Finite Element Analysis of Vertical Bearing Performance in RC Slab–Column Joints: Effects of Bottom Reinforcement and Concealed Beams
Abstract
1. Introduction
2. Finite Element Simulation
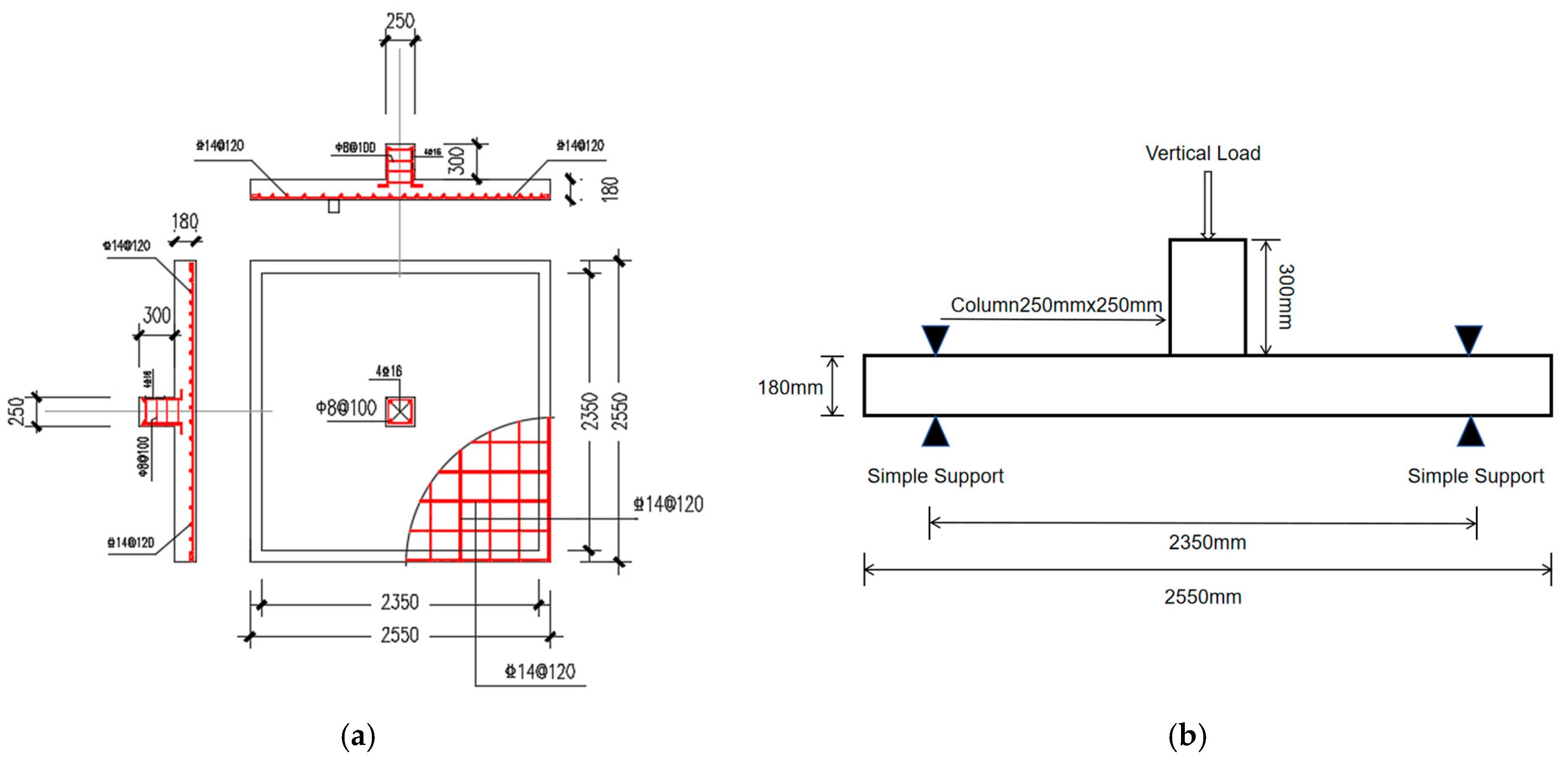
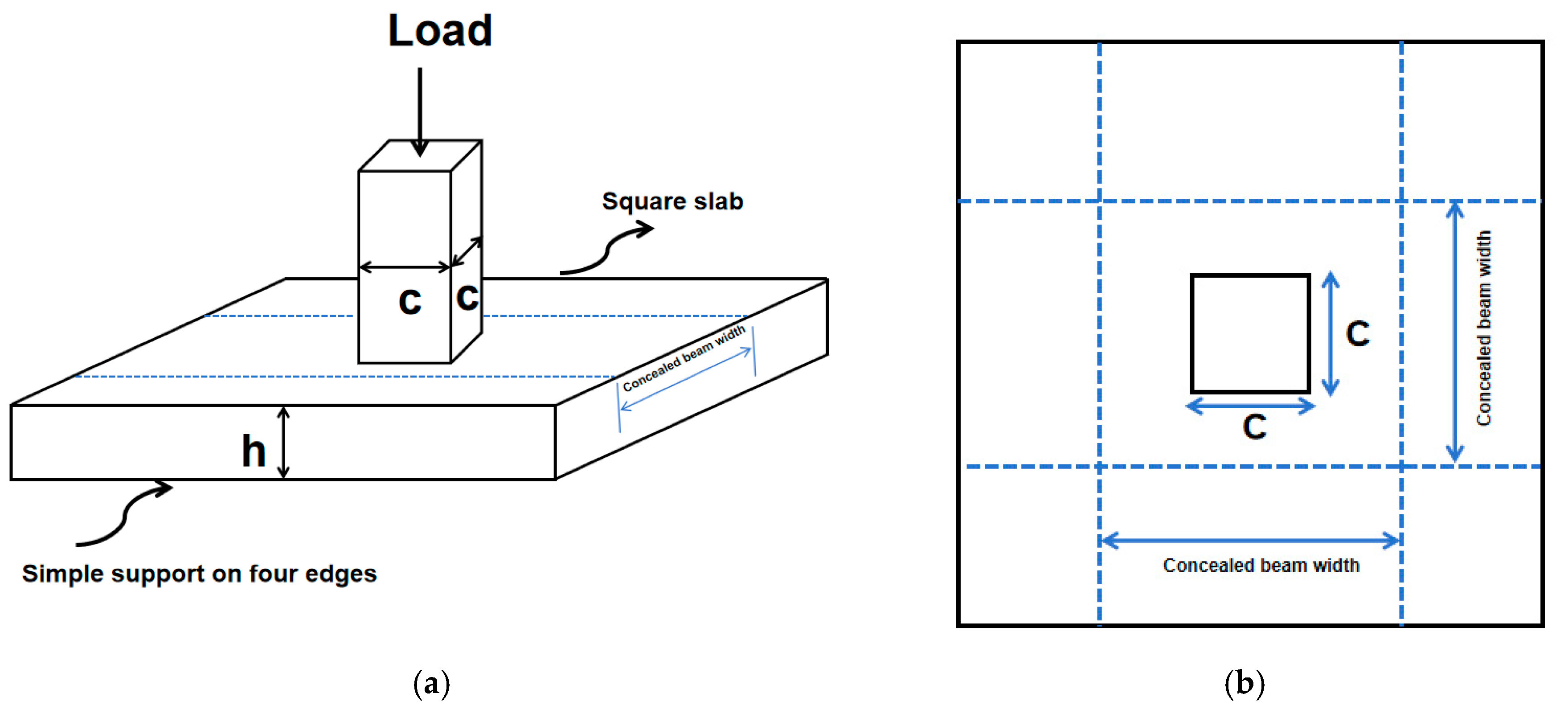
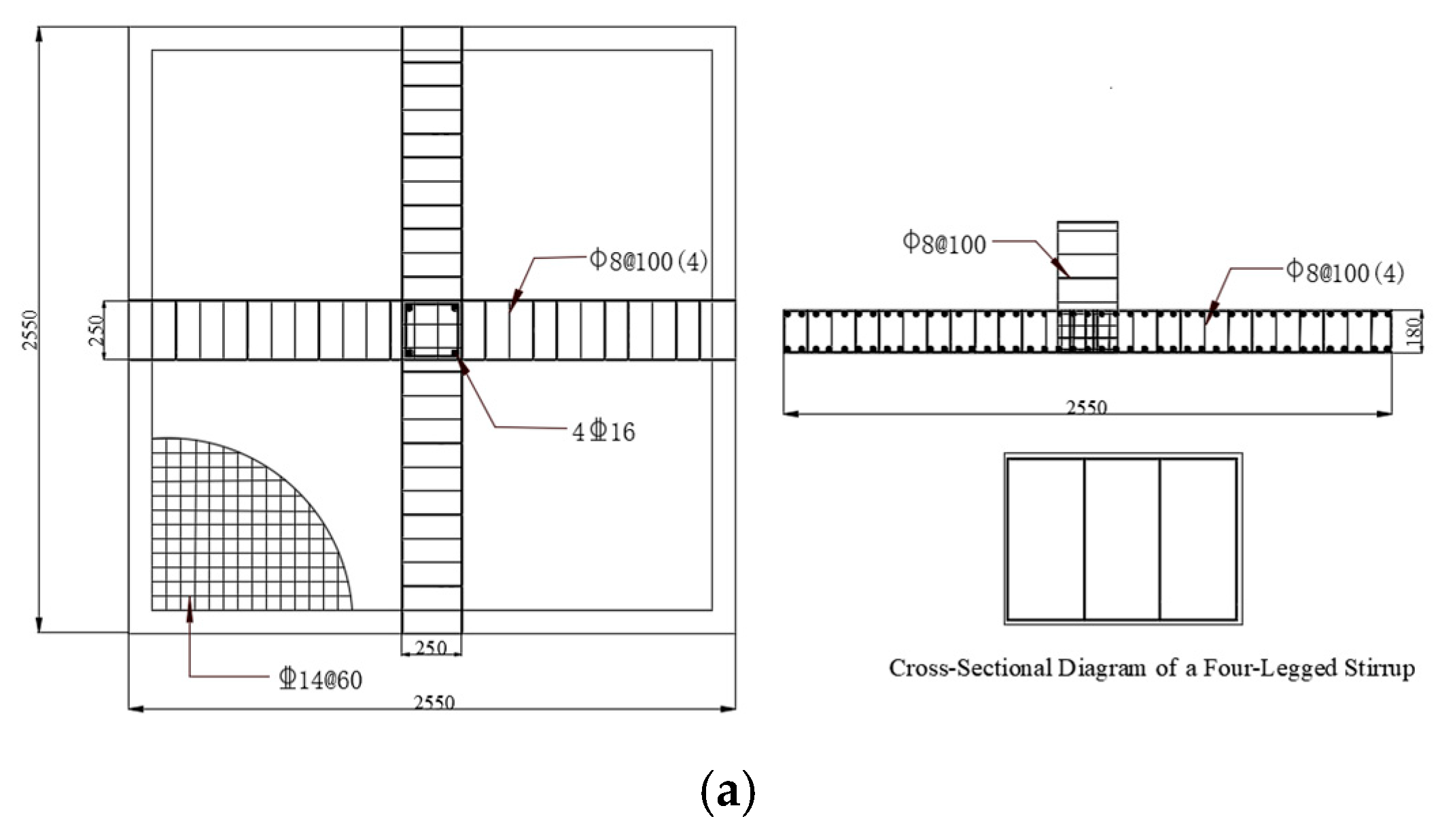
2.1. Test Description
2.2. Methodology
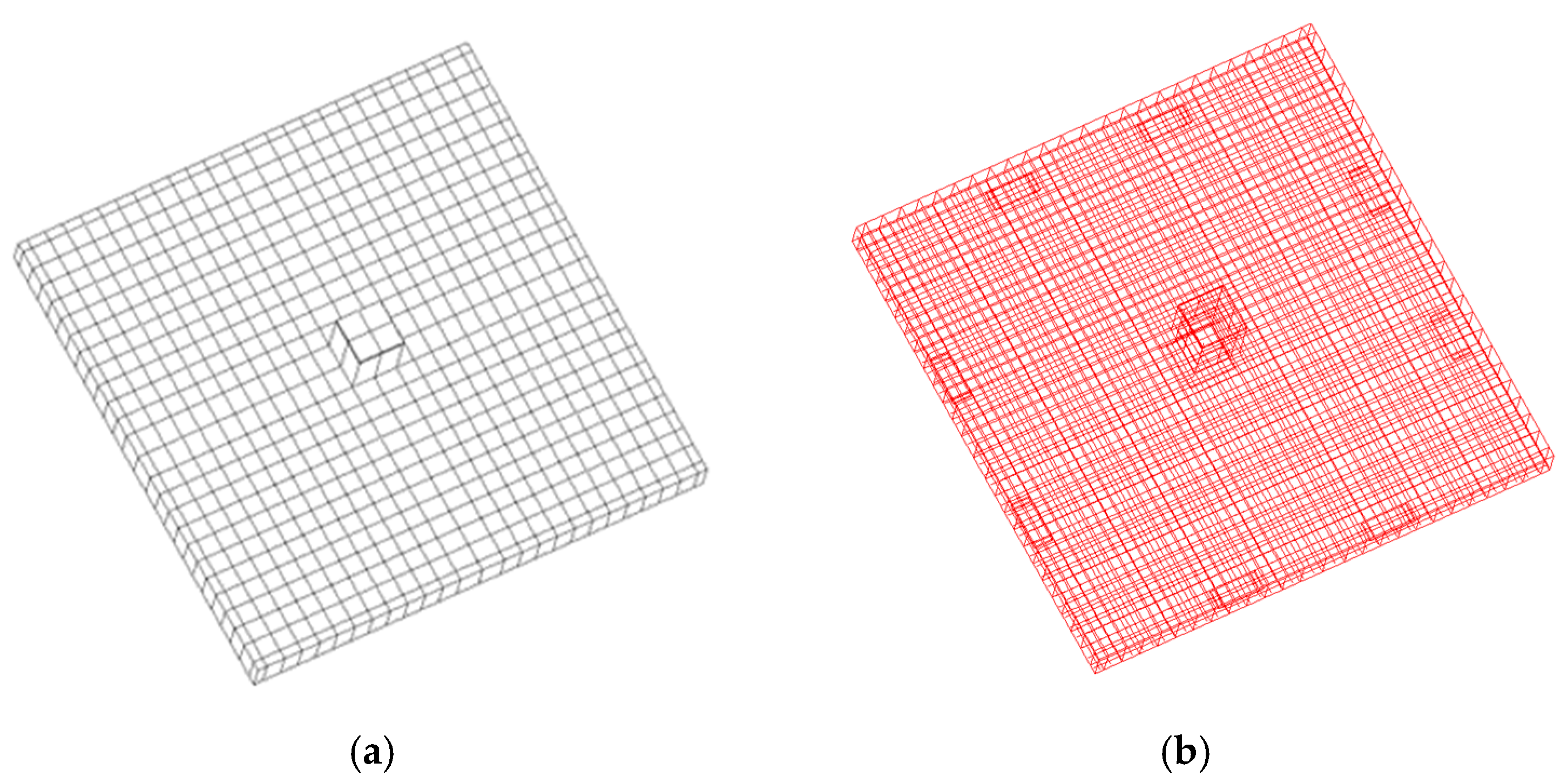
2.2.1. Element Types and Division
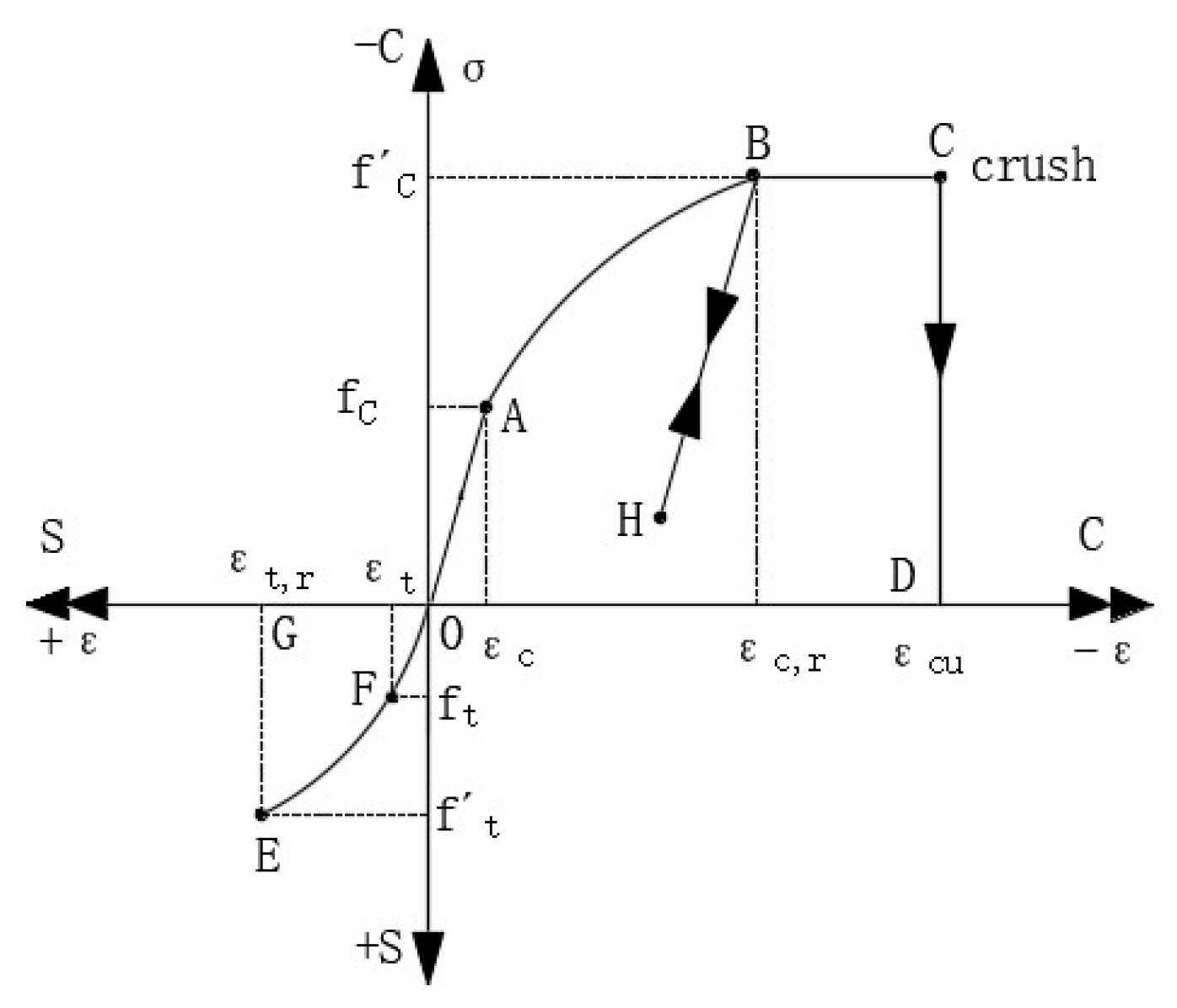
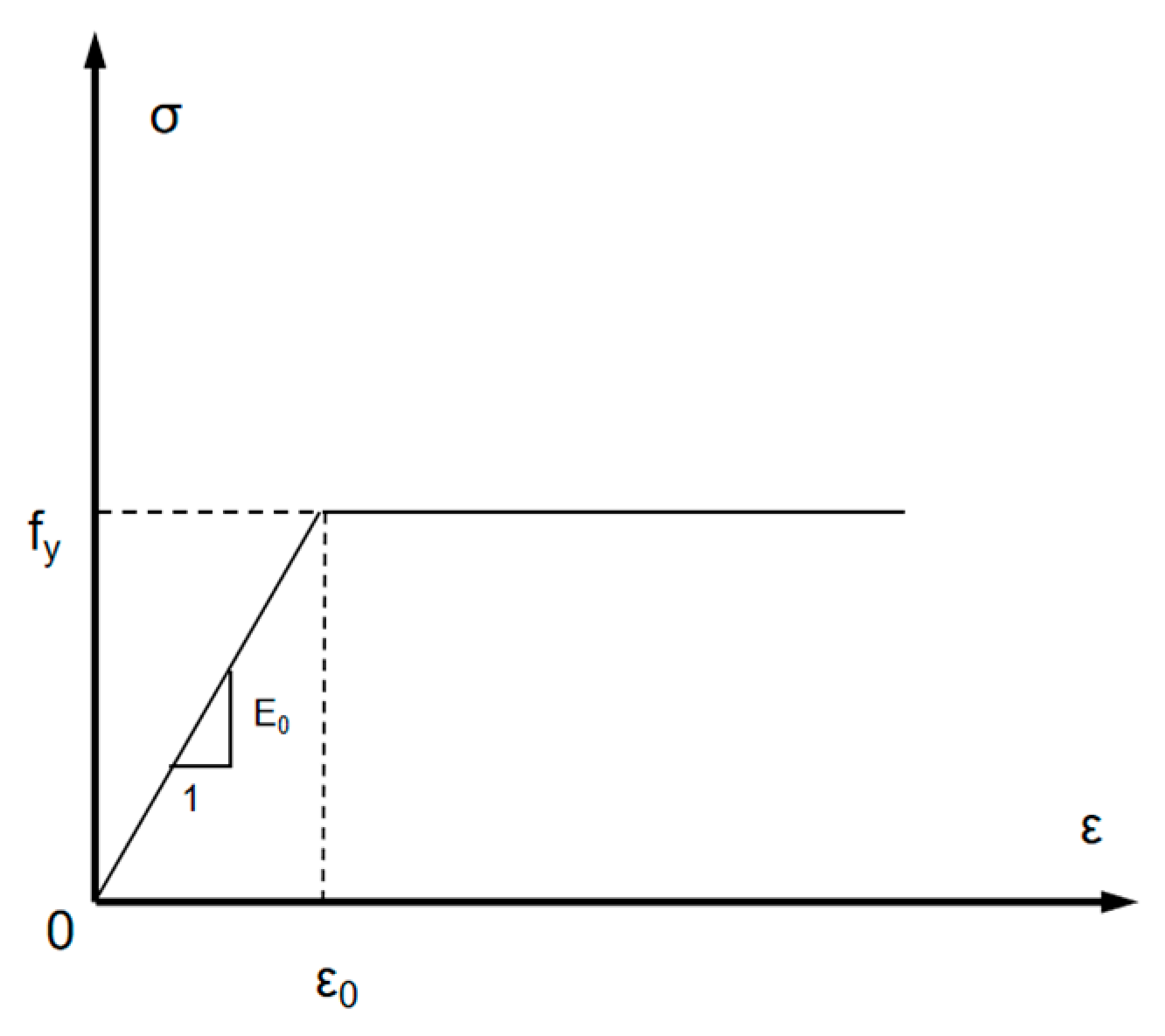
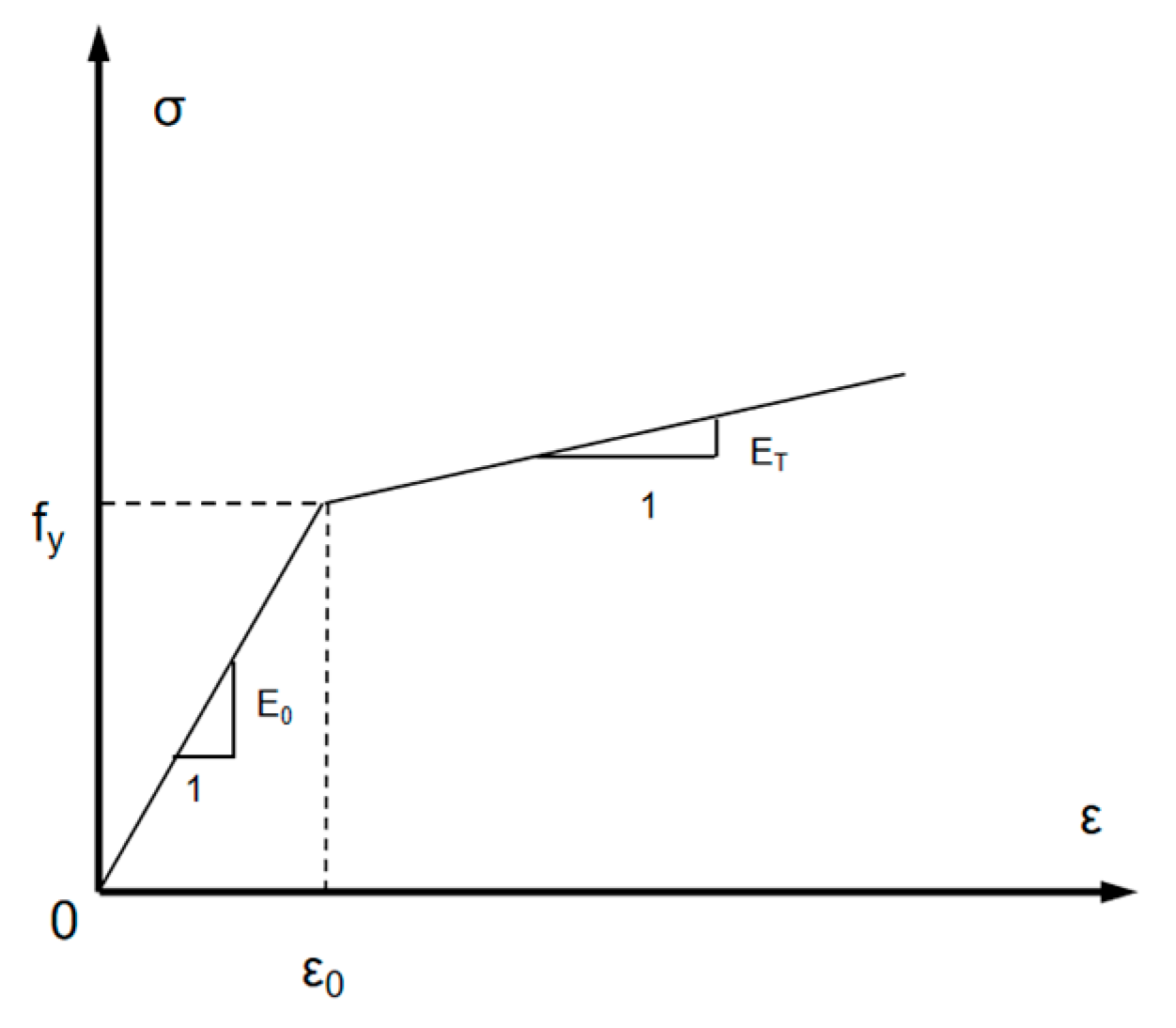
2.2.2. Constitutive Relationships of the Materials
Concrete
Rebar
2.2.3. Loading and Boundary Conditions
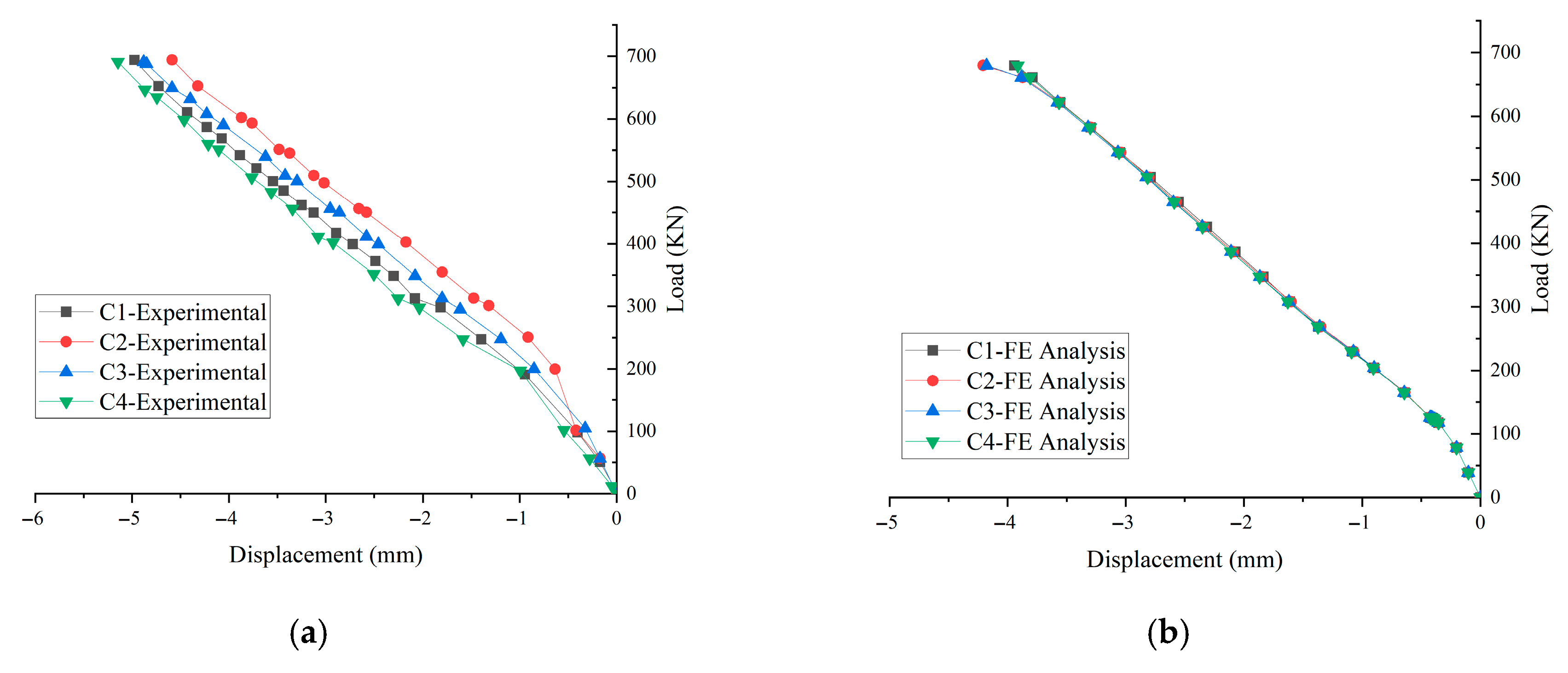
2.3. Validation of the FE Model
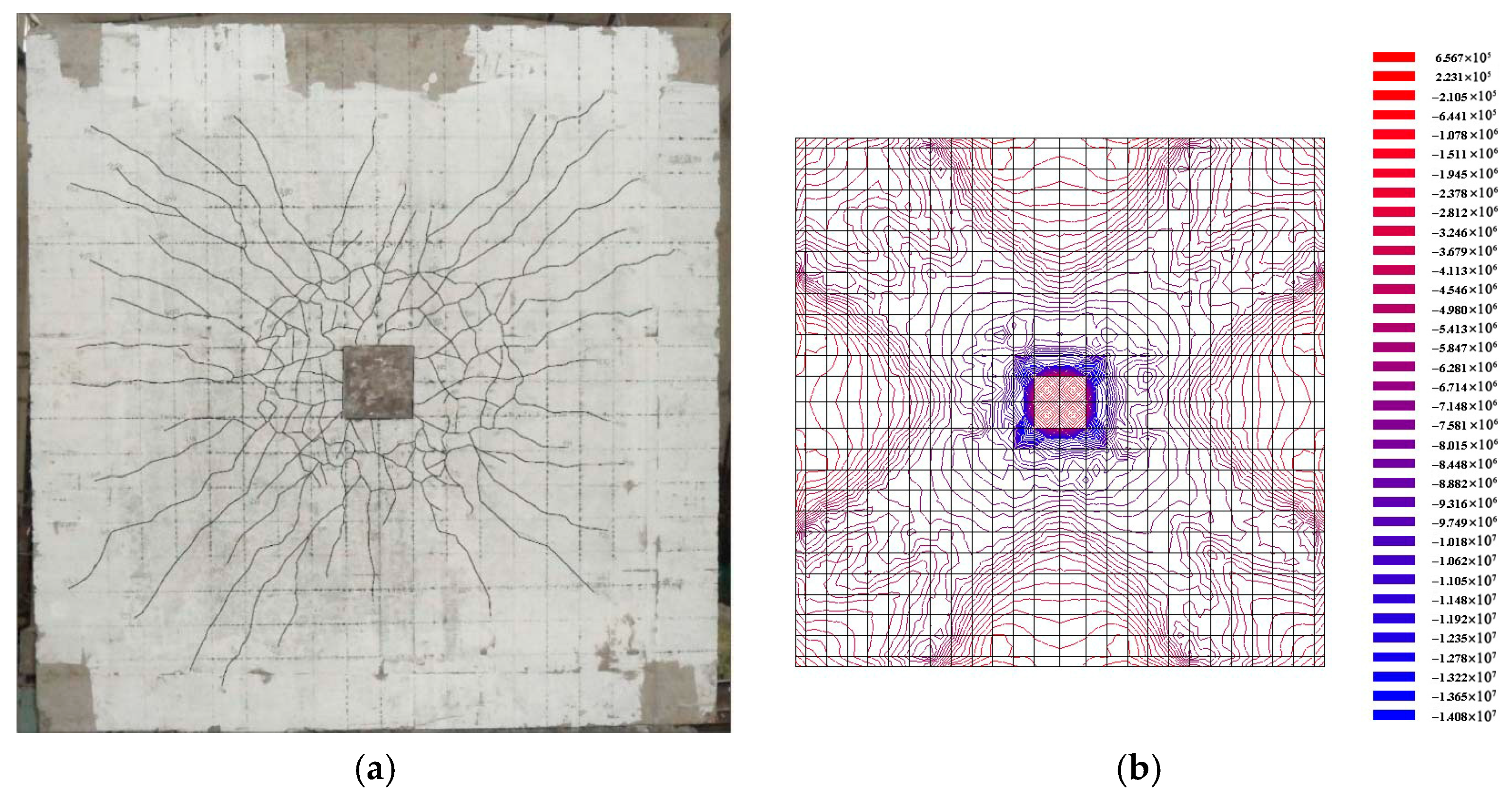
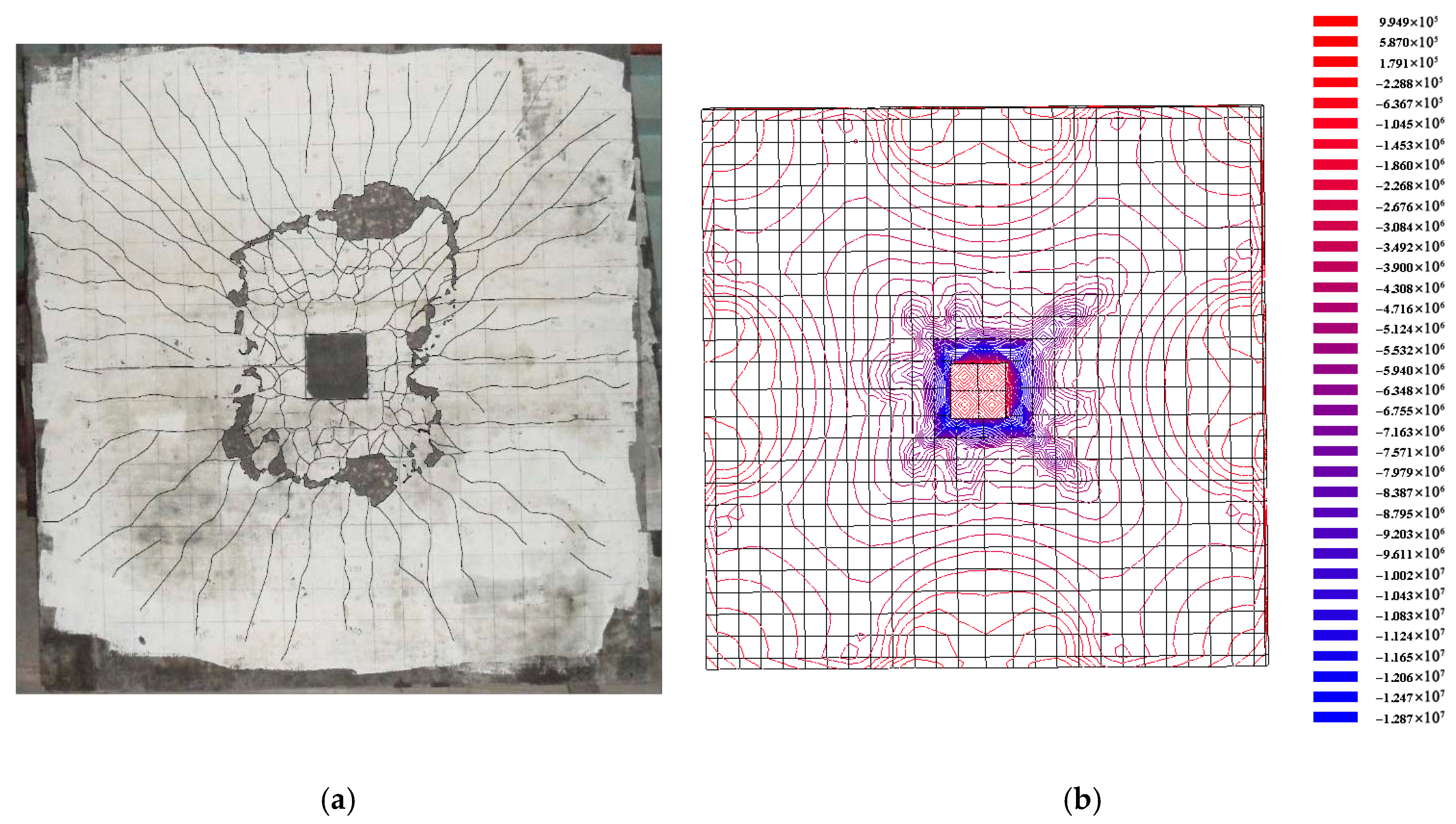
2.3.1. Crack Pattern
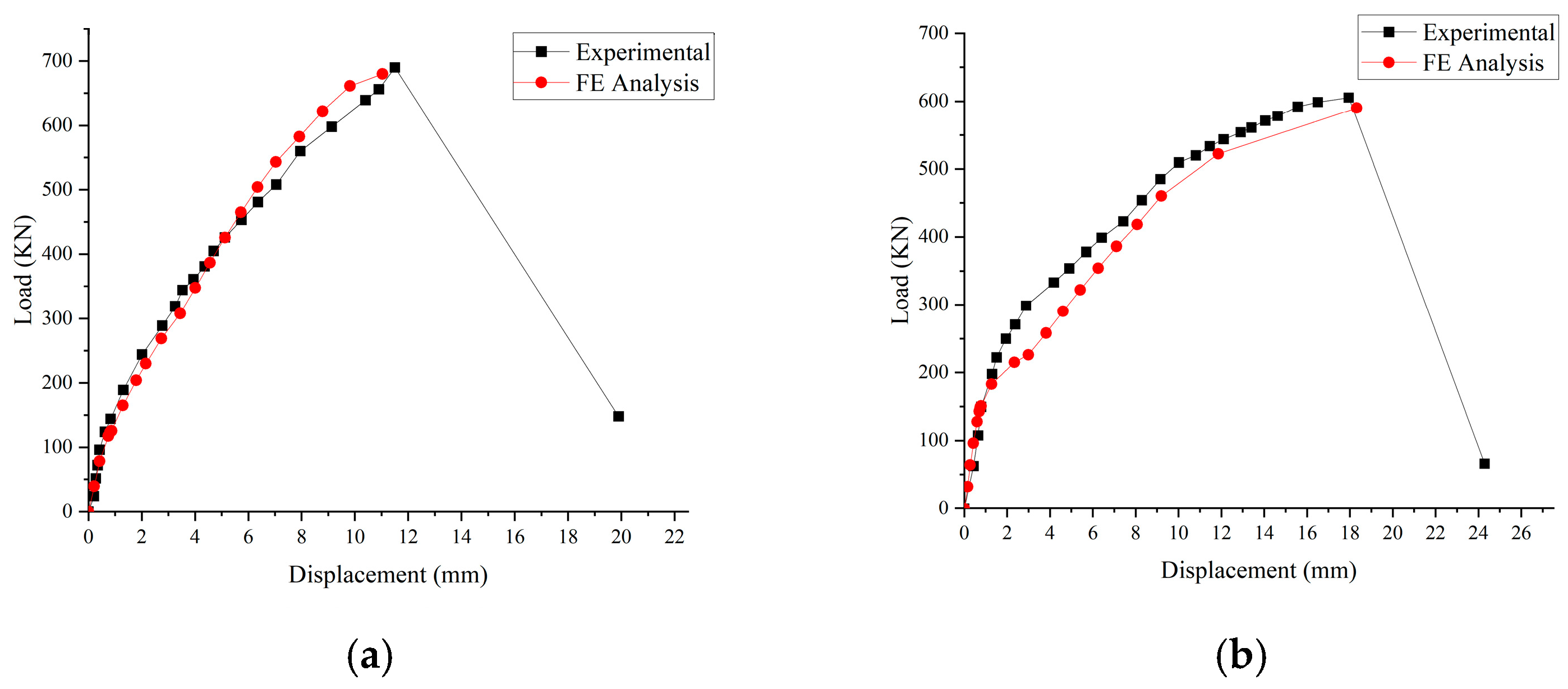
2.3.2. Load–Displacement Response
3. The Parametric Study
3.1. Modeling and Parameterization
3.2. Simulation Analysis
3.3. Discussing the Results
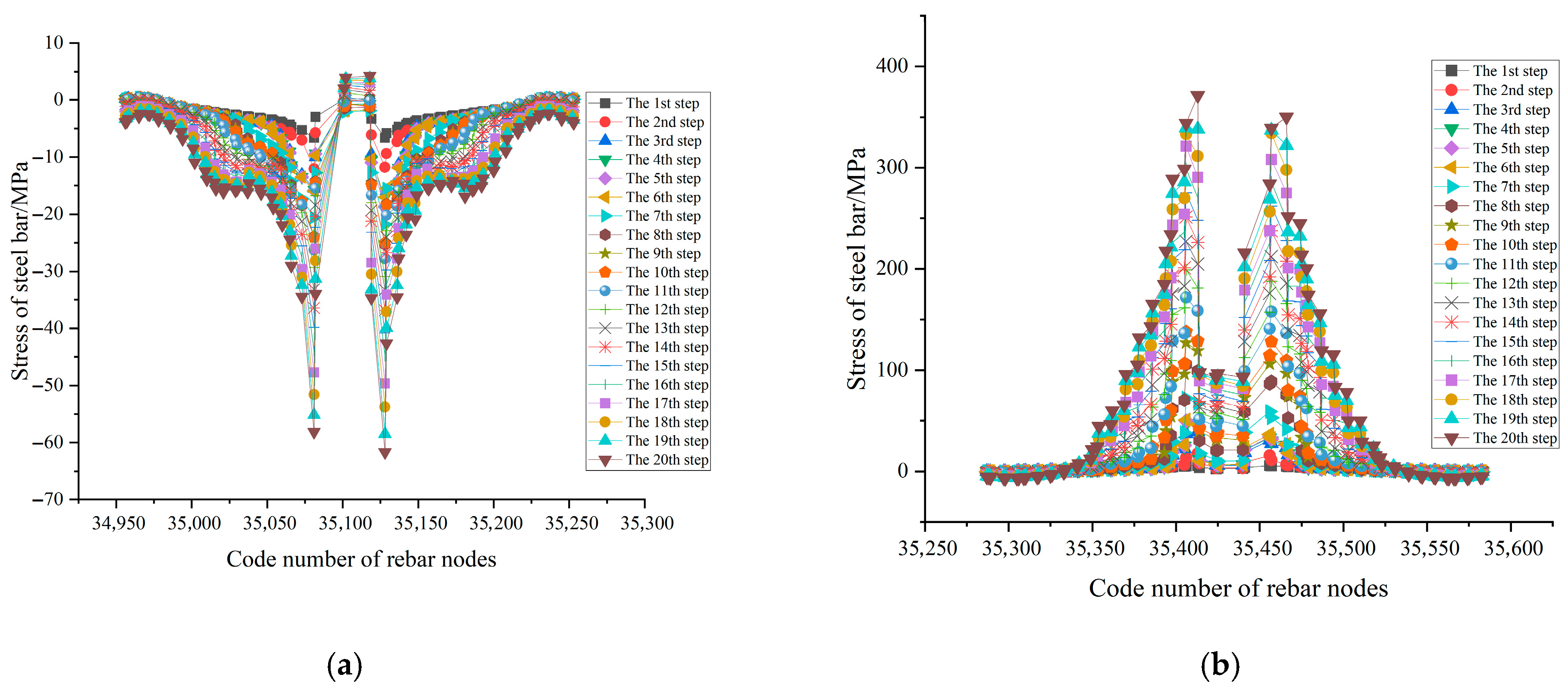
3.3.1. Failure Mechanism Analysis of Slab–Column Joints
3.3.2. Influence of the Bottom Reinforcement
3.3.3. Influence of Reinforcement Ratios Between Top and Bottom
3.3.4. Influence of the Width of Concealed Beams
3.3.5. Influence of Punch–Span Ratio
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Talbot, A.N. Reinforced Concrete Wall Footings and Column Footings. In Charge of Theoretical & Applied Mechanics; University of Illinois: Champaign, IL, USA, 1925. [Google Scholar]
- Zheng, S.; Du, Y.; Liang, Z. Research progress of punching shear performance of reinforced concrete slab-column joints. J. Archit. Civ. Eng. 2024, 41, 52–68. [Google Scholar] [CrossRef]
- Jiang, M.; Shi, Q.; Jing, X. State-of-the-art on punching shear capacity of concrete slab -column connections. China Civ. Eng. J. 2024, 57, 1–18. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Zhou, D.; Yan, W. Experimental Study on Post-Punching Mechanical Performance of Flat Slab-Column Joints with Drop Panel and Embedded Beam. Earthq. Eng. Eng. Dyn. 2025, 40, 178–186. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, G.; Wang, Y. Research Progress in Bearing Capacity Calculation Methods of Slab-Column Connections. J. Harbin Inst. Technol. 2022, 54, 1–7. [Google Scholar] [CrossRef]
- Zhang, J. Research on Punching Strength of Side Slab-Column Joints of RC Slab-Column Structures with Hidden Beams; South China University of Technology: Guangzhou, China, 2019. [Google Scholar]
- Kang, S.-M.; Na, S.-J.; Hwang, H.-J. Punching Shear Strength of Reinforced Concrete Transfer Slab-Column Connections with Shear Reinforcement. Eng. Struct. 2021, 243, 112610. [Google Scholar] [CrossRef]
- Wang, J.; Gong, C.; Tan, X. Research on Flexural Performance of Edge Joint of Column-Slab Structure with Steel Concealed-Beam. Struct. Eng. 2024, 40, 50–60. [Google Scholar] [CrossRef]
- De Oliveira, V.H.D.; de Lima, H.J.N.; Melo, G.S. Punching Shear Resistance of Flat Slabs with Different Types of Stirrup Anchorages Such as Shear Reinforcement. Eng. Struct. 2022, 253, 113671. [Google Scholar] [CrossRef]
- Shatarat, N.; Salman, D. Investigation of Punching Shear Behavior of Flat Slabs with Different Types and Arrangements of Shear Reinforcement. Case Stud. Constr. Mater. 2022, 16, e01028. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Chen, H.; Zhou, Y.; Mansour, W.; Wang, X.; Wang, P. Effects of Concrete-Stirrup Interaction on Shear Behavior of RC Beams under Varying Shear Span-Depth Ratio Scenarios. Structures 2024, 61, 106071. [Google Scholar] [CrossRef]
- Tang, M. Study on Seismic Behavior of RC Slab-Column Connections; Hunan University: Changsha, China, 2021. [Google Scholar]
- Zhao, J.; Yi, W. Calculation and Study on Punching Bearing Capacity of Slab-Column Joints without Shear Reinforcement. Build. Struct. 2019, 49, 120–123. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, J.; Jia, Y.; Wu, G.; Ke, N.; Wei, X. A Study on the Bearing Performance of an RC Axial Compression Shear Wall Strengthened by a Replacement Method Using Local Reinforcement with an Unsupported Roof. Buildings 2024, 14, 2926. [Google Scholar] [CrossRef]
- Wei, X.; Lu, L.; Ke, N.; Jia, Y.; Wu, G. A Study on the Effects of Punch-to-Span Ratio and Longitudinal Reinforcement Eigenvalues on the Bearing Capacity of RC Slab–Column Connections. Buildings 2024, 14, 208. [Google Scholar] [CrossRef]
- Jia, Y.; Lu, L.; Wu, G.; Liu, Y.; Mo, X. Spatial Nonlinear Simulation Analysis on the Temperature Shrinkage Effect of a Super-Long Frame Structure Considering the Construction Process. Processes 2022, 10, 1874. [Google Scholar] [CrossRef]
- Hong, F. Experimental Study on Punching Shear Failure of Reinforced Concrete Slabs-Column Connection; Hunan University: Changsha, China, 2015. [Google Scholar]
- GB 50010-2010; Code for the Design of Coagulation Structures. Construction Science and Technology. Standardization Administration of China (SAC): Beijing, China, 2015; pp. 28–30.
- Lin, D.; Zhang, J.; Xiang, Y.; Xu, X. Virtual Layered Module Method and Its Application in Bridge Construction Application in Bridge Engineering. Chin. Civ. Eng. J. 1998, 31, 1–8. [Google Scholar] [CrossRef]
- Xu, X.; Guo, Y.; Shen, Y. Nonlinear Finite Element and Programming; Zhejiang University Press: Hangzhou, China, 1993. [Google Scholar]
- Xu, X.; Lin, D. Physical Degradation Unit Series. Chin. J. Solid Mech. 2001, 22, 1–12. [Google Scholar]
- Lu, L. Three-Dimensional Nonlinear Analysis of Time-Varying Fire Behavior of RC Frame Structures Considering the Spatial Coordinated Interaction of Beam-Slab-Column; Nanchang University: Nanchang, China, 2025. [Google Scholar]
- Zhan, M. Study on Load-Carrying Mechanism to Resist Progressive Collapse of RC Structures Considering Cast-in-Place Slab; Nanchang University: Nanchang, China, 2021. [Google Scholar]
- Deng, J. Research on Normal Section Bearing Capacity of RC Vertical Members Strengthened by Enclosure Method and Unbraced Local Reinforcement Replacement Method Considering Stress Lag; Nanchang University: Nanchang, China, 2023. [Google Scholar]
- Hu, Q. Simulation Study on Continuous Collapse of PC Frame Structure Considering Spatial Synergy; Nanchang University: Nanchang, China, 2023. [Google Scholar]
- Willam, K. Plasticity in Reinforced Concrete. Comput. Methods Appl. Mech. Eng. 1982, 31, 363. [Google Scholar] [CrossRef]
- Bergan, P.; Holand, I.; Soreide, T. Use of Current Stiffness Parameter in Solution of Nonlinear Problems, Energy Methods in Finite Element Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1979. [Google Scholar]










| Specimens | Concrete Compressive Strength (MPa) | Concrete Tensile Strength (MPa) | Reinforcement Yield Strength (MPa) | Reinforcement Ultimate Strength (MPa) |
|---|---|---|---|---|
| C7-30-3 | 35.56 | 2.82 | 453.6 | 611 |
| C7-70-1 | 70.11 | 3.69 | 453.6 | 611 |
| Specimens | Mechanical Property | Experimental | FE Analysis | Deviation |
|---|---|---|---|---|
| C7-30-3 | ultimate load (KN) | 690.01 | 679.12 | 1.60% |
| ultimate displacement(mm) | 11.50 | 11.03 | 4.26% | |
| C7-70-1 | ultimate load (KN) | 605.50 | 590.13 | 2.61% |
| ultimate displacement (mm) | 17.95 | 18.31 | 1.97% |
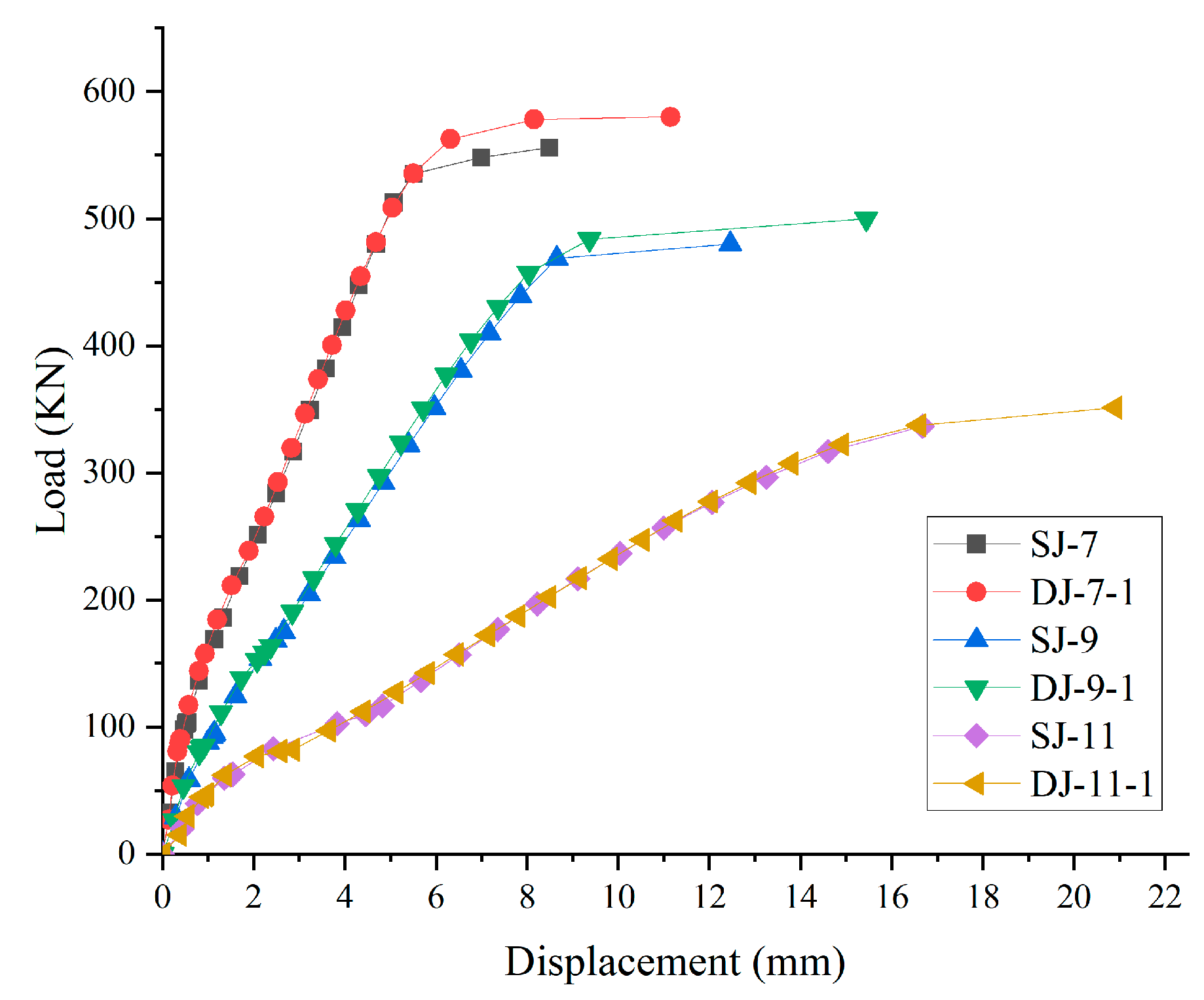
| Specimens | L/mm | a/mm | h0 | λ | Concrete Strength | Top Reinforcement of the Slab | Bottom Reinforcement of the Slab | Concealed Beam width/mm |
|---|---|---|---|---|---|---|---|---|
| SJ-7 | 2550 | 250 | 150 | 7 | C30 | 14@60 | - | 0 |
| DJ-7-1 | 2550 | 250 | 150 | 7 | C30 | 14@60 | 14@60 | 0 |
| DJ-7-1-250 | 2550 | 250 | 150 | 7 | C30 | 14@60 | 14@60 | 250 |
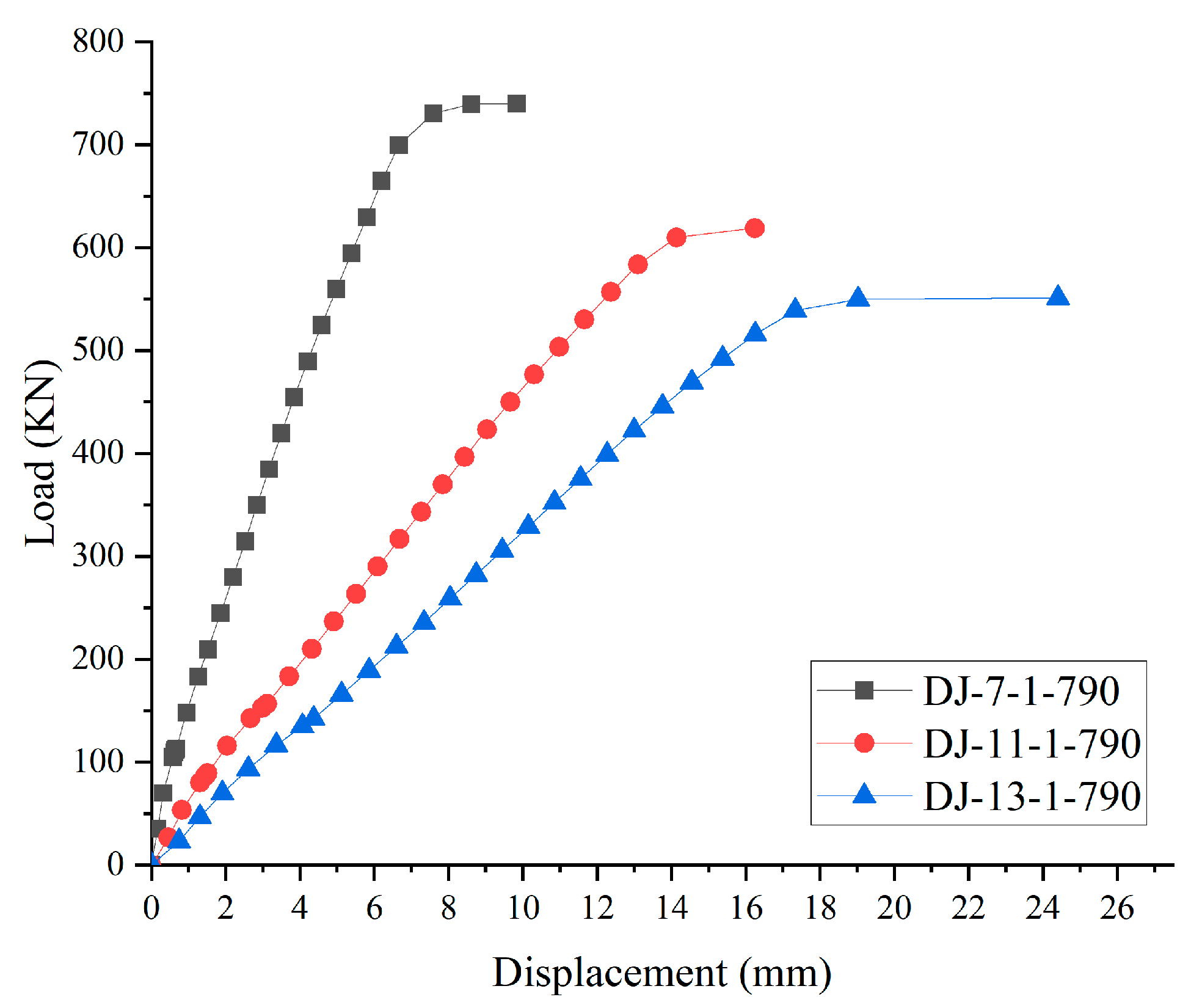
| DJ-7-1-790 | 2550 | 250 | 150 | 7 | C30 | 14@60 | 14@60 | 790 |
| DJ-7-1-970 | 2550 | 250 | 150 | 7 | C30 | 14@60 | 14@60 | 970 |
| SJ-9 | 3150 | 250 | 150 | 9 | C30 | 14@60 | - | 0 |
| DJ-9-1 | 3150 | 250 | 150 | 9 | C30 | 14@60 | 14@60 | 0 |
| SJ-11 | 3750 | 250 | 150 | 11 | C30 | 14@120 | - | 0 |
| DJ-11-1 | 3750 | 250 | 150 | 11 | C30 | 14@120 | 14@120 | 0 |
| DJ-11-1.5 | 3750 | 250 | 150 | 11 | C30 | 14@80 | 14@120 | 0 |
| DJ-11-2 | 3750 | 250 | 150 | 11 | C30 | 14@60 | 14@120 | 0 |
| DJ-11-1-790 | 3750 | 250 | 150 | 11 | C30 | 14@60 | 14@60 | 790 |
| DJ-13-1-790 | 3750 | 250 | 150 | 13 | C30 | 14@60 | 14@60 | 790 |
| Specimens | Cracking Load/KN | Ultimate Load/KN | Failure Characteristics | Stress Contour Plot Characteristics | Reinforcement Yield Condition | Failure Mode |
|---|---|---|---|---|---|---|
| SJ-7 | 103.7 | 555.75 | Sunken column head | No plastic hinge line | Unyielded | Punching shear |
| DJ-7-1 | 90.2 | 580.1 | Sunken column head | No plastic hinge line | Neither the top nor the bottom of the slab has yielded | Punching shear |
| DJ-7-1-250 | 100.2 | 599.5 | Sunken column head | The column circumference 1/2 damage is obvious; no plastic hinge line | Unyielded | Punching shear |
| DJ-7-1-790 | 113.1 | 774.9 | Sunken column head | 3/4 of the column circumference was significantly damaged; no plastic hinge line | Unyielded | Punching shear |
| Specimens | Cracking load/KN | Ultimate load/KN | Failure characteristics | Stress contour plot characteristics | Reinforcement yield condition | Failure mode |
| DJ-7-1-970 | 124.1 | 883.6 | Sunken column head | Around the column is clearly damaged; no plastic hinge line | Unyielded | Punching shear |
| SJ-9 | 95.1 | 480.1 | Sunken column head | No plastic hinge line | Unyielded | Punching shear |
| DJ-9-1 | 84.9 | 499.9 | Sunken column head | Partial plastic hinge lines | Neither the top nor the bottom of the slab has yielded | Flexural–punching |
| SJ-11 | 62.9 | 336.7 | Column head crushed by inward sinking | Obvious plastic hinge lines | Yield | Flexural |
| DJ-11-1 | 47.1 | 351.4 | Column head crushed by inward sinking | Obvious plastic hinge lines | Bottom of slab not yielding; top of slab yielding | Flexural |
| DJ-11-1.5 | 54.7 | 405 | Column head crushed by inward sinking | Obvious plastic hinge lines | Bottom of slab not yielding; top of slab yielding | Flexural |
| DJ-11-2 | 58.2 | 447 | Column head crushed by inward sinking | Plastic hinge lines are evident | Bottom of slab not yielding; top of slab yielding | Flexural |
| DJ-11-1-790 | 89.1 | 618.9 | Sunken column head | Plastic hinge lines are evident | Unyielded | Flexural–punching |
| DJ-13-1-790 | 142.3 | 551.3 | Sunken column head | Plastic hinge lines are evident | Unyielded | Flexural–punching |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Cai, G.; Ke, N.; Liu, Y.; Wu, G.; Jia, Y. Finite Element Analysis of Vertical Bearing Performance in RC Slab–Column Joints: Effects of Bottom Reinforcement and Concealed Beams. Buildings 2025, 15, 2905. https://doi.org/10.3390/buildings15162905
Wei X, Cai G, Ke N, Liu Y, Wu G, Jia Y. Finite Element Analysis of Vertical Bearing Performance in RC Slab–Column Joints: Effects of Bottom Reinforcement and Concealed Beams. Buildings. 2025; 15(16):2905. https://doi.org/10.3390/buildings15162905
Chicago/Turabian StyleWei, Xianglan, Gaowang Cai, Naiwen Ke, Yuanwen Liu, Guangyu Wu, and Yigang Jia. 2025. "Finite Element Analysis of Vertical Bearing Performance in RC Slab–Column Joints: Effects of Bottom Reinforcement and Concealed Beams" Buildings 15, no. 16: 2905. https://doi.org/10.3390/buildings15162905
APA StyleWei, X., Cai, G., Ke, N., Liu, Y., Wu, G., & Jia, Y. (2025). Finite Element Analysis of Vertical Bearing Performance in RC Slab–Column Joints: Effects of Bottom Reinforcement and Concealed Beams. Buildings, 15(16), 2905. https://doi.org/10.3390/buildings15162905





