A Simplified Multi-Linear Spring Model for Cross-Plate Joint in Diaphragm Walls Based on Model Tests
Abstract
1. Introduction
2. Experimental Program and Results
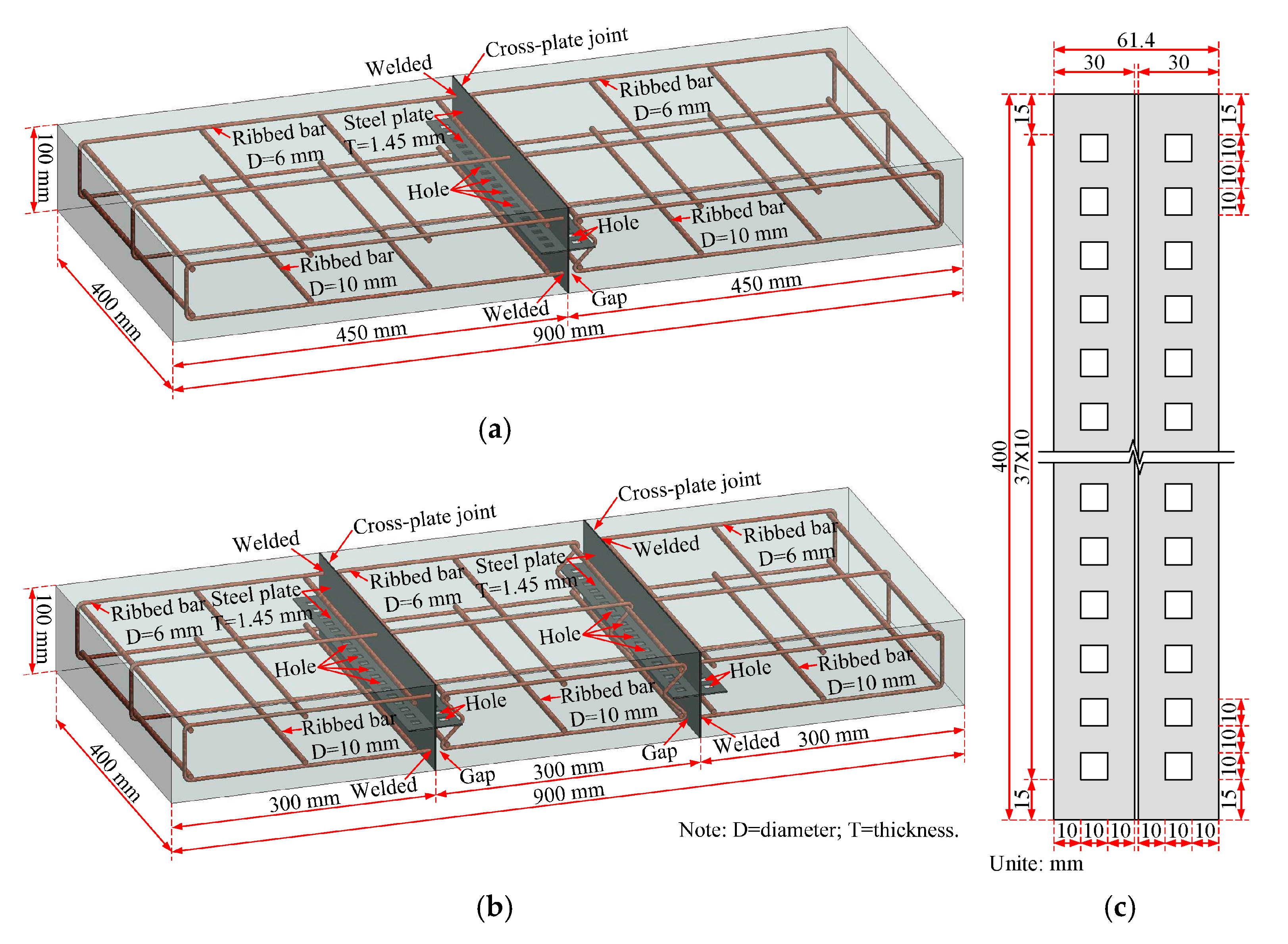
2.1. Fabrication of Specimens
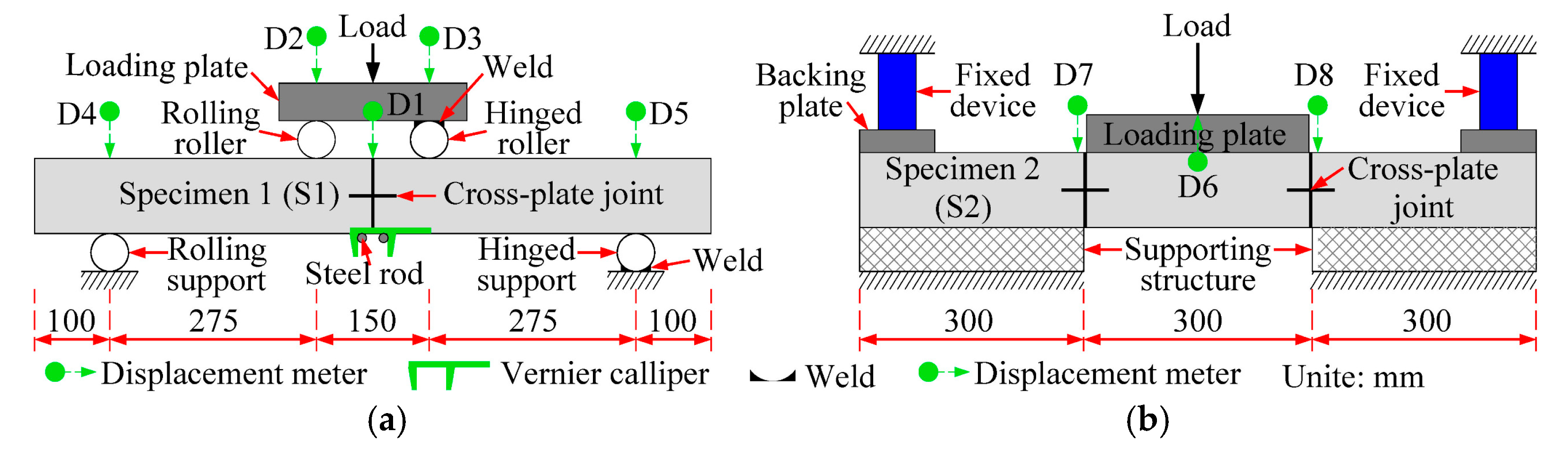
2.2. Test Setup and Instrumentation
2.3. Experimental Results
3. Simplified Mechanical Model
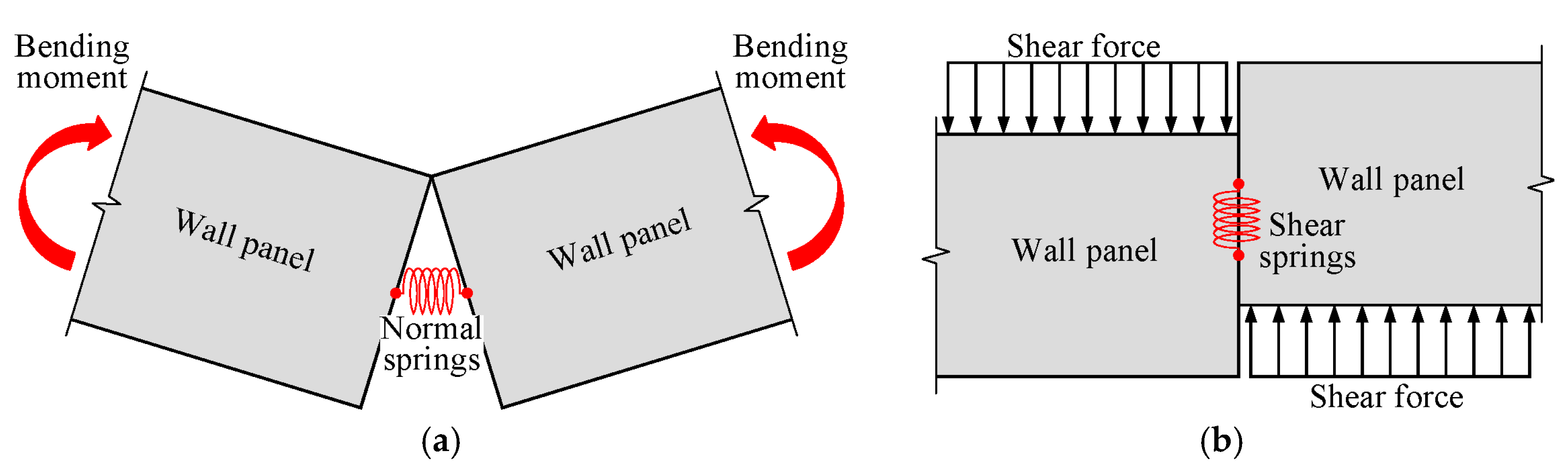
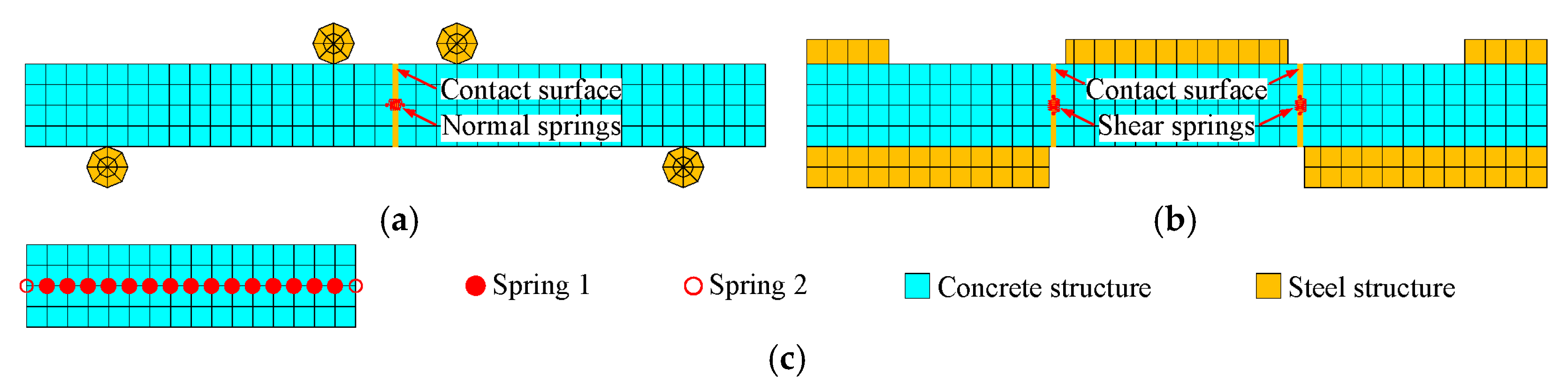
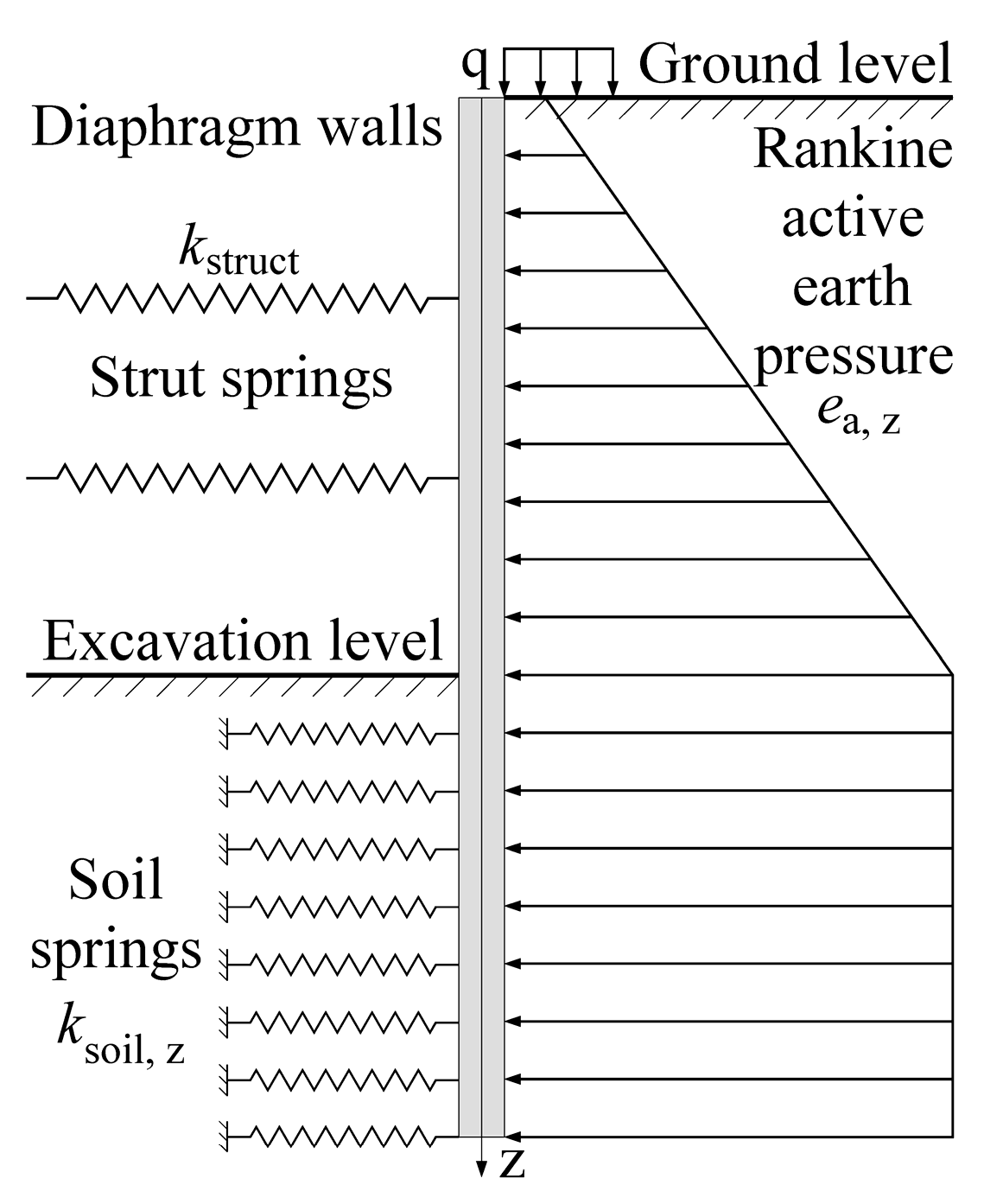
3.1. Multi-Linear Spring Model
3.2. Stiffness of the Multi-Linear Spring
4. Case Study
4.1. Basic Information
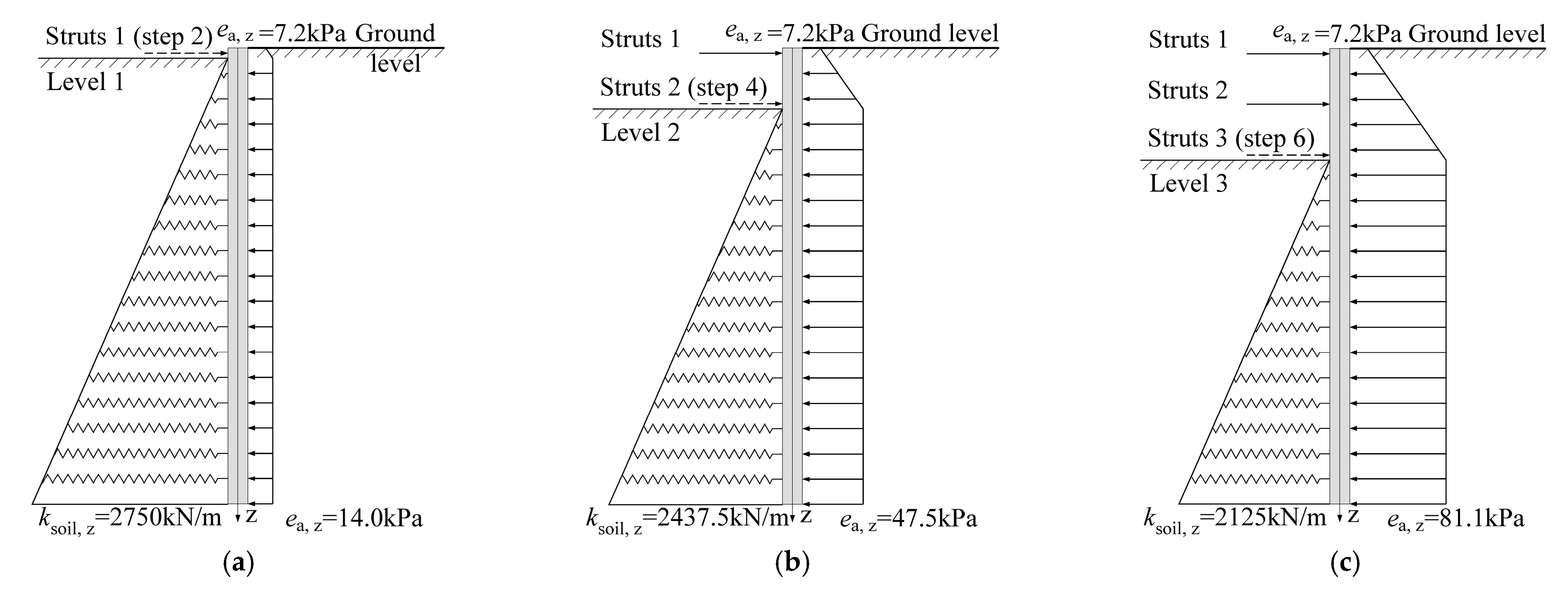
4.2. Numerical Modelling
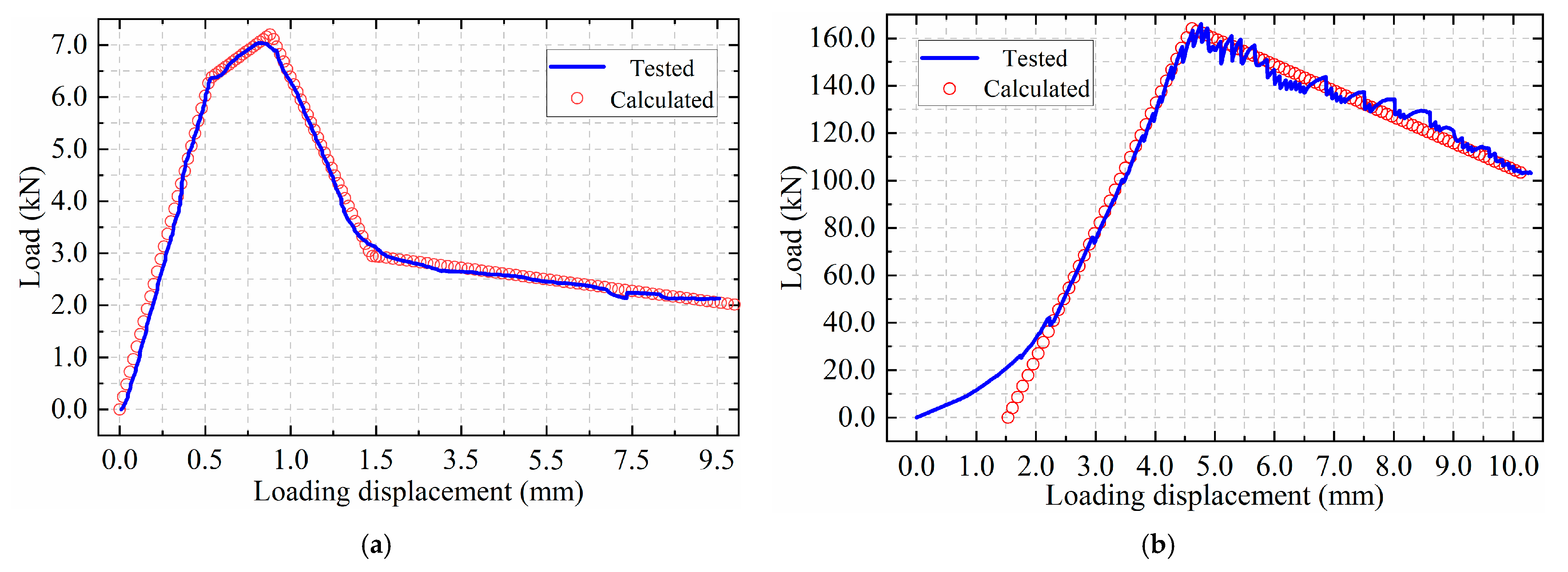
4.3. Results and Discussion
4.4. Study Limitation
5. Conclusions
- (1)
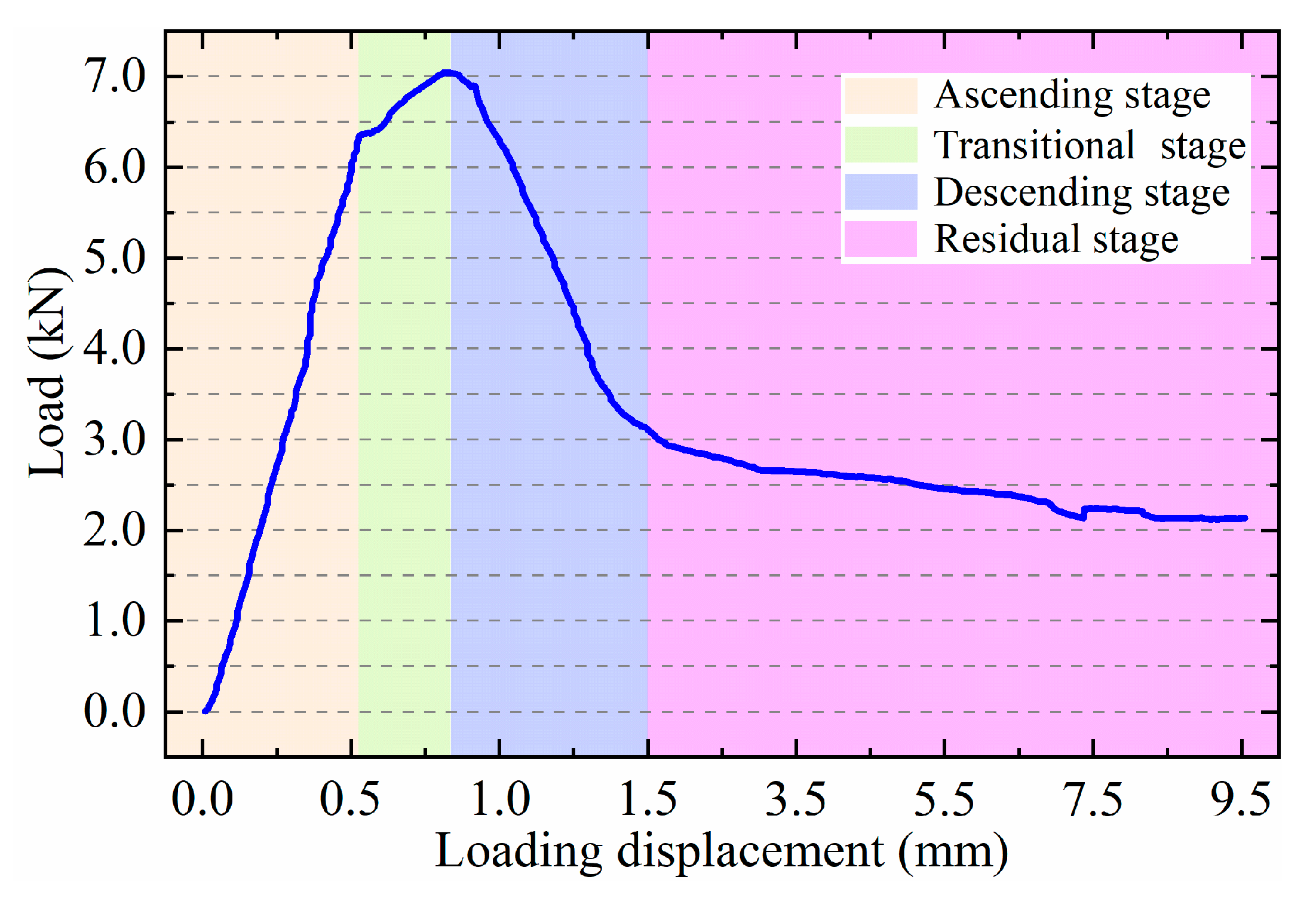
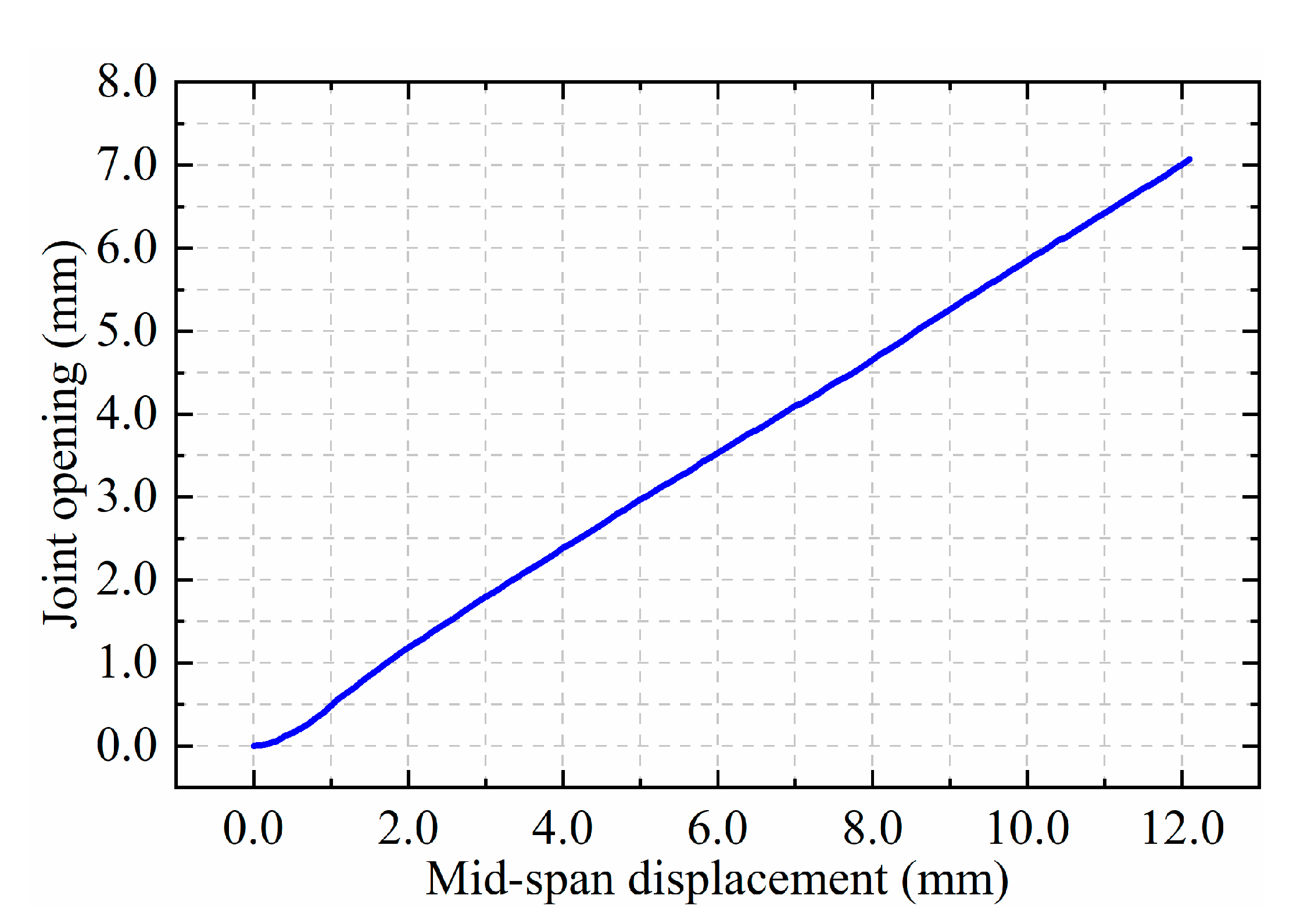
- When the joint is subjected to a bending test, the load–displacement curve obtained can be categorised into four stages: ascending, transitional, descending, and residual. Each stage can be approximated by a linear trend. The joint opening showed an approximate linear growth pattern, with an increase in mid-span displacement. When the joint fails, the longitudinal plate is pulled out of the concrete on one side, the concrete below the longitudinal plate separates from the plate, and the concrete above the longitudinal plate cracks along a curved surface extending from the end of the longitudinal plate to the end of the transverse plate.
- (2)
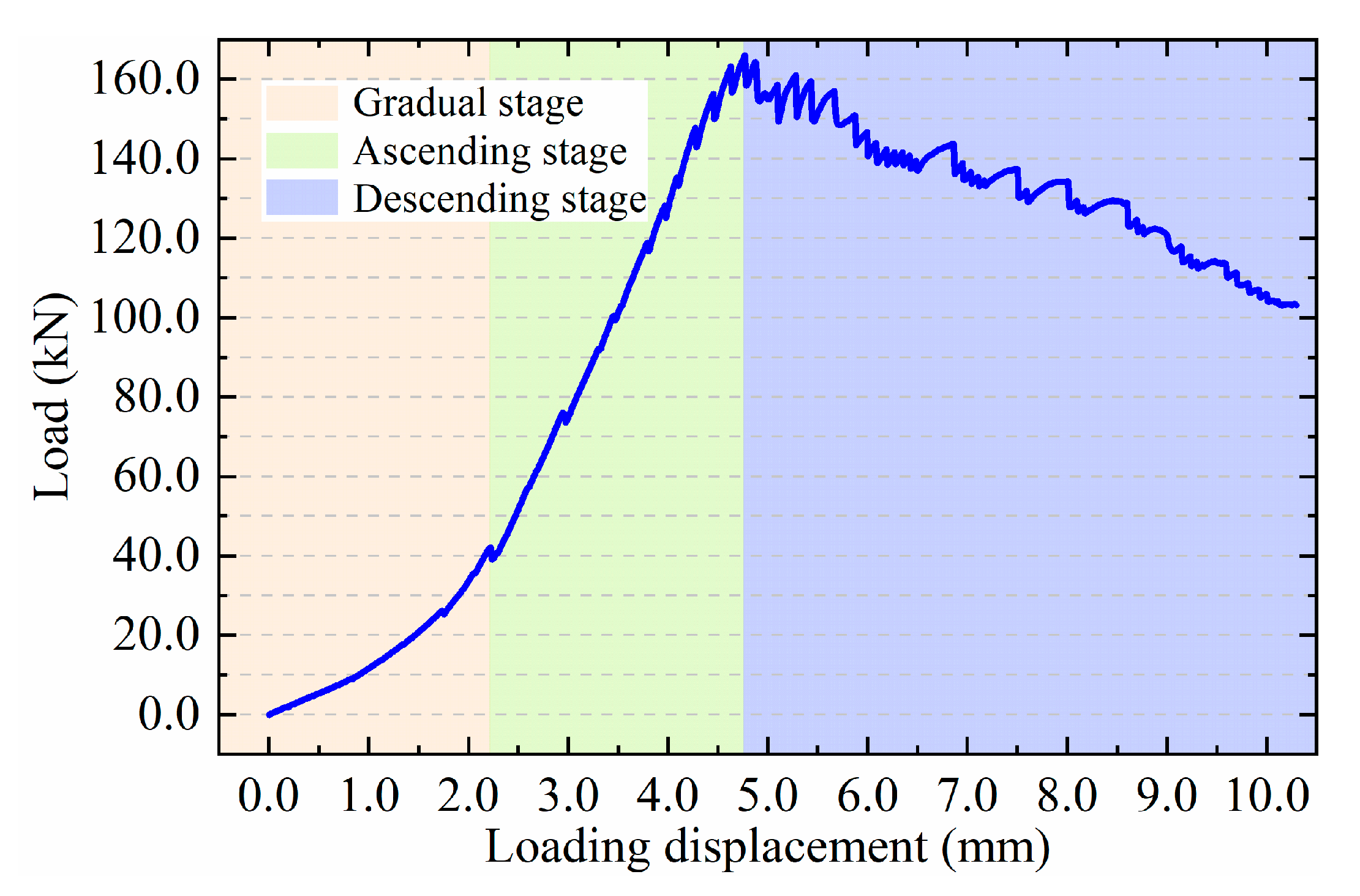
- In the shear test, the load–displacement curve can be divided into three stages: gradual, ascending, and descending. With the exception of the gradual stage, which is non-linear due to deviations in specimen manufacture, the other two stages can also be approximated to be linear. When the joint breaks, the longitudinal plate exhibits substantial shear deformation. The concrete beneath the longitudinal plate cracks along a curved surface, extending to the longitudinal steel plate, and then, the cracking continues along the interface between the concrete and the longitudinal plate. The concrete above the longitudinal plate cracks, originating from the edge of the loading steel plate, extending to the transverse plate, and subsequently propagating along the interface between the concrete and the longitudinal plate.
- (3)
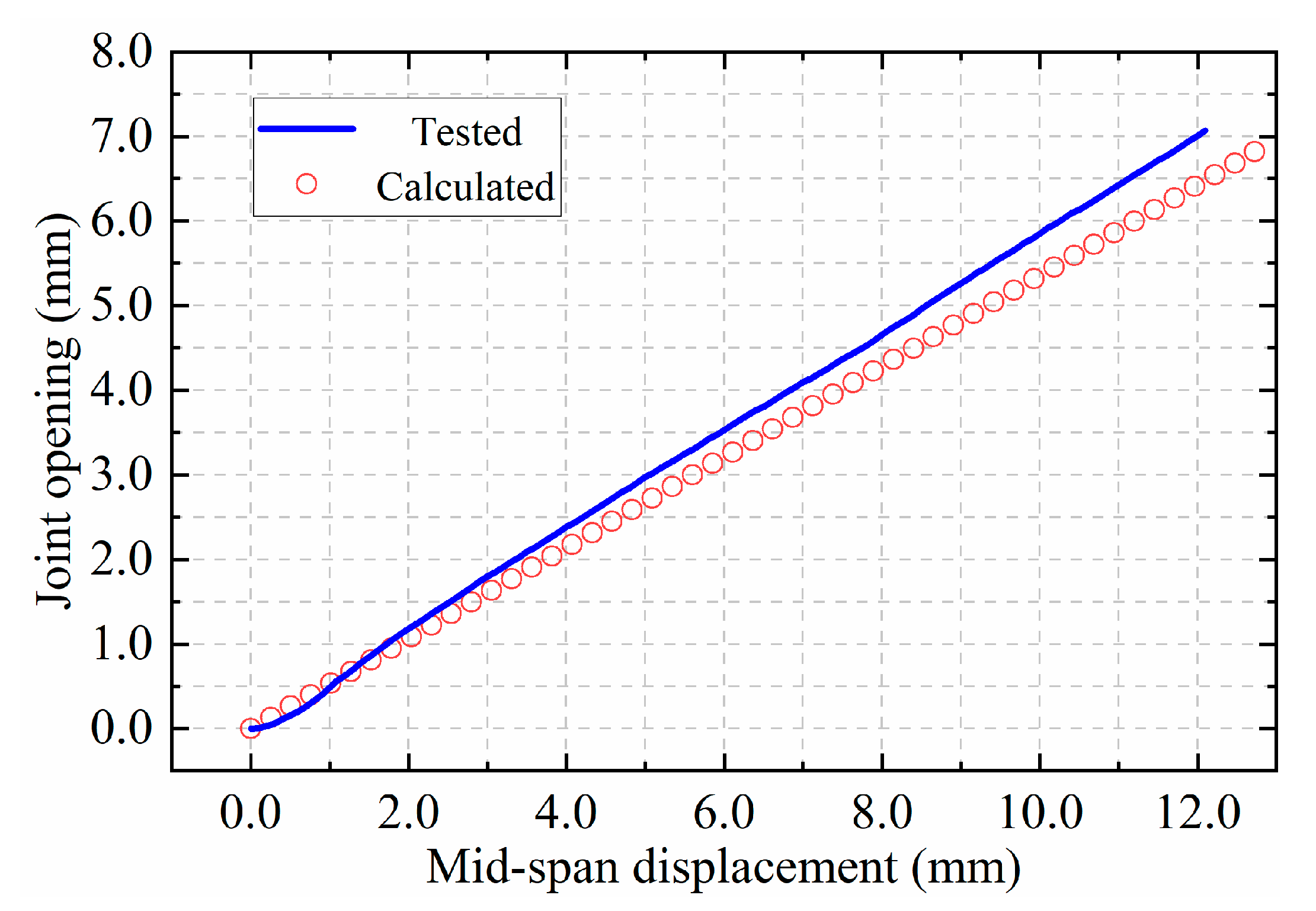
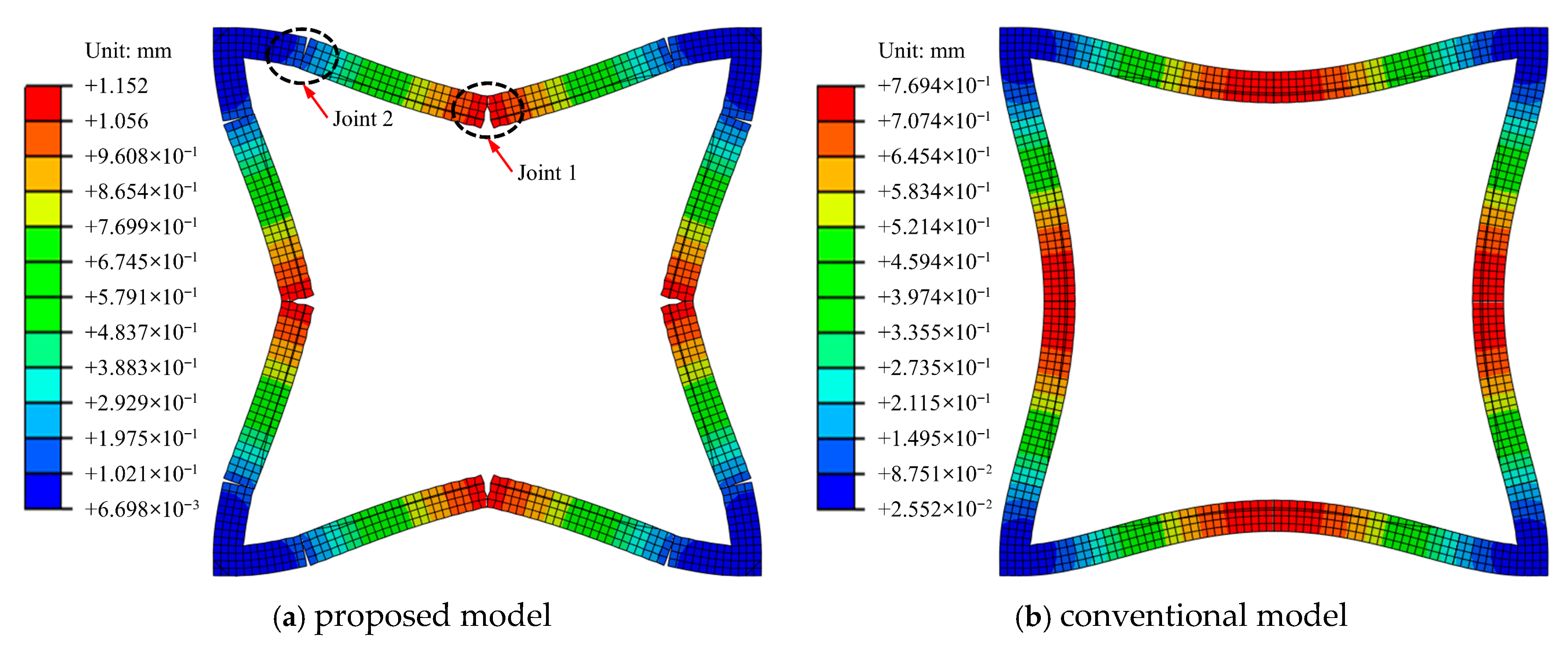
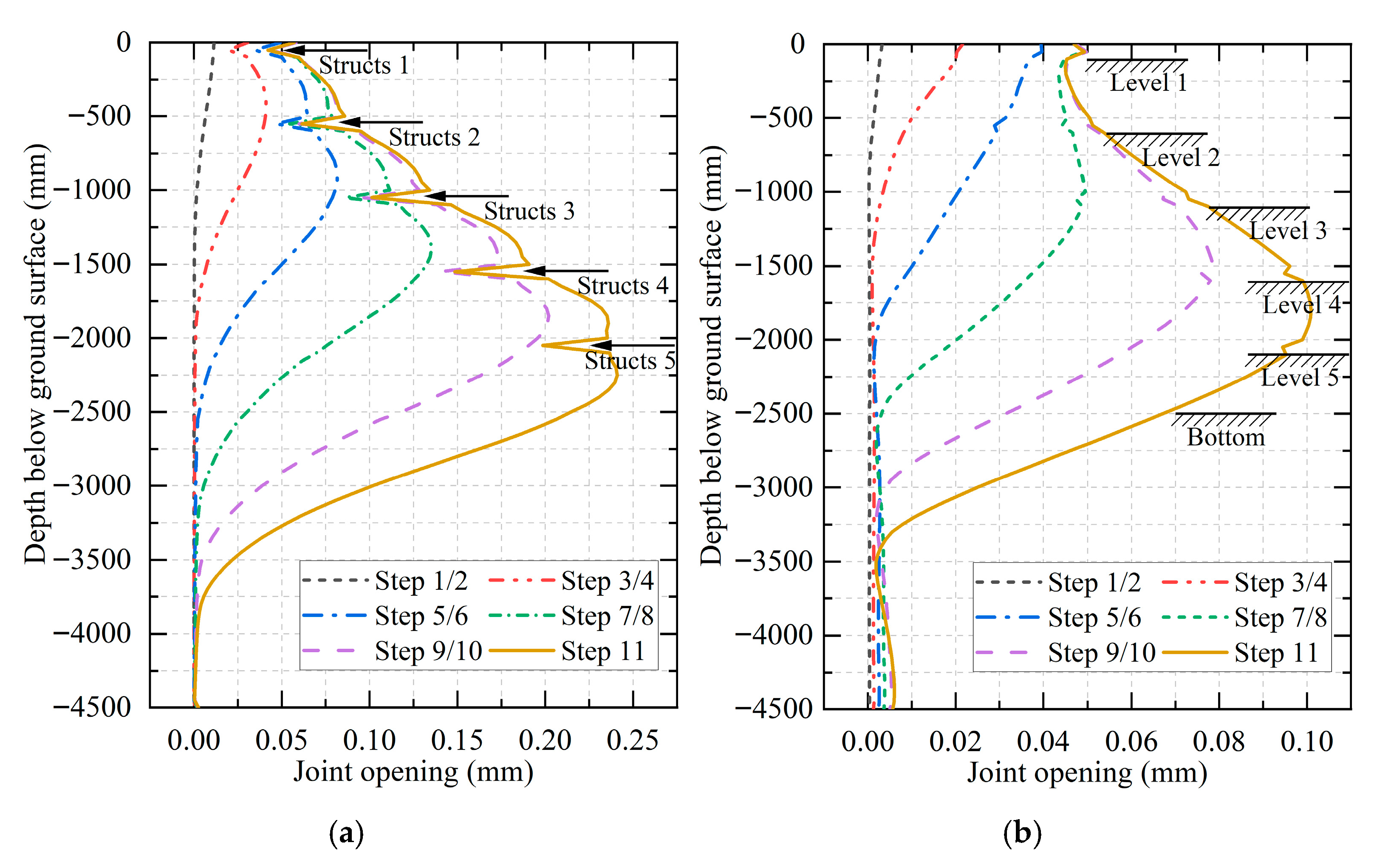
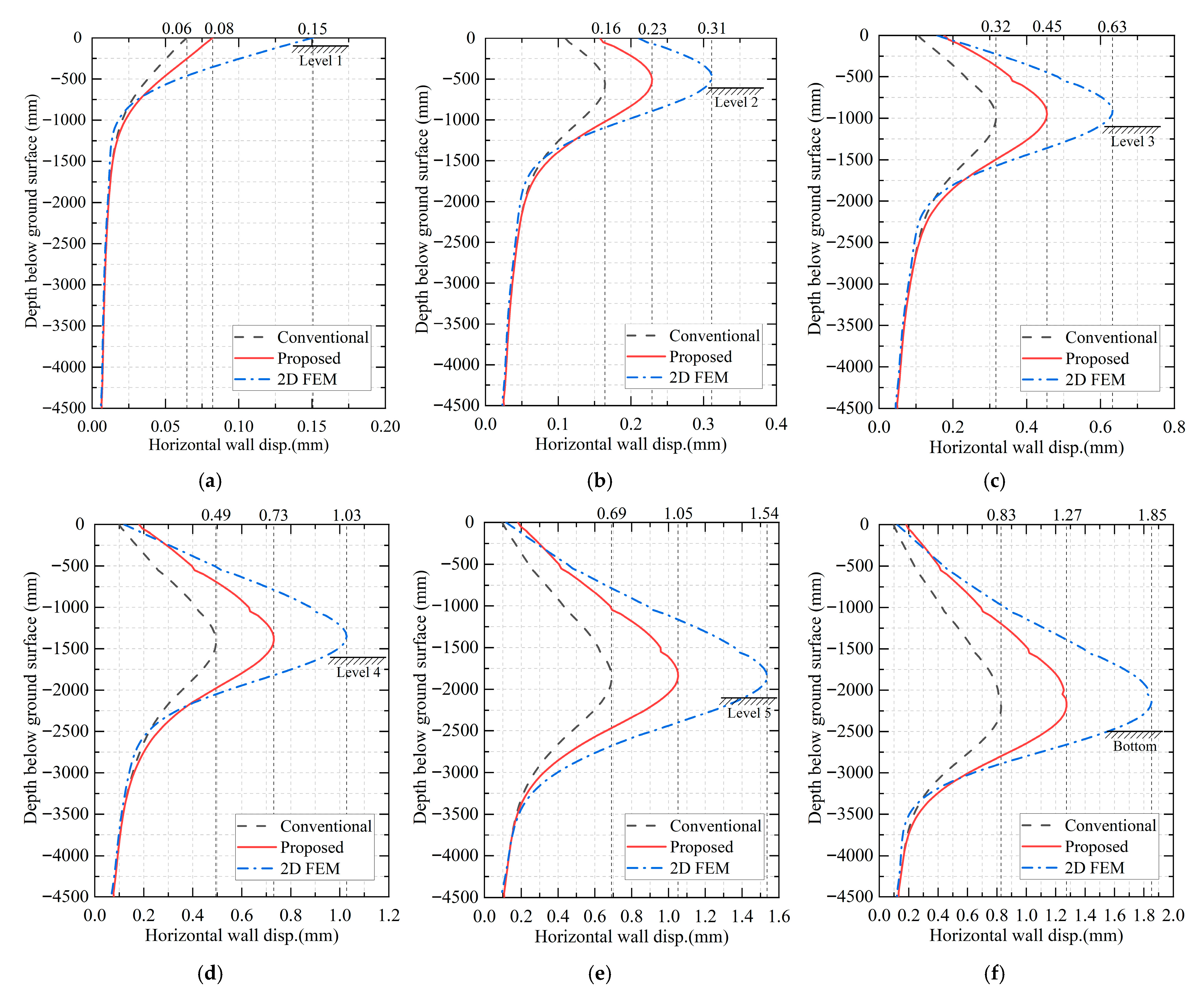
- In comparison to the conventional 3D and 2D models, the deformation of the diaphragm wall obtained by the proposed model can provide a superior representation of the joint opening phenomenon. For the joint located at the midpoint, the maximum joint opening generally occurred near the excavation level. For the joint near the corner, the maximum joint opening was observed at the top of the diaphragm wall during the initial stages. Subsequently, the location where the maximum joint opening occurred shifted deeper into the excavation yet remained significantly higher than the excavation level. Furthermore, it is evident that the midpoint joints exhibit a substantially greater degree of opening in comparison to the joints near the corners.
- (4)
- The 3D model, incorporating the multi-linear spring model, is capable of accounting for the spatial effect of the excavation and the reduction in horizontal stiffness of the diaphragm wall resulting from the joints simultaneously. The calculated displacements of the model fall between those of conventional 3D and 2D calculations and are more in line with the actual deformation of the diaphragm wall. Moreover, the calculation time of the proposed model is only 1.52 times that of the conventional 3D model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gunn, M.J.; Clayton, C.R.I. Installation effects and their importance in the design of earth-retaining structures. Geotechnique 1992, 42, 137–141. [Google Scholar] [CrossRef]
- El-Razek, M.E.A. New method for construction of diaphragm walls. J. Constr. Eng. Manag. 1999, 125, 233–241. [Google Scholar] [CrossRef]
- Brown, A.J.; Bruggemann, D.A. Arminou Dam, Cyprus, and construction joints in diaphragm cut-off walls. Géotechnique 2002, 52, 3–13. [Google Scholar] [CrossRef]
- Comodromos, E.M.; Papadopoulou, M.C.; Konstantinidis, G.K. Effects from diaphragm wall installation to surrounding soil and adjacent buildings. Comput. Geotech. 2013, 53, 106–121. [Google Scholar] [CrossRef]
- Ewald, K.; Schneider, N. Avoid of damage to diaphragm wall joints through the use of appropriate quality assurance systems. Bautechnik 2015, 92, 631–637. [Google Scholar] [CrossRef]
- Wu, G.; Chen, W.; Bian, H.; Yuan, J. Structure optimisation of a diaphragm wall with special modelling methods in a large-scale circular ventilating shaft considering shield crossing. Tunn. Undergr. Space Technol. 2017, 65, 35–41. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Shao, Y.; Zhang, Y. Leakage detection and long-term monitoring in diaphragm wall joints using fiber Bragg grating sensing technology. Tunn. Undergr. Space Technol. 2020, 98, 103331. [Google Scholar] [CrossRef]
- Shao, Y.; Chen, C.; Lu, Z.; Zheng, Y.; Zhang, Y. An intelligent leakage detection method for diaphragm wall joints based on fiber Bragg grating sensors and intelligent algorithms. Measurement 2022, 197, 111339. [Google Scholar] [CrossRef]
- JGJ 120-2012; Technical Specification for Retaining and Protection of Building Foundation Excavations. China Architecture Press: Beijing, China, 2012; pp. 24–25+163. (In Chinese)
- DG/TJ 508-61-2018; Technical Code for Excavation Engineering. Tongji University Press: Shanghai, China, 2018; pp. 59–61+248. (In Chinese)
- 11SG814; Specification for the Structure of Building Excavation. China Planning Press: Beijing, China, 2011; p. 41. (In Chinese)
- Chen, J.J.; Wang, J.H.; Qiao, P.; Hou, Y.M.; Gu, Q.Y. Shear bearing of cross-plate joints between diaphragm wall panels–I: Model tests and shear behaviour. Mag. Concr. Res. 2016, 68, 902–915. [Google Scholar] [CrossRef]
- Chen, J.J.; Hou, Y.M.; Wang, J.H.; Qiao, P. Shear bearing of cross-plate joints between diaphragm wall panels–II: Numerical analysis and prediction formula. Mag. Concr. Res. 2016, 68, 1025–1039. [Google Scholar] [CrossRef]
- Valente, I.; Cruz, P.J. Experimental analysis of perfobond shear connection between steel and lightweight concrete. J. Constr. Steel Res. 2004, 60, 465–479. [Google Scholar] [CrossRef]
- Vianna, J.D.C.; De Andrade, S.A.L.; Vellasco, P.D.S.; Costa-Neves, L.F. Experimental study of perfobond shear connectors in composite construction. J. Constr. Steel Res. 2013, 81, 62–75. [Google Scholar] [CrossRef]
- Zou, Y.; Peng, H.; Zhang, Z.; Jiang, J.; Guo, J. Effect of additional constraints of push-out test on the mechanical properties of perfobond shear connectors. Structures 2023, 47, 991–1004. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Zhu, S.; Deng, K.; Li, Z.; Yuan, X. Shear resistance of perfobond rib shear connectors under cyclic loading. J. Struct. Eng. 2024, 150, 4023218. [Google Scholar] [CrossRef]
- Yang, M.; Wu, R.; Tong, C.; Chen, J.; Tang, B. Displacement analyses of diaphragm wall in small-scale deep excavation considering joints between panels. Buildings 2024, 14, 1449. [Google Scholar] [CrossRef]
- Wang, Q.; Geng, P.; Guo, X.; Zeng, G.; Chen, C.; He, C. Experimental study on the tensile performance of circumferential joint in shield tunnel. Tunn. Undergr. Space Technol. 2021, 112, 103937. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, W.; Li, S.; Qiao, Y. Effect of oblique bolt arrangement on flexural behavior of segmental joint for shield tunnel. Tunn. Undergr. Space Technol. 2023, 135, 105043. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, M. Experimental study on the mechanical properties of longitudinal joints of shield tunnels under large deformation conditions. Tunn. Undergr. Space Technol. 2024, 144, 105447. [Google Scholar] [CrossRef]
- Qiu, T.; Zhang, J.; Chen, X.; Xu, Z.; Su, D.; Song, R.; Cui, T. Experimental investigation and mechanical model for assembled joints of prefabricated two-wall-in-one diaphragm walls. Eng. Struct. 2023, 275, 115285. [Google Scholar] [CrossRef]
- Han, G.; Zhang, Y.; Zhang, J.; Zhang, H. Numerical analysis and optimization of displacement of enclosure structure based on midas finite element simulation software. Buildings 2025, 15, 1462. [Google Scholar] [CrossRef]
- Zhuang, Y.; Cui, X.; Hu, S. Numerical simulation and simplified analytical method to evaluate the displacement of adjacent tunnels caused by excavation. Tunn. Undergr. Space Technol. 2023, 132, 104879. [Google Scholar] [CrossRef]
- Bozkurt, S.; Abed, A.; Karstunen, M. Finite element analysis for a deep excavation in soft clay supported by lime-cement columns. Comput. Geotech. 2023, 162, 105687. [Google Scholar] [CrossRef]
- Zdravkovic, L.; Potts, D.M.; St John, H.D. Modelling of a 3D excavation in finite element analysis. Géotechnique 2005, 55, 497–513. [Google Scholar] [CrossRef]
- Dong, Y.P.; Burd, H.J.; Houlsby, G.T. Finite-element analysis of a deep excavation case history. Géotechnique 2016, 66, 1–15. [Google Scholar] [CrossRef]
- Dong, Y.; Burd, H.; Houlsby, G.; Hou, Y. Advanced finite element analysis of a complex deep excavation case history in Shanghai. Front. Struct. Civ. Eng. 2014, 8, 93–100. [Google Scholar] [CrossRef]
- Dong, Y.P.; Burd, H.J.; Houlsby, G.T. Finite element parametric study of the performance of a deep excavation. Soils Found. 2018, 58, 729–743. [Google Scholar] [CrossRef]
- Jin, X.F.; Zhang, Y.L.; Liang, S.T.; Zhu, X.J. Simplified calculation method for mechanical performance of type Ⅱ joint of diaphragm wall. J. Southeast Univ. 2015, 45, 929–934. (In Chinese) [Google Scholar]
- Wang, F.; Huang, H.; Soga, K.; Li, Z. 3D modelling of concrete tunnel segmental joints and the development of a new bolt-spring model. Tunn. Undergr. Space Technol. 2021, 110, 103835. [Google Scholar] [CrossRef]
- Sun, H.; Li, B.; Wang, Z.; Wang, S.; Wang, H.; Meng, X. Centrifugal model tests on characteristics of deep foundation pits in starting. Chin. J. Geotech. Eng. 2024, 46, 244–248. (In Chinese) [Google Scholar]
- Wang, Z.; Yu, H.; Zhang, Z.; Song, Y.; Liu, S. Shaking table test for near-valley underground station: Influence of diaphragm walls. Tunn. Undergr. Space Technol. 2024, 153, 106030. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Z.; Zhang, Z.; Song, Y.; Liu, S. Shaking table test for subway station considering the influence of diaphragm walls. Earthq. Eng. Struct. Dyn. 2024, 53, 2710–2733. [Google Scholar] [CrossRef]
- Kumbasaroğlu, A.; Budak, A. An experimental study on impact of anchor bars at the steel frames with infilled walls. Chall. J. Struct. Mech. 2016, 2, 129–138. [Google Scholar]
- He, J.; Liu, Y.; Pei, B. Experimental study of the steel-concrete connection in hybrid cable-stayed bridges. J. Perform. Constr. Facil. 2014, 28, 559–570. [Google Scholar] [CrossRef]
- Mirghaderi, S.R.; Eghbali, N.B.; Ahmadi, M.M. Moment-connection between continuous steel beams and reinforced concrete column under cyclic loading. J. Constr. Steel Res. 2016, 118, 105–119. [Google Scholar] [CrossRef]
- GB/T 50152-2012; Standard for Test Method of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012; p. 13. (In Chinese)
- GB 50497-2019; Technical Standard for Monitoring of Building Excavation Engineering. China Planning Press: Beijing, China, 2020; p. 35. (In Chinese)
- Cho, J.R.; Park, S.Y.; Cho, K.; Kim, S.T.; Kim, B.S. Pull-out test and discrete spring model of fibre-reinforced polymer perfobond rib shear connector. Can. J. Civ. Eng. 2012, 39, 1311–1320. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Kou, L.; Zhang, B.; Jiang, Y.; Yu, H. Experimental study of the short-term and long-term behavior of perfobond connectors. J. Constr. Steel Res. 2018, 150, 462–474. [Google Scholar] [CrossRef]
- Deng, W.; Xiong, Y.; Liu, D.; Zhang, J. Static and fatigue behavior of shear connectors for a steel-concrete composite girder. J. Constr. Steel Res. 2019, 159, 134–146. [Google Scholar] [CrossRef]
- Jin, H.; Yu, S.; Zhou, S.; Xiao, J. Research on mechanics of longitudinal joint in shield tunnel by the nonlinear spring equivalent method. KSCE J. Civ. Eng. 2019, 23, 902–913. [Google Scholar] [CrossRef]
- Li, Z.; Soga, K.; Wang, F.; Wright, P.; Tsuno, K. Behaviour of cast-iron tunnel segmental joint from the 3D FE analyses and development of a new bolt-spring model. Tunn. Undergr. Space Technol. 2014, 41, 176–192. [Google Scholar] [CrossRef]
- Karam, M.S.; Nakamura, H.; Yamamoto, Y.; Miura, T. Numerical evaluation of the perfobond (PBL) shear connector with transverse rebar using coupled rigid Body spring model (RBSM) and solid finite element method (FEM). Structures 2022, 45, 1544–1560. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Mashiri, F.; Mirza, O. Parametric study of innovative bolted shear connectors using 3D finite element modelling. J. Constr. Steel Res. 2021, 179, 106565. [Google Scholar] [CrossRef]
- Xue, X.; Hu, S.W.; Qi, H.; Shan, C.X. Study on the normal bonding performance of the steel-concrete interface. Eng. Mech. 2022, 39, 65–74. (In Chinese) [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture Press: Beijing, China, 2015; pp. 19–20. (In Chinese)
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture Press: Beijing, China, 2017; p. 28. (In Chinese)
- Guo, P.; Gong, X.; Wang, Y. Displacement and force analyses of braced structure of deep excavation considering unsymmetrical surcharge effect. Comput. Geotech. 2019, 113, 103102. [Google Scholar] [CrossRef]
- Tu, B.; Han, M.; Jia, J.; Xiao, Z.; Liu, L. Improved mobilized strength design method for multi-support excavation deformation analysis. Buildings 2024, 14, 3630. [Google Scholar] [CrossRef]
- Yang, D.; Ma, Y. Test for Building Structure; Wuhan University of Technology Press: Wuhan, China, 2013; p. 86. (In Chinese) [Google Scholar]
- Li, Z.; Han, M.; Liu, L.; Li, Y.; Yan, S. Corner and partition wall effects on the settlement of a historical building near a supported subway excavation in soft soil. Comput. Geotech. 2020, 128, 103805. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, R.; Liang, C. Size effects of small-scale model tests on bearing capacity of strip foundation. Chin. J. Geotech. Eng. 2024, 46, 1289–1299. (In Chinese) [Google Scholar]







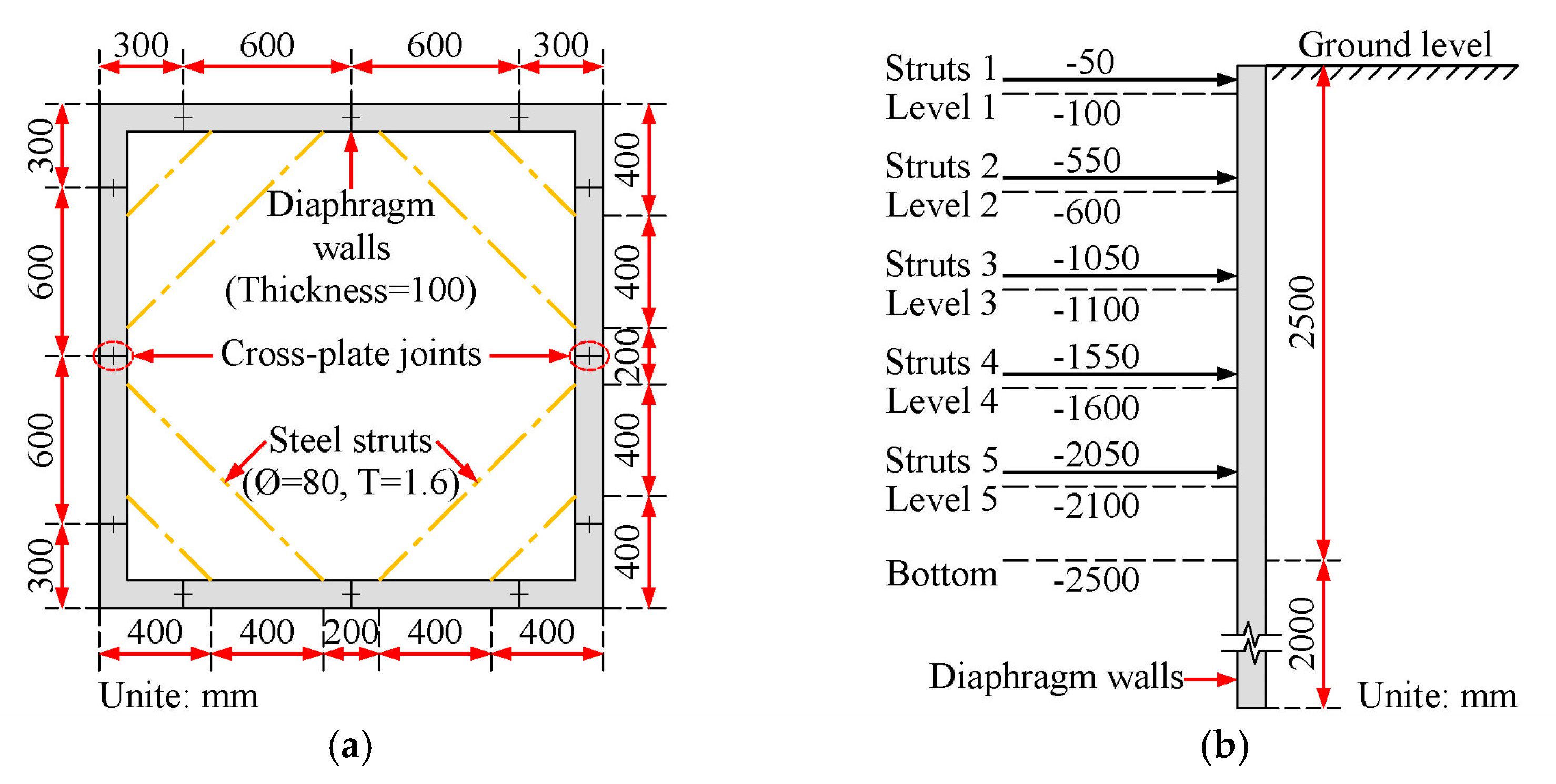

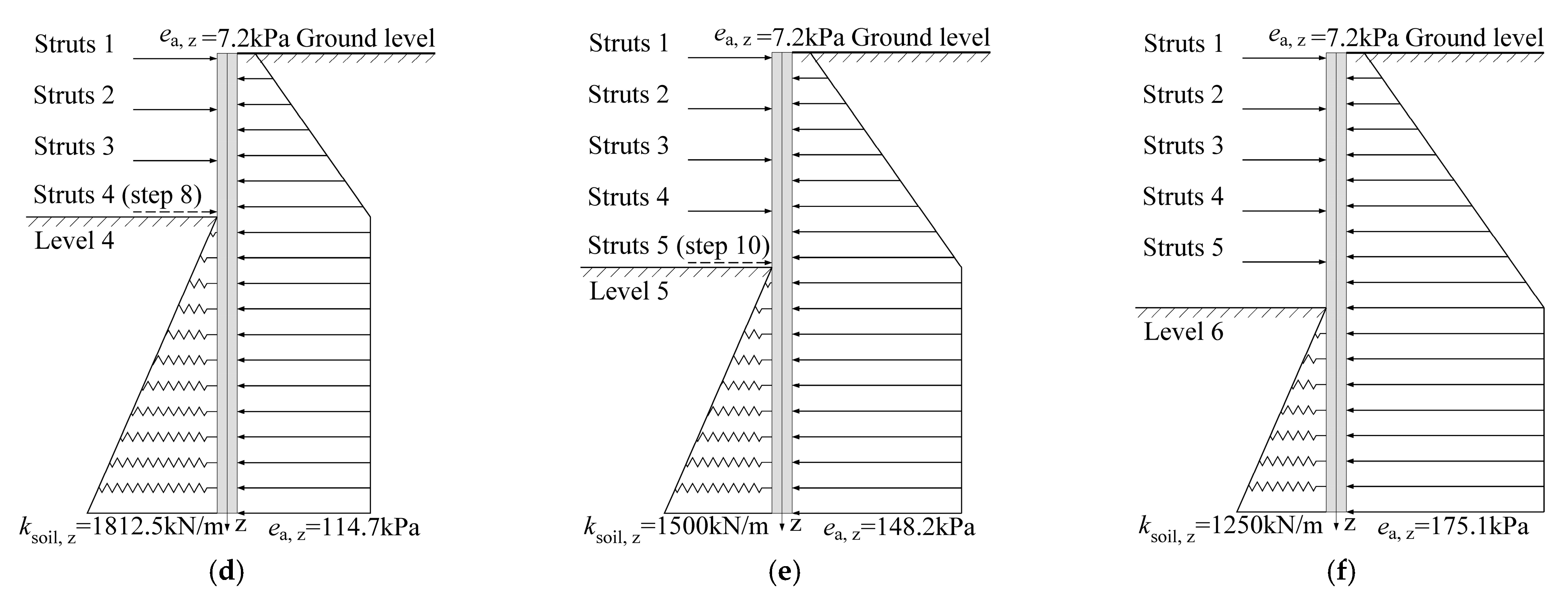
| Step | Description |
|---|---|
| 1 | Excavate to the level 1 at −100 mm. |
| 2 | Install struts 1 at −50 mm. |
| 3 | Excavate to the level 2 at −600 mm. |
| 4 | Install struts 2 at −550 mm. |
| 5 | Excavate to the level 3 at −1100 mm. |
| 6 | Install struts 3 at −1050 mm. |
| 7 | Excavate to the level 4 at −1600 mm. |
| 8 | Install struts 4 at −1550 mm. |
| 9 | Excavate to the level 5 at −2100 mm. |
| 10 | Install struts 5 at −2050 mm. |
| 11 | Excavate to the level 6 at −2500 mm. |
| Type | Physical Quantity | Similarity Relationship [52] |
|---|---|---|
| Material Properties | Stress σ | Sσ = SE |
| Strain ε | 1.0 | |
| Elasticity modulus E | SE | |
| Poisson’s ratio υ | 1.0 | |
| Geometric Properties | Length L | SL |
| Displacement x | Sx = SL | |
| Rotation θ | 1.0 | |
| Area A | SA = SL2 | |
| Load | Point load P | SP = SESL2 |
| Line load ω | Sω = SESL2 | |
| Surface load q | Sq = SE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Tong, C.; Wu, R.; Wang, G.; Tong, S. A Simplified Multi-Linear Spring Model for Cross-Plate Joint in Diaphragm Walls Based on Model Tests. Buildings 2025, 15, 2890. https://doi.org/10.3390/buildings15162890
Yang M, Tong C, Wu R, Wang G, Tong S. A Simplified Multi-Linear Spring Model for Cross-Plate Joint in Diaphragm Walls Based on Model Tests. Buildings. 2025; 15(16):2890. https://doi.org/10.3390/buildings15162890
Chicago/Turabian StyleYang, Ming, Chenxi Tong, Rongxing Wu, Gaoke Wang, and Shenglei Tong. 2025. "A Simplified Multi-Linear Spring Model for Cross-Plate Joint in Diaphragm Walls Based on Model Tests" Buildings 15, no. 16: 2890. https://doi.org/10.3390/buildings15162890
APA StyleYang, M., Tong, C., Wu, R., Wang, G., & Tong, S. (2025). A Simplified Multi-Linear Spring Model for Cross-Plate Joint in Diaphragm Walls Based on Model Tests. Buildings, 15(16), 2890. https://doi.org/10.3390/buildings15162890





