Semi-Analytical Method for the Response of Existing Tunnels to Tunneling Considering the Tunnel–Soil Interaction Based on the Modified Gaussian Function
Abstract
1. Introduction
2. The Elastic Continuum Solution of Existing Tunnel Deformation
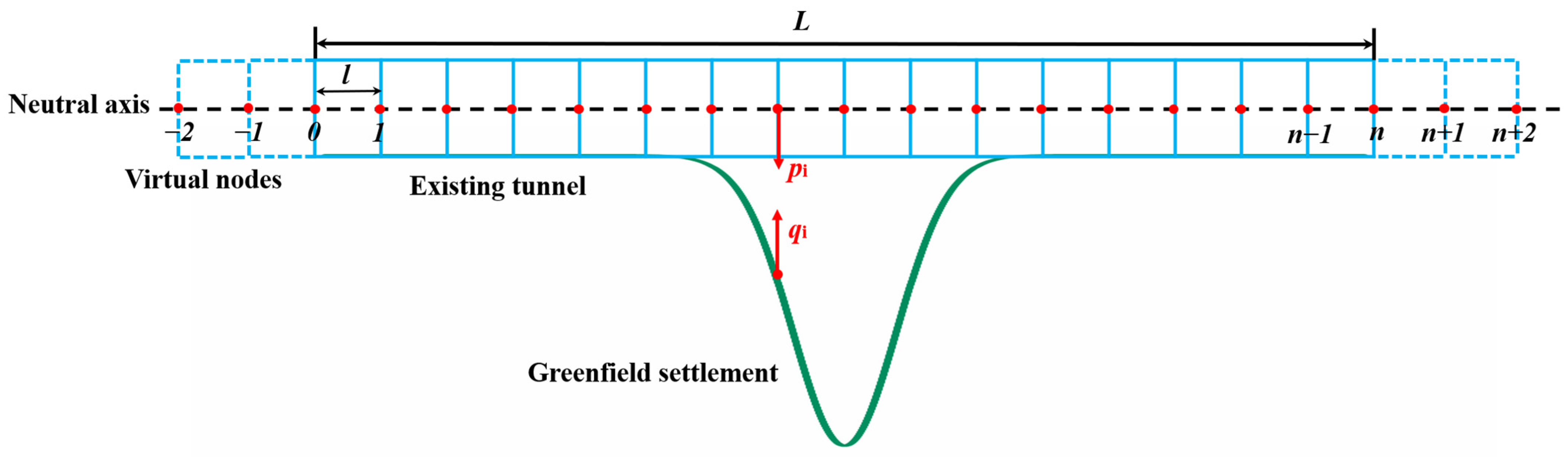
2.1. Single-Variable Formulation of a Timoshenko Beam
2.2. Elastic Continuum Solution of Existing Tunnel Deformation
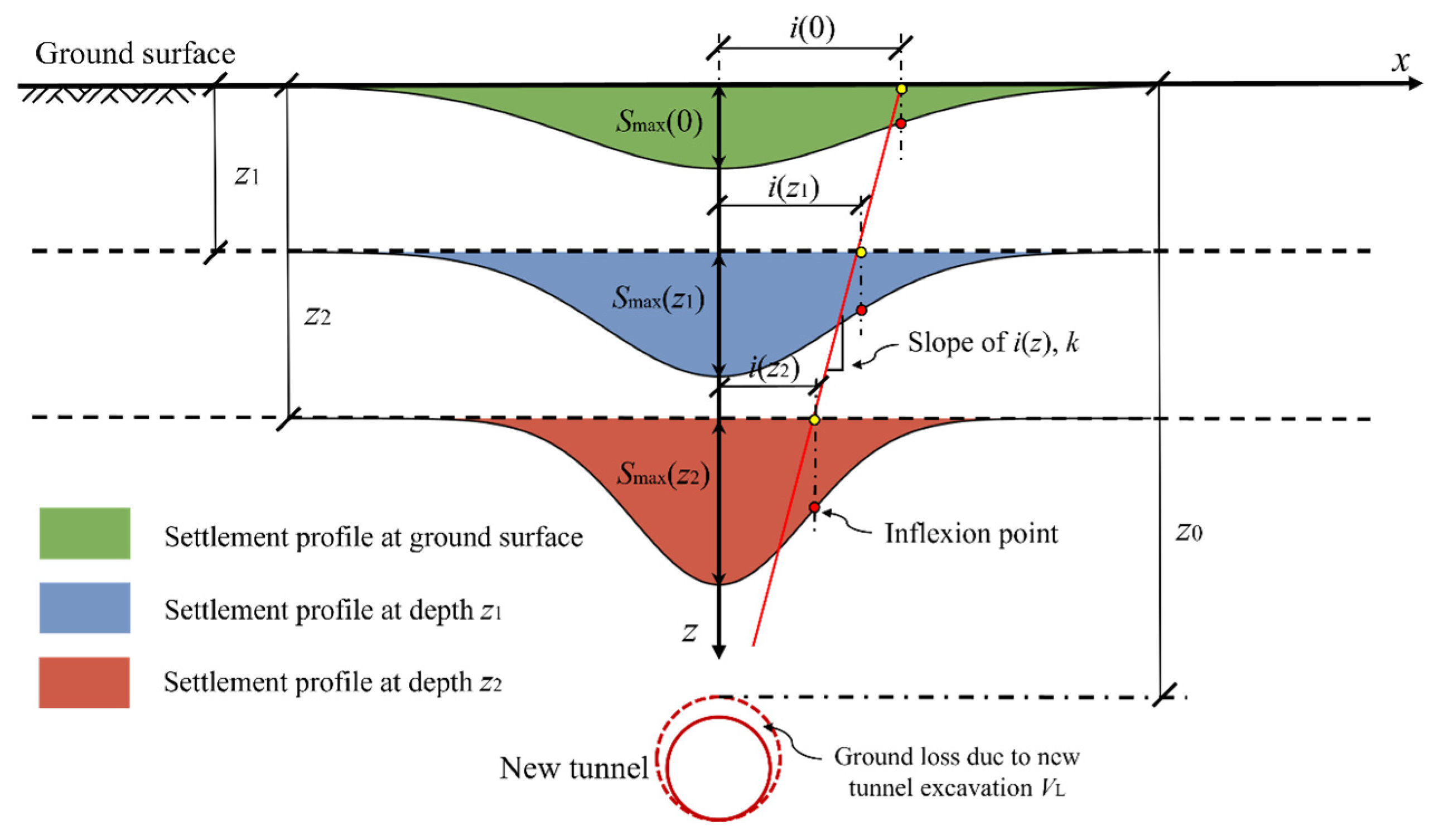
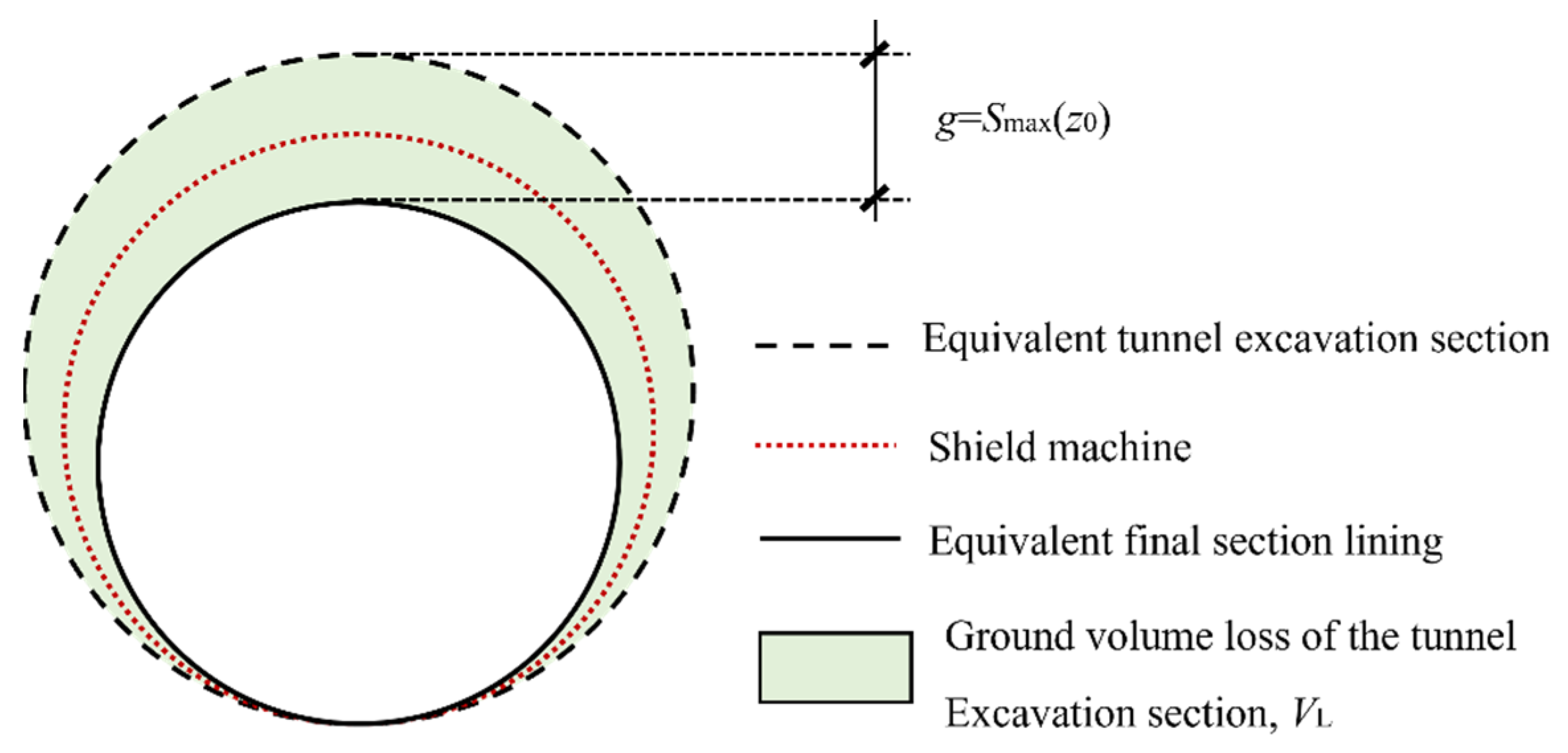
2.3. Greenfield Settlement at the Existing Tunnel Axis
2.4. Simplification to the Winkler–Timoshenko Solution
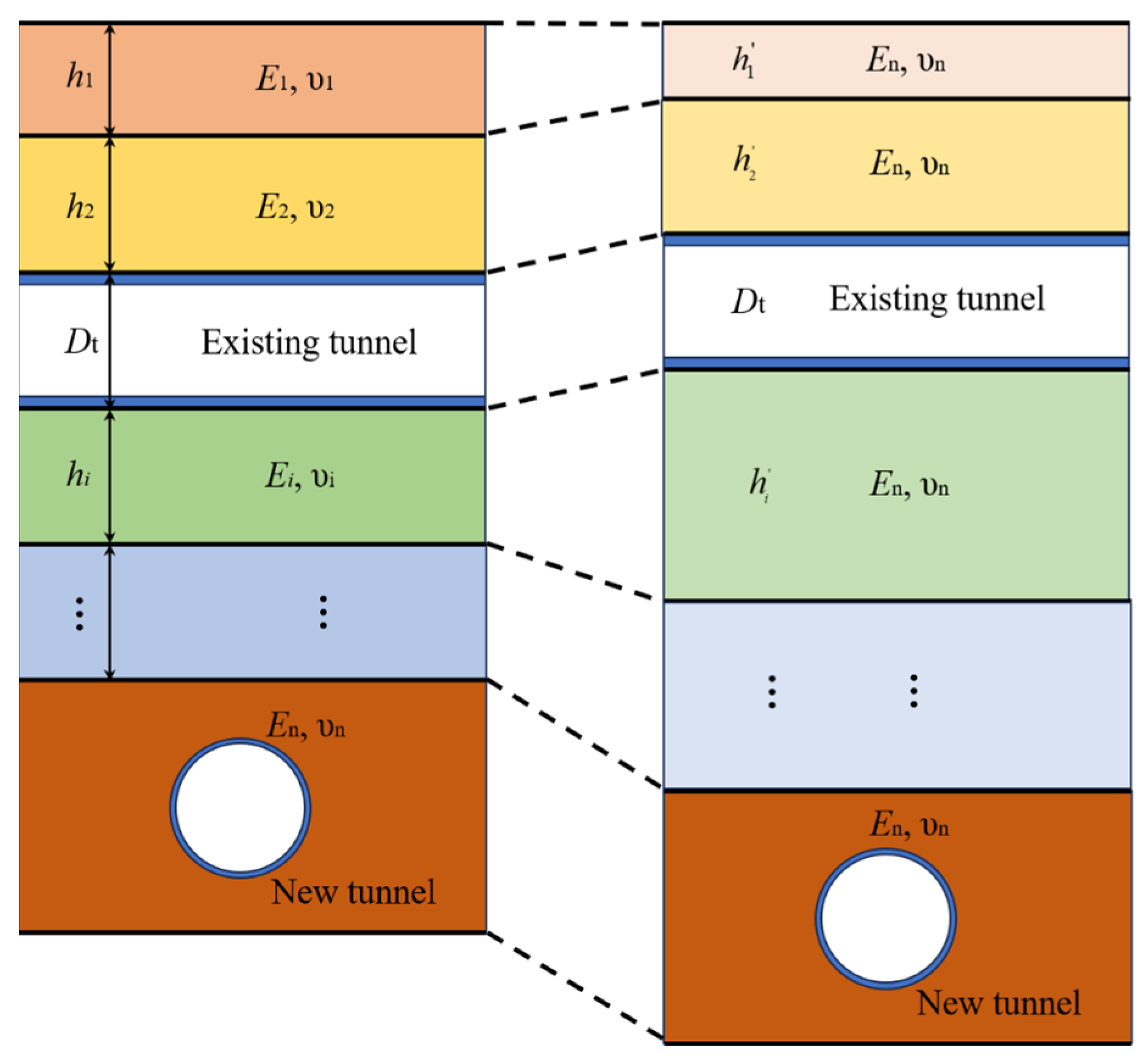
2.5. Equivalent Bending Stiffness and Shear Stiffness of the Existing Tunnel
3. Verification
3.1. Case 1: Shenzhen Metro Line 1 Under-Crossed by Line 9
3.2. Case 2: Shenzhen Metro Line 3 Under-Crossed by Line 9
3.3. Case 3: Shanghai Metro Line 4 Under-Crossed by Line 11
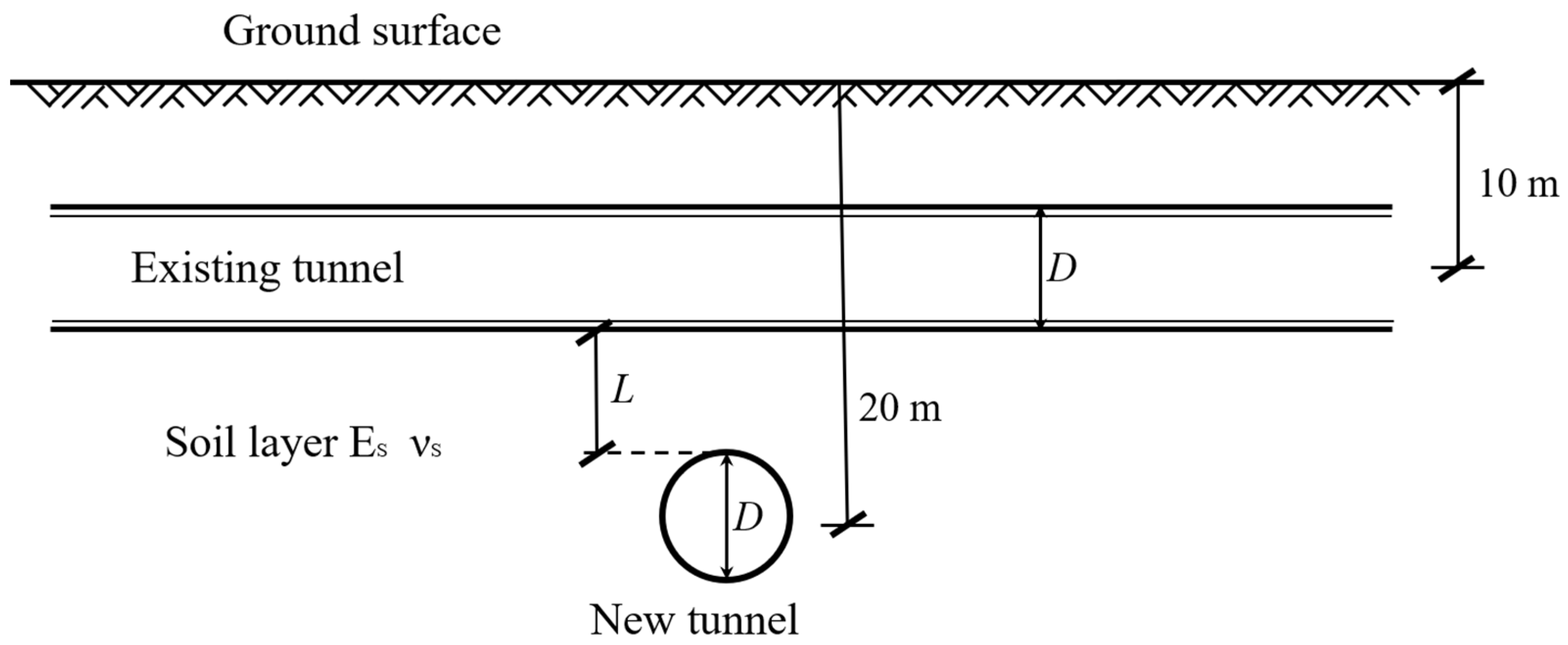
4. Parametric Analysis
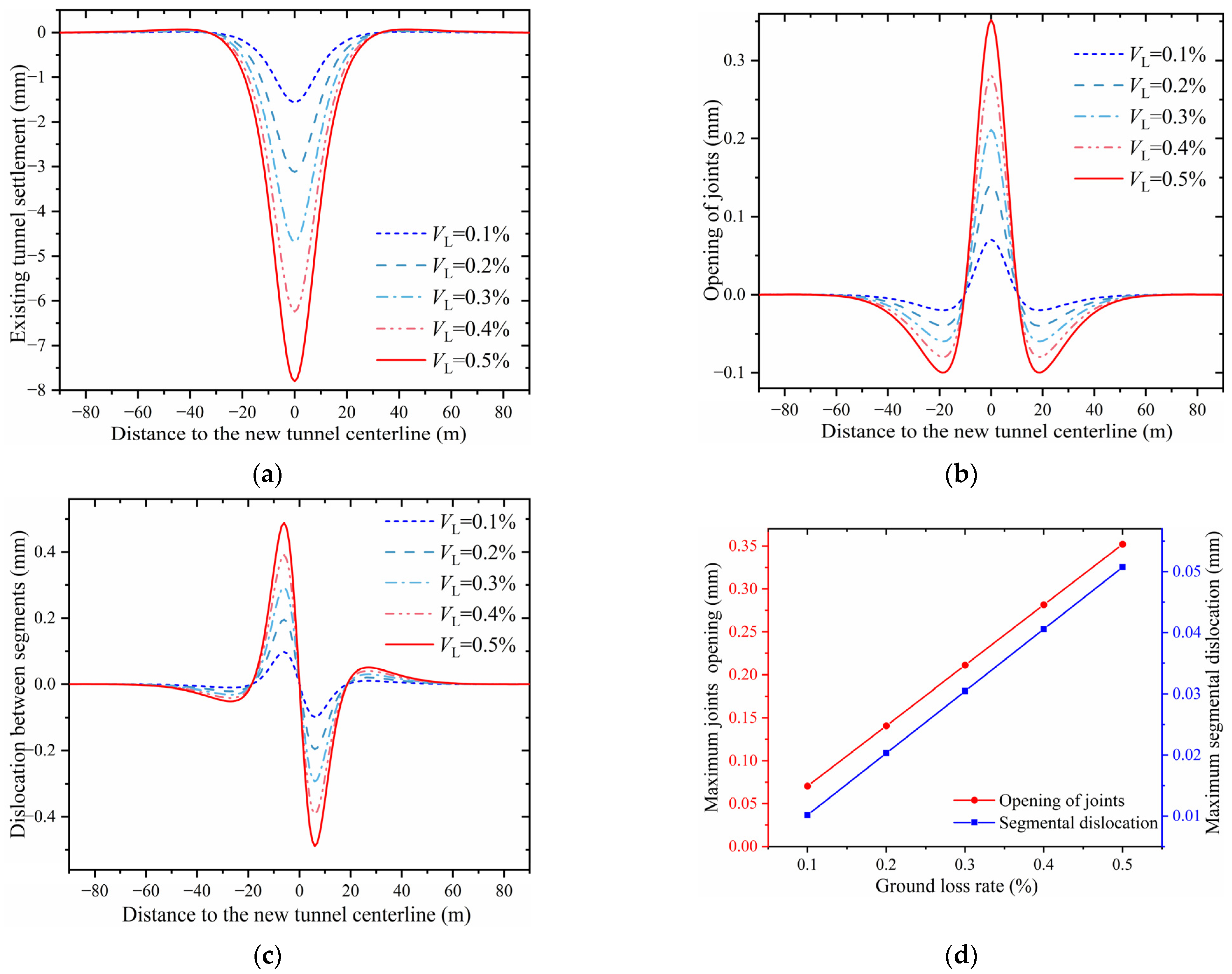
4.1. Influence of the Ground Loss Rate
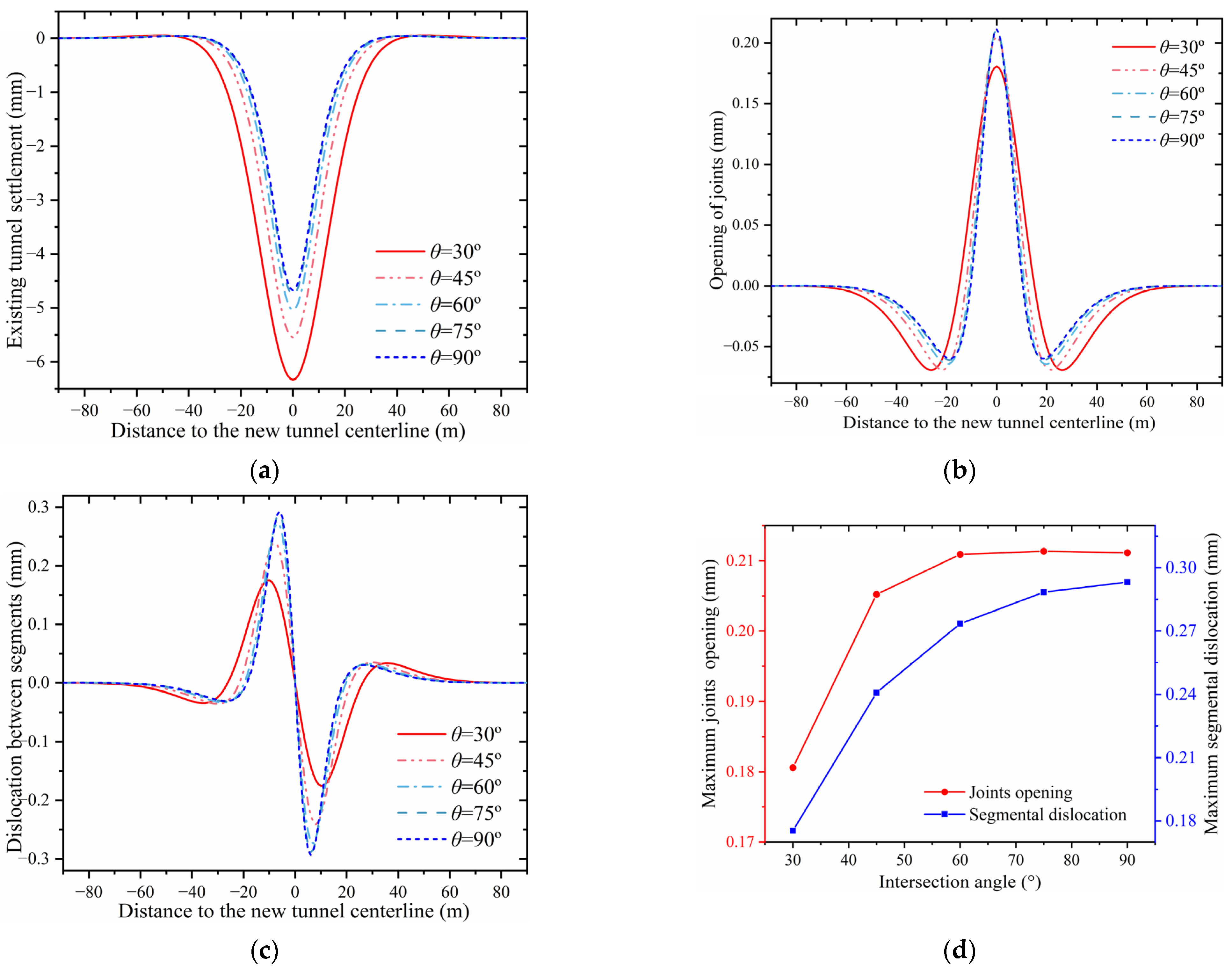
4.2. Influence of the Intersection Angle
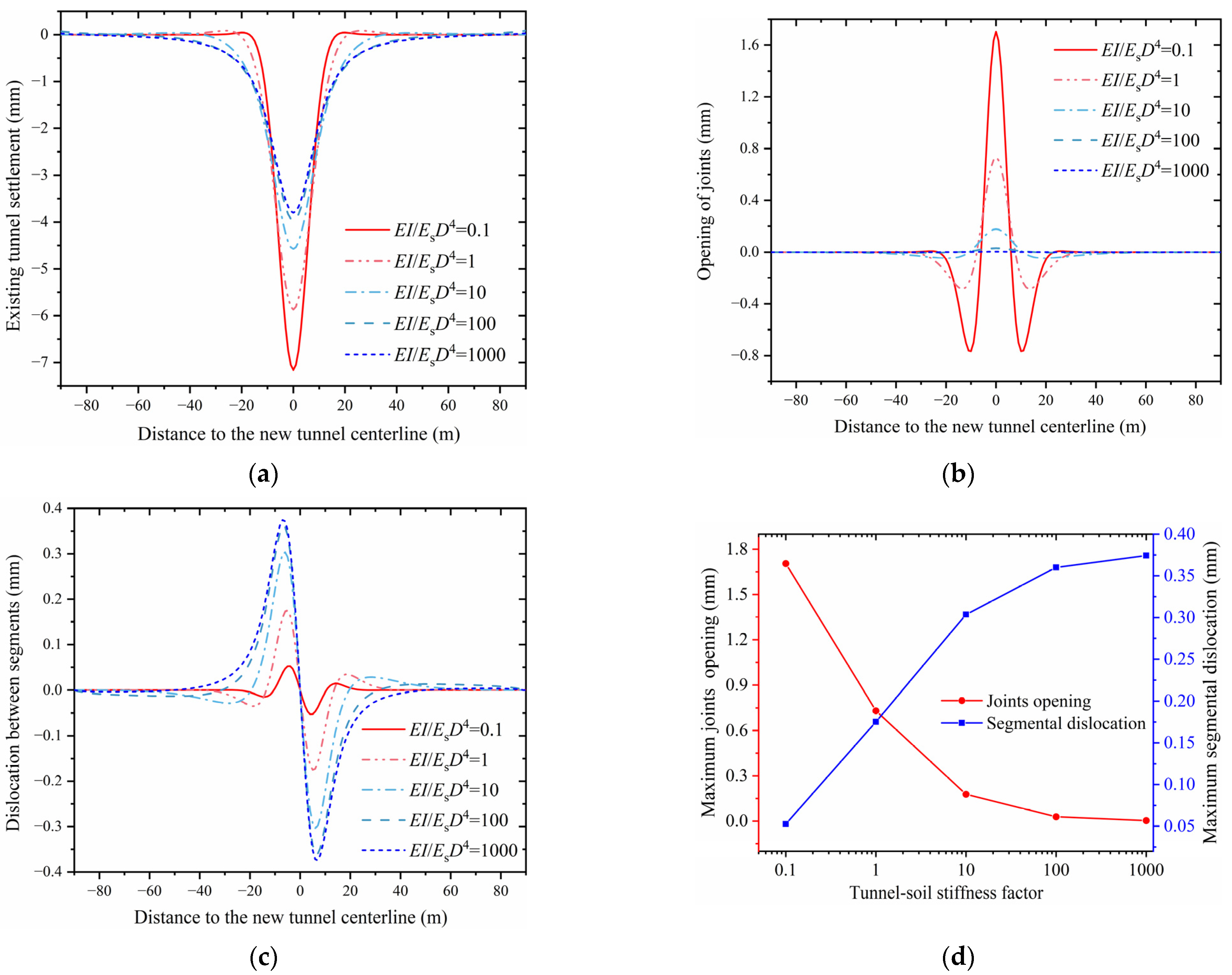
4.3. Influence of the Tunnel–Soil Stiffness Factor
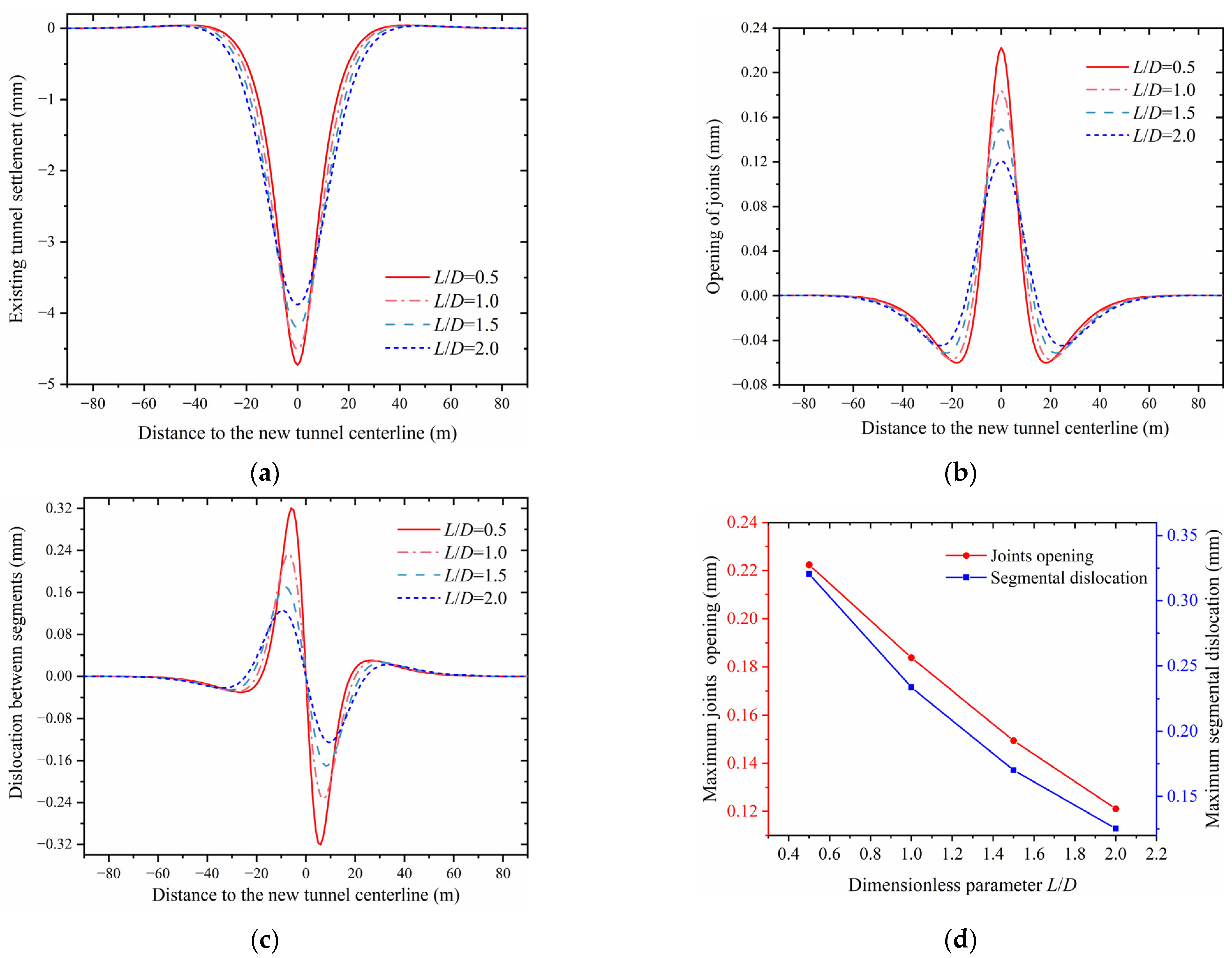
4.4. Influence of the Vertical Clearance Between the New and Existing Tunnels
5. Conclusions
- (1)
- The proposed elastic continuum method considers the tunnel–soil interaction, unlike the degrading Winkler–Timoshenko method. The modified Gaussian function is validated by measured greenfield settlement data. Compared with the elastic continuum solution, the Winkler model significantly underestimates both joint openings and segmental dislocations;
- (2)
- Existing tunnel deflection, maximum joint opening, and segmental dislocation strongly depend on the ground loss rate, exhibiting a positive correlation. Conversely, an inverse relationship is observed with the intersection angle: a larger intersection angle leads to a broader and more pronounced tunnel settlement profile, indicating that the disturbance zone expands as the intersection angle increases. Thus, under-crossing existing tunnels at a large intersection angle and selecting appropriate shield types based on ground conditions to minimize soil disturbance are preconditions for ensuring the safe operation of existing metro lines;
- (3)
- The tunnel–soil stiffness factor analysis reveals that the existing tunnel deformation mode transitions to bending-dominated as the stiffness factor decreases, whereas it becomes shear-deformation-dominated with increasing stiffness factor. Additionally, decreasing vertical clearance leads to marginal changes in tunnel settlement but induces significant growth in both maximum joint openings and segmental dislocations. Therefore, adopting different reinforcement measures for varying foundation soil conditions and ensuring a reasonable arrangement of the new tunnel position are cost-effective strategies to prevent existing tunnel diseases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Verruijt, A.; Booker, J.R. Surface Settlements Due to Deformation of a Tunnel in an Elastic Half Plane. Geotechnique 1996, 46, 753–756. [Google Scholar] [CrossRef]
- Loganathan, N.; Poulos, H.G. Analytical Prediction for Tunneling-Induced Ground Movements in Clays. J. Geotech. Geoenviron. Eng. 1998, 124, 846–856. [Google Scholar] [CrossRef]
- Vorster, T.E.B.; Klar, A.; Soga, K.; Mair, R.J. Estimating the Effects of Tunneling on Existing Pipelines. J. Geotech. Geoenviron. Eng. 2005, 131, 1399–1410. [Google Scholar] [CrossRef]
- Pinto, F.; Whittle, A.J. Ground Movements Due to Shallow Tunnels in Soft Ground. I: Analytical Solutions. J. Geotech. Geoenviron. Eng. 2014, 140, 04013040. [Google Scholar] [CrossRef]
- Franza, A.; Marshall, A.M.; Zhou, B. Greenfield Tunnelling in Sands: The Effects of Soil Density and Relative Depth. Geotechnique 2019, 69, 297–307. [Google Scholar] [CrossRef]
- Lu, D.; Wang, G.; Du, X.; Wang, Y. A Nonlinear Dynamic Uniaxial Strength Criterion That Considers the Ultimate Dynamic Strength of Concrete. Int. J. Impact Eng. 2017, 103, 124–137. [Google Scholar] [CrossRef]
- Wang, G.; Lu, D.; Du, X.; Zhou, X.; Cao, S. A True 3D Frictional Hardening Elastoplastic Constitutive Model of Concrete Based on a Unified Hardening/Softening Function. J. Mech. Phys. Solids 2018, 119, 250–273. [Google Scholar] [CrossRef]
- Lu, D.; Liang, J.; Du, X.; Ma, C.; Gao, Z. Fractional Elastoplastic Constitutive Model for Soils Based on a Novel 3D Fractional Plastic Flow Rule. Comput. Geotech. 2019, 105, 277–290. [Google Scholar] [CrossRef]
- Shen, S.-L.; Wu, H.-N.; Cui, Y.-J.; Yin, Z.-Y. Long-Term Settlement Behaviour of Metro Tunnels in the Soft Deposits of Shanghai. Tunn. Undergr. Space Technol. 2014, 40, 309–323. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M. Geotechnical Influence on Existing Subway Tunnels Induced by Multiline Tunneling in Shanghai Soft Soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Cooper, M.L.; Chapman, D.N.; Rogers, C.D.F.; Chan, A.H.C. Movements in the Piccadilly Line Tunnels Due to the Heathrow Express Construction. Geotechnique 2002, 52, 243–257. [Google Scholar] [CrossRef]
- Mohamad, H.; Bennett, P.J.; Soga, K.; Mair, R.J.; Bowers, K. Behaviour of an Old Masonry Tunnel Due to Tunnelling-Induced Ground Settlement. Geotechnique 2010, 60, 927–938. [Google Scholar] [CrossRef]
- Chakeri, H.; Hasanpour, R.; Hindistan, M.A.; Unver, B. Analysis of Interaction between Tunnels in Soft Ground by 3D Numerical Modeling. Bull. Eng. Geol. Environ. 2011, 70, 439–448. [Google Scholar] [CrossRef]
- Avgerinos, V.; Potts, D.M.; Standing, J.R. Numerical Investigation of the Effects of Tunnelling on Existing Tunnels. Geotechnique 2017, 67, 808–822. [Google Scholar] [CrossRef]
- Lu, D.; Zhou, X.; Du, X.; Wang, G. A 3D Fractional Elastoplastic Constitutive Model for Concrete Material. Int. J. Solids Struct. 2019, 165, 160–175. [Google Scholar] [CrossRef]
- Lu, D.; Zhou, X.; Du, X.; Wang, G. 3D Dynamic Elastoplastic Constitutive Model of Concrete within the Framework of Rate-Dependent Consistency Condition. J. Eng. Mech. 2020, 146, 04020124. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, D.; Du, X.; Wang, G.; Meng, F. A 3D Non-Orthogonal Plastic Damage Model for Concrete. Comput. Methods Appl. Mech. Eng. 2020, 360, 112716. [Google Scholar] [CrossRef]
- Liu, D.; Tian, C.; Wang, F.; Hu, Q.; Zuo, J. Longitudinal Structural Deformation Mechanism of Shield Tunnel Linings Considering Shearing Dislocation of Circumferential Joints. Comput. Geotech. 2021, 139, 104384. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, R.; Wu, H.; Meng, F.; Yi, Y. General Solutions for the Longitudinal Deformation of Shield Tunnels with Multiple Discontinuities in Strata. Tunn. Undergr. Space Technol. 2021, 107, 103652. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Li, L.; Wang, J. Failure Mechanism of Tunnel Lining Joints and Bolts with Uneven Longitudinal Ground Settlement. Tunn. Undergr. Space Technol. 2014, 40, 300–308. [Google Scholar] [CrossRef]
- Shi, C.; Cao, C.; Lei, M.; Peng, L.; Ai, H. Effects of Lateral Unloading on the Mechanical and Deformation Performance of Shield Tunnel Segment Joints. Tunn. Undergr. Space Technol. 2016, 51, 175–188. [Google Scholar] [CrossRef]
- Chen, R.-P.; Lin, X.-T.; Kang, X.; Zhong, Z.-Q.; Liu, Y.; Zhang, P.; Wu, H.-N. Deformation and Stress Characteristics of Existing Twin Tunnels Induced by Close-Distance EPBS under-Crossing. Tunn. Undergr. Space Technol. 2018, 82, 468–481. [Google Scholar] [CrossRef]
- Chen, R.-P.; Chen, S.; Wu, H.-N.; Liu, Y.; Meng, F.-Y. Investigation on Deformation Behavior and Failure Mechanism of a Segmental Ring in Shield Tunnels Based on Elaborate Numerical Simulation. Eng. Fail. Anal. 2020, 117, 104960. [Google Scholar] [CrossRef]
- Marshall, A.M.; Klar, A.; Mair, R.J. Tunneling beneath Buried Pipes: View of Soil Strain and Its Effect on Pipeline Behavior. J. Geotech. Geoenvironmental Eng. 2010, 136, 1664–1672. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Boonyarak, T.; Masin, D. Three-Dimensional Centrifuge and Numerical Modeling of the Interaction between Perpendicularly Crossing Tunnels. Can. Geotech. J. 2013, 50, 935–946. [Google Scholar] [CrossRef]
- Li, P.; Du, S.-J.; Ma, X.-F.; Yin, Z.-Y.; Shen, S.-L. Centrifuge Investigation into the Effect of New Shield Tunnelling on an Existing Underlying Large-Diameter Tunnel. Tunn. Undergr. Space Technol. 2014, 42, 59–66. [Google Scholar] [CrossRef]
- Boonyarak, T.; Ng, C.W.W. Effects of Construction Sequence and Cover Depth on Crossing-Tunnel Interaction. Can. Geotech. J. 2015, 52, 851–867. [Google Scholar] [CrossRef]
- Liang, R.; Xia, T.; Hong, Y.; Yu, F. Effects of Above-Crossing Tunnelling on the Existing Shield Tunnels. Tunn. Undergr. Space Technol. 2016, 58, 159–176. [Google Scholar] [CrossRef]
- Liang, R.; Xia, T.; Huang, M.; Lin, C. Simplified Analytical Method for Evaluating the Effects of Adjacent Excavation on Shield Tunnel Considering the Shearing Effect. Comput. Geotech. 2017, 81, 167–187. [Google Scholar] [CrossRef]
- Liu, X.; Fang, Q.; Zhang, D. Mechanical Responses of Existing Tunnel Due to New Tunnelling below without Clearance. Tunn. Undergr. Space Technol. 2018, 80, 44–52. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Huang, Z.-K.; Li, Z.-L.; Zong, X.; Zhang, D.-M. Analytical Solution for the Response of an Existing Tunnel to a New Tunnel Excavation Underneath. Comput. Geotech. 2019, 108, 197–211. [Google Scholar] [CrossRef]
- Klar, A.; Vorster, T.E.B.; Soga, K.; Mair, R.J. Soil-Pipe Interaction Due to Tunnelling: Comparison between Winkler and Elastic Continuum Solutions. Geotechnique 2005, 55, 461–466. [Google Scholar] [CrossRef]
- Klar, A.; Vorster, T.E.B.; Soga, K.; Mair, R.J. Elastoplastic Solution for Soil-Pipe-Tunnel Interaction. J. Geotech. Geoenvironmental Eng. 2007, 133, 782–792. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Xu, C.; Jiang, Y.; Wang, W. Simplified Solution for Tunnel-Soil-Pile Interaction in Pasternak’s Foundation Model. Tunn. Undergr. Space Technol. 2018, 78, 146–158. [Google Scholar] [CrossRef]
- Gan, X.; Yu, J.; Gong, X.; Liu, N.; Zheng, D. Behaviours of Existing Shield Tunnels Due to Tunnelling underneath Considering Asymmetric Ground Settlements. Undergr. Space 2022, 7, 882–897. [Google Scholar] [CrossRef]
- Franza, A.; Viggiani, G.M.B. Role of Shear Deformability on the Response of Tunnels and Pipelines to Single and Twin Tunneling. J. Geotech. Geoenvironmental Eng. 2021, 147, 04021145. [Google Scholar] [CrossRef]
- Mair, R.; Taylor, R.; Bracegirdle, A. Subsurface Settlement Profiles Above Tunnels in Clays. Geotechnique 1993, 43, 315–320. [Google Scholar] [CrossRef]
- Lee, K.; Rowe, R.; Lo, K. Subsidence Owing to Tunneling. I. Estimating the Gap Parameter. Can. Geotech. J. 1992, 29, 929–940. [Google Scholar] [CrossRef]
- Han, X. The Analysis and Prediction of Tunnelling-Induced Building Deformations. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2008. (In Chinese). [Google Scholar]
- Lu, D.; Lin, Q.; Tian, Y.; Du, X.; Gong, Q. Formula for Predicting Ground Settlement Induced by Tunnelling Based on Gaussian Function. Tunn. Undergr. Space Technol. 2020, 103, 103443. [Google Scholar] [CrossRef]
- Lin, Q.; Song, T.; Lu, D.; Du, X. A Novel Analytical Method for Describing Ground Motion Behaviour Caused by Tunnel Excavation. Tunn. Undergr. Space Technol. 2025, 161, 106546. [Google Scholar] [CrossRef]
- Ma, S.; Shao, Y.; Liu, Y.; Jiang, J.; Fan, X. Responses of Pipeline to Side-by-Side Twin Tunnelling at Different Depths: 3D Centrifuge Tests and Numerical Modelling. Tunn. Undergr. Space Technol. 2017, 66, 157–173. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, Y.; Liu, Z.; Miao, L. Theoretical Prediction Model for Deformations Caused by Construction of New Tunnels Undercrossing Existing Tunnels Based on the Equivalent Layered Method. Comput. Geotech. 2020, 123, 103565. [Google Scholar] [CrossRef]
- Lu, D.; Meng, F.; Zhou, X.; Wang, G.; Du, X. Double Scalar Variables Plastic-Damage Model for Concrete. J. Eng. Mech. 2022, 148, 04021143. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, D.; Zhang, Y.; Du, X.; Rabczuk, T. An Open-Source Unconstrained Stress Updating Algorithm for the Modified Cam-Clay Model. Comput. Methods Appl. Mech. Eng. 2022, 390, 114356. [Google Scholar] [CrossRef]
- Kiendl, J.; Auricchio, F.; Hughes, T.J.R.; Reali, A. Single-Variable Formulations and Isogeometric Discretizations for Shear Deformable Beams. Comput. Methods Appl. Mech. Eng. 2015, 284, 988–1004. [Google Scholar] [CrossRef]
- Liang, R.; Zhang, Z.; Wu, J.; Li, Z.; Cao, S.; Wu, W. Probabilistic Assessment of Existing Shield Tunnel Longitudinal Responses to Tunnelling. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 2493–2520. [Google Scholar] [CrossRef]
- Cao, S.; Liang, R.; Kang, C.; Wu, W.; Ke, Z.; Guo, Y. Analytical Prediction for Longitudinal Deformation of Shield Tunnel Subjected to Ground Surface Surcharge Considering the Stiffness Reduction. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 925–950. [Google Scholar] [CrossRef]
- Mindlin, R.D. Force at a Point in the Interior of a Semi-Infinite Solid. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Wang, J.C. Mechanical Response and Its Control of Overlying Existing Underground Structure with Shallow Tunnel Construction. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2014. [Google Scholar]
- Lin, C.; Huang, M. Tunnelling-Induced Response of a Jointed Pipeline and Its Equivalence to a Continuous Structure. Soils Found. 2019, 59, 828–839. [Google Scholar] [CrossRef]
- O’reilly, M.P.; New, B.M. Settlements Above Tunnels in The United Kingdom—Their Magnitude and Prediction; Institution of Mining & Metallurgy: London, UK, 1982. [Google Scholar]
- Deng, H.-S.; Fu, H.-L.; Yue, S.; Huang, Z.; Zhao, Y.-Y. Ground Loss Model for Analyzing Shield Tunneling-Induced Surface Settlement along Curve Sections. Tunn. Undergr. Space Technol. 2022, 119, 104250. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, C. Subsidence in Taipei Basin Due to Shield Tunneling. In Proceedings of The Tenth Southeast Asian Geotechnical Conference, Volume 1; Asian Institute Technology: Bangkok, Thailand, 1990; pp. 501–506. [Google Scholar]
- Yi, X.; Rowe, R.; Lee, K. Observed and Calculated Pore Pressures and Deformations Induced by an Earth Balance Shield. Can. Geotech. J. 1993, 30, 476–490. [Google Scholar] [CrossRef]
- Toombs, A.F. Settlement Caused by Tunnelling Beneath a Motorway Embankment. Supplementary Report 547, Transport and Road Research Laboratory, Department of Transport, London. 1995. Available online: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=PASCALBTP8080364421 (accessed on 9 August 2025).
- Moh, Z.C.; Hwang, R.N.; Ju, D.H. Ground Movements around Tunnels in Soft Ground. In Proceedings of the Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, London, UK, 15–17 April 1996. [Google Scholar]
- Romo, M.P. Soil Movements Induced by Slurry Shield Tunneling. In Proceedings of the Fourteenth International Conference on Soil Mechanics and Foundation Engineering, Hamburg, Germany, 6–12 September 1997. [Google Scholar]
- Park, K.H. Analytical Solution for Tunnelling-Induced Ground Movement in Clays. Tunn. Undergr. Space Technol. 2005, 20, 249–261. [Google Scholar] [CrossRef]
- Chen, R.P.; Zhu, J.; Liu, W.; Tang, X.W. Ground Movement Induced by Parallel EPB Tunnels in Silty Soils. Tunn. Undergr. Space Technol. 2011, 26, 163–171. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, M.-B.; Zhang, X.; Wei, X.-J. Theoretical Analysis on the Deformation of Existing Tunnel Caused by Under-Crossing of Large-Diameter Slurry Shield Considering Construction Factors. Tunn. Undergr. Space Technol. 2023, 133, 104913. [Google Scholar] [CrossRef]
- Vesić, A.B. Bending of Beams Resting on Isotropic Elastic Solid. J. Eng. Mech. Div. 1961, 87, 35–53. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, C.; Huang, M. Soil-Pipe Interaction Due to Tunnelling: Assessment of Winkler Modulus for Underground Pipelines. Comput. Geotech. 2013, 50, 17–28. [Google Scholar] [CrossRef]
- Liang, R.; Wu, W.; Yu, F.; Jiang, G.; Liu, J. Simplified Method for Evaluating Shield Tunnel Deformation Due to Adjacent Excavation. Tunn. Undergr. Space Technol. 2018, 71, 94–105. [Google Scholar] [CrossRef]
- Wu, H.-N.; Shen, S.-L.; Liao, S.-M.; Yin, Z.-Y. Longitudinal Structural Modelling of Shield Tunnels Considering Shearing Dislocation between Segmental Rings. Tunn. Undergr. Space Technol. 2015, 50, 317–323. [Google Scholar] [CrossRef]
- Xu, L. Study on the Longitudinal Settlement of Shield Tunnel in Soft Soil. Ph.D. Thesis, Tongji University, Shanghai, China, 2005. [Google Scholar]
- Wu, H.-N.; Shen, S.-L.; Yang, J.; Zhou, A. Soil-Tunnel Interaction Modelling for Shield Tunnels Considering Shearing Dislocation in Longitudinal Joints. Tunn. Undergr. Space Technol. 2018, 78, 168–177. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the Settlement of an Existing Tunnel Induced by Shield Tunneling Underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Zhou, X.; Wang, J.; Zhong, Z.; Liu, P.; Xiong, F.; He, C. E-M Calculation Model and Its Application of Calculating Deformation in a New Tunnel Orthogonally Undercrossing an Existing Tunnel. Tunn. Undergr. Space Technol. 2022, 123, 104418. [Google Scholar] [CrossRef]

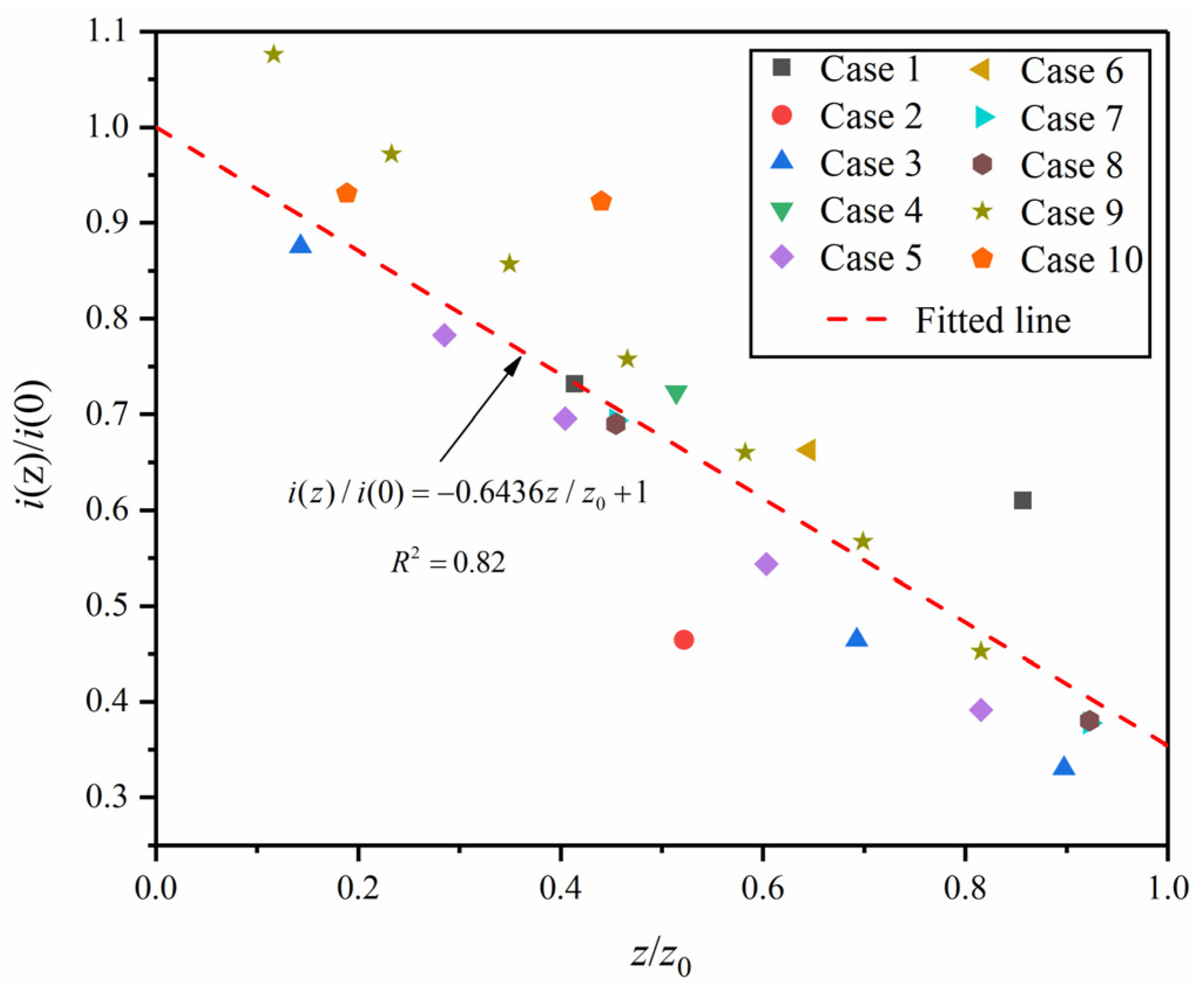
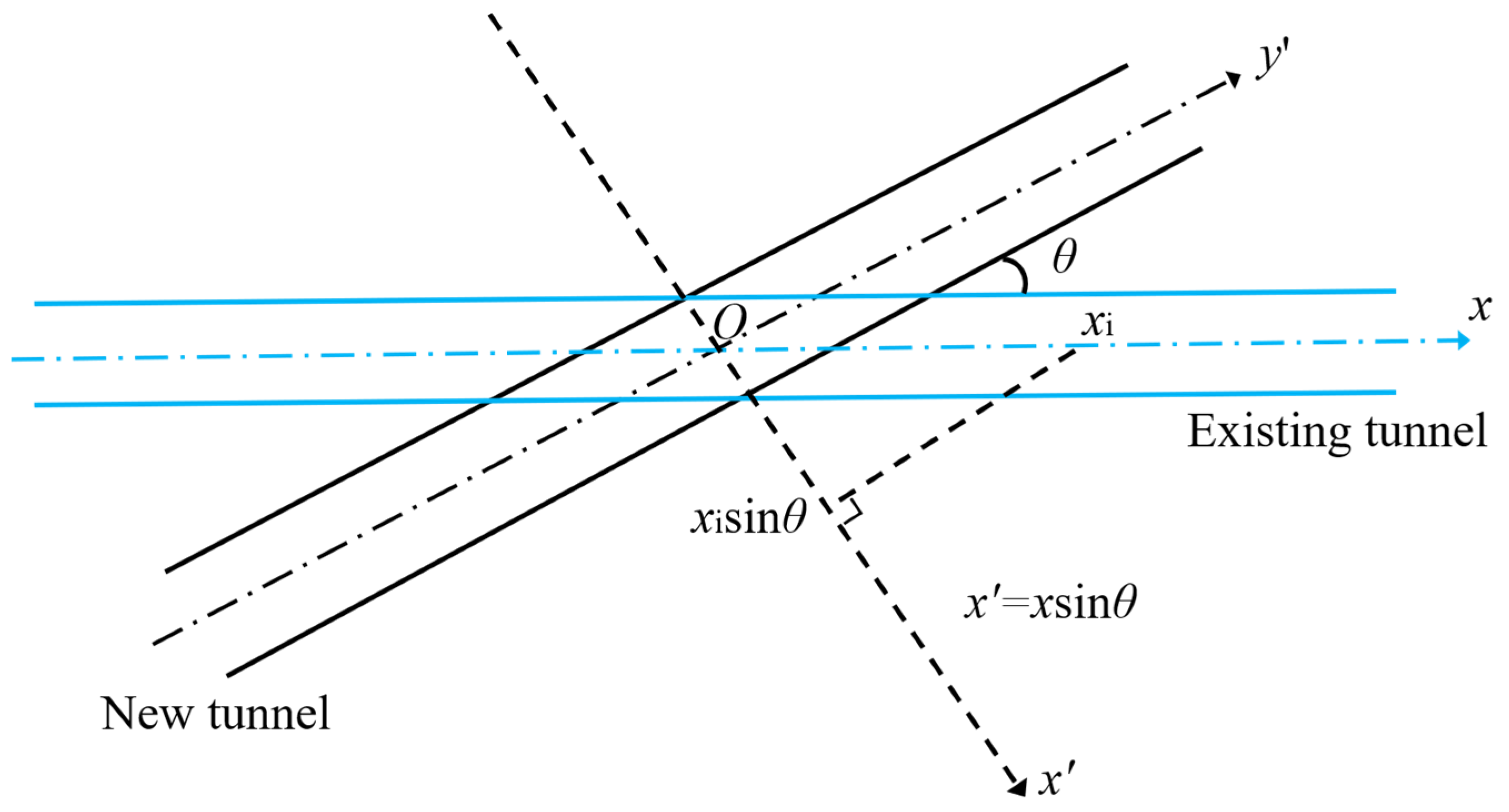

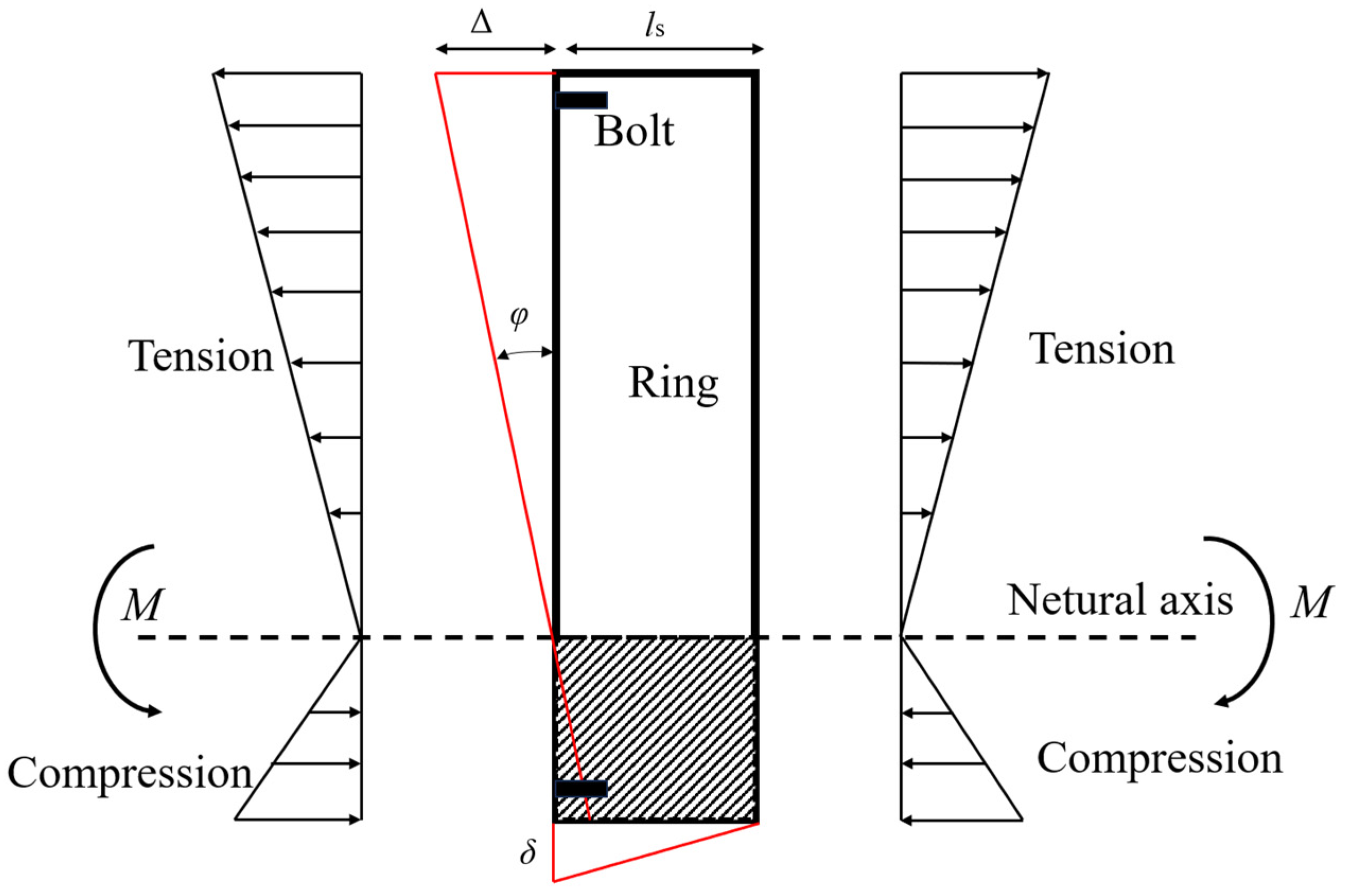
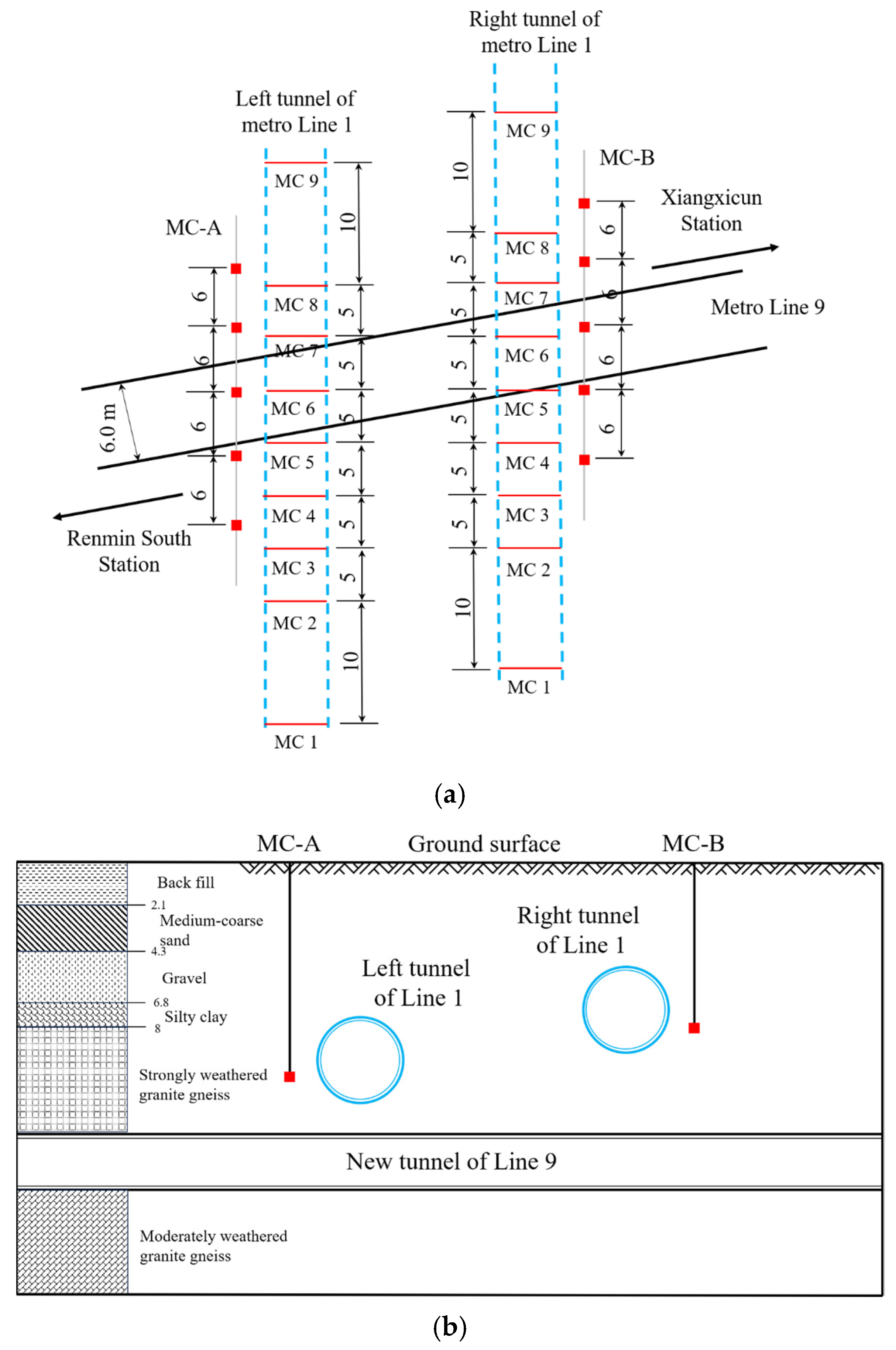


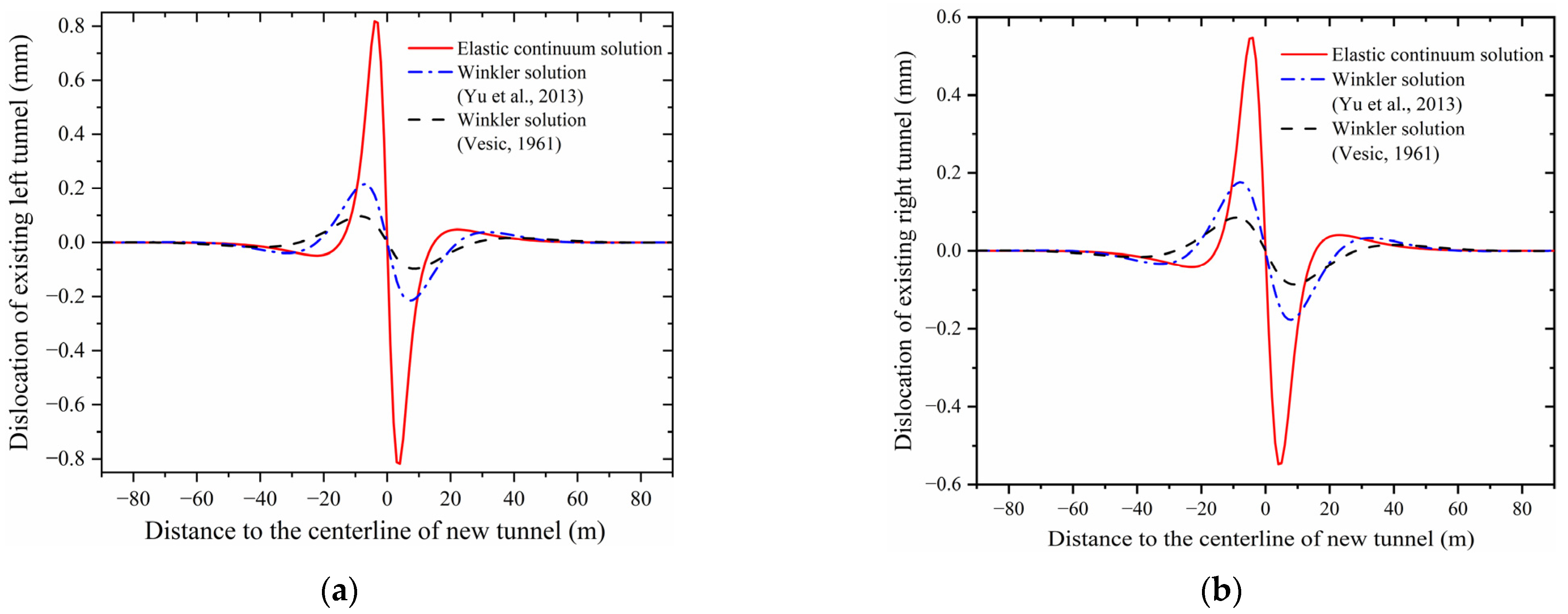
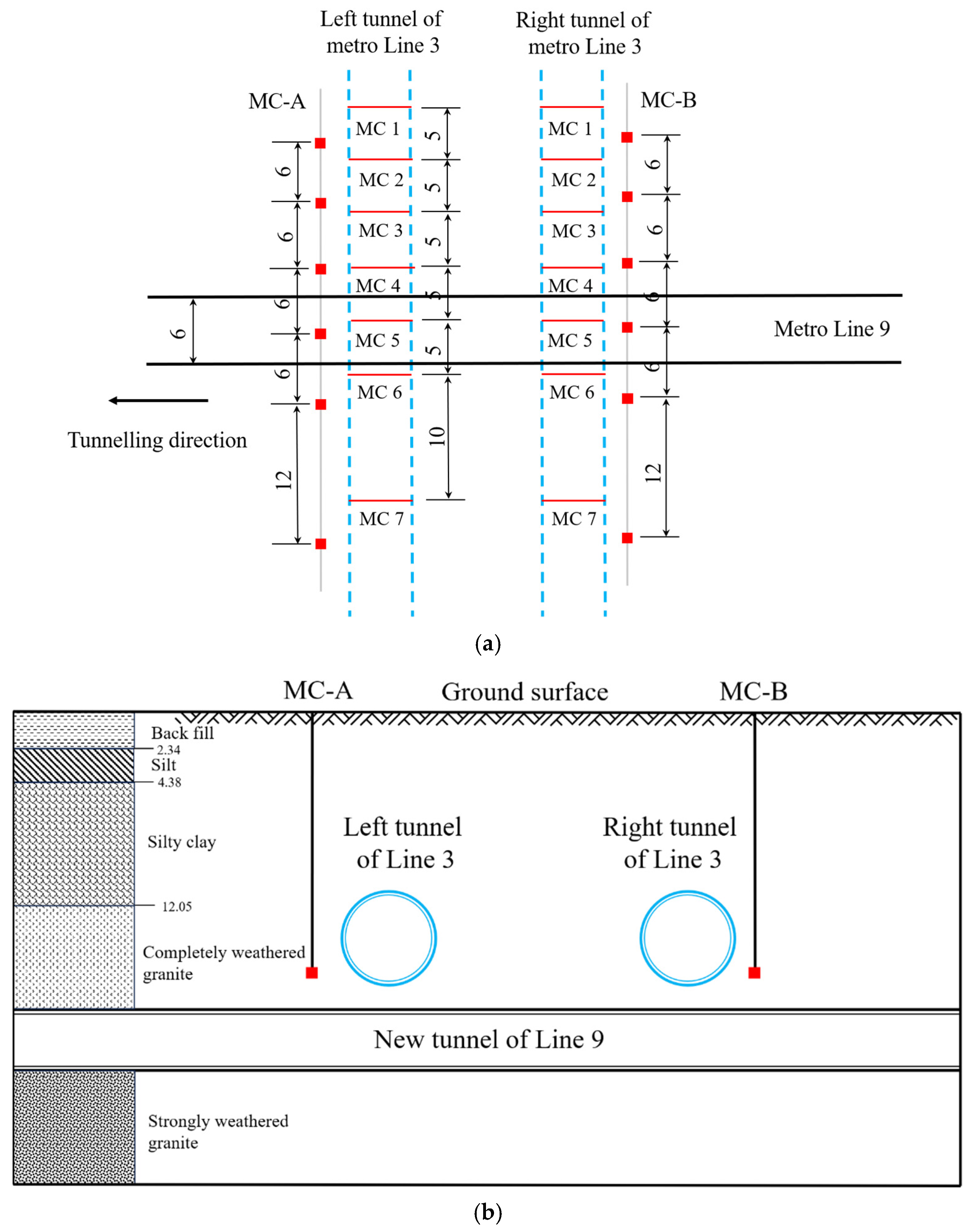

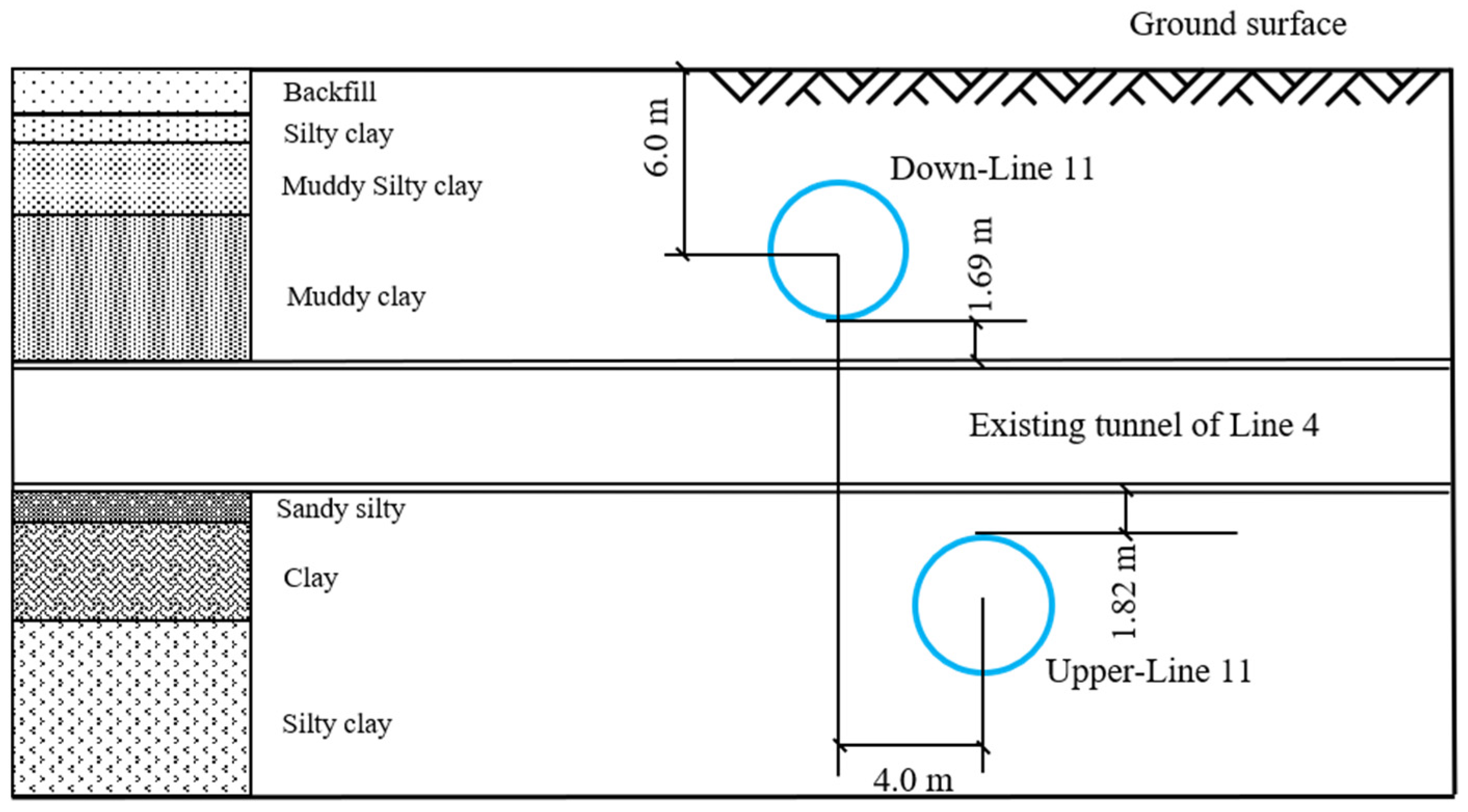
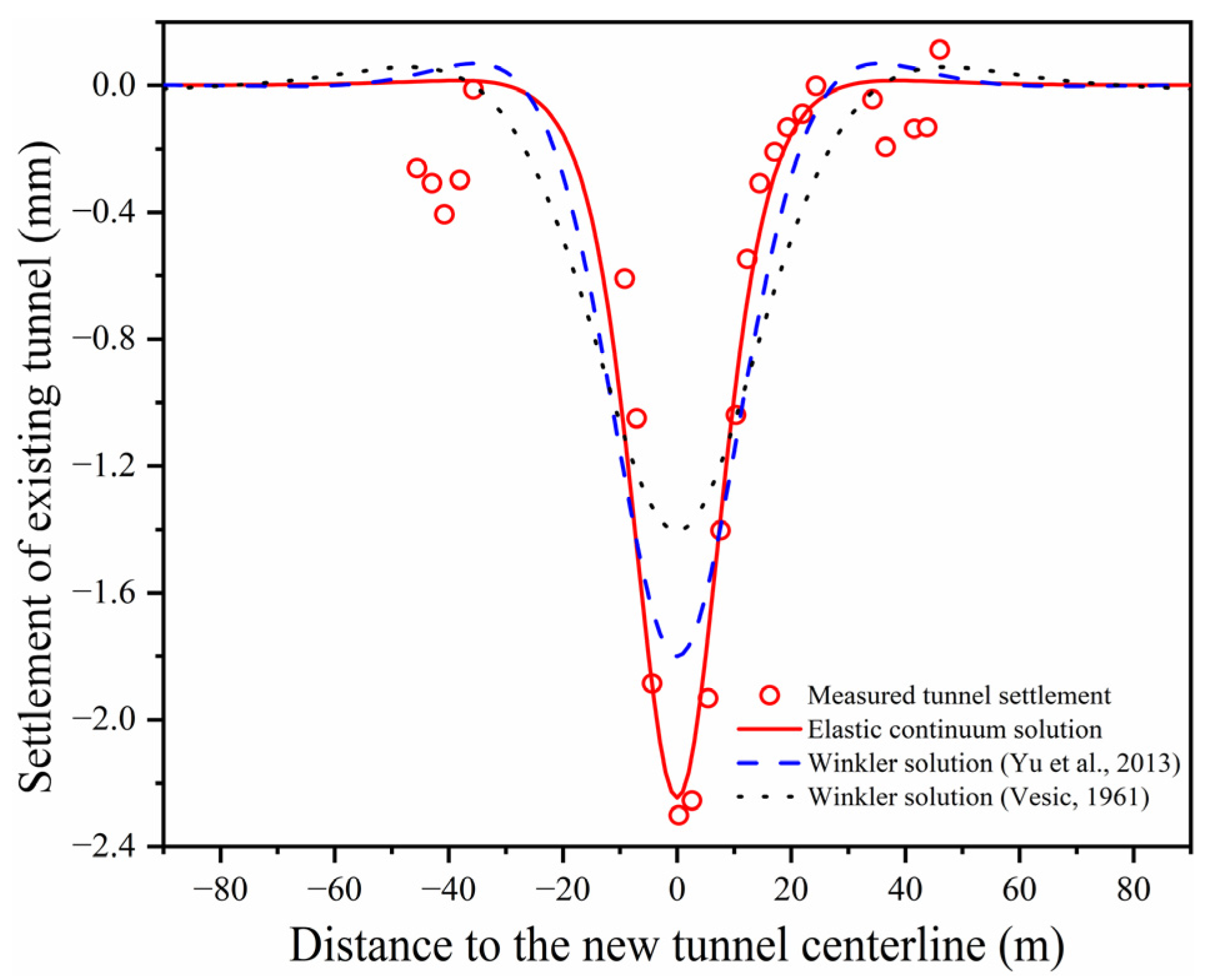
| Case No. | Ground Condition | Shield Type | Tunnel Depth h (m) | Tunnel Diameter 2R (m) | Depth z (m) | Width Parameter i(z) (m) | References |
|---|---|---|---|---|---|---|---|
| 1 | Clay | EPB shield | 9 | 4 | 0 | 4.1 | Fang and Chen [54] |
| 2.9 | 3.0 | ||||||
| 6 | 2.5 | ||||||
| 2 | Silty clay | Slurry shield | 12 | 4.83 | 0 | 9.9 | Lee et al. [38] |
| 5.0 | 4.6 | ||||||
| 11.0 | 4.3 | ||||||
| 3 | London clay | EPB shield | 41.0 | 7.8 | 0.0 | 11.2 | Mair et al. [37] |
| 5.3 | 9.8 | ||||||
| 25.7 | 5.2 | ||||||
| 33.3 | 3.7 | ||||||
| 4 | Clay | EPB shield | 5.6 | 4.2 | 0.0 | 3.18 | Yi et al. [55] |
| 0.91 | 2.5 | ||||||
| 1.8 | 2.3 | ||||||
| 2.5 | N/A | ||||||
| 5 | Clay | N/A | 16.9 | 3.63 | 0.0 | 4.6 | Toombs [56] |
| 4.3 | 3.6 | ||||||
| 6.1 | 3.2 | ||||||
| 9.1 | 2.5 | ||||||
| 12.3 | 1.8 | ||||||
| 6 | Clay | EPB shield | 18.5 | 6.0 | 0.0 | 8.9 | Moh et al. [57] |
| 10.0 | 5.9 | ||||||
| 7 | Soft clay | Slurry shield | 13.0 | 4.0 | 0.0 | 9.8 | Romo [58] |
| 5.0 | 6.8 | ||||||
| 10.15 | 3.7 | ||||||
| 8 | Soft clay | Slurry shield | 13.0 | 4.0 | 0.0 | 10 | Romo [58] |
| 5.0 | 6.9 | ||||||
| 10.15 | 3.8 | ||||||
| 9 | Soft clay | EPB shield | 18.5 | 2.66 | 0.0 | 4.62 | Park [59] |
| 2.0 | 4.97 | ||||||
| 4.0 | 4.49 | ||||||
| 6.0 | 3.96 | ||||||
| 8.0 | 3.5 | ||||||
| 10.0 | 3.05 | ||||||
| 12.0 | 2.62 | ||||||
| 14.0 | 2.09 | ||||||
| 10 | Silty clay | EPB shield | 19.0 | 6.20 | 0.0 | 10.43 | Chen et al. [60] |
| 3.0 | 9.71 | ||||||
| 7.0 | 9.62 |
| Existing Tunnel Lining Parameters | Magnitude |
|---|---|
| External diameter D (m) | 6.0 |
| Inner diameter Di (m) | 5.4 |
| Young’s modulus Ec (MPa) | 3.45 × 104 |
| Lining width ls (m) | 1.5 |
| Number of longitudinal joints nb | 10 |
| Diameter of bolts Db (mm) | 24 |
| Length of bolts lb (mm) | 400 |
| Young’s modulus of bolts Eb (MPa) | 2.06 × 105 |
| Existing Tunnel Lining Parameters | Magnitude |
|---|---|
| External diameter D (m) | 6.2 |
| Inner diameter Di (m) | 5.5 |
| Young’s modulus Ec (MPa) | 3.45 × 104 |
| Lining width ls (m) | 1.2 |
| Number of longitudinal joints nb | 17 |
| Diameter of bolts Db (mm) | 30 |
| Length of bolts lb (mm) | 400 |
| Young’s modulus of bolts Eb (MPa) | 2.06 × 105 |
| Parameters | Magnitude |
|---|---|
| Burial depth of new tunnel axis zn (m) | 20 |
| Diameter of new tunnel Dn (m) | 6 |
| Ground loss rate VL (%) | 0.3 |
| Burial depth of existing tunnel axis ze (m) | 10 |
| Outer diameter of existing tunnel D (m) | 6 |
| Inner diameter of existing tunnel Di (m) | 5.4 |
| Length of each segmental ring l (m) | 1.5 |
| Elastic modulus of soil Es (MPa) | 15 |
| Poisson’s ratio of soil υ | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Hussain, A.A.H.S.; Liu, L.; Huang, C.; Huang, D.; Liang, R.; Wu, W. Semi-Analytical Method for the Response of Existing Tunnels to Tunneling Considering the Tunnel–Soil Interaction Based on the Modified Gaussian Function. Buildings 2025, 15, 2849. https://doi.org/10.3390/buildings15162849
Zhang H, Hussain AAHS, Liu L, Huang C, Huang D, Liang R, Wu W. Semi-Analytical Method for the Response of Existing Tunnels to Tunneling Considering the Tunnel–Soil Interaction Based on the Modified Gaussian Function. Buildings. 2025; 15(16):2849. https://doi.org/10.3390/buildings15162849
Chicago/Turabian StyleZhang, Hualin, Ahmed Altaib Hussain Suliman Hussain, Lv Liu, Chaoqun Huang, Dong Huang, Rongzhu Liang, and Wenbing Wu. 2025. "Semi-Analytical Method for the Response of Existing Tunnels to Tunneling Considering the Tunnel–Soil Interaction Based on the Modified Gaussian Function" Buildings 15, no. 16: 2849. https://doi.org/10.3390/buildings15162849
APA StyleZhang, H., Hussain, A. A. H. S., Liu, L., Huang, C., Huang, D., Liang, R., & Wu, W. (2025). Semi-Analytical Method for the Response of Existing Tunnels to Tunneling Considering the Tunnel–Soil Interaction Based on the Modified Gaussian Function. Buildings, 15(16), 2849. https://doi.org/10.3390/buildings15162849









