Discrete Modeling of Aging Creep in Concrete

Abstract

Understanding concrete creep aging is essential for ensuring structural safety and long-term durability, while the lack of robust numerical models limits the ability to thoroughly investigate and accurately predict time-dependent deformation and cracking behaviors. This study proposes a numerical framework integrating a discrete model and the microprestress solidification (MPS) theory to describe the aging creep and quasi-static performance of concrete at early-age and beyond. Hydration kinetics were formulated into constitutive equations to consider the time-dependent evolution of elastic modulus, strength, and fracture properties. Derived from the MPS theory, a unified creep model is developed within the equivalent rheological framework based on strain additivity. This formulation accounts for both visco-elastic and purely viscous creep phases while coupling environmental humidity effects with aging through the hydration degree. The proposed model is validated against experimental datasets encompassing diverse curing conditions, loading histories, and environmental exposures. The simulation results demonstrate that extended curing age enhances concrete strength (compression and fracture), while increased curing temperature has minimal impact due to the competing effects of microstructural refinement and thermal microcracking; both drying-induced transient creep and thermally induced microcracking contribute to increased creep deformation, driven by changes in microprestress resulting from variations in the chemical potential of nanopore water. The proposed numerical model can provide an effective tool to design and predict the long-term performance of concrete under various environmental conditions.

1. Introduction

As one of the most widely utilized construction materials in civil engineering, concrete exhibits complex mechanical behaviors due to its heterogeneous quasi-brittle nature [1,2,3]. Time-dependent deformations, such as creep, critically influence concrete serviceability, potentially causing excessive deflections, prestress loss, and detrimental cracking [4,5,6]. While more and more constitutive models are being developed for quasi-brittle performance of concrete, it remains challenging to accurately capture time-dependent mechanical properties, failure modes, and creep deformations of concrete in a numerical model [7,8]. This is crucial in terms of structural design, project planning, and building optimization.

The early-age strength development of cement-based composites like concrete involves complex, multiscale chemo-physical mechanisms, coupling hydration, thermal effects, and deformation across nanometers to meters and seconds to years [9,10,11]. The interplay between hydration-induced aging and environmental exposure governs the time-varying behavior of concrete, transforming it from a static material into a dynamically evolving system [12,13,14]. For instance, the hydration process governs the temporal evolution of stiffness and strength of concrete [15,16,17]. While numerous models address environmental impacts on concrete deformation (e.g., drying shrinkage or thermal expansion), few incorporate their impact on hydration kinetics and subsequent effects on material strength evolution. This simplification hinders their ability to predict scenarios where coupled chemo-thermo-mechanical processes dominate [18,19], such as in early-age concrete or structures exposed to cyclic environmental loads.

Over the past century, numerous models have been developed to characterize the visco-elastic–viscoplastic behavior of concrete [20,21]. Early formulations were rooted in thermodynamic principles [22,23], while subsequent studies employed diverse approaches to unravel the mechanisms governing creep and shrinkage [24]. These include colloid-based representations of C-S-H gel at the nanoscale [25], multiscale modeling of early-age creep [26], continuum micro-visco-elasticity [27], and retardation spectra approximations [28]. Among contemporary theories, the microprestress solidification (MPS) theory [29]—an extension of the classical solidification theory [30] incorporating microprestress effects—has gained prominence. Its adaptability is evidenced by subsequent refinements, such as enhancements for cyclic thermal loading [31] and modifications for high-performance concretes containing pozzolanic materials, where creep aging is linked to a generalized chemical reaction degree encompassing both hydration and pozzolanic reactions [32]. Recent advancements and more explanations of the theory can be found in Ref. [33].

Despite significant advances in concrete creep modeling, few existing formulations successfully integrate comprehensive environmental effects. While temperature and humidity impacts on volumetric deformation are commonly accounted for, their influence on ongoing hydration processes and microstructural evolution remains largely overlooked. This limitation leads to an inadequate representation of the coupling between creep aging and material property development—particularly the time-dependent evolution of concrete strength and stiffness. Combining MPS with a discrete approach would provide a promising way to simulate concrete creep under diverse environmental conditions, as well as associated cracking behavior. To address these challenges, this study proposes a numerical framework integrating two advanced theoretical approaches. First, the Lattice Discrete Particle Model (LDPM) is employed to characterize the aging-dependent quasi-static mechanical behavior of concrete. By explicitly incorporating hydration kinetics into LDPM constitutive formulation, the time-varying evolution of elastic modulus, strength, and fracture properties is systematically captured. Second, a unified creep model is developed within the framework of strain additivity, derived from the MPS theory. This formulation accounts for both visco-elastic and purely viscous creep phases while coupling environmental humidity effects with aging through the hydration degree. The synergistic integration of these two components enables simulating time-dependent stiffness development, strength growth, and nonlinear creep behavior of concrete under variable environmental conditions. The proposed model is validated against experimental datasets encompassing diverse curing conditions, loading histories, and environmental exposures.

2. Numerical Modeling

2.1. Mechanical Model

The Lattice Discrete Particle Model (LDPM), originally proposed by Cusatis and colleagues [34,35], is a meso-scale model designed to simulate the mechanical behavior and fracture processes of quasi-brittle heterogeneous materials, such as concrete, granular rocks, and polymers.

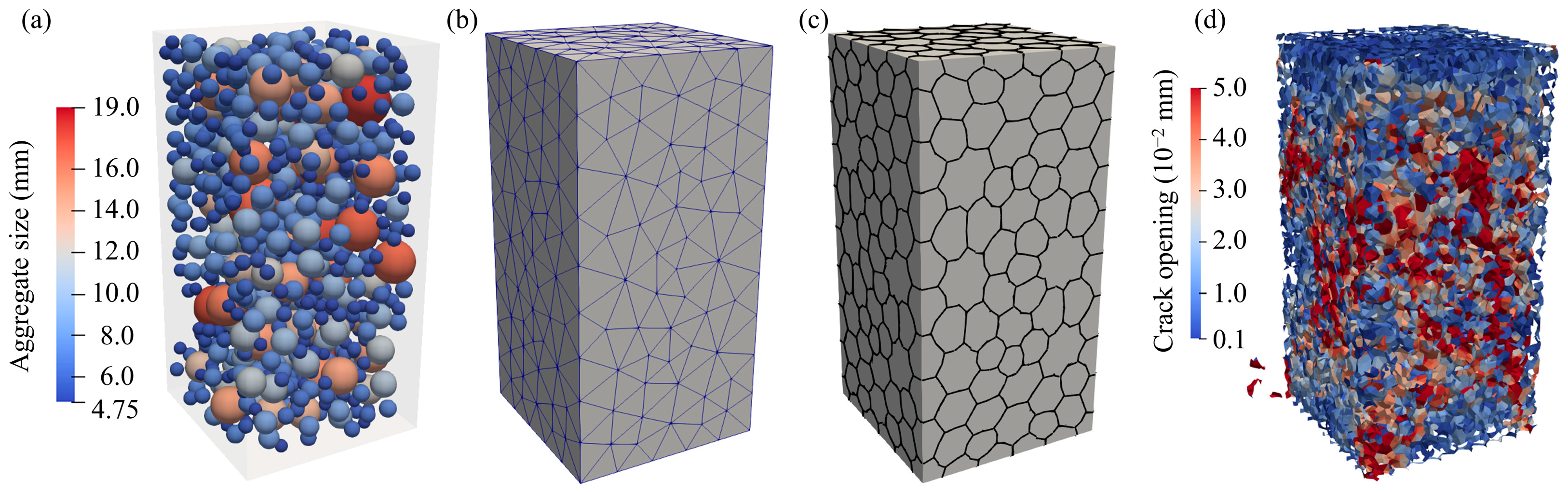
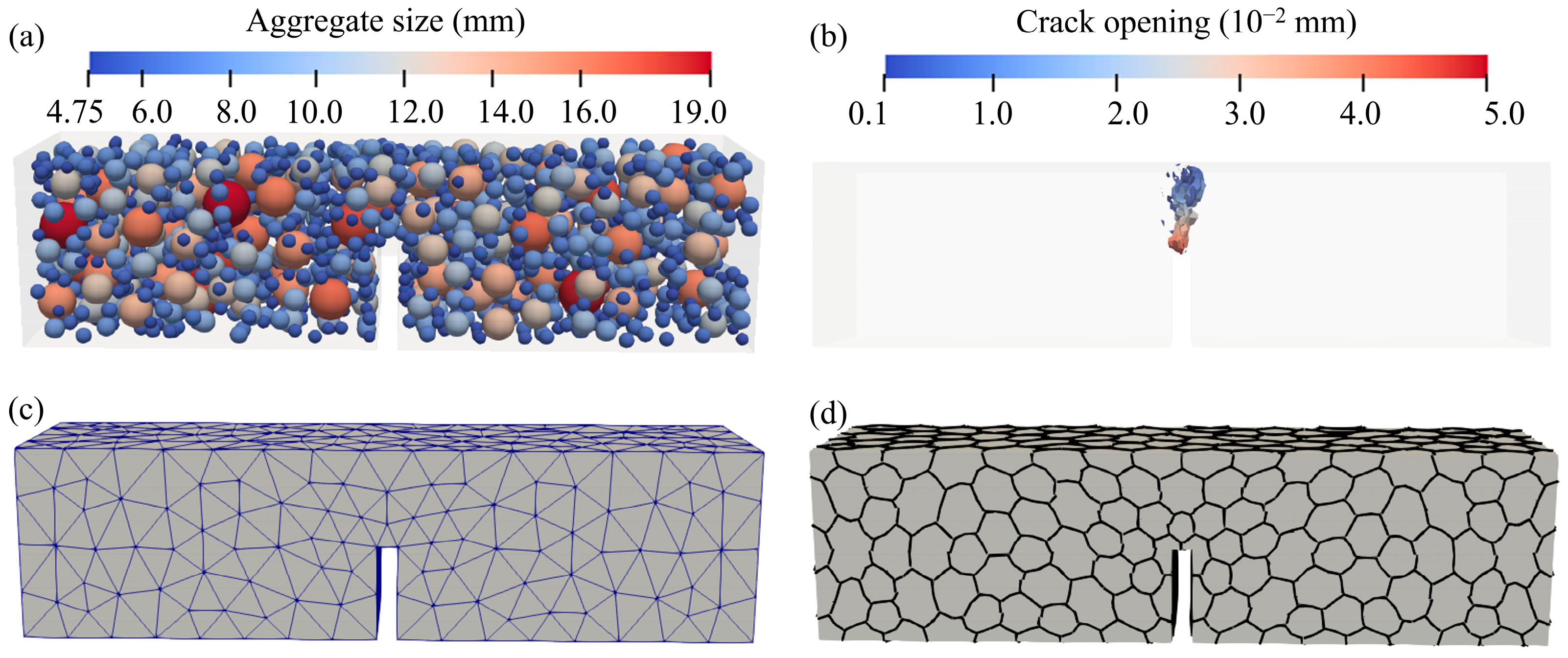
2.1.1. Mesostructure

LDPM captures the internal meso-scale structure of materials, such as coarse aggregates in concrete [36]. Its construction involves four steps: (1) Spherical aggregate particles are randomly distributed within the specimen volume. Their size distribution follows a Fuller curve [37,38] or a piecewise linear sieve curve [39,40] (see the circles in Figure 1a for a 2D representation). (2) A constrained Delaunay tetrahedralization connects the particle centers, generating a gap-free space-filling mesh (see the solid thin lines of the triangular mesh in Figure 1b for a 2D representation) [41,42]. (3) A domain tessellation subdivides the domain into polyhedral cells, each of them enclosing one spherical particle (see Figure 1h for a 2D visualization and Figure 1g for a 3D visualization). The surface of each polyhedral cell consists of triangles (see facet element E₁₂F₄T in Figure 1f), called hereinafter facet and describing potential crack locations (see Figure 1i for a 3D visualization) [43]. Each facet is defined by one on each edge of the tetrahedron (edge-point; see point E₁₂ on the edge P₁P₂ in Figure 1c), one on each face of the tetrahedron (face-point; see point F₄ on the face P₁P₂P₃ in Figure 1d), and one vertex inside the tetrahedron (tet-point; see point T in tetrahedron P₁P₂P₃P₄ in Figure 1e). (4) The interaction between cells is described through the triangular facets of the polyhedral cells and the generated lattice that connects the centers of the particles (also called nodes).

2.1.2. Constitutive Equations

In the LDPM framework, the facet strains between two adjacent cells are defined as $e={\left[\begin{array}{ccc}{e}_N& e_M& e_L\end{array}\right]}^{\mathrm{T}}$ to describe the heterogeneous deformation of the cell system (as shown in Figure 1g), where $e_N=n^{\mathrm{T}}u/l$ is the normal strain component, $e_M=m^{\mathrm{T}}u/l$ and $e_L=l^{\mathrm{T}}u/l$ are the tangential strain components, u is the displacement jump at the centroid of the facet, l is the length of tetrahedron edge associated with the facet, and n, m, and l are unit vectors normal and tangential to each facet.

Instantaneous elasticity and damage. In the elastic regime, the LDPM assumes the mechanical facet stress components are proportional to the corresponding strain components as

$$t_N=E_N{e}_N^{\ast }, t_M=E_T{e}_M^{\ast }, t_L=E_T{e}_L^{\ast },$$

(1)

where $E_N=E_0$, $E_T=\alpha E_0$, α is the shear–normal coupling parameter, and $E_0$ is the effective normal modulus.

Fracture and damage. Fracturing behavior is simulated by positive tensile normal strains $(e_N^{\ast }>0)$. The constitutive equation is formulated by using an effective strain and an effective stress, defined as

$$e={\left[e_N^{\ast 2}+\alpha \left(e_M^{\ast 2}+e_L^{\ast 2}\right)\right]}^{{\displaystyle \frac{1}{2}}},$$

(2)

$$t={\left(t_N^2+{\displaystyle \frac{t_M^2+t_L^2}{\alpha }}\right)}^{{\displaystyle \frac{1}{2}}},$$

(3)

$$t_N={\displaystyle \frac{t{e}_N^{\ast }}{e}}, t_M={\displaystyle \frac{\alpha t{e}_M^{\ast }}{e}}, t_L={\displaystyle \frac{\alpha t{e}_L^{\ast }}{e}},$$

(4)

Within a limiting strain-dependent boundary, the effective stress t is incrementally elastic as

$$\dot{t}=E_0\dot{e}, 0\le t\le {\sigma }_{bt}(e,\omega ),$$

(5)

where ω represents the ratio between normal and shear stress as

$$\omega =\arctan \left[{\displaystyle \frac{e_N^{\ast }}{{\alpha }^{1/2}{(e_M^{\ast 2}+e_L^{\ast 2})}^{1/2}}}\right]=\arctan \left({\displaystyle \frac{t_N{\alpha }^{1/2}}{t_T}}\right),$$

(6)

When the effective stress t meets Equation (5), the initial boundary ${\sigma }_{bt}(e,\omega )$ is reported as

$${\sigma }_{bt}(e,\omega )={\sigma }_0(\omega )\exp \left[-H_0(\omega ){\displaystyle \frac{〈e-e_0(\omega )〉}{{\sigma }_0(\omega )}}\right],$$

(7)

where $H_0$ is the softening modulus, governing the post peak behaviors, and is defined as

$$H_0={\displaystyle \frac{H_s}{\alpha }}+\left(H_t-{\displaystyle \frac{H_s}{\alpha }}\right){\left({\displaystyle \frac{2\omega }{\pi }}\right)}^{n_t},$$

(8)

where $n_t$ is the softening exponent; $H_t=2E_0/\left({\mathcal{l}}_t/l-1\right)$; $H_s=r_s{E}_0$; l is the length of the tetrahedron edge (P₁P₂ in Figure 1c); $r_s$ is the shear softening modulus ratio; ${\mathcal{l}}_t$ is the tensile characteristic length, defined as

$${\mathcal{l}}_t={\displaystyle \frac{2E_0{G}_t}{{\sigma }_t^2}},$$

(9)

where $G_t$ is the meso-scale fracture energy.

The effective strength is defined as

$${\sigma }_0(\omega )={\sigma }_t{\displaystyle \frac{{\left[{\sin }^2\left(\omega \right)+4\alpha {\cos }^2\left(\omega \right)/r_{st}^2\right]}^{1/2}-\sin \left(\omega \right)}{2\alpha {\cos }^2\left(\omega \right)/r_{st}^2}},$$

(10)

where $r_{st}={\sigma }_s/{\sigma }_t$, ${\sigma }_s$ is the shear strength, and ${\sigma }_t$ is the tensile strength.

Compaction and pore collapse. For $e_N^{\ast }<0$, LDPM simulates pore collapse and frictional behavior. With the following strain-dependent boundary, the strain-hardening behavior in compression is simulated as

$${\dot{t}}_N=E_N{\dot{e}}_N, -{\sigma }_{bc}(e_D^{\ast },e_V^{\ast }) \le t_N \le 0,$$

(11)

where the stress boundary of pore collapse ${\sigma }_{bc}$ is defined as

$${\sigma }_{bc}=\left\{\begin{array}{c}\begin{array}{cc}{\sigma }_{c0}+H_c〈-e_V^{\ast }-e_{c0}〉; & \hspace{1em}\hspace{1em}(-e_V^{\ast }\le e_{c1})\end{array}\\ \begin{array}{cc}{\sigma }_{c1}\exp \left[(-e_V^{\ast }-e_{c1})H_c/{\sigma }_{c1}\right];& \mathrm{otherwise}\end{array}\end{array}\right.,$$

(12)

where ${\sigma }_{c0}$ is the meso-scale yielding compressive stress, and $H_c$ is further defined as

$$H_c=H_{c1}+{\displaystyle \frac{H_{c0}-H_{c1}}{1+{\kappa }_{c2}〈r_{DV}-{\kappa }_{c1}〉}},$$

(13)

where ${\sigma }_{c1}={\sigma }_{c0}+H_c\left(e_{c1}-e_{c0}\right)$, $e_V^{\ast }=\left(V-V_0\right)/3V_0$, $e_{c0}={\sigma }_{c0}/E_0$, $e_{c1}={\kappa }_{c0}{e}_{c0}$, and

$$r_{DV}=\left\{\begin{array}{cc}{\displaystyle \frac{|e_N^{\ast }-e_V^{\ast }|}{0.1e_{c0}-e_V^{\ast }}},& e_N^{\ast }-e_V^{\ast }\le 0\\ {\displaystyle \frac{|e_N^{\ast }-e_V^{\ast }|}{0.1e_{c0}}},& e_N^{\ast }-e_V^{\ast }>0\end{array}\right.,$$

(14)

where $H_{c0}$, $H_{c1}$, ${\kappa }_{c0}$, ${\kappa }_{c1}$, and ${\kappa }_{c2}$ are material parameters.

Friction behavior. The frictional behavior is simulated by a nonlinear Mohr–Coulomb model as follows:

$${\sigma }_{bs}\left(t_N\right)={\sigma }_s+{\mu }_0{\sigma }_{N0}-{\mu }_0{\sigma }_{N0}\exp \left({\displaystyle \frac{t_N}{{\sigma }_{N0}}}\right),$$

(15)

where ${\sigma }_{N0}$ is the transitional stress governing the evolution of the friction coefficient.

2.2. Aging Law of Strength Proporties

To overcome the limitation of conventional constitutive models that cannot capture the evolution of material properties, an aging function is incorporated into the model to account for the time-dependent behavior of concrete as an aging material.

2.2.1. Hydration Evolution

The degree of cement hydration, denoted as ${\alpha }_c$, is defined as the ratio of the mass of reacted cement to its initial mass. This definition represents an average of the hydration degrees associated with each individual clinker phase. According to previous research [44,45,46], the rate of cement hydration degree can be calculated as

$${\dot{\alpha }}_c=A_{c1}(A_{c2}+{\alpha }_c)〈{\alpha }_c^{\infty }-{\alpha }_c〉\exp \left(-{\displaystyle \frac{{\eta }_c{\alpha }_c}{{\alpha }_c^{\infty }}}\right)\exp \left(-{\displaystyle \frac{E_{ac}}{RT}}\right),$$

(16)

$${\alpha }_c^{\infty }(h)={\tilde{\alpha }}_c^{\infty }\exp \left[-{\zeta }_c(1/h-1)\right],$$

(17)

where $〈x〉=\max (0,x)$; $A_{c1}$, $A_{c2}$, ${\eta }_c$, and ${\zeta }_c$ are material parameters; $E_{ac}$ is the hydration activation energy; ${\tilde{\alpha }}_c^{\infty }$ is the asymptotic hydration degree at saturation.

2.2.2. Aging Law

The evolution of concrete’s mechanical behavior due to hydration is considered in the LDPM [47,48]. This is governed by the aging degree in constitutive equations, which is defined as the ratio between the normal modulus value at any given time and its asymptotic value: $\lambda =E_0/E_0^{\infty }$. One can write [49]

$${\sigma }_t={\sigma }_t^{\infty }{\lambda }^{n_a}, {\sigma }_{c0}={\sigma }_{c0}^{\infty }{\lambda }^{n_a}, {\sigma }_{N0}={\sigma }_{N0}^{\infty }{\lambda }^{n_a}, r_{st}=r_{st}^{\infty }{\lambda }^{m_a},$$

(18)

$${\mathcal{l}}_t={\mathcal{l}}_t^{\infty }\left[{\kappa }_a\left(1-\lambda \right)+1\right],$$

(19)

where $n_a$, $m_a$, and ${\kappa }_a$ are material parameters; $E_0^{\infty }$, ${\sigma }_t^{\infty }$, ${\sigma }_{c0}^{\infty }$, ${\sigma }_{N0}^{\infty }$, $r_{st}^{\infty }$. and ${\mathcal{l}}_t^{\infty }$ are the asymptotic values of the aforementioned parameters at a certain reference temperature $T_{\mathrm{ref}}^a$ usually assumed to be room temperature (23 °C).

The aging degree is governed as a function of hydration degree and temperature as

$$\dot{\lambda }={\dot{\alpha }}_c\left[A_{\lambda 0}+A_{\lambda }\left({\alpha }_c^{\infty }+{\alpha }_0-2{\alpha }_c\right)\right]{\left({\displaystyle \frac{T_{\max }-T}{T_{\max }-T_{\mathrm{ref}}^a}}\right)}^{n_{\lambda }},$$

(20)

where $A_{\lambda }$ is a material parameter, ${\alpha }_0$ represents the critical hydration degree at which concrete starts to achieve a solid consistency: for ${\alpha }_c\le {\alpha }_0$, $\dot{\lambda }=0$; $A_{\lambda 0}={\left({\alpha }_c^{\infty }-{\alpha }_c\right)}^{-1}$, $T_{\max }$ is the maximum temperature at which concrete can harden.

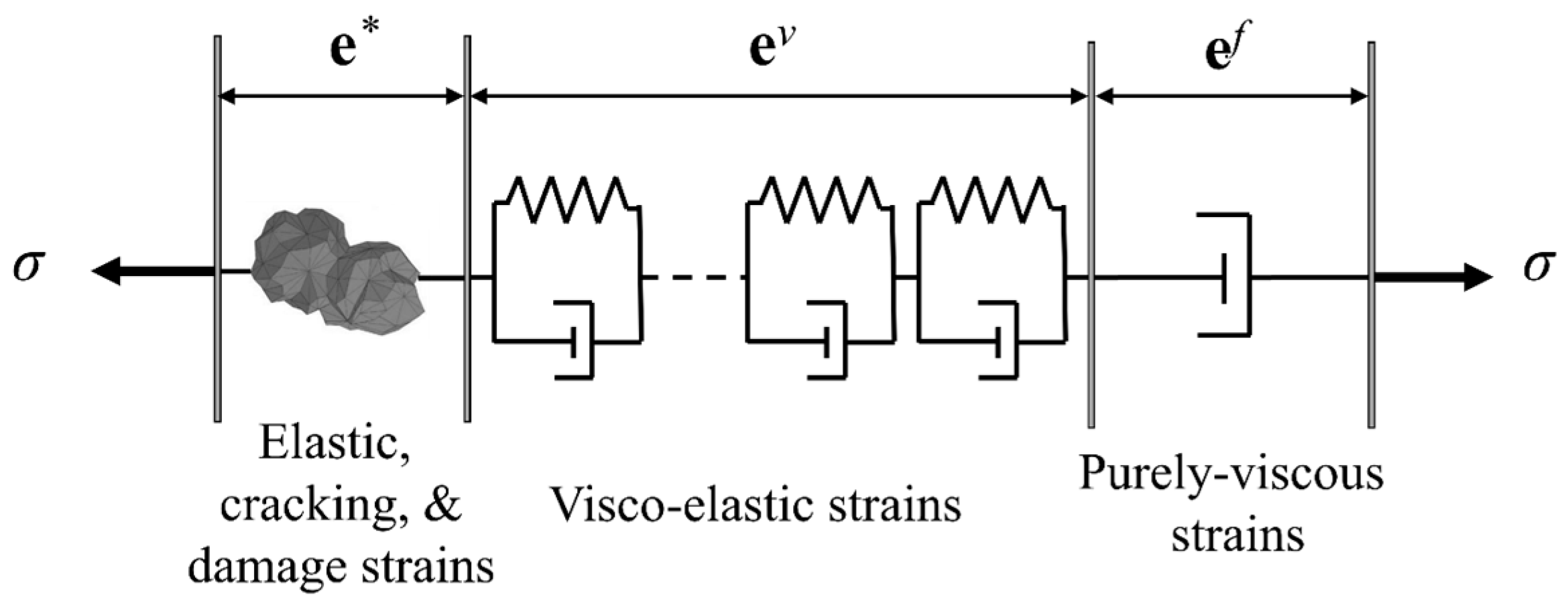
2.3. Creep Model

In the microprestress solidification (MPS) theory [50,51], creep strain consists of both visco-elastic and pure-viscous strains. The LDPM constitutive equations are based on the classical assumption of strain additivity [52], as shown in Figure 2, and it reads

$$\dot{e}={\dot{e}}^{\ast }+{\dot{e}}^v+{\dot{e}}^f,$$

(21)

where ${\dot{e}}^{\ast }$ represents the strain rate due to instantaneous elasticity and damage, which goes into constitutive equations of LDPM, as reported in Section 2.1.2; ${\dot{e}}^v$ represents the strain rate due to the visco-elastic deformation, and ${\dot{e}}^f$ represents the strain rate due to the purely viscous deformation. One can observe that creep strains ($e^v+e^f$) and other strains ($e^{\ast }$) are coupled within the same element (i.e., LDPM facet element).

2.3.1. Visco-Elastic Strains

The visco-elastic strain rate can be reported as

$${\dot{e}}^v={\displaystyle \frac{1}{v\left({\alpha }_c\right)}}\dot{\gamma }, \gamma ={\displaystyle {\int }_0^t\mathsf{\Phi }\left(t_r(t)-t_r(\tau )\right)G\dot{t}\mathrm{d}\tau },$$

(22)

where $v\left({\alpha }_c\right)={\left({\alpha }_c/{\alpha }_c^{\infty }\right)}^{n_{\alpha }}$ is associated with the volume fraction of cement gel from early-age hydration reactions; $\dot{\gamma }$ is the cement gel visco-elastic micro-strain rate; $\Phi (t-t_0)={\xi }_1\ln \left[1+{(t-t_0)}^{0.1}\right]$ is the non-aging micro-compliance function of cement gel, $t_r(t)={\displaystyle {\int }_0^t\psi (\tau )\mathrm{d}\tau }$, $\psi (t)=\left[0.1+0.9h^2\right]\exp \left[Q_v/\left(R{T}_{\mathrm{ref}}^{ve}\right)-Q_v/\left(RT\right)\right]$, and $G_{11}=1$, $G_{22}=G_{33}=1/\alpha$, $G_{ij}=0$ for $i\ne j$.

2.3.2. Purely Viscous Strains

The purely viscous strain rate can be written as

$${\dot{e}}^f={\xi }_2{\kappa }_{0}S\psi (t)Gt,$$

(23)

where S is the microprestress that can be computed by the differential equation $\dot{S}+{\psi }_s(t){\kappa }_0{S}^2={\kappa }_1\left|\dot{T}\ln \left(h\right)+T\dot{h}/h\right|$, where ${\kappa }_0$, ${\kappa }_1$, and the initial value $S_0$ at time $t=t_0$ are model parameters. In addition, ${\psi }_s(t)=\left[0.1+0.9h^2\right]\exp \left[Q_s/\left(R{T}_{\mathrm{ref}}^{pv}\right)-Q_s/\left(RT\right)\right]$.

The numerical model proposed in this study reproduces the time-dependent behavior of concrete under various environmental conditions, including aging effects, hygrothermal strains, and creep deformation. Unlike previous work [32], the MPS theory is implemented within a discrete framework, allowing for explicit crack representation. Additionally, the model incorporates hydration kinetics and the aging effect on creep, enabling it to capture the coupled interaction between hydration and creep. It should be noted that moisture transport and heat transfer are not considered; instead, the temperature and relative humidity of the concrete specimens are assumed to remain constant throughout the simulation. As a result, the predictions may deviate when applied to large-size concrete structures.

3. Results and Discussions

The experimental campaign of Bousikhane [53] investigated the effect of curing age, temperature, and relative humidity on the compression, fracture, and creep behaviors of concrete. The casting and storage of specimens were conducted as ASTM C192 [54], as shown in

Table 1. Mix design summary.

Materials	Specific Information	Quantity (kg/m3)
Portland cement	Holcim St. Genevieve Type 1	420.0
Coarse aggregate	Size range: 4.75~19.0 mm	1078.6
Fine aggregate	Size range: 0.15~4.75 mm	718.5
Water	Potable	176.2
w/c	Water/Cement	0.42 (-)
Superplasticizer	BASF Glenium 7500	3.2

.

Table 2. Size distribution of coarse aggregate in concrete.

Size (mm)	4.75	9.5	12.5	19.0
Pasing	0	33.3%	66.7%	100%

shows the size distribution of coarse aggregate in concrete. After casting, the concrete samples were demolded after 24 h and kept at 100% RH and 23 °C for 28 days. Then, concrete specimens were moved to different environmental chambers and compression, three-point bending, and creep tests were conducted at different curing ages.

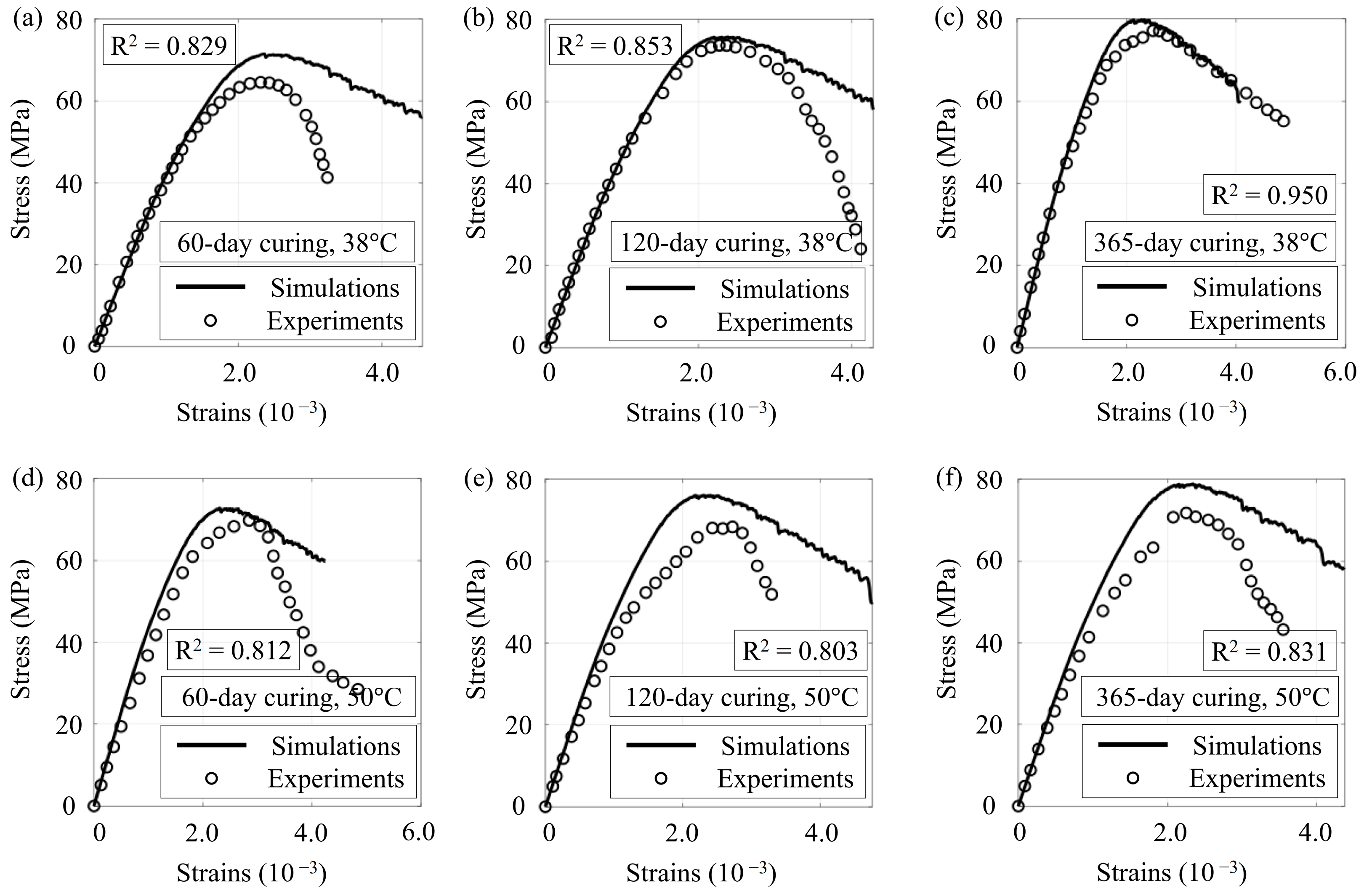
3.1. Compression Tests

After 28 days of curing at room temperature, concrete prism specimens with 75 × 75 × 150 mm were then placed in environments with a relative humidity of 100% and temperature of 38 °C and 50 °C, respectively, for continued curing. Compression tests were conducted at the ages of 60 days, 120 days, and 365 days.

Figure 3a–c shows the particle model, tetrahedron discretization, and discrete cell system for concrete specimens in compression tests, respectively. Figure 3d illustrates the crack pattern of concrete specimens under compression.

Table 3. Model parameters to simulate age-dependent mechanical behaviors of concrete.

Parameters	Values	Parameters	Values	Parameters	Values
$\alpha$	0.25	$n_t$	1.460	$E_0^{\infty }$	96,522 MPa
$H_{c0}/E_0$	0.4	$H_{c1}/E_0$	0.1	$A_{\lambda }$	0.5
${\kappa }_{c0}$	2.0	${\kappa }_{c1}$	1.0	$r_{st}^{\infty }$	3.409
${\kappa }_{c2}$	5.0	${\sigma }_{c0}$	200.0 MPa	$m_a$	0.338
${\sigma }_{N0}$	750.0 MPa	${\mu }_0$	0.2	${\kappa }_a$	0.228
${\alpha }_0$	0.165	$n_a$	0.318	${\sigma }_t^{\infty }$	8.378 MPa
${\mathcal{l}}_t^{\infty }$	76.475 mm	$A_{c1}$	7.125 × 106 1/h	$A_{c2}$	0.005
${\eta }_c$	7.171	${\zeta }_c$	0.400	$E_{ac}$	45.656 kJ/mol
${\tilde{\alpha }}_c^{\infty }$	0.876

shows the model parameters to simulate age-dependent mechanical behaviors of concrete, in which the hydration parameters were identified by using the ONIX model [44] according to the cement type.

Figure 4a–c shows the comparison between the simulation results and experimental data of the stress–strain curves of concrete specimens under axial compression at the age of 60 days, 120 days, and 365 days under 38 °C, respectively. One can observe that the model can accurately simulate the mechanical behavior of specimens under compression at different ages. Moreover, the slope of the stress–strain curve in the elastic stage increases with age, and the peak value of the curve also gradually increases with age. This indicates that the material strength of concrete under uniaxial compression increases as the age progresses. According to the simulation results, the age-dependent numerical framework can effectively capture this time-dependent compressive property of concrete.

Figure 4d–f shows the comparison between the simulation results and experimental data of the stress–strain curves of concrete specimens under axial compression at the age of 60 days, 120 days, and 365 days under 50 °C, respectively. These results demonstrate that the simulation results are in good agreement with the experimental data and that the model can capture accurately the temperature dependence of compressive strength.

3.2. Three-Point Bending Tests

After 28 days of curing, concrete prism specimens with 75 × 75 × 285 mm were then placed in environments with a relative humidity of 100% and temperature of 38 °C and 50 °C, respectively, for continued curing. Three-point bending tests were conducted at the age of 60 days, 120 days, and 365 days, respectively. Figure 5a,c,d shows the particle model, tetrahedron discretization, and discrete cell system for concrete specimens in three-point bending tests, respectively. Figure 5b illustrates the crack pattern of concrete specimens under three-point bending.

Figure 6a–c shows the comparison between the simulation results and experimental data of the Force-CMOD curves of concrete specimens under three-point bending at the age of 60 days, 120 days, and 365 days under 38 °C, respectively. One can observe that the model can accurately simulate the mechanical behavior of specimens under three-point bending at different ages. Moreover, the peak value of the Force-CMOD curve increases with age. According to the simulation results, the age-dependent numerical framework can effectively capture this time-dependent fracture property of concrete.

Figure 6d–f shows the comparison between the simulation results and experimental data of the Force-CMOD curves of concrete specimens under three-point bending at the ages of 60 days, 120 days, and 365 days under 50 °C, respectively. These results demonstrate that the simulation results are in good agreement with the experimental data and that the model can capture accurately the effect of temperature on three-point bending performance.

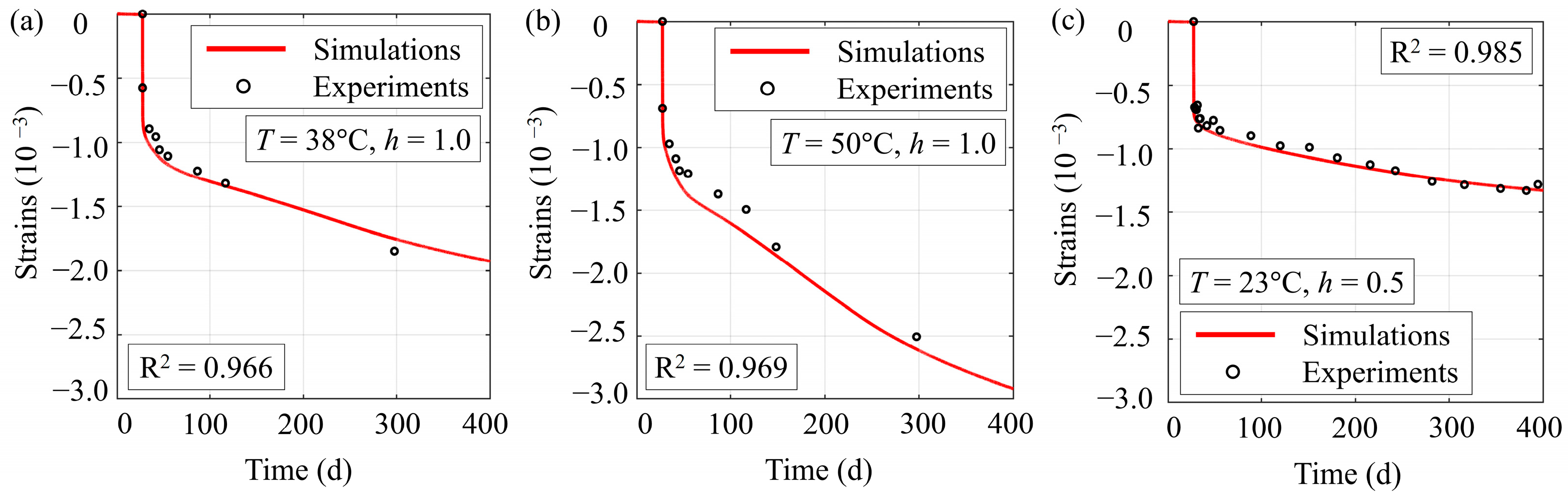
3.3. Creep Tests

After 28 days of curing, a constant axial compressive load of 23.2 MPa (0.4 f_c) was applied to both ends of concrete prism specimens with 75 × 75 × 150 mm. The creep specimens were subjected to different environmental conditions, i.e., (a) under 38 °C and 100% relative humidity, (b) under 50 °C and 100% relative humidity, and (c) under 23 °C and 50% relative humidity, respectively; the creep deformation was monitored over a period of 400 days.

Table 4. Model parameters to simulate creep behavior of concrete.

Parameters	Values	Parameters	Values
$n_{\alpha }$	2.867	${\xi }_1$	2.800 × 10−12 m2/N
${\kappa }_0$	2.315 × 10−14 m2/N/s	${\xi }_2$	2.809 × 10−13 m2/N
$Q_v$	86.158 kJ/mol	$Q_s$	33.031 kJ/mol
${\kappa }_1$	58.561 km/N/°C

shows the model parameters to simulate the creep behavior of concrete.

The creep deformation of concrete under different curing conditions is shown in Figure 7. These results demonstrate that the simulation results are in good agreement with the experimental data and that the LDPM can capture accurately the creep behavior of concrete subjected to different temperatures and relative humidity levels. By comparing Figure 7a–c, one can observe that, under a constant load, an increase in ambient temperature leads to greater creep deformation in concrete, while a decrease in ambient humidity also results in increased creep deformation.

3.4. Discussion

According to the simulation results, one can observe that the curing age plays an important role in the material strength (compression and fracture behaviors), while the curing temperature did not have a significant effect on the mechanical behavior. It might be caused by both the promotion effect on microstructure evolution [48,55] and more thermal microcracks [36,56] as the environmental temperature increases.

The effect of temperature and relative humidity on creep deformation is obvious. The relative humidity dependence can be explained by the Pickett effect, where transient creep increases due to drying [22,24]. Similarly, temperature dependence is often linked to thermally induced microcracking [51]. Both effects can be explained by the microprestress solidification theory (MPS) [29,32,50], which accounts for the buildup and relaxation of microprestress within the material. These microprestress changes are driven by variations in the chemical potential of nanopore water [51,57], highlighting the coupled influence of moisture and temperature on the visco-elastic behavior of concrete.

This study proposed a numerical model, combining MPS theory within a discrete framework, to investigate concrete creep aging behavior, and formulate the coupling effect between creep aging and material property development. The numerical model can provide an effective tool to design and predict structural safety and long-term durability under various environmental conditions.

4. Conclusions

This study presents an integrated numerical framework combining the Lattice Discrete Particle Model (LDPM) with microprestress solidification (MPS) theory to characterize both quasi-static mechanical behavior and aging creep in concrete. Compared with the experimental data, the proposal model is validated. The results suggest the following conclusions:

(1)

The numerical framework consists of the aging formulation of the LDPM to formulate the mechanical behavior, and the creep formulation based on MPS theory to formulate the time-dependent creep deformation. The elastic, cracking and damage strains, visco-elastic strains, and purely viscous strains are formulated in the constitutive equations based on the classical assumption of strain additivity.

(2)

The model provides accurate representations of the time-dependent mechanical properties of concrete under compression and three-point bending. The typical failure modes and crack pattern in compression and three-point bending tests were well reproduced.

(3)

The material strength and creep deformations of concrete increase with the increase in environmental temperature. The proposed model can simulate the temperature dependence of strength evolution and creep behavior.