Failure Mechanism of Progressive Collapse Induced by Hanger Fracture in Through Tied-Arch Bridge: A Comparative Analysis
Abstract
1. Introduction
2. The Engineering Background and Finite Element Model Validation
2.1. Bridge Design
- Nanfang’ao bridge
- 2.
- Liujiang bridge
2.2. Bridge Model Verification
- Nanfang’ao Bridge
- 2.
- Liu Jiang Bridge
3. Comparative Study on the Structural Dynamic Behavior Considering the Breakage of Hangers
3.1. Structural Design and Dynamic Characteristics of Hangers
3.1.1. The Importance Assessment of Hangers
3.1.2. Dynamic Response and Redundancy Evaluation of Remaining Hangers
3.2. Force Analysis of Remaining Structure Under Systematic Failure of Hangers
3.2.1. Arch Rib
3.2.2. Bridge Deck System
4. Comparative Analysis of Stress Mechanism and Failure Mode
4.1. Stress Mechanism
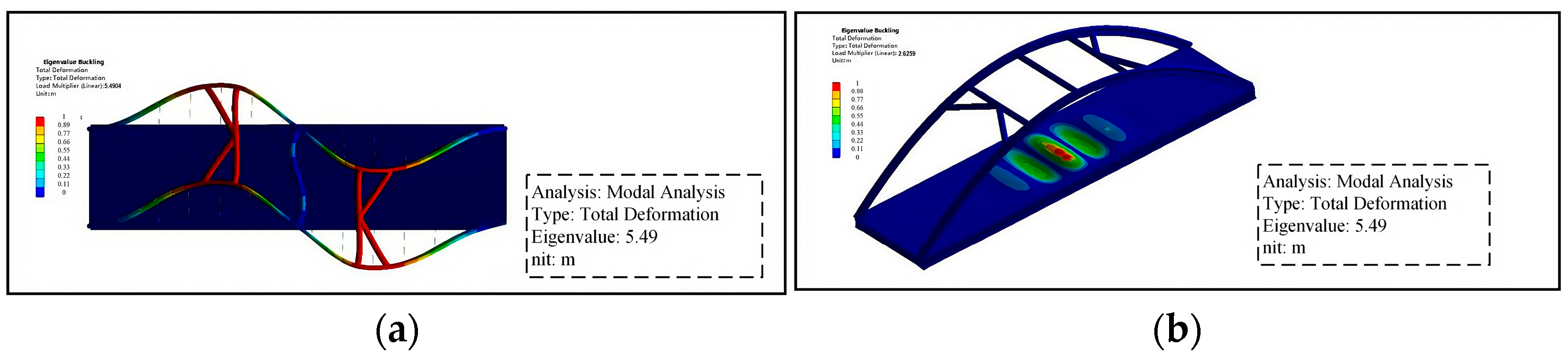
4.2. Failure Mode
5. Discussion
- Design of hangers
- 2.
- Design of arch rib
- 3.
- Design of bridge deck system
- 4.
- Design of the tie bar
6. Conclusions
- (1)
- Mechanical performance comparisons demonstrate that the non-cross diagonal hanger configuration outperforms the vertical hanger design. Specifically, under identical hanger failure paths, the Nanfang’ao Bridge with diagonal hangers remains stable after the failure of four hangers without experiencing progressive collapse, whereas the Liujiang Bridge with vertical hangers undergoes continuous failure following the rupture of only three hangers. This comparison confirms the significant advantage of diagonal hangers in enhancing resistance against progressive collapse. Therefore, in the design of long-span tied-arch bridges, the mechanical benefits of diagonal hanger layouts should be fully incorporated to achieve improved structural safety and stability.
- (2)
- Mechanism analysis of progressive collapse reveals that, when the hanger system undergoes failure, the Nanfang’ao Bridge experiences a V-shaped collapse pattern. This is attributed to insufficient flexural stiffness in both the mid-span section of the bridge deck system and the single-rib double-fork arch rib, combined with the absence of anti-drop beam measures at the bearings. These deficiencies lead to a dramatic alteration in the structural system and load transfer path, leaving no alternative load-carrying pathways to prevent collapse. In the case of the Liujiang Bridge, upon disruption of hanger force transmission, compressive stresses develop in the bridge deck system, initiating localized concrete cracking. The cracks propagate laterally toward both sides and longitudinally through the bridge deck. As a result, the reinforcing steel transitions from the elastic stage to plastic yielding, ultimately leading to crack coalescence and beam drop, exhibiting characteristics of progressive collapse. Therefore, it is critical to enhance the maintenance and inspection of hangers and associated structural components, preventing such progressive failure modes in similar bridge structures.
- (3)
- For arch-girder composite structures, the structural layout should be optimized during the design phase to mitigate stress concentrations and eliminate potential weak links. The use of double-fork arch ribs is discouraged, and critical vulnerable components such as girder supports and joints should be reinforced to enhance structural integrity. Furthermore, redundancy principles should be integrated into the design process by increasing structural redundancy, thereby ensuring that the system retains a certain load-bearing capacity even in the event of sudden component failure. This approach would effectively prevent rapid structural collapse within a short timeframe.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Lai, Z.; Yang, X.; Li, Q.; Zhang, Z. Dynamic Analyses and Simplified Methods for Evaluating Complicated Suspend-dome Structures Subjected to Sudden Cable Failure. Int. J. Steel Struct. 2023, 23, 18–36. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, K.; Ren, Y. Analying the reason and renovating project of "little south door Jinsha River bridqe of Yibin City" collapsing. Henan Urban Constr. Jr. Coll. 2002, 11, 15–17. (In Chinese) [Google Scholar] [CrossRef]
- Fan, B.; Wang, S.; Chen, B.; Chao, P.; Sun, Q. Robustness-based Condition Evaluation Framework for Through Tied-arch Bridge. Perform. Constr. Fac. 2023, 37, 06023001. [Google Scholar] [CrossRef]
- Jiang, J.; Lv, D.; Lu, X. Research progress and development trends on progressive collapse resistance of building structures. Build. Struct. 2022, 43, 1–28. (In Chinese) [Google Scholar] [CrossRef]
- Cao, A.; Esser, L.; Frangi, A. Modelling progressive collapse of timber buildings. Structure 2024, 62, 106279. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, K.; Yuan, H.; Yang, Y. The suspended bridge deck system of a through arch bridge reinforced by truss steel structure stiffened longitudinal beams. CN202120159934.5, 21 January 2021. (In Chinese). [Google Scholar]
- Lu, X.; Tian, B.; Song, L. Reinforcement, maintenance and renovation design of Nanmen Bridge over Jinsha River in Yibin City. South High. 2018, 29, 14–20. [Google Scholar]
- Zhang, W.; Wu, Y. Rehabilitation techniques for dynamically suspended main girder structure of a CFST arch bridge. Bridge Construc. 2016, 46, 103–108. (In Chinese) [Google Scholar]
- Fan, B.; Sun, Q. Robustness Design of Multi-span Through tied-arch bridge considering systematic failure of hangers. J. Traffic Transp. Eng. 2025, 25, 204–217. (In Chinese) [Google Scholar]
- Derseh, S.; Mohammed, T. Bridge Structures Under Progressive Collapse: A Comprehensive State-of-the Art-review. Res. Eng. 2023, 18, 101090. [Google Scholar] [CrossRef]
- Ran, C.; Sherif, E.; Anil, K. Miami Pedestrian Bridge Collapse: Computational Forensic Analysis. Bridge Eng. 2020, 25, 04019134. [Google Scholar] [CrossRef]
- Nicola, S.; Roberto, S.; Matteo, M. Collapse Analysis of The Multi-span Reinforced Concrete Arch Bridge of Caprigliola, Italy. Eng. Struct. 2022, 251 Pt A, 113375. [Google Scholar] [CrossRef]
- Domaneschi, M.; Pellecchia, C.; De Iuliis, E. Collapse analysis of the Polcevera viaduct by the applied element method. Eng. Struct. 2020, 214, 110659. [Google Scholar] [CrossRef]
- Salem, H.; Helmy, H. Numerical investigation of collapse of the Minnesot a I-35W bridge. Eng. Struct. 2014, 59, 635–645. [Google Scholar] [CrossRef]
- Whelan, M.J.; Janoyan, K.D. In-Service Diagnostics of a Highway Bridge from a Progressive Damage Case Study. J. Bridge Eng. 2010, 15, 597–607. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.W.; Mousavi, A.A. Nonlinear numerical analysis and progressive damage assessment of a cable-stayed bridge pier subjected to ship collision. Mar. Struct. 2020, 69, 102662. [Google Scholar] [CrossRef]
- Xi’an Changda Highway Detection Center. Zhengzhou Liujiang Yellow River Highway Bridge (BG–2015–Q2–TS 0507); Xi’an Changda Highway Detection Center: Xi’an, China, 2015. [Google Scholar]
- Zheng, X.; Zhang, G.; Huang, L.; Tang, C.; Xiong, X.; Ding, Y. Research on the Progressive Failure collapse Dynamic Behavior of Steel Truss concrete Composite Bridge. China J. Highw. Transp. 2022, 35, 147–159. [Google Scholar] [CrossRef]
- Huang, S.; Lu, X.; Zheng, J.; Zhu, W. Overload-induced progressive collapse simulation for a reinforced concrete arch bridge. Eng. Mech. 2012, 29, 122–127. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, D.; Qi, L.; Chen, X.; Zhao, Y. Complex Network Invulnerability and Node Importance Evaluation Model Based on Redundancy. Compl. Syst. Complex. Sci. 2020, 17, 78–85. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Q.; Agrawal, A.K.; El-Tawil, S.; Bhattacharya, B.; Wong, W. Dynamic Response and Progressive Collapse of a Long-Span Suspension Bridge Induced by Suspender Loss. J. Struct. Eng. 2022, 148, 05022001. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, J.; He, H.; Wang, X. Simulation Calculation of Strip Descaling Based on Birth-Death Element Method. J. Phys. Conf. Ser. 2022, 2174, 012080. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Z. An approach for evaluation of the structural robustness of steel frames. Chin. Civ. Eng. J. 2012, 29, 122–127+138. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Z.; Lv, Z. Compara tive study on the tied-arch bridges with vertical and inclined hangers. Chin. Civ. Eng. J. 2000, 33, 63–68. (In Chinese) [Google Scholar] [CrossRef]
- Wu, Q.X.; Yu, Y.G.; Chen, B.C. Dynamic Analysis for Cable Loss of a Rigid-frame Tied Through Concrete-filled Steel Tubular Arch Bridge. Vib. Shock. 2014, 33, 144–149. (In Chinese) [Google Scholar] [CrossRef]
- GB 50923-2013; Technical Code for Concrete-Filled Steel Tube Arch Bridges. MOHURD: Beijing, China, 2013. (In Chinese)








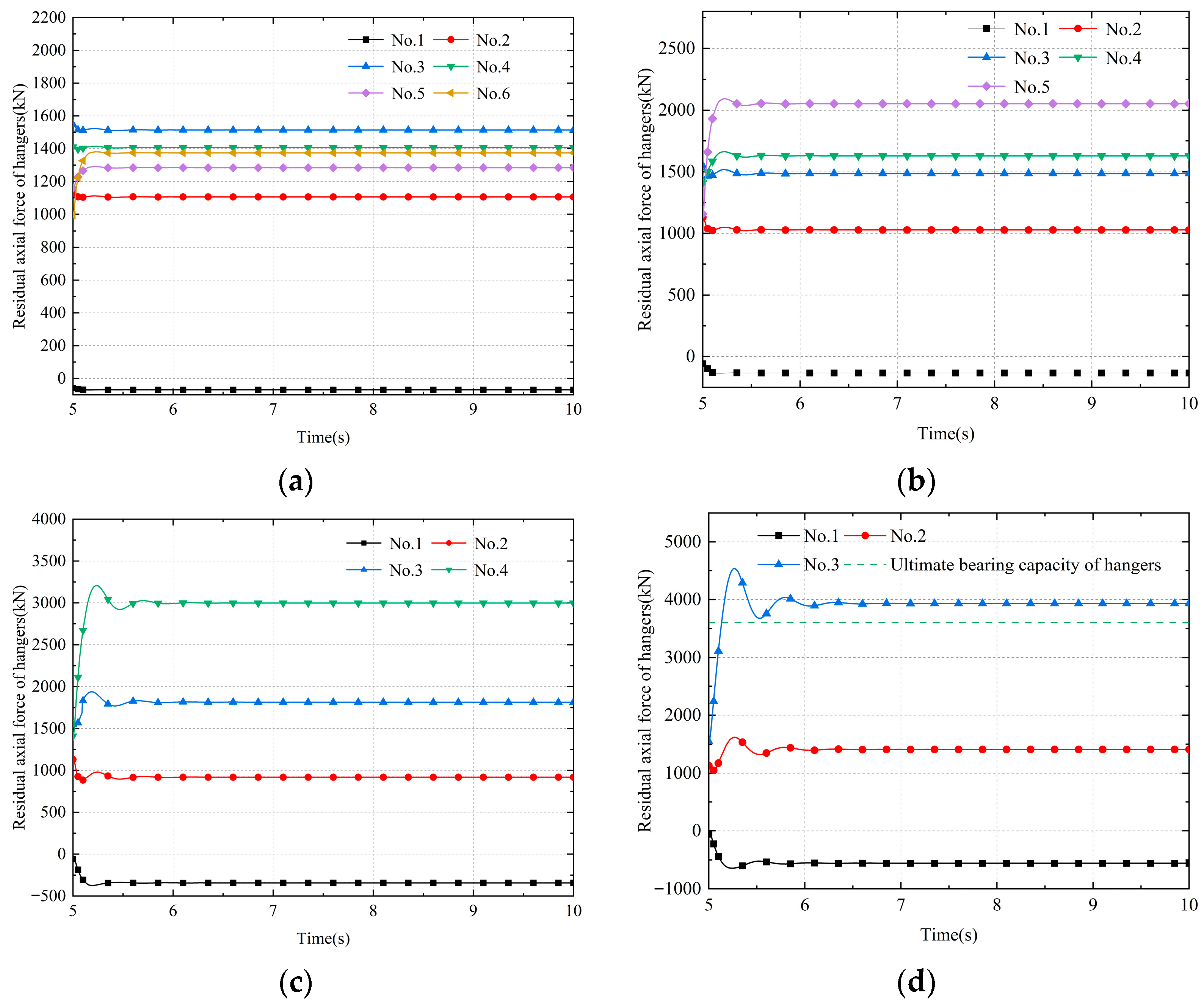











| Hanger Number | Yield Load | Ultimate Tensile | Ultimate Tensile Load of Anchorage System | Hanger Tension (Measured Value/Finite Element Value) | ||
|---|---|---|---|---|---|---|
| Breakage of No. 6 and No. 7 Hangers | Breakage of No. 4 and No. 5 Hangers | Breakage of No. 3 Hanger | ||||
| 1 | 3748.40 | 4243.60 | 3872.37 | 353.39/356.92 | 0/0 | 844.27/852.71 |
| 2 | 2866.50 | 3245.17 | 2853.27 | 452.07/456.59 | 180.61/182.42 | 2676.77/2703.54 |
| 3 | 2866.50 | 3245.17 | 2853.27 | 678.45/685.24 | 1114.36/1125.50 | 6285.13/6347.98 |
| 4 | 2866.50 | 3245.17 | 2853.27 | 1117.40/1128.56 | 2873.56/2902.29 | / |
| 5 | 2548.00 | 2884.53 | 2853.27 | 1801.04/1819.05 | 5063.17/5113.80 | / |
| 6 | 2866.50 | 3245.17 | 2853.27 | 3651.38/3687.90 | / | / |
| 7 | 980.00 | 1109.46 | 2853.27 | 2073.97/2094.71 | / | / |
| Name | Number of Broken Hangers | Breaking the Sequence of Hangers | Extreme Values of the Dynamic Response of Adjacent Hangers | Redundancy of Adjacent Hangers |
|---|---|---|---|---|
| Liujiang bridge | 3 | D6 and d6 were broken | D5, d5: 2697.8 kN | 0.556 |
| D5 and d5 were broken | D4, d4: 4474 kN | 0.923 | ||
| D4 and d4 were broken | D3, d3: 5891.5 kN | 1.215 | ||
| Nanfang’ao bridge | 4 | No. 7 was broken | No. 6: 1376.9 kN | 0.382 |
| No. 6 was broken | No. 5: 2089.2 kN | 0.579 | ||
| No. 5 was broken | No. 4: 3202.7 kN | 0.888 | ||
| No. 4 was broken | No. 3: 4523.5 kN | 1.255 |
| Name | Axial Force | Displacement | Bending Moment | Stability | |||
|---|---|---|---|---|---|---|---|
| Location | Maximum | Location | Maximum | Location | Maximum | ||
| Nanfang’ao bridge | The connection point between the arch ring and the arch column | −112.32 kN | The connection point between the arch ring and the arch column | 0.02 m | Arch springing | 6425.9 kN·m | Instability |
| Liujiang bridge | Cross brace | 10.99 kN | Cross brace | 0.02 m | Cross brace | 931.28 kN·m | Stability |
| Name | Axial Force | Displacement | Bending Moment | |||
|---|---|---|---|---|---|---|
| Location | Maximum | Location | Maximum | Location | Maximum | |
| Nanfang’ao bridge | At both ends of the bridge deck | 149.19 kN | At the 1/2 mark | 0.47 m | No. 3 hanger | 2.08 × 105 kN·m |
| Liujiang bridge | At the 1/2 mark | 26,533 kN | At the 1/2 mark | 0.37 m | Arch springing | 275,490 kN·m |
| Material | Material Model | Parameters | Value |
|---|---|---|---|
| Prestressed steel bar | MAT 098 | Density/(kg·m−3) | 7.8 × 103 |
| Elastic modulus/Mpa | 2.06 × 105 | ||
| Poisson’s ratio | 0.3 | ||
| Failure stress/Mpa | 420 | ||
| Bulk modulus/Mpa | 1.67 × 105 | ||
| Failure strain | 0.002 | ||
| Concrete | Density/(kg·m−3) | 2.6 × 103 | |
| Elastic modulus/Mpa | 3.55 × 105 | ||
| Poisson’s ratio | 0.1667 | ||
| Failure stress/Mpa | 420 | ||
| Bulk modulus/Mpa | 1.67 × 105 | ||
| Failure strain | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, B.-H.; Sun, Q.; Chen, Q.; Zhou, B.-B.; Wu, Z.-J.; Zou, J.-Q. Failure Mechanism of Progressive Collapse Induced by Hanger Fracture in Through Tied-Arch Bridge: A Comparative Analysis. Buildings 2025, 15, 2810. https://doi.org/10.3390/buildings15162810
Fan B-H, Sun Q, Chen Q, Zhou B-B, Wu Z-J, Zou J-Q. Failure Mechanism of Progressive Collapse Induced by Hanger Fracture in Through Tied-Arch Bridge: A Comparative Analysis. Buildings. 2025; 15(16):2810. https://doi.org/10.3390/buildings15162810
Chicago/Turabian StyleFan, Bing-Hui, Qi Sun, Qiang Chen, Bin-Bin Zhou, Zhi-Jiang Wu, and Jin-Qi Zou. 2025. "Failure Mechanism of Progressive Collapse Induced by Hanger Fracture in Through Tied-Arch Bridge: A Comparative Analysis" Buildings 15, no. 16: 2810. https://doi.org/10.3390/buildings15162810
APA StyleFan, B.-H., Sun, Q., Chen, Q., Zhou, B.-B., Wu, Z.-J., & Zou, J.-Q. (2025). Failure Mechanism of Progressive Collapse Induced by Hanger Fracture in Through Tied-Arch Bridge: A Comparative Analysis. Buildings, 15(16), 2810. https://doi.org/10.3390/buildings15162810







