Rapid Identification Method for Concrete Defect Boundaries Based on Acoustic-Mode Gradient Analysis
Abstract
1. Introduction
2. Theoretical Analysis and Algorithm Principles
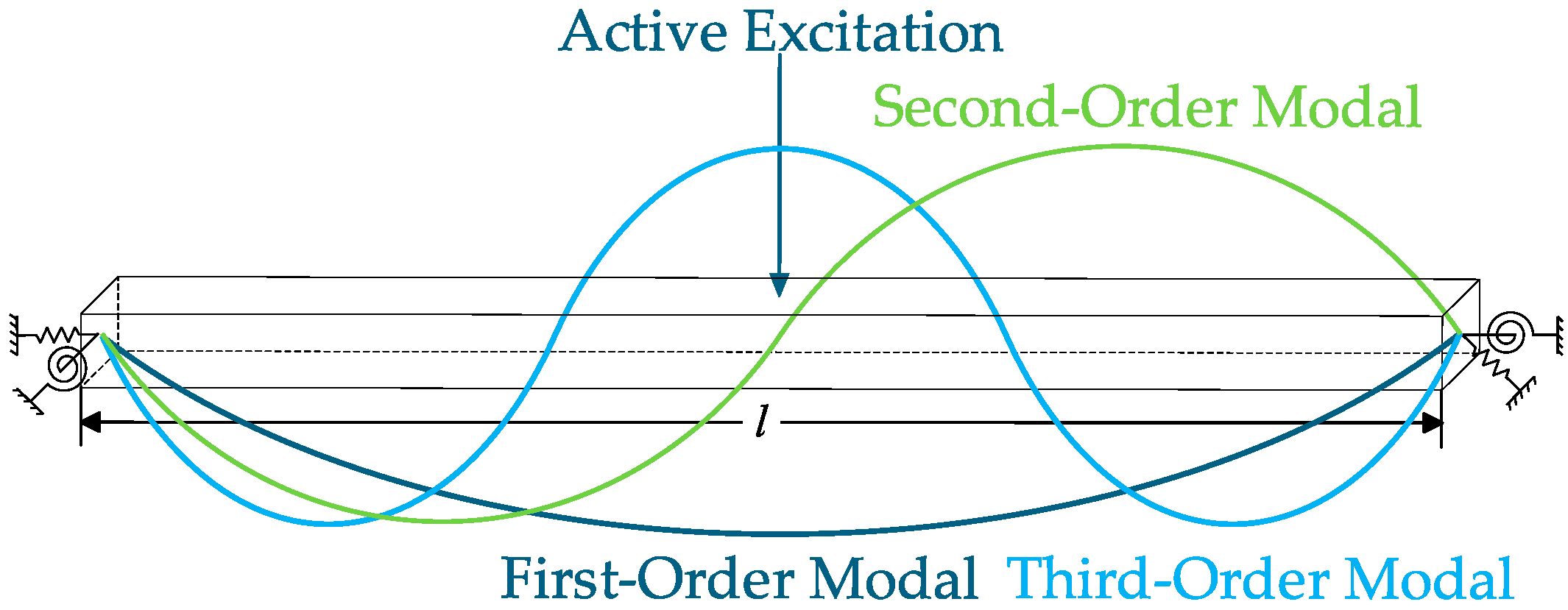
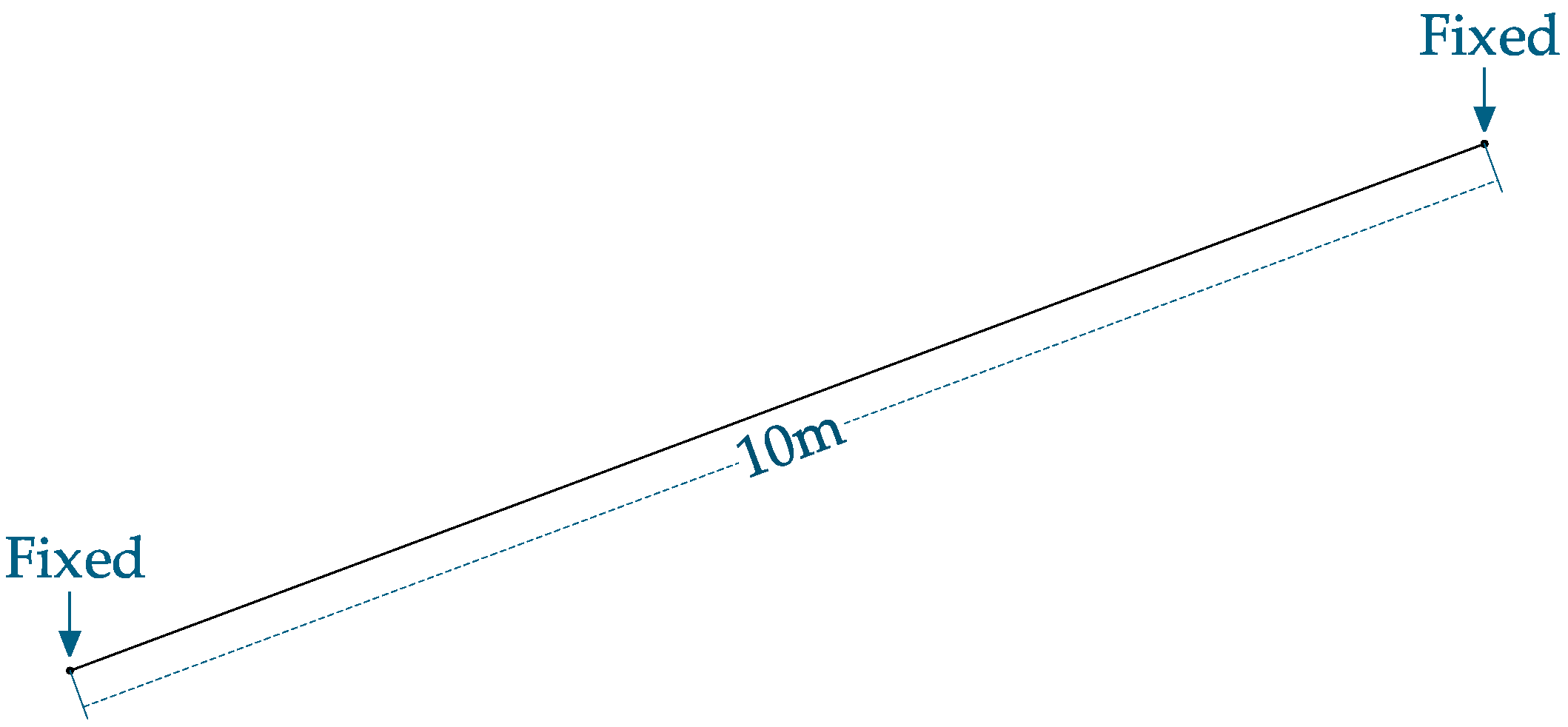
2.1. Forced Vibration of Beams
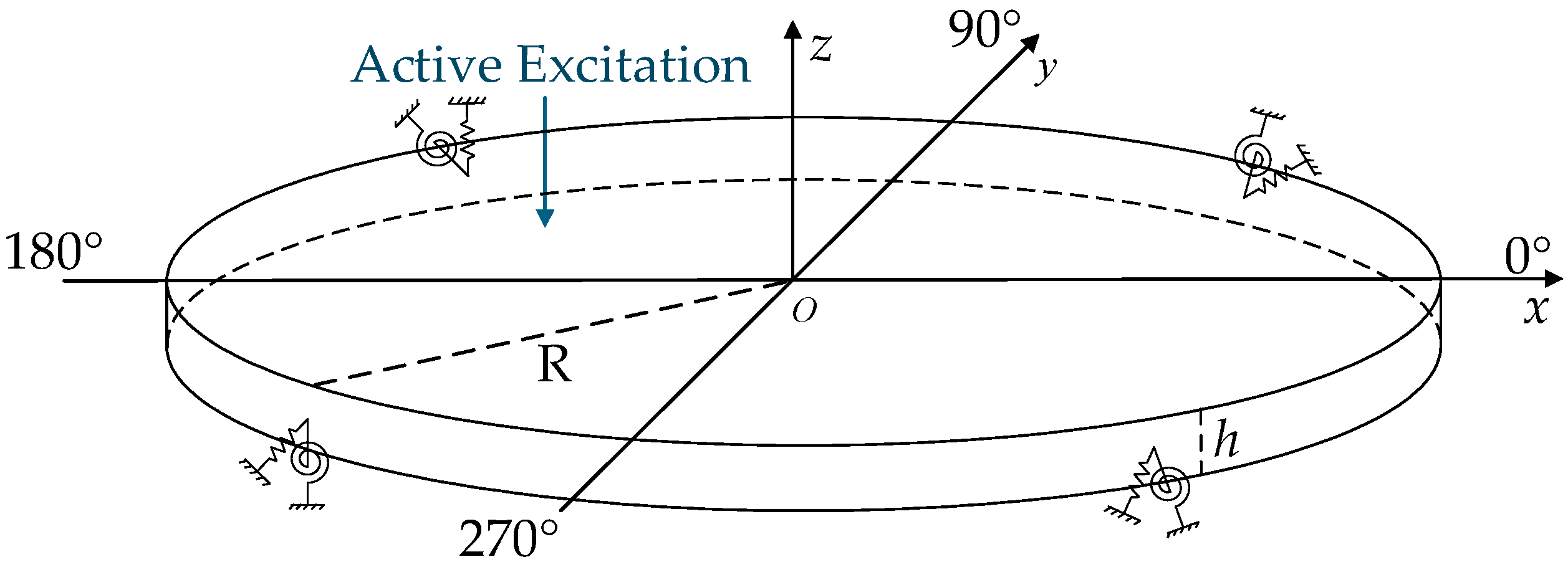
2.2. Natural Vibration of Circular Thin Plates
2.3. Theoretical Analysis
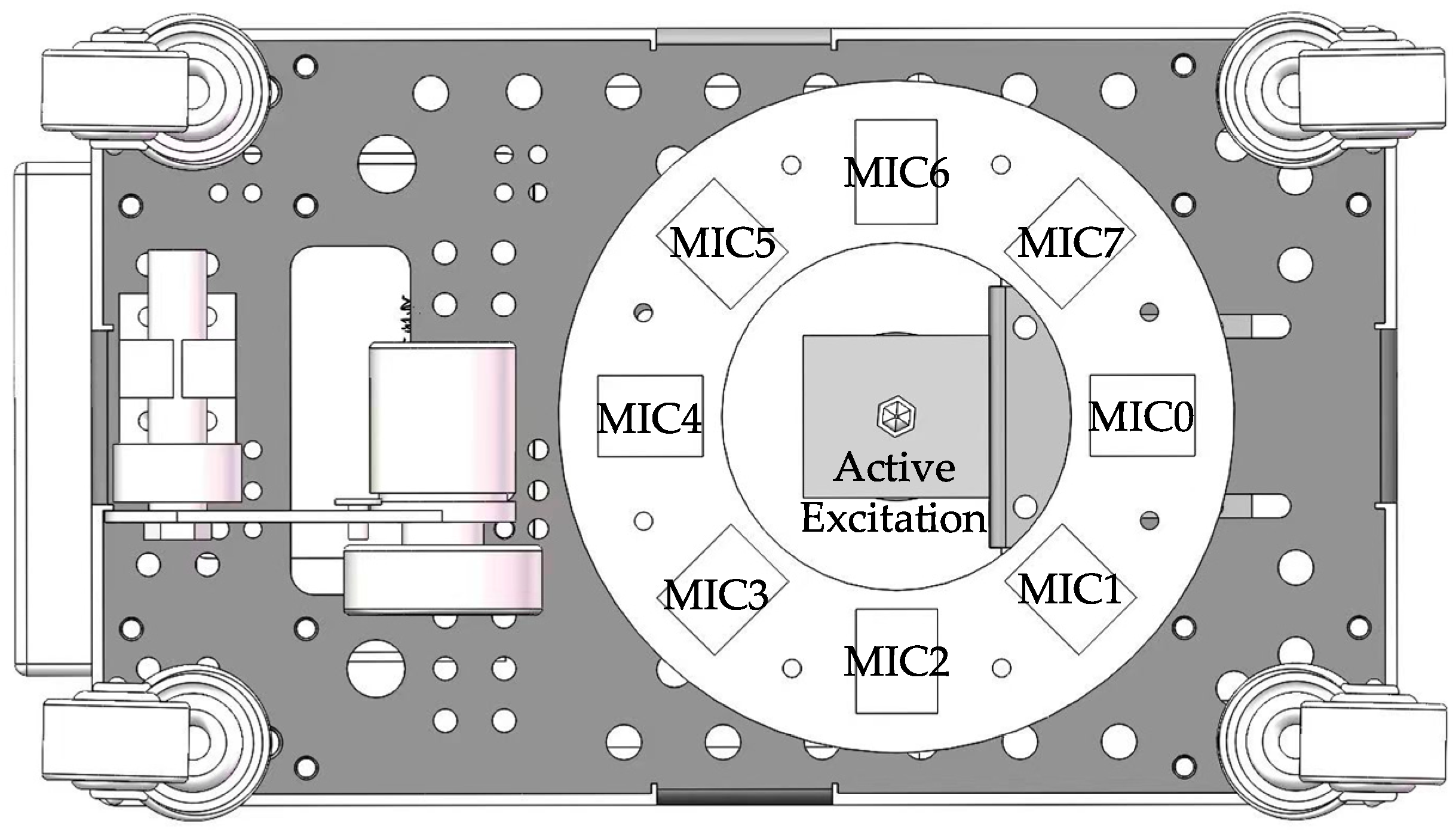
2.3.1. Comparison of Array Technology and Single-Point Technology
2.3.2. Acoustic Component Analysis
2.3.3. Determining the Center Direction Using Gradient
2.4. Acoustic Signal Processing
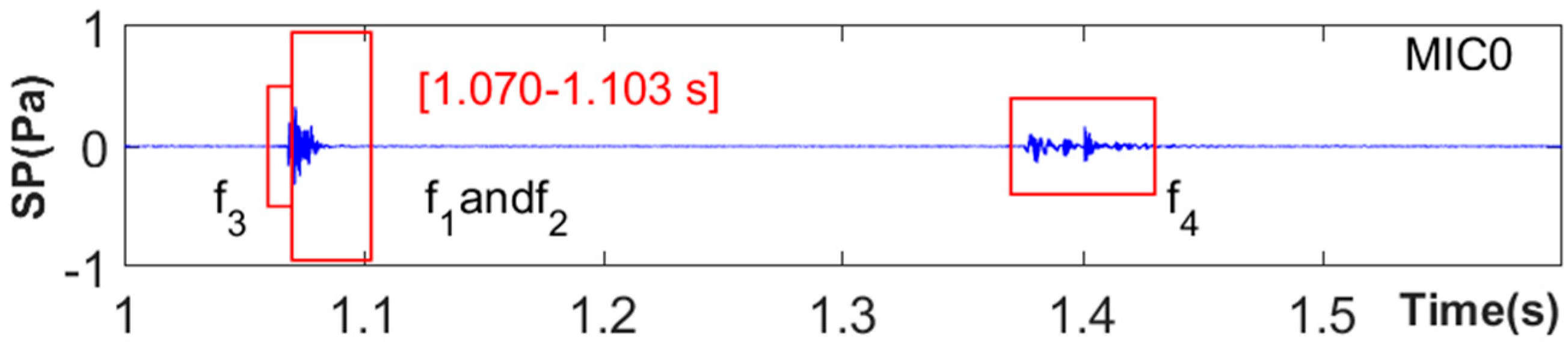
2.4.1. Synchronous Interception of Multi-Channel Acoustic Signals
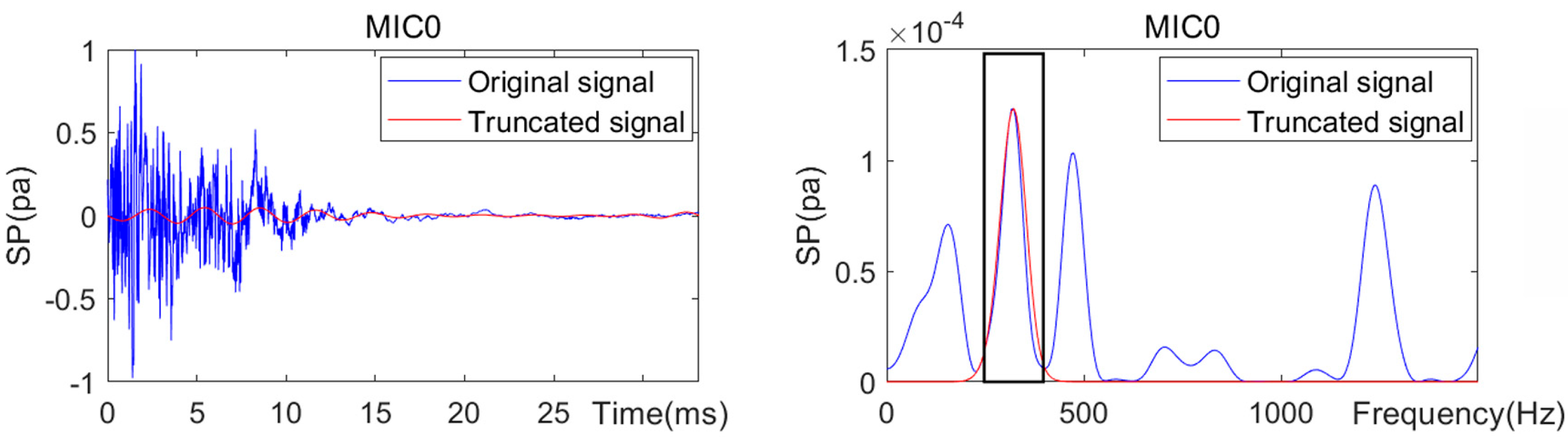
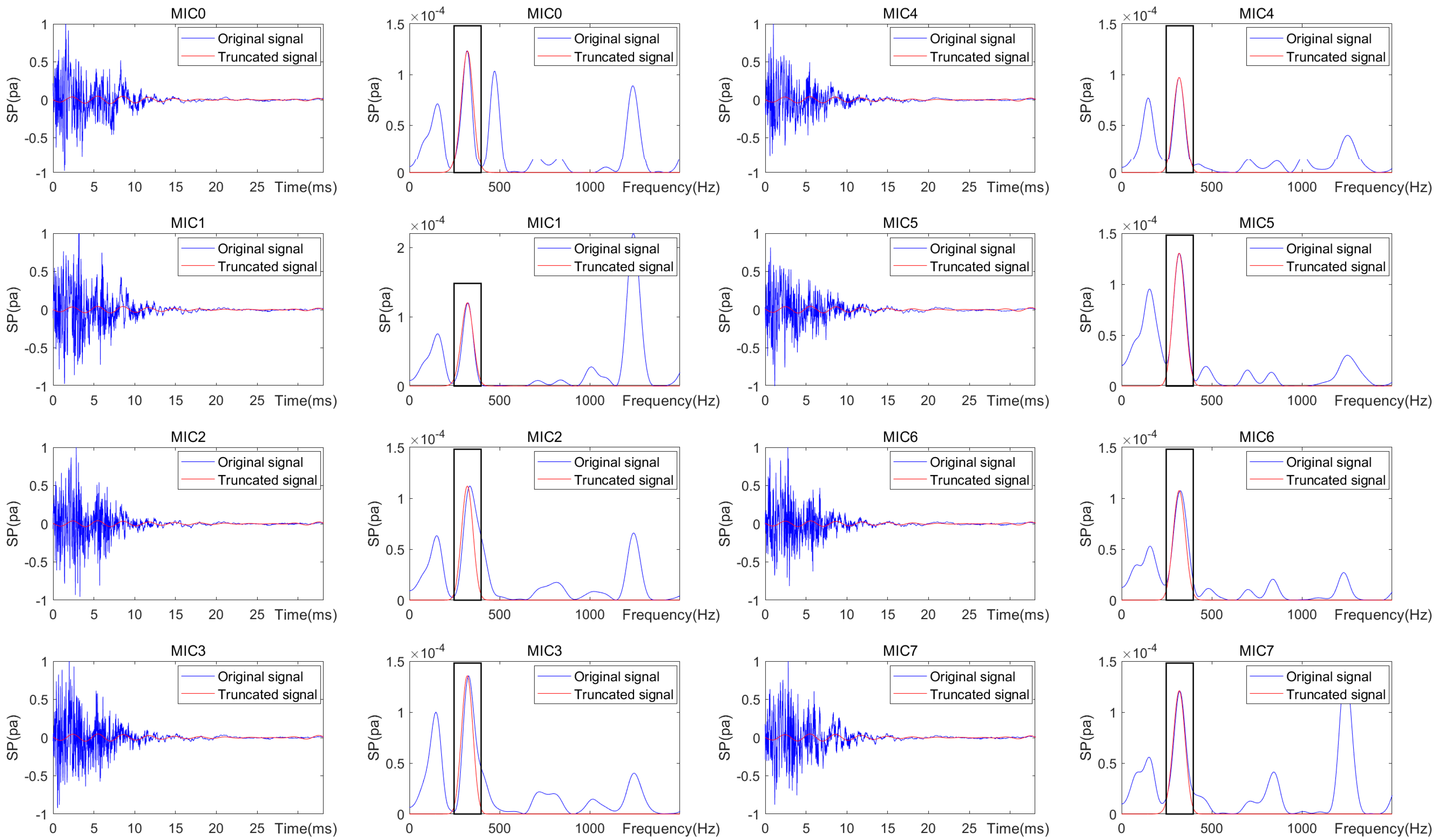
2.4.2. Extraction of First-Order Modal Response Under Mechanical Vibration Interference
2.4.3. Selection of the Maximal Gradient
3. Simulation Analysis
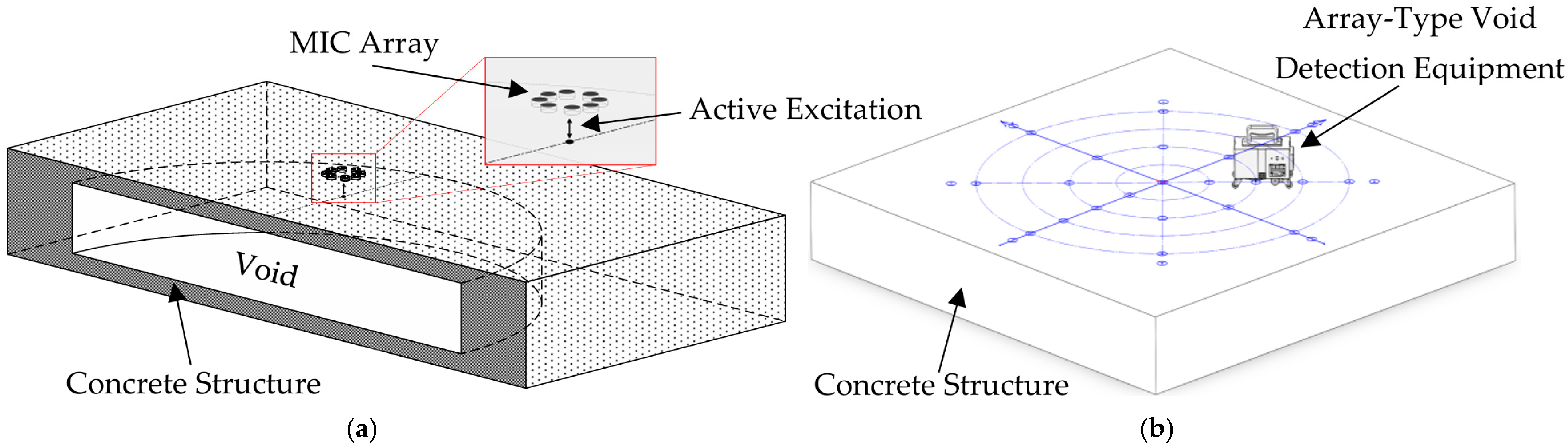
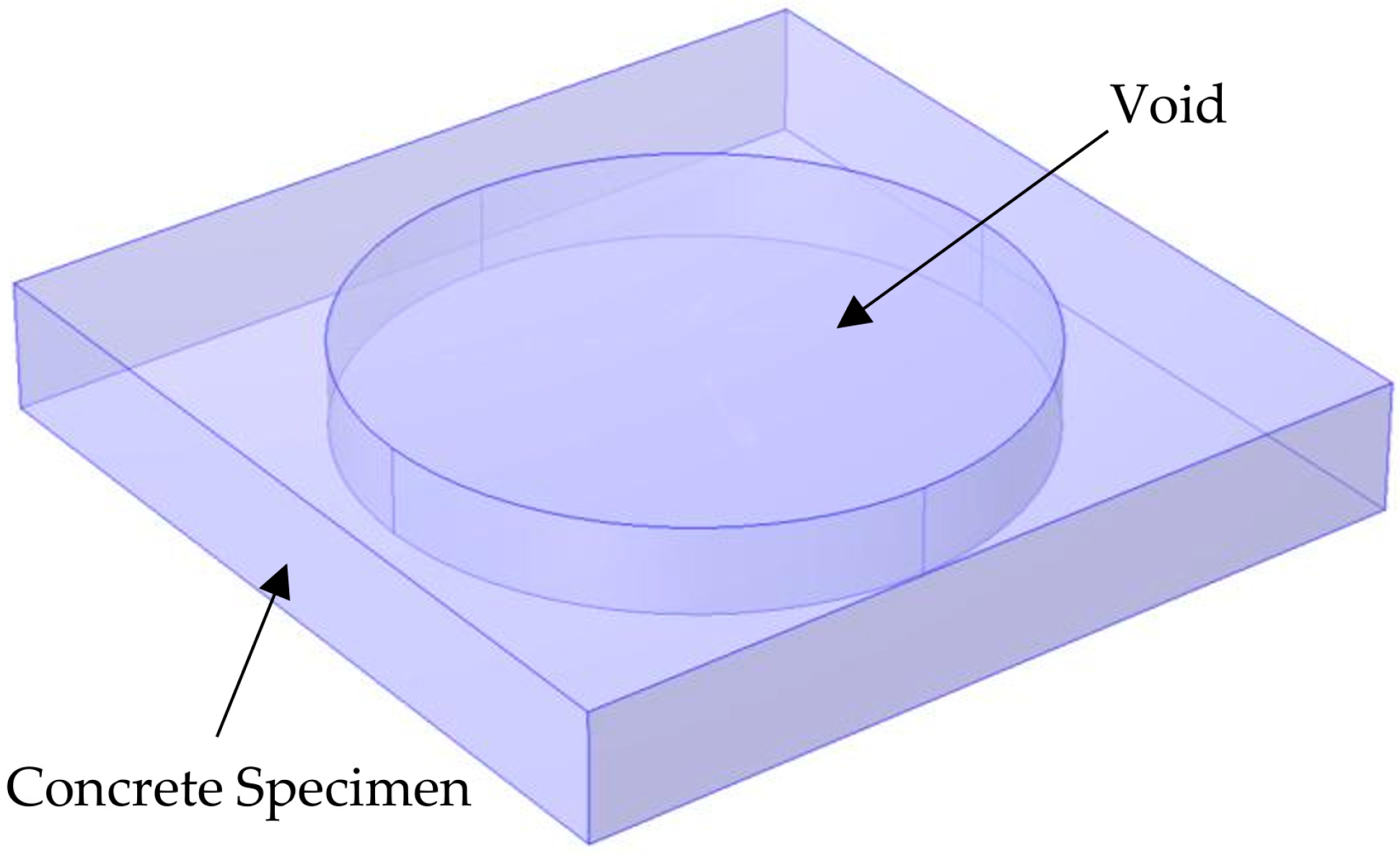
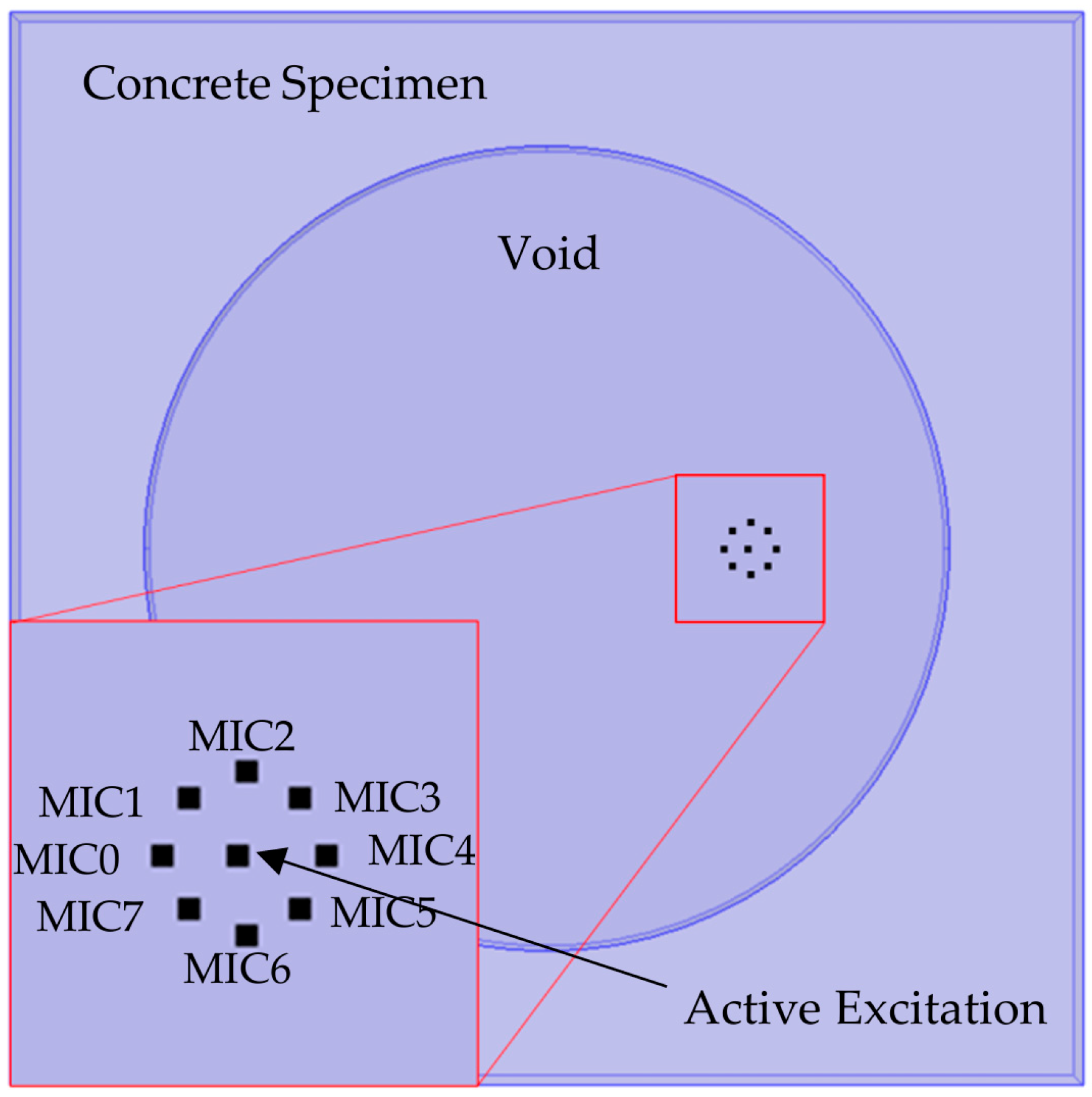
4. Concrete Specimen Experiment
5. Data Processing and Analysis
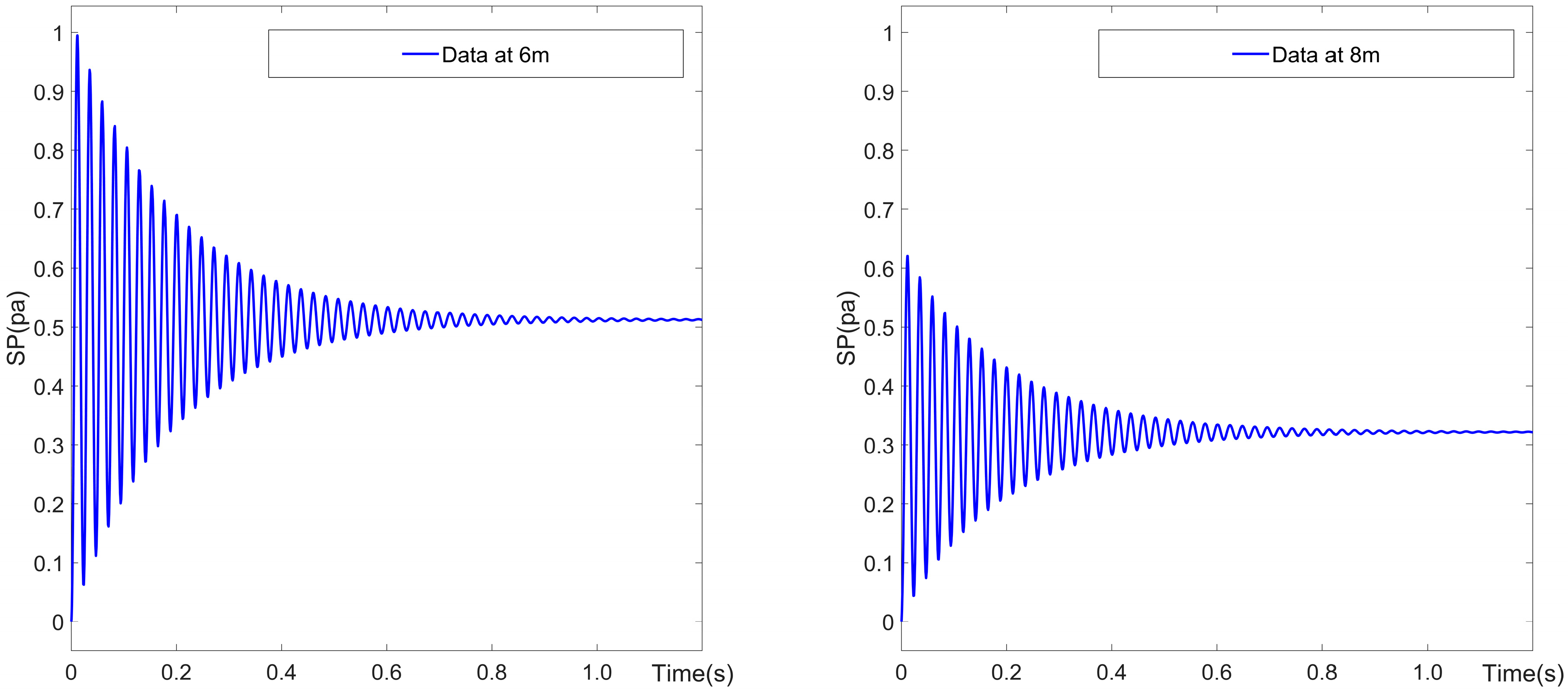
5.1. Data Preprocessing
5.2. Analysis of Central Measurement Point Data
5.3. Multi-Channel Acoustic Data Analysis of Axial Measurement Points on High-Order Rotationally Symmetric Structures
5.3.1. Ninety-Degree Axial Acoustic Data Analysis
5.3.2. Analysis of 315° Axial Acoustic Data
6. Conclusions
- Adaptive Global Synchronous Time Window Construction Technique: A technique is introduced for creating a global synchronous analysis time window that comprehensively encompasses all relevant acoustic signals from every channel. This is accomplished by accurately determining the start time of the tapping excitation through peak detection of transient acoustic response signals gathered by the microphone array, and by integrating the data from the initial and final moments of the response waveforms observed in each channel of the array.
- Precise Decoupling of Target Modes from Complex Responses: A new effective algorithm for modal separation is created to tackle the intricate forced vibration acoustic signals that arise from tapping concrete plates, which include multiple modes and noise. This algorithm excels at accurately extracting the first-order vibration modal characteristic signal, successfully eliminating non-target modal information even in the presence of significant background noise.
- Rapid Identification Method for Defect Boundaries: This method seamlessly integrates MIC array acoustic signal collection technology, acoustic vibration analysis, and gradient field analysis to create a specific method for identifying internal void boundaries based on a gradient field. The essence of this method is in using the extracted pure first-order modal acoustic signals to compute and examine the characteristics of the spatial distribution gradient field.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Niu, F.; Liu, Y.; Xue, F.; Sun, H.; Liu, T.; He, H.; Kong, X.; Chen, Y.; Liao, H. Ultra-high performance concrete: A review of its material properties and usage in shield tunnel segment. Case Stud. Constr. Mater. 2025, 22, e04194. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, A.-X.; Hou, Y.-Q.; Wang, S.-Y. Calculation model of shotcrete support thickness based on elastic thin plate theory. Case Stud. Constr. Mater. 2022, 17, e01232. [Google Scholar] [CrossRef]
- Alsuhaibani, E. Nondestructive testing of externally bonded FRP concrete structures: A comprehensive review. Polymers 2025, 17, 1284. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Huang, Z.; Deng, X.; Liu, H.; Fang, H.; Liu, C.; Zhang, X.; Cui, J. Leakage detection and localization of buried water pipe using ground penetrating radar. Measurement 2025, 254, 117902. [Google Scholar] [CrossRef]
- Tosti, F.; Ferrante, C. Using ground penetrating radar methods to investigate reinforced concrete structures. Surv. Geophys. 2020, 41, 485–530. [Google Scholar] [CrossRef]
- Wu, C.; Liu, Y.; Shao, S.-A.; Ma, S. Research on ultrasonic tomography of concrete hole defects based on multi-parameter coupling and inversion initial value correction. Ind. Constr. 2023, 53, 184–189. [Google Scholar] [CrossRef]
- Ma, Y. Infrared thermal imaging detection and recognition technology for defects in concrete structure. J. Highw. Transp. Res. Dev. 2017, 34, 59–65. [Google Scholar]
- Sirca, G.F., Jr.; Adeli, H. Infrared thermography for detecting defects in concrete structures. J. Civ. Eng. Manag. 2018, 24, 508–515. [Google Scholar] [CrossRef]
- Cui, B.; Wang, C.; Li, Y.; Li, H.; Li, C. Application of computer vision techniques to damage detection in underwater concrete structures. Alex. Eng. J. 2024, 104, 745–752. [Google Scholar] [CrossRef]
- Xiao, Z.; Liu, Z.; Guo, X.; Liu, J. An intelligent non-destructive method to identify the quality of self-compacting concrete based on convolutional neural networks via image recognition. Case Stud. Constr. Mater. 2025, 22, e04442. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Lv, S.; Yu, J.; Ge, D.; Guo, J.; Li, L. YOLOv11-CAFM model in ground penetrating radar image for pavement distress detection and optimization study. Constr. Build. Mater. 2025, 485, 141907. [Google Scholar] [CrossRef]
- Bettayeb, F.; Rachedi, T.; Benbartaoui, H. An improved automated ultrasonic NDE system by wavelet and neuron networks. Ultrasonics 2004, 42, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.-L.; Lee, K.-H.; Wu, T.-T.; Kuo, M.-K. Scan of surface-opening cracks in reinforced concrete using transient elastic waves. NDT E Int. 2001, 34, 219–226. [Google Scholar] [CrossRef]
- Mazzeo, B.A.; Patil, A.N.; Guthrie, W.S. Acoustic impact-echo investigation of concrete delaminations using liquid droplet excitation. NDT E Int. 2012, 51, 41–44. [Google Scholar] [CrossRef]
- Gao, Z.; Chang, Y.; Ren, F. The micro-shearing mechanism of the rock-concrete interface from acoustic emission using the improved Hilbert-Huang transform. Constr. Build. Mater. 2025, 489, 142301. [Google Scholar] [CrossRef]
- Ju, J.; Zhao, W.; Tian, X.; Wang, Z. Research on the identification method based on energy distribution of adaptive WPD for railway tunnel lining void. Nondestruct. Test. Eval. 2024, 39, 2138–2160. [Google Scholar] [CrossRef]
- Fan, B.; Zhao, W.; Ju, J.; Tian, X. Research on wavelet packet energy entropy extraction method for acoustic signal of tunnel lining cavity, Measurem. Sci. Technol. 2024, 35, 106133. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Q.; Zhang, K.; Liu, Y.; Liu, H. Selection refines diagnosis: Mamba for acoustic weak fault diagnosis combining feature mode decomposition and selection. Adv. Eng. Inform. 2025, 66, 103421. [Google Scholar] [CrossRef]
- Chen, H.; Xue, J.; Gan, S.; Wang, J.; Li, Y.; Nie, X. Interfacial debonding detection for steel-concrete composite structures Part II: Scanning Doppler laser-based MASW and microphone combination-based impact-acoustic vibration. Structures 2024, 61, 106124. [Google Scholar] [CrossRef]
- Carrera, E. Use of the integration by part to derive beam/plate equilibrium equations from elasticity with ap-plications to beams. Mech. Adv. Mater. Struct. 2025, 32, 2535–2547. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, W. Analysis on identifying thin-plate void parameters in concrete based on vibro-acoustic method. Measurement 2025, 242, 116281. [Google Scholar] [CrossRef]
- Cabada, A.; Jebari, R.; López-Somoza, L. Existence results for a fourth order problem with functional perturbed clamped beam boundary conditions. Math. Slovaca 2024, 74, 895–916. [Google Scholar] [CrossRef]
- Liu, E.G.; Shao, Y.F.; Dou, B.; Cui, J.F.; Ding, H. High-Order Modal Vibration Control of Timoshenko Beams Based on Nonlinear Energy Sink Cells. J. Vib. Eng. Technol. 2024, 12, 6809–6819. [Google Scholar] [CrossRef]
- Gómez-Silva, F.; Zaera, R.; Loya, J.A. Buckling and free vibration modes of a multi-cracked variable stiffness Euler–Bernoulli beam in a Winkler foundation with piecewise constant stiffnesses. Eng. Struct. 2025, 340, 120717. [Google Scholar] [CrossRef]
- Régal, X.; Cumunel, G.; Bornert, M.; Quiertant, M. Assessment of 2D digital image correlation for experimental modal analysis of transient response of beams using a continuous wavelet transform method. Appl. Sci. 2023, 13, 4792. [Google Scholar] [CrossRef]
- Luna Vera, O.S.; Kim, C.W.; Oshima, Y. Energy dissipation and absorption capacity influence on experimental modal parameters of a PC girder. J. Phys. Conf. Ser. 2017, 842, 012038. [Google Scholar] [CrossRef]
- Chen, T.; Yang, X.-M.; Yang, S.-H.; Yao, X.-J.; Zheng, Y.-X. Variational mode extraction-guided automated asynchronous operational modal analysis for bridges. Struct. Control Health Monit. 2025, 32, 1–15. [Google Scholar] [CrossRef]
- Liu, Z.; Rao, B.; Zhang, Q. Polynomial stability of the Rao-Nakra beam with a single internal viscous dam-ping. J. Differ. Equ. 2020, 269, 6125–6162. [Google Scholar] [CrossRef]
- Li, L.; Chen, L.; Yi, H. Vibration characteristic analysis of a circular thin plate with complex pre-stress distribution. J. Vibroengineering 2018, 20, 2951–2965. [Google Scholar] [CrossRef]
- Poozesh, P.; Aizawa, K.; Niezrecki, C.; Baqersad, J.; Inalpolat, M.; Heilmann, G. Structural health monitoring of wind turbine blades using acoustic microphone array. Struct. Health Monit. 2017, 16, 471–485. [Google Scholar] [CrossRef]
- Chiariotti, P.; Martarelli, M.; Castellini, P. Acoustic beamforming for noise source localization—Reviews, methodology and applications. Mech. Syst. Signal Process. 2019, 120, 422–448. [Google Scholar] [CrossRef]
- Chae, K.-S.; Ih, J.-G. Prediction of vibrational energy distribution in the thin plate at high-frequency bands by using the ray tracing method. J. Sound Vib. 2001, 240, 263–292. [Google Scholar] [CrossRef]
- Omologo, M.; Svaizer, P. Use of the crosspower-spectrum phase in acoustic event location. IEEE Trans. Speech Audio Process. 1997, 5, 288–292. [Google Scholar] [CrossRef]
- Barros, J.; Diego, R.I. On the use of the Hanning window for harmonic analysis in the standard framework. IEEE Trans. Power Deliv. 2006, 21, 538–539. [Google Scholar] [CrossRef]
- Hou, J.; Xu, D.; Jankowski, Ł. Structural modal parameter identification with the Power-Exponential window function. Mech. Syst. Signal Process. 2025, 222, 111771. [Google Scholar] [CrossRef]








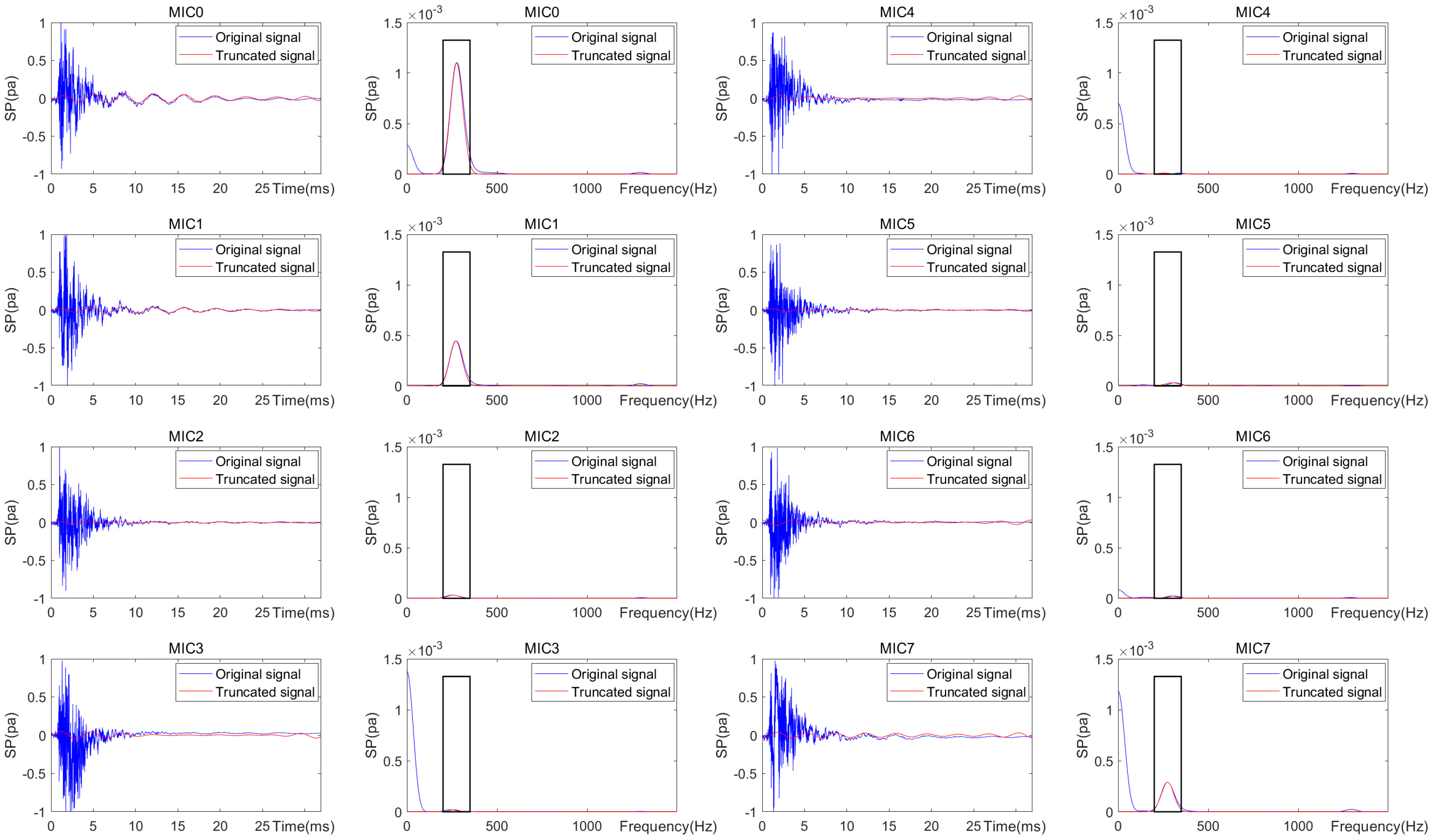
| MIC0 | MIC1 | MIC2 | MIC3 | MIC4 | MIC5 | MIC6 | MIC7 | |
|---|---|---|---|---|---|---|---|---|
| SP(point 00) |
| MIC0 | MIC1 | MIC2 | MIC3 | MIC4 | MIC5 | MIC6 | MIC7 | |
|---|---|---|---|---|---|---|---|---|
| SP(point 07) | ||||||||
| SP(point 15) | ||||||||
| SP(point 23) |
| MIC0 | MIC1 | MIC2 | MIC3 | MIC4 | MIC5 | MIC6 | MIC7 | |
|---|---|---|---|---|---|---|---|---|
| SP(point 12) | ||||||||
| SP(point 20) | ||||||||
| SP(point 28) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Shen, P.; Qi, Z.; Liu, S. Rapid Identification Method for Concrete Defect Boundaries Based on Acoustic-Mode Gradient Analysis. Buildings 2025, 15, 2569. https://doi.org/10.3390/buildings15142569
Yang Y, Shen P, Qi Z, Liu S. Rapid Identification Method for Concrete Defect Boundaries Based on Acoustic-Mode Gradient Analysis. Buildings. 2025; 15(14):2569. https://doi.org/10.3390/buildings15142569
Chicago/Turabian StyleYang, Yong, Peixuan Shen, Ziming Qi, and Shiqi Liu. 2025. "Rapid Identification Method for Concrete Defect Boundaries Based on Acoustic-Mode Gradient Analysis" Buildings 15, no. 14: 2569. https://doi.org/10.3390/buildings15142569
APA StyleYang, Y., Shen, P., Qi, Z., & Liu, S. (2025). Rapid Identification Method for Concrete Defect Boundaries Based on Acoustic-Mode Gradient Analysis. Buildings, 15(14), 2569. https://doi.org/10.3390/buildings15142569





