Abstract
Energy is a critical resource, and its optimization is central to sustainable building design. Occupant comfort, significantly influenced by factors, including mean radiant temperature (MRT), alongside air temperature, velocity, and humidity, is another key consideration. This paper introduces a hybrid crow search optimization (CSA) and penguin search optimization algorithm (PeSOA), termed (HCRPN), designed to simultaneously optimize building energy consumption and achieve MRT levels conducive to thermal comfort by adjusting HVAC system parameters. We first validate HCRPN using ZDT-1 and Shaffer N1 multi-objective benchmarks. Subsequently, we employ EnergyPlus simulations, utilizing a single-objective Particle Swarm Optimization (PSO) for initial parameter analysis to generate a dataset. Following correlation analyses to understand parameter relationships, we implement our hybrid multi-objective approach. Comparative evaluations against state-of-the-art algorithms, including MoPso, NSGA-II, hybrid Nsga2/MOEAD, and Mo-CSA, validated the effectiveness of HCRPN. Our findings demonstrate an average 7% reduction in energy consumption and a 3% improvement in MRT-based comfort relative to existing methods. While seemingly small, even minor enhancements in MRT can have a noticeable positive impact on well-being, particularly in large, high-occupancy buildings.
1. Introduction
In the current global scenario, the issue of reducing energy consumption in buildings has taken center stage. With the growing awareness of the finite nature of energy resources and the escalating concerns regarding climate change, the building sector has been identified as a key area for intervention. Buildings, in their various forms and functions, consume a significant portion of the world’s total energy supply. This consumption is not only a drain on valuable resources but also a major contributor to greenhouse gas emissions. From commercial high-rises in bustling urban centers to educational institutions like universities and residential complexes, every building type presents unique challenges and opportunities for energy conservation. The imperative to optimize energy use in buildings stems from multiple factors. Firstly, it is a matter of environmental stewardship. By reducing energy consumption, we can mitigate the carbon footprint associated with building operations, thereby contributing to the global effort to combat climate change. Secondly, it has direct economic benefits for the owners and occupants of the building. Lower energy bills translate into cost savings that can be redirected to other productive or essential areas. Moreover, buildings with better energy performance ratings are more attractive to tenants and buyers in an increasingly competitive market, enhancing their market value. In the case of energy reduction studies of buildings, several investigations have been carried out on EnergyPlus as a powerful energy simulation software. Although the studies have been performed and several meta-heuristic algorithms were used to solve the problem of optimization with EnergyPlus, an automated framework for analyzing results and using EnergyPlus is required to improve the speed of studies.
1.1. Background
The imperative to curtail energy consumption in the building sector has become a global priority in the face of escalating climate change and dwindling energy resources. Buildings, encompassing a diverse range of typologies, account for a significant portion of worldwide energy demand and associated greenhouse gas emissions [1]. While energy efficiency remains paramount, ensuring occupant well-being through optimal indoor environmental quality is equally crucial. Among the factors influencing thermal comfort, mean radiant temperature (MRT) plays a critical role in how occupants perceive the thermal environment, often independently of air temperature [2]. The accurate assessment and optimization of thermal comfort, considering MRT, present a significant challenge in building design and operation. Building energy simulation tools, such as EnergyPlus, are indispensable for analyzing energy performance; however, their validation often prioritizes energy consumption over the nuanced aspects of indoor microclimatic conditions responsible for thermal comfort [3]. Significant energy is used when Heating Ventilation and Air Conditioning (HVAC) systems are operating in crowded areas. Higher ventilation rates and more stringent indoor air quality regulations in the post-pandemic environment significantly raise energy usage. The energy retrofit of a partial recirculation all-air HVAC system that supplies air to a lecture hall in a Southern Italian university was studied. By using a Multi-Objective Optimization and a Multi-Criterion Decision-Making (MCDM) algorithm, two distinct decision-makers, assessments of public and private buildings were made [4]. In another study, thermal ventilation in multiple-floor office buildings was investigated to improve energy consumption using computational fluid dynamics simulations with phase change materials [5].
A study by D’Agostino et al. examined HVAC retrofits in an Italian office building, assessing their energy and cost impact, and their role in mitigating COVID-19 transmission via increased outdoor air exchange. Using dynamic simulation, an optimal outdoor air change rate was identified to reduce infection risk, energy, and cost, also combining system interventions with envelope efficiency measures to offset these drawbacks [6].
Consequently, a performance gap frequently exists between simulated and measured thermal comfort conditions [7], highlighting the need for more sophisticated approaches that concurrently address both energy efficiency and occupant thermal comfort, with a specific focus on MRT.
1.2. Objectives
To overcome the limitations identified in the state-of-the-art, this research work aims to develop a novel hybrid meta-heuristic algorithm, synergizing the crow search algorithm and the penguin optimization algorithm, specifically tailored for the concurrent optimization of building energy consumption and mean radiant temperature. Establish an automated framework that seamlessly integrates the proposed hybrid algorithm with the EnergyPlus building simulation software to facilitate detailed and efficient analysis. We validate the performance of the novel algorithm and the automated framework through comprehensive comparisons with well-established optimization algorithms (MoPso, Nsga-II, Nsga-II/MOEAD, and Mo-Csa) [8,9,10,11,12,13,14] across relevant case studies. We provide valuable insights into the trade-offs between energy efficiency and occupant thermal comfort, with a specific emphasis on the influence of mean radiant temperature. This research contributes to the field of building energy optimization by offering a more holistic approach that simultaneously addresses energy efficiency and occupant thermal comfort, leveraging a novel hybrid meta-heuristic algorithm within an automated simulation framework. This has the potential to drive the development of more sustainable and comfortable building designs, reducing the environmental impact of the built environment and enhancing the well-being of its occupants. In Section 2, previous works based on optimization energy in buildings and their methods are categorized and reviewed in detail. In Section 3, our novel method and levels in this study are explained in detail. Section 4 depicts experiments and comparison results of the algorithms. Finally, Section 5 concludes the studies in our research and Section 6 states the future direction of the study.
2. State-of-the-Art
In this section, recent research on energy optimization is explored. Studies are categorized into five different areas: building energy optimization methods, energy simulations optimizations, energy optimization in the field of machine learning (especially in neural networks), multi-objective and hybrid energy optimizations, and, finally, energy optimization research in other fields.
2.1. Building Energy Optimization Methods
There are numerous ways to approach the optimization of building energy consumption. One fundamental aspect is the improvement of the building envelope. This involves enhancing the insulation properties of walls, roofs, and floors to prevent heat loss during the colder months and heat gain during warmer periods. High-quality insulation materials, such as advanced fiberglass or spray foam insulation, can significantly reduce the need for excessive heating and cooling. Furthermore, the use of energy-efficient windows with low-emissivity coatings and proper glazing techniques can further enhance the performance of the envelope [15,16].
Efficient lighting systems also play a crucial role. The transition from traditional incandescent bulbs to more energy-efficient alternatives such as compact fluorescent lamps (CFLs) and light-emitting diodes (LEDs) has been a significant step forward. LEDs, in particular, offer high luminous efficacy, long lifetimes, and the ability to integrate with smart lighting controls. Studies, such as [17,18], have shown that the widespread adoption of LED lighting in buildings can result in substantial energy savings without compromising the quality of illumination.
Another area of focus is the optimization of HVAC systems. These systems are responsible for maintaining comfortable indoor temperatures and air quality but can be significant energy consumers if not properly designed and controlled. The implementation of variable refrigerant flow (VRF) systems, which can modulate cooling and heating capacity based on the actual demand, has been shown to improve energy efficiency. Additionally, the integration of energy recovery ventilators (ERVs) can recover heat or coolness from exhaust air, pre-conditioning the incoming fresh air and reducing the load on the HVAC system [19,20].
In recent years, meta-heuristic methods, especially nature-inspired and hybrid ones, have emerged as promising techniques for building energy optimization. Nature-inspired algorithms, such as genetic algorithms (GAs), PSO, and ant colony optimization (ACO), mimic the behavior of natural phenomena to search for optimal solutions. For example, a GA emulates the process of natural selection and genetic recombination to evolve better solutions over generations [21,22,23,24].
2.2. Energy Simulation Optimizations
In the pursuit of optimizing building energy consumption, several simulation software tools have been developed and utilized. One such software is DOE-2.3 It has been widely used for many years and offers a comprehensive set of features for whole-building energy analysis. Its strength lies in its extensive library of building components and systems, allowing for detailed modeling. However, it has been criticized for its relatively complex user interface, which may pose a challenge for novice users. DOE-2.3 has been a staple in the industry but is gradually being superseded by more modern alternatives in some applications due to its dated interface and certain limitations in handling advanced building technologies [25].
Another tool is TRNSYS, which is a simulation program that is mainly utilized in renewable energy engineering and building simulation, particularly for both passive and active solar design. Originating from the University of Wisconsin as a commercial software package, it initially served the purpose of conducting dynamic simulations of solar hot water systems over a typical meteorological year. Although it has some advantages, such as flexibility and customization, granular results, and built-in optimization tools, it has a high learning curve, which causes complexity for beginners, limited visualization capabilities, system modeling constraints, and a lack of direct data import/export [26].
2.3. Machine Learning-Based Methods
Zhang et al. developed a method for predicting energy utilization in buildings based on plug load electricity. They used a neural network-based method, Long Short-Term Memory (LSTM) and Bi-directional LSTM (Bi-LSTM) for this purpose. To increase the prediction accuracy, the swarm intelligent algorithm known as the Whale Optimization algorithm (WO) was applied. They compared their results based on four different combinations of these algorithms: LSTM, Bi-LSTM, LSTM-WO, and Bi-LSTM-WO. Their predictions were evaluated based on metrics such as the coefficient of determination (R), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), and Coefficient-of-Variation of Root Mean Square Error (CV-RMSE). Better achievements were reached in R, MAPE, and CV-RMSE evaluation metrics [27].
In another study, authors addressed the need for sustainable urban energy management by proposing an advanced building energy consumption prediction system. They introduced the concept of region-wide occupant energy-use behavior probability to capture real-time interactions in building environments. Additionally, they employed the squeeze-and-excitation attention mechanism, the sparrow search algorithm, and the convolutional neural network to enhance data processing and hyperparameter selection. Testing on seven buildings showed improved accuracy, reducing MAPE and CV-RMSE, with only a slight increase in processing time. Applied to 45 buildings in a university setting, the system achieved remarkable MAPE and CV-RMSE, demonstrating its effectiveness [28].
Rufuss et al. examined electricity consumption trends in Tamil Nadu, India, over three decades, identifying a linear increase in demand. They focused on optimizing energy resources with an emphasis on maximizing the Energy Received On Energy Invested (EROI), a factor often overlooked in prior studies. Their econometric model showed that population, GDP, and electricity prices significantly influenced demand, with projections indicating a sharp rise by 2040–2041. Their optimization model suggested that increasing renewable energy contributions could help to reverse the declining EROI trend. The model’s reliability was confirmed through uncertainty analysis, showing minor deviations from actual data. The study also discussed policy recommendations for sustainable energy planning to support policymakers and industry stakeholders [29].
2.4. Multi-Objective and Hybrid Energy Optimizations
In five distinct Chinese towns with varying climates, researchers examined an office building equipped with Building-Integrated Photovoltaic (BIPV) windows. Building Orientation (BO), Window Size (WZ), Window Visible-Light Transmittance (VLT), and PV Type (TOPV) were the four variables taken into consideration in the study. The goal was to reduce the additional investment cost of BIPV windows as well as the Annual Net Electricity Cost (ANEC). jEPlus v2.0.0 software was used to simulate the objective functions and design variables. For the sensitivity analysis of design parameters, the jEPlus + EA program also employed the Morris and Standard Regression Coefficient (SRC) algorithms. The genetic-based algorithm known as NSGA-II was used to solve the multi-objective problem. A collection of Pareto optimum solutions was produced through optimization. According to the findings, the building with BIPV windows might reduce its yearly electricity expenses. Additionally, the static investment payback durations for all cities ranged from 7 to 14 years, proving the economic feasibility of implementing the BIPV window [30].
A framework named AnFiS-MoH introduced, which was an innovative framework combining the adaptive neuro-fuzzy inference system (ANFIS) with metaheuristic optimization algorithms to improve parameter tuning in complex, nonlinear modeling. Traditional ANFIS models faced optimization challenges as the problem size grew, so AnFiS-MoH leveraged the global search abilities of algorithms like ant colony optimization, particle swarm optimization, genetic algorithm, and simulated annealing. Testing on benchmark datasets (Boston Housing and Wine Quality) by authors showed that AnFiS-MoH significantly improved prediction accuracy and generalization, with a reduction in Mean Squared Error and increase in scores. The study highlighted the effectiveness of hybrid approaches for high-dimensional, noisy data in intelligent systems [31].
2.5. Energy Optimization in Other Scopes
Ghorbannia Delavar et al. presented a method to reduce energy and costs in instance-intensive cloud workflows via virtual machine migration. Their approach introduced input classification, real execution time calculation, distance parameters, and an intelligent threshold detector (ITD), surpassing previous methods in efficiency. The HDECO method used an objective function to enhance energy efficiency by integrating parameters into the fitness function. Improvements were achieved by dynamically adjusting thresholds, enhancing prediction accuracy, and refining resource allocation. By categorizing inputs based on processing power and optimizing load balancing, their method significantly reduced execution time, energy consumption, and costs [32,33]. In their other research, they presented a novel hybrid bat and genetic algorithm to reduce energy while maximizing throughput in networks [34,35,36]. Another research work introduced a multi-objective crow search algorithm (CSA), called CSAMOMC, to optimize makespan and costs in scientific cloud workflows. A comparative analysis was conducted with the commonly used HEFT and TC3pop algorithms, known for minimizing makespan and costs. The results showed that the proposed algorithm achieved an average reduction in makespan and in cost, demonstrating its superior performance over existing methods [10].
In response to the growing demands for energy reduction in Internet of Things (IoT) applications and the need for efficient resource management, Khaledian et al. explored workflow scheduling approaches in fog-cloud environments to optimize energy use and makespan. In one study, they developed a workflow scheduling method using a multi-objective krill herd algorithm, leveraging fog-cloud architecture to reduce response delays, energy consumption, and costs. The proposed approach showed improvement in makespan over IHEFT, HEFT, and IWO-CA methods, along with reduced energy and monetary costs. In another study, they introduced a hybrid particle swarm optimization and simulated annealing (PSO-SA) algorithm to prioritize tasks within IoT workflows, addressing resource constraints and energy consumption. Their method enhanced makespan and energy efficiency [37,38,39,40,41].
3. Methodology
In this section, the levels, which were used during the experiments and the results, are explained step by step. Table 1 lists the notations used in the research.

Table 1.
Notations for parameters in the algorithms.
3.1. EnergyPlus Simulations
EnergyPlus is a sophisticated software program for building energy analysis, predicting energy use, indoor conditions, and system performance. Its application is valuable on university campuses with diverse and complex building energy needs, offering insights for efficiency and cost reduction. Developed by the U.S. Department of Energy in the late 1990s, EnergyPlus combined features of BLAST 3.0 (HVAC) and DOE-2 (whole-building analysis). Continuous development by a global community has enhanced its accuracy and applicability to various building types, including those on university campuses [42].
3.2. Meta-Heuristic Algorithms
Meta-heuristic algorithms have an important role in the optimization of different fields. In this section, single- and multi-objective meta-heuristic algorithms are reviewed.
3.2.1. Particle Swarm Optimization (PSO)
PSO is a metaheuristic optimization technique inspired by the social behavior of bird flocking or fish schooling. It has gained significant attention in the field of building energy optimization due to its simplicity and effectiveness in solving complex problems. The algorithm works by initializing a population of particles, each representing a potential solution to the optimization problem. These particles move through a search space, adjusting their positions based on their own best-known position and the global best position found by the swarm. This process continues iteratively until a stopping criterion is met, typically when a satisfactory solution is obtained or a maximum number of iterations is reached [43,44].
The method for updating the speed of particles is written in Equation (1), where is the velocity of particle i in dimension d at iteration t, w is the inertia weight, and are acceleration coefficients, and are random numbers in the range [0, 1], is the personal best position of particle i in dimension d, is the position of particle i in dimension d at iteration t, and is the global best position in dimension d.
The position of each particle is updated based on Equation (2):
Algorithm 1 shows PSO.
| Algorithm 1 Particle Swarm Optimization (PSO) |
|
In the context of building energy management, PSO has been applied to various aspects such as optimizing the control strategies of HVAC systems, determining the optimal sizing and configuration of renewable energy systems integrated with buildings, and improving the energy efficiency of building envelopes. For example, in HVAC control, PSO can be used to find the optimal setpoints for temperature and humidity to minimize energy consumption while maintaining occupant comfort. Renewable energy system design can help to determine the most efficient placement and sizing of solar panels or wind turbines to maximize energy generation and reduce the building’s reliance on grid electricity.
For multi-objective PSO, instead of one objective function, there are multiple ones that might directly or inversely affect each other. There are different ways to handle multiple objective functions in PSO, sSuch as looking for the Pareto front and dominated solution or opposition-based and dynamic multi-objective PSO [8,9].
3.2.2. Multi-Objective Crow Search Optimization (MoCsa)
A meta-heuristic optimization algorithm that has gained popularity because of its special features and benefits is the crow search algorithm. It draws inspiration from the clever way that crows conceal and retrieve food, offering a fun and practical method for resolving challenging optimization issues.
The CSA’s ease of use and simplicity are among its many noteworthy benefits. The algorithm does not need as much parameter adjustment as some other optimization algorithms. Researchers and practitioners, even those with little background in optimization techniques, can use it because of its simplicity. Its comparatively small number of parameters to modify lessens the computational load and complexity of the optimization process compared to fine-tuning several parameters.
Each crow has a memory and awareness property. Based on its awareness of itself, it decides whether or not to move to its hidden food resource. In some situations, he understands that another crow is following him, so he tries to deceive that crow and go somewhere else, but, in some circumstances, it does not, and the following crow will find his hidden food resource. Based on random number , and awareness property , crow i with a position in dimension j at the iteration will be set. Equation (3) shows setting crow position based on the awareness property:
Pseudocode for the algorithm is written in Algorithm 2. For adding more objective functions to the crow search algorithm, multiple functions will be calculated, set as the current fitness value of the selected crow and based on the memory of the current crow, which is an n-dimensional space; its memory is also calculated by objective functions. Finally, if all values of current fitness are lower than current memory values, the memory will be updated. Algorithm 3 shows the process.
When evaluating fitness, all objective functions will be called to perform multi-objective optimization in the CSA algorithm. This is a simple way of converting CSA from single-objective to multi-objective. In our previous article [10], we utilized hyper-volume computation between two parameters of optimization. This is one of the accurate ways to achieve multi-objective optimization. There are other methods such as weighted sum [45,46], Pareto-based [47], and non-dominated sorting [48].
| Algorithm 2 Crow Search Algorithm (CSA) |
|
| Algorithm 3 Update Memory (CSA) |
|
3.3. Proposed Method
In this research, a new hybrid algorithm, which combines adaptive memory management (AMM) with the crow search and the penguin optimization algorithm, is presented. Dynamically modifying memory size preserves a wide range of superior solutions and boosts optimization effectiveness. According to simulations, the proposed algorithm performs better than CSA and POA separately in terms of energy and MRT parameters. The novel method is a viable solution for building energy management because of its adaptive memory strategy, which enables it to strike a balance between exploration and exploitation [49].
We chose to hybridize the CSA and POA to form HCRPN based on three key reasons. Firstly, this hybrid approach provides an enhanced balance between exploration (from CSA’s global search) and exploitation (from POA’s local search), which is crucial for navigating the complex, multi-modal landscape of building energy and thermal comfort optimization. Secondly, the distinct search behaviors of CSA and POA are particularly well-suited for the highly nonlinear objective functions and interacting parameters inherent in optimizing dynamic thermal comfort and energy in buildings. Finally, this novel combination represents a significant contribution to the field by exploring the efficacy of less commonly hybridized metaheuristics for this specific problem, as validated by our superior performance compared to other state-of-the-art algorithms.
There are multiple advantages to synthesizing the crow search algorithm with penguin search. First of all, the search speed of crows and the wide area of search can be added as an advantage to the penguin algorithm. Secondly, although penguins are searching for food resources, finding the largest resource is performed by crows. On top of this, implementing the crow search algorithm is simpler than other meta-heuristic algorithms, which have more parameters and are more complicated. Third, by changing awareness and random parameters, the behavior of searching the crows can be changed, which leads to more convexity of the program. Finally, penguins have the ability to escape from local optima traps because of their grouping attribute in the algorithm.
3.3.1. Penguin Search Optimization Algorithm
As CSA was explained in previous sections, POA is looked at in more detail in the following section. POA is an emerging meta-heuristic optimization algorithm that draws inspiration from the behavior of penguins in the Antarctic environment. This algorithm has the potential to offer unique advantages and contribute novel perspectives to the field of optimization, making it a relevant addition to certain research studies.
Behavioral Inspiration: Penguins exhibit social behaviors such as huddling to conserve heat and foraging in groups. In the POA algorithm, these behaviors are mimicked to guide the search for optimal solutions. For example, the movement and interaction of penguins within a colony are translated into mathematical operations that govern how candidate solutions move and converge in the search space.
Search Mechanism: The algorithm initializes a population of “penguins” considered as candidate solutions in the search space. Each penguin has a position and a velocity. Similar to other swarm-based algorithms, the position of a penguin is updated based on its current position and velocity, as well as the influence of the best positions found by itself and its neighboring penguins. The velocity update takes into account factors like the distance to the best positions and a random factor to introduce exploration.
Advantages: One of the key advantages of POA is its ability to balance exploration and exploitation. The social behavior-inspired interactions allow the algorithm to explore different regions of the search space while also converging towards promising areas. It has shown good performance in handling complex and multimodal optimization problems, where there are multiple local optima. Additionally, POA is relatively simple to implement compared to some other advanced optimization algorithms, making it accessible for researchers and practitioners in various fields.
Applications: POA has been applied in diverse domains such as engineering design optimization, energy management, and image processing. In engineering, it can be used to optimize the design parameters of structures or mechanical systems to achieve better performance and cost-efficiency. In energy management, it can help in optimizing the operation of power systems or energy-efficient building systems.
POA acts as collective intelligence, which consists of several groups of penguins looking for food resources. Each group of penguins gathers around a hole in the ice, and penguins in the group start diving into the hole and searching for food resources. They continue until their oxygen is finished. Penguins in the group inform each other about how many fish they hunt, and, based on this, the group decides whether that hole has enough food resources or not, and they change the hole in the case of a lack of enough food. Updating the penguin position will be based on Equation (4) [50]:
where is the position of penguin j allocated to the i-th group at the t-th instance, is the oxygen reserve of the j-th penguin of the i-th group, and is the best solution found by the i-th group.
Algorithm 4 shows an overview of the penguin search optimization algorithm. At the start of the process, they will be distributed among groups, and then they will start fishing. At each iteration, they inform each other about the food resources and the membership of groups that might be changed based on the situation. This process will happen until the condition is met [50,51].
| Algorithm 4 Penguin Search Optimization Algorithm (POA) |
|
Through the utilization of both CSA’s and POA’s benefits, the proposed hybrid approach maximizes the optimization of functions. The algorithm’s detailed levels are shown in Algorithm 5. The first step is to configure the settings for both hybrid algorithms. Certain factors, including population size and the total number of iterations, are the same for both approaches, while others are exclusive to each one. The while loop is started in the following step, and the number of iterations is determined by the input parameters. Two stages will occur. These are for the penguin algorithm in the first place and crow search in the second. In POA, it walks randomly for every group of penguins, updates its location, and uses the optimal solution to verify target function values. If the method produces better outcomes, it updates the local best. Next, the CSA algorithm selects a random memory location for the crow populations and performs the crow search algorithm levels in the second phase. The original CSA method produces a random number to compare the awareness probability. Without taking into account certain environmental circumstances, this random number generation may not achieve satisfactory results. A True Random Number Generator (TRNG) was thus used [52,53]. Based on an image’s input color channels and statistical noise analysis, TRNG produces random numbers. This attribute was inspired by this research to enhance the decision process of crows for following other ones or not. In fact, the field of view of each crow has an impact on its memory and awareness. Some images from the point of view of the flying objects in the sky were selected as crow views and, based on their noise, random numbers were generated by TRNG to affect the awareness and memory of crows. After generating random number, algorithm checks the awareness property of the crow to see if crow understands that it is being followed by another crow or not. If the awareness value of the crow will be larger than random value, this means that the crow knows that another crow is following him, so it will change its position to deceive following crow; in the other case, it moves to the location of the food based on his memory. After carrying out this process for each crow, fitness values of the crows will be calculated and, based on the better new fitness value, memory will be updated. At the end of the iterations of the POA and CSA algorithms, both algorithms share and compare their solutions and objective function values to choose the global best.
| Algorithm 5 Hybird Crow, Penguin Search Algorithm |
|
As an example of an algorithm working with EnergyPlus, first, specific input parameters such as populations, groups, and awareness for both POA and CSA are set. Next, EnergyPlus will be called by the generated code. For calling EnergyPlus, some input parameters for calculating HVAC energy are set by each CSA and POA. These selected parameters will be modified inside the .idf file, and one simulation of EnergyPlus will be run until it finishes. After finishing the simulation, EnergyPlus will generate an HTML report file that has multiple tables of different parts of the experiment. Then, our implemented code extracts total energy and MRT, uses it as a result of an objective function, and checks it with previous iterations. These iterations will be carried out until it reaches total iteration. Both POA and CSA compare returned results with previous ones and, if each one is reduced, the the new returned value is replaced as the global optimum of the objective function.
Figure 1 shows the steps and flowchart of the proposed algorithm. At the beginning, it receives the IDF file of a model, which is the input of the EnergyPlus simulator. Then, it initializes parameter values of the meta-heuristic algorithm. These parameters can be changed by an expert or researcher who wants to carry out simulations. After that, iterations start, and the meta-heuristic algorithm changes its parameters. In every step, it calls EnergyPlus and, from the output, calculates objective functions. In our case, functions are energy and comfort. The meta-heuristic algorithm changes its values in each iteration to reach optimal values in each step until the total iterations are finished.
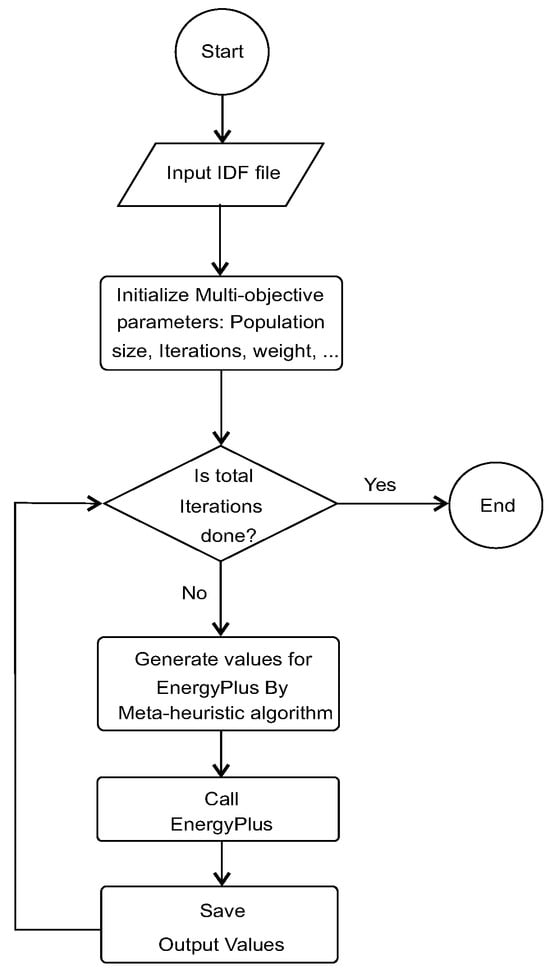
Figure 1.
Flowchart of hybrid proposed algorithm.
Figure 2 presents a comprehensive and innovative framework that bridges the power of multiple meta-heuristic algorithms with the advanced capabilities of the EnergyPlus simulator. This integration is designed to address complex challenges in the domain of building energy optimization, providing a more efficient and accurate approach to problem-solving.
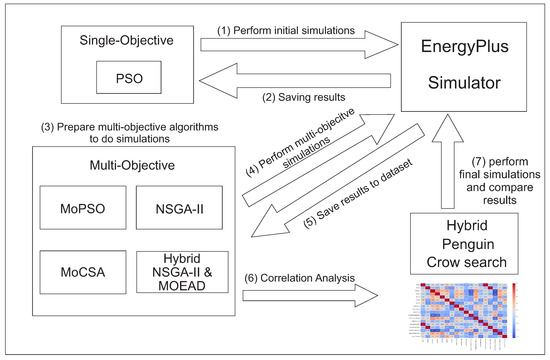
Figure 2.
TPMCD framework analysis.
At the core of the framework lies the EnergyPlus simulator, which is renowned for its ability to model and predict the energy performance of buildings with a high degree of detail. It takes into account various factors such as building geometry, materials, and HVAC systems to generate accurate energy consumption and comfort level forecasts. Surrounding the simulator are several meta-heuristic algorithms. For single-objective energy optimization, we used the PSO algorithm. PSO, with its swarm-based approach, explores building design and operation parameters to minimize energy consumption [22].
In multi-objective scenarios, we incorporated the Multi-Objective Particle Swarm Optimization (MoPSO) algorithm. It extends PSO to balance energy consumption and occupant comfort by maintaining an archive of non-dominated solutions [54]. NSGA-II is another key multi-objective algorithm. It uses non-dominated sorting to classify solutions, providing a range of optimal and near-optimal solutions for energy and comfort trade-offs [12]. MoCSA, inspired by the crow’s behavior, introduces memory and awareness to balance exploration and exploitation in the multi-objective search space [11]. The Hybrid NSGA-II-MOEAD algorithm, which combines NSGA-II and MOEAD, was also employed in the experiments. It can find diverse Pareto-optimal solutions by decomposing problems [13,14]. However, a novel hybrid penguin crow search algorithm (HCRPN) stands out. This hybrid combines the strengths of the penguin optimized algorithm and the crow search algorithm. Its hybrid nature and utilization of a True Random Number Generator (TRNG) enable it to explore the search space more comprehensively and converge towards better solutions [52].
The interaction of these algorithms with the EnergyPlus simulator occurs in a cyclic fashion. The meta-heuristic algorithms generate sets of potential solutions, which are then fed into the EnergyPlus simulator as input parameters. The simulator evaluates these solutions based on predefined energy and comfort metrics and returns the results to the algorithms. This feedback loop enables the algorithms to learn from the simulator’s output and adjust their search strategies accordingly, continuously refining the solutions until an optimal or near-optimal result is achieved.
Overall, this proposed framework holds great promise for revolutionizing the way that we approach building energy optimization based on EnergyPlus and automatic input parameter tuning, offering a synergistic combination of meta-heuristic optimization and detailed energy simulation that can lead to significant improvements in energy efficiency, cost savings, and occupant satisfaction.
3.3.2. Energy
Accurate energy calculation is paramount for effective building energy optimization. The fidelity of the building energy model, along with its detailed configuration within simulation software, directly impacts the precision and relevance of the predicted energy consumption. In this study, building energy performance was rigorously assessed using EnergyPlus version 24.2.0. Our building energy model, representing one floor of a university campus with HVAC facilities with different properties, with a 48-person capacity in the environment that will rarely be full and most of the time will be filled with to around 70% of capacity with students and employees, was meticulously constructed within EnergyPlus. Key parameters defining the thermal characteristics of the building envelope, internal gains such as lighting power density, equipment load, and detailed HVAC system configurations were precisely defined. For this research, the HVAC system was modeled to accurately capture the energy dynamics associated with heating, cooling, and ventilation.
The optimization objectives of this study primarily focus on minimizing total building energy consumption while enhancing thermal comfort through MRT adjustments. Consequently, the energy consumption calculation emphasized components directly influenced by HVAC system operation and internal loads. The total energy consumption for each simulation run was extracted from EnergyPlus outputs and is defined as the sum of the following key components in Equation (5), which collectively represent the dominant energy demands of the building during operation:
where is the total energy consumed specifically for space cooling. This term is highly responsive to setpoint changes and outdoor conditions. is the electrical energy consumed by interior lighting, modeled based on specified lighting power densities and operational schedules. is the electrical energy consumed by miscellaneous internal equipment such as computers and office appliances, modeled based on equipment power densities and usage schedules. is the electrical energy consumed by all fans within the HVAC system, crucial for air distribution and directly impacted by airflow rates, which are varied for ventilation and comfort. is the electrical energy consumed by pumps in the HVAC system, typically associated with chilled water loops, condenser water loops, or hot water circulation. is the energy associated with heat rejection, primarily from cooling towers or other condenser systems, representing the energy required to dissipate heat from the cooling process.
EnergyPlus calculated these individual terms based on the detailed physics of heat transfer, fluid flow, and system performance as defined by the model inputs over the simulation period. This comprehensive breakdown allowed for a precise evaluation of the energy impacts of our proposed HVAC parameter optimizations.
3.3.3. Thermal Comfort
Thermal comfort in mechanically conditioned buildings is typically evaluated using indices such as the Predicted Mean Vote (PMV), which integrates various environmental and personal factors, including air temperature, humidity, air velocity, metabolic rate, clothing insulation, and, crucially, the MRT. MRT is not a comfort index itself but rather a measure of the radiant heat exchange between an occupant and the surrounding surfaces. It represents the uniform temperature of an imaginary enclosure in which an occupant would exchange the same amount of radiant heat as in the actual non-uniform 1 environment. Therefore, accurately determining and influencing MRT is essential for achieving optimal thermal comfort.
Our research recognizes the significant impact of MRT on thermal comfort and, alongside energy consumption, considers it as a key parameter to be influenced through our optimization process. While the evaluation of MRT within building simulation tools like EnergyPlus and DesignBuilder has been extensively discussed in the literature [55], our work aims to surpass standard evaluation by actively optimizing building design parameters to achieve desired MRT levels that contribute to enhanced thermal comfort (potentially as reflected in improved PMV values) while simultaneously minimizing energy use.
The fundamental formula for calculating MRT is
where MRT is the Mean Radiant Temperature, N is the number of surfaces in the space, is the emissivity of surface j, is the view factor between the occupant (represented as surface i) and surface j, and is the temperature of surface j in Kelvin.
For simplicity and consistency with typical building energy simulation practices, EnergyPlus often calculates MRT based on a linearized form of the radiative heat exchange equation, approximating the fourth-power relationship. Our methodology utilizes the MRT values calculated by EnergyPlus within our automated optimization framework.
The accurate determination of remains a critical aspect of MRT calculation, particularly in complex geometries. EnergyPlus employs sophisticated algorithms to compute these factors. Our research leverages the capabilities of EnergyPlus for MRT calculation and focuses on how our novel hybrid optimization algorithm can manipulate building design variables to achieve optimal MRT values that contribute to overall thermal comfort and energy efficiency. By considering MRT directly in our optimization objectives, we aim to address a critical aspect of indoor environmental quality that is often secondary to pure energy consumption metrics in building design optimization.
3.3.4. Objective Function
Every multi-objective algorithm decides the calculation of objective functions based on multiple functions that might be minimized or maximized. In this research, energy consumption should be minimized while higher MRT values are better. The calculation of the objective function is based on the hyper-volume indicator for Pareto-front values [10]. The formula is written in Equation (7).
where is the hyper-volume of the two parameters and and are coefficients of energy and MRT, respectively. These coefficients can be changed based on the weight of objectives. In some cases, low energy usage is more important than people’s comfort; in other situations, people’s comfort in the building has a higher weight than energy consumption. Thus, these values are modifiable by experts who want to reach their preferred results.
4. Experiments and Results
All the experiments were performed on a PC with an Intel CPU i5-6500 3.20GHz and 8 gigabytes of RAM in Windows 10 Pro. The Python 3.7 programming language is used to generate simulations and analyze results.
For the purpose of this study, a representative building model, designated as “Building 1”, is situated in Dalian City, Liaoning Province, China, specifically at the Dalian Zhoushuizi International Airport site (Latitude: 38.908°, Longitude: 121.66°, Elevation: 32.6 m). This location is characterized by a monsoon-influenced humid continental climate, with design conditions ranging from a winter heating dry-bulb of −12.2 °C to a summer cooling dry-bulb of 31.1 °C. The building’s envelope incorporates constructions typical for a commercial or institutional structure, utilizing pre-defined EnergyPlus constructions such as ASHRAE 189.1-2009 ExtWall Mass ClimateZone 7-8 [56] for exterior walls, ASHRAE 189.1-2009 ExtRoof IEAD ClimateZone 7-8 for the roof [56], and ExtSlabCarpet 4in ClimateZone 1-8 for floors [56]. Windows are modeled with ASHRAE 189.1-2009 ExtWindow ClimateZone 7-8 3 construction [56]. Internal loads are defined by Office Bldg Light and Office Bldg Occ schedules, with default profiles indicating typical office hours and an Office Activity Default Schedule of 132 for metabolic rate. The HVAC system, although specific components are auto-sized by EnergyPlus to meet loads for zones like “Thermal Zone 1” through “Thermal Zone 15”, is designed to incorporate outdoor air ventilation according to ASHRAE 189.1-2009-Office-OpenOffice-CZ4-8 [56].
Ventilation standards, signifying a focus on mechanical ventilation for indoor air quality. The simulation runs annually from 15 May 2022 to 30 September 2022, using a 1 h timestep.
The model of the building is generated from DesignBuilder v7.0.2.006 software and contains 4 HVAC systems. The parameters for Air Loop HVAC 1 in the university building model are significant. Designated as an “AirLoop Name” with a focus on sensible load sizing, its design outdoor air flow rate is “Autosize”. Key values include a 0.47 central heating maximum system air flow ratio, along with specific preheat and precool temperatures and humidity ratios, 4.2° and 26.9° for central cooling and heating design supply air temperatures, respectively. Furthermore, 100% outdoor air is used in both cooling and heating. Supply air flow rate methods follow “DesignDay”, with defined fractions and per-unit values. Cooling and heating design capacities are autosized, and the central cooling capacity control method is “OnOff”, while occupant diversity is “Autosize”. Altogether, these parameters shape the system’s operation for optimal energy efficiency and comfort.
In every run, the objective function is called from the meta-heuristic algorithm, and EnergyPlus simulation is started. After finishing the simulation, the generated results from EnergyPlus are saved in a folder.
4.1. Computational Complexity
For the complexity analysis of the proposed algorithm, the pseudocode of Algorithm 5 is reviewed. Although using a hybrid approach will require more computations, its final results will overcome the number of resources. The main loop in the algorithm is in line 5, which is the “while NOT” termination condition. Let us set the condition to perform iterations T times. In the inner body of the loop, we have two hybrid algorithms of POA and CSA. For the penguins, there are g groups and p penguins in each group, and, for the nested “for loops”, it runs for POA. The next phase will be for the CSA algorithm, which will run for each crow c, so it runs c times, which is equal to the number of populations of the crows. The computational complexity of the algorithm will be . But it can be run more efficiently with a bit of code change, as mentioned in the comment after the 6th line of the algorithm. When running each group of penguins, groups do not interact with each other until the computation is finished, so group computation can run in parallel, and, after all groups finish their calculations, solutions between them will be shared. Therefore, groups can run in parallel with a simple software coding change. In this case, the complexity of the algorithm will be , where g is set equal to 1 because of the parallel manner.
In the case of CPU time, regarding how much time each iteration requires to execute on average, for the CSA, POA, and hybrid HCRPN algorithms, the average time of running for each iteration is around 15 s. It is the same for all three algorithms because all of them call the EnergyPlus simulator with the same model, but change some of the parameter values in the model. Therefore, the number of iterations and population of each algorithm have the most effect on execution time.
The complexity analysis of MOPSO gives , where N is the population size [57,58]. For NSGA-II, it is , where M is the number of objectives and N is population size [12]. MoCsa also has the complexity of , where N is the number of crows and t is the number of iterations. For Hybrid NSGA-II-MOEA/D algorithm complexity, two steps are considered: one is for NSGA-II, which has a complexity of , and the other one is MOEA/D, which has a complexity of , where M is the number of objectives, N is the population size, and T is neighborhood size. The hybrid approach that uses both algorithms has the complexity of [14]. Comparing the four algorithms, our proposed method has linear complexity like MoCsa, while MOPSO, NSGA-II, and Hybrid NSGA-II-MOEA/D algorithms have nonlinear complexity, requiring more computations and a longer time to reach the expected results.
4.2. Convergence Analysis
For the starting point, we decided to perform experiments on the energy optimization of the algorithms and compare the convergence. A total of 200 iterations was considered and all algorithms started with 217.7 of total energy, as Figure 3 shows. Over the first 7 iterations, all algorithms reached a large decline in energy and HCRPN had a lower decrease. Until 40 to 60 iterations, all algorithms have a steady value of energy and, after that, they have a regular decrement every 10 steps. Although MOPSO had a lower decline at the end, optimization steps were closer for fewer iterations than 10. NSGA-II and Hybrid NSGA-II-MOEA/D sometimes dominate each other, and this is the cause of their similarity, but, in the end, Hybrid NSGA-II-MOEA/D has a lower energy value because of the hybrid approach and the help of MOEA/D to reach a better optimum value. Our proposed algorithm resulted in lower energy than others with the help of the parallel groups in the penguin search algorithm and the adaptability of crows to their memory and flying length.
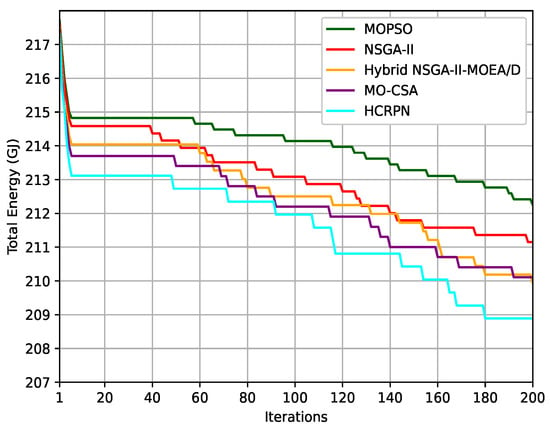
Figure 3.
Energy usage per iteration.
4.3. Benchmark Functions
Benchmark functions play a pivotal role in the field of multi-objective optimization. They serve as standardized test beds to assess the efficacy of diverse optimization algorithms. Among them, the ZDT-1 benchmark function is highly prominent. It comprises two objective functions and is defined over a set of decision variables. These objectives typically conflict with each other, mirroring real-world scenarios where trade-offs must be made. For example, in engineering designs, one objective could be minimizing resource consumption while the other aims to maximize product quality.
This study conducted experiments using several state-of-the-art multi-objective optimization algorithms. Firstly, the multi-objective particle swarm optimization (MOPSO) was implemented. MOPSO extends the fundamental PSO by maintaining an archive of non-dominated solutions. As its particles navigated the search space, they aimed to populate this archive with solutions that offered optimal trade-offs for the ZDT-1 objectives. The swarm behavior inherent in MOPSO enabled both exploration and exploitation.
The NSGA-II was also employed. Utilizing non-dominated sorting to categorize solutions selectively chooses individuals for the next generation. This process is crucial in generating a diverse set of solutions that approximated the Pareto front, thereby facilitating the understanding of the objective trade-offs.
The Hybrid NSGA-II-MOEA/D combined the strengths of NSGA-II and MOEA/D. The latter decomposed the problem into sub-problems. The hybrid algorithm effectively tackled the ZDT-1 problem, uncovering Pareto-optimal solutions and providing insights into the trade-offs.
The multi-objective crow search algorithm (MO-CSA), inspired by the behavior of crows, incorporated memory and awareness. Crows remembered their best positions and made decisions based on an awareness probability. In the context of ZDT-1, this feature contributed to a more balanced exploration of the search space in search of better solutions.
Finally, the hybrid crow search and penguin optimization (HCRPN) algorithm was tested. It integrated the unique behaviors of crows and penguins, leveraging the memory-based approach of crows and the social foraging-inspired behavior of penguins. Notably, HCRPN incorporated the use of a TRNG for picture noise to generate a random value based on the field of view of the crow and the decision of his awareness. In the context of optimizing the ZDT-1 function, the TRNG added an element of unpredictability. When dealing with the search space, the random perturbations from the TRNG, akin to introducing picture noise, disrupted potential stagnation points and helped the algorithm to explore more diverse regions. This, in turn, accelerated the convergence towards the Pareto front as particles shared information about advantageous regions.
In these experiments, metrics such as the generational distance and spread of solutions were utilized to evaluate the performance of the algorithms. These comparisons provided valuable insights into the strengths and weaknesses of each algorithm in optimizing the ZDT-1 function, furthering the knowledge in the field of multi-objective optimization.
Figure 4a compares the performance of MOPSO, NSGA-II, Hybrid NSGA-II-MOEA/D, MO-CSA, and HCRPN. Based on this figure, HCRPN and MO-CSA appear to be promising candidates for solving the ZDT1 problem. Their close approximation to the Pareto front suggests they effectively balance exploration and exploitation of the search space. However, it is important to remember that the performance of any multi-objective algorithm can vary depending on the specific problem characteristics and parameter settings.
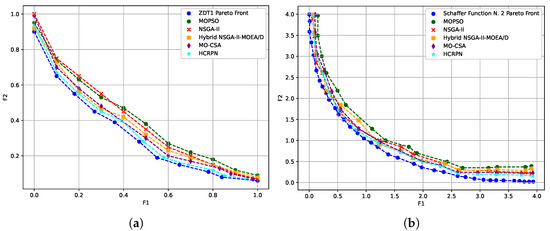
Figure 4.
Benchmark function tests. (a) Results of ZDT1 benchmark function. (b) Results of Shaffer N1 benchmark function.
The superior performance of hybrid crow search and penguin and MO-CSA can be attributed to several factors. Both algorithms incorporate mechanisms that effectively balance exploration and exploitation, enabling them to efficiently search the solution space and identify high-quality solutions. Additionally, their inherent diversity-preserving mechanisms help to maintain a broad range of solutions along the Pareto front, ensuring a comprehensive representation of the trade-off space. This is crucial for the Shaffer N1 function, which presents a complex, non-convex Pareto front with multiple local optima.
Figure 4b presents the Pareto fronts obtained by several multi-objective algorithms on the Shaffer N1 function. The Shaffer N1 function is a challenging bi-objective optimization problem characterized by a non-convex Pareto front with a complex shape.
Based on the visual analysis of the chart, our proposed algorithm and MO-CSA demonstrate a strong potential for solving the Shaffer N1 benchmark function effectively. Their ability to closely approximate the Pareto front and maintain diversity suggests their suitability for tackling complex multi-objective optimization problems with challenging landscapes. However, a more rigorous quantitative analysis, including the consideration of computational cost and sensitivity to parameter settings, is necessary for a comprehensive evaluation of their performance.
4.4. Correlation Analysis
The experiment was carried out as mentioned previously in Figure 2. After calling EnergyPlus several times with a multi-objective algorithm that generated different values of input parameters, a dataset was generated to analyze the impact of input parameters on energy. Duplicated rows were emitted, resulting in a dataset with 1008 rows and 73 input parameter values as columns, plus one column that iwa the result of the energy.
Input column names are mentioned in Table 2. The abbreviation of the input parameter is in the first column, and the detailed explanation of it is written in the second. Influencing parameters are the maximum and minimum setpoints for temperature, a fraction of heating, cooling, and air flow rate.

Table 2.
Generated dataset columns definitions.
The correlation analysis, as depicted in Figure 5, provided critical insights into the relationship between HVAC system parameters and total site energy consumption, moving beyond mere statistical values to interpret their physical implications. Notably, Cooling Coil Design Supply Air Temperature (CCDSAT) exhibited the strongest positive correlation (0.46), underscoring that a higher supply air temperature demands increased airflow to maintain thermal comfort, consequently escalating fan energy consumption—a major component of HVAC energy use. Similarly, Preheat Coil Air Outlet Temperature (PreHeat, 0.34) showed a substantial positive correlation, directly linking higher preheat setpoints to increased heating energy consumption, particularly during colder periods. The correlation with Chiller Maximum Airflow (CHMaxAir, 0.26) further reinforced the significant impact of fan energy on overall consumption, as moving more air, even for cooling, requires considerable electricity.
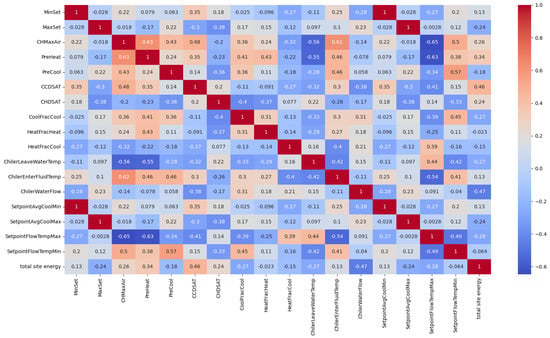
Figure 5.
Correlation analysis of input variables.
These findings offer a clear strategic direction for the optimization algorithm, emphasizing the dominant influence of air distribution and temperature setpoints on building energy use. By strategically manipulating parameters with higher correlations, such as CCDSAT and PreHeat, the HCRPN algorithm can efficiently target areas with the greatest potential for energy reduction. While other parameters also contribute, the highlighted correlations demonstrate the robustness of our simulation model and the validity of our optimization approach, as these observed relationships align well with fundamental principles of building physics.
4.5. Hyperparameters
For the input of the crow search, penguin search, and hybrid proposed algorithm, some parameters exist that should be set before running the simulations. Some of them can be initialized like default values, but in some cases they can be changed to reach better outcomes. Although they might be changed by trial and error, they can be set consciously if the person has deep knowledge about meta-heuristic algorithms. Table 3 shows the input parameters for the hybrid crow search and penguin algorithm.

Table 3.
Hyperparameters for hybrid crow and penguin algorithm.
We selected an awareness radius of 0.21 for the crow algorithm based on trial analyses, indicating that smaller values led to premature convergence, while larger values reduced convergence speed without further improving solution quality. The number of crows was set to 40, which was chosen by testing different values between 10 and 100 using trial and error, with a number of 40 resulting in better values. Input parameters of POA were set based on [51].
4.6. Energy and MRT Experiments Setup
For the first steps, we started with 50 iterations of each algorithm and ended with 200, adding 50 each step. In the second step, we decided to increase the number of steps from 50 to 100 and start from 300 iterations, ending with 600. All experiments were performed 20 times, and the average values of parameters are shown in the figures.
4.7. Energy Comparison
Experiments were performed with different iteration values for the simulation of energy values. Figure 6a shows the results. Over the first 50 iterations, all the algorithms have approximately the same value of energy, around 217.75 gigajoules, except NSGA-II, which is 217.25, showing a little decrease of around 0.5 gigajoules—this is because of its non-dominated sorting feature, causing it to converge more quickly. At the second level, NSGA-II has also reached a greater decrease, equal to 214, while others are 215.5 to 216.5; on the other hand, MOCSA, Hybrid NSGA-II-MOEAD/D, and HCRPN have higher values, even greater than MOPSO, and this is because of their complexity. When iterations reach 150 and 200, the substituting results happen, and the two hybrid algorithms and MOCSA reach better results than the first two algorithms. This is because they are hybrid, and more computations are required to catch the global optima. In 150 and 200 iterations, our proposed algorithm reached better results than the others, and this is because of their linear complexity, helping to reach better optimization. MOCSA with 208.5 gigajoules surpassed Hybrid NSGA-II-MOEAD/D with 209 gigajoules at 150 iterations, but, with 200 iterations, NSGA-II-MOEAD/D improved because of the greater global space exploration.
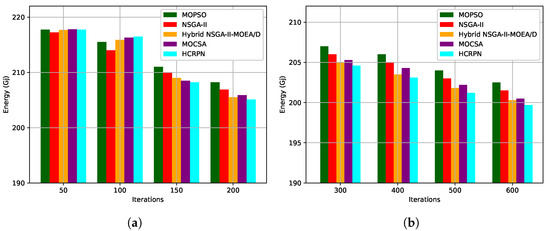
Figure 6.
(a) Energy comparison of algorithms with 50–200 iterations. (b) Energy comparison Of algorithms with 300–600 iterations.
Experiments were also tested with more iterations. Figure 6b depicts the results with 300 to 600 iterations with a step of 100. At 300 iterations, HCRPN had 204.6 Gj while Hybrid NSGA-II-MOEA/D had 205 Gj at the second rate; the largest value was MOCPSO with 207 Gj. At 400 iterations, the ranking of the algorithms was the same, with 203.1 Gj for our proposed algorithm as the first one and 206 Gj for MOPSO as the last, i.e., the one with the largest value of energy. At 500 iterations, 204, 203, 201.8, 202.2 and 201.2 were the values for MOCPSO, NSGA-II, Hybrid NSGA-II-MOEA/D, and HCRPN, respectively. Finally, at 600 iterations, our algorithm reached 199.7 Gj, with the lowest energy value of all algorithms. By increasing the number of iterations in the meta-heuristic algorithms, it is clear that the results of the two hybrid algorithms and also MOCSA became better than the first two. In all steps, Hybrid NSGA-II-MOEA/D and HCRPN have the nearest results to each other, but our proposed method was ultimately the best.
4.8. MRT Comparison
The calculation of MRT was carried out after executing the number of iterations in EnergyPlus. It was computed from the final HTML file generated as a report from EnergyPlus. Figure 7a shows five levels, from 50 iterations to 200 with a step of 50. In the beginning, NSGA-II showed a better comfort value 691,039.7 than other algorithms because of its fast convergence at the starting iterations. Other methods had the same value of 691,040. In the second step, with 100 iterations, NSGA-II also reached 691,039.1, while MOCSA was 691,039.4 and MOPSO was 691,039.7 at the second and third ranks. By performing more experiments at iteration 150, MOCSA reached a better MRT value of 691,035 at 150 iterations, which was the first rank, but, with a final number of 200 iterations, our algorithm surpassed others with value of 691,031 because of its better exploration and exploitation of the hybrid penguins and crows.
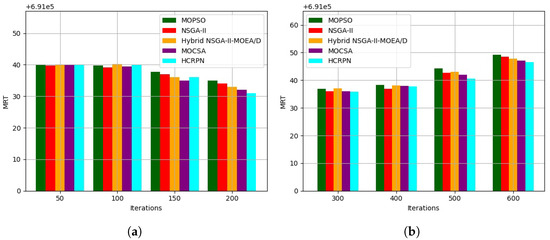
Figure 7.
(a) MRT comparison Of algorithms with 50–200 iterations. (b) MRT comparison Of algorithms with 300–600 iterations.
Figure 7b shows the rest of the experiments, with different steps of 100 that range from 300 to 600. By increasing the number of iterations, MOPSO had a higher MRT value, from 691,036.8 with 300 iterations to 691,049.2 with 600 iterations, than other algorithms; this is because of its weakness in finding optimal points with more iterations and its tendency to stick to non-global optimum points. On the other hand, NSGA-II resulted in better values because of its smart ability to search over a wide solution space. At 300 and 400 iterations, with values of 691,036 and 691,036.8, respectively, NSGA-II had acceptable MRT compared to other algorithms, but, at 500 and 600 iterations, other advanced algorithms reached better values. Hybrid NSGA-II MOEAD/D with 691,047.8 was better than its sibling NSGA-II with 691,048.5 at iteration 600; it is shown that hybrid approaches will obtain a better outcome with an increase in the number of iterations. MOCSA values were near Hybrid NSGA-II MOEAD/D with a slightly better value of MRT. Finally, our proposed algorithm resulted in better values in all steps and showed that, with more iterations, HCRPN had better convergence in the case of MRT optimization.
Finally, the results of all experiments for the energy and MRT values are written in Table 4 and Table 5. Columns under each iteration number show the average value of 20 runs and, inside each set of parentheses, the standard deviation of multiple runs is shown. The average of four algorithms is calculated from four compared ones: MOPSO, NSGA-II, Hybrid NSGA-II MOEAD/D, and MOCSA, and improvement in percent is computed from the numerical difference values of HCRPN and this average.

Table 4.
Energy values of algorithms in the experiments.

Table 5.
MRT values of algorithms in the experiments.
At the beginning of the experiments in Table 4 with 50 and 100 iterations, NSGA-II achieved better energy values of 217.25 and 214, respectively, compared to the other four algorithms. This is due to the fast convergence of NSGA-II with fewer iterations. Also, in the parentheses, 0.2 and 0.7 show the lower standard deviation obtained by calculating Pareto fronts. By increasing the number of iterations, our proposed algorithm overcame the others because of its hybrid approach and random TRNG position search in the crow search algorithm. For its standard deviation, it had lower values than others, except with 150 and 200 iterations—MOCSA had 0.3 and 1 as lower values. This may be the result of original random values instead of TRNG, as is the nature of random number generation.
For MRT in Table 5, NSGA-II had better average values of 691,039.7 and 691,039.1 at 50 and 100 iterations, respectively. As mentioned before, this is because of its fast convergence to Pareto fronts in lower iterations. By increasing the number of iterations to 150, the average value of MRT for MOCSA of 691,035 overcame others, while from 200 to 600 iterations our proposed method resulted in better MRT, except at 400, at which point NSGA-II had a better value of 691,036.8. For standard deviation, different behaviors happened for different algorithms. At 50, 100, and 150 iterations, NSGA-II had the lowest standard deviation, while at 200 and 300 iterations HCRPN had the lowest. At 400 and 500, Hybrid NSGA-II MOEAD/D and, at 600, MOCSA had the lowest standard deviation. The random values generated by meta-heuristic at every step and initializing the input parameters of the algorithms resulted in different standard deviations while performing 20 tests continuously.
5. Conclusions
This study addressed the critical challenge of simultaneously optimizing building energy consumption and occupant thermal comfort, with a specific focus on MRT. To achieve this, we developed a novel hybrid meta-heuristic algorithm, HCRPN, which leverages the efficient global exploration of the crow search algorithm, enhanced with a TRNG random noise generator, and the robust local-optimum avoidance of the penguin search optimization algorithm.
In the first steps, the interaction of the EnergyPlus simulator with the Python programming language was developed and, as an initial experiment, the single-objective PSO algorithm was implemented in Python to test multiple simulations in EnergyPlus automatically. In the second stage, simulated results were saved for further analysis and a dataset was generated to study the relation of parameters and their impact on energy and MRT, after which correlation analysis was performed. Finally, multi-objective algorithms were developed beside our proposed algorithm to carry out several experiments, and results were saved, studied, and compared in detail.
Through rigorous EnergyPlus simulations, our results demonstrate that HCRPN significantly outperformed the average of state-of-the-art multi-objective algorithms, namely, MOSPSO, NSGA-II, Hybrid NSGA-II MOEAD/D, and MOCSA, achieving a 7% reduction in energy consumption and a 3% improvement in MRT values, which are conducive to comfort. These improvements hold considerable potential for reducing operational costs and carbon emissions in buildings, while even the seemingly small enhancement in MRT can positively impact occupant thermal sensation and overall well-being. The ability of HCRPN to effectively balance these often-conflicting objectives highlights its value for designing more sustainable and comfortable built environments. Additionally, we aim to make the framework independent of a specific model, allowing it to work with various input models. Furthermore, we plan to extend it as a recommendation system that offers the selection and modification of input parameters from a large set.
6. Future Work
Looking ahead, future work will be centered around exploring and implementing a more computationally efficient alternative to EnergyPlus. Given the time-consuming nature of EnergyPlus simulations, especially when dealing with large-scale projects or numerous optimization iterations, substituting it with a faster method is crucial. This new approach could potentially reduce the overall time required for energy and comfort analysis and optimization, enabling more rapid decision-making in building design and operation. Additionally, benefiting from machine learning features such as predicting outputs from the input parameters of EnergyPlus can improve the speed of the experiments, but extensive knowledge and data from the simulation are required to avoid faulty results. Further research will be carried out to validate the new method’s accuracy and reliability in comparison with EnergyPlus, ensuring that the high-quality results obtained in this study can be maintained or even improved upon. This will be the focus of our future study. In summary, our HCRPN algorithm achieved on average a 7% reduction in energy consumption and a 3% improvement in MRT comfort compared to four baseline algorithms, reflecting a meaningful balance of building energy efficiency and occupant well-being.
Author Contributions
Conceptualization, T.Z., Y.R., and A.G.; methodology, T.Z., A.G., and R.A.; software, R.A.; validation, Y.S.R.; formal analysis, Y.R.; investigation, Y.R. and R.A.; resources, T.Z.; data curation, A.G.; writing—original draft preparation, R.A.; writing—review and editing, R.A.; visualization, R.A.; supervision, T.Z., Y.R., and A.G.; project administration, T.Z.; funding acquisition, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Dalian University of Technology, Dalian, China.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
This research was conducted during Reza Akraminejad visiting research period at Dalian University of Technology, supported by the Institute of Building Energy. He would likes to express his sincere gratitude to Tianyi Zhao, Yacine Rezgui, and Ali Ghoroghi for their guidance and support during his visit. He also thanks the Department of Building Energy at Dalian University of Technology for providing the necessary resources and infrastructure.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, Z.; Zhang, W.; Tang, R.; Wang, H.; Korolija, I. Reinforcement learning in building controls: A comparative study of algorithms considering model availability and policy representation. J. Build. Eng. 2024, 90, 109497. [Google Scholar] [CrossRef]
- Dogan, A.; Kayaci, N.; Kanbur, B.B.; Demir, H. Experimental investigation of mean radiant temperature trends for a ground source heat pump-integrated radiant wall and ceiling heating system. Buildings 2023, 13, 2420. [Google Scholar] [CrossRef]
- Huerto-Cardenas, H.; Leonforte, F.; Aste, N.; Del Pero, C.; Evola, G.; Costanzo, V.; Lucchi, E. Validation of dynamic hygrothermal simulation models for historical buildings: State of the art, research challenges and recommendations. Build. Environ. 2020, 180, 107081. [Google Scholar] [CrossRef]
- D’Agostino, D.; Minelli, F.; Minichiello, F. HVAC System Energy Retrofit for a University Lecture Room Considering Private and Public Interests. Energies 2025, 18, 1526. [Google Scholar] [CrossRef]
- Mokhberi, P.; Mokhberi, P.; Izadi, M.; Nesaii, M.B.; Yaici, W.; Minelli, F. Thermal regulation enhancement in multi-story office buildings: Integrating phase change materials into inter-floor void formers. Case Stud. Therm. Eng. 2024, 60, 104792. [Google Scholar] [CrossRef]
- D’Agostino, D.; Minelli, F.; Minichiello, F.; Musella, M. Improving the indoor air quality of office buildings in the post-pandemic era—impact on energy consumption and costs. Energies 2024, 17, 855. [Google Scholar] [CrossRef]
- d’Ambrosio Alfano, F.R.; Olesen, B.W.; Pepe, D.; Palella, B.I. Working with different building energy performance tools: From input data to energy and indoor temperature predictions. Energies 2023, 16, 743. [Google Scholar] [CrossRef]
- Gao, Y.; Peng, L.; Li, F.; Liu, M.; Li, W. Multi-objective opposition-based learning fully informed particle swarm optimizer with favour ranking. In Proceedings of the 2013 IEEE International Conference on Granular Computing (GrC), Beijing, China, 13–15 December 2013; pp. 114–119. [Google Scholar]
- Kouka, N.; Fdhila, R.; Hussain, A.; Alimi, A.M. Dynamic Multi Objective Particle Swarm optimization with Cooperative Agents. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Akraminejad, R.; Khaledian, N.; Nazari, A.; Voelp, M. A multi-objective crow search algorithm for optimizing makespan and costs in scientific cloud workflows (CSAMOMC). Computing 2024, 106, 1777–1793. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Srinath, N.; Yilmazlar, I.O.; Kurz, M.E.; Taaffe, K. Hybrid multi-objective evolutionary meta-heuristics for a parallel machine scheduling problem with setup times and preferences. Comput. Ind. Eng. 2023, 185, 109675. [Google Scholar] [CrossRef]
- Vaseghi, A.; Capano, C.D. Comparative analysis of insulation strategies for improving thermal performance of wall to parkade suspended slab. Energy Built Environ. 2025, 6, 147–160. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Chen, Z.; Cui, Y.; Zheng, H.; Ning, Q. Optimization and prediction of energy consumption, light and thermal comfort in teaching building atriums using NSGA-II and machine learning. J. Build. Eng. 2024, 86, 108687. [Google Scholar] [CrossRef]
- Wagiman, K.R.; Abdullah, M.N.; Hassan, M.Y.; Mohammad Radzi, N.H. A new metric for optimal visual comfort and energy efficiency of building lighting system considering daylight using multi-objective particle swarm optimization. J. Build. Eng. 2021, 43, 102525. [Google Scholar] [CrossRef]
- Homod, R.Z.; Yaseen, Z.M.; Hussein, A.K.; Almusaed, A.; Alawi, O.A.; Falah, M.W.; Abdelrazek, A.H.; Ahmed, W.; Eltaweel, M. Deep clustering of cooperative multi-agent reinforcement learning to optimize multi chiller HVAC systems for smart buildings energy management. J. Build. Eng. 2023, 65, 105689. [Google Scholar] [CrossRef]
- Nasruddin; Sholahudin; Satrio, P.; Mahlia, T.M.I.; Giannetti, N.; Saito, K. Optimization of HVAC system energy consumption in a building using artificial neural network and multi-objective genetic algorithm. Sustain. Energy Technol. Assessments 2019, 35, 48–57. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-international conference on neural networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway Township, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Makhadmeh, S.N.; Al-Betar, M.A.; Dalbah, L.M.; Al-Redhaei, A.; Kouka, S.; Enshassi, O.S. Multi-objective Ant Colony Optimization. Arch. Comput. Methods Eng. 2024, 32, 995–1037. [Google Scholar] [CrossRef]
- Pan, Y.; Zhu, M.; Lv, Y.; Yang, Y.; Liang, Y.; Yin, R.; Yang, Y.; Jia, X.; Wang, X.; Zeng, F.; et al. Building energy simulation and its application for building performance optimization: A review of methods, tools, and case studies. Adv. Appl. Energy 2023, 10, 100135. [Google Scholar] [CrossRef]
- Oueslati, F. Hybrid renewable system based on solar wind and fuel cell energies coupled with diesel engines for Tunisian climate: TRNSYS simulation and economic assessment. Int. J. Green Energy 2021, 18, 402–423. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, L.; Luo, Z.; Han, X.; Zhao, T. Forecasting building plug load electricity consumption employing occupant-building interaction input features and bidirectional LSTM with improved swarm intelligent algorithms. Energy 2024, 288, 129651. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, Z.; Rezgui, Y.; Zhao, T. Enhancing building energy consumption prediction introducing novel occupant behavior models with sparrow search optimization and attention mechanisms: A case study for forty-five buildings in a university community. Energy 2024, 294, 130896. [Google Scholar] [CrossRef]
- Dsilva Winfred Rufuss, D.; Sonu Ashritha, K.; Suganthi, L. Green energy revolution: A unique approach for energy forecasting and optimization towards sustainable energy planning and social development. Environ. Dev. Sustain. 2024, 1–28. [Google Scholar] [CrossRef]
- Qiao, X.; Zhao, T.; Zhang, X.; Li, Y. Multi-objective optimization of building integrated photovoltaic windows in office building. Energy Build. 2024, 318, 114459. [Google Scholar] [CrossRef]
- Wang, H.; Chen, B.; Sun, H.; Li, A.; Zhou, C. AnFiS-MoH: Systematic exploration of hybrid ANFIS frameworks via metaheuristic optimization hybridization with evolutionary and swarm-based algorithms. Appl. Soft Comput. 2024, 167, 112334. [Google Scholar] [CrossRef]
- Delavar, A.G.; Akraminejad, R.; Mozafari, S. HDECO: A method for Decreasing energy and cost by using virtual machine migration by considering hybrid parameters. Comput. Commun. 2022, 195, 49–60. [Google Scholar] [CrossRef]
- Ghorbannia Delavar, A.; Akraminejad, R.; Mozafari, S. WSTMOS: A Method For Optimizing Throughput, Energy, And Latency In Cloud Workflow Scheduling. J. Inf. Commun. Technol. 2023, 57, 62. [Google Scholar]
- Delavar, A.G.; Akraminejad, R.; Kazemipour, F. MHSC: A meta-heuristic method to optimize throughput and energy using sensitivity rate computing. Future Gener. Comput. Syst. 2025, 166, 107624. [Google Scholar] [CrossRef]
- Delavar, A.G.; Bagheri, H. EDLIoT: A method for decreasing energy consumption and latency using scheduling algorithm in Internet of Things. J. Ind. Inf. Integr. 2024, 42, 100719. [Google Scholar] [CrossRef]
- GhorbanniaDelavar, A.; Jormand, Z. FMORT: The Meta-Heuristic routing method by integrating index parameters to optimize energy consumption and real execution time using FANET. Comput. Networks 2024, 255, 110869. [Google Scholar] [CrossRef]
- Khaledian, N.; Khamforoosh, K.; Azizi, S.; Maihami, V. IKH-EFT: An improved method of workflow scheduling using the krill herd algorithm in the fog-cloud environment. Sustain. Comput. Informatics Syst. 2023, 37, 100834. [Google Scholar] [CrossRef]
- Khaledian, N.; Khamforoosh, K.; Akraminejad, R.; Abualigah, L.; Javaheri, D. An energy-efficient and deadline-aware workflow scheduling algorithm in the fog and cloud environment. Computing 2024, 106, 109–137. [Google Scholar] [CrossRef]
- Khaledian, N.; Razzaghzadeh, S.; Haghbayan, Z.; Völp, M. Hybrid Markov chain-based dynamic scheduling to improve load balancing performance in fog-cloud environment. Sustain. Comput. Informatics Syst. 2025, 45, 101077. [Google Scholar] [CrossRef]
- Kosari, S.; Hosseini Shirvani, M.; Khaledian, N.; Javaheri, D. A Hybrid Discrete Grey Wolf Optimization Algorithm Imbalance-ness Aware for Solving Two-dimensional Bin-packing Problems. J. Grid Comput. 2024, 22, 1–36. [Google Scholar] [CrossRef]
- Abbasi, S.; Khaledian, N.; Rahmani, A.M. Trust management in the internet of vehicles: A systematic literature review of blockchain integration. Int. J. Inf. Secur. 2024, 23, 3065–3088. [Google Scholar] [CrossRef]
- Energyplus, I. EnergyPlus™ Version 23.1.0 Documentation. 2023. Available online: https://energyplus.net/assets/nrel_custom/pdfs/pdfs_v23.1.0/GettingStarted.pdf (accessed on 28 March 2023).
- Bannoud, M.A.; da Silva, C.A.M.; Martins, T.D. Applications of metaheuristic optimization algorithms in model predictive control for chemical engineering processes: A systematic review. Annu. Rev. Control 2024, 58, 100973. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Nobahari, H.; Bighashdel, A. MOCSA: A Multi-Objective Crow Search Algorithm for Multi-Objective optimization. In Proceedings of the 2017 2nd Conference on Swarm Intelligence and Evolutionary Computation (CSIEC), Kerman, Iran, 7–9 March 2017; pp. 60–65. [Google Scholar]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Wilm, T.; Normann, P.; Stepprath, F. Pareto Front Approximation for Multi-Objective Session-Based Recommender Systems. In Proceedings of the 18th ACM Conference on Recommender Systems, Bari, Italy, 14–18 October 2024; pp. 809–812. [Google Scholar]
- Bao, C.; Xu, L.; Goodman, E.D.; Cao, L. A novel non-dominated sorting algorithm for evolutionary multi-objective optimization. J. Comput. Sci. 2017, 23, 31–43. [Google Scholar] [CrossRef]
- Singh, H.; Tyagi, S.; Kumar, P. Crow–penguin optimizer for multiobjective task scheduling strategy in cloud computing. Int. J. Commun. Syst. 2020, 33, e4467. [Google Scholar] [CrossRef]
- Gheraibia, Y.; Moussaoui, A.; Yin, P.Y.; Papadopoulos, Y.; Maazouzi, S. PeSOA: Penguins search optimisation algorithm for global optimisation problems. arXiv 2018, arXiv:1809.09895. [Google Scholar]
- Gheraibia, Y.; Moussaoui, A. Penguins search optimization algorithm (PeSOA). In Proceedings of the Recent Trends in Applied Artificial Intelligence: 26th International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, IEA/AIE 2013, Amsterdam, The Netherlands, 17–21 June 2013; Proceedings 26; Springer: Berlin/Heidelberg, Germany, 2013; pp. 222–231. [Google Scholar]
- Li, R. A true random number generator algorithm from digital camera image noise for varying lighting conditions. In Proceedings of the SoutheastCon 2015, Fort Lauderdale, FL, USA, 9–12 April 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 1–8. [Google Scholar]
- Akraminejad, R.; Kazemipour, F.; Davoodi, M.K. A Hybrid Crow Search And Penguin Optimization Algorithm (CPMM) for Efficient Cloud Workflow Scheduling. In Proceedings of the 2024 15th International Conference on Information and Knowledge Technology (IKT), Isfahan, Iran, 24–26 December 2024; pp. 121–126. [Google Scholar]
- Coello Coello, C.; Lechuga, M. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Alfano, F.R.d.; Pepe, D.; Riccio, G.; Vio, M.; Palella, B.I. On the effects of the mean radiant temperature evaluation in the assessment of thermal comfort by dynamic energy simulation tools. Build. Environ. 2023, 236, 110254. [Google Scholar] [CrossRef]
- ASHRAE 189.1-2009; Standard for the design of high-performance green buildings. ASHRAE: Peachtree Corners, GA, USA, 2017.
- Knowles, J.D.; Corne, D.W. Approximating the nondominated front using the Pareto archived evolution strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef] [PubMed]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).