Seismic Performance of Self-Centering Frame Structures with Additional Exterior Wall Panels Connected by Flexible Devices
Abstract
1. Introduction
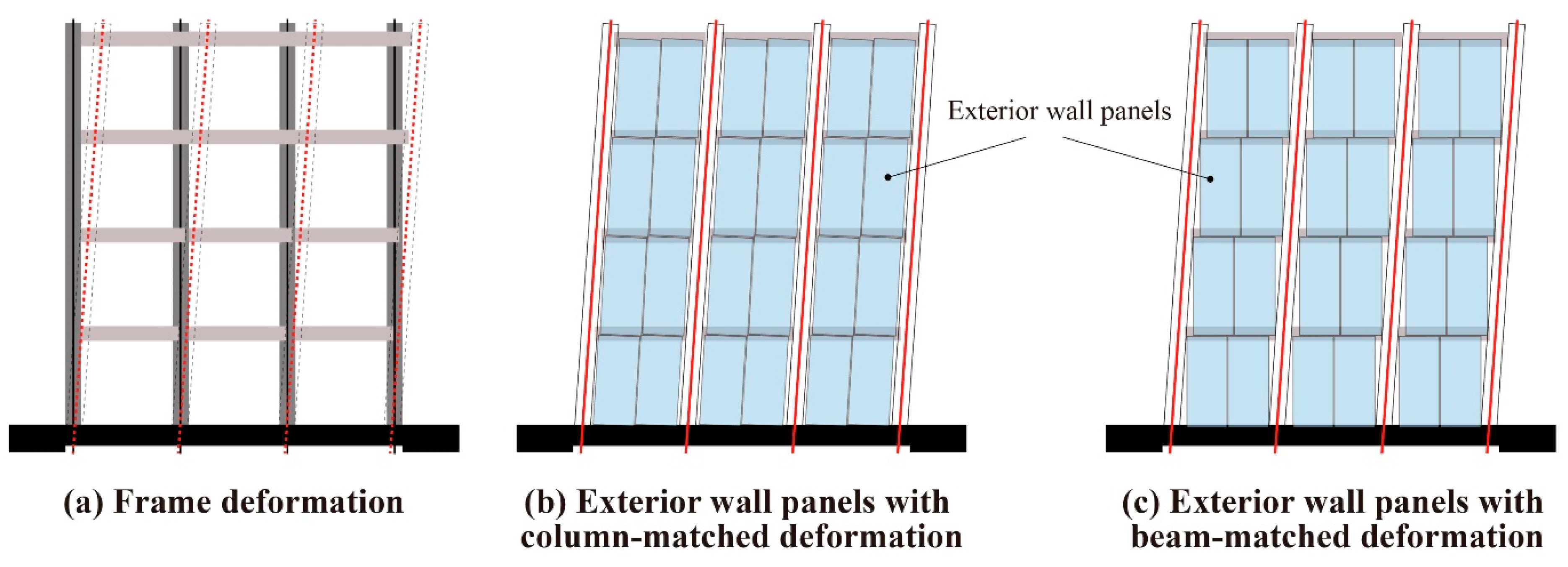
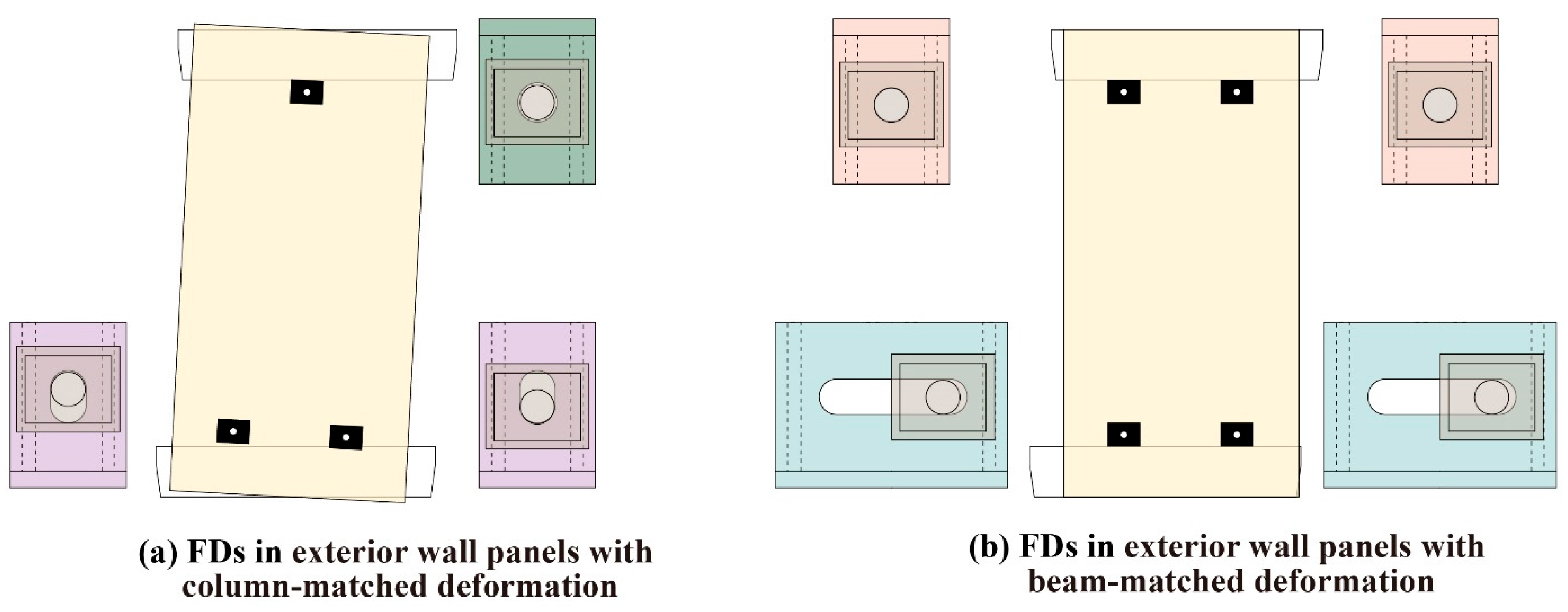
2. Design Concept of Flexible Devices
3. Overview of the Experiment
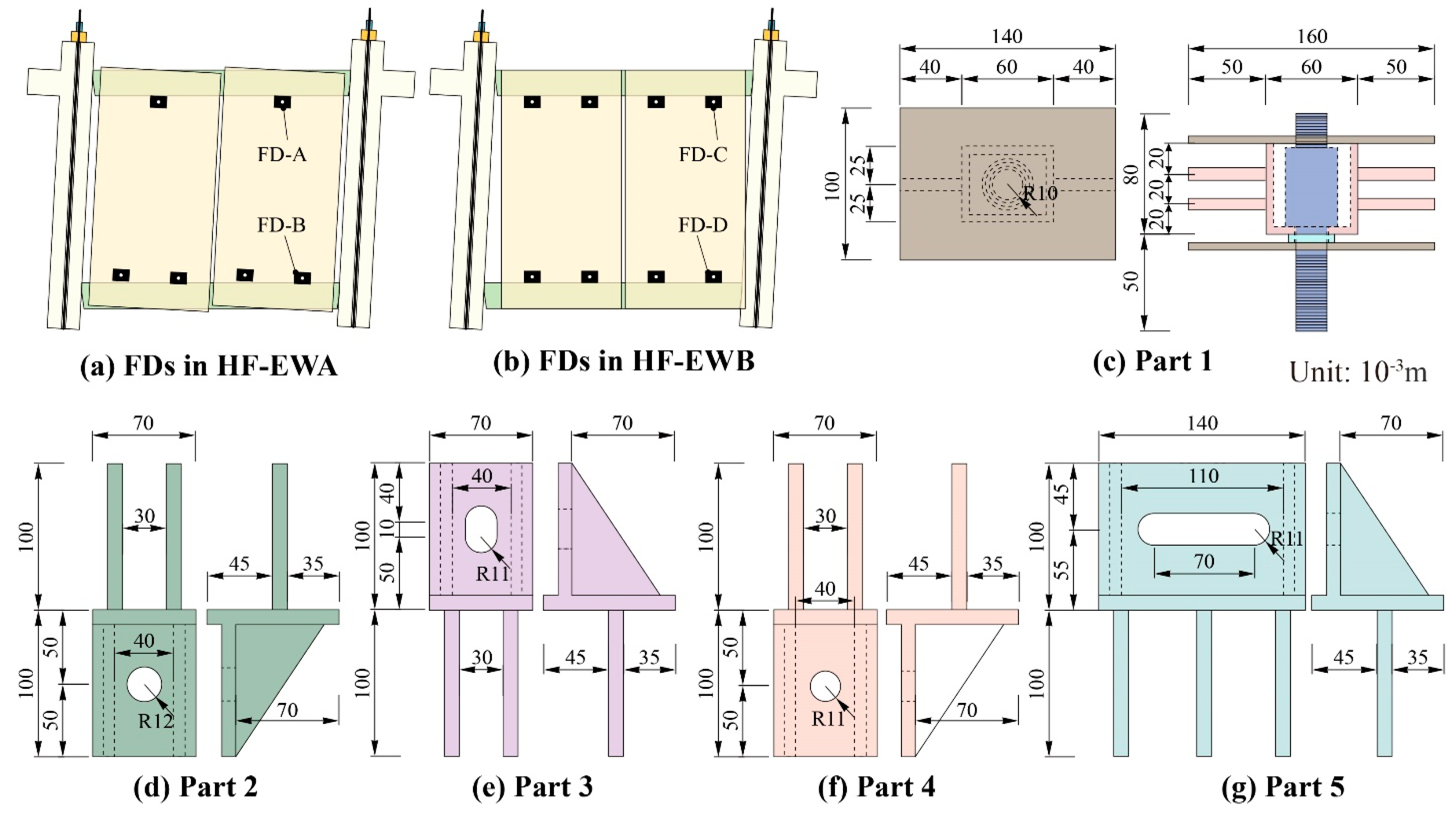
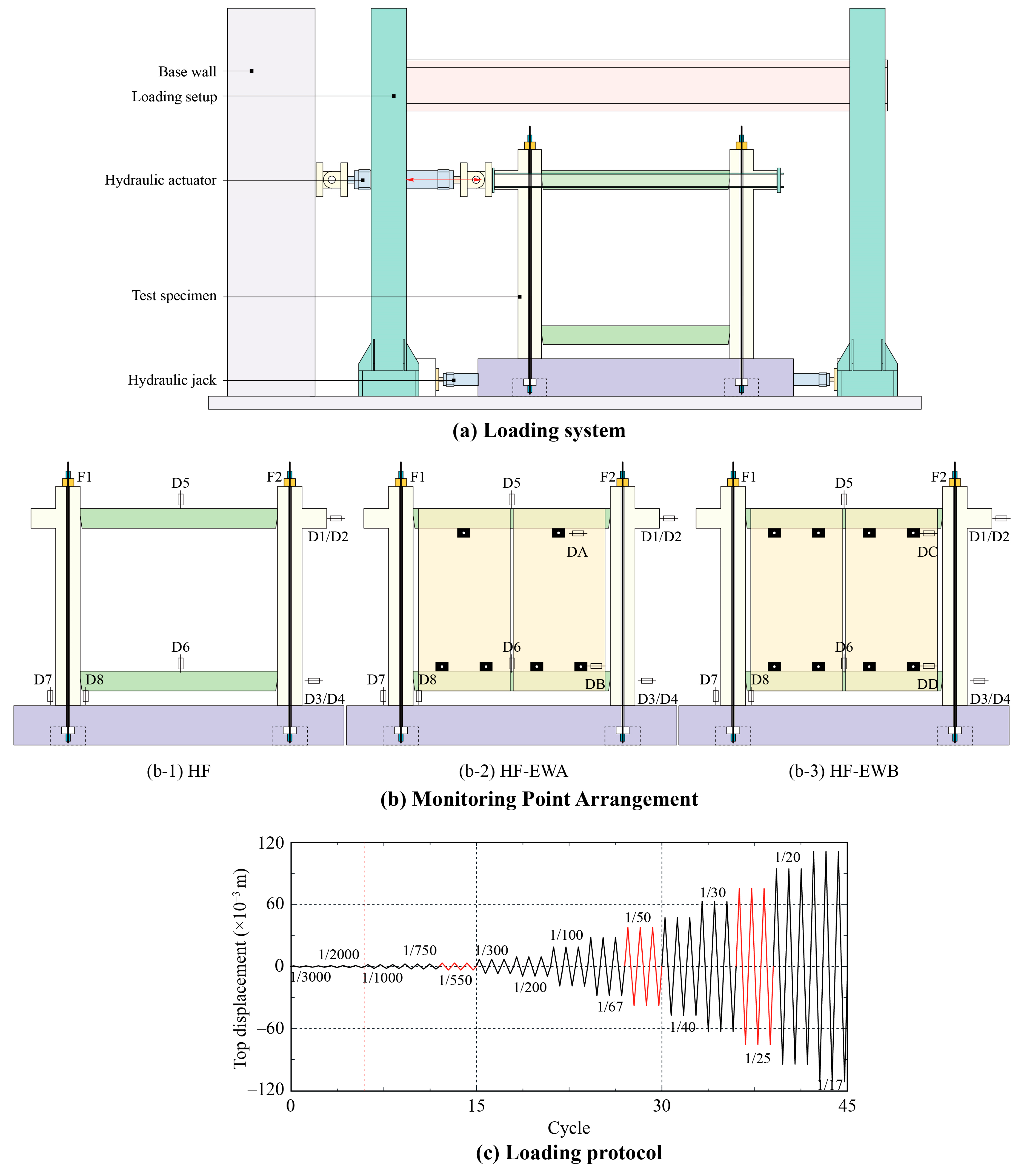
3.1. Specimen Design
3.2. Loading Scheme
4. Experimental Results
4.1. Failure Characteristics
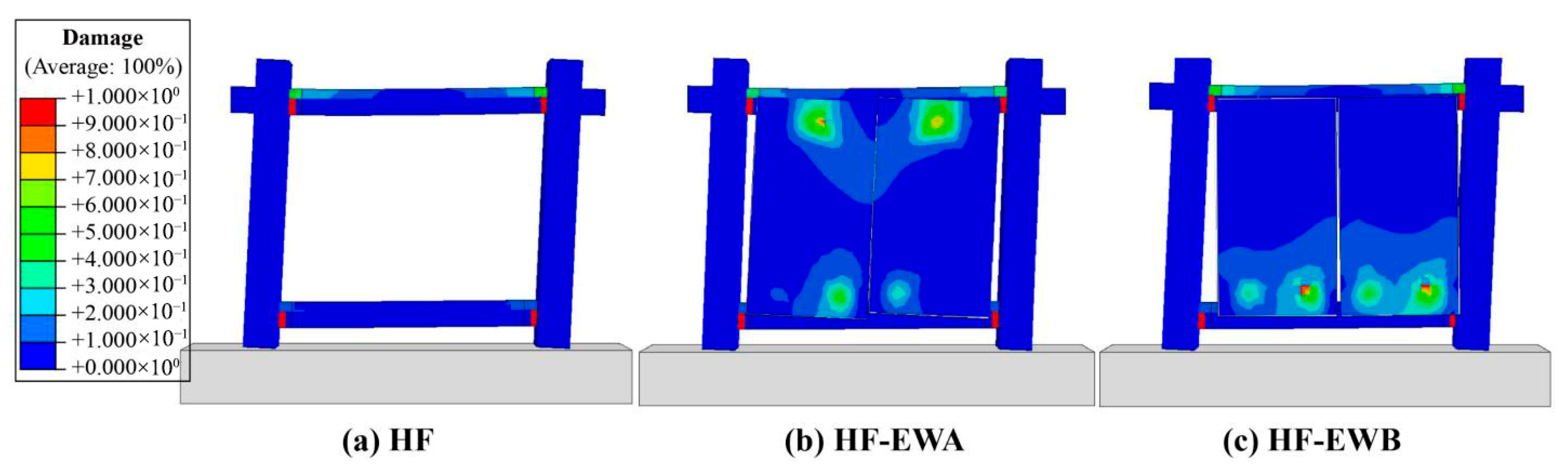
4.1.1. HF Specimen
4.1.2. HF-EWA Specimen
4.1.3. HF-EWB Specimen
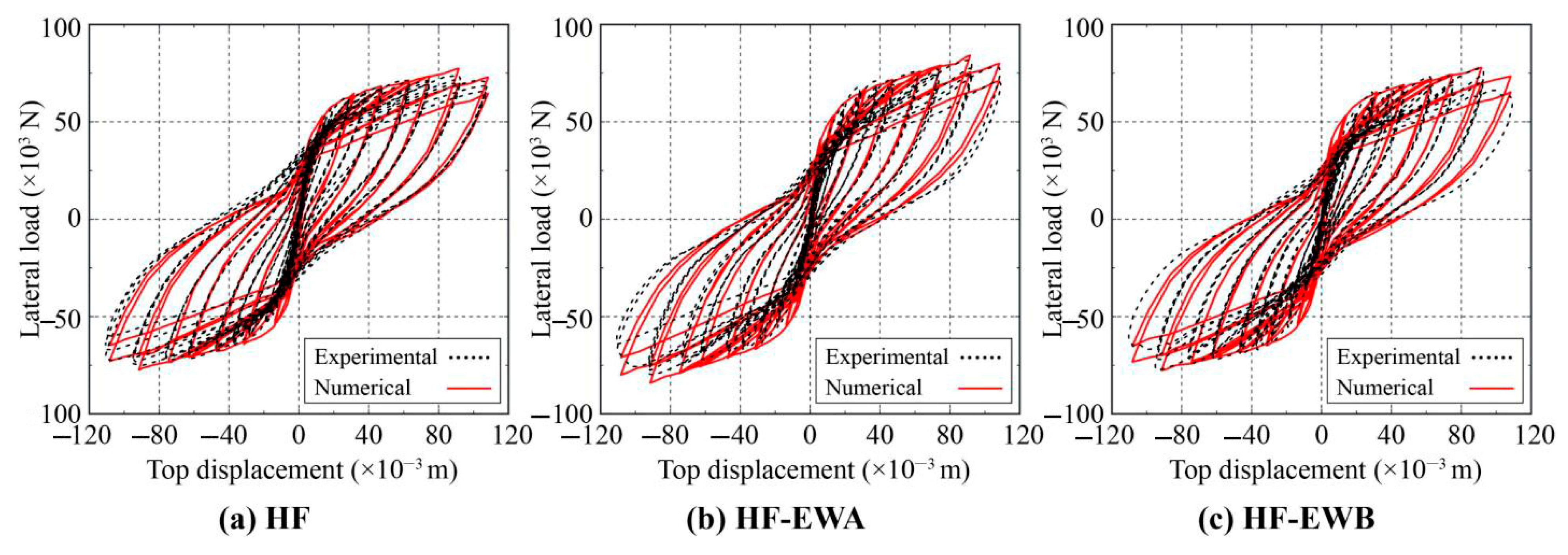
4.2. Hysteretic and Skeleton Curves
4.3. Stiffness Degradation and Energy Dissipation
4.4. Displacement of FDs
5. Finite Element Simulation
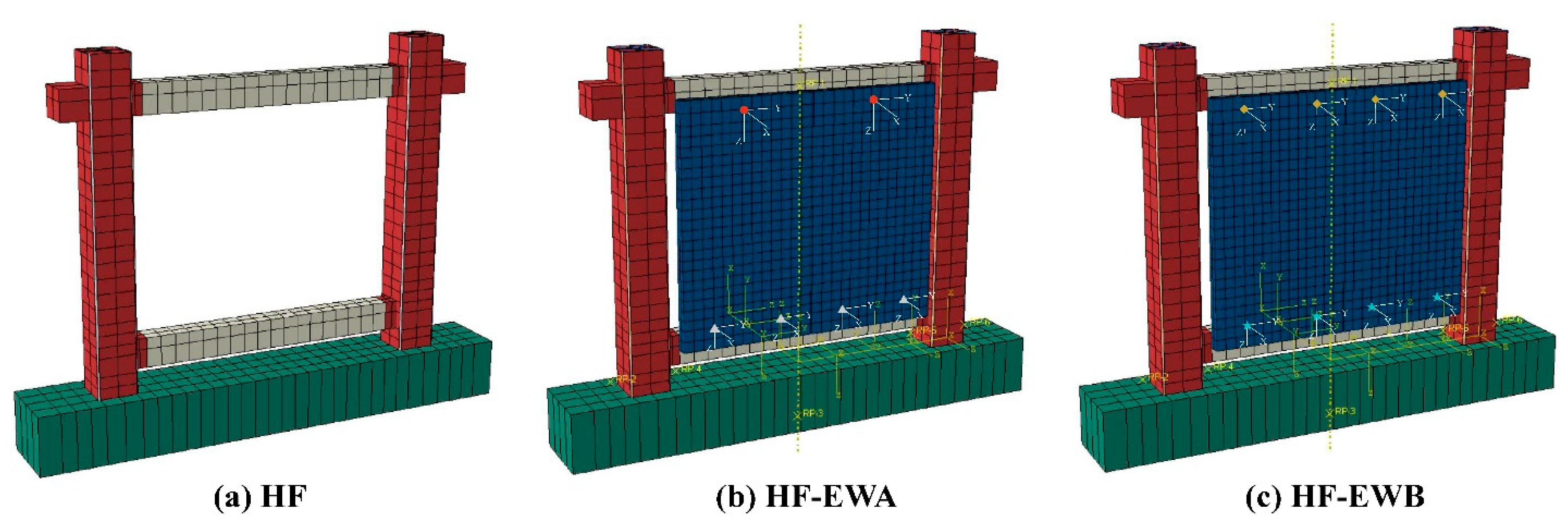
5.1. Numerical Analysis Model
5.2. Correctness Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dhakal, R.P.; Pourali, A.; Tasligedik, A.S.; Yeow, T.; Baird, A.; MacRae, G.; Pampanin, S.; Palermo, A. Seismic performance of non-structural components and contents in buildings: An overview of NZ research. Earthq. Eng. Eng. Vib. 2016, 15, 1–17. [Google Scholar] [CrossRef]
- Nader, K.A.; Zargaran, M.; Jahromi, K.K.; Bayat, M.R.; Jahanmohammadi, A. Seismic evaluation of cladded exterior walls considering the effects of facade installation details and out-of-plane behavior of walls. Structures 2020, 24, 317–334. [Google Scholar] [CrossRef]
- Braga, F.; Manfredi, V.; Masi, A.; Salvatori, A.; Vona, M. Performance of non-structural elements in RC buildings during the L’Aquila, 2009 earthquake. Bull. Earthq. Eng. 2011, 9, 307–324. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. A review of the performance of infilled RC structures in recent earthquakes. Appl. Sci. 2021, 11, 5889. [Google Scholar] [CrossRef]
- Kam, W.Y.; Pampanin, S. The seismic performance of RC buildings in the 22 February 2011 Christchurch earthquake. Struct. Concr. 2011, 12, 223–233. [Google Scholar] [CrossRef]
- Ercolino, M.; Magliulo, G.; Manfredi, G. Failure of a precast RC building due to Emilia-Romagna earthquakes. Eng. Struct. 2016, 118, 262–273. [Google Scholar] [CrossRef]
- Senel, S.M.; Haydar, K.A.; Mehmet, P.; Demir, A. Assessment of Damages in Precast Industrial Buildings in the Aftermath of Pazarcık and Elbistan Earthquakes. J. Earthq. Eng. 2024, 1–30. [Google Scholar] [CrossRef]
- Dal Lago, B.; Lamperti Tornaghi, M. Sliding channel cladding connections for precast structures subjected to earthquake action. Bull. Earthq. Eng. 2018, 16, 5621–5646. [Google Scholar] [CrossRef]
- Palsson, H.; Goodno, B.J.; Craig, J.I.; Will, K.M. Cladding influence on dynamics response of tall buildings. Earthq. Eng. Struct. Dyn. 1984, 12, 215–228. [Google Scholar] [CrossRef]
- Biondini, F.; Dal Lago, B.; Toniolo, G. Role of wall panel connections on the seismic performance of precast structures. Bull. Earthq. Eng. 2013, 11, 1061–1081. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, H.; Feng, Y.; Chong, X.; Huang, J.; Liu, Y. Enhancing the seismic performance of precast RC frames with cladding panels through setting U-shaped dampers and rocking walls. Shock Vib. 2020, 2020, 4182094. [Google Scholar] [CrossRef]
- Sellers, V.A. Experimental Testing of a Rotational Friction Connection for Use with Precast Concrete Cladding Panels in Metal Building Systems. Master’s Thesis, Auburn University, Auburn, AL, USA, 2017. [Google Scholar]
- Karadogan, F.; Yüksel, E.; Khajehdehi, A.; Ozkaynak, H.; Gullu, A.; Senol, E. Cyclic behavior of reinforced concrete cladding panels connected with energy dissipative steel cushions. Eng. Struct. 2019, 189, 423–439. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R.; Peloso, S. Evaluation of the seismic response of precast wall connections: Experimental observations and numerical modeling. J. Earthq. Eng. 2020, 24, 1057–1082. [Google Scholar] [CrossRef]
- Hou, H.; Yan, X.; Qu, B.; Du, Z.; Lu, Y. Cyclic tests of steel tee energy absorbers for precast exterior wall panels in steel building frames. Eng. Struct. 2021, 242, 112561. [Google Scholar] [CrossRef]
- Rahmanishamsi, E.; Soroushian, S.; Maragakis, E.M.; Shirazi, R. Analytical model for seismic assessment of nonstructural partition walls with returns. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Xie, L.; Sha, H.; Chong, X.; Jia, J. Seismic performance comparison between reinforced concrete frame structures with and without energy dissipating cladding panel system: Shaking table test and numerical simulation. J. Build. Eng. 2022, 62, 105414. [Google Scholar] [CrossRef]
- Su, R.K.L.; Chandler, A.M.; Sheikh, M.N.; Lam, N.T.K. Influence of non-structural components on lateral stiffness of tall buildings. Struct. Des. Tall Spec. Build. 2005, 14, 143–164. [Google Scholar] [CrossRef]
- Li, B.; Hutchinson, G.L.; Duffield, C.F. The influence of non-structural components on tall building stiffness. Struct. Des. Tall Spec. Build. 2011, 20, 853–870. [Google Scholar] [CrossRef]
- Pinelli, J.-P.; Craig James, I.; Goodno Barry, J. Energy-based seismic design of ductile cladding systems. J. Struct. Eng. 1995, 121, 567–578. [Google Scholar] [CrossRef]
- Dal Lago, B.; Biondini, F.; Toniolo, G. Seismic performance of precast concrete structures with energy dissipating cladding panel connection systems. Struct. Concr. 2018, 19, 1908–1926. [Google Scholar] [CrossRef]
- Toniolo, G.; Dal Lago, B. Conceptual design and full-scale experimentation of cladding panel connection systems of precast buildings. Earthq. Eng. Struct. Dyn. 2017, 46, 2565–2586. [Google Scholar] [CrossRef]
- Baird, A. Seismic Performance of Precast Concrete Cladding Systems. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2014. [Google Scholar]
- Dal Lago, B.; Biondini, F.; Toniolo, G. Friction-based dissipative devices for precast concrete panels. Eng. Struct. 2017, 147, 356–371. [Google Scholar] [CrossRef]
- Dal Lago, B.; Biondini, F.; Toniolo, G. Experimental investigation on steel W-shaped folded plate dissipative connectors for horizontal precast concrete cladding panels. J. Earthq. Eng. 2018, 22, 778–800. [Google Scholar] [CrossRef]
- Biondini, F.; Palermo, A.; Toniolo, G. Seismic performance of concrete structures exposed to corrosion: Case studies of low-rise precast buildings. Struct. Infrastruct. Eng. 2011, 7, 109–119. [Google Scholar] [CrossRef]
- Yarmohamadi, P.; Javadi, P.; Aziminejad, A. Improvement of seismic performance of self-centering mid-rise RC frames by adding semi-rigid rocking columns. Bull. Earthq. Eng. 2023, 21, 5991–6028. [Google Scholar] [CrossRef]
- Li, S.; Liu, H.; Wang, H.; Zar, A.; Zhai, C. Experimental Research on the Seismic Performance of Self-Centering Precast Concrete Frames With Infill Walls. Earthq. Eng. Struct. Dyn. 2025, 54, 2303–2324. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, P.; Zhu, X.; Cui, J.; Liu, X. Seismic performance of steel frames with different configurations of self-centering joints. Structures 2025, 74, 108480. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Lasowicz, N.; Jankowski, R. Development and experimental validation of a novel double-stage yield steel slit damper-buckling restrained brace. Eng. Struct. 2024, 315, 118427. [Google Scholar] [CrossRef]




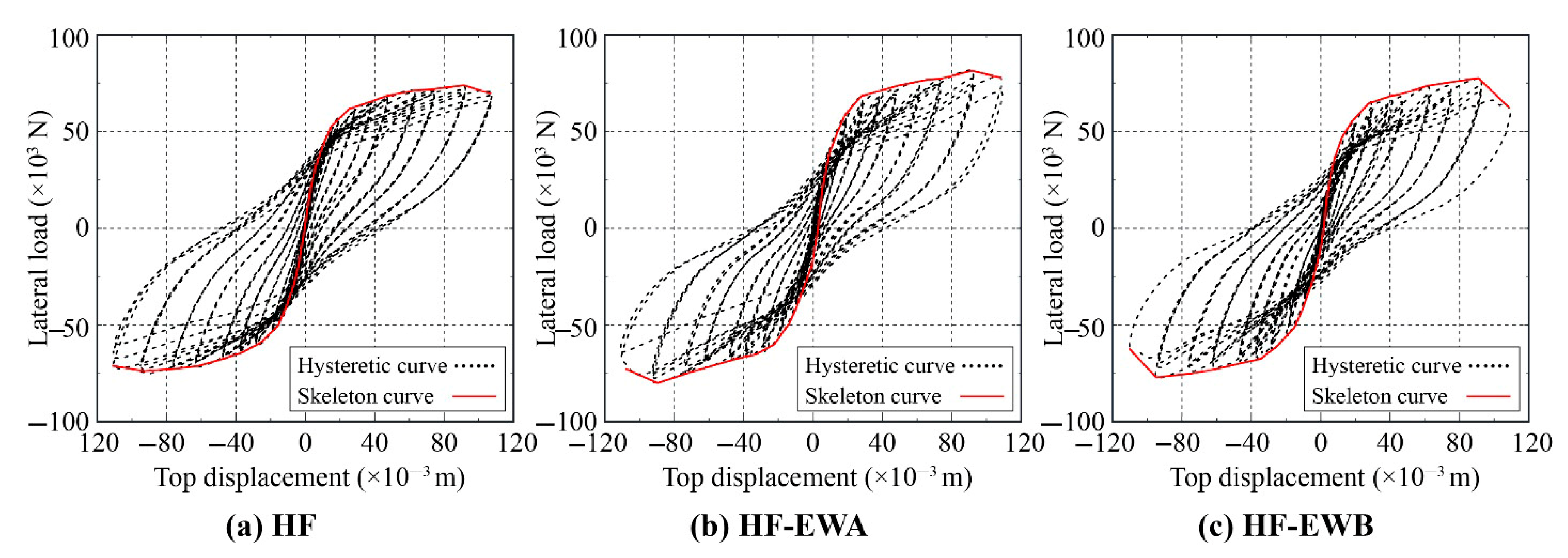
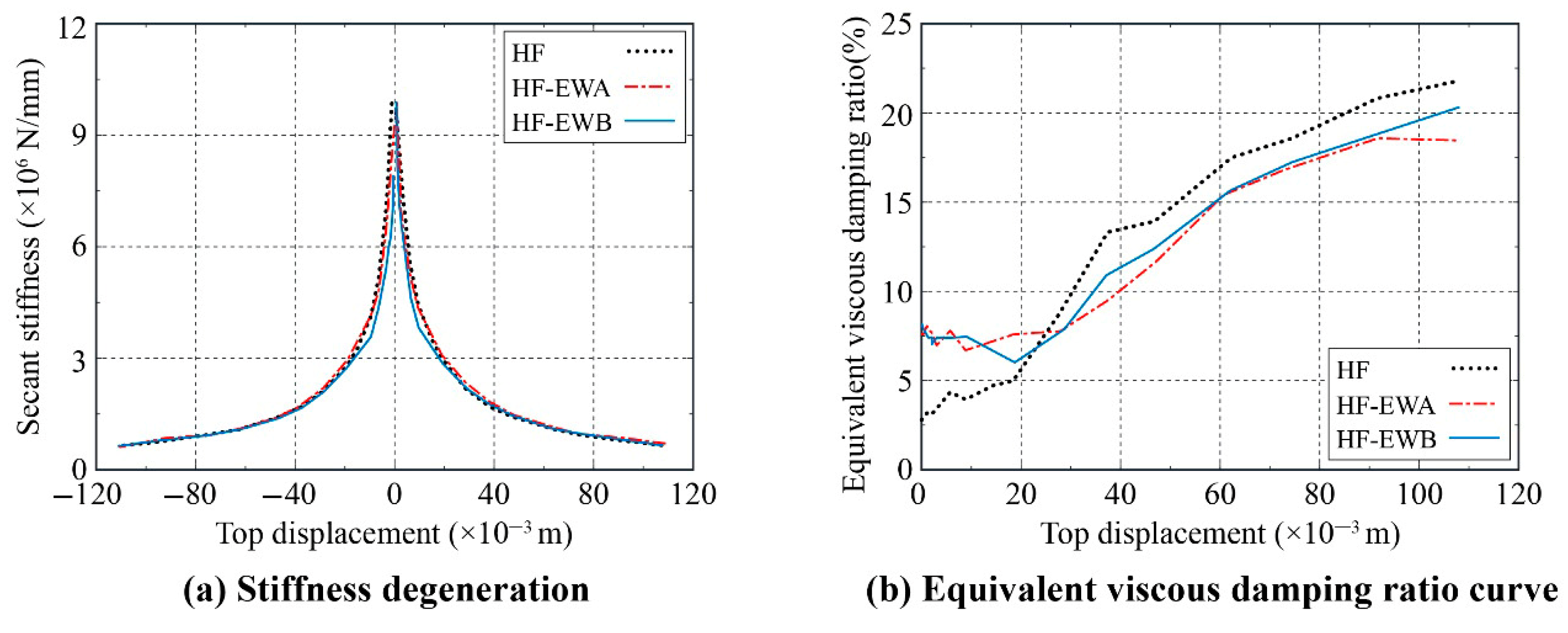
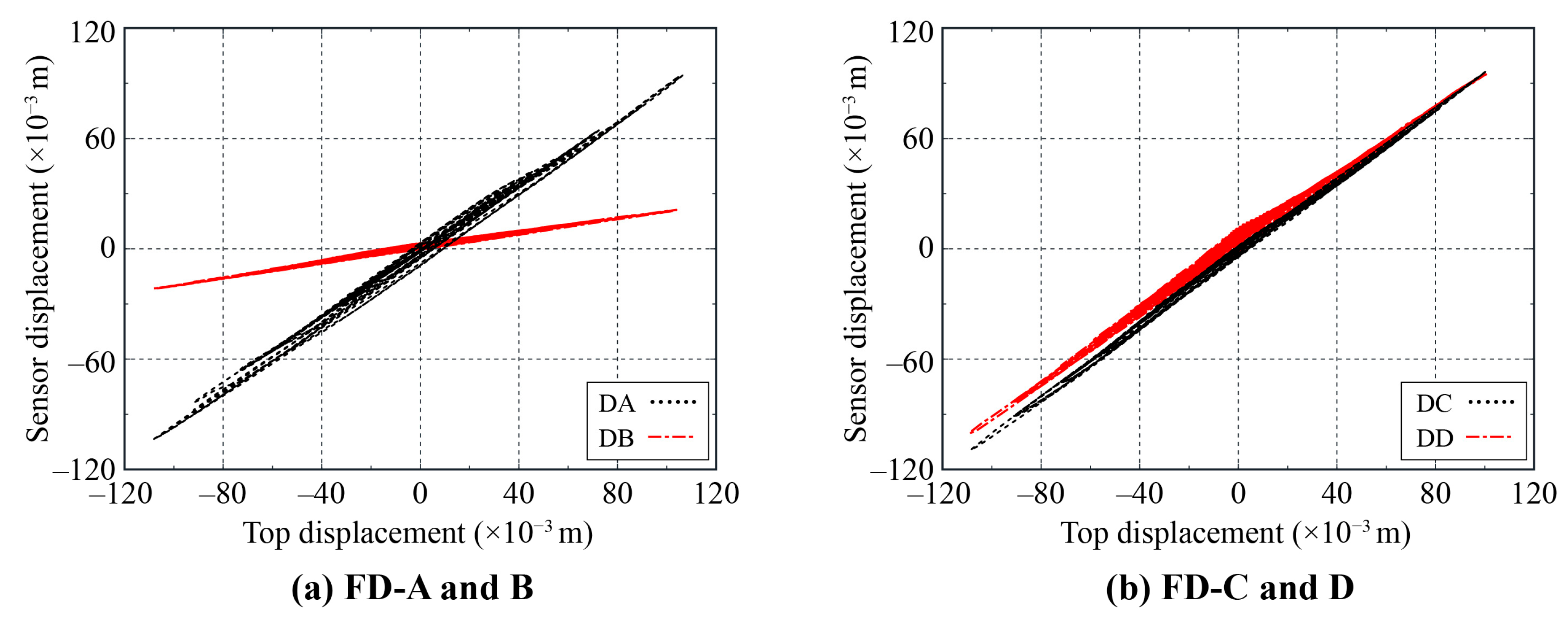
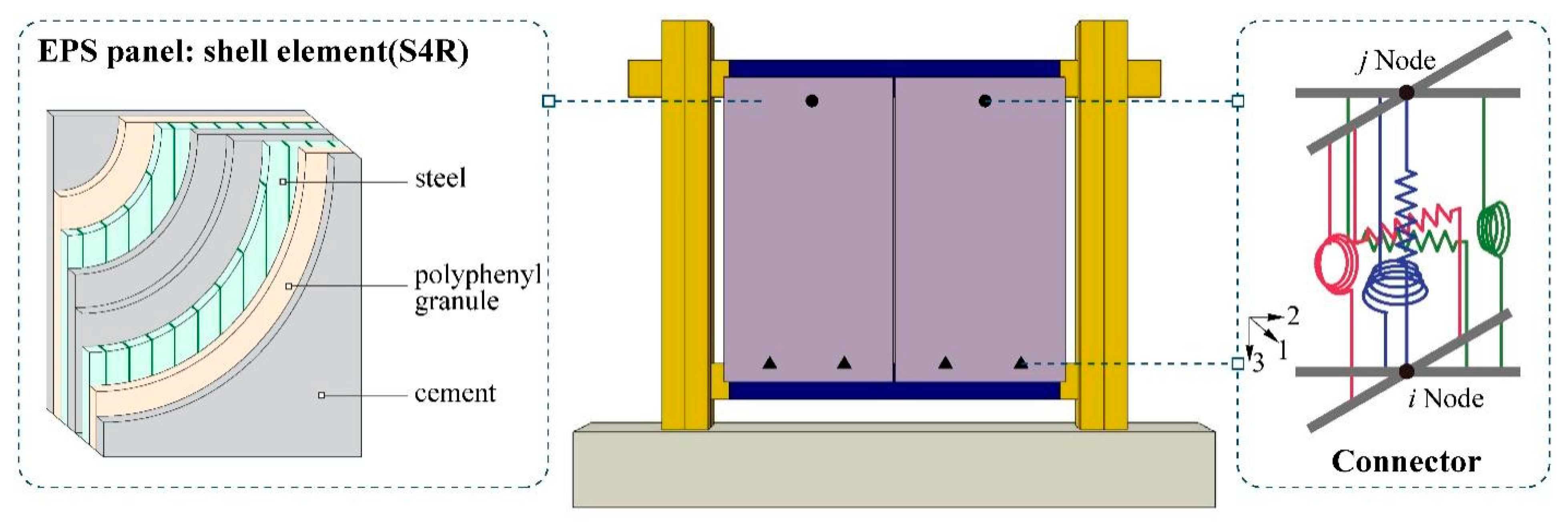
| Fy/kN | Δy/mm | Fm/kN | Δm/mm | Fu/kN | Δu/mm | ||
|---|---|---|---|---|---|---|---|
| HF | Forward | 45.82 | 10.92 | 71.48 | 92.24 | 70.08 | 107.55 |
| Reverse | −46.14 | −13.33 | −70.96 | −94.95 | −70.81 | −110.81 | |
| HF-EWA | Forward | 51.96 | 15.63 | 79.91 | 92.57 | 73.10 | 109.16 |
| Reverse | −56.16 | −16.87 | −85.58 | −91.20 | −77.71 | −106.55 | |
| HF-EWB | Forward | 54.05 | 17.96 | 82.94 | 91.57 | 74.94 | 107.98 |
| Reverse | −57.85 | −20.21 | −88.63 | −90.22 | −80.46 | −105.40 |
| Direction | 1(ux) | 2(uy) | 3(uz) | 4(urx) | 5(ury) | 6(urz) |
|---|---|---|---|---|---|---|
| FD-A | × | × | × | √ | × | × |
| FD-B | × | × | √ | √ | × | × |
| FD-C | × | × | × | × | × | × |
| FD-D | × | √ | √ | √ | × | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Lai, X.; Gao, W. Seismic Performance of Self-Centering Frame Structures with Additional Exterior Wall Panels Connected by Flexible Devices. Buildings 2025, 15, 2478. https://doi.org/10.3390/buildings15142478
Zhang C, Lai X, Gao W. Seismic Performance of Self-Centering Frame Structures with Additional Exterior Wall Panels Connected by Flexible Devices. Buildings. 2025; 15(14):2478. https://doi.org/10.3390/buildings15142478
Chicago/Turabian StyleZhang, Caiyan, Xiao Lai, and Weihang Gao. 2025. "Seismic Performance of Self-Centering Frame Structures with Additional Exterior Wall Panels Connected by Flexible Devices" Buildings 15, no. 14: 2478. https://doi.org/10.3390/buildings15142478
APA StyleZhang, C., Lai, X., & Gao, W. (2025). Seismic Performance of Self-Centering Frame Structures with Additional Exterior Wall Panels Connected by Flexible Devices. Buildings, 15(14), 2478. https://doi.org/10.3390/buildings15142478






