Abstract
The compressive capacity of helical anchors constitutes a pivotal performance parameter in geotechnical design. To precisely predict the compressive bearing behavior of helical anchors in aeolian sand, this study integrates in situ testing with finite element numerical analysis to systematically elucidate the non-linear evolution of its load-bearing mechanisms. The XGBoost algorithm enabled the rigorous quantification of the governing geometric features of compressive capacity, culminating in a computational framework for the bearing capacity factor (Nq) and lateral earth pressure coefficient (Ku). The research findings demonstrate the following: (1) Compressive capacity exhibits significant enhancement with increasing helix diameter yet displays limited sensitivity to helix number. (2) Load–displacement curves progress through three distinct phases—initial quasi-linear, intermediate non-linear, and terminal quasi-linear stages—under escalating pressure. (3) At embedment depths of H < 5D, tensile capacity diminishes by approximately 80% relative to compressive capacity, manifesting as characteristic shallow anchor failure patterns. (4) When H ≥ 5D, stress redistribution transitions from bowl-shaped to elliptical contours, with ≤10% divergence between uplift/compressive capacities, establishing 5D as the critical threshold defining shallow versus deep anchor behavior. (5) The helix spacing ratio (S/D) governs the failure mode transition, where cylindrical shear (CS) dominates at S/D ≤ 4, while individual bearing (IB) prevails at S/D > 4. (6) XGBoost feature importance analysis confirms internal friction angle, helix diameter, and embedment depth as the three parameters exerting the most pronounced influence on capacity. (7) The proposed computational models for Nq and Ku demonstrate exceptional concordance with numerical simulations (mean deviation = 1.03, variance = 0.012). These outcomes provide both theoretical foundations and practical methodologies for helical anchor engineering in aeolian sand environments.
1. Introduction
Helical anchors represent a quintessential deep foundation system that is widely employed across the construction, power transmission, and transportation sectors due to their operational efficiencies, geological adaptability, and reusability [1,2]. Compressive capacity constitutes a critical performance metric directly governing structural integrity. Aeolian sand—prevalent in China’s Gansu Province, the U.S. West Coast, and Australian inland regions—exhibits distinctive geomechanical properties, including a coarse-grained skeletal structure, high permeability, an elevated compression modulus, and negligible cohesion. These attributes induce the following systemic engineering risks: significant bearing capacity dispersion, heightened seepage deformation sensitivity, and compromised long-term stability.
Contemporary research has extensively investigated helical anchor behavior, with Merifield et al. [3,4,5] employing numerical methods to analyze pullout resistance in cohesive soils, while Pratama et al. [6] utilized axisymmetric FEM to elucidate diameter/spacing effects on axial capacity in medium-dense sands. Schiavon et al. [7] further examined cyclic loading impacts via centrifuge testing. In recent years, Ho et al. analyzed the load response of screw piles and straight piles under compressive loading in dense sand through numerical simulations, clarifying the load transfer mechanism and bearing capacity variation patterns [8]. Shuman et al. conducted numerical simulations of helical anchor settlement under various soil parameters, demonstrating that over 90% of the helical anchor’s bearing capacity is undertaken by the helix plates [9]. Garakani et al. investigated the bearing behavior of helical anchors in unsaturated soils (sandy soil and clay) through numerical simulations and in situ tests, proposed the transition boundaries of failure modes for helical anchors in sandy soil and clay, and elucidated the load transfer mechanism of helical anchors [10]. However, the research methodologies adopted in the aforementioned literature exhibit singularization. Nevertheless, studies have predominantly addressed conventional soils, leaving aeolian sand systems insufficiently characterized.
Axial capacity assessment primarily employs two theoretical frameworks: the cylindrical shear (CS) method—applicable to multi-helix configurations where resistance derives from base bearing and cylindrical soil shear [2,11,12,13]—and the individual bearing (IB) method—suitable for single/multi-helix anchors. Crucially, failure mode transitions from CS to IB occur at spacing ratios (S/D) between 1.5 and 3, although the precise thresholds for aeolian sand remain undetermined.
Despite advances through numerical simulations [14,15,16], centrifuge testing [17,18], and machine learning [14,17], predictive models exhibit limited generalizability and accuracy [19].
To resolve these deficiencies, we integrated in situ static load tests and calibrated FEM simulations for Gansu’s aeolian sand, systematically revealing the following: (1) load convergence mechanisms and failure mode evolution; (2) the critical embedment depth ratio (H/D = 5) distinguishing shallow failure characteristics (80% tensile capacity reduction) from deep anchor behavior (<10% uplift-compression divergence); (3) a CS–IB transition threshold at S/D = 4, where failure shifts from cylindrical shear to individual bearing; (4) Bayesian-optimized XGBoost models identifying internal friction angle, helix diameter, and embedment depth as dominant parameters; and (5) the formulation of Nq (bearing capacity factor) and Ku (lateral pressure coefficient) equations validated across four density states (mean deviation = 1.03, variance = 0.012).
Distinguished from existing studies, this research introduces a novel tripartite methodology integrating in situ testing, numerical analysis, and machine learning (ML). The ML-curated dataset dramatically expands the sample size for formula derivation while circumventing intensive numerical modeling efforts, thereby establishing a new research paradigm for investigating helical anchor-bearing behavior.
2. Field Testing Program
2.1. In Situ Testing Conditions
The in situ testing site was located in a desert region east of Wuwei City, Gansu Province (Figure 1), and comprised mobile dune terrain. Field investigations revealed four distinct aeolian sand strata exhibiting progressively increasing density from the surface downward: loose, slightly dense, medium dense, and dense. All strata demonstrated homogeneous distribution characteristics.

Figure 1.
Topographic features of the test site.
Geotechnical characterization of site strata was derived from laboratory testing per GB 50123-2019 [20], comprising Standard Proctor compaction, direct shear, and triaxial compression tests. The compaction tests yielded a minimum dry density of 1.60 g/cm3 and a maximum dry density of 1.90 g/cm3. Triaxial compression testing employed a TSZ-3 strain-controlled triaxial apparatus (Figure 2), wherein four specimen groups with dry densities, , of 1.60, 1.70, 1.80, and 1.90 g/cm3 (39.1 mm × 80 mm height; h/d = 2.05) underwent consolidated–drained (CD) testing at a shear rate of 0.5 mm/min under confinement pressures of 100, 200, and 300 kPa. The test termination criteria were as follows: (1) attainment of peak stress or (2) stabilization followed by approximately 5% additional axial strain. Strength interpretation was as follows: (1) peak strength adopted for distinct stress–strain peaks or (2) deviator stress at 15% axial strain for non-peaking curves. Complete experimental configurations and results are detailed in Table 1.

Figure 2.
Test specimen and TSZ-3 strain-controlled triaxial apparatus. (a) Specimen preparation; (b) TSZ-3 strain-controlled triaxial system.

Table 1.
Geological parameters of test site.
To thoroughly investigate the compression capacity of helical anchors in aeolian sand, the specimen design incorporated key parameters including varied helix diameters, multiple helix configurations, and installation inclination angles. Ten helical anchor specimens were fabricated with helix spacings ranging from 3 to 4.5 times the helix diameter. The central shaft featured an outer diameter of 219 mm with 16 mm wall thickness, while the helices were 18 mm thick. Both shaft and helices utilized Q355 structural steel (equivalent to EN S355 [21]). Detailed specimen parameters are provided in Table 2.

Table 2.
Parameters of helical anchor test specimens.
2.2. Static Load Test
At the test site, helical anchors served as temporary reaction piles. The ends of vertical reaction beams were bolted to these reaction piles, while horizontal loading utilized reaction beams secured by mechanical equipment. Hydraulic jacks applied both vertical and horizontal loads at the anchor heads. For inclined helical anchors, synchronized proportional vertical–horizontal loading was implemented (Figure 3). The static load test for helical anchors adopted the slow-maintained load method. Loading was performed according to the Code for Design of Building Foundation (GB 50007-2011) [22], Design Code for Foundations of Overhead Transmission Lines (DL/T 5219-2023) [23], and the Technical Code for Testing of Building Foundation Piles (JGJ 106-2014) [24]. The vertical static load test for single piles required that the graded loading increment was 1/10~1/15 of the estimated ultimate bearing capacity, with each load stage maintained for at least 2 h.

Figure 3.
Test scheme of helical anchor. (a) Axial compressive load test; (b) axial tensile load test.
For working conditions C1, C2, and C3, the loading stages were sequentially increased by 90 kN; for C4, C5, and C6 by 120 kN; for C7 by 200 kN; and for C8, C9, and C10 by 260 kN. Each load stage was maintained for at least 2 h [22,23,24]. Loading ceased when either (a) vertical displacement exceeded 10% of the helix diameter or (b) settlement surpassed twice that of the previous stage after 24 h without stabilization.
Unloading then proceeded in stages at twice the incremental load until completed. Jack pressures were converted into applied loads via calibrated gauges. Vertical displacements were measured using displacement transducers (e.g., LVDTs) mounted on anchor heads.
2.3. Test Results and Analysis
The load–displacement curves (Figure 4) demonstrated that all helical anchors underwent three distinct behavioral phases: an initial quasi-linear stage → non-linear progression → a secondary quasi-linear stage. During initial loading, the anchors exhibited pronounced linear elasticity. As the load increased, the progressive development of plastic zones in the surrounding soil induced a non-linear response. Upon reaching displacements equivalent to 10% of the helix diameter (10%), the curves transitioned into a secondary quasi-linear segment with a persistent positive slope. This indicated residual load-bearing capacity mobilization. Concurrently, the progressively decreasing slope of the curves signified the degradation of the soil–structure interface interaction with increasing displacement.
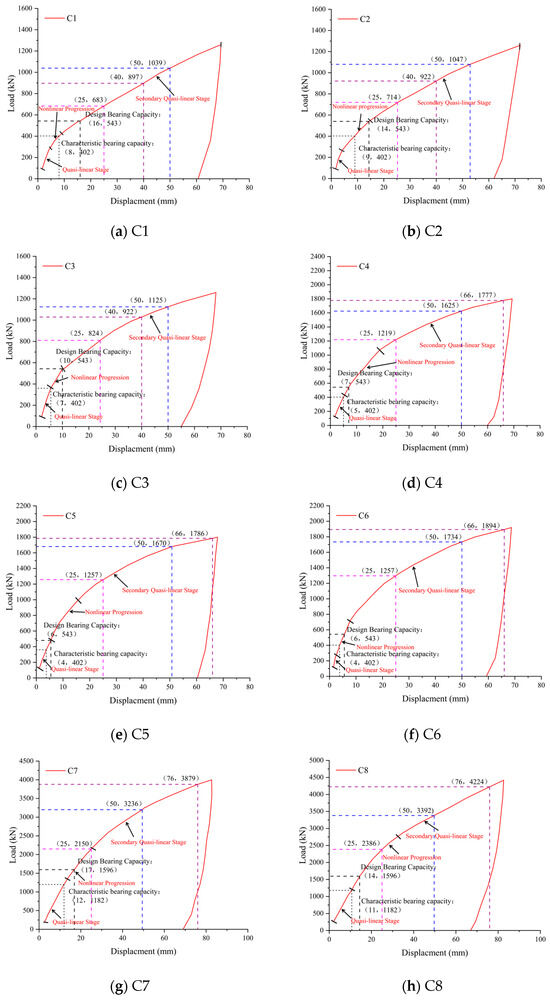
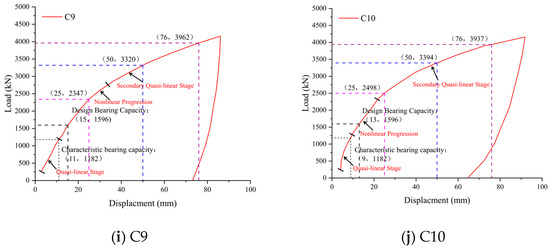
Figure 4.
Load–displacement curves.
Table 3 documents the in situ test results. Specimens under identical configurations demonstrated strong data consistency: groups C1–C3, C4–C6, and C8–C10 exhibited ≤10% deviation in ultimate load at 10% helix diameter displacement. Accounting for inherent soil stratigraphy variations (±15% layer thickness across the test site), this margin fell within the acceptable experimental error, confirming the validity of the results. Analysis revealed the following:

Table 3.
Field test performance data.
- (1)
- Diameter effect: The three-helix anchors (C1, C4, and C7) showed capacity scaling with diameter—C4 (65% larger diameter; 172% greater base area) achieved 92% higher capacity than C1; C7 (90% larger diameter, 261% greater base area) exhibited a 309% capacity increase. These measurements defined an exponential capacity–diameter relationship (R2 > 0.98).
- (2)
- Helix quantity effect: Despite identical top-helix embedment and diameters, the four-helix anchor (C8) provided merely 4% higher axial compressive capacity than the three-helix configuration (C7), indicating the negligible influence of helix count.
Collectively, helical anchor axial compressive capacity demonstrated pronounced exponential dependence on helix diameter while remaining effectively independent of helix quantity beyond three plates.
2.4. Bearing Capacity Calculation Methods
Current helical anchor designs primarily employ the cylindrical shear (CS) and individual bearing (IB) models. The CS failure mechanism assumes shear failure develops between the uppermost and lowermost helices, forming a cylindrical surface [13]. Consequently, total axial capacity comprises shaft resistance, tip bearing, and cylindrical shear resistance along this failure plane [11,12,13]. Figure 5 illustrates load distribution patterns for both models. Critically, when helix spacing exceeds a threshold, failure transitions from the CS to the IB mechanism [12,13]. Empirical studies confirm that IB failure occurs at spacing ratios (S/D) of 1.5–3, with exact thresholds dependent on soil stratigraphy [25,26,27]. The specific threshold values are quantified in Section 4 of this study.
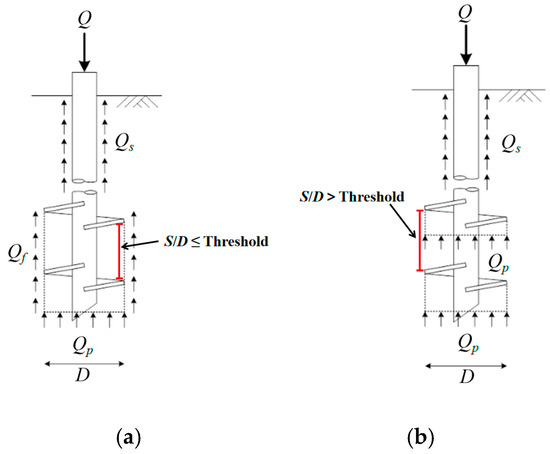
Figure 5.
Load distribution patterns of CS and IB models. (a) CS model; (b) IB model.
The CS model adopts a calculation formula corresponding to the cylindrical shear failure mode for deeply embedded anchors, expressed as follows:
where Qp is the characteristic value of the compressive bearing capacity at the bottom helix plate (kN); Qs is the frictional resistance along the anchor shaft (kN); and Qf is the frictional resistance of soil layers between helix plates (kN).
The calculation formula for compressive bearing capacity in the IB model is as follows:
where Qpi is the compressive bearing capacity mobilized by the anchor plate (counted from top to bottom), in kN, and Qs is the frictional resistance along the anchor shaft, in kN.
In the above formula, the frictional resistance of inter-helix soil layers, Qf, and the characteristic value of the compressive bearing capacity for a single helix plate, Qp, are calculated as follows:
where D is the helix plate diameter (m); γ in the Qp formula represents the weighted average unit weight of soil between the top and bottom helix plates, while in the Qf formula, it denotes the weighted average unit weight of soil above the bottom helix plate (kN/m3); Ku is the lateral earth pressure coefficient; θ is the internal friction angle of the soil; A is the area of the bottom helix plate (m2); and Nqu is the compressive bearing capacity factor for helical anchors in sandy soils.
The two prediction models apply to distinct operational conditions. The CS model incorporates side resistance along the soil cylinder between adjacent helical plates—a critical component when cylindrical shear failure develops—as the fundamental bearing capacity. When the anchor spacing exceeds the threshold, inhibiting cylindrical shear failure formation, the IB model becomes applicable, summing the bearing capacities of individual plates. The critical S/D values for aeolian sand anchors are detailed in Section 4.
As indicated by the equations above, calculating the axial compressive capacity of helical anchors via the CS and IB models requires two critical coefficients: the lateral earth pressure coefficient (Ku) and the bearing capacity factor (Nqu). However, the current practice for determining these coefficients predominantly relies on empirically derived values due to the absence of precise computational formulations, with reference values adopted from the Chinese Design Code DL/T 5219-2023 Technical Specification for Foundation Design of Overhead Transmission Lines [23] and the IEEE Guide for Transmission Structure Foundation Design and Testing (IEEE Std 691-2001) [28], as exemplified in Figure 6. These lack rigorous predictive equations. To address this limitation, our study integrates in situ static load tests, coupled Eulerian–Lagrangian (CEL) numerical simulations, and XGBoost machine learning modeling to develop precise predictive equations for Ku and Nqu.
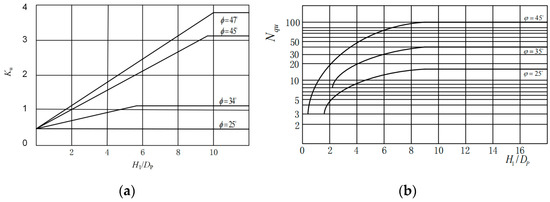
Figure 6.
Reference coefficients in design codes. (a) Lateral earth pressure coefficient; (b) compression bearing capacity coefficient.
The theoretical ultimate capacity was calculated per Chinese design code DL/T 5219-2023 Technical Specification for Foundation Design of Overhead Transmission Lines [23]. As summarized in Table 3, the mean ratio of code-calculated to experimental capacities was 0.712 with a variance of 0.019. The low variance indicated that this deviation was not attributable to random error but revealed a systematic bias in the code methodology. Statistically significant systematic deviations between code predictions and measured data were evident, signaling a requirement for the systematic refinement of the design formulae.
3. Numerical Analysis
3.1. Model Overview
A numerical model for analyzing the uplift and compressive bearing capacity of helical anchors in aeolian sand was developed using ABAQUS (Figure 7). The boundary conditions were optimized based on existing research. Following Kwon et al.’s modeling approach [29], the bottom boundary was set at 6D (where D represents the helix plate diameter) for uplift conditions, while for compressive conditions, it was extended to 30D according to Schiavon et al.’s findings [30] to ensure that boundary effects remained below 3%. To ensure numerical accuracy, a 2D-height void layer was incorporated above the soil domain to prevent material overflow [31], with horizontal boundaries uniformly set at 6D. Mesh refinement zones were established in the central regions (3D horizontal extent × 11D depth for the uplift model and 3D × 35D for the compression model), employing a uniform element size of 0.08 m in refined zones and implementing bilinear graded mesh discretization in transition zones (with the element size gradually decreasing from 0.5 m at boundaries to 0.08 m at refinement zone interfaces). Furthermore, validation through a boundary effect-free benchmark model (20D horizontal × 50D bottom boundaries) demonstrated that boundary effects in the primary model were effectively controlled within 2%, fully meeting the accuracy requirements for subsequent parametric studies. Non-reflective Eulerian outflow boundaries were applied to the side and bottom surfaces. The bottom boundary was fully constrained (U1 = U2 = U3 = UR1 = UR2 = UR3 = 0). The soil model was discretized using EC3D8R elements (8-node linear brick elements with reduced integration), and the helical anchor was meshed with C3D4 elements (4-node linear tetrahedral elements with full integration). A reference point was defined at the anchor head to apply displacement-controlled loading.
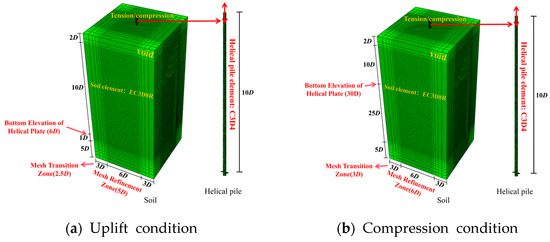
Figure 7.
Numerical model.
The helical anchor in this model was assigned an ideal elastic constitutive model [32,33]. Both the anchor shaft and plates were modeled as Lagrangian bodies, with the specific parameters detailed in Table 4. To ensure model accuracy, Mohr–Coulomb constitutive parameters were implemented for soil layers, calibrated against field investigation data (Table 5). The soil domain was modeled as an Eulerian body.

Table 4.
Parameters of helical anchor.

Table 5.
Parameters of soil layer.
To address the non-linear contact behavior between the helical anchor and soil, the interaction was defined using a Coulomb penalty contact formulation. The tangential behavior incorporated a friction coefficient of tanφ [34], while the normal direction adopted a hard contact definition (allowing for separation upon tensile stress). The dilatancy angle was set to half of the internal friction angle (ψ = φ/2) [35].
3.2. Model Validation
Numerical models for uplift (T-series) and compression (C-series) conditions were established based on field test scenarios. The accuracy of the numerical models was validated by comparing simulation results with field test data. Figure 8 presents the displacement–load comparison curves between field tests and numerical simulations (where T denotes uplift models, C denotes compression models, and identical indices correspond to identical anchor dimensions). The curves exhibited close alignment in overall trends, with both demonstrating distinct linear growth phases followed by non-linear growth phases.
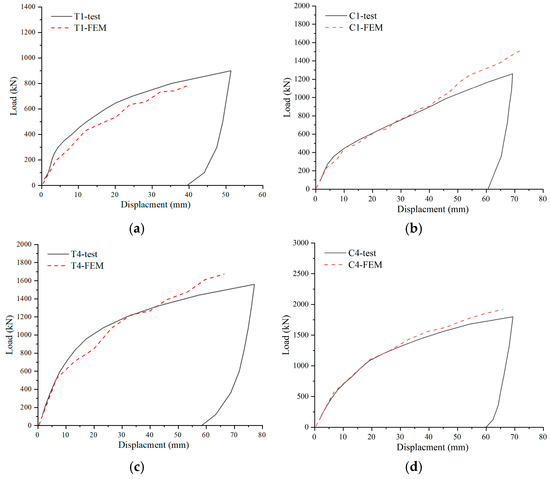
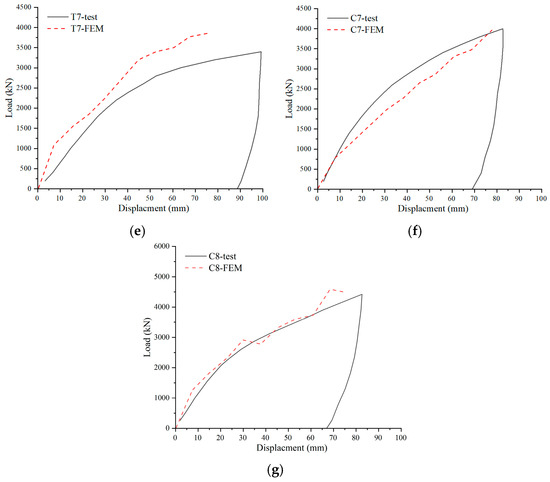
Figure 8.
Load–displacement comparison curves between numerical simulations and field tests. (a) Uplift condition T1; (b) compression condition C1; (c) uplift condition T4; (d) compression condition C4; (e) uplift condition T7; (f) compression condition C7; (g) compression condition C8.
Multiple experimental validations confirmed that the simulation results exhibited excellent agreement with the measured data, with deviations consistently controlled within approximately 10% (Figure 8). It should be emphasized that due to inherent geological heterogeneity and site-specific variability, inevitable discrepancies existed between the actual soil parameters obtained during testing and those from the geotechnical investigation reports (e.g., friction angle and soil density) [36], which consequently affected the accuracy of the numerical simulations. As quantitatively demonstrated in Formulas (3) and (4), such parameter variations systematically influenced the ultimate bearing capacity calculations. Therefore, the observed deviation range was deemed acceptable, and the proposed model demonstrated sufficient reliability for subsequent research applications.
3.3. Failure Mechanism
Figure 9 displays the equivalent plastic strain (PEEQ) distribution contours at the ultimate bearing capacity of helical anchors under various working conditions. Soil regions with cumulative PEEQ exceeding 0.05 are identified as mobilized zones that govern the foundation-bearing capacity [37]. Consequently, all output PEEQ contours exhibited minimum values >0.05.
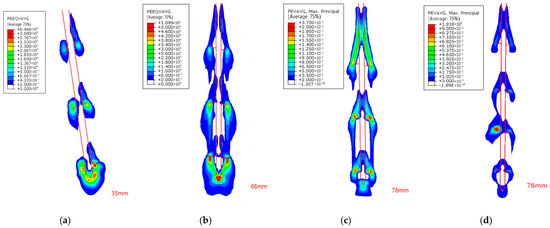
Figure 9.
PEEQ (equivalent plastic strain) contours at ultimate bearing capacity. (a) Cases C1–C3 (S/D = 4.5); (b) cases C4–C6; (S/D = 3.0); (c) case C7 (S/D = 3.0); (d) cases C8–C10 (S/D = 3.0).
A detailed contour analysis revealed the following:
- (1)
- For C4–C10 cases (Figure 9b–d), plastic strain concentrated around anchor plates, forming maximum high-PEEQ zones beneath the bottom plate, consistent with the end-bearing mechanism in the CS model. Progressively expanding continuous shear bands developed along plate edges, exhibiting embedment depth-dependent spatial distribution that aligned with lateral earth pressure effects. The axisymmetric cylindrical plastic zone distribution matched the CS-predicted failure mode.
- (2)
- For C1–C3 cases (Figure 9a), isolated plastic strain zones between plates showed no interconnected shear bands, conforming to the localized punch-through failure of the IB model. The linear correlation between the bottom plate plastic zone radius and the geometric radius indicated plate-area-dominated end resistance.
Key design implications:
- (1)
- CS failure mode: The compression capacity exhibits positive correlations with the bottom plate radius (R) and embedment depth (H):
- (2)
- IB failure mode: Capacity follows an exponential relationship with plate radius:
This research establishes geometric linkages between the CS/IB theoretical models and physical failure patterns, quantifying the governing roles of plate diameter, embedment depth, and plate area in compression capacity development.
Figure 10 presents Mises stress contours at different displacement stages for case C4. Under multi-plate helical anchor conditions, enhanced stress transfer beneath the anchor plates occurred with increasing embedment depth (Figure 10).
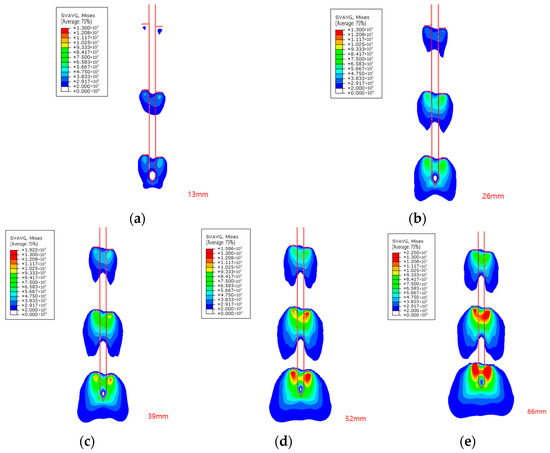
Figure 10.
von Mises stress contours for case C4. (a) At 13 mm displacement; (b) at 26 mm displacement; (c) at 39 mm displacement; (d) at 52 mm displacement; (e) at 66 mm displacement.
From the CS model perspective, this phenomenon stemmed from the depth-dependent evolution of lateral earth pressure coefficients, governed by the theoretical formulation derived later (Formula (12)).
Alternatively, the IB model attributed this behavior to the depth-proportional capacity enhancement of individual plates, consistent with the single-plate bearing capacity equation in the design codes (Formula (4)).
The ability of both models to explain this stress redistribution demonstrated their theoretical validity and fundamental complementarity.
Figure 11 presents plastic strain contours at 13 mm displacement for case C4. Comparative analysis with Figure 10 indicated that during the initial displacement phase, while no significant plastic strain was observed beneath the top anchor plate (Figure 11a), a fully developed stress field existed in this region (Figure 10a). This apparent contradiction arose from two factors: (i) the stress magnitude remained below the yield threshold of the aeolian sand material, and (ii) the strain values were beneath the minimum contour visualization limit (0.05 m PEEQ as defined in Section 3.3).
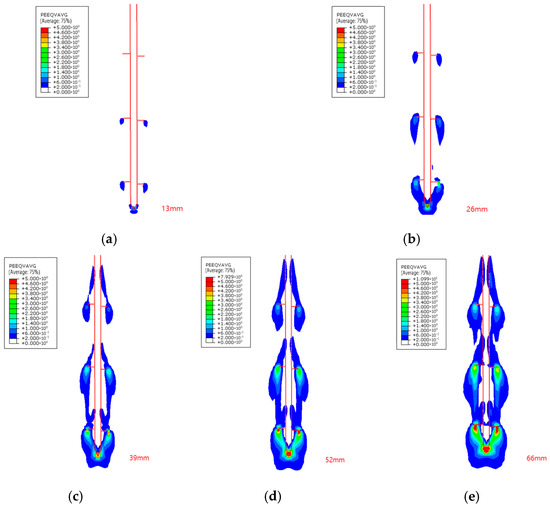
Figure 11.
PEEQ (equivalent plastic strain) contours for case C4. (a) At 13 mm displacement; (b) at 26 mm displacement; (c) at 39 mm displacement; (d) at 52 mm displacement; (e) at 66 mm displacement.
Consequently, although compression capacity was predominantly controlled by the bottom plate geometry and embedment depth, all helical plates participated in load transfer. This demonstrated a collaborative bearing mechanism among multi-plate helical anchors during loading progression.
4. Parametric Analysis
Based on the validated numerical model, parametric studies were performed to investigate helical anchor-bearing behavior and establish a robust dataset for machine learning applications. Simulations encompassed the four aeolian sand density states (loose, slightly loose, medium dense, and dense) defined in Table 5. For single-plate anchors, 168 numerical models were established, systematically covering all density states, with six plate diameters (500–1000 mm in 100 mm increments) and fourteen embedment ratios (H/D = 2–20). This yielded 336 unique combinations (4 densities × 6 diameters × 14 H/D ratios), as detailed in Table 6. For multi-plate anchors, 80 models were developed, comprising two configurations for 500 mm diameter anchors (top plate depths: 1000 mm [2D] and 3000 mm [6D]) and two for 800 mm diameter anchors (top plate depths: 1600 mm [2D] and 4800 mm [6D]). For each top plate depth, five plate spacings ranging from 2D to 6D were simulated, all replicated across the four density states (2 diameters × 2 depths × 5 spacings × 4 densities = 80 models; Table 7). Collectively, this comprehensive parametric matrix of 184 simulations quantified the effects of plate diameter, embedment depth, plate spacing, and soil density on bearing capacity.

Table 6.
Numerical modeling parameters for single-plate helical anchors.

Table 7.
Numerical modeling parameters for twin-plate helical anchors.
Through the systematic experimental investigation, the influence of embedment depth on the bearing capacity and failure mechanism of 800 mm diameter helical anchors in S1 soil was revealed. The results indicated that both the bearing capacity and failure mode of the helical anchor underwent fundamental changes with increasing H/D ratio. Under shallow embedment conditions (H = 2D), the compressive bearing capacity versus displacement curve exhibited an approximately linear relationship, without distinct fluctuation points or a peak plateau. Conversely, the uplift bearing capacity versus displacement curve showed a staged, approximately linear relationship with a pronounced peak plateau. The bearing capacity demonstrated significant direction dependency, with the difference between uplift and compressive capacities reaching up to 80% (Figure 12a). As the H/D ratio increased, the uplift peak plateau gradually elevated, and the disparity between uplift and compressive capacities diminished. A detailed analysis of strain contour plots (with red lines outlining the anchor rod and soil boundaries) indicated that this disparity primarily stemmed from distinct failure mechanisms. Under uplift, the strain exhibited a symmetrical bowl-shaped distribution, whereas under compression, the strain showed an elliptical distribution (Figure 13a).
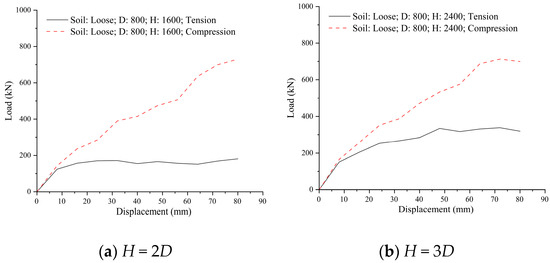
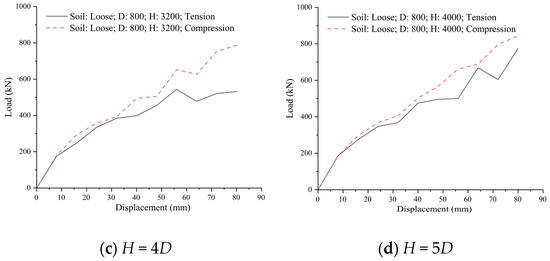
Figure 12.
Comparison of bearing capacity under uplift versus compressive loading conditions at various embedment depths.
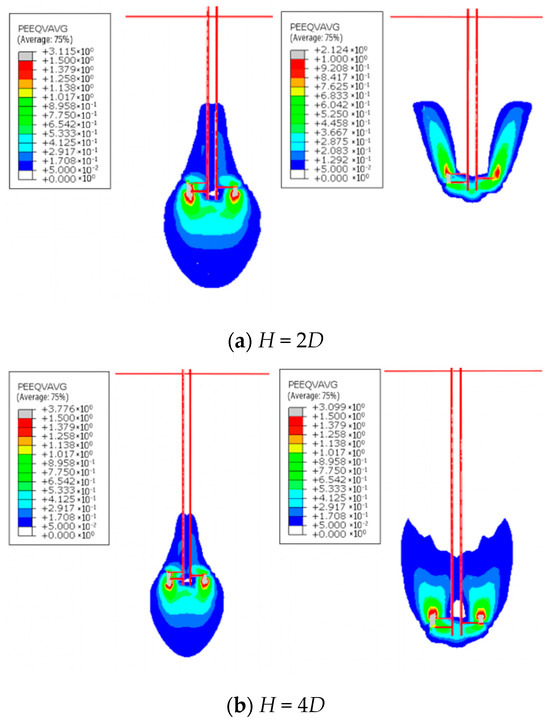
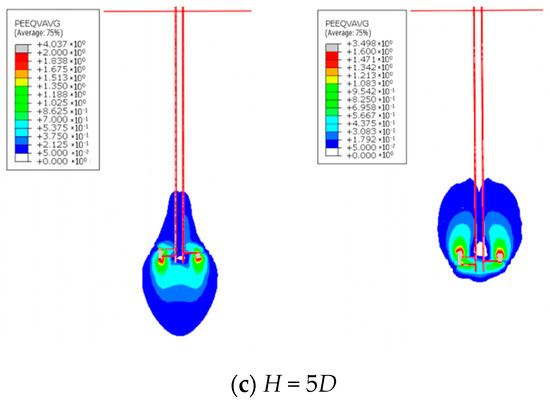
Figure 13.
Plastic strain contours under uplift and compressive loading (anchor rod and soil boundaries outlined in red).
Under deep embedment conditions (H = 5D), both the uplift and compressive bearing capacities versus displacement curves displayed an approximately linear relationship, lacking distinct fluctuation points or peak plateaus. The direction dependency of the bearing capacity disappeared, as the uplift and compressive capacity curves showed a high degree of coincidence. Overall, the compressive capacity differed from the uplift capacity by less than 10% (Figure 12d). A detailed strain contour plot analysis (with red lines outlining the anchor rod and soil boundaries) revealed elliptical strain distributions for both uplift and compressive loading conditions (Figure 13c). Integrating the strain contours from shallow conditions explained that the pronounced direction dependency observed in shallow embedment arose from differing soil failure modes around the anchor plate. Furthermore, as embedment depth increased, the soil failure mode under uplift gradually transitioned toward an elliptical pattern, with the critical transition occurring at H = 5D.
When the embedment ratio did not reach the transitional boundary, the compression bearing capacity curve exhibited two distinct stages (non-directional sensitivity stage → directional sensitivity stage), with a clear directional sensitivity initiation point. In the non-directional sensitivity stage, the uplift and compression bearing capacity curves coincided. After the directional sensitivity initiation point, the curve entered the directional sensitivity stage; the growth rate of compression bearing capacity showed no significant change initially, then markedly decelerated, and eventually ceased to increase (Figure 14).
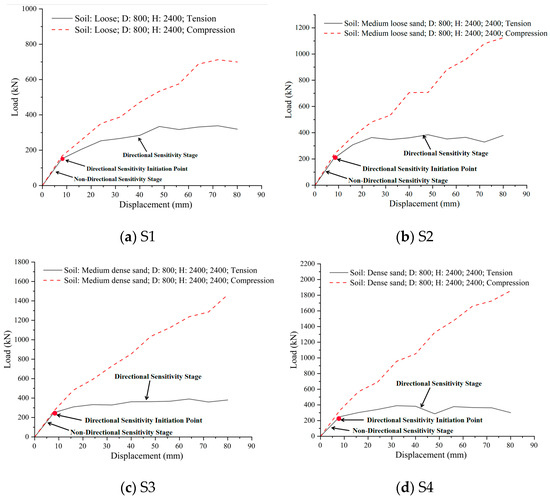
Figure 14.
Comparison of uplift versus compressive bearing capacities in sand with varying density states.
Under identical working conditions with embedment ratios below the transitional boundary, the directional sensitivity of the helical anchor bearing capacity became progressively pronounced with increasing soil density. In the S1 soil layer, the discrepancy between uplift and compression bearing capacities was 50% (Figure 14a); in the S4 soil layer, this discrepancy reached 80% (Figure 14d). The displacement at the directional sensitivity initiation point remained constant at 10% of the ultimate bearing capacity displacement, independent of soil density (Figure 14).
Under identical specimen parameters, the compressive ultimate bearing capacity of the helical anchors exhibited significant soil-dependent characteristics. With increasing soil density and internal friction angle, the compressive capacity demonstrated a marked positive correlation, progressively increasing from approximately 700 kN (Figure 14a) to 1100 kN (Figure 14b), 1500 kN (Figure 14c), and 1900 kN (Figure 14d). By contrast, the uplift ultimate bearing capacity showed no substantial soil dependence, remaining consistently stable at 300 kN (Figure 14) regardless of variations in soil density and internal friction angle, indicating negligible correlation with the latter parameter. The complete geotechnical parameters for soil types S1–S4 are detailed in Table 1.
Through systematic numerical modeling of double-helix anchors with 800 mm plate diameters, this study defines the critical spacing ratio threshold at which the failure mechanism in aeolian sand transitions from the CS model to the IB model. Detailed analysis of plastic strain contours (with red lines delineating the anchor rod profile and soil boundaries) revealed that at S/D < 4 (Figure 15a,b), a distinct cylindrical continuous shear slip zone developed between the anchor plates, characteristic of the CS failure mode. At S/D = 4 (Figure 15c), this inter-plate cylindrical shear slip zone was disrupted yet incompletely destroyed—partially compromised on the left side under compressive loading and fully disrupted under uplift conditions. When S/D = 5 (Figure 15d), independent symmetric plastic strain zones formed around each plate, with the cylindrical continuous shear slip zone entirely eliminated, demonstrating the IB failure mode. Strain at the bottom plate concentrated primarily beneath its lower surface, while strain surrounding the upper plate localized at its periphery. This investigation conclusively established S/D ≥ 4 as the transition threshold between the CS and IB failure mechanisms for helical anchors.
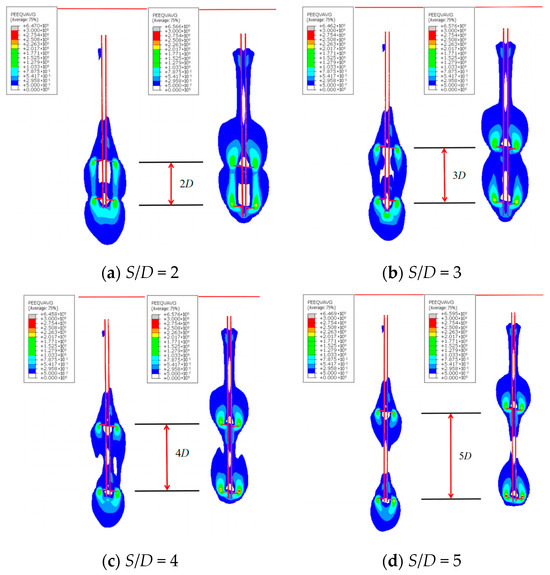
Figure 15.
Numerical plastic strain contours for double-helix anchors with 800 mm plate diameters.
5. Formula Fitting
5.1. Key Parameter Extraction
The bearing capacity factor of helical anchors is influenced by multiple characteristics, including soil parameters, plate diameter, embedment depth, and load direction. To elucidate the core influencing features governing helical anchor capacity, this study leveraged an in-house machine learning platform. Utilizing a database of 832 data points from parametric analyses, the XGBoost algorithm was employed to identify the dominant factors controlling bearing capacity.
The database comprised 832 numerical simulations from parametric analyses and incorporated dry density (ρ), internal friction angle (φ), initial cohesion (c), compression modulus (Es), helical plate diameter (D), and embedment depth (H) as predictive features, with compressive capacity designated as the target variable. Dataset partitioning allocated 70% for training, 20% for validation, and 10% for testing to establish the XGBoost framework. Model performance evaluation for single-plate anchor compressive capacity employed K-fold cross-validation [38,39] (Figure 16), wherein the dataset underwent random uniform division into K mutually exclusive subsets. Each iteration reserved one subset for validation while utilizing the remaining K-1 subsets for training, with ultimate performance metrics derived from averaged results across all K iterations. Feature importance rankings were quantified following established methodologies.
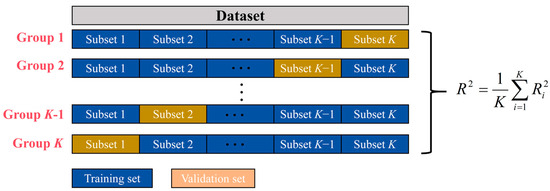
Figure 16.
Schematic diagram of K-fold cross-validation.
Bayesian optimization determined the optimal hyperparameters (Table 8) by sequentially reducing function evaluations. This probabilistic approach leveraged Gaussian processes to construct the posterior distributions of the objective function, strategically selecting subsequent sampling points via acquisition function maximization to achieve global convergence. The optimization cycle iteratively refined hyperparameter space exploration while minimizing computational expenditure, ultimately yielding the finalized predictive model.

Table 8.
Hyperparameter values of the optimal model.
Iteratively training the XGBoost dataset yielded the final model, which was employed to predict the compressive ultimate capacity of helical anchors across the entire dataset. The predictions were then compared with the numerical analysis results (Figure 17). The machine learning model demonstrated accurate predictions for the compression capacity of the helical anchors, with the predictions showing excellent agreement with the numerical analysis results. The prediction error remained within ±10%, satisfying the precision requirements of this study.
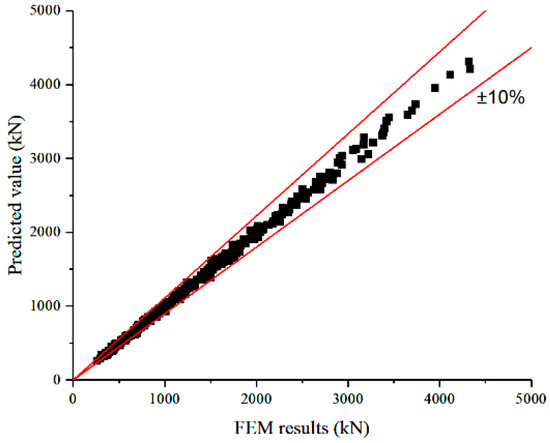
Figure 17.
Comparison of machine learning prediction accuracy.
To elucidate the core features influencing the bearing capacity of helical anchors, the finalized model was interpreted and analyzed using feature importance analysis [40] within the XGBoost framework. To ensure the comprehensiveness of features for model training, parameters including the internal friction angle (φ), sand density (ρ), initial cohesion (c), compression modulus (E), helix diameter (D), and embedment depth (H) were selected as input features. Subsequently, the key importance metrics for each feature—namely, gain, weight, and cover—were extracted (Figure 18).
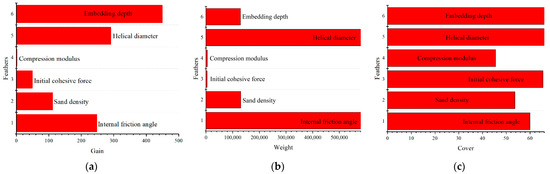
Figure 18.
Feature importance in the machine learning-based compressive capacity prediction model. (a) Feature importance (gain); (b) feature importance (weight); (c) feature importance (cover).
Under compressive loading, the embedment depth (H) exhibited the highest gain importance (Figure 18a), while the helix diameter (D) and internal friction angle (φ) demonstrated the greatest weight importance (Figure 18b). The cover importance was dominated by the embedment depth (H), helix diameter (D), and internal friction angle (φ) (Figure 18c). In summary, the internal friction angle, helix diameter, and embedment depth were the three most significant features influencing the compressive capacity of helical anchors in sandy soils. As demonstrated by the bearing capacity formulations for the CS and IB models (Formulas (3) and (4)), the internal friction angle (φ) governed Formula (3), while the embedment depth (H) was essential to Formulas (3) and (4). Given that the helix diameter (D) functionally determines the helical plate area, D likewise constituted a fundamental parameter in both equations. The machine learning-identified critical parameters aligned precisely with these theoretical formulations, validating the accuracy of the determined key features.
5.2. Compressive Capacity Factor
Formula (4) was applied to analyze 336 sets of model data to determine the compressive capacity factor, Nqu, for helical anchors in the four aeolian sand states. As shown in the compressive capacity factor (Nqu) versus embedment ratio (H/D) plot, Nqu exhibited an exponential decay trend with increasing embedment ratio (Figure 19). This trend contradicted the reference compressive capacity factor (Nqu) curve in Figure 6, indicating that existing design codes provide reference curves with limited applicability. These standardized curves fail to adequately characterize the relationship between the compressive capacity factor (Nqu) and embedment ratio (H/D) in aeolian sands.
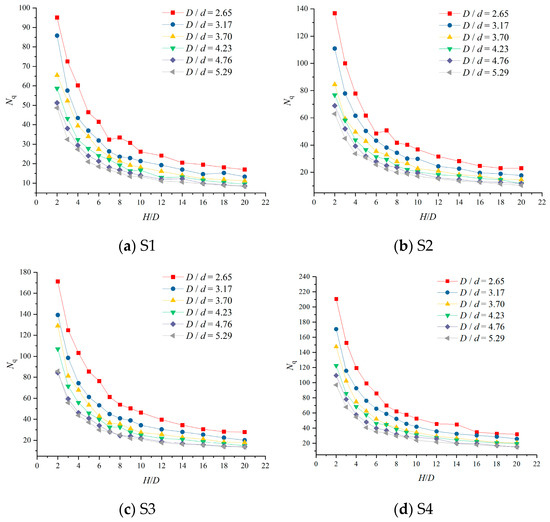
Figure 19.
Compressive capacity factor (Nqu) versus embedment ratio (H/D).
Building upon the three most significant features identified by the aforementioned machine learning analysis, the helix diameter (D), anchor shaft diameter (d), and embedment depth (H) were selected as variable parameters. By integrating the numerical model data from parametric analyses (Table 6 and Table 7), computational formulas for the compressive capacity factor (Nqu) were derived for the four aeolian sand types specified in Table 5. This formula system quantified the mathematical relationships between the key variables and the compressive capacity factor across four aeolian sand density states—loose, medium-loose, medium-dense, and dense—through a regression analysis of the parametric results. The derivation workflow is illustrated in Figure 20. The formulas are as follows:

Figure 20.
Derivation workflow for the compressive capacity factor (Nqu) formulation.
Within these formulations, Nqu denotes the compressive capacity factor of the helical anchor; D represents the plate diameter (m); d corresponds to the anchor shaft diameter (m); and H signifies the embedment depth of the bottom plate (m).
5.3. Lateral Earth Pressure Coefficient
To determine the lateral earth pressure coefficient, Ku, for the four aeolian sand density states listed in Table 5, the CS model bearing capacity prediction method was applied. Based on parametric analysis data, the overall frictional resistance of sand between the two plates was calculated by subtracting the bearing capacity contribution of the bottom plate from that of the double-helix anchor. This approach was used to establish Ku values for loose, medium-loose, medium-dense, and dense aeolian sands.
Building on the three most significant bearing capacity features identified through machine learning, the helix diameter (D) and embedment depth (H) were selected as variable parameters. Regression analysis of parametric results yielded computational formulas for Ku corresponding to the four aeolian sand types in Table 5. The fitting curves are presented in Figure 21, and the derivation workflow is shown in Figure 22. The formulas are provided below:
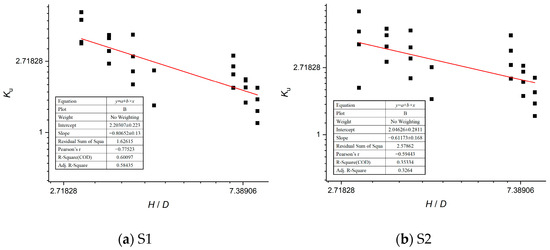
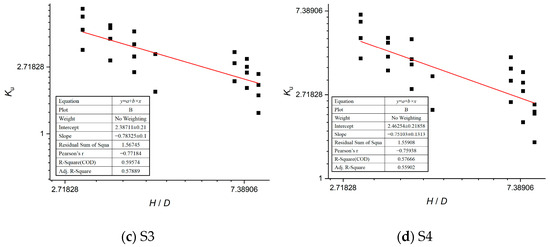
Figure 21.
Fitting curves for lateral earth pressure coefficients in aeolian sands.

Figure 22.
Derivation workflow for the lateral earth pressure coefficient formulation.
In these expressions, Ku represents the lateral earth pressure coefficient; D denotes the helix diameter (m); and H signifies the embedment depth at the centroid of the soil column between the helices (m).
5.4. Formula Validation
The proposed formulas for the compressive capacity factor (Nqu) and lateral earth pressure coefficient (Ku) were validated against ten field test scenarios. Theoretical calculations employing the CS model were compared with numerical analysis results (benchmark) and conventional code-based predictions. For stratified soil columns within the shear zone, frictional resistance was calculated segmentally with final superposition. Conventional code calculations adopted reference curves from Figure 5.
The mean value of the ratio of the conventional formula predictions to the numerical analysis results was 1.51 with a variance of 0.06. By contrast, the proposed formulas yielded a mean ratio of 1.03 and a variance of 0.012 when compared against numerical benchmarks. The proposed methodology exhibited significantly enhanced accuracy, reliably predicting the compressive capacity of helical anchors and providing reliable formula support for engineering design (Table 9).

Table 9.
Comparison of computational results using different methods.
6. Conclusions
This study systematically investigates the compressive bearing capacity characteristics of helical anchors in aeolian sand through integrated in situ testing, numerical simulations, and machine learning. It establishes the transition boundary between cylindrical shear (CS) and individual bearing (IB) failure modes and proposes novel calculation formulas for the bearing capacity factor and lateral earth pressure coefficient across four aeolian sand relative densities: loose, slightly loose, medium-dense, and dense. The principal findings are as follows:
- (1)
- During compressive loading, the load–displacement curve progresses through sequential phases: an initial near-linear stage, a non-linear transition, and a subsequent near-linear stage. The curve slope decreases with displacement, indicating the progressive degradation of soil–helix interlock. Compressive capacity exhibits an exponential relationship with helix diameter.
- (2)
- Under CS failure mode, a maximum high-plastic-strain zone develops near the bottom helix, reflecting its end-bearing function. Progressively expanding shear slip bands form at helix edges, with spatial distribution positively correlating with embedment depth, consistent with lateral earth pressure mechanisms. Under the IB mode, plastic strain localizes beneath helices. CS capacity correlates positively with bottom helix radius and embedment depth, while IB capacity shows an exponential relationship with helix radius. This elucidates the geometric correspondence between CS/IB models and physical failure mechanisms, providing a theoretical foundation for failure mode analysis.
- (3)
- For multi-helix anchors, soil stress beneath helices increases significantly with embedment depth. This phenomenon is attributed to depth-dependent variation in the lateral earth pressure coefficient (CS model perspective) and depth-dependent helix bearing capacity (IB model perspective), confirming both the model’s validity and their fundamental interrelation.
- (4)
- The shallow-to-deep embedment transition is defined as H = 5D. Shallow conditions (H < 5D) exhibit bowl-shaped axisymmetric failure zones and significant directional capacity sensitivity (deviations ≤ 80%). Deep conditions (H ≥ 5D) demonstrate elliptical axisymmetric failure zones with markedly reduced directional sensitivity (deviations ≈ 10%).
- (5)
- The CS-to-IB failure mode transition occurs at S/D ≥ 4. When S/D < 4, failure manifests as a CS mode with progressive shear slip bands at helix edges. When S/D ≥ 4, the IB mode prevails with stress concentration beneath helices (compression) or above them (tension), enabling independent bearing contribution.
- (6)
- Embedment depth, helix diameter, and internal friction angle are the most influential capacity parameters. Feature importance analysis revealed that embedment depth has the highest gain (450); helix diameter and internal friction angle show the highest weight (580,000); and all three parameters exhibit maximum cover (65).
- (7)
- Innovative formulas are proposed for calculating compressive bearing capacity and lateral earth pressure coefficients across the four sand densities. Compared with current design codes (mean calculated/analyzed ratio = 1.51; variance = 0.06), the proposed formulas demonstrate superior accuracy (mean ratio = 1.03) and reduced dispersion (variance = 0.012).
This study delivers important contributions, establishing the first critical depth criterion (H = 5D) and CS–IB transition boundary (S/D = 4) for aeolian sand through integrated in situ testing, numerical analysis, and machine learning while developing reliability-verified computational methods. Our methodology demonstrates broad applicability across soil types, providing a universal research framework for helical anchor-bearing capacity characterization. For aeolian sand engineering design, spiral anchor foundations should be embedded at H ≥ 5D based on the critical depth and directional sensitivity of the bearing capacity. Concurrently, helical plate spacing must be optimized using the model transition threshold S/D = 4. These outcomes fundamentally advance performance-based helical anchor design methodologies in aeolian sand regions, offering critical design benchmarks that bridge key knowledge gaps with significant scientific and practical implications.
Research Limitations and Future Perspectives
Limitations: (1) This study focuses specifically on aeolian sand, with the proposed equations validated solely for granular soils. Validation in cohesive soils (e.g., silty clays) requires reapplication of the methodology. (2) While establishing a generalized research framework for helical anchor-bearing mechanisms, the applicability of conventional CS/IB models in special soils—including frost-susceptible soils, expansive clays, and collapsible loess—remains uncertain due to their unique properties, necessitating methodology modifications.
Future Perspectives: (1) We will extend the model’s validation to silt–clay transitional soils and develop corresponding bearing capacity formulations for cohesive media. (2) We will enhance the XGBoost dataset scope through machine learning integration. Note: The ML algorithms advanced herein will be presented separately.
Author Contributions
Methodology, W.L., L.L. and S.Q.; Software, F.L.; Validation, Q.C., W.L., L.L., Y.W., Y.Z. (Yi Zhang) and S.Q.; Formal analysis, Q.C., W.L., Y.W. and S.Q.; Investigation, W.L., Y.Z. (Yi Zhang) and S.Q.; Resources, Q.C., W.L., S.Q., Y.Z. (Yue Zhang) and Y.G.; Writing—original draft, W.L. and S.Q.; Project administration, W.L. and S.Q.; Funding acquisition, W.L. and S.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [the Key Technology Research on the Application of Helical Anchor Foundations for Transmission Lines in Inner Mongolia] grant number [K2023-05], [National Natural Science Foundation of China] grant number [52208165], [the Henan Province Higher Education Young Core Teacher Training Program] grant number [2024GGJS125], [the Natural Science Foundation of Henan Province of China] grant number [222300420105] and [Henan University of Urban Construction] grant number [YCJQNGGJS202101 and YCJXSJSDTR202202].
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
We gratefully acknowledge the Structural Engineering Laboratory at Henan University of Urban Construction for providing experimental facilities. Special gratitude is extended to Gang CAO and Zhengwei MA for their technical assistance throughout the testing phase.
Conflicts of Interest
Author Yonghua Guo was employed by the company Henan Electric Power Survey and Design Institute Co., Ltd., China Electric Power Construction Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Livneh, B.; El Naggar, M.H. Axial testing and numerical modeling of square shaft helical piles under compressive and tensile loading. Can. Geotech. J. 2008, 45, 1142–1155. [Google Scholar] [CrossRef]
- Mohajerani, A.; Bosnjak, D.; Bromwich, D. Analysis and design methods of screw piles: A review. Soils Found. 2016, 56, 115–128. [Google Scholar] [CrossRef]
- Merifield, R.S. Ultimate uplift capacity of multiplate helical type anchors in clay. J. Geotech. Geoenviron. Eng. 2011, 137, 704–716. [Google Scholar] [CrossRef]
- Tang, C.; Phoon, K.K. Model uncertainty of cylindrical shear method for calculating the uplift capacity of helical anchors in clay. Eng. Geol. 2016, 207, 14–23. [Google Scholar] [CrossRef]
- Tang, C.; Phoon, K.K. Statistics of model factors and consideration in reliability-based design of axially loaded helical piles. J. Geotech. Geoenviron. Eng. 2018, 144, 04018050. [Google Scholar] [CrossRef]
- Pratama, I.T.; Lestari, A.S.; Oktavianus, I. Numerical study on the effects of helix diameter and spacing on the helical pile axial bearing capacity in cohesionless soils. Proc. Civ. Eng. Forum 2024, 10, 173–186. Available online: https://api.semanticscholar.org/CorpusID:268949950 (accessed on 11 July 2025). [CrossRef]
- Schiavon, J.A. Behaviour of Helical Anchors Subjected to Cyclic Loadings. Ph.D. Thesis, École centrale de Nantes, Universidade de São Paulo, São Paulo, Brazil, 2016. Available online: https://theses.hal.science/tel-02185307v1 (accessed on 11 July 2025).
- Ho, H.M.; Malik, A.A.; Kuwano, J.; Brasile, S.; Tran, T.V.; Mazhar, M.A. Experimental and Numerical Study on Pressure Distribution. Int. J. Geomech. 2022, 22, 9. [Google Scholar] [CrossRef]
- Shuman, N.M.; Khan, S.; Amini, F. Settlement based load capacity curve for single helix helical pile in c-ϕ soil. Soils Found. 2023, 63, 101265. [Google Scholar] [CrossRef]
- Garakani, A.A.; Serjoie, K.A. Ultimate Bearing Capacity of Helical Piles as Electric Transmission Tower Foundations in Unsaturated Soils: Analytical, Numerical, and Experimental Investigations. Int. J. Geomech. 2023, 9, 04023119. [Google Scholar] [CrossRef]
- Sakr, M. Performance of helical piles in oil sand. Can. Geotech. J. 2009, 46, 1046–1061. [Google Scholar] [CrossRef]
- Sakr, M. Installation and performance characteristics of high capacity helical piles in cohesionless soils. DFI J. 2011, 5, 39–57. [Google Scholar] [CrossRef]
- Vignesh, V.; Mayakrishnan, M. Design parameters and behavior of helical piles in cohesive soils—A review. Arab. J. Geosci. 2020, 13, 1194. [Google Scholar] [CrossRef]
- Igoe, D.; Zahedi, P.; Soltani-Jigheh, H. Predicting the compression capacity of screw piles in sand using machine learning trained on finite element analysis. Geotechnics 2024, 4, 807–823. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, A.; Zhao, H.; Gong, C.; Sun, H.; Cai, J. Model and numerical analyses of screw pile uplift in dry sand. Can. Geotech. J. 2024, 61, 1144–1158. [Google Scholar] [CrossRef]
- Cheng, L.; Han, Y.R.; Wu, Y.Q.; Kim, Y.H. Numerical investigation of pullout capacity for inclined strip plate anchors in sand. Appl. Ocean Res. 2023, 130, 103414. [Google Scholar] [CrossRef]
- Wang, L.; Wu, M.; Chen, H.; Hao, D.; Tian, Y.; Qi, C. Efficient machine learning models for the uplift behavior of helical anchors in dense sand for wind energy harvesting. Appl. Sci. 2022, 12, 10397. [Google Scholar] [CrossRef]
- Yuan, C.; Hao, D.; Chen, R.; Zhang, N. Numerical investigation of uplift failure mode and capacity estimation for deep helical anchors in sand. J. Mar. Sci. Eng. 2023, 11, 1547. [Google Scholar] [CrossRef]
- Lin, Y.; Xiao, J.; Le, C.; Zhang, P.; Chen, Q.; Ding, H. Bearing characteristics of helical pile foundations for offshore wind turbines in sandy soil. J. Mar. Sci. Eng. 2022, 10, 889. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD). Standard for Geotechnical Testing Method. China Electric Power Press: Beijing, China, 2019.
- BS EN 1993-1-1:2022; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. British Standards Institution (BSI): London, UK, 2022.
- GB 50007-2011; Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD). Code for Design of Building Foundation. China Architecture & Building Press: Beijing, China, 2011.
- DL/T 5219-2023; National Energy Administration of China. Technical Code for Basic Design of Overhead Transmission Line. China Electric Power Press: Beijing, China, 2024.
- JGJ 106-2014; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Code for Testing of Building Foundation Piles SS. China Architecture & Building Press: Beijing, Chian, 2014.
- Lutenegger, A.J. Cylindrical shear or plate bearing uplift behavior of multi-helix screw anchors in clay. In Contemporary Topics in Deep Foundations; Iskander, M., Laefer, D.F., Hussein, M.H., Eds.; ASCE Library: Reston, VA, USA, 2009; pp. 456–463. [Google Scholar] [CrossRef]
- Salhi, L.; Nait-Rabah, O.; Deyrat, C.; Roos, C. Numerical modeling of single helical pile behavior under compressive loading in sand. Electron. J. Geotech. Eng. 2013, 18, 4319–4338. [Google Scholar]
- Nabizadeh, F.; Choobbasti, A.J. Field study of capacity helical piles in sand and silty clay. Transp. Infrastruct. Geotechnol. 2017, 4, 3–17. [Google Scholar] [CrossRef]
- IEEE Std 691-2001; IEEE Standards Association (IEEE SA). IEEE Guide for Transmission Structure Foundation Design and Testing. IEEE: Piscataway, NJ, USA, 2001.
- Kwon, O.; Lee, J.; Kim, G.; Kim, I.; Lee, J. Investigation of pullout load capacity for helical anchors subjected to inclined loading conditions using coupled Eulerian-Lagrangian analyses. Comput. Geotech. 2019, 111, 66–75. [Google Scholar] [CrossRef]
- Schiavon, J.A.; Tsuha, C.H.C.; Thorel, L. Scale effect in centrifuge tests of helical anchors in sand. J. Phys. Model. Geotech. 2016, 16, 185–196. [Google Scholar] [CrossRef]
- Dassault Systèmes. ABAQUS Analysis User’s Guide, Version 2019; Dassault Systèmes Simulia Corp: Johnston, RI, USA, 2019.
- Sui, C.Y.; Shen, Y.S.; Wen, Y.M.; Gao, B. Application of the modified Mohr-Coulomb yield criterion in seismic numerical simulation of tunnels. Shock. Vib. 2021, 2021, 9968935. [Google Scholar] [CrossRef]
- Fan, C.; Yang, P.Y.; Li, L.; Wang, R. Poisson’s ratio of granular materials for Mohr-Coulomb elastoplastic model. Int. J. Min. Reclam. Environ. 2023, 37, 780–804. [Google Scholar] [CrossRef]
- Ghiba, I.D.; Rizzi, G.; Madeo, A.; Neff, P. Cosserat micropolar elasticity: Classical Eringen vs. dislocation form. J. Mech. Mater. Struct. 2023, 18, 93–123. [Google Scholar] [CrossRef]
- Andersen, K.H.; Schjetne, K. Database of friction angles of sand and consolidation characteristics of sand, silt, and clay. J. Geotech. Geoenviron. Eng. 2013, 139, 1140–1155. [Google Scholar] [CrossRef]
- Mortazavi Bak, H.; Mostafaei, H.; Shahbodagh, B.; Vahab, M.; Hashemolhosseini, H.; Khoshghalb, A. Effect of Sample Preparation on the Reliability of Large-Scale Physical Modeling in Geotechnical Systems: A Case Study. Geotech. Geol. Eng. 2024, 42, 2693–2707. Available online: https://link.springer.com/article/10.1007/s10706-023-02699-9 (accessed on 11 July 2025). [CrossRef]
- Hossain, M.S.; Randolph, M.F. Effect of strain rate and strain softening on the penetration resistance of spudcan foundations on clay. Int. J. Geomech. 2009, 9, 122–132. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).