Seismic Response Characteristics of High-Speed Railway Hub Station Considering Pile-Soil Interactions
Abstract
1. Introduction
2. Establishment of Finite Element Model of Station Structure System
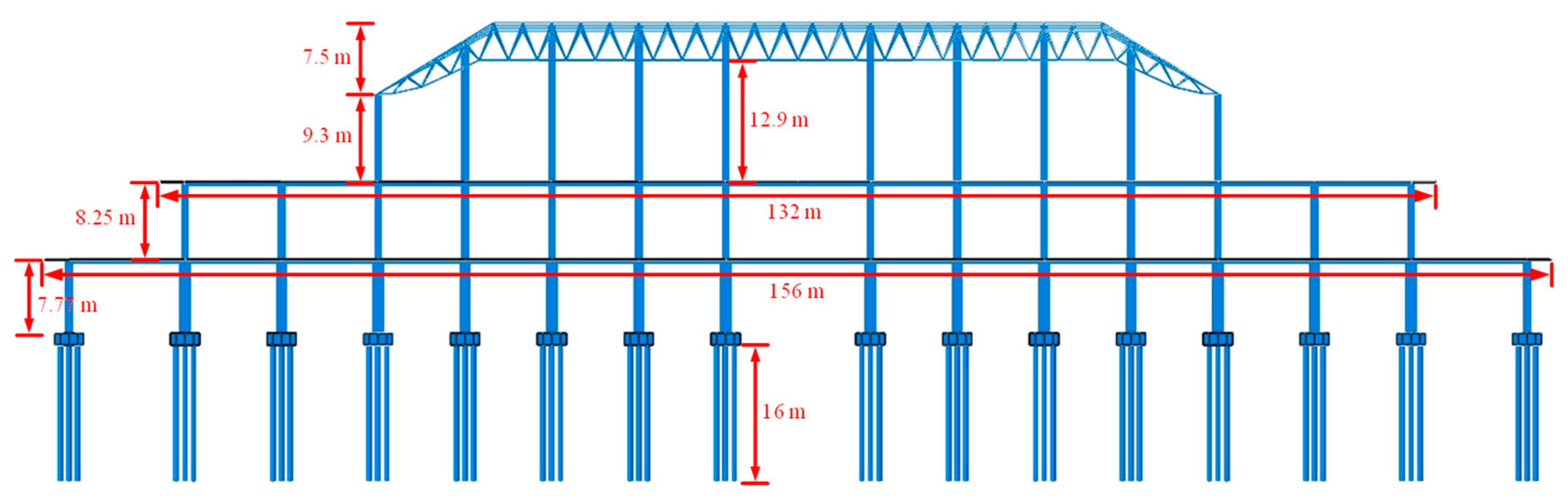
2.1. Engineering Backgrounds and Model Establishment
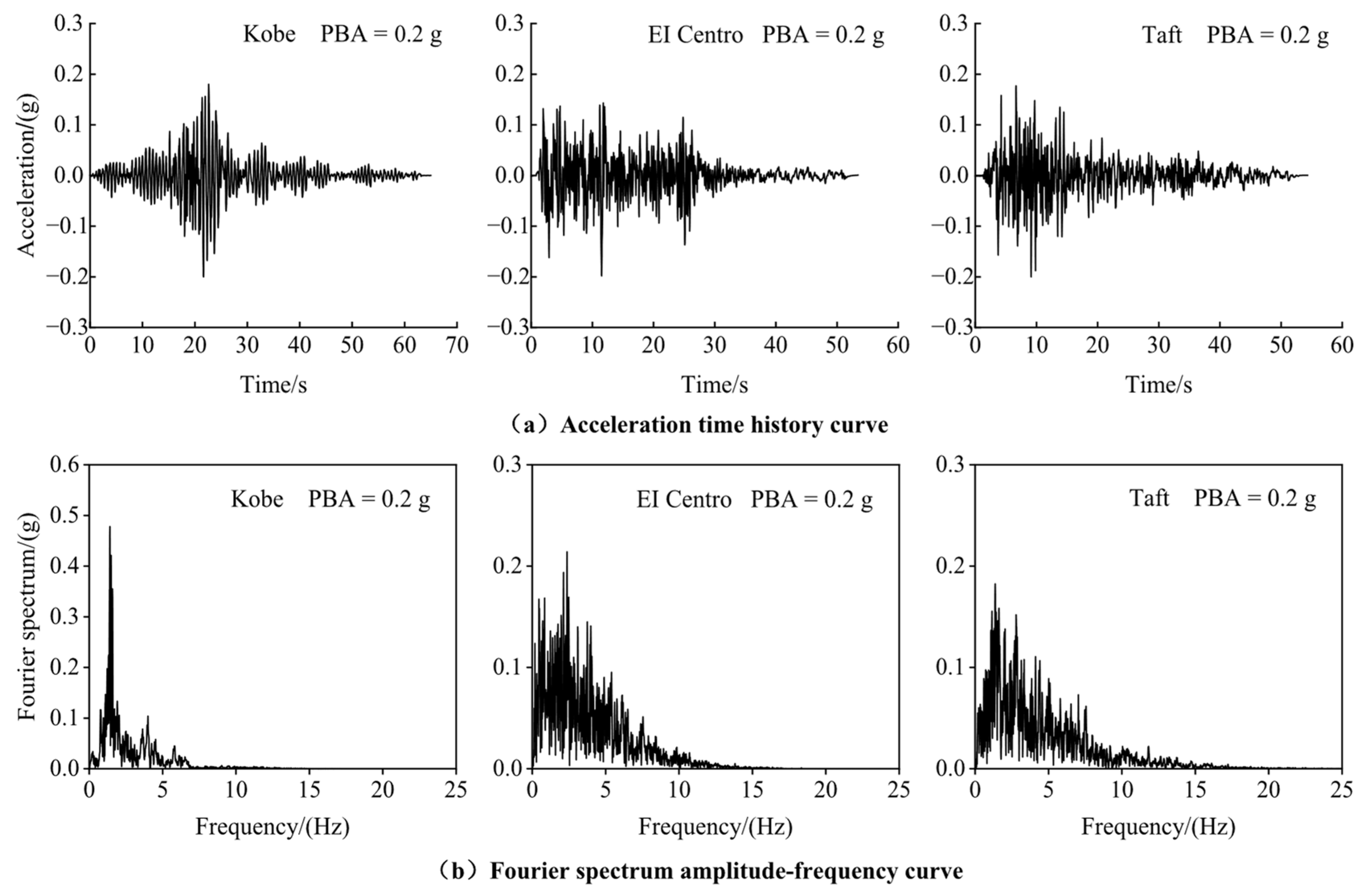
2.2. The Mesh Layout and the Input Earthquake Motion of the Model
2.3. Artificial Boundary Conditions
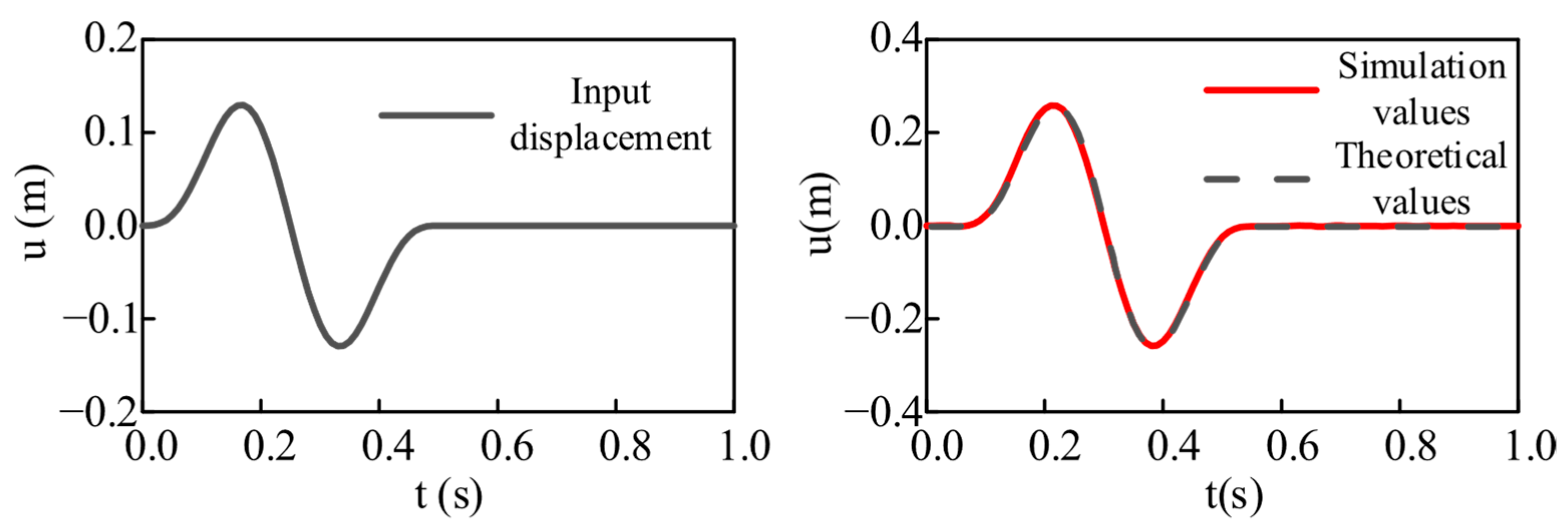
2.4. Verification of the Site Soil Model
2.5. Cyclic Constitutive Model of Soil
3. Natural Vibration Characteristics of the Hub Station Structure
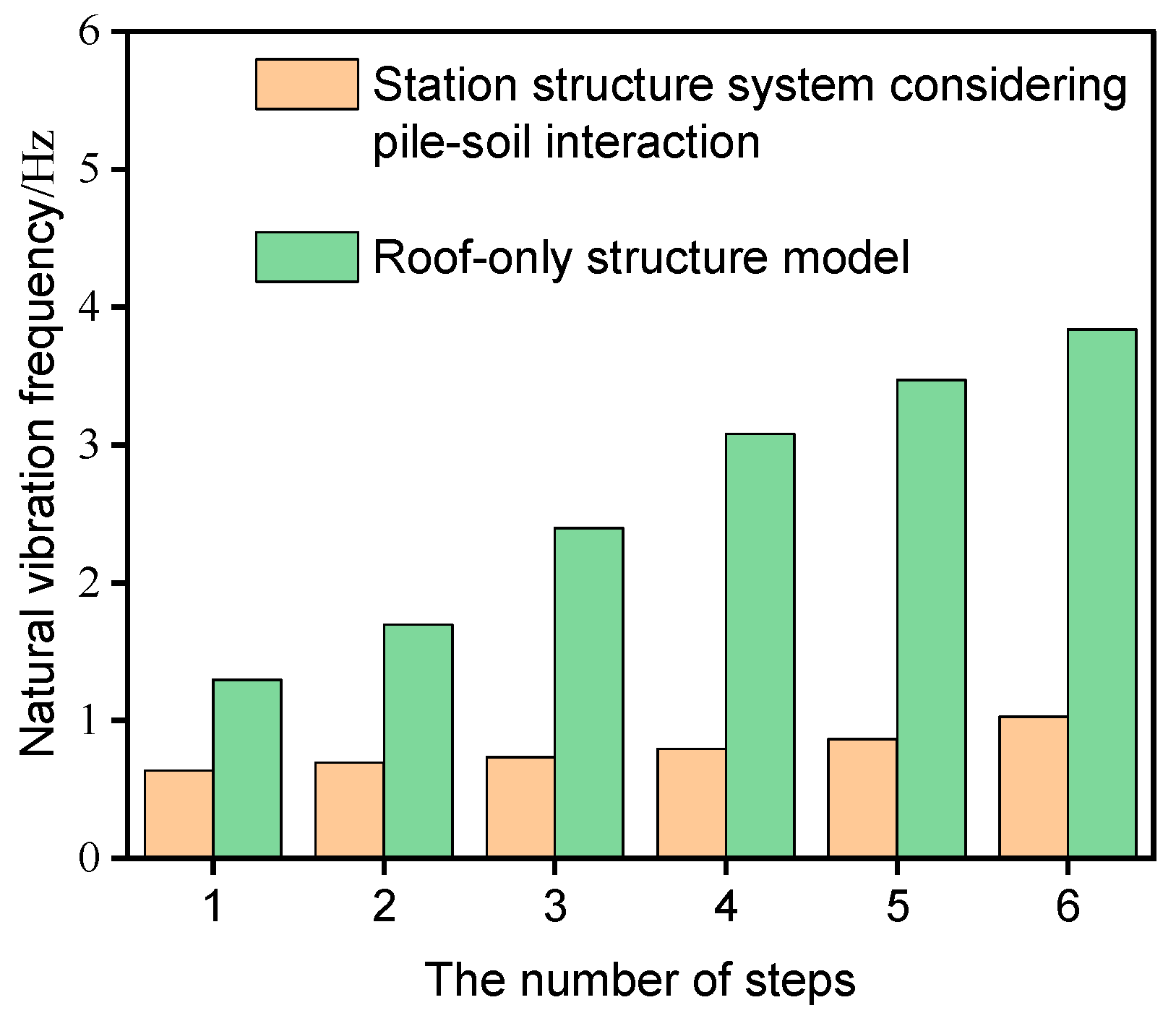
3.1. Influence of Pile-Soil Interaction and the Base Frame Structure of the Station on the Natural Vibration Characteristics of the Roof Structure
3.2. Realization of Material Damping
4. Seismic Response Characteristics of High-Speed Railway Hub Station Structure System
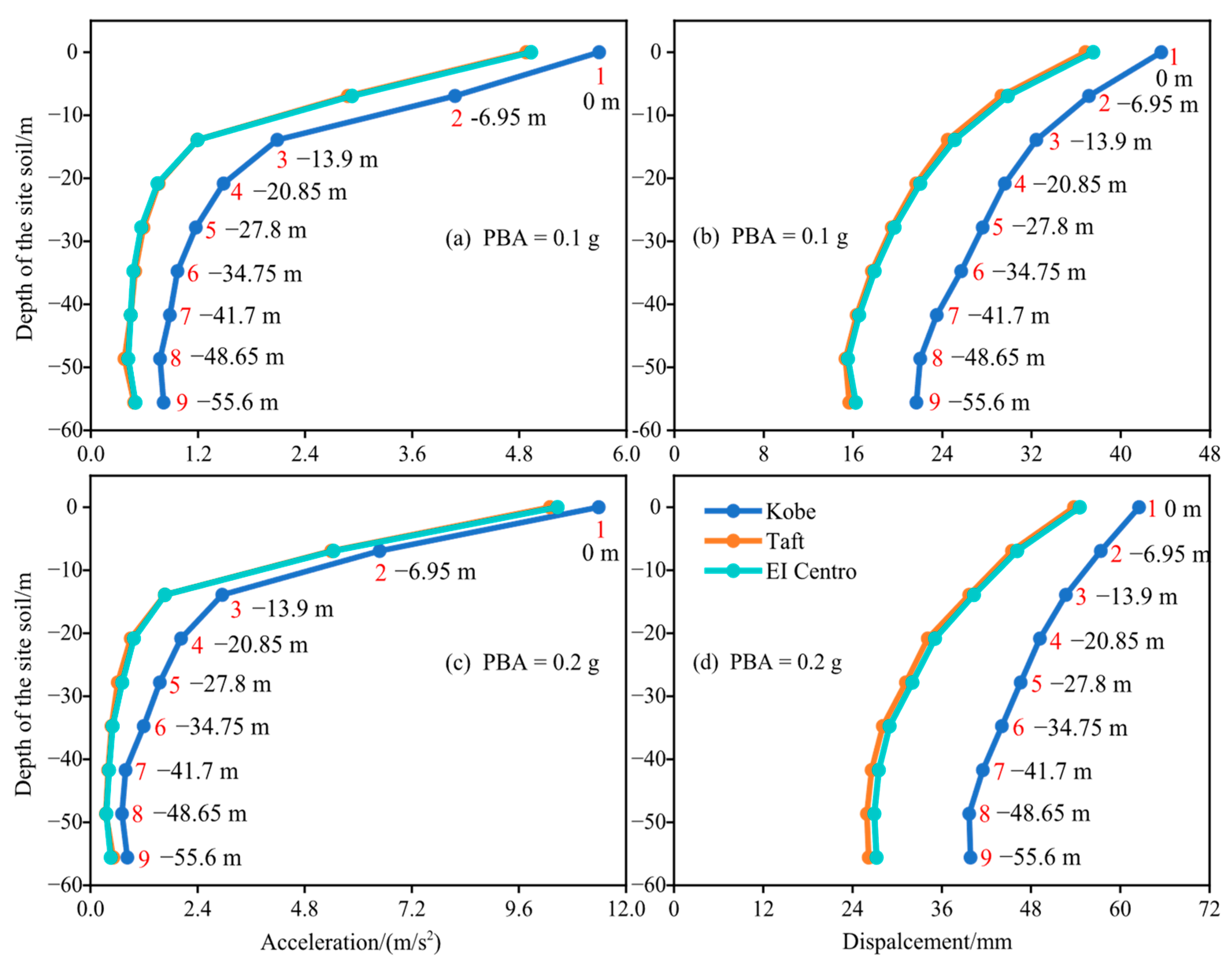
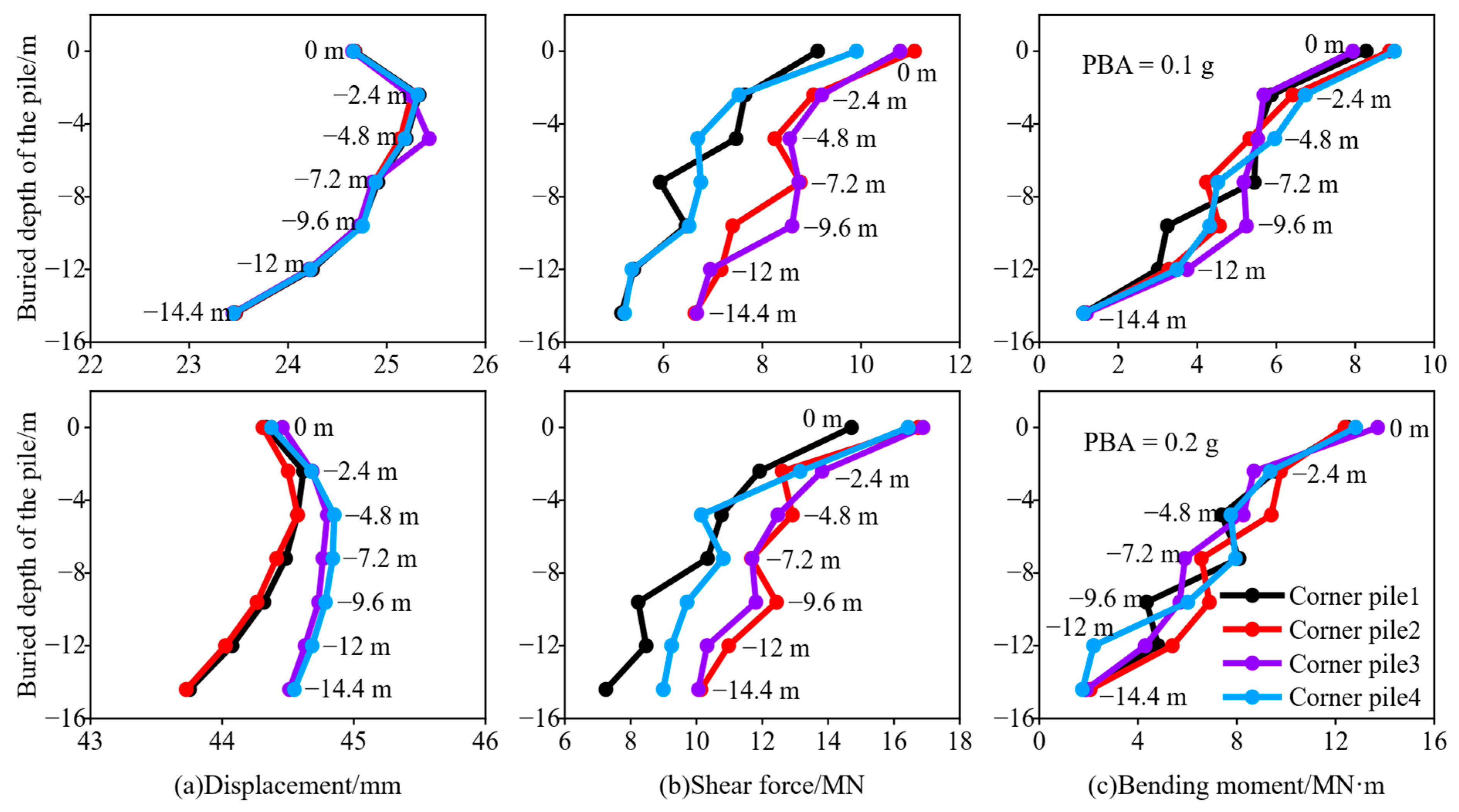
4.1. Seismic Response of Pile-Soil System
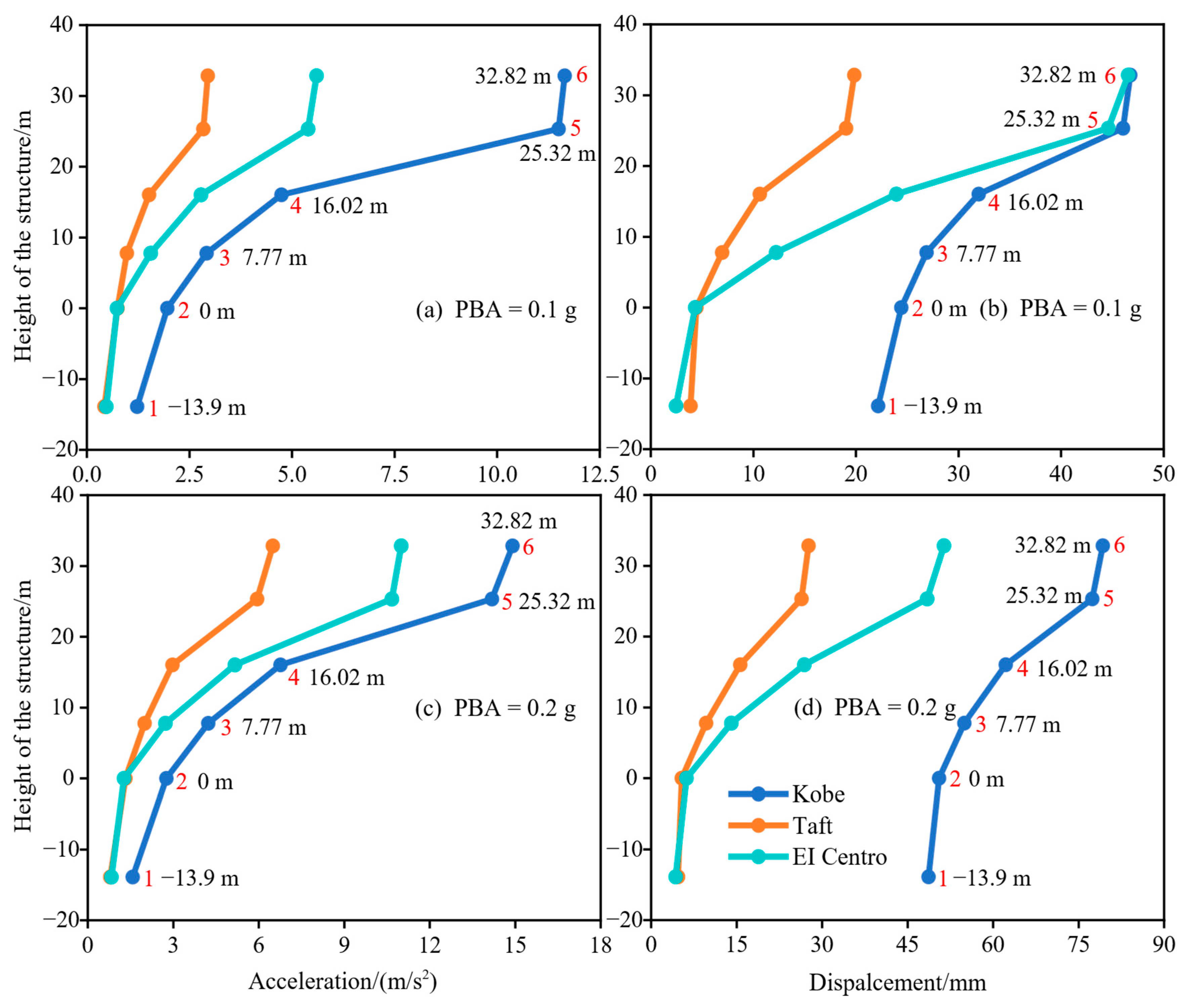
4.2. Seismic Response of Station Roof Structure
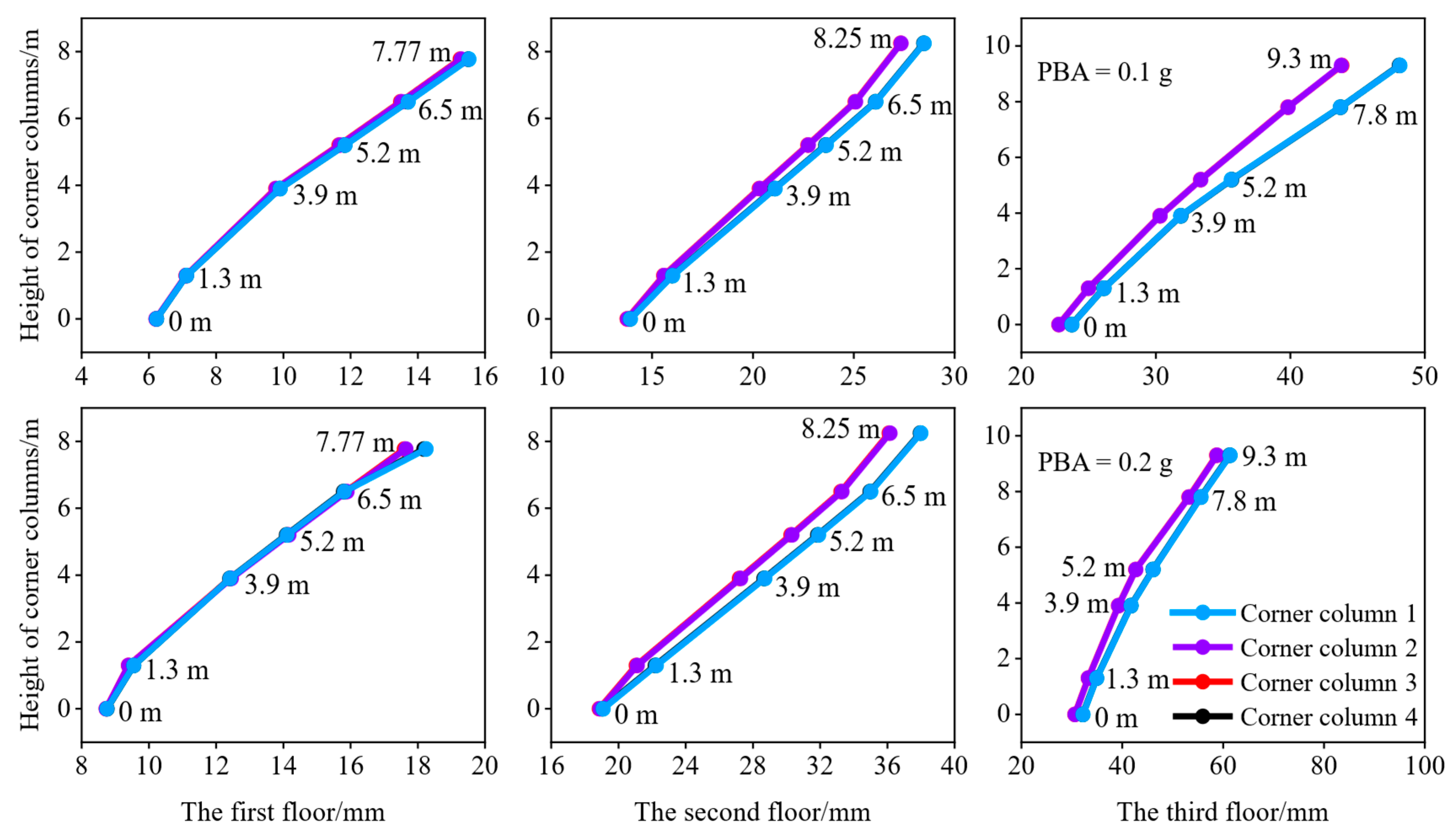
4.3. Seismic Response of Station Frame Structure
5. Conclusions
- (1)
- The pile-soil interaction has a significant influence on the dynamic characteristics of the high-speed railway hub station structure system. Due to the existence of the main frame structure, the natural vibration of the high-speed railway hub station system is significantly reduced compared with the roof-only structure.
- (2)
- Under the three earthquake motion records with PBA of 0.1 g and 0.2 g, the seismic response of the site soil gradually decreases with the increase of depth. The interaction between pile and soil resists the deformation of the foundation, and the nonlinear degree of pile-soil interaction increases with the increase of earthquake motion intensity.
- (3)
- Among the three kinds of earthquake motion records, the spectral characteristics of the Kobe earthquake are the closest to the natural vibration of a high-speed railway station structure system, followed by the El Centro earthquake. The displacement responses of the roof structure of Changde high-speed railway hub station, considering pile-soil interaction, are significantly larger than those without considering pile-soil interaction.
- (4)
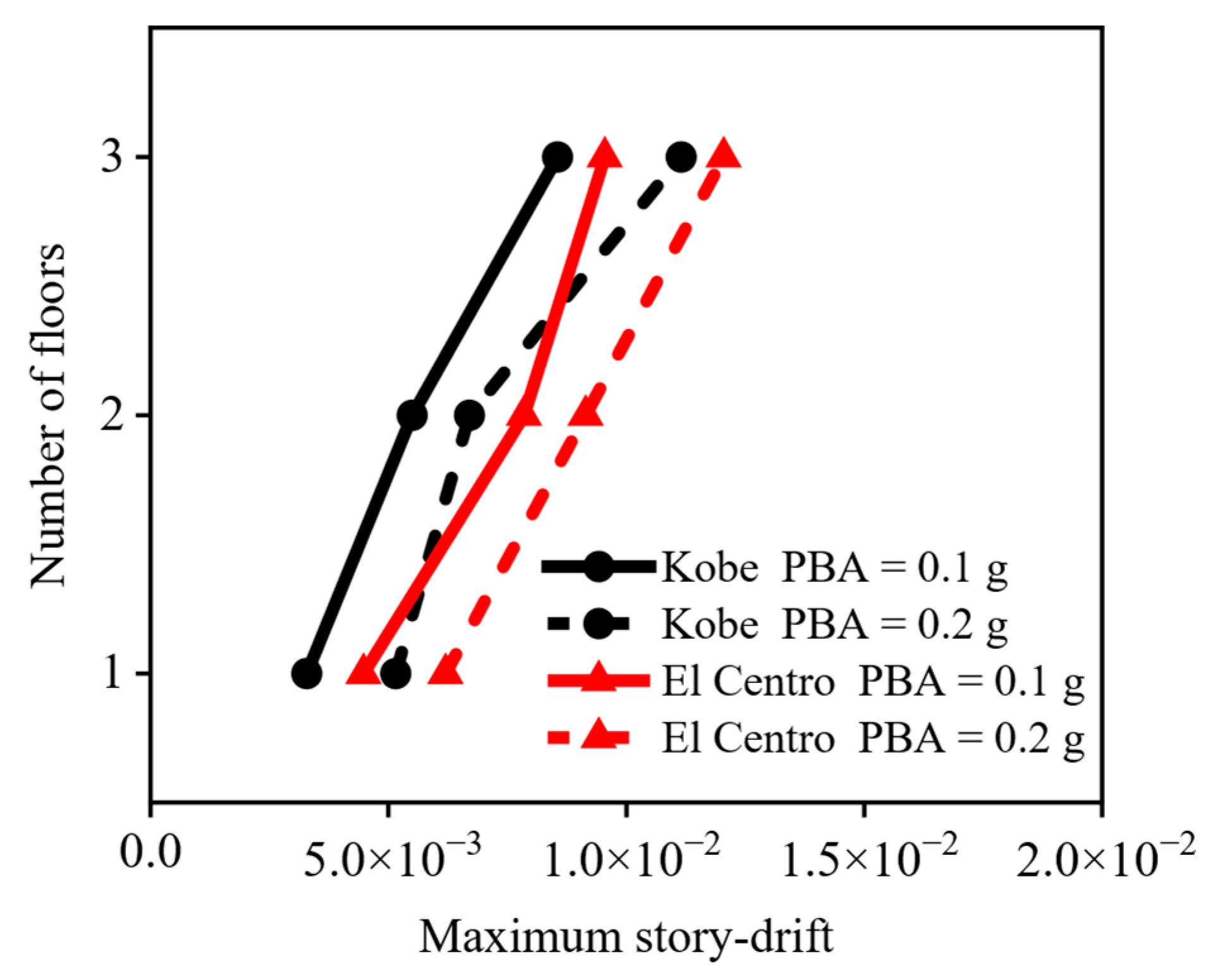
- The roof structure has a significant effect on the seismic response of the base frame structure, and the seismic response of the connection between the roof structure and the base frame structure is seriously amplified. The seismic response of the high-speed railway station structure increases gradually with the increase in the height of the frame structure. The maximum story drift angle at the top floor of the station structure is also greater than that at the bottom floor.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, M.; Fan, F.; Zhi, X.; Kong, D. Analysis on dynamic response of quadrangular pyramid grid structure with supporting columns. China Civil. Eng. J. 2014, 47, 9–15. [Google Scholar]
- Sun, B.R. Shaking Table Test of “Integrated Station-Bridge” High-Speed Railway Station Structure; China University of Mining and Technology: Xuzhou, China, 2021. [Google Scholar]
- Su, L.; Dong, S.L. Seismic analysis of two typical spatial structures under multi-support vertical excitations. Eng. Mech. 2007, 24, 85–90. [Google Scholar]
- Liu, J.H.; Deng, H. Elasto-plastic dynamic response analysis for double-layer spherical reticulated shells under rare earthquake. J. Vib. Shock. 2012, 31, 161–167. [Google Scholar]
- Nakazawa, S.; Kato, S.; Yagi, Y. Evaluation of seismic damage of single layer lattice dome supported by ductile braces. J. Struct. Constr. Eng. 2012, 77, 593–601. [Google Scholar] [CrossRef]
- Nakazawa, S.; Yanagisawa, T.; Kato, S. Seismic loads for single layer reticular domes and seismic performance evaluation. J. Struct. Constr. Eng. 2014, 79, 1287–1297. [Google Scholar] [CrossRef][Green Version]
- Jiang, S.F.; Li, H.J.; Long, T.T. Stability of single-layer three-way reticulated barrel vaults considering global geometric imperfection, member imperfection and eccentricity. Eng. Mech. 2022, 39, 178–188. [Google Scholar]
- Ye, Y.P. Analysis of dynamic characteristics and seismic performance of high-speed railway station structure. Rail. Cons. Tech. 2024, 10, 188–192. [Google Scholar]
- Palermo, A.; Krödel, S.; Matlack, K.H.; Zaccherini, R.; Dertimanis, V.K.; Chatzi, E.N.; Marzani, A.; Daraio, C. Hybridization of guided surface acoustic modes in unconsolidated granular media by a resonant metasurface. Phys. Rev. Appl. 2018, 9, 054026. [Google Scholar] [CrossRef]
- Ding, H.; Huang, N.; Xu, C.; Xu, Y.; Cao, Z.; Zeng, C.; Tong, L. A locally resonant metamaterial and its application in vibration isolation: Experimental and numerical investigations. Earthq. Eng. Struct. Dyn. 2024, 53, 15. [Google Scholar] [CrossRef]
- Yu, J.K. Dynamic Interaction Test and Numerical Simulation of Pile-Soil-Structure; The Institute of Engineering Mechanics, China Earthquake Administration: Harbin, China, 2023. [Google Scholar]
- Liu, J.Y.; Jing, L.P.; Qi, W.H. Analysis of dynamic interaction influence factors of pile-soil-structure. Earth. Eng. Eng. Dyn. 2024, 44, 210–221. [Google Scholar]
- Xu, S.Y. Study on Seismic Performance of Frame Structure Considering Pile Soil-Structure Interaction; Lanzhou Jiaotong University: Lanzhou, China, 2024. [Google Scholar]
- Wang, G.; Zhang, J.M.; Wei, X. Seismic response analysis of a subway station in liquefiable soil. Chin. J. Geotech. Eng. 2011, 33, 1623–1627. [Google Scholar]
- Muhammad; Lim, C.W.; Reddy, J.N. Built-up structural steel sections as seismic metamaterials for surface wave attenuation with low frequency wide bandgap in layered soil medium. Eng. Struct. 2019, 188, 440–451. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Hu, Z.H.; Wang, X.J.; Chen, G.X. Seismic response of a large underground structure in liquefied soils by FEM numerical modelling. Bull. Earth. Eng. 2015, 13, 3645–3688. [Google Scholar] [CrossRef]
- Zhuang, H.; Ren, J.; Miao, Y.; Jing, L.; Yao, E.; Xu, C. Seismic performance levels of a large underground subway station in different soil foundations. J. Earth. Eng. 2021, 25, 2808–2833. [Google Scholar] [CrossRef]
- Zhuang, H.; Wang, W.; Jin, L.; Li, S.; Chen, G. Seismic performance of two-story subway station structures with different isolating systems. Earth. Res. Adv. 2022, 2, 100155. [Google Scholar] [CrossRef]
- Zhuang, H.; Zhao, D.; Chen, G.; Wang, Y.; Zhao, K. Three-dimensional numerical investigation on seismic response of subway station in liquefied soil by the loosely coupled effective stress model. J. Earth. Eng. 2023, 27, 3607–3631. [Google Scholar] [CrossRef]
- Chen, G.X.; Chen, S.; Zuo, X.; Du, X.L.; Qi, C.Z.; Wang, Z.H. Shaking-table tests and numerical simulations on a subway structure in soft soil. Soil. Dyn. Earth. Eng. 2015, 76, 13–28. [Google Scholar]
- Chen, G.; Chen, S.; Qi, C.; Du, X.; Wang, Z.; Chen, W. Shaking table tests on a three-arch type subway station structure in a liquefiable soil. Bull. Earth. Eng. 2015, 13, 1675–1701. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Zhao, D.; Zhao, K.; Yang, J. A new effective stress method for nonlinear site response analyses. Earthq. Eng. Struct. Dyn. 2021, 50, 1595–1611. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Zhao, D.; Zhao, K.; Yang, J. 3D seismic response characteristics of a pile-mat-founded AP1000 nuclear-island building considering nonlinear hysteretic behavior of soil. Bull. Earth. Eng. 2022, 20, 7077–7106. [Google Scholar] [CrossRef]
- Wang, G.B.; Hao, P.F.; Sun, F.X. Spatial influence scope of end wall of metro station structures. Chin. J. Geotech. Eng. 2020, 42, 1435–1445. [Google Scholar]
- Jing, Y.; Zhuang, H.Y.; Wang, W.; Zhou, Z.H.; Chen, G.X. Seismic performance and effective isolation of a large multilayered underground subway station. Soil. Dyn. Earth. Eng. 2021, 142, 106560. [Google Scholar] [CrossRef]
- Zhao, K.; Xia, G.X.; Wang, Y.Z.; Zhao, D.F.; Zhuang, H.Y.; Chen, G.X. Three-dimensional loosely coupled effective stress method for seismic soil-structure interactions. Chin. J. Geotech. Eng. 2022, 44, 861–869. [Google Scholar]
- Gholizadeh, S.; Milany, A.; Hasancebi, O. Seismic optimization and performance assessment of special steel moment-resisting frames considering nonlinear soil-structure interaction. Steel Comp. Str. 2023, 47, 339–353. [Google Scholar]
- Zhu, S.D.; Chen, G.X.; Chen, W.Y.; Gao, W.S.; Li, W.B. Influence of soil secondary nonlinearity on 3D seismic responses of a pile-founded nuclear island structure. Rock. Soil. Mech. 2023, 44, 1501–1511. [Google Scholar]
- Song, Z.W. Research on the structure design for the central station track level of newly built Shenyang South railway station. J. Rail. Eng. Soc. 2014, 31, 81–86. [Google Scholar]
- Zhang, L.L.; Xu, J.H.; Zhang, Y.Y.; Sun, B.R.; Wang, Y. Seismic vulnerability analysis of “integrated station-bridge” high-speed railway station structure based on IDA. Earth. Resistant Eng. Retro. 2023, 45, 86–94. [Google Scholar]
- Zhao, K.; Zhu, S.; Bai, X.; Wang, Q.; Chen, S.; Zhuang, H.; Chen, G. Seismic response of immersed tunnel in liquefiable seabed considering ocean environmental loads. Tunn. Undergr. Space Technol. 2021, 115, 104066. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, Q.; Chen, S.; Zhuang, H.; Chen, G. Dynamic response of pipelines in liquefiable seabed under nature loadings: Waves and currents. Ocean. Eng. 2021, 230, 109051. [Google Scholar] [CrossRef]
- Zhang, X.L.; Li, X.J.; Chen, G.X.; Zhou, Z.H. An improved method of the calculation of equivalent nodal forces in viscous-elastic artificial boundary. Chin. J. Theor. Appl. Mech. 2016, 48, 1126–1135. [Google Scholar]
- Chen, G.; Ruan, B.; Zhao, K.; Chen, W.; Zhuang, H.; Du, X.; Khoshnevisan, S.; Juang, C.H. Nonlinear response characteristics of undersea shield tunnel subjected to strong earthquake motions. J. Earth. Eng. 2020, 24, 351–380. [Google Scholar] [CrossRef]
- GB50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010; pp. 23–25.
- Kuhlemeyer, R.L.; Lysmer, J. Fine element method accuracy for wave propagation problems. J. Soil. Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Zhu, S.D.; Chen, G.X.; Jiang, P.C.; Chen, W.Y.; Gao, W.S. 3D nonlinear response characteristics of the pile-raft-supported AP1000 nuclear island building in soft deposits subjected to strong earthquake motions. Eng. Mech. 2021, 38, 129–142. [Google Scholar]
- Zhu, S.D.; Chen, G.X.; Chen, W.Y.; Gao, W.S. 3D seismic response characteristics of piles of a nuclear island building considering nonlinearity of soil. China Civil. Eng. J. 2023, 56, 124–136. [Google Scholar]
- Zhao, D.F.; Ruan, B.; Chen, G.X.; Xu, L.Y.; Zhuang, H.Y. Validation of modified irregular loading-unloading rules based on Davidenkov skeleton curve and its equivalent shear strain algorithm implemented in ABAQUS. Chin. J. Geotech. Eng. 2017, 39, 888–895. [Google Scholar]
- Wang, Y.Z.; Zhao, D.F.; Chen, G.X.; Liang, K. A new nonlinear effective stress method for one-dimensional seismic site response analysis and its validation. Chin. J. Geotech. Eng. 2021, 43, 502–510. [Google Scholar]
- Chen, W.; Luo, Z.; Zheng, Y.; Xu, L.; Huang, L. Seismic response analysis of liquefiable seabed sites: Effects of seawater-seabed interaction and bidirectional seismic motion. Ocean. Eng. 2025, 324, 120717. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Li, X.X.; Zhao, K.; Wu, S.L.; Li, Z.Y.; Chen, G.X. Liquefaction-induced lateral spreading characteristics of the fluvial terraces at the lower reaches of Yangtze River. Eng. Geol. 2025, 346, 107900. [Google Scholar]
- Hudson, M.; Idriss, I.M.; Beikae, M. User Manual for QUAD4m: A Computer Program to Evaluate the Seismic Response of Soil Structures Using Finite Element Procedures and Incorporating A Compliant Base; University of California: Berkeley, CA, USA, 1994. [Google Scholar]
- Zou, D.G.; Xu, B.; Kong, X.J. Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response. Rock. Soil. Mech. 2011, 32, 797–803. [Google Scholar]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of seismic soil-pile-structure interaction on mid-and high-rise steel buildings resting on a group of pile foundations. Int. J. Geomech. 2018, 18, 04018103.1–04018103.27. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced seismic analysis of soil-foundation-structure interaction for shallow and pile foundations in saturated and dry deposits: Insights from 3D parallel finite element modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Asgari, A.; Sorkhi, S.F.A. Wind turbine performance under multi-hazard loads: Wave, wind, and earthquake effects on liquefiable soil. Results Eng. 2025, 26, 104647. [Google Scholar] [CrossRef]
- Asgari, A.; Ranjbar, F.; Bagheri, M. Seismic resilience of pile groups to lateral spreading in liquefiable soils: 3D parallel finite element modeling. Structures 2025, 74, 108578. [Google Scholar] [CrossRef]






| Constituent | Density /(kg/m3) | Elastic Modulus /(GPa) | Poisson Ratio | Ultimate Tensile Strength /(MPa) | Ultimate Tensile Strain | Ultimate Compressive Strength /(MPa) | Peak Compressive Strain | Limit Compressive Strain |
|---|---|---|---|---|---|---|---|---|
| C40 concrete | 2500 | 32.5 | 0.2 | 2.39 | 7.35 × 10–5 | 26.8 | 0.002 | 0.0033 |
| Steel | 7900 | 210 | 0.3 | 650 | 0.18 | 420 | 0.002 | 0.02 |
| Constituent. | Category of Soils | Depth/ (m) | Density/ (kg/m3) | Shear Wave Velocity/ (m/s) | Poisso Ratio | A | B | Reference Shear Strain | Damping Ratio Under Small Strain |
|---|---|---|---|---|---|---|---|---|---|
| Surface layer | Backfill | 2.6 | 1900 | 176 | 0.47 | 1.05 | 0.42 | 0.00031 | 0.025 |
| Middle layer | Clay | 14.6 | 1950 | 236 | 0.45 | 1.06 | 0.44 | 0.00053 | 0.024 |
| Sublayer | Mealy sand | 33.6 | 2000 | 289 | 0.43 | 1.07 | 0.46 | 0.00082 | 0.022 |
| Bottom layer | Sandy soil 1 | 50.6 | 2030 | 458 | 0.43 | 1.10 | 0.47 | 0.00093 | 0.020 |
| Sandy soil 2 | 55.6 | 2045 | 546 | 0.42 | 1.12 | 0.45 | 0.00111 | 0.019 |
| Constituent | Category of Soils | PBA = 0.1 g | PBA = 0.2 g | ||||
|---|---|---|---|---|---|---|---|
| Kobe | Taft | El Centro | Kobe | Taft | El Centro | ||
| Transverse | Characteristic coefficient/(%) | 2.72 | 5.86 | 25.29 | 3.29 | 5.48 | 18.46 |
| Longitudinal | Characteristic coefficient/(%) | 243 | 140.99 | 166.80 | 315 | 139.70 | 165.86 |
| Vertical | Characteristic coefficient/(%) | 220.88 | 743.13 | 570.43 | 146.42 | 639.52 | 411.56 |
| Constituent | Category of Soils | PBA = 0.1 g | PBA = 0.2 g | ||||
|---|---|---|---|---|---|---|---|
| Kobe | Taft | El Centro | Kobe | Taft | El Centro | ||
| Transverse | Characteristic coefficient/(%) | 2.66 | 5.52 | 24.39 | 3.25 | 5.47 | 18.16 |
| Longitudinal | Characteristic coefficient/(%) | 1458.12 | 1221.78 | 1568.15 | 2025.69 | 1175.47 | 1519 |
| Vertical | Characteristic coefficient/(%) | 2054.62 | 5018.46 | 4419.73 | 1199 | 4326.49 | 3164.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Chen, Z. Seismic Response Characteristics of High-Speed Railway Hub Station Considering Pile-Soil Interactions. Buildings 2025, 15, 2466. https://doi.org/10.3390/buildings15142466
Zhang N, Chen Z. Seismic Response Characteristics of High-Speed Railway Hub Station Considering Pile-Soil Interactions. Buildings. 2025; 15(14):2466. https://doi.org/10.3390/buildings15142466
Chicago/Turabian StyleZhang, Ning, and Ziwei Chen. 2025. "Seismic Response Characteristics of High-Speed Railway Hub Station Considering Pile-Soil Interactions" Buildings 15, no. 14: 2466. https://doi.org/10.3390/buildings15142466
APA StyleZhang, N., & Chen, Z. (2025). Seismic Response Characteristics of High-Speed Railway Hub Station Considering Pile-Soil Interactions. Buildings, 15(14), 2466. https://doi.org/10.3390/buildings15142466







