Abstract
A novel endplate bolted rigid joint is proposed in this study for connecting circular concrete-filled steel tube (CCFT) columns to wide-flange (WF) steel beams. The seismic performance and potential failure mechanisms of the proposed joint were investigated through quasi-static cyclic tests and finite element (FE) simulations. This study aims to address several engineering challenges commonly observed in existing joint configurations, including an irrational force-resisting mechanism, complicated detailing and installation, on-site construction difficulties, constraints on beam size, and limited repairability. By optimizing the force transfer path, the new joint effectively reduces the number of critical tension welds, thereby enhancing the ductility and reliability. The experimental results indicate that the joint exhibits adequate flexural strength, stiffness, and ductility, with stable moment–rotation hysteresis loops under cyclic loading. Moreover, full restoration of the joint can be achieved by replacing only the steel beam and endplate, facilitating post-earthquake repair. FE analysis reveals that, under the ultimate bending moment at the beam end, multiple through cracks develop in the high-strength grout—which serves as a key load-transferring component—and significant debonding occurs between the grout and the surrounding steel members. However, due to confinement from adjacent components, these internal cracks do not compromise the overall strength and stiffness of the joint. This research provides an efficient and practical connection solution, along with valuable experimental insights, for the application of CCFT columns in moment-resisting frames located in high seismic zones.
1. Introduction
Extensive research has demonstrated that circular concrete-filled steel tube (CCFT) columns exhibit excellent seismic performance [1,2]. The core concrete effectively mitigates the local buckling and instability of the steel tube wall, thereby enhancing the flexural stiffness of the member. Simultaneously, the confining effect of the circular steel tube significantly increases the compressive strength of the core concrete and restricts the development of its plastic strains, which leads to the improved ductility and energy dissipation capacity of the composite member. In addition, structural systems employing CCFT columns can reduce steel consumption and minimize cross-sectional dimensions. Furthermore, the absence of formwork during the casting of the core concrete simplifies construction, shortens the construction period, and reduces the overall costs [3].
Compared to other concrete-filled steel tube (CFST) cross-sectional shapes, CCFT columns demonstrate superior confinement capacity [4], more stable moment–rotation hysteresis behavior, and enhanced fire resistance [5,6]. However, their closed sections and curved surfaces often complicate the rigid connection with conventional wide-flange (WF) steel beams. Existing connection types for such joints can generally be classified into two categories: (1) those that transfer loads entirely to the outer wall of the circular steel tube through welding or bolting, and (2) those that utilize embedded components to partially transfer loads directly into the core concrete.
The first category features relatively simple detailing but often suffers from irrational force-resisting mechanisms, leading to insufficient joint stiffness or ductility, making them unsuitable for high seismic zones. Stephen and Yousef [7] demonstrated experimentally that directly welding a connection stub to the outer wall of the steel tube tends to cause brittle failure in the tube wall, beam flange, and welds. Azizinamini et al. [8] and Cheng [9] showed that using external ring plates can result in the premature degradation of flexural strength and brittle weld failure. Although enlarging the external ring plate may enhance seismic performance [10,11], it can interfere with curtain wall arrangements at the joint. Similarly, using blind fasteners to bolt curved endplates directly onto the steel tube wall can cause early yielding under significant radial tension [12,13,14], and such connections typically fail to meet the stiffness requirements of fully rigid joints [15]. Li et al. [16] and Ng et al. [17] attempted to improve the strength and stiffness of blind fasteners in rectangular CFST columns by anchoring the embedded ends, but this method has yet to be verified for CCFT columns.
The second category of connections offers improved seismic performance but introduces issues such as complicated detailing and installation, on-site construction difficulties, or constraints on beam size. Connection configurations involving through-beam flanges [18], through-entire beam [19,20], or pre-welded embedded rebars on beam flanges [21] require complex cutting of the steel tube, followed by extensive welding [22] for rejoining, which disrupts the continuity of the tube and introduces unpredictable welding residual stresses, ultimately compromising ductility [9]. For joints with through-beam flanges, additional anti-slip components are required at the upper and lower flanges to prevent flange sliding to meet moment frame requirements [7], further increasing the complexity. Moreover, embedded components such as through-flange or through-diaphragm [9] can obstruct core concrete placement, potentially leading to compaction defects in the joint panel zone. Penetration of only the beam web [8] simplifies construction but fails to meet the seismic requirements for rigid moment connections [7]. Welding shear studs to the inner wall of the steel tube at the beam flange elevation can partially restrain radial deformation [23], but inner-wall welding is inherently complex. Sheet et al. [24] proposed a connection combining curved endplates and partially cut long bolts; however, due to space constraints, only two bolts can be arranged at each elevation, limiting applicable beam sizes. Other curved endplate joints include the use of hooked blind bolts by Yao et al. [25] to transfer flange tension to the core concrete, and the use of curved washers by Zhong et al. [26] to allow parallel arrangement of long bolts. However, curved endplates inevitably introduce additional horizontal shear forces and bending moments in the bolts, a topic that remains insufficiently studied. Li et al. [27] used welded ribbed plates to provide a flat connection surface for the beam endplate, but limited weld space hinders their extension to biaxial bending joints. Additionally, many of the above joint types are difficult to repair once damaged. The first category of joints may cause significant radial deformation or tearing of the steel tube wall. The second category involves embedded parts that are nearly impossible to replace once damaged. Replacing a damaged CCFT column is highly difficult and costly, making repair impractical.
To overcome the challenges associated with rigidly connecting CCFT columns and WF steel beams, this study proposes a novel joint configuration that integrates a conventional extended endplate moment connection [28] with long through bolts. The proposed design addresses several critical issues found in existing joints, including insufficient stiffness or ductility due to irrational force-resisting mechanisms, complicated detailing and installation, interference with concrete placement, limitations on applicable beam sizes, and poor repairability. Furthermore, the new joint exhibits promising potential for extension to biaxial bending scenarios. Its development promotes the broader application of CCFT columns in special moment frames. Replacing traditional steel columns in steel moment frames with CCFT columns—known for their superior seismic performance—can significantly enhance the seismic resilience of such frames in high seismic zones.
2. Design Concept
Brittle fracture of welds is one of the major causes of steel structure collapse during earthquakes [29,30,31]. In addition to improving weld quality, reducing the number of primary tension welds within the joint by optimizing the force transfer path can also effectively lower the risk of weld fatigue failure. As illustrated in Figure 1, this study proposes a novel joint based on the conventional extended endplate bolted connection. A square steel tube is sleeved around a circular steel tube, and high-strength grout is filled in the annular space to form a planar surface for beam connection. The beam endplates are then fastened using high-strength through bolts. All welding and grout casting can be completed in the factory, requiring only core concrete casting and bolt installation on-site. Factory prefabrication ensures superior quality control and consistent welding performance while reducing construction cost and duration.
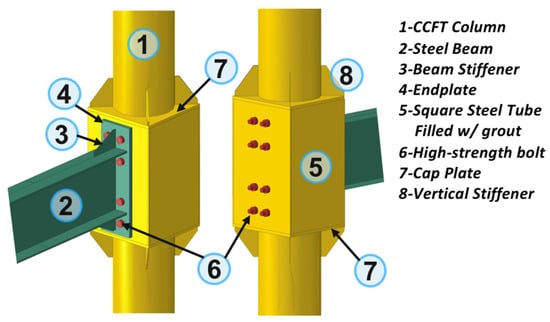
Figure 1.
Proposed connection detail for CCFT columns.
Under the beam-end moment, the tensile force in the beam flange is transferred through long through bolts to the opposite side of the column. This force acts as compression on the wall of the square tube and is subsequently transmitted to the CCFT column via the high-strength grout. Only the high-strength bolts and the full-penetration welds between the beam and endplate are subjected to tensile force. The beam-end shear is transferred through the high-strength bolts, the square tube wall, and the grout to the vertical stiffeners, and finally to the circular tube wall via vertical shear welds. This novel joint configuration effectively avoids radial tension on the circular tube wall and minimizes the number of primary tension welds. In this joint, the primary tensile members are high-strength bolts, and the primary compressive member is the high-strength grout. The force transfer path is simple and well-defined, allowing each component to fully utilize its material properties.
As one of the most reliable seismic-resistant joint types, the conventional endplate moment connection differs from the proposed joint primarily in the way it supports the beam endplate. In the new joint, the beam endplate is supported by high-strength grout. Therefore, the seismic performance of the grout is crucial to the overall behavior of the joint. If it can be demonstrated that the grout possesses sufficient strength and stiffness to provide reliable support to the beam endplate, it is reasonable to infer that this novel joint also has the potential to become one of the most reliable joints for seismic design. This study adopts both quasi-static tests and finite element analysis to evaluate the seismic performance of the high-strength grout and verify whether it meets the expected requirements.
3. Prototype Connection
The novel joint proposed in this study is an evolution of the traditional endplate bolted steel joint, with the primary difference being the support method for the beam endplate. Instead of relying on the flange of an H-shaped steel column, the support is provided by high-strength grout encased in a square steel tube. The design methods for the beam endplate, beam flange stiffeners, and high-strength bolts remain largely the same between the two configurations. The design process begins with analyzing the structural system to determine the required sizes of the frame beams and columns. Subsequently, following the design methodology outlined in ANSI/AISC 358 [28] for endplate bolted steel joints, the maximum flexural strength of the beam plastic hinge, the diameter of the high-strength bolts, the dimensions of the beam endplate, and the beam flange stiffeners are determined sequentially. Finally, based on the code’s assumptions regarding the location of the beam’s plastic hinge, the sectional flexural capacity of the circular concrete-filled steel tube column is verified.
A prototype joint was designed using the aforementioned methodology to conduct quasi-static tests and finite element analyses, aiming to investigate the seismic performance and potential failure modes of the novel joint. The prototype joint is situated at the mid-story of an exterior column in a 3-span, 5-story moment-resisting frame. The frame has a story height of 3.5 m and a column space of 5 m. The steel beam uses a wide-flange (WF) hot-rolled section with a designation of HN450×200×9×14, featuring a beam height of 450 mm, flange width of 200 mm, web thickness of 9 mm, and flange thickness of 14 mm. The CCFT column uses a circular steel tube with a diameter of 406 mm and a wall thickness of 10 mm. The core concrete has a strength grade of C40, with a specified cube compressive strength . High-strength bolts were designed with a shank diameter of 30 mm, a length of 600 mm, and an effective thread cross-sectional area of 5.61 cm2. The beam endplate is a steel plate measuring 770 mm in height, 240 mm in width, and 30 mm in thickness. The beam flange stiffeners are steel plates measuring 225 mm in length, 130 mm in height, and 10 mm in thickness. Except for the high-strength bolts, all other steel components in this study are made of Q235-grade steel, with a nominal yield strength of 235 MPa, nominal tensile strength of 370 MPa, and a design yield strength of 215 MPa. The high-strength bolts are fabricated from grade 10.9S steel, with a yield strength corresponding to 0.2% residual strain of 940 MPa and a tensile strength of 1040 MPa [32].
Additionally, the design of the novel connection includes determining the strength grade of the high-strength grout, the dimensions of the square steel tube, the upper and lower cap plates of the square steel tube, the vertical stiffeners, and the welds. The strength grade is undoubtedly one of the most critical factors influencing the compressive capacity and stiffness of the high-strength grout. The confinement effect of the square steel tube also enhances the strength and toughness of the grout to some extent. In this study, high-strength grout with a grade of C35 is selected, with a specified cube compressive strength of . This grout strength is practical and achievable in engineering applications. Moreover, with the dimensions of the CCFT column fixed, the size of the high-strength grout is uniquely determined by the dimensions of the square steel tube. Changes in the square steel tube’s dimensions could potentially affect the seismic performance of the high-strength grout. This study initially tests the seismic performance of the novel connection using the minimum square steel tube size required for construction. Subsequent research in the future can explore the effects on the connection performance of varying the square steel tube dimensions to identify the optimal design. During grout casting, the upper cap plate of the square steel tube must include a grout pouring hole with a diameter of at least 60 mm and a vent hole, determining the minimum side length of the square steel tube to be 520 mm. The wall thickness of the square steel tube is set to 10 mm, matching the wall thickness of the circular steel tube. The shear force at the beam end is primarily transferred to the square steel tube wall through the bearing capacity of the high-strength bolts and subsequently transferred to the CCFT column via the upper and lower cap plates and the vertical stiffeners. Preliminary analysis shows that the stresses in the cap plates and vertical stiffeners are relatively small, with limited impact on the overall connection performance. In this study, the thicknesses of the cap plates and vertical stiffeners are set to 20 mm and 10 mm, respectively. The dimensions of the vertical stiffeners are designed following the guidelines in ANSI/AISC 358 [28] for beam flange stiffeners, with a height and width of 260 mm and 150 mm, respectively.
The welding work for the novel joint can be entirely completed in the factory. Based on the load distribution within the joint, the weld between the steel beam and the endplate must be capable of transferring the beam sectional maximum moment; hence, a full-penetration butt weld is employed. The other welds, bearing relatively limited loads, can utilize fillet welds. These primarily include the following: (1) welds between the beam flange stiffeners and both the beam flange and endplate; (2) welds between the cap plate and the square steel tube; (3) welds between the cap plate and the circular steel tube; and (4) welds between the vertical stiffeners and both the cap plate and circular steel tube. The fillet welds use gas-shielded arc welding, with J422 electrodes providing a tensile strength of no less than 430 MPa. The weld requirements for this novel joint are relatively low, effectively mitigating the brittle fracture risk often associated with steel structures during earthquakes. The dimensions of the prototype joint components are determined based on the design strengths of the materials, as shown in Figure 2 and Table 1. The actual material strengths measured during the experimental tests, which serve as the basis for quasi-static tests and finite element analysis, are also presented in Table 1.
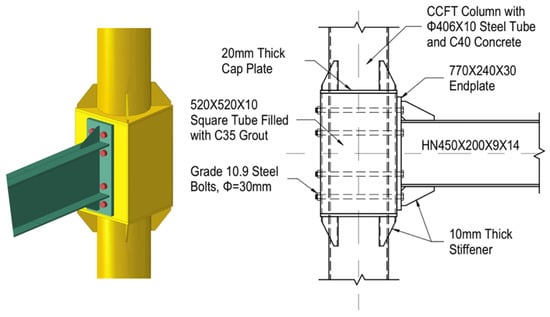
Figure 2.
Prototype connection details (length unit: mm).

Table 1.
Prototype connection dimensions and actual material properties.
In this study, freshly mixed ordinary Portland cement with a strength grade of 42.5 was used. The fly ash met the Class I requirements specified in Chinese Standard GB/T 1596-2005 [33], while the silica fume complied with GB/T 21236-2007 [34], featuring a specific surface area of 1.5 × 105 cm2/g and a SiO2 content of no less than 96%. The coarse aggregate ranged in size from 10 to 30 mm. Medium-grade river sand with a particle size distribution of 0–5 mm was used as the fine aggregate. A polycarboxylate-based superplasticizer from ShanXi FeiKe Company in Yun Cheng, China was used to improve the workability of the mix. The detailed mix proportions of the concrete and high-strength grout are listed in Table 2.

Table 2.
Mixing proportions of concrete and high-strength grout mixtures.
4. Quasi-Static Test
4.1. Test Method
To evaluate the seismic performance of the novel connection and explore its post-earthquake repairability, this study conducted two consecutive full-scale quasi-static tests on the same CCFT column. In the first test, the entire connection employed new components to simulate the seismic behavior of the novel connection during its initial exposure to an earthquake. In the second test, only the severely damaged steel beam and its pre-welded endplate were replaced, while all other components were retained, to assess the seismic performance of the repaired connection. The prototype connection is located on an exterior column in the middle story of a five-story frame, and the test setup is shown in Figure 3.
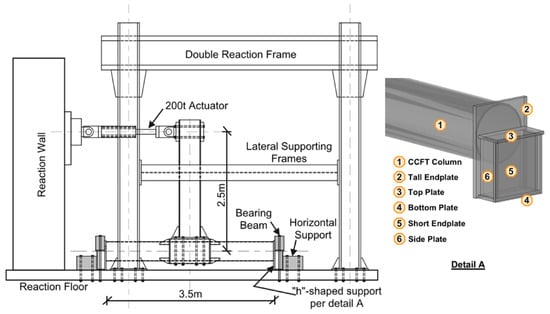
Figure 3.
Test layout and setup.
To facilitate the measurement of the flatness of the square steel tube walls after being subjected to repeated compression from the beam endplate using a spirit level, the CCFT column was placed horizontally during the test, while the steel beam was positioned vertically. At both ends of the CCFT column, “h”-shaped supports were welded to lift the square steel tube 135 mm off the ground, accommodating the high-strength bolts and eliminating the influence of the reaction foundation on the normal functioning of the connection. As shown in Detail A of Figure 3, the “h”-shaped support consists of six Q235 steel plates welded together, including one tall and one short endplate, two horizontal plates (top and bottom), and two side plates, ensuring a flat-bottom surface. The dimensions of these six plates are detailed in Table 3. The vertical and horizontal displacements of the “h”-shaped supports were constrained by a bearing beam and horizontal supports, respectively. The bearing beam, 2 m long, spanned over the top plate of the “h”-shaped supports and was hinged at both ends to the reaction foundation using vertical steel rods measuring 940 mm in length and 60 mm in diameter. Proper prestress was applied to the steel rods to firmly press the “h”-shaped supports onto the reaction foundation. The action centers of the bearing beam and the horizontal supports on the “h”-shaped supports correspond to the midlines of the top plate and the short endplate, respectively, with eccentric distances of 0.095 m and 0.2 m from the center of the column ends. The column height and space are 3.5 m and 5 m, respectively. If the connection moment at the column centerline is M, the vertical reactions provided by the bearing beam and the reaction foundation are , and the horizontal reactions from the horizontal supports are . Consequently, the bending moments at the two column ends provided by the “h”-shaped supports are and , respectively. These results demonstrate that the maximum moment provided by the “h”-shaped supports at the column ends is only 5.1% of the connection moment at the column centerline, closely approximating pin support conditions at the column ends. A 200-ton hydraulic actuator was placed horizontally, connecting the free end of the steel beam to the reaction wall. Under the actuator’s action, the beam’s free end underwent horizontal cyclic loading. Since the tested prototype connection is located on a lower-story frame exterior column with relatively low axial force, its influence on the connection’s performance is negligible, and no axial force was applied to the column during the test. To prevent out-of-plane instability of the beam under cyclic loading, a lateral bracing frame was provided near the beam’s free end. Sliding pads were placed between the beam and the lateral bracing frame to ensure free horizontal movement of the beam’s free end.

Table 3.
Plate size for “h”-shaped support (unit: mm).
The loading diagram is shown in Figure 4. The actuator applies the load at the beam end under displacement control. The displacement at the loading point of the beam end is denoted as , with the distance from the load application point to the outer surface of the square steel tube being . The corresponding joint rotation is defined as the ratio of displacement to beam length, . In the initial elastic phase, the displacement increment is set to 3.73 mm, corresponding to a rotation increment of 0.167%, with each load cycle applied once. After 12 cycles, the displacement reaches 44.8 mm, equivalent to a rotation of 2%, and the current load cycle is applied three times. In the subsequent primary yielding phase, the displacement increment is set to 22.4 mm, corresponding to a rotation increment of 1%, with each load cycle applied twice. When the displacement reaches 89.6 mm, equivalent to a rotation of 4%, the current load cycle is applied two and a half times. Afterward, the number of load cycles per increment returns to two, continuing until the rotation reaches 5% or the joint fails prematurely, at which point the test is terminated. The loading history for tests is shown in Figure 5.
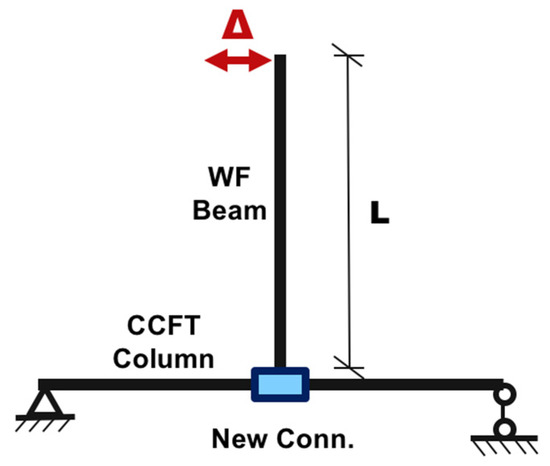
Figure 4.
Loading diagram.
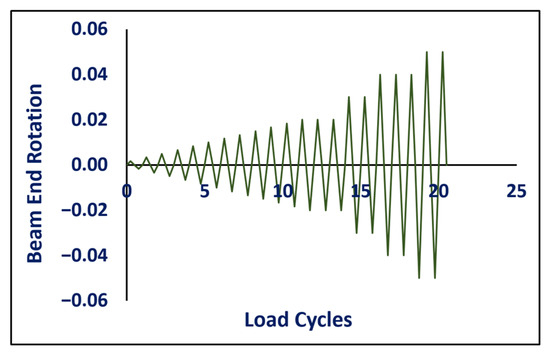
Figure 5.
Loading history for tests.
During the test, deformation of the components was monitored and recorded using displacement meters (DMs) and strain gauges. As shown in Figure 6, seven DMs were used, with DM-1~3 measuring horizontal deformations and DM-4~7 measuring vertical deformations. DM-1 and DM-2 were positioned at the same height as the column centerline and aligned with the beam flange, perpendicular to the sidewalls of the square steel tube, to measure the lateral bulging of the tube sidewall and the internal high-strength grout under beam flange pressure. DM-3 was used to measure the horizontal displacement of the horizontal support under the action of the hydraulic actuator. DM-4 and DM-7 were vertically positioned on the bearing beam at the center of the “h”-shaped support to monitor its vertical deformation. DM-5 and DM-6 were placed on the top surface of the square steel tube as close to the beam endplate as possible, aligned with the beam flange, and inclined at a 6° angle from the vertical direction to avoid collision with the beam flange. These DMs were used to measure the vertical deformations in the square steel tube wall and the internal grout under beam flange pressure. Strain gauges were installed at critical locations, including the outer side of the beam flange, near the beam flange on the endplate, and on the beam flange stiffeners, to capture significant strain distributions.
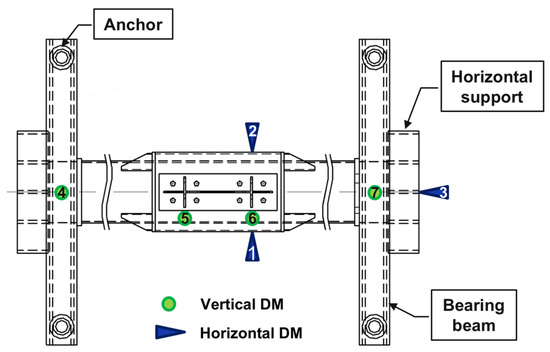
Figure 6.
Displacement meter (DM) layout.
4.2. Test Results
4.2.1. Test-1
The results of the first quasi-static test are shown in Figure 7. The results indicate that the novel joint produced stable and robust hysteresis curves under the bending moment at the beam end. Based on the beam flange yield strength of 285 MPa, the theoretical yield strength of the beam cross-section was estimated to be 416 kN·m. Assuming the plastic hinge forms at the tip of the beam flange stiffener, the beam-end yield strength was calculated to be 469 kN·m. The experimental results showed that noticeable hysteresis occurred when the beam-end moment reached approximately 445 kN·m, indicating the onset of steel beam yielding, which deviates by only 5.1% from the theoretical value. Based on the tensile strength of the beam flange at 374 MPa, the theoretical ultimate strength of the beam cross-section was estimated at 606 kN·m, corresponding to a beam-end ultimate strength of 683 kN·m. The test results showed a maximum beam-end moment of 580 kN·m, which reached 85% of the theoretical estimate. The theoretical values were estimated based on the fully plastic section theory and were influenced by the location of the plastic hinge. However, during the test, local buckling of the compressed flange occurred before reaching the ultimate strength, preventing the theoretical ultimate strength from being fully achieved. When the joint rotation exceeded 0.02 rad, the steel beam entered a fully yielded state, forming a distinct plastic hinge. The beam-end moment peaked at approximately 0.03 rad of joint rotation. The plastic hinge maintained its maximum moment up to a joint rotation of about 0.04 rad. Beyond this, during the increase to 0.05 rad, the plastic hinge exhibited gradual stiffness degradation, with the maximum drop in the ultimate moment being less than 19%. This satisfies the seismic requirements for frame structures specified in ANSI/AISC 341 [35]. These results demonstrate that the novel joint provides sufficient strength and stiffness for the steel beam to fully yield.
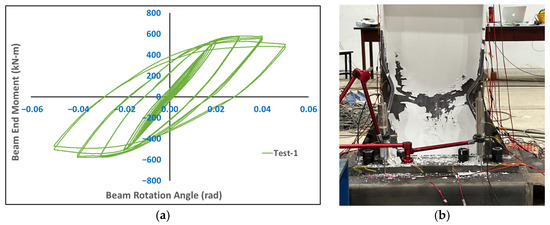
Figure 7.
Results of Test-1. (a) Hysteresis loops; (b) beam plastic hinge.
During the test, the horizontal and vertical displacements at the column ends were measured using DM-3 and DM-7, as shown in Figure 8 and Figure 9. The maximum horizontal and vertical displacements were 4.1 mm and 1.8 mm, respectively, corresponding to impacts on the joint rotation angle of 4.1% and 1.2%, both within the permissible error range. When the force at the beam end was applied toward the direction close to DM-7, the vertical reaction force on the column-end support on the DM-7 side was directly provided by the reaction foundation. As shown in Figure 9, the maximum deformation of the reaction foundation under the column-end support pressure was −0.5 mm, which had a negligible impact on the joint rotation angle.
Figure 8.
Column-end horizontal displacement at DM-3.
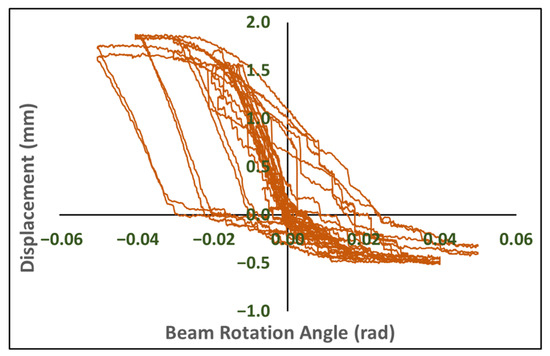
Figure 9.
Column-end vertical displacement at DM-7.
The deformation of the square steel tube wall and the filled high-strength grout under the pressure of the beam endplate is critical to the stiffness of the novel joint. The vertical deformation of the square steel tube wall at the potential maximum deformation point, measured by DM-5 during the test, is shown in Figure 10a. The base of DM-5 was fixed on the outer wall of the circular steel tube and positioned as close to the square steel tube as possible to ensure that the measured vertical deformation reflected only the relative deformation of the square steel tube wall, effectively excluding the combined displacement of the square steel tube and CCFT column. As shown in Figure 10a, regardless of which flange is under compression, the square steel tube wall exhibits vertical downward deformation, indicating that the infilled high-strength grout is under pressure. However, the relative deformation measured when the flange on the same side as DM-5 is under compression is noticeably greater. When the beam-end moment is small, the deformation of the square steel tube wall remains within the elastic stage, resulting in minimal residual deformation. As illustrated in Figure 10a, when the joint rotation angle is within ±0.02 rad, the deformation of the square steel tube wall is less than 1.23 mm, and the residual deformation does not exceed 0.52 mm, remaining predominantly in the elastic stage. As the beam-end moment increases, the deformation of the square steel tube wall gradually grows. The maximum deformation measured by DM-5 is 2.11 mm when the flange on the same side as DM-5 is under compression and 1.64 mm when the opposite flange is under compression, with the residual deformation correspondingly increasing. During the final quarter cycle of the test, the joint rotation angle reduced from 0.05 rad to 0 rad under the action of the actuator. However, significant plastic deformation in the beam plastic hinge area resulted in the specimen being fully unloaded when the joint rotation angle decreased to approximately 0.025 rad, leaving the square steel tube wall with a residual deformation of 0.94 mm. As the rotation angle returned to 0 rad, the specimen effectively entered a reloading phase, causing the deformation of the square steel tube wall to rebound to 1.4 mm.
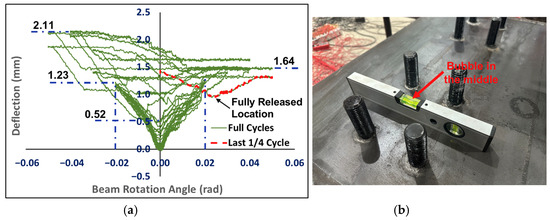
Figure 10.
Square tube top face deflection and flatness at DM-5. (a) Deflection; (b) flatness.
Post-test inspection of the flatness of the square steel tube wall’s load-bearing surface using a spirit level, as shown in Figure 10b, revealed no visible deformation affecting the joint connection. The spirit level adhered closely to the tube wall, with the air bubble aligned at the center of the scale. From a construction accuracy perspective, the square steel tube wall did not exhibit any deformation impairing joint repair feasibility, satisfying the condition for joint restoration by replacing only the steel beam. Therefore, the square steel tube and the internal high-strength grout provided sufficient stiffness for the novel joint, and their deformation had a negligible impact on the joint stiffness.
Under the simultaneous application of pressure from the beam endplate on the load-bearing surface of the square steel tube, the sidewalls of the square steel tube undergo out-of-plane bulging due to the applied load. The extent of this bulging was measured using DM-1, as illustrated in Figure 11a. The support base of DM-1 was securely mounted on the outer wall of the circular steel tube and positioned as close as possible to the square steel tube. This setup ensured that the measured horizontal deformation exclusively reflected the relative deformation of the square steel tube walls, while effectively excluding the combined displacement of the square steel tube and the CCFT column. The lateral displacement generated when the beam flange on the same side as DM-1 was under compression was slightly larger than that observed when the opposite beam flange was under compression. The maximum lateral displacements were 1.14 mm and 0.94 mm, respectively. When the joint rotation angle is within ±0.02 rad, the deformation of the square steel tube sidewalls was less than 0.28 mm, with residual deformation remaining below 0.06 mm, indicating that the deformation was confined to the elastic range. However, when the joint rotation angle reached 0.03 rad, the deformation of the square steel tube sidewalls transitioned into the plastic range. In this phase, even when the cyclic loading amplitude was maintained constant between consecutive cycles, the residual deformation exhibited a slight increase. During the final quarter-cycle of the test, the joint rotation angle, driven by the actuator, recovered from 0.05 rad to 0 rad. Owing to significant plastic deformation in the plastic hinge region of the beam, the specimen was fully unloaded when the joint rotation angle decreased to approximately 0.025 rad. At this point, the ultimate residual deformation of the square steel tube sidewall was recorded as 0.9 mm. Upon reloading by the actuator during the recovery to 0 rad, the deformation of the square steel tube sidewall reached 1.0 mm at the conclusion of the test.

Figure 11.
Square tube sidewall deflection and flatness at DM-1. (a) Deflection; (b) flatness.
After the test, the flatness of the square steel tube sidewalls was assessed using a spirit level, as shown in Figure 11b. Visual inspection revealed that the spirit level adhered closely to the square steel tube sidewalls, with the air bubble aligned at the center of the scale. From the perspective of construction accuracy, no deformation was observed in the square steel tube sidewalls that could compromise the integrity of the joint connections. Consequently, in practical engineering applications, other structural components connected to the square steel tube sidewalls remain unaffected by any deformation of the square steel tube.
4.2.2. Test-2
Based on the original specimen from the first test, a new specimen for the second quasi-static test was prepared by replacing only the steel beam and the endplate. The replaced steel beam and endplate were identical to those in the original specimen. The results of the second quasi-static test are shown in Figure 12. During the fabrication of the new specimen, defects were introduced in the full-penetration weld between one steel beam flange and the endplate. As a result, the ultimate moment capacity of the steel beam was lower when the flange with the weld defect was under tension compared to when it was under compression. Unlike the first test, the loading procedure for the second test was adjusted as the experiment progressed. Initially, the displacement increment and the number of loading cycles in the elastic stage were kept consistent with the first test. The results showed that the joint stiffness during the elastic stage was identical in both tests, indicating that the first test did not cause any significant damage affecting the joint stiffness. When the beam-end displacement reached 33.6 mm, corresponding to a joint rotation angle of 1.5%, a slight reduction in joint stiffness was observed due to the presence of weld defects. To verify this change, the current load cycle was repeated twice. Subsequently, the displacement increment was set to 27 mm, and three cycles of loading were conducted. When the beam-end displacement first reached 60.6 mm, corresponding to a rotation angle of 2.7%, the beam-end moment was only 455 kN·m, representing a significant 20% reduction compared to the 568 kN·m observed at the same rotation angle in the first test. Conversely, when the rotation angle reached −2.7%, the beam-end moment was 540 kN·m, differing by less than 4% from the 562 kN·m recorded in the first quasi-static test. This indicates that the weld defect between the beam flange and the endplate significantly affected the joint strength and stiffness when the defective flange was under tension, while the impact was relatively limited when the flange was under compression. When the joint rotation angle again reached 2.7% and −2.7%, the beam-end moment showed no significant change compared to the previous load cycle. However, during the subsequent loading to −2.7%, as the joint rotation angle varied from 0.1 rad to −0.26 rad, the joint stiffness exhibited a decrease followed by an increase. It was believed that this phenomenon was attributed to the closure of micro-cracks in the weld under compressive stress.
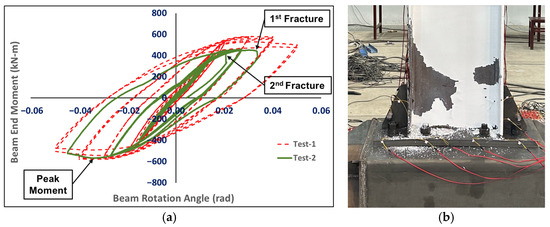
Figure 12.
Results of Test-2. (a) Hysteresis loops; (b) beam plastic hinge.
As the joint rotation angle continued to increase, the cracks in the defective weld between the flange and the endplate rapidly propagated under tensile forces, ultimately leading to a brittle fracture, which was accompanied by a distinct audible sound, when the joint rotation angle first reached 3.34%. At this point, the joint moment dropped abruptly from 441.5 kN·m to 385 kN·m, a reduction of 12.8%. The stiffener connecting the beam flange remained intact. The weld fracture originated from the flange edge on one side, with a visible length of less than 20 mm and a depth of less than 1 mm near the initiation point. The width of the fractured weld was minimal, making the fracture surface difficult to detect with the naked eye. Following the fracture, the test was gradually unloaded. Since the weld on the opposite flange remained intact and capable of sustaining load, loading continued in the reverse direction after unloading, with the joint rotation angle reaching −4.5%. During reverse loading, the closure of weld cracks once again caused the joint stiffness to exhibit a significant decrease followed by an increase as the moment changed direction. When the joint rotation angle reached −3.4%, the beam-end moment achieved a peak value of −567 kN·m, which was within 2% of the peak value of −578 kN·m observed at the same rotation angle in the first test. This demonstrates that the novel joint retained its capacity to bring the steel beam to its ultimate strength even after the first quasi-static test. The joint’s strength and stiffness showed no significant deterioration, further confirming that the first test did not cause substantial damage to the joint. The innovative joint design allows for complete restoration by simply replacing the steel beam and endplate. Subsequently, the loading direction of the beam-end force was reversed, and a second brittle fracture occurred when the joint rotation angle reached 2%. This fracture was most prominently observed in the weld between the flange stiffener and the beam flange, accompanied by further propagation of the crack in the weld between the beam flange and the endplate. As shown in Figure 13, more than 90% of the weld between the flange and the stiffener fractured, and the two components were nearly completely separated. The fracture propagated along the heat-affected zone (HAZ) between the stiffener and the weld metal, with a relatively smooth fracture surface. The fracture length of the weld between the flange and the endplate extended to nearly 85 mm, occurring only on the outer side of the flange without forming a through-thickness crack. The crack width was minimal, and the fracture surface could not be clearly identified with the naked eye. With the onset of this fracture, the beam-end moment dropped sharply from 431 kN·m to 337 kN·m, a reduction of 21.8%. At this point, the specimen was deemed to have failed completely, and the test was terminated after unloading. Post-test measurements using a spirit level revealed no significant deformation on the top surface or sidewalls of the square steel tube, as illustrated in Figure 14 and Figure 15.

Figure 13.
Weld fractures along beam flange and flange stiffener during Test-2. (a) Along beam flange; (b) along flange stiffener.

Figure 14.
Square tube top and sidewall flatness after Test-2. (a) Top face 1; (b) top face 2; (c) sidewall.

Figure 15.
High-strength grout infill condition after Test-2. (a) Bottom face; (b) side face w/DM-1; (c) top face; (d) side face w/DM-2.
To further investigate the damage condition of the high-strength grout infill after the two tests, the sidewalls of the square steel tube were removed using gas cutting. The condition of the load-bearing surface (top face), the surface opposite the load-bearing face (bottom face), and the side faces of the high-strength grout infill are shown in Figure 15. From a visual inspection, no significant crushing or large cracks were observed on any of the faces. Only two minor cracks were detected on the bottom face between two rows of high-strength bolts located on the inner side of the beam flanges. Additionally, since no endplate was used on the bottom face and the high-strength bolts acted directly on the square steel tube wall, slight annular compressive deformation was observed around the bolt holes due to the high local pressure. This deformation matched the outer diameter of the bolt heads, with a depth of less than 1 mm. On the other hand, due to reduced flowability of the high-strength grout during the later stages of casting, a casting gap was observed between the grout and the top cap plate (indicated by the red-dashed region in Figure 15), measuring approximately 480 mm × 150 mm × 25 mm. However, the test results show that this casting gap did not significantly affect the performance of the joint. Since no non-destructive testing was conducted, the internal cracking condition of the high-strength grout could not be fully assessed. To compensate for this limitation, the potential cracking behavior of the grout was further investigated through finite element analysis.
5. Finite Element Analysis
As discussed earlier, the compressive strength and stiffness of the high-strength grout determine the effectiveness of the support for the beam endplate. This section employs finite element analysis (FEA) to further investigate the seismic performance and potential failure modes of the high-strength grout infill under cyclic loading of the beam’s ultimate bending strength to provide critical insights for the design of the novel joint.
5.1. FEA Model
The simulated joint is located on the exterior column of a middle story within a moment-resisting frame. Under seismic-equivalent loads, the inflection points of the frame beams and columns are assumed to be at the midpoints of their respective lengths. A T-shaped joint model was established in ABAQUS, with a column height of 3.5 m, the column centerline 2.5 m away from the beam’s free end, and the beam positioned at mid-height of the column. The dimensions and material properties of the components are detailed in Table 1. To reduce the computational cost of the finite element analysis, the model leveraged the joint’s symmetry by using the central plane of the beam web as the symmetry plane, thus modeling only half of the joint, as shown in Figure 16. In the finite element model, solid elements are used to simulate three components: the core concrete inside the circular steel tube, the high-strength grout filling between the two steel tubes, and the high-strength bolts. All other components, including the circular steel tube, square steel tube, beam, endplate, cap plates, and stiffeners, are modeled using shell elements. Specifically, C3D8R elements are employed for the solid elements, while S4R elements are used for the shell elements. A mesh size sensitivity analysis conducted in the preliminary stages determined that the mesh size should not exceed 40 mm. The meshing configuration of each component is shown in Figure 17.
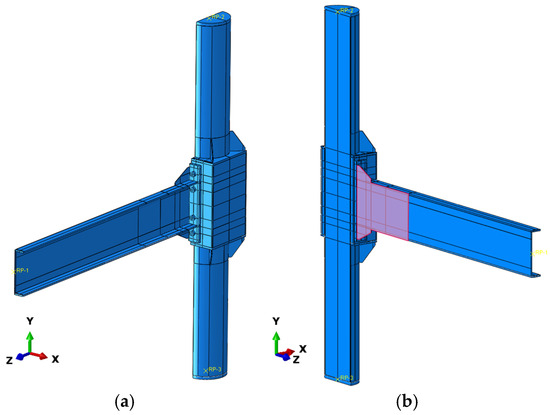
Figure 16.
FEA model in ABAQUS. (a) View-1; (b) view-2. (Pink region refers to the location where plane symmetry boundary condition is not applied.).

Figure 17.
FEA model assembly and meshing condition.
In the finite element model, connections and interactions between components are primarily established through three methods: Merge, Contact, and Constrain. The analysis does not consider the effects of weld failure, and the Merge connection method is mainly used to simulate welded joints. This includes connections between the beam flange and web, beam and endplate, beam stiffener and endplate, square steel tube and upper/lower cap plates, circular steel tube and upper/lower cap plates, and circular steel tube and vertical stiffeners. Gaps are introduced between certain components to account for plate thickness effects, such as between the beam flange and flange stiffeners and between the vertical stiffeners and the upper/lower cap plates. The gap sizes correspond to the beam flange thickness and cap plate thickness, respectively. Components on both sides of these gaps are connected using the Tie constraint method.
Similarly, the Tie constraint is used to connect steel components with core concrete and high-strength grout, enabling the assessment of separation between steel and core concrete or high-strength grout based on their surface damage, including connections between the core concrete and the circular steel tube, high-strength grout and the circular steel tube, high-strength grout and the square steel tube, and high-strength grout and the upper/lower cap plates. The nuts of the high-strength bolts are tied to the beam endplate using the Tie constraint, ensuring that the nuts move with the beam endplate without separation. On the other side, the bolts are in direct contact with the square steel tube wall, connected using a surface-to-surface contact method, allowing separation after residual deformation of the bolts. The contact surface’s compressive stiffness is set to a high value to prevent nodes on either side of the contact surface from penetrating the opposing component. The coefficient of friction between steel components is set to 0.3 [32]. Due to tensile forces in the beam flange, deformation of the endplate and partial separation from the square steel tube wall are inevitable. Thus, surface-to-surface contact is used between the endplate and square steel tube wall, allowing for free separation. Surface-to-surface contact is also used between the bolt shanks and surrounding components to allow lateral support from these components while permitting axial sliding of the bolt shanks. These surrounding components include the core concrete, circular steel tube wall, high-strength grout, and square steel tube wall. The contact between the bolt shanks and the walls of the circular and square steel tubes is defined as line-to-surface contact, with a discretization method set to node-to-surface. The coefficient of friction between the steel and concrete is set to 0.45.
The steel material adopts a simplified three-segment stress–strain curve model, which is an improvement based on the elastic–perfectly plastic material model (as shown in Figure 18). The yield strength and ultimate strength of each steel component are listed in Table 1, with the strain corresponding to the ultimate strength () set at 0.1. The elastic modulus and Poisson’s ratio are set to 200 GPa and 0.3, respectively. The yield surface is defined using the von Mises yield criterion, and the isotropic hardening method is employed to account for the effects of material behavior in the plastic state.
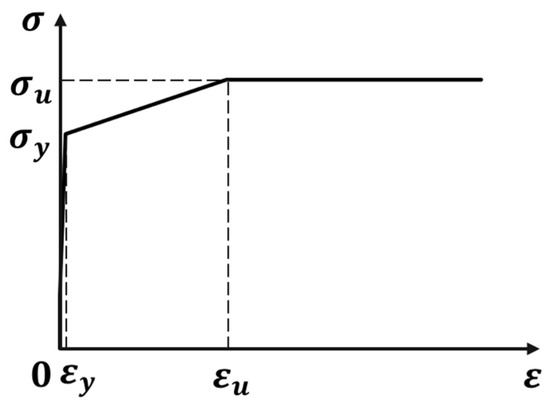
Figure 18.
Simplified stress–strain curve for steel.
In this study, the interaction between the steel tubes, core concrete, and high-strength grout is explicitly simulated in the finite element model based on actual conditions. Therefore, the triaxial stress state of the core concrete and high-strength grout inherently accounts for the confinement effect of the steel tubes. To avoid redundant consideration of this confinement, the material properties of the core concrete and high-strength grout are defined using unconfined uniaxial stress–strain curves. The unconfined uniaxial compressive stress–strain curves for the core concrete and high-strength grout are derived from experimental data, which terminates when the stress drops by approximately 6% from the peak value. The measured cube compressive strengths are listed in Table 1. In the finite element analysis, the uniaxial compressive strength of the concrete is defined as , where
- ○
- : Ratio of prism strength to cube strength. It is 0.76 for ordinary concrete with strength grade C50 and below, 0.82 for high-strength concrete with strength grade C80 and above, and linearly interpolated for intermediate grades.
- ○
- : Brittleness reduction coefficient. It is 1.0 for ordinary concrete with strength grade C40 and below, 0.87 for high-strength concrete with strength grade C80 and above, and linearly interpolated for intermediate grades.
Therefore, the uniaxial compressive strength of the core concrete and high-strength grout was taken as 28.2 MPa and 22.5 MPa, respectively, with corresponding strains of and . According to the Chinese Code for Design of Concrete Structures [36], the axial tensile strength of the core concrete and high-strength grout was taken as 1.66 MPa and 1.48 MPa, respectively, with corresponding strains of and . The unconfined stress–strain curves for both materials are shown in Figure 19. Considering the confinement provided by the steel tubes, which significantly enhances the ductility, the post-peak portions of the curves are extrapolated based on the recommendations in the design code [36] and the experimental trends, extending the curves until the stress drops to less than 10% of the peak value (indicated by dashed lines in Figure 19). The ultimate compressive and tensile strains for both materials were set to 0.011 and 0.003, respectively. The elastic moduli of the core concrete and high-strength grout are 32.5 GPa and 31.5 GPa, respectively, with a Poisson’s ratio of 0.2.
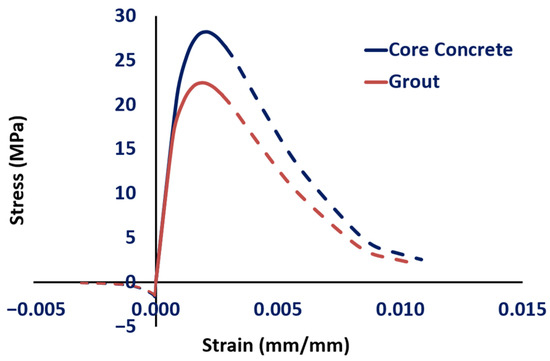
Figure 19.
Unconfined uniaxial stress–strain curve for concrete and grout.
The deformation and failure behavior of the core concrete and high-strength grout are described using the Concrete Damaged Plasticity (CDP) model. This model integrates plastic flow and damage mechanics, assuming isotropic damage under tensile and compressive conditions. It uses the concepts of tensile and compressive damage to reduce material stiffness and describes the constitutive behavior of quasi-brittle materials like concrete. The CDP model effectively captures the nonlinear behavior of concrete during tensile cracking and compressive crushing and accounts for strength enhancement effects under complex multiaxial stress states. A damage value of 0.99 is defined as full damage.
A reference point is established at each end of the column, and all degrees of freedom of the column-end sections are coupled to their respective reference points. A pin constraint (Ux, Uy, and Uz) is applied at the reference point at the bottom of the column, while a lateral constraint (Ux and Uz) is applied at the reference point at the top of the column, allowing for free axial deformation of the column. Additionally, a plane symmetry boundary condition is applied to the symmetric face of the model. To simulate the free buckling deformation of the beam’s plastic hinge region under the beam-end moment, no plane symmetry boundary condition is applied within the region influenced by the beam plastic hinge (highlighted in pink in Figure 16b). A reference point is established at the free end of the beam, with all degrees of freedom of the beam-end section coupled to this reference point. A cyclic vertical displacement load () is applied at the reference point at the beam’s free end. The distance from the beam’s free end to the square steel tube outer wall is L = 2240 mm. When the beam-end displacement reaches Δ1 = 112 mm, the joint rotation angle reaches L/Δ = 0.05 rad. The loading schematic is shown in Figure 20, and the cyclic loading pattern is illustrated in Figure 21. Also, a pretension of 177.5 kN is applied to each high-strength bolt.
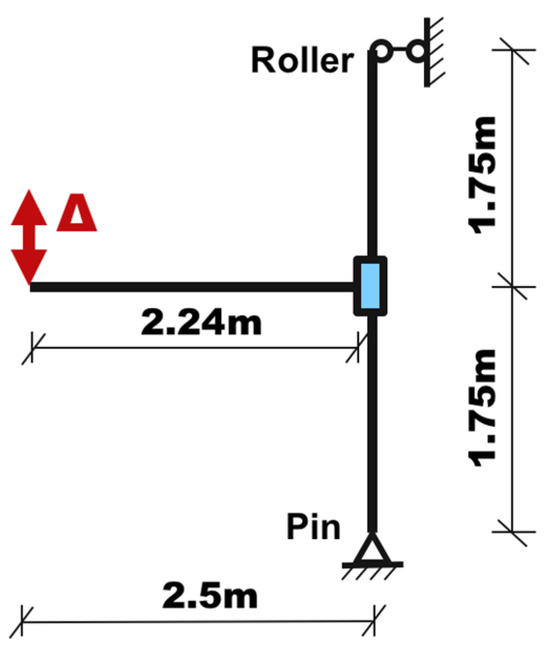
Figure 20.
Loading condition for FE analysis.
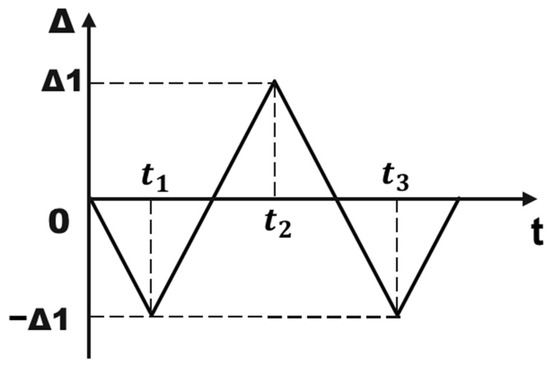
Figure 21.
Loading history for FE analysis.
5.2. Model Verification
The moment–rotation relationship of the FEA model under the cyclic displacement load ∆ at the beam end is shown in Figure 22. A comparison with the Test-1 results indicates that both the average joint stiffness in the elastic phase and the ultimate joint strength in the plastic phase are in good agreement with those from Test-1. The FEA results reveal that the rotational acceleration of the joint increases significantly after the beam-end moment reaches approximately 450 kN·m, suggesting this value is close to the yield strength of the model. This result differs from the theoretical beam-end yield strength of 469 kN·m by 4.1%, while it differs from the experimentally measured yield strength of 445 kN·m by only 1.1%. The joint rotations corresponding to the yield strengths in the FEA and the test are 0.0137 rad and 0.0156 rad, respectively. Consequently, the average elastic stiffnesses obtained from the FEA and the test are 32,847 kN·m/rad and 28,526 kN·m/rad, differing by 8.7%. The FEA shows an ultimate beam-end moment of 571 kN·m, differing by only 1.6% from the experimental value of 580 kN·m. The formation of the plastic hinge in the beam is accurately simulated by the finite element model, as shown in Figure 22b.
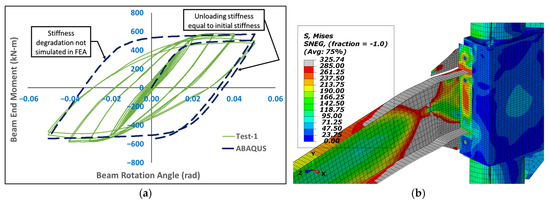
Figure 22.
Results comparison between experimental Test-1 and FE analysis. (a) Hysteresis loops; (b) beam plastic hinge.
Although the FEA results show good agreement with both the theoretical predictions and experimental data, the validity of the analysis heavily depends on the selected material models and corresponding parameters. A sensitivity analysis was conducted in this study on key parameters such as plastic strains and friction coefficients, which are used to define material behaviors. The results indicate that a variation of approximately 5% in these parameters typically leads to less than 2% variation in the analysis outcomes. This suggests that the FE model exhibits low sensitivity to parameter variations, and the analysis results can be considered relatively reliable.
The discrepancy between the finite element model and Test-1, as shown in Figure 22, lies in the loading and unloading stiffness after the joint reaches its yield strength. This difference is attributed to the significant variation in the loading process. The pseudo-static test involved 21.5 load cycles, with the displacement gradually increasing to the maximum connection rotation. In contrast, the finite element analysis only applied 1.5 cycles, directly applying the displacement load up to the maximum connection rotation. Stiffness degradation depends on the number of load cycles [37]. Due to the limited cycles applied, the degradation observed in the pseudo-static test could not be accurately captured in the FE analysis, leading to discrepancies in the loading/unloading stiffness between the two after the joint reaches its yield strength. Without considering stiffness degradation, the unloading/reloading stiffness from the FEA closely matches the initial stiffness observed in the pseudo-static test, which is also consistent with the material model setup, as expected (shown in Figure 22).
In this study, two consecutive pseudo-static tests demonstrated that the proposed joint can be fully restored simply by replacing the steel beam and endplate. This indirectly indicates that the observed stiffness degradation was mainly attributable to the steel beam, while the degradation experienced by the core concrete and high-strength grout was minimal. The FEA was primarily conducted as a supplement to the pseudo-static tests, aiming to further investigate the stress state and damage extent of the high-strength grout under ultimate loading. The stiffness degradation of the steel beam had limited influence on the objectives of this study, in contrast to its greater impact on the structural system analysis. To reduce the computational cost, the full loading history of the pseudo-static test was not simulated. Instead, the FE model only included a limited number of loading cycles under the ultimate load level. While the FE model effectively captured key characteristics such as the joint’s ultimate strength and initial stiffness, it did not account for damage accumulation that may result from smaller amplitude load cycles. In general, structural damage during seismic events is predominantly caused by a few large load cycles. Therefore, the adopted cyclic loading strategy at the ultimate load level was considered adequate for achieving the intended analytical goals. Nonetheless, the results may have certain limitations when applied to joints subjected to high-cycle seismic loading, and further analyses are needed for validation.
5.3. Analysis Results
As shown in the loading history in Figure 21, the joint rotation angle first reaches 0.05 rad at , then −0.05 rad at , and finally 0.05 rad again at .
The square steel tube and the upper and lower cap plates confine the high-strength grout, enhancing its strength and toughness. The high-strength grout is classified as C35, with a uniaxial compressive strength () of 22.47 MPa. The stress distribution of the high-strength grout at a joint rotation angle of ±0.05 rad is shown in Figure 23. The stress distribution reveals that the primary compression zones of the high-strength grout are concentrated in the bearing areas under the compressed beam flange and the bearing areas of the tensioned bolts. Under confinement, the grout’s compressive strength is effectively increased beyond its uniaxial compressive strength (). In the bearing area under the compressed beam flange, the grout’s stress ranges from 25 MPa to 45 MPa, with a maximum stress of 74 MPa. In contrast, due to the lack of force distribution provided by an endplate, localized stress concentration around the bearing bolts results in stress levels ranging from 35 MPa to 75 MPa, with a maximum stress of 165 MPa. Outside the primary compression zones, most of the grout experiences stress levels below 5 MPa. Despite the high stresses in the main compression zones exceeding the grout’s uniaxial compressive strength, the grout’s plastic strain remains at a relatively low level under the triaxial compressive stress state, preventing severe compressive failure. The grout’s final compressive damage is illustrated in Figure 24. The compression damage coefficient stays below 0.99, which represents complete failure. From the analysis results, the primary compression damage occurs in three regions: ① areas directly under the bearing bolts; ② the inner surface at joint mid-height where the grout interfaces with the column; and ③ the inner and outer surfaces at the top and bottom edges of the grout near the joint’s vertical symmetry plane. Notably, regions ② and ③ do not exhibit the highest stresses but are more prone to compressive damage due to relatively unbalanced principal triaxial stresses, resulting in large plastic strain. In the finite element analysis (FEA), the stiffness of damaged elements is significantly reduced, weakening their confinement effect on adjacent elements, which in turn exacerbates damage in surrounding areas. In real-world conditions, however, the damaged concrete remains within the structure and continues to provide some degree of confinement to adjacent materials. Consequently, the actual damage to the high-strength grout is likely to be less severe than that predicted by FEA.
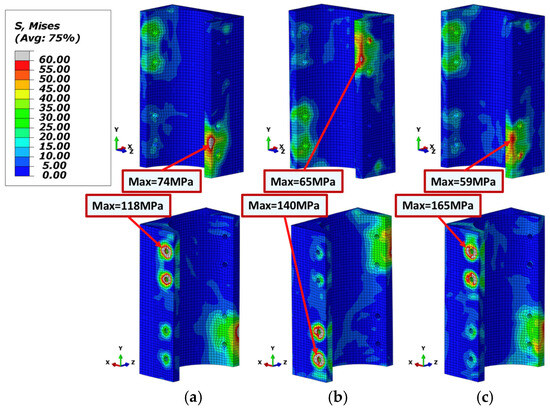
Figure 23.
Grout stress deformation (SF = 5). (a) ; (b) ; (c) .
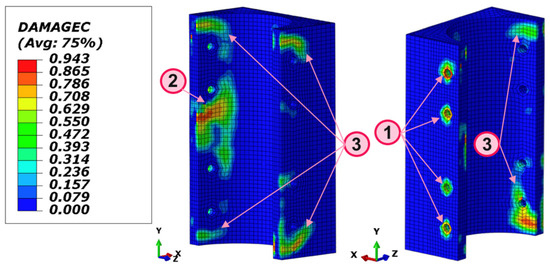
Figure 24.
Grout compressive damage at (SF = 5).
Moreover, the CCFT column provides sufficient shear resistance to counteract the panel zone shear force induced by the beam-end moment. The high-strength grout, confined by the outer square steel tube, is tightly bonded to the panel zone of the CCFT column and deforms compatibly with the column. As shown in Figure 25a, the panel zone shear force Vs is given by the difference between the beam flange axial force and the column-end horizontal reaction force , expressed as , where is the beam-end moment, is the beam height, is the flange thickness, and is the column height. A schematic representation of the shear deformation and resulting cracks in the high-strength grout is shown in Figure 25b. Under the shear force illustrated, the grout transitions from its initial shape ABCD to A′B′C′D′, with diagonal AD elongating to A′D′. Due to the limited tensile deformation capacity of the grout, crack C1 forms, starting from the midpoint of side AC and extending toward corners B and C. As shown in Figure 25a, under the bending moment at the beam end, the column exhibits the bending deformation indicated by the dashed line. Consequently, the high-strength grout experiences compression at corners B and C, while it is subjected to tension at corners A and D. Therefore, the crack does not propagate entirely to corners B and C. Similarly, when the beam-end moment changes direction, crack C2 forms. Cracks C1 and C2 intersect near the plane of the column’s central axis, where the grout’s thickness is minimal. Stress concentration at this thinnest section causes cracks C1 and C2 to coalesce into crack C3.
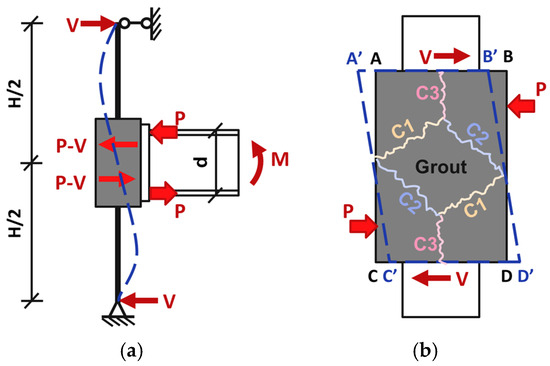
Figure 25.
Grout shear and cracking diagrams. (a) Shear diagram; (b) cracking diagram.
The tensile damage of the high-strength grout under a joint rotation angle of ±0.05 rad is illustrated in Figure 26. A damage coefficient of 0.99 signifies complete tensile failure of the grout, with its tensile strength and stiffness reduced by 99%. The cracks observed in section a-a align with the distribution and formation sequence shown in Figure 25b. Additionally, on the beam endplate’s bearing surface side, section b-b exhibits several through-thickness transverse cracks. On the high-strength bolt’s bearing surface side, section c-c shows non-penetrating fragmentation cracks, primarily concentrated at the grout’s mid-height. From the joint moment–rotation hysteresis curves, it is evident that despite the formation of multiple through-thickness cracks in the grout under the action of the beam-end moment, the confinement provided by the circular steel tube, square steel tube, and upper and lower cap plates ensures its overall integrity. This integrity allows the grout to continuously and stably support the beam endplate.
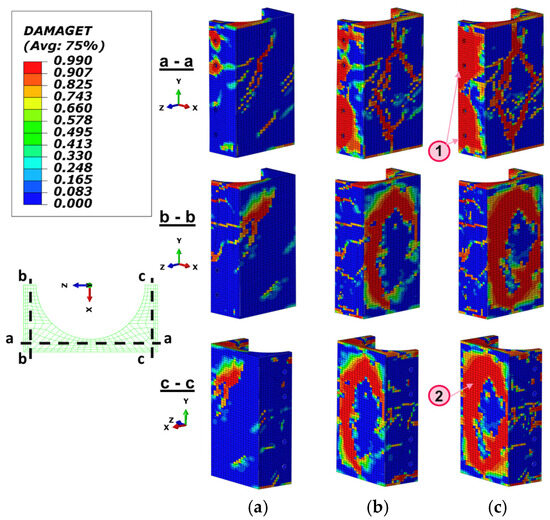
Figure 26.
Grout interior tensile damage. (a) ; (b) ; (c) .
In addition to multiple through cracks forming internally, the high-strength grout also exhibits significant cracking and separation between its external surfaces and surrounding components under the bending moment at the beam end. At a joint rotation angle of ±0.05 rad, the tensile damage conditions between the high-strength grout and the circular steel tube, as well as the upper and lower cap plates, are shown in Figure 27. The tensile damage on other external surfaces can be referenced from the uncut surfaces in Figure 26. Interfacial separation primarily results from the mismatch in the elastic modulus between the high-strength grout and the surrounding steel components, leading to incompatible deformations at the contact interface. This phenomenon is particularly pronounced in regions where the square steel tube wall is directly subjected to significant compressive forces, and in areas where its low out-of-plane stiffness limits its confinement effectiveness on the grout. The analysis indicates that large-scale separation mainly occurs in the following areas: ① the bearing surface of the endplate; ② the perimeter of the square steel tube’s sidewalls; ③ the circular steel tube wall on the side of the square steel tube’s sidewall; ④ the circular steel tube wall at the mid-height of the joint on the side of the high-strength bolt’s bearing surface; and ⑤ the upper and lower cap plates of the square steel tube. Despite severe separation, the moment–rotation hysteresis curves of the joint show that, due to the constraint effect of surrounding components, the high-strength grout is still capable of providing stable and continuous support to the beam endplate.
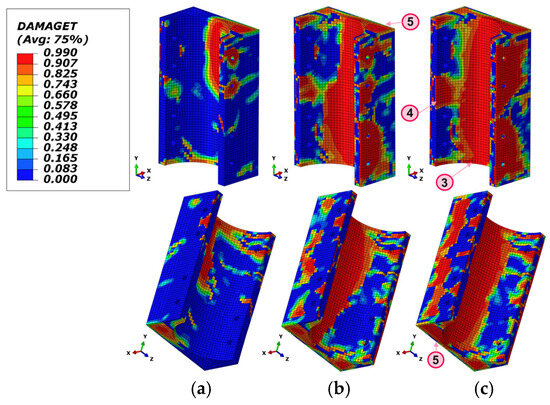
Figure 27.
Grout tensile damage on exterior surface. (a) ; (b) ; (c) .
6. Conclusions
A novel joint for rigid connections between circular concrete-filled steel tube columns and wide-flange steel beams is proposed. In this joint, a square steel tube is sleeved over the circular steel tube, and high-strength grout is filled between the two tubes to support the beam endplate. Through bolts are used to connect the beam and column, effectively reducing the number of critical tension welds and simplifying fabrication and installation. Based on the experimental and analytical studies of full-scale connections at exterior columns, the seismic behavior, failure modes, and repairability of the proposed joint were investigated, leading to the following conclusions:
- Under cyclic loading, the proposed joint achieved a plastic rotation of up to 0.05 rad and exhibited stable and full hysteresis loops. The joint provided sufficient flexural strength, stiffness, deformation capacity, and energy dissipation, meeting the seismic performance requirements for composite special moment-resisting frames as specified by ANSI/AISC 341 [35].
- Two consecutive pseudo-static tests demonstrated that the proposed joint could fully recover its initial strength and stiffness by replacing only the steel beam and endplate. Plastic deformation was primarily concentrated in the steel beam, while the deformation in the high-strength grout and square steel tube was negligible. The joint is therefore considered fully repairable.
- Although several through cracks developed in the high-strength grout under the ultimate bending moment at the beam end, and large areas deboned from the steel tube walls, the confinement provided by the steel tubes enabled the grout to continuously offer stable and reliable support to the beam endplate throughout the loading process.
- Weld failure was limited to the regions between the steel beam, endplate, and flange stiffeners. All other welds remained intact.
The conclusions derived from the quasi-static cyclic tests are applicable to structures subjected to moderate to strong seismic impacts characterized by low-cycle loading and significant plastic deformation demands, particularly in near-fault regions or design scenarios with limited displacement cycles. The materials used in this study are based on commonly used types such as Q235 steel, C40 concrete, and C35 high-strength grout. Further research is required for applications involving special or non-standard materials. From a structural configuration perspective, the proposed joint does not impose limitations on beam or column dimensions; however, further experimental validation is needed to confirm this.
This study has certain limitations due to practical constraints in both the experiments and finite element analysis. These include the lack of non-destructive testing for high-strength grout, the omission of stiffness degradation under limited cyclic loading in the FEA, casting voids between the grout and cover plate, and welding defects between the beam and endplate. These issues have been discussed in the relevant sections.
7. Future Work
To further advance the research, future work will include non-destructive testing to examine post-test internal defects or cracking in the high-strength grout. Additional efforts may focus on increasing the number of test specimens, optimizing key parameters affecting joint performance (e.g., grout strength, square tube dimensions and thickness, column axial force), investigating the shear contribution of the high-strength grout and square steel tube, and evaluating the potential effects of fabrication and installation tolerances, temperature variation, long-term loading, and repair requirements such as time and labor.
Author Contributions
Conceptualization, Y.G. and P.Z.; methodology, Y.G. and P.Z.; software, J.L.; validation, P.Z., F.L. and J.L.; formal analysis, Y.G.; data curation, Y.G.; writing—original draft preparation, Y.G.; writing—review and editing, J.L. and F.L.; supervision, J.L. and F.L.; project administration, P.Z.; funding acquisition, Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Peilin Zhu and Feng Lou were employed by the company Zhejiang Dadongwu Construction Science & Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Shams, M.; Saadeghvaziri, M.A. State of the art of concrete-filled steel tubular columns. Struct. J. 1997, 94, 558–571. [Google Scholar] [CrossRef]
- Aslani, F.; Uy, B.; Tao, Z.; Mashiri, F. Predicting the axial load capacity of high-strength concrete filled steel tubular columns. Steel Compos. Struct. 2015, 19, 967–993. [Google Scholar] [CrossRef]
- Inai, E.; Mukai, A.; Kai, M.; Tokinoya, H.; Fukumoto, T.; Mori, K. Behavior of concrete-filled steel tube beam columns. J. Struct. Eng. 2004, 130, 189–202. [Google Scholar] [CrossRef]
- Song, T.Y.; Han, L.H.; Yu, H.X. Concrete filled steel tube stub columns under combined temperature and loading. J. Constr. Steel Res. 2010, 66, 369–384. [Google Scholar] [CrossRef]
- Tao, Z.; Han, L.H.; Uy, B.; Chen, X. Post-fire bond between the steel tube and concrete in concrete-filled steel tubular columns. J. Constr. Steel Res. 2011, 67, 484–496. [Google Scholar] [CrossRef]
- Alostaz, Y.M.; Schneider, S.P. Analytical behavior of connections to concrete-filled steel tubes. J. Constr. Steel Res. 1996, 40, 95–127. [Google Scholar] [CrossRef]
- Azizinamini, A.; Schneider, S.P. Moment connections to circular concrete-filled steel tube columns. J. Struct. Eng. 2004, 130, 213–222. [Google Scholar] [CrossRef]
- Cheng, C.T.; Chung, L.L. Seismic performance of steel beams to concrete-filled steel tubular column connections. J. Constr. Steel Res. 2003, 59, 405–426. [Google Scholar] [CrossRef]
- Schneider, S.P.; Alostaz, Y.M. Experimental behavior of connections to concrete-filled steel tubes. J. Constr. Steel Res. 1998, 45, 321–352. [Google Scholar] [CrossRef]
- Ramirez Ortiz, C.; Areiza Palma, G.; Gutierrez Amador, A.D.; Ramirez Duque, J.L.; Cano Buitron, R.E.; Gonzales Escobar, L.F. Seismic behavior of a steel beam-to-concrete-filled steel tubular column connection using external diaphragms. Appl. Sci. 2022, 12, 3618. [Google Scholar] [CrossRef]
- Wang, J.F.; Han, L.H.; Uy, B. Behaviour of flush end plate joints to concrete-filled steel tubular columns. J. Constr. Steel Res. 2009, 65, 925–939. [Google Scholar] [CrossRef]
- Wang, J.F.; Chen, L.P. Experimental investigation of extended end plate joints to concrete-filled steel tubular columns. J. Constr. Steel Res. 2012, 79, 56–70. [Google Scholar] [CrossRef]
- Li, Y.L.; Chan, T.M.; Zhao, X.L. Review on blind bolted connections to concrete-filled steel tubes. Thin-Walled Struct. 2023, 183, 110444. [Google Scholar] [CrossRef]
- Wang, Z.B.; Tao, Z.; Li, D.S.; Han, L.H. Cyclic behaviour of novel blind bolted joints with different stiffening elements. Thin-Walled Struct. 2016, 101, 157–168. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhao, X.L. Study on stainless steel blind bolted T-stub to concrete-filled stainless steel tube connections. Eng. Struct. 2022, 257, 114107. [Google Scholar] [CrossRef]
- Ng, W.H.; Kong, S.Y.; Chua, Y.S.; Bai, Y. Tensile behaviour of innovative one-sided bolts in concrete-filled steel tubular connections. J. Constr. Steel Res. 2022, 191, 107165. [Google Scholar] [CrossRef]
- Koloo, F.A.; Badakhshan, A.; Fallahnejad, H.; Jamkhaneh, M.E.; Ahmadi, M. Investigation of proposed concrete filled steel tube connections under reversed cyclic loading. Int. J. Steel Struct. 2018, 18, 163–177. [Google Scholar] [CrossRef]
- Elremaily, A.; Azizinamini, A. Design provisions for connections between steel beams and concrete filled tube columns. J. Constr. Steel Res. 2001, 57, 971–995. [Google Scholar] [CrossRef]
- Khanouki, M.A.; Sulong, N.R.; Shariati, M.; Tahir, M. Investigation of through beam connection to concrete filled circular steel tube (CFCST) column. J. Constr. Steel Res. 2016, 121, 144–162. [Google Scholar] [CrossRef]
- Beutel, J.; Thambiratnam, D.; Perera, N. Cyclic behaviour of concrete filled steel tubular column to steel beam connections. Eng. Struct. 2002, 24, 29–38. [Google Scholar] [CrossRef]
- Morino, S.; Tsuda, K. Design and construction of concrete-filled steel tube column system in Japan. Earthq. Eng. Eng. Seismol. 2003, 4, 51–73. [Google Scholar]
- DBJ 13-51; Technical Specification for Concrete-Filled Steel Tubular Structures. The Construction Department of Fujian Province: Fuzhou, China, 2003.
- Sheet, I.S.; Gunasekaran, U.; Macrae, G.A. Experimental investigation of CFT column to steel beam connections under cyclic loading. J. Constr. Steel Res. 2013, 86, 167–182. [Google Scholar] [CrossRef]
- Yao, H.; Goldsworthy, H.; Gad, E. Experimental and numerical investigation of the tensile behavior of blind-bolted T-stub connections to concrete-filled circular columns. J. Struct. Eng. 2008, 134, 198–208. [Google Scholar] [CrossRef]
- Tao, Z.; Li, W.; Shi, B.L.; Han, L.H. Behaviour of bolted end-plate connections to concrete-filled steel columns. J. Constr. Steel Res. 2017, 134, 194–208. [Google Scholar] [CrossRef]
- Li, X.; Xiao, Y.; Wu, Y.T. Seismic behavior of exterior connections with steel beams bolted to CFT columns. J. Constr. Steel Res. 2009, 65, 1438–1446. [Google Scholar] [CrossRef]
- ANSI/AISC 358; Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications. American Institute of Steel Construction: Chicago, IL, USA, 2022.
- Miller, D.K. Lessons learned from the Northridge earthquake. Eng. Struct. 1998, 20, 249–260. [Google Scholar] [CrossRef]
- Bertero, V.V. Performance of Steel Building Structure During the Northridge Earthquake; UCB/EERC-94/09; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 1994. [Google Scholar]
- Bertero, V.V. Seismological and Engineering Aspects of the January 17, 1995 Hyogoken-Nanbu (Kobe) Earthquake; UCB/EERC-95/10; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 1995. [Google Scholar]
- GB 50017; Code for Design of Steel Structures. China Standard Press: Beijing, China, 2017.
- GB/T 1596; Code for Fly Ash Used for Cement and Concrete. China Standard Press: Beijing, China, 2005.
- GB/T 21236; Code for Silica Fume from Electric-Furnace. China Standard Press: Beijing, China, 2007.
- ANSI/AISC 341; Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2016.
- GB 50010; Code for Design of Concrete Structures. China Standard Press: Beijing, China, 2015.
- Wang, C.; Liu, J.; Lu, B.; Zhang, Y.; Ma, Z. Stiffness degradation and mechanical behavior of microfiber-modified high-toughness recycled aggregate concrete under constant load cycling. Eng. Fract. Mech. 2024, 312, 110608. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).