Experimental Investigation of the Seismic Behavior of a Multi-Story Steel Modular Building Using Shaking Table Tests
Abstract
1. Introduction
2. Experimental Design and Preparation
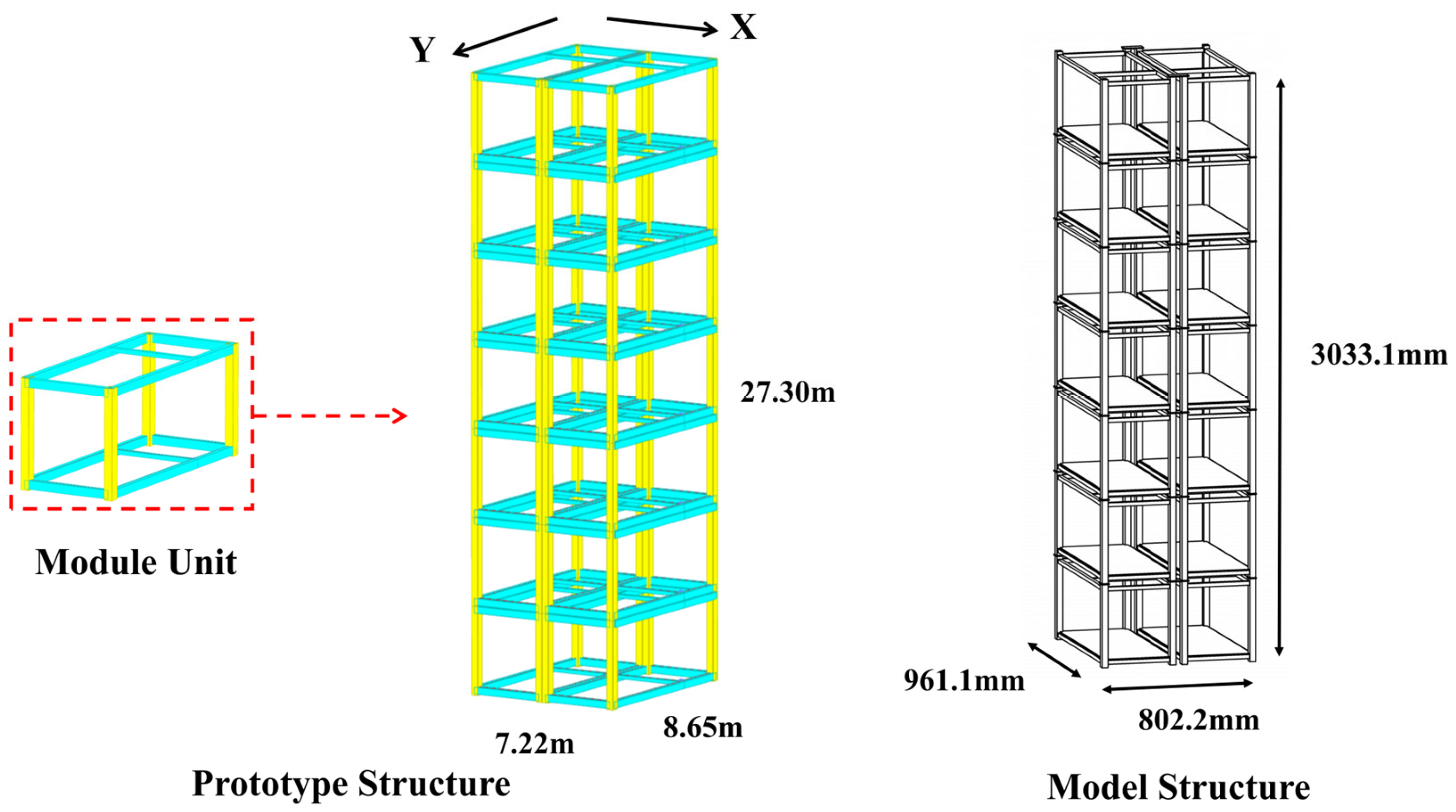
2.1. Prototype Description
2.2. Similitude Relationship
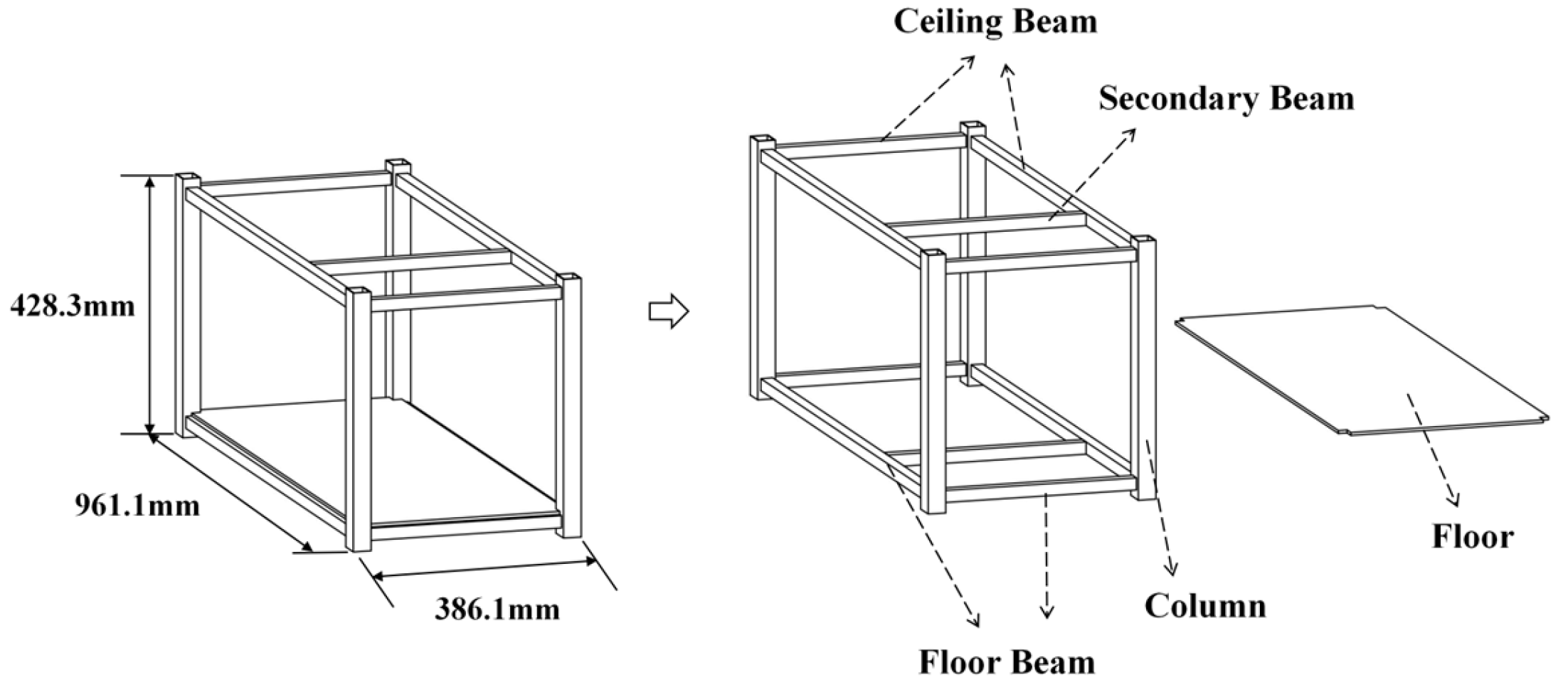
2.3. Design and Fabrication of the Physical Model
2.3.1. Structural Component Design
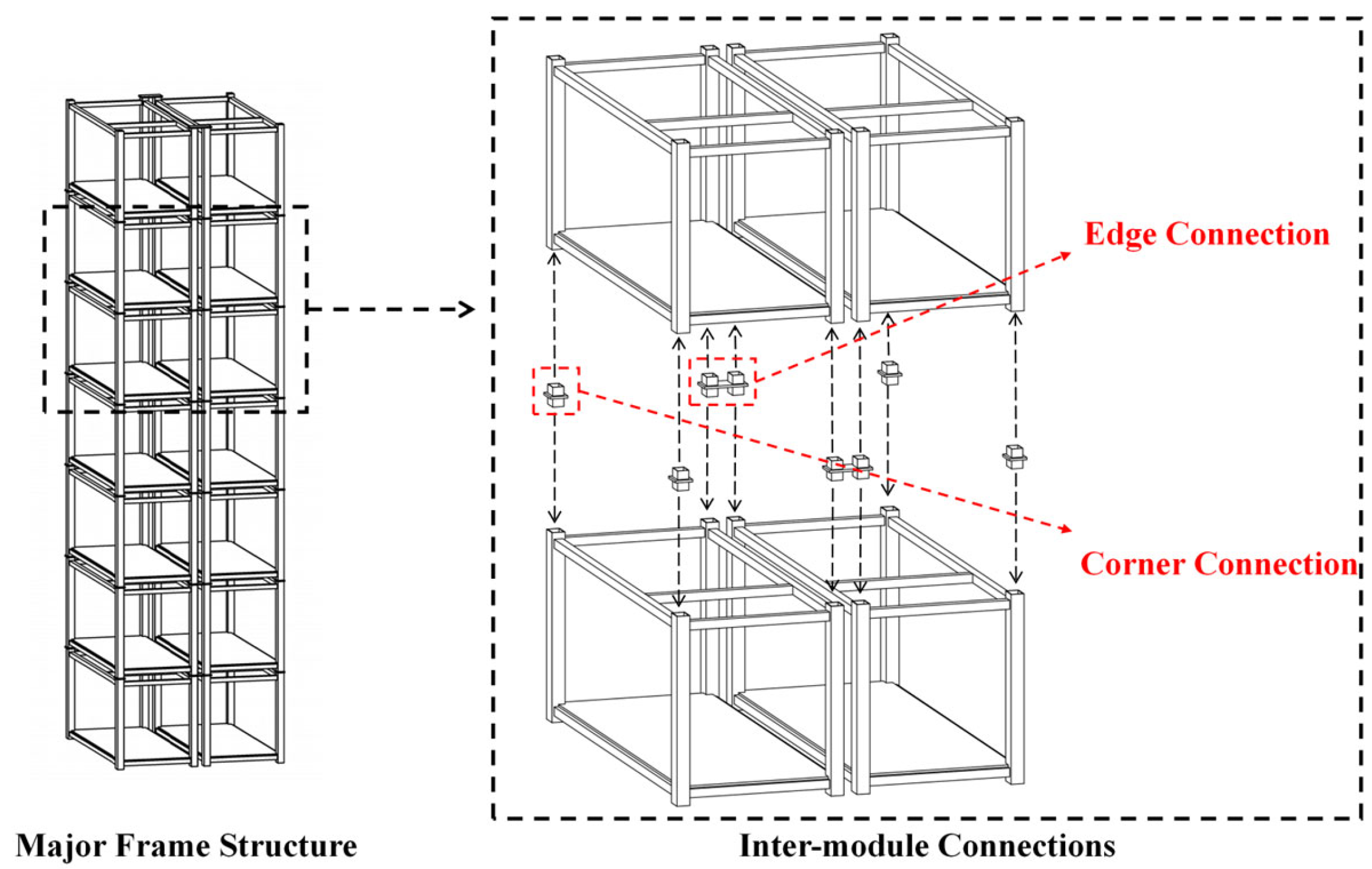
2.3.2. Major Frame Design
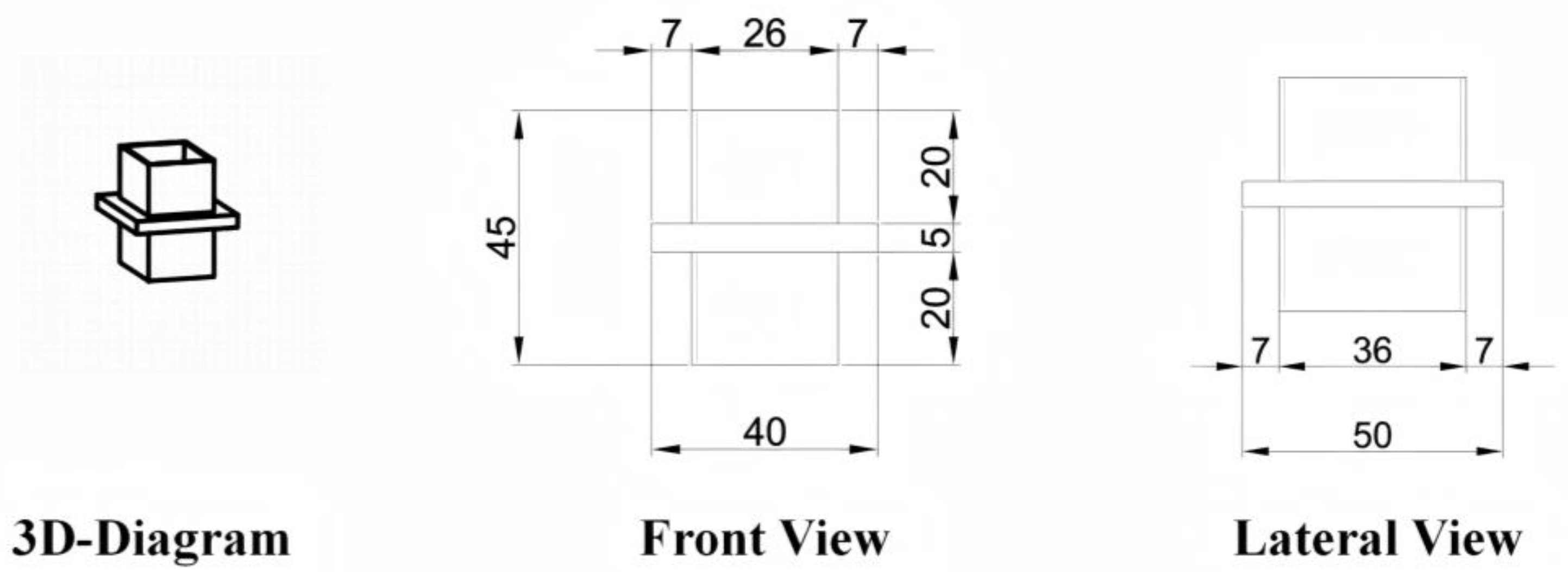
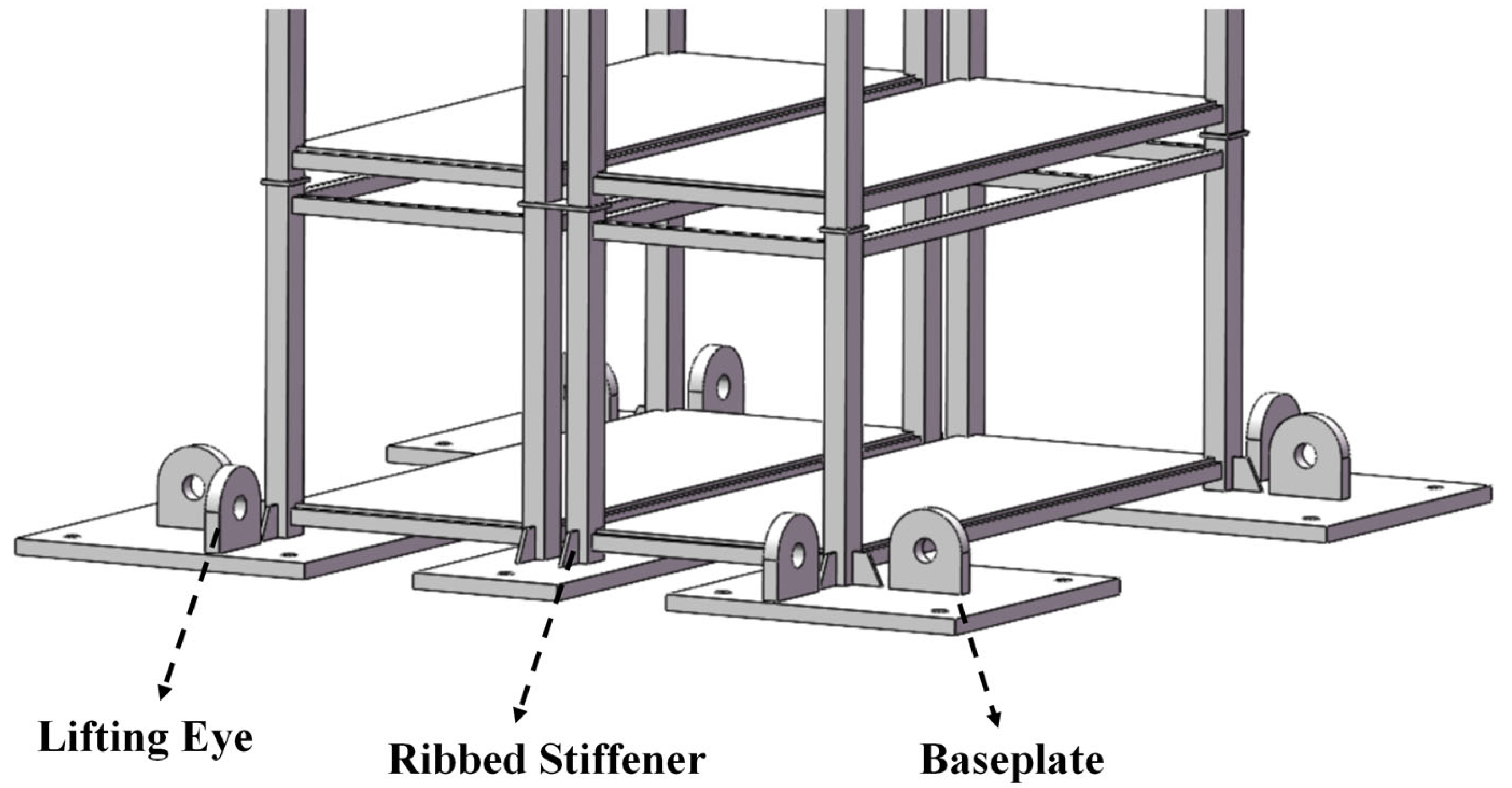
2.3.3. Fabrication
2.4. Measurement Scheme
2.4.1. Sensors
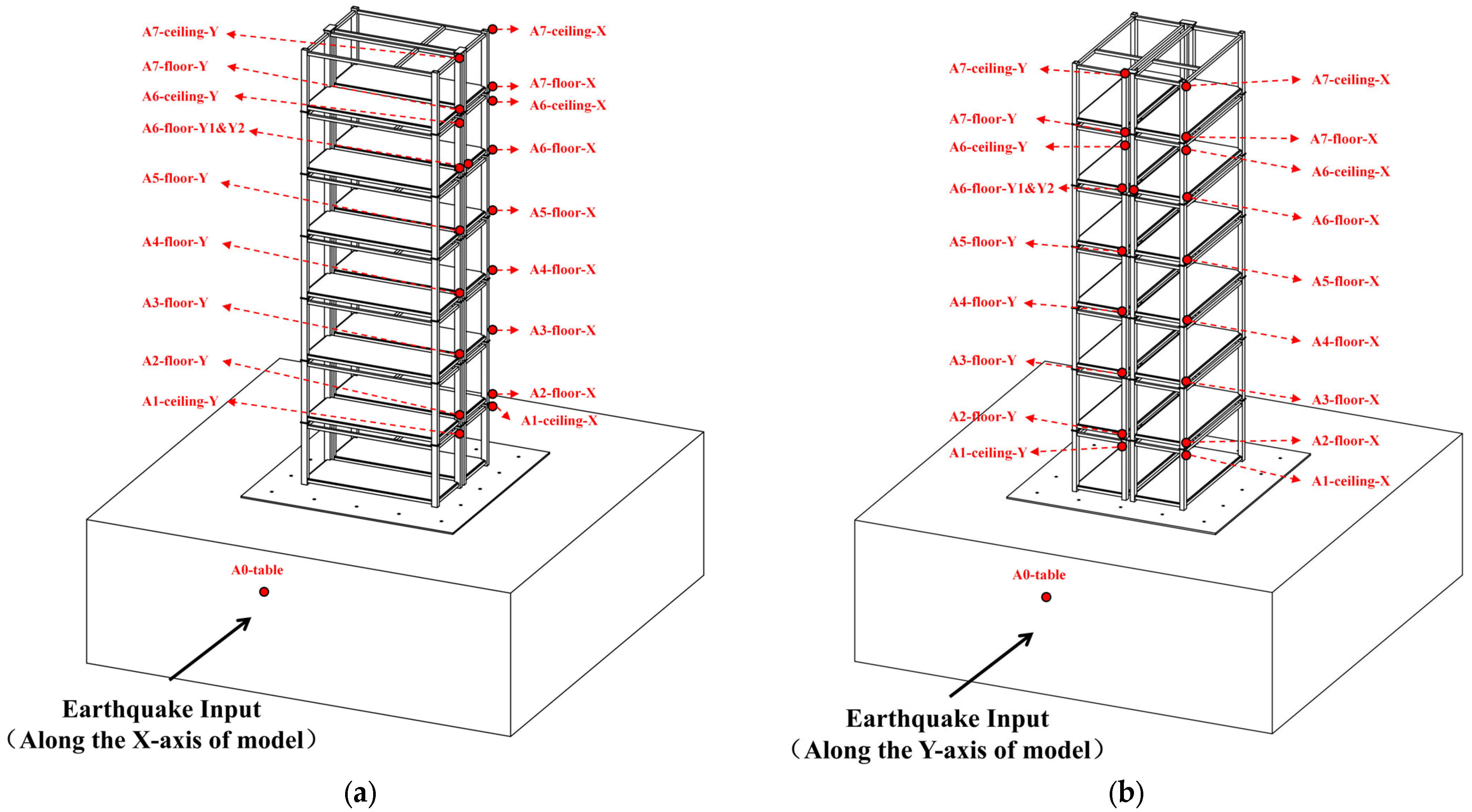
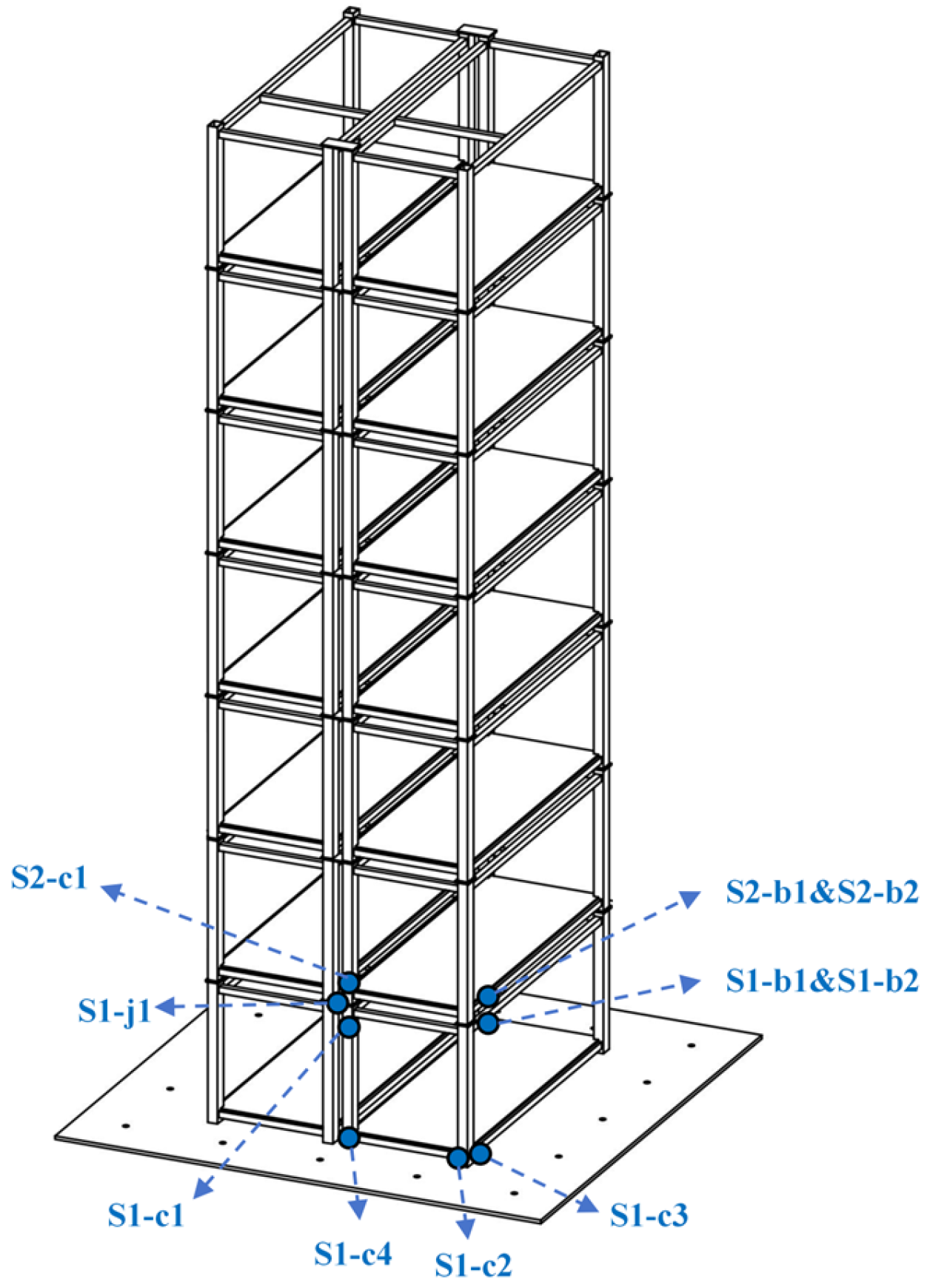
2.4.2. Sensor Arrangement
2.5. Load Scheme
2.5.1. Shaking Table
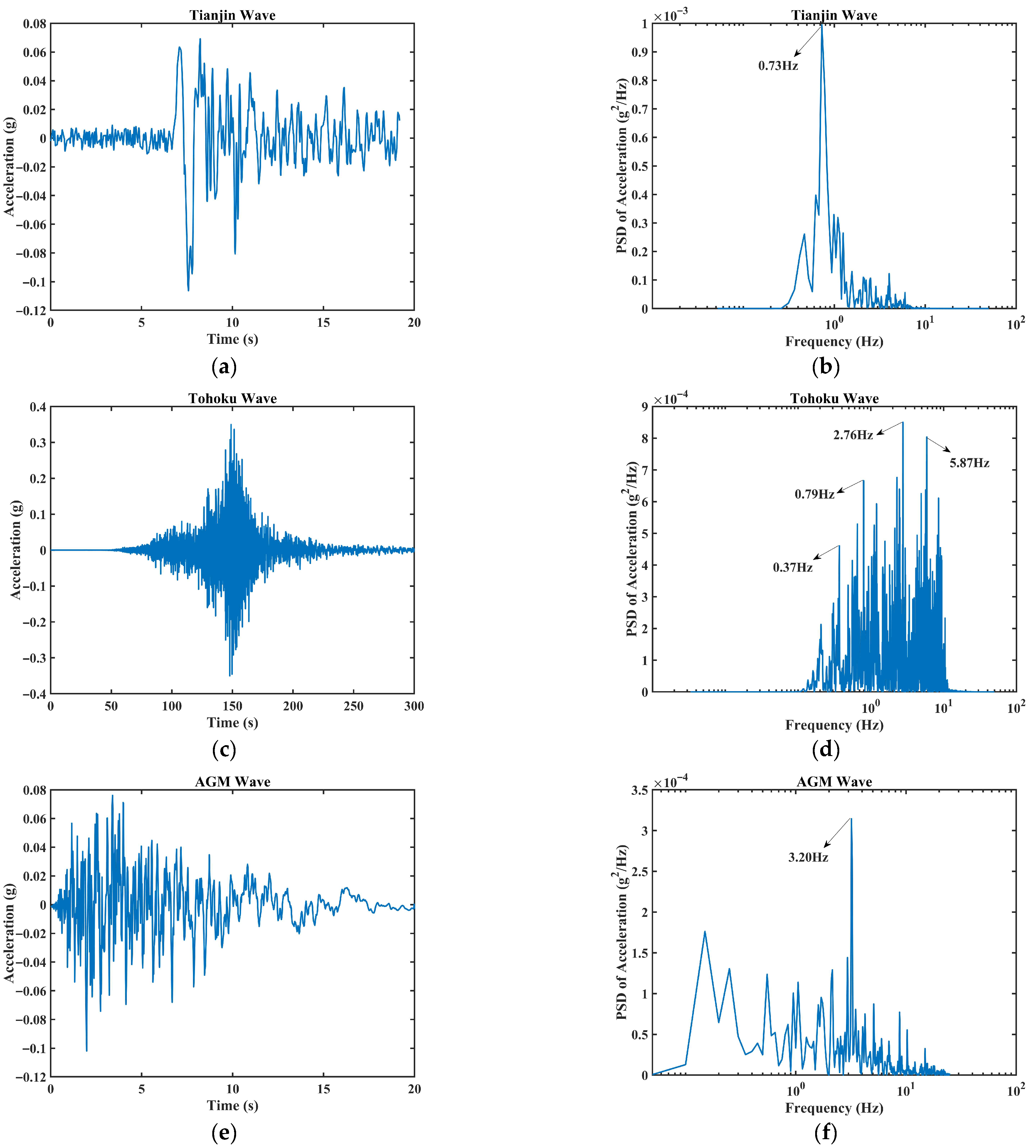
2.5.2. Selection of Seismic Waves
2.5.3. Test Loading Scheme
3. Results and Discussion
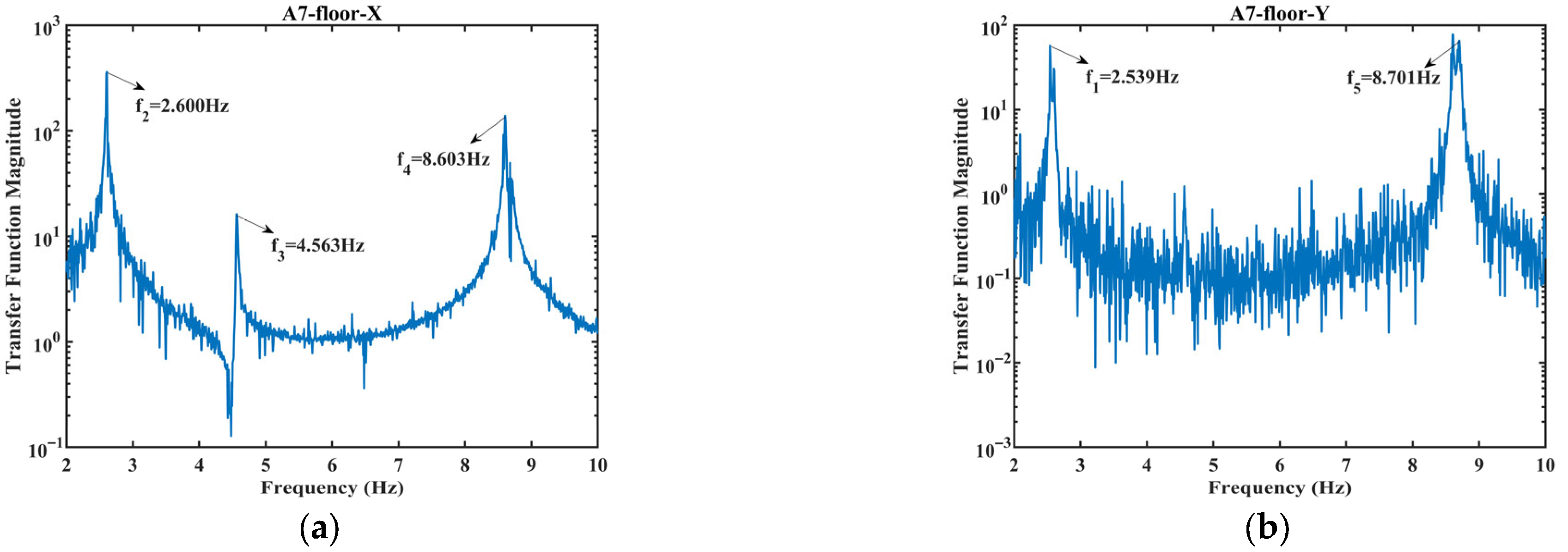
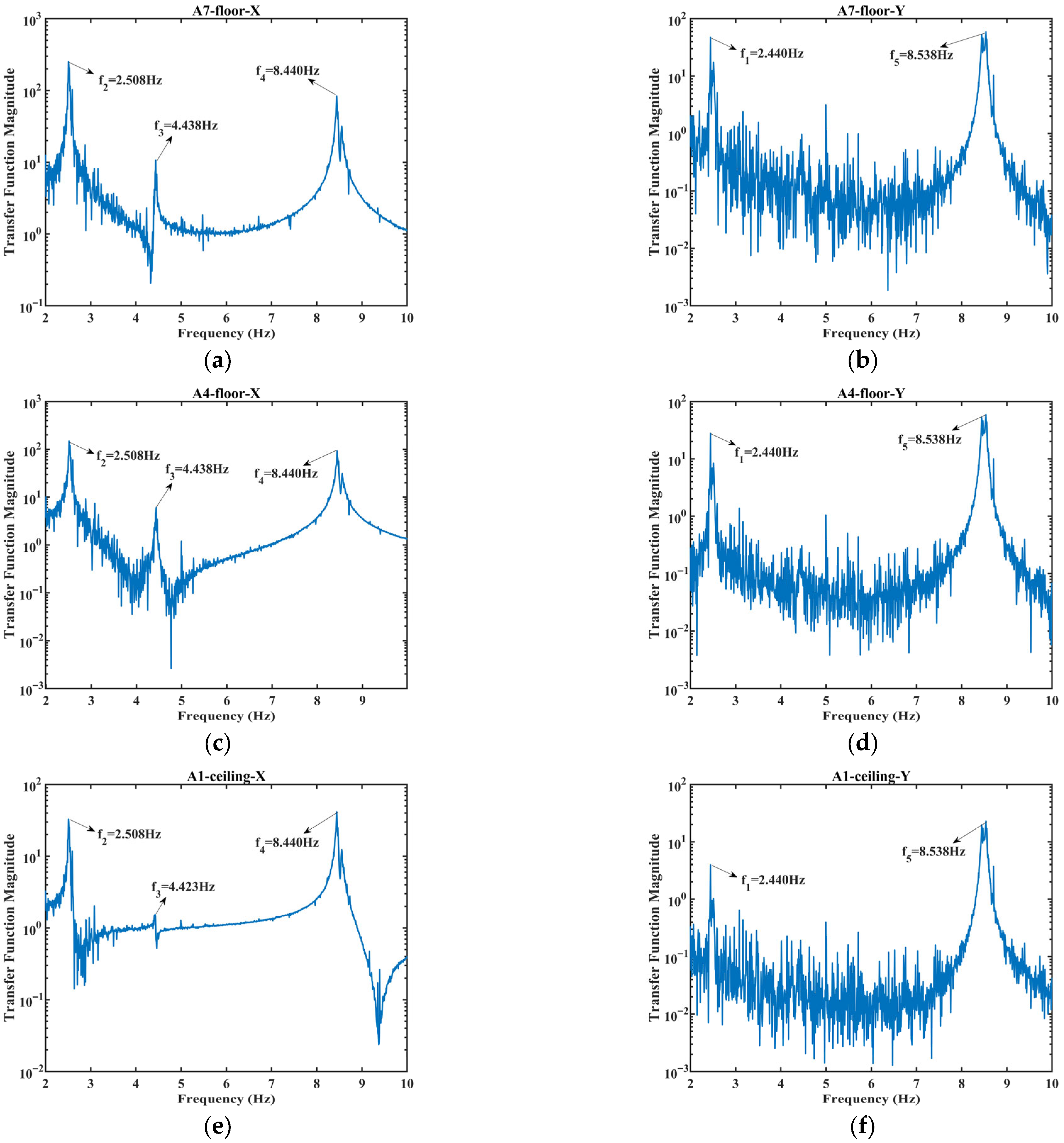
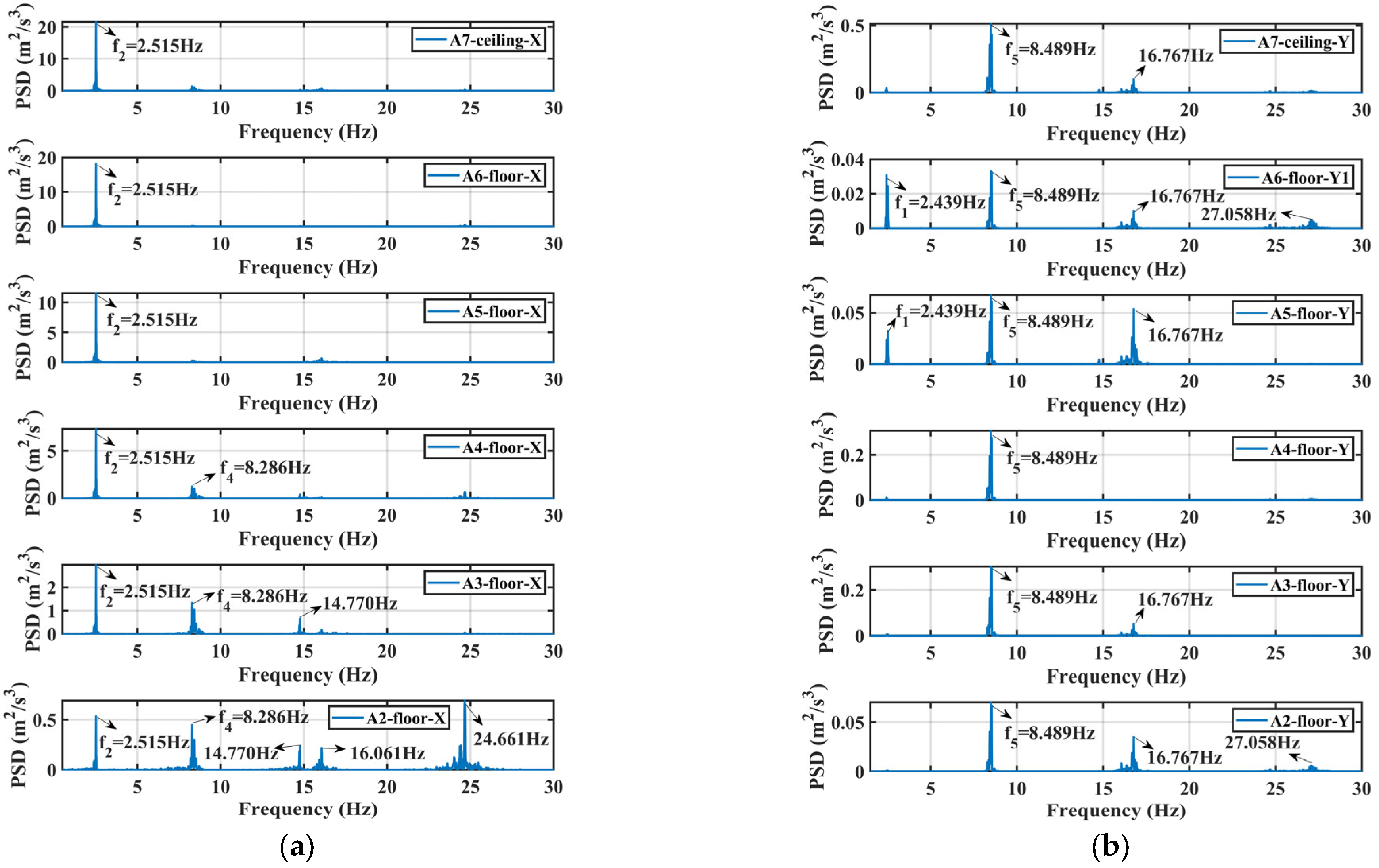
3.1. Dynamic Characteristics
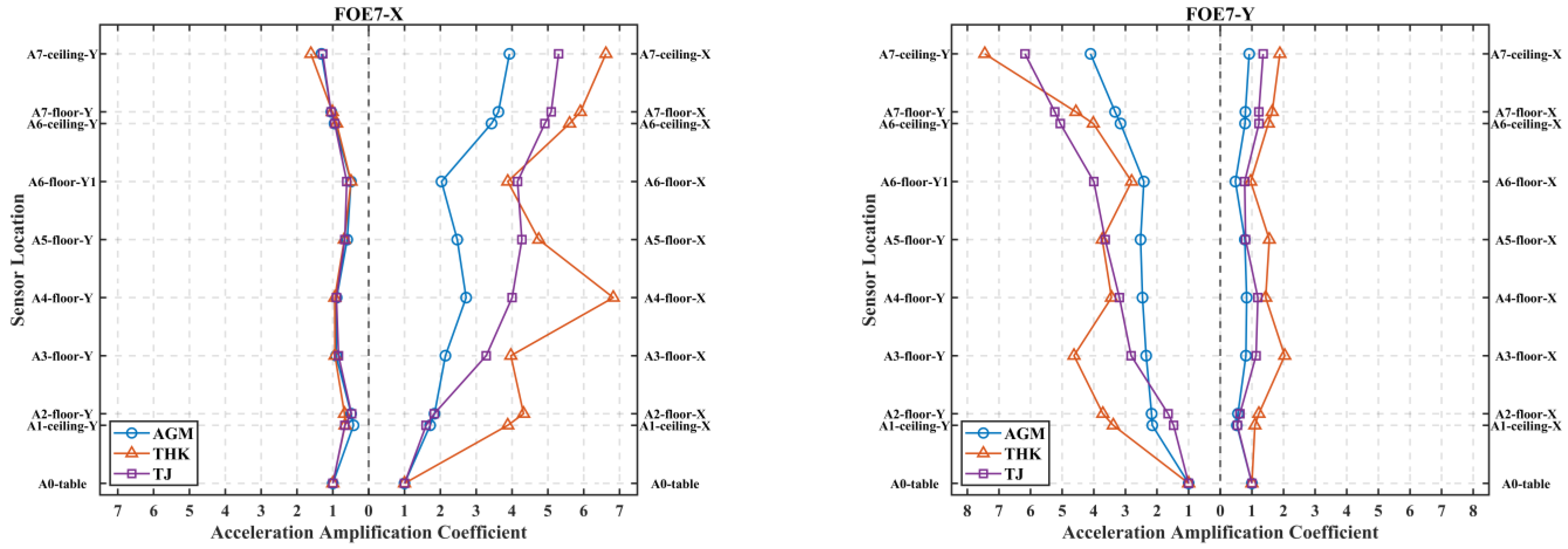
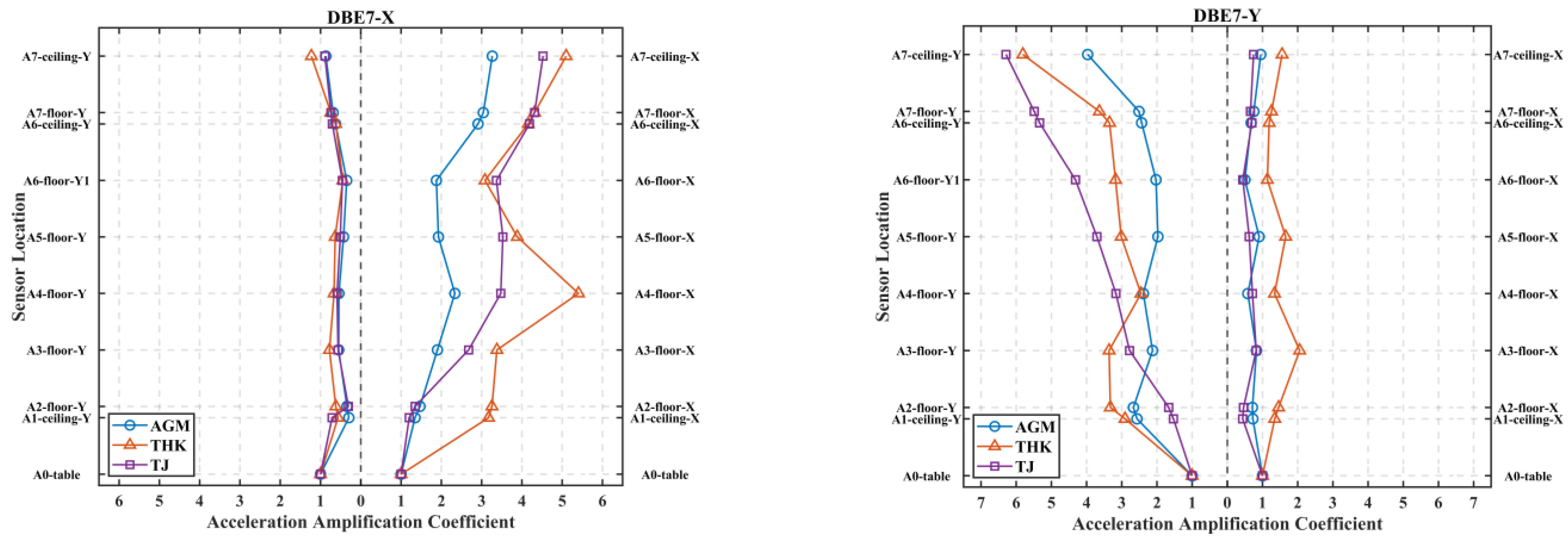
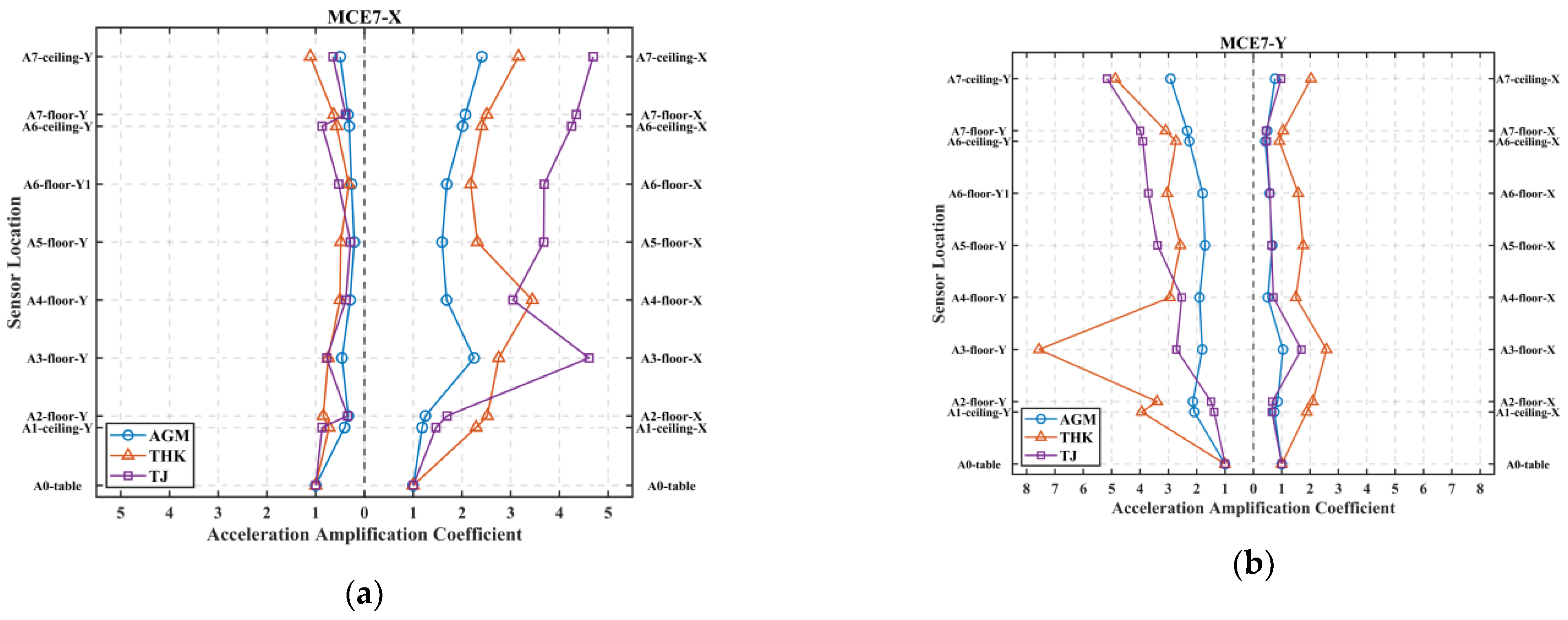
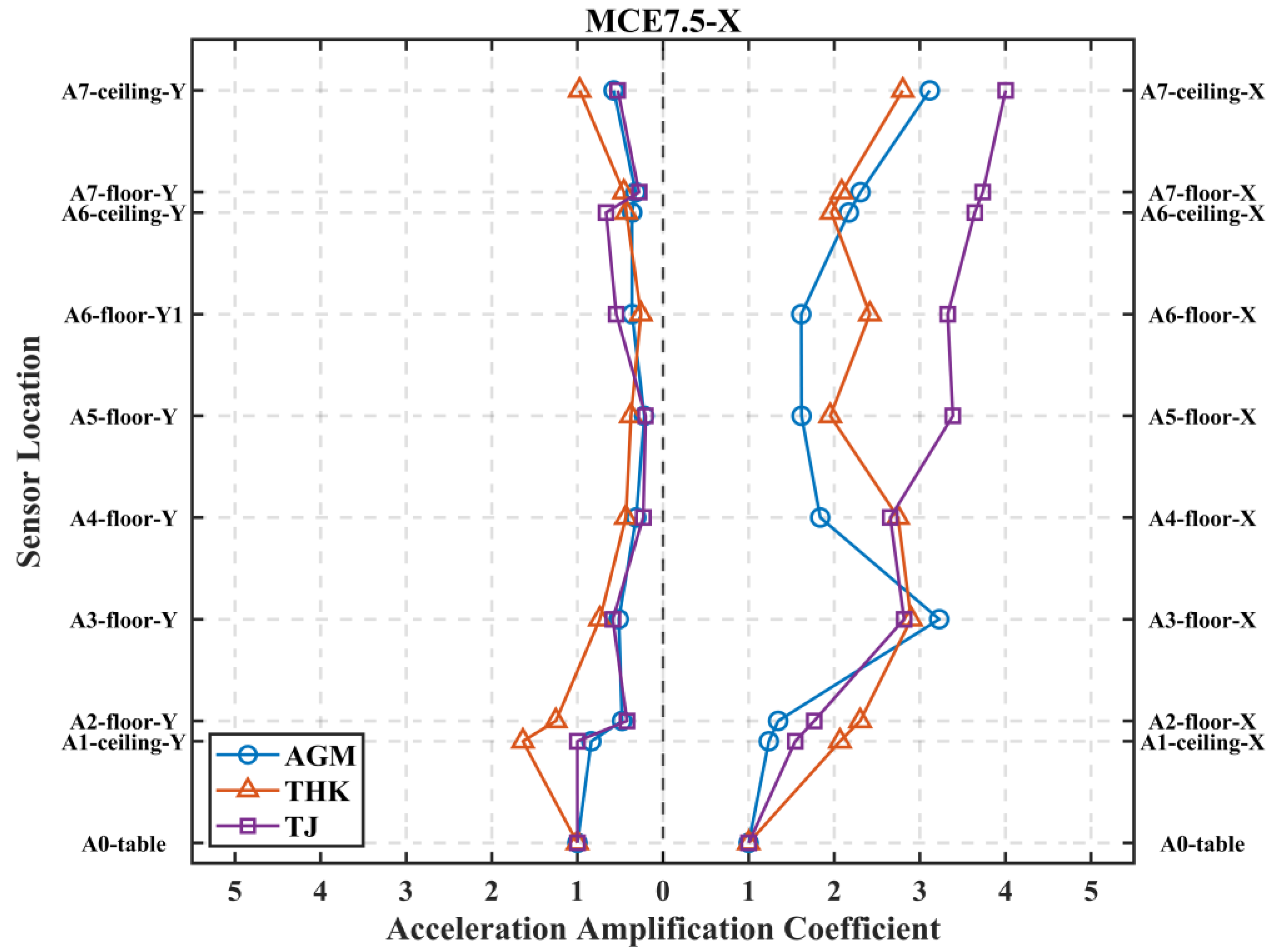
3.2. Acceleration Amplification Coefficient
3.3. Acceleration Response Spectrum Analysis
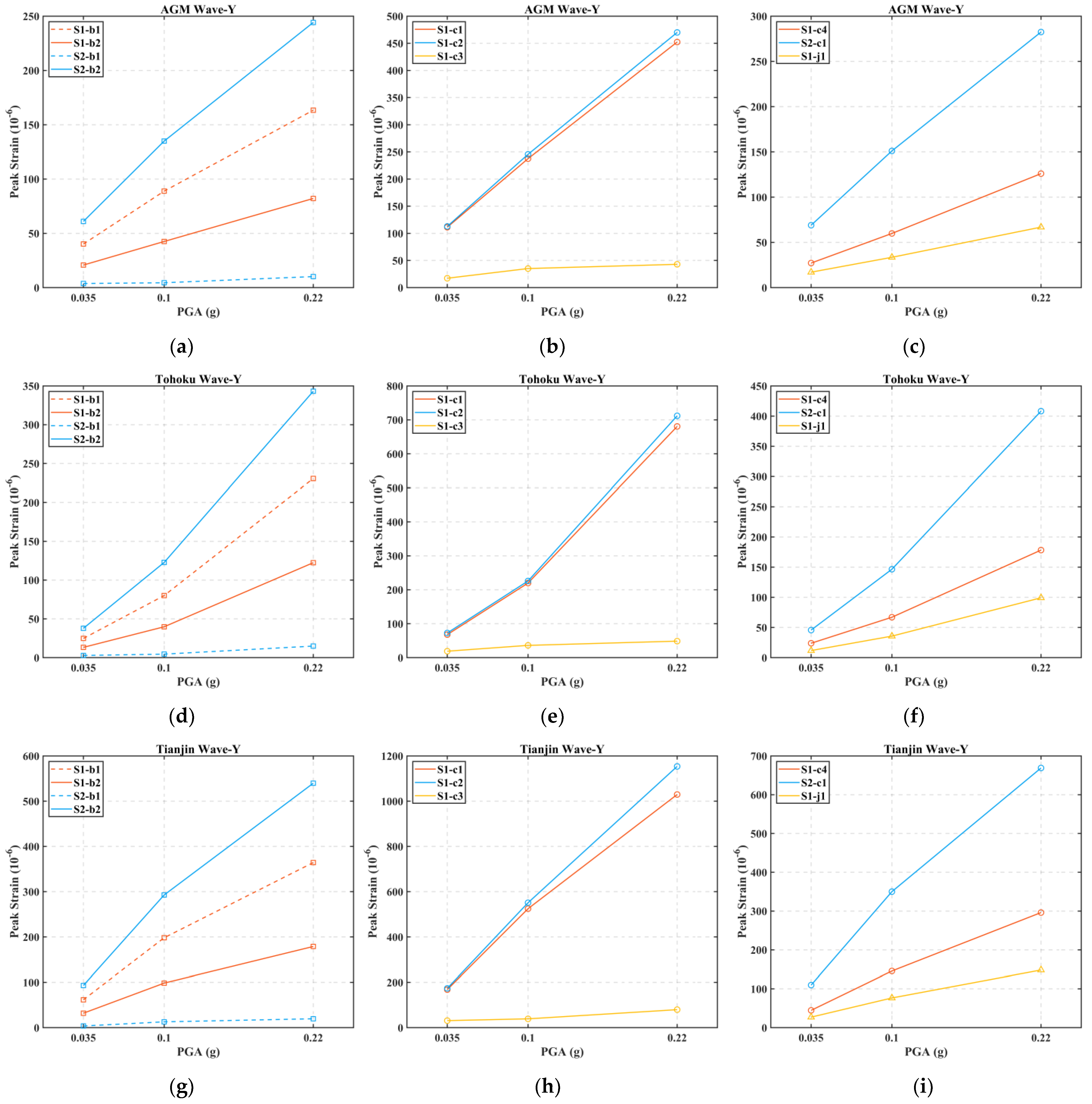
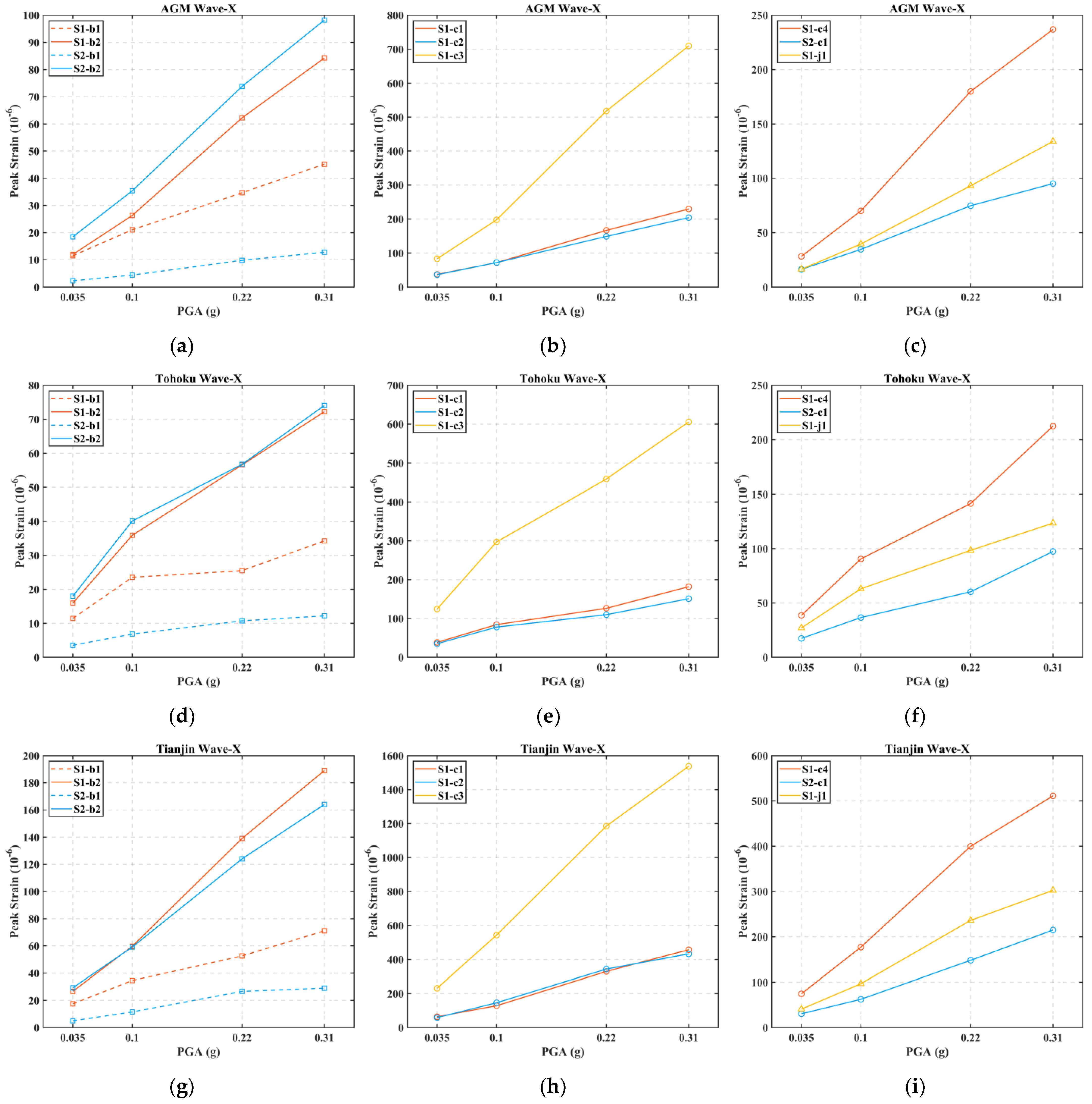
3.4. Strain Response
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, E.F. Seismic Behavior of Corrugated Steel Plate Shear Wall and Innovative Connection in Integrated Modular Steel Construction. Ph.D. Thesis, Tianjin University, Tianjin, China, 8 June 2018. [Google Scholar]
- Deng, E.F.; Wang, Y.H.; Gao, J.D. Numerical study on seismic performance of modular steel structures with FPLC. Structures 2025, 71, 108076. [Google Scholar] [CrossRef]
- Qin, J.J.; Tan, P.; Cai, G.J.; Zhou, C.H.; Mi, P.; Tang, M.X.; Zhou, F.L. Seismic performance investigation on simplified modular loading-bearing and energy-dissipating joints for modular steel buildings. Structures 2025, 79, 109409. [Google Scholar] [CrossRef]
- Kirkayak, L.; De Souza, V.A.; Suzuki, K.; Ando, H.; Sueoka, H. On the vibrational characteristics of a two-tier scaled container stack. J. Mar. Sci. Technol. 2011, 16, 354–365. [Google Scholar] [CrossRef]
- De Souza, V.A.; Kirkayak, L.; Suzuki, K.; Ando, H.; Sueoka, H. Experimental and numerical analysis of container stack dynamics using a scaled model test. Ocean Eng. 2012, 39, 24–42. [Google Scholar] [CrossRef]
- Srisangeerthanan, S.; Hashemi, M.J.; Rajeev, P.; Gad, E.; Fernando, S. Numerical study on the effects of diaphragm stiffness and strength on the seismic response of multi-story modular buildings. Eng. Struct. 2018, 163, 25–37. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, W. A hybrid coupled wall system with replaceable steel coupling beams for high-rise modular buildings. J. Build. Eng. 2020, 31, 101355. [Google Scholar] [CrossRef]
- Shi, F.; Wang, H.; Zong, L.; Ding, Y.; Su, J. Seismic behavior of high-rise modular steel constructions with various module layouts. J. Build. Eng. 2020, 31, 101396. [Google Scholar] [CrossRef]
- Sanches, R.; Tao, J.; Fathieh, A.; Mercan, O. Investigation of the seismic performance of braced low-, mid- and high-rise modular steel building prototypes. Eng. Struct. 2021, 234, 111986. [Google Scholar] [CrossRef]
- GB 50017-2017; Standard for design of steel structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2017.
- GB 50017-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
- GB/T 50018-2025; Technical Standard of Cold-Formed Steel Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2025.
- SJG 129-2023; Technical Specification for Steel Modular Buildings. Housing and Construction Bureau of Shenzhen Municipality: Shenzhen, China, 2023.
- Zheng, X.Y.; Li, H.; Rong, W.; Li, W. Joint earthquake and wave action on the monopile wind turbine foundation: An experimental study. Mar. Struct. 2015, 44, 125–141. [Google Scholar] [CrossRef]
- Chi, S.C.; Lin, S.S. Validation of similitude laws for dynamic structural model test. World Earthq. Eng. 2004, 20, 10. [Google Scholar]
- Feng, L.Q.; Li, F.; Niu, C.L.; Wei, H.L.; Ji, S.Y.; Yang, P.; Wang, G.J. Design and shaking table test of a ten-storey building with steel plate shear walls partially connected to columns. J. Build. Eng. 2022, 49, 103982. [Google Scholar] [CrossRef]
- Li, Z.Y. Shaking Table Test and Finite Element Optimization of Steel Frame Bent Structure with Buckling Restrained Brace. Master’s Thesis, Beijing University of Technology, Beijing, China, 22 June 2022. [Google Scholar]
- Zhang, A.L.; Xie, Z.Q.; Zhang, Y.X.; Lin, H.P. Shaking table test of a prefabricated steel frame structure with all-bolted connections. Eng. Struct. 2021, 248, 113273. [Google Scholar] [CrossRef]
- Wu, F.W.; Li, Y.Q. Large-scale shaking table tests of a six-story floor-by-floor assembled CFS frame-framing shear wall structure. Eng. Struct. 2023, 293, 116608. [Google Scholar] [CrossRef]
- Zhou, X.; Yao, X.; Xu, L.; Shi, Y.; Ke, K.; Liu, L. Shake table tests on a full-scale six-storey cold-formed thin-walled steel-steel plate shear wall structure. Thin-Walled Struct. 2022, 181, 110009. [Google Scholar] [CrossRef]
- Shang, Q.X.; Zheng, J.Y.; Li, J.C.; Wang, T. Comparative study of relevant specifications on peak floor acceleration in current codes of different countries. Eng. Mech. 2020, 37, 91–96. [Google Scholar]
- Huang, B.; Hua, X.; Lu, W.; Zhang, Q. Floor acceleration amplification factor in the instrumented buildings under historical earth-quake excitations. China Civ. Eng. J. 2020, 53, 16–27. [Google Scholar]
- JGJ 339-2015; Code for Seismic Design of Non-Structural Components. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015.
- Yu, H.; Zhang, W.; Zhang, Y.; Sun, Y. Shaking table test and numerical analysis of a 1:12 scale model of a special concentrically braced steel frame with pinned connections. Earthq. Eng. Eng. Vib. 2010, 9, 51–63. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Wu, B.L.; Zhang, A.L.; Li, Y.L.; Zhang, H.; Xiao, C.Y. Shaking table test and structural dynamic analysis for resilient steel frames with seismically isolated floor under bi-directional seismic action. J. Build. Struct. 2025, 46, 30–50. [Google Scholar]





| Component Type | Prototype Section | Model Section |
|---|---|---|
| Column | Box-shaped 250 × 450 × 16 | Box-shaped 30 × 40 × 2.0 |
| Main beam-Y | Box-shaped 200 × 250 × 10 | Box-shaped 20 × 20 × 2.0 |
| Main beam-X | Box-shaped 200 × 200 × 10 | Box-shaped 20 × 20 × 2.0 |
| Secondary beam | Box-shaped 150 × 200 × 10 | Box-shaped 20 × 20 × 1.2 |
| Mode | Natural Frequency (Hz) | Mode Shape |
|---|---|---|
| Mode 1 | 0.848 | Translation along the Y-axis |
| Mode 2 | 0.873 | Translation along the X-axis |
| Mode 3 | 1.117 | Torsion around the Z-axis |
| Mode 4 | 2.691 | Translation along the X-axis |
| Mode 5 | 2.833 | Translation along the Y-axis |
| Physical Parameter | Relationship | Scale Factor |
|---|---|---|
| Length | 1/9 | |
| Mass density | 9 | |
| Elastic modulus | 1 | |
| Poisson’s ratio | 1 | |
| Stress | 1 | |
| Mass | 1/81 | |
| Time | 1/3 | |
| Frequency | 3 | |
| Displacement | 1/9 | |
| Velocity | 1/3 | |
| Acceleration | 1 |
| Type | Sensitivity (mv/g) | Amplitude Range (g) | Frequency Range (Hz) |
|---|---|---|---|
| AI-050 | 500 | 10 | 0.2–2500 |
| AI-100 | 1000 | 5 | 0.2–2000 |
| AI-500 | 5000 | 1 | 0.2–2000 |
| CA-YD-188T | 500 | 10 | 0.6–5000 |
| Type | Resistance (Ω) | Coefficient of Sensitivity | Limiting Strain (μm/m) |
|---|---|---|---|
| BMB120-5AA | 120 ± 0.5 | 2.11 ± 1% | 20,000 |
| BMB120-3CA | 120 ± 0.5 | 2.11 ± 1% | 20,000 |
| Type | Specification | Type | Specification |
|---|---|---|---|
| Shaking direction | Unidirectional horizontal | Operating frequency | 0.1–50 Hz |
| Table size | 3 m × 3 m | Driving method | Electro-hydraulic |
| Load-bearing capacity | 15 t | Max displacement | 150 mm |
| Overturning moment | 45 t × m | Full load acceleration | 1.5 g |
| Name | Nation | Magnitude | Duration | Time Interval | Peak Frequency | PGA |
|---|---|---|---|---|---|---|
| Tianjin | China | 6.9 | 19.19 s | 0.01 s | 0.73 Hz | 0.106 g |
| Tohoku | Japan | 9.0 | 300.00 s | 0.01 s | 2.76 Hz | 0.352 g |
| AGM | - | - | 20.00 s | 0.02 s | 3.20 Hz | 0.102 g |
| Name | Effective Duration | Entire Duration | Time Interval | Peak Frequency |
|---|---|---|---|---|
| Tianjin | 6.40 s | 10.0 s | 0.001 s | 2.19 Hz |
| Tohoku | 100.00 s | 100.0 s | 0.001 s | 8.28 Hz |
| AGM | 6.67 s | 10.0 s | 0.001 s | 9.60 Hz |
| Sequence | Loading Label | Seismic Wave | Input Direction | Intensity | PGA (g) |
|---|---|---|---|---|---|
| 1 | WN-X1 | White Noise | X | - | - |
| 2 | AGM-FOE7-X | AGM | X | FOE7 | 0.035 |
| 3 | THK-FOE7-X | Tohoku | X | FOE7 | 0.035 |
| 4 | TJ-FOE7-X | Tianjin | X | FOE7 | 0.035 |
| 5 | AGM-DBE7-X | AGM | X | DBE7 | 0.1 |
| 6 | THK-DBE7-X | Tohoku | X | DBE7 | 0.1 |
| 7 | TJ-DBE7-X | Tianjin | X | DBE7 | 0.1 |
| 8 | AGM-FOE7-Y | AGM | Y | FOE7 | 0.035 |
| 9 | THK-FOE7-Y | Tohoku | Y | FOE7 | 0.035 |
| 10 | TJ-FOE7-Y | Tianjin | Y | FOE7 | 0.035 |
| 11 | AGM-DBE7-Y | AGM | Y | DBE7 | 0.1 |
| 12 | THK-DBE7-Y | Tohoku | Y | DBE7 | 0.1 |
| 13 | TJ-DBE7-Y | Tianjin | Y | DBE7 | 0.1 |
| 14 | AGM-MCE7-Y | AGM | Y | MCE7 | 0.22 |
| 15 | THK-MCE7-Y | Tohoku | Y | MCE7 | 0.22 |
| 16 | TJ-MCE7-Y | Tianjin | Y | MCE7 | 0.22 |
| 17 | AGM-MCE7-X | AGM | X | MCE7 | 0.22 |
| 18 | THK-MCE7-X | Tohoku | X | MCE7 | 0.22 |
| 19 | TJ-MCE7-X | Tianjin | X | MCE7 | 0.22 |
| 20 | AGM-MCE7.5-X | AGM | X | MCE7.5 | 0.31 |
| 21 | THK-MCE7.5-X | Tohoku | X | MCE7.5 | 0.31 |
| 22 | TJ-MCE7.5-X | Tianjin | X | MCE7.5 | 0.31 |
| 23 | WN-X2 | White Noise | X | - | - |
| Natural Frequency | Mode Shape | Design Value | Measured Value | Error |
|---|---|---|---|---|
| Mode 1: f1 | Translation along the Y-axis | 2.544 Hz | 2.539 Hz | 0.20% |
| Mode 2: f2 | Translation along the X-axis | 2.619 Hz | 2.600 Hz | 0.73% |
| Mode 3: f3 | Torsion around the Z-axis | 3.351 Hz | 4.563 Hz | 26.56% |
| Mode 4: f4 | Translation along the X-axis | 8.073 Hz | 8.603 Hz | 6.16% |
| Mode 5: f5 | Translation along the Y-axis | 8.499 Hz | 8.701 Hz | 2.32% |
| Natural Frequency | Mode Shape | Before the Tests | After the Tests | Reduction |
|---|---|---|---|---|
| Mode 1: f1 | Translation along the Y-axis | 2.539 Hz | 2.440 Hz | 3.90% |
| Mode 2: f2 | Translation along the X-axis | 2.600 Hz | 2.508 Hz | 3.54% |
| Mode 3: f3 | Torsion around the Z-axis | 4.563 Hz | 4.423 Hz | 3.07% |
| Mode 4: f4 | Translation along the X-axis | 8.603 Hz | 8.440 Hz | 1.89% |
| Mode 5: f5 | Translation along the Y-axis | 8.701 Hz | 8.538 Hz | 1.87% |
| Seismic Wave | A1-Ceiling | A2-Floor | A3-Floor | A4-Floor | A5-Floor | A6-Floor | A6-Ceiling | A7-Floor | A7-Ceiling | |
|---|---|---|---|---|---|---|---|---|---|---|
| Formula of code: = 1 + Z/h | 1.14 | 1.16 | 1.30 | 1.44 | 1.58 | 1.73 | 1.85 | 1.87 | 2.00 | |
| FOE7-X | AGM | 1.71 | 1.84 | 2.14 | 2.72 | 2.47 | 2.03 | 3.43 | 3.62 | 3.93 |
| THK | 3.88 | 4.32 | 3.97 | 6.83 | 4.75 | 3.88 | 5.61 | 5.91 | 6.62 | |
| TJ | 1.60 | 1.83 | 3.28 | 4.00 | 4.28 | 4.15 | 4.92 | 5.09 | 5.30 | |
| FOE7-Y | AGM | 0.53 | 0.56 | 0.81 | 0.83 | 0.78 | 0.48 | 0.78 | 0.80 | 0.92 |
| THK | 1.10 | 1.22 | 2.04 | 1.44 | 1.55 | 0.96 | 1.52 | 1.64 | 1.89 | |
| TJ | 0.54 | 0.62 | 1.13 | 1.19 | 0.80 | 0.77 | 1.23 | 1.22 | 1.36 | |
| DBE7-X | AGM | 1.35 | 1.47 | 1.90 | 2.34 | 1.93 | 1.88 | 2.91 | 3.04 | 3.26 |
| THK | 3.17 | 3.26 | 3.38 | 5.40 | 3.88 | 3.08 | 4.16 | 4.31 | 5.10 | |
| TJ | 1.20 | 1.35 | 2.68 | 3.47 | 3.53 | 3.37 | 4.19 | 4.31 | 4.52 | |
| DBE7-Y | AGM | 0.73 | 0.71 | 0.83 | 0.58 | 0.90 | 0.50 | 0.68 | 0.75 | 0.95 |
| THK | 1.35 | 1.46 | 2.06 | 1.34 | 1.66 | 1.14 | 1.19 | 1.26 | 1.56 | |
| TJ | 0.44 | 0.46 | 0.82 | 0.71 | 0.62 | 0.44 | 0.70 | 0.66 | 0.75 | |
| MCE7-X | AGM | 1.18 | 1.25 | 2.25 | 1.69 | 1.59 | 1.69 | 2.02 | 2.07 | 2.41 |
| THK | 2.29 | 2.52 | 2.75 | 3.44 | 2.32 | 2.18 | 2.41 | 2.51 | 3.16 | |
| TJ | 1.47 | 1.69 | 4.61 | 3.05 | 3.68 | 3.69 | 4.25 | 4.34 | 4.69 | |
| MCE7-Y | AGM | 0.74 | 0.85 | 1.04 | 0.51 | 0.66 | 0.57 | 0.42 | 0.49 | 0.76 |
| THK | 1.88 | 2.09 | 2.58 | 1.50 | 1.75 | 1.58 | 0.92 | 1.05 | 2.03 | |
| TJ | 0.65 | 0.67 | 1.70 | 0.71 | 0.63 | 0.58 | 0.47 | 0.44 | 0.98 | |
| MCE7.5-X | AGM | 1.24 | 1.34 | 3.23 | 1.84 | 1.62 | 1.61 | 2.17 | 2.31 | 3.11 |
| THK | 2.07 | 2.30 | 2.90 | 2.75 | 1.95 | 2.42 | 1.96 | 2.09 | 2.80 | |
| TJ | 1.54 | 1.77 | 2.82 | 2.65 | 3.38 | 3.32 | 3.64 | 3.73 | 4.00 | |
| Seismic Wave | A1-Ceiling | A2-Floor | A3-Floor | A4-Floor | A5-Floor | A6-Floor | A6-Ceiling | A7-Floor | A7-Ceiling | |
|---|---|---|---|---|---|---|---|---|---|---|
| Formula of code: = 1 + Z/h | 1.14 | 1.16 | 1.30 | 1.44 | 1.58 | 1.73 | 1.85 | 1.87 | 2.00 | |
| FOE7-X | AGM | 0.42 | 0.49 | 0.91 | 0.89 | 0.60 | 0.49 | 0.95 | 1.04 | 1.32 |
| THK | 0.66 | 0.67 | 0.94 | 0.95 | 0.68 | 0.49 | 0.90 | 1.01 | 1.61 | |
| TJ | 0.67 | 0.48 | 0.84 | 0.90 | 0.67 | 0.61 | 0.95 | 1.05 | 1.28 | |
| FOE7-Y | AGM | 2.15 | 2.17 | 2.34 | 2.46 | 2.52 | 2.42 | 3.16 | 3.33 | 4.10 |
| THK | 3.38 | 3.71 | 4.63 | 3.44 | 3.73 | 2.80 | 4.02 | 4.56 | 7.45 | |
| TJ | 1.48 | 1.65 | 2.82 | 3.19 | 3.64 | 4.00 | 5.06 | 5.23 | 6.18 | |
| DBE7-X | AGM | 0.30 | 0.34 | 0.55 | 0.54 | 0.43 | 0.35 | 0.63 | 0.69 | 0.87 |
| THK | 0.57 | 0.62 | 0.78 | 0.66 | 0.64 | 0.45 | 0.62 | 0.74 | 1.23 | |
| TJ | 0.71 | 0.31 | 0.56 | 0.59 | 0.51 | 0.46 | 0.71 | 0.74 | 0.89 | |
| DBE7-Y | AGM | 2.57 | 2.67 | 2.13 | 2.39 | 1.97 | 2.03 | 2.44 | 2.51 | 3.97 |
| THK | 2.91 | 3.32 | 3.36 | 2.45 | 3.02 | 3.18 | 3.35 | 3.64 | 5.81 | |
| TJ | 1.53 | 1.67 | 2.78 | 3.17 | 3.71 | 4.32 | 5.34 | 5.49 | 6.29 | |
| MCE7-X | AGM | 0.41 | 0.33 | 0.46 | 0.29 | 0.21 | 0.26 | 0.31 | 0.34 | 0.50 |
| THK | 0.73 | 0.84 | 0.74 | 0.50 | 0.49 | 0.32 | 0.57 | 0.63 | 1.11 | |
| TJ | 0.87 | 0.35 | 0.77 | 0.38 | 0.29 | 0.53 | 0.87 | 0.39 | 0.65 | |
| MCE7-Y | AGM | 2.08 | 2.13 | 1.81 | 1.90 | 1.70 | 1.79 | 2.26 | 2.34 | 2.92 |
| THK | 3.94 | 3.40 | 7.56 | 2.94 | 2.58 | 3.04 | 2.73 | 3.10 | 4.87 | |
| TJ | 1.38 | 1.50 | 2.71 | 2.53 | 3.38 | 3.71 | 3.90 | 4.00 | 5.17 | |
| MCE7.5-X | AGM | 0.84 | 0.48 | 0.52 | 0.31 | 0.22 | 0.36 | 0.36 | 0.32 | 0.58 |
| THK | 1.64 | 1.25 | 0.74 | 0.43 | 0.37 | 0.26 | 0.43 | 0.46 | 0.97 | |
| TJ | 1.00 | 0.42 | 0.59 | 0.23 | 0.20 | 0.55 | 0.66 | 0.28 | 0.53 | |
| AAF | Modular Steel Structure | Conventional Steel Structure | Difference |
|---|---|---|---|
| Second floor | 1.67 | 1.40 | 19.3% |
| Third floor | 2.78 | 1.24 | 124.2% |
| Fourth floor | 3.17 | 1.30 | 143.8% |
| Fifth floor | 3.71 | 1.90 | 95.3% |
| Sixth floor | 4.32 | 2.37 | 82.2% |
| Seventh floor | 5.49 | 3.42 | 60.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Nie, Y.; Qian, K.; Xie, X.; Zhao, M.; Zhao, Z.; Zheng, X.Y. Experimental Investigation of the Seismic Behavior of a Multi-Story Steel Modular Building Using Shaking Table Tests. Buildings 2025, 15, 2661. https://doi.org/10.3390/buildings15152661
Zhang X, Nie Y, Qian K, Xie X, Zhao M, Zhao Z, Zheng XY. Experimental Investigation of the Seismic Behavior of a Multi-Story Steel Modular Building Using Shaking Table Tests. Buildings. 2025; 15(15):2661. https://doi.org/10.3390/buildings15152661
Chicago/Turabian StyleZhang, Xinxin, Yucong Nie, Kehao Qian, Xinyu Xie, Mengyang Zhao, Zhan Zhao, and Xiang Yuan Zheng. 2025. "Experimental Investigation of the Seismic Behavior of a Multi-Story Steel Modular Building Using Shaking Table Tests" Buildings 15, no. 15: 2661. https://doi.org/10.3390/buildings15152661
APA StyleZhang, X., Nie, Y., Qian, K., Xie, X., Zhao, M., Zhao, Z., & Zheng, X. Y. (2025). Experimental Investigation of the Seismic Behavior of a Multi-Story Steel Modular Building Using Shaking Table Tests. Buildings, 15(15), 2661. https://doi.org/10.3390/buildings15152661






