Hysteresis Model for Flexure-Shear Critical Circular Reinforced Concrete Columns Considering Cyclic Degradation
Abstract
1. Introduction
2. Selection of Specimens and Hysteretic Characteristics
2.1. Selection of Experimental Specimens
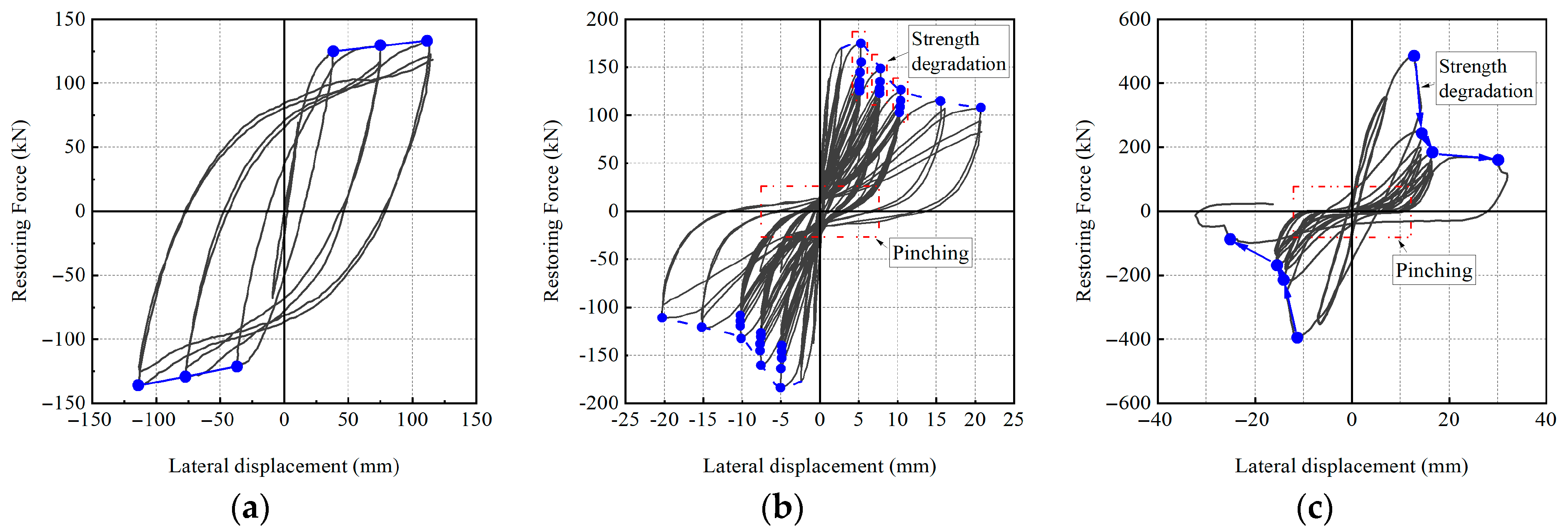
2.2. Hysteretic Characteristics of Flexure-Shear Critical Columns
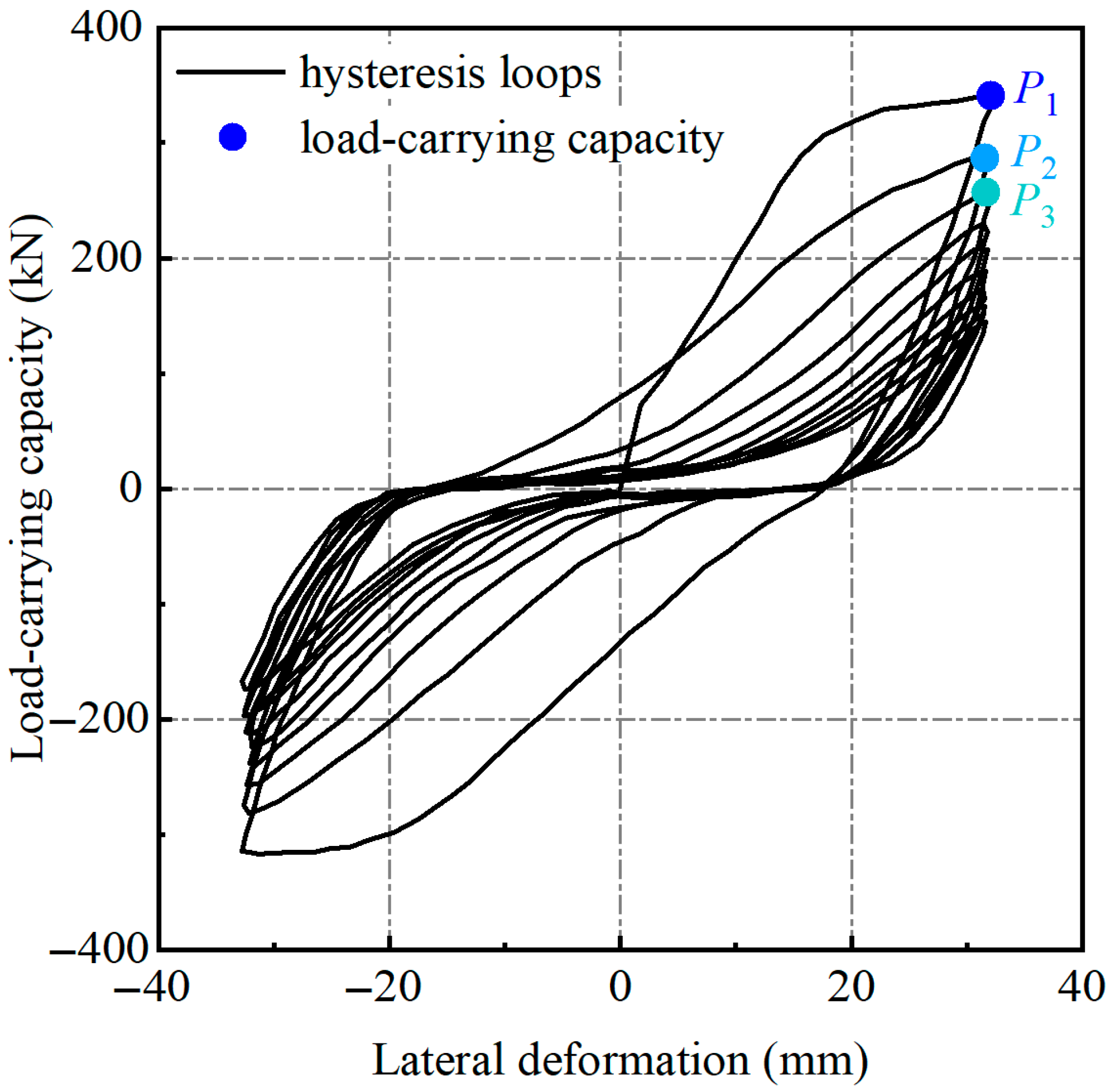
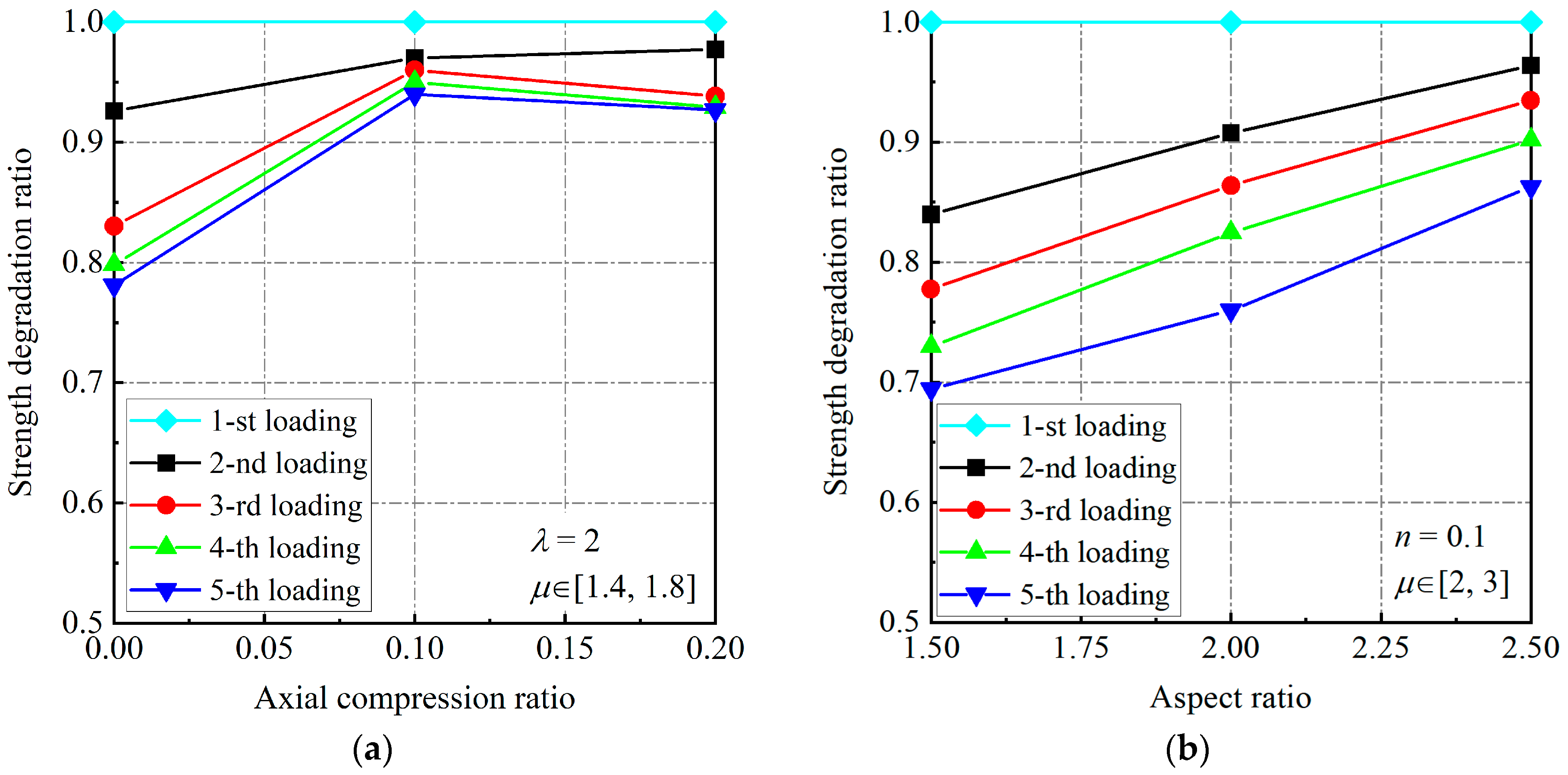
2.2.1. Nonlinear Strength Degradation
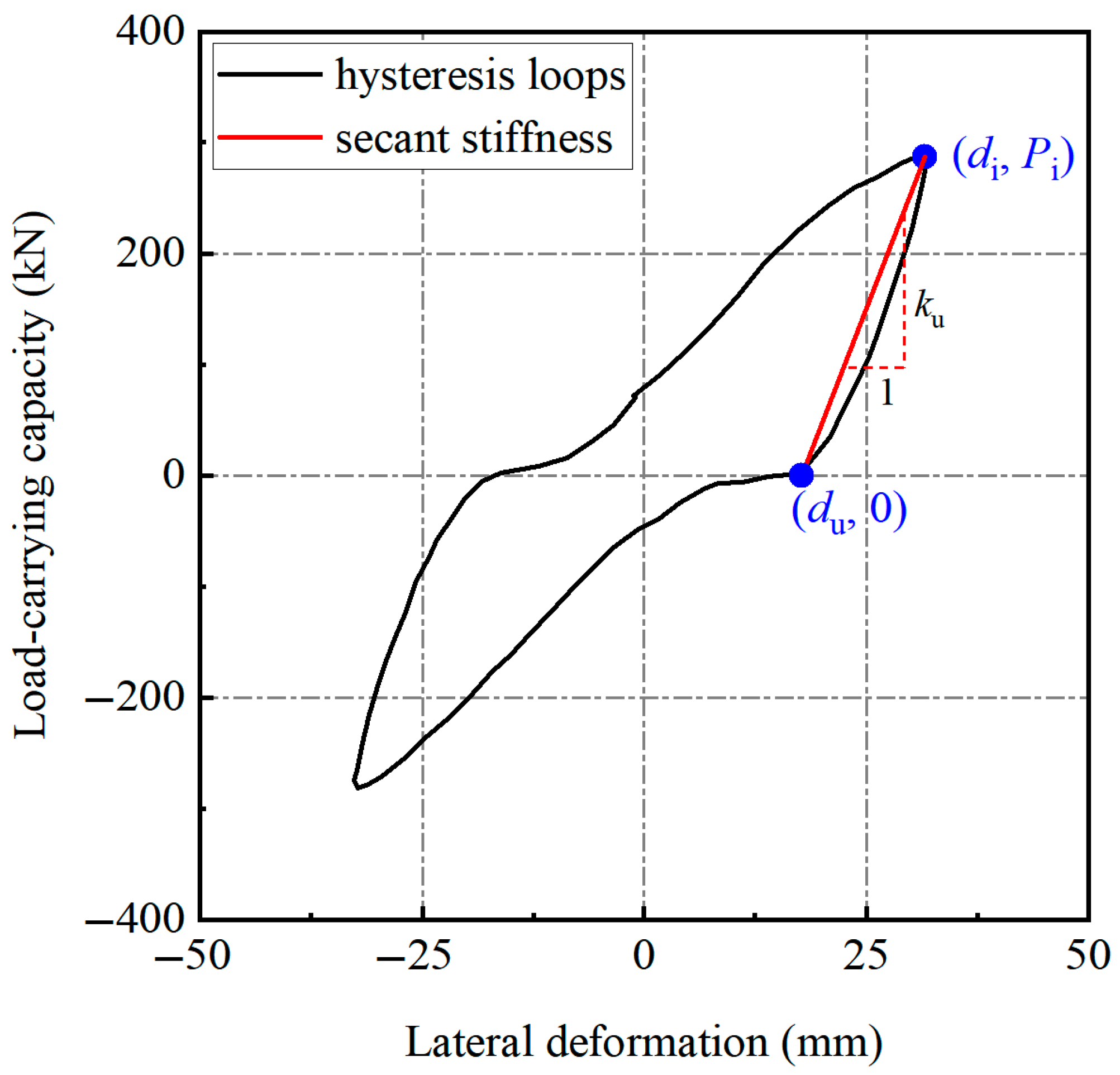
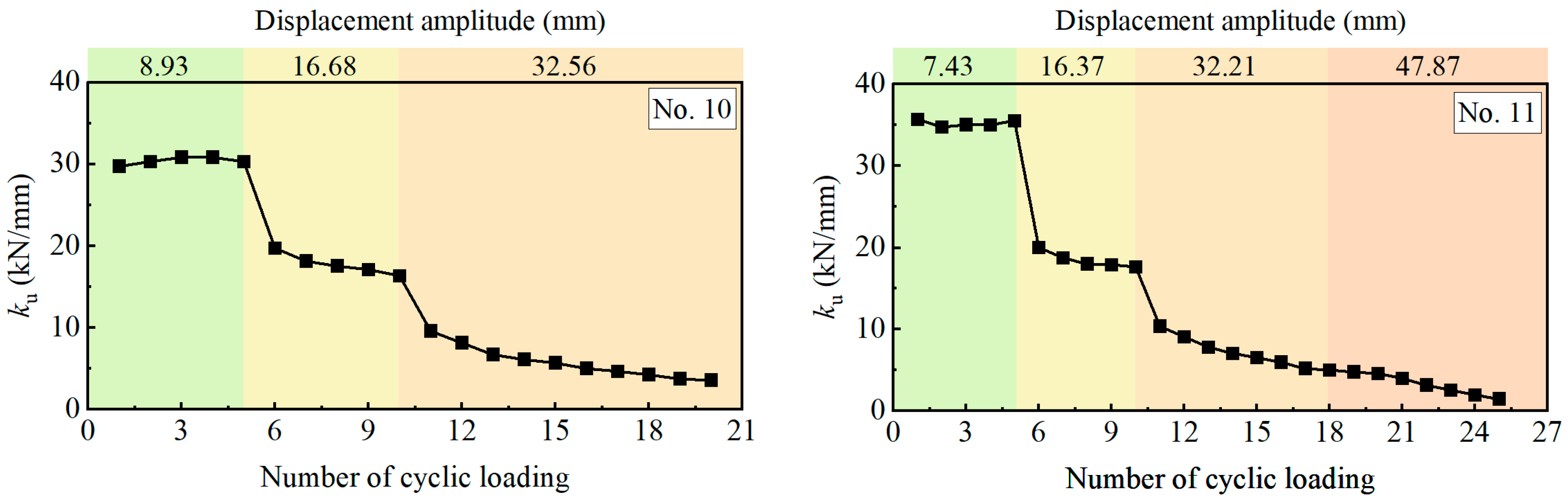
2.2.2. Stiffness Degradation
2.2.3. Hysteretic Energy Dissipation
3. Model Framework for Degradation and Pinching Effect
3.1. Energy-Based Strength Degradation Model
3.2. Stiffness Degradation Model
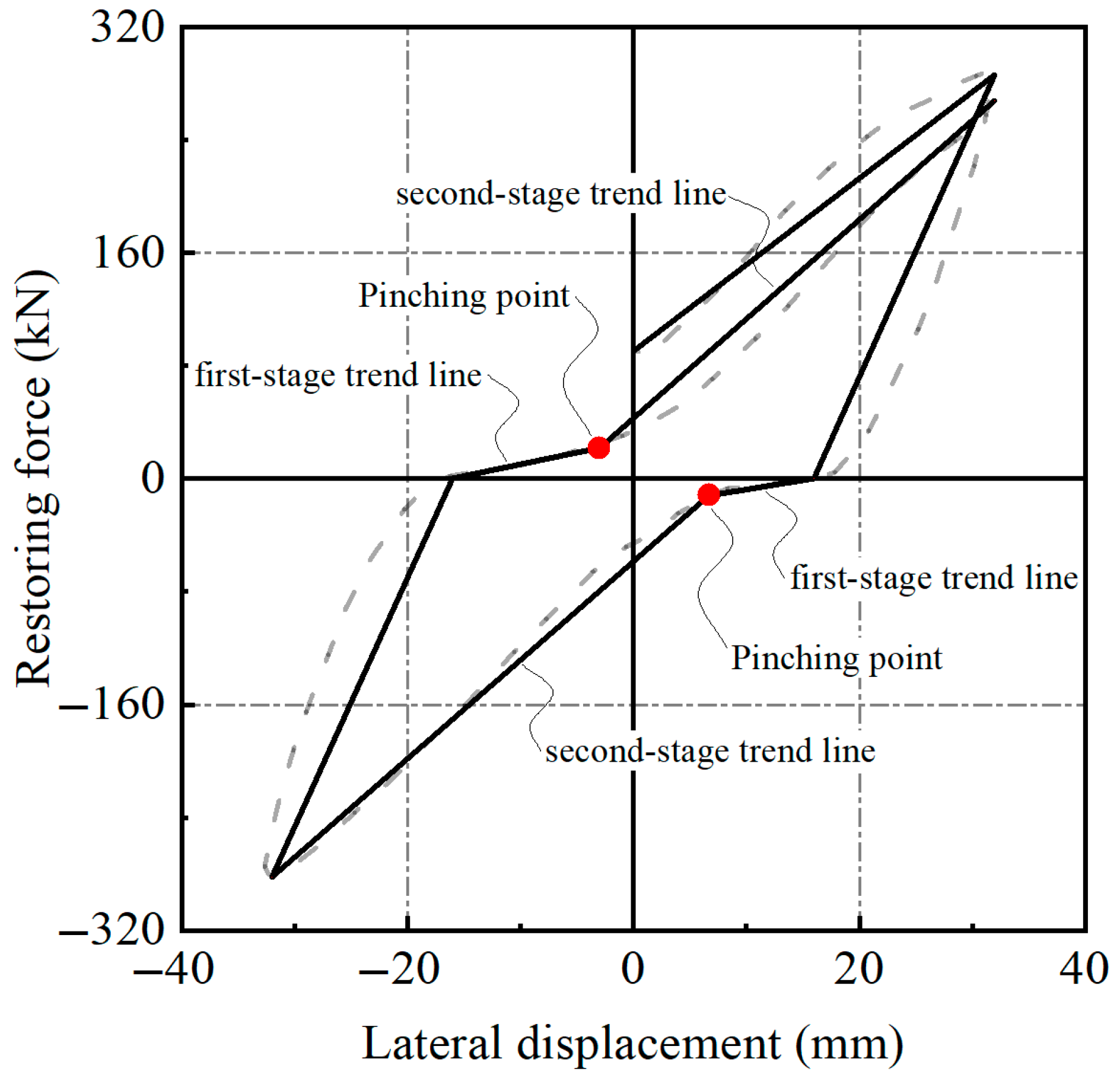
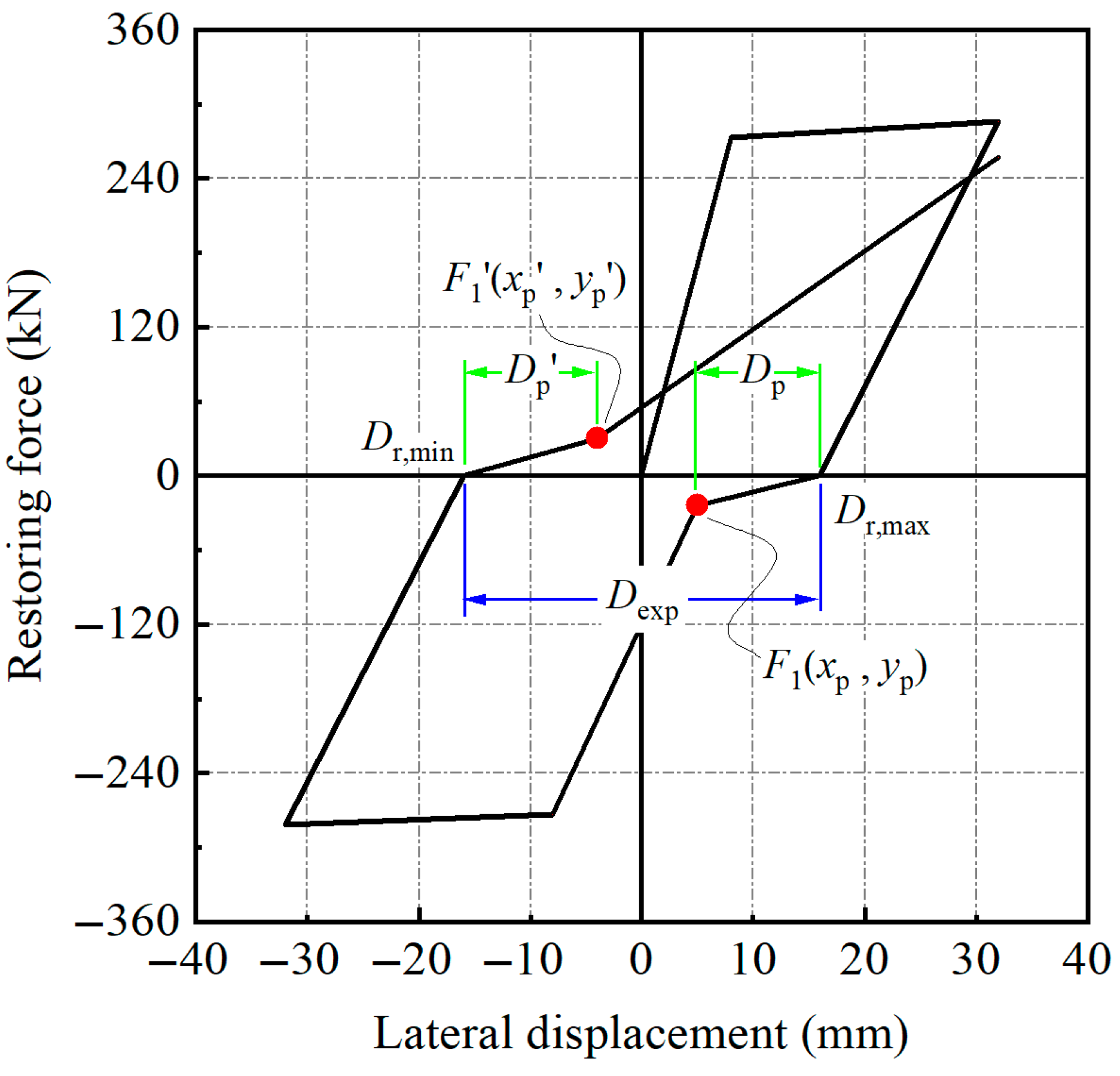
3.3. Pinching Behavior Characterization
4. Hysteresis Model Considering Cyclic Degradation
5. Verification and Application Extension
5.1. Verification of the Proposed Model
5.2. Application Extension
5.3. Limitations and Further Research Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yoshikawa, H.; Miyagi, T. Ductility and failure modes of singly reinforced concrete columns. In Modeling of Inelastic Behavior of RC Structures Under Seismic Loads; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 35–368. [Google Scholar]
- Ma, Y.; Gong, J. Seismic failure modes and deformation capacity of reinforced concrete columns under cyclic loads. Period. Polytech. Civ. Eng. 2018, 62, 80–91. [Google Scholar]
- Zhang, Q.; Chen, M.; Li, W.; Gu, X.; Gong, J. Seismic performance and damage properties of flexure–shear critical RC columns with various loading cycles. Bull. Earthq. Eng. 2023, 21, 5083–5113. [Google Scholar] [CrossRef]
- Yan, H.; Peng, J.; Zhou, S.; Qin, Y.; Kang, S.; Chen, Y. Behaviour of reinforced ultra-high performance concrete columns with medium shear span ratios under reversed cyclic loading. Eng. Fail. Anal. 2025, 179, 109769. [Google Scholar] [CrossRef]
- Hu, B.; Wang, X.; Zhou, Y.; Huang, X.; Zhu, Z. Seismic performance of shear-critical RC columns strengthened by multiple composites considering shifted failure zone. Case Stud. Constr. Mater. 2024, 20, e02971. [Google Scholar] [CrossRef]
- Gurbuz, T.; Ilki, A.; Thambiratnam, D.P.; Perera, N. Low-elevation impact tests of axially loaded reinforced concrete columns. ACI Struct. J. 2019, 116, 118–128. [Google Scholar] [CrossRef]
- Jeon, J.S.; Lowes, L.N.; DesRoches, R.; Brilakis, I. Fragility curves for non-ductile reinforced concrete frames that exhibit different component response mechanisms. Eng. Struct. 2015, 85, 127–143. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, J. Hysteretic shear–flexure interaction model of reinforced concrete columns for seismic response assessment of bridges. Earthq. Eng. Struct. Dyn. 2011, 40, 315–337. [Google Scholar] [CrossRef]
- Munro, I.; Park, R.; Priestley, M.J.N. Seismic Behaviour of Reinforced Concrete Bridge Piers; Department of Civil Engineering, University of Canterbury: Christchurch, New Zealand, 1976; pp. 76–79. [Google Scholar]
- Siryo, K.K. A Seismic Analysis of Building Structural Members: A List of Experimental Results on Deformation Ability of Reinforced Concrete Columns Under Large Deflection (No. 3); Building Research Institute, Ministry of Construction: Tsukuba, Japan, 1978. [Google Scholar]
- Ghee, A.B.; Priestley, M.J.N.; Paulay, T. Seismic Shear Strength of Circular Reinforced Concrete Columns. ACI Struct. J. 1985, 86, 45–59. [Google Scholar]
- Ma, F.; Zhang, H.; Bockstedte, A.; Foliente, G.C.; Paevere, P. Parameter analysis of the differential model of hysteresis. J. Appl. Mech. 2004, 71, 342–349. [Google Scholar] [CrossRef]
- Cai, G.; Sun, Y.; Takeuchi, T.; Takeuchi, T.; Zhang, J. Proposal of a complete seismic shear strength model for circular concrete columns. Eng. Struct. 2015, 100, 399–409. [Google Scholar] [CrossRef]
- Azadi Kakavand, M.R.; Allahvirdizadeh, R. Enhanced empirical models for predicting the drift capacity of less ductile RC columns with flexural, shear, or axial failure modes. Front. Struct. Civ. Eng. 2019, 13, 1251–1270. [Google Scholar] [CrossRef]
- Ang, B.G. Seismic Shear Strength of Circular Bridge Piers. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1985. [Google Scholar]
- Setzler, E.J.; Sezen, H. Model for the lateral behavior of reinforced concrete columns including shear deformations. Earthq. Spectra 2008, 24, 493–511. [Google Scholar] [CrossRef]
- Ma, Y. Study on Failure Modes and Seismic Behavior of Reinforced Concrete Columns. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
- Mullapudi, T.R.S.; Ayoub, A. Analysis of reinforced concrete columns subjected to combined axial, flexure, shear, and torsional loads. J. Struct. Eng. 2013, 139, 561–573. [Google Scholar] [CrossRef]
- Xu, J.; Feng, D.; Wu, G.; Demitrios, M.C.; Lu, Y. Analytical modeling of corroded RC columns considering flexure-shear interaction for seismic performance assessment. Bull. Earthq. Eng. 2020, 18, 2165–2190. [Google Scholar] [CrossRef]
- Ling, Y.; Mogili, S.; Hwang, S. Parameter optimization for Pivot hysteresis model for reinforced concrete columns with different failure modes. Earthq. Eng. Struct. Dyn. 2022, 51, 2167–2187. [Google Scholar] [CrossRef]
- Yi, W.; Liu, Y.; Zhou, Y. Behavior of reinforced concrete columns under different loading histories. In Proceedings of the 12th International Symposium on Structural Engineering, Wuhan, China, 16 November 2012. [Google Scholar]
- Zhang, Q.; Gong, J.; Ma, Y. Seismic shear strength and deformation of RC columns failed in flexural shear. Mag. Concr. Res. 2014, 66, 234–248. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, M.; Gu, X.; Li, Y.; Li, W.; Gong, J. Low-Cycle Fatigue Properties and Model for Flexure-Shear Critical Reinforced Concrete Columns Considering Cyclic Damage Effects. J. Struct. Eng. 2024, 150, 04024071. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, J.; Zhang, Q.; Han, S. Equivalent damping ratio model of flexure-shear critical RC columns. Eng. Struct. 2017, 130, 52–66. [Google Scholar] [CrossRef]
- Zhu, J.; Tang, G. Experimental investigation and load-deformation analysis of reinforced concrete bridge columns under various loading cycles. Structures 2023, 49, 570–582. [Google Scholar] [CrossRef]
- Ozcebe, G.; Saatcioglu, M. Hysteretic shear model for reinforced concrete members. J. Struct. Eng. 1989, 115, 132–148. [Google Scholar] [CrossRef]
- Takayanagi, T.; Schnobrich, W.C. Computed Behavior of Reinforced Concrete Coupled Shear Walls; Civil Engineering Studies, University of Illinois, Urbana: Champaign, IL, USA, 1976; pp. 60–97. [Google Scholar]
- Sezen, H.; Chowdhury, T. Hysteretic model for reinforced concrete columns including the effect of shear and axial load failure. J. Struct. Eng. 2009, 135, 139–146. [Google Scholar] [CrossRef]
- Lee, D.H.; Elnashai, A.S. Seismic analysis of RC bridge columns with flexure-shear interaction. J. Struct. Eng. 2001, 127, 546–553. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, S. Hysteretic Model for flexure-shear critical reinforced concrete columns. J. Earthq. Eng. 2018, 22, 1639–1661. [Google Scholar] [CrossRef]
- Sae-Long, W.; Limkatanyu, S.; Hansapinyo, C.; Imjai, T.; Kwon, M. Forced-based shear-flexure-interaction frame element for nonlinear analysis of non-ductile reinforced concrete columns. J. Appl. Comput. Mech. 2020, 6, 1151–1167. [Google Scholar]
- Sae-Long, W.; Limkatanyu, S.; Panedpojaman, P.; Prachasaree, W.; Damrongwiriyanupap, N.; Kwon, M.; Hansapinyo, C. Nonlinear Winkler-based frame element with inclusion of shear-flexure interaction effect for analysis of non-ductile RC members on foundation. J. Appl. Comput. Mech. 2021, 7, 148–164. [Google Scholar]
- Limkatanyu, S.; Sae-Long, W.; Damrongwiriyanupap, N.; Imjai, T.; Chaimahawan, P.; Sukontasukkul, P. Shear-flexure interaction frame model on Kerr-type foundation for analysis of non-ductile RC members on foundation. J. Appl. Comput. Mech. 2022, 8, 1076–1090. [Google Scholar]
- Limkatanyu, S.; Sae-Long, W.; Damrongwiriyanupap, N.; Sukontasukkul, P.; Imjai, T.; Chompoorat, T.; Hansapinyo, C. Nonlinear shear-flexure-interaction RC frame element on Winkler-Pasternak foundation. Geomech. Eng. 2023, 32, 69–84. [Google Scholar]
- Pacific Earthquake Engineering Research Center (PEER) Structural Performance Database. Available online: https://peer.berkeley.edu/spd (accessed on 20 February 2025).
- Priestley, M.J.N.; Benzoni, G. Seismic performance of circular columns with low longitudinal reinforcement ratios. ACI Struct. J. 1996, 93, 474–485. [Google Scholar]
- Vu, N.D.; Priestley, M.J.N.; Seible, F.; Benzoni, G. Seismic response of well confined circular reinforced concrete columns with low aspect ratios. In Proceedings of the 5th Caltrans Seismic Research Workshop, San Diego, CA, USA, 9–11 June 1998. [Google Scholar]
- Hamilton, C.H.; Pardoen, G.C.; Kazanjy, R.P. Experimental Testing of Bridge Columns Subjected to Reversed-Cyclic and Pulse-Type Loading Histories; Technical Report; Department of Civil and Environmental Engineering, University of California: Irvine, CA, USA, 2002. [Google Scholar]
- Baber, T.T.; Noori, M.N. Random vibration of degrading, pinching systems. J. Eng. Mech. 1985, 111, 1010–1026. [Google Scholar] [CrossRef]
- Erberik, M.A. Fragility-based assessment of typical mid-rise and low-rise RC buildings in Turkey. Eng. Struct. 2008, 30, 1360–1374. [Google Scholar] [CrossRef]
- Takeda, T.; Sozen, M.A.; Nielsen, N.N. Reinforced concrete response to simulated earthquakes. J. Struct. Div. 1970, 96, 2557–2573. [Google Scholar] [CrossRef]
- Montuori, R.; Nastri, E.; Palese, M.I.; Piluso, V. Comparison among different software for the evaluation of moment-curvature of RC columns. Comput. Concr. 2019, 24, 259–269. [Google Scholar]
- An, D.; Qin, Z.; Yang, Y.; Yu, X.; Li, C. Hybrid Compensation Method for Non-Uniform Creep Difference and Hysteresis Nonlinearity of Piezoelectric-Actuated Machine Tools Under S-Shaped Curve Trajectory. Appl. Sci. 2025, 15, 4207. [Google Scholar] [CrossRef]
- Lu, Y.; Xiong, F.; Zhong, J. Uniaxial hysteretic spring models for static and dynamic analyses of self-centering rocking shallow foundations. Eng. Struct. 2022, 272, 114995. [Google Scholar] [CrossRef]
- Chen, P.; Bai, X.; Qian, L.; Choi, S.B. A new hysteresis model based on force–displacement characteristics of magnetorheological fluid actuators subjected to squeeze mode operation. Smart Mater. Struct. 2017, 26, 06LT01. [Google Scholar] [CrossRef]
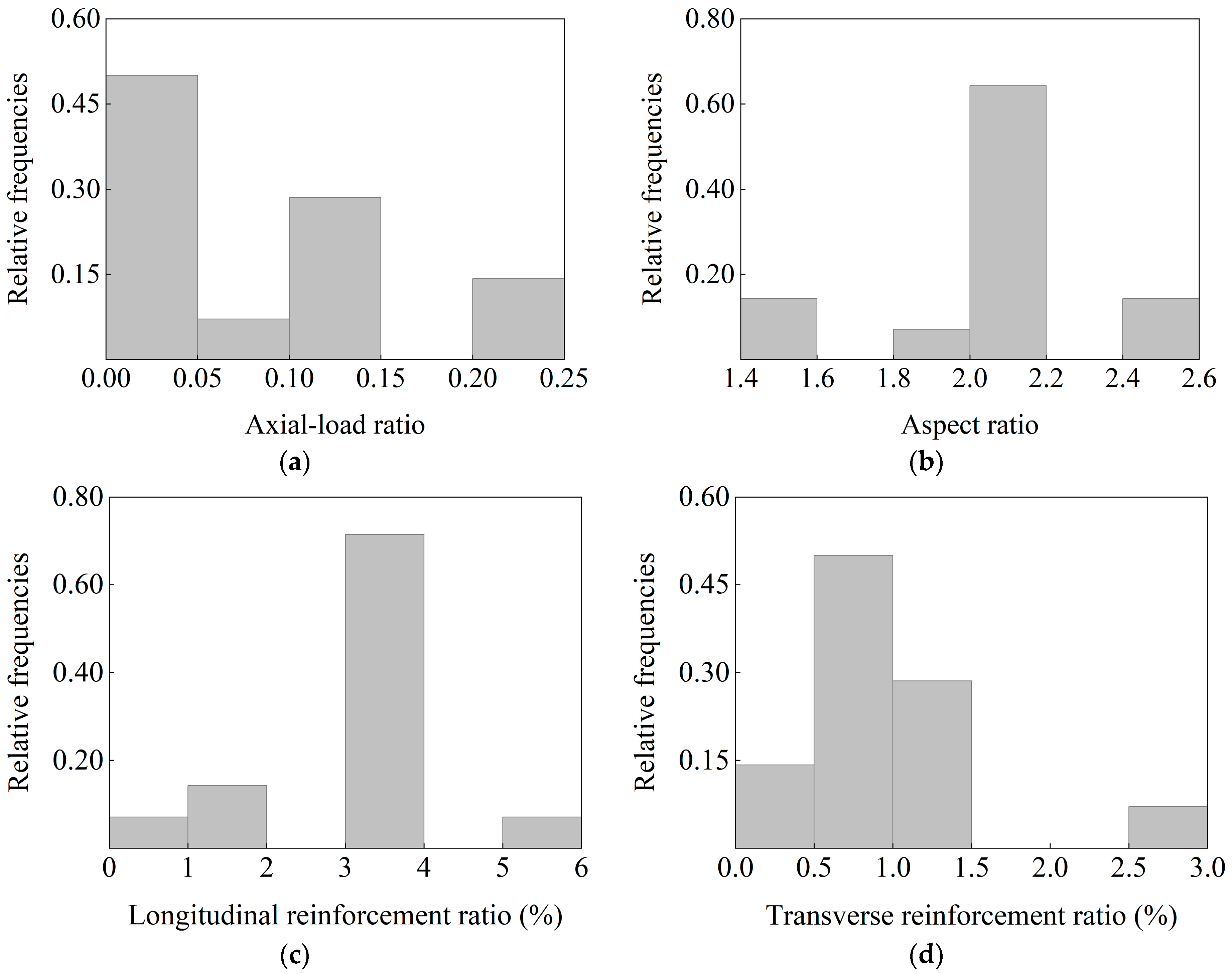














| Test Number | Experimenters | Column Designation | D (mm) | H (mm) | N (kN) | n | λ | fc’ (MPa) | LRR (%) | TRR (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Ghee et al. (1985) [11] | No. 1 | 400 | 800 | 0 | 0 | 2 | 37.5 | 3.2 | 0.51 |
| 2 | Ghee et al. (1985) [11] | No. 5 | 400 | 800 | 0 | 0 | 2 | 31.1 | 3.2 | 0.76 |
| 3 | Ghee et al. (1985) [11] | No. 8 | 400 | 800 | 721 | 0.2 | 2 | 28.7 | 3.2 | 1.02 |
| 4 | Ghee et al. (1985) [11] | No. 10 | 400 | 800 | 784 | 0.2 | 2 | 31.2 | 3.2 | 1.02 |
| 5 | Ghee et al. (1985) [11] | No. 12 | 400 | 600 | 359 | 0.1 | 1.5 | 28.6 | 3.2 | 1.02 |
| 6 | Ghee et al. (1985) [11] | No. 13 | 400 | 800 | 455 | 0.1 | 2 | 36.2 | 3.2 | 1.02 |
| 7 | Ghee et al. (1985) [11] | No. 14 | 400 | 800 | 0 | 0 | 2 | 33.7 | 3.2 | 0.51 |
| 8 | Ghee et al. (1985) [11] | No. 15 | 400 | 800 | 0 | 0 | 2 | 34.8 | 1.9 | 0.51 |
| 9 | Ghee et al. (1985) [11] | No. 17 | 400 | 1000 | 431 | 0.1 | 2.5 | 34.3 | 3.2 | 0.51 |
| 10 | Ghee et al. (1985) [11] | No. 23 | 400 | 800 | 0 | 0 | 2 | 32.3 | 3.2 | 0.76 |
| 11 | Ghee et al. (1985) [11] | No. 24 | 400 | 800 | 0 | 0 | 2 | 33.1 | 3.2 | 0.77 |
| 12 | Priestley et al. (1994) [36] | NR1 | 610 | 914.5 | 503 | 0.057 | 1.5 | 30 | 0.5 | 0.28 |
| 13 | Vu et al. (1998) [37] | NH4 | 457 | 910 | 850 | 0.148 | 1.99 | 35 | 5.2 | 2.7 |
| 14 | Hamilton (2002) [38] | UC15 | 406.4 | 1047.8 | 0 | 0 | 2.58 | 35.4 | 1.2 | 0.26 |
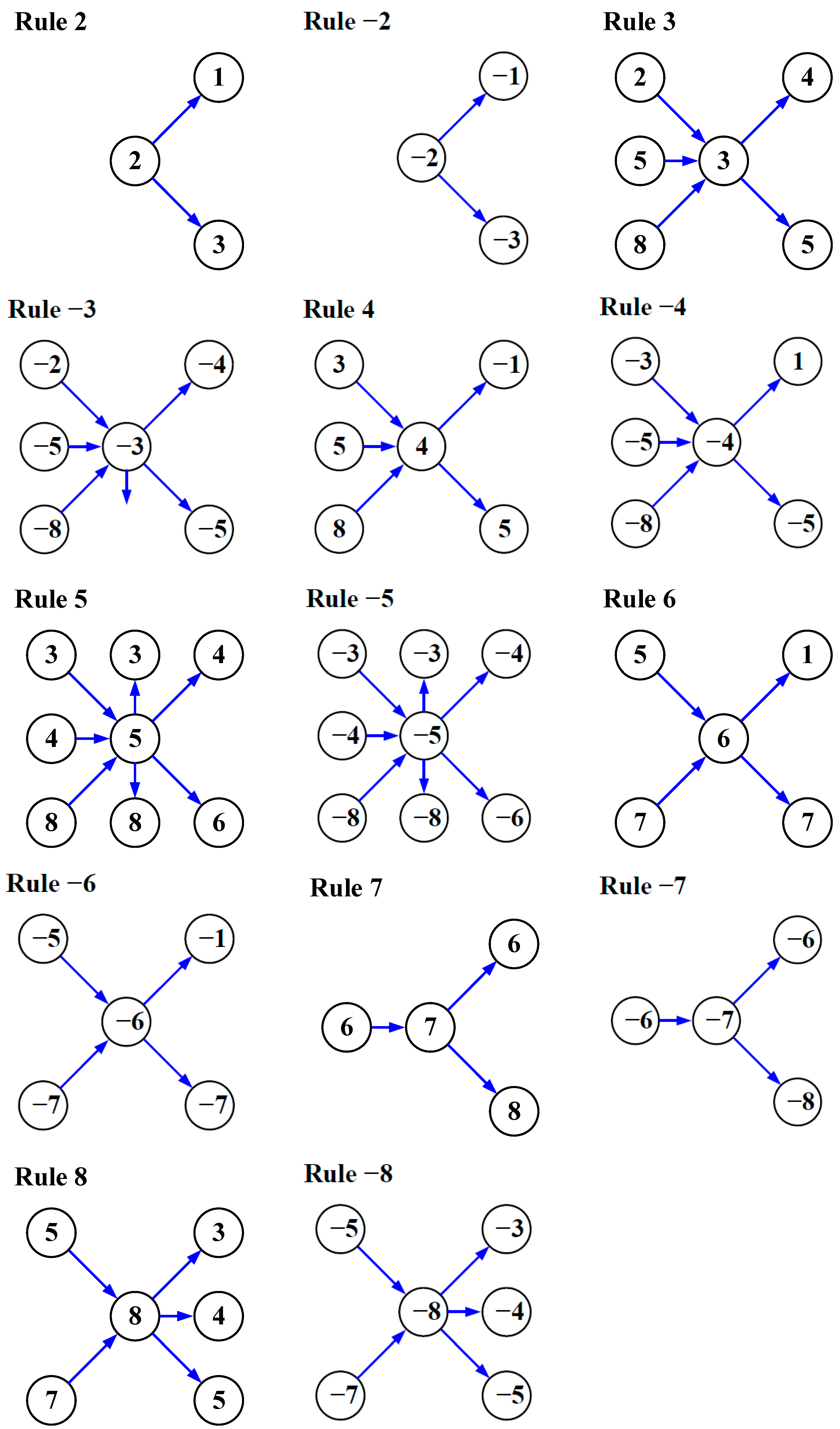
| Rule | Stage | Loading | Unloading |
|---|---|---|---|
| 0 | Elastic | Condition: d > dy Toward: 1 Stiffness: S(YU) | Condition: Δd < 0 Toward: 0 Stiffness: S(OY) |
| 1 | Primary curve up to yielding | Condition: Δd > 0 Toward: 1 Stiffness: S(YU) | Condition: Δd < 0 Toward: 2 Stiffness: S(UR) |
| 2 | Unloading from point U on primary curve | Condition: d > Dmax Toward: 1 Stiffness: S(YU) | Condition: F < 0 Toward: 3 Stiffness: S(RP) |
| 3 | Reloading toward pinching point P | Condition: d < Dp Toward: 4 Stiffness: S(PY–) | Condition: Δd > 0 Toward: 5 Stiffness: S(UR) |
| 4 | Reloading toward yielding point Y– | Condition: d < –dy Toward: –1 Stiffness: S(Y–U–) | Condition: Δd > 0 Toward: 5 Stiffness: S(UR) |
| 5 | Unloading from line RP or PY– | Condition: [d > Du1 & Du1 > Dp] or [d > Du2 & Du2 < Dp] Toward: 3 or 4 Stiffness: S(RP) or S(PY–) | Condition: F > 0 Toward: 6 Stiffness: S(QPd) |
| 6 | Loading toward strength degradation point Pd | Condition: F > Fdmax Toward: 1 Stiffness: S(YU) | Condition: Δd < 0 Toward: 7 Stiffness: S(UR) |
| 7 | Unloading from small amplitude cycles | Condition: d > Du1 Toward: 6 Stiffness: S(QPd) | Condition: F < 0 Toward: 8 Stiffness: S(TU1) |
| 8 | Reloading from small amplitude cycles | Condition: [d < Du1 & Du1 > Dp] or [d < Du2 & du2 < Dp] Toward: 3 or 4 Stiffness: S(RP) or S(PY–) | Condition: Δd > 0 Toward: 5 Stiffness: S(UR) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Wang, J.; Huang, H.; Liang, W.; Zhou, Y.; Zhang, Q.; Gong, J. Hysteresis Model for Flexure-Shear Critical Circular Reinforced Concrete Columns Considering Cyclic Degradation. Buildings 2025, 15, 2445. https://doi.org/10.3390/buildings15142445
Feng Z, Wang J, Huang H, Liang W, Zhou Y, Zhang Q, Gong J. Hysteresis Model for Flexure-Shear Critical Circular Reinforced Concrete Columns Considering Cyclic Degradation. Buildings. 2025; 15(14):2445. https://doi.org/10.3390/buildings15142445
Chicago/Turabian StyleFeng, Zhibin, Jiying Wang, Hua Huang, Weiqi Liang, Yingjie Zhou, Qin Zhang, and Jinxin Gong. 2025. "Hysteresis Model for Flexure-Shear Critical Circular Reinforced Concrete Columns Considering Cyclic Degradation" Buildings 15, no. 14: 2445. https://doi.org/10.3390/buildings15142445
APA StyleFeng, Z., Wang, J., Huang, H., Liang, W., Zhou, Y., Zhang, Q., & Gong, J. (2025). Hysteresis Model for Flexure-Shear Critical Circular Reinforced Concrete Columns Considering Cyclic Degradation. Buildings, 15(14), 2445. https://doi.org/10.3390/buildings15142445






