Calculation of Shear-Bearing Capacity of Aluminum Alloy-Concrete Composite Beam
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
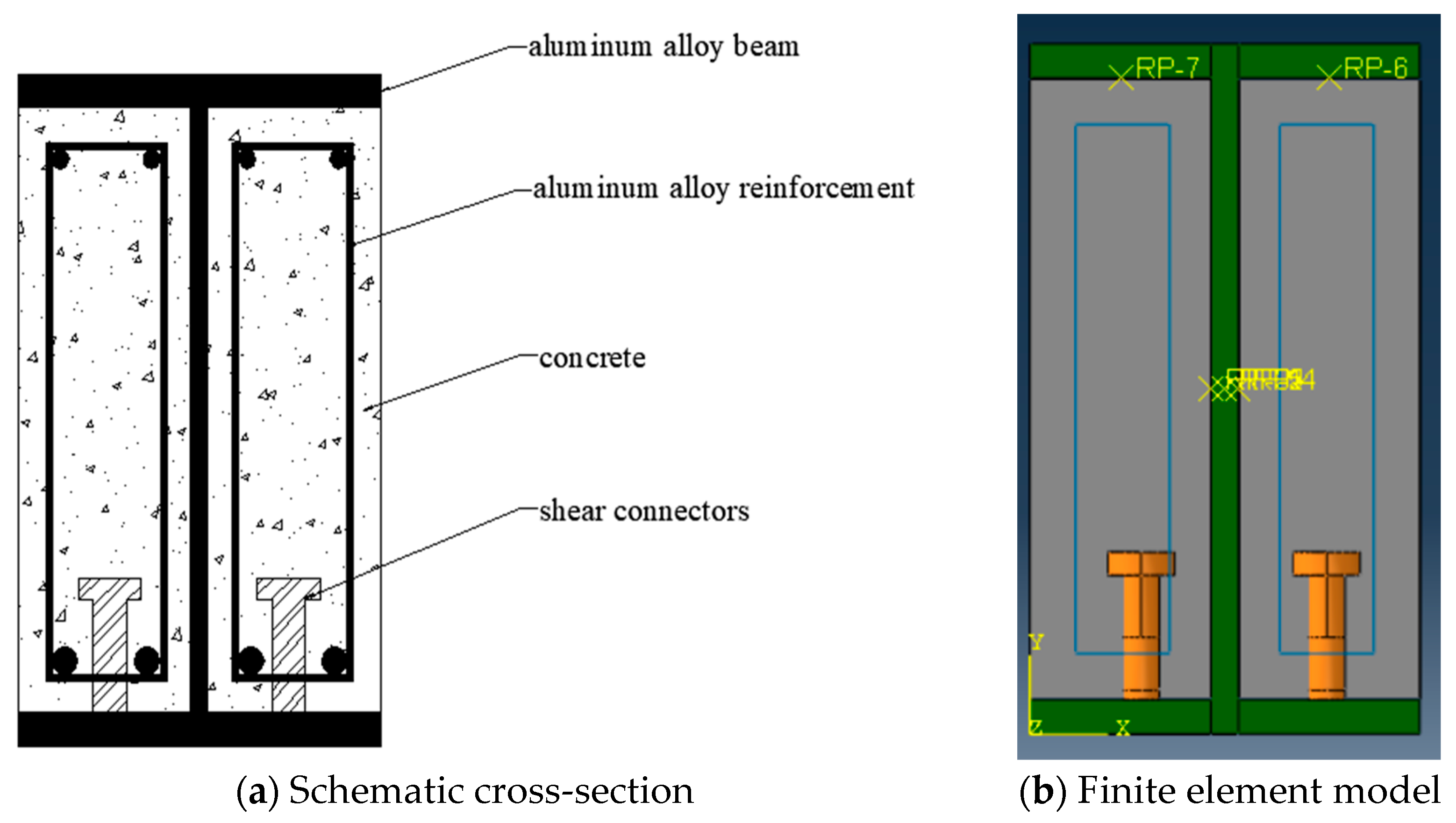
3.1. Modeling Method
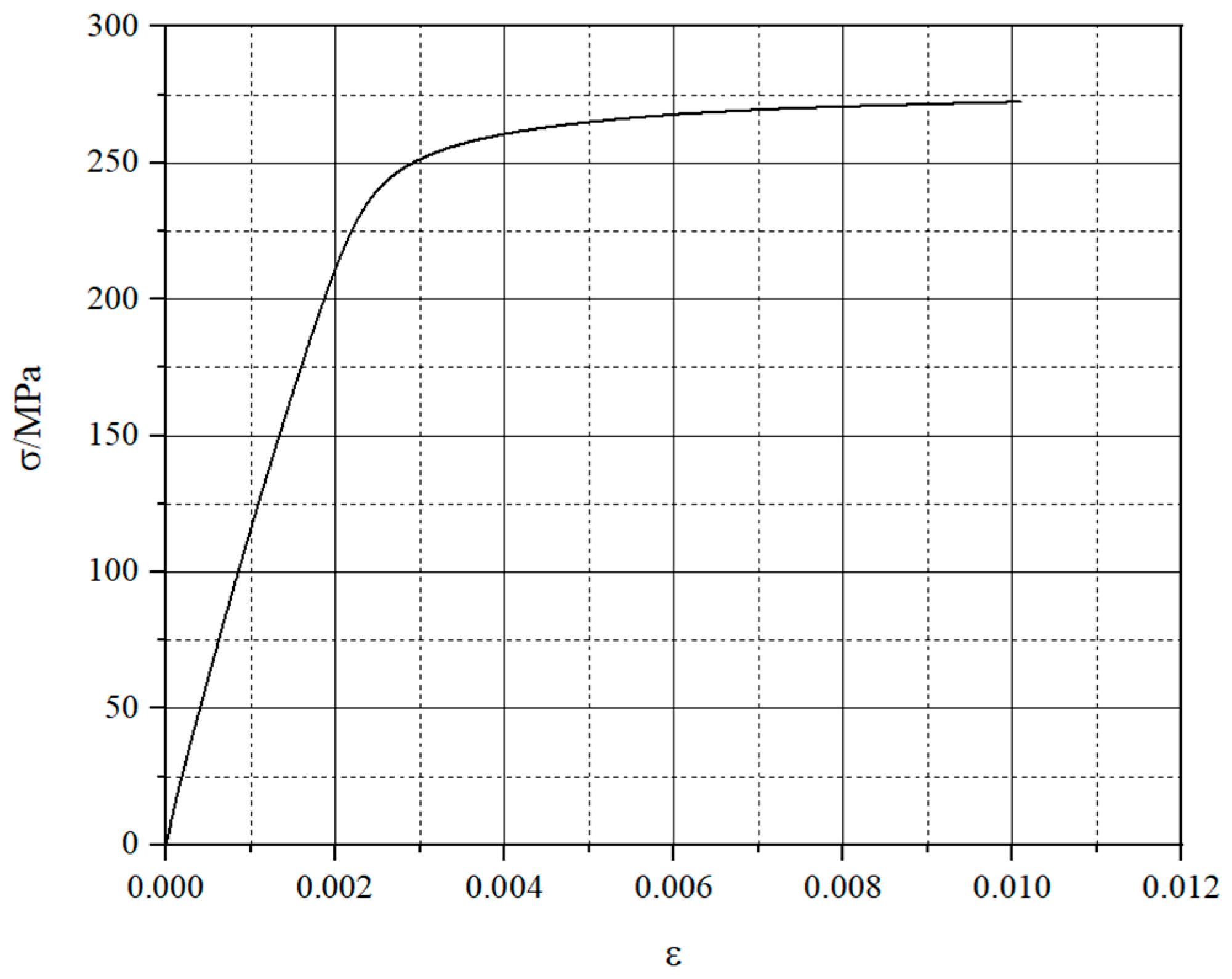
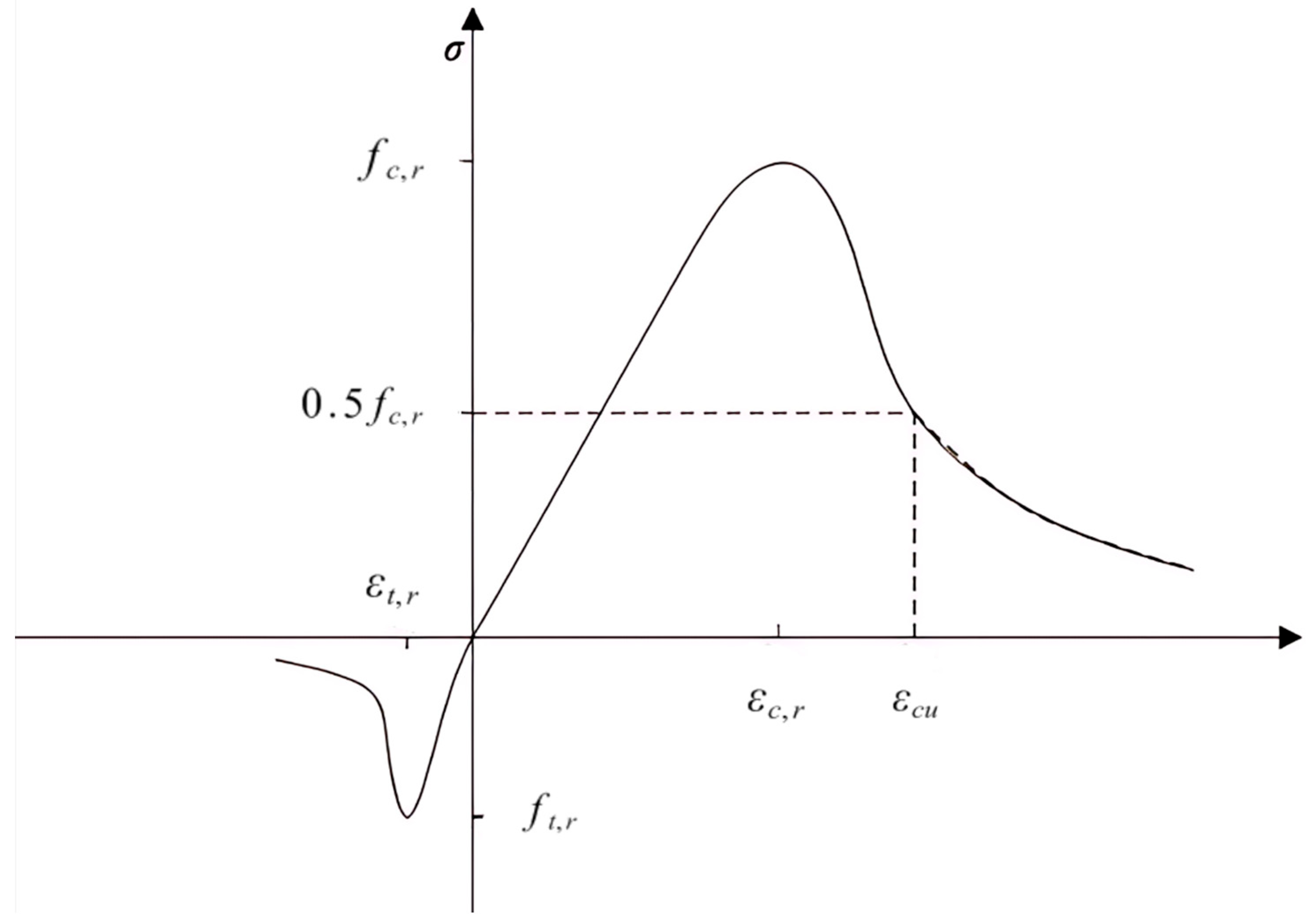
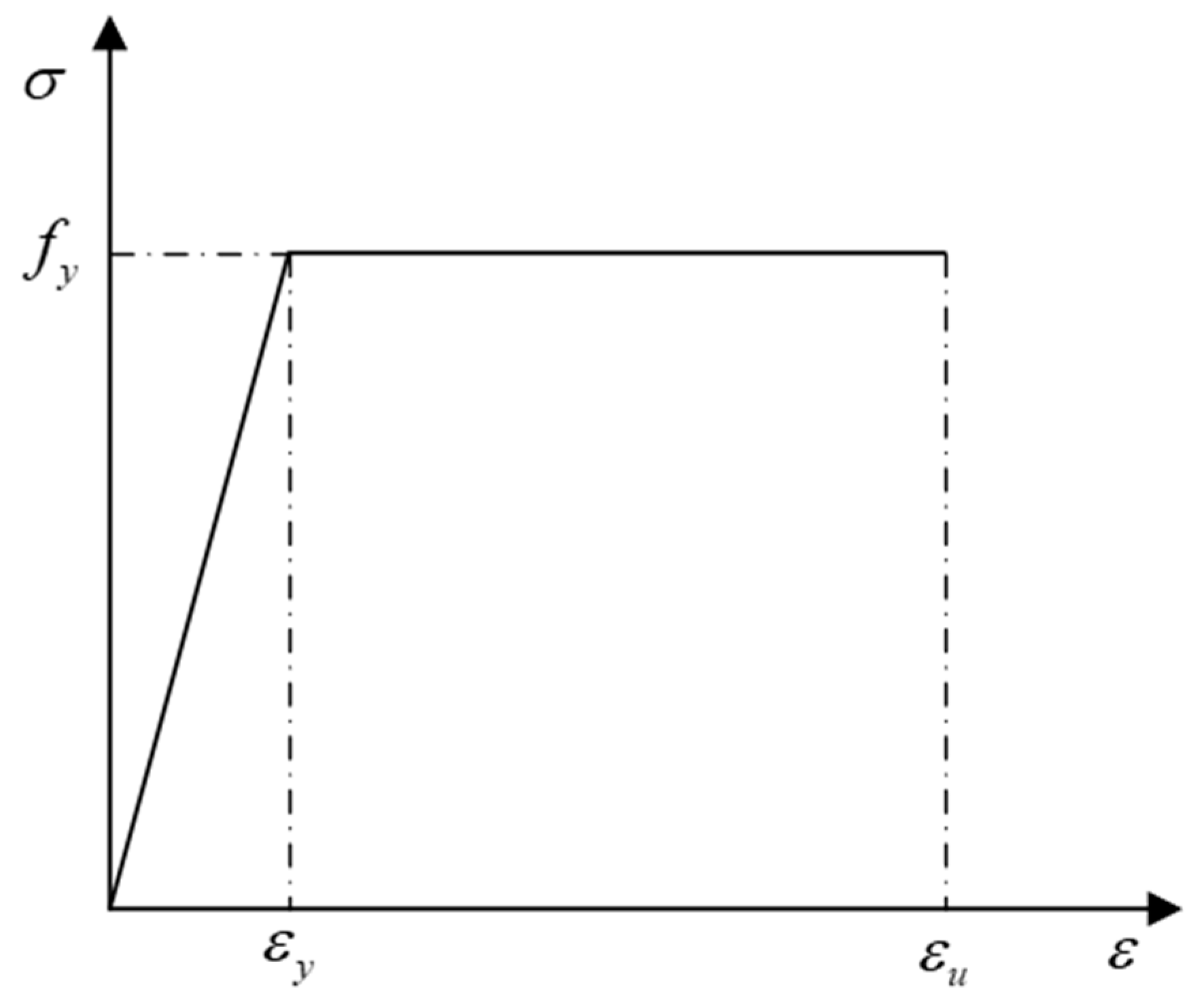
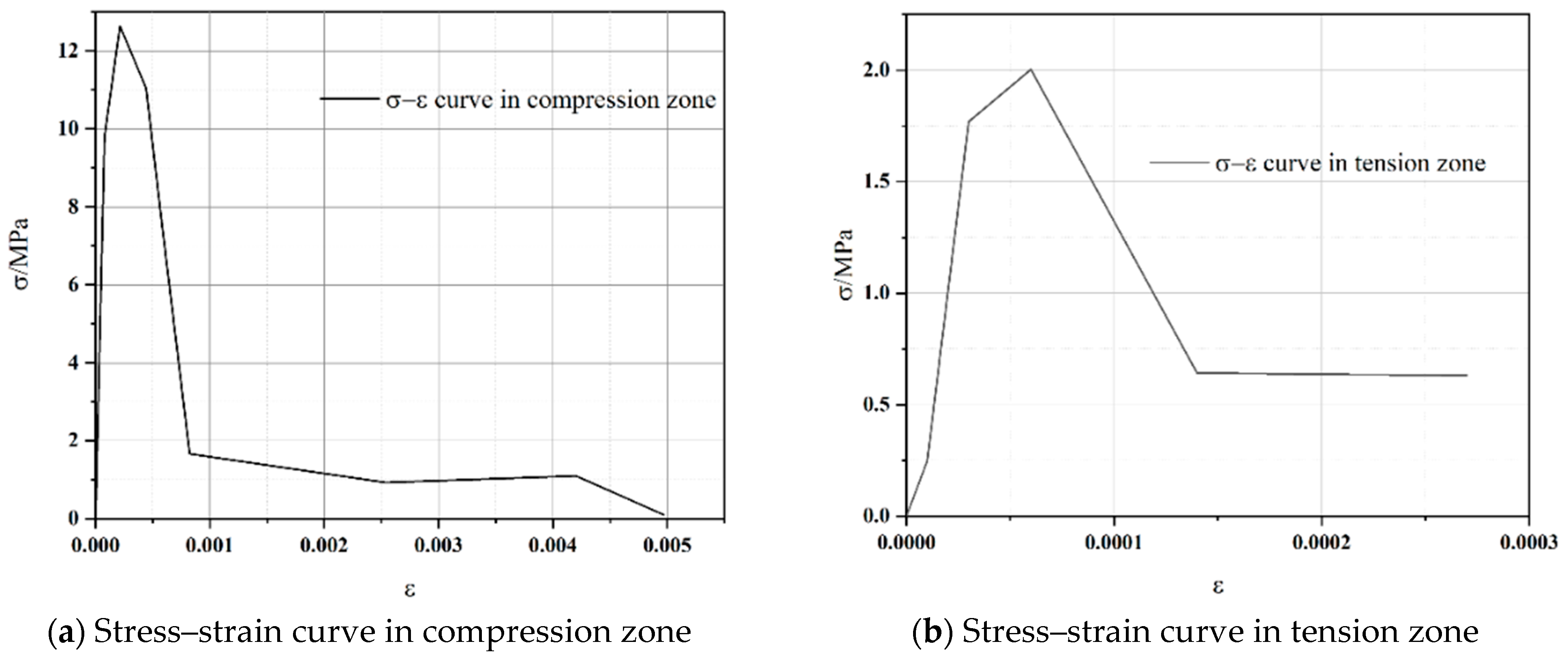
3.2. Constitutive Model
3.3. Parameter Analysis
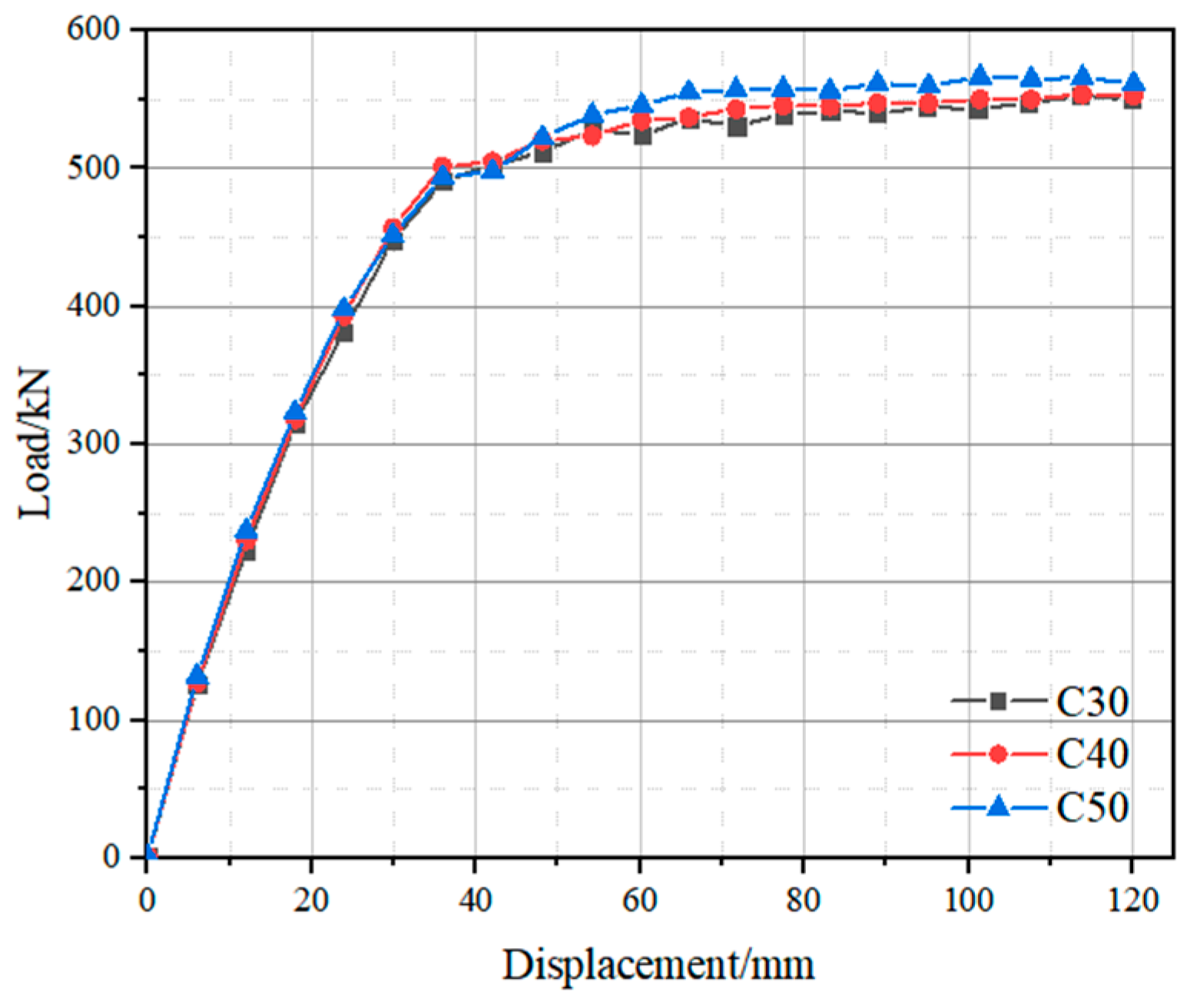
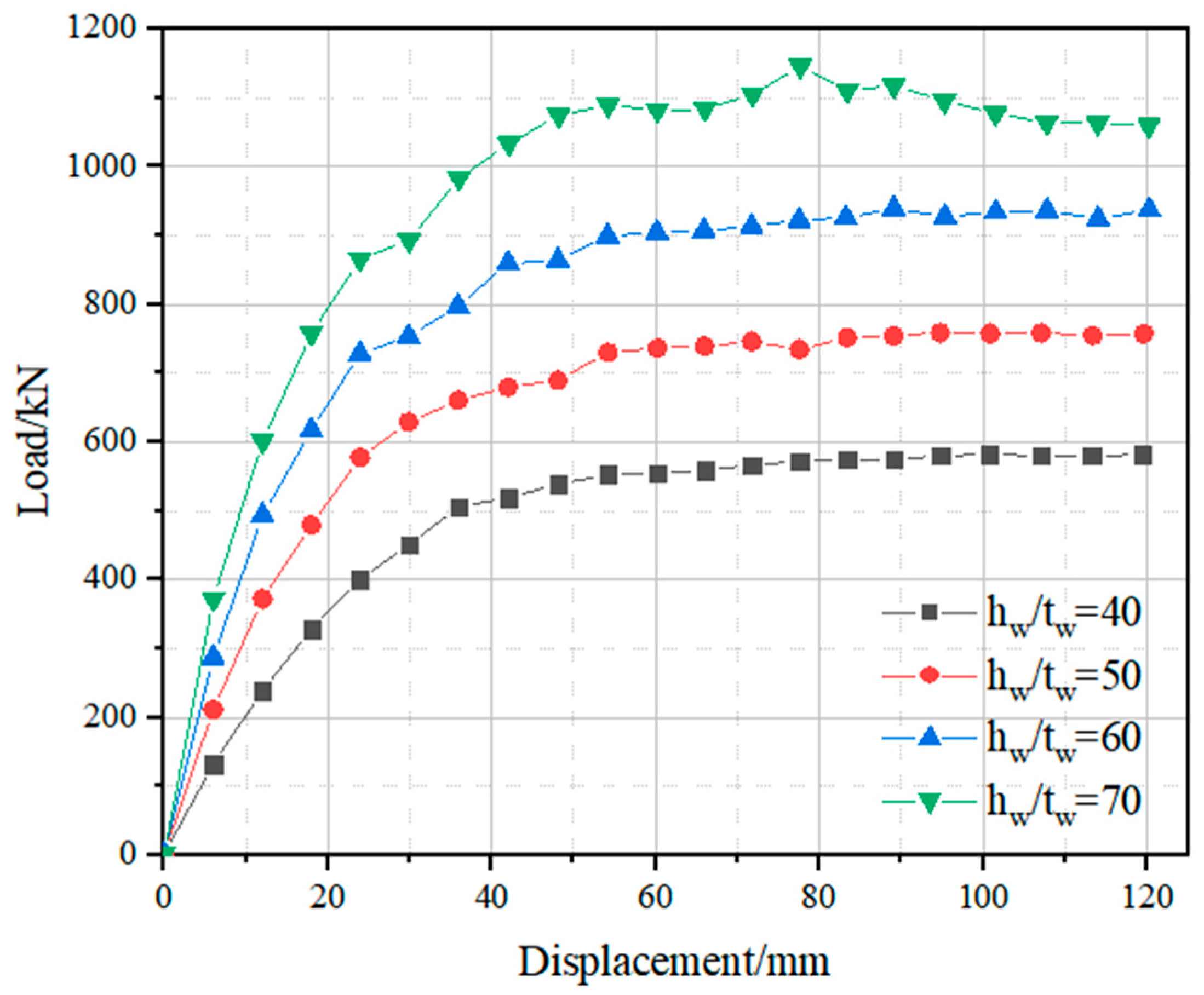
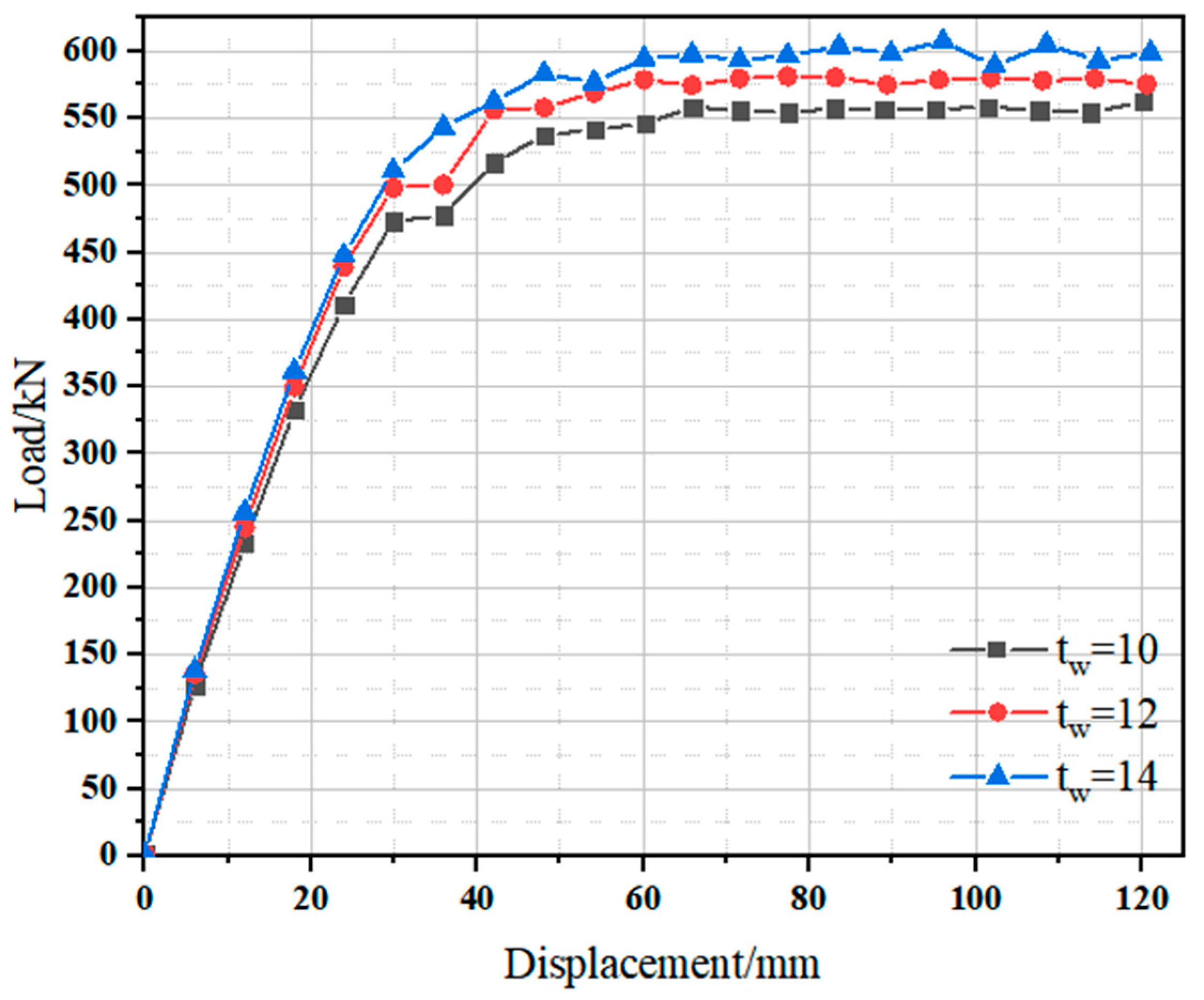
3.3.1. Material Strength and Geometric Dimension
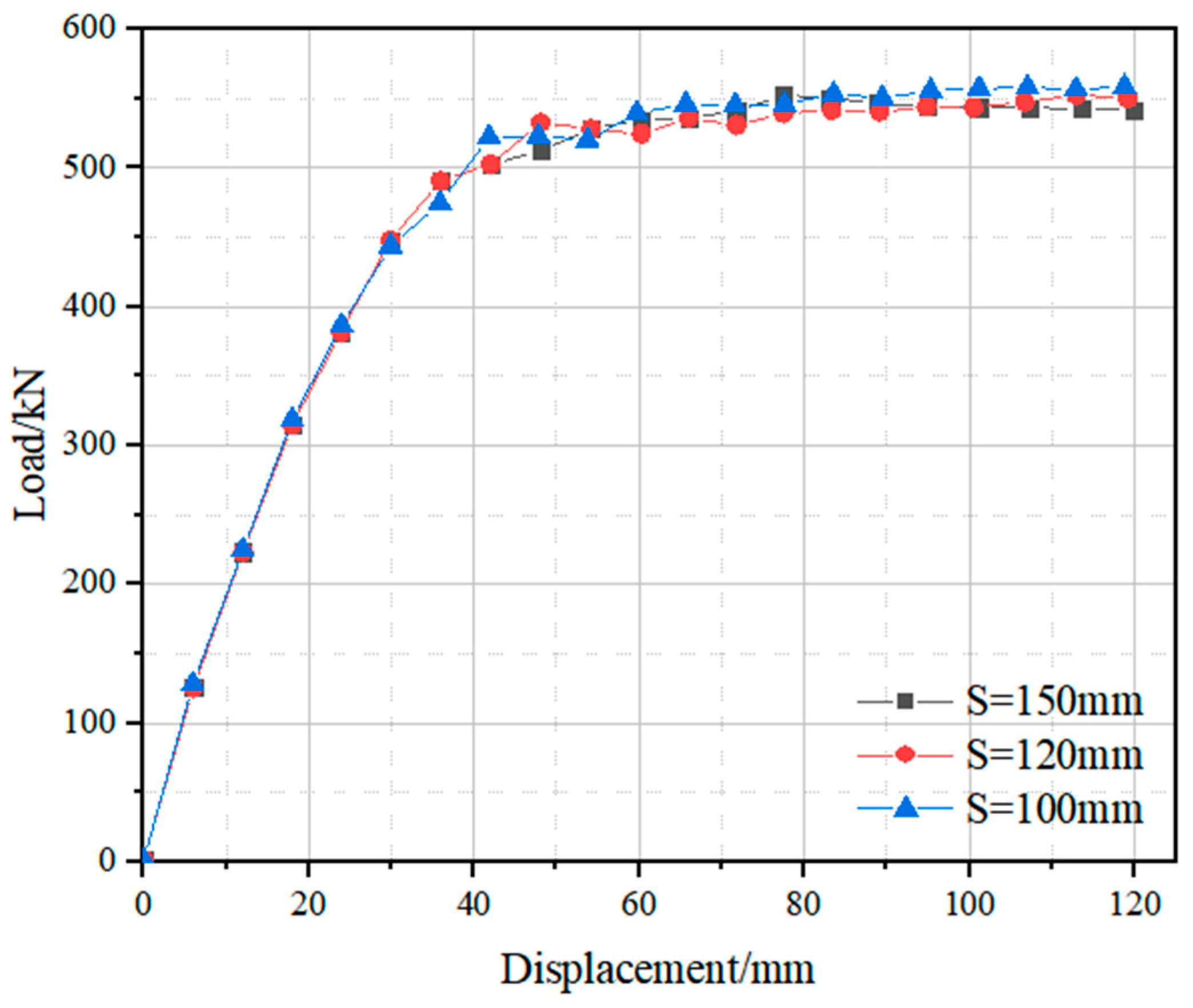
3.3.2. Stirrup Spacing
3.3.3. Shear Span Ratio
4. Numerical Results and Analysis
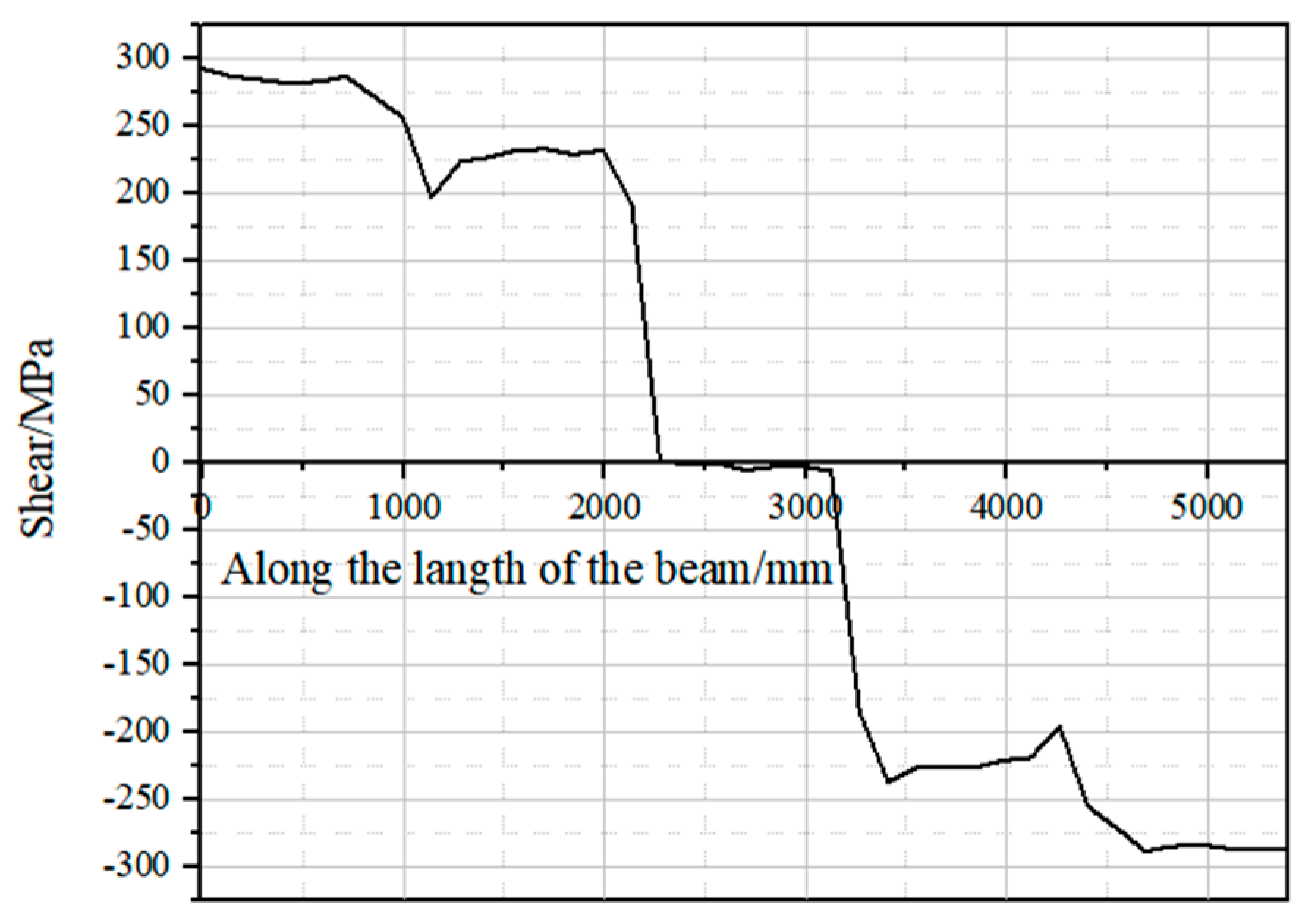
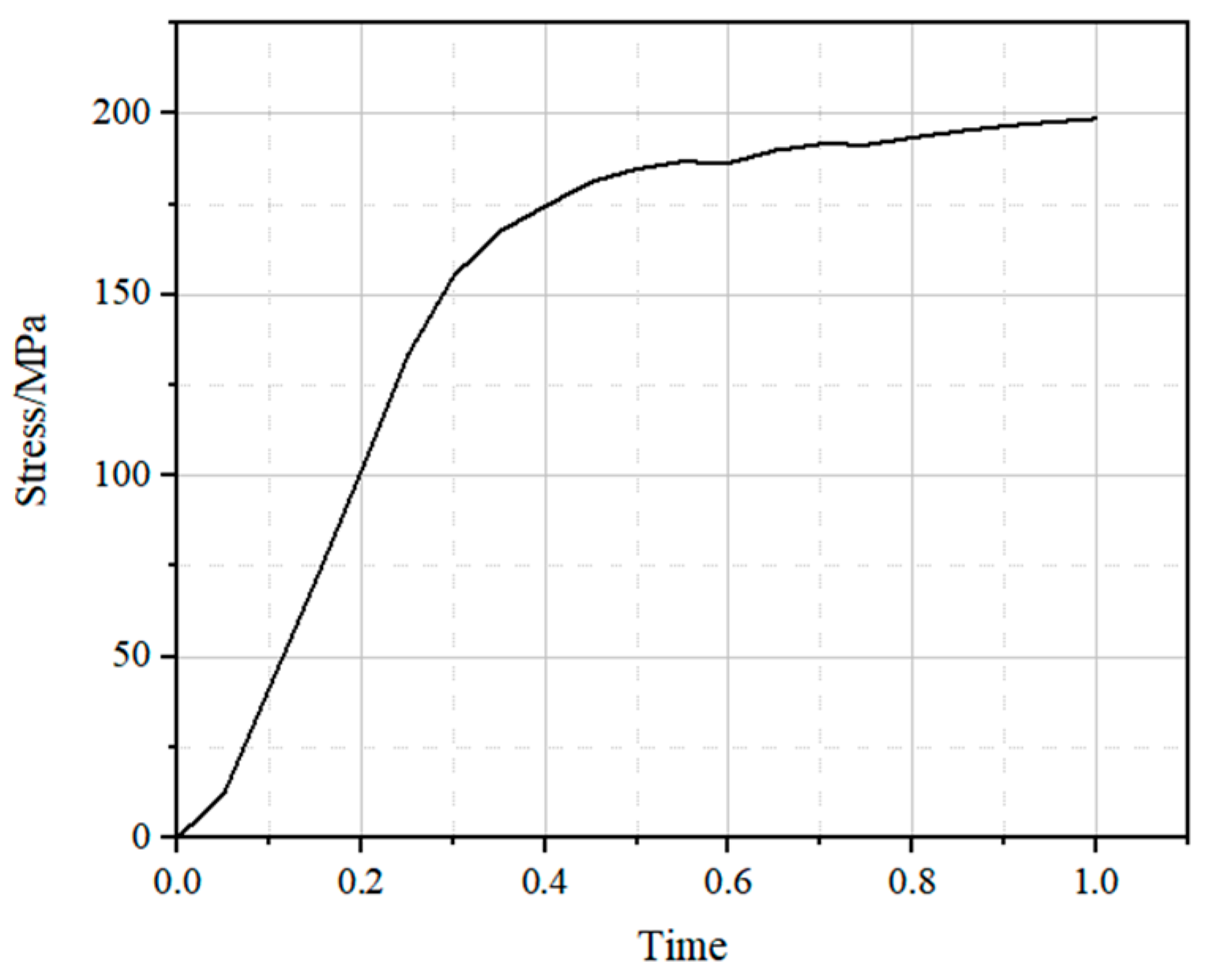
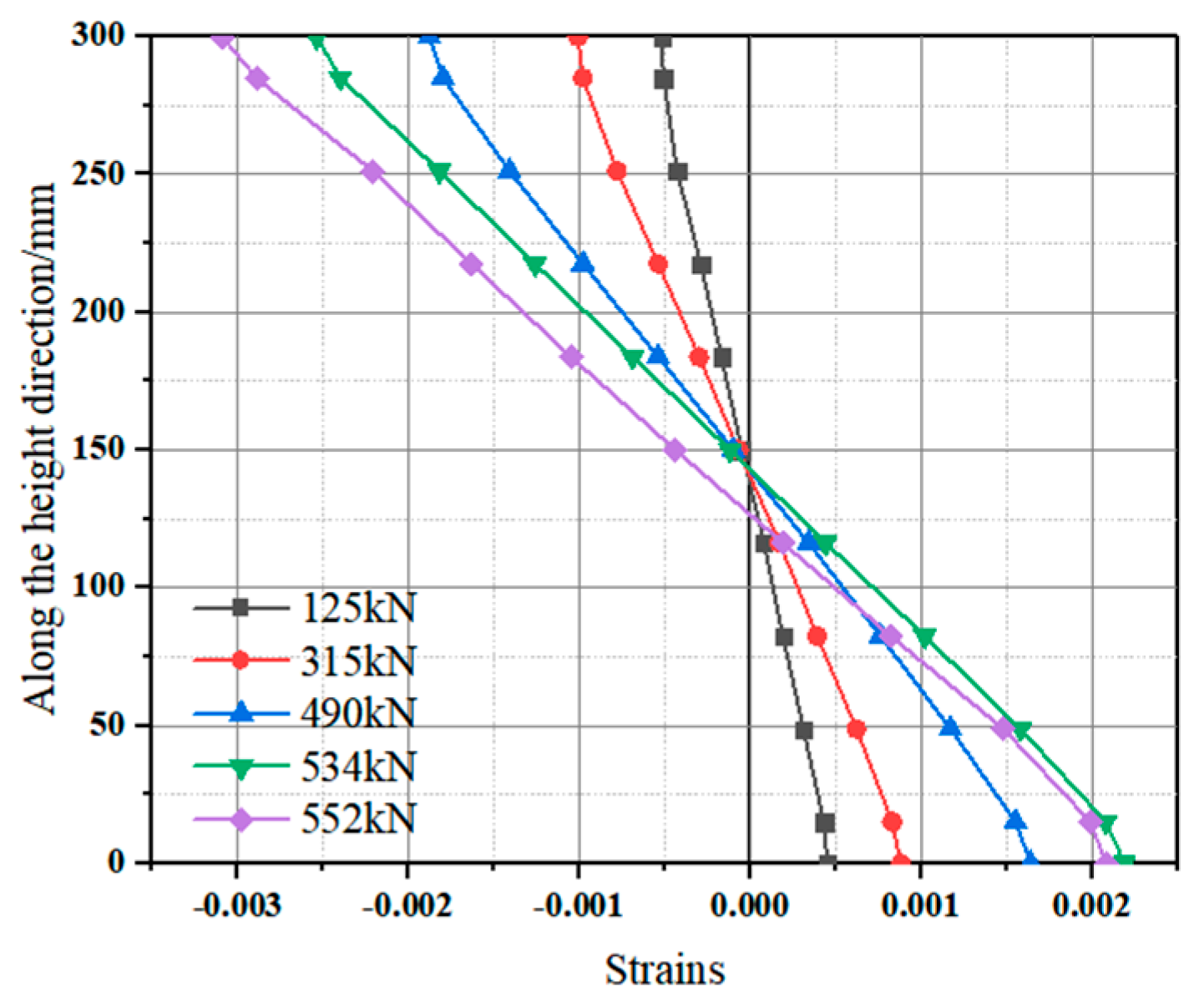
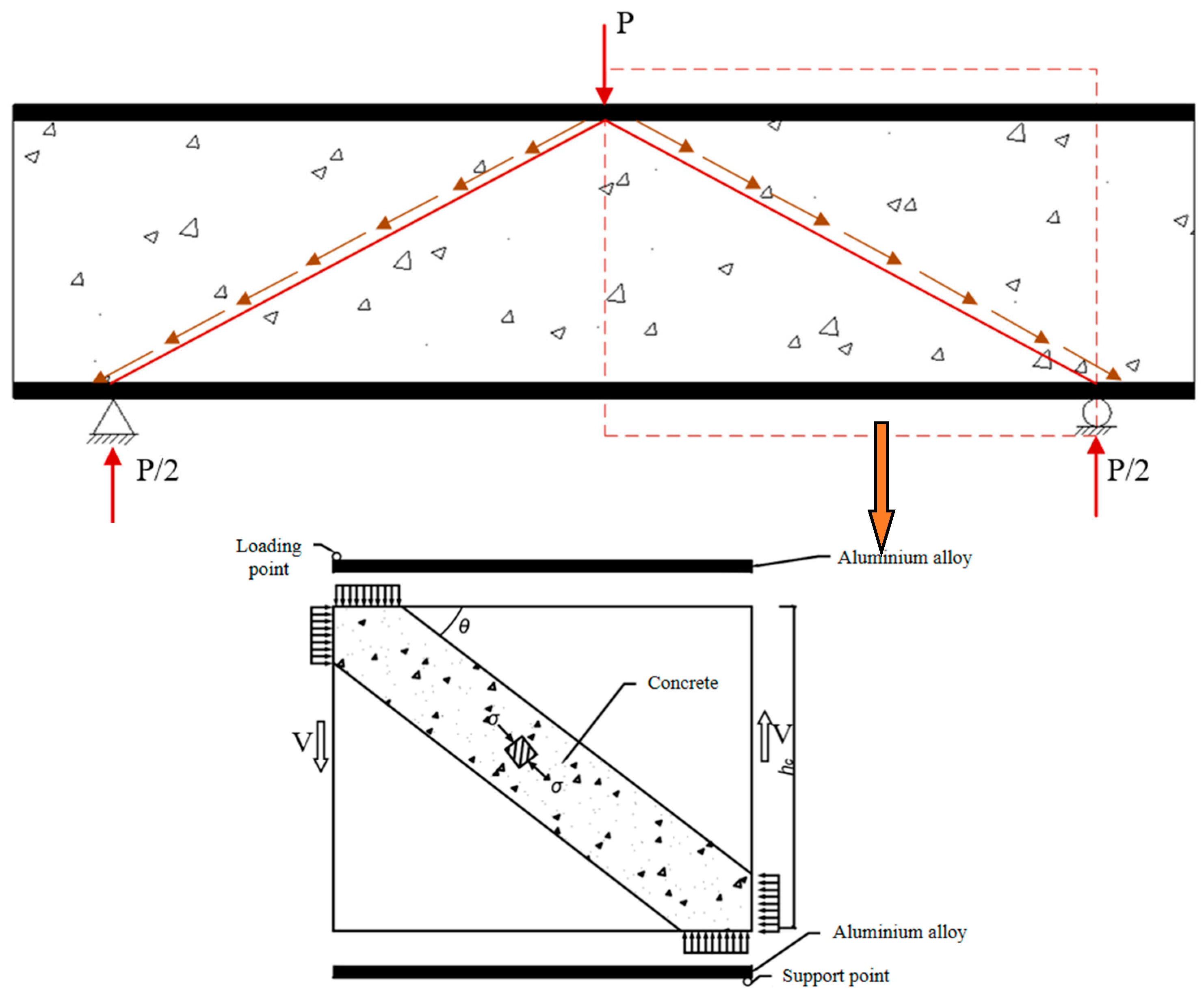
Shear Analysis of Aluminum Alloy-Concrete Composite Beam
- (1)
- Stress and strain analysis of the section
- (2)
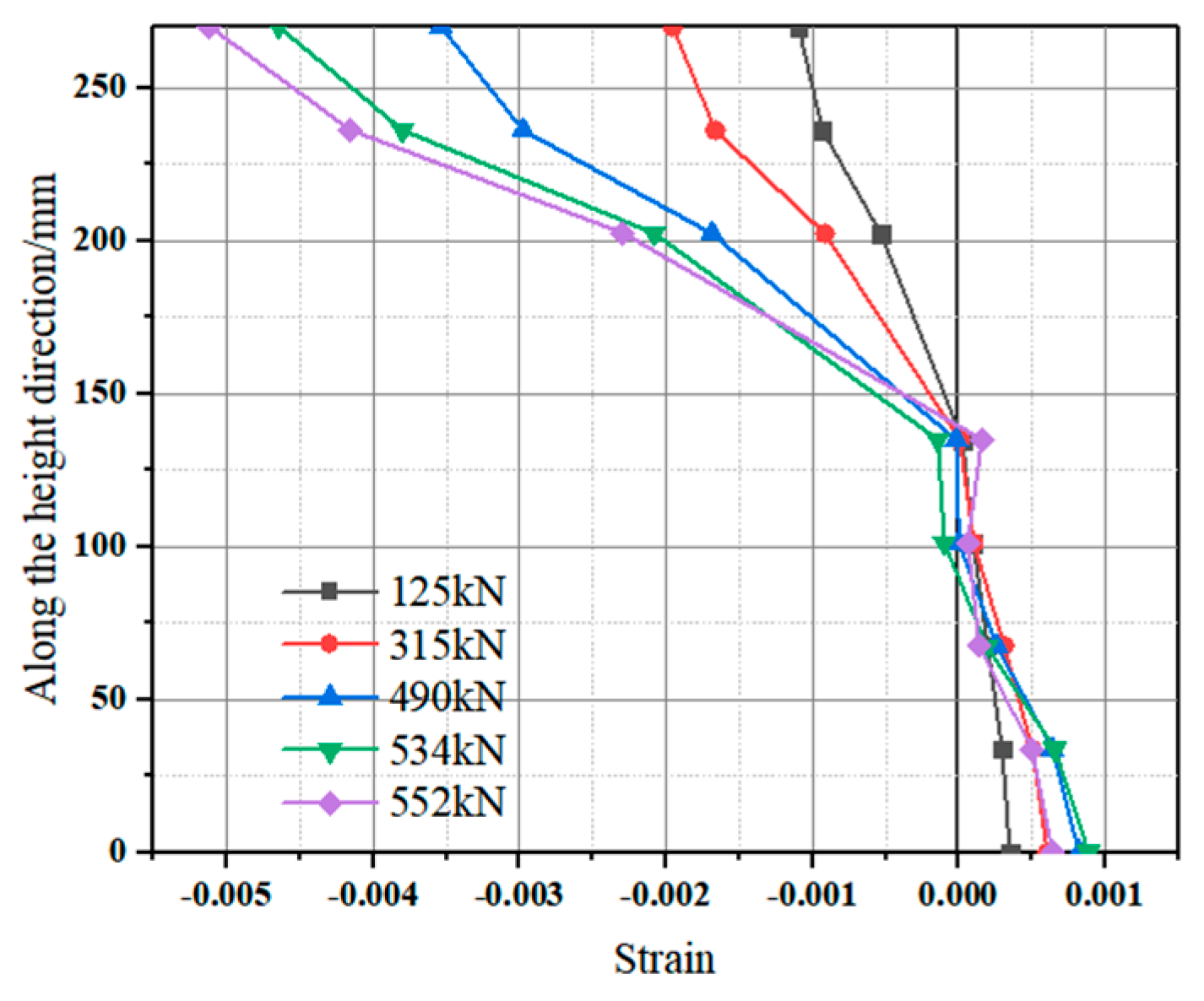
- Load strain analysis
5. Theoretical Derivation and Validation
5.1. Derivation of Shear Bearing Capacity Calculation Formula of Aluminum Alloy-Concrete Composite Beam
5.2. Derivation and Verification of Shear Bearing Capacity Calculation Formula of Aluminum Alloy-Concrete Composite Beam
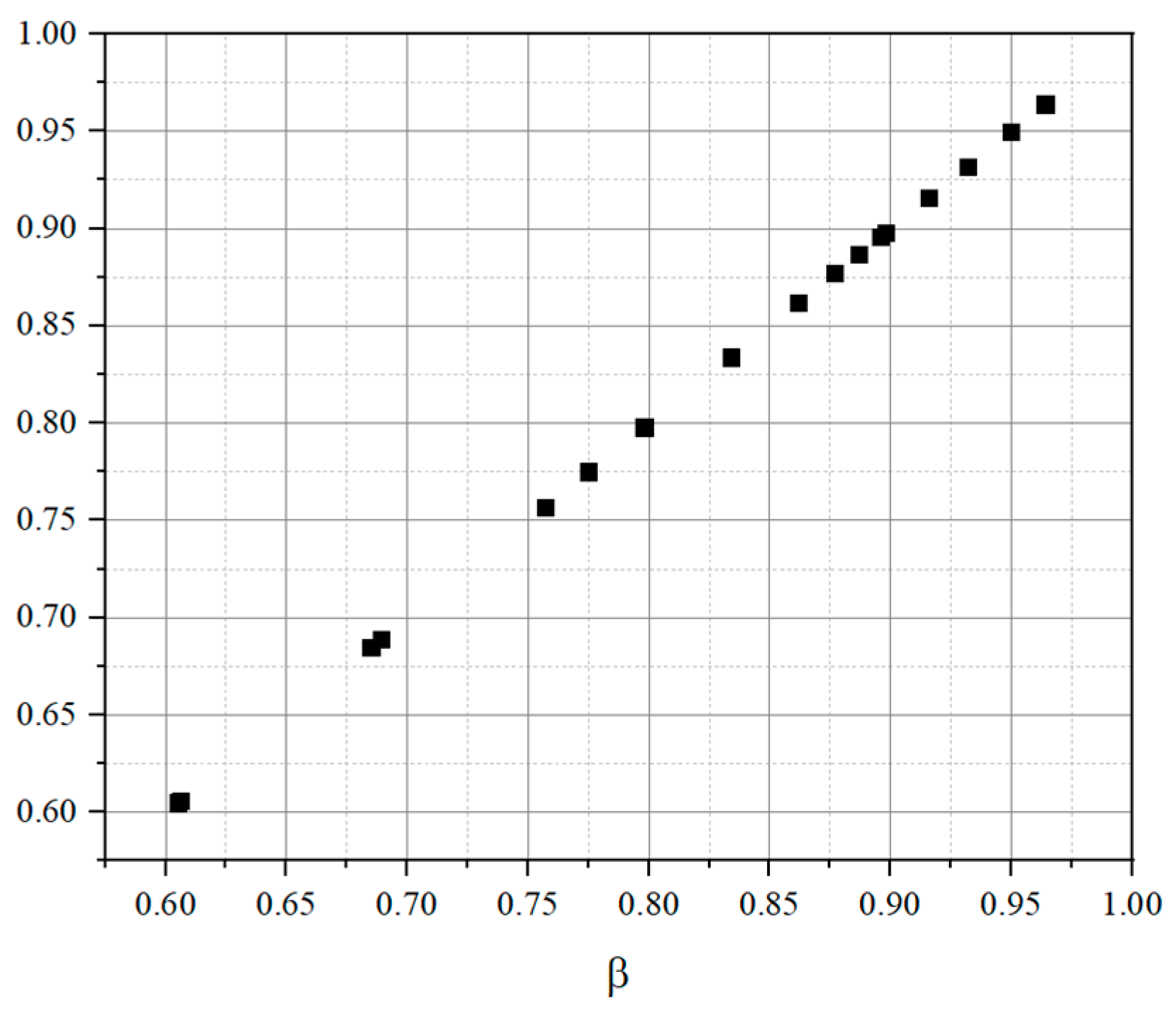
5.3. Correction and Verification of Calculation Formula of Aluminum Alloy-Concrete Composite Beam
6. Discussion and Limitations
6.1. Limitations
- (1)
- Post-buckling behavior of the aluminum alloy web is not included in the finite element model or theoretical derivation. The model only considers pre-buckling shear resistance, which may underestimate or overestimate capacity in slender web sections.
- (2)
- Perfect bonding is assumed between the aluminum alloy and the concrete interface. No slip, debonding, or relative movement is modeled, which may affect accuracy in real composite structures with incomplete connections or interface degradation.
- (3)
- Flange contribution to shear resistance is neglected. The flanges are treated as axial force components, while their potential shear capacity is considered a strength reserve and not quantified in this model.
- (4)
- Material model simplifications: The concrete is modeled using the Concrete Damaged Plasticity (CDP) model without considering long-term effects such as creep or shrinkage.
- (5)
- Parameter range limitations: The formula is verified only for shear span ratios between 1.0 and 5.0, concrete grades between C30 and C50, and the specific geometric configuration studied. Application outside this range requires further verification.
- (6)
- No experimental validation has been conducted. All verification is based on finite element simulations. While a strong correlation with FEA results is shown, real-world factors may introduce additional variability.
6.2. Practical Applications
7. Conclusions
- (1)
- The shear bearing capacity increases by a maximum of 6.55% with higher concrete strength. It also increases by up to 25.6% and 7.45% with a greater web height-to-thickness ratio and web thickness, respectively. An increase in bolt diameter results in a maximum shear capacity increase of 2.6%. Reducing stirrup spacing leads to a maximum increase of 5.41% in shear capacity. As the shear span ratio increases from 1 to 3, the shear bearing capacity of aluminum alloy–concrete composite (ACC) beams decreases; when the shear span ratio exceeds 3, the rate of decrease slows.
- (2)
- A calculation formula for the shear bearing capacity of aluminum alloy–concrete composite beams was established using the superposition method. The total shear capacity primarily comprises contributions from the aluminum alloy beam web, concrete, and stirrups. Comparison of the formula results with finite element analysis (FEA) values showed a relatively large initial error. After introducing a strength reduction coefficient for correction, the final average ratio of the formula solution to the FEA value was 1.018, with a standard deviation of 0.151, indicating low dispersion and improved accuracy of the formula and the proposed formula was validated against 22 FEA models, demonstrating excellent agreement with numerical results and confirming its reliability for practical engineering applications.
- (3)
- This study addresses a key gap in the current literature: the lack of a validated shear capacity formula tailored specifically for aluminum alloy–concrete composite beams. By developing and verifying a new theoretical model based on an improved tension–compression bar mechanism and supporting it with finite element analysis, the research contributes both methodologically and practically. The proposed formula enables more accurate and material-specific shear capacity assessment, facilitating the application of aluminum–concrete composite structures in environments where corrosion resistance is critical. Future research may expand on this work through experimental validation and extension to dynamic or fatigue loading scenarios. Furthermore, recent advances such as the application of engineered cementitious composites [30,31,32], optimization of shear behavior in hybrid and corrugated systems [33,34], and the use of intelligent design methods like morphable components and machine-learning-based multiscale modeling [35,36] provide promising directions for further refinement and application of aluminum–concrete composite structures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, Y.J.; Cheng, M.; Wang, Y.Q. Application and study of aluminum alloy in building structures. Build. Sci. 2005, 21, 7–11+20. [Google Scholar]
- Yang, L.P.; Wei, S.; Zhang, Q.L. Aluminum reticulated spatial structures: State of the art and key issues. J. Build. Struct. 2013, 34, 1–19+60. [Google Scholar]
- Yang, F.Q. Closed-loop recycling boosts the leapfrog development of the secondary aluminum industry. Resour. Recycl. 2020, 18–21. (In Chinese) [Google Scholar]
- Siwowski, T. Test and Finite Element Analysis of an ‘Aluminium-Lightweight Concrete’ Composite Girder. Struct. Eng. Int. 2006, 16, 319–325. [Google Scholar] [CrossRef]
- Polus, Ł.; Szumigała, M. A Numerical Analysis of the Resistance and Stiffness of the Aluminium and Concrete Composite Beam. Civ. Environ. Eng. Rep. 2014, 15, 99–112. [Google Scholar] [CrossRef][Green Version]
- Polus, Ł.; Szumigała, M. Tests of shear connectors used in aluminium-concrete composite structures. In Recent Progress in Steel and Composite Structures—Proceedings of the 13th International Conference on Metal Structures, Zielona Góra, Poland, 15–17 June 2016; ICMS: Sydney, Australia, 2014. [Google Scholar]
- Szumigała, M.; Polus, Ł. An Numerical Simulation of an Aluminium-concrete Beam. Procedia Eng. 2017, 172, 1086–1092. [Google Scholar] [CrossRef]
- Polus, Ł.; Szumigała, M. Theoretical and Numerical Analyses of an Aluminium-Concrete Composite Beam with Channel Shear Connectors. Eng. Trans. 2019, 57, 535–556. [Google Scholar]
- Polus, Ł.; Szumigała, M. An experimental and numerical study of aluminium–concrete joints and composite beams. Arch. Civ. Mech. Eng. 2019, 19, 375–390. [Google Scholar] [CrossRef]
- Eurocode 4; Design of Composite Steel and Concrete Structures: Part 1.1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- AISI S100; North American Specification for the Design of Cold-Formed Steel Structural Members. American Iron and Steel Institute: Washington, DC, USA, 2012.
- Gong, W.Z. Experimental Study on Flexural Behavior of Concrete Filled Aluminum Alloy Tube. Ph.D. Dissertation, Hua Qiao University, Quanzhou, China, 2016. [Google Scholar]
- Xing, G.H.; Luo, X.B.; Jun, M.; Zhang, W.L.; Chen, R.X.; Li, J.H.; Deng, Y.L.; Wang, T.; Sun, K.; Ma, L. Study on bonding performance and debonding capacity of RC beam strengthened with NSM aluminum alloy bars. J. Archit. Civ. Eng. 2021, 38, 41–50. (In Chinese) [Google Scholar]
- Zhang, Y.T. Study on Bond Properties Between Aluminum Alloy and Concrete. Ph.D. Dissertation, Chang’an University, Xi’an, China, 2015. [Google Scholar]
- Badawi, M.; Abdelmgeed, F.A.; Elsamak, G.; Alharthai, M.; Bahrami, A.; Ghalla, M. Numerical study on enhancing shear performance of RC beams with external aluminum alloy plates bonded using steel anchors. Results Eng. 2024, 22, 102143. [Google Scholar]
- Hu, T.; Zeng, X.; Liu, H.B.; Zhang, Y.; Li, S.; Ma, K.; Xu, J.; Wang, R.; Zhao, L.; Chen, H.; et al. Review on aluminum alloy–concrete composite structure research progress. Concrete 2020, 5, 5–8. (In Chinese) [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; NACA TN-902: Washington, DC, USA, 1943. [Google Scholar]
- Steinhardt, O. Aluminum constructions in civil engineering. Aluminum 1971, 47, 131–139. [Google Scholar]
- GB 50017-2017; Code for Design of Concrete Structures. Architecture and Architecture Press: Beijing, China, 2018.
- Chen, Y.; Wang, J. Finite element analysis and design recommendations for aluminum alloy–concrete composite beams under shear. Thin-Walled Struct. 2023, 182, 110245. [Google Scholar]
- Wu, K.; Lin, S.; Liu, X.; Mao, F.; Tan, C. Experimental Study on Load Bearing Capacity of Prefabricated Partially Encased Composite Beams. Int. J. Struct. Stab. Dyn. 2021, 21, 2150104. [Google Scholar] [CrossRef]
- BS EN 1999-1-1:2007; Eurocode 9 (EC9): Design of Aluminium Structures, Part 1-1: General Structural Rules—General Structural Rules and Rules for Buildings. European Committee for Standarization (CEN): Brussels, Belgium, 2007.
- Shi, Q.J.; Cheng, M.; Wang, Y.Q. Shear buckling design of webs in aluminum beams. J. Tsinghua Univ. (Sci. Technol.) 2008, 2008, 918–921. [Google Scholar]
- Eurocode 3; Design of Steel Structures: Part 1.1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- He, J.; Liu, Y.Q.; Chen, A.R.; Yoda, T. Shear behavior of partially encased composite I-girder with corrugated steel web: Experimental study. J. Constr. Steel 2012, 77, 193–209. [Google Scholar] [CrossRef]
- Eurocode 2; Design of Concrete Structures: Part 1.1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Zhou, F.; Young, B. Shear buckling resistance of aluminum alloy beams: Experimental tests and reliability analysis. J. Struct. Eng. (ASCE) 2023, 149, 04022259. [Google Scholar]
- Wang, Y.; Shi, Y. Post-buckling behavior of aluminum alloy beams under shear: Numerical and analytical studies. Thin-Walled Struct. 2020, 157, 107083. [Google Scholar]
- Yuan, L.; Zhang, Q.L.; Luo, X.Q.; Ouyang, Y.; Yin, J. Shear resistance of aluminum alloy extruded H-Section beams. Thin-Walled Struct. 2020, 159, 107279. [Google Scholar] [CrossRef]
- Mo, C.; Huang, J.; Huang, J.; Tan, J. Finite element analysis on flexural performance of the bending capacity for concrete beams reinforced with ECC and aluminum alloy bars. Highlights Sci. Eng. Technol. 2023, 62, 22–30. [Google Scholar] [CrossRef]
- Cheng, K.; Du, Y.; Wang, H.; Liu, R.; Sun, Y.; Lu, Z.; Chen, L. Experimental Study of the Shear Performance of Combined Concrete–ECC Beams without Web Reinforcement. Materials 2023, 16, 5706. [Google Scholar] [CrossRef] [PubMed]
- Maheswaran, J.; Chellapandian, M.; Sivasubramanian, M.V.; Murali, G.; Vatin, N.I. Experimental and Numerical Investigation on the Shear Behavior of Engineered Cementitious Composite Beams with Hybrid Fibers. Materials 2022, 15, 5059. [Google Scholar] [CrossRef] [PubMed]
- Sharaky, I.A.; Alharthi, Y.M.; Elamary, A.S. Effect of Shear and Pure Bending Spans on the Behaviour of Steel Beams with Corrugated Webs. Materials 2022, 15, 4675. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Z.; Li, J.; Mou, X.; Wang, T.; Baktheer, A.; Feldmann, M. Experimental and Theoretical Study of Thin-covered Composite Dowels considering Multiple Load Conditions. arXiv 2025, arXiv:2502.18956. [Google Scholar] [CrossRef]
- Huo, W.; Liu, C.; Liu, Y.; Du, Z.; Zhang, W.; Guo, X. A novel explicit design method for complex thin-walled structures based on embedded solid moving morphable components. arXiv 2023, arXiv:2306.10449. [Google Scholar] [CrossRef]
- Wei, H.; Wu, C.T.; Hu, W.; Su, T.H.; Oura, H.; Nishi, M.; Naito, T.; Chung, S.; Shen, L. LS-DYNA Machine Learning-based Multiscale Method for Nonlinear Modeling of Short Fiber-Reinforced Composites. arXiv 2023, arXiv:2301.02738. [Google Scholar] [CrossRef]





| Dilation Angle | Eccentricity | k | Viscosity Parameter | |
|---|---|---|---|---|
| 30 | 0.1 | 1.16 | 0.6667 | 1 × 10−5 |
| Concrete Grade | Peak Load (kN) | Shear Capacity (kN) | Increase (%) |
|---|---|---|---|
| C30 | 264.00 | 281.18 | — |
| C40 | 272.00 | 288.20 | +2.49% |
| C50 | 299.40 | 299.60 | +6.55% |
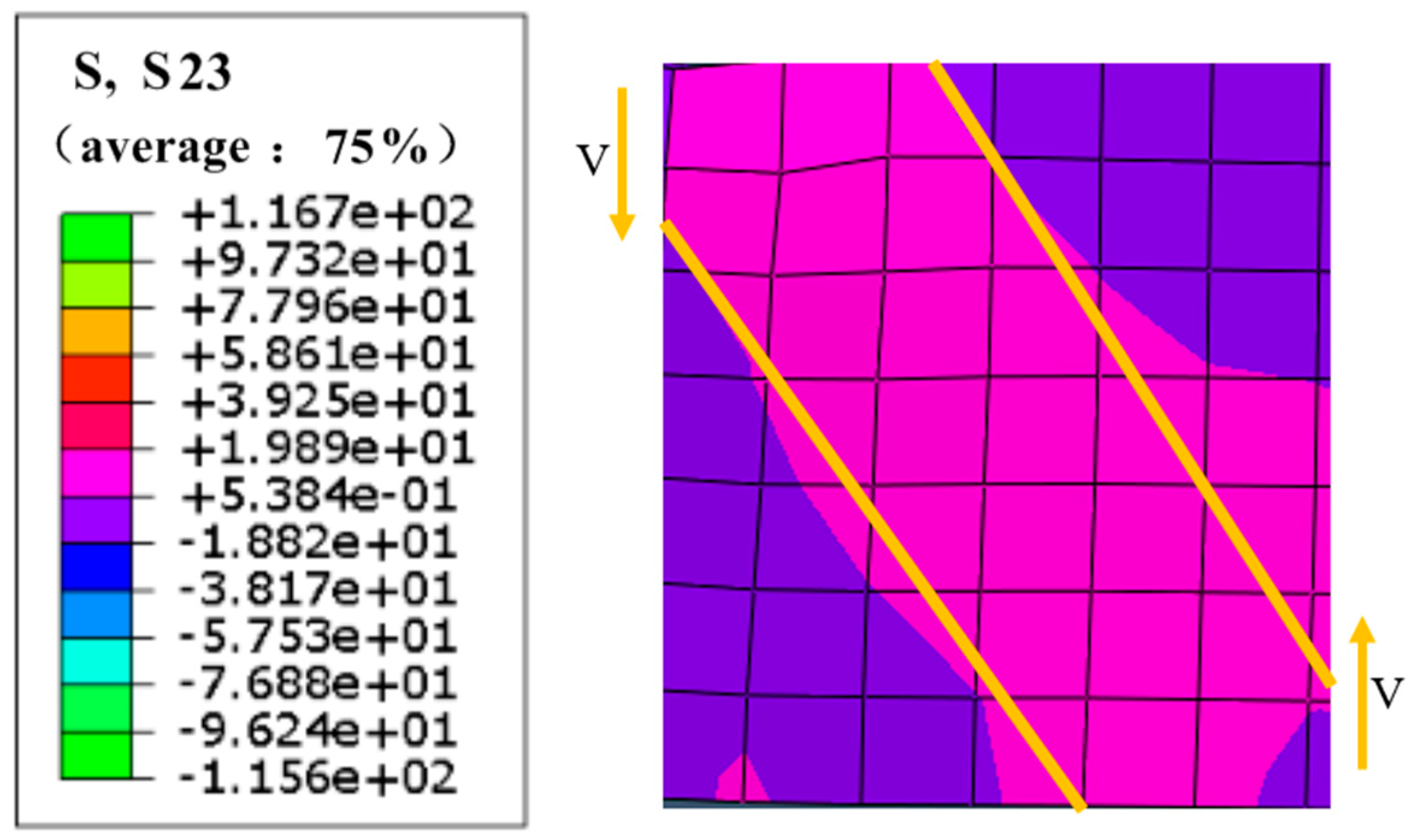
| Path No. | Location | Peak Shear Stress (MPa) |
|---|---|---|
| Path 1 | Outer concrete edge | ~0.00 |
| Path 2 | Near web (left side) | 3.25 |
| Path 3 | Near web (right side) | 4.10 |
| Path 4 | Outer concrete edge | ~0.00 |
| Model Number | (MPa) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (MPa) | (MPa) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC2-1 | 14.3 | 3.6 | 270 | 8 | 15 | 81 | 16 | 150 | 281.18 | 344.98 | 1.227 |
| ACC2-2 | 19.1 | 3.6 | 270 | 8 | 15 | 81 | 16 | 150 | 288.20 | 359.60 | 1.248 |
| ACC2-3 | 23.1 | 3.6 | 270 | 8 | 15 | 81 | 16 | 150 | 299.60 | 371.78 | 1.241 |
| ACC2-4 | 14.3 | 3.6 | 320 | 8 | 15 | 81 | 16 | 150 | 318.40 | 367.27 | 1.182 |
| ACC2-5 | 14.3 | 3.6 | 400 | 8 | 15 | 81 | 16 | 150 | 400.00 | 456.42 | 1.162 |
| ACC2-6 | 14.3 | 3.6 | 480 | 8 | 15 | 81 | 16 | 150 | 477.10 | 545.57 | 1.167 |
| ACC2-7 | 14.3 | 3.6 | 560 | 8 | 15 | 81 | 16 | 150 | 564.80 | 634.72 | 1.169 |
| ACC2-8 | 14.3 | 3.6 | 270 | 10 | 15 | 81 | 16 | 150 | 291.70 | 348.13 | 1.193 |
| ACC2-9 | 14.3 | 3.6 | 270 | 12 | 15 | 81 | 16 | 150 | 295.60 | 351.28 | 1.188 |
| ACC2-10 | 14.3 | 3.6 | 270 | 14 | 15 | 81 | 16 | 150 | 300.30 | 354.43 | 1.180 |
| ACC2-11 | 14.3 | 3.6 | 270 | 8 | 15 | 81 | 19 | 150 | 285.79 | 360.25 | 1.164 |
| ACC2-12 | 14.3 | 3.6 | 270 | 8 | 15 | 81 | 22 | 150 | 288.50 | 352.62 | 1.217 |
| ACC2-13 | 14.3 | 3.6 | 270 | 8 | 15 | 81 | 16 | 100 | 311.70 | 363.82 | 0.697 |
| ACC2-14 | 14.3 | 3.6 | 270 | 8 | 15 | 81 | 16 | 120 | 295.70 | 361.57 | 0.873 |
| ACC2-15 | 14.3 | 1 | 270 | 8 | 15 | 81 | 16 | 150 | 521.90 | 355.42 | 0.940 |
| ACC2-16 | 14.3 | 1.5 | 270 | 8 | 15 | 81 | 16 | 150 | 414.00 | 350.34 | 1.137 |
| ACC2-17 | 14.3 | 2 | 270 | 8 | 15 | 81 | 16 | 150 | 378.00 | 347.01 | 1.166 |
| ACC2-18 | 14.3 | 2.5 | 270 | 8 | 15 | 81 | 16 | 150 | 308.10 | 344.56 | 1.330 |
| ACC2-19 | 14.3 | 3 | 270 | 8 | 15 | 81 | 16 | 150 | 297.70 | 344.83 | 1.427 |
| ACC2-20 | 14.3 | 4 | 270 | 8 | 15 | 81 | 16 | 150 | 262.40 | 345.78 | 1.543 |
| ACC2-21 | 14.3 | 4.5 | 270 | 8 | 15 | 81 | 16 | 150 | 260.30 | 344.98 | 1.227 |
| ACC2-22 | 14.3 | 5 | 270 | 8 | 15 | 81 | 16 | 150 | 259.10 | 359.60 | 1.248 |
| Vcal/VFEA | 1.173 | ||||||||||
| σ | 0.175 |
| Model Number | |||
|---|---|---|---|
| ACC2-1 | 298.66 | 281.18 | 1.062 |
| ACC2-2 | 313.28 | 288.20 | 1.087 |
| ACC2-3 | 325.46 | 299.60 | 1.086 |
| ACC2-4 | 318.07 | 318.40 | 1.024 |
| ACC2-5 | 395.73 | 400.00 | 1.008 |
| ACC2-6 | 473.39 | 477.10 | 1.013 |
| ACC2-7 | 551.05 | 564.80 | 1.015 |
| ACC2-8 | 301.27 | 291.70 | 1.033 |
| ACC2-9 | 303.88 | 295.60 | 1.028 |
| ACC2-10 | 306.49 | 300.30 | 1.021 |
| ACC2-13 | 313.93 | 311.70 | 1.014 |
| ACC2-14 | 306.29 | 295.70 | 1.057 |
| ACC2-15 | 317.50 | 521.90 | 0.608 |
| ACC2-16 | 315.24 | 414.00 | 0.761 |
| ACC2-17 | 309.09 | 378.00 | 0.818 |
| ACC2-18 | 304.01 | 308.10 | 0.987 |
| ACC2-19 | 300.68 | 297.70 | 1.010 |
| ACC2-20 | 298.24 | 262.40 | 1.151 |
| ACC2-21 | 298.51 | 260.30 | 1.235 |
| ACC2-22 | 299.46 | 259.10 | 1.336 |
| Vcal/VFEA | 1.018 | ||
| σ | 0.151 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Lu, Z. Calculation of Shear-Bearing Capacity of Aluminum Alloy-Concrete Composite Beam. Buildings 2025, 15, 2393. https://doi.org/10.3390/buildings15142393
Li C, Lu Z. Calculation of Shear-Bearing Capacity of Aluminum Alloy-Concrete Composite Beam. Buildings. 2025; 15(14):2393. https://doi.org/10.3390/buildings15142393
Chicago/Turabian StyleLi, Chenghua, and Ziliang Lu. 2025. "Calculation of Shear-Bearing Capacity of Aluminum Alloy-Concrete Composite Beam" Buildings 15, no. 14: 2393. https://doi.org/10.3390/buildings15142393
APA StyleLi, C., & Lu, Z. (2025). Calculation of Shear-Bearing Capacity of Aluminum Alloy-Concrete Composite Beam. Buildings, 15(14), 2393. https://doi.org/10.3390/buildings15142393





