Abstract
To enhance the economic and safety aspects of tunnel structural design, this study optimizes the mix proportion of steel fiber-reinforced concrete (SFRC). It investigates the stress characteristics and support parameters of SFRC secondary lining structures via small-scale model tests and finite element analysis. The research focuses on the cracking process, deformation, and stress characteristics of SFRC linings under various loads. Compared with conventional reinforced concrete tunnels, SFRC tunnels show a significant increase in lining stiffness and load capacity, with a 20% reduction in reinforcement yielding load. When the damage factor is 0.43, the addition of steel fibers increases compressive stress by 22.18%. Using ABAQUS, simulations of SFRC linings with thicknesses ranging from 400 mm to 600 mm and reinforcement ratios of 0% to 0.28% were conducted. The results indicate that a 450 mm thick SFRC lining matches the mechanical performance of a 600 mm thick conventional reinforced concrete lining. Notably, an SFRC lining with a 0.20% circumferential reinforcement ratio equals a conventional lining with a 0.28% reinforcement ratio in overall mechanical performance.
1. Introduction
Traditional tunnel construction often faces challenges with concrete lining cracking due to various factors during construction and fatigue loads. Crack propagation can lead to reinforcement corrosion and arch rusting, as well as carbonation at crack sites [1]. This can result in concrete spalling, delamination, and water leakage in tunnels, as illustrated in Figure 1. These defects not only reduce the load-bearing capacity of the tunnel structure but also compromise its durability, posing potential threats to tunnel safety [2].

Figure 1.
Tunnel engineering disasters. (a) Corrosion of steel reinforcement. Image source: Journal of Building Engineering. Author: Huaijin Wang. (b) Tunnel water leakage collapse. Image source: China News Network. Author: Dongsheng Wei.
Steel fiber-reinforced concrete (SFRC) tunnel lining technology has gained widespread adoption in tunnel engineering due to its excellent crack resistance, toughness, and ease of construction [3]. Steel fibers create a three-dimensional dispersed reinforcement system within the concrete structure [4], significantly enhancing its tensile, flexural, and impact resistance properties. This effectively improves the structural performance and durability of tunnel linings while reducing maintenance costs [4]. As a result, SFRC has emerged as a potential alternative to traditional reinforced concrete for the design and construction of tunnel linings.
In recent years, the growing scale of tunnel engineering has led to higher demands for the performance of initial support structures. As a novel composite material, steel fiber-reinforced concrete (SFRC) has increasingly gained attention. Many scholars have carried out extensive research on it. Gao Zhe [5], through material substitution experiments, shake table tests, and finite element numerical simulations, demonstrated that the addition of steel fibers significantly enhances the crack resistance and durability of subway tunnel lining segments. It effectively limits crack propagation and exhibits good ductility and energy dissipation capacity under earthquake and train loading. Guo Yanhua [6], employing four-point bending tests, compression–shear failure tests, and finite element simulations, investigated the toughening and crack resistance properties of steel fiber-reinforced concrete. The study found that steel fiber-reinforced concrete effectively enhances the tensile and flexural strength of concrete, as well as fracture elongation, significantly improving its brittleness. By incorporating material tensile softening curves and shear softening curves into finite element models, the study confirmed that the application of steel fiber-reinforced concrete in tunnel support systems can significantly improve lining durability and economic benefits. Hu Xinchao [7], through the design of the steel fiber shotcrete mix ratio, finite element simulation analysis, and research on critical construction process parameters, confirmed the advantages of steel fiber shotcrete in enhancing tunnel surrounding rock stability and reducing displacement deformation. The mechanical performance and surrounding rock stability of single-layer shotcrete lining structures with steel fiber were validated through experiments and simulations. Zhang Hannan [8], employing experimental research and numerical simulation methods, investigated the influence of steel fibers on concrete mechanical properties. While the compressive strength enhancement was limited, the steel fibers significantly strengthened the concrete’s flexural properties, tensile properties, and ductility, improving the concrete’s failure mode. Furthermore, numerical simulations using ABAQUS (2021) software have validated experimental results and showed that the application of steel fiber-reinforced concrete in initial tunnel development can support in practical engineering. The effectiveness in enhancing tunnel support performance was confirmed through measurements and simulation analysis of surrounding rock pressure and structural stress. Hu Lei [9], through fiber reinforcement theory analysis, ultimate state load capacity comparison, bending toughness tests, and seismic dynamic response numerical simulations, concluded that steel fiber-reinforced concrete exhibits better seismic resistance performance and requires thinner sections in tunnels and underground structures. It showed a reduced bending moment and axial force response under seismic action, validating its effectiveness in improving tunnel lining seismic performance. Li Wenwu [10] found that, under specific blending ratios, hybrid fibers significantly enhance the working performance and durability of tunnel lining concrete. Particularly, the combination of 0.5% steel fiber and 0.3% polypropylene fiber is recommended to maximize crack resistance and the impermeability of tunnel linings. Li Yunhua [11] studied the mechanical behavior of single-layer linings of ordinary concrete and steel fiber-reinforced concrete under surrounding rock pressure through scaled model tests, proving that steel fiber-reinforced concrete effectively enhances the initial cracking load of the lining structure. Wu Liming [12] used LS-DYNA (R13.1.0) software to establish numerical models of plain concrete, ordinary concrete, and steel fiber-reinforced concrete and conducted numerical analyzes under different quantities of explosives. The results showed that steel fiber-reinforced concrete tunnel linings outperformed the other two types of concrete in tunnel construction. Tiberti et al. [13] investigated the adoption of SFRC as a partial replacement for mesh-reinforced linings containing steel mesh, and the study confirmed the feasibility of using SFRC linings to reinforce the critical connection zone between the tunnel invert and bench. Kooiman et al. [14] pointed out that steel fiber-reinforced concrete (SFRC) exhibits significant tensile strength. The appropriate addition of fibers effectively reduces ductile failure and decreases the amount of steel reinforcement required in concrete construction. Under favorable geological conditions, a certain thickness of single-layer SFRC lining is sufficient to maintain tunnel stability [15]. Larive et al. [16] further indicated that improvements in equipment, quality control, and design methods have provided opportunities for the long-term use of SFRC linings, potentially reducing lining thickness and tunnel excavation cross-sectional area. Wang Xiuling [17] summarized the advantages of using SFRC linings in tunnel engineering, emphasizing key design considerations and practical application cases, validating significant benefits in controlling rock displacement, reducing lining pressures, and enhancing overall and local support structure stability.
Traditional tunnel support methods have limitations. Plain concrete has a high compressive strength but a low tensile strength and ductility, making it prone to cracking and brittle failure under complex stresses. This compromises tunnel stability and durability. Reinforced concrete (RC), despite adding steel bars to enhance tensile strength, has complex reinforcement arrangements. In some geological conditions, the steel bars are prone to corrosion, which shortens the structure’s lifespan. To meet support requirements, plain and reinforced concrete often need thick lining structures in specific tunnels. This increases the excavation and construction difficulty, causes material waste, and raises costs.
In comparison, steel fiber-reinforced concrete (SFRC) has unique advantages. Adding steel fibers significantly improves concrete’s mechanical properties. It increases the tensile and flexural strength and fracture elongation, and enhances toughness and crack resistance. SFRC also absorbs and dissipates more energy, showing good seismic performance. In construction, SFRC has a simple process similar to plain concrete, is easy to operate and control, and improves construction efficiency. This shortens construction periods and enhances economic efficiency. Moreover, SFRC allows for a reduction in lining thickness, reducing concrete usage and excavation cross-sectional area, thus further lowering project costs.
The studies above show that these scholars have investigated various applications of steel fiber-reinforced concrete (SFRC) in tunnel structures through experiments and numerical simulations. These applications include improving the crack resistance, ductility, and seismic performance of tunnel linings, and enhancing the economic benefits. However, the main focus has been on the application of SFRC in primary support structures, with limited reports on its application in secondary lining structures. Further analysis and research are needed to explore the mechanical properties and optimal support parameters of SFRC for secondary lining structures.
2. Experimental Study on Secondary Lining Structure of Tunnels
2.1. Engineering Background
This paper is based on a highway tunnel located in Hezuo City, Gansu Province, China. The tunnel is designed with separate left and right lanes, spaced approximately 30 m apart. The entrance of the left tunnel is located at station ZK119+73, and its exit is at station ZK120+655, making the total length of the tunnel 925 m. Correspondingly, the entrance of the right tunnel is marked at station K119+730, and its exit at station K120+685, with a total length of 955 m, so the tunnels are classified as middle tunnels.
2.2. Similarity Ratio Design and Material Selection
This study [18] designed a tunnel section prototype for experimentation based on the relevant provisions of the Code for Design of Highway Tunnels (JTG/T 3660-2020). The lining structure shown in Figure 2 was designed for Class V surrounding rock.
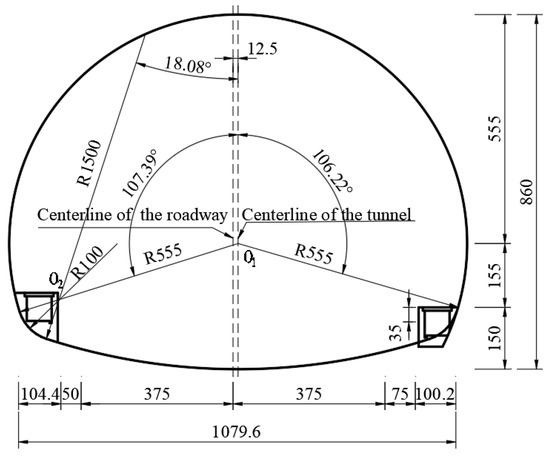
Figure 2.
Tunnel cross-sectional dimensions.
2.2.1. Similarity Ratio Design
To reduce the impact of model boundary effects on the test results, and to account for the test box size and tunnel model span, the geometric similarity ratio for the test is 1:20. The similarity ratios for the other physical parameters are shown in Table 1.

Table 1.
Similarity ratio used in model experiments.
2.2.2. Material Selection
The silicomanganese used in the tests is the Borun brand product from Henan Borun Casting Materials Co., Ltd., Gongyi City, Henan Province, China. The cement used is Hongshi brand PO42.5 ordinary Portland cement. The fine aggregate had a fineness modulus between 2.0 and 3.7. The coarse aggregate is well-graded natural crushed stone with a particle size distribution of 5–10 mm. The water-reducing agent is a polycarboxylate-based high-efficiency water-reducing agent. The secondary lining reinforced concrete specimens are simulated using a concrete mix with a water-to-binder ratio of 0.4 and a 10% silicomanganese addition. The reinforcing bars are simulated using 6 mm diameter hot-rolled plain bars, spaced at 15 cm intervals, as shown in Figure 3.

Figure 3.
Pouring of the secondary lining model of reinforced concrete soil. (a) Install the mold; (b) binding steel bars; (c) concrete pouring; (d) finished product.
Next, 1% of steel fiber was added to the concrete to produce the secondary steel fiber concrete lining and steel fiber-reinforced concrete lining. The steel fiber used in the test was Class b milled steel fiber from Hebei Steel Fiber Factory. The length of the steel fiber used in the test is 32 mm, the width is 0.5 mm, the elastic modulus is 210 GPa, and the tensile strength is 1100 MPa. As shown in Figure 4, the mechanical parameters of the lining model specimens are presented in Table 2 below.

Figure 4.
Tunnel lining structure model.

Table 2.
Main mechanical parameters of model specimen.
2.3. Experimental Testing Instruments and Testing Methods
The experimental setup utilizes the DH3821 Static Strain Testing Analysis System. Strain was measured using strain gauges, which were configured in a 1/4 bridge state. The displacements at the tunnel vault, haunches, and arch foot are measured using YHD-100 displacement sensors, also configured in a 1/4 bridge state [19]. Refer to Figure 5 for details.

Figure 5.
Physical map of test equipment. (a) DH3821 Static Strain Testing Analysis System; (b) displacement sensor.
At the highest point of the tunnel vault, a strain gauge is positioned to measure maximum vertical stress and vertical deformation, which is crucial for monitoring the overall load-bearing capacity and stability of the tunnel vault [20]. Two strain gauges are placed on either side of the haunch to detect horizontal stress distribution and symmetry between the left and right sides of the tunnel. Additionally, one strain gauge is positioned on each side of the tunnel at the foot to monitor strain in both the vertical and horizontal directions. Refer to Figure 6 for details.
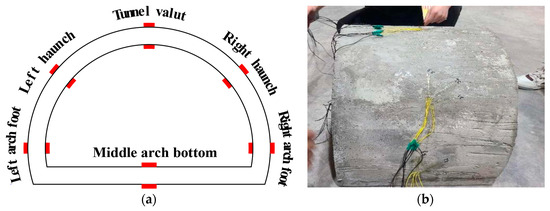
Figure 6.
Distribution map of measuring points for lining structure. (a) Strain gauge installation locations; (b) installation of strain gauges.
2.4. Model Load Testing
To simulate the soil pressure acting on the tunnel linings in actual engineering projects, a specialized experimental setup was designed for this study. A reaction frame was used to apply load to a steel plate above the soil, which transmits the load to the tunnel lining model. During the experiment, a testing instrument for static strain is used to monitor and record strain changes on the surface of the tunnel lining model continuously. This data is analyzed to understand the distribution of strains in the tunnel lining model under the combined effects of the reaction frame and soil pressure, allowing inference of the stress state at different positions of the tunnel lining. The experimental procedure is illustrated in Figure 7.


Figure 7.
Experimental process. (a) Installing tunnel lining; (b) placing soil; (c) applying load on top; (d) collecting data.
3. Analysis of Experimental Results
3.1. Analysis of Outer Lining Stress in Tunnels
As shown in Figure 8a–c, for the conventional concrete lining, yielding occurred at the left arch foot when the load reached 3.0 MPa, with a maximum tensile stress of 4.0 MPa. At 3.5 MPa, yielding occurred at the arch bottom, with a maximum compressive stress of 36.0 MPa. At 4.0 MPa, yielding occurred at the tunnel vault, with a maximum compressive stress of 37.0 MPa. For the steel fiber-reinforced and reinforced concrete, the yielding occurred at 4.0 MPa, with the maximum compressive stresses at the tunnel vault and arch bottom reduced to 33.0 MPa and 26.0 MPa, respectively. At the right arch foot, the maximum tensile stress at the 4.0 MPa yielding point was 3.0 MPa.
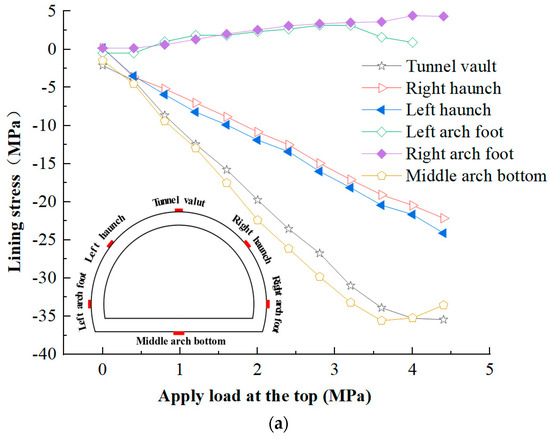
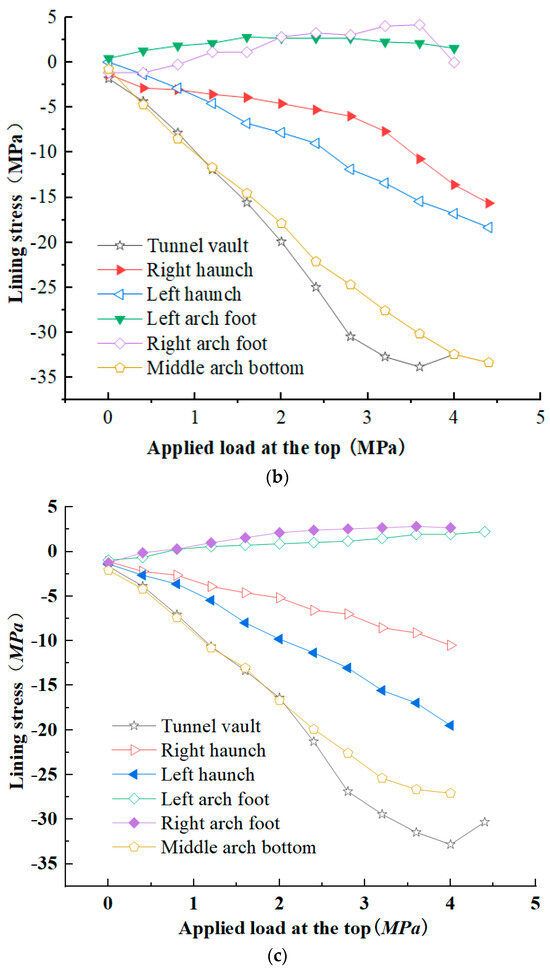
Figure 8.
(a) Stress on the outer side of reinforced concrete tunnel lining; (b) stress on the outer side of steel fiber concrete tunnel lining; (c) stress on the outer side of steel fiber-reinforced concrete tunnel lining.
The addition of steel fibers significantly improved the compressive and tensile performance, reduced stress concentrations, and resulted in a substantial increase in the load-bearing capacity and service life of the structure.
3.2. Analysis of Inner Lining Stress in Tunnel
According to Figure 9a–c, the inner lining of ordinary concrete exhibited primarily tensile stresses at the tunnel vault and middle arch bottom, while the haunch area sustained compressive stresses that showed a basic linear increase with increasing loads. Under lower to moderate loads (1.0 MPa to 3.5 MPa), cracks and concrete spalling gradually appeared in the lining, progressing to significant structural damage and crushing under high loads 4.0 MPa and above, resulting in a loss of load-bearing capacity.
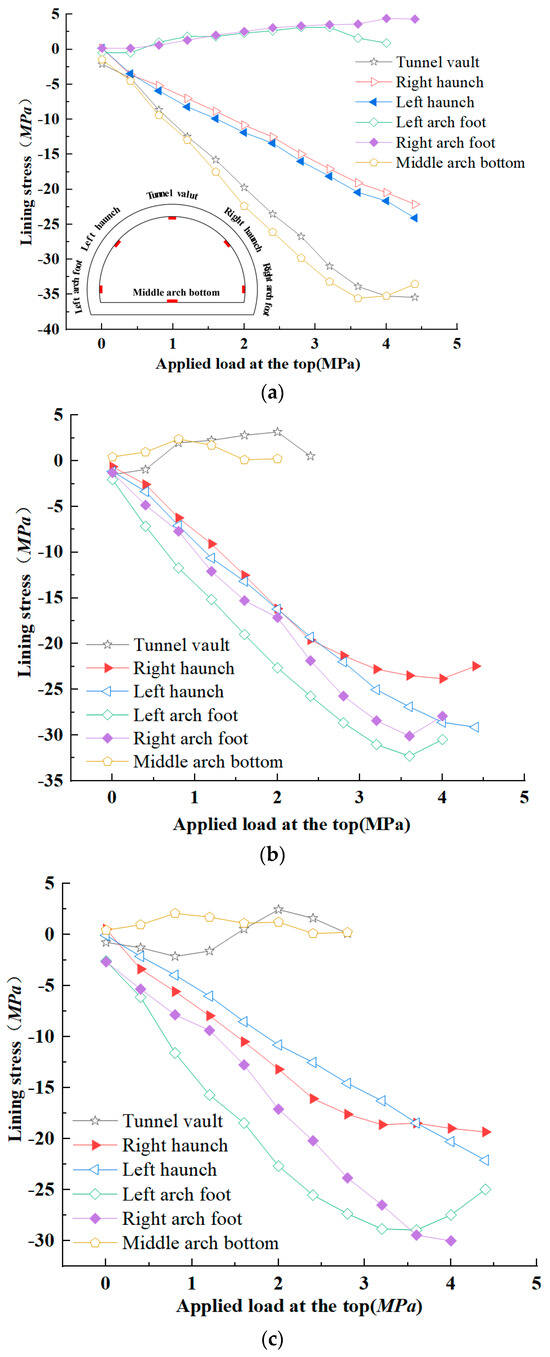
Figure 9.
(a) Stress on the outer side of reinforced concrete tunnel lining; (b) stress on the inner side of steel fiber concrete tunnel lining; (c) stress on the inner side of steel fiber-reinforced concrete tunnel lining.
In contrast, the steel fiber and steel fiber-reinforced concrete linings similarly exhibited tensile stresses at the tunnel vault and middle arch bottom, with compressive stresses at the haunch. However, under equivalent loads, the steel fibers formed a three-dimensional network within the concrete matrix, enhancing material toughness and tensile strength. This effectively suppressed crack propagation, demonstrating a superior performance with higher tensile strength and load-bearing capacity.
3.3. Verification and Comparison of Numerical Model Results
To compare the simulation results with the actual bending moments experienced by the scaled model, we calculated the internal force distribution of the tunnel lining under a top load of 0.5 MPa. Additionally, numerical calculations and analyses of the internal stress state of the tunnel secondary lining were performed using Midas (2022) software with a load structure calculation method.
3.3.1. Internal Force Calculations for the Secondary Lining
Based on the strain measurement data from the inner and outer surfaces of the lining, the following equations were used to calculate the axial force (N) and bending moment (M) acting on the lining structure [21]:
In the formula:
—the longitudinal unit length of the lining, m;
—the thickness of the lining, m;
, —the strains on the inner and outer sides of the lining, respectively.
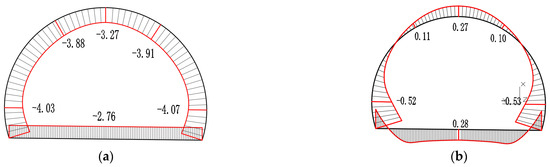
Figure 10.
Internal force diagram of ordinary reinforced concrete lining structure (scaled model). (a) Axial force (kN); (b) bending moment (kN·m).
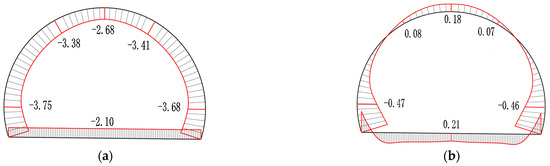
Figure 11.
Internal force diagram of steel fiber-reinforced steel lining structure (scaled model). (a) Axial force (kN); (b) bending moment (kN·m).
3.3.2. Numerical Model Calculation
In the computational model, the secondary lining is treated as a series of discrete beam elements, each with a thickness of 0.6 m. The concrete density is set to 24.5 kN/m3. The elastic moduli for the ordinary concrete and steel fiber-reinforced concrete are 30 GPa and 40 GPa, respectively, with a Poisson’s ratio of 0.2. The foundation reaction coefficient K is set to 200 MPa/m. To accurately reflect the structural loading conditions, the horizontal displacements at the nodes of the tunnel vault and arch bottom are constrained, simulating practical boundary conditions encountered in engineering. Based on these settings, the internal force distributions of the secondary linings made of ordinary reinforced concrete and steel fiber-reinforced concrete are computed under the same loading conditions. The calculation results are shown in Figure 12 and Figure 13.
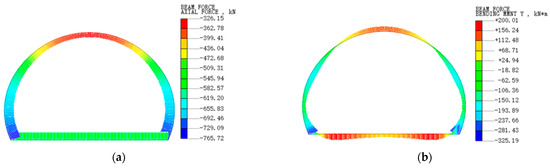
Figure 12.
Internal force diagram of ordinary reinforced concrete lining structure (numerical model). (a) Axial force (kN); (b) bending moment (kN·m).
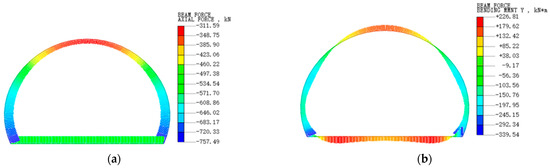
Figure 13.
Internal force diagram of steel fiber-reinforced steel lining structure (numerical model). (a) Axial force (kN); (b) bending moment (kN·m).
According to Figure 10, Figure 11, Figure 12 and Figure 13, the axial forces obtained from the three types of tunnel model experiments and numerical simulations are all overall compressive behavior. The results of the tunnel model and simulation analysis show that the tunnel, left and right haunches, and middle arch bottom exhibit consistent bending directions. The left and right arch foot also exhibit consistent bending directions, proving that the simulation method can reliably predict the mechanical behavior of the actual structure, providing a guarantee for the safety, economy, and feasibility of the design scheme.
4. Finite Element Simulation and Optimization Analysis of Support Parameters
Through a comparative analysis of the experimental and simulation results of the scaled model, it was found that the mechanical behavior of the scaled model exhibits consistent patterns with the actual model. This finding supports the potential use of steel fiber material as an alternative to ordinary reinforced concrete. Building on this, further research was conducted to develop a full-scale finite element tunnel model, where its load-bearing capacity was analyzed and evaluated. Additionally, the optimization of lining thickness and reinforcement ratio was studied.
4.1. Constitutive Relationship
In this study, the concrete damage plasticity (CDP) model was used to simulate the mechanical behavior of reinforced concrete and fiber-reinforced concrete lining structures. As a quasi-brittle material, concrete exhibits nonlinear mechanical properties under complex stresses, with significant differences between its tensile and compressive behavior. Based on plasticity mechanics and continuum damage mechanics, the CDP model can effectively describe the plastic deformation and damage evolution of concrete during loading, caused by internal microcracking [22]. This aligns with the mechanical responses of lining structures subjected to various load combinations in actual service. The plasticity parameters used are shown in Table 3.

Table 3.
Plasticity parameters of CDP model.
- (1)
- Constitutive relationship of concrete plastic damage inelasticity
Based on the stress characteristics of concrete structures, the mechanical properties of concrete are simulated by defining the stress–strain relationships for uniaxial compression and tension, along with the corresponding damage factors [23,24]. The uniaxial compression constitutive model for concrete damage stages adopts the calculation formula suggested by E. Hognestad [25]:
In the formula, represents the design compressive strength of concrete (kPa); denotes the yield strain, taken as 0.002; and signifies the ultimate strain, taken as 0.0038.
- (2)
- Constitutive relationship of steel fiber reinforcement
When conducting segregated modeling, it is necessary to develop separate models for both concrete and steel fibers, followed by defining their contact conditions. Therefore, distinct material properties must be assigned to each, including appropriate damage criteria and loading methods, to ensure the accuracy of finite element computations.
During the reinforcement stage, the elastic modulus E of steel fibers is 0.01 E0, where E0 is the initial modulus and equals 230 GPa. The Poisson’s ratio is taken as 0.21, and the tensile strength is 800 MPa. The constitutive relationship of steel fibers is illustrated in Figure 14.
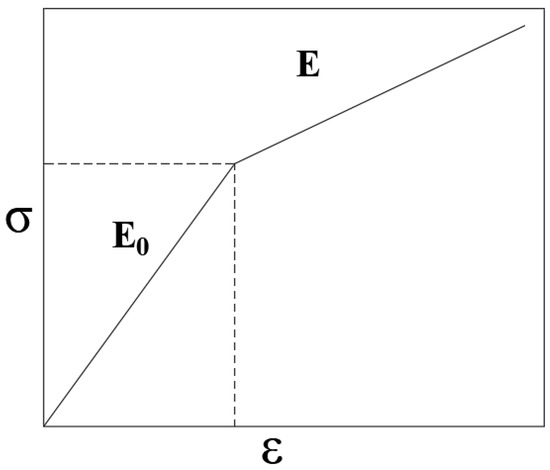
Figure 14.
Constitutive relationship of steel fibers.
- (3)
- Constitutive soil modeling
Different soil constitutive models vary greatly in complexity. Due to the inherent complexity of soil materials and field conditions, determining soil model parameters is often subject to some error. Thus, the proper choice of constitutive model and material parameters is crucial for numerical simulation results [26]. Common soil constitutive models are mainly categorized into elastic and plastic types. The linear elastic model, assuming a linear stress–strain relationship, is simple but neglects plastic deformation. The Mohr–Coulomb model, based on Coulomb’s fracture criterion and Mohr’s circle theory, effectively describes soil shear failure but is less accurate for volume changes. The modified Mohr–Coulomb model improves upon the original by integrating nonlinear elasticity and elastoplastic characteristics. It also accounts for soil buckling under specific conditions and introduces a cap to enable shear strengthening under high stress, making it widely applicable. The Drucker–Prager model, with a conical paraboloid yield surface, is suitable for complex stress states and considers the middle principal stress but has complex parameter determination. The MCC model, though yielding good results in simulating soil hardening, softening, and volume changes, involves complex expressions and numerous parameters, posing challenges in parameter selection.
Considering the pros and cons of these models, this study selects the modified Mohr–Coulomb model as the constitutive model for numerical simulation to balance model applicability and result accuracy.
The concrete structure adopts a concrete damage plasticity model for its constitutive relationship, while the reinforcement material is simulated using an ideal elastoplastic model. The specific parameters are detailed in Table 4.

Table 4.
Material model parameters.
4.2. Finite Element Model Establishment
4.2.1. Model Scale
This article adopts a geotechnical–structural model to analyze the mechanical performance of a steel fiber-reinforced concrete lining [27]. A three-dimensional tunnel model with dimensions of 84 m × 90 m × 10 m was developed using ABAQUS (Version 2021). This model is composed of three primary components: the surrounding rock mass, the secondary lining, and the steel reinforcement cage. The tunnel lining has a thickness of 0.6 m and spans 10.9 m in width, with a height of 9.4 m, and a longitudinal length consistent with the experimental section at 6.0 m. The secondary lining structure employs a double-layered reinforcement configuration as per design requirements, with both longitudinal and circumferential reinforcements spaced at 300 mm. The finite element models are shown in Figure 15 and Figure 16.

Figure 15.
Tunnel holistic model.

Figure 16.
Structural secondary lining. (a) Reinforced concrete lining structure; (b) lining reinforcement.
4.2.2. Model Meshing and Element Selection
The simulation of the secondary lining structure in the tunnel employs eight-node hexahedral incompatible solid elements (C3D8I). The reinforcement cage is simulated using two-node three-dimensional truss elements (T3D2), while the rock mass is represented by eight-node reduced integration solid elements (C3D8R). In the finite element analysis of concrete structures, mesh size affects both accuracy and computational efficiency. Smaller meshes enhance accuracy by better capturing concrete’s nonlinear behavior and damage evolution but raise computational costs. Larger meshes improve efficiency but may reduce result accuracy [28,29]. Based on these considerations, the maximum structural unit mesh size was set at 0.05 m, as shown in Table 5. The interface between the rock mass and the secondary lining is modeled using a tied contact, which ensures the compatibility of the displacements at the contact surfaces. The interaction between the reinforcement and the secondary lining is simulated using an embedded region approach, allowing them to resist the applied external loads together [30].

Table 5.
Number and type of structural units.
4.2.3. Boundary Conditions
The boundary conditions for the model include: the lateral, front, and back boundaries of the rock mass limit vertical displacement; and fixed constraints at the bottom, assuming homogeneous behavior for the rock and soil mass providing overall restraint to the lining structure. Uniformly distributed loads are applied at the top and lateral boundaries [31,32], with a lateral pressure coefficient set at 0.4.
4.3. Analysis of Results
Under the standard design condition, the load applied to the top of the model is increased until the reinforcement yields. The corresponding stress contour plot is shown in Figure 17.
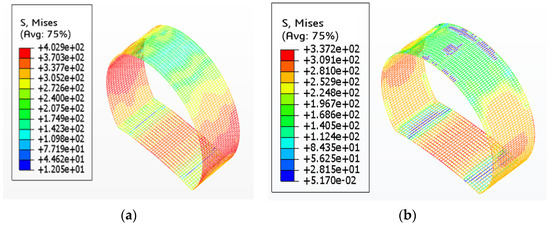
Figure 17.
Stress of steel fiber-reinforced concrete reinforcement under yield load of ordinary concrete reinforcement. (a) Plain reinforced concrete; (b) steel fiber-reinforced concrete reinforcement.
According to the data in Figure 17, under a uniformly distributed load of 5.37 MPa, the stress of plain reinforced concrete reaches a yield stress of 400 MPa, whereas for steel fiber-reinforced concrete reinforcement, the stress is 337 MPa. This indicates that the addition of steel fibers enhances the ultimate bearing capacity of the reinforcement and improves the overall structural performance of the lining. This is because the added steel fibers form a 3D net-like structure in the matrix. When concrete is under tension or bending, the matrix, with its low tensile strength, cracks first. At this point, the fiber bridging effect becomes the key mechanism for inhibiting crack propagation and reducing the stress concentration.
According to Figure 18, concrete components reinforced with steel fibers show stronger deformation resistance under identical loading conditions, with displacement deformations becoming more stable and significantly reduced.
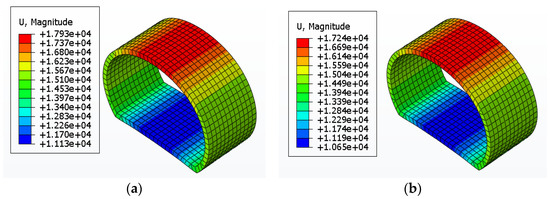
Figure 18.
Under the yield load of reinforced concrete, the stress of steel fiber-reinforced concrete with steel bars. (a) Reinforced concrete lining with ordinary steel reinforcement; (b) steel fiber-reinforced concrete lining.
According to reference [21], when the stiffness reduction factor of the lining structure drops to 0.57, it indicates the occurrence of minor cracking and damage. In this case, local reinforcement of the damaged areas is required to ensure the stability and safety of the structure. The present study investigates the concrete compressive damage parameter, and when its value reaches 0.43, the corresponding compressive stress level is considered the ultimate pressure that the lining structure can withstand. This implies that when the concrete is subjected to a pressure reaching the ultimate value, the lining structure may undergo failure. Figure 19 and Figure 20 show the stress contour plots under this condition.
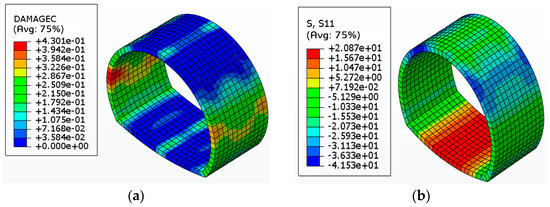
Figure 19.
Compression stress cloud map of ordinary reinforced concrete lining structure under standard design. (a) Damage factor cloud map of masonry structures; (b) cloud map of compressive stresses in masonry structures.

Figure 20.
Compression stress cloud map of steel fiber-reinforced concrete lining structure under standard design. (a) Damage factor contour map of masonry structures; (b) damage factor contour map of masonry structures.
According to Figure 19 and Figure 20, it can be observed that in the secondary masonry structure, the regions near the left and right arch foot bear the most significant pressure damage, followed by the tunnel vault and middle arch bottom regions. When the damage factor reaches 0.43, the compressive stress in ordinary reinforced concrete at the arch foot is 41.53 MPa. In contrast, in the same location, the compressive stress in steel fiber-reinforced concrete increases to 50.74 MPa, indicating a 22.18% increase due to the addition of steel fibers. This study provides strong support for optimizing the thickness of the secondary lining and the reinforcement ratio of the circumferential steel in tunnels
4.4. Optimization of Secondary Lining Thickness in Tunnels
Based on the optimal mix design conditions of 1% steel fiber content and 0.28% circumferential reinforcement ratio, this study designed six different thicknesses of secondary tunnel linings: 350 mm, 400 mm, 450 mm, 500 mm, 550 mm, and 600 mm. Using a numerical model, stress data for the steel fiber-reinforced concrete lining structure were extracted under consistent strain conditions (refer to Figure 21). Horizontal reference lines indicate stress levels at the ultimate load for ordinary reinforced concrete with a thickness of 600 mm.
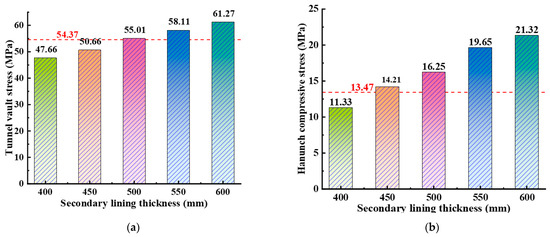
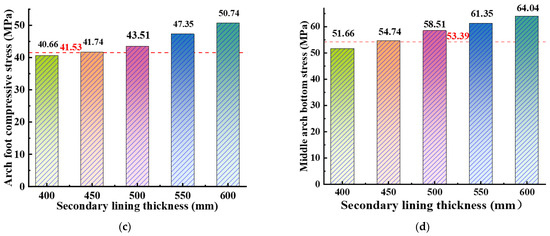
Figure 21.
Comparison of stresses of steel fiber-reinforced concrete secondary lining with different thicknesses. (a) Tunnel vault stress (MPa); (b) haunch compressive stress (MPa); (c) arch foot compressive stress (MPa); (d) middle arch bottom stress (MPa).
According to Figure 21, as the thickness of the lining increases, the stress at the tunnel vault shows a positive correlation trend, with a maximum and minimum stress difference of 28.81%. The reduction in the stressed area of the structure leads to a decrease in stress with decreasing lining thickness. When the lining thickness is 500 mm, the stress at the tunnel vault approaches 55.01 MPa, similar to that of ordinary concrete. However, for thicknesses less than 450 mm, the stress at the tunnel vault is significantly lower than in ordinary concrete.
Additionally, with increasing lining thickness, the stress levels at the haunch and arch foot also rise. Particularly noticeable is that at thicknesses less than 400 mm, the observed compressive stresses are significantly lower compared with thicker linings. The maximum and minimum compressive stresses at the arch waist differ by 24.79%, and at the arch foot by 46.85%. Based on the above analysis, under identical engineering application conditions, setting the thickness of the steel fiber-reinforced concrete lining to 450 mm enables it to withstand stress levels equivalent to those of conventional concrete lining at a thickness of 600 mm. By incorporating steel fiber-reinforced concrete in structural design, the lining thickness can be reduced by approximately 33.33% while maintaining structural performance. This advantage not only reduces material usage and construction costs but also enhances flexibility and efficiency in structural design.
4.5. Optimization of Circumferential Steel Reinforcement
Under the fixed condition of a 600 mm thick lining, this study investigated the influence of the circumferential reinforcement ratio on the stress state of the lining structure by designing seven different cases. These cases were based on the optimal 1% steel fiber content, with the circumferential reinforcement ratios being 0%, 0.04%, 0.08%, 0.12%, 0.16%, 0.20%, 0.24%, and 0.28%. The stress distributions for each reinforcement ratio are shown in Figure 22. Figure 22 presents the stresses in the steel fiber-reinforced concrete with different circumferential reinforcement ratios, under the condition where the reinforcement in the plain concrete reaches the yield (note that the red dashed line represents the stress in the plain concrete with 0.28% reinforcement).
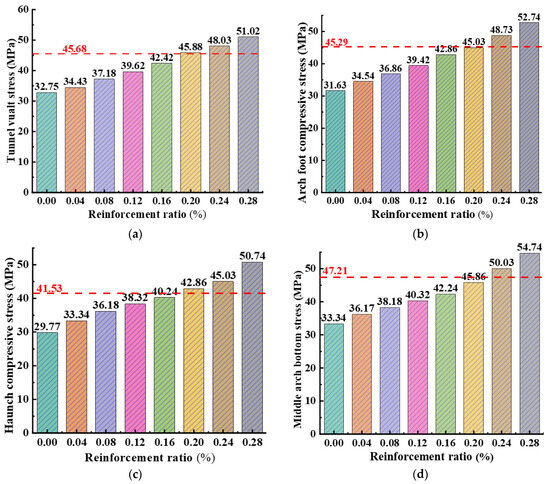
Figure 22.
Comparison of compressive stress with different mesocyclic reinforcement rates for steel fiber-reinforced concrete lining structures. (a) Tunnel vault stress (MPa); (b) arch foot compressive stress (MPa); (c) haunch compressive stress (MPa); (d) middle arch bottom stress (MPa).
According to Figure 22, it is evident that with an increase in the reinforcement ratio of the tunnel lining structure, the stress level of the structure also increases. In particular, there is a significant positive correlation between the circumferential reinforcement ratio and the compressive stress of the lining. This indicates that adjusting the reinforcement ratio, especially the circumferential reinforcement ratio, can effectively control the stress state of the tunnel lining.
When the circumferential reinforcement ratio of steel fiber-reinforced concrete structure is 0.20%, the stresses at the tunnel vault, haunch, arch foot, and middle arch bottom are 45.88 MPa, 42.86 MPa, 45.03 MPa, and 45.86 MPa, respectively. These stresses are equivalent to the compressive stresses in conventional concrete lining structures with a reinforcement ratio of 0.28%. This comparative analysis demonstrates that under equivalent performance requirements, the use of steel fiber-reinforced concrete can achieve a reduction in circumferential steel reinforcement ratio, specifically reducing it by approximately 26%.
5. Conclusions and Outlook
5.1. Conclusions
This study utilized a tunnel model experiment to study the deformation behavior and load-bearing characteristics of SFRC-reinforced tunnels and conventional reinforced concrete (RC) tunnels. Through a comparative analysis of three sets of material tunnel model experiments, as well as Abaqus finite element simulations, the following conclusions were drawn:
(1) Through the comparative analysis of tunnel model experiments and finite element simulations, it was found that the SFRC-reinforced tunnel exhibited an enhanced stiffness and load-bearing capacity compared with the conventional reinforced concrete (RC) tunnel. Specifically, the yield load of the reinforcement was reduced by approximately 20% in the SFRC-reinforced tunnel. When the damage factor reached 0.43, the addition of steel fibers resulted in a 22.18% increase in the compressive stress. The incorporation of steel fibers significantly improved the deformation resistance and crack resistance of the tunnel lining.
(2) Through the parameter optimization analysis using ABAQUS software on steel fiber-reinforced concrete tunnel linings, it was proved that under equivalent engineering conditions, a 450 mm steel fiber-reinforced concrete secondary lining can replace a 600 mm ordinary concrete secondary lining. This substitution allows for a material savings of 33.33% while maintaining structural performance. With a steel fiber content of 1%, a circumferential reinforcement ratio of 0.20% is sufficient to meet the strength standards of reinforced concrete.
5.2. Outlook
This article has achieved certain results, but there are still some problems and shortcomings in research depth that need further exploration. During the experiment, a scaled-down tunnel model was used. Due to the limitations of experimental equipment and human factors, the data is bound to have certain errors, which cannot accurately verify the accuracy and feasibility of the simulation experiment. It is recommended to use a full-scale experimental model if conditions permit.
Author Contributions
Conceptualization, Z.W. and B.R.; Funding acquisition, L.W., B.Z.; Validation, Z.W., X.W. and B.Z.; Investigation, Y.W. and L.W.; Writing—original draf, Y.W.; Software, Y.W.; Supervision, X.W. and B.Z.; Writing—review & editing, X.W. and L.W.; Datacuration, C.J., Z.H. and B.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by key project of science and technology research program of Chongqing Education Commission of China (Nos. KJZD-K202504002 and KJZD-M202204001). This research was supported by Young project of science and technology research program of Chongqing Education Commission of China (No. KJQN202501522). This research was supported by Chongqing University of Science and Technology Graduate Innovation Program (No. YKJCX2420607).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Chaolin Jia and Zihang Huang were employed by the company Chongqing Chuanjiu Mine Construction Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Al-Kheetan, M.J.; Al-Tarawneh, M.A.; Ghaffar, S.H.; Chougan, M.; Jweihan, Y.S.; Rahman, M.M. Resistance of hydrophobic concrete with different moisture contents to advanced freeze–thaw cycles. Struct. Concr. 2021, 22, E1050–E1061. [Google Scholar] [CrossRef]
- Deng, X. Study on Mechanical Properties of Fiber Reinforced Concret Confined by Reinforced Mesh with Low Modulus and Strong Joints. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2022. [Google Scholar] [CrossRef]
- Zhang, E. Experiment Study on Mechanical Properties and Durability of Complex Fiber Concrete. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2007. [Google Scholar]
- Li, D. Application of steel fiber reinforced concrete technology in road and bridge construction. China High-Tech. 2024, 2, 9897–98101. [Google Scholar]
- Gao, Z. Dynamic Performance Study of Subway with Steel Fiber Concrete Lining Based on SSI Theory. Ph.D. Thesis, Liaoning Technical University, Liaoning, China, 2023. [Google Scholar] [CrossRef]
- Guo, Y. Research on the Ductility of the Steel Fiber Reinforced Concrete and Its Application in the Underground Structure Calculation. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2008. [Google Scholar]
- Hu, X. Application and Research of Steel Fiber Concrete in Tunnel Construction. Master’s Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2023. [Google Scholar] [CrossRef]
- Zhang, H. Steel Fiber Reinforced Concrete Application Research in the Tunnel Weak Positions Primary Support. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2018. [Google Scholar]
- Hu, L. Seismic Dynamic Response Research on Steel Fiber Reinforced Concrete in Tunnel Lining Structure. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Li, W. Experimental Research of Waterproof for Shotcrete with Hybrid Fibers in the Structure of Tunnel Lining. Master’s Thesis, Wuhan Polytechnic University, Wuhan, China, 2015. [Google Scholar]
- Li, H.; Wu, Y.; Zhou, A.; Lu, F.; Lei, Z.; Zeng, B.; Zhu, K. Cracking Pattern and Bearing Capacity of Steel Fiber-Reinforced Concrete Single-Layer Tunnel Lining. Sustainability 2023, 15, 10665. [Google Scholar] [CrossRef]
- Wu, L.-M.; Wang, Z.-J.; Chang, Y.-Z.; Gao, F.; Zhang, B.; Wu, Y.; Fan, H.-X. Vibration Performance of Steel Fiber Concrete Tunnel Lining by Adjacent Tunnel Blasting Construction. Appl. Sci. 2023, 13, 4201. [Google Scholar] [CrossRef]
- Tiberti, G.; Minelli, F.; Plizzari, G. Reinforcement optimization of fiber reinforced concrete linings for ordinary tunnels. Compos. B Eng. 2014, 58, 199–207. [Google Scholar] [CrossRef]
- Kooiman, A.G. Modelling Steel Fibre Reinforced Concrete for Structural Design. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2000. [Google Scholar]
- Nanakorn, P.; Horii, H. A fracture-mechanics-based design method for SFRC tunnel linings. Tunn. Undergr. Space Technol. 1996, 11, 39–43. [Google Scholar] [CrossRef]
- Larive, C.; Bouteille, S.; Berthoz, N.; Zappelli, S. Fiber-reinforced sprayed concrete as a permanent tunnel lining. Struct. Eng. Int. 2020, 30, 498–505. [Google Scholar] [CrossRef]
- Wang, X.; Fan, F.; Lai, J.; Xie, Y. Steel fiber reinforced concrete: A review of its material properties and usage in tunnel lining. Structures 2021, 34, 1080–1098. [Google Scholar] [CrossRef]
- JTG/T 3660-2020; Technical Specifications for Construction of Highway Tunnel. Ministry of Transport of the People’s Republic of China: Beijing, China, 2020.
- Wang, Z. Experimental Study on the Equivalent Fracture Length of Time-Dependent Fracture of Concret. Master’s Thesis, Hainan University, Haikou, China, 2019. [Google Scholar]
- Tian, Y.; Man, J.; An, J.; Liao, H.; Dou, L. Study on Dynamic Mechanical Properties and Failure Mode of Shotcrete under Cyclic Impact Loading. Study Dyn. Mech. Prop. Fail. Mode 2024, 20, 221–225. [Google Scholar]
- Bo, M. Study on the Cracking Characteristic of Asymmetric Double-Arch Tunnel Linings and its Influence on Structural Bearing Capacity. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar] [CrossRef]
- Chen, F.; Yu, Z.; Yu, Y.; Liu, Q. Study on the bond-slip numerical simulation in the analysis of reinforced concrete wall-beam-slab joint under cyclic loading. Constr. Build. Mater. 2024, 449, 15. [Google Scholar] [CrossRef]
- Guo, S.; Huang, R. The AHP method of orthogonal trial. Coll. Math. 2004, 20, 114–117. [Google Scholar]
- Jia, L.; Fan, H.; Mi, X.; Shang, S.; Li, L.; Li, Z. Comprehensive performance evaluation of ceramsite concrete based on AHP weight analysis. J. Mater. Sci. Eng. 2022, 40, 774–778. [Google Scholar]
- Abubakar, A.; Idongesit, U.R.; Konitufe, C.; Mohammed, A. Prediction of Strength Properties of Concrete Containing Calcined Black Cotton Soil Using Response Surface Methodology. Am. J. Mater. Synth. Process. 2020, 5, 17. [Google Scholar] [CrossRef]
- Çetindemir, O. Nonlinear constitutive soil models for the soil–structure interaction modeling issues with emphasis on shallow tunnels: A review. Arab. J. Sci. Eng. 2023, 48, 12657–12691. [Google Scholar] [CrossRef]
- Wang, J. The Application of Abaqus in Civil Engineering; Zhejiang University Press: Hangzhou, China, 2006. [Google Scholar]
- Kuang, Z.; Liu, Z. Study on the mesh size determination method of blast wave numerical simulation with strong applicability. Heliyon 2023, 9, e13714. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Li, X.; Wang, Z.; Wang, Y.; Yan, C.; Jin, H. Numerical Analysis of Temperature Stress Generated by Hydration Heat in Massive Concrete Pier. Period. Polytech. Civ. Eng. 2025, 69, 461–469. [Google Scholar] [CrossRef]
- Jayaprakash, S.; Jegatheeswaran, D.; Paul, A.; Shanmugam, B. Prediction of the Mechanical Properties of Fibre-Reinforced Quarry Dust Concrete Using Response Surface and Artificial Neural Network Techniques. Adv. Civ. Eng. 2023, 2023, 8267639. [Google Scholar]
- Liu, X.; Chen, P.; Deng, Z.; Lian, N.; Xie, Y. Experimental study on the mechanical properties of polypropylene fiber-steel bar reinforced concrete pipe. Acta Mater. Compos. Sin. 2021, 38, 4349–4361. [Google Scholar]
- Ren, L. Mechanical Properties of Polypropylene Fiber Reinforced Concrete and its Application in Tunnel Secondary Lining. Master’s Thesis, Chongqing University, Chongqing, China, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).