Macro-Mesoscale Submodeling Approach for Analysis of Large Masonry Structures

Abstract

In this work, a sub-modeling technique is proposed for the analysis of large-scale masonry structures. The approach couples an anisotropic macroscale formulation, derived by incorporating the notion of a fabric tensor for an orthotropic material, with mesoscale analysis. The latter employs distinct inelastic constitutive relations assigned to the brick material and brick-mortar interfaces, which enable the tracing of localized damage propagation. The mechanical properties at the macro-level are identified from the ‘virtual’ set of data generated through mesoscale analysis, ensuring consistency between the two approaches in representing the masonry material across different scales. In the numerical analysis, the macroscale approach is first applied over the entire domain to interpolate the kinematic boundary conditions in a local region of interest, which is then re-analyzed based on the mesoscale framework. The developed strategy is illustrated by simulating the shear response of a large-scale unreinforced masonry wall with multiple window openings.

1. Introduction

The simulation of large-scale masonry structures (e.g., hydropower structures, historical buildings, and arch bridges) cannot be conducted at the scale of constituents as this would be computationally prohibitive. Therefore, a macroscale analysis is typically employed, which incorporates various homogenization/volume averaging schemes. Such an analysis is efficient; however, it is not very accurate in representing the local deformation field, particularly when it involves the onset and discrete propagation of damage.

In order to improve the accuracy of the solution, various special techniques have been used, which include substructuring and the stiffness separation method. Substructuring involves dividing a structure into smaller units that are analyzed independently, and their results are subsequently assembled (cf. ref. [1]). The stiffness separation method, on the other hand, focuses on partitioning the global stiffness operator into sub-stiffness matrices [2]. Both these approaches reduce the computational cost; however, the overall complexity can remain significant, particularly for very large and intricate systems. A viable alternative is the sub-modeling technique, which involves the remeshing of a coarse finite element discretization into smaller elements at different scales and locations. In this case, the nodal variables along the sub-model boundaries are constrained to match the results of the global model [3,4,5]. For additional boundary nodes, the interpolation order is usually determined by the type of elements used. The sub-modeling technique is currently the most common method for analyzing large-scale structures. It has been employed in a broad range of practical problems in the areas of composite mechanics [6,7,8], mechanical engineering [9,10], as well as civil engineering [11,12,13,14,15]. This approach is computationally efficient, while its performance is affected by the accuracy of mapping the boundary condition for the local model.

The main conceptual difficulty in the standard sub-modeling approach is that the mechanical properties at the global scale are generally not the same as those in the sub-model. This is particularly the case for materials with a heterogeneous mesostructure, such as masonry, where the global response is strongly anisotropic and size-dependent, while the constituents themselves remain isotropic and obey the principle of local action. In a typical macroscale approach, masonry is considered a continuum with an a priori defined internal structure. In this case, the equivalent properties are a function of properties of the constituents and the geometric layout. The most common approach for deriving the constitutive relation is the mathematical theory of homogenization or its practical implementation, i.e., volume averaging. Homogenization has been applied primarily in the context of periodic media by invoking the notion of a representative elementary volume (REV), from which the equivalent (i.e., volume-averaged) properties are acquired (cf. refs. [16,17,18,19,20]). Some attempts have also been made to assess the equivalent properties of non-periodic media [21], and a comprehensive review of different volume-averaging strategies is provided in ref. [22].

Apparently, the primary difficulty in the homogenization approach is the assessment of properties in the inelastic range, which requires the implementation of an incremental numerical scheme. In this case, an alternative methodology is the formulation of phenomenologically based macroscopic failure/yield criteria. Examples in the context of structural masonry include the studies reported in refs. [23,24,25,26,27]. In this approach, the major issue is the identification of the anisotropic strength parameters employed in the framework. The latter requires complex experiments on masonry panels, which can be quite expensive and are often subject to the strong influence of boundary conditions, so that the scatter in the data can be significant. Thus, this approach is typically combined with the generation of ‘virtual data’, which is obtained via a mesoscale analysis [28].

The analysis at the meso-level is conducted by examining all constituents (i.e., brick units, mortar joints, and brick–mortar interface) and their interactions. In this case, the properties of constituents can be directly acquired from standard mechanical tests. The weakest links in structural masonry are the brick–mortar interfaces, which require a contact law relating the traction rate to velocity discontinuity. The failure of constituents often involves the onset and propagation of localized damage associated with unstable strain-softening behavior, which must be accounted for. Common strategies for modeling damage propagation at the mesoscale include discrete and continuum methods. The former approaches consider the masonry assembly as individual blocks interacting through frictional joints (cf. refs. [29,30]), while the latter employ either standard or extended finite element schemes, often combined with the use of interface elements [31,32].

The present paper, which focuses on coupling an anisotropic macroscale formulation with mesoscale analysis, is organized as follows. In Section 2, a global plasticity framework is outlined, incorporating the notion of a microstructure/fabric tensor, which is employed in the functional form of the failure criterion. In Section 3, the mesoscale framework is discussed, in which irreversible plastic deformation is said to be triggered by failure along the brick-mortar interfaces. These interfaces are considered to be embedded in the adjacent intact zone, and a constitutive law with embedded discontinuity is employed. The mathematical framework is illustrated by a numerical example that involves macro-mesoscale sub-modeling applied to a large unreinforced masonry wall with multiple window openings.

2. Global Analysis: Macroscale Formulation

In the macroscale approach, masonry is treated as a continuum with a distinct internal structure. In this case, it is convenient to invoke the notion of a microstructure/fabric tensor, whose spectral decomposition may be written in the form

$$F_{ij}={(\lambda }_1-{\lambda }_3)t_i{t}_j+{(\lambda }_2-{\lambda }_3)n_i{n}_j+{\lambda }_3{\delta }_{ij}$$

(1)

where $n_i$,$t_i$ are the eigenvectors and $\lambda$’s are the eigenvalues. The tensor $F_{ij}$ can be normalized such that $F_{ii}=1$, which implies ${\lambda }_3=1-{\lambda }_1-{\lambda }_2$. In this case, the deviatoric part $D_{ij}$ of this tensor becomes

$$D_{ij}={3F}_{ij}-{\delta }_{ij}=3{(\lambda }_2-{2\lambda }_1-1)t_i{t}_j+{3(\lambda }_1+{2\lambda }_2-1)n_i{n}_j+(2-3{\lambda }_1-3{\lambda }_2){\delta }_{ij}$$

(2)

In order to correlate the strength properties with the fabric, an anisotropy parameter η is defined, which represents a projection of $D_{ij}$ on the so-called loading direction $l_i$. Thus,

$$\mathsf{\eta }=a_0+a_1{D}_{ij}{l}_i{l}_j; l_i=L_i/{\left(L_k{L}_k\right)}^{1/2}$$

(3)

where a’s are constants and the components of $L_i$ are the traction moduli on planes normal to the material axes. Substituting Equation (2) into Equation (3) leads, after some algebraic transformations, to

$$\mathsf{\eta }=\widehat{\eta }(1+C_1{\zeta }^2+C_2{\xi }^2+C_3); \zeta =n_i{l}_i, \xi =t_i{l}_i$$

(4)

where

$$C_1={\displaystyle \frac{3a_1{(\lambda }_1+{2\lambda }_2-1)}{a_0}}, C_2={\displaystyle \frac{3a_1{(\lambda }_2+{2\lambda }_1-1)}{a_0}}, C_3={\displaystyle \frac{a_1{(2-3\lambda }_1-3{\lambda }_2)}{a_0}},\widehat{\eta }=a_0$$

The above expression defines the value of the anisotropy parameter for an orthotropic material. Note that in the case of transverse isotropy, when $n_i$ is the preferred orientation, there is

$$F_{ii}=1 \Rightarrow { \lambda }_1={\lambda }_3; {2\lambda }_1+{\lambda }_2=1 \Rightarrow C_1=3a_1(1-{3\lambda }_1)/a_0,{ C}_2=0, { C}_3=-C_1/3$$

(5)

so that, the representation (4) reduces to

$$\mathsf{\eta }=\widehat{\eta }[1+b_1\left(3{\zeta }^2-1)\right]; \zeta =n_i{l}_i$$

(6)

where $b_1=C_1/3=a_1(1-3{\lambda }_1)/a_0$. In general, the functional form (3) may be enhanced by incorporating the higher-order terms in the dyadic product $l_i{l}_j$. In this case, Equation (6) becomes

$$\mathsf{\eta }=a_0+{\sum }_{m-1}^n{a}_m{\left(D_{ij}{l}_i{l}_j\right)}^m=\widehat{\eta }\left[1+{\sum }_{m-1}^n{b}_m{\left(3{\zeta }^2-1\right)}^m\right]$$

(7)

where $b_m=a_m(1-3{\lambda }_1)/a_0;(m=1,\dots ,n)$.

Given the representation above, the formulation follows now the framework outlined in refs. [27,28]. In particular, the conditions at failure are defined by the Mohr-Coulomb criterion with a Rankine cut-off in the tensile regime, both functions enhanced by the notion of anisotropy of strength. Thus, the failure criterion $F=0$ assumes the form

$$F=\mathit{max}(F_1,F_2)=0; F_1=\left({\sigma }_1-{\sigma }_2\right){+\eta }_s\left({\sigma }_1+{\sigma }_2\right)-2C{\eta }_s; F_2={\sigma }_1-{\eta }_t$$

(8)

where σ’s are the major and minor principal stresses, ${\eta }_s=sin \varphi$, where $\varphi$ is the friction angle, and ${\eta }_t$ is the tensile strength. For an anisotropic material, the parameter C, which is associated with hydrostatic pressure, is a constant, while the scalar strength parameters ${\eta }_s$ and ${\eta }_t$ are defined by the polynomial form (7). The deformation process is described using a plasticity formulation. The latter incorporates the notion of a yield/loading surface, which is defined in a functional form similar to that of Equation (8), i.e.,

$$f_1=\left({\sigma }_1-{\sigma }_2\right)+\mu \left({\sigma }_1+{\sigma }_2\right)-2C\mu =0; \mu ={\eta }_s{\displaystyle \frac{\vartheta \kappa }{B+\kappa }}; f_2=F_2=0$$

(9)

where B and $\vartheta$ are material constants, and $\kappa$ is the hardening parameter identified with accumulated plastic distortion. Note that the parameter $\vartheta$ is used here to determine the onset of localized deformation that is assumed to occur at $\mu ={\eta }_s$, so that the conditions of failure are consistent with Mohr-Coulomb criterion, i.e., $f_1=F_1$. The formulation incorporates a non-associated flow rule, whose functional form is analogous to that used in refs. [26,28]. In the tensile range, the material is considered elastic-brittle, with the onset of brittle response occurring at $F_2=0$. Finally, the mechanical response in the presence of discontinuous (i.e., localized) deformation is modeled using a constitutive law with an embedded discontinuity. The latter is briefly outlined in Section 3 below.

3. Local Analysis: An Overview of the Mesoscale Formulation

In the mesoscale framework, irreversible plastic deformation is assumed to result from failure along the brick-mortar interfaces, which are the weakest links in the masonry mesostructure. The interfaces are considered to be nested in the adjacent intact zone, and a constitutive law with embedded discontinuity (CLED) is employed [33,34]. In the CLED approach, the averaged mechanical properties in a referential domain containing a discrete macro-fracture with unit normal $e_i$, are established. The methodology incorporates the volume averaging of the gradient of the discontinuous velocity field. The relation between the velocity jump and the average macroscopic strain rate is then obtained by imposing the continuity of traction across the macrocrack. The governing constitutive relation takes the general form [34]

$${\dot{\sigma }}_{ij}={\overline{D}}_{ijkl}{\dot{\epsilon }}_{kl}; {\overline{D}}_{ijkl}=D_{ijpq}^e\left({\delta }_{pk}{\delta }_{ql}-\chi e_p{E}_{qr}{D}_{rskl}^e{e}_s\right); E_{ij}={(K_{ij}+\chi D_{ijpq}^e{e}_p{e}_q)}^{-1}$$

(10)

Here, ${\overline{D}}_{ijkl}$ is the equivalent tangential stiffness operator whose components are functions of properties of the intact material ($D_{ijpq}^e$), the interfacial stiffness ($K_{ij}$) and a length scale parameter $\chi$, the latter defined as the ratio of the surface area of the macrocrack to the referential volume, i.e., that associated with the corresponding finite element. The intact material is perceived as elastic, while the stiffness of the brick-mortar bond is established based on a strain softening plasticity framework. By analogy to the macroscale formulation, the onset of irreversible deformation along the interface is defined by Coulomb criterion with tension cut-off, i.e.,

$$\tilde{F}=\max \left({\tilde{F}}_1,{\tilde{F}}_2\right)=0; {\tilde{F}}_1=\tau +\upsilon \left(\sigma +C\right); {\tilde{F}}_2=\sigma -f_t$$

(11)

where $\tau$ and σ are the shear and normal components of the traction acting at the discontinuity surface, $f_t$ is the tensile strength, while C and $\upsilon$ are the strength parameters for the Coulomb criterion. In formulating the stiffness operator $K_{ij}$ an associated flow rule is employed, and the degradation functions are selected in an exponential form similar to that used in ref. [35], viz.

$$\upsilon ={\upsilon }_r+\left({\upsilon }_0-{\upsilon }_r\right)e^{(-\alpha g_T)}; f_t=f_t^0{e}^{(-\beta g_N)}$$

(12)

Here, $g_T=\left|g_i-g_k{e}_k{e}_i\right|$ and $g_N=g_i{e}_i$ are the tangential and normal components of $g_i$, i.e., the irreversible part of the displacement discontinuity. Moreover, ${\upsilon }_0,f_t^0$ are the values of $\upsilon ,f$ at the onset of strain-softening, ${\upsilon }_r$ is the residual friction coefficient, and $\alpha ,\beta$ are the material constants. It should be pointed out that, in the case of macrocracks forming in the brick material, similar evolution laws may be employed; however, in this case, the initial values of ${\upsilon }_0,f_t^0$ are defined by the stress state at the onset of softening.

The CLED formulation, as defined by Equation (10), can also be employed to model localized deformation at the macroscale. In this case, the onset of localization is governed by the condition $f_1=F_1$ or $f_2=F_2$, cf. Equation (9), and the analysis typically incorporates a ‘smeared’ approach, i.e., without a discrete tracing of crack propagation. It is also worth mentioning that, in general, since the global solution serves primarily the purpose of specification of kinematic boundary conditions for the sub-model, it may be sufficiently accurate to conduct the macroscale analysis assuming $\vartheta =1$ in Equation (9). The latter implies that the conditions at failure are approached asymptotically, i.e., no strain localization occurs in the global model.

Both the macro-and mesoscale constitutive relations incorporate several material parameters that need to be identified. In general, the specification of strength anisotropy parameters ${\eta }_s\left(\zeta \right)$ and ${\eta }_t\left(\zeta \right)$ requires generation of ‘virtual data’ based on the mesoscale analysis of masonry panels subjected to axial/biaxial compression-tension at different orientations relative to the direction of loading. At the same time, the identification of the parameters appearing in the mesoscale formulation requires standard tests on constituent materials, i.e., axial compression/tension of the brick samples and shear tests involving failure along the brick-mortar bond. The numerical examples provided in this work are heuristic, and the specification of the material parameters/functions is largely based on the results reported in ref. [28].

4. Numerical Analysis Involving the Sub-Modeling Approach

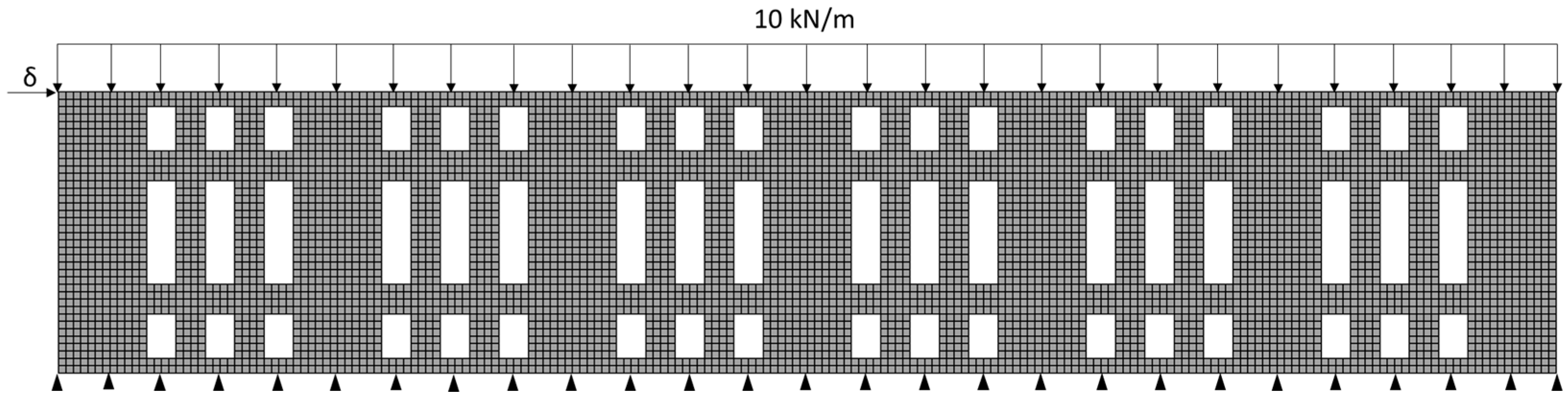
In this section, the sub-modeling framework incorporating distinct macro-and mesoscale approaches is applied to the finite element analyses of a large masonry wall with multiple window openings. The geometry of the structure, as depicted in Figure 1, resembles the general layout of the units of the Beauharnois hydropower generating station located along the St. Lawrence Seaway in Quebec, Canada. The analyzed part of the wall has a span of 102 m, a height of 19 m, and a thickness of 0.5 m. The large window openings measure 7 m × 2 m, while the smaller ones are 3 m × 2 m. The bricks have dimensions of 24 × 12 × 4 cm and are arranged in a running-bond pattern.

The elastic and strength properties of the constituents (i.e., bricks and brick-mortar joints) incorporated in the analysis were similar to those reported in ref. [28] and are provided in

Table 1. Mechanical properties of the masonry constituents.

	Bricks	Brick-Mortar Bond
Young’s modulus (MPa)	6750	N/A
Poisson’s ratio	0.17	N/A
Tensile strength ${\eta }_t,f_t$ (MPa)	2.2	0.2
Friction coefficients ${\eta }_s,\upsilon$	0.78	0.7
Constant C (MPa)	4.5	0.4
Interface normal stiffness, $k_n$ (N/m)	N/A	1.3*108
Interface shear stiffness, $k_t$ (N/m)	N/A	6.2*108

. These properties were also employed to identify the macroscale parameters, including the approximation coefficients appearing in the definitions of the scalar anisotropy functions, Equations (7) and (8). For the latter purpose, the results of mesoscale simulations (cf. ref. [28]) were first used to assess the ultimate strength of masonry panels under biaxial tests with a fixed ratio r of tensile to compressive stress. This data was then employed to find the best-fit approximations to both functions ${\eta }_s\left(\zeta \right)$ and ${\eta }_t\left(\zeta \right)$. The corresponding polynomial approximations of the 3rd and 4th order, respectively, are shown in Figure 2 and yield the following sets of coefficients

$$\begin{array}{l}{\eta }_s={\eta }_s\left(\zeta \right)\to \widehat{\eta }=1.97, { b}_1=-0.24, { b}_2=-0.10, { b}_3=0.09\\ {\eta }_t={\eta }_t\left(\zeta \right)\to \widehat{\eta }=0.59, { b}_1=-0.68, { b}_2=-0.15, { b}_3=0.41, { b}_4=-0.12\end{array}$$

The deformation properties at the macroscale were assigned based on data generated from external artificial neural networks (ANNs), as described in ref. [28]. These ANNs, which incorporate the constituent properties as inputs, were trained using an extensive set of data generated virtually through numerical simulations. Details of their architecture, input-output structure, training dataset, and validation are provided in the original reference. Thus, the equivalent elastic transversely isotropic properties were assessed as

$$E_x=5100 \mathrm{M}\mathrm{P}\mathrm{a}, E_y=5400 \mathrm{M}\mathrm{P}\mathrm{a}, {\upsilon }_{xy}=0.12, {\upsilon }_{xz}=0.14, G_{xy}=2300 \mathrm{M}\mathrm{P}\mathrm{a}$$

while the hardening parameters, Equation (9), were defined as B $=1.2\times {10}^{-6},\vartheta =1.025$.

For the mesoscale analysis, the softening parameters for the brick-mortar bond were taken as $\alpha ={5000 \mathrm{m}}^{-1},{\upsilon }_r=0.7{\upsilon }_0$ and $\beta ={7500 \mathrm{m}}^{-1}$ (cf. ref. [28]). These parameters can be identified by fitting the corresponding traction-displacement relations in the softening regime using the exponential functions given in Equation (12). In general, the same strain-softening properties were also assigned to the fracture zone in the macroscale simulations. In this case, the post-localization behavior was described using the CLED formulation (cf. Equation (10)), which, as mentioned earlier, incorporates a ‘smeared’ approach without the discrete tracking of the crack propagation.

Figure 3 shows the discretization of the macroscale model and the boundary conditions adopted. The wall was considered fixed at the base and was initially subjected to a gravitational load corresponding to a unit weight of 20 kN/m³, as well as a uniformly distributed vertical load of 10 kN/m. In the second stage, a lateral displacement δ was applied at the top until ultimate conditions were reached. A non-structured mesh was employed, incorporating a total of 5880 eight-node cubic elements with an element size of 0.5 m.

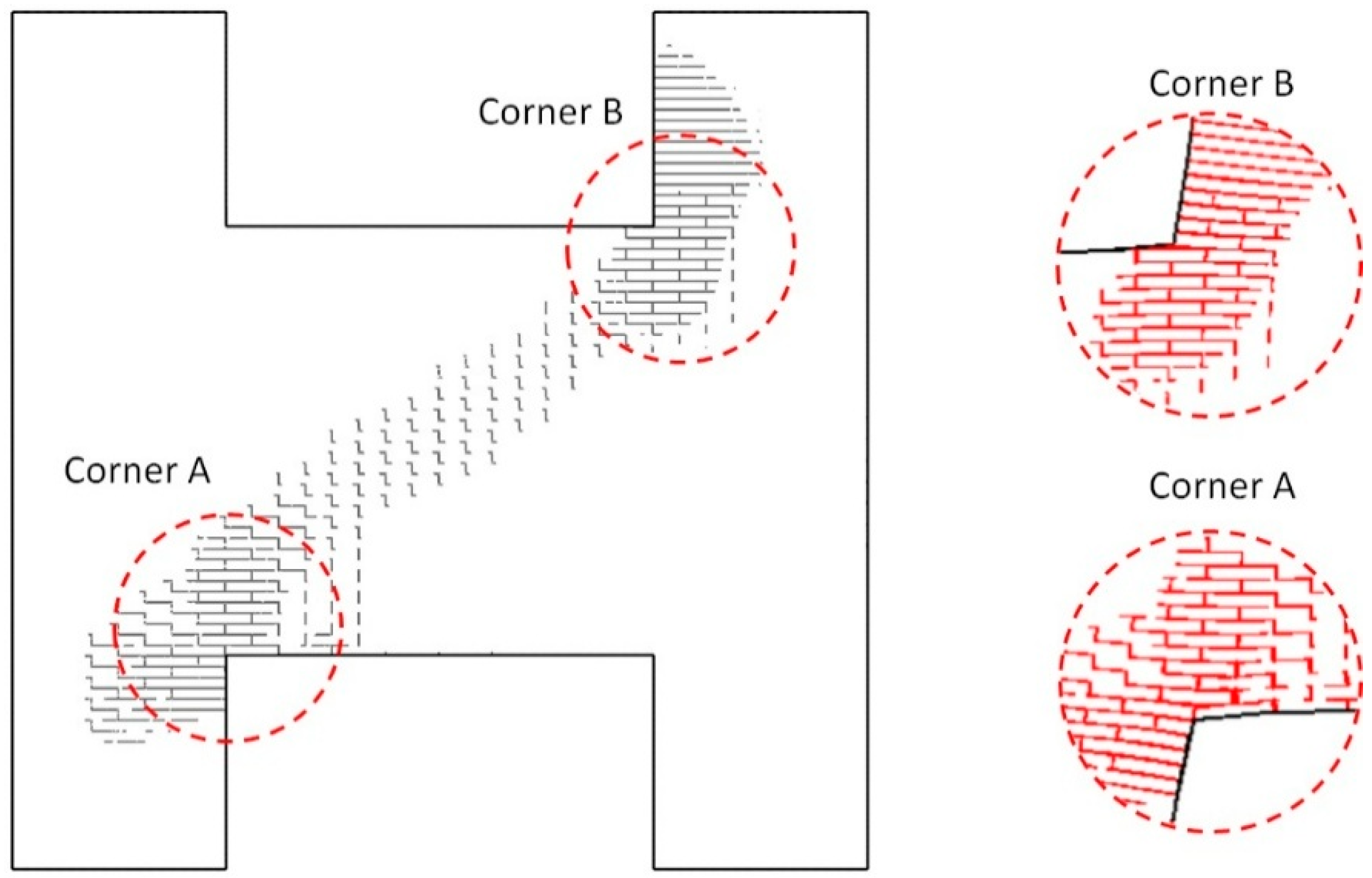
The results of the global simulations are presented in Figure 4. The figure shows the relation between the applied horizontal displacement and the resultant lateral shear force. It is evident that the response becomes unstable after reaching the peak, and the predicted ultimate load has a value of approximately 3700 kN. The corresponding evolution of the damage pattern is shown in the adjacent figure. At the initial stages of loading, fracture zones develop around the top-left and bottom-right corners of the window openings. As the load increases, a significant propagation of damage occurs, leading to a loss of stability at the macroscale. Note that the bottom picture in this figure shows the extent of damage at the ultimate load.

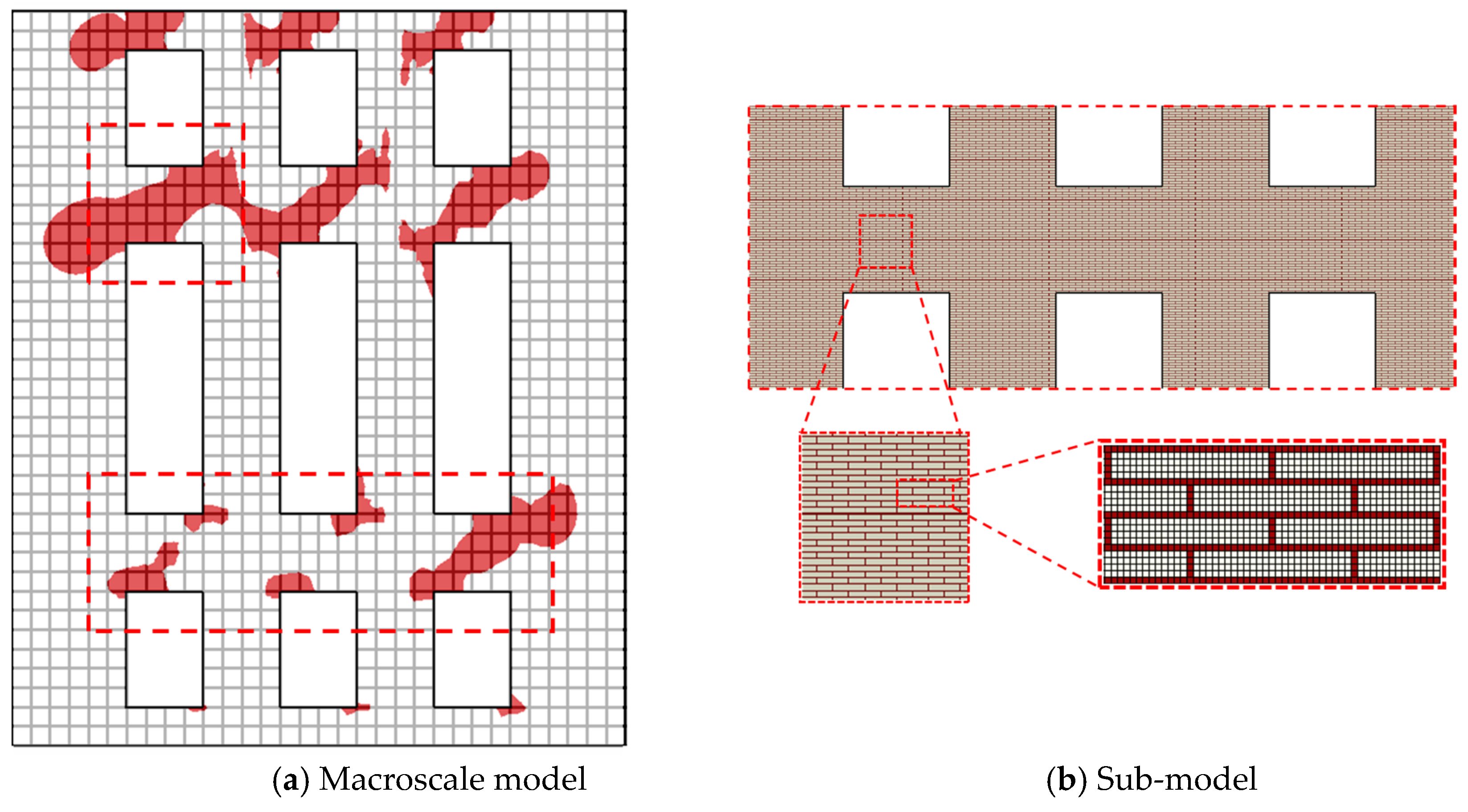
Sub-modeling simulations incorporating a detailed FE mesh at the meso-level were performed for the parts of the structure that experienced the most significant damage. Figure 5a shows the two subdomains selected for analysis. Both incorporate the region confined to the vicinity of the window openings, and the boundary conditions are constrained to match the results from the global model. The simulations were based on the mesoscale formulation and employed a non-structured mesh with up to 624,000 cubic elements, as shown in Figure 5b.

It should be emphasized again that the global and local analyses were conducted independently, with the global model solved first to capture the overall structural response. The resulting displacement history was then transferred to the boundary nodes of the refined region, which are referred to as the driven nodes. A key factor affecting the accuracy of this approach is the interpolation of the boundary displacements. In general, when the global and local models have a matching node-to-node topology, the displacement values can be transferred directly, thereby minimizing interpolation errors. For the additional nodes in the local model, linear interpolation was employed to estimate the values at the boundary of the refined region. This is illustrated in Figure 6, which shows the geometry of the sub-model for the top part of the structure, along with the boundary displacements at the driven nodes. Note that the latter refer to the stage at which the ultimate lateral shear force (3700 kN) is reached.

The two main aspects examined in the local models involve a more precise assessment of the fracture pattern and evaluation of local stability within the considered subdomains. Figure 7 shows the distribution of the cracked zones at the ultimate lateral load in the top section of the unit. The extent of the damage is similar to that predicted by the macro-model. However, the fractured zones have a more localized nature, and it is evident that the mechanism involves failure along the brick-mortar interfaces. In general, damage along the bed joint interfaces is associated with a shear mode (viz. Coulomb criterion, Equation (11)), while the head joints experience a tensile fracture (Rankine criterion, Equation (11)). The adjacent figure shows a zoom-in of the region close to the corner of the window opening. Here, a deformed configuration is displayed, which shows the non-homogeneity in the fracture aperture.

Figure 8 presents a similar set of results for the bottom subdomain, which contains parts of all three rows of window openings. The results are qualitatively similar to those shown in Figure 7; however, the damage is less pronounced as it remains confined to some corners of the openings. The zoom-in shows again a more detailed picture of the deformed configuration.

The structural integrity within the considered subdomains may be assessed by examining the second rate of internal work $\ddot{w}={\int }_{\Omega }{\dot{\sigma }}_{ij}{\dot{\epsilon }}_{kl}d\Omega$ (cf. ref. [35]). Physical stability is associated with a positive value, i.e., $\ddot{w}>0$, while the onset of instability corresponds to $\ddot{w}=0$. In the latter case, the global stiffness matrix becomes singular (i.e., its determinant is equal to zero). 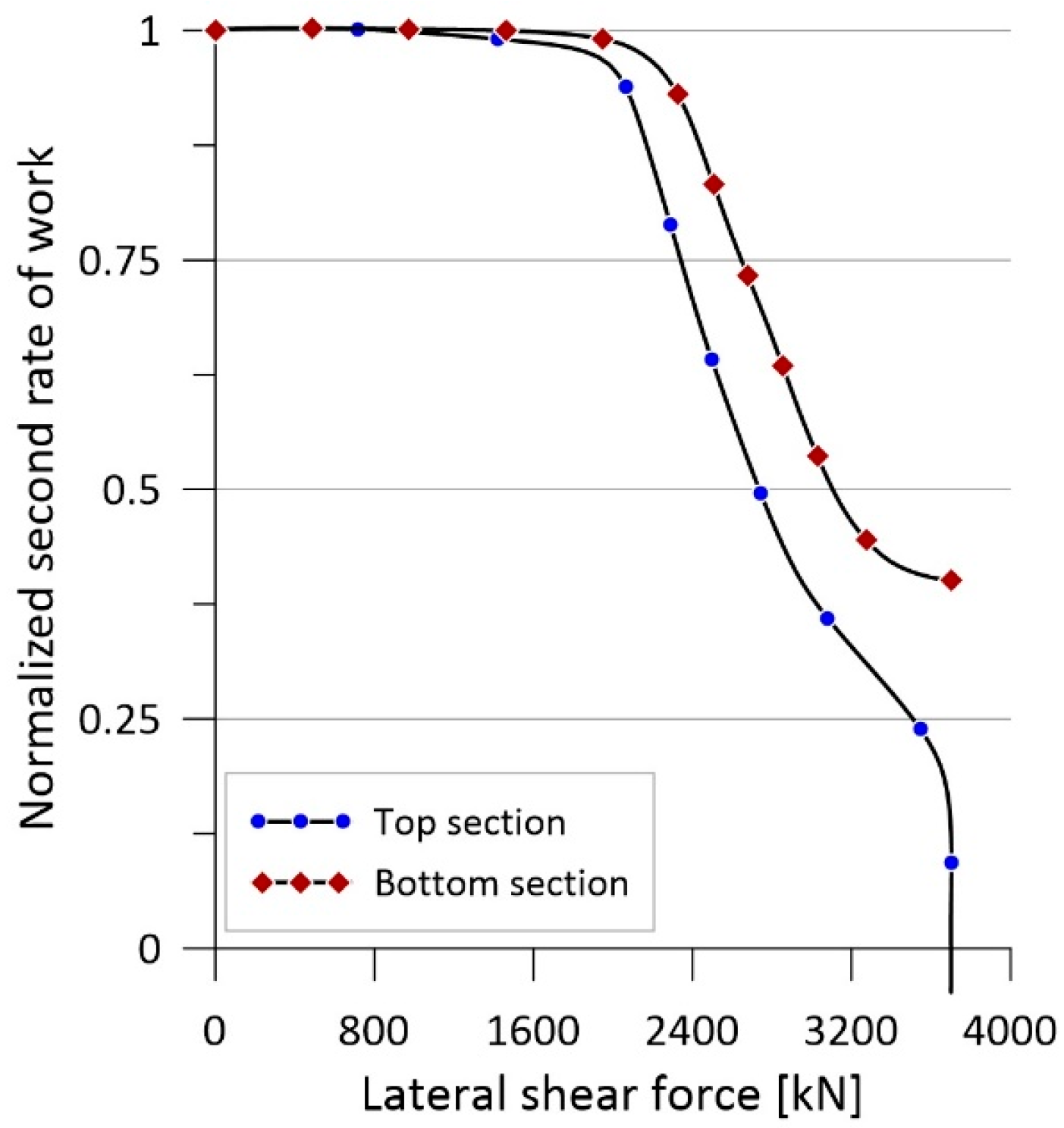Figure 9 shows the evolution of $\ddot{w}$ normalized with respect to that corresponding to the elastic solution, i.e., ${\ddot{w}}_0={\int }_{\Omega }{\dot{\sigma }}_{ij}^e{\dot{\epsilon }}_{kl}d\Omega$, so that $1\ge \ddot{w}/{\ddot{w}}_0\ge 0$. Plots are provided for both subdomains considered in the analysis. It is evident here that for the top section, the second rate of work becomes negative when the ultimate load is approached, which is indicative of the loss of stability. For the bottom section, however, $\ddot{w}$ remains positive, which implies that the observed extent of damage is still associated with a stable response within this subdomain.

5. Final Remarks

The main focus of this work was the development and implementation of a sub-modeling technique for the analysis of large-scale masonry structures. The proposed methodology requires the assignment of distinct constitutive relations at the macro and meso levels. This is consistent with the fact that masonry is a structured medium, and its properties at both scales are different. At the macro level, the material is heterogeneous, and its response is strongly anisotropic, while the constituents themselves may be considered isotropic. The formulation is phrased such that the specification of anisotropy parameters at the global scale requires the generation of ‘virtual data’ based on the local mesoscale analysis. Thus, there is an implicit interaction between the two scales, and the boundary conditions for the sub-model can be predicted fairly accurately.

The sub-modeling approach is practical and effective for examining the fracture mode and local displacement field. This is particularly significant in the context of large engineering structures of strategic importance. In this case, a local analysis can be performed for selected parts of the structure to assess their stability and the extent of damage. Note that the latter requires accounting for the onset and discrete propagation of localized deformation. This was done here by invoking a constitutive law with embedded discontinuity, which has a non-local nature, as it incorporates an internal scale parameter.

The numerical example provided in Section 4 demonstrates the pragmatic aspects of the proposed approach. For the given geometry, the mesoscale analysis of the entire wall, as shown in Figure 1, is computationally not feasible, while the macroscale approach alone does not provide adequate insight into the local phenomena (cf. Figure 4). In contrast, the sub-modeling scheme incorporating the CLED approach is efficient and does not require the use of interface elements. As a result, a simple non-structured mesh can be employed, which incorporates a manageable number of degrees of freedom (viz. Figure 5). The analysis allows the fracture mode to be traced in a discrete manner, and the evolution of the second rate of internal work can assist in examining the stability of the considered subdomain.