Sustainable Reinforcement Methods for Brick Masonry Walls: An Experimental and Finite Element Analysis Approach
Abstract
1. Introduction
2. Materials and Experimental Framework
2.1. Material Characteristics
2.2. Wall Preparation
2.3. Fiberglass/Steel Strengthening
2.4. Test Setup and Instrumentation
2.4.1. Axial Compression
2.4.2. Diagonal Compression
3. Experimental Results
3.1. Failure Modes and Peak Capacity of Walls
3.1.1. Reference Specimens Without Plaster
3.1.2. Plastered Specimens
3.1.3. Walls Strengthened with Steel Mesh Under Axial Load
3.1.4. Walls Strengthened with Steel Mesh Under Diagonal Load
3.1.5. Walls Strengthened with Fiberglass Mesh Under Axial Load
3.1.6. Walls Strengthened with Fiberglass Mesh Under Diagonal Load
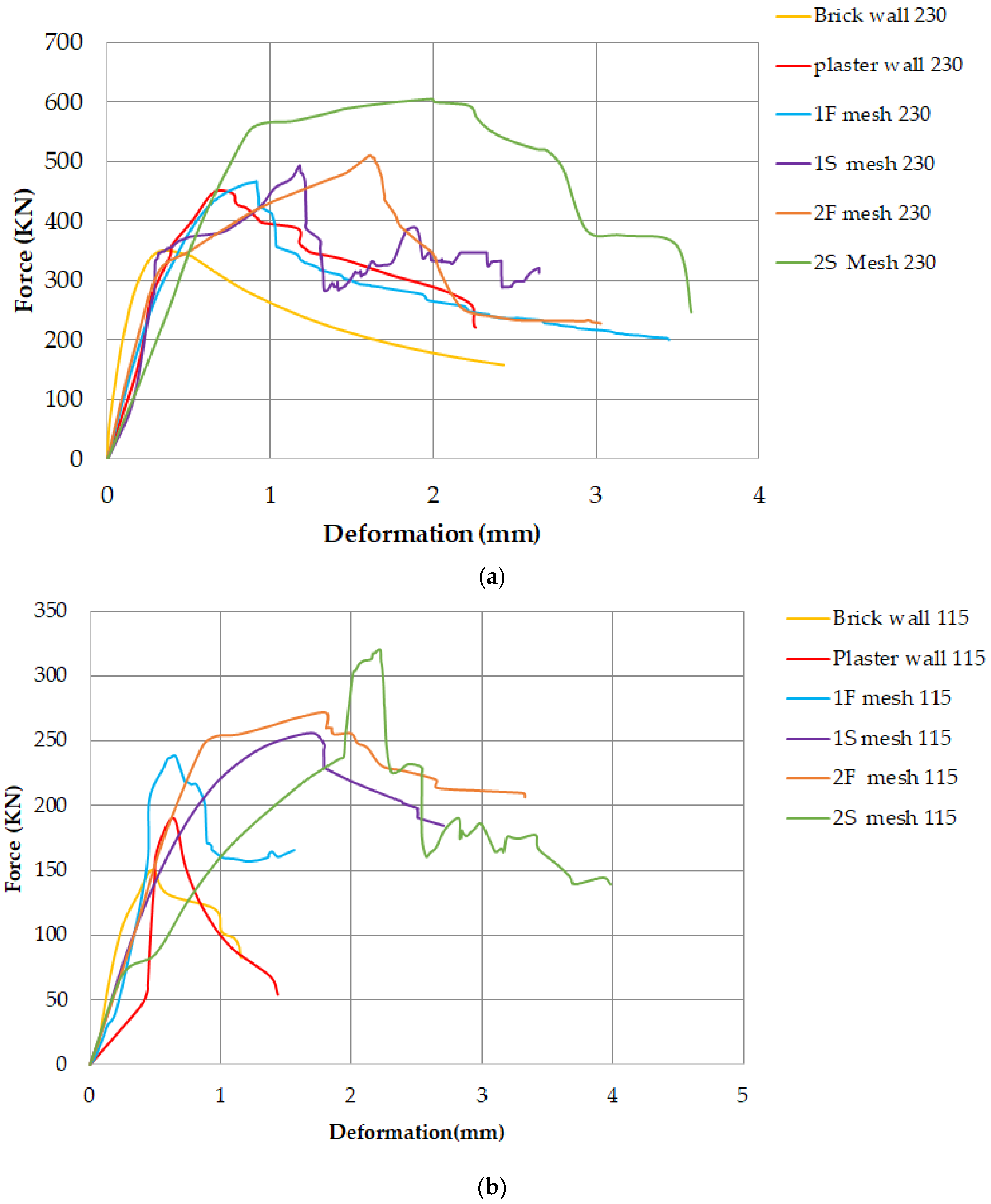
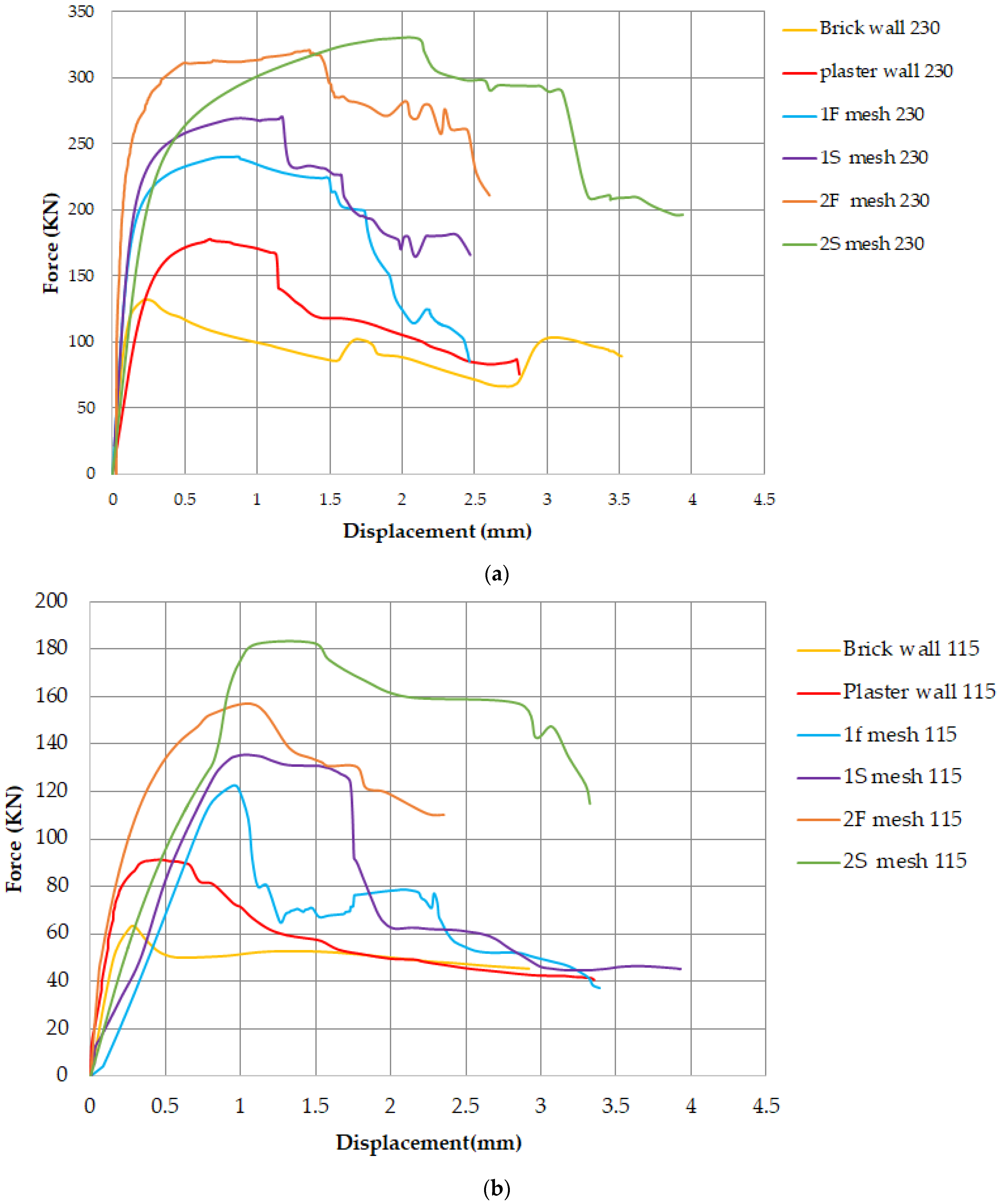
3.2. Peak Capacity and Load vs. Deflection Curves
3.2.1. Walls Under Axial Compression
3.2.2. Walls Under Diagonal Compression
3.3. Load vs. Deflection Curves
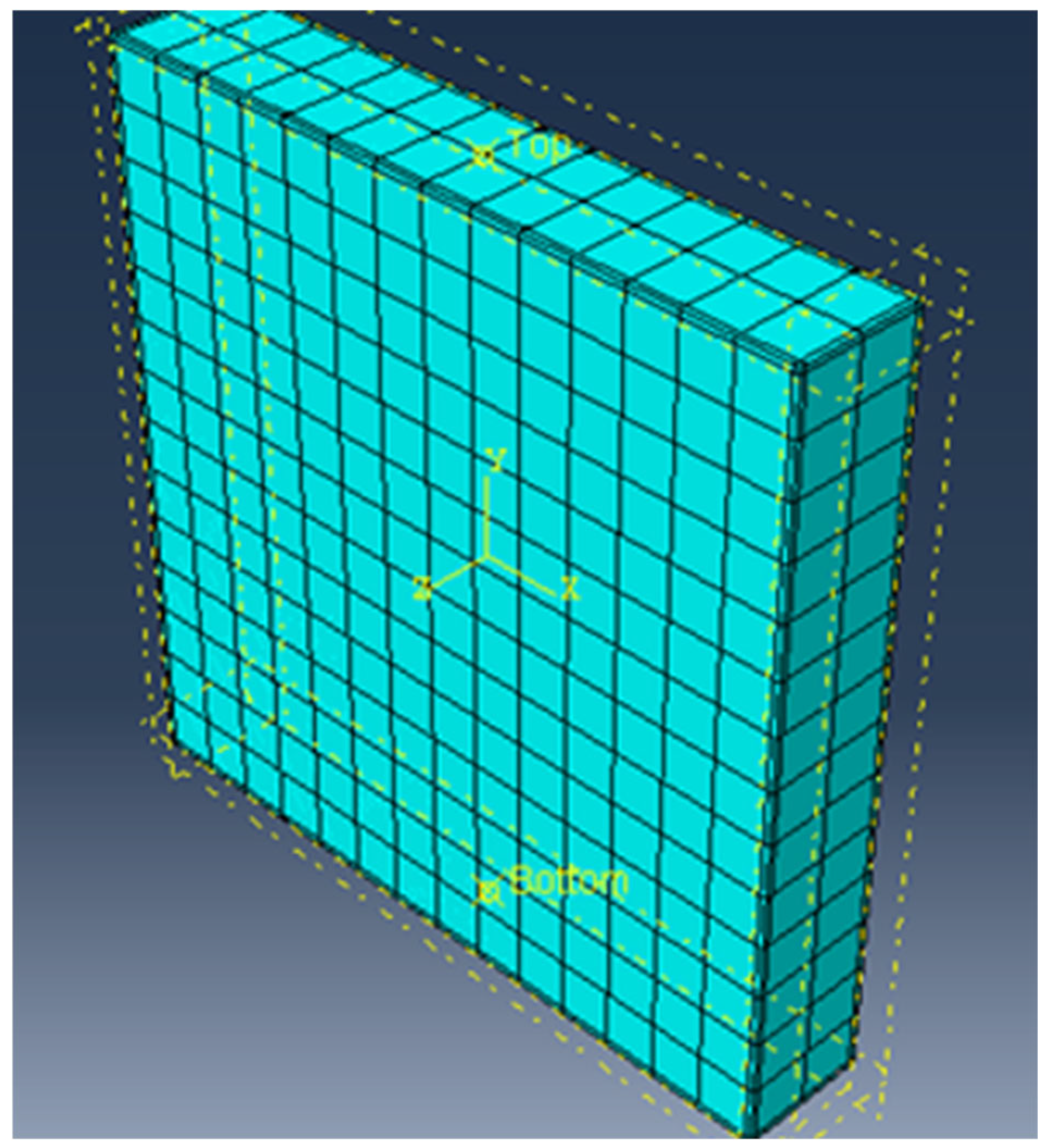
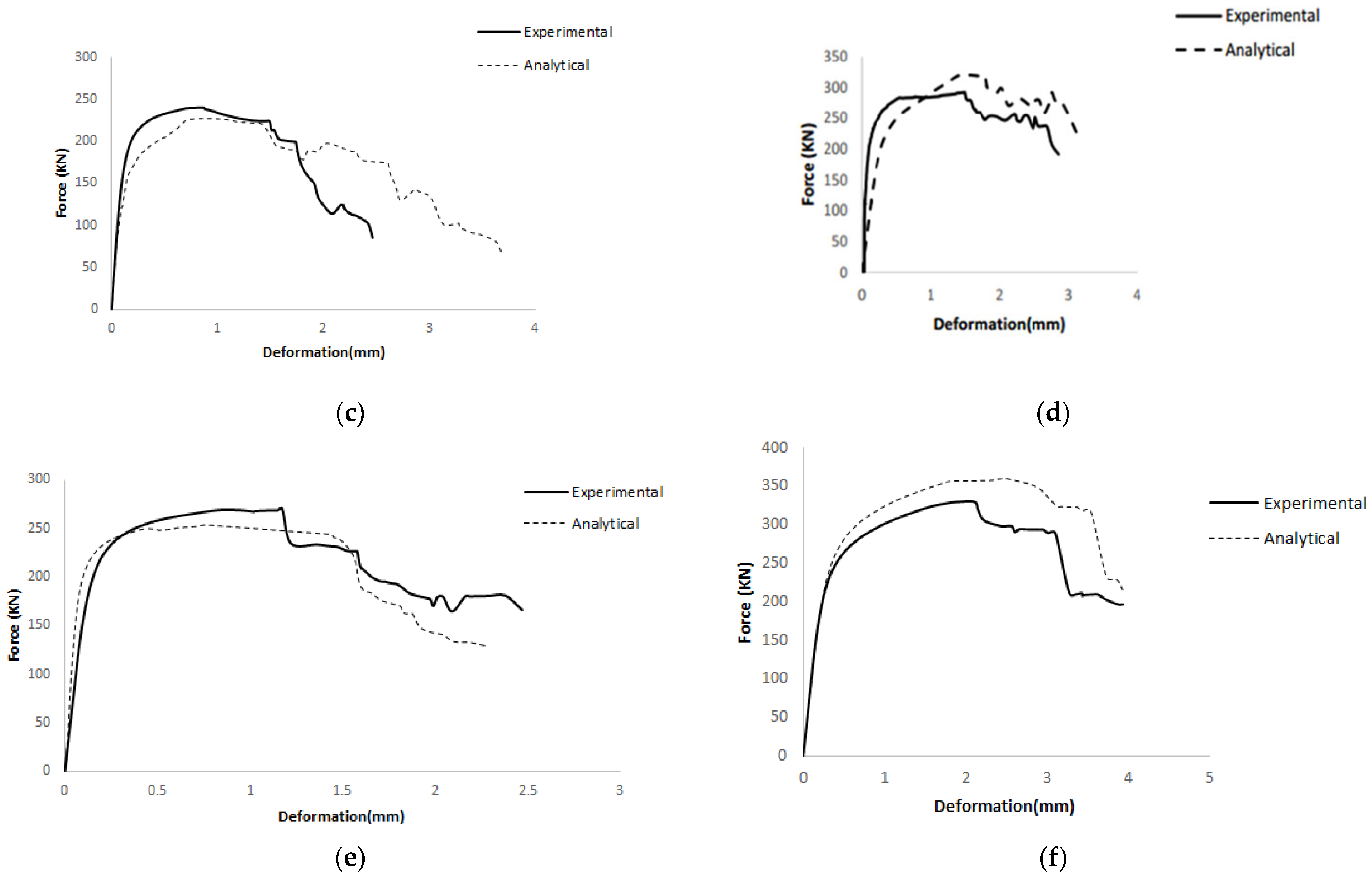
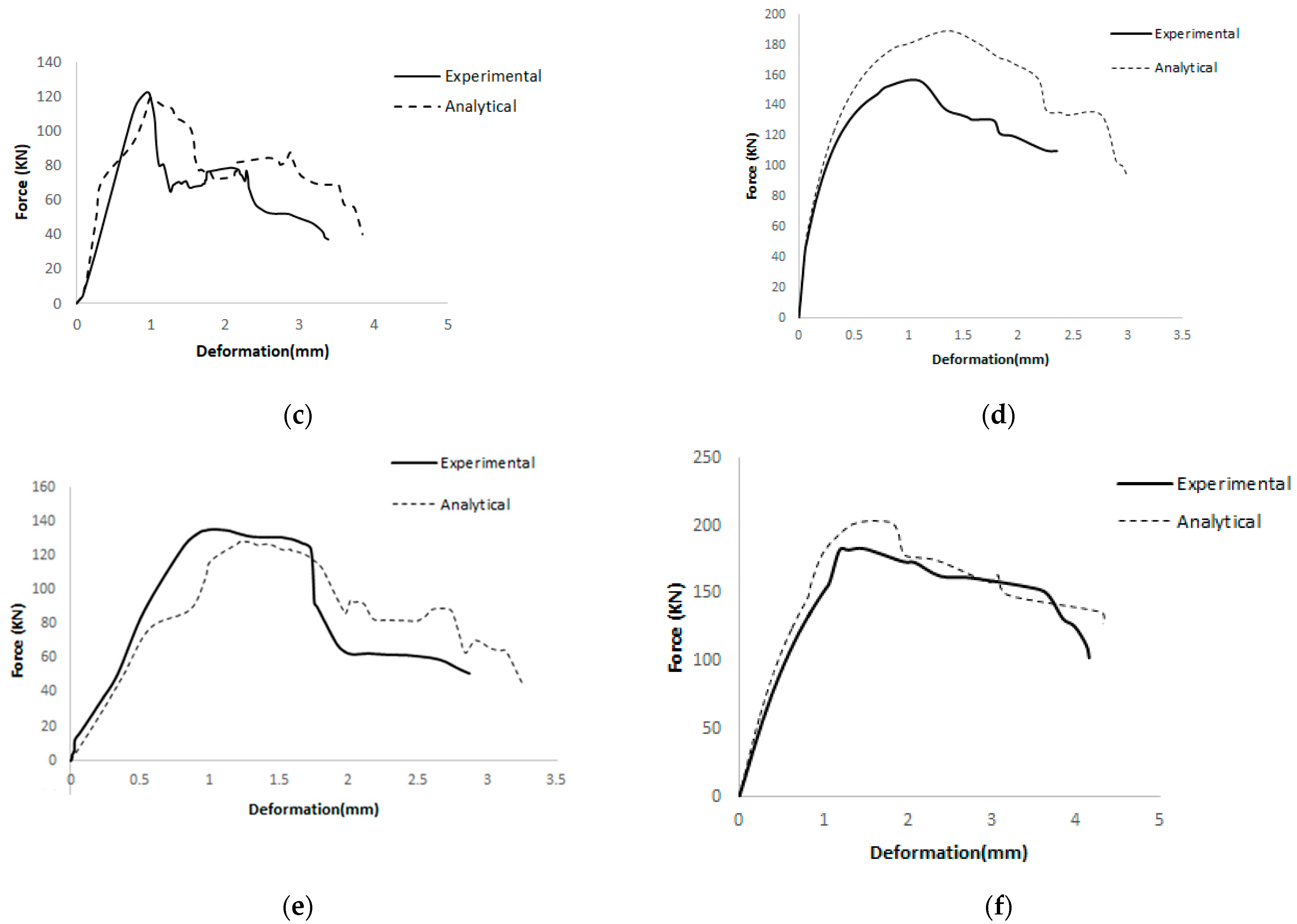
4. Numerical Modeling
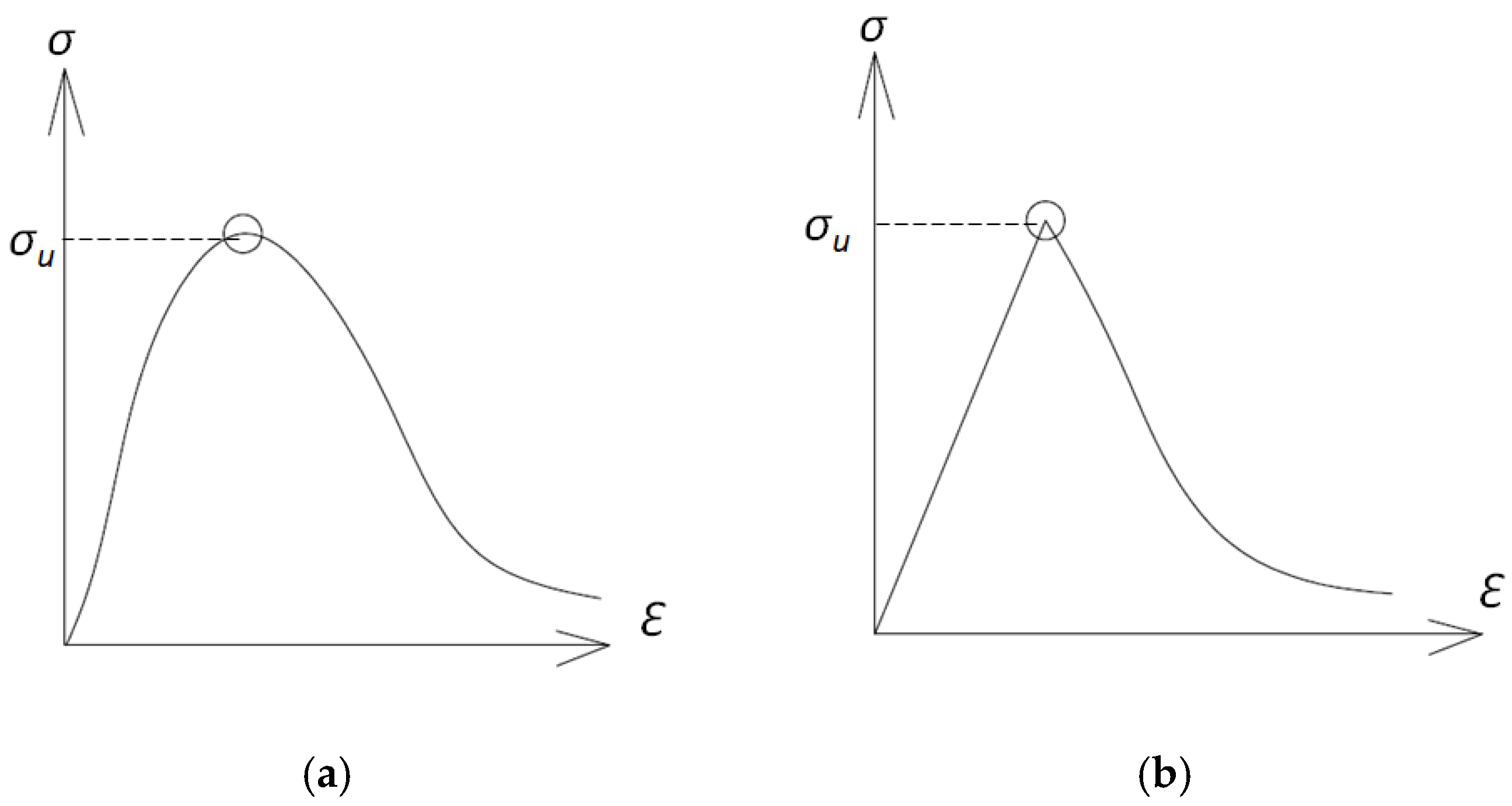
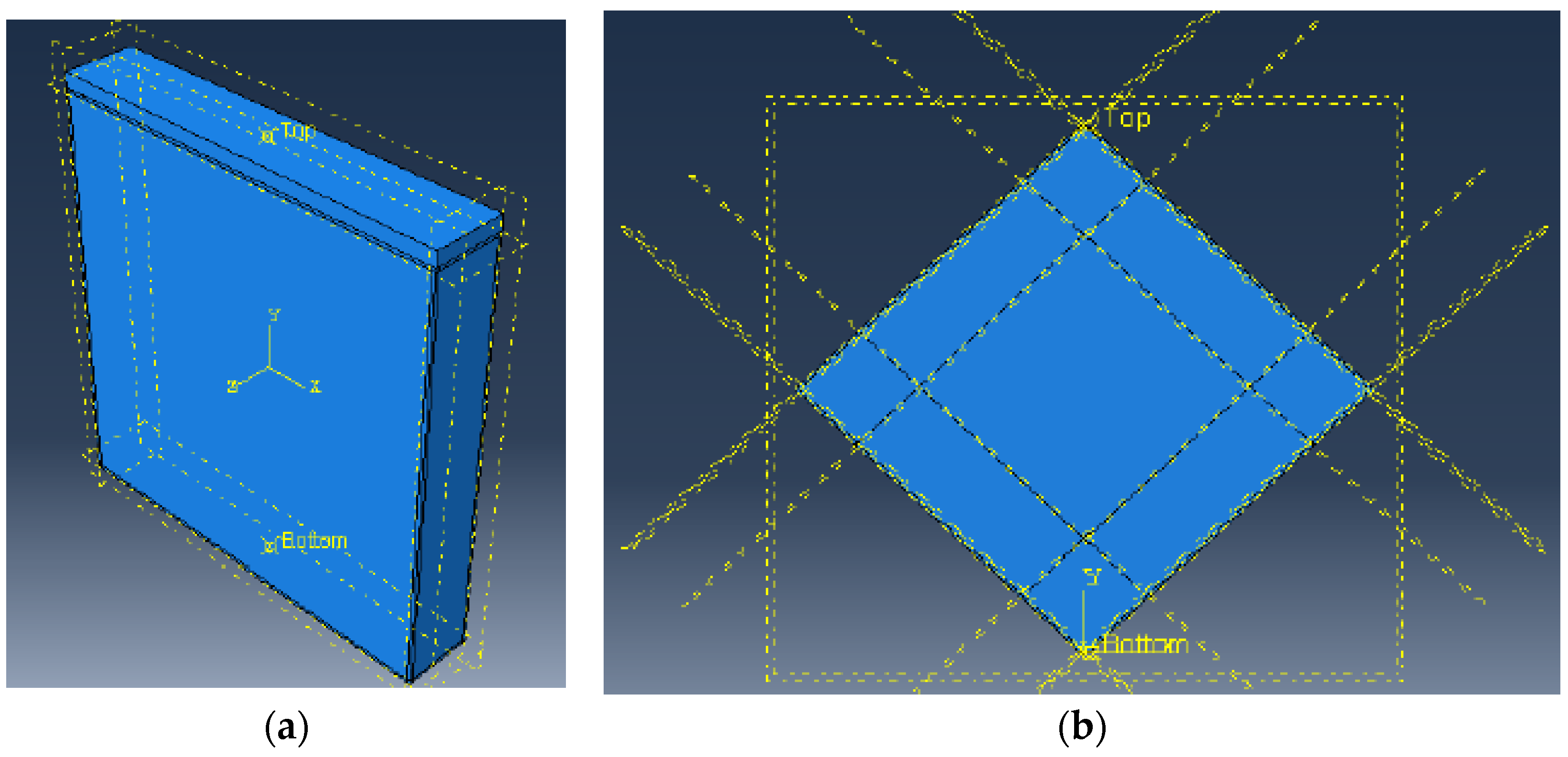
4.1. Modeling Strategy
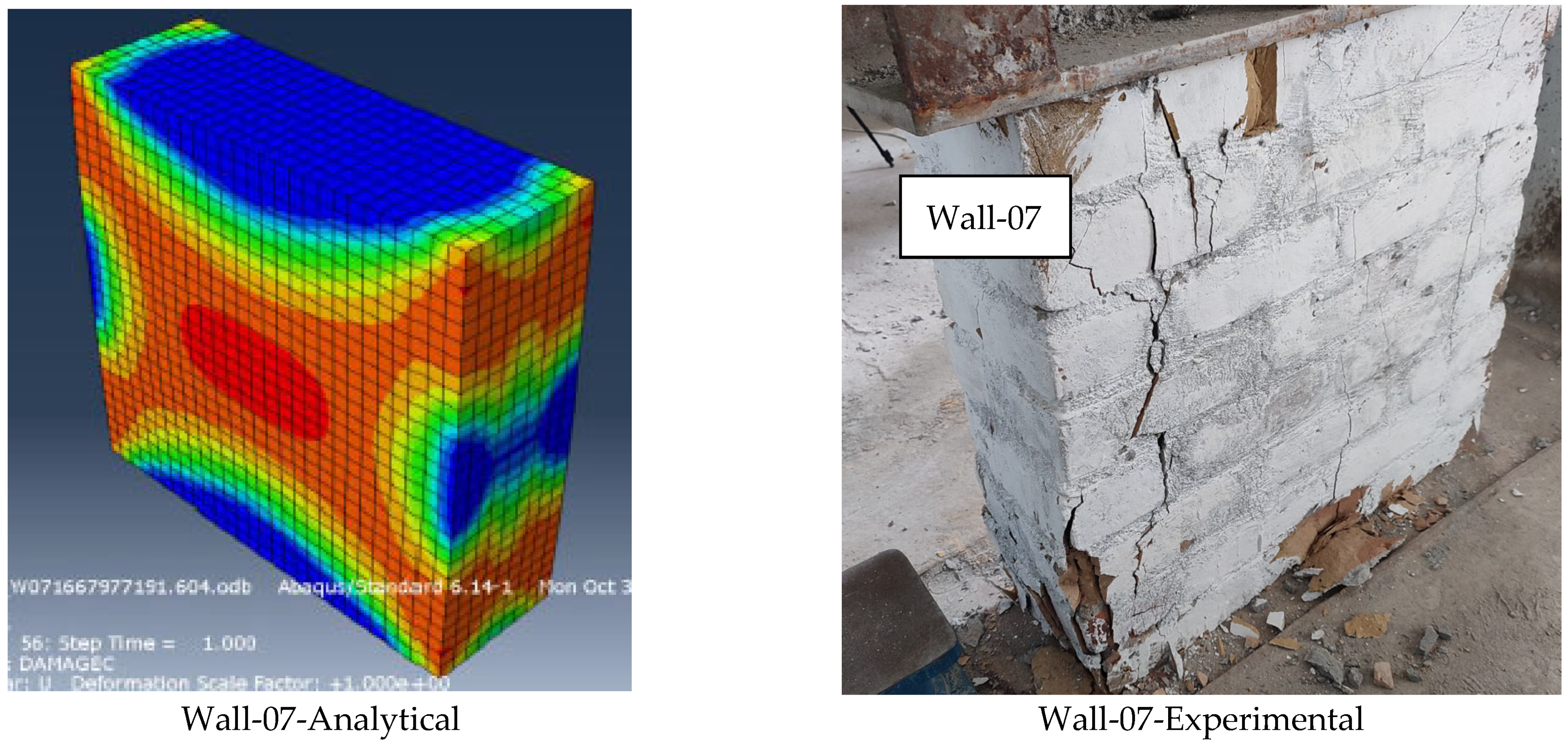
4.2. Axial Compression Behavior of Brick Walls with Abaqus
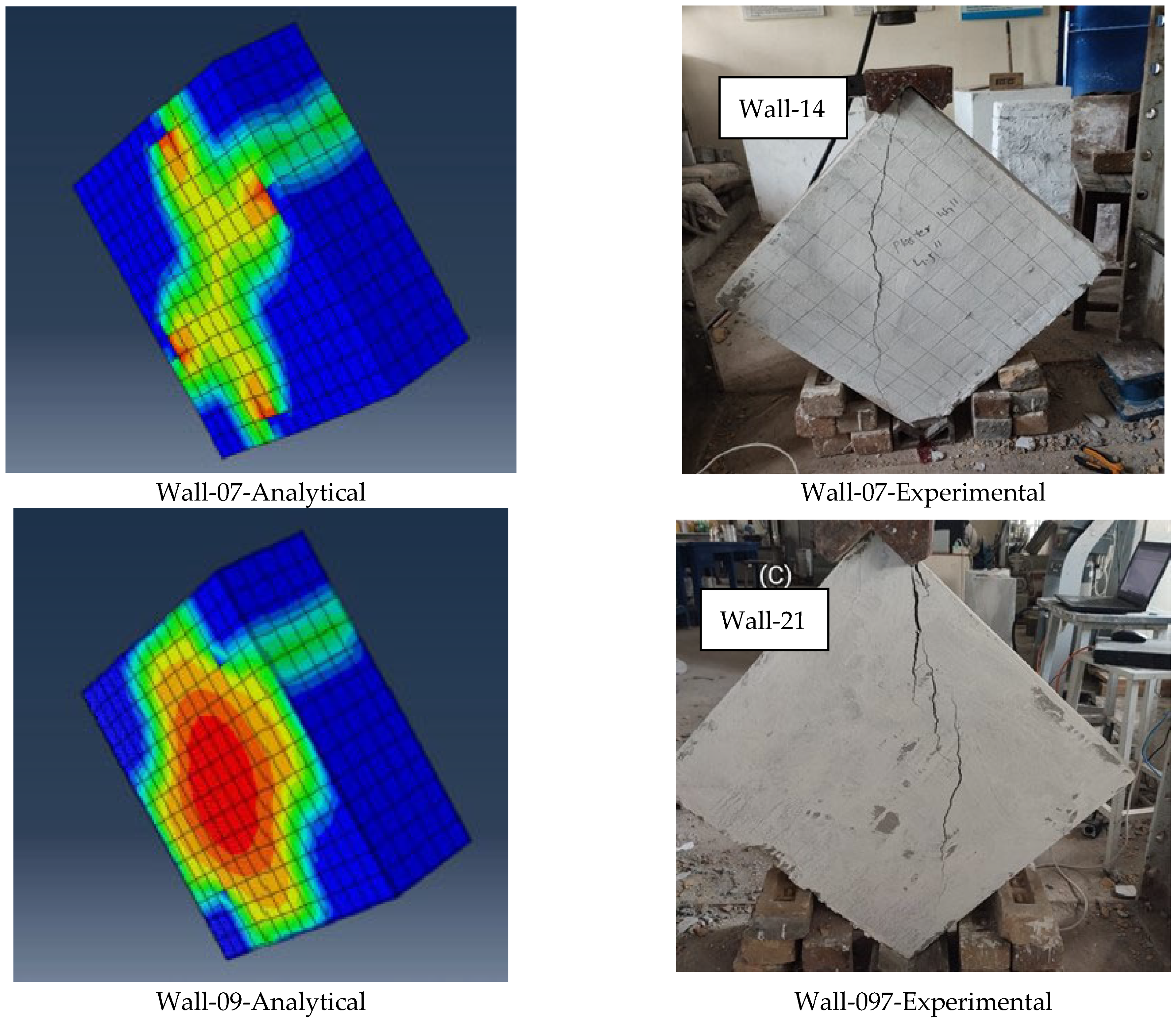
4.3. Diagonal Compression Behavior of Brick Walls with Abaqus
5. Conclusions
- Double-layer steel mesh exhibited the highest axial and shear strength among all reinforcement types, outperforming double-layer fiberglass mesh, single-layer steel mesh, single-layer fiberglass mesh, plaster walls, and unreinforced brick walls in both single and double brick masonry walls. The brittleness of brick masonry walls was reduced with the application of steel and fiberglass mesh, which, in turn, enhanced the deformation capacity of the walls. The increased strength and enhanced deformation capacity observed in walls reinforced with steel and fiberglass meshes can be attributed to the reduced ductility of the members.
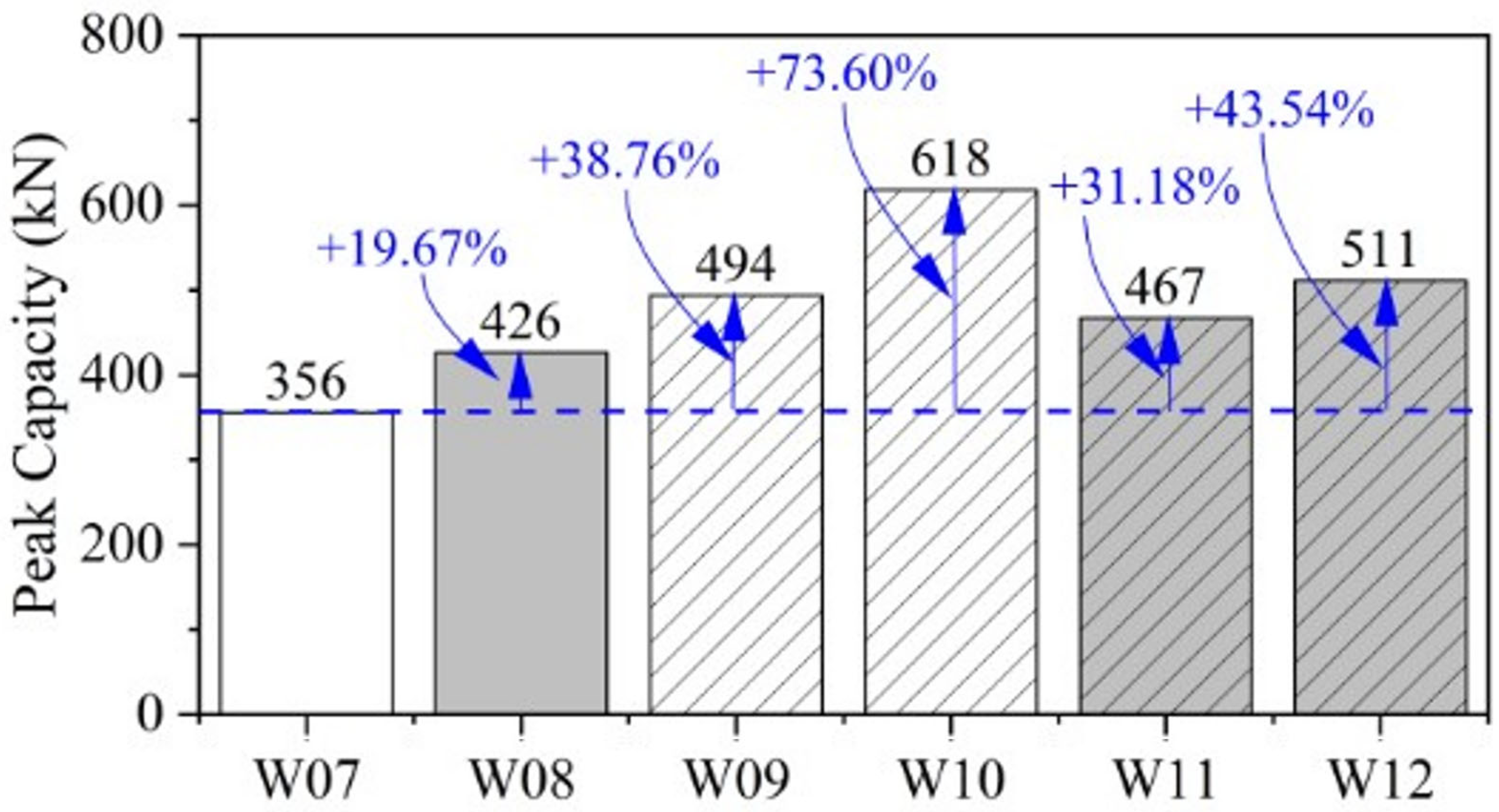
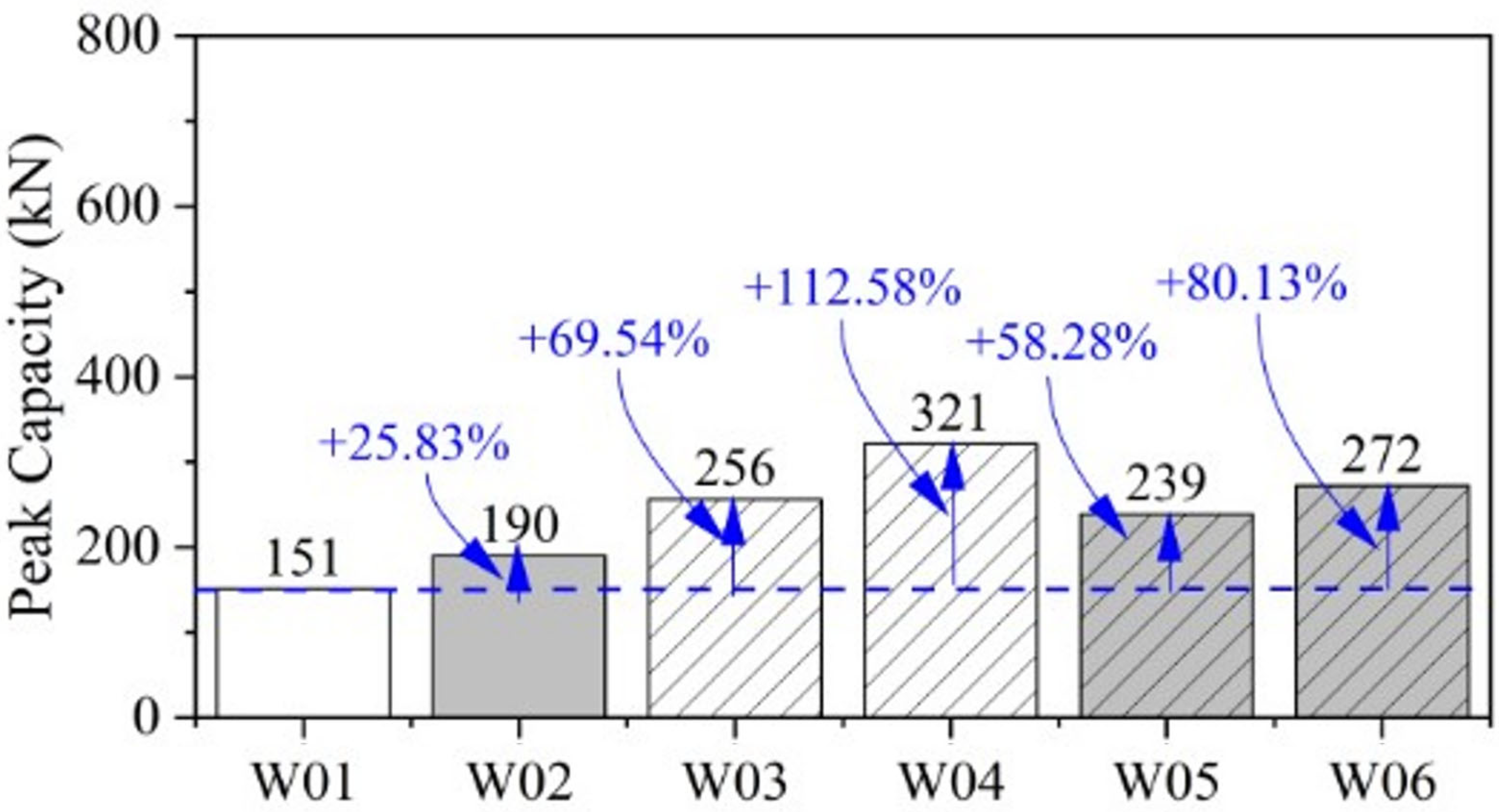
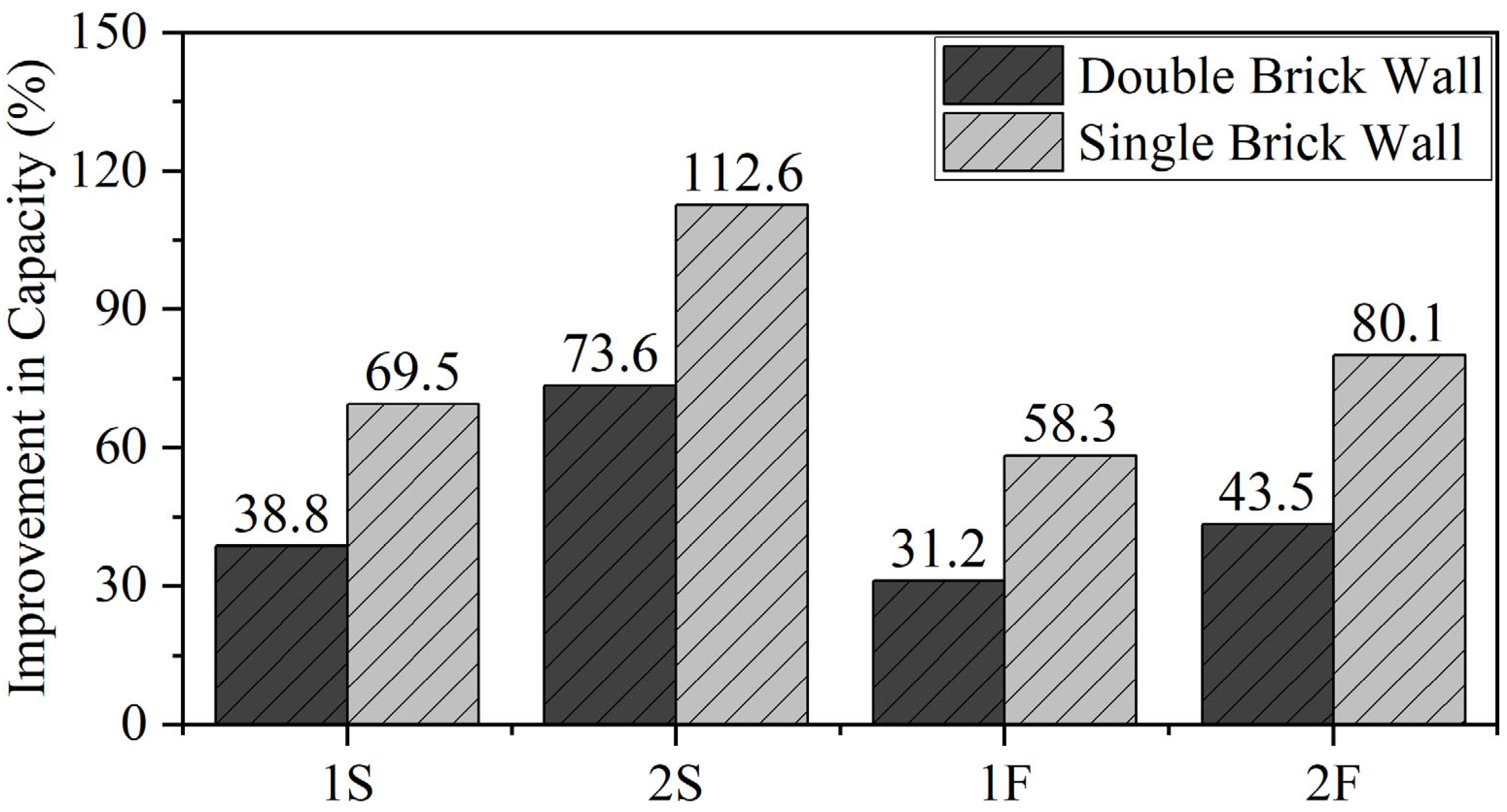
- The use of single-layer steel mesh, fiberglass mesh, and plaster improved the compressive strength of unreinforced masonry walls by 69.54%, 58.28%, and 25.83%, respectively. Additionally, the application of double-layer steel and fiberglass mesh increased the compressive strength by 112.58% and 80.13%, respectively, in single-brick walls. For double-brick walls, the compressive strength was enhanced by 38.76%, 31.18%, and 19.67% with single-layer steel mesh, fiberglass mesh, and plaster, respectively, compared to the control samples. Furthermore, the use of double-layer steel and fiberglass meshes increased the compressive strength of double-brick walls by 73.60% and 43.54%, respectively, compared to unreinforced counterparts. The greater percentage increase in compressive strength in single-brick walls is attributed to the fact that load transfer from the brick to the steel mesh occurs at lower loads compared to the load transfer mechanism in double brick walls.
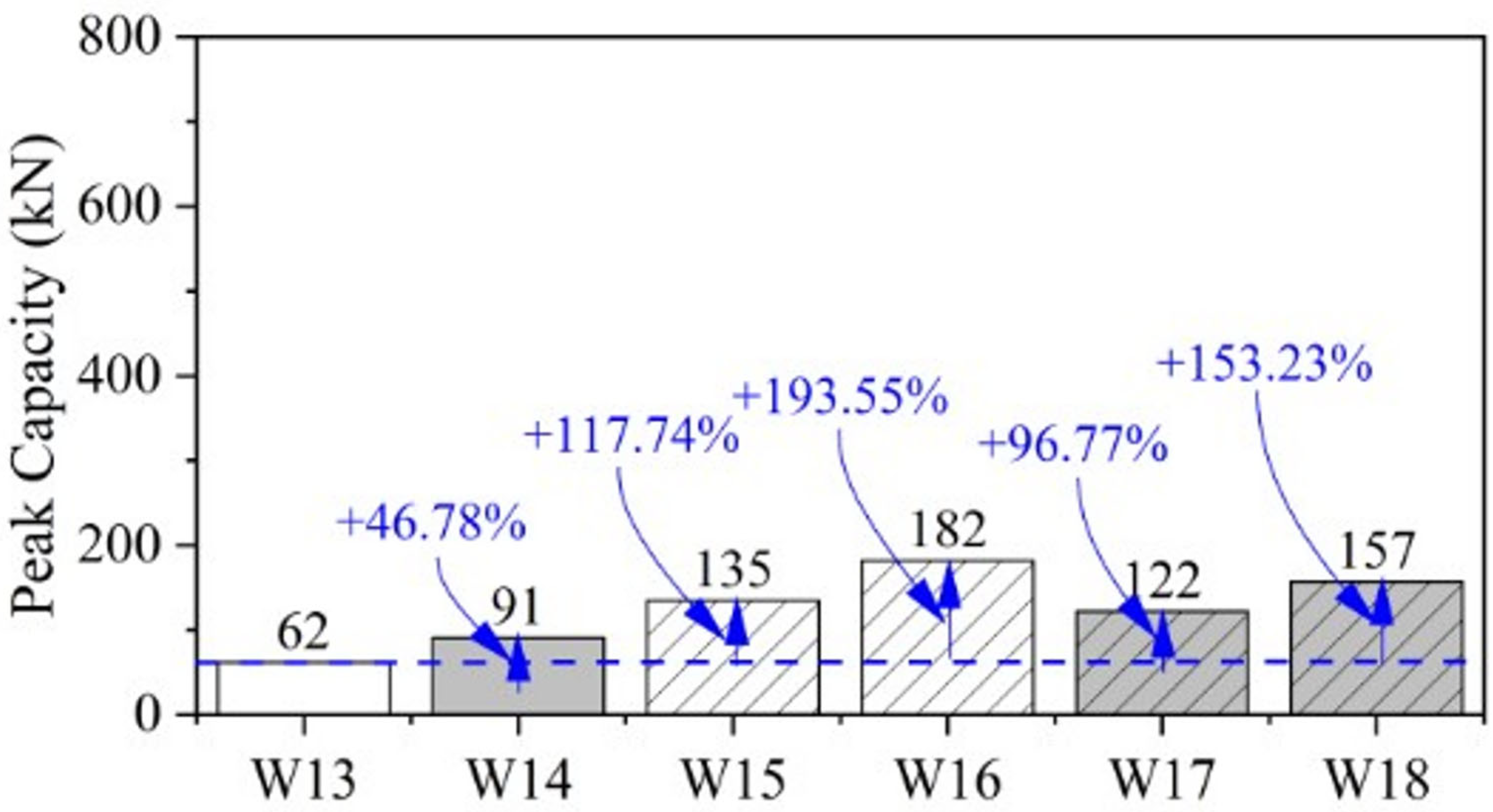
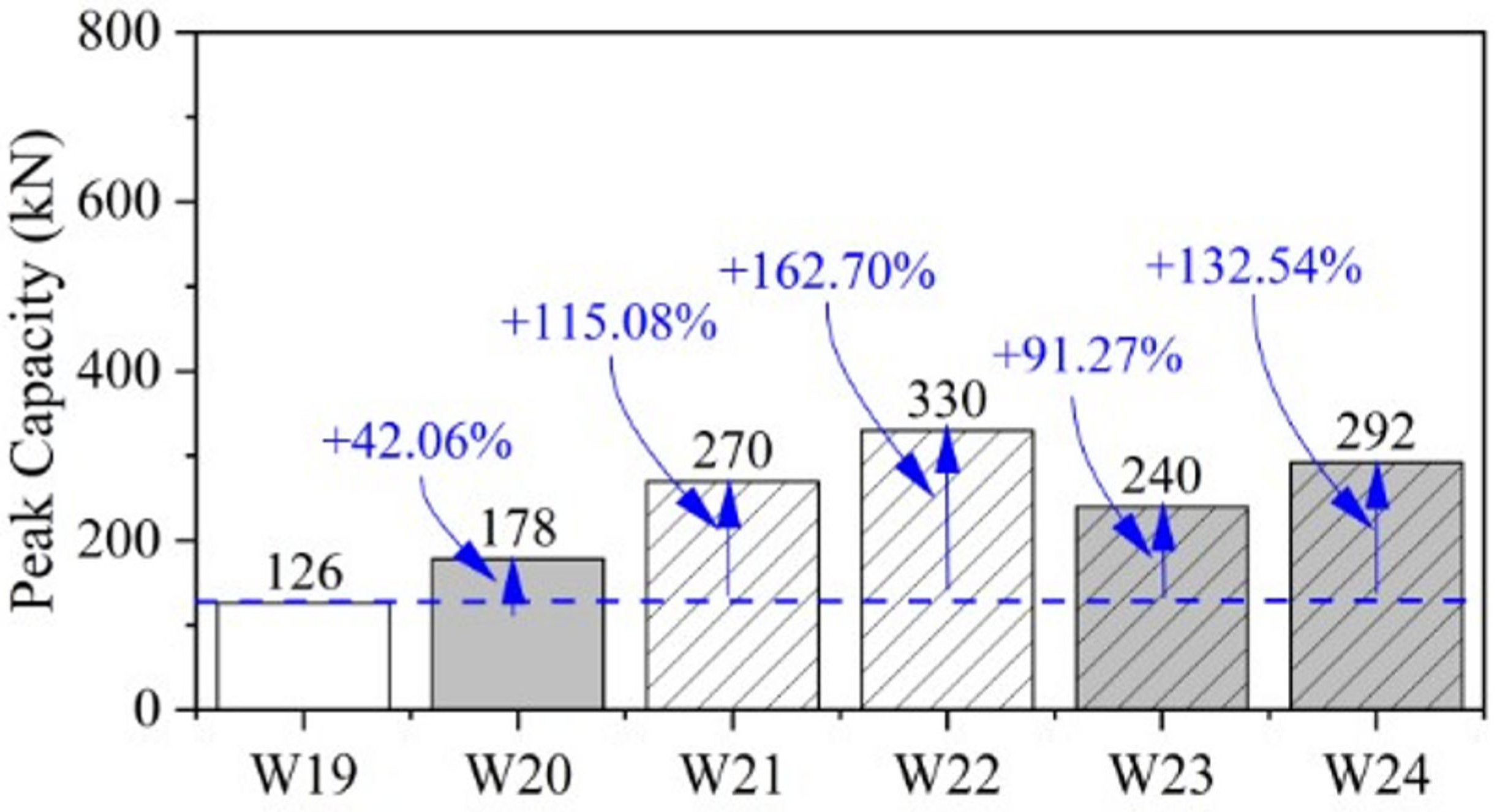
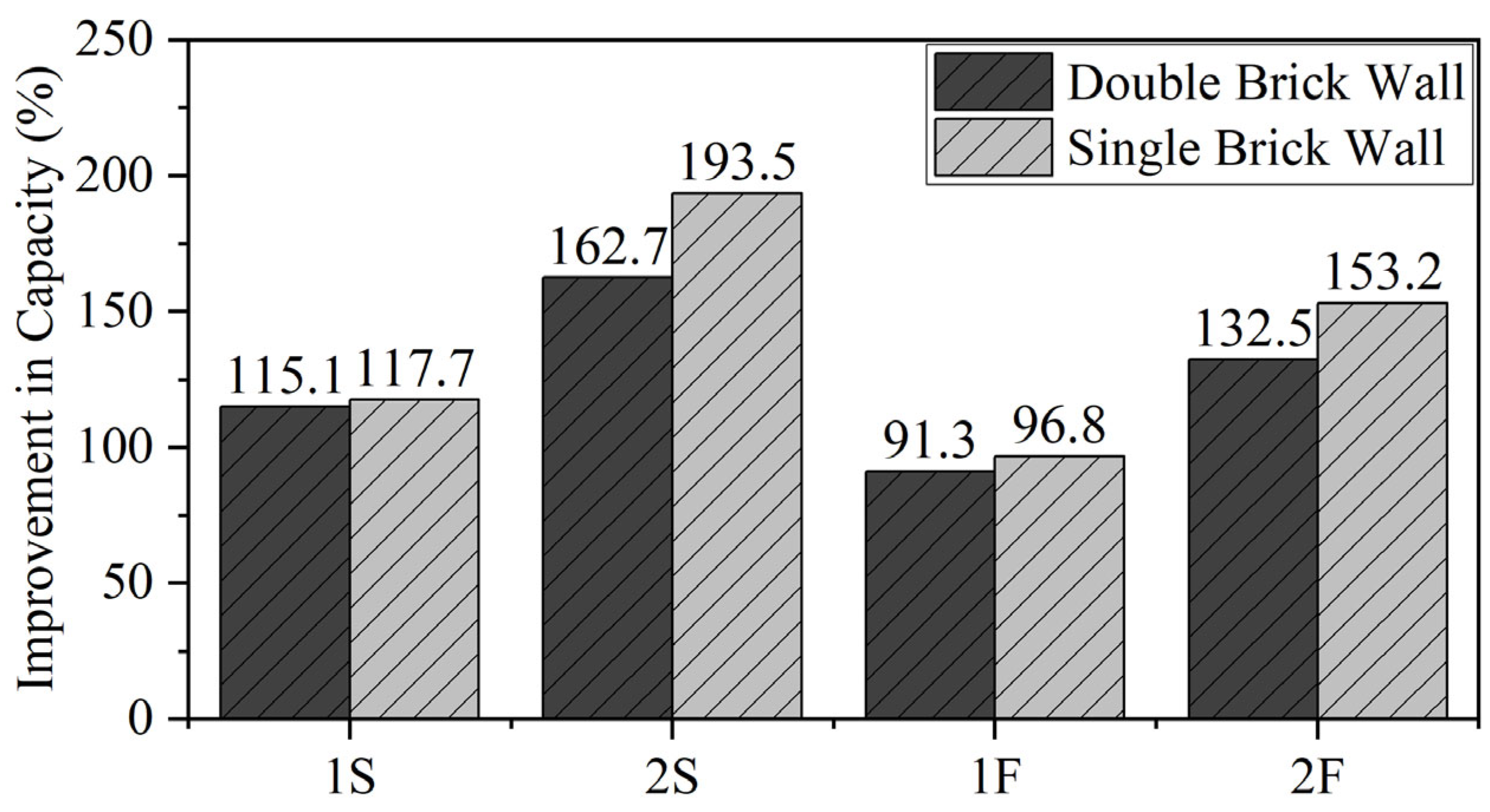
- The use of single-layer steel mesh, fiberglass mesh, and plaster enhanced the shear strength of double-brick walls by 117.74%, 96.77%, and 46.78%, respectively, compared to the control samples. Additionally, double-layer steel mesh and double-layer fiberglass mesh increased the shear strength by 193.55% and 153.23%, respectively, due to the mesh wires being oriented parallel to the direction of stresses, allowing them to behave in tension.
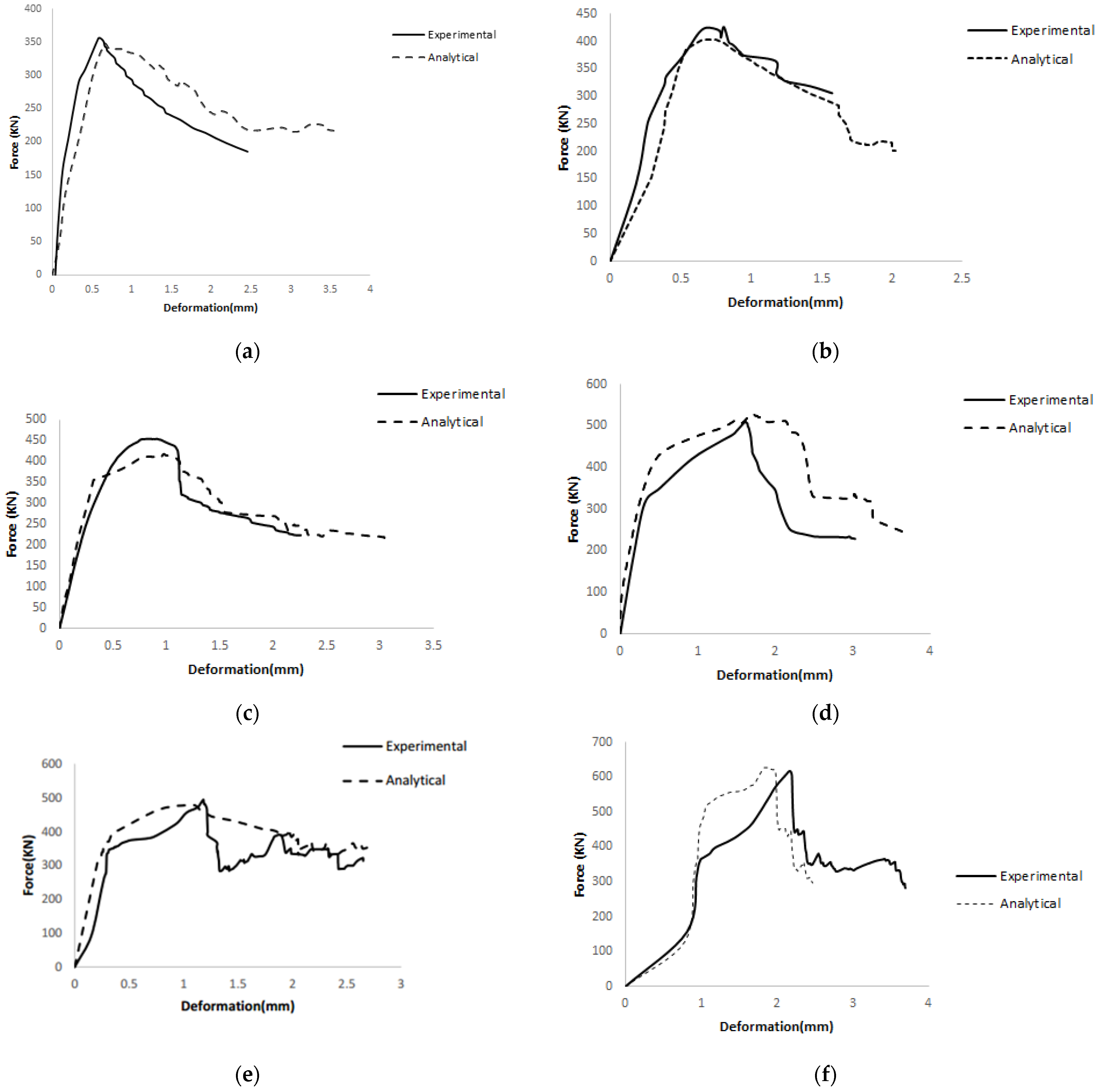
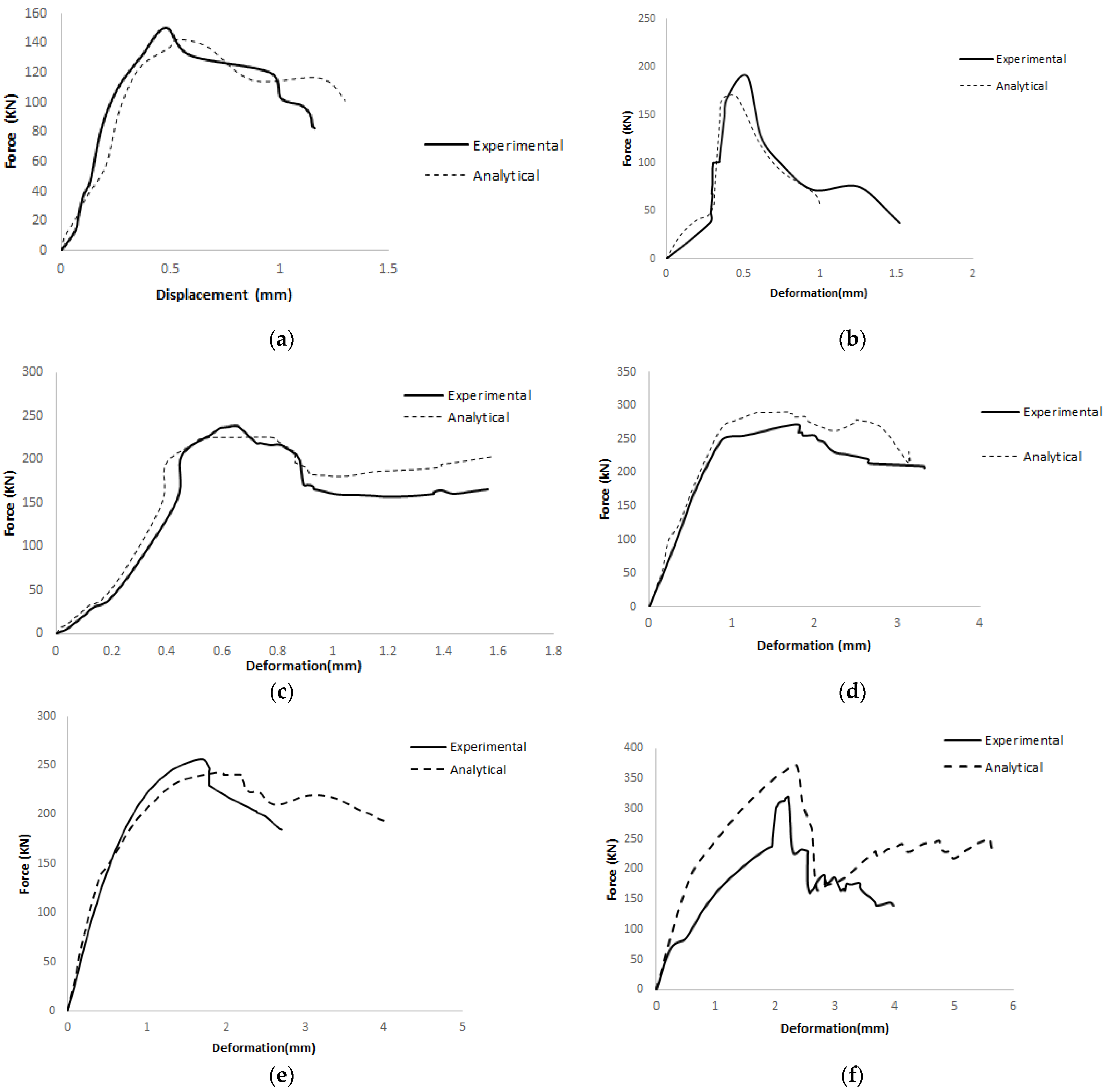
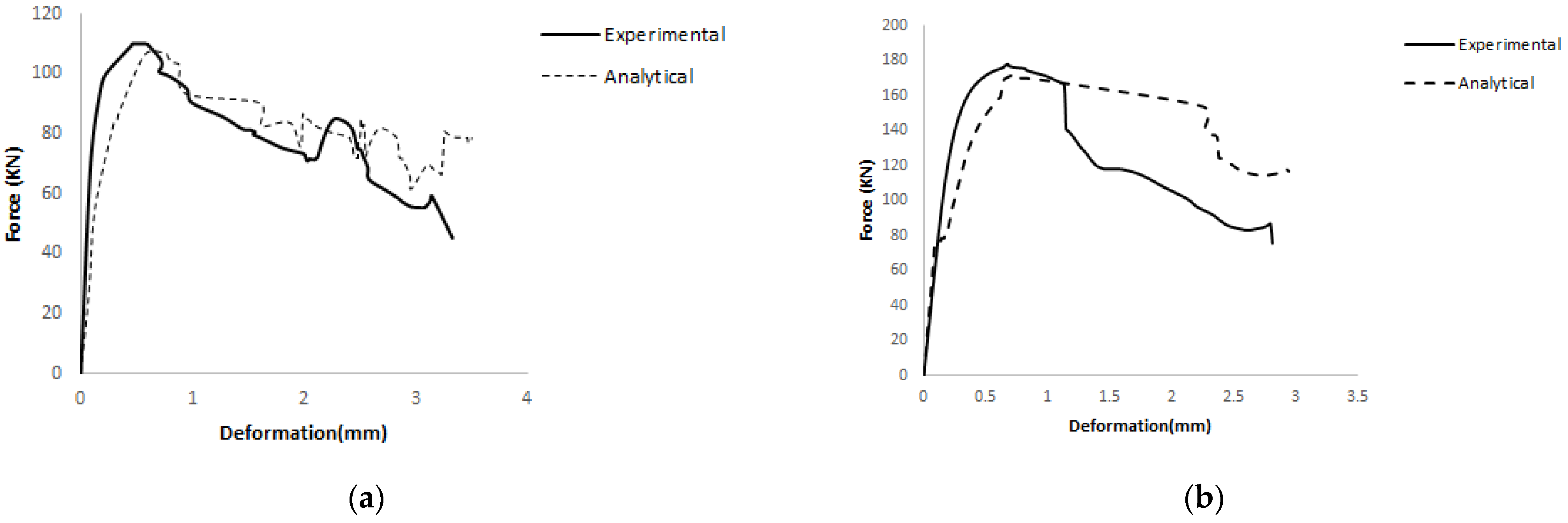
- The results obtained from Abaqus software showed good agreement with the experimental findings. The experimental results for double-layer steel mesh, double-layer fiberglass mesh, single-layer steel mesh, and single-layer fiberglass mesh were compared and validated using commercial software. The overall percentage difference between the experimental and analytical results was less than 10%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Almssad, A.; Almusaed, A.; Homod, R.Z. Masonry in the Context of Sustainable Buildings: A Review of the Brick Role in Architecture. Sustainability 2022, 14, 14734. [Google Scholar] [CrossRef]
- Maione, A.; Casapulla, C.; Di Ludovico, M.; Prota, A.; Ceroni, F. Efficiency of injected anchors in connecting T–shaped masonry walls: A modelling approach. Constr. Build. Mater. 2021, 301, 124051. [Google Scholar] [CrossRef]
- Papanicolaou, C.G.; Triantafillou, T.; Papathanasiou, M.; Karlos, K. Textile reinforced mortar (TRM) versus FRP as strengthening material of URM walls: Out-of-plane cyclic loading. Mater. Struct. 2007, 41, 143–157. [Google Scholar] [CrossRef]
- D’aLtri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arch. Comput. Methods Eng. 2019, 27, 1153–1185. [Google Scholar] [CrossRef]
- Deng, M.; Dong, Z.; Dai, J.; Zhao, X. Out-of-plane strengthening of URM walls using different fiber-reinforced materials. Constr. Build. Mater. 2022, 362, 129597. [Google Scholar] [CrossRef]
- Mughal, U.A.; Qazi, A.U.; Ahmed, A.; Abbass, W.; Abbas, S.; Salmi, A.; Sayed, M.M. Impact of openings on the in-plane strength of confined and unconfined masonry walls: A sustainable numerical study. Sustainability 2022, 14, 7467. [Google Scholar] [CrossRef]
- Asteris, P.; Chronopoulos, M.; Chrysostomou, C.; Varum, H.; Plevris, V.; Kyriakides, N.; Silva, V. Seismic vulnerability assessment of historical masonry structural systems. Eng. Struct. 2014, 62–63, 118–134. [Google Scholar] [CrossRef]
- Joyklad, P.; Ali, N.; Yooprasertchai, E.; Jaffar, S.T.A.; Magbool, H.M.; Hussain, Q.; Chaiyasarn, K. An investigative study for the prediction of compressive strength of cement-clay interlocking (CCI) hollow brick masonry walls. Case Stud. Constr. Mater. 2022, 16, e01001. [Google Scholar] [CrossRef]
- Gul, A.; Alam, B.; Shahzada, K. Seismic performance evaluation of unconfined dry stacked block masonry structure. Eng. Struct. 2022, 265, 114529. [Google Scholar] [CrossRef]
- Ullah, S.; Farooq, S.H.; Usman, M.; Ullah, B.; Hussain, M.; Hanif, A. In-Plane Seismic Strengthening of Brick Masonry Using Steel and Plastic Meshes. Materials 2022, 15, 4013. [Google Scholar] [CrossRef]
- Waseem, M.; Khan, M.A.; Khan, S. Seismic sources for southern Pakistan and seismic hazard assessment of Karachi. Nat. Hazards 2019, 99, 511–536. [Google Scholar] [CrossRef]
- Pararas-carayannis, G. pakistan’s earthquake and tsunami hazards potential impact on infrastructure. J. Infect. Dis. 2011, 2, 19–29. [Google Scholar]
- Andrabi, T.; Das, J. In Aid We Trust: Hearts and Minds and the Pakistan Earthquake of 2005. Rev. Econ. Stat. 2017, 99, 371–386. [Google Scholar] [CrossRef]
- Rossetto, T.; Peiris, N. Observations of damage due to the Kashmir earthquake of October 8, 2005 and study of current seismic provisions for buildings in Pakistan. Bull. Earthq. Eng. 2009, 7, 681–699. [Google Scholar] [CrossRef]
- Godio, M.; Portal, N.W.; Flansbjer, M.; Magnusson, J.; Byggnevi, M. Experimental and numerical approaches to investigate the out-of-plane response of unreinforced masonry walls subjected to free far-field blasts. Eng. Struct. 2021, 239, 112328. [Google Scholar] [CrossRef]
- Garofano, A.; Ceroni, F.; Pecce, M. Modelling of the in-plane behaviour of masonry walls strengthened with polymeric grids embedded in cementitious mortar layers. Compos. Part B Eng. 2016, 85, 243–258. [Google Scholar] [CrossRef]
- Zhou, Y.; Sui, L.; Huang, X.; Guo, M.; Luo, M.; Hu, B.; Chen, C. Enhancing the EB-FRP strengthening effectiveness by incorporating a cracking-control layer of ECC with different thicknesses. Constr. Build. Mater. 2021, 286, 122975. [Google Scholar] [CrossRef]
- Haldar, P.; Singh, Y.; Paul, D. Identification of seismic failure modes of URM infilled RC frame buildings. Eng. Fail. Anal. 2013, 33, 97–118. [Google Scholar] [CrossRef]
- Di Nino, S.; Luongo, A. A simple homogenized orthotropic model for in-plane analysis of regular masonry walls. Int. J. Solids Struct. 2019, 167, 156–169. [Google Scholar] [CrossRef]
- Joyklad, P.; Ali, N.; Verre, S.; Magbool, H.M.; Elnemr, A.; Qureshi, M.I.; Hussain, Q.; Chaiyasarn, K. Experimental study on the out-of-plane behavior of brick masonry walls strengthened with mortar and wire mesh: A pioneer study. Infrastructures 2021, 6, 165. [Google Scholar] [CrossRef]
- Joyklad, P.; Hussain, Q. Development of strength models for brick walls: Experimental and theoretical study. Results Eng. 2023, 18, 101103. [Google Scholar] [CrossRef]
- Hussain, Q.; Ruangrassamee, A.; Joyklad, P.; Wijeyewickrema, A.C. Shear enhancement of RC beams using low-cost natural fiber rope reinforced polymer composites. Buildings 2022, 12, 602. [Google Scholar] [CrossRef]
- Mercedes, L.; Bernat-Maso, E.; Gil, L. In-plane cyclic loading of masonry walls strengthened by vegetal-fabric-reinforced cementitious matrix (FRCM) composites. Eng. Struct. 2020, 221, 111097. [Google Scholar] [CrossRef]
- Angiolilli, M.; Gregori, A. Assessment of the FRCM in-plane behavior in masonry retrofit applications. Procedia Struct. Integr. 2023, 44, 2174–2181. [Google Scholar] [CrossRef]
- Triwiyono, A.; Eratodi, I.G.L.B.; Wibowo, D.E.; Siswosukarto, S. Investigation of Confined Masonry Using Non-standard Quality of Concrete and Reinforcement. Lect. Notes Civ. Eng. 2022, 215, 187–199. [Google Scholar] [CrossRef]
- Zhang, L. Production of bricks from waste materials—A review. Constr. Build. Mater. 2013, 47, 643–655. [Google Scholar] [CrossRef]
- Meli, R. Behavior of masonry walls under lateral loads. In Proceedings of the Fifth World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1973; pp. 853–862. [Google Scholar]
- Naseer, M.A.; Qazi, A.U.; Mughal, U.A.; Ajmal, M.M.; Ahmed, A. Characteristics of unconfined masonry walls under in-plane static and reverse-cyclic loading: A comparative numerical study. Eur. J. Environ. Civ. Eng. 2023, 28, 150–175. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Meftah, F.; Chammas, R.; Mebarki, A. The behaviour of masonry walls subjected to fire: Modelling and parametrical studies in the case of hollow burnt-clay bricks. Fire Saf. J. 2009, 44, 629–641. [Google Scholar] [CrossRef]
- Haach, V.G.; Vasconcelos, G.; Lourenço, P.B. Parametrical study of masonry walls subjected to in-plane loading through numerical modeling. Eng. Struct. 2011, 33, 1377–1389. [Google Scholar] [CrossRef]
- Haach, V.G.; Vasconcelos, G.; Lourenço, P.B. Experimental Analysis of Reinforced Concrete Block Masonry Walls Subjected to In-Plane Cyclic Loading. J. Struct. Eng. 2010, 136, 452–462. [Google Scholar] [CrossRef]
- Kalali, A.; Kabir, M.Z. Experimental response of double-wythe masonry panels strengthened with glass fiber reinforced polymers subjected to diagonal compression tests. Eng. Struct. 2012, 39, 24–37. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced seismic analysis of soil-foundation-structure interaction for shallow and pile foundations in saturated and dry deposits: Insights from 3D parallel finite element modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of seismic soil–pile–structure interaction on mid- and high-rise steel buildings resting on a group of pile foundations. Int. J. Géoméch. 2018, 18. [Google Scholar] [CrossRef]
- Najam, F.A.; Qureshi, M.I.; Warnitchai, P.; Mehmood, T. Prediction of nonlinear seismic demands of high-rise rocking wall structures using a simplified modal pushover analysis procedure. Struct. Des. Tall Spéc. Build. 2018, 27, e1506. [Google Scholar] [CrossRef]
- Khalil, U.; Aslam, B.; Kazmi, Z.A.; Maqsoom, A.; Qureshi, M.I.; Azam, S.; Nawaz, A. Integrated support vector regressor and hybrid neural network techniques for earthquake prediction along Chaman fault, Baluchistan. Arab. J. Geosci. 2021, 14, 2192. [Google Scholar] [CrossRef]
- Khan, S.U.; Qureshi, M.I.; Rana, I.A.; Maqsoom, A. Seismic vulnerability assessment of building stock of Malakand (Pakistan) using FEMA P-154 method. SN Appl. Sci. 2019, 1, 1625. [Google Scholar] [CrossRef]
- Qureshi, M.I.; Warnitchai, P. Reduction of inelastic seismic demands in a mid-rise rocking wall structure designed using the displacement-based design procedure. Struct. Des. Tall Spéc. Build. 2016, 26, e1307. [Google Scholar] [CrossRef]
- Qureshi, M.I.; Khan, S.U.; Rana, I.A.; Ali, B.; Rahman, A.U. Determinants of people’s seismic risk perception: A case study of Malakand, Pakistan. Int. J. Disaster Risk Reduct. 2021, 55, 102078. [Google Scholar] [CrossRef]
- Abbas, S.N.; Qureshi, M.I.; Alkharisi, M.K.; Alturki, M.; Ahmad, Z. Combined effect of silica fume and various fibers on fresh and hardened properties of concrete incorporating HDPE aggregates. Constr. Build. Mater. 2024, 445, 137940. [Google Scholar] [CrossRef]
- Ali, K.; Saingam, P.; Qureshi, M.I.; Saleem, S.; Nawaz, A.; Mehmood, T.; Maqsoom, A.; Malik, M.W.; Suparp, S. Influence of recycled plastic incorporation as coarse aggregates on concrete properties. Sustainability 2023, 15, 5937. [Google Scholar] [CrossRef]
- Khan, A.A.; Rana, I.A.; Nawaz, A.; Waheed, A. Gender-based emergency preparedness and awareness: Empirical evidences from high-school students of Gilgit, Pakistan. Environ. Hazards 2020, 20, 416–431. [Google Scholar] [CrossRef]
- Van Noort, J.R. Computational Modelling of Masonry Structures. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- ASTM International. ASTM C1314-23a Standard Test Method for Compressive Strength of Masonry Prisms. 2023. Available online: https://www.astm.org/DATABASE.CART/HISTORICAL/C1314-16.htm (accessed on 28 September 2021).
- ASTM. ASTM C109/C109M-21–Standard Test Method for Compressive Strength of Hydraulic Cement Mortars. 2021. Available online: https://store.astm.org/c0109_c0109m-21.html (accessed on 4 January 2022).
- EN 1998-1; Eurocode 8, Design of Structures for Earthquake Resistance. British Standard: London, UK, 2005.
- ASTM C1717-19; Standard Test Methods for Conducting Strength Tests of Masonry Wall Panels. American Society for Testing Materials: West Conshohocken, PA, USA, 2019.
- ASTM E519/E519M-22; Standard Test Method for Diagonal Tension (Shear) in Ma-Sonry Assemblages. American Society for Testing Materials: West Conshohocken, PA, USA, 2022.
- Garcia-Ramonda, L.; Pelá, L.; Roca, P.; Camata, G. In-plane shear behaviour by diagonal compression testing of brick masonry walls strengthened with basalt and steel textile reinforced mortars. Constr. Build. Mater. 2020, 240, 117905. [Google Scholar] [CrossRef]
- George, J.; Rama, J.K.; Kumar, M.S.; Vasan, A. Behavior of plain concrete beam subjected to three point bending using concrete damaged plasticity (CDP) model. Mater. Today Proc. 2017, 4, 9742–9746. [Google Scholar] [CrossRef]
- Le Thanh, C.; Minh, H.-L.; Sang-To, T. A nonlinear concrete damaged plasticity model for simulation reinforced concrete structures using ABAQUS. Frat. Ed Integrita Strutt. Struct. Integr. 2021, 16, 232–242. [Google Scholar] [CrossRef]
- Fakeh, M.; Jawdhari, A.; Fam, A. Calibration of ABAQUS Concrete Damage Plasticity (CDP) Model for UHPC Material. In Proceedings of the Third International Interactive Symposium on Ultra-High Performance Concrete, Wilmington, DE, USA, 4–7 June 2023. [Google Scholar]
- Işık, E.; Avcil, F.; Harirchian, E.; Arkan, E.; Bilgin, H.; Özmen, H.B. Architectural characteristics and seismic vulnerability assessment of a historical masonry minaret under different seismic risks and probabilities of exceedance. Buildings 2022, 12, 1200. [Google Scholar] [CrossRef]
- Systèmes, D. Abaqus USER Subroutines Reference Guide; Version 6.14; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2014. [Google Scholar]


















| ID | Thickness (mm) | Mortar Ratio | Wire Mesh | |
|---|---|---|---|---|
| Cement | Sand | |||
| Walls for Axial Compressive Behavior | ||||
| W01 | 115 | 1 | 4 | N/A |
| W02 | 115 | 1 | 4 | N/A |
| W03 | 115 | 1 | 4 | Single steel layer (1S) |
| W04 | 115 | 1 | 4 | Double steel layer (2S) |
| W05 | 115 | 1 | 4 | Single fiberglass layer (1F) |
| W06 | 115 | 1 | 4 | Double fiberglass layer (2F) |
| W07 | 230 | 1 | 4 | N/A |
| W08 | 230 | 1 | 4 | N/A |
| W09 | 230 | 1 | 4 | Single steel layer (1S) |
| W10 | 230 | 1 | 4 | Double steel layer (2S) |
| W11 | 230 | 1 | 4 | Single fiberglass layer (1F) |
| W12 | 230 | 1 | 4 | Double fiberglass layer (2F) |
| Walls for Diagonal Compressive Behavior | ||||
| W13 | 115 | 1 | 4 | N/A |
| W14 | 115 | 1 | 4 | N/A |
| W15 | 115 | 1 | 4 | Single steel layer (1S) |
| W16 | 115 | 1 | 4 | Double steel layer (2S) |
| W17 | 115 | 1 | 4 | Single fiberglass layer (1F) |
| W18 | 115 | 1 | 4 | Double fiberglass layer (2F) |
| W19 | 230 | 1 | 4 | N/A |
| W20 | 230 | 1 | 4 | N/A |
| W21 | 230 | 1 | 4 | Single steel layer (1S) |
| W22 | 230 | 1 | 4 | Double steel layer (2S) |
| W23 | 230 | 1 | 4 | Single fiberglass layer (1F) |
| W24 | 230 | 1 | 4 | Double fiberglass layer (2F) |
| ID | Type | Peak Load (kN) | Compressive Strength (MPa) | Axial Deformation at Peak (mm) | |
|---|---|---|---|---|---|
| Thickness (mm) | Strengthening | ||||
| W01 | 115 | Control | 151 | 1.88 | 0.58 |
| W02 | 115 | Plaster Only | 190 | 2.36 | 0.80 |
| W03 | 115 | 1 Layer Steel | 256 | 3.18 | 1.18 |
| W04 | 115 | 2 Layer Steel | 321 | 3.99 | 2.17 |
| W05 | 115 | 1 Layer Fiberglass | 239 | 2.97 | 0.92 |
| W06 | 115 | 2 Layer Fiberglass | 272 | 3.38 | 1.60 |
| W07 | 230 | Control | 356 | 2.21 | 0.48 |
| W08 | 230 | Plaster Only | 426 | 2.65 | 0.52 |
| W09 | 230 | 1 Layer Steel | 494 | 3.07 | 1.75 |
| W10 | 230 | 2 Layer Steel | 618 | 3.84 | 2.10 |
| W11 | 230 | 1 Layer Fiberglass | 467 | 2.90 | 0.96 |
| W12 | 230 | 2 Layer Fiberglass | 511 | 3.17 | 1.81 |
| ID | Type | Peak Load (kN) | Shear Strength (MPa) | Axial Deformation at Peak (mm) | |
|---|---|---|---|---|---|
| Thickness (mm) | Strengthening | ||||
| W13 | 115 | Control | 62 | 0.77 | 0.33 |
| W14 | 115 | Plaster Only | 91 | 1.13 | 0.67 |
| W15 | 115 | 1 Layer Steel | 135 | 1.68 | 1.17 |
| W16 | 115 | 2 Layer Steel | 182 | 2.26 | 2.11 |
| W17 | 115 | 1 Layer Fiberglass | 122 | 1.52 | 0.87 |
| W18 | 115 | 2 Layer Fiberglass | 157 | 1.95 | 1.49 |
| W19 | 230 | Control | 126 | 0.78 | 0.28 |
| W20 | 230 | Plaster Only | 178 | 1.11 | 0.47 |
| W21 | 230 | 1 Layer Steel | 270 | 1.68 | 1.03 |
| W22 | 230 | 2 Layer Steel | 330 | 2.05 | 1.49 |
| W23 | 230 | 1 Layer Fiberglass | 240 | 1.49 | 0.94 |
| W24 | 230 | 2 Layer Fiberglass | 292 | 1.81 | 1.10 |
| ID | Peak Load—EXP (kN) | Peak Load—Analytical (kN) | Difference (%) | Axial Deformation at Peak—EXP (mm) | Axial Deformation at Peak— Analytical (mm) | Difference (%) |
|---|---|---|---|---|---|---|
| W01 | 151 | 140 | 7.86 | 0.58 | 0.65 | −10.77 |
| W02 | 190 | 175 | 8.57 | 0.8 | 0.75 | 6.67 |
| W03 | 256 | 245 | 4.49 | 1.18 | 1.2 | −1.67 |
| W04 | 321 | 330 | −2.73 | 2.17 | 2.01 | 7.96 |
| W05 | 239 | 225 | 6.22 | 0.92 | 1.05 | −12.38 |
| W06 | 272 | 289 | −5.88 | 1.6 | 1.51 | 5.96 |
| W07 | 356 | 345 | 3.19 | 0.48 | 0.52 | −7.69 |
| W08 | 426 | 405 | 5.19 | 0.52 | 0.56 | −7.14 |
| W09 | 494 | 475 | 4.00 | 1.75 | 1.85 | −5.41 |
| W10 | 618 | 630 | −1.90 | 2.1 | 2.3 | −8.70 |
| W11 | 467 | 445 | 4.94 | 0.96 | 0.94 | 2.13 |
| W12 | 511 | 480 | 6.46 | 1.81 | 1.75 | 3.43 |
| W13 | 62 | 54 | 14.81 | 0.33 | 0.38 | −13.16 |
| W14 | 91 | 83 | 9.64 | 0.67 | 0.75 | −10.67 |
| W15 | 135 | 125 | 8.00 | 1.17 | 1.26 | −7.14 |
| W16 | 182 | 192 | −5.21 | 2.11 | 2.2 | −4.09 |
| W17 | 122 | 115 | 6.09 | 0.87 | 0.99 | −12.12 |
| W18 | 157 | 165 | −4.85 | 1.49 | 1.59 | −6.29 |
| W19 | 126 | 118 | 6.78 | 0.28 | 0.32 | −12.50 |
| W20 | 178 | 170 | 4.71 | 0.47 | 0.51 | −7.84 |
| W21 | 270 | 260 | 3.85 | 1.03 | 1.15 | −10.43 |
| W22 | 330 | 345 | −4.35 | 1.49 | 1.6 | −6.88 |
| W23 | 240 | 230 | 4.35 | 0.94 | 1.01 | −6.93 |
| W24 | 292 | 305 | −4.26 | 1.1 | 1.19 | −7.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, T.; Abid, M.A.; Chatveera, B.; Sua-Iam, G.; Saingam, P.; Ejaz, A.; Hussain, Q.; Joyklad, P.; Suparp, S. Sustainable Reinforcement Methods for Brick Masonry Walls: An Experimental and Finite Element Analysis Approach. Buildings 2025, 15, 2180. https://doi.org/10.3390/buildings15132180
Mehmood T, Abid MA, Chatveera B, Sua-Iam G, Saingam P, Ejaz A, Hussain Q, Joyklad P, Suparp S. Sustainable Reinforcement Methods for Brick Masonry Walls: An Experimental and Finite Element Analysis Approach. Buildings. 2025; 15(13):2180. https://doi.org/10.3390/buildings15132180
Chicago/Turabian StyleMehmood, Tahir, Muhammad Amer Abid, Burachat Chatveera, Gritsada Sua-Iam, Panumas Saingam, Ali Ejaz, Qudeer Hussain, Panuwat Joyklad, and Suniti Suparp. 2025. "Sustainable Reinforcement Methods for Brick Masonry Walls: An Experimental and Finite Element Analysis Approach" Buildings 15, no. 13: 2180. https://doi.org/10.3390/buildings15132180
APA StyleMehmood, T., Abid, M. A., Chatveera, B., Sua-Iam, G., Saingam, P., Ejaz, A., Hussain, Q., Joyklad, P., & Suparp, S. (2025). Sustainable Reinforcement Methods for Brick Masonry Walls: An Experimental and Finite Element Analysis Approach. Buildings, 15(13), 2180. https://doi.org/10.3390/buildings15132180








