Seismic Damage Mechanism of Five-Story and Three-Span Underground Complex in Soft Soil Site
Abstract
1. Introduction
2. Experimental Investigation
2.1. Facility and Scaling Laws
2.2. Model Soil and Model Structure
2.3. Sensor Scheme and Loading Cases
3. Time-Frequency Evolution Analysis of the Free Field Experiments
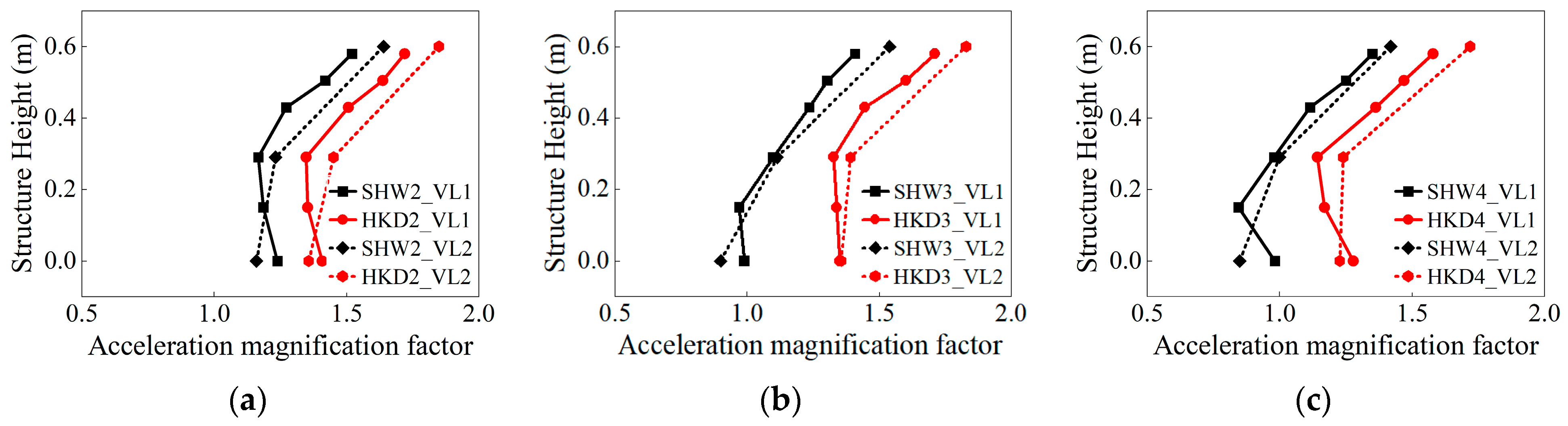
3.1. Acceleration Magnification Factor Analysis
3.2. Response Spectra Evolution Analysis
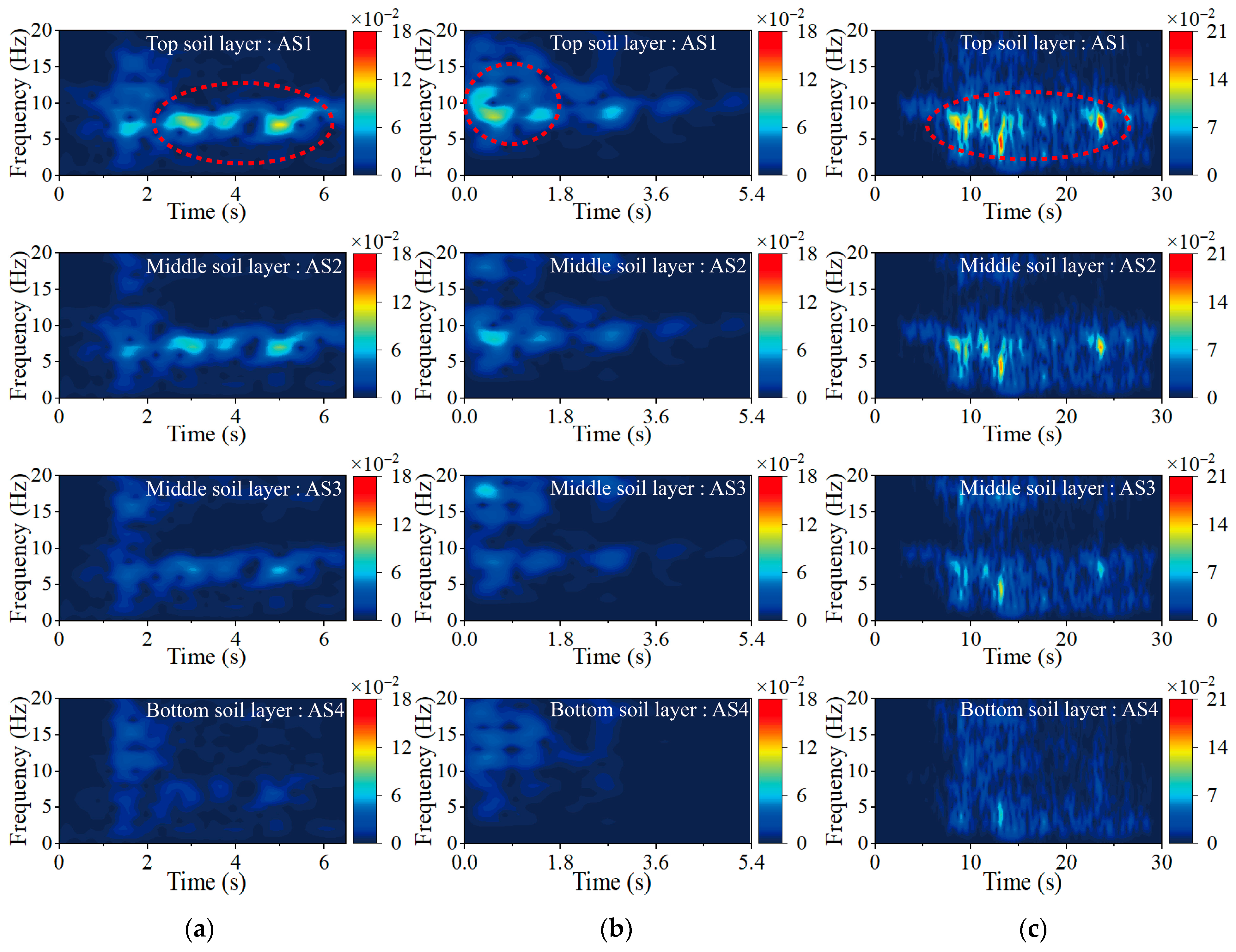
3.3. Time–Frequency Distribution and Evolution Analysis
4. Experimental Results and Numerical Model Validation on the Soil–Underground Complex Interaction System
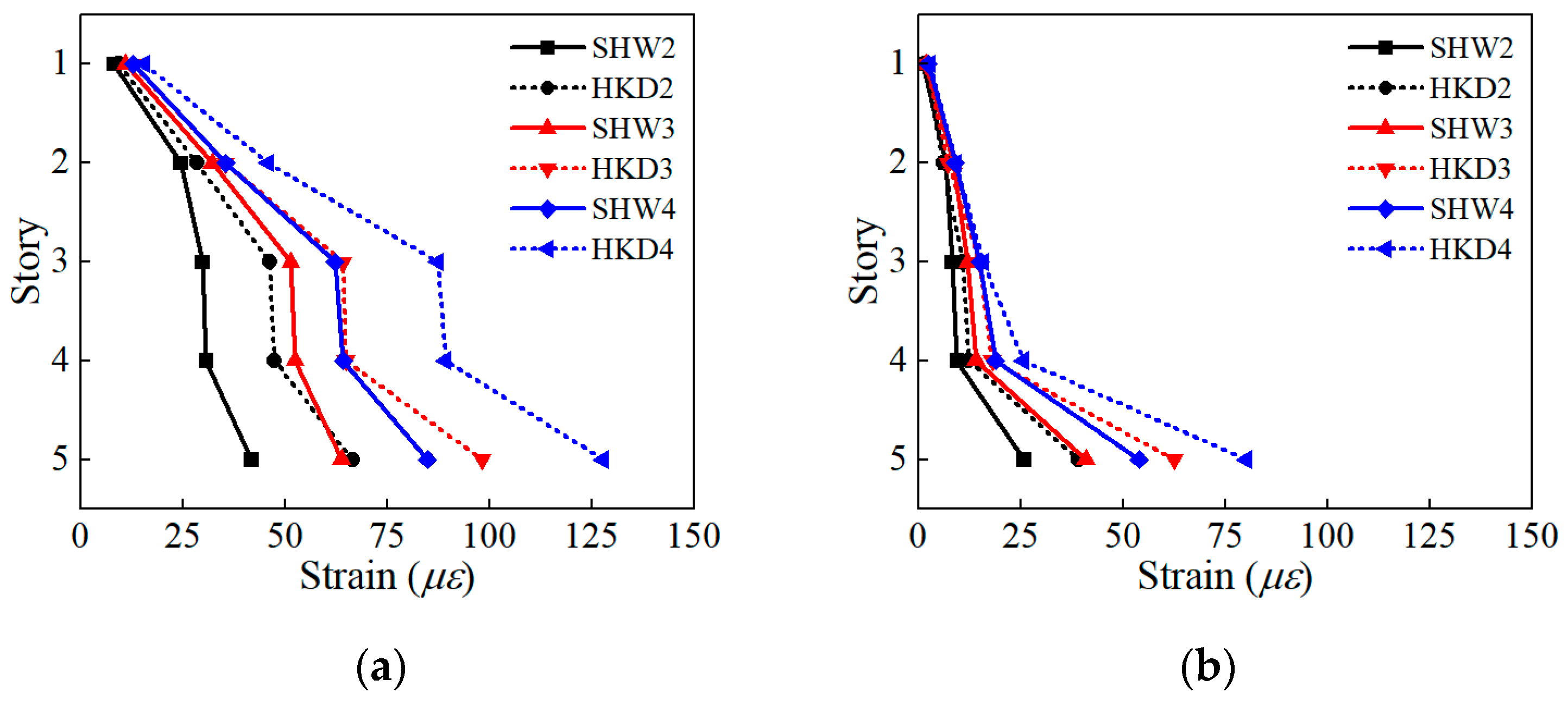
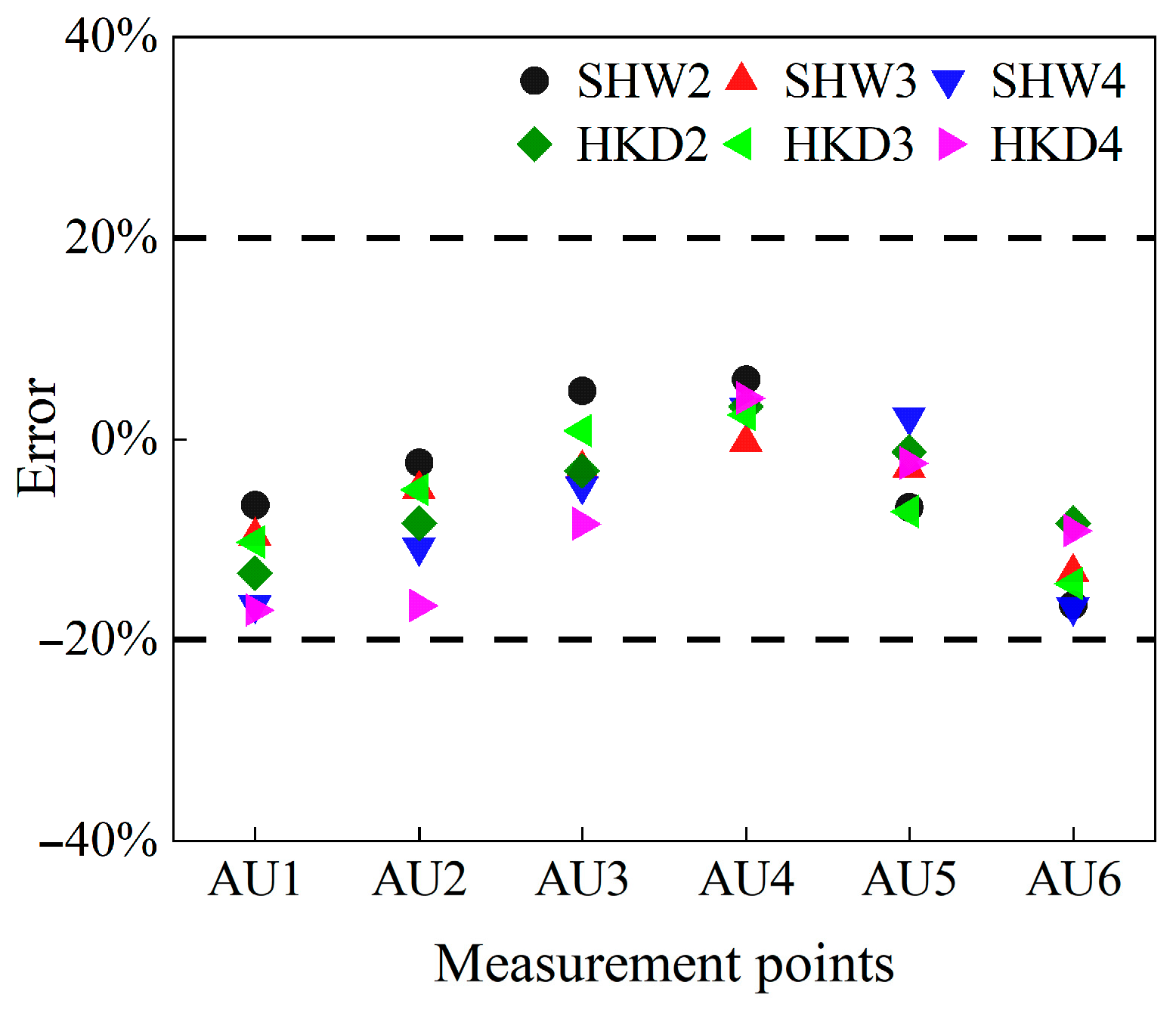
4.1. Experimental Results
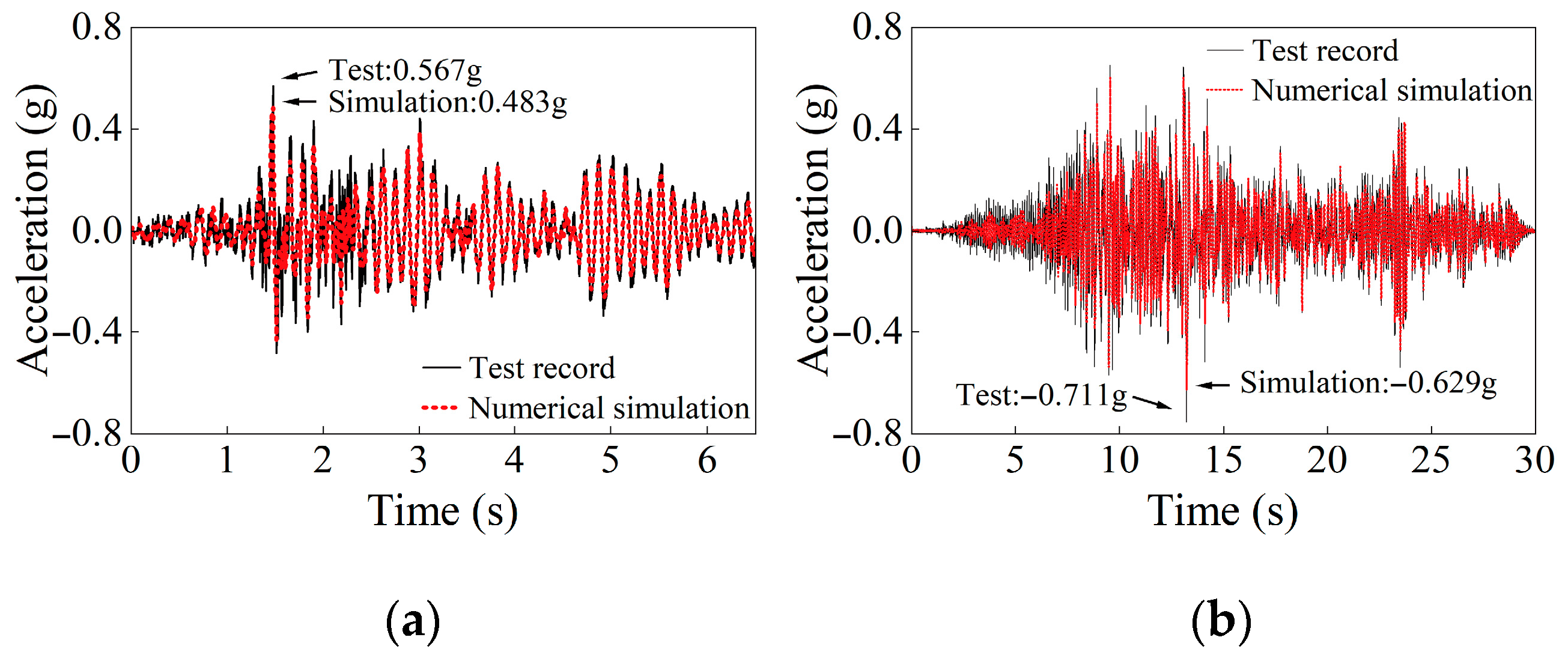
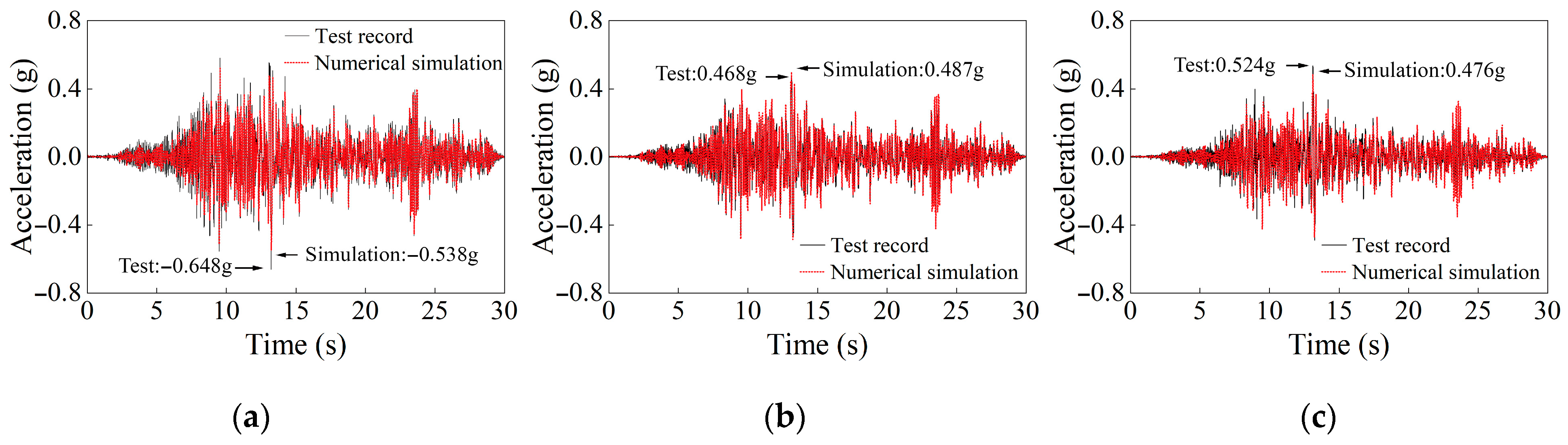
4.2. Numerical Simulation and Validation
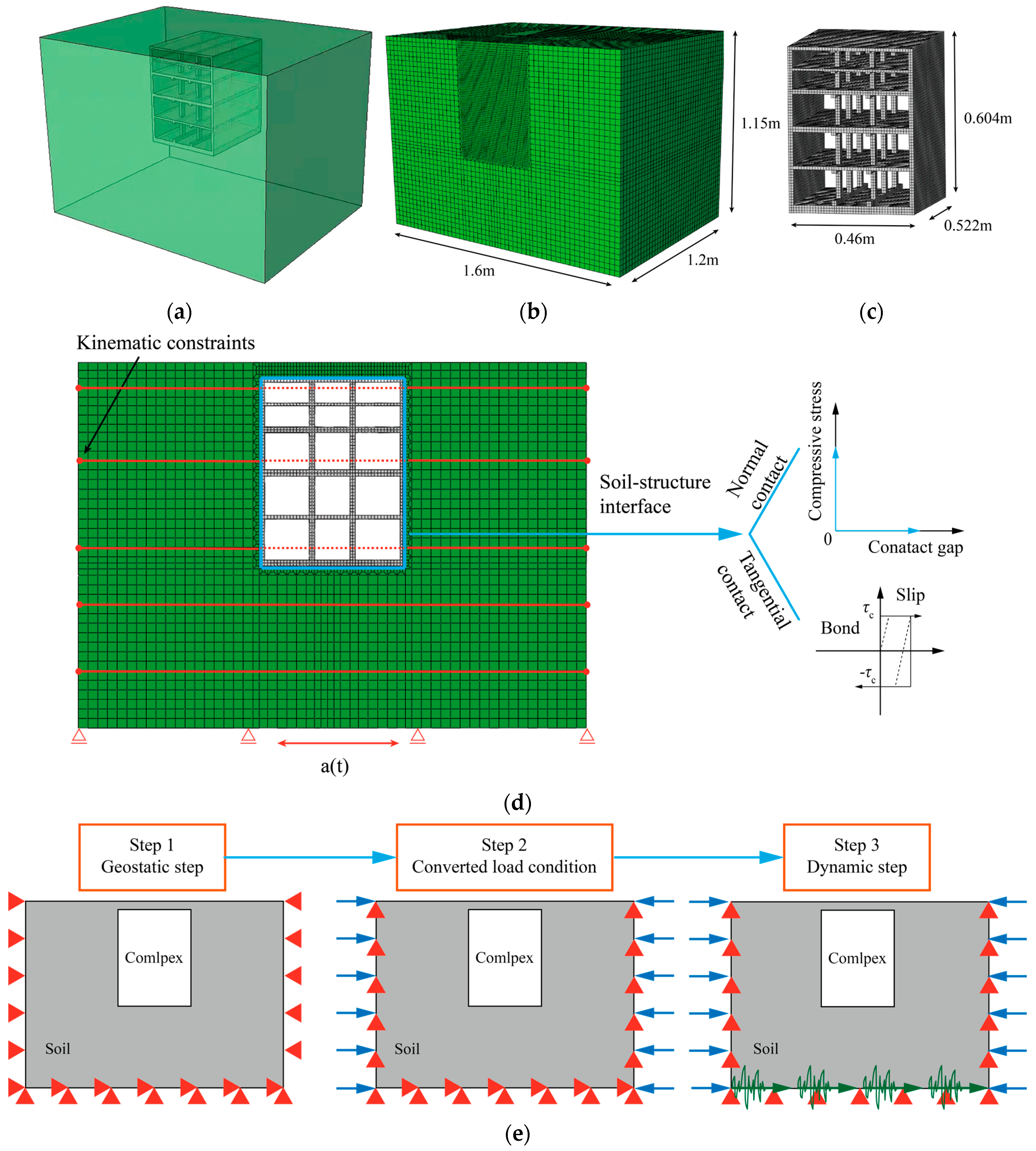
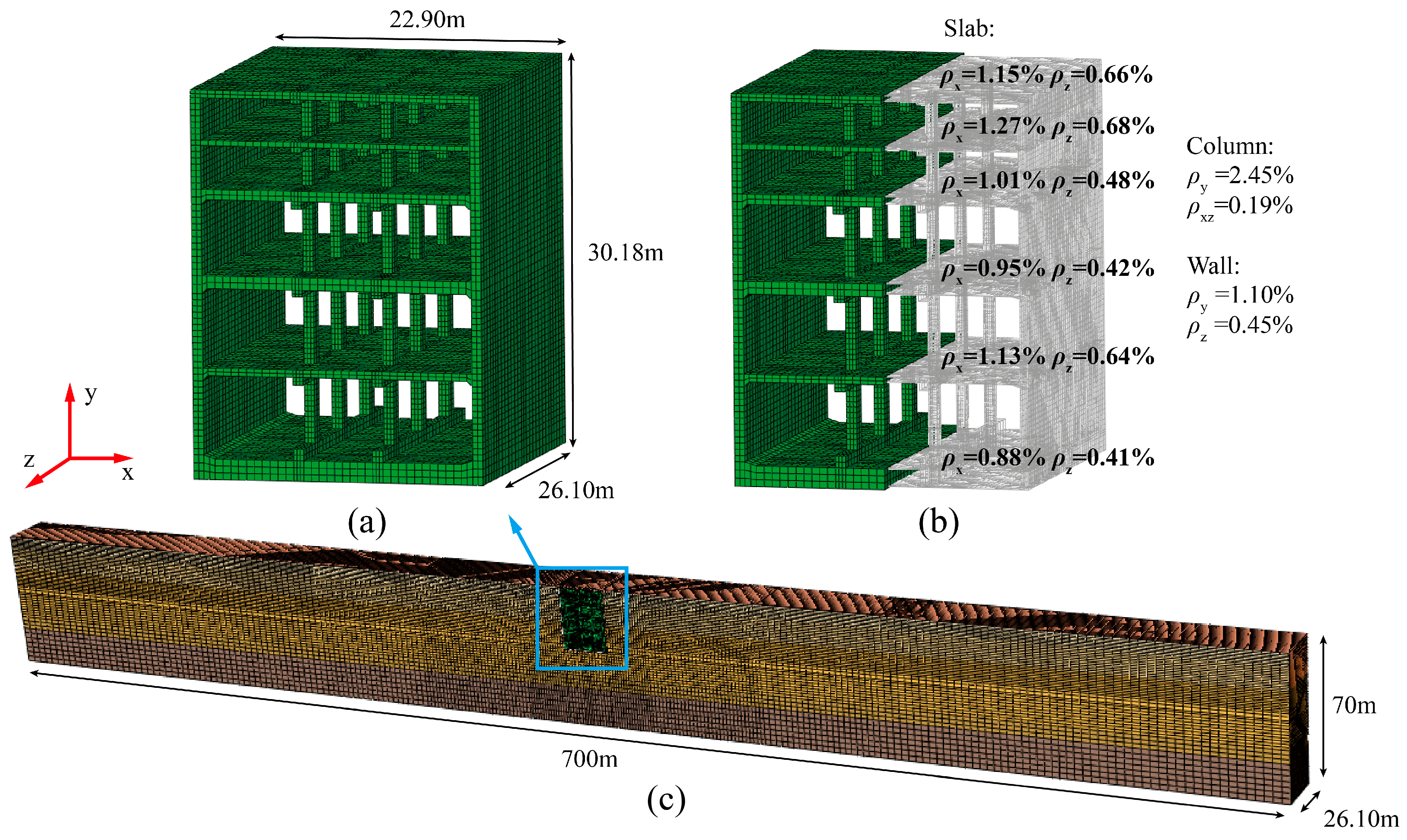
4.2.1. Establishment of the Finite Element Model (FEM)
4.2.2. Numerical Simulation and FEM Validation of Model Tests
5. Seismic Damage Mechanism of the Underground Complex
5.1. Numerical Models of the Soil–Underground Complex Interaction System
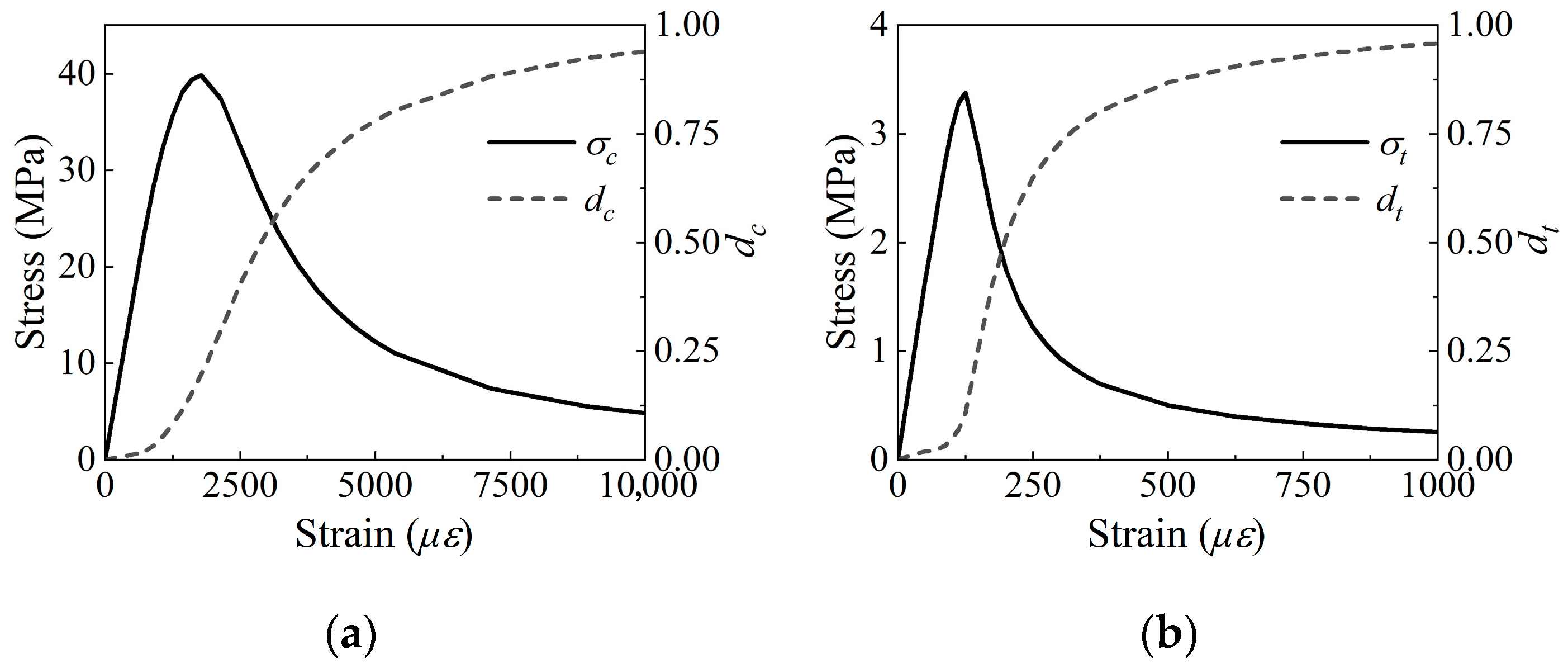
5.2. Structural Damage Mechanism
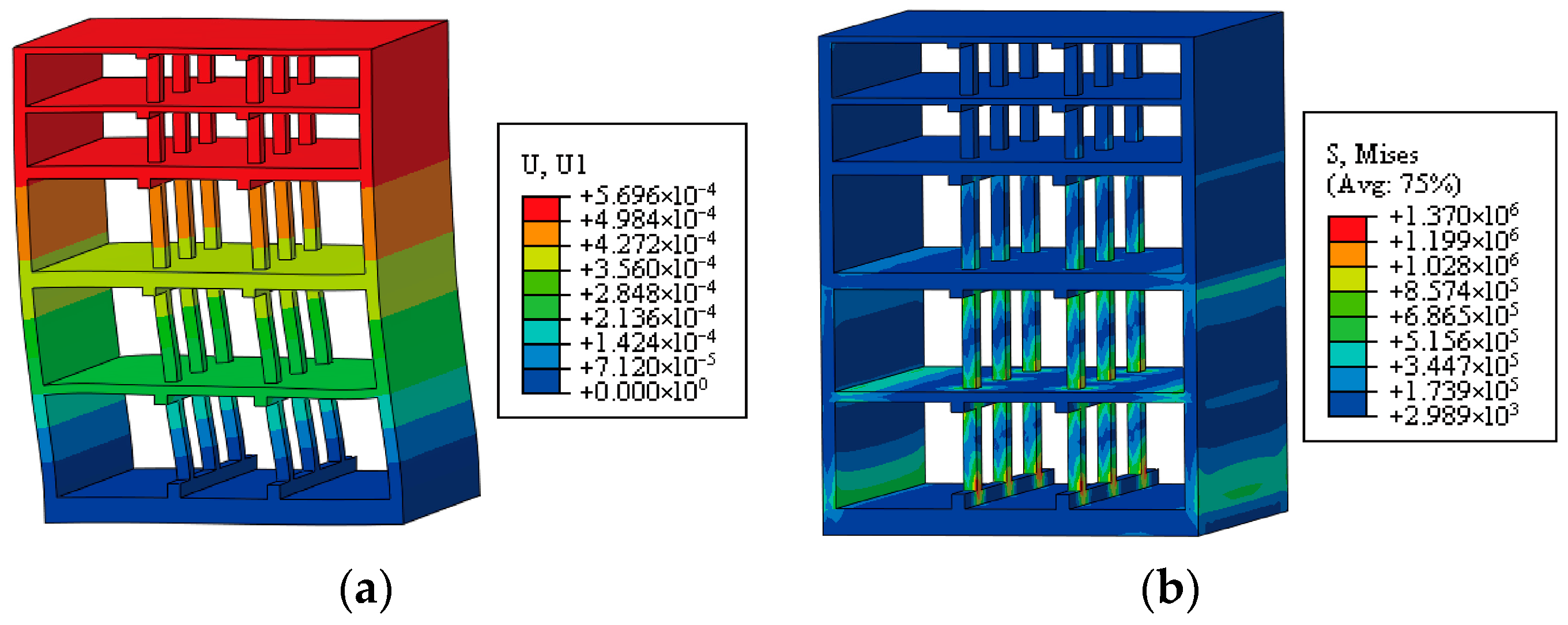
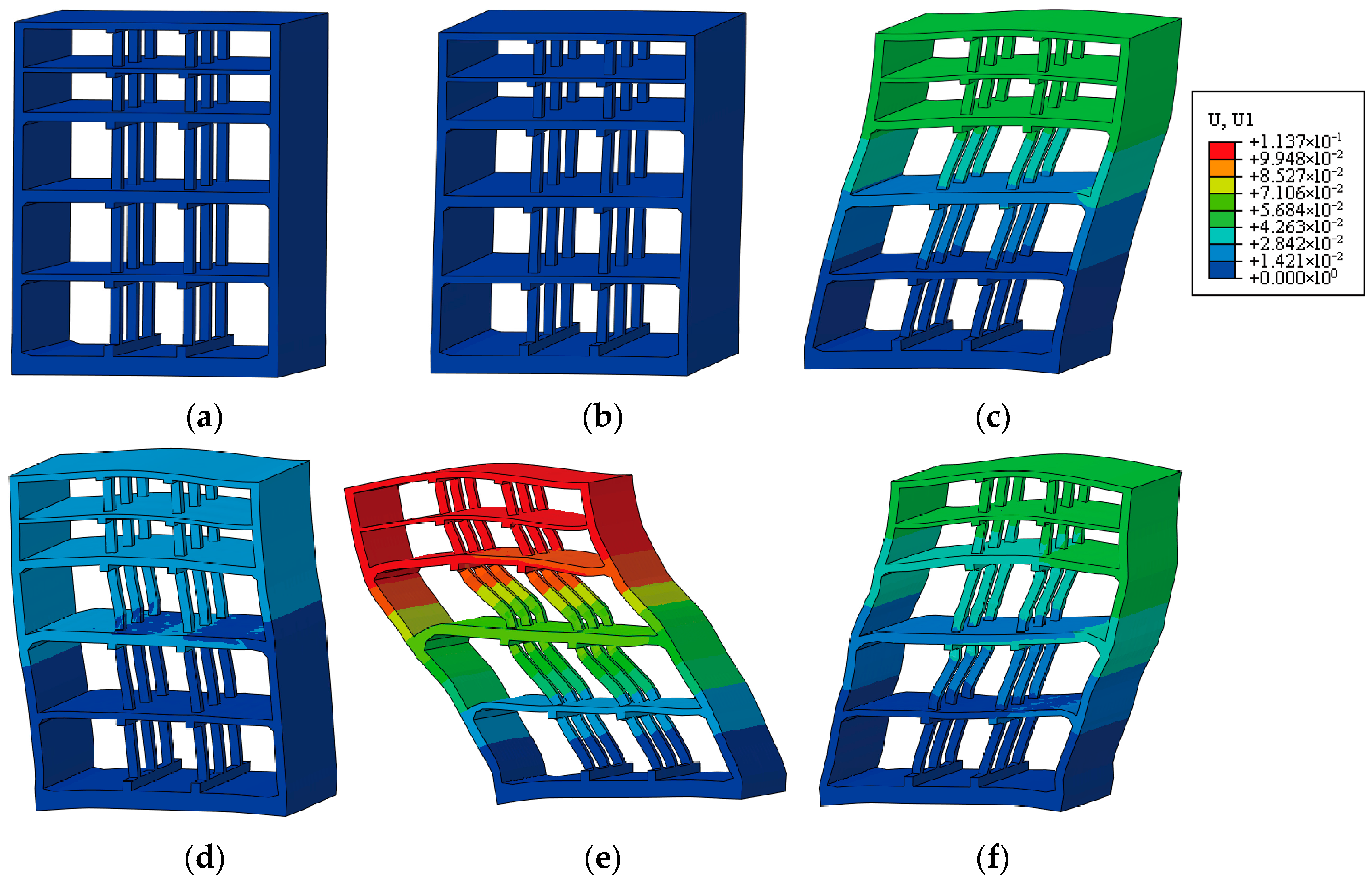
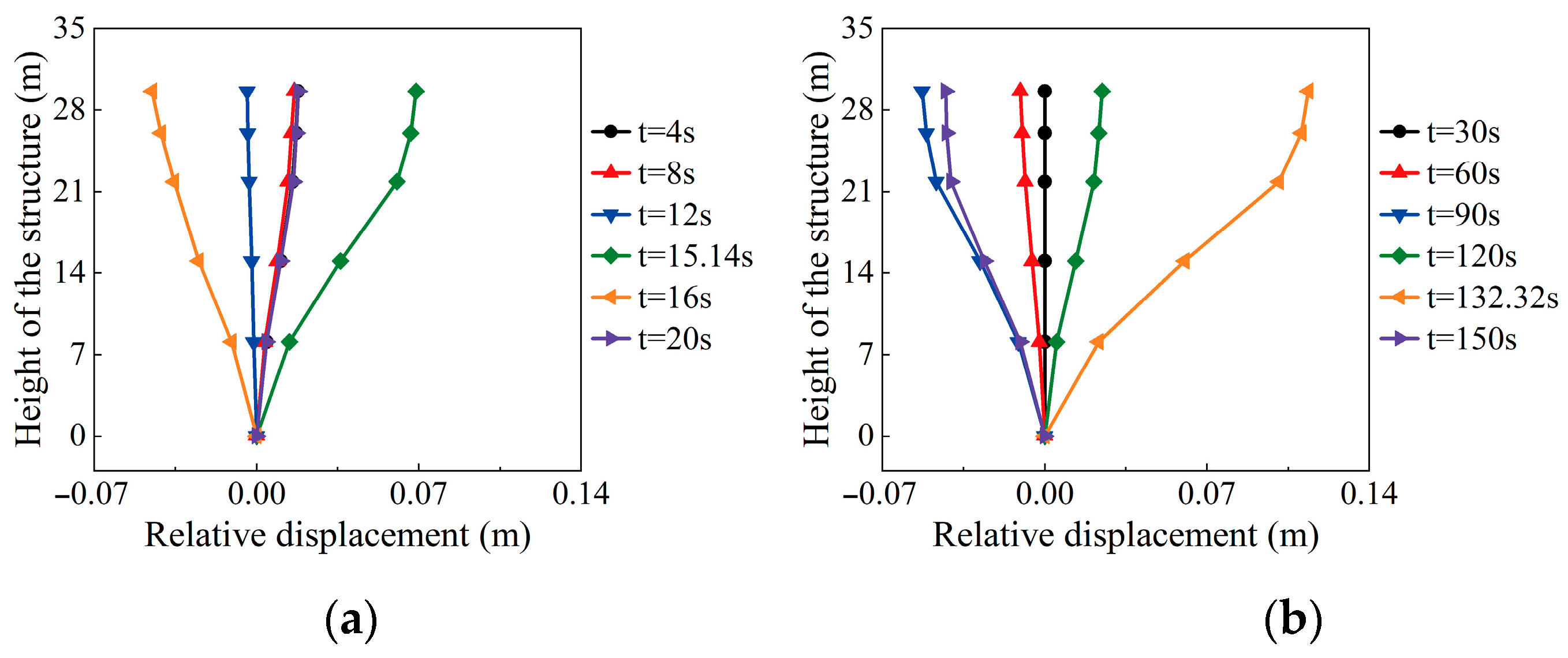
5.2.1. Structural Deformation Evolution
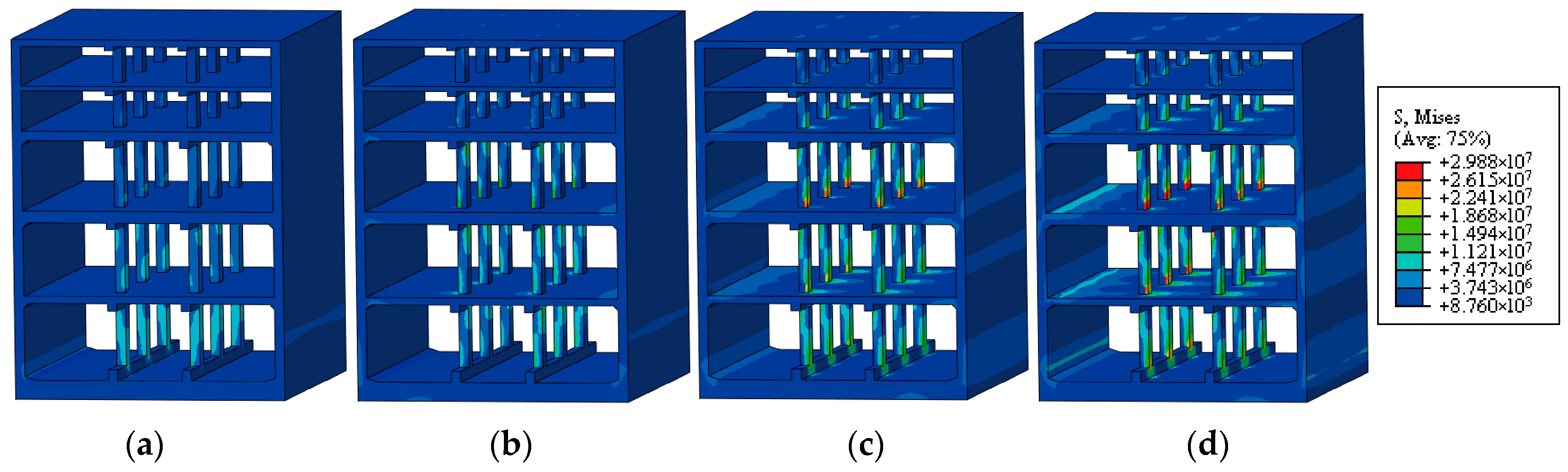
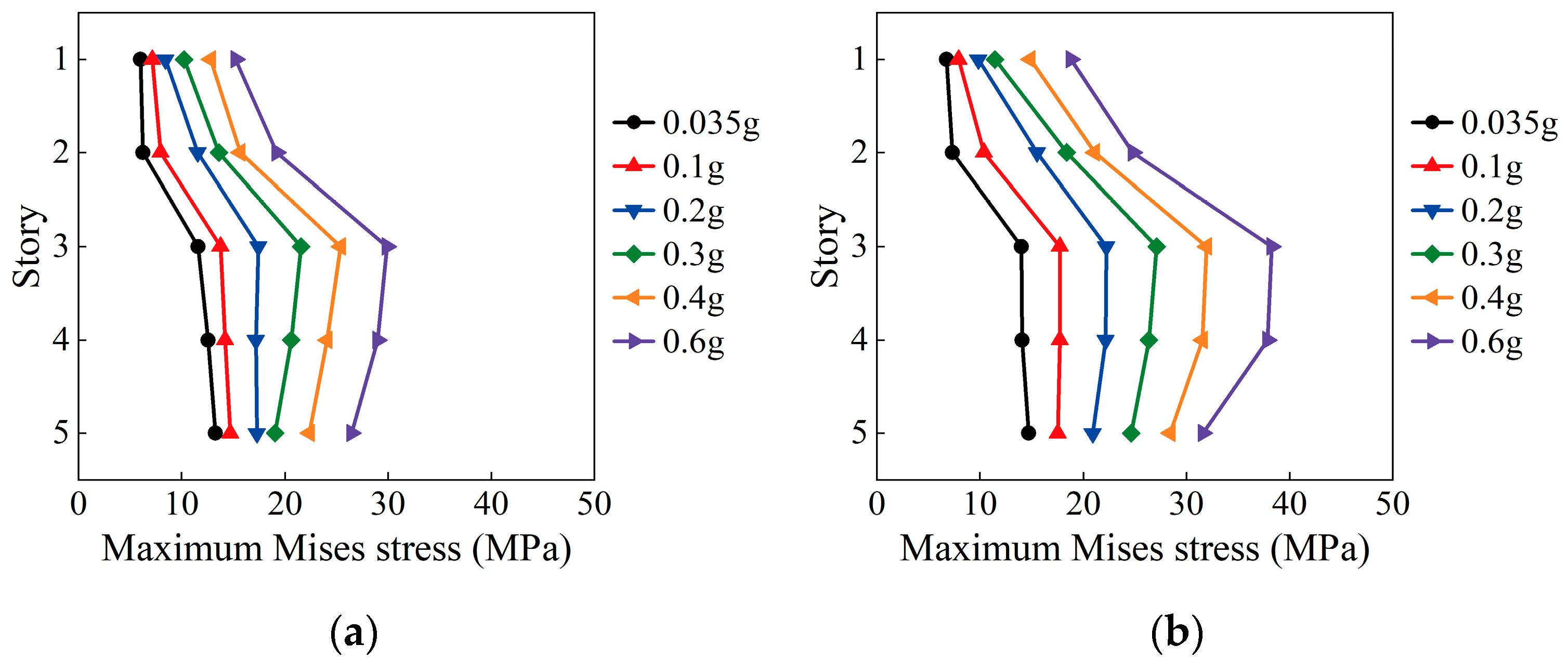
5.2.2. Stress Distribution and Damage Evolution Analysis
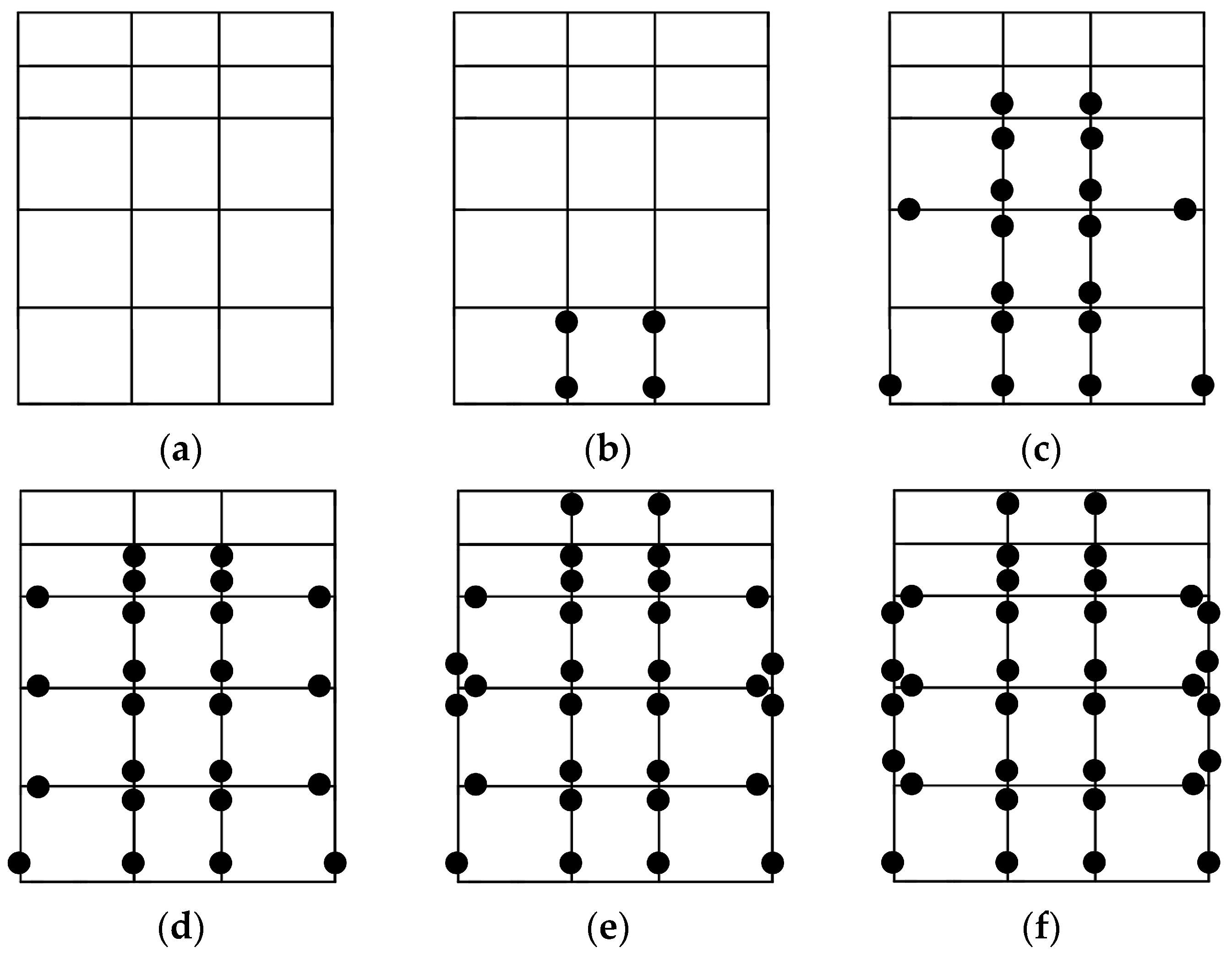
5.2.3. Development Process of Plastic Damage in the Structure
6. Conclusions
- (1)
- The acceleration amplification factor, response spectrum, and time–frequency evolution characteristics of the soft soil under the Shanghai artificial wave are similar to those under El Centro but differ notably from the far-field long-period ground motion HKD095. The peak time–frequency spectral energy under HKD095 reaches 1.66 times that of the Shanghai artificial wave. The time–frequency evolution of the soft soil indicates that the soft soil site exhibits a more significant energy amplification effect under far-field long-period seismic motions.
- (2)
- The acceleration amplification factors of the underground complex and surrounding soil are generally consistent, except for localized discrepancies. This indicates that the structural seismic response is primarily governed by the surrounding soil’s confinement effect, while localized extrusion and separation may occur at the soil–structure interface. The seismic deformation of the underground complex is dominated by shear behavior, with greater horizontal deformation under HKD095 than under the Shanghai artificial wave.
- (3)
- Plastic damage is primarily concentrated at the column-to-slab and wall-to-slab connections, where abrupt stiffness changes are located. Under strong seismic excitation, it first initiates at bottom-story column ends and then extends to these connections. For the five-story and three-span underground complex examined in this paper, the structural plastic damage progresses as follows: (i) ends of bottom-story columns, (ii) ends of columns from the second to fifth stories, base of bottom-story sidewalls and edges of third-story slabs, (iii) edges of second- to fourth-story slabs, and (iv) wall-to-slab connections from the third to fourth stories.
- (4)
- Under various types of seismic motions, the time–frequency evolution of the free field site response, structural deformation, stress distribution, and damage evolution of the underground complex all indicate that the response of the soft soil site and the structure under the far-field long-period seismic motion is significantly greater than that under the Shanghai artificial wave. Therefore, how to ensure the seismic safety of major engineering structures in soft soil sites under far-field strong seismic motions still requires further research in seismic design.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, K.; Zhang, L.; Li, S.; Huang, Y.P.; Ding, X.; Hao, J.N.; Huang, S.Q.; Li, X.J.; Lu, F.; Zhang, H.W. Urban rail transit in china: Progress report and analysis (2015–2023). Urban Rail Transit 2025, 11, 1–27. [Google Scholar] [CrossRef]
- Cheng, X.J.; Xu, X.; Hu, Z.N.; Jing, L.P.; Liang, H.A.; Cui, J. Seismic response of a liquefiable site-underground structure system. Buildings 2022, 12, 1751. [Google Scholar] [CrossRef]
- Chen, X.; Xiong, Z.M.; Ren, C.H.; Liu, Y. Experimental investigations of the seismic response of a large underground structure at a soft loess site. Buildings 2023, 13, 1710. [Google Scholar] [CrossRef]
- Iida, H.; Hiroto, T.; Yoshida, N.; Iwafuji, M. Damage to daikai subway station. Soils Found. 1996, 36, 283–300. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the taiwan chi-chi earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Kontoe, S.; Zdravkovic, L.; Potts, D.M.; Menkiti, C.O. Case study on seismic tunnel response. Can. Geotech. J. 2008, 45, 1743–1764. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Bobet, A.; Yuan, Y. Damage observation and assessment of the longxi tunnel during the wenchuan earthquake. Tunn. Undergr. Space Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Wu, C.Y.; Lu, D.C.; El Naggar, M.H.; Ma, C.; Li, Q.; Du, X.L. Upgrading seismic performance of underground frame structures based on potential failure modes. Soil Dyn. Earthq. Eng. 2022, 153, 107116. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Vasiliadis, L.K. Structural damage prediction of a reinforced concrete frame under single and multiple seismic events using machine learning algorithms. Appl. Sci. 2022, 12, 3845. [Google Scholar] [CrossRef]
- Quan, D.Z.; Chai, S.B.; Wang, Y.L.; Fan, Z.S.; Bu, Y.H. 3-d numerical simulation of seismic response of the induced joint of a subway station. Buildings 2023, 13, 1244. [Google Scholar] [CrossRef]
- Yang, J.; Zhuang, H.Y.; Zhang, G.Y.; Tang, B.Z.; Xu, C.J. Seismic performance and fragility of two-story and three-span underground structures using a random forest model and a new damage description method. Tunn. Undergr. Space Technol. 2023, 135, 104980. [Google Scholar] [CrossRef]
- Hou, C.; Jin, X.G.; Ge, Y.; He, J. Shaking table test on the seismic response of a frame-type subway station in composite soil. Int. J. Geomech. 2021, 21, 04021220. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Ren, J.W.; Miao, Y.; Jing, L.G.; Yao, E.L.; Xu, C.J. Seismic performance levels of a large underground subway station in different soil foundations. J. Earthq. Eng. 2021, 25, 2808–2833. [Google Scholar] [CrossRef]
- Yang, Y.F.; Cao, J.J.; Qu, R.Q.; Xu, Z.G. Numerical simulation of the seismic damage of daikai station based on pushover analyses. Buildings 2023, 13, 760. [Google Scholar] [CrossRef]
- Yamato, T.; Umehara, T.; Aoki, H.; Nakamura, S.; Ezaki, J.; Suetomi, I. Damage to daikai subway station of kobe rapid transit system and estimation of its reason during the 1995 hyogoken-nanbu earthquake. Doboku Gakkai Ronbunshu 1996, 1996, 303–320. [Google Scholar] [CrossRef]
- Lu, C.C.; Hwang, J.H. Nonlinear collapse simulation of daikai subway in the 1995 kobe earthquake: Necessity of dynamic analysis for a shallow tunnel. Tunn. Undergr. Space Technol. 2019, 87, 78–90. [Google Scholar] [CrossRef]
- Nguyen, V.Q.; Nizamani, Z.A.; Park, D.; Kwon, O.S. Numerical simulation of damage evolution of daikai station during the 1995 kobe earthquake. Eng. Struct. 2020, 206, 110180. [Google Scholar] [CrossRef]
- An, X.H.; Shawky, A.A.; Maekawa, K. The collapse mechanism of a subway station during the great hanshin earthquake. Cem. Concr. Compos. 1997, 19, 241–257. [Google Scholar] [CrossRef]
- Huo, H.; Bobet, A.; Fernández, G.; Ramírez, J. Load transfer mechanisms between underground structure and surrounding ground: Evaluation of the failure of the daikai station. J. Geotech. Geoenviron. Eng. 2005, 131, 1522–1533. [Google Scholar] [CrossRef]
- Ma, C.; Lu, D.C.; Du, X.L.; Qi, C.Z.; Zhang, X.Y. Structural components functionalities and failure mechanism of rectangular underground structures during earthquakes. Soil Dyn. Earthq. Eng. 2019, 119, 265–280. [Google Scholar] [CrossRef]
- Dong, R.; Jing, L.P.; Li, Y.Q.; Yin, Z.Y.; Wang, G.; Xu, K.P. Seismic deformation mode transformation of rectangular underground structure caused by component failure. Tunn. Undergr. Space Technol. 2020, 98, 103298. [Google Scholar] [CrossRef]
- Ma, C.; Lu, D.C.; Du, X.L.; Qi, C.Z. Seismic performance of a rectangular subway station with earth retaining system. Earthq. Eng. Eng. Vib. 2022, 21, 221–236. [Google Scholar] [CrossRef]
- Yue, F.; Liu, B.W.; Zhu, B.; Jiang, X.L.; Chen, L.; Liao, K. Shaking table test and numerical simulation on seismic performance of prefabricated corrugated steel utility tunnels on liquefiable ground. Soil Dyn. Earthq. Eng. 2021, 141, 106527. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, W.; Li, Y.; Yuan, Y. Shaking table test of a multi-story subway station under pulse-like ground motions. Soil Dyn. Earthq. Eng. 2016, 82, 111–122. [Google Scholar] [CrossRef]
- Chen, S.; Zhuang, H.Y.; Qu, D.Z.; Yuan, J.; Zhao, K.; Ruan, B. Shaking table test on the seismic response of large-scale subway station in a loess site: A case study. Soil Dyn. Earthq. Eng. 2019, 123, 173–184. [Google Scholar] [CrossRef]
- Yu, H.T.; Yan, X.; Bobet, A.; Yuan, Y.; Xu, G.P.; Su, Q.K. Multi-point shaking table test of a long tunnel subjected to non-uniform seismic loadings. Bull. Earthq. Eng. 2018, 16, 1041–1059. [Google Scholar] [CrossRef]
- Yue, C.Z.; Zheng, Y.L.; Deng, S.X. Shaking table test study on seismic performance improvement for underground structures with center column enhancement. J. Earthq. Tsunami 2019, 13, 1950009. [Google Scholar] [CrossRef]
- Liu, S.T.; Lu, Z.; Li, P.Z.; Ding, S.W.; Wan, F. Shaking table test and numerical simulation of eddy-current tuned mass damper for structural seismic control considering soil-structure interaction. Eng. Struct. 2020, 212, 110531. [Google Scholar] [CrossRef]
- DGJ08-9-2013; Code for Seismic Design of Buildings. Tongji University Press: Shanghai, China, 2013.
- Wang, J.N.; Yang, J.; Zhuang, H.Y.; Ma, G.W.; Sun, Y.J. Seismic responses of a large unequal-span underground subway station in liquefiable soil using shaking table test. J. Earthq. Eng. 2022, 26, 8446–8467. [Google Scholar] [CrossRef]
- Kramer, S.L.; Stewart, J.P. Geotechnical Earthquake Engineering; CRC Press: Boca Raton, FL, USA, 2024; pp. 368–370. [Google Scholar] [CrossRef]
- Li, X.J.; Pan, D.G.; Huang, Y.; Cheng, Y.; Fu, X.Q. Shaking table test and numerical simulation of free field in sand-sawdust mixed soil. Soil Dyn. Earthq. Eng. 2023, 165, 107707. [Google Scholar] [CrossRef]
- ABAQUS Inc. Abaqus Analysis User’s Guide; ABAQUS 6.14 HTML Documentation; ABAQUS Inc.: Palo Alto, CA, USA, 2014. [Google Scholar]
- Martin, P.P.; Seed, H.B. One-dimensional dynamic ground response analyses. J. Geotech. Eng.-Asce 1982, 108, 935–952. [Google Scholar] [CrossRef]
- Li, W.T.; Chen, Q.J. Effect of vertical ground motions and overburden depth on the seismic responses of large underground structures. Eng. Struct. 2020, 205, 110073. [Google Scholar] [CrossRef]
- Chen, Q.J.; Hong, N.; Zhang, T.Y.; Zhao, Z.P. Experiment-based performance evaluation framework for isolated structures in underground subway station-soil-aboveground structure interaction system under seismic excitations. J. Build. Eng. 2022, 56, 104790. [Google Scholar] [CrossRef]
- Qiu, D.P.; Wang, P.; Ren, W.J.; Chen, J.Y.; Zhao, C.F. Seismic responses and failure mechanism of the superstructure-integrated underground structure considering the seismic aboveground-underground interaction. Soil Dyn. Earthq. Eng. 2023, 175, 108259. [Google Scholar] [CrossRef]
- Wu, W.F.; Ge, S.P.; Yuan, Y.; Ding, W.Q.; Anastasopoulos, I. Seismic response of subway station in soft soil: Shaking table testing versus numerical analysis. Tunn. Undergr. Space Technol. 2020, 100, 103389. [Google Scholar] [CrossRef]
- Xu, C.S.; Zhang, Z.H.; Li, Y.; Du, X.L. Validation of a numerical model based on dynamic centrifuge tests and studies on the earthquake damage mechanism of underground frame structures. Tunn. Undergr. Space Technol. 2020, 104, 103538. [Google Scholar] [CrossRef]
- Yan, G.Y.; Xu, C.S.; Zhang, Z.H.; Du, X.L.; Wang, X.L. Numerical analysis on seismic performance of underground structures in liquefiable interlayer sites from centrifuge shaking table test. Earthq. Eng. Eng. Vib. 2024, 23, 781–798. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Hu, Z.N.; Wang, X.L.; Chen, G.X. Seismic responses of a large underground structure in liquefied soils by fem numerical modelling. Bull. Earthq. Eng. 2015, 13, 3645–3668. [Google Scholar] [CrossRef]
- Cui, Z.D.; Zhang, L.J.; Hou, C.Y. Seismic behavior of subway station in the soft clay field before and after freeze-thaw cycle. Soil Dyn. Earthq. Eng. 2023, 175, 108222. [Google Scholar] [CrossRef]
- Chen, Q.J.; Zhang, T.Y.; Hong, N.; Huang, B. Seismic performance of a subway station-tunnel junction structure: A shaking table investigation and numerical analysis. KSCE J. Civ. Eng. 2021, 25, 1653–1669. [Google Scholar] [CrossRef]
- DG/TJ08-2064-2022; Standard for Seismic Design of Subway Structure. Tongji University Press: Shanghai, China, 2022.
- Lee, J.H.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech.-ASCE 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Chopra, A.K.; Chintanapakdee, C. Inelastic deformation ratios for design and evaluation of structures: Single-degree-of-freedom bilinear systems. J. Struct. Eng. 2004, 130, 1309–1319. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, Q.J. Parametric fitting of soft soil sites’ davidenkov model based on pso algorithm and its application. J. Vib. Shock. 2019, 38, 8–16. [Google Scholar] [CrossRef]
- Chen, Q.J.; Chen, X.; Zhao, Z.P. Simulation of near-fault pulse-like ground motion and investigation of seismic response characteristics in subway stations. J. Earthq. Eng. 2024, 28, 3648–3680. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- Zhuang, H.Y.; Zhao, C.; Chen, S.; Fu, J.S.; Zhao, K.; Chen, G.X. Seismic performance of underground subway station with sliding between column and longitudinal beam. Tunn. Undergr. Space Technol. 2020, 102, 103439. [Google Scholar] [CrossRef]
- Wei, S.M.; Wang, C.; Cui, Z.D.; Liang, F.Y.; Qin, T.X. Seismic behavior of a shallow underground station with internal soil erosion. Eng. Struct. 2025, 328, 119706. [Google Scholar] [CrossRef]

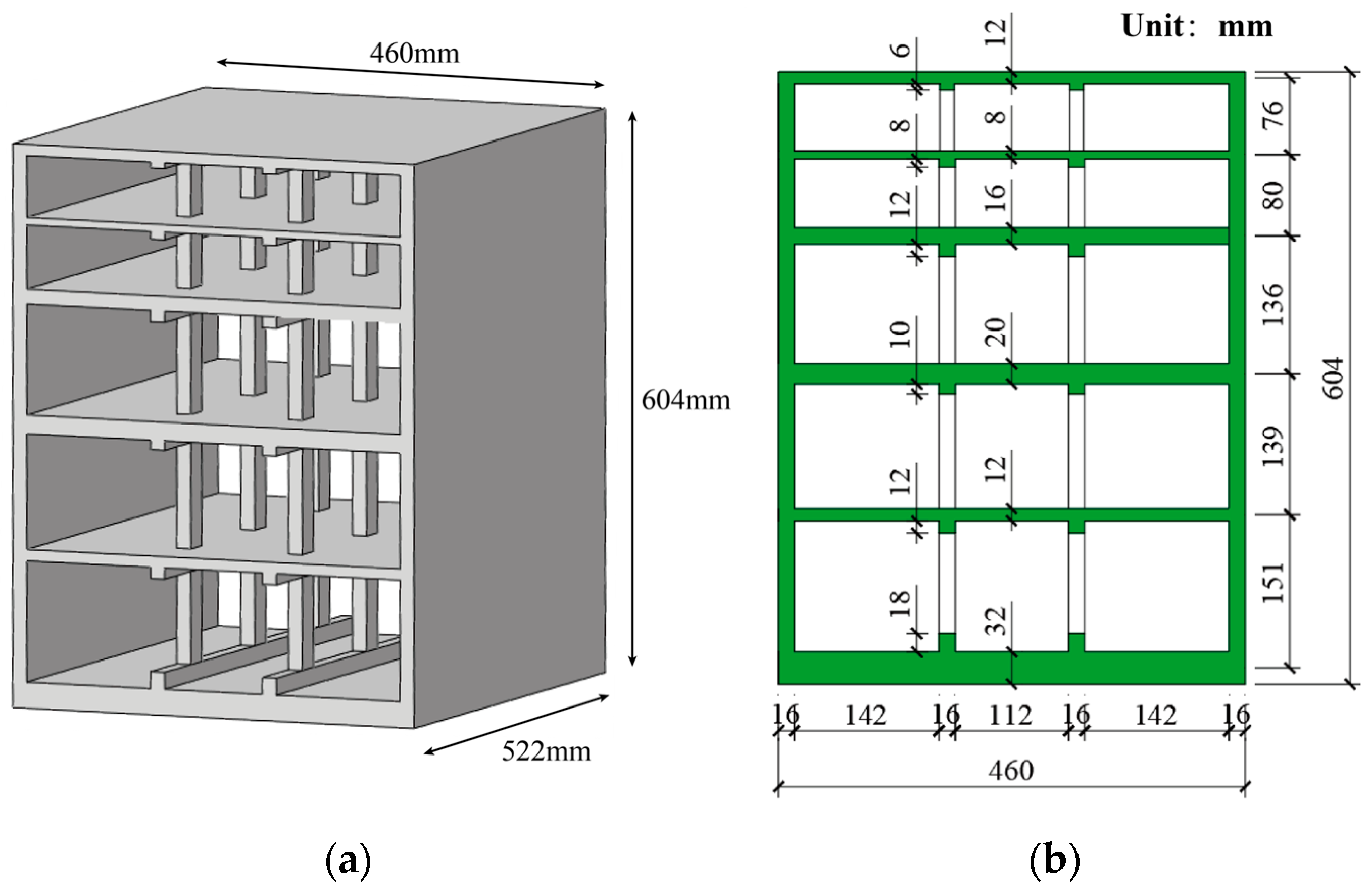


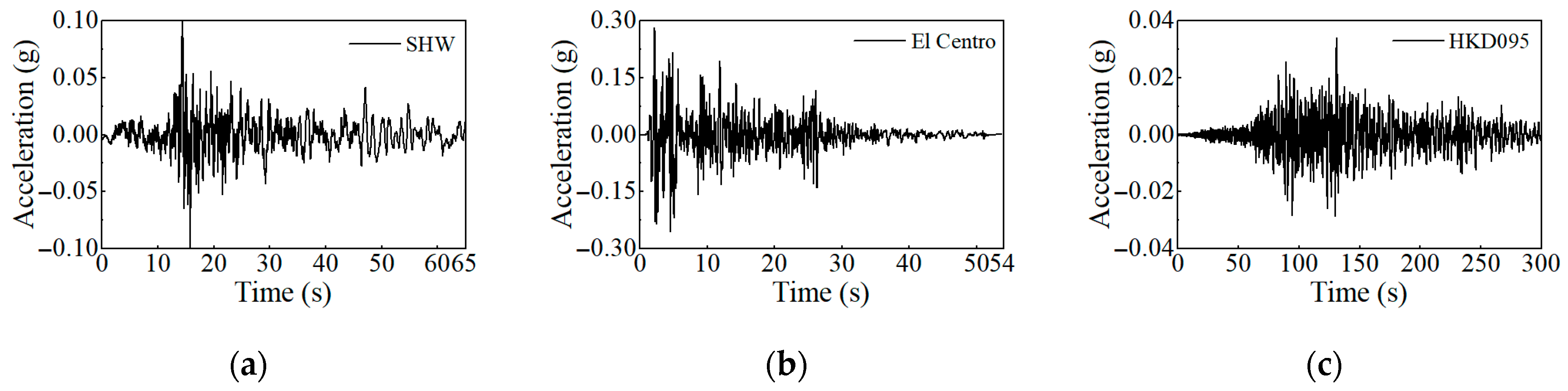
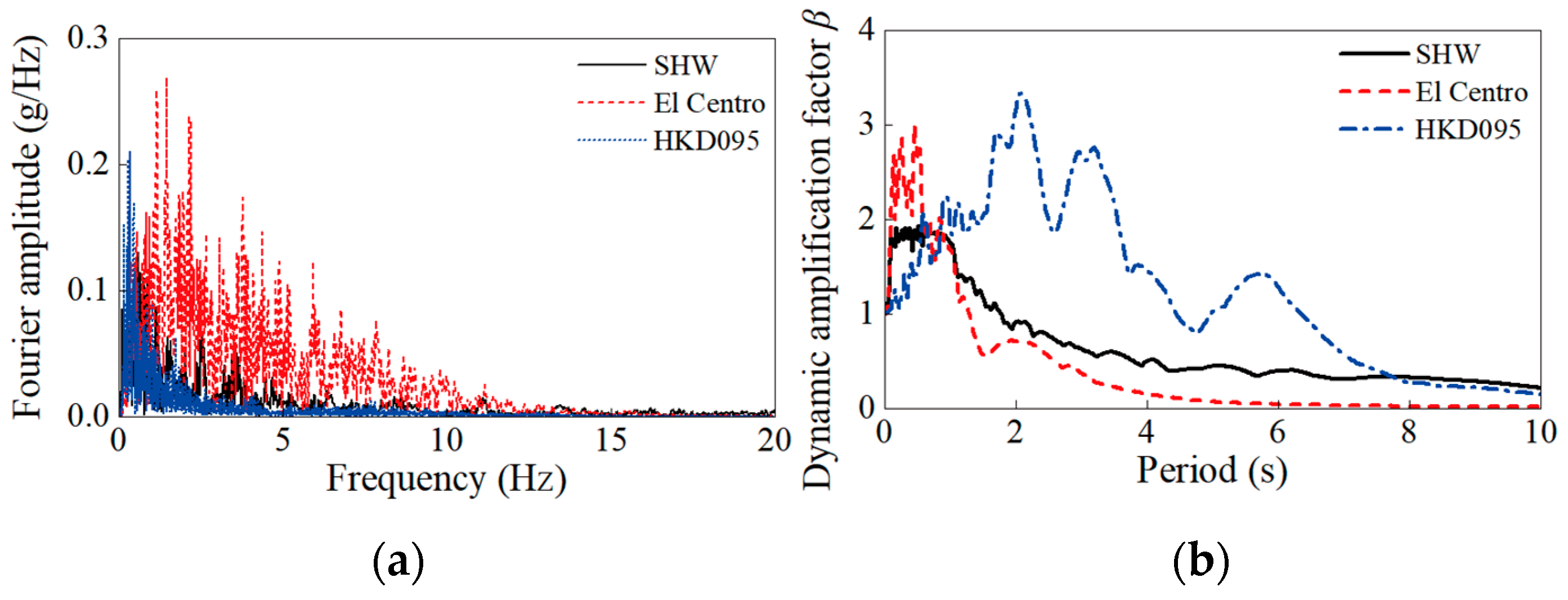
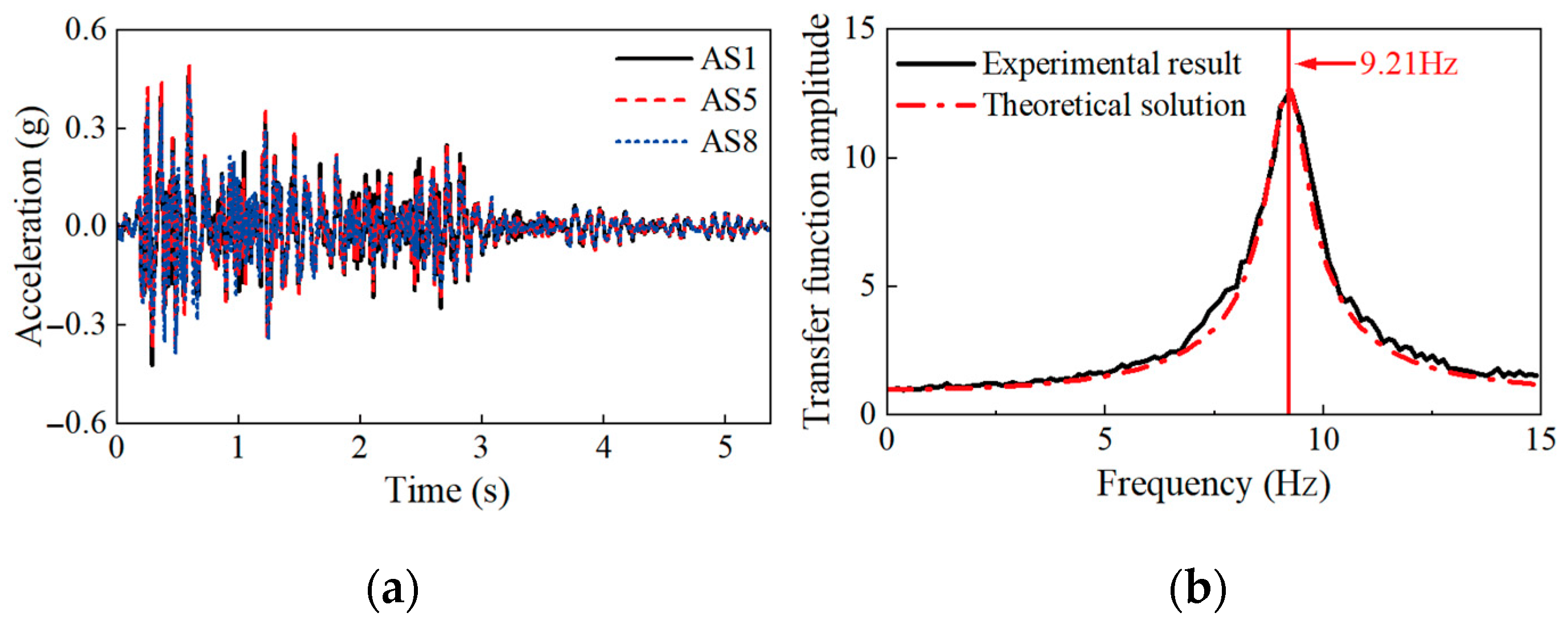







| Type | Physical Quantity | Symbol | Similarity Ratio |
|---|---|---|---|
| Geometry properties | Length | 0.02 | |
| Material properties of the model structure | Strain | 1 | |
| Elastic modulus | 0.1 | ||
| Stress | 0.1 | ||
| Density | 2.5 | ||
| Mass | 2 × 10−5 | ||
| Material properties of the model soil | Shear modulus | 0.0147 | |
| Density | 0.368 | ||
| Loading | Linear load | 2 × 10−3 | |
| Area load | 0.1 | ||
| Dynamic properties | Duration | 0.1 | |
| Frequency | 10 | ||
| Velocity | 0.2 | ||
| Acceleration | 2 |
| Test No. | Ground Motion | Peak Acceleration (g) | Test No. | Ground Motion | Peak Acceleration (g) |
|---|---|---|---|---|---|
| WN1 | White noise | 0.05 | HKD3 | HKD095 | 0.3 |
| EL2 | El Centro | 0.2 | WN3 | White noise | 0.05 |
| SHW2 | SHW | 0.2 | EL4 | El Centro | 0.4 |
| HKD2 | HKD095 | 0.2 | SHW4 | SHW | 0.4 |
| WN2 | White noise | 0.05 | HKD4 | HKD095 | 0.4 |
| EL3 | El Centro | 0.3 | WN4 | White noise | 0.05 |
| SHW3 | SHW | 0.3 |
| Concrete Strength Grade | Elastic Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Dilatancy Angle | Initial Compression Yield Stress (MPa) | Limited Compression Yield Stress (MPa) | Limited Tensile Stress (MPa) |
|---|---|---|---|---|---|---|---|
| C35 | 31.5 | 0.15 | 2400 | 30° | 19.85 | 32.05 | 3.01 |
| C45 | 33.5 | 0.15 | 2400 | 30° | 23.17 | 39.82 | 3.38 |
| Soil Layer | Depth (m) | Soil Property | Density (kg/m3) | Shear Wave Velocity (m/s) | Poisson’s Ratio |
|---|---|---|---|---|---|
| S1 | 1.00 | Miscellaneous fill | 1890 | 74 | 0.40 |
| S2 | 6.40 | Silty clay | 1850 | 87 | 0.35 |
| S3 | 17.66 | Muddy silty clay | 1830 | 110 | 0.38 |
| S4 | 44.06 | Silty clay | 1820 | 220 | 0.35 |
| S5 | 51.46 | Clay | 2040 | 195 | 0.35 |
| S6 | 70.00 | Silty fine sand | 1935 | 225 | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, Q.; Chen, X.; Liao, C. Seismic Damage Mechanism of Five-Story and Three-Span Underground Complex in Soft Soil Site. Buildings 2025, 15, 2380. https://doi.org/10.3390/buildings15142380
Liu Y, Chen Q, Chen X, Liao C. Seismic Damage Mechanism of Five-Story and Three-Span Underground Complex in Soft Soil Site. Buildings. 2025; 15(14):2380. https://doi.org/10.3390/buildings15142380
Chicago/Turabian StyleLiu, Yikun, Qingjun Chen, Xi Chen, and Cong Liao. 2025. "Seismic Damage Mechanism of Five-Story and Three-Span Underground Complex in Soft Soil Site" Buildings 15, no. 14: 2380. https://doi.org/10.3390/buildings15142380
APA StyleLiu, Y., Chen, Q., Chen, X., & Liao, C. (2025). Seismic Damage Mechanism of Five-Story and Three-Span Underground Complex in Soft Soil Site. Buildings, 15(14), 2380. https://doi.org/10.3390/buildings15142380






