Mechanical Response Analysis of High-Pile Wharf on Deep Soft Soil Foundation Under Complex Multi-Factor Interactions
Abstract
1. Introduction
2. Numerical Model Construction
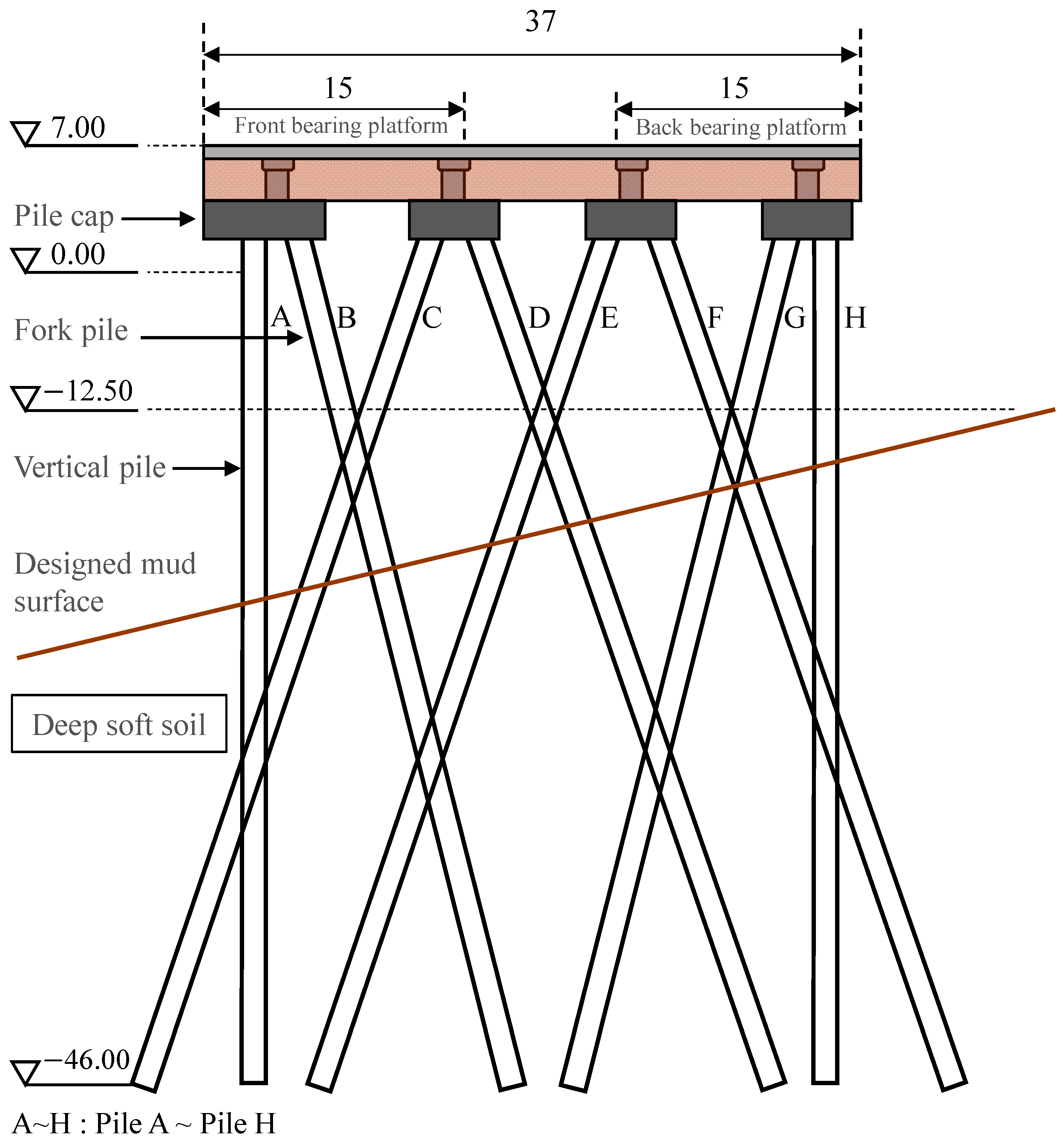
2.1. Project Description
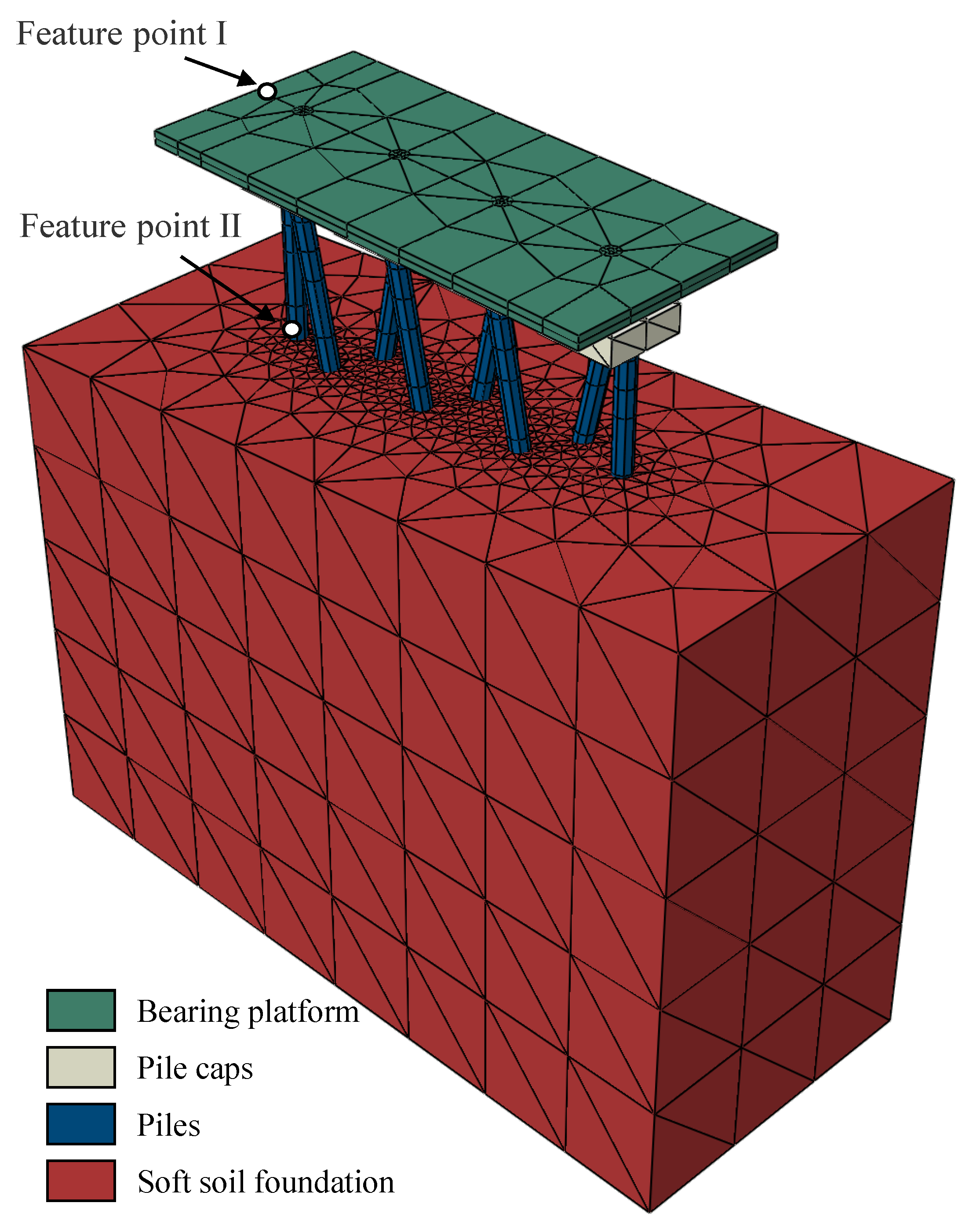
2.2. Finite Element Model Construction
2.3. Calculation Procedure
3. Results and Discussion
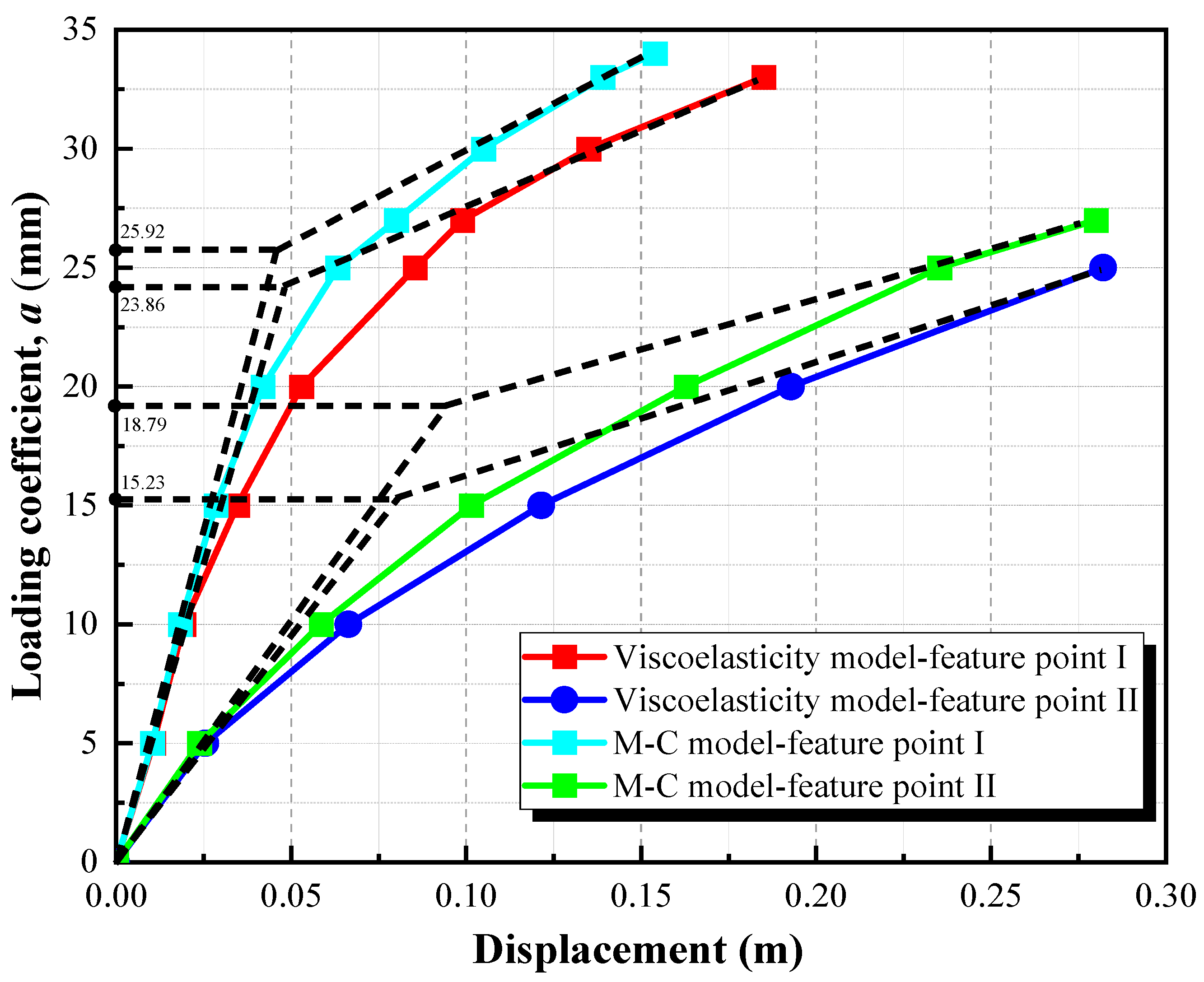
3.1. Soft Foundation Analysis
3.2. Wave Analysis
3.3. Stacking Surface Load Analysis
3.4. Multi-Factor Comparative Numerical Analysis
4. Conclusions
- 1
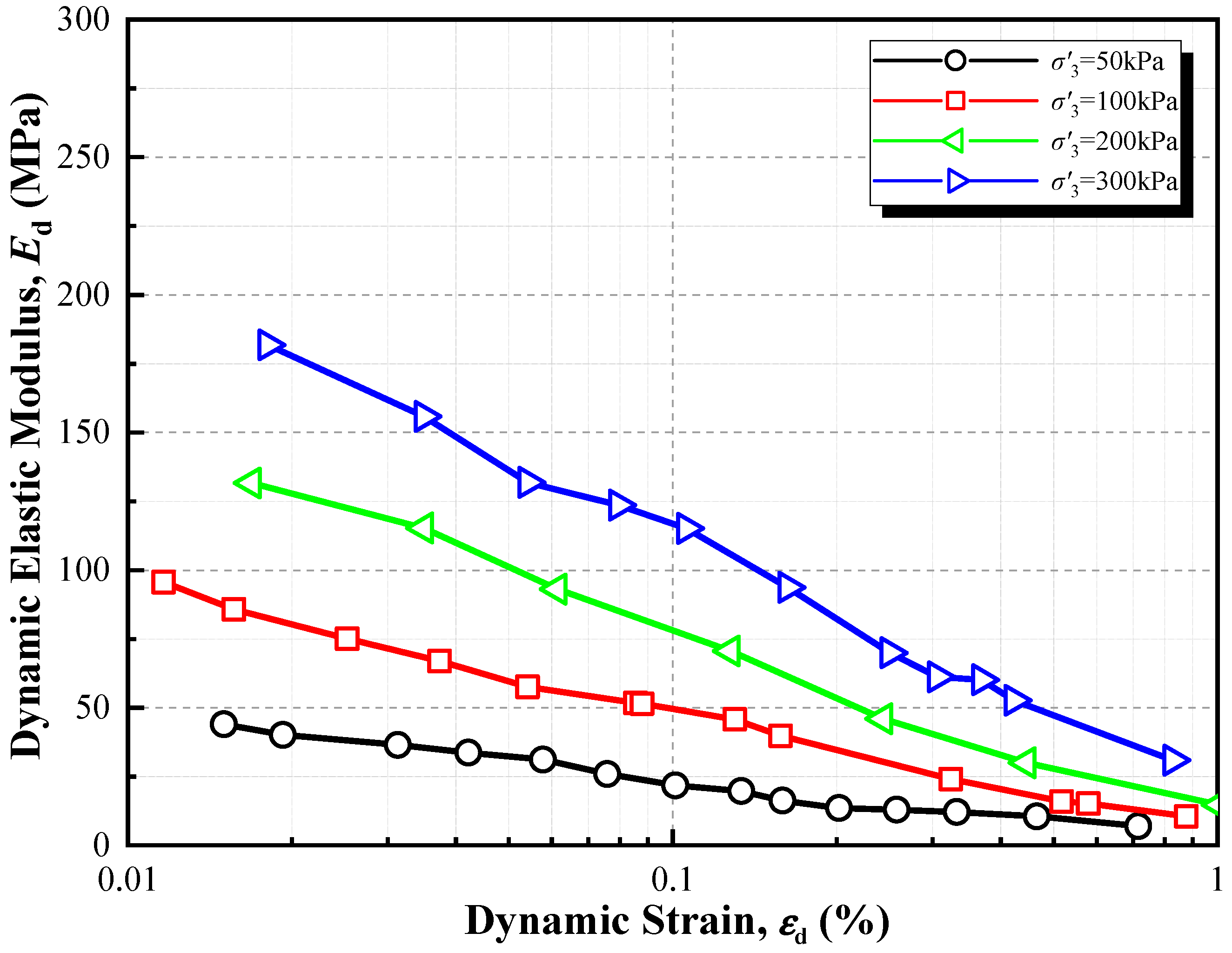
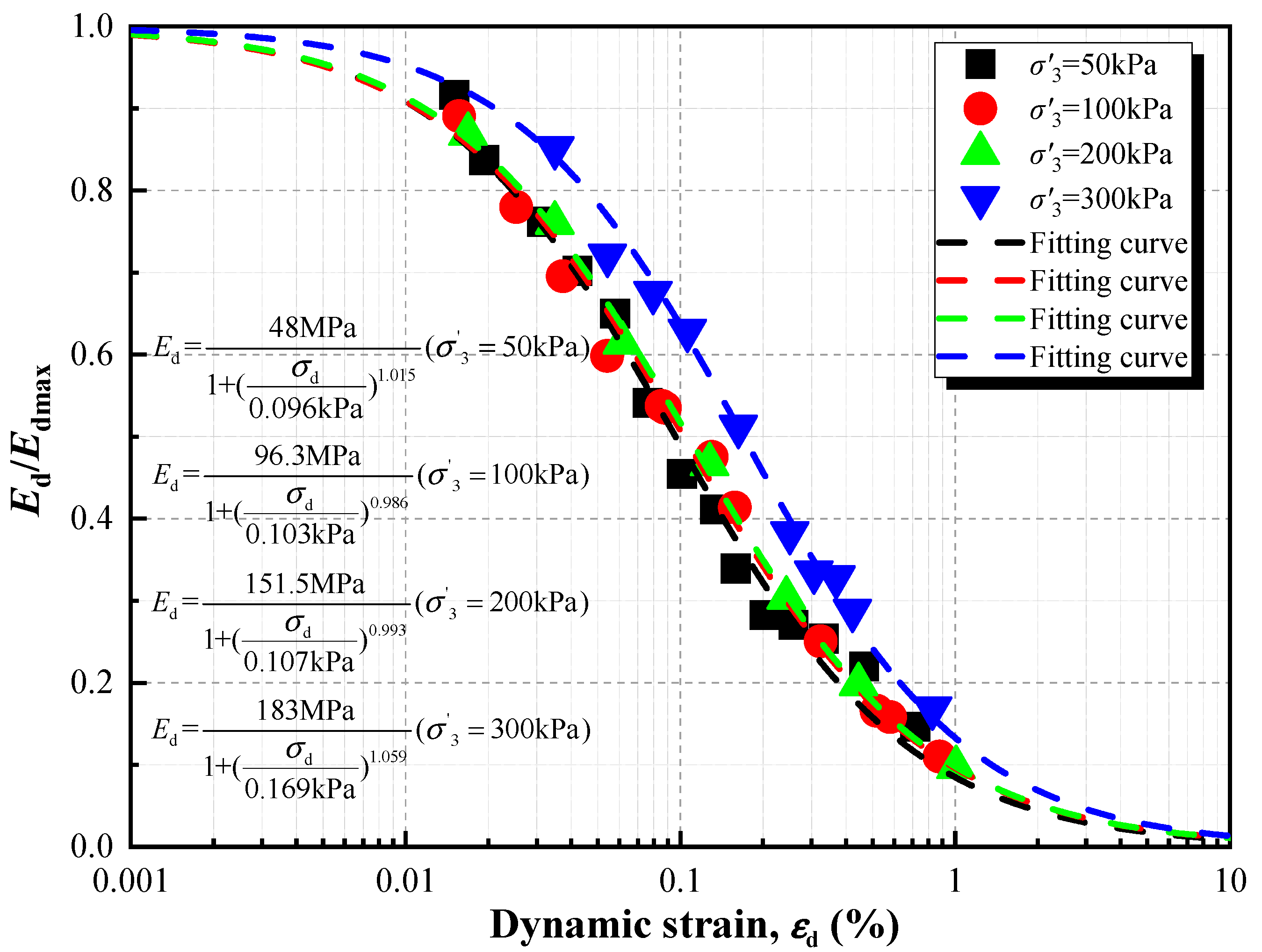
- Considering the hysteretic behavior and stiffness degradation characteristics of deep soft soil foundations for high-pile wharves, the Darendeli viscoelastic constitutive model was adopted. The safety factor at critical locations of the wharf structure decreased by up to 18.95%, highlighting the necessity of accounting for large deformation and hysteretic effects of soft soil in high-pile wharf design.
- 2
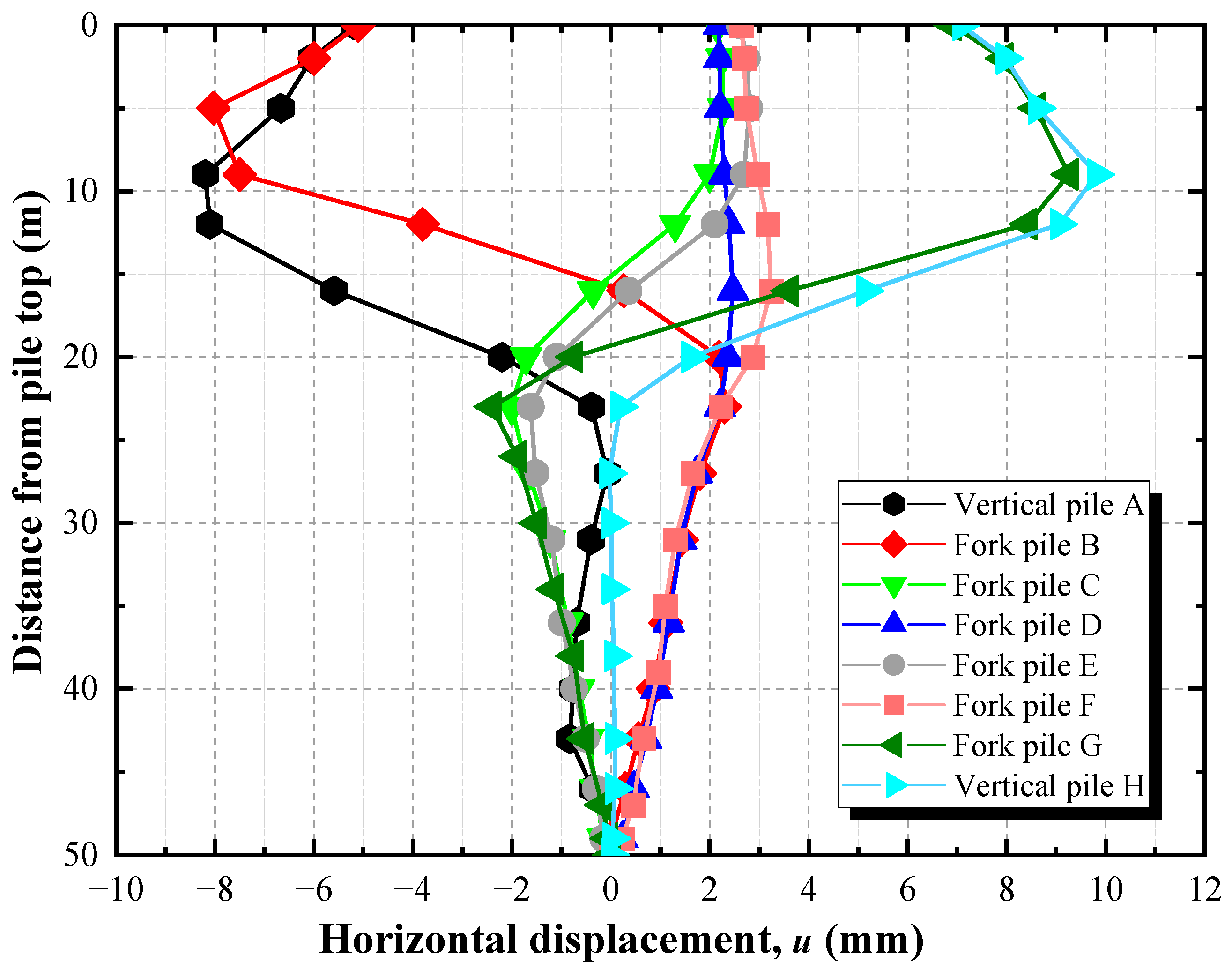
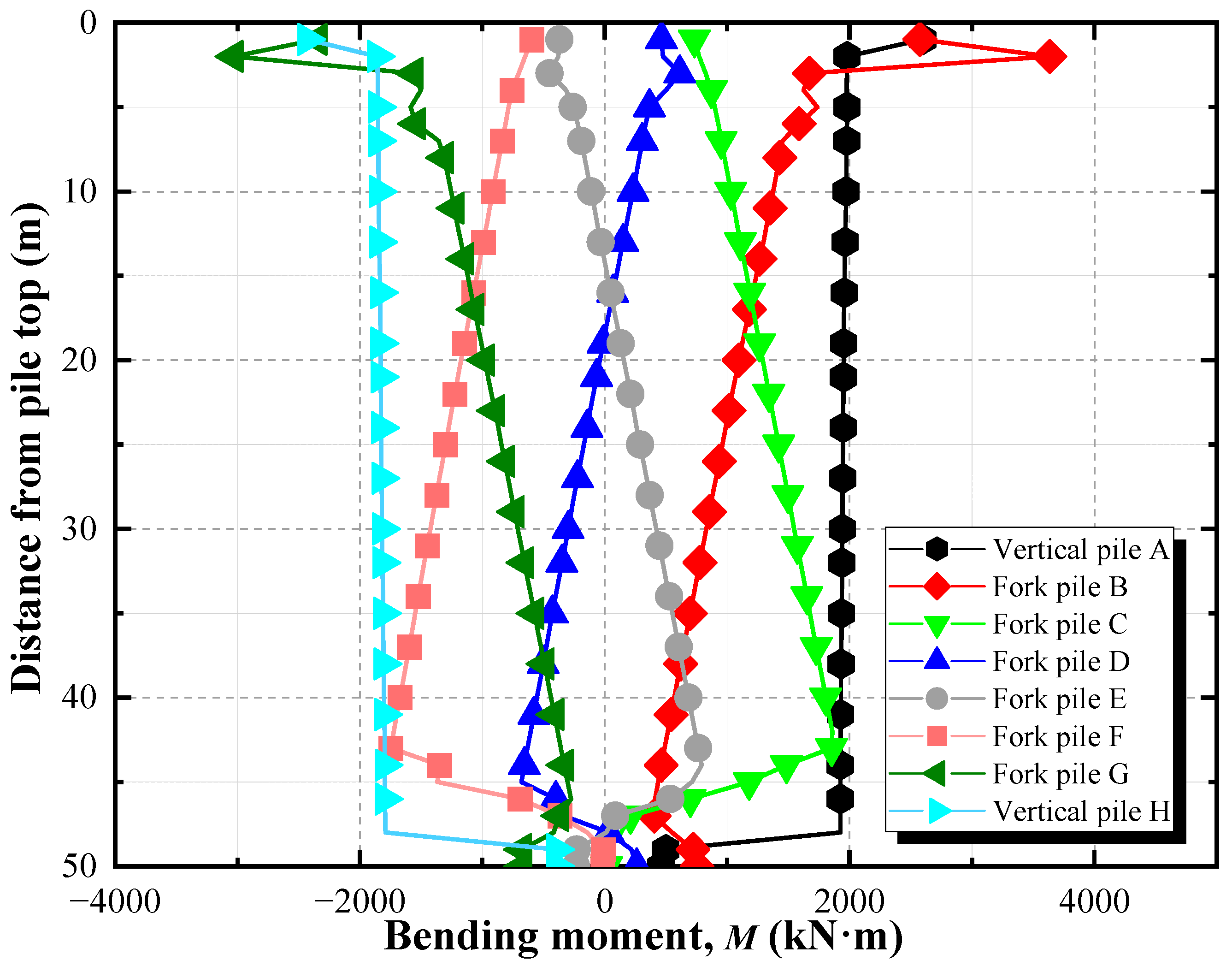
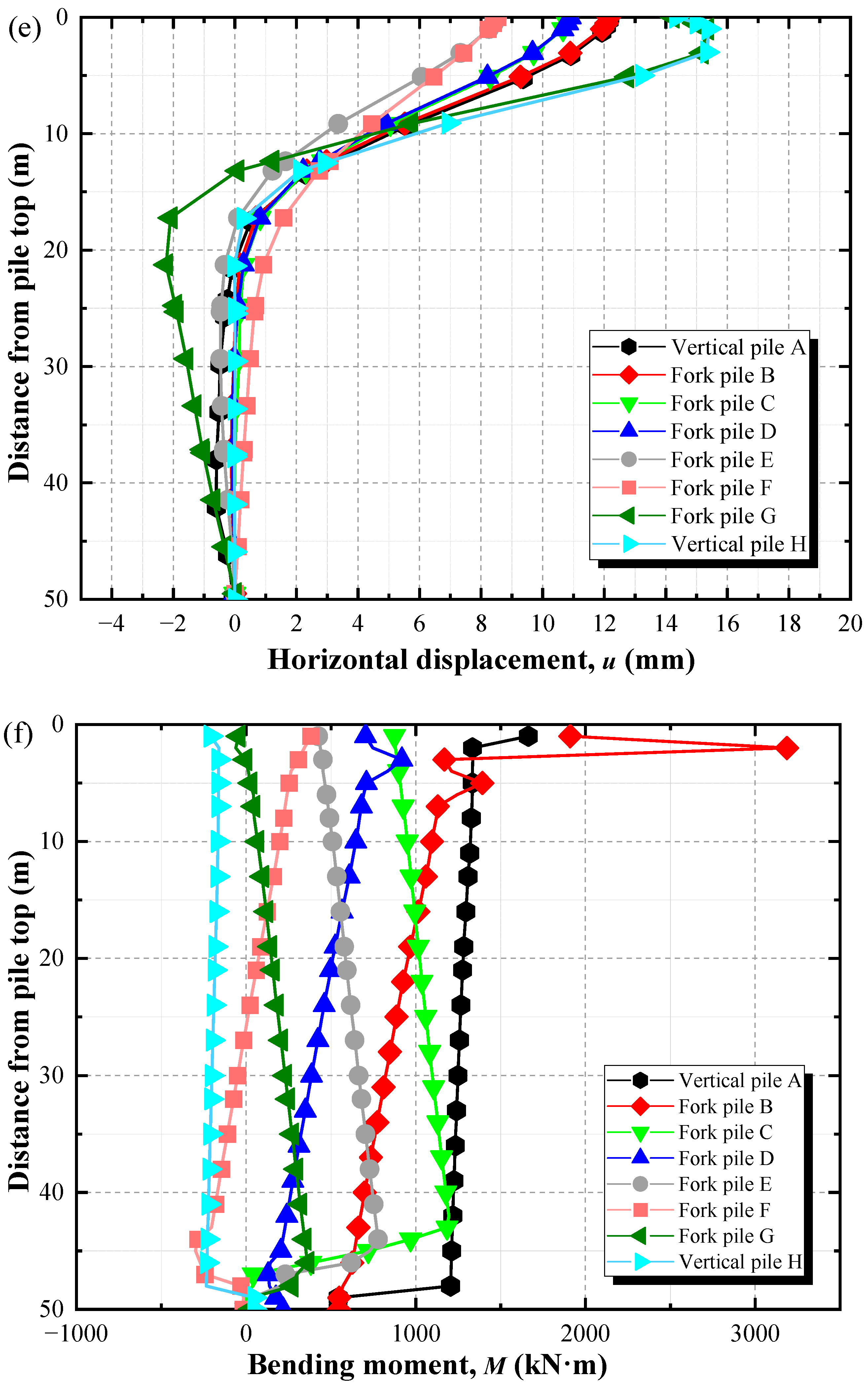
- Based on the Morison equation, wave loads were applied to the steel pipe piles of the high-pile wharf through the distributed load subroutine DLOAD. The horizontal displacements of piles A, B, G, and H were significantly larger than those of the four middle cross piles. The bending moments of the vertical piles were more uniform compared to those of the batter piles, while piles B and F exhibited distinct zones of abrupt bending moment change. The maximum displacement and maximum bending moments of the wharf were both located within the wave load action zone.
- 3
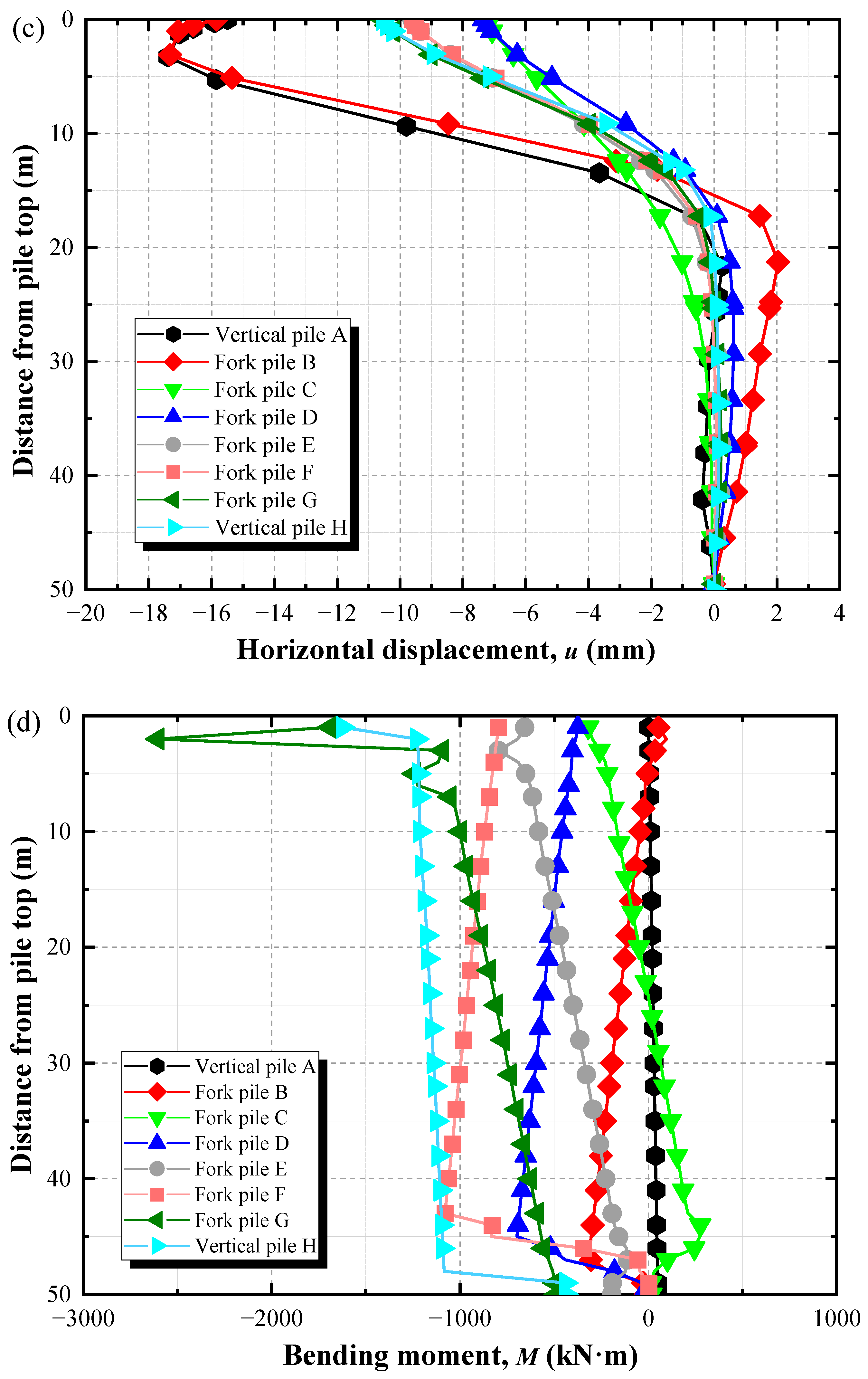
- The impact of surface loads on the deformation and internal force responses of the wharf structure was evident. Under the global surface load, the horizontal displacements and bending moments of piles A and H were larger, while piles B and G showed distinct zones of abrupt bending moment change. Under local loading conditions, the horizontal displacement on the loaded side was larger, while the bending moment on the opposite side was relatively higher.
- 4
- The coupling analysis of multiple external factors affecting the high-pile wharf reveals that surface loads have the greatest impact on the deformation and internal forces of the wharf. The soft foundation model and wave loads primarily affected the maximum displacement of the structure, with no significant impact on the maximum bending moment. Therefore, during the initial design of the wharf, the engineering characteristics of the deep soft soil foundation must be thoroughly considered. During the operational period of the wharf, the selection of the surface cargo placement is crucial, and special attention should be given to the areas affected by wave action, with focused prevention measures and monitoring.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, Z.; Cong, S.; Cheng, Z. Recent Advances in Composite Caisson–Pile Foundation. Mar. Georesour. Geotechnol. 2025, 1–14. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Q.; Zhu, R.; Li, C.; Wang, N. Real-Time Identification of Foundation Damage in High-Pile Wharves: Nonlinear Feature Change Point Analysis in Dynamic Characteristics under Wave Excitation. Measurement 2025, 243, 116365. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, R.; Gong, X.; Yu, J. Field Study on Uplift Bearing Capacity of Pre-Bored Grouted Planted Pile and Bored Pile in Deep Soft Soil. Ocean Eng. 2025, 322, 120477. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, S.; Ren, Y.; Qi, Z.; Yang, Q. Characterization of Engineering Properties of Deep-Water Soils in the South China Sea. Eng. Geol. 2023, 320, 107138. [Google Scholar] [CrossRef]
- Lin, Y.; Qin, H.; Guo, J.; Chen, J. Study on the Rheological Behavior of a Model Clay Sediment. J. Mar. Sci. Eng. 2021, 9, 81. [Google Scholar] [CrossRef]
- Han, Y.; Li, J. Study of Deformation Performance and Seismic Damage on Pile-Supported Wharf by Shaking Table Test. Integr. Ferroelectr. 2024, 240, 1298–1314. [Google Scholar] [CrossRef]
- Jingyu, R.E.N.; Kunpeng, W.; Chunyi, C.U.I.; Hailong, L.I.U.; Min, Z. Analysis of Force Deformation in Wharf Pile Foundation-Slope System under Siltation Conditions. Hydro-Sci. Eng. 2024, 5, 113–123. [Google Scholar]
- Wu, M.; Zheng, J.; Liu, Q.; Zheng, L.; Deng, T. Calculation Method of Flow Drag around a Pile in Soft Soil Considering Bingham Fluid Properties and Analysis of Single Pile Response. Ocean Eng. 2025, 317, 120031. [Google Scholar] [CrossRef]
- Li, B.; Chen, F.; Chen, L.; Fu, J.; Shan, Z.; Chen, J. The Engineering Characteristics of Uplift Piles in Soft Clay. J. Perform. Constr. Facil. 2025, 39, 6025002. [Google Scholar] [CrossRef]
- Tan, Y.; Fan, X. Statistical Analyses on a Database of Deep Excavations in Shanghai Soft Clays. In Databases for Data-Centric Geotechnics; CRC Press: Boca Raton, FL, USA, 2024; pp. 600–630. [Google Scholar]
- Peng, X.-B.; Ren, W.-J.; Li, T.-Q.; Xue, Y.-Y.; Tao, X.-S.; Xu, L.-Y. Seismic Response of Deep Soft Soil Sites with Varying Shear Wave Velocities. Front. Earth Sci. 2024, 12, 1488519. [Google Scholar] [CrossRef]
- Fu, X.; Li, J.; Liu, J.; Hu, Z.; Tang, C. Influence of Complex Hydraulic Environments on the Mechanical Properties of Pile-Soil Composite Foundation in the Coastal Soft Soil Area of Zhuhai. Buildings 2023, 13, 563. [Google Scholar] [CrossRef]
- Yan, Z.; Sun, X.P.; Yang, Z.X.; Fu, D.F. Lateral Bearing Performance of a Defective Pile-Supported Wharf with Batter Piles. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 4020035. [Google Scholar] [CrossRef]
- Zhu, D.T. Hydrodynamic Characteristics of Offshore and Pile Breakwaters. Ocean Eng. 2015, 104, 257–265. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, L.; Liu, X. Deformation Response of a High-Pile Wharf Foundation the Process of Slope Siltation. J. Water Resour. Water Eng. 2022, 33, 159–163. [Google Scholar]
- Yi, J.H.; Kim, S.B.; Yoon, G.L.; Andersen, L.V. Natural Frequency of Bottom-Fixed Offshore Wind Turbines Considering Pile-Soil-Interaction with Material Uncertainties and Scouring Depth. Wind Struct. 2015, 21, 625–639. [Google Scholar] [CrossRef]
- Zhao, M.; Wu, G.; Wang, K. Comparative Analysis of Dynamic Response of Damaged Wharf Frame Structure under the Combined Action of Ship Collision Load and Other Static Loads. Buildings 2022, 12, 1131. [Google Scholar] [CrossRef]
- Zhao, J.; Cui, C.; Zhang, P.; Wang, K.; Zhao, M. Parameter Sensitivity Analysis of the Seismic Response of a Piled Wharf Structure. Buildings 2023, 13, 349. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, W.; Qiu, W.; Jiang, M. Experimental Study on Wave-Induced Loads and Nonlinear Effects for Pier-Pile Group Foundations of Sea-Crossing Bridges: Wave Slamming and Suction Effect. Coast. Eng. 2024, 192, 104567. [Google Scholar] [CrossRef]
- Li, R.; Huo, Y. Three-Dimensional Finite Element Analysis of Pile-Supported Wharf Considering Sediment Deposition. Port Waterw. Eng. 2016, 10, 95–99. [Google Scholar]
- He, L.; Wang, Y.; Li, S.; Wang, Z. Practical Method and Application Study for Predicting Cyclic Accumulative Deformations of the Saturated Soft Clay. J. Mt. Sci. 2017, 14, 2348–2358. [Google Scholar] [CrossRef]
- Xie, L.; Su, L.; Wan, H.-P.; Wang, J.; Bi, J.; Ling, X. Experimental Study on Dynamic Response of Pile-Supported Wharf under Wave and Ship Berthing Collision. Appl. Ocean Res. 2023, 135, 103561. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, C.; Gao, S.; Tang, J.; Chen, Y. Lateral Load Bearing Capacity of Offshore High-Piled Wharf with Batter Piles. Ocean Eng. 2017, 142, 377–387. [Google Scholar] [CrossRef]
- de Macêdo Wahrhaftig, A.; Plevris, V.; Mohamad, B.A.; Pereira, D.L. Minimum Design Bending Moment for Systems of Equivalent Stiffness. Structures 2023, 57, 105224. [Google Scholar] [CrossRef]
- Systèmes, D. Abaqus 6.10: Analysis User’s Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2010. [Google Scholar]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves; The University of Texas at Austin: Austin, TX, USA, 2001; ISBN 0-493-36697-0. [Google Scholar]
- Ju, L.; Xu, R.; Zhu, J.; Tao, Y.; Yu, T. An Elastoplastic Model with Egg-Shaped Yield Surface for Coastal Soft Clay. Appl. Ocean Res. 2024, 146, 103975. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Zhao, D.; Zhao, K.; Yang, J. A New Effective Stress Method for Nonlinear Site Response Analyses. Earthq. Eng. Struct. Dyn. 2021, 50, 1595–1611. [Google Scholar] [CrossRef]
- Cheng, X.; Li, M.; Ma, C.; El Naggar, M.H.; Wang, P.; Sun, X. Dynamic Analysis of Tripod Pile Foundation in Clays for Offshore Wind Turbines. Ocean Eng. 2023, 287, 115832. [Google Scholar] [CrossRef]
- Ma, K.; Gao, Z.; Wang, J.; Zhang, Y.; Zong, M.; Wu, W.; Mei, G. Nonlinear Consolidation Finite Element Analysis of a Layered Soft Soil Foundation under Multistage Loading Based on the Continuous Drainage Boundary. Comput. Geotech. 2024, 169, 106220. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, H.; Cai, Y.; Yu, X.; Zhao, J. Seismic Subsidence of Soft Subgrade with Considering Principal Stress Rotation. Int. J. Civ. Eng. 2022, 20, 827–837. [Google Scholar] [CrossRef]
- Chanda, D.; Saha, R.; Haldar, S. Behaviour of Piled Raft Foundation in Sand Subjected to Combined V-M-H Loading. Ocean Eng. 2020, 216, 107596. [Google Scholar] [CrossRef]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Reeve, D.; Chadwick, A.; Fleming, C. Coastal Engineering: Processes, Theory and Design Practice; CRC Press: Boca Raton, FL, USA, 2018; ISBN 1-351-16552-6. [Google Scholar]
- Zhang, H.C.; Li, G.; Geng, J.; Zhao, X.L.; Liu, S.X.; Li, J.X. Wave Force Characteristics of Fixed Photovoltaic Pile Structures under Multi-Directional Irregular Waves. In Innovations in Renewable Energies Offshore; CRC Press: Boca Raton, FL, USA, 2024; pp. 139–145. [Google Scholar]


| Working Condition | Maximum Horizontal Displacement umax (mm) | Maximum Bending Moment of Pile B MBmax (kN·m) | Maximum Bending Moment of Pile G MGmax (kN·m) |
|---|---|---|---|
| MC + UF | [16.79, 16.92] | [303.9, 311.5] | [2600.7, 2612.6] |
| MC + UB | [14.89, 15.23] | [3196.0, 3209.3] | [370.7, 376.6] |
| MC + UG | [8.59, 8.66] | [3637.5, 3645.2] | [3015.0, 3039.7] |
| MC + Wave + UF | [16.89, 17.09] | [302.1, 305.9] | [2621.1, 2623.9] |
| MC + Wave + UB | [16.97, 17.15] | [3215.1, 3217.9] | [383.1, 386.9] |
| MC + Wave + UG | [9.48, 9.63] | [3660.3, 3673.7] | [3040.0, 3047.3] |
| VM + UF | [17.35, 17.47] | [230.8, 235.8] | [2605.3, 2615.7] |
| VM + UB | [15.33, 15.50] | [3181.7, 3192.3] | [358.9, 366.1] |
| VM + UG | [8.56, 8.76] | [3599.0, 3617.4] | [3010.1, 3029.9] |
| VM + Wave + UF | [17.01, 17.22] | [300.9, 310.1] | [2617.6, 2626.4] |
| VM + Wave + UB | [17.17, 17.32] | [3218.6, 3227.4] | [379.6, 390.4] |
| VM + Wave + UG | [9.78, 9.88] | [3626.1, 3647.9] | [3015.9, 3036.1] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Cao, C.; Bai, R.; Ma, H. Mechanical Response Analysis of High-Pile Wharf on Deep Soft Soil Foundation Under Complex Multi-Factor Interactions. Buildings 2025, 15, 2379. https://doi.org/10.3390/buildings15132379
Yang K, Cao C, Bai R, Ma H. Mechanical Response Analysis of High-Pile Wharf on Deep Soft Soil Foundation Under Complex Multi-Factor Interactions. Buildings. 2025; 15(13):2379. https://doi.org/10.3390/buildings15132379
Chicago/Turabian StyleYang, Kezheng, Chenyue Cao, Rui Bai, and Huihuan Ma. 2025. "Mechanical Response Analysis of High-Pile Wharf on Deep Soft Soil Foundation Under Complex Multi-Factor Interactions" Buildings 15, no. 13: 2379. https://doi.org/10.3390/buildings15132379
APA StyleYang, K., Cao, C., Bai, R., & Ma, H. (2025). Mechanical Response Analysis of High-Pile Wharf on Deep Soft Soil Foundation Under Complex Multi-Factor Interactions. Buildings, 15(13), 2379. https://doi.org/10.3390/buildings15132379








