Non-Linear Behaviour and Analysis of Innovative Suspension Steel Roof Structures
Abstract
1. Introduction
2. Innovative Suspension Roof System
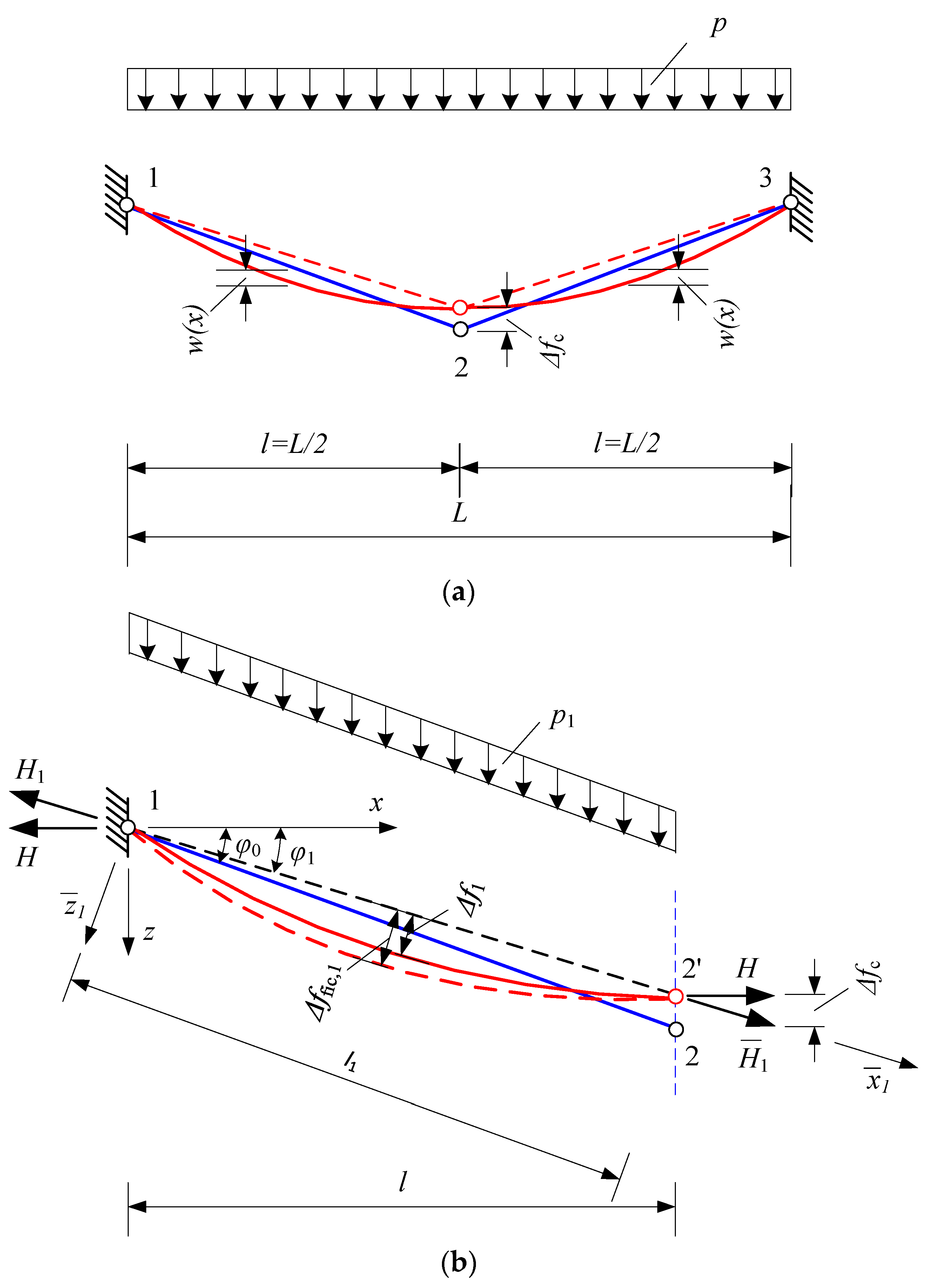
2.1. Analysis of Suspension System with Two Straight “Rigid” Elements
2.2. Parameters of Innovative Suspension Cable-Strut Systems of Straight Elements
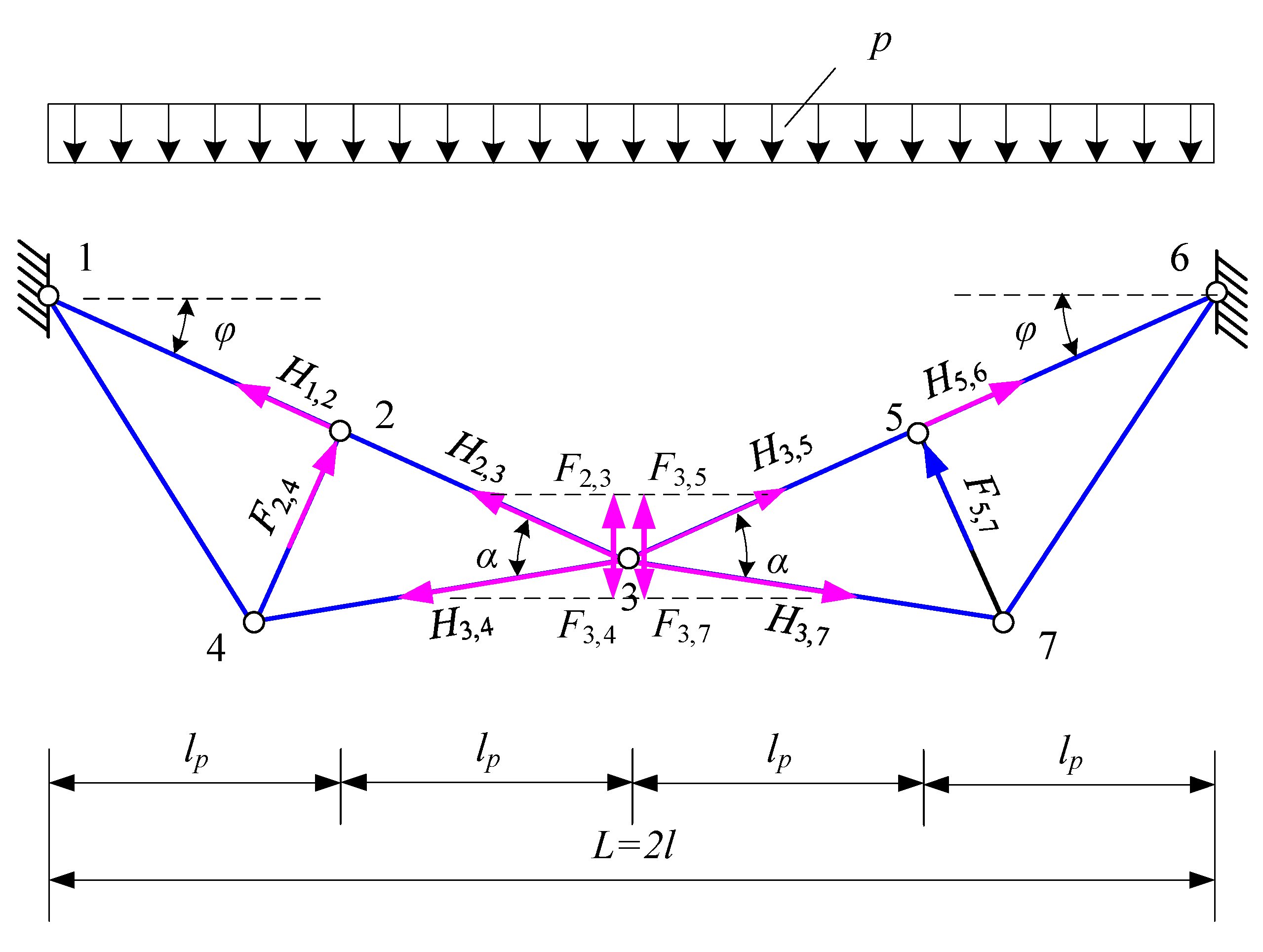
2.3. Non-Linear Analysis of Innovative Suspension Single-Level Cable-Strut System
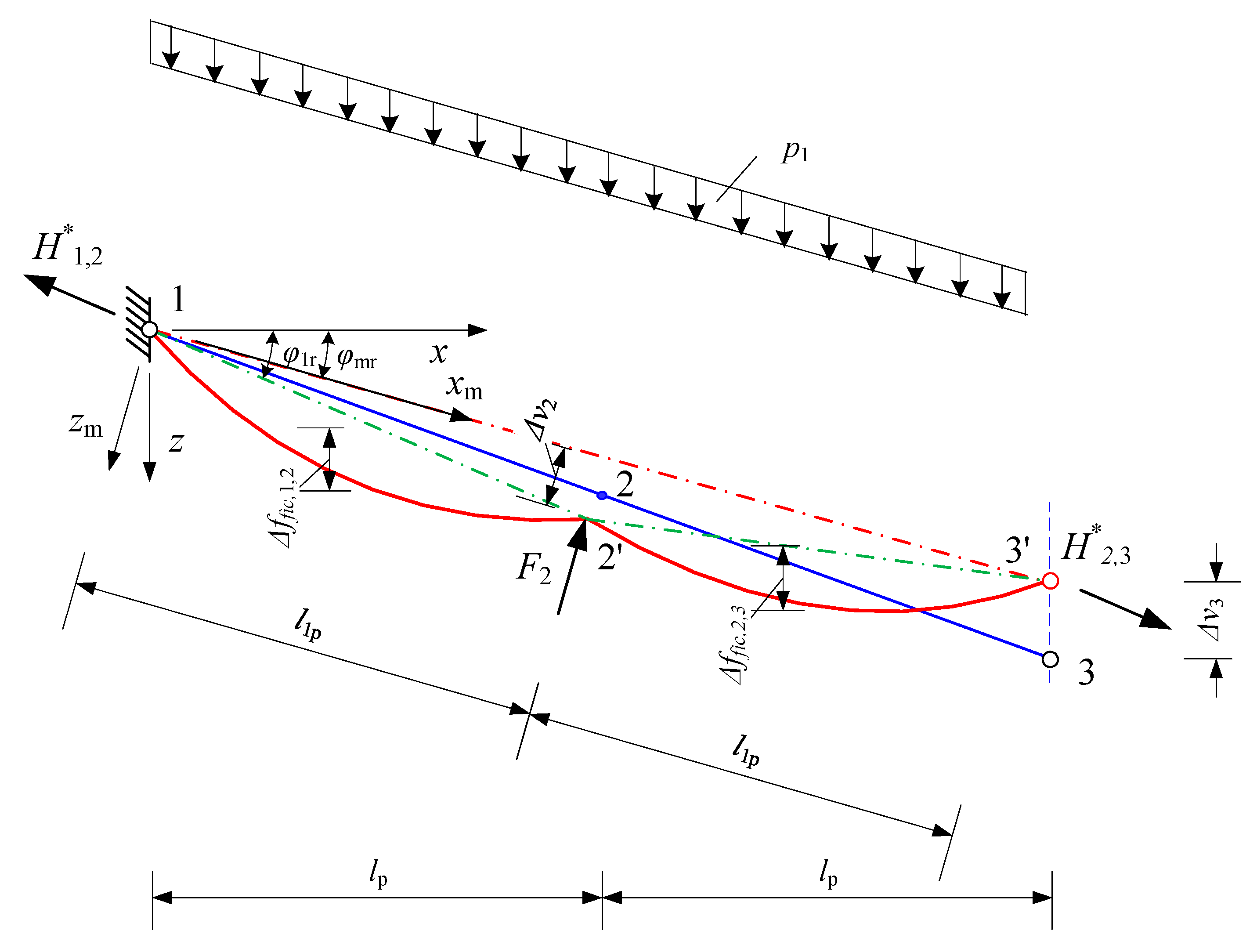
2.3.1. Non-linear Analysis of Upper Hord Elements
2.3.2. Non-Linear Analysis of the Lower Hord
2.3.3. Non-Linear Analysis of the Suspension Cable-Strut System
- (1)
- An initial value of the central hinge vertical displacement is assumed;
- (2)
- Using Formulas (24), (25), and (23), the average fictitious displacement of the upper hord is calculated iteratively;
- (3)
- The kinematic displacement of the lower hord node “4” is calculated using Formula (37), the elastic displacement by using Formula (36), and the total displacement is calculated using Formula (39);
- (4)
- The axial force of the strut is calculated using expression (38);
- (5)
- The tensile forces and in the lower hord are calculated using Formulas (27) and (30);
- (6)
- The displacement of the upper hord and the tensile force are calculated according to (20);
- (7)
- The convergence conditions (41) and (42) are checked. If they are not satisfied, return to step 1. If they are satisfied, calculate the remaining structural system element axial forces and displacements: .
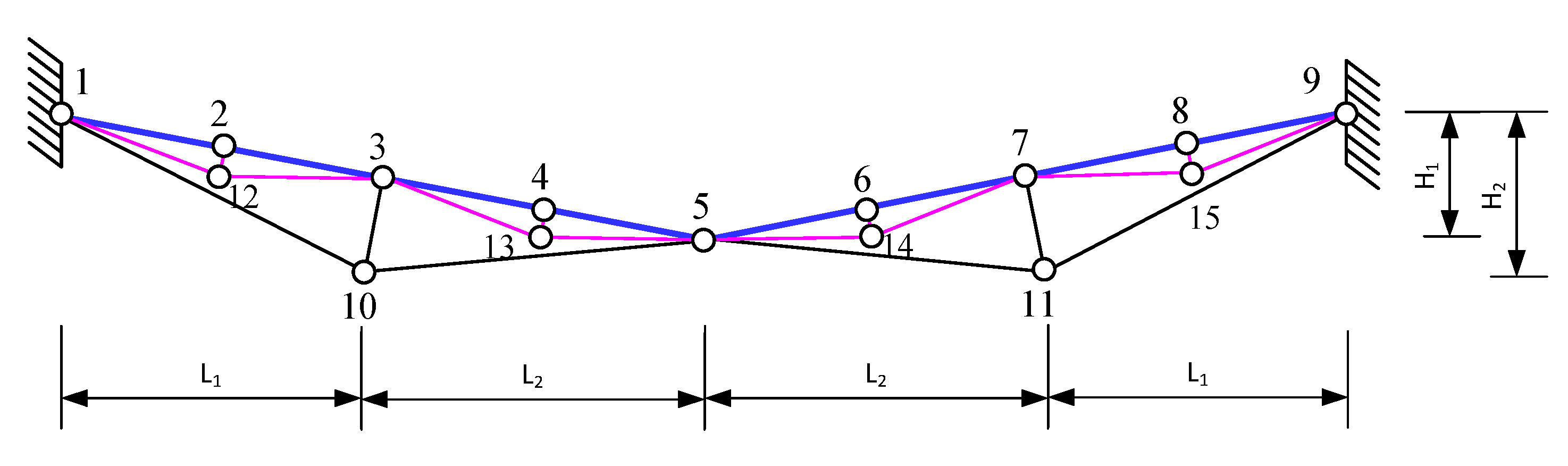
2.4. New Combined Two-Level Cable-Strut Suspension System
3. Comparative Study of Analytical Calculation and FEM Results
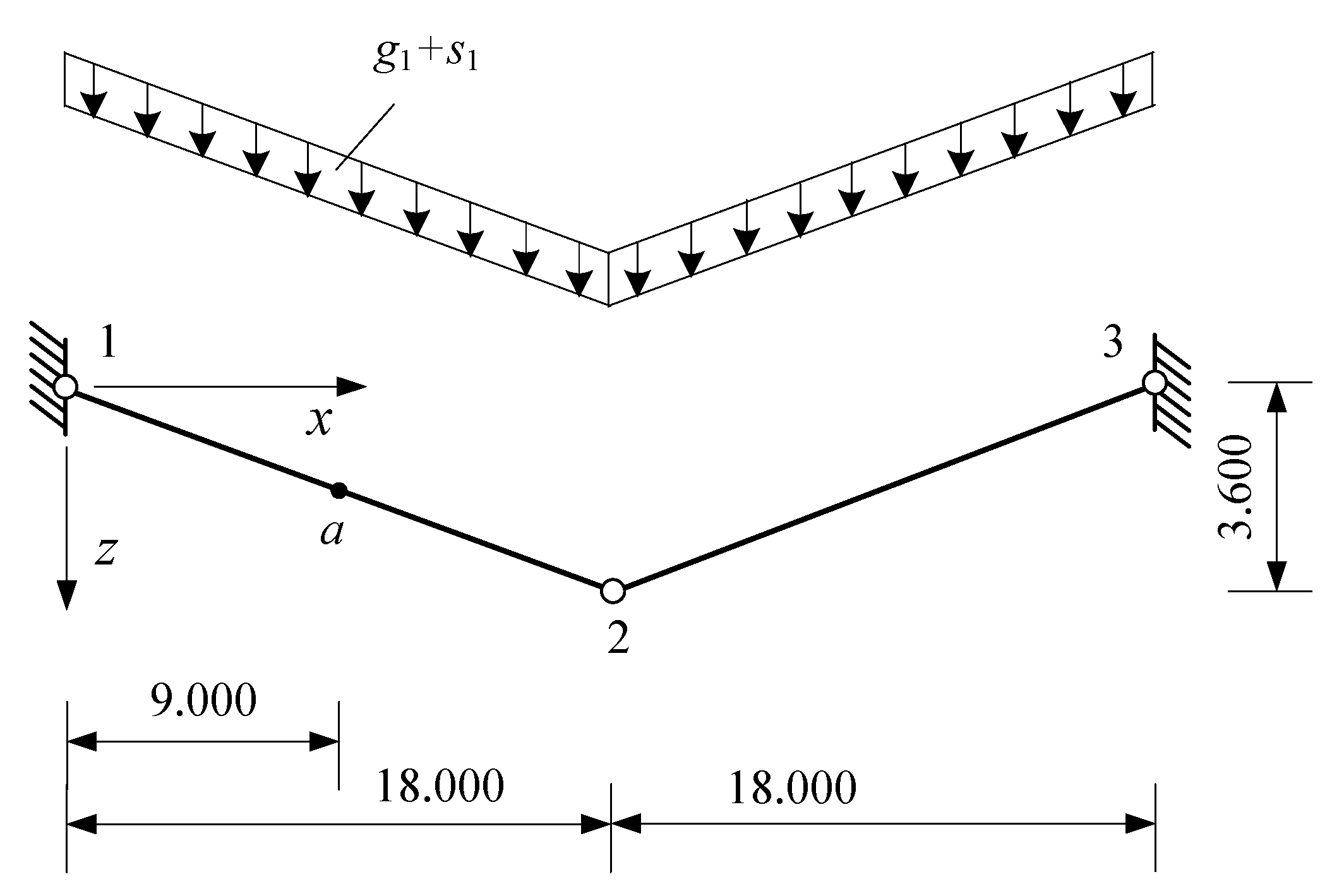
3.1. Suspension Structures with Two Straight Elements
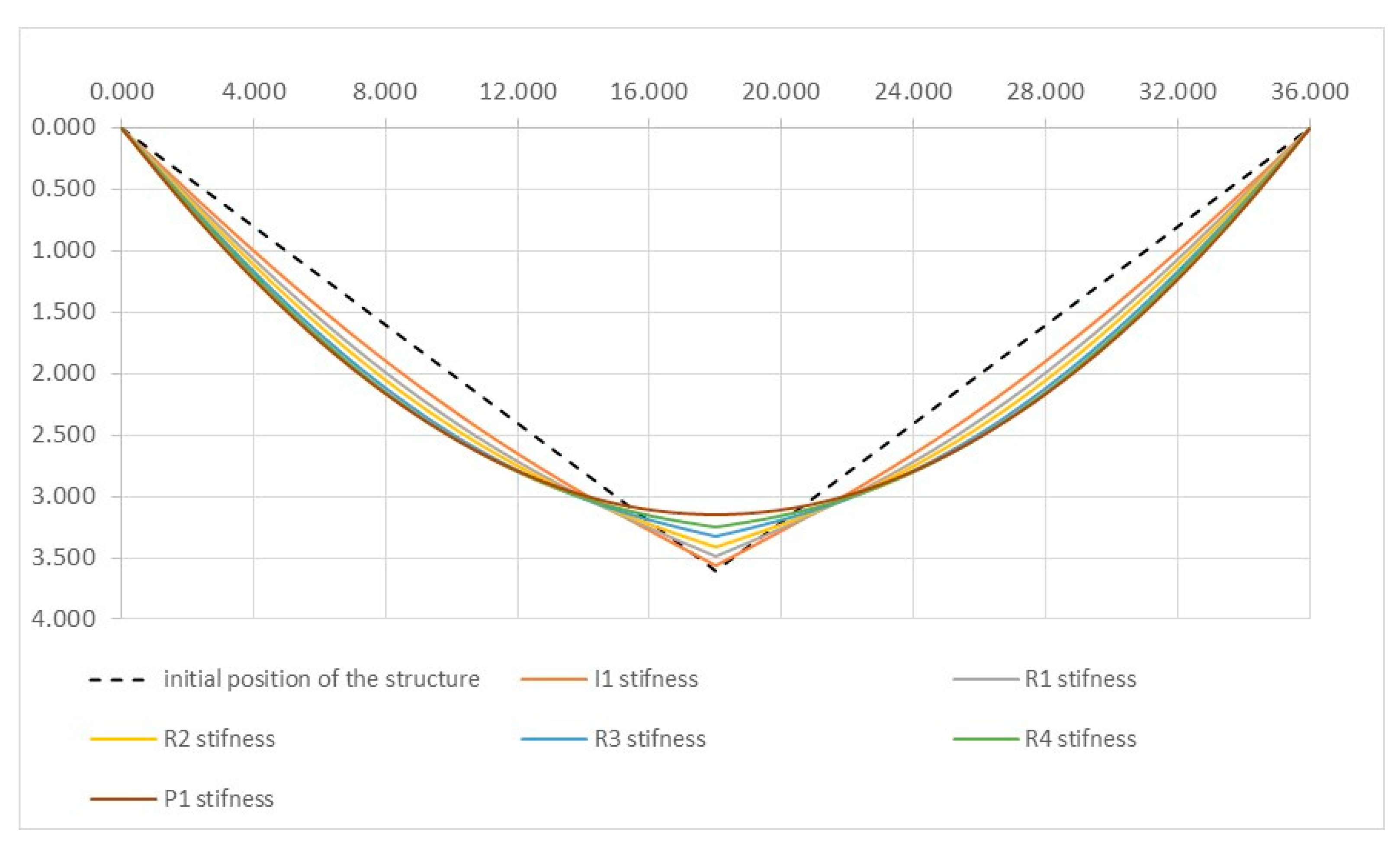
3.2. Suspension Single-Level Cable-Strut Systems
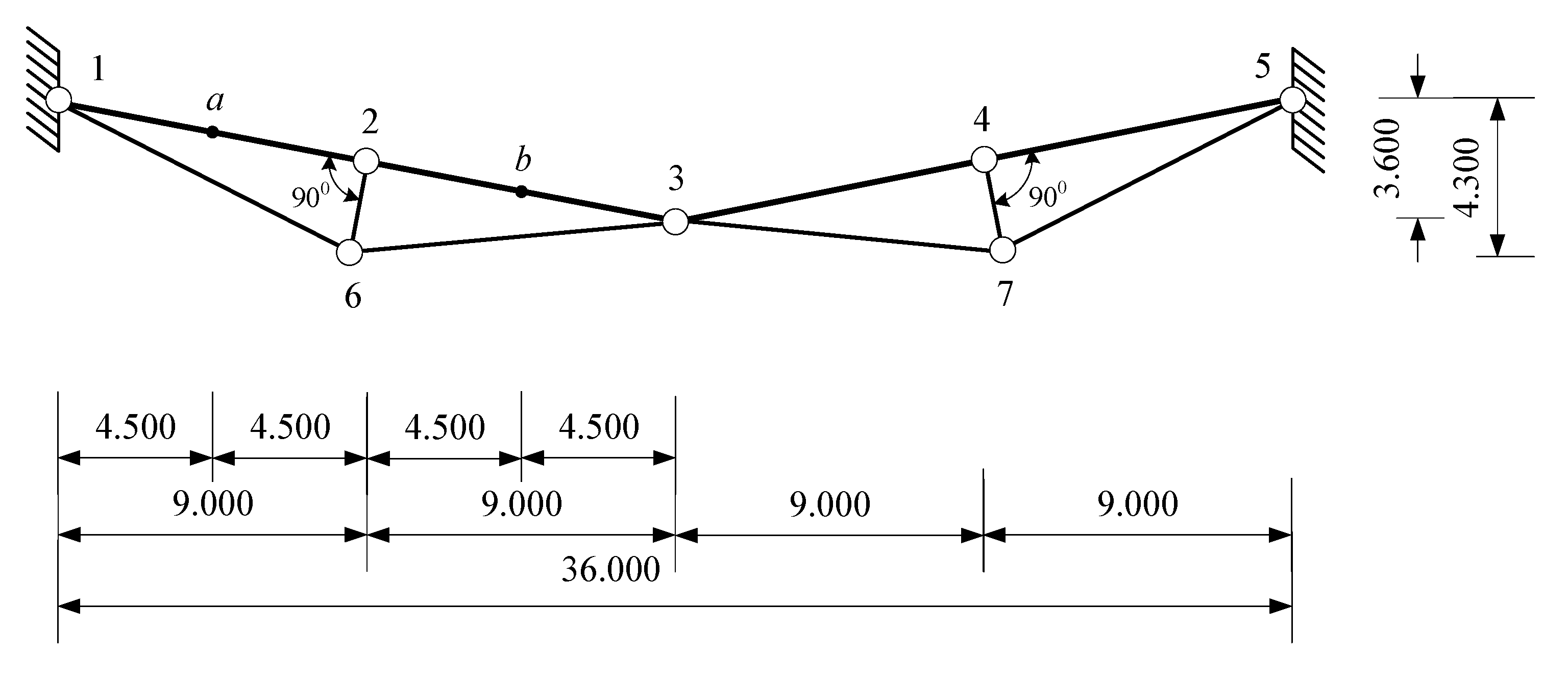
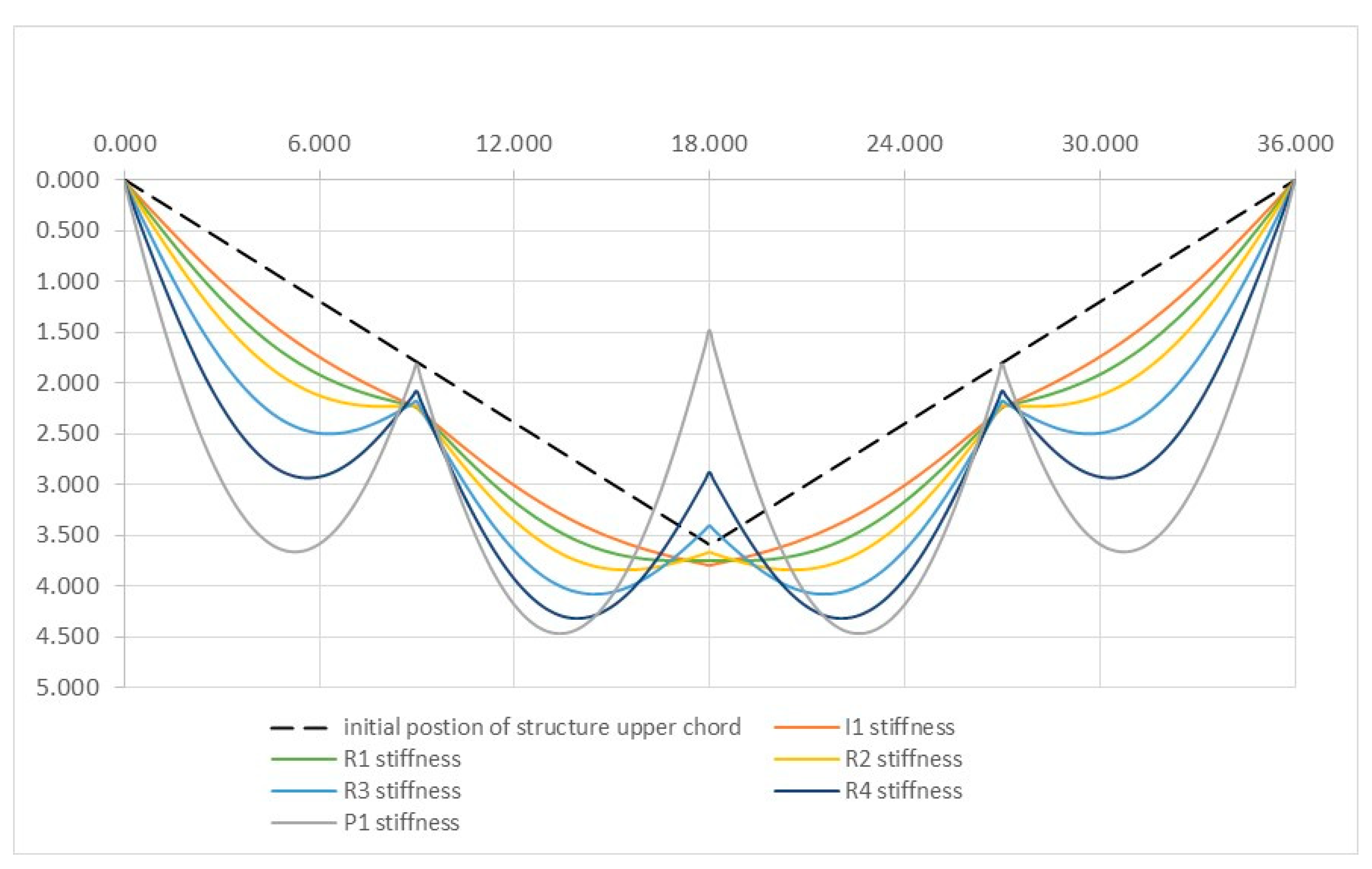
3.3. Suspension Two-Level Cable-Strut System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bucholdt, H.A. An Introduction to Cable Roof Structures, 2nd ed.; Thomas Telford: London, UK, 1999. [Google Scholar]
- Engel, H. Tragsysteme/Structure Systems; Hatje Cantz Verlag GmbH: Berlin, Germany, 2009. [Google Scholar]
- Krishna, P. Tension Roofs and Bridges. J. Constr. Steel Res. 2001, 57, 1123–1140. [Google Scholar] [CrossRef]
- Schlaich, J.; Bergermann, R.; Leich, W. Light Structures, 2nd ed.; Prestel: Munich, Germany, 2005. [Google Scholar]
- Schlaich, J. Conceptual design of light structures. J. Int. Assoc. Shell Spat. Struct. 2004, 45, 157–168. [Google Scholar]
- Krishna, P.; Agrawal, T.P. Cable-Suported Roof; McGaw-Hill: Kingsport, TN, USA; New York, NY, USA, 1978. [Google Scholar]
- Lewis, W. Tension Structures: Form and Behavior; Thomas Telford Ltd.: London, UK, 2003. [Google Scholar]
- Irvine, H.M. Cable Structures; Dover Publications: New York, NY, USA, 1992. [Google Scholar]
- González Quelle, I. Cable Roofs. Evolution, Classification and Future Trends. In Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium, Valencia, Spain, 28 September 2009. [Google Scholar]
- Otto, F. Gestalt Finden; Edition Axel Menges: Fellbach, Germany, 2001. (In German) [Google Scholar]
- Kulbach, V. Cable Structures. Design and Analysis; Estonian Academy Publisher: Tallinn, Estonia, 2007. [Google Scholar]
- Göppert, K.; Stein, M. A spoke wheel roof for the World’s largest convertible roof. The new Commerzbank Arena in Frankfurt, Germany. Struct. Eng. Int. 2007, 4, 282–287. [Google Scholar] [CrossRef]
- Berger, H. Light Structures-Structures of Light: The Art and Engineering of Tensile Architecture; Birkhauser: Basel, Switzerland, 2002. [Google Scholar]
- Pakrastinsh, L.; Rocens, K.; Serdjuks, D. Deformability of hierarchic cable roof. J. Constr. Steel Res. 2006, 62, 1295–1301. [Google Scholar] [CrossRef]
- Shimoda, M.; Yamane, K.; Shi, J.X. Non-parametric shape optimization method for designing cable net structures in form finding and stiffness maximization problems. Int. J. Solids Struct. 2018, 146, 167–179. [Google Scholar] [CrossRef]
- Schlaich, M.; Golenhofen, D. Hanging Glass Roof in Heilbronn, Germany. Struct. Eng. Int. 2018, 12, 179–181. [Google Scholar] [CrossRef]
- Zhang, N.; Luo, B.; Liu, H.; Zhang, M. Prestress Self-Equilibrium Force-Finding Method for Cable-Supported Grid Structures Considering Zero-Stress State Form-Finding and the Construction Process. Buildings 2022, 12, 749. [Google Scholar] [CrossRef]
- Jennings, A. Deflection theory analysis of different cable profiles for suspension bridges. Eng. Struct. 1987, 9, 84–94. [Google Scholar] [CrossRef]
- Cao, J.; Shao, X.; Zhan, J.; Zhang, J.; Wang, Y. A simplified analysis method for long-span suspension bridges within the deck overlay retrofitting process from asphalt to UHPC. Eng. Struct. 2023, 289, 116122. [Google Scholar] [CrossRef]
- Juozapaitis, A.; Norkus, A. Displacement analysis of asymmetrically loaded cable. J. Civ. Eng. Manag. 2004, 10, 277–284. [Google Scholar] [CrossRef]
- Ernst, H.J. Der E-Modul von Seilen unter Berücksichtigung des Durchhanges. Der Bauingenieu 1965, 40, 52–55. [Google Scholar]
- EN 1993-11. Design of Steel Structures, Part 1-11: Design of Structures with Tension Components. CEN: Brussels, Belgium, 2005.
- Rizzo, F.; D’Asdia, P.; Lazzari, M.; Procino, L. Wind action evaluation on tension roofs of hyperbolic paraboloid shape. Eng. Struct. 2011, 33, 445–461. [Google Scholar] [CrossRef]
- Xue, S.; Zhao, Z.; Li, X.; Liu, R.; Dezhkam, M.; Lu, Z.; Liu, T.; Fan, Q.; Jing, H. Shaking Table Test Research on the Influence of Center-Hung Scoreboard on Natural Vibration Characteristics and Seismic Response of Suspen-Dome Structures. Buildings 2022, 12, 1231. [Google Scholar] [CrossRef]
- Peil, U. Statik der Dachtragwerke von Stadien. Stahlbau 2005, 74, 159–177. [Google Scholar] [CrossRef]
- Rizzo, F.; Sadhu, A.; Abasi, A.; Pistol, A.; Flaga, Ł.; Venanzi, I.; Ubertini, F. Construction and dynamic identification of aeroelastic test models for flexible roofs. Arch. Civ. Mech. Eng. 2023, 23, 16. [Google Scholar] [CrossRef]
- Rizzo, F.; Sepe, V. Static loads to simulate dynamic effects of wind on hyperbolic paraboloid roofs with square plan. J. Wind Eng. Ind. Aerodyn. 2015, 137, 46–57. [Google Scholar] [CrossRef]
- Li, S.; Yao, G.; Wang, W.; Yu, X.; He, X.; Ran, C.; Long, H. Research on the Diffusion Model of Cable Corrosion Factors-Based on Optimized BP Neural Network Algorithm. Buildings 2023, 13, 1485. [Google Scholar] [CrossRef]
- Xu, J.; Chen, W. Behavior of wires in parallel wire stayed cable under general corrosion effects. J. Constr. Steel Res. 2013, 85, 40–47. [Google Scholar] [CrossRef]
- Ludescher, G.; Braun, F.; Bachmann, U. Stress-ribbon roof structures of the new Stuttgart trade fair exhibition halls. Struct. Eng. Int. 2007, 1, 22–27. [Google Scholar] [CrossRef]
- Zimmermann, M.; Deillon, A. A new roof for the Émile Cohl Art School in Lyon. Struct. Eng. Int. 2018, 28, 171–177. [Google Scholar] [CrossRef]
- Furtado, R.; Quinaz, C.; Bastos, R. New Braga Municipal Stadium, Braga. Struct. Eng. Int. 2005, 15, 72–76. [Google Scholar] [CrossRef]
- Ban, S.; Tsubota, H.; Motohashi, S.; Yoshida, A. Suspended roof for the Olympic Skating Arena, Nagano. Struct. Eng. Int. 2018, 8, 187–188. [Google Scholar] [CrossRef]
- Shimanovsky, A.V.; Shilinsky, V.V.; Shaban, N.A. Mechanics of Suspension System; Stal: Kiyv, Russia, 2010. (In Russian) [Google Scholar]
- Strasky, J. Stress-Ribbon and Supported Cable Pedestrian Bridges; Thomas Telford Ltd.: London, UK, 2005. [Google Scholar]
- Juozapaitis, A.; Sandovič, G.; Jakubovskis, R.; Gribniak, V. Effects of flexural stiffness on deformation behaviour of steel and FRP stress-ribbon bridges. Appl. Sci. 2021, 11, 2585. [Google Scholar] [CrossRef]
- Budziński, R. Numerical analysis of cable net structure with application of different pretensioning methods. Czasopismo Inżynierii Lądowej, Środowiska i Architektury/J. Civ. Eng. Environ. Archit. 2019, 66, 47–64. Available online: https://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-01dc5e98-f87d-458f-9d19-c4cab649044e (accessed on 10 January 2023.).
- Stauske, D. Drahtseile für Seilbauwerke. Stahlbau 2000, 69, 612–618. [Google Scholar] [CrossRef]
- EN 1993-1-8; Eurocode 3, Design of Steel Structures, Part 1-8: Design of Joints. CEN: Brussels, Belgium, 2005.
- Petersen, C. Stahlbau: Grundlagen der Berechnung und Baulichen Ausbildung von Stahlbauten (German Edition); Springer Vieweg: Wiesbaden, Germany, 2013. [Google Scholar]
- Bučmys, Ž.; Daniūnas, A.; Jaspart, J.-P.; Demonceau, J.-F. A component method for cold-formed steel beam-to-column bolted gusset plate joints. Thin-Walled Struct. 2018, 123, 520–527. [Google Scholar] [CrossRef]
- Juozapaitis, A.; Sharaskin, V.; Grigorjeva, T.; Valiunas, B. Analysis and arrangement of suspension structures from straight-line elements of finite flexural stiffness. In Theoretical Foundations of Civil Engineering; Szczesniak, W., Ed.; Warsaw University of Technology: Warsaw, Poland, 2002; Volume 2, pp. 887–896. [Google Scholar]
- Pałkowski, S. Statik der Seilkonstruktionen; Springer: Berlin/Heidelberg, Germany, 1990. (In German) [Google Scholar] [CrossRef]
- Pałkowski, S. Some problem of calculation and design of cable structures. In Proceedings of the 11th International Conference on Metal Structures ICMS-2006, Rzeszow, Poland, 21–23 June 2006. [Google Scholar]
- Ruchwa, M.; Matuszkiewicz, M. Zastosowanie Metody Elementow Skończonych w obliczeniach statycznych. Biuletyn WAT 2010, LIX, 363–377. [Google Scholar]
- Rezaiee-Pajand, M.; Mokhtari, M.; Masoodi, A.R. A novel cable element for nonlinear thermo-elastic analysis. Eng. Struct. 2018, 167, 431–444. [Google Scholar] [CrossRef]
- Qin, J.; Ju, Z.; Liu, F.; Zhang, Q. Cable Force Identification for Pre-Stressed Steel Structures Based on a Multi-Frequency Fitting Method. Buildings 2022, 12, 1689. [Google Scholar] [CrossRef]
- Šaraškinas, V.; Kvedaras, A.K. Course and results of testing a suspended composite structure. Statyba 2000, 6, 315–321. [Google Scholar] [CrossRef]
- Qin, K.; Zhao, F.; Luo, Y.; Fang, B.; Chen, S. Aeolian Vibration Dynamic Analysis of Large-Span, Relaxed Antenna Cable Net Based on Finite Particle Method. Buildings 2024, 14, 105. [Google Scholar] [CrossRef]
- Rizzo, F.; Kopp, G.A.; Giaccu, G.F. Investigation of wind-induced dynamics of a cable net roof with aeroelastic wind tunnel tests. Eng. Struct. 2021, 229, 111569. [Google Scholar] [CrossRef]
- Costa, R.S.; Lavall, A.C.C.; da Silva, R.G.L.; dos Santos, A.P.; Viana, H.F. Cable structures: An exact geometric analysis using catenary curve and considering the material nonlinearity and temperature effect. Eng. Struct. 2022, 253, 113738. [Google Scholar] [CrossRef]
- Wei, J.; Guan, M.; Cao, Q.; Wang, R. Spatial combined cable element for cable-supported bridges. Eng. Comput. 2019, 36, 204–225. [Google Scholar] [CrossRef]
- Vu, T.-V.; Lee, H.-E.; Bui, Q.-T. Nonlinear analysis of cable-supported structures with a spatial catenary cable element. Struct. Eng. Mech. 2012, 43, 583–605. [Google Scholar] [CrossRef]
- Gwon, S.-G.; Choi, D.-H. Three-dimensional parabolic cable element for static analysis of cable structures. J. Struct. Eng. 2015, 142, 06015004. [Google Scholar] [CrossRef]
- Ding, M.; Luo, B.; Ding, S.; Shen, Y.; Huang, L. Experimental Investigation and Numerical Simulation of a Levy Hinged-Beam Cable Dome. Buildings 2021, 11, 110. [Google Scholar] [CrossRef]
- Gimsing, N.J. Cable Suported Bridges—Concept and Design, 2nd ed.; John Wiley & Sons: Chichester, UK, 1997. [Google Scholar]
- Fürst, A.; Marti, P.; Ganz, H.R. Bending of stay cables. Struct. Eng. Int. 2018, 13, 42–46. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, X.; Chen, Z. A simplified finite element model for structural cable bending mechanism. Int. J. Mech. Sci. 2016, 113, 196–210. [Google Scholar] [CrossRef]
- Zhou, B.; Hu, Y.; Zheng, X.; Zhu, H. Bending behavior of a frictional single-layered spiral strand subjected to multi-axial loads: Numerical and experimental investigation. Appl. Sci. 2022, 12, 4792. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, Y.; Wang, X.; Wu, X.; Liu, H. Experimental research on bending performance of structural cable. Constr. Build. Mater. 2015, 96, 279–288. [Google Scholar] [CrossRef]
- Farkas, J.; Jármai, K. 5—Large-span suspended roof members. In Design and Optimization of Metal Structures; Harwood Publishing: Chichester, UK, 2008; pp. 47–56. [Google Scholar] [CrossRef]
- Kmet, S.; Tomko, M.; Bin, M. Experimental and theoretical behaviour analysis of steel suspension members subjected to tension and bending. Steel Compos. Struct. 2012, 13, 343–365. [Google Scholar] [CrossRef]
- Cui, W.; Caracoglia, L.; Zhao, L.; Ge, Y. Examination of occurrence probability of vortex-induced vibration of long-span bridge decks by Fokker–Planck–Kolmogorov equation. Struct. Saf. 2023, 105, 102369. [Google Scholar] [CrossRef]
- Zhang, C. The active rotary inertia driver system for flutter vibration control of bridges and various promising applications. Sci. China Technol. Sci. 2023, 66, 390–405. [Google Scholar] [CrossRef]




| Stiffness | Analysis Method | Displacement, Axial Force, Bending Moment, Stresses | ||||||
|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (kN) | (kNm) | (MPa) | ||||
| I1 | Analytical | 0.30901 | L/116.5 | −0.039296 | L/916.1 | 731.21 | 371.28 | 511.5 |
| FEM | 0.29779 | L/120.9 | −0.038085 | L/945.3 | 742.33 | 364.67 | 505.7 | |
| Difference (%) | 3.63 | 3.08 | −1.52 | 1.78 | ||||
| R1 | Analytical | 0.40484 | L/88.9 | −0.11367 | L/316.7 | 749.24 | 263.25 | 481.00 |
| FEM | 0.39128 | L/92.0 | −0.11056 | L/325.6 | 758.03 | 259.00 | 476.1 | |
| Difference (%) | 3.35 | 2.73 | −1.17 | 1.61 | ||||
| R2 | Analytical | 0.46670 | L/77.1 | −0.18739 | L/192.1 | 765.74 | 184.63 | 454.7 |
| FEM | 0.45253 | L/79.6 | −0.18314 | L/196.6 | 772.61 | 181.94 | 450.5 | |
| Difference (%) | 3.08 | 2.27 | −0.90 | 1.46 | ||||
| R3 | Analytical | 0.52241 | L/68.9 | −0.28490 | L/126.4 | 786.28 | 102.14 | 399.2 |
| FEM | 0.50805 | L/70.9 | −0.28024 | L/128.5 | 790.95 | 100.83 | 396.1 | |
| Difference (%) | 2.75 | 1.63 | −0.59 | 1.28 | ||||
| R4 | Analytical | 0.55044 | L/65.4 | −0.36086 | L/99.8 | 801.69 | 49.107 | 311.0 |
| FEM | 0.53655 | L /67.1 | −0.35678 | L/100.9 | 804.83 | 48.524 | 309.1 | |
| Difference (%) | 2.52 | 1.13 | −0.39 | 1.19 | ||||
| P1 | Analytical | 0.56373 | L/63.9 | −0.44031 | L/81.8 | 817.32 | 4.3835 | 204.8 |
| FEM | 0.55183 | L/65.2 | −0.44853 | L/80.3 | 819.89 | 4.0334 | 197.9 | |
| Difference (%) | 2.11 | 1.87 | 0.31 | 7.98 | ||||
| Stiffness of the Upper Chord | Displacements | ||||||
|---|---|---|---|---|---|---|---|
(m) | (m) | (m) | (m) | ||||
| I1 | 0.050248 | L/716.4 | 0.044002 | 0.060207 | L/598.0 | 0.019554 | L/1841.1 |
| R1 | 0.070657 | L/509.5 | 0.043197 | 0.078601 | L/458.0 | 0.014889 | L/2417.9 |
| R2 | 0.094352 | L/381.5 | 0.041677 | 0.098494 | L/365.5 | 0.0061287 | L/5874.00 |
| R3 | 0.13784 | L/261.2 | 0.037054 | 0.13052 | L/275.8 | −0.020192 | L/1782.9 |
| R4 | 0.18998 | L/189.5 | 0.027686 | 0.16000 | L/225.0 | −0.072094 | L/499.3 |
| P1 | 0.26759 | L/134.5 | 0.00066073 | 0.17576 | L/204.8 | −0.21255 | L/169.4 |
| Stiffness of the Upper Chord | Axial Force, Bending Moment, and Stresses | |||||
|---|---|---|---|---|---|---|
(kN) | (kN) | (kNm) | (kNm) | (MPa) | (MPa) | |
| I1 | 501.33 | 473.11 | 143.40 | 144.33 | 227.7 | 224.8 |
| R1 | 503.27 | 475.05 | 130.27 | 131.72 | 256.3 | 254.6 |
| R2 | 506.75 | 478.55 | 115.29 | 117.18 | 287.9 | 287.6 |
| R3 | 516.35 | 488.18 | 88.267 | 90.549 | 322.5 | 325.1 |
| R4 | 532.84 | 504.72 | 56.087 | 58.150 | 302.5 | 307.0 |
| P1 | 569.49 | 541.46 | 5.4182 | 5.6987 | 192.0 | 193.9 |
| Stiffness of the Upper Chord | Displacements | |||||||
|---|---|---|---|---|---|---|---|---|
(m) | (m) | (m) | (m) | (m) | (m) | (m) | (m) | |
| I2 | 0.046807 | 0.038352 | 0.071273 | 0.048326 | 0.082774 | 0.061785 | 0.081741 | 0.044666 |
| R5 | 0.084372 | 0.042302 | 0.10669 | 0.041533 | 0.10994 | 0.046725 | 0.093739 | 0.0049378 |
| I3z | 0.10931 | 0.046149 | 0.12905 | 0.03364 | 0.12321 | 0.029656 | 0.089988 | −0.039917 |
| P2 | 0.12337 | 0.048945 | 0.14078 | 0.026986 | 0.12737 | 0.015487 | 0.080134 | −0.076673 |
| Stiffness of the Upper Chord | Axial Force, Bending Moment | |||||||
|---|---|---|---|---|---|---|---|---|
(kN) | (kN) | (kN) | (kN) | (kNm) | (kNm) | (kNm) | (kNm) | |
| I2 | 349.07 | 334.96 | 321.02 | 306.91 | 28.435 | 28.706 | 29.138 | 29.504 |
| R5 | 366.42 | 352.33 | 338.74 | 324.65 | 14.258 | 14.633 | 15.014 | 15.429 |
| I3z | 381.85 | 367.78 | 354.76 | 340.69 | 5.4873 | 5.6776 | 5.8654 | 6.0822 |
| P2 | 393.05 | 378.99 | 366.45 | 352.39 | 0.52709 | 0.54738 | 0.56687 | 0.59013 |
| Stiffnessof the Upper Chord | (MPa) | (MPa) | (MPa) | (MPa) |
|---|---|---|---|---|
| I2 | 435.4 | 430.9 | 427.9 | 424.3 |
| R5 | 444.1 | 444.1 | 444.5 | 445.3 |
| I3z | 519.2 | 523.7 | 528.4 | 534.4 |
| P2 | 275.6 | 271.6 | 268.3 | 264.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juozapaitis, A.; Daniūnas, A.; Ustinovichius, L. Non-Linear Behaviour and Analysis of Innovative Suspension Steel Roof Structures. Buildings 2024, 14, 661. https://doi.org/10.3390/buildings14030661
Juozapaitis A, Daniūnas A, Ustinovichius L. Non-Linear Behaviour and Analysis of Innovative Suspension Steel Roof Structures. Buildings. 2024; 14(3):661. https://doi.org/10.3390/buildings14030661
Chicago/Turabian StyleJuozapaitis, Algirdas, Alfonsas Daniūnas, and Leonas Ustinovichius. 2024. "Non-Linear Behaviour and Analysis of Innovative Suspension Steel Roof Structures" Buildings 14, no. 3: 661. https://doi.org/10.3390/buildings14030661
APA StyleJuozapaitis, A., Daniūnas, A., & Ustinovichius, L. (2024). Non-Linear Behaviour and Analysis of Innovative Suspension Steel Roof Structures. Buildings, 14(3), 661. https://doi.org/10.3390/buildings14030661






