Fire Resistance of Steel Beams with Intumescent Coating Exposed to Fire Using ANSYS and Machine Learning
Abstract
1. Introduction
1.1. Fire Protection of Steel Members
1.2. Machine Learning Methods Used for Modelling Fire Loading
1.3. Objectives of the Study
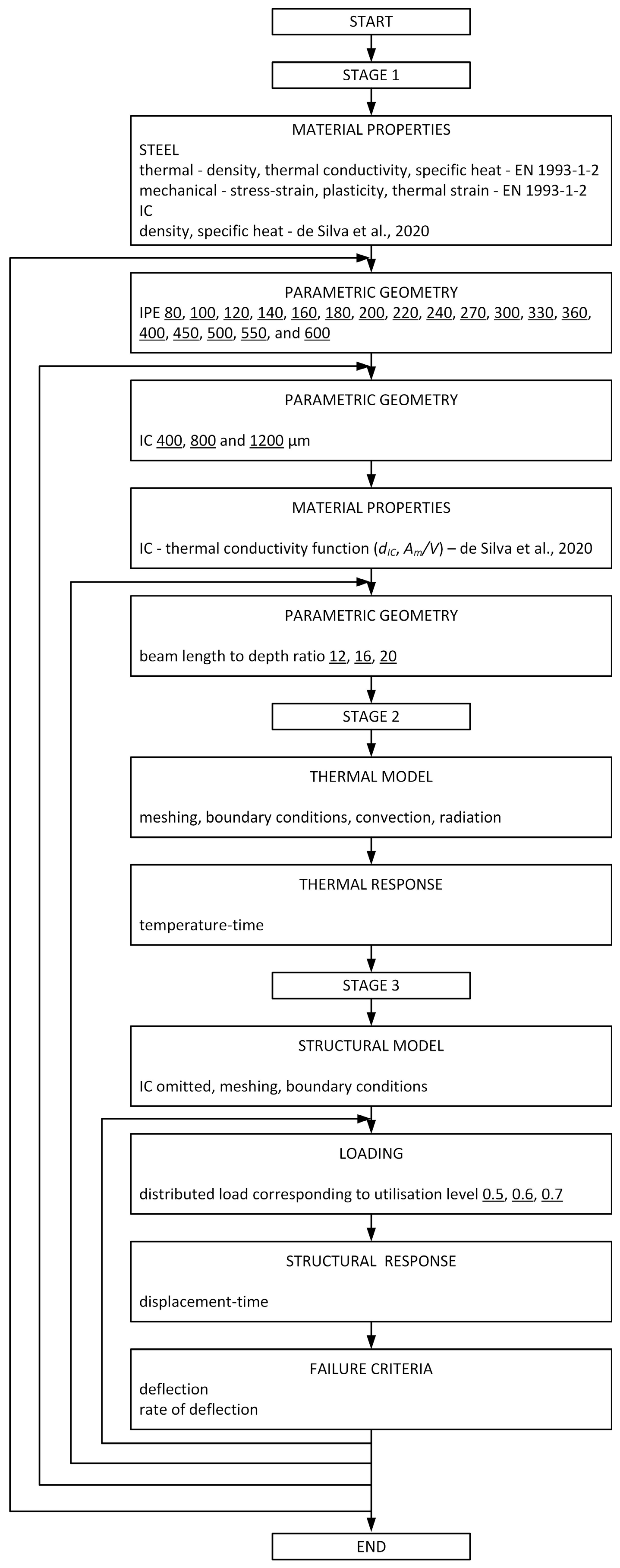
2. Numerical Simulations in ANSYS
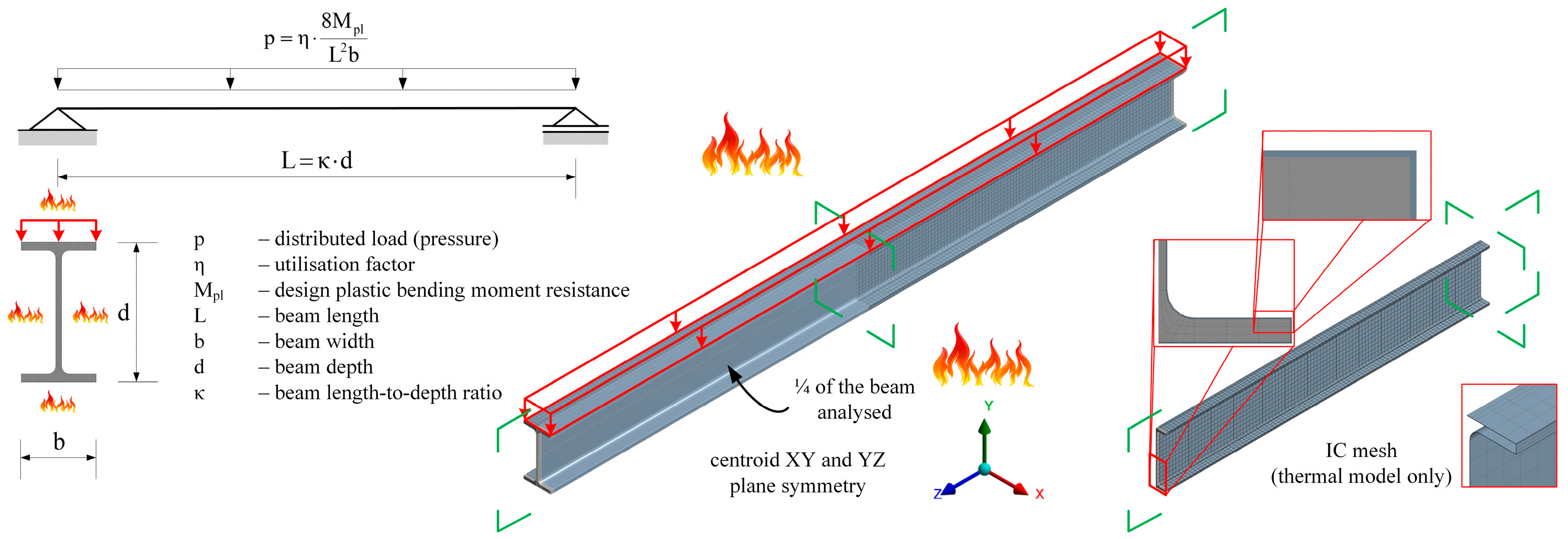
2.1. Thermal and Structural System Scenario
2.2. Numerical Model Development
2.2.1. Thermal and Structural Model Development
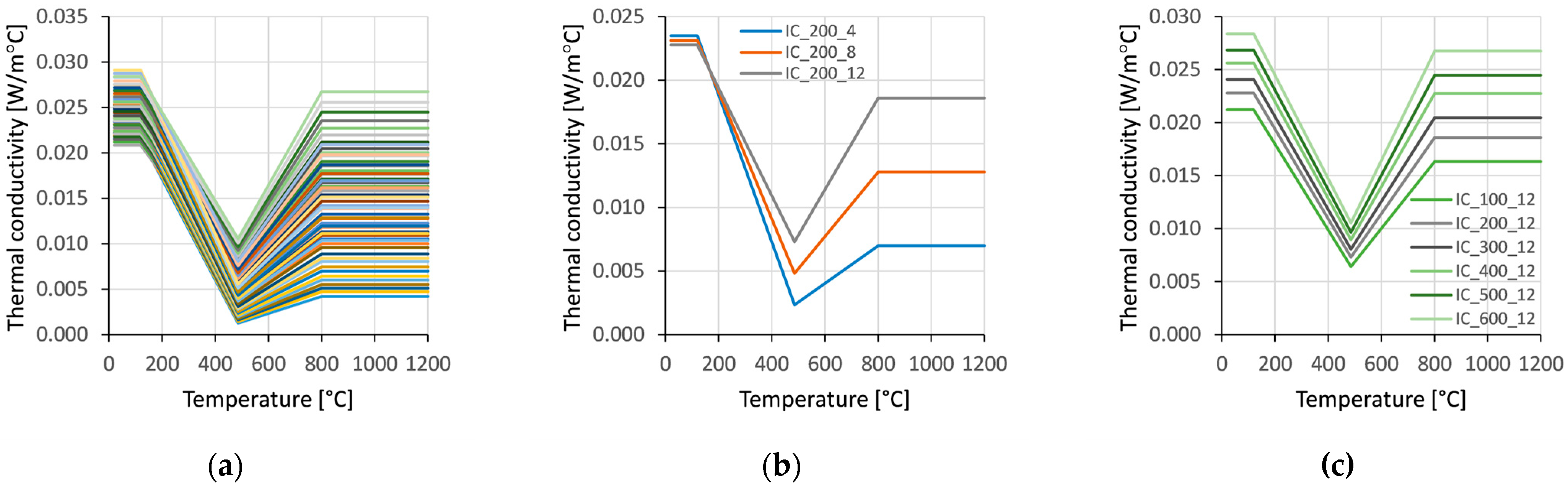
2.2.2. IC Material Model Development
2.2.3. Failure Criteria
2.3. Parametric Analysis
3. Machine Learning
3.1. Artificial Neural Networks
3.1.1. Dataset
3.1.2. ANN Models
4. Results and Discussion
4.1. Model Verification and Validation
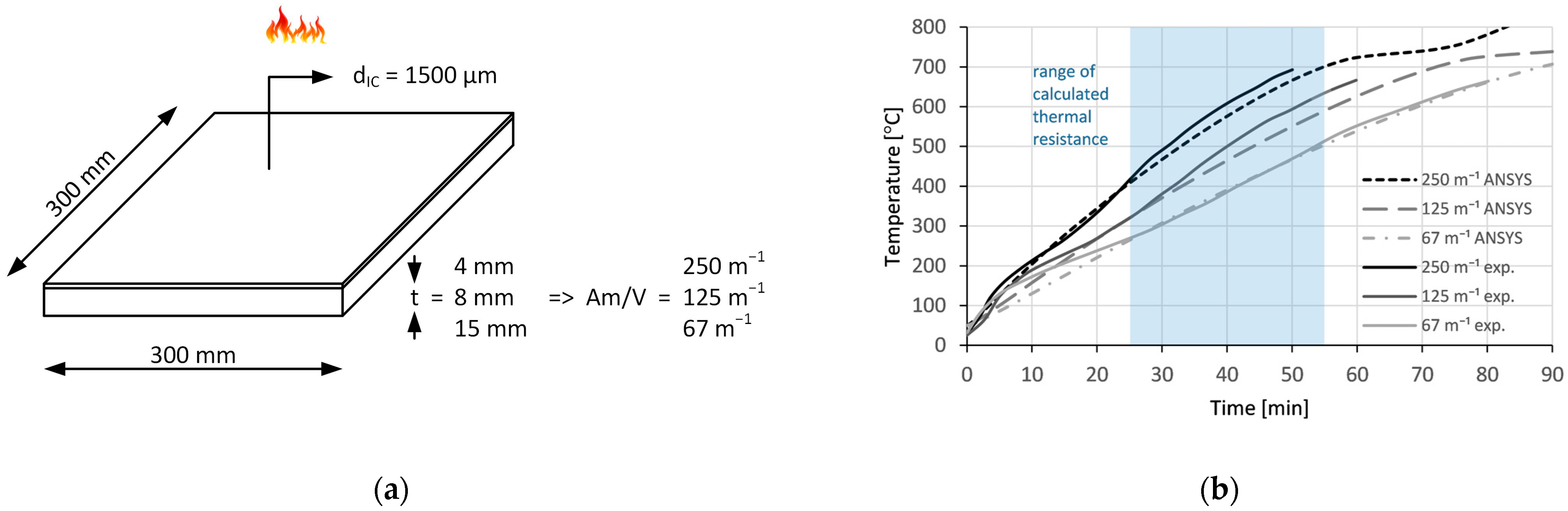
4.1.1. Thermal Model Validation
4.1.2. Structural Model Verification
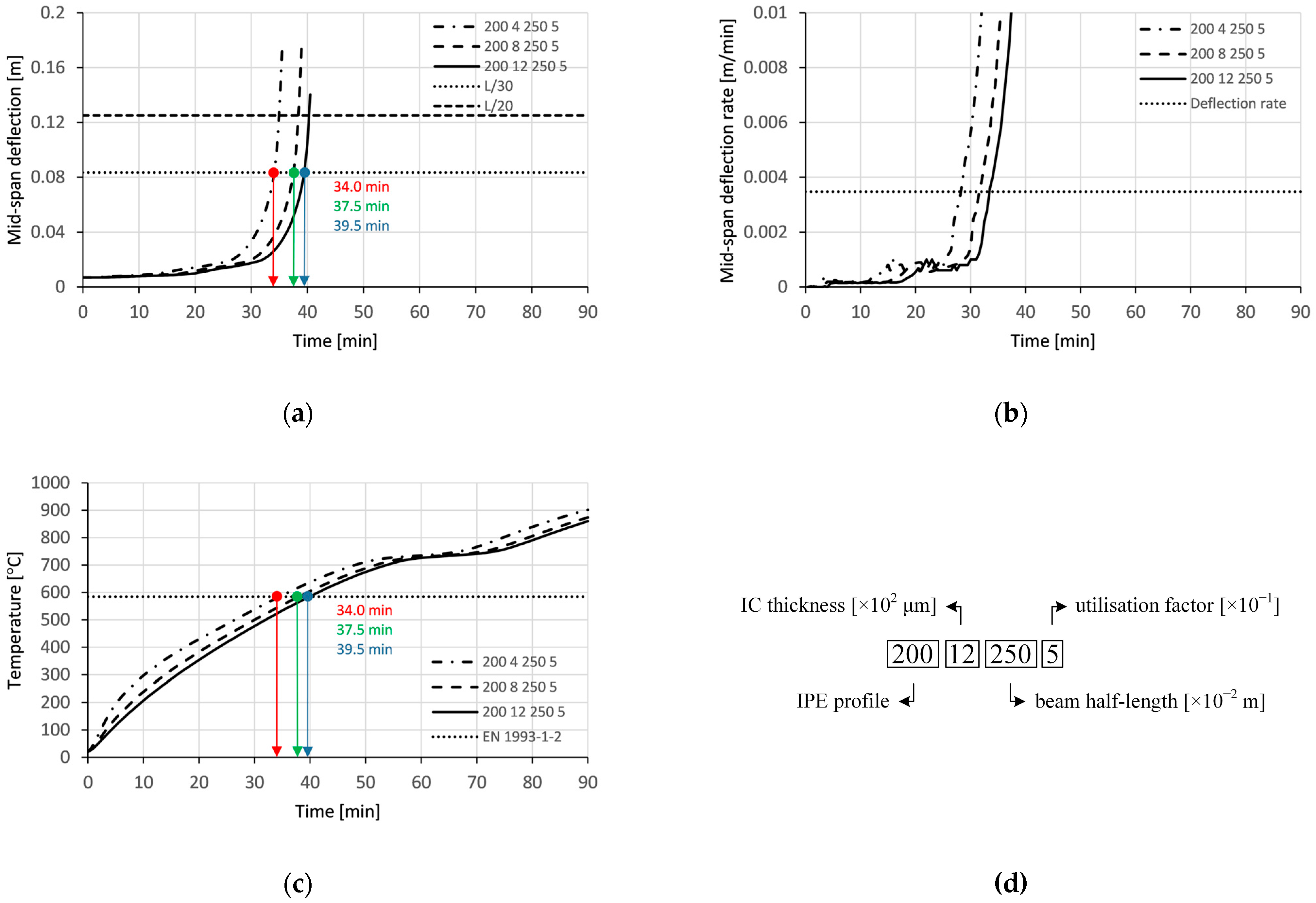
4.2. Parametric Response
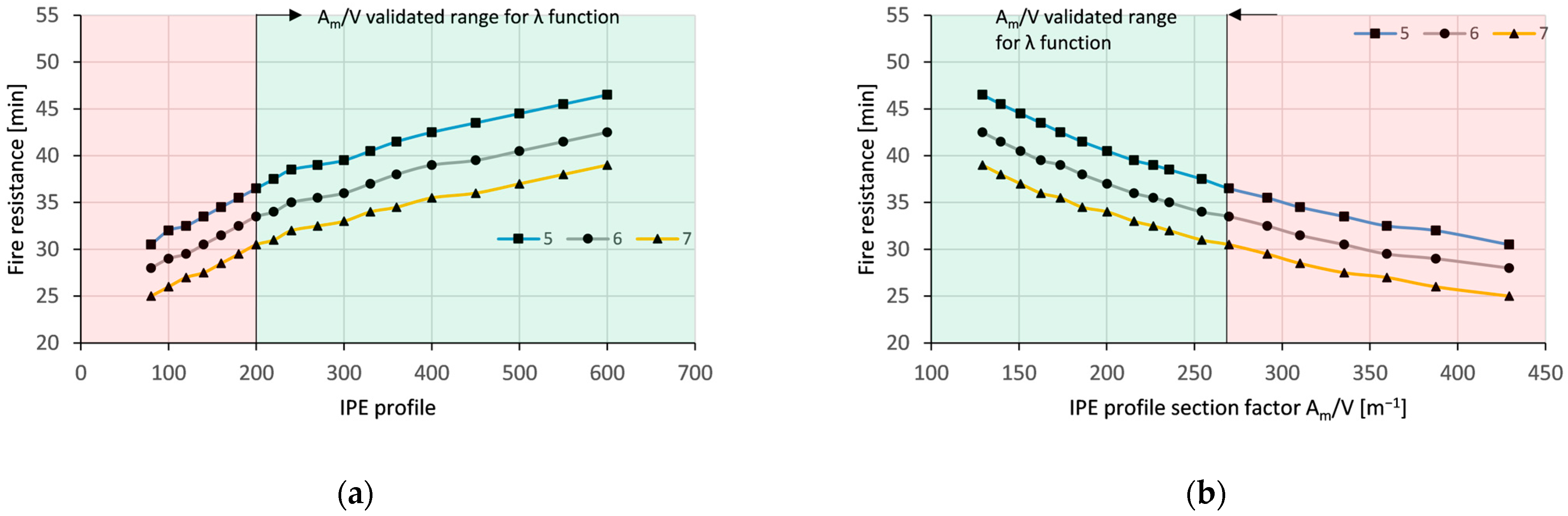
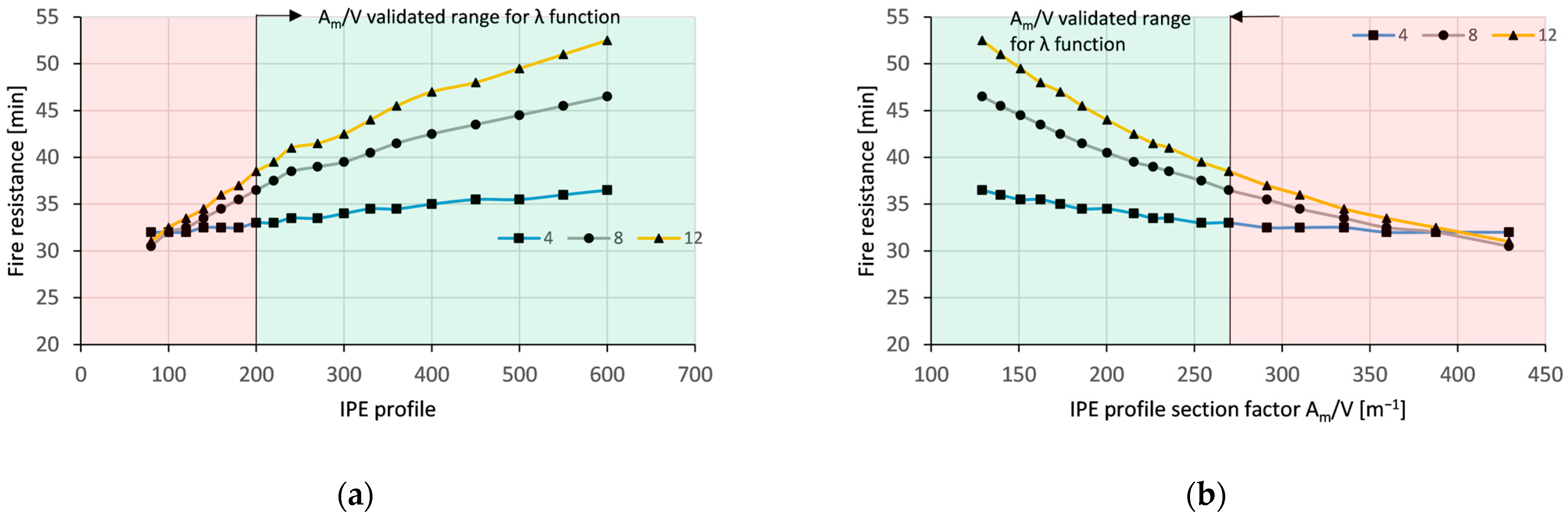
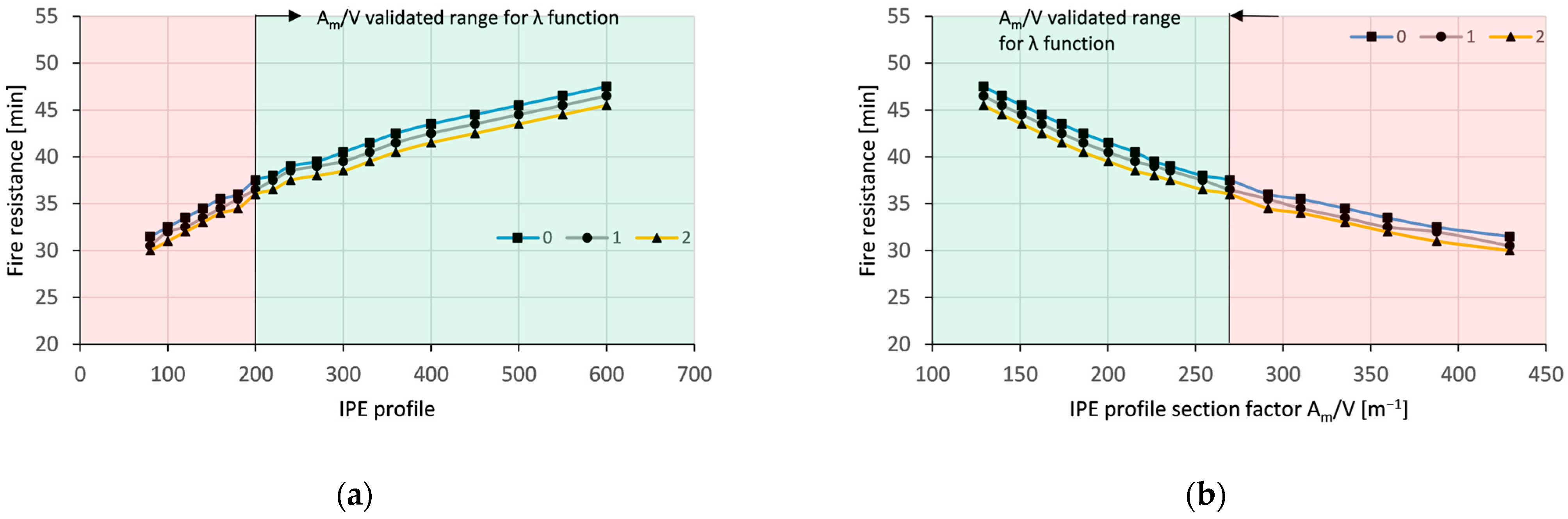
4.2.1. Influence of Beam Section Factor, Utilisation, Length-to-Depth Ratio, and IC Thickness on Beam Failure
4.2.2. Limitations of the Mathematical Model with Respect to High Section Factors
4.3. ANN Models Response
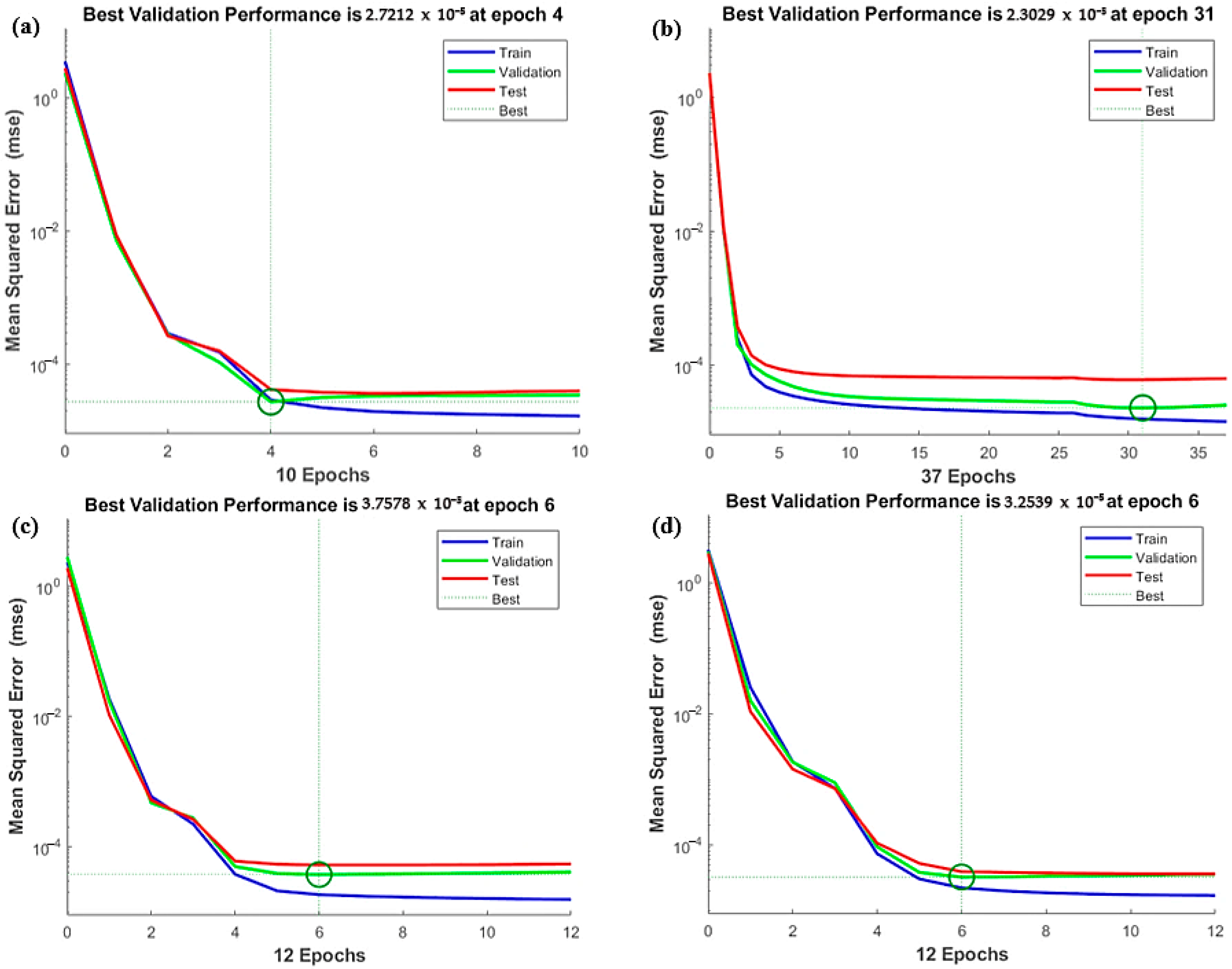
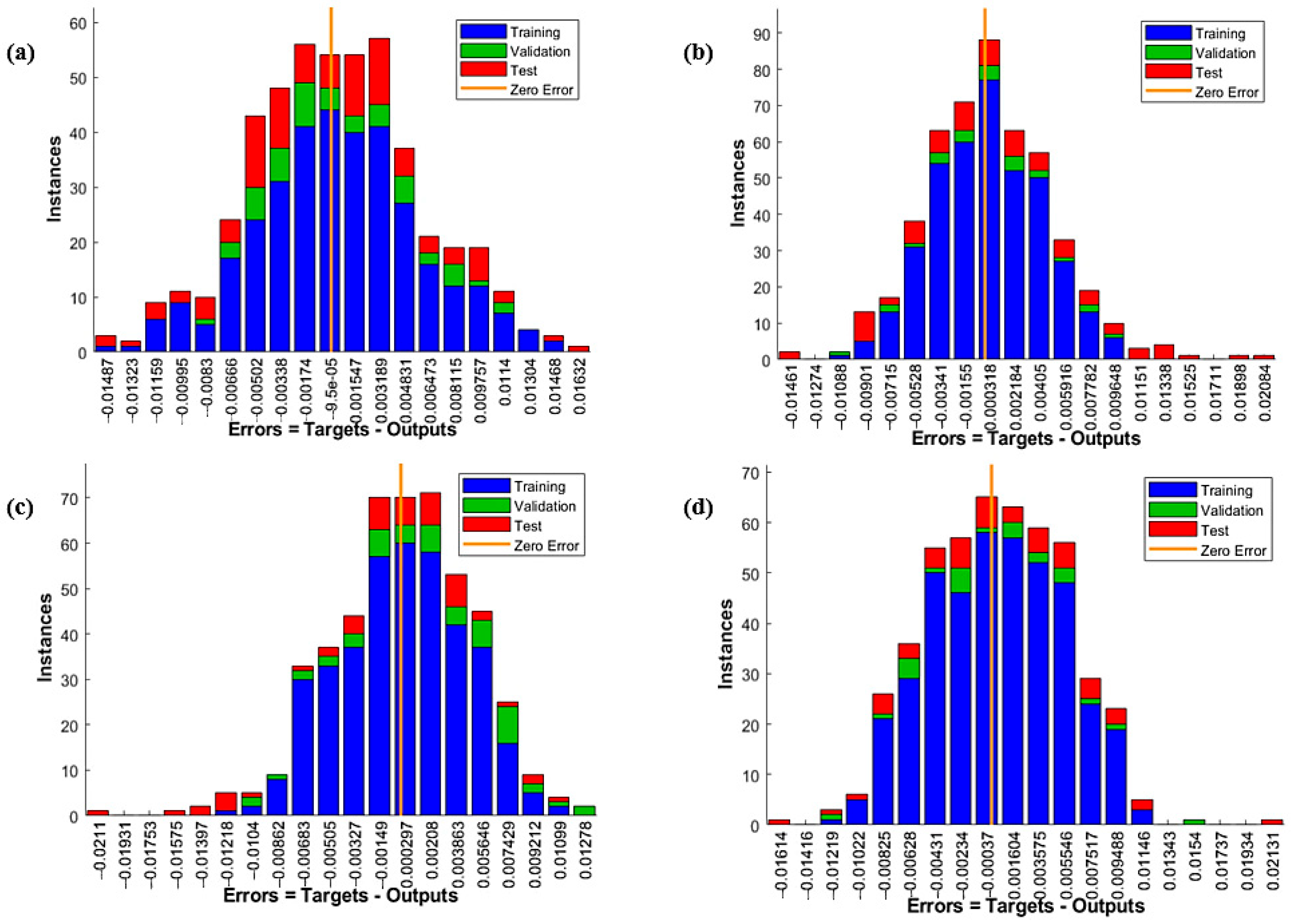
4.4. Evaluation of ANN Models
5. Conclusions
- Extrapolation of the section factor succeeded to provide appropriate values of thermal conductivity (Equation (1)).
- Efficiency of the applied IC protection is higher for larger profiles, i.e., for lower profile section factors. This is particularly observed for higher IC thicknesses, while in the case of thin IC, the influence of profile size is less pronounced. The fire protection efficiency is not linearly proportional to the thickness of the coating; moreover, it becomes less efficient for higher coating thicknesses.
- As expected, fire resistance depends on the degree of utilisation of the member and is reduced as the utilisation increases.
- In terms of the beam length, practically, minor variations in the fire resistance are obtained, giving preference to the beams with a higher depth-to-length ratio.
- Satisfactory behaviour of all machine learning models confirms a high-quality dataset, implying the suitability of the thermal conductivity function and the rate of deflection limitations that are applied for the parametric analysis.
- The input purposefully included numerical description of the members’ geometry instead of using a simple designation, e.g., IPE80. Therefore, ANN models may be generalized for other types of I steel beams, such as HEA or HEB, for prediction of fire resistance time.
- ANN model NN_85_10_5-14 included 85% of the dataset for training, 10% for testing, and 5% for validation, with 14 hidden neurons. This model showed optimal performance, including good generalization properties after the initial training and after further evaluation. Hence, this model is recommended for the prediction of fire resistance time for I steel profiles with water-based IC in standard fire.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IC | Intumescent coating |
| ANN | Artificial neural network |
| SVM | Support vector machine |
| DT | Decision tree |
| FE | Finite element |
| ISO | International Organization for Standardization |
| EN | European Standard |
| MSE | Mean squared error |
References
- Hua, Y.; Duan, L.; Zhao, J. Performance-based fire protection of clustered individual members within a steel frame structure. J. Constr. Steel Res. 2024, 218, 108691. [Google Scholar] [CrossRef]
- Häßler, D.; Hothan, S. Performance of intumescent fire protection coatings applied to structural steel tension members with circular solid and hollow sections. Fire Saf. J. 2022, 131, 103605. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Y.; Shao, W.; Xiao, F. Benign design of intumescent fire protection coatings for steel structures containing biomass humic acid as carbon source. Constr. Build. Mater. 2023, 409, 134001. [Google Scholar] [CrossRef]
- Lucherini, A.; Cristian, M. Intumescent coatings used for the fire-safe design of steel structures: A review. J. Constr. Steel Res. 2019, 162, 105712. [Google Scholar] [CrossRef]
- Lucherini, A.; Hidalgo, J.P.; Torero, J.L.; Maluk, C. Influence of heating conditions and initial thickness on the effectiveness of thin intumescent coatings. Fire Saf. J. 2021, 120, 103078. [Google Scholar] [CrossRef]
- Lucherini, A.; Hidalgo, J.P.; Torero, J.L.; Maluk, C. A novel approach to model the thermal and physical behaviour of swelling intumescent coatings exposed to fire. In Proceedings of the 11th International Conference Structures in Fire SiF, Brisbane, Australia, 30 November—2 December 2020. [Google Scholar] [CrossRef]
- Lucherini, A.; Giuliani, L.; Jomaas, G. Experimental study of the performance of intumescent coatings exposed to standard and non-standard fire conditions. Fire Saf. J. 2018, 95, 42–50. [Google Scholar] [CrossRef]
- Xu, Q.; Li, G.-Q.; Wang, Y.; Bisby, L. An Experimental Study of the Behavior of Intumescent Coatings under Localized Fires. Fire Saf. J. 2020, 115, 103003. [Google Scholar] [CrossRef]
- ISO 834-1; Fire-Resistance Tests—Elements of Building Construction—Part 1: General Requirements. International Organization for Standardization (ISO): Geneve, Switzerland, 1999.
- Gurney, K. An Introduction to Neural Networks, 1st ed.; UCL Press Limited: London, UK, 1997. [Google Scholar]
- Hammer, B. Neural Networks. In Academic Press Library in Signal Processing; Diniz, P.S.R., Suykens, J.A.K., Chellappa, R., Theodoridis, S., Eds.; Chapter 15; Elsevier: Oxford, UK, 2014; Volume 1, pp. 817–855. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, S.; Athaiya, A. Activation Functions in Neural Networks. Int. J. Eng. Appl. Sci. Technol. 2020, 4, 310–316. [Google Scholar] [CrossRef]
- Kecman, V. Learning and Soft Computing: Support Vector Machines, Neural Networks, and Fuzzy Logic Models, 1st ed.; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Shamisi, M.H.A.; Assi, A.H.; Hejase, H.A.N. Using MATLAB to develop Artificial Neural Network for Predicting Global Solar Radiation in Al Ain City—UAE. In Engineering Education and Research Using MATLAB; Chapter 9; Assi, A., Ed.; InTech: London, UK, 2011; pp. 219–238. [Google Scholar] [CrossRef]
- Gupta, T.; Patel, K.A.; Siddique, S.; Sharma, R.K.; Chaudhary, S. Prediction of mechanical properties of rubberised concrete exposed to elevated temperature using ANN. Measurement 2019, 147, e106870. [Google Scholar] [CrossRef]
- Tanyildizi, H. Prediction of the Strength Properties Carbon Fiber-Reinforced Lightweight Concrete Exposed to the High Temperature using Artificial Neural Network and Support Vector Machine. Adv. Civ. Eng. 2018, 2018, 5140610. [Google Scholar] [CrossRef]
- Chaabene, W.B.; Flah, M.; Nehdi, M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020, 260, 119889. [Google Scholar] [CrossRef]
- Lazarevska, M.; Cvetkovska, M.; Gavriloska, A.T.; Knežević, M.; Milanović, M. Neural-Network-Based Approach for Prediction of the Fire Resistance of Centrically Loaded Composite Columns. Teh. Vjesn. 2016, 23, 1475–1480. [Google Scholar] [CrossRef]
- Moradi, M.J.; Daneshvar, K.; Ghazi-nader, D.; Hajiloo, H. The prediction of fire performance of concrete-filled steel tubes (CFST) using artificial neural network. Thin–Walled Struct. 2021, 161, 107499. [Google Scholar] [CrossRef]
- Quevedo, R.L.; Pardo, Y.L.; Silva, V.P.; Cabrera, Y.F.; Mota, Y.C. Using Numerical Modelling and Artificial Intelligence for Predicting the Degradation of the Resistance to Vertical Shear in Steel—Concrete Composite Beams Under Fire. In Applied Computer Sciences in Engineering, (WEA 2020), Communications in Computer and Information Science; Figueroa-García, J.C., Garay-Rairán, F.S., Hernández-Pérez, G.J., Díaz-Gutierrez, Y., Eds.; Springer: Cham, Switzerland, 2020; Volume 1274, pp. 35–47. [Google Scholar] [CrossRef]
- Fahmi, A.S.; El-Mandawy, M.E.; Gobran, Y.A. Using artificial neural networks in the design of orthotropic bridge decks. Alex. Eng. J. 2016, 55, 3195–3203. [Google Scholar] [CrossRef]
- Fu, F. Fire induced progressive collapse potential assessment of steel framed buildings using machine learning. J. Constr. Steel Res. 2020, 166, 105918. [Google Scholar] [CrossRef]
- Naser, M.Z. Properties and material models for common construction materials at elevated temperatures. Constr. Build. Mater. 2019, 215, 192–206. [Google Scholar] [CrossRef]
- Han, Z.; Fina, A.; Malucelli, G.; Camino, G. Testing fire protective properties of intumescent coatings by in-line temperature measurements on a cone calorimeter. Prog. Org. Coat. 2010, 69, 475–480. [Google Scholar] [CrossRef]
- Griffin, G.J. The modelling of heat transfer across intumescent polymer coatings. J. Fire Sci. 2010, 28, 249–277. [Google Scholar] [CrossRef]
- Bailey, C.G. The behaviour of asymmetric slim floor steel beam in fire. J. Constr. Steel Res. 1999, 50, 235–257. [Google Scholar] [CrossRef]
- Alam, N.; Maraveas, C.; Tsavdaridis, K.D.; Nadjai, A. Performance of Ultra Shallow Floor Beams (USFB) exposed to standard and natural fires. J. Build. Eng. 2021, 38, 102192. [Google Scholar] [CrossRef]
- Kolšek, J.; Češarek, P. Performance-based fire modelling of intumescent painted steel structures and comparison to EC3. J. Constr. Steel Res. 2015, 104, 91–103. [Google Scholar] [CrossRef]
- de Silva, D.; Bilotta, A.; Nigro, E. Experimental investigation on steel elements protected with intumescent coating. Constr. Build. Mater. 2019, 205, 232–244. [Google Scholar] [CrossRef]
- de Silva, D.; Bilotta, A.; Nigro, E. Approach for modelling thermal properties of intumescent coating applied on steel members. Fire Saf. J. 2020, 116, 103200. [Google Scholar] [CrossRef]
- ANSYS® Academic Teaching Mechanical. ANSYS Help Documentation, Release 16.0; ANSYS, Inc.: Canonsburg, PA, USA, 2015. Available online: https://www.ansys.com/ (accessed on 1 September 2024).
- EN 1991-1-2; Eurocode 1: Actions on Structures: Part 1-2: General Actions—Actions on Structures Exposed to Fire. CEN—European Committee for Standardization (ISO): Geneve, Switzerland, 2012.
- EN 1993-1-2; Eurocode 3: Design of Steel Structures, Part 1-2: General Rules, Structural Fire Design. CEN—European Committee for Standardization (ISO): Geneve, Switzerland, 2012.
- Gernay, T.; Franssen, J.M. A formulation of the Eurocode 2 concrete model at elevated temperature that includes an explicit term for transient creep. Fire Saf. J. 2012, 51, 1–9. [Google Scholar] [CrossRef]
- Nguyen, H.L.; Kohno, M. Numerical model of heat transfer for protected steel beam with cavity under ISO 834 standard fire. Fire Saf. J. 2023, 140, 103876. [Google Scholar] [CrossRef]
- Allam, A.; Nassif, A.; Nadjai, A. Behavior of restrained steel beam at elevated temperature—Parametric studies. J. Struct. Fire Eng. 2019, 10, 324–339. [Google Scholar] [CrossRef]
- Rackauskaite, E.; Kotsovinos, P.; Jeffers, A.; Rein, G. Computational analysis of thermal and structural failure criteria of a multistorey steel frame exposed to fire. Eng. Struct. 2019, 180, 524–543. [Google Scholar] [CrossRef]
- Karlik, B.; Olgac, A.V. Performance Analysis of Various Activation Functions in Generalized MLP Architectures of Neural Networks. Int. J. Artif. Intell. 2011, 1, 111–122. [Google Scholar]
- The MathWorks Inc. Optimization Toolbox, Version: 9.4 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022. Available online: https://www.mathworks.com (accessed on 1 September 2024).
- Özturan, M.; Kutlu, B.; Özturan, T. Comparison of Concrete Strength Prediction Techniques with Artificial Neural Network Approach. Build. Res. J. 2008, 56, 23–36. [Google Scholar]


| Coefficient | θIC (°C) | ||
|---|---|---|---|
| 120 | 486 | 800 | |
| a0 | 0.0187 | −0.0031 | −0.0063 |
| a1 | −0.90 | 6.32 | 14.50 |
| a2 | 1.39 | 0.80 | 2.02 |
| Input Neurons | Minimum Value | Maximum Value |
|---|---|---|
| H—height of cross-section [mm] | 80 | 600 |
| B—width of cross-section [mm] | 46 | 220 |
| Tw—thickness of web [mm] | 3.8 | 12 |
| Tf—thickness of flange [mm] | 5.2 | 19 |
| r—root radius [mm] | 5 | 24 |
| L—length of beam [m] | 1 | 12 |
| Am/V—section factor [m−1] | 129.18 | 429.32 |
| Nfi—loading factor | 0.5 | 0.7 |
| dIC—thickness of dry IC film [mm] | 0.4 | 1.2 |
| λIC,20 [W/m°C] | 0.020858 | 0.0291 |
| λIC,120 [W/m°C] | 0.020858 | 0.0291 |
| λIC,486 [W/m°C] | 0.001243 | 0.010533 |
| λIC,800 [W/m°C] | 0.004205 | 0.026737 |
| λIC,1200 [W/m°C] | 0.004205 | 0.026737 |
| Output neuron | Minimum value | Maximum value |
| RT—resistance time [min] | 24 | 53.5 |
| Model | Hidden Neurons | Training % (#) | Validation % (#) | Testing % (#) |
|---|---|---|---|---|
| NN70_10_20-14 | 14 | 70 (340) | 10 (49) | 20 (97) |
| NN70_10_20-29 | 29 | 70 (340) | 10 (49) | 20 (97) |
| NN70_10_20-42 | 42 | 70 (340) | 10 (49) | 20 (97) |
| NN80_5_15-14 | 14 | 80 (389) | 5 (24) | 15 (73) |
| NN80_5_15-29 | 29 | 80 (389) | 5 (24) | 15 (73) |
| NN80_5_15-42 | 42 | 80 (389) | 5 (24) | 15 (73) |
| NN80_10_10-14 | 14 | 80 (389) | 10 (49) | 10 (49) |
| NN80_10_10-29 | 29 | 80 (389) | 10 (49) | 10 (49) |
| NN80_10_10-42 | 42 | 80 (389) | 10 (49) | 10 (49) |
| NN85_5_10-14 | 14 | 85 (413) | 5 (24) | 10 (49) |
| NN85_5_10-29 | 29 | 85 (413) | 5 (24) | 10 (49) |
| NN85_5_10-42 | 42 | 85 (413) | 5 (24) | 10 (49) |
| Model | Regression—Training | Regression—Validation | Regression—Testing | Regression—Total | MSE | Epoch |
|---|---|---|---|---|---|---|
| NN70_10_20-14 | 0.99978 | 0.99947 | 0.99951 | 0.99970 | 0.0000381 | 29 |
| NN70_10_20-29 | 0.99966 | 0.99975 | 0.99939 | 0.99963 | 0.0000272 | 10 |
| NN70_10_20-42 | 0.99977 | 0.99938 | 0.99937 | 0.99965 | 0.0000440 | 12 |
| NN80_5_15-14 | 0.99976 | 0.99935 | 0.99950 | 0.99971 | 0.0000346 | 29 |
| NN80_5_15-29 | 0.99978 | 0.99977 | 0.99952 | 0.99974 | 0.0000319 | 23 |
| NN80_5_15-42 | 0.99981 | 0.99969 | 0.99927 | 0.99972 | 0.0000231 | 37 |
| NN80_10_10-14 | 0.99973 | 0.99976 | 0.99950 | 0.99971 | 0.0000300 | 33 |
| NN80_10_10-29 | 0.99978 | 0.99963 | 0.99963 | 0.99974 | 0.0000381 | 36 |
| NN80_10_10-42 | 0.99977 | 0.99965 | 0.99952 | 0.99971 | 0.0000376 | 12 |
| NN85_5_10-14 | 0.99970 | 0.99974 | 0.99910 | 0.99966 | 0.0000387 | 15 |
| NN85_5_10-29 | 0.99975 | 0.99949 | 0.99940 | 0.99971 | 0.0000325 | 12 |
| NN85_5_10-42 | 0.99984 | 0.99939 | 0.99950 | 0.99978 | 0.0000485 | 35 |
| Model | Training Results | Evaluation Results | ||||||
|---|---|---|---|---|---|---|---|---|
| R Training | R Validation | R Testing | R Total | MSE | Epoch | R Total | MSE | |
| EV-NN70_10_20-29 | 0.99967 | 0.99908 | 0.9993 | 0.9995 | 0.000077 | 11 | 0.9987 | 0.0017 |
| EV-NN80_5_15-42 | 0.99993 | 0.99846 | 0.9993 | 0.9998 | 0.00008 | 25 | 0.9983 | 0.0017 |
| EV-NN80_10_10-42 | 0.99987 | 0.99909 | 0.9977 | 0.9996 | 0.000104 | 11 | 0.9986 | 0.0017 |
| EV-NN85_5_10-14 | 0.99981 | 0.99968 | 0.9994 | 0.9998 | 0.000024 | 17 | 0.9993 | 0.0016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Džolev, I.; Kekez-Baran, S.; Rašeta, A. Fire Resistance of Steel Beams with Intumescent Coating Exposed to Fire Using ANSYS and Machine Learning. Buildings 2025, 15, 2334. https://doi.org/10.3390/buildings15132334
Džolev I, Kekez-Baran S, Rašeta A. Fire Resistance of Steel Beams with Intumescent Coating Exposed to Fire Using ANSYS and Machine Learning. Buildings. 2025; 15(13):2334. https://doi.org/10.3390/buildings15132334
Chicago/Turabian StyleDžolev, Igor, Sofija Kekez-Baran, and Andrija Rašeta. 2025. "Fire Resistance of Steel Beams with Intumescent Coating Exposed to Fire Using ANSYS and Machine Learning" Buildings 15, no. 13: 2334. https://doi.org/10.3390/buildings15132334
APA StyleDžolev, I., Kekez-Baran, S., & Rašeta, A. (2025). Fire Resistance of Steel Beams with Intumescent Coating Exposed to Fire Using ANSYS and Machine Learning. Buildings, 15(13), 2334. https://doi.org/10.3390/buildings15132334








