Abstract
Train–bridge dynamic interaction analysis is critical for the dynamic design of bridges and the safety and comfort assessment of trains. This study introduces a train–bridge dynamic model of a straddle monorail train and a steel–concrete composite track beam to investigate the dynamic performance of the bridge and train. It explores the influence of track irregularities and passenger loads on the dynamic response of train–bridge systems at various traveling speeds. The numerical results indicate that there is no significant resonance between the straddle monorail train and the steel–concrete composite bridge. However, track irregularities and train speed significantly amplify the responses of the train and bridge, including displacement, acceleration, and impact coefficient. Additionally, increased passenger load leads to a substantial rise in the vertical displacement of the bridge while reducing the vibration of the train, thereby improving riding comfort. The findings of this study provide valuable scientific insights and have significant practical applications for the use of steel–concrete composite bridges in straddle monorail systems.
1. Introduction
Urban rail transport is an efficient avenue for reducing urban congestion and fostering high-quality urban development in the context of the rapid growth of urbanization [1]. A straddle-type monorail with medium traffic volume is a popular alternative mode of the rail transit system for its many advantages [2] such as low investment, fast construction, less land occupation, and low noise, and it has been applied in some countries, including China, Japan, and Brazil. The straddle monorail has the traveling characteristics of beam–track integration, in which the train is supported, stabilized, and guided through the track beam while the car body travels on the track beam using pneumatic tires. Its unique traveling mechanism specifies that the train–bridge dynamic interaction behavior of the straddle monorail concerning the service performance of the bridge and the riding comfort of the train differs from that of the conventional rail transit system [3,4]. Thus, it is essential to examine the dynamic coupling vibration behavior of the straddle monorail train–bridge system.
A larger number of studies associated with train–bridge coupling analysis have been conducted over the years. Zhai and Cai [5] proposed a numerical simulation technique for analyzing the train–track–bridge dynamic interaction and evaluated the dynamic performance of three extraordinarily large bridges under high-speed railway train load. Taking into account the China-Star high-speed train with 27 degrees of freedom (DOFs) and a bridge with a span of 24 m simply supported by prestressed concrete, Xia and Zhang [6] established a numerical model of the railway vehicle–bridge system and verified the simulated results with field measurements. Zhang et al. [7] developed a linear wheel–rail interaction model for exploring the dynamic response of the train–bridge interaction system. Zhang et al. [8] presented an accurate and efficient calculation for analyzing the non-stationary random dynamic behavior of train–bridge systems combined with the pseudo-excitation method and precise integration algorithm. Considering the random track irregularity and wheel–rail contact geometry, Mao et al. [9] created a three-dimensional train–track–bridge random interaction model through the probability density evolution method. Furthermore, many studies [10,11,12,13,14,15,16,17,18] have reported on the dynamic characteristics and traveling safety of train–bridge systems subjected to stochastic winds, earthquakes, and collisions.
With the rapid development of urban rail transit infrastructure, the train–bridge dynamic interaction problems of the straddle monorail system have also attracted a great deal of attention in recent years. Lee et al. [19,20] derived the motion equation of straddle monorail vehicle–bridge dynamics early on to examine the riding comfort of trains by measuring the surface roughness in the field. Kim and Kawatani [21] further considered the effects of ground motion on a steel monorail bridge using a train–bridge coupling interaction model. Naeimi et al. [22] developed a computational model of train–guideway interaction and assessed the dynamic behavior of the monorail–bridge system under different loading conditions. Zhang et al. [23] explored the pre-load effects of guiding and stabilizing wheels on the anti-overturning performance of a straddle-type monorail train and discussed the limited speed of the train on a curved track. Gou et al. [24] set up a numerical model for studying the dynamic behavior of a concrete-filled steel tubular arch bridge on which a straddle monorail train travels and discussed the traveling comfort of the vehicle. Yang et al. [25] carried out a field test on the Chongqing straddle monorail and proposed a stable wheel overturning coefficient to evaluate the anti-overturning stability of trains. Using commercial software, Jiang et al. [26] proposed a prediction method for the wheel wears of two types of articulated monorail trains. Zhou et al. [27] reported on the parameter optimization of straddle-type monorail trains with a single-axle bogie with the use of a multibody dynamic simulation. Sirisonthi et al. [28] conducted a full-scale test of the load–deformation characteristics of a continuous girder for the straddle monorail, and Zhou et al. [29] also introduced a co-simulation technique to compute the vibration response of a straddle monorail train–bridge system. Notably, most prior studies on straddle monorail train–bridge systems have focused on prestressed concrete track beams with spans of 22–26 m. However, few studies have investigated the dynamic behavior of steel–concrete composite bridges under straddle monorail loads, especially for the larger spans required in urban intersections or river crossings. This study fills this gap by systematically analyzing the train–bridge interaction of a steel–concrete composite bridge, which offers advantages in terms of cost efficiency and the construction cycle for monorail systems.
The dynamic interaction between the straddle monorail train and bridge is influenced not only by the train’s motion but also by the combined mass, stiffness, and damping properties of the coupled system. This pure dynamic interaction, often overlooked in railway studies but more commonly addressed in road bridge research [30], introduces complexities in predicting system responses. Understanding this interaction is essential for accurate dynamic modeling, and this study is the first to examine the dynamic interaction of a straddle monorail train with a steel–concrete composite track beam, introducing a novel coupling model that accounts for passenger-load-induced mass effects and track irregularity excitations, and finally, the impact coefficient of the bridge and the traveling comfort of a straddle monorail train are evaluated. The calculated results reveal that the steel–concrete composite bridge has great potential and advantages in the straddle monorail transportation system as a result of the good dynamic behavior and riding comfort of the train–bridge system when compared to the traditional simply supported bridge.
2. The Dynamic Interaction Model of a Straddle Monorail Train–Bridge System
2.1. Train Model
In general, the multibody dynamic method is widely applied to model the straddle monorail train, and it assumes that the whole train is assembled by several independent vehicle elements, where each vehicle element consists of a car body and two bogies connected by a simplified suspension system with springs and dampers, as shown in Figure 1. Differing from the conventional rail transit system, the straddle monorail train rides on the track beam with the use of pneumatic tires. Thus, there are three types of wheels: traveling wheels that provide driving force and support the weight of trains, steering wheels that guide the traveling direction, and stabilizing wheels that prevent the train from rolling over. In addition, some assumptions are used to simplify the calculation in the train model, as follows:
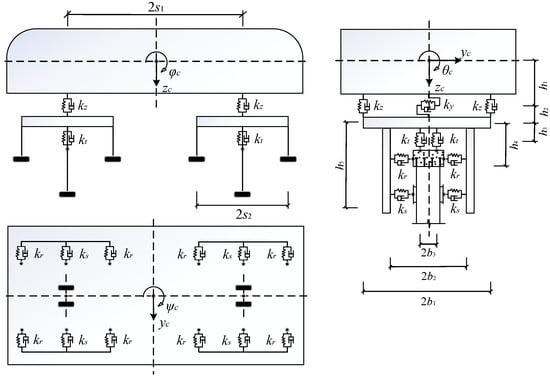
Figure 1.
Vehicle element model of straddle monorail trains.
(1) The car body and bogies are regarded as rigid elements without any elastic deformation.
(2) The mass, damping, and stiffness parameters in the train model are assumed to be constant.
(3) The wheels are neglected, and the interaction characteristics between rubber wheels and bridges are simplified as a single contact point with a spring and damper.
There are 5 DOFs for each car body in the directions of y, z, θ, φ, and ψ (transverse, vertical, rolling, pitching, and yawing). It should be noted, however, that the pitching DOF of each bogie is not considered in this study on account of the use of a single-axle bogie, which differs from the conventional dual-axle designs in prior studies [3,24]. The total number of DOFs is 13 for each vehicle element, as illustrated in Table 1. The detailed parameters of straddle monorail trains are listed in Table 2.

Table 1.
DOFs of each vehicle element with single-axle bogies.

Table 2.
Parameters of straddle monorail trains. (Some data were sourced from Gou et al. [24].
With the use of D’Alembert’s principle, we can derive the following motion equations of the car body in the DOFs of y, z, θ, φ, and ψ:
where j = 1, 2 represents the front and rear bogies, respectively; ηj is the sign function, where η1 = 1 for the front bogie, and η2 = −1 for the rear bogie.
Analogously, the motion equations of the bogie in the DOFs of y, z, θ, and ψ can be established as follows:
where rRjl (l = 1, 2, 3, 4) is the displacement of the l-th steering wheel at the j-th bogie, which can be expressed as
rrjl and ybjl are the track irregularity and displacement of bridges at the l-th steering wheel and j-th bogie, respectively; rSjm (m = 1, 2) and rTjn (n = 1, 2) can refer to the definition of rRjl.
From Equations (1)–(9) we can obtain the following motion equation of the vehicle element concerning straddle monorail trains:
where XV is the displacement vector of the vehicle element:
MV is the mass matrix of the vehicle element:
KV is the stiffness matrix of the vehicle element:
FV is the force vector of the vehicle element:
The form of the damping matrix CV and ctr is identical to that of the stiffness matrix KV and ktr, which can be obtained by substituting the respective stiffness parameters.
2.2. Bridge Model
The bridge model is based on the operational straddle monorail system in Wuhu, China, with dimensions and properties drawn from as-built engineering data. The steel–concrete composite bridge for straddle monorails is made up of two separate track beams simply supported on the piers and linked together by plan bracing systems. The span of bridges is 28.71 m, and there is 4.6 m in the center between two separate track beams. To meet the traveling requirement of the straddle monorail vehicle with single-axle bogies, the concrete deck is set to 0.69 m in width, and the total height of the beam is 2 m. Figure 2 demonstrates the detailed layouts and dimensions of the straddle monorail bridge.
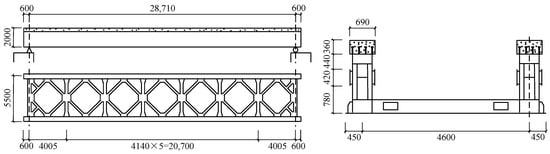
Figure 2.
The layouts and dimensions of the steel–concrete composite bridge for straddle monorails (units: mm).
The finite element method is adopted to set up the monorail bridge, and all substructures of the bridge, including track beams, bracing systems, and piers, are established by the spatial beam element with 6 DOFs, as shown in Figure 3. The steel–concrete composite bridge uses C50 concrete (elastic modulus Ec = 34.5 GPa; density ρc = 2400 kg/m3) and Q345 steel (Es = 206 GPa; ρs = 7850 kg/m3). The bridge bearings are modeled as spring elements with vertical stiffness 1 × 108 N/m and transverse stiffness 5 × 107 N/m, while piers are fully fixed to the ground (fixed support). In total, the bridge model is divided into 122 nodes and 132 elements. The motion equation of the bridge can be expressed as follows:
where XB is the displacement vector of the bridge; MB, KB, and CB are the mass, stiffness, and damping matrices of the bridge, respectively, which can be obtained from the finite element model; FB is the force vector, which probably results from the moving vehicle or external crosswinds, earthquakes, impacts, etc.
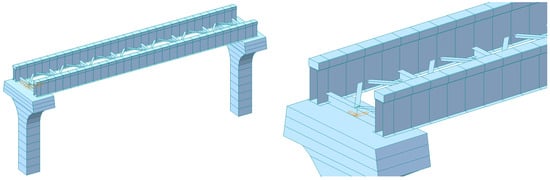
Figure 3.
Finite element model of monorail bridges.
For a linear system, the mode superposition method can be adopted to significantly improve solving efficiency. Thus, XB can be written as follows:
where ϕi is the i-th mode shape vector; qi is the i-th modal coordinate; NB is the total number of DOFs. It is important to note that the response of the bridge is mainly determined by several low-order modes. It is a fact that the first N (N < NB) order modes are only considered in practice to simplify the calculation. Therefore, the displacement vector is calculated approximatively using the following expression:
With the use of the orthogonal condition of the natural modes, the motion equation of the modal coordinates is obtained:
where ξi and ωi are the damping ratio and natural circular frequency of mode i, respectively. In general, the natural frequency and mode shape of the bridge are straightforwardly calculated through the finite element model, and the damping ratio is considered to be 3% for the steel–concrete structure. The main natural frequencies and mode shape of monorail bridges are visualized in Table 3, where the first-order mode is the symmetric transverse bending of piers with 3.323 Hz frequency, and Modes 3–5 correspond to the vertical (5.771 Hz), torsional (7.338 Hz), and transverse (8.853 Hz) bending of track beams, respectively. The first 30 order modes (the ratio of effective mass to total mass is more than 90% in each direction) are extracted to calculate the dynamic response of the bridge in this study.

Table 3.
Main natural frequencies and modes of monorail bridges.
2.3. Interaction Equations
The wheel–rail interaction is critical to the coupling train–bridge system, which determines the interaction force between the train and bridge systems. Based on the contact relationship of a single point between the wheel and track beam, we can calculate the wheel–rail force vector of the straddle monorail for the steering wheel at the j-th bogie:
That for the stabilizing wheel at the j-th bogie is as follows:
That for the traveling wheel at the j-th bogie is as follows:
The damping matrix in the above equations can be derived by replacing the corresponding stiffness parameter in the stiffness matrix. According to the results of the wheel–rail interaction force, the force vector FB on the bridge can also be obtained. Finally, the simultaneous equations of the train–bridge coupling system for straddle monorails are expressed as follows:
where subscripts V, B, and VB (or BV) represent the train, bridge, and train–bridge interaction, respectively. The train–bridge dynamic interaction equation can be effectively solved using the intersystem iteration method developed by Zhang and Xia [31]. This approach has demonstrated robustness and is widely adopted in prior research [14,29] due to its ability to treat the train and bridge subsystems as fully independent entities.
2.4. Track Irregularity
Track irregularity is a crucial excitation in the vehicle–bridge dynamic analysis, which refers to random deviations from the ideal track profile. Lee et al. [19] carried out field measurements and fitted the power spectral density function of the track irregularity for straddle monorails, expressed as follows:
where Ω is the spatial frequency (cycle/m); α, β, and n are the fitted coefficients for determining the shape and distribution of the power spectral density, which can be estimated to be 0.0005, 0.35, and 3.00 for traveling wheels; 0.0006, 0.50, and 2.80 for steering wheels; and 0.0006, 0.50, and 2.60 for stabilizing wheels.
In general, track irregularity is assumed to be a stationary Gauss random process. Thus, with the use of the trigonometric series superposition method, the track irregularity sample can be simulated by the following expression:
where x denotes the mileage coordinate; Ωk (k = 1, 2, …, N) is the discrete frequency point; ∆Ω is the frequency interval; φk is the random phase that follows the uniform distribution and ranges from 0 to 2π. Figure 4 shows the simulated time history sample of track irregularity for the traveling, steering, and stabilizing wheels over a length of 500 m.
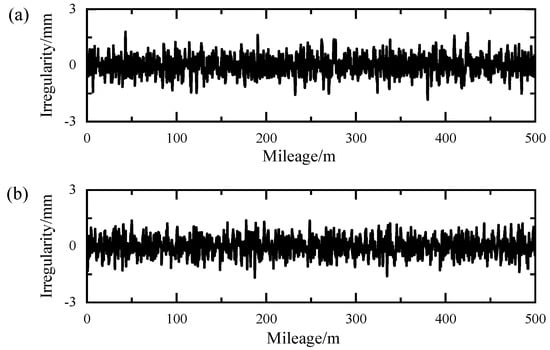
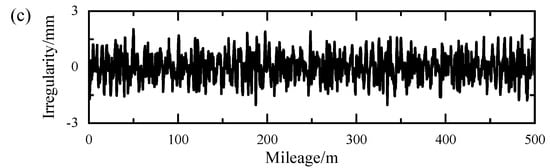
Figure 4.
Simulated track irregularity sample: (a) traveling wheel; (b) steering wheel; (c) stabilizing wheel.
3. Numerical Results and Discussions
3.1. Time History Response
Based on the established monorail train–bridge interaction model, Figure 5 and Figure 6 present the calculated dynamic response time histories of the train and bridge at a running speed of 80 km/h. It can be seen that the vertical displacement of the bridge is significantly larger than the transverse displacement due to the vertical static load of the train. However, the bridge accelerations in both the transverse and vertical directions are consistent. One possible explanation for this is that the accelerations are determined by track irregularity. Similar results can also be observed in the acceleration response of the car body.
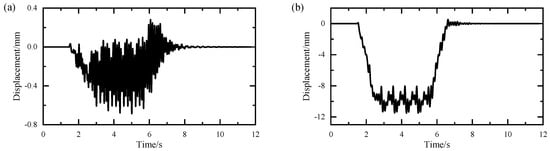
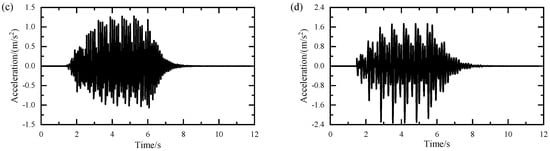
Figure 5.
Calculated time history response of bridge at mid-span: (a) transverse displacement; (b) vertical displacement; (c) transverse acceleration; (d) vertical acceleration.
Figure 6.
Calculated acceleration time history of car body at mid-span: (a) transverse; (b) vertical.
3.2. Track Irregularity Effect
To explore the effects of track irregularity on the bridge dynamic responses, Figure 7 illustrates the displacement and acceleration amplitudes of the bridge in the transverse and vertical directions for various running speeds. It can clearly be observed that the dynamic responses of the bridge with track irregularity are considerably greater than those without. Also, the influence of track irregularity on the displacement and acceleration of the bridge is likely to increase with an increasing traveling speed, especially for the transverse acceleration response, whereas there is little variation when track irregularity is not considered. It is important to note that the response amplitude does not increase linearly with the traveling speed but exhibits some local peaks at traveling speeds (e.g., 30 km/h, 60 km/h), indicating slight resonance between the train and bridge due to the coincidence of the train’s passing frequency and the bridge’s natural frequencies. In addition, we can observe that the vertical displacement of the bridge resulting from the static load of the train is approximately 10.5 mm.
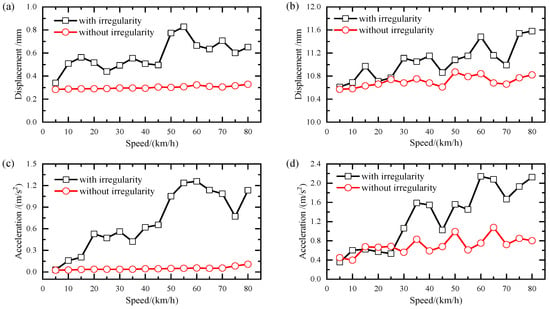
Figure 7.
Bridge response amplitudes at mid-span with and without track irregularities: (a) transverse displacement; (b) vertical displacement; (c) transverse acceleration; (d) vertical acceleration.
The obvious influence of track irregularities on train acceleration can also be observed in Figure 8. In the absence of track irregularities, the transverse train acceleration response remains steady as the moving speed increases but increases approximately linearly while taking track irregularity into account. Also, the vertical acceleration amplitudes of trains with track irregularities are greater than those without.
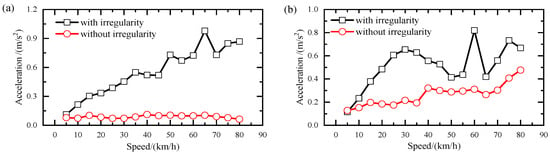
Figure 8.
Train acceleration amplitudes with and without track irregularities: (a) transverse; (b) vertical.
3.3. Passenger Load Effect
Due to the light weight of the car body, passenger capacity is another fundamental factor in determining the dynamic behavior of the straddle monorail train–bridge interaction system. This study examines three types of passenger load, including empty passenger, standard passenger, and overload passenger, which correspond to static mass increments of 0 kg, 7550 kg, and 10,550 kg, respectively. Figure 9 shows the displacement and acceleration responses of the bridge for various passenger loads. What can be seen is that there is a great increase in vertical bridge displacement on account of the increasing train weight resulting from the passenger loads, and the transverse displacement response of the bridge slightly rises to a higher level. Nevertheless, it should also be noted that the passenger load has almost no effect on the transverse acceleration, and only a slight increase is seen in the vertical acceleration amplitude. One potential explanation for this is that the effect of passenger load is equivalent to that of changing the train mass, which is effective for vertical bridge displacement but ineffective for dynamic bridge acceleration.
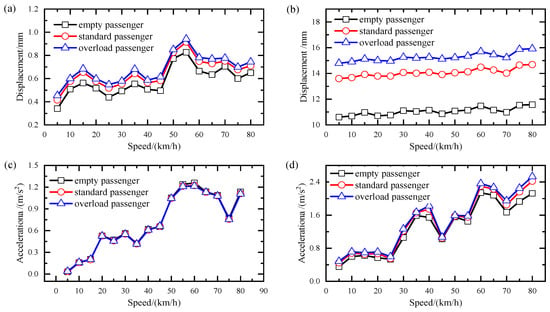
Figure 9.
Bridge response amplitudes at mid-span with different passenger loads: (a) transverse displacement; (b) vertical displacement; (c) transverse acceleration; (d) vertical acceleration.
Observably, with an increase in passenger capacity, the bridge displacement amplitude rises to a higher level. However, the passenger load has almost no effect on the bridge acceleration response. One potential explanation for this is that the effect of passenger load is equivalent to that of changing the train mass, which is effective for static bridge displacement but ineffective for dynamic bridge acceleration. On the other hand, the acceleration response of the car body is also sensitive to the passenger load. Also, it can be seen that the transverse and vertical acceleration amplitudes under empty passenger conditions are greater than those of the standard and overloaded passenger conditions on account of the small vibration mass of the car body.
Figure 10 shows the effect of passenger load on the acceleration response of trains. Observably, the transverse and vertical acceleration amplitudes under empty passenger conditions are greater than those of the standard and overloaded passenger conditions due to the small vibration mass of the car body.
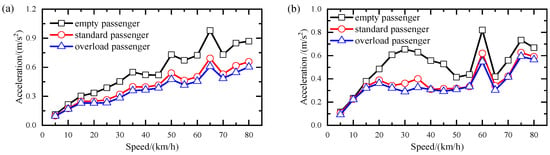
Figure 10.
Car body acceleration amplitudes at different passenger loads: (a) transverse; (b) vertical.
3.4. Impact Coefficients
When a train passes over a bridge, the bridge response is significantly amplified due to the impact effect resulting from the moving load. Thus, the impact coefficient, a dimensionless number, is usually used to describe the dynamic amplification effect of the moving train load on the bridge response, defined as the ratio of the maximum dynamic response to the maximum static response:
where Rdmax and Rsmax are the peak dynamic and static responses, respectively. In this study, the impact coefficient is calculated based on the vertical displacement at the mid-span.
Based on the vertical displacement response data, Figure 11 shows the calculated impact coefficient of the bridge with considerations of the effects of track irregularity and passenger load. Compared with prior studies [24], the impact coefficients (1.0–1.2) are within a similar range and tend to increase with some local fluctuations as train speed increases. Similarly to the bridge displacement and acceleration, the impact coefficient is much greater with track irregularities than without. However, it is possible for an increase in the load of passengers to slightly decrease the impact coefficient of the bridge. Also, the impact coefficient results reveal that there is no obvious resonance between the train and bridge in the transverse and vertical directions.
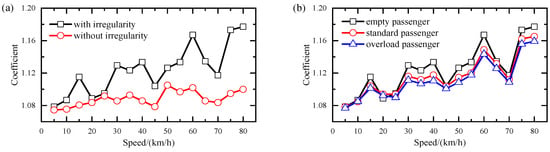
Figure 11.
Bridge impact coefficients under different conditions: (a) track irregularity; (b) passenger load.
3.5. Riding Comfort
An evaluation of passenger riding comfort is a crucial step in the dynamic interaction analysis of train–bridge systems. Nevertheless, there are no specific evaluation criteria for the comfort of straddle monorail trains. The Sperling index, commonly applied in evaluating the riding comfort of rolling stock [32,33], is utilized in this study to assess the traveling comfort of a straddle monorail train. For the i-th vibration frequency, the Sperling index can be written as follows:
where Ai is the acceleration amplitude of the car body at the position of the mass center in the i-th frequency fi; F(fi) is the frequency correction factor, which indicates the weight of frequency on passenger riding comfort and can be obtained from Table 4. Given that the acceleration of the car body is a random process composed of many frequency components, the overall Sperling index can be determined as follows:
where n is the total frequency number. Table 5 shows the evaluation criteria of riding comfort using the Sperling index.

Table 4.
The frequency correction factor of the Sperling index [32].

Table 5.
The evaluation criteria of the Sperling index [32].
Figure 12 illustrates the transverse and vertical Sperling indices for monorail trains with and without track irregularities at various train speeds. As would be expected, the track irregularity and traveling speed can increase the Sperling index of trains, implying that passenger comfort decreases accordingly. Furthermore, it can also be obtained that the transverse Sperling index is greater in comparison to the vertical Sperling index, which means that riding comfort is worse in the transverse direction for monorail trains. The overall Sperling index of trains ranges from 0 to 2.5, and the corresponding riding comfort does not exceed the “not uncomfortable feeling” level.
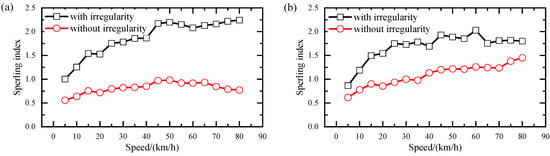
Figure 12.
Sperling index of trains with and without track irregularities: (a) transverse; (b) vertical.
Figure 13 shows the effect of passenger load on the Sperling index of trains. It is found that an increase in passenger load can reduce the Sperling index of trains in the transverse and vertical directions, hence enhancing the comfort of train riding. Under standard and overload passenger load conditions, the train comfort level mainly falls between “slight feeling” and “obvious feeling”. These results imply that the steel–concrete composite track beam can provide good riding comfort on the train.
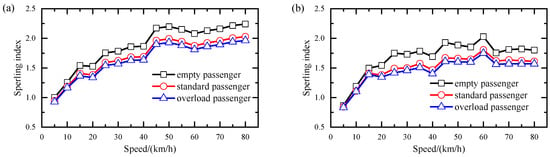
Figure 13.
Sperling index of trains with various passenger loads: (a) transverse; (b) vertical.
4. Conclusions and Further Works
This study presents a methodology for analyzing the dynamic behavior of the straddle monorail train–bridge system, where a multibody dynamic model of a monorail train with a single-axle bogie and a finite element model of a steel–concrete composite bridge are the first detailed derivations made to investigate the influence of track irregularity and passenger load on the response of the bridge and the riding comfort of the train. The following conclusions can be drawn:
(1) Track irregularity and train speed are crucial to the dynamic response of the train and bridge, which can result in a substantial increase in dynamic response, including displacement, acceleration, and impact coefficient. There is no obvious resonance between the train and the bridge in the transverse and vertical directions.
(2) The passenger load might increase the train mass, resulting in a greater vertical deflection of the bridge. In contrast, the acceleration value of the train diminishes as the number of passengers increases due to the decreased vibration mass.
(3) The transverse and vertical riding comfort decrease with track irregularity and travel speed but increase with passenger load. The overall riding comfort of a straddle monorail train traveling over a steel–concrete composite track beam does not exceed the “not uncomfortable feeling” level.
The outputs of this study imply that the steel–concrete composite bridge can allow for the good dynamic behavior and riding comfort of the train, which has great potential and advantages in the application of the straddle monorail transportation system. The numerical results can also provide important scientific insights as well as significant practical applications for the steel–concrete composite bridge in the straddle monorail. Nevertheless, it should be noted that the results are only based on the numerical calculation. Our further works will focus on the following: (1) Conducting scaled model experiments and field tests to validate the numerical model under real-world conditions, including measurements of bridge vibrations and train accelerations. (2) Investigating the effects of complex environmental loads (e.g., crosswinds, earthquakes) on the steel–concrete composite bridge–train system, particularly for long-span configurations. (3) Optimizing the design parameters of steel–concrete composite bridges (e.g., span length, section dimensions) to balance dynamic performance and construction costs for monorail applications.
Author Contributions
Methodology, Z.Y.; Software, Z.L.; Validation, Z.Y.; Formal analysis, Z.Z.; Investigation, Z.Y. and Z.Z.; Data curation, Z.L.; Writing—original draft, Z.Y.; Writing—review & editing, Z.L.; Supervision, Z.L.; Project administration, Z.Y.; Funding acquisition, Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Tertiary Education Scientific research project of Guangzhou Municipal Education Bureau (Grant No. 2024312488), National Natural Science Foundation of China (Grant No. 52208309) and Scientific Research Platforms and Projects of Guangdong Provincial Education Department (Grant No. 2024KTSCX297).
Data Availability Statement
The data supporting the results of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
No potential conflicts of interest are reported by the authors.
References
- Bhattacharjee, S.; Goetz, A.R. The rail transit system and land use change in the Denver metro region. J. Transp. Geogr. 2016, 54, 440–450. [Google Scholar] [CrossRef]
- He, X. Application and prospect of straddle monorail transit system in China. Urban Rail Transit 2015, 1, 26–34. [Google Scholar] [CrossRef]
- Gao, Q.; Cui, K.; Li, Z.; Li, Y. Numerical investigation of the dynamic performance and riding comfort of a straddle-type monorail subjected to moving trains. Appl. Sci. 2020, 10, 5258. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, E.; Chen, Z. Dynamic response analysis of the straddle-type monorail bridge–vehicle coupling system. Urban Rail Transit 2017, 3, 172–181. [Google Scholar] [CrossRef]
- Zhai, W.M.; Cai, C.B. Train/track/bridge dynamic interactions: Simulation and applications. Veh. Syst. Dyn. 2002, 37 (Suppl. S1), 653–665. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, N. Dynamic analysis of railway bridge under high-speed trains. Comput. Struct. 2005, 83, 1891–1901. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, H.; Guo, W.; De Roeck, G. A vehicle–bridge linear interaction model and its validation. Int. J. Struct. Stab. Dyn. 2010, 10, 335–361. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Lin, J.H.; Zhang, Y.H.; Howson, W.P.; Williams, F.W. Non-stationary random vibration analysis of three-dimensional train–bridge systems. Veh. Syst. Dyn. 2010, 48, 457–480. [Google Scholar] [CrossRef]
- Mao, J.; Yu, Z.; Xiao, Y.; Jin, C.; Bai, Y. Random dynamic analysis of a train-bridge coupled system involving random system parameters based on probability density evolution method. Probabilistic Eng. Mech. 2016, 46, 48–61. [Google Scholar] [CrossRef]
- Carbonari, S.; Nicoletti, V.; Martini, R.; Gara, F. Dynamics of bridges during proof load tests and determination of mass-normalized mode shapes from OMA. Eng. Struct. 2024, 310, 118111. [Google Scholar] [CrossRef]
- Du, X.T.; Xu, Y.L.; Xia, H. Dynamic interaction of bridge–train system under non-uniform seismic ground motion. Earthq. Eng. Struct. Dyn. 2012, 41, 139–157. [Google Scholar] [CrossRef]
- Guo, X.; Tang, J. Effects of wind barrier porosity on the coupled vibration of a train-bridge system in a crosswind. Struct. Eng. Int. 2019, 29, 268–275. [Google Scholar] [CrossRef]
- Li, Y.; Qiang, S.; Liao, H.; Xu, Y.L. Dynamics of wind–rail vehicle–bridge systems. J. Wind Eng. Ind. Aerodyn. 2005, 93, 483–507. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Barbosa, D.; Carvalho, H.; Calçada, R. Dynamic effects on a train-bridge system caused by stochastically generated turbulent wind fields. Eng. Struct. 2020, 211, 110430. [Google Scholar] [CrossRef]
- Xia, C.Y.; Xia, H.; De Roeck, G. Dynamic response of a train–bridge system under collision loads and running safety evaluation of high-speed trains. Comput. Struct. 2014, 140, 23–38. [Google Scholar] [CrossRef]
- Xiang, P.; Ma, H.; Zhao, H.; Jiang, L.; Xu, S.; Liu, X. Safety analysis of train-track-bridge coupled braking system under earthquake. Structures 2023, 53, 1519–1529. [Google Scholar] [CrossRef]
- Yao, Z.; Zhang, N.; Zhu, M.; Li, X. Dynamic Interaction Analysis and Running Safety Assessment of the Wind–Train–Bridge System Considering the Moving Train’s Aerodynamic Coupling with Crosswind. Int. J. Struct. Stab. Dyn. 2023, 23, 2350173. [Google Scholar] [CrossRef]
- Žitný, J.; Ryjáček, P.; Sýkora, M.; Pospíšil, S.; Hračov, S. Probabilistic Assessment of the Equilibrium of a Steel Railway Bridge Based on Wind Tunnel and Traffic Records. Struct. Eng. Int. 2023, 34, 34–44. [Google Scholar] [CrossRef]
- Lee, C.H.; Kim, C.W.; Kawatani, M.; Nishimura, N.; Kamizono, T. Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains. Eng. Struct. 2005, 27, 1999–2013. [Google Scholar] [CrossRef]
- Lee, C.H.; Kawatani, M.; Kim, C.W.; Nishimura, N.; Kobayashi, Y. Dynamic response of a monorail steel bridge under a moving train. J. Sound Vib. 2006, 294, 562–579. [Google Scholar] [CrossRef]
- Kim, C.W.; Kawatani, M. Effect of train dynamics on seismic response of steel monorail bridges under moderate ground motion. Earthq. Eng. Struct. Dyn. 2006, 35, 1225–1245. [Google Scholar] [CrossRef]
- Naeimi, M.; Tatari, M.; Esmaeilzadeh, A.; Mehrali, M. Dynamic interaction of the monorail–bridge system using a combined finite element multibody-based model. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2015, 229, 132–151. [Google Scholar] [CrossRef]
- Zhang, R.; Ji, Y.; Ren, L. Pre-load on the guiding/stabilizing wheels and the critical lateral force of a straddle-type monorail vehicle. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 160–169. [Google Scholar] [CrossRef]
- Gou, H.; Zhou, W.; Yang, C.; Bao, Y.; Pu, Q. Dynamic response of a long-span concrete-filled steel tube tied arch bridge and the riding comfort of monorail trains. Appl. Sci. 2018, 8, 650. [Google Scholar] [CrossRef]
- Yang, Z.; Du, Z.; Xu, Z.; Zhou, J.; Hou, Z. Research on dynamic behavior of train dynamic model of straddle-type monorail. Noise Vib. Worldw. 2020, 51, 195–207. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhong, W.; Wu, P.; Zeng, J.; Zhang, Y.; Wang, S. Prediction of wheel wear of different types of articulated monorail based on co-simulation of MATLAB and UM software. Adv. Mech. Eng. 2019, 11, 1687814019856841. [Google Scholar] [CrossRef]
- Zhou, J.; Du, Z.; Yang, Z.; Xu, Z. Dynamic parameters optimization of straddle-type monorail vehicles based multiobjective collaborative optimization algorithm. Veh. Syst. Dyn. 2020, 58, 357–376. [Google Scholar] [CrossRef]
- Sirisonthi, A.; Suparp, S.; Joyklad, P.; Hussain, Q.; Julphunthong, P. Experimental study of the load-deformation behaviour of the precast post-tensioned continuous girder for straddle monorail: Full-scale load test under service and ultimate loading conditions. Case Stud. Constr. Mater. 2021, 15, e00666. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, C.; Deng, J.; Zhang, J.; Zhang, L. A co-simulation approach for straddle monorail vehicle–bridge interaction subjected to nonlinear excitation. Adv. Eng. Softw. 2023, 180, 103458. [Google Scholar] [CrossRef]
- Chang, K.C.; Kim, C.W.; Borjigin, S. Variability in bridge frequency induced by a parked vehicle. Smart Struct. Syst. 2014, 13, 755–773. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, H. Dynamic analysis of coupled vehicle–bridge system based on inter-system iteration method. Comput. Struct. 2013, 114, 26–34. [Google Scholar] [CrossRef]
- GB/T-5599-2019; Specification for Dynamic Performance Assessment and Testing Verification of Rolling Stock. Standardization Administration: Beijing, China, 2019.
- Wu, Z.; Zhang, N.; Yao, J.; Poliakov, V. Analysis of Train Car-Body Comfort Zonal Distribution by Random Vibration Method. Appl. Sci. 2022, 12, 7442. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).