Analysis of Disturbance and Safety Risk Assessment of Shallow-Buried Pressure Pipelines Utilizing the Shield Tunneling Method
Abstract
1. Introduction
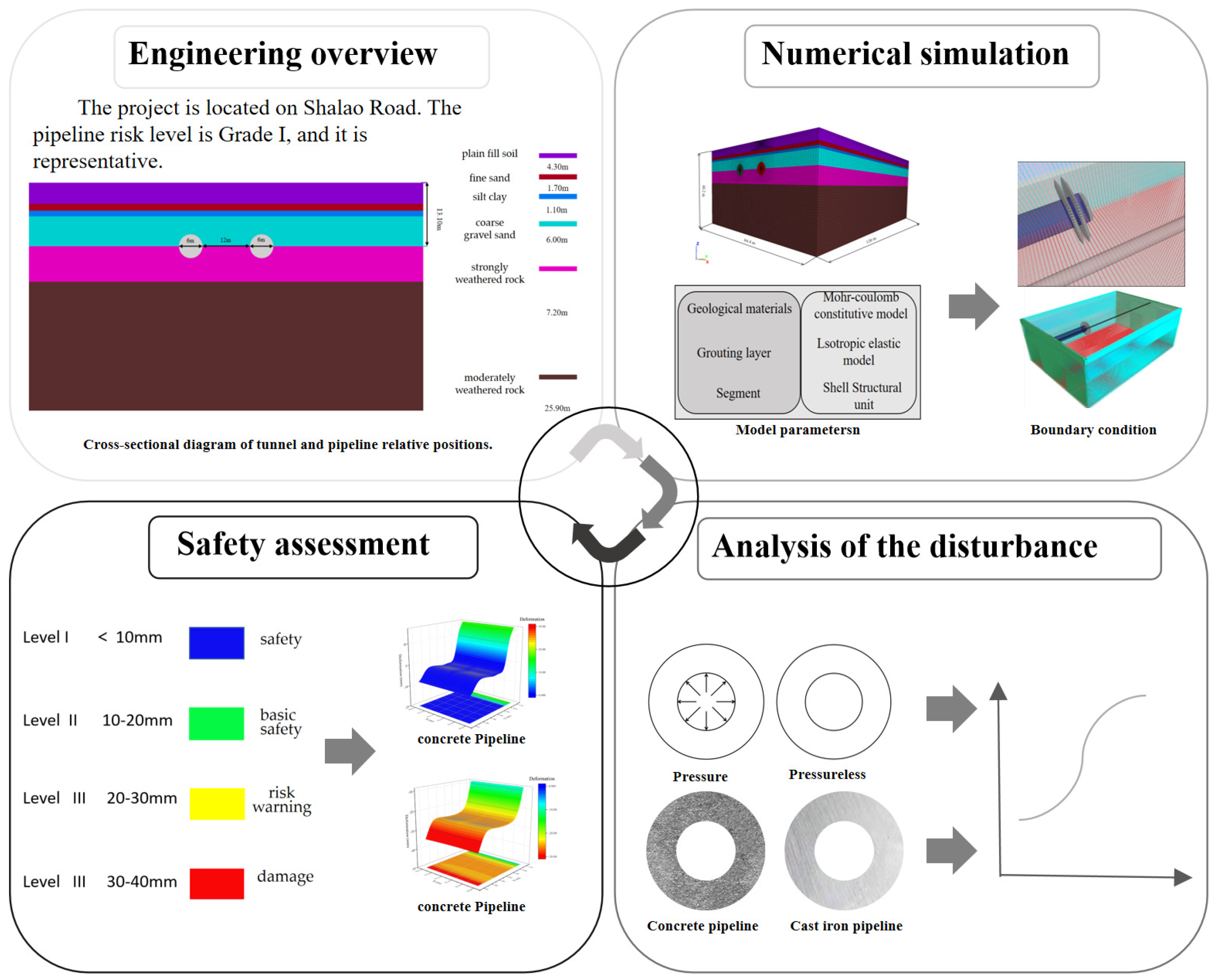
2. Numerical Simulation Methods
2.1. Engineering Overview
2.2. Model Parameters
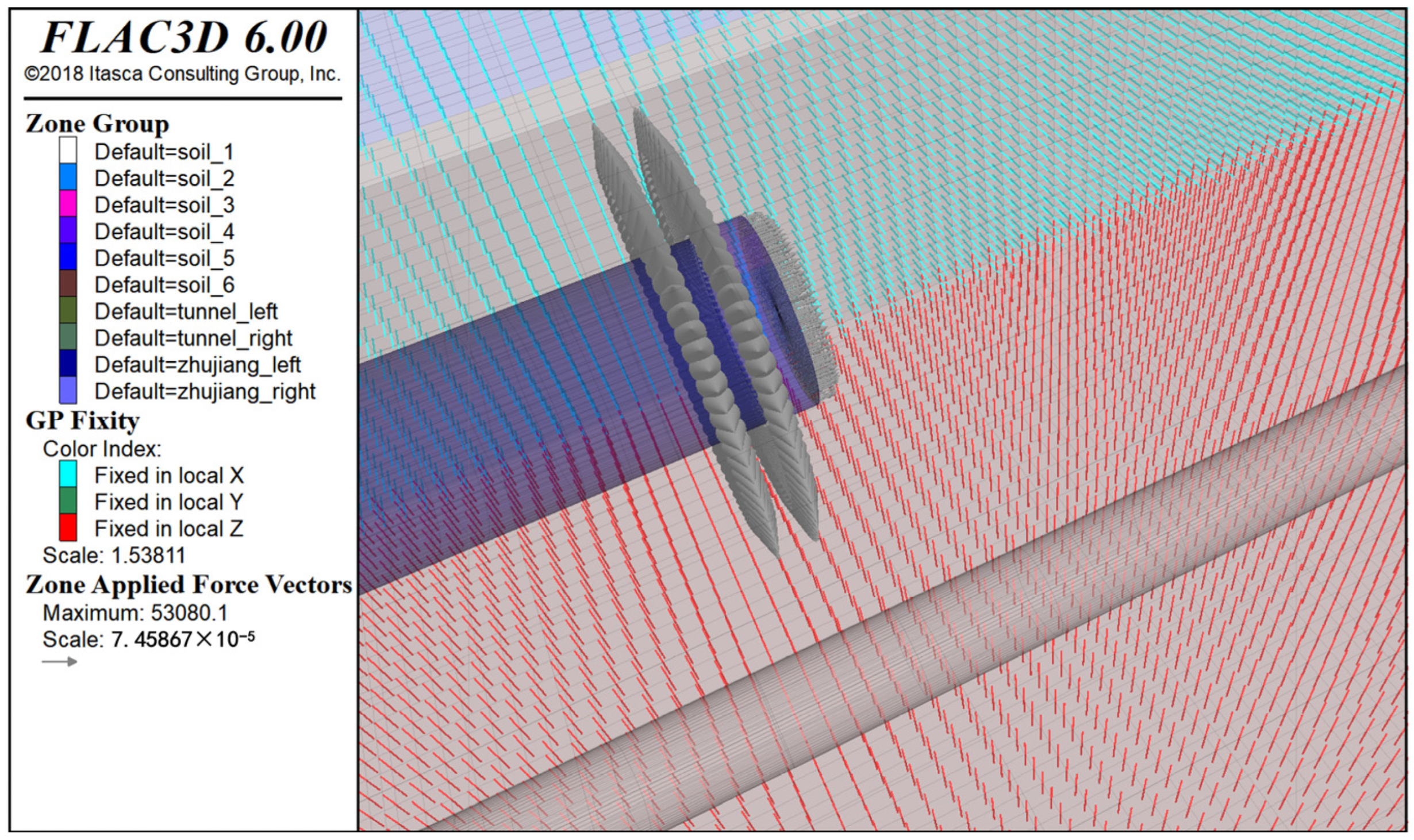
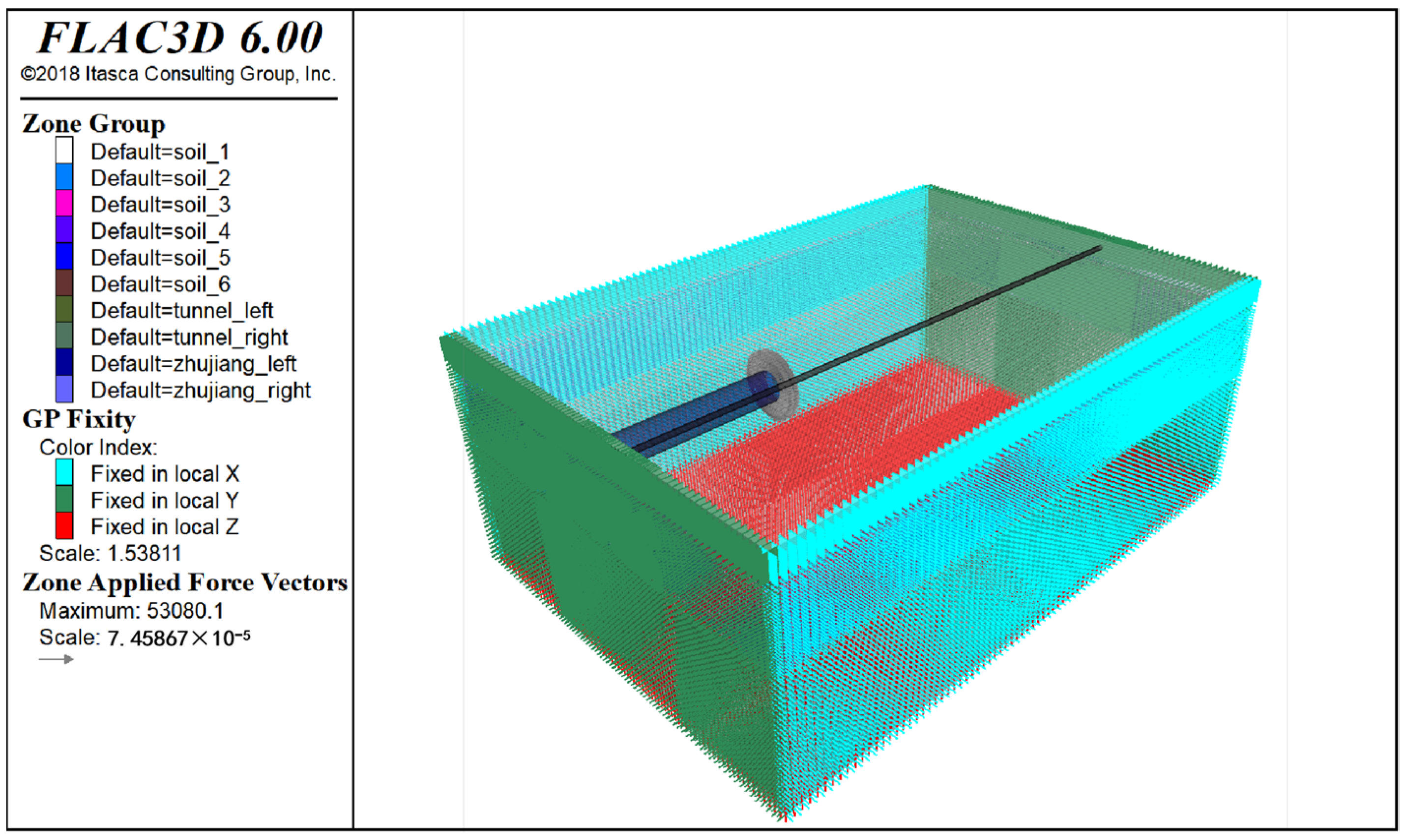
2.3. Load Boundary Conditions of the Model
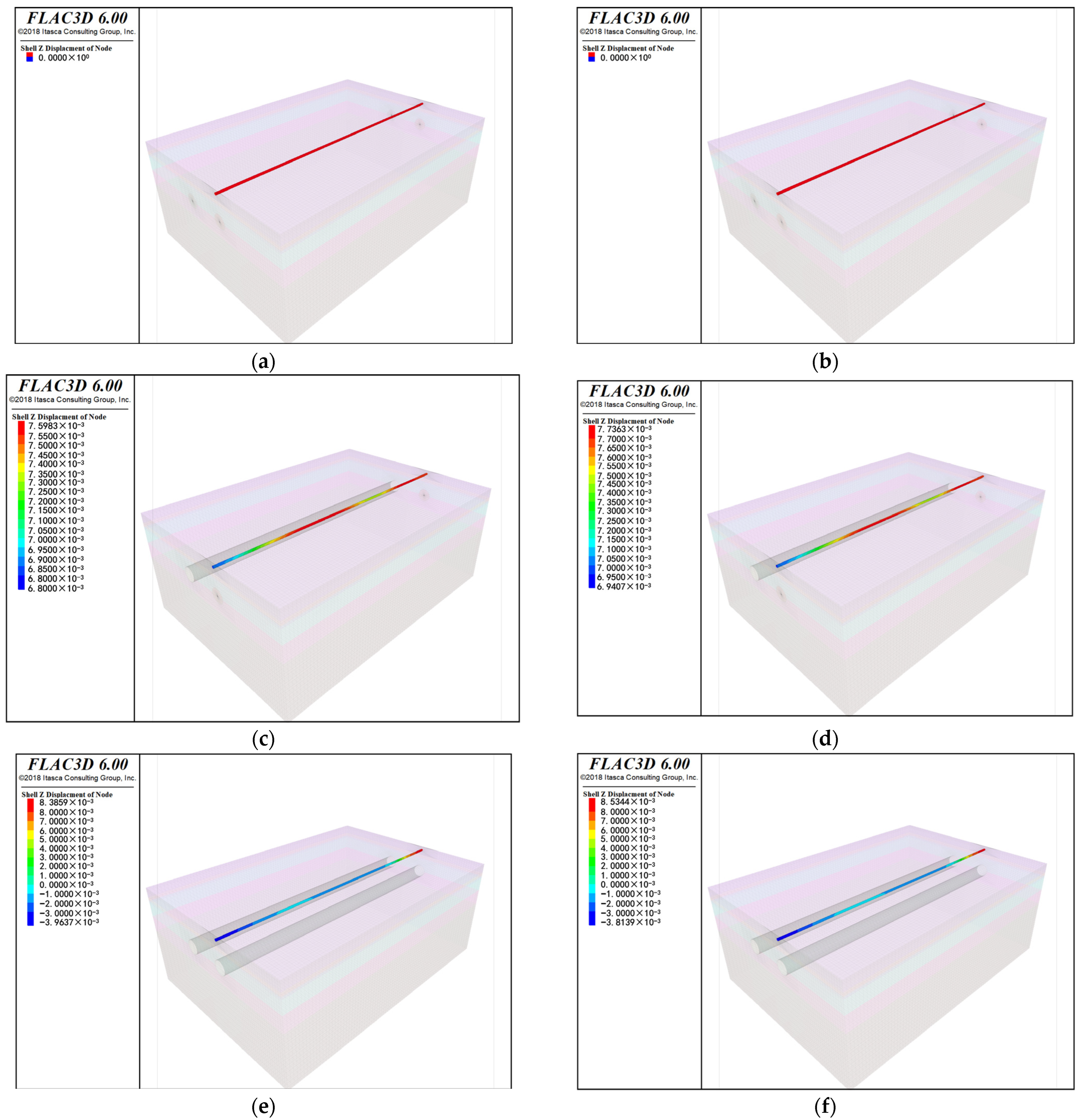
3. Disturbance of Pressure Pipelines by Shield Tunneling Construction
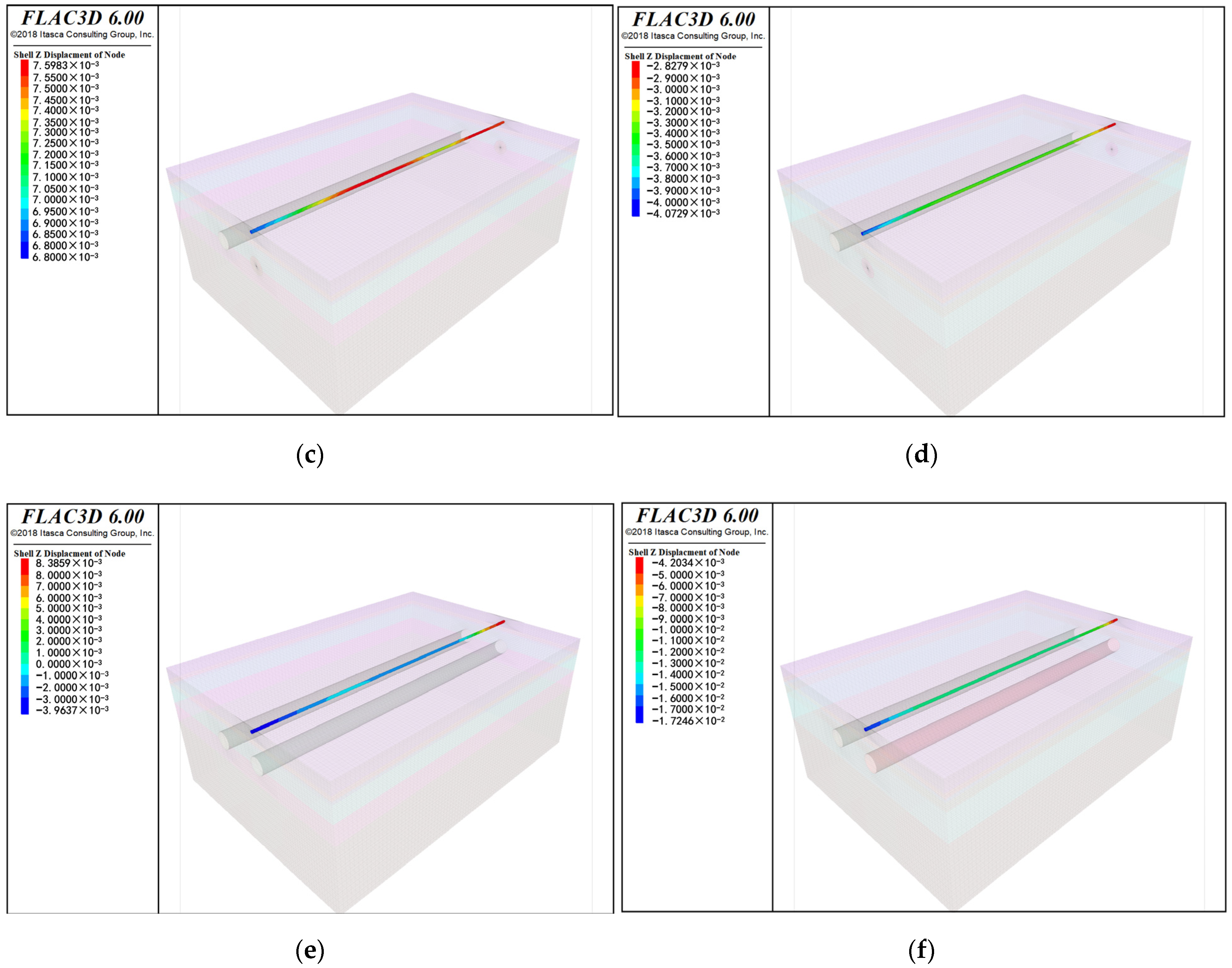
3.1. Analysis of Disturbance to Pressure Pipelines by Shield Tunneling Construction
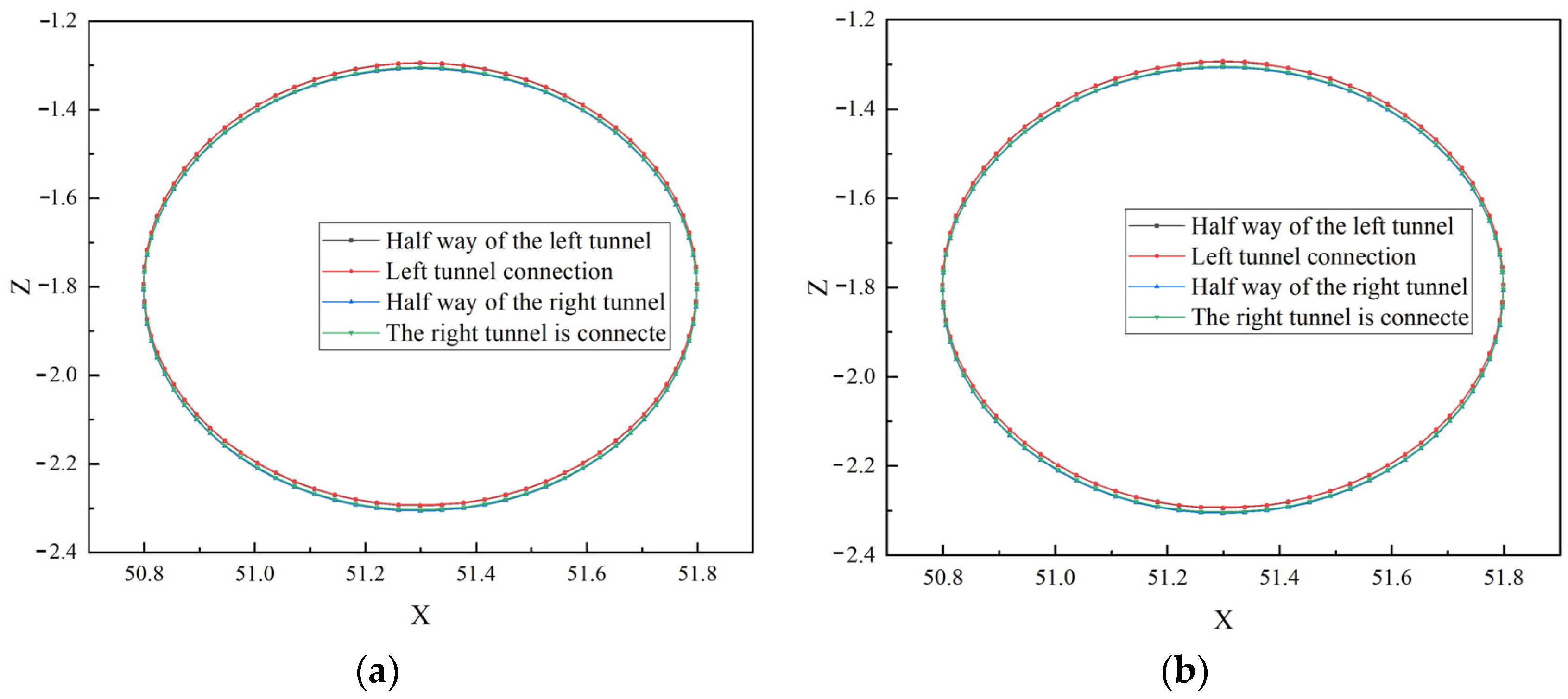
3.2. Analysis of the Disturbance Caused by Shield Tunneling to Pipelines of Different Materials
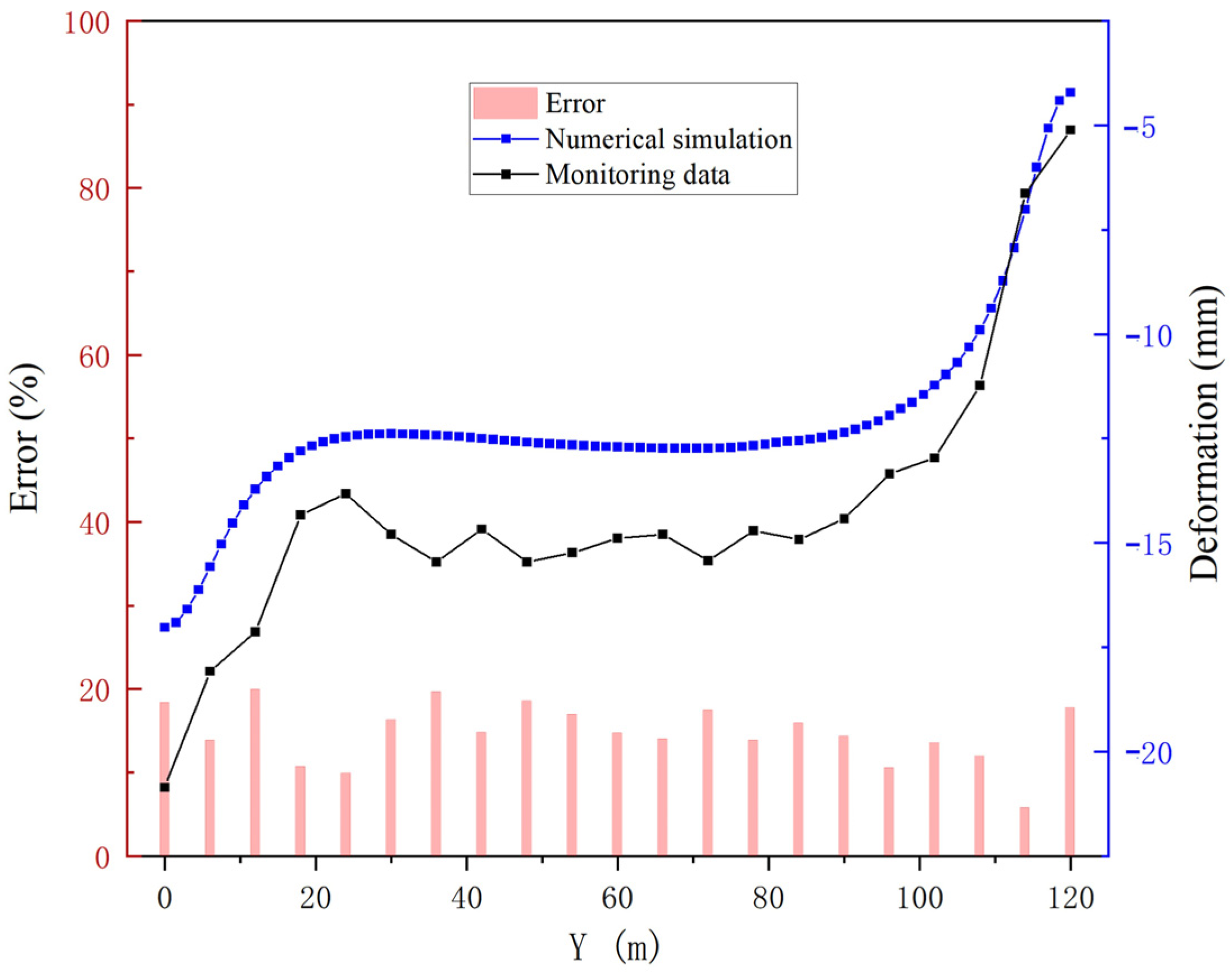
3.3. Model Validation and Error Analysis
4. Safety Risk Assessment of Shallow-Buried Pressure Pipelines Using the Shield Tunneling Method
4.1. Classification of Pipeline Safety Risk Levels
4.2. Safety Risk Assessment of Pipelines During Shield Tunneling Construction
5. Conclusions
- ①
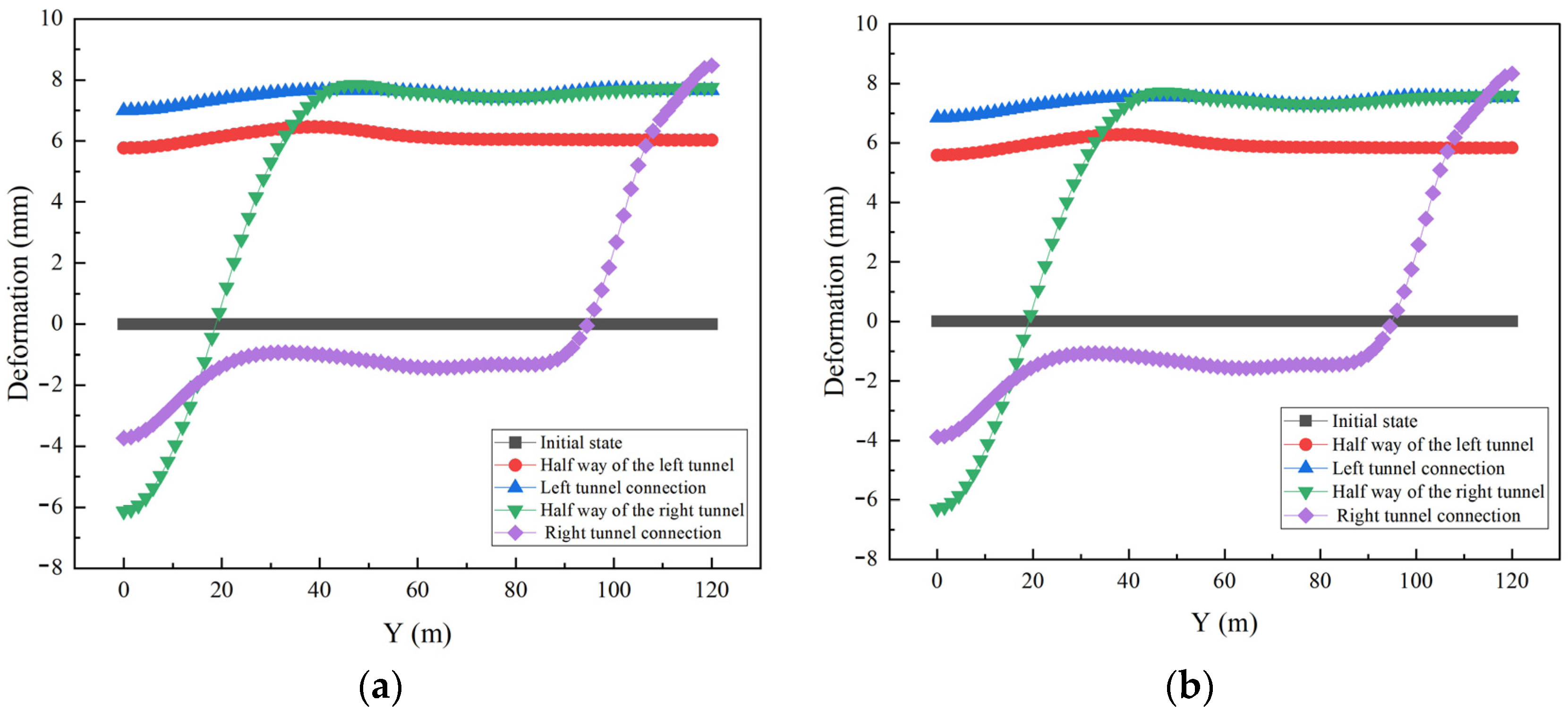
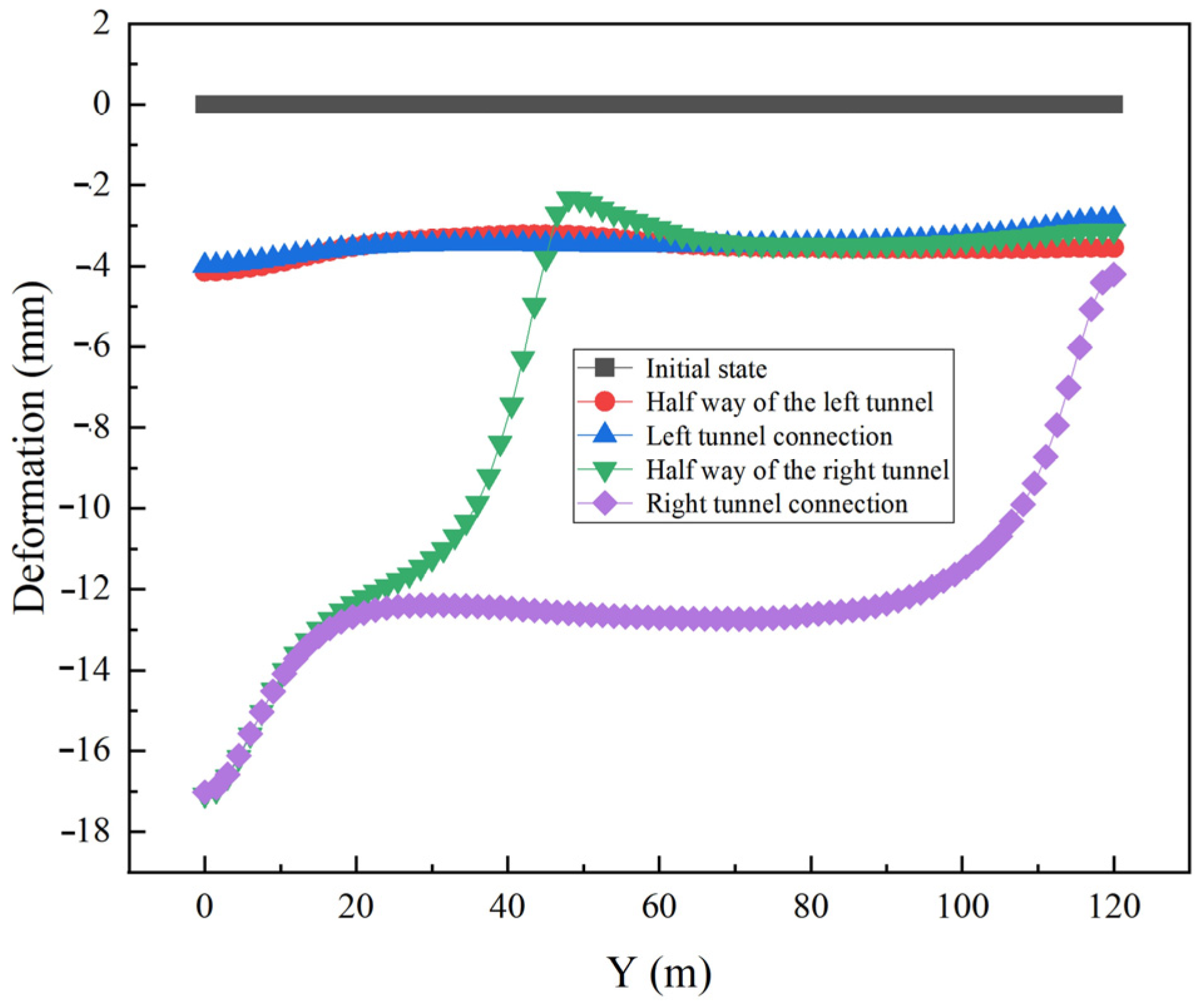
- The presence or pressure less does not cause variations in the vertical deformation of the pipeline during the tunneling process. During the entire excavation process of the left tunnel, the pipeline experiences an overall upward deformation, with the amount of deformation gradually decreasing as excavation progresses; at the half way of the right tunnel excavation, a significant downward deformation of the pipeline can be observed, with the deformation extending gradually smaller along the pipeline, and deformation stopping behind the tunnel face, indicating a clear lag effect in the pipeline deformation. When the excavation of the right tunnel is completed, the pipeline deformation in the 0 m to 90 m area is basically stable, while in the 90 m to 120 m range, the pipeline gradually transitions from upward deformation to downward deformation. The maximum deformation of the cast iron pipeline does not occur at the moment when the shield tunneling is completed, but rather during the tunneling process, close to the position of the tunnel’s starting shaft.
- ②
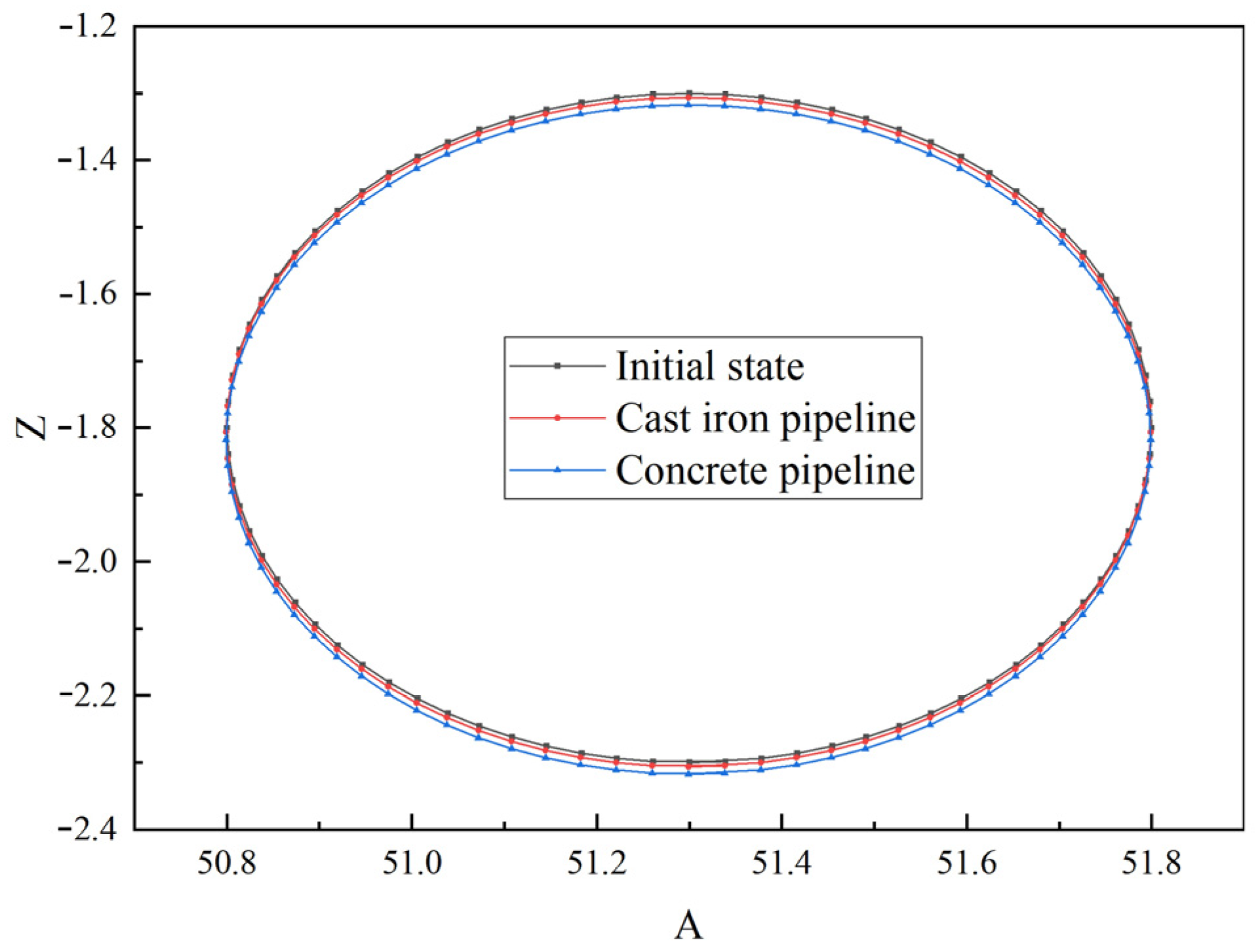
- Sensitivity of pipeline materials to shield tunneling is quite high. Both axial and lateral deformations of the pipeline show significant variations in concrete pipelines. The main reason for this phenomenon is that cast iron pipelines have better stability and can withstand larger disturbances, while the stiffness of concrete pipelines is much lower than that of cast iron pipelines, making them more susceptible to the impacts of shield tunnel construction.
- ③
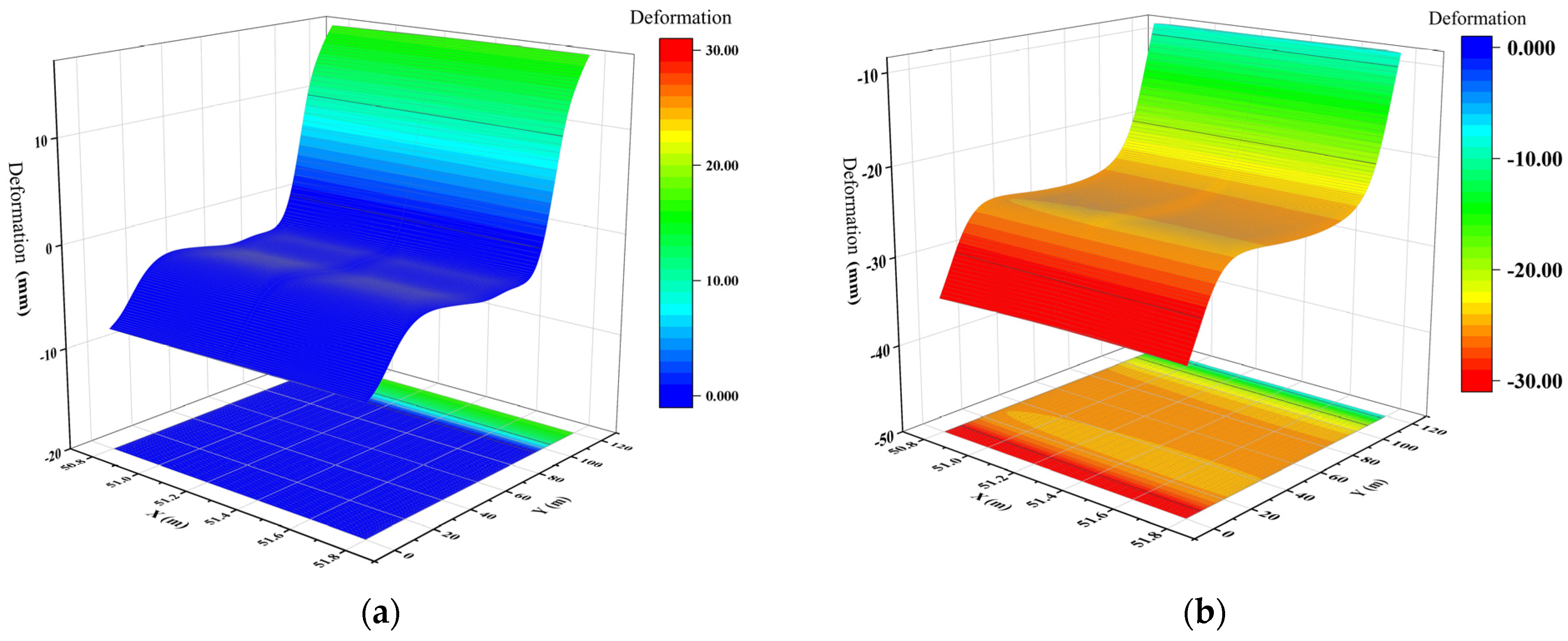
- By analyzing and discussing the literature and local norms, safety risk levels of pipelines can be determined using pipeline deformation values as criteria. A deformation of 0 to 10 mm is classified as a safe state (Level I), 10 to 20 mm as a basic safe state (Level II), 20 to 30 mm as a risk warning zone (Level III), and greater than 30 mm as a damage zone (Level IV). Corresponding safety measures for each risk level should also be proposed.
- ④
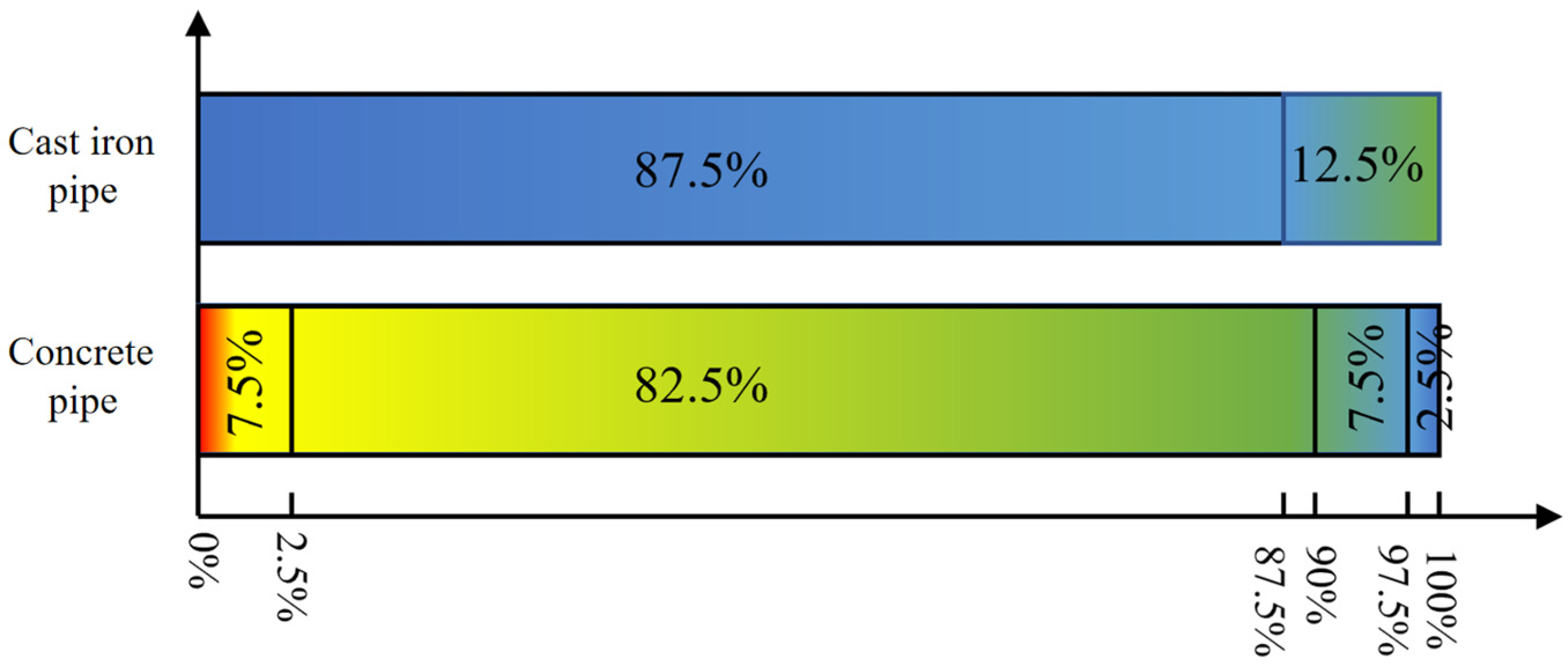
- Through the assessment of the pipelines on site, it is found that the safety level of cast iron pipelines is I and II along the pipeline extension direction, accounting for 87.5% and 12.5% respectively, and the pipelines at the start of the shield have the highest safety. The safety level of concrete pipelines is Class IV, Class III, Class II, and Class I along the pipeline extension direction, accounting for 7.5%, 82.5%, 7.5% and 2.5% respectively, and the safety of pipelines at the beginning of the shield is the lowest.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mu, H.X.; Feng, K.; Guo, W.Q.; Yang, S.; Zhang, L. Study on the Structural Mechanical Behavior and Failure Characteristics of Ultra-Large Diameter Shield Tunnel Segments. Mod. Tunn. Technol. 2025, 62, 125–134. [Google Scholar] [CrossRef]
- Liu, Y.B.; Zhang, J.E. Experience in Operation and Maintenance Support of Urban Side Sewage Systems for the Hangzhou Asian Games. Water Supply Drain. 2024, 60, 45–52+57. [Google Scholar] [CrossRef]
- Xu, J.B.; Wu, X.; Qiao, W.; Wang, S.; Chen, X.; Zhao, D.; Zeng, X.; Shu, S. Life cycle carbon emission assessment for ecological protection slopes: Focus on construction and maintenance phases. J. Clean. Prod. 2025, 497, 145174. [Google Scholar] [CrossRef]
- Tian, Y.; Wei, L.F.; Fu, Y.P.; Fang, Y.; Liu, L. Research on the Calculation Method of Pipeline Settlement and Pipeline-Soil Displacement Law during the Construction of Slurry Shield Near Underground Pipelines. China Saf. Prod. Sci. Technol. 2023, 19, 31–38. [Google Scholar]
- Zhang, Z.G.; Jiang, K.M.; Wang, Z.W.; Xing, L.; Wei, G.; Ding, Z. Theoretical Analysis of Longitudinal Deformation of Existing Tunnels Induced by Excavation of Foundation Pits Considering the Pasternak Foundation Model. Tunn. Constr. 2020, 40, 57–67. [Google Scholar]
- Feng, X.; Yang, X.; Li, Y.; Ding, X. Influence of Underground Tunnel Excavation on Upper-level Existing Pipelines. Adv. Civ. Eng. 2022, 2022, 5469345. [Google Scholar] [CrossRef]
- Zhang, D.M.; Huang, Z.K.; Li, Z.L.; Zong, X.; Zhang, D.M. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath. Comput. Geotech. 2019, 108, 197–211. [Google Scholar] [CrossRef]
- Bondarev, E.A.; Rozhin, I.I.; Argunova, K.K. Generalized mathematical model of hydrate formation in gas pipelines. J. Appl. Mech. Tech. Phys. 2019, 60, 503–509. [Google Scholar] [CrossRef]
- Huang, X.K.; Wang, W.D.; Zhu, D.Y.; Lu, K.L. Model Test Study on the Impact of Metro Shield Construction on Underground Pipelines. J. Hefei Univ. Technol. 2018, 41, 805–811. [Google Scholar]
- Hu, Y.; Yao, A.J.; Zhang, J.T.; Guo, H.F. Experimental and Numerical Analysis of the Impact of Metro Shield Construction on Overlying Parallel Rain and Sewage Pipelines. Tunn. Constr. 2018, 38, 797–804. [Google Scholar]
- Peng, H.; Liu, Y.; Chen, H. Creep rupture assessment of cyclically heated 3D pressure pipelines with volumetric defects using a direct numerical approach. Int. J. Press. Vessel. Pip. 2021, 192, 104387. [Google Scholar] [CrossRef]
- Deng, H.; Fu, H.; Shi, Y.; Huang, Z.; Huang, Q. Analysis of asymmetrical deformation of surface and oblique pipeline caused by shield tunneling along curved section. Symmetry 2021, 13, 2396. [Google Scholar] [CrossRef]
- Hu, B.; Li, X.; Huang, D. Safety risk analysis and protective control of existing pipelines affected by deep pit excavation in metro construction. Model. Simul. Eng. 2019, 2019, 3643808. [Google Scholar] [CrossRef]
- Zhao, S.W.; Li, X.L.; Li, X.; Chen, L.-G. Analysis of pipeline deformation caused by shield tunnel excavation that obliquely crosses existing pipelines. Arab. J. Geosci. 2022, 15, 227. [Google Scholar] [CrossRef]
- Shen, J.; Yan, L.; Fu, J.Y.; Yang, J.S. Impact Analysis of Parallel Underpassing Gas Pipelines by Stacked Shield Tunnels. J. Undergr. Space Eng. 2021, 17, 449–456. [Google Scholar]
- Chen, Z.M.; Fan, C.H.; Wen, Y.; Huang, L.X.; Ren, Y. Study on Settlement Deformation and Control Standards of Superficially Buried Tunnels Underpassing Pipelines. Highways 2021, 66, 371–378. [Google Scholar]
- Sun, L.W.; Fang, Y.X.; Shen, W. Analysis of the Instability Mechanism of Shield Tunneling Face Underpassing Existing Pipelines. J. Undergr. Space Eng. 2020, 16, 278–284. [Google Scholar]
- Wang, X.Y.; Lei, K.; Wang, T.; Zhang, J. Settlement Prediction of Existing Pipeline Engineering Underneath Stations Using the Bored Pile Method. J. Civ. Eng. 2021, 54, 65–75. [Google Scholar] [CrossRef]
- Ren, Y.R.; Wang, X.H. ABAQUS Influence of Trench shield construction on adjacent pipelines in subway. Civ. Eng. 2023, 12, 559–564. [Google Scholar]
- Zhang, K.; Chavez Torres, J.L.; Zang, Z. Numerical analysis of pipeline settlement induced by tunneling. Adv. Civ. Eng. 2019, 2019, 4761904. [Google Scholar] [CrossRef]
- Sun, A.J. Research on surface settlement and neighbouring pipeline deformation law of double-line shield tunnel construction. Shijiazhuang Railw. Univ. 2023. [Google Scholar] [CrossRef]
- Guan, X.M.; Zhang, L.; Wang, L.M.; Fu, H.X.; Yu, D.M.; Chen, G.; Ding, Y.; Jiang, W.L. Characteristics of Blasting Vibration and Safety Standards for Tunnels Close to Underpassing Pipelines. J. Cent. South Univ. 2019, 50, 2870–2885. [Google Scholar]
- Wu, W.Y.; Sun, Y.K.; Zhang, T.Q. Analysis on the influence of shield tunnel construction on nearby underground pipelines. China Railw. Sci. 2008, 58–62. [Google Scholar]
- Weng, G.Y.; Ding, J.F.; Cao, J.T.; Hui, Y. Experiment and numerical simulation of stress detection for oil and gas pipelines based on magnetic stress coupling of pipeline steel. Structures 2023, 55, 2478–2490. [Google Scholar] [CrossRef]
- Cen, K.; Chen, S.Y.; Chen, K.; Li, Q.; Zhu, L.; Shen, J. Application of super-efficient SBM-Malmquist model in the evaluation of gas pipeline integrity management effectiveness. J. Saf. Environ. 2024, 24, 3144–3153. [Google Scholar]
- Tang, L.Y.; Wei, R.R.; Wang, F.; Zhang, W.Y.; Bie, Q.; Tian, Z.J.; Mei, W. Construction of safety evaluation index system for high steel grade pipelines. Oil Gas Storage Transp. 2023, 42, 1137–1148. [Google Scholar]
- Wang, Y.; Wang, K.X. Study on Safety Control of Pipeline with Rigid Interface under Metro Tunnel Excavation. China Saf. Sci. J. 2021, 31, 97–103. [Google Scholar]
- Liu, C.Z.; Su, Y.H. Deformation pattern of pipeline caused by shield construction and safety risk assessment. J. Railw. Sci. Eng. 2020, 17, 2882–2891. [Google Scholar]
- Ni, Z.H.; Feng, Q.Q.; Huang, W.Z. Application of distributed optical fiber sensing technology in structural health monitoring of municipal drainage pipes. China Munic. Eng. 2024, 22, 56–58+64+160+161. [Google Scholar]
- Bao, C.; Hao, H.; Li, Z. Vibration-based structural health monitoring of offshore pipelines: Numerical and experimental study. Struct. Control Health Monit. 2013, 20, 769–788. [Google Scholar] [CrossRef]
- Li, L.; Ma, H.; Jing, H. Vertical displacement monitoring and safety evaluation of oil pipelines in permafrost region. J. Geosci. Environ. Prot. 2018, 6, 247–256. [Google Scholar] [CrossRef][Green Version]
- Han, J.Y.; Zhao, M.Q.; Li, L.Y. Mechanical Response and Parameter Analysis of Shield Tunnelling Through Existing Steel Pipelines. J. Harbin Eng. Univ. 2025, 1–9. [Google Scholar]
- Su, H.; Zhao, W.; Zhu, L. Mechanical Characteristics of Enclosing Edge Pile Construction for Shield Structure Penetrating Existing Metro Station. Highway 2025, 417–425. [Google Scholar]
- Huang, K.; Fu, T.J.; Wang, K.W.; Liu, R.; Zhou, J. Analysis on the influence of shield tunnel construction on the overlying parallel pipelines. Highw. Mot. Transp. 2025, 41, 118–123. [Google Scholar] [CrossRef]
- Li, Y.K.; Han, T.H.; Zhao, S.X.; Chang, J.; Peng, Q. Study on Stress and Deformation Effects of Pressure Pipeline Laying Methods Based on ABAQUS. Pipeline Technol. Equip. 2023, 1–10. [Google Scholar] [CrossRef]
- Hu, J.L.; Zhao, Y.X.; Zhou, Y.X.; Leng, F.; Du, X. Dynamic properties and constitutive model fitting analysis of geopolymer stabilized soil. Mater. Bull. 2025, 1–15. [Google Scholar]
- Xu, P.; Zhang, A.; Zhang, R.; Wang, X. Study on the reinforcement effect of MJS for pipeline underpass with large large-section rectangular pipe. J. Undergr. Space Eng. 2024, 20, 463–471. [Google Scholar] [CrossRef]
- Niu, D.C.; Zhang, L.R.; Jia, J.; Gao, W.; Lu, Y.; Qiu, T. Dynamic flutter deformation test of wind turbine blades under off-balance conditions. Renew. Energy 2024, 42, 1491–1497. [Google Scholar]
- Guo, Y.H.; Li, S.Y. Safety study of tunnel double shield-dark excavation under close distance through lake bottom. J. Undergr. Space Eng. 2024, 20, 900–906. [Google Scholar] [CrossRef]
- Wang, Y. Analysis of influencing factors on subway construction in sandy and silty soil layers based on FLAC3D. J. Liaoning Tech. Univ. 2024, 43, 179–186. [Google Scholar]
- Si, X.D.; Xiao, W.B.; Zheng, Q.P. Study on deformation law of existing highway subgrade under porous tunnel. Highway 2023, 68, 29–39. [Google Scholar]
- Huang, Z.Q.; Liu, C.; Zhang, N.; Wang, G.L.; Yu, F.L. Impact of Reverse Construction of Deep Foundation Pit Cover in Water-Rich Sand Layer on the Surrounding Environment. Urban Rail Transit Res. 2024, 27, 188–195. [Google Scholar]
- Wu, X.G.; Zeng, T.M.; Zhang, L.M.; Song, R.X. Research on safety risk management of pipeline near subway construction. J. Railw. Eng. 2013, 127–132. [Google Scholar]
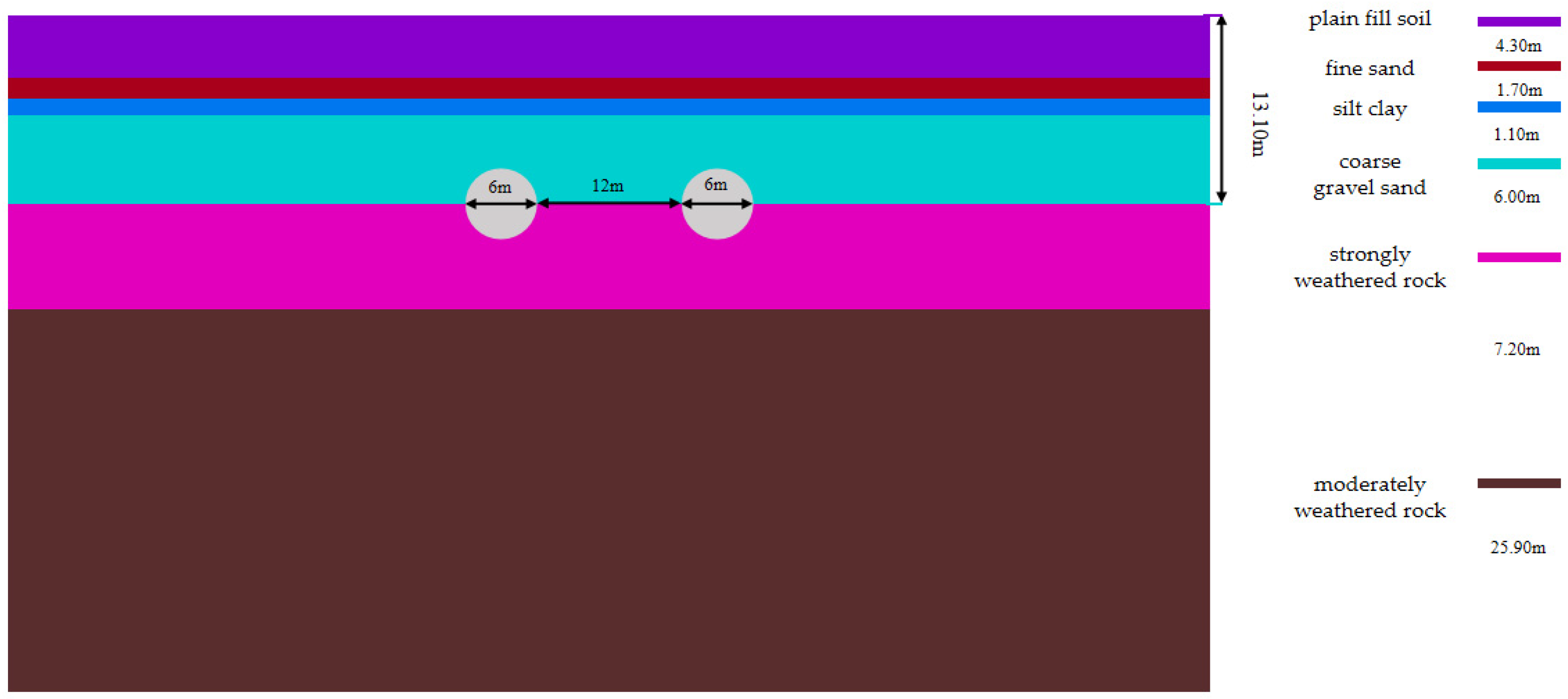







| Stratum | Elastic Modulus (106 Pa) | Poisson’s Ratio (μ) | Density (kg·m−3) | Bulk Modulus (K/MPa) | Shear Modulus (G/MPa) | C (kPa) | Φ (°) | Soil Layer Thickness (m) |
|---|---|---|---|---|---|---|---|---|
| plain fill soil | 20 | 0.35 | 1800 | 22 | 7 | 19.2 | 18 | 4.3 |
| fine sand | 35 | 0.3 | 1750 | 29 | 13 | 0 | 22 | 1.7 |
| silt clay | 25 | 0.33 | 1970 | 25 | 9 | 23 | 20 | 1.1 |
| coarse gravel sand | 54 | 0.28 | 2050 | 41 | 21 | 80 | 35 | 6.0 |
| strongly weathered rock | 15,000 | 0.21 | 2500 | 8621 | 6198 | 500 | 40 | 7.2 |
| moderately weathered rock | 32,000 | 0.2 | 2650 | 17,778 | 13,333 | 2000 | 45 | 25.9 |
| slightly weathered rock | 94 | 0.22 | 2100 | 56.2 | 38.7 | — | — | — |
| slurry | 10,500 | 0.25 | 2500 | 7000 | 4200 | — | — | — |
| Safety Risk Level | Status Description | Protective Measures |
|---|---|---|
| Level I (safety) | The deformation value is less than 10 mm, and the pipeline is not significantly affected by construction disturbance, with its function remaining unaffected. | No protective measures are required. |
| Level II (basic safety) | The deformation value is between 10 mm and 20 mm, and the pipeline experiences minor deformation due to construction disturbance, but its function can still be achieved normally. | Simple protection: regularly monitor key pipeline sections to keep track of their condition. |
| Level III (risk warning) | The deformation value is between 20 mm and 30 mm, and the pipeline undergoes obvious deformation, reaching the deformation limit, with its function barely achieved. | Key protection: comprehensively monitor the pipeline and appropriately reinforce the local and surrounding strata. |
| Level IV (damage) | The deformation value exceeds 30 mm, and the pipeline deformation surpasses the safety standard, resulting in functional damage and necessitating immediate maintenance or replacement. | Professional protection: conduct a comprehensive inspection of pipeline damage and leakage points, promptly maintain damaged areas, and replace the pipeline if necessary. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Wu, W.; Wu, X.; Xu, J.; Li, J.; Qi, Q.; Sun, W. Analysis of Disturbance and Safety Risk Assessment of Shallow-Buried Pressure Pipelines Utilizing the Shield Tunneling Method. Buildings 2025, 15, 2253. https://doi.org/10.3390/buildings15132253
Yang H, Wu W, Wu X, Xu J, Li J, Qi Q, Sun W. Analysis of Disturbance and Safety Risk Assessment of Shallow-Buried Pressure Pipelines Utilizing the Shield Tunneling Method. Buildings. 2025; 15(13):2253. https://doi.org/10.3390/buildings15132253
Chicago/Turabian StyleYang, Hanxi, Wenjia Wu, Xiong Wu, Jiangbo Xu, Jisheng Li, Quan Qi, and Wen Sun. 2025. "Analysis of Disturbance and Safety Risk Assessment of Shallow-Buried Pressure Pipelines Utilizing the Shield Tunneling Method" Buildings 15, no. 13: 2253. https://doi.org/10.3390/buildings15132253
APA StyleYang, H., Wu, W., Wu, X., Xu, J., Li, J., Qi, Q., & Sun, W. (2025). Analysis of Disturbance and Safety Risk Assessment of Shallow-Buried Pressure Pipelines Utilizing the Shield Tunneling Method. Buildings, 15(13), 2253. https://doi.org/10.3390/buildings15132253







