Development and Numerical Implementation of Plastic Damage Constitutive Model for Concrete Under Freeze–Thaw Cycling
Abstract
1. Introduction
2. CDP Model Development and Parameter Selection
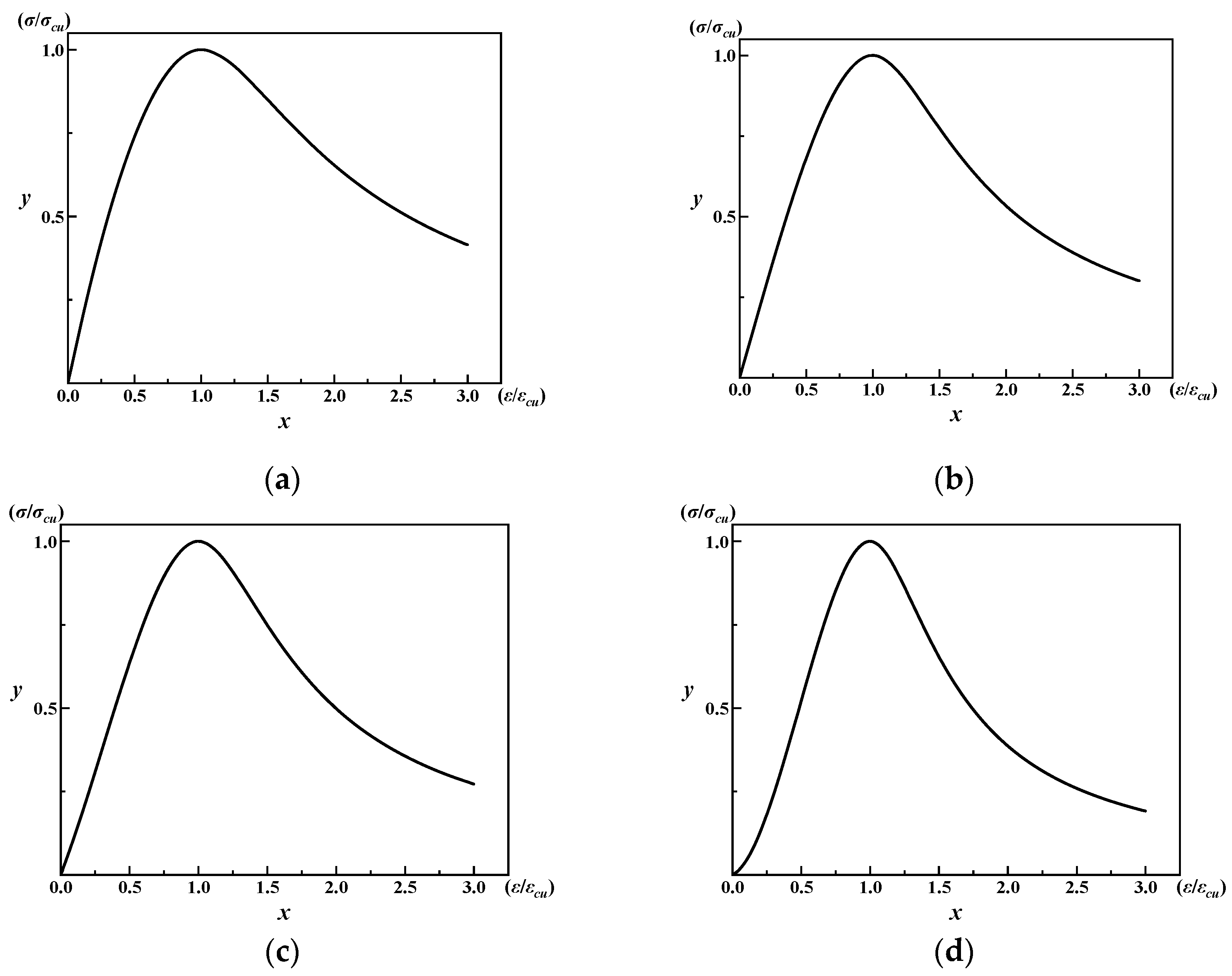
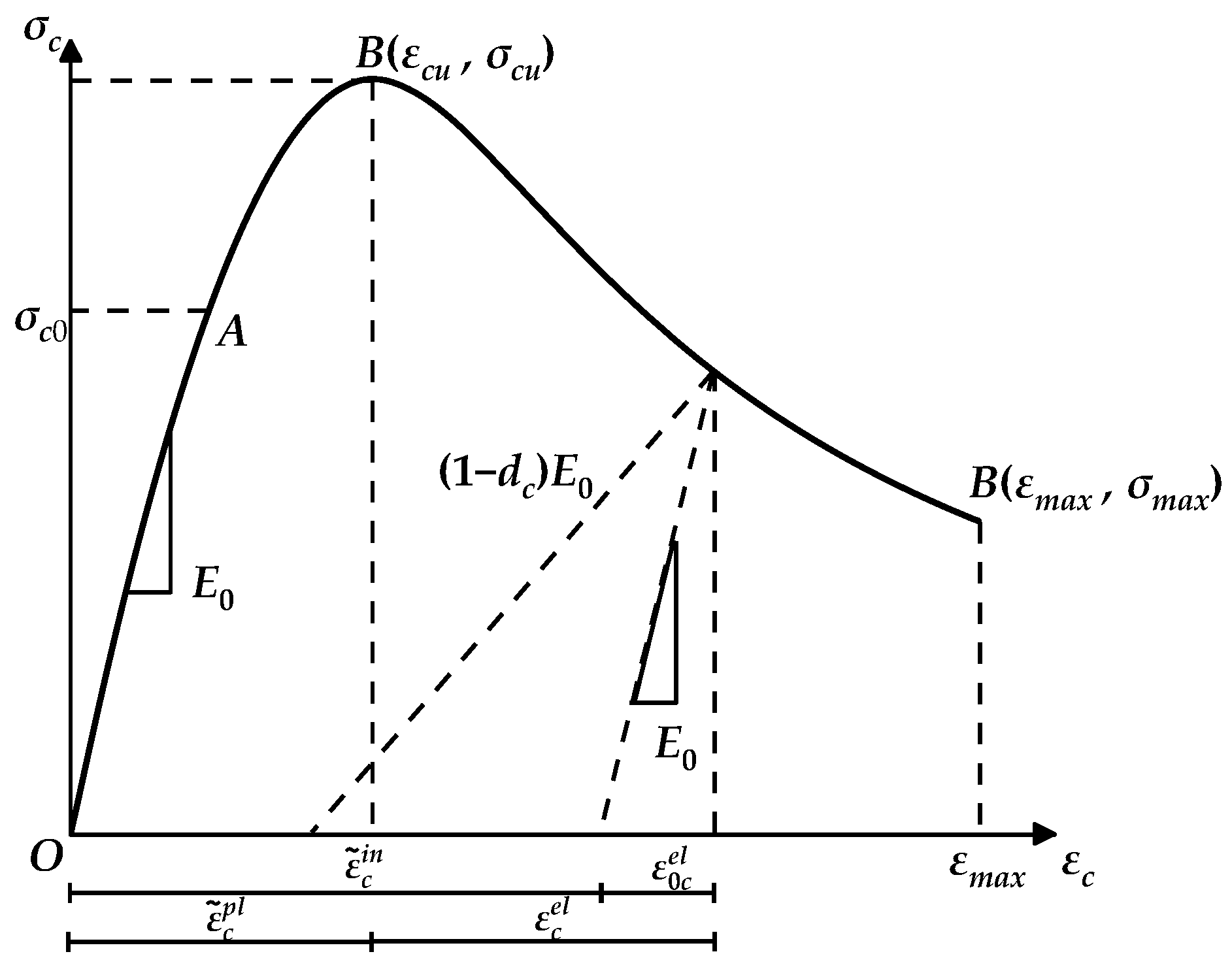
2.1. Axial Compressive Stress–Strain Relationship of Concrete
2.2. Correction of Axial Compressive Stress–Strain Relationship of Concrete
- (1)
- Elastic stage (OA segment): represented by a linear elastic constitutive model;
- (2)
- Hardening stage (AB segment): exhibits nonlinear strengthening behavior;
- (3)
- Softening stage (BC segment): post-peak stiffness degradation reflects the accumulation of damage.
- (i)
- linear elasticity prevails within 0 ≤ x ≤ 0.378;
- (ii)
- damage initiates beyond the critical threshold of x > 0.378.
- (a)
- 25 cycles: 0–0.431;
- (b)
- 50 cycles: 0–0.470;
- (c)
- 75 cycles: 0–0.553.
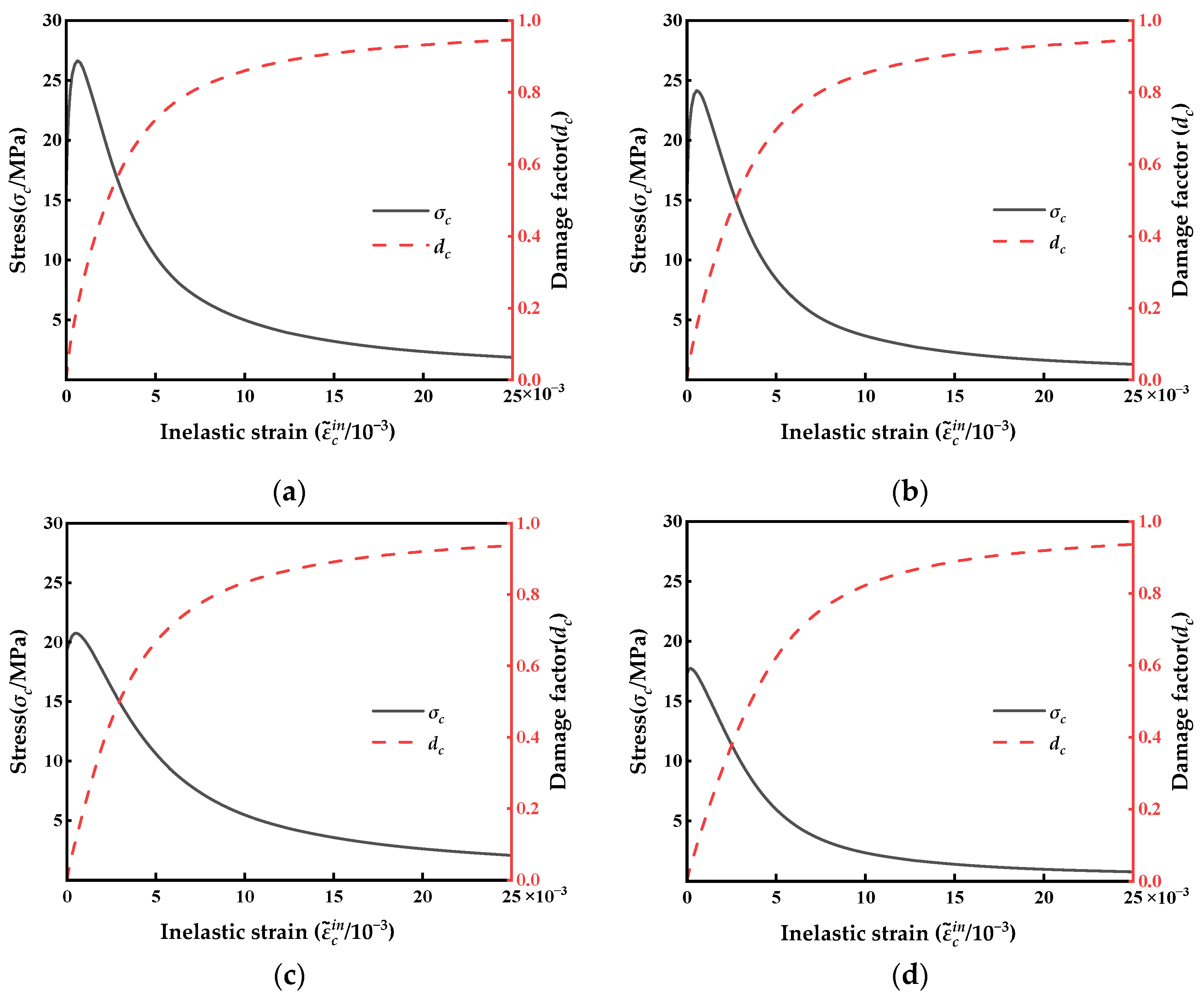
2.3. Plastic Damage Factor Determination
2.4. Plasticity Parameters Calibration
2.4.1. Yield Condition
2.4.2. Expansion Angle and Eccentricity
3. Macroscopic Modeling Analysis of Freeze–Thaw Induced Compressive Response
3.1. The Development of the Macroscopic Model
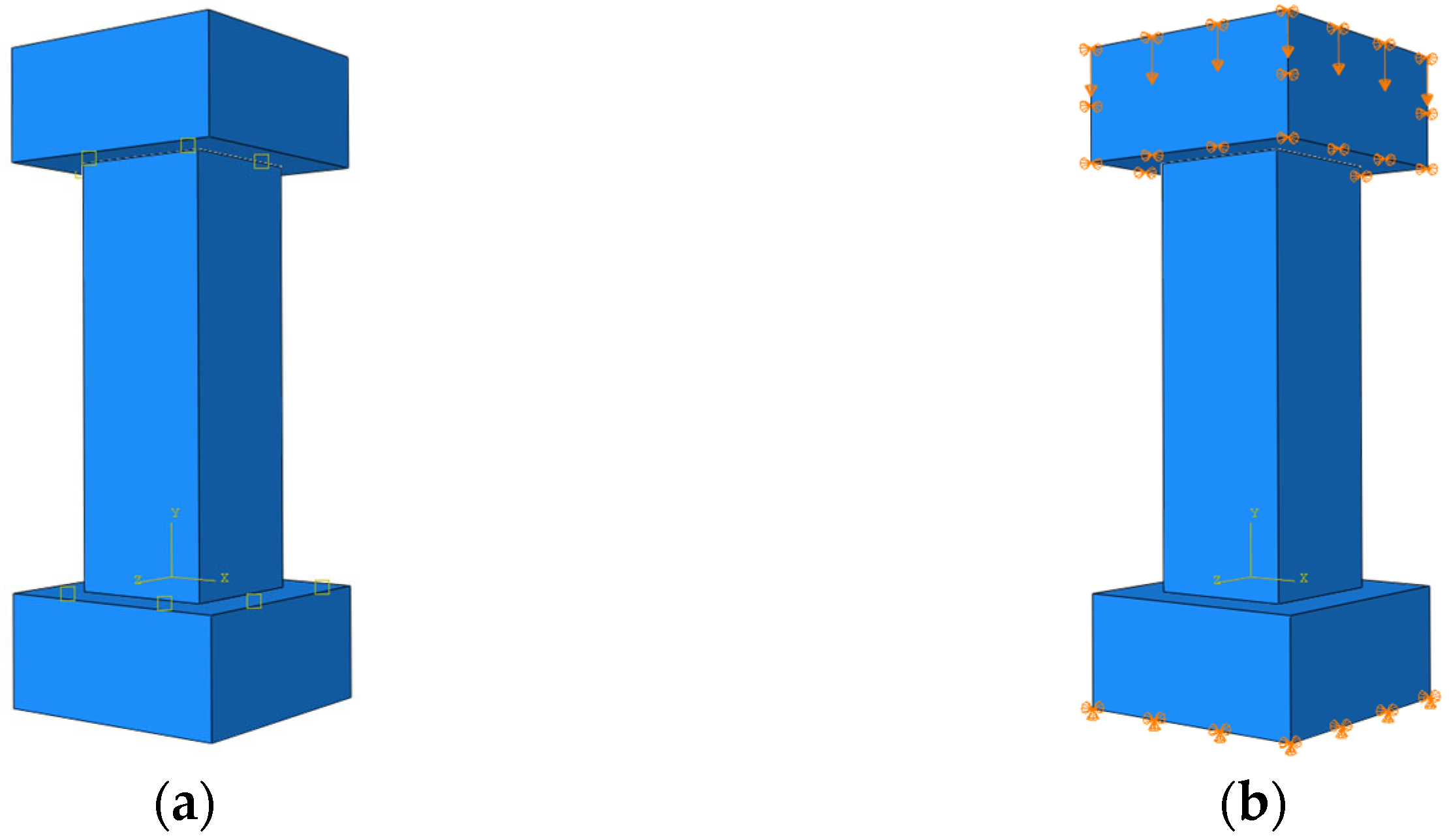
3.1.1. Modeling and Meshing
3.1.2. Implementation of Freeze–Thaw Damage
3.1.3. Boundary Conditions and Loading Mode
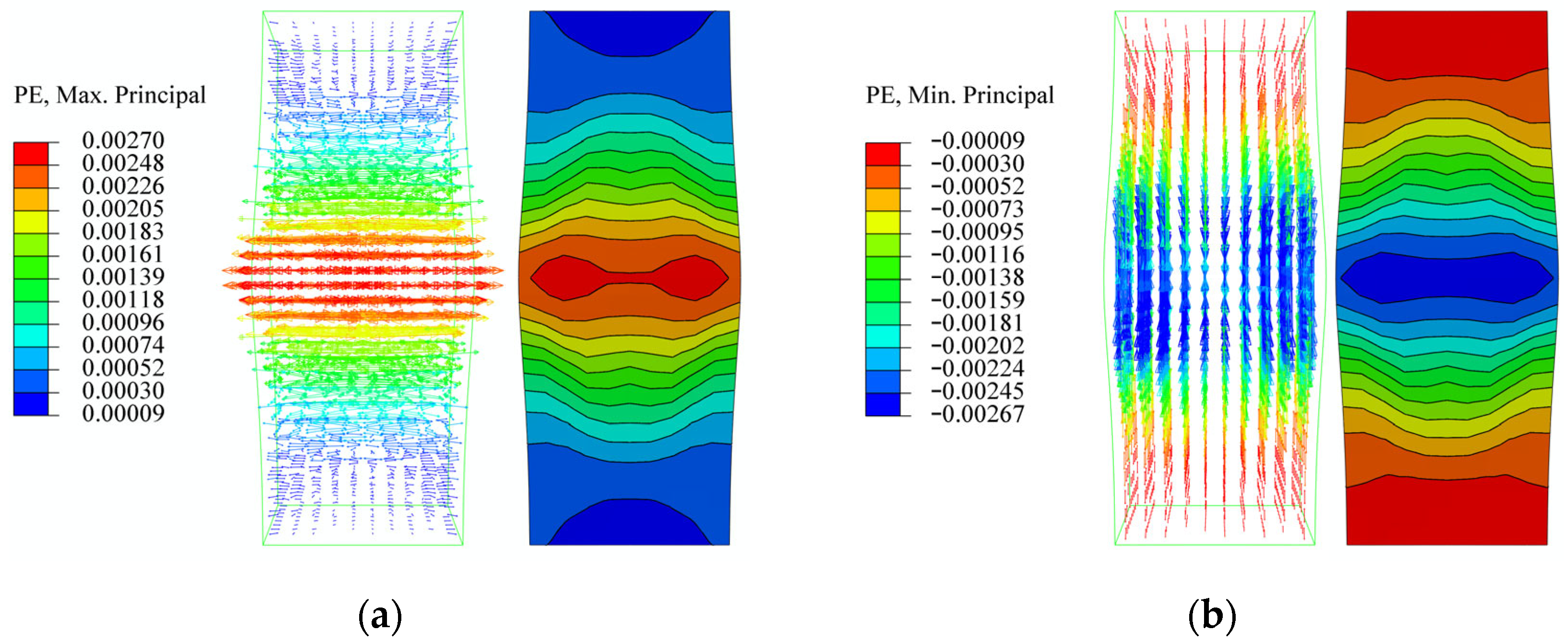
3.2. Macroscopic Simulation Results
4. Mesoscale Modeling Analysis of Freeze–Thaw-Induced Compressive Response
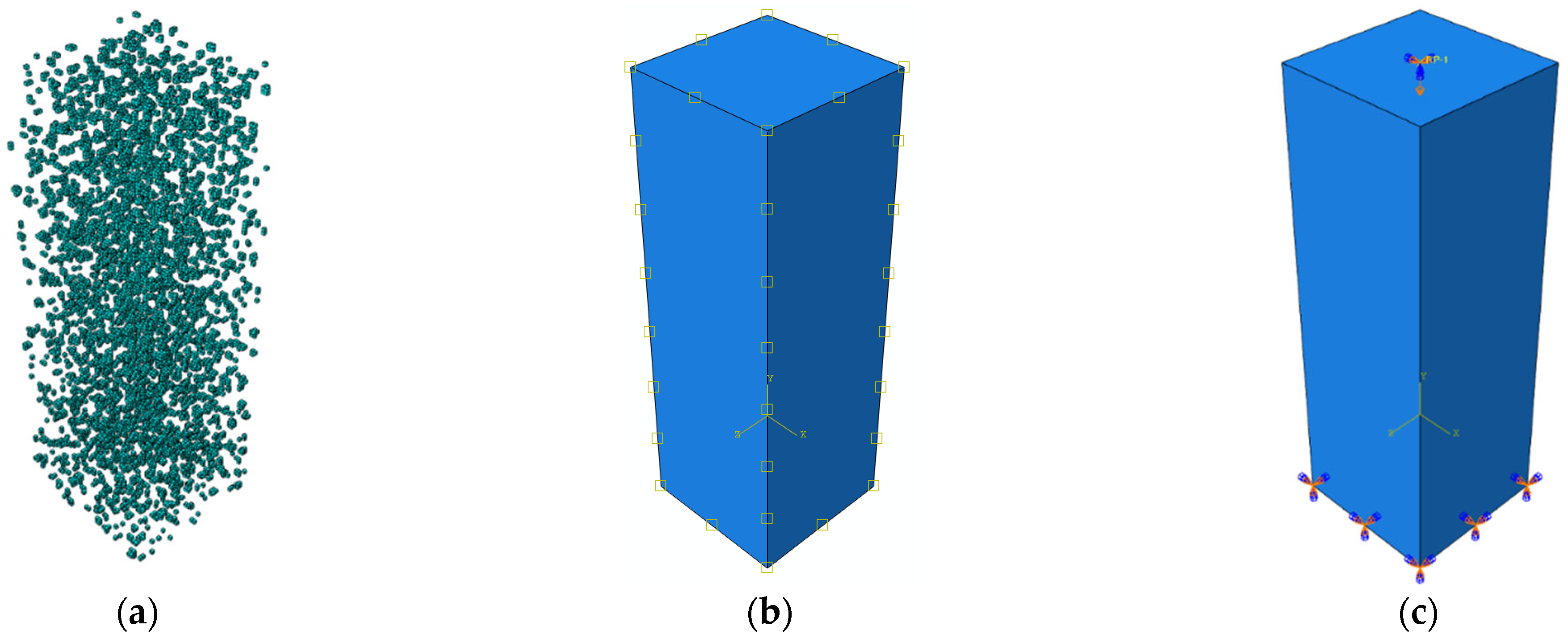
4.1. Development of Mesoscale Model
4.1.1. Advanced Freeze–Thaw Modeling Methodology
4.1.2. Pore Water Assignment and Boundary Implementation
4.2. Mesoscopic Simulation Results
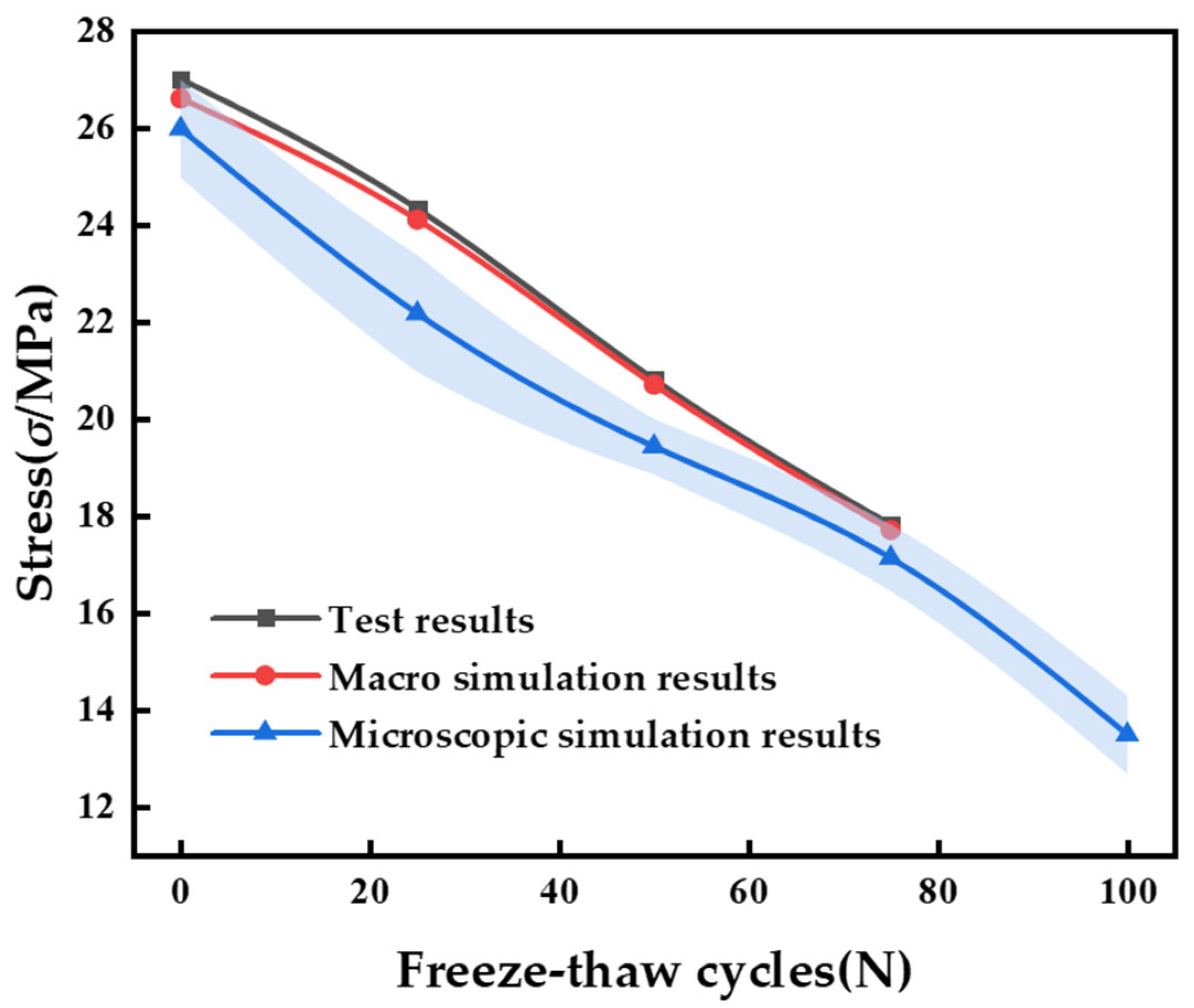
5. Comparison Between Simulations and Experiment
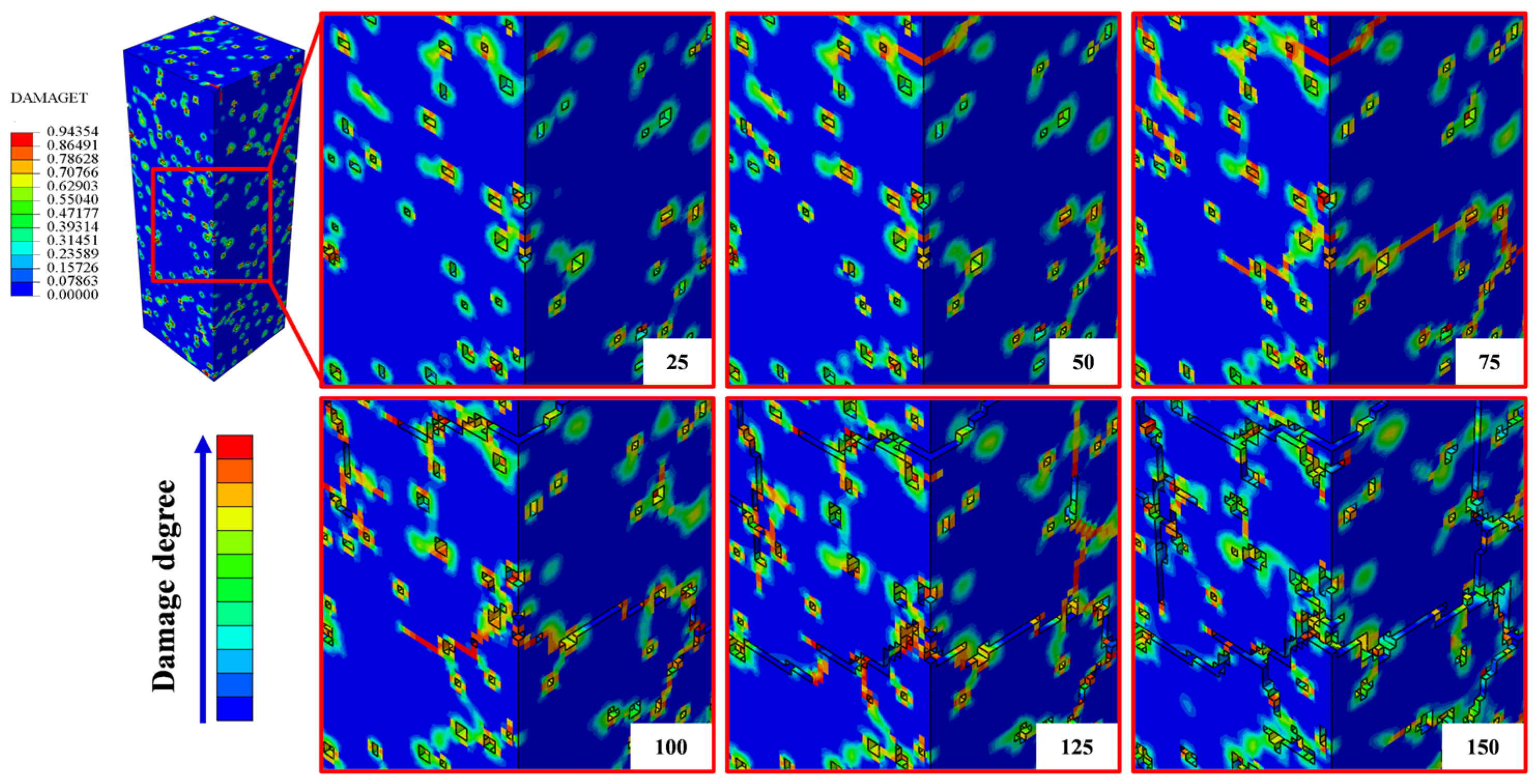
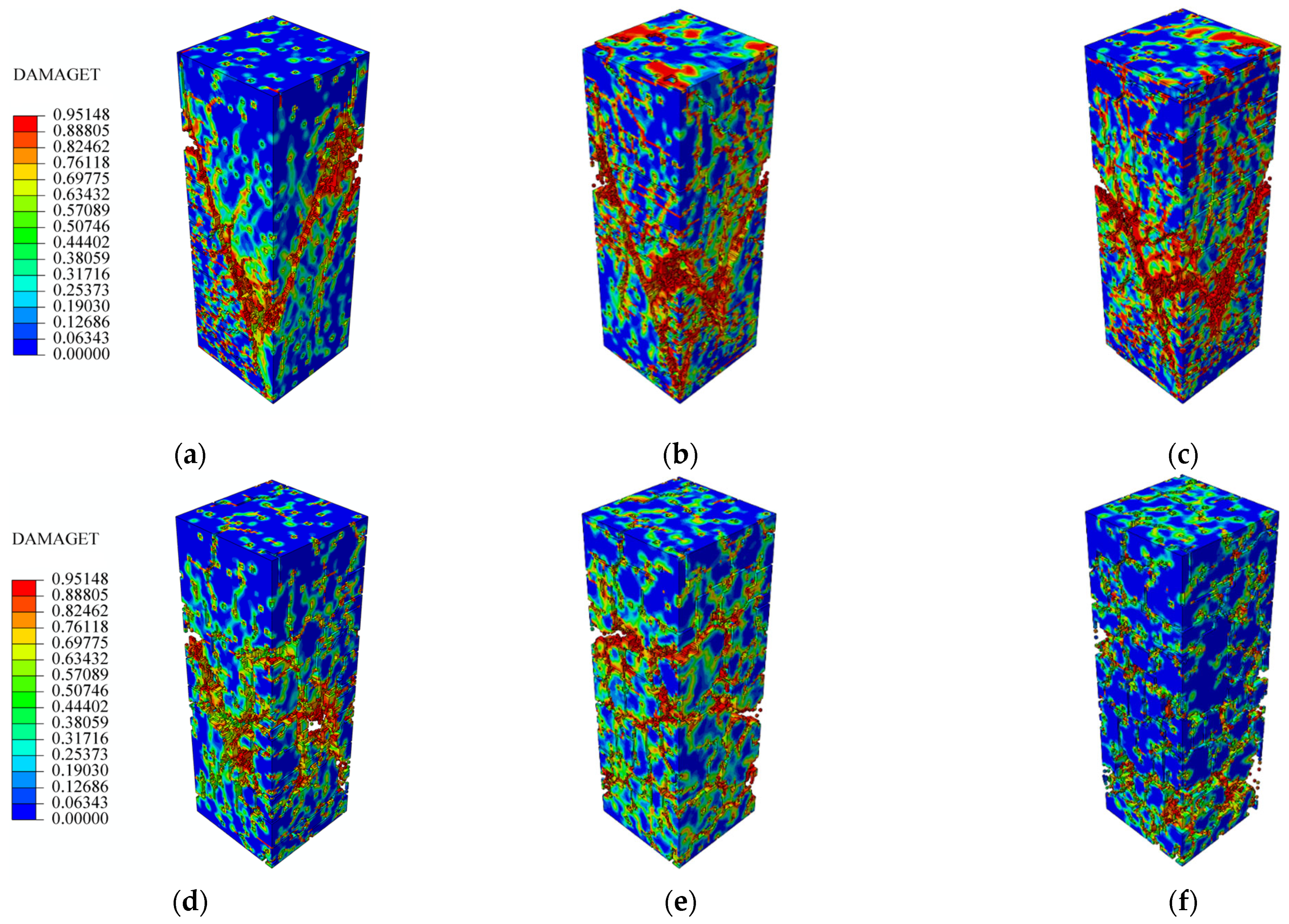
5.1. Damage Evolution and Failure Pattern Comparison
5.2. Analysis of Axial Compressive Stress–Strain
5.3. Result Analysis
6. Conclusions
- (1)
- Based on experimental data, the constitutive relationship was refined to define the elastic yield point (σc0 = 0.6σcu) and initial modulus (E0), yielding a model applicable to 0–75 freeze–thaw cycles. A mathematical relationship between the compressive damage factor (dc) and stress–inelastic strain was derived, and the proper calibration of dc significantly improved the model’s convergence and suitability for the finite element analysis.
- (2)
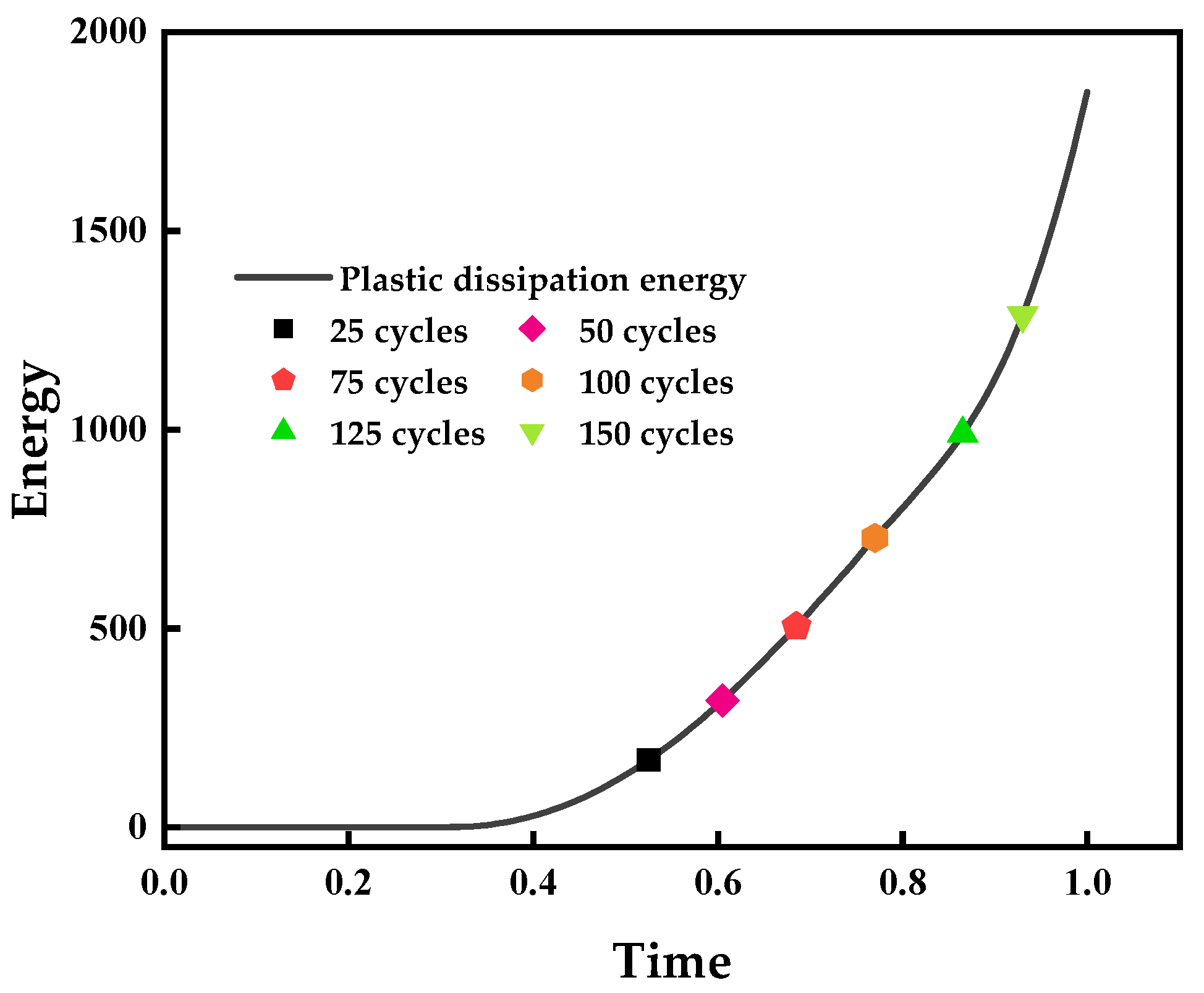
- The macroscale model accurately captured the global mechanical response of concrete after varying freeze–thaw cycles, with a relative error of 1.61%. Meanwhile, the mesoscale model successfully reproduced the internal damage evolution and crack propagation using equivalent plastic dissipation energy, achieving an average error of 5.81%. This confirms the effectiveness of the CDP model in both types of finite element simulations and its accuracy in characterizing the freeze–thaw damage evolution, with an improved accuracy compared to the results of existing simulation studies, validating its applicability to freezing environments.
- (3)
- The macroscale and mesoscale models demonstrate complementary analytical capabilities: the macroscale model is primarily used to investigate the macrostructural mechanical response of concrete after freeze–thaw cycling, while the mesoscale model is more suitable for exploring the material’s microstructure and freezing resistance mechanisms. Moreover, model parameters exhibit a significant sensitivity on simulation results. The further optimization of plastic parameters and the mesh sensitivity analysis will be the focus of future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| CDP | Concrete Damaged Plasticity |
References
- Ebrahimi, K.; Daiezadeh, M.J.; Zakertabrizi, M.; Zahmatkesh, F.; Habibnejad Korayem, A. A Review of the Impact of Micro- and Nanoparticles on Freeze-Thaw Durability of Hardened Concrete: Mechanism Perspective. Constr. Build. Mater. 2018, 186, 1105–1113. [Google Scholar] [CrossRef]
- Liu, J.; Wang, M.; Yang, Y.; Liu, Q.; Chen, Z.; Shi, C. Freeze–Thaw Durability of Concrete—A Short Review. J. Chin. Ceram. Soc. 2025, 53, 190–211. [Google Scholar] [CrossRef]
- Mobaraki, B.; Ma, H.; Lozano Galant, J.A.; Turmo, J. Structural Health Monitoring of 2D Plane Structures. Appl. Sci. 2021, 11, 2000. [Google Scholar] [CrossRef]
- Mobaraki, B.; Vaghefi, M. The Effect of Protective Barriers on the Dynamic Response of Underground Structures. Buildings 2024, 14, 3764. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A Plastic-Damage Model for Concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Shi, X.; Yao, Y.; Wang, L.; Zhang, C. The influence of CDP model parameters based on the numerical simulation of uniaxial loading test. Build. Struct. 2021, 51, 999–1007. [Google Scholar]
- Yao, Z.; Cui, T.; Dang, F.; Wen, S.; Linghu, T.; Qi, Y. Plastic Damage Performance of Recycled Concrete Based on ABAQUS. J. Yangtze River Sci. Res. Inst. 2022, 39, 131–136, 143. [Google Scholar]
- Zhang, F.; Ma, J.; Nan, Y. Parameters Selection and Verification Calculation of Concrete Plastic Damage Model. China Concr. Cem. Prod. 2021, 29, 7–11. [Google Scholar] [CrossRef]
- Zhou, Z.; Luo, J.; Kang, Y. Damaged plastic analysis of concrete around dowel bars at joint in cement pavement. J. Traffic Transp. Eng. 2022, 22, 117–127. [Google Scholar] [CrossRef]
- Chen, X.; Yang, S.; Han, M. Uniaxial compression simulation of concrete under the coupled actions of sulfate, dry-wet cycles and freeze-thaw cycles. Sci. Technol. Eng. 2023, 23, 6158–6166. [Google Scholar]
- Sun, M.; Xin, D.; Zou, C. Damage Evolution and Plasticity Development of Concrete Materials Subjected to Freeze-Thaw during the Load Process. Mech. Mater. 2019, 139, 103192. [Google Scholar] [CrossRef]
- Qiu, W.-L.; Teng, F.; Pan, S.-S. Damage Constitutive Model of Concrete under Repeated Load after Seawater Freeze-Thaw Cycles. Constr. Build. Mater. 2020, 236, 117560. [Google Scholar] [CrossRef]
- Yang, Z. Reaserch about Uniaxial Compression Performance of Concrete Under Freeze-Thaw Cycle. Master’s Thesis, Yangzhou University, Yangzhou, China, 2010. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Architecture & Building Press: Beijing, China, 2014.
- Guo, Z.; Zhang, X.; Zhang, D.; Wang, R. Experimental Investigation of The Complete Stress-strain relationship of Concrete. J. Build. Struct. 1982, 1, 1–12. [Google Scholar] [CrossRef]
- Yu, Z.; Ding, F. Unified calculation method of compressive mechanical properties of concrete. J. Build. Struct. 2003, 24, 41–46. [Google Scholar]
- Ding, F.; Yu, Z. Unified Calculation Method of Mechanical Properties of Concrete in Tension. J. Civ. Eng. Manag. 2004, 21, 29–34. [Google Scholar]
- Li, Y.; Wang, X.; Chen, S. Comparison of Stress-strain relationships for Concrete under Uniaxial Stresses. J. Highw. Transp. Res. Dev. 2005, 10, 75–78. [Google Scholar]
- Popovics, S. A Numerical Approach to the Complete Stress-strain relationship of Concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Ortiz, M. A Constitutive Theory for the Inelastic Behavior of Concrete. Mech. Mater. 1985, 4, 67–93. [Google Scholar] [CrossRef]
- Hordijk, D.A. Tensile and Tensile Fatigue Behaviour of Concrete; Experiments, Modelling and Analyses. Heron 1992, 37, 79. [Google Scholar]
- Zhang, J.; Ren, H.; Wang, S. Finite element analysis for confinement behavior of hybrid FRP tube-concrete-steel tube composite bushing. J. Dalian Univ. Technol. 2016, 56, 375–381. [Google Scholar]
- GB/T 50082-2009; Standard for Test Methods for Long-Term Performance and Durability of Concrete. China Standards Press (CSP): Beijing, China, 2009.
- Krajcinovic, D.; Lemaitre, J. (Eds.) Continuum Damage Mechanics Theory and Application; Springer: Vienna, Austria, 1987; ISBN 978-3-211-82011-7. [Google Scholar]
- Wang, Z.; Yu, Z. Concrete Damage Model Based on Energy Loss. J. Build. Mater. 2004, 7, 365–369. [Google Scholar] [CrossRef]
- Sidoroff, F. Description of Anisotropic Damage Application to Elasticity. In Physical Non-Linearities in Structural Analysis, Proceedings of the Symposium, Senlis, France, 27–30 May 1980; Hult, J., Lemaitre, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 237–244. [Google Scholar]
- Birtel, V.; Mark, P. Parameterised Finite Element Modelling of RC Beam Shear Failure. In Proceedings of the ABAQUS Users’ Conference, Providence, RI, USA, 16 November 2006; Volume 14. [Google Scholar]
- Wang, G.; Liu, Q.; Wang, H.; Wang, J.; Dong, F. Preliminary analysis of mechanical properties of subway station under fire after earthquake. Chin. J. Geotech. Eng. 2022, 44, 30–35. [Google Scholar]
- Lei, T.; Qian, J.; Liu, C. Application of Damaged Plasticity Model for Concrete. Struct. Eng. 2008, 24, 22–27. [Google Scholar] [CrossRef]
- Lan, W. Study on the Numerical Simulation of Freeze-Thaw Cycles for Concrete. Master’s Thesis, Hebei Agricultural University, Hebei, Shijiazhuang, China, 2014. [Google Scholar]
- Liang, K. Research on Freeze-thaw Damage Model and Numerical Simulation of Concrete in High Cold Area. Master’s Thesis, Xi’an Technological University, Xi’an, China, 2022. [Google Scholar]
- Zhou, Y. Dynamic Numerical Simulation Analysis of Concrete Under Freeze-Thaw Environment. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Peng, R.; Qiu, W.; Teng, F. Three-Dimensional Meso-Numerical Simulation of Heterogeneous Concrete under Freeze-Thaw. Constr. Build. Mater. 2020, 250, 118573. [Google Scholar] [CrossRef]
- Hover, K.C. The Influence of Water on the Performance of Concrete. Constr. Build. Mater. 2011, 25, 3003–3013. [Google Scholar] [CrossRef]









| Freeze–Thaw Cycles (N) | Peak Compressive Stress (MPa) | Peak Compression Strain | Ultimate Compressive Strain |
|---|---|---|---|
| 0 | 26.6 | 0.001708 | 0.004083 |
| 25 | 24.1 | 0.002042 | 0.004292 |
| 50 | 20.7 | 0.002375 | 0.004792 |
| 75 | 17.7 | 0.002708 | 0.004917 |
| Freeze–Thaw Cycles (N) | 0 | 25 | 50 | 75 | |
|---|---|---|---|---|---|
| Control Parameter | |||||
| a | 1.91 | 1.45 | 1.09 | 0.18 | |
| b | 1.06 | 1.75 | 2.01 | 3.18 | |
| Freeze–Thaw Cycles (N) | Normalized Strain (x = ε/εcu) | Damage Factor (dc) | Stage | Key Parameters |
|---|---|---|---|---|
| 0 | 0.000–0.378 | 0.000 | Elastic stage | a = 1.91, b = 1.06 ρc = 0.630 |
| 0.378–1.000 | Hardening stage | |||
| >1.000 | Softening stage | |||
| 25 | 0.000–0.431 | 0.000 | Elastic stage | a = 1.45, b = 1.75 ρc = 0.719 |
| 0.431–1.000 | Hardening stage | |||
| >1.000 | Softening stage | |||
| 50 | 0.000–0.470 | 0.000 | Elastic stage | a = 1.09, b = 2.01 ρc = 0.784 |
| 0.470–1.000 | Hardening stage | |||
| >1.000 | Softening stage | |||
| 75 | 0.000–0.553 | 0.000 | Elastic stage | a = 0.18, b = 3.18 ρc = 0.922 |
| 0.553–1.000 | Hardening stage | |||
| >1.000 | Softening stage |
| Expansion Angle ψ/(°) | Eccentricity | fb0/fc0 | K | μ |
|---|---|---|---|---|
| 36 | 0.1 | 1.16 | 0.667 | 0.0005 |
| Freeze–Thaw Cycles (N) | σc | dc | |
|---|---|---|---|
| 0 | 15.97027 | 0.00000 | 0.00000 |
| 19.66753 | 0.00000 | 0.03514 | |
| 25.49418 | 0.00033 | 0.13177 | |
| 26.64543 | 0.00063 | 0.20622 | |
| 21.53629 | 0.00186 | 0.43611 | |
| 15.76317 | 0.00311 | 0.58880 | |
| 12.00375 | 0.00429 | 0.68209 | |
| 4.17241 | 0.01172 | 0.88188 | |
| 2.54784 | 0.01851 | 0.92662 | |
| 1.61371 | 0.02856 | 0.95326 | |
| 25 | 14.47263 | 0.00000 | 0.00000 |
| 18.99476 | 0.00007 | 0.02873 | |
| 22.74894 | 0.00025 | 0.07966 | |
| 24.14921 | 0.00057 | 0.15204 | |
| 20.14075 | 0.00163 | 0.34579 | |
| 12.90583 | 0.00329 | 0.56212 | |
| 8.89727 | 0.00475 | 0.68132 | |
| 3.68880 | 0.00993 | 0.85239 | |
| 1.45728 | 0.02212 | 0.93782 | |
| 1.04071 | 0.03011 | 0.95518 | |
| 50 | 13.18601 | 0.00000 | 0.00000 |
| 17.67961 | 0.00007 | 0.02232 | |
| 20.36691 | 0.00030 | 0.07477 | |
| 20.74916 | 0.00050 | 0.11416 | |
| 16.88915 | 0.00180 | 0.32487 | |
| 12.12393 | 0.00317 | 0.49577 | |
| 7.88112 | 0.00497 | 0.64818 | |
| 5.66508 | 0.00659 | 0.73339 | |
| 1.38246 | 0.02103 | 0.92449 | |
| 0.78629 | 0.03493 | 0.95620 | |
| 75 | 17.27507 | 0.00000 | 0.00000 |
| 17.62447 | 0.00008 | 0.01786 | |
| 17.74793 | 0.00020 | 0.03944 | |
| 16.05562 | 0.00098 | 0.16621 | |
| 13.03120 | 0.00194 | 0.30475 | |
| 8.34775 | 0.00368 | 0.50951 | |
| 5.77826 | 0.00512 | 0.63108 | |
| 4.31476 | 0.00641 | 0.70691 | |
| 1.60519 | 0.01322 | 0.87150 |
| Freeze–Thaw Cycles (N) | Peak Stress (σ/MPa) | Peak Strain (ε) | ||||
|---|---|---|---|---|---|---|
| Test Results | Modeling Results | Relative Error (%) | Test Result | Modeling Results | Relative Error (%) | |
| 0 | 26.6 | 27.001 | 1.49% | 0.001708 | 0.001733 | 1.44% |
| 25 | 24.1 | 24.323 | 0.92% | 0.002042 | 0.002064 | 1.07% |
| 50 | 20.7 | 20.809 | 0.52% | 0.002375 | 0.002323 | 2.1% |
| 75 | 17.7 | 17.810 | 0.61% | 0.002708 | 0.002658 | 1.84% |
| Freeze–Thaw Cycles (N) | Peak Stress (σ/MPa) | ||
|---|---|---|---|
| Test Results | Simulated Mean Results | Relative Error (%) | |
| 0 | 26.6 | 25.975 | 2.35% |
| 25 | 24.1 | 22.165 | 8.03% |
| 50 | 20.7 | 19.424 | 6.16% |
| 75 | 17.7 | 17.125 | 3.25% |
| 100 | - | 13.482 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, X.; Shao, X.; Han, J.; Liu, Y. Development and Numerical Implementation of Plastic Damage Constitutive Model for Concrete Under Freeze–Thaw Cycling. Buildings 2025, 15, 2155. https://doi.org/10.3390/buildings15132155
Wang Z, Liu X, Shao X, Han J, Liu Y. Development and Numerical Implementation of Plastic Damage Constitutive Model for Concrete Under Freeze–Thaw Cycling. Buildings. 2025; 15(13):2155. https://doi.org/10.3390/buildings15132155
Chicago/Turabian StyleWang, Zhixuan, Xiao Liu, Xiaoquan Shao, Jianyong Han, and Yu Liu. 2025. "Development and Numerical Implementation of Plastic Damage Constitutive Model for Concrete Under Freeze–Thaw Cycling" Buildings 15, no. 13: 2155. https://doi.org/10.3390/buildings15132155
APA StyleWang, Z., Liu, X., Shao, X., Han, J., & Liu, Y. (2025). Development and Numerical Implementation of Plastic Damage Constitutive Model for Concrete Under Freeze–Thaw Cycling. Buildings, 15(13), 2155. https://doi.org/10.3390/buildings15132155






