Three-Dimensional Printing Experiments and Particle-Based Meshless Numerical Investigations on the Failure Modes of Tunnel-Lining Structures Containing Fissures

Abstract

The presence of fissures poses significant threats to tunnel-lining structures, and the interaction between tunnels and linings under complex stress conditions remains poorly understood. This study investigated the failure modes of tunnel-lining structures with prefabricated fissures via 3D-printed samples, uniaxial compression experiments using DIC technology for full-field strain monitoring, and a particle-based meshless (SPH) numerical method to simulate tunnel–fissure interactions. The results show that under uniaxial compression, three crack types (main, upper/lower side cracks) initiate from the tunnel, while only wing cracks form at pre-existing fissures; wing crack initiation suppresses upper-side cracks, whereas more lining cracks (upper, middle, lower, corner, bottom) emerge without fissure-induced propagation. Fissure orientation (β) and inclination (α) significantly affect crack distributions: β = 90° induces maximum stress concentration and asymmetric deformation, while α ≥ 45° promotes wing crack initiation and reduces lining crack density. Along with our findings, we offer design recommendations to prioritize fissure orientation in tunnel engineering and expand SPH applications for predicting crack propagation in underground structures with complex fissures.

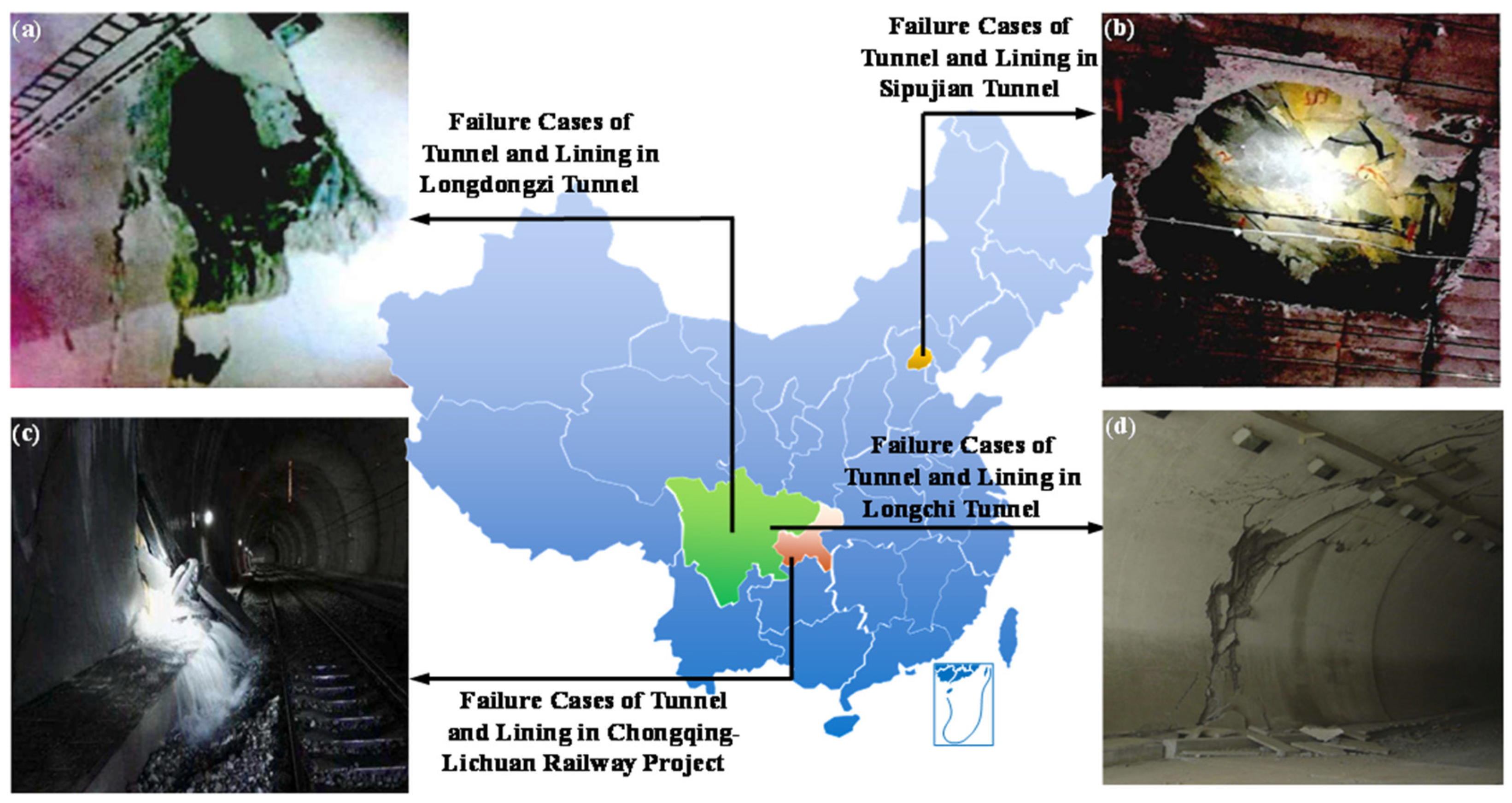
1. Introduction

With the promotion of construction in Central and Western China, more and more underground space has been developed and utilized. As an important carrier of transportation and water conservancy construction, tunnels have played a pivotal role in China’s economic development [1]. By 2022, there were already 24,850 road tunnels in China, including 1752 extremely long tunnels and 6715 long tunnels, showing a trend of continuous growth regarding construction scale. However, in the context of tunnel projects with a large burial depth and complex geological conditions, fissures are widely distributed inside rock masses. Under complex stress conditions, crack propagation and penetration lead to stress redistributions in the tunnel, thus affecting the lining structures, which results in the lining cracking and affects the safe and stable operations of the tunnel projects [2,3]. For example, after the Wenchuan earthquake, the Longdongzi tunnel in Sichuan Province, whose section crosses the fault, dislocated, resulting in serious disasters such as the misalignment of the tunnel body and the collapse of the lining structures [4], as shown in Figure 1a. Some sections of the Sifujian Tunnel of the Shuohuang Railway in North China have large cavities behind their linings, and there are obvious cracks in the arch lining, which result in water leakage [5], as shown in Figure 1b. On 17 June 2015, the tunnel that passed through Fangdou Mountain as part of the Chongxi–Lichuan Railway Project suffered serious lining damage [6], as shown in Figure 1c. Obvious spalling occurred on the side wall of the lining of the Longchi Tunnel, and the crack extended to the arch top [7], as shown in Figure 1d. Hence, grasping the failure mechanisms of tunnels and their linings will undoubtedly provide references for the design, construction, and engineering of tunnels.

Investigations on the combined action of the tunnel and lining under complex stress conditions focus on three parts: experimental investigations, theoretical research, and numerical simulations. Experimental investigations can directly reveal the deformation laws and failure morphologies of the tunnel-lining structures, which can be divided into field investigations and laboratory tests. Field investigations can obtain real tunnel-lining failure laws: for example, Huang et al. [8] analyzed the distribution laws of highway tunnel-lining cracks in detail through field investigations; meanwhile, Wang et al. [9] discussed the mechanical effects of faults on tunnel and lining damage through field investigations. However, field investigations take a long time, and only local damage can be observed, so it is difficult to grasp the damage distributions of whole tunnel and lining structures. Laboratory tests can “move” large-scale tunnels into the laboratory through scale reduction. For example, Liu et al. [10] carried out a shaking table test to explore the structural response of a tunnel and lining that cross the fault under the action of an earthquake; Liu et al. [11] conducted geo-mechanical tests on tunnel and lining structures under a normal fault stick–slip dislocation with 75° inclination angles; and Zhang et al. [12] designed a fully enclosed hydraulic pressure device and conducted experimental studies on the mechanical properties, deformation, and crack propagation processes of tunnel-lining structures during tunnel mining. However, laboratory tests can only obtain the superficial crack distributions of tunnel-lining structures. Meanwhile, an understanding of the influences of different fissure orientations and inclinations is still lacking. Theoretical research is based on experimental investigations, which summarize and extract the general mathematical expressions of the damage range or the initiation conditions of tunnel-lining structures. For example, Wang et al. [13] conducted a safety evaluation of tunnel-lining cracks and established a prediction formula considering the degradations of tunnel lining; Zhu et al. [14] derived an elastic–plastic damage model of a tunnel lining and analyzed the damage distributions; Wen et al. [15] proposed a coupled seepage–stress–damage model for tunnel linings and applied it to tunnel health monitoring; and Bian et al. [16] established a coupled seepage–stress–damage model for the hydraulic fracturing of tunnel linings. However, theoretical research is suitable for problems which deal with simple boundary conditions and geometries, while it is almost impossible for dealing with complex problems.

As an alternative method to theoretical research and experimental research, numerical simulation has gained more and more acclaim in modelling the interactions between the tunnel and lining. The commonly used numerical methods include the following: (1) Finite element method (FEM). For instance, Asgari et al. [17] employed three-dimensional parallel finite elements to assess the seismic response and resilience of various pile group configurations; Liu et al. [18] used a refined 3D model to study the dynamic responses of tunnel lining under earthquake action; Liu et al. [19] established a tunnel model containing damaged lining based on FEM and studied the deformation laws of the tunnel and the development of the plastic zones during the processes of long-distance lining replacements. However, during the numerical treatments of the discontinuous features of tunnel and lining, grid-based methods should re-divide mesh grids, and the calculation amount is huge. In the case of complex fissure interactions, mesh re-divisions can easily fail, which leads to calculation errors. The discrete element method (DEM) overcomes the problems of re-meshing in traditional FEM, so it can be easily used to simulate the failure processes of tunnel-lining structures. For example, Fan et al. [20] investigated the influences of lining on stress distributions of surrounding rock around the tunnel based on DEM; Yang et al. [21] established a simplified model of a railway tunnel and studied the microscopic evolutions of the concrete structures at the bottom of the tunnel. However, DEM relies heavily on simulation experiences. The recent popular modelling schemes, such as PD method [22,23,24], NMM method [25,26], PF method [27,28], all possess certain applications in the tunnel-lining damage simulations, but they also have certain limitations. SPH is another kind of meshless method, which not only possesses the advantages of traditional FEM in numerical calculation but can also simulate large deformation and discontinuous problems, and the interaction states can be directly reflected by the damage variable, so it is very suitable for simulating discontinuous crack propagation processes. Therefore, some scholars have made improvements to SPH, so as to model the rock damage, such as the GPD method developed from SPH [29,30,31,32,33,34,35,36,37]. Nevertheless, SPH has not yet involved applications of the simulations of tunnel-lining failure processes.

In our work, to grasp the failure mechanisms of the tunnel and lining, 3DP is used to prepare the tunnel-lining samples containing fissures with various inclinations as well as orientations; meanwhile, the lining structures adapted to the tunnel are also printed. The deformation and failure laws of various fissure properties are investigated based on DIC technology. The tunnel-lining models are also established by the SPH method, and the progressive damage processes are simulated. The influences of prefabricated fissure inclinations as well as orientations on the final fracture morphologies are discussed in detail. Findings in this work can offer the correct understanding of cooperative working mechanisms in tunnel-lining structures and expand the use of the SPH method into underground structures.

2. Experimental Schemes

2.1. Principles of DIC

Digital image correlation technology (DIC) is a non-destructive optical measurement method, and its basic principles are illustrated in Figure 2. Firstly, before applying the load on the tunnel-lining specimen, an N × N pixel rectangle subregion can be defined to be the reference subset, whose center point is defined as P (x_i, y_i). During the loading processes of the tunnel-lining specimen, it is necessary to find the target region of the specimen image after deformation that has the greatest correlation with the image before deformation, and the center region is denoted as P^′ (x_i^′, y_i^′). Therefore, P^′ is regarded as the position of P before the deformation of the tunnel-lining specimen [38]. Based on the above methods, the corresponding positions of the images before and after deformation can be obtained, and the strain information of the tunnel-lining sample surface can be displayed.

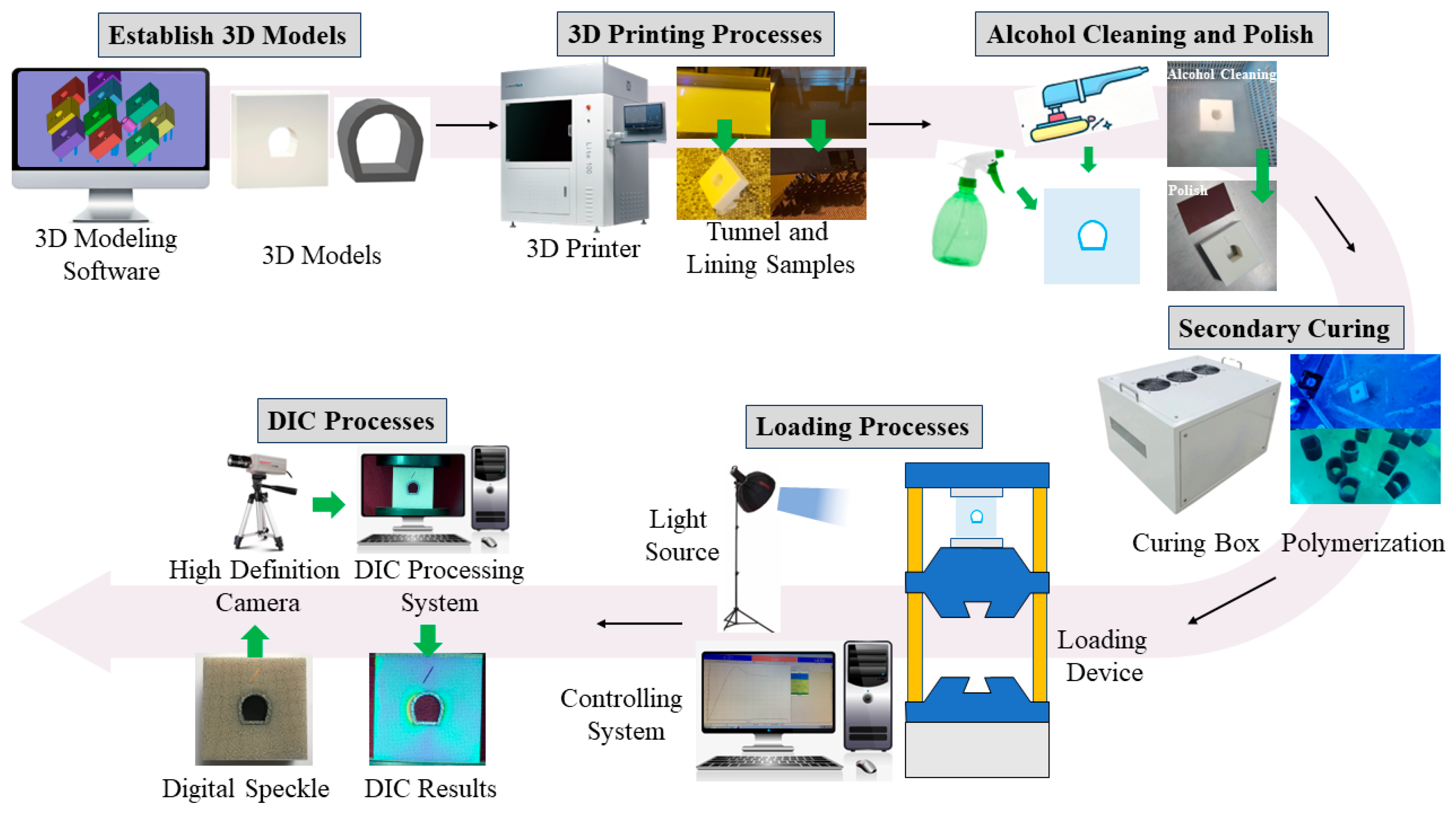
2.2. Specimen Preparations and Experimental Processes

The specimen preparations and test processes are shown in Figure 3. Their main steps include the following: (1) establish 3D models; (2) 3D-printing processes; (3) alcohol cleaning and polish; (4) secondary curing; (5) loading processes; (6) DIC processes. The details are as follows:

(1)

Establish 3D models: Establish 3D models of tunnels and linings that meet the requirements through 3D modeling software (such as Catia).

(2)

3D-printing processes: The established 3D modes (tunnel model and lining model) are imported into Lite3D printer; the tunnel and lining samples will be printed layer by layer.

(3)

Alcohol cleaning and polish: Remove the support of the printed sample, wash the excess liquid resin with alcohol, and polish the uneven surface of the sample with sandpaper.

(4)

Secondary curing: Put the polished tunnel and lining samples into the UV curing box to further cure and improve the brittleness of the samples.

(5)

Loading processes: Spray speckles on the surface of the tunnel and lining specimens, and put them into the uniaxial loading system after splice. Control the loading rate at 0.5 mm/min. Use the light source to fill light on the specimen surface, and the controlling system is used to monitor the stress and displacement changes during the loading processes.

(6)

DIC processes: The images of tunnel and lining samples are captured in real time, and the DIC systems are used to calculate the strain on the sample surfaces.

2.3. Schemes

To investigate the influences of different fissure inclination and orientation angles on the deformation and damage of the tunnel-lining structures, specimens are prepared using 3D-printing technology described in Section 2.2. The shape of the specimen is a cuboid with dimensions of 30 mm × 80 mm, which is referred to the experience from previous works [39]. A horseshoe-shaped tunnel is designed, and the lining is also set inside the tunnel. Various prefabricated fissure inclination angles α as well as orientation angles β are set. The specific schemes are shown in

Table 1. Specimen sizes.

Specimen Sizes with No Fissures	Specimen Sizes Containing Fissures

and

Table 2. Experimental schemes.

Specimen Number	Experimental Schemes	Specimen Number	Experimental Schemes
A	No fissures	B5	β = 180°
B1	β = 0°	C1	α = 0°
B2	β = 45°	C2	α = 30°
B3	β = 90°	C3	α = 60°
B4	β = 135°	C4	α = 90°

.

3. Numerical Strategy for Simulating Material Failure

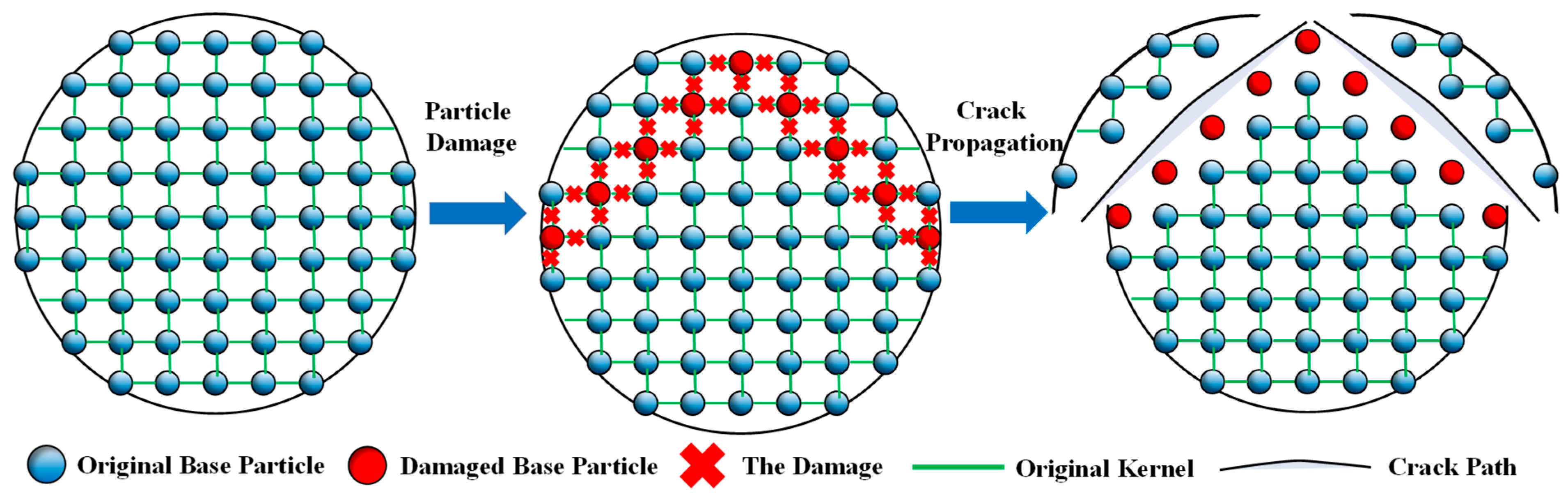
3.1. Numerical Treatments of Crack Propagation in SPH

SPH discretizes the entire computational domain into finite particles. It is necessary to select a suitable fracture criterion to simulate the tunnel-lining damage processes. The tensile stress criterion is utilized in our work [40], which has been widely applied in previous works and has achieved good results. Once maximum principal stress σ₁ exceeds the particle tensile strength σ_t, it is assumed to be in the “failure” state. Mathematical equations of maximum tensile stress criterion are listed below:

$${\sigma }_1={\sigma }_t$$

(1)

Modelling the interaction damage of the tunnel-lining structures also needs to determine the particle failure treatment method in SPH. In our work, a fracture mode coefficient γ is used in this section, and its principle is illustrated in Figure 4. Moreover, The improved kernel function can be expressed in the following form:

$$E(\mathit{x}-{\mathit{x}}^{\prime }, h)=\gamma \cdot W(\mathit{x}-{\mathit{x}}^{\prime }, h)$$

(2)

By substituting Formula (2) into traditional SPH momentum equation to replace the original W, an improved SPH governing equation can be listed below:

$${\displaystyle \frac{d{v}_i^{\alpha }}{dt}}={\displaystyle \sum _{j\in \mathrm{S}}{m}_j}({\displaystyle \frac{{\sigma }_{ij}^{\alpha \beta }}{{\rho }_i^2}}+{\displaystyle \frac{{\sigma }_{ij}^{\alpha \beta }}{{\rho }_j^2}}+T_{ij})\partial E_{ij,\beta }+{\displaystyle \sum _{j\in \mathrm{D}}{m}_j}({\displaystyle \frac{{\sigma }_{ij}^{\alpha \beta }}{{\rho }_i^2}}+{\displaystyle \frac{{\sigma }_d^{\alpha \beta }}{{\rho }_j^2}}+T_{ij})\partial E_{ij,\beta }$$

(3)

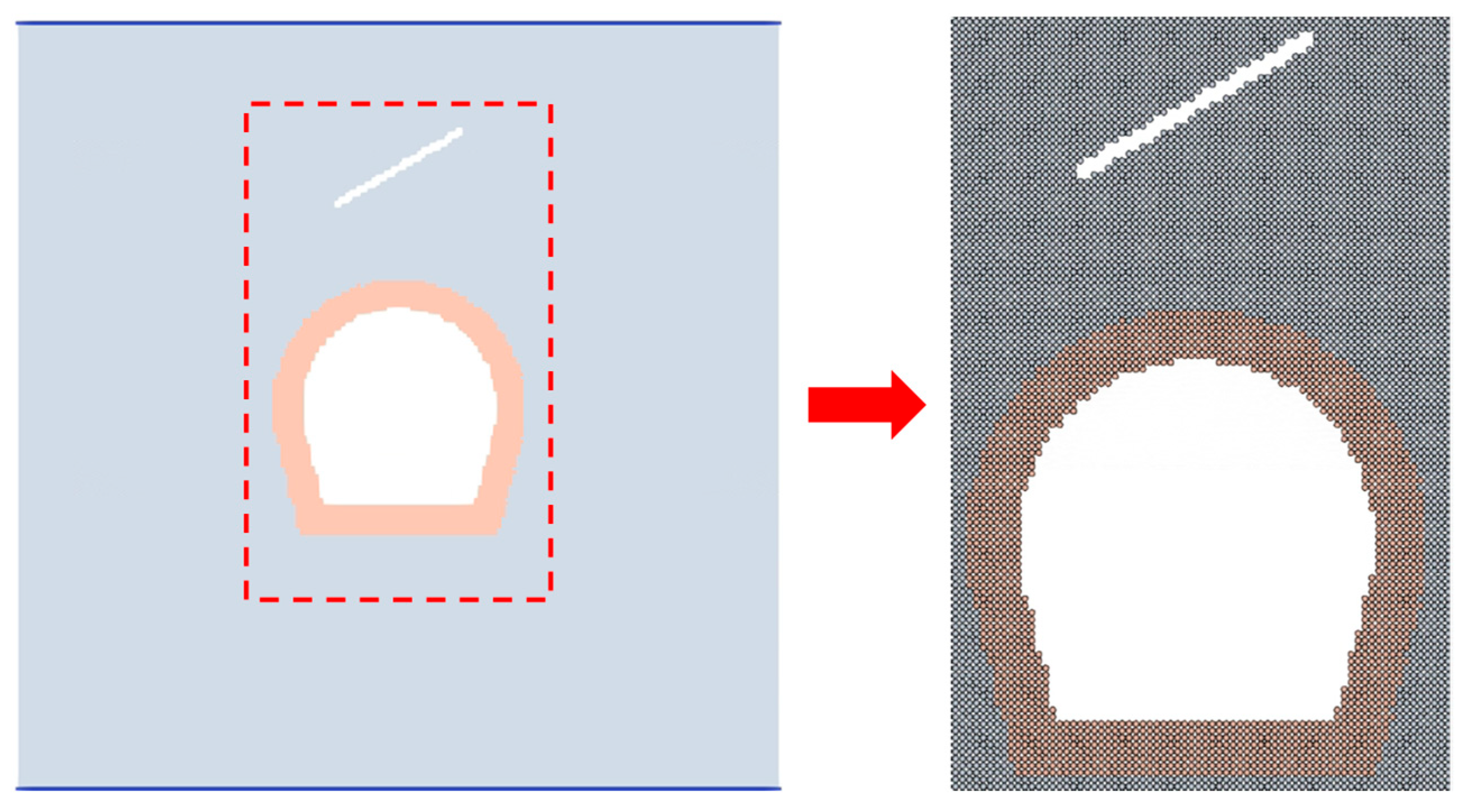
3.2. Model Dimension and Particle Divisions

Established simulation models are illustrated in Figure 5 (taking scheme C2 as an example). The model size is consistent with the experimental sizes in Section 2.3. The numerical parameters used in our simulations are listed below: (1) the elastic modulus of the tunnel model E_T = 17 GPa, the Poisson’s ratio of the tunnel model μ_T = 0.2, and the tensile strength of the tunnel model σ_tT = 4 MPa; (2) the elastic modulus of the lining model E_L = 34 GPa, the Poisson’s ratio of the lining model μ_L = 0.2, and lining tensile strength is set to be σ_tL = 8 MPa.

4. Experimental and Numerical Results

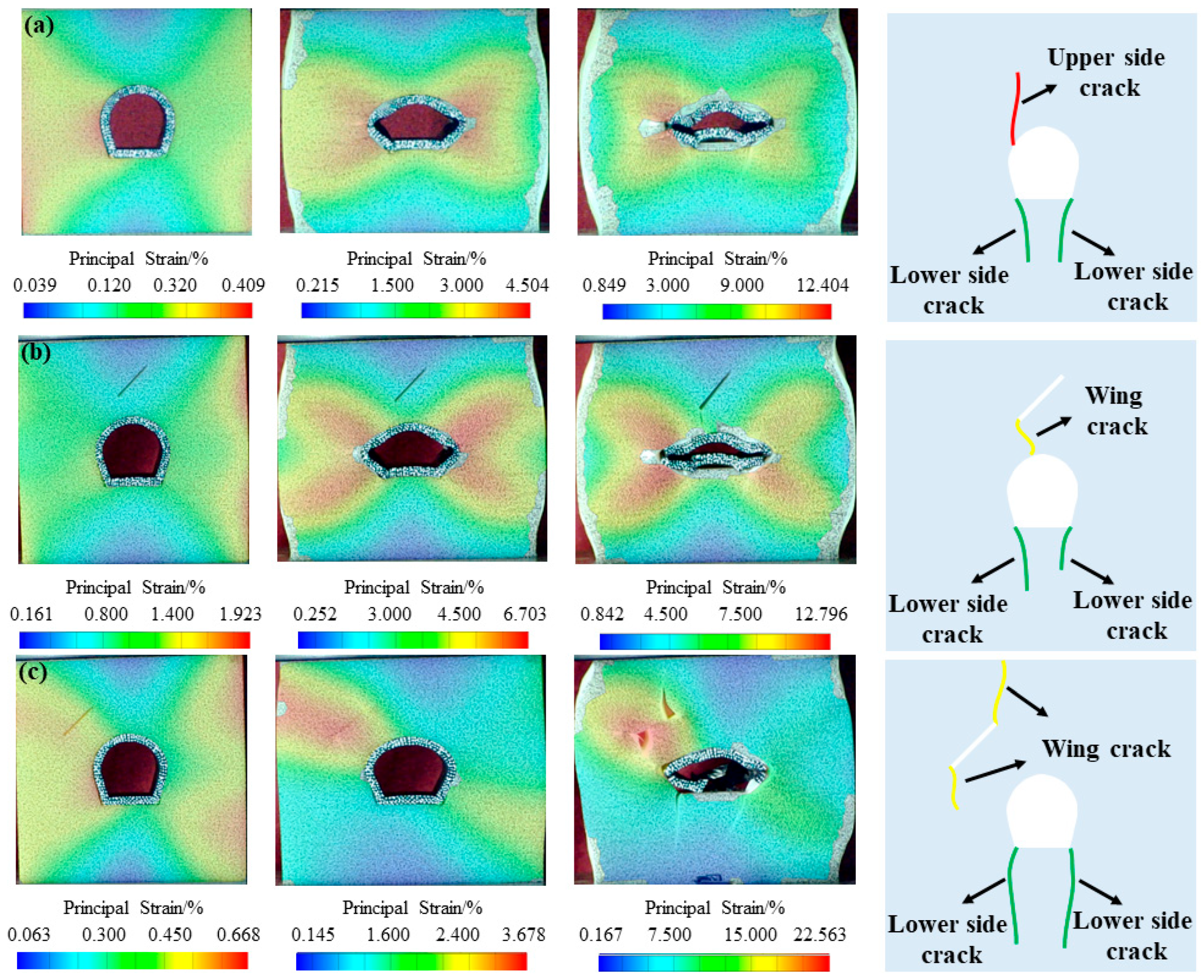
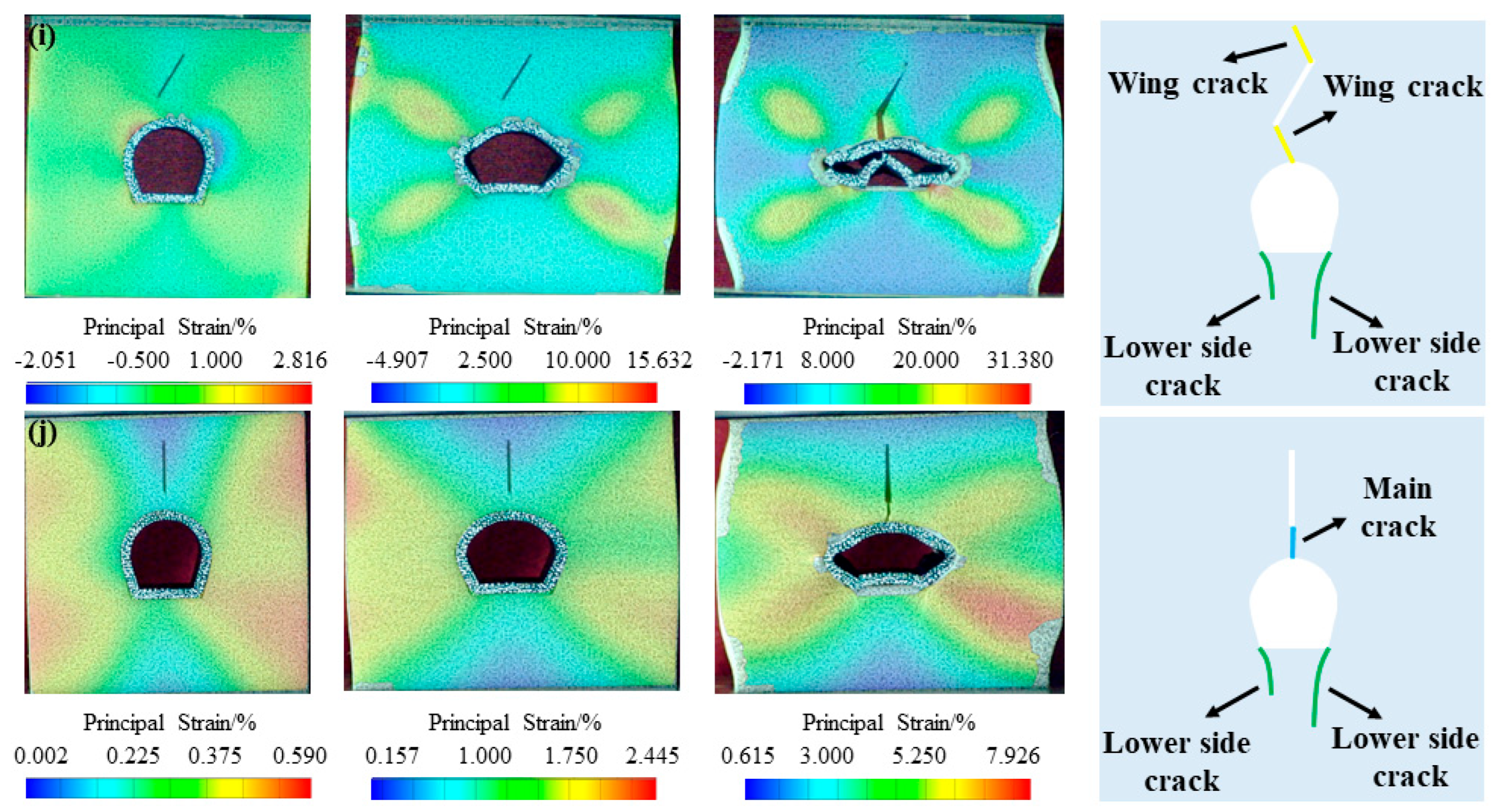
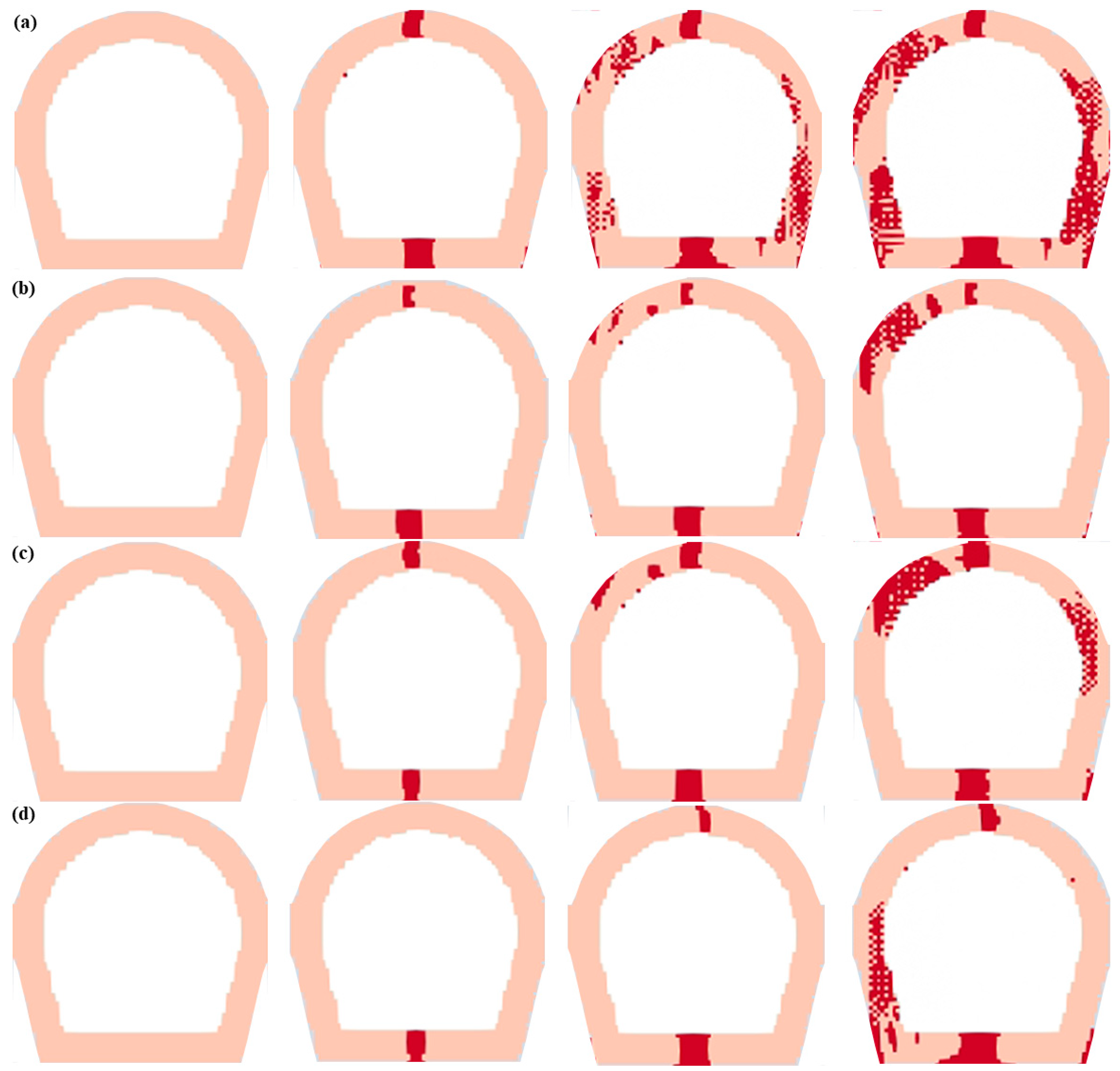
4.1. Crack Propagation of the Tunnel Structure

Figure 6 shows the experimental laws on tunnel crack propagation processes. We can see from the figure that the fissure inclination and orientation angles pose great influences on the failure morphologies. For the non-fissure circumstances, there are two kinds of cracks around the tunnel, namely, the upper-side crack and the lower-side crack, in which the two lower-side cracks present an approximate symmetric distribution along the tunnel model.

Under the circumstances of various fissure orientations β, (1) as for β = 0°, the presence of fissure changes the crack morphologies in the upper part of the tunnel. Firstly, one wing crack initiates at the lower end of the fissure, which propagates and connects with the tunnel. Subsequently, two symmetrical lower-side cracks appear in the lower part of the model, indicating that the prefabricated fissure in the upper part has little impact on crack propagation paths in the lower part of the tunnel. (2) When β = 45°, two anti-symmetric wing cracks are formed at the upper and lower ends of the pre-existing fissure, wherein a wing crack at the lower end stops when it extends to the tunnel left side; however, the upper end position wing crack propagates to the model top. (3) When β = 90°, two wing cracks appear in the fissure upper and lower ends, while the two lower-side cracks at the lower part are no longer symmetrically distributed. The lower-side crack near the prefabricated fissure in the lower-left part of the tunnel is affected by the wing crack, whose propagation length is relatively smaller. The lower-side crack away from the wing crack has a larger propagation length and is less affected by the wing crack. (4) When β = 135°, in this condition, the fissure is close to the tunnel’s lower-left corner, the lower-side crack first occurs between the fissure’s right upper end, and the tunnel’s lower left corner. Then, a wing crack appears at the fissure’s lower-left end. In addition to the lower-side crack in the lower-left corner, no other cracks appear around the tunnel. (5) When β = 180°, the upper-side crack as well as the lower-side crack are similar to those circumstances without prefabricated fissures appearing around the tunnel. However, unlike the scheme without prefabricated fissures, two lower-side cracks are not symmetrically distributed, indicating that the prefabricated fissure in the lower part of the tunnel has a certain influence on the propagation of the lower-side cracks.

Under the circumstances with variations of α, (1) as for α = 0° and 30°, fissure inclination is lower than in other conditions, and there is no wing crack produced from prefabricated fissure tips. An upper-side crack and two lower-side cracks are generated around the tunnel. (2) When α = 45°, two antisymmetric wing cracks are produced, where the upper-wing crack extends to the model top, and the lower-wing crack overlaps with the tunnel top. Affected by the prefabricated fissure, the upper-side cracks do not appear, while two lower-side cracks are generated. (3) When α = 90°, one main crack appears in the fissure’s lower end and overlaps with the tunnel top. The upper part of the tunnel is also affected by a pre-existing fissure, and no upper-side cracks occur, but two lower-side cracks appear.

Figure 7 shows the numerical results of tunnel crack propagation processes. For Scheme A, crack growth occurs at the tunnel top and bottom but stops after it propagates to a certain degree. Subsequently, two lower-side cracks and the upper-side crack lead to the final failure, which is consistent with the test results of Scheme A.

Under the circumstances of various fissure orientations β, (1) as for β = 0°, damage first happens at tunnel sites. Among them, the main crack appears at the bottom of the tunnel and stops after a certain length of expansion. Subsequently, two lower-side cracks and one upper-side crack appear and then expand. At this time, one wing crack appears at the fissure’s lower end and gradually expands to overlap with the top of the tunnel, while the propagation degrees of other wing cracks at the prefabricated fissure upper end are relatively smaller. (2) When β = 45°, two wing cracks with antisymmetric distributions first appear at both fissure ends, and then a crack propagates at tunnel sites, in which two main cracks on the top and bottom have a small propagation degree, while two upper-side cracks as well as one lower-side crack have a larger propagation length, and, finally, they contribute to the model failure. (3) As for β = 90°, the extension degree of two wing cracks is the largest. Then, the main cracks appear, which propagate for a short distance and then stop. Finally, two lower-side cracks appear. (4) When β = 135°, two wing cracks first appear, but their expansion degree is smaller than that of the condition with β = 90°. The wing crack extends to the tunnel’s lower-left corner. The top and bottom of the tunnel produce the main crack with a small expansion distance, and the lower-side crack initiates. (5) As for β = 180°, the tunnel’s top and bottom first produce two main cracks. Subsequently, two lower-side cracks are produced, overlapping with the fissure at the bottom, while one upper-side crack initiates at the tunnel’s upper right.

Under the circumstances of various α, (1) as for α = 0°, cracks are first produced from the fissure’s middle, followed by an upper-side crack. Finally, two lower-side cracks are formed at the bottom of the tunnel. (2) When α = 30°, two upper-side cracks as well as two lower-side cracks are produced. Wing cracks initiating from pre-existing fissure tips stop propagating after extending to a small degree. Finally, two upper-side cracks as well as two lower-side cracks contribute to the final failure. (3) When α = 45°, the upper-side cracks and lower-side cracks are first produced, and then a wing crack is formed from the pre-existing fissure’s lower end, which propagates to the tunnel’s top. (4) When α = 90°, one main crack is formed from the tunnel’s bottom; then, two lower-side cracks propagate from two tunnel corners. Finally, one main crack is formed at the lower end of the prefabricated fissure and runs through the tunnel top.

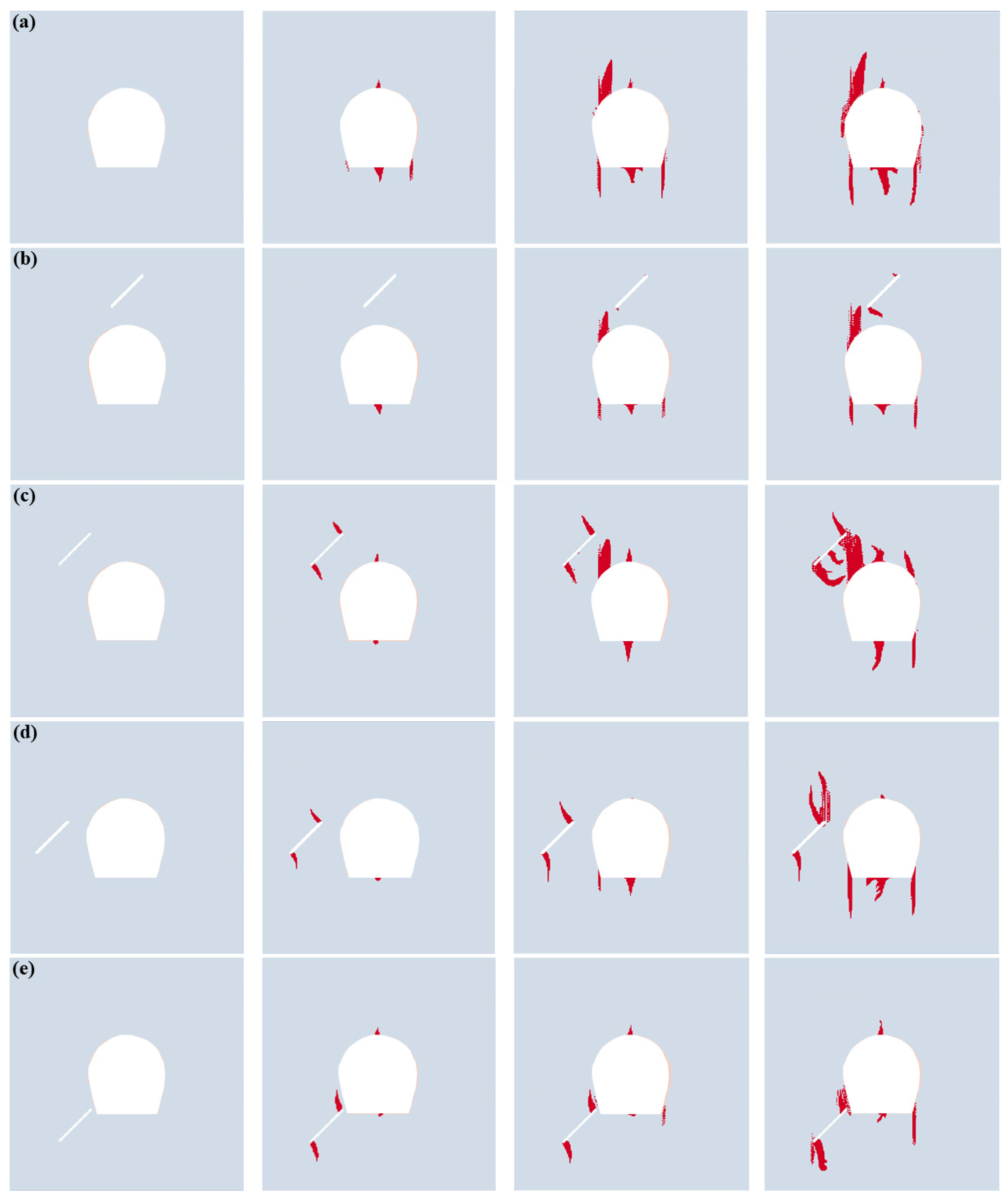
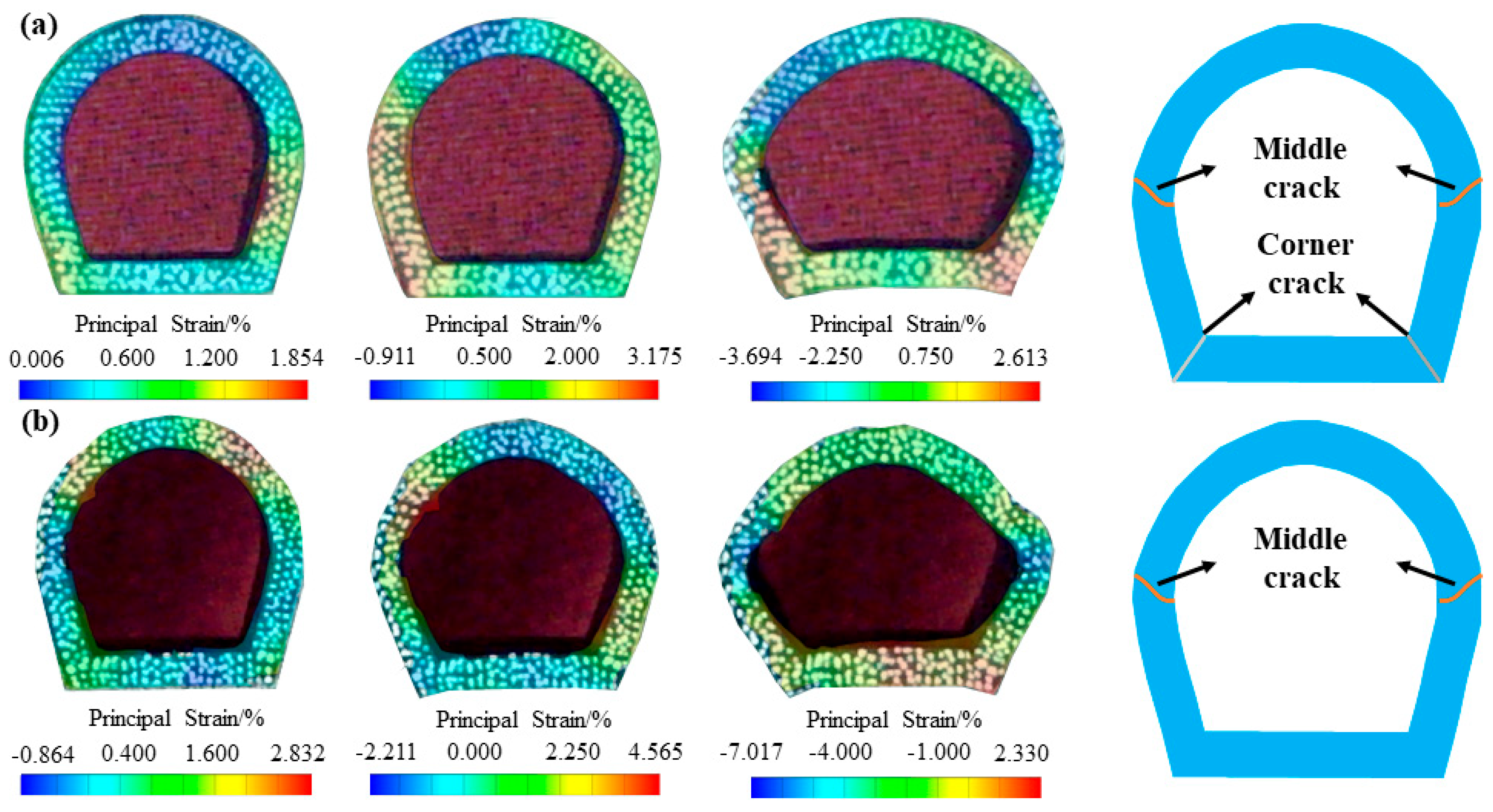
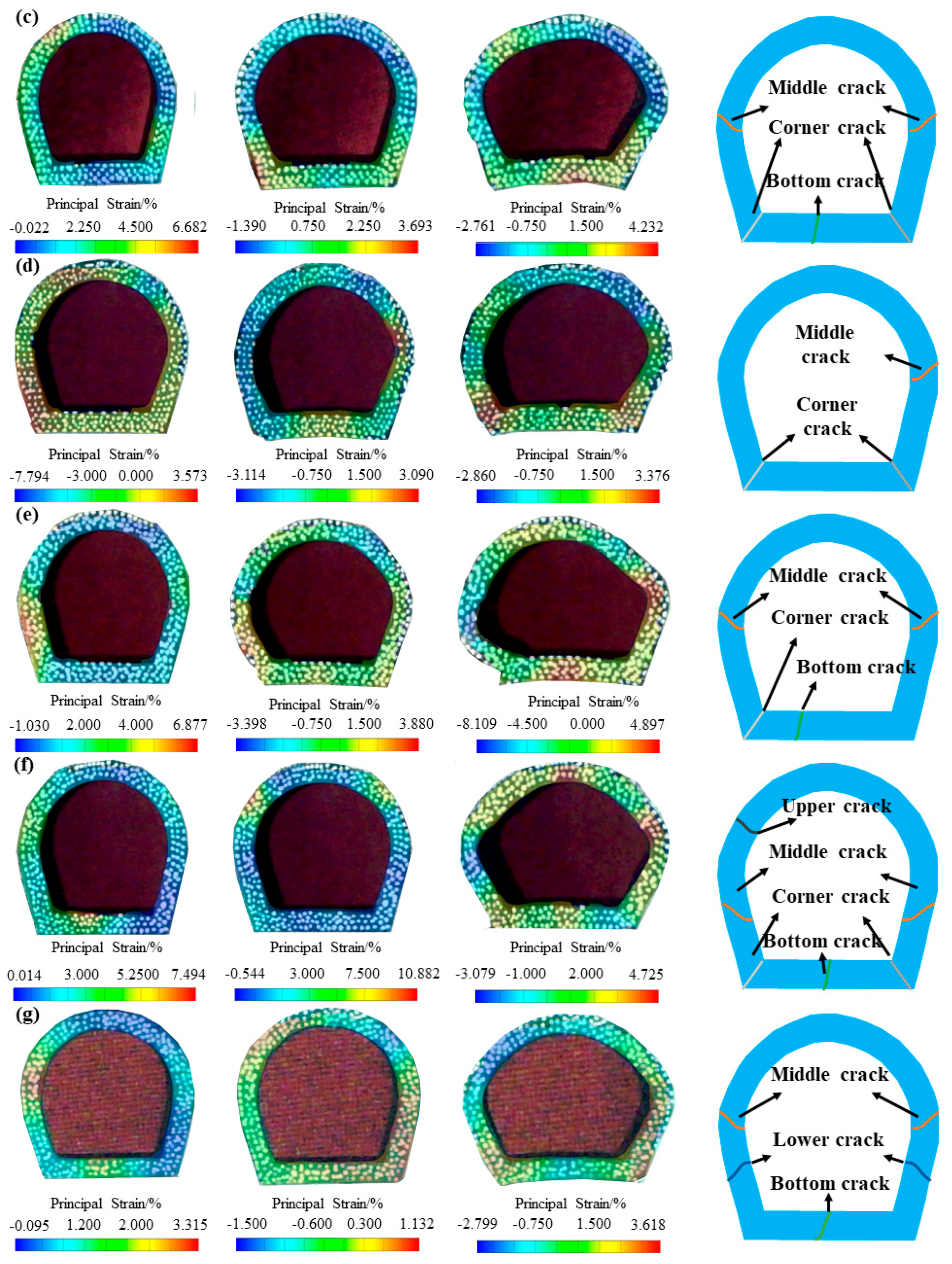
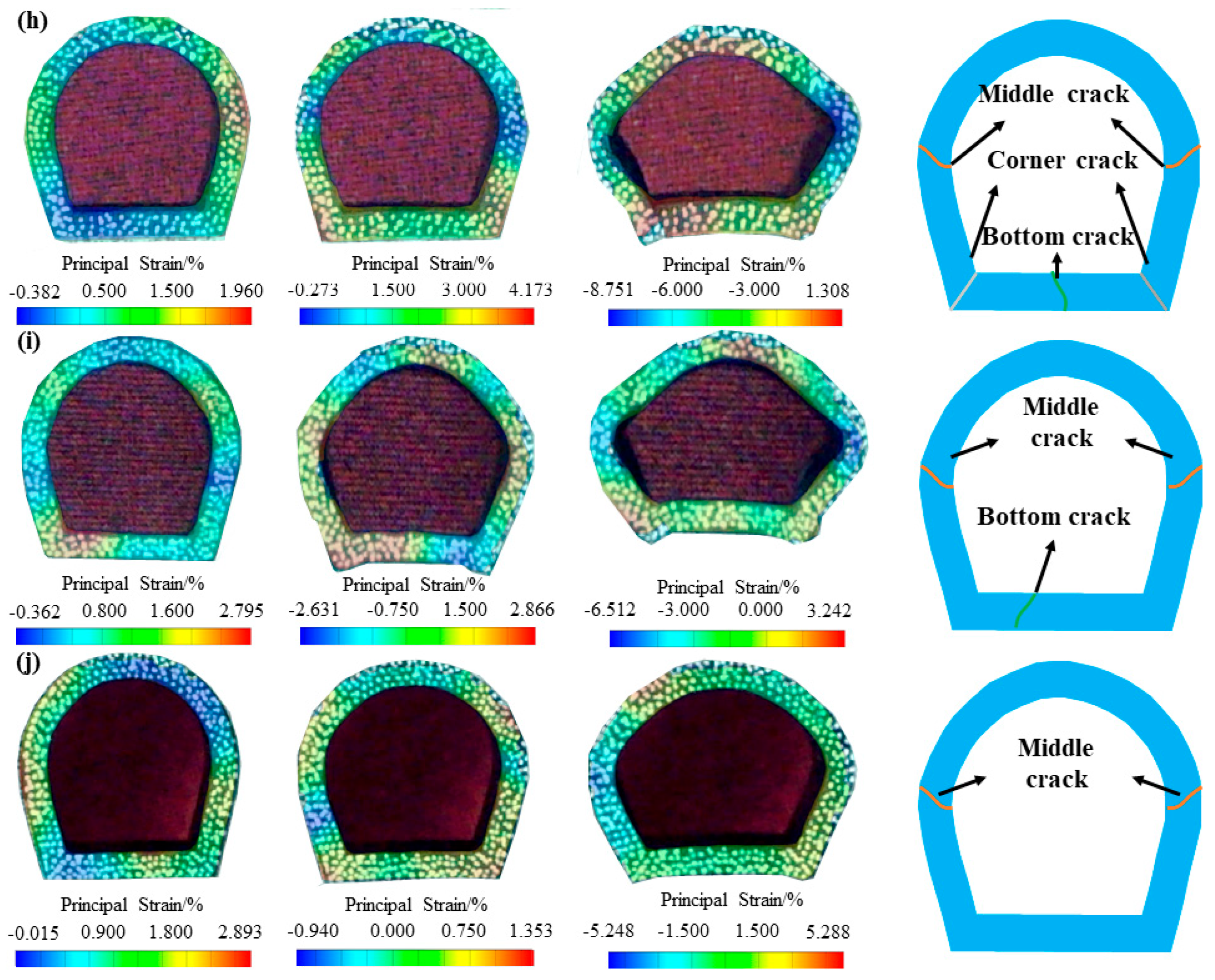
4.2. Crack Propagation Processes of the Lining Structure

Figure 8 shows the damage morphologies of lining structures in various conditions. In general, the crack types mainly include the following: upper crack, middle crack, lower crack, corner crack and bottom crack. The existence of prefabricated fissures with different properties also exerts great impacts on the failure morphologies of the lining. For Scheme A, strain localization occurs at the middle and bottom corners of the lining, resulting in two middle cracks propagating from the lining middle and two middle cracks propagating from the lining corner.

Under the condition of various β, (1) as for β = 0°, the pre-existing fissure is located above the lining in this circumstance; the lining structure basically deforms symmetrically. Strain localization happens in the middle of the lining, so two symmetrical middle cracks are generated in the middle of the lining. (2) When β = 45°, the prefabricated fissure is not located above the lining; therefore, the lining structure begins to undergo asymmetric deformations. However, the main strain localization parts are still in the middle and bottom corner of the lining, and they also appear in the bottom of the lining. As a result, there are two middle cracks initiating from the lining middle, two corner cracks initiating from the lining corners, and one bottom crack initiating from the lining bottom. (3) When β = 90°, the prefabricated fissures are on the lining’s left, and the whole lining is deformed to the right. The strain localization happens at two corner points and the right side; therefore, one middle crack is generated on the right side of the lining, and two corner cracks are generated at the corner points of the lining. (4) When β = 135°, since the prefabricated fissures are close to the lining’s lower-left corner, lining asymmetric deformation in this scheme is the largest, and the entire lining tilts to the lower-left corner, resulting in strain localization in the middle of the lining structure, the lower-left corner and the bottom. Therefore, two middle cracks are generated in the middle of the lining, one corner crack is generated in the lining’s lower-left corner, and one bottom crack is also produced.

Under the condition of various α, (1) as for α = 0°, almost no cracks occur from the pre-existing fissures. Strain localization occurs in the middle, lower and bottom of the lining. Therefore, two middle cracks occur in the middle of the lining, two lower cracks occur in the lower part of the lining, and one bottom crack appears at the bottom of the lining. (2) When α = 30°, the existence of the prefabricated fissure has little influence on the lining structure. Strain localization occurs in the middle, corner and bottom of the lining, corresponding to two middle cracks, two corner cracks and one bottom crack in the lining structure. (3) When α = 45°, wing crack propagation occurs at the prefabricated fissure, which has certain effects on the overall stress distributions of the lining structure. Strain localization occurs in the middle and bottom of the lining, so that two middle cracks occur in the middle of the lining and one bottom crack occurs in the bottom of the lining. (4) When α = 90°, the main crack is produced, resulting in strain localization only in the middle of the lining. Therefore, two middle cracks occur in the middle of the lining.

Figure 9 shows the numerical results of the lining crack propagation processes. For Scheme A, the top crack and bottom crack are first generated at the lining’s top and bottom sites, while two middle cracks are generated at the lining’s middle, and two corner cracks are generated.

Under the condition of various β, (1) as for β = 0°, top and bottom cracks first occur at the top and bottom of the lining structure, respectively. Then, the middle cracks occur at the lining’s middle. (2) When β = 45°, a top crack and bottom crack appear on the top and bottom of the lining. Then, two middle cracks occur in the lining middle, and one corner crack initiates in the lining’s lower-right corner. (3) When β = 90° and 135°, a top crack and bottom crack appear at the top and bottom of the lining structure, respectively. Subsequently, two middle cracks appear in the middle of the lining, and one corner crack is also produced. (4) When β = 180°, in this condition, a pre-existing fissure is located below the lining; this situation is similar to that when β = 0°. A top crack and bottom crack are first generated at the lining’s top and bottom. Then, the upper crack is produced on the upper-right side of the lining structure. Meanwhile, two middle cracks are generated in the lining’s middle, and two lower cracks propagate in the lining bottom.

Under the condition of various α, (1) as for α = 0°, upper cracks, middle cracks and lower cracks are generated at the right side of the lining. Meanwhile, two corner cracks are produced on the bottom corner of the lining. (2) When α = 30°, top cracks and bottom cracks are first produced at the lining’s top and bottom, followed by two middle cracks at the lining’s middle. (3) When α = 45°, upper cracks and lower cracks first appear at the lining’s top and bottom, and the middle cracks and lower cracks are produced at the lining side. (4) When α = 90°, the top and bottom of the lining produce upper and lower cracks, while the lining side produces two lower cracks.

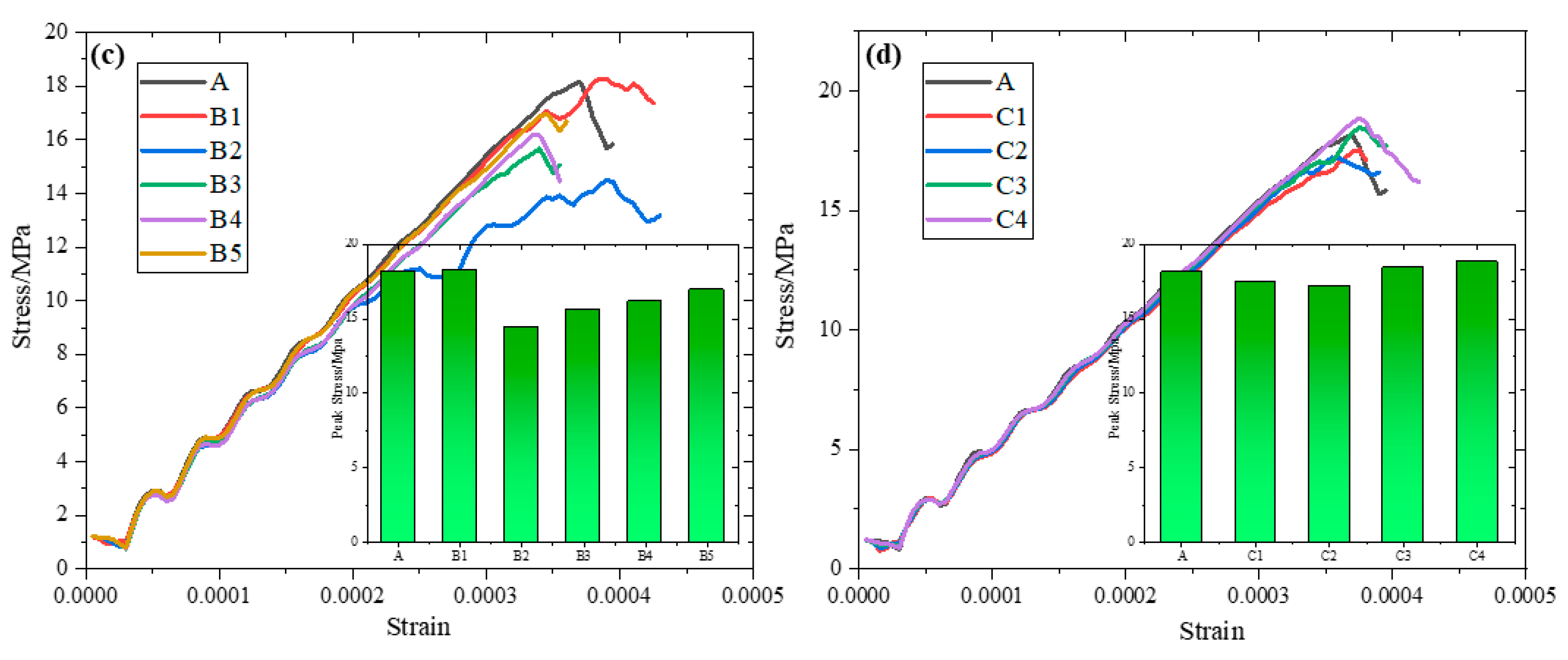
4.3. Influences of Fissure Inclination and Orientation Angles on Tunnel-Lining Structure Strength

Figure 10 illustrates the stress–strain curves of tunnel-lining structures. The stress–strain curve of the tunnel-lining structure mainly presents four different periods: (1) initial compression period, where the curve is concave, showing that the cracks in the specimen are compressed in this period; (2) elastic deformation period, where the curve presents a linear relationship, and the specimen is in recoverable elastic deformation, indicating that there are no cracks initiating in the specimen; (3) elastoplastic deformation period, where the curve of the sample presents a lower concave shape, indicating that the specimen has unrecoverable plastic deformation and internal cracks initiate and propagate; (4) post-peak period, where the sample strain increases, while the stress gradually decreases, indicating that the sample is damaged at this time.

Under the condition of various β (Scheme B), with an increase in β, the peak strength shows a trend of first decreasing and then increasing. This is because when β is close to 90°, the prefabricated fissure is located on tunnel’s left; hence, the asymmetric deformation is the largest. Therefore, a larger stress concentration occurs, and its peak strength reduces greatly. However, under the condition of different α (Scheme C), the sample’s peak strengths are almost the same. This is because the prefabricated fissure is located right above the tunnel-lining structure, so the deformation of the sample is basically symmetrical. Therefore, the prefabricated fissure has less influence on the tunnel-lining structures. In the SPH simulation, the peak strength also shows a trend of first decreasing and then increasing with β and has no obvious changes for different fissure inclination angles α.

5. Discussions on Cracking Mechanisms

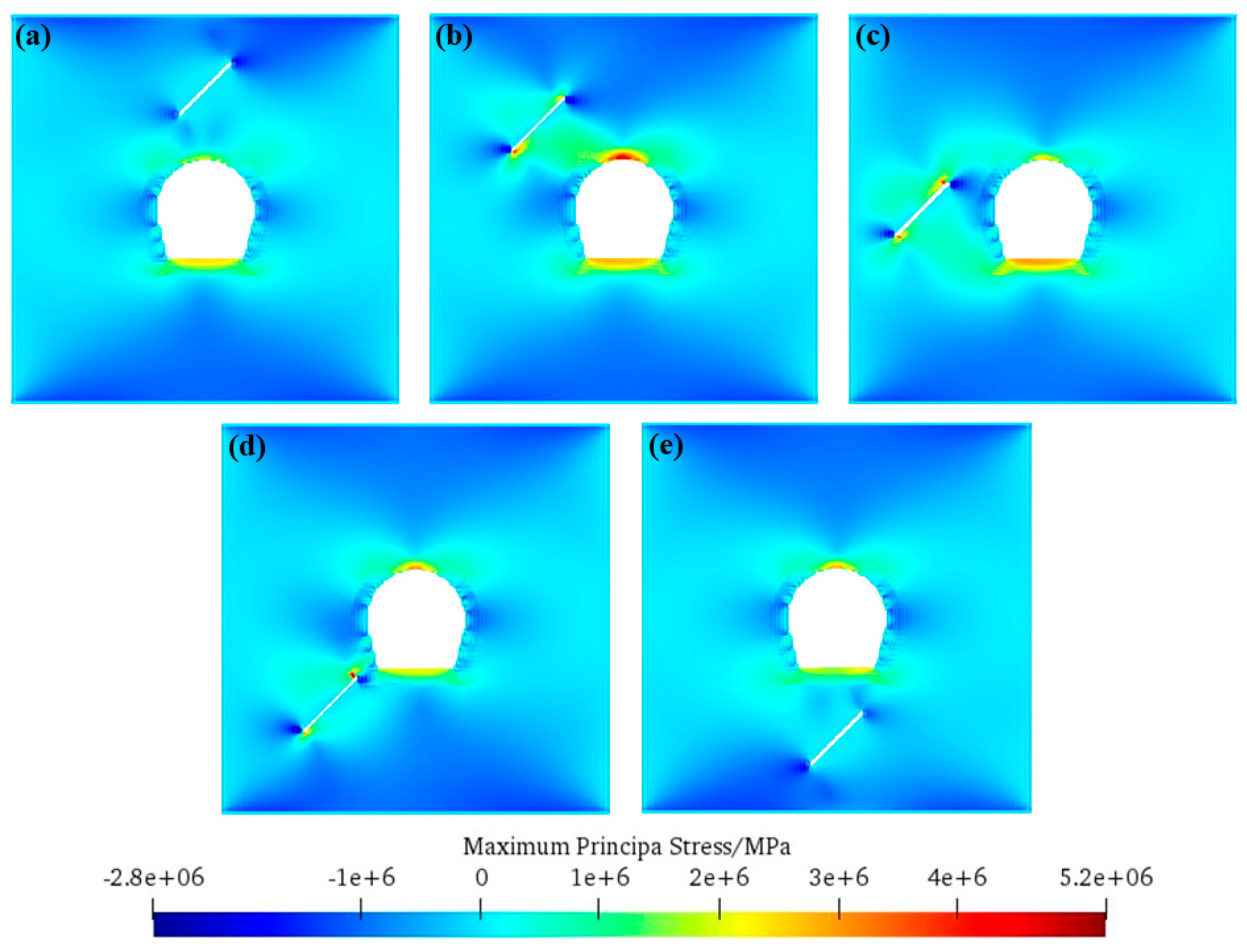
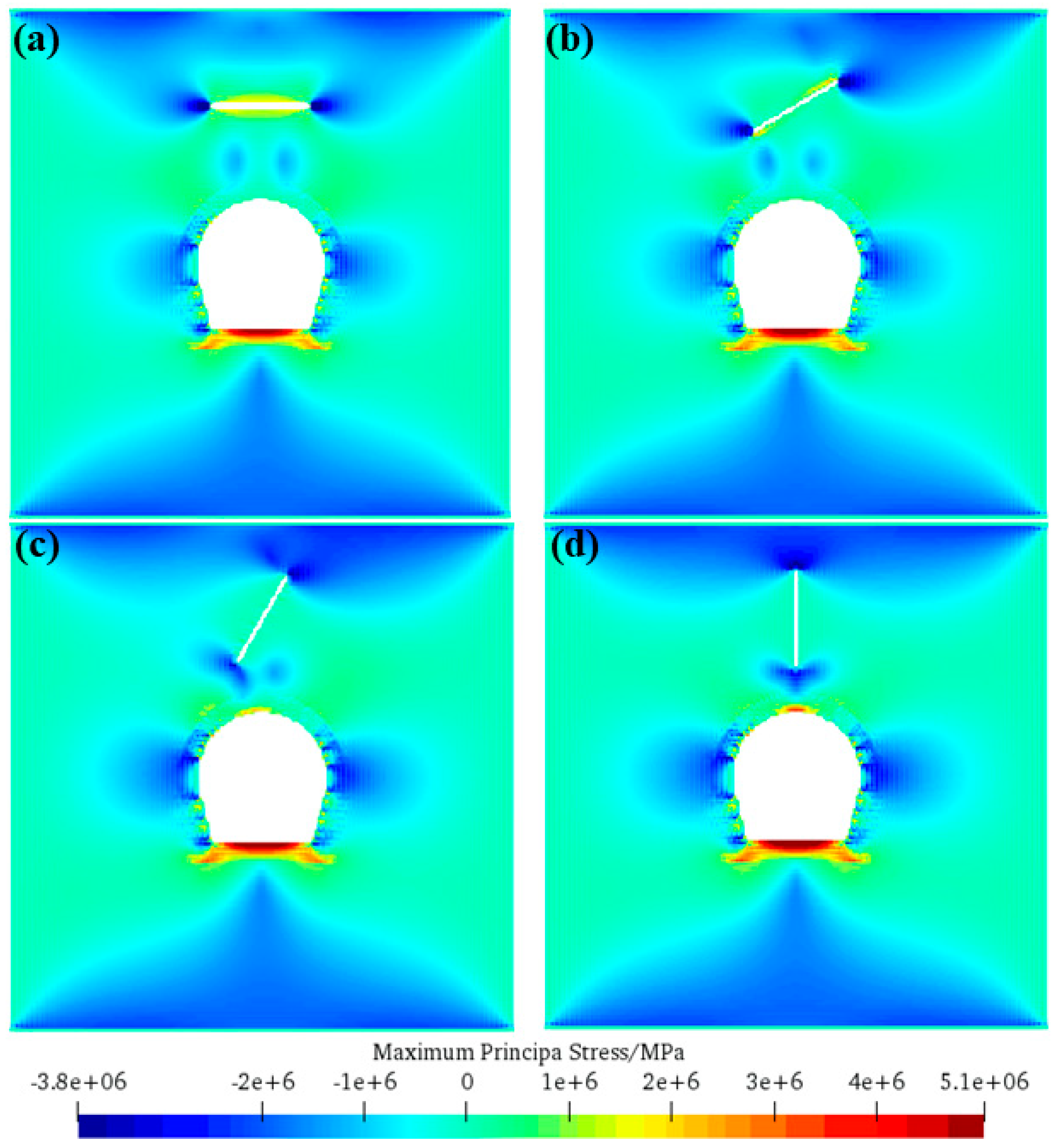
5.1. Crack Initiation Mechanisms of Tunnel-Lining Structures in Scheme A

Figure 11 shows the distributions of the maximum principal stress of the tunnel-lining structures without prefabricated fissures (Scheme A) prior to crack initiation (Step 20) and after crack initiation (Step 50). We can infer from the presented results that, before a crack appears in the model, the tensile stress concentration occurs at the top and bottom of the lining; therefore, a top crack and bottom crack are produced at the lining’s top and bottom sites, respectively. Then, after the propagation of the top crack and bottom crack, a higher tensile stress concentration occurs from the tunnel’s upper and lower sides, which is also the cause of upper- and lower-side cracks around the tunnel. In addition, tensile stress is also concentrated at the bottom corner of the lining, which is also the reason for the formations of corner cracks at the bottom of the lining.

5.2. Crack Initiation Mechanisms of Tunnel-Lining Structures with Various Orientations

Figure 12 shows the maximum principal stress distributions of the tunnel-lining structures before crack initiation under different fissure orientations (Scheme B). We can infer from the presented results that, when the orientation β approaches 90°, the tensile stress concentration degree at both pre-existing fissure ends becomes the largest, so that wing crack propagation first occurs. At this time, the tunnel-lining structure has asymmetric deformation, leading to a larger stress concentration, so that the peak strength in this circumstance is smaller.

When the prefabricated fissure orientation angle β is 0° or 180°, the tensile stress concentration mentioned in the above position is smaller, while the concentration around the tunnel and lining is larger. Therefore, crack propagation first occurs in the tunnel-lining structures, and these schemes are close to the conditions containing no prefabricated fissures (Scheme A).

5.3. Crack Initiation Mechanisms of Tunnel-Lining Structures with Various Inclinations

Figure 13 shows the distributions of maximum principal stress for the tunnel-lining structures before crack initiation under different fissure inclinations (Scheme C). We can infer from the presented results that the tensile stress mentioned in the above position is obviously much smaller than that around the tunnel-lining structures; therefore, different fissure inclinations have limited influences on the stress distributions on the specimens. This is also the reason why there are few differences in peak strength under different prefabricated fissure inclinations.

5.4. Limitations of SPH Method for Simulating Crack Propagation

The SPH model employed in this study relies on a linear elastic–brittle framework with a maximum principal stress criterion to simulate crack propagation, which inherently involves several simplifications that may affect its accuracy in capturing real-world tunnel-lining failure mechanisms. These limitations are discussed as follows.

5.4.1. Neglecting the Rate Dependency and Time Effects

The current model assumes instantaneous stress transfer and static loading conditions, ignoring rate-dependent behaviors such as strain rate effects on material strength and viscous dissipation during crack propagation. In reality, tunnel linings may undergo dynamic loading (e.g., seismic events or blasting) or time-dependent creep deformation under sustained stress, which can alter crack initiation and propagation paths. For example, dynamic loading can induce inertial effects that lead to different crack patterns compared to static uniaxial compression. The absence of rate dependency in the SPH model limits its applicability to scenarios involving time-varying loads, such as long-term serviceability assessments of tunnels in active fault zones.

5.4.2. Simplified Treatment of Mixed-Mode Fracture

The model uses a pure tensile stress criterion to trigger crack initiation, neglecting mixed-mode (tension-shear) fracture mechanisms that are common in tunnel-lining structures. In practice, prefabricated fissures or defects in surrounding rock masses often induce combined tensile and shear stresses at crack tips, leading to complex propagation paths that deviate from the purely tensile-dominated wing cracks observed in this study (e.g., shear-driven crack coalescence in Figure 6 for β = 45°). More sophisticated criteria, such as the Mohr–Coulomb or Griffith criterion, would be required to account for shear effects on crack behavior, especially in cases where fissure orientations are oblique to the principal stress direction.

5.4.3. Lack of Plastic Deformation and Damage Evolution

The linear elastic–brittle assumption implies instantaneous failure once the tensile strength is exceeded, ignoring progressive damage accumulation and plastic deformation in the lining material. Real concrete or rock-like materials exhibit nonlinear behavior, including micro-crack nucleation, yielding, and post-peak stress softening, which are critical for predicting the full failure process (e.g., the transition from elastic deformation to strain localization in Figure 10). For instance, the experimental stress–strain curves show an elastoplastic deformation stage (Section 4.3), whereas the SPH model simulates abrupt failure, without capturing the gradual stiffness degradation observed in tests. Incorporating damage mechanics (e.g., continuum damage models) into SPH could improve the representation of such behaviors.

5.4.4. Inadequate Representation of Material Heterogeneity

The model assumes homogeneous material properties, while actual tunnel linings and surrounding rocks exhibit microscale heterogeneity (e.g., aggregate distribution, voids), which can significantly influence crack branching and arrest. For example, the symmetric crack patterns in Scheme A (Figure 6a) may not fully reflect the randomness of crack paths in heterogeneous materials. Advanced particle-based methods, such as the Generalized Particle Dynamics (GPD) approach, could introduce randomness in particle properties to simulate heterogeneity, but this was beyond the scope of the current study.

6. Conclusions

(1)

Uniaxial compression fracture tests of tunnel-lining structures containing prefabricated fissures are carried out based on 3D-printing technology and DIC technology, and the impacts of various fissure properties on the failure laws of tunnel-lining structures are explored.

(2)

Three types of cracks occur at tunnel sites, namely main crack, upper-side crack and lower-side crack.

(3)

Five types of cracks occur around the lining, namely upper crack, middle crack, lower crack, corner crack and bottom crack. When a wing crack propagation occurs in prefabricated fissures, the crack propagation degree around the lining is relatively small, while when wing cracks do not initiate from prefabricated fissures, more cracks are produced around the lining.

(4)

Crack initiation mechanisms of tunnel-lining structures under different schemes are discussed: The tension stress concentration at the bottom of the tunnel-lining structure is the cause of the bottom crack. After the initiation of the bottom crack, a stress concentration occurs at the tunnel’s upper and lower parts, which is the cause of the upper- and lower-side crack around the tunnel. When the fissure orientation angle β is close to 90°, tensile stress concentrations are larger, contributing to wing crack extensions prior to the crack propagation in tunnel-lining structures.