Abstract
This study presents a closed-form solution for the dynamic response of a sandwich beam subjected to arbitrary impact loading, with a particular focus on energy harvesting from an attached piezoelectric layer. A thin piezoelectric patch is bonded to the bottom surface of the beam to convert mechanical vibrations into electrical energy. The governing equations of motion are derived using Hamilton’s principle, considering a non-symmetric sandwich cross-section and incorporating higher-order shear deformation effects. The state–space method is employed to obtain the exact dynamic response of the beam under impact excitation. The differential equations governing the output voltage and harvested power are solved analytically based on the derived response. The natural frequencies and dynamic responses are validated against classical beam theory, highlighting the significance of shear deformation. Numerical examples are provided to evaluate the generated voltage and energy harvesting efficiency. The results demonstrate the strong potential for energy harvesting from sandwich beam vibrations and elucidate the influence of impact loading conditions, distributed load amplitude, and the geometric dimensions of the beam on the harvested output.
1. Introduction
Piezoelectric materials possess the remarkable property of generating electricity in response to mechanical strain [1]. A layer of piezoelectric material is adhered to the surface of vibrating bodies, such as beams, plates, bridges, buildings, or mechanical machinery and equipment. When subjected to external excitations such as loads [2], earthquakes [3], or motors [4], deformation is induced in the piezoelectric layer, enabling the harvesting of useful energy from the vibrations of the structure or mechanical device. This process represents a form of energy regeneration where excess vibration is converted into electrical energy. Additionally, piezoelectric materials have numerous applications in structural control [5,6].
Sandwich beams, with material distribution optimized for specific loading conditions, are widely used in construction. Numerous studies have been conducted on sandwich beams in general [7], as well as on their dynamic behavior. V.T.A. Ninh [8] and P.T.B. Lien [9] investigated the natural frequencies of vibration of functionally graded sandwich beams resting on an elastic foundation. T.D. Hien [10] calculated the dynamic response of sandwich beams under moving loads using the finite element method. T.T. Thanh et al. [11] investigated the static bending and stability of unsymmetric functionally graded sandwich beams using higher-order finite element methods.
Recent studies by Huan Duong Thanh et al. [12] indicate that piezoelectric layers in small-scale systems, such as mobile devices, can achieve significant energy-harvesting efficiency. Advances in piezoelectric materials are opening new opportunities, not only in vibration-based energy harvesting but also in applications in transportation, infrastructure, and portable devices. Recent work by Wang Zuowei et al. [13] and Song Jiawen et al. [14] has highlighted new materials that enhance energy-harvesting performance, underscoring the ongoing development of this field. Research trends increasingly focus on optimizing piezoelectric materials and application structures in real-world systems. Studies by Tonan Michele et al. [15] and Frýba L. [16] continue to advance design optimization methods, making vibration-based energy harvesting a viable solution for smart and sustainable systems.
Energy harvesting from beam vibrations has emerged as a prominent area of research due to its potential applications in structural health monitoring and powering low-energy devices. The study by Du et al. [17] focuses on acoustic black hole piezoelectric energy harvesting under Gaussian white noise excitation, demonstrating high efficiency under stochastic conditions. Similarly, Zhang et al. [18] and Mousavi et al. [19] explore energy harvesting from bridge and beam vibrations under dynamic loads, leveraging bi-stable characteristics to enhance energy conversion efficiency in transportation infrastructure applications. Hassan et al. [20] investigate energy harvesting from environmental noise in traffic areas, utilizing an array of piezoelectric cantilever plates, which proves effective in regions with high vehicular activity. Meanwhile, Adoukatl et al. [21] develop a high-order nonlinear model for piezoelectric beams subjected to parametric and direct excitations, providing insights into optimizing energy harvesting under complex dynamic conditions. Other studies, such as those by Song et al. [14] and Wang et al. [22], focus on optimizing harvester designs, including the width-splitting method for coupled bending-torsion vibrations and semi-analytical models for flexural wave propagation in piezoelectric composite beams. Lu et al. [23] and Amini et al. [24] analyze energy harvesting capabilities in multi-span beams or beams under moving loads, offering both theoretical and experimental insights to improve system performance. The work by Paknejad et al. [25] provides an analytical solution for energy harvester patches on multilayer composite beams.
Previous research indicates that analyzing the vibrations of beams under moving loads is essential for optimizing energy harvesting performance. Theoretical and experimental models, such as those by Erturk [26] and Ali et al. [27], offer a clearer understanding of beam vibration mechanisms, facilitating the design of more efficient energy-harvesting systems. The high-order shear deformation theory (HSDT) has been successfully applied to model complex beam structures, especially in cases of thick or heterogeneous materials. Studies by Kadivar and Mohebpour [28] demonstrate that HSDT enhances the accuracy of vibration analysis and energy-harvesting calculations, further optimizing beam structures for applications such as infrastructure-based energy harvesting.
The primary objective of this study is to develop an analytical framework for investigating the dynamic response and energy harvesting performance of a sandwich beam with an asymmetric cross-section, incorporating higher-order shear deformation effects. Specifically, the study aims to (i) derive exact solutions for the natural frequencies and dynamic responses of the beam subjected to arbitrary impact loads using a state–space method and (ii) analytically compute the voltage and electrical power harvested from a piezoelectric layer attached to the bottom surface of the beam. This research seeks to provide a comprehensive understanding of the influence of shear deformation, impact load characteristics, distributed load amplitude, and the geometric dimensions of the beam on both the dynamic behavior and energy harvesting efficiency of asymmetric sandwich beam systems.
2. Equation of Motion for Unsymmetric Sandwich Beam Based on a Refined Shear Deformation Theory
2.1. Governing Equations
An unsymmetric sandwich beam of length L is considered, whose cross-section consists of a core layer, an upper face sheet, and a lower face sheet, as illustrated in Figure 1. A thin piezoelectric layer is attached to the bottom surface of the beam. Since the elastic modulus of the piezoelectric material is significantly lower than that of the beam’s face sheets, its stiffness is neglected in the structural analysis.
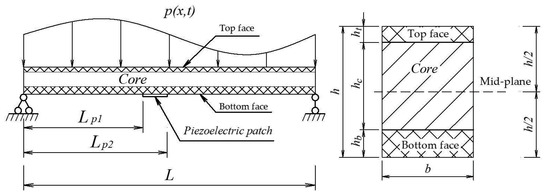
Figure 1.
Unsymmetrical sandwich beam model.
Numerous studies have demonstrated that accounting for shear deformation significantly improves the accuracy of displacement, natural frequency, and critical load predictions in beam analysis. In the present work, a higher-order shear deformation theory (HSDT) incorporating trigonometric functions, as proposed in [29], is employed. The displacement fields U, W of the beam are expressed as follows:
where are the displacement components on the mid-plane, respectively.
The kinetic energy of the system comprises the kinetic energy of both the core layer and the face sheets, expressed as follows:
The potential energy of the applied load q is
The strain energy of the beam includes the strain energy of the core layer and the face layer:
where A, B, etc., are the beam stiffness defined by
For sandwich beams with cross-sections composed of multiple distinct materials, each layer—namely the core and face sheets—possesses its own elastic modulus, mass density, and other mechanical properties. Consequently, when performing integration along the thickness direction z, these parameters cannot be treated as continuous throughout the entire domain. Instead, the integration must be partitioned into separate subdomains, each corresponding to a specific material layer.
In Equation (6), the domains Ac and AF represent the cross-sectional areas of the core and face layers, respectively. The elastic moduli of the core and face layers are denoted by Ec and EF, while GC and GF refer to the corresponding shear moduli of the core and face materials.
Using Hamilton’s principle to write the differential equation of motion:
The differential equations of motion are
where q is the transverse load, are the stress resultants, and the inertias are defined by:
2.2. Analytical Solution for Dynamic Response
The simple support boundary conditions are
The sinusoidal function is chosen to satisfy all the boundary conditions as follows:
where are the displacement coefficients, .
The uniformly distributed transverse load is expanded in Fourier series as
where Pn:
Substituting the displacement in Equation (11) into the equation of motion Equation (8), and using the orthogonality property of trigonometric functions, the equation of motion can be written as follows:
where
By multiplying both sides of Equation (14) by Equation (16) is obtained.
Equation (16) is rewritten in the form of Equation (17).
The matrices involved in Equation (17) are expressed in the following form:
By substituting Equation (18) into Equation (17), Equation (19) is obtained as follows:
Next, Equation (19) is rewritten in the form of
The matrices appearing in Equation (20) are defined as follows:
The state vector represents the instantaneous dynamic condition of the structural system through the displacement and velocity of a vibration mode. The system matrix characterizes the intrinsic dynamic behavior, capturing the relationship between stiffness and structural response. Together, and form the foundation of the state–space approach in vibration analysis.
Substituting Equations (21) and (22) into Equation (20) results in Equation (23).
Solving Equation (23) by state space method, we can obtain the solution as follows:
where are eigenvalues and Eigen matrix of matrix .
2.3. Energy Harvesting from the Piezoelectric Layer
The electromechanical outputs of the piezoelectric response from vibrations of the structure under open circuit conditions applying the approach of Erturk and Inman [1], the relationships for piezoelectric materials are
where ε is the strain, E is the external electric vector, D is the electric displacement vector, and is the elastic compliance tensor.
When there is no external voltage (E = 0), electric displacement takes the form:
The voltage obtained from the piezoelectric pad across the resistive load can be described by the equation according to Erturk and Inman [1]:
where Cp is the piezoceramic patch capacitance, and is the plane stress piezoelectric stress.
The transform Formula (29) is as follows:
where
The solution of the first-order differential Equation (31) is formed:
The harvested power due to beam vibration is
3. Results
3.1. Numerical Example for Validation
3.1.1. Comparison of Natural Vibration Frequencies
Verification Example 1
Consider a sandwich beam composed of a concrete core layer and steel face sheets at the top and bottom. The beam is simply supported with a span length L = 8 m, height h varying from 0.4 m to 0.8 m, and width b = 0.3 m. The thickness of the top face sheet is ht = 1 cm, while that of the bottom face sheet is hb = 2 cm. The material properties of the core and face layers are taken as given in Table 1.

Table 1.
Material properties of the face sheets and the core layer.
The comparison results of the first three vibration modes of the sandwich beam, considering higher-order shear deformation, with those calculated by the classical beam theory as presented in Reddy’s textbook [30], are shown. Table 2 displays the natural frequencies of the first three modes for beam heights ranging from 40 cm to 80 cm. The results clearly indicate that the error progressively increases with both the vibration mode number and the beam height. This can be explained by the increasing influence of shear deformation as the beam height increases, which leads to larger discrepancies in natural frequencies compared to the classical beam theory.

Table 2.
Comparison of natural vibration frequencies: higher-order shear deformation theory and classical beam theory.
3.1.2. Comparison of Vibration Behavior
To compare the dynamic responses, the study employs the finite element model of a sandwich beam under moving loads from the reference [10] to formulate the dynamic problem of the sandwich beam subjected to dynamic loading. A classical beam element with six degrees of freedom, as shown in Figure 2, is used to establish the finite element equations for the dynamic analysis of the sandwich beam.
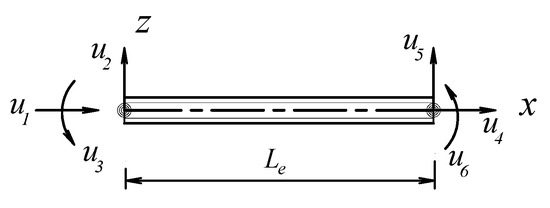
Figure 2.
The element model of the asymmetric sandwich beam.
The axial displacement u(x) at the mid-span and the vertical displacement v(x) are approximated as follows:
where the interpolation functions Ni are
From these shape functions, the stiffness matrix [K], mass matrix [M], damping matrix [C], and load vector [21] are formulated. The equation of motion of the beam is derived based on the variational principle as follows:
The dynamic response is obtained by solving the equation of motion 37 using the Newmark algorithm, as presented in the reference [31]. The dynamic load applied in this example is a uniformly distributed force along the entire length of the beam, and the function of times is considered as follows:
For sine loading
For step loading
For triangular loading
To perform the comparison of the beam’s dynamic responses, the dimensions and material properties of the beam are taken as in Section 3.1.1, with a beam height of h = 60 cm and a uniformly distributed load intensity of .
Figure 3 illustrates the vibration response at the mid-span of the beam under three types of loading: sine loading, step loading, and triangular loading, obtained using both the analytical method and the finite element method. The results clearly show that the discrepancy between the two methods is minimal. Moreover, the analytical method employed in this study, which incorporates higher-order shear deformation, tends to predict slightly larger responses compared to the finite element method based on classical beam theory that neglects shear deformation.
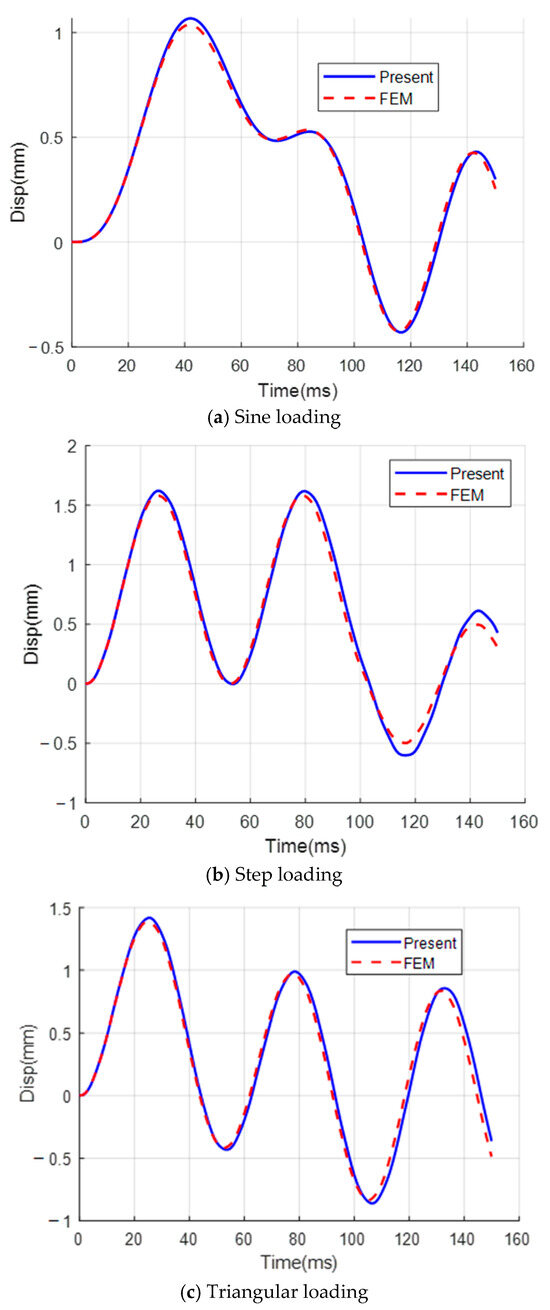
Figure 3.
Comparison of the dynamic response at the mid-span of the beam analyzed using FEM and the closed-form solution.
3.2. Energy Harvesting Analysis Based on Beam Vibration
In this section, the study calculates the energy harvested from the piezoelectric material layer attached to the bottom surface of the beam, as illustrated in Figure 1. The piezoelectric material used is lead zirconate titanate (PZT-5A), as referenced in [26], with its properties listed in Table 3.

Table 3.
Properties of piezoelectric material.
Using the analytical approach presented in Section 2, the voltage and harvested power are calculated, as shown in Figure 4, Figure 5 and Figure 6, corresponding to sinusoidal loading, step loading, and triangular loading, respectively.
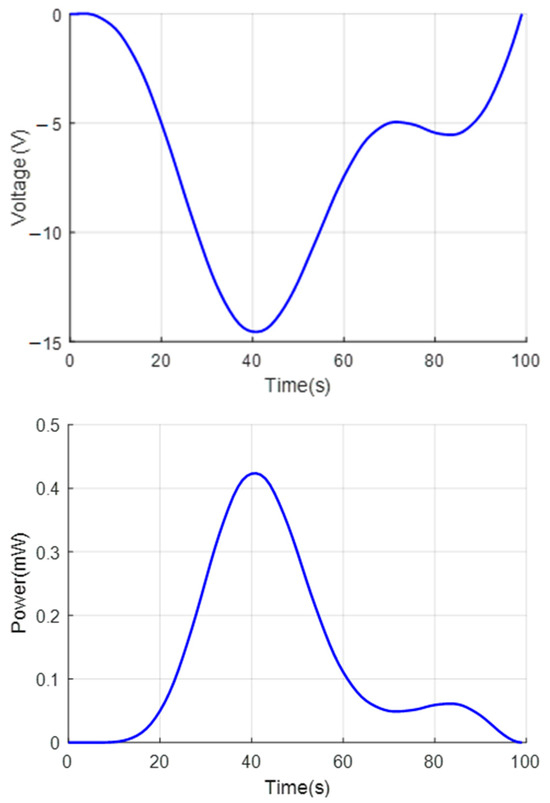
Figure 4.
Voltage and harvested energy power under sinusoidal load conditions.
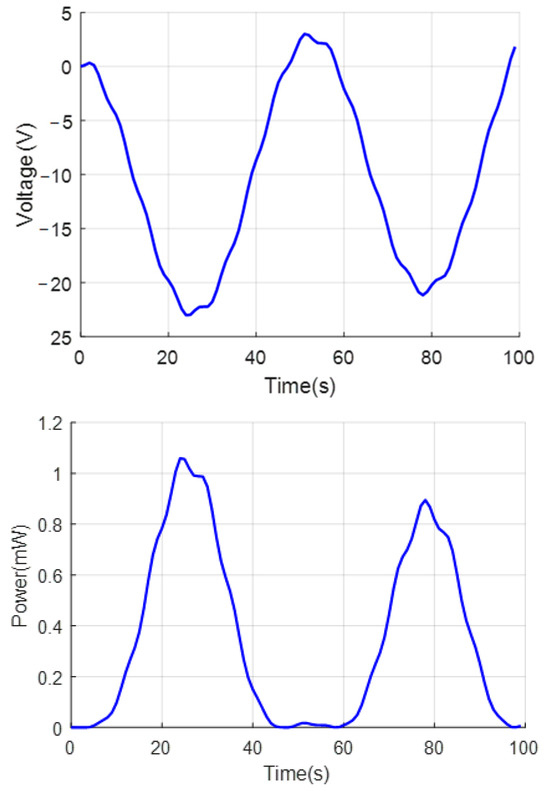
Figure 5.
Voltage and harvested energy power under step load conditions.
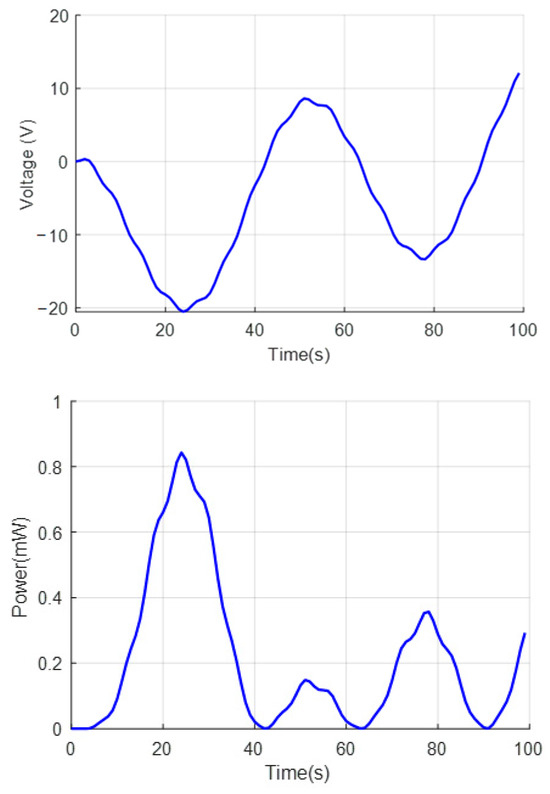
Figure 6.
Voltage and harvested energy power under triangular load conditions.
The results illustrated in Figure 4, Figure 5 and Figure 6 depict the variations in voltage and harvested power from the piezoelectric layer affixed to the bottom surface of the sandwich beam under three different types of dynamic loading: sinusoidal, step, and triangular loads. Overall, both the generated voltage and harvested power exhibit a strong dependence on the time-dependent characteristics of the applied load. Notably, the step loading condition yields the highest energy harvesting performance among the three cases, characterized by a rapid rise and sustained high levels of both voltage and power. This behavior reflects the effectiveness of abrupt excitation in inducing significant and persistent structural vibrations. In contrast, sinusoidal loading results in a periodic fluctuation of voltage and power, with harmonic amplitude patterns corresponding to the regular nature of the excitation, making it well-suited for systems operating under steady-state oscillations. Meanwhile, triangular loading produces a gradual increase and decrease in both voltage and power, aligning with the linearly varying nature of the load and leading to moderate energy harvesting performance. These findings highlight the critical influence of load waveform characteristics on energy harvesting efficiency, emphasizing that loads with sharp, sustained excitation, such as step loads, are most favorable for maximizing power output in vibration-based energy harvesting systems.
Table 4 displays the energy harvested from the piezoelectric layer due to the vibrations of the beam under dynamic loads of varying intensities, taking into account different ratios of beam height to length. The data clearly demonstrate a proportional relationship between load intensity and the amount of harvested energy. Specifically, as the dynamic load intensity increases, the induced strain within the piezoelectric layer also increases, leading to greater mechanical deformation. This increased deformation enhances electric charge generation via the piezoelectric effect, resulting in higher voltage output and, consequently, improved energy harvesting performance. These findings underscore the critical role of load magnitude in optimizing the efficiency of piezoelectric energy harvesters embedded in vibrating beam structures.

Table 4.
Impact of the h/L ratio and load magnitude on the energy harvesting performance.
Furthermore, the analysis results in Table 4 indicate that the geometric ratio h/L plays a significant role in the energy harvesting performance of the sandwich beam system with an attached piezoelectric layer. As the h/L ratio increases (i.e., as the beam height becomes larger relative to its span), the amount of energy harvested from the piezoelectric layer decreases markedly across all types of dynamic loading examined, including sinusoidal, step, and triangular excitations. This trend can be attributed to the fact that an increase in beam height leads to a corresponding increase in structural stiffness, which, in turn, reduces both the vibration amplitude and the mechanical strain at the location of the piezoelectric patch. Since the generated voltage is directly dependent on the mechanical strain within the piezoelectric material, reduced strain results in lower electric charge generation and, thus, decreased harvested energy. This effect is particularly pronounced under low-amplitude loading conditions, where the induced strain may be insufficient to effectively activate the piezoelectric response. Therefore, to optimize energy harvesting efficiency, it is essential to select an appropriate h/L ratio that balances structural stiffness with the beam’s deformation capability.
4. Conclusions
This work successfully analyzes a sandwich beam with an asymmetric cross-section, considering higher-order shear deformation, with two main objectives:
- An analytical method is used to determine the natural vibration frequencies and obtain exact solutions for the dynamic response of the beam subjected to arbitrary impact loads.
- Calculating the energy harvested from a piezoelectric layer attached to the bottom of the beam using an analytical approach, specifically determining the voltage and the harvested electrical power.
The natural vibration frequencies were validated by comparison with results from classical beam theory, showing that the natural frequencies decrease as the height-to-span ratio of the beam increases due to the effects of shear deformation and changes in beam stiffness. As the beam height increases, the influence of shear deformation on the frequencies becomes significant.
The dynamic response under step, sine, and triangular impact loads was also validated with the finite element method using classical beam theory, confirming the reliability of the dynamic response when using higher-order beam theory.
Numerical results indicate that different types of impact loads significantly affect beam displacement and the energy harvesting capability of the piezoelectric layer. For the same amplitude of impact load, voltage variations increase, and power output strongly depends on the time-dependent characteristics of the applied load. The voltage depends on the deformation of the piezoelectric layer, thus exhibiting a pattern similar to the vibration curve of the beam at the location of the piezoelectric layer. The results of this study indicate that the energy harvesting power tends to be maximized under step loading conditions. In addition, the analysis indicates that the geometric ratio h/L has a significant influence on the energy harvesting efficiency. As h/L increases, the harvested energy decreases due to the increased stiffness of the beam, which limits structural deformation and reduces the mechanical strain in the piezoelectric layer. Since the generated voltage is directly dependent on mechanical strain, this results in a lower energy output.
Future research will focus on experimental investigations to validate the theoretical models and develop optimization methods to enhance energy harvesting efficiency in practical applications.
Author Contributions
Conceptualization, S.-D.D. and D.-K.T.; methodology, validation, S.-D.D.; formal analysis, S.-D.D. and D.-D.N.; investigation, D.-D.N.; writing—original draft preparation, S.-D.D. and D.-D.N.; writing—review and editing, D.-K.T.; visualization, N.-L.N.; supervision, D.-K.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available in the article.
Acknowledgments
This research is funded by the Ministry of Education and Training (MOET), Vietnam under the grant number B2023-GHA-09.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting: Modelling and Application; Wiley: Chicester, UK, 2011. [Google Scholar]
- Biglari, H.; Teymouri, H.; Shokouhi, A. Dynamic Response of Sandwich Beam with Flexible Porous Core Under Moving Mass. Mech. Compos. Mater. 2024, 60, 163–182. [Google Scholar] [CrossRef]
- Quan, H.V.; Canh, T.M.; Van Phuc, L. Vehicle Model Dynamic Analysis under Random Excitation of Uneven Pavement as Measured by the International Roughness Index. Transp. Commun. Sci. J. 2023, 74, 866–880. [Google Scholar]
- Chen, J.; Yuan, K.; Zhu, L.; Zhao, X. Dynamic Modelling and Stability Analysis of Aero-Engine Rotor System Considering Aerodynamics. Aerosp. Sci. Technol. 2024, 151, 109294. [Google Scholar] [CrossRef]
- Geiger, F.; Bathel, H.; Spors, S.; Bader, R.; Kluess, D. Monitoring of Hip Joint Forces and Physical Activity after Total Hip Replacement by an Integrated Piezoelectric Element. Technologies 2024, 12, 51. [Google Scholar] [CrossRef]
- Kanchan, M.; Santhya, M.; Bhat, R.; Naik, N. Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review. Technologies 2023, 11, 155. [Google Scholar] [CrossRef]
- Yang, K.; Liu, Z.; Yang, Y.; Zhou, G.; Su, C.; Feng, H. Mechanical Properties Test and Failure Analysis of Composite Foam Sandwich Structure in Ramp-Down Zone. Mech. Compos. Mater. 2024, 60, 1027–1040. [Google Scholar] [CrossRef]
- Ninh, V.T.A. Fundamental Frequencies of Bidirectional Functionally Graded Sandwich Beams Partially Supported by Foundation Using Different Beam Theories. Transp. Commun. Sci. J. 2021, 72, 452–467. [Google Scholar]
- Lien, P.T.B. Free Vibration of Porous Functionally Graded Sandwich Beams on Elastic Foundation Based Ontrigonometric Shear Deformation Theory. Transp. Commun. Sci. J. 2023, 74, 946–961. [Google Scholar]
- Hien, T.D.; Hung, N.D.; Hiep, N.T.; Van Tan, G.; Van Thuan, N. Finite Element Analysis of a Continuous Sandwich Beam resting on Elastic Support and Subjected to Two Degree of Freedom Sprung Vehicles. Eng. Technol. Appl. Sci. Res. 2023, 13, 10310–10315. [Google Scholar] [CrossRef]
- Tran, T.T.; Nguyen, N.H.; Van Do, T.; Van Minh, P.; Duc, N.D. Bending and Thermal Buckling of Unsymmetric Functionally Graded Sandwich Beams in High-Temperature Environment Based on a New Third-Order Shear Deformation Theory. J. Sandw. Struct. Mater. 2021, 23, 906–930. [Google Scholar] [CrossRef]
- Huan, D.T.; Huong, L.Q.; Khiem, N.T. Modal Analysis of Cracked Beam with a Piezoelectric Layer. Vietnam J. Mech. 2021, 43, 105–120. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, T. A Semi-Analytical Model for Energy Harvesting of Flexural Wave Propagation on Thin Plates by Piezoelectric Composite Beam Resonators. Mech. Syst. Signal Process. 2021, 147, 107137. [Google Scholar] [CrossRef]
- Song, J.; Sun, G.; Zeng, X.; Li, X.; Bai, Q.; Zheng, X. Piezoelectric Energy Harvester with Double Cantilever Beam Undergoing Coupled Bending-Torsion Vibrations by Width-Splitting Method. Sci. Rep. 2022, 12, 583. [Google Scholar] [CrossRef]
- Tonan, M.; Pasetto, A.; Doria, A. Vibration Energy Harvesting from Plates by Means of Piezoelectric Dynamic Vibration Absorbers. Appl. Sci. 2024, 14, 402. [Google Scholar] [CrossRef]
- Frýba, L. Vibration of Solids and Structures Under Moving Loads; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 1. [Google Scholar]
- Du, W.; Xiang, Z.; Qiu, X. Stochastic Analysis of an Acoustic Black Hole Piezoelectric Energy Harvester Under Gaussian White Noise Excitation. Appl. Math. Model. 2024, 131, 22–32. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, W.; Zhou, Z.; Zhu, P.; Du, W. Piezomagnetoelastic Energy Harvesting from Bridge Vibrations Using Bi-Stable Characteristics. Energy 2023, 263, 125859. [Google Scholar] [CrossRef]
- Mousavi, M.; Ziaei-Rad, S.; Karimi, A.H. Piezoelectric-Based Energy Harvesting from Bridge Vibrations Subjected to Moving Successive Vehicles by Functionally Graded Cantilever Beams—Theoretical and Experimental Investigations. Mech. Syst. Signal Process. 2023, 188, 110015. [Google Scholar] [CrossRef]
- Hassan, E.; Kouritem, S.A.; Amer, F.Z.; Mubarak, R.I. Acoustic Energy Harvesting Using an Array of Piezoelectric Cantilever Plates for Railways and Highways Environmental Noise. Ain Shams Eng. J. 2023, 15, 102461. [Google Scholar] [CrossRef]
- Adoukatl, C.; Ntamack, G.E.; Azrar, L. High Order Analysis of a Nonlinear Piezoelectric Energy Harvesting of a Piezo Patched Cantilever Beam Under Parametric and Direct Excitations. Mech. Adv. Mater. Struct. 2023, 30, 4835–4861. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, C.; Lai, L.; Dong, X.; Li, Y. Design, Manufacture and Test of Piezoelectric Cantilever-Beam Energy Harvesters with Hollow Structures. Micromachines 2021, 12, 1090. [Google Scholar] [CrossRef]
- Lu, Z.-Q.; Jie, C.; Hu, D.; Li-Qun, C. Two-Span Piezoelectric Beam Energy Harvesting. Int. J. Mech. Sci. 2020, 175, 105532. [Google Scholar] [CrossRef]
- Amini, Y.; Heshmati, M.; Fatehi, P.; Habibi, S. Piezoelectric Energy Harvesting from Vibrations of a Beam Subjected to Multi-moving Loads. Appl. Math. Model. 2017, 49, 1–16. [Google Scholar] [CrossRef]
- Paknejad, A.; Rahimi, G.; Farrokhabadi, A.; Khatibi, M.M. Analytical Solution of Piezoelectric Energy Harvester Patch for Various Thin Multilayer Composite Beams. Compos. Struct. 2016, 154, 694–706. [Google Scholar] [CrossRef]
- Erturk, A. Piezoelectric Energy Harvesting for Civil Infrastructure System Applications: Moving Loads and Surface Strain Fluctuations. J. Intell. Mater. Syst. Struct. 2011, 22, 1959–1973. [Google Scholar] [CrossRef]
- Ali, S.F.; Friswell, M.I.; Adhikari, S. Analysis of Energy Harvesters for Highway Bridges. J. Intell. Mater. Syst. Struct. 2011, 22, 1929–1938. [Google Scholar] [CrossRef]
- Kadivar, M.; Mohebpour, S. Finite Element Dynamic Analysis of Unsymmetric Composite Laminated Beams with Shear Effect and Rotary Inertia Under the Action of Moving Loads. Finite Elem. Anal. Des. 1998, 29, 259–273. [Google Scholar] [CrossRef]
- Ta, H.-D.; Noh, H.-C. Analytical Solution for the Dynamic Response of Functionally Graded Rectangular Plates Resting on Elastic Foundation Using a Refined Plate Theory. Appl. Math. Model. 2015, 39, 6243–6257. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 2nd ed.; Computers and Structures: Berkeley, CA, USA, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).