Shear Force–Displacement Curve of a Steel Shear Wall Considering Compression
Abstract
1. Introduction
2. Shear Capacity Model
2.1. Strain of the Tensile Strips
2.2. Yield Stress
2.3. Stress Under Compression
2.4. Stress Analysis of the Wall Under Compression and Shear
3. Finite Element Analysis
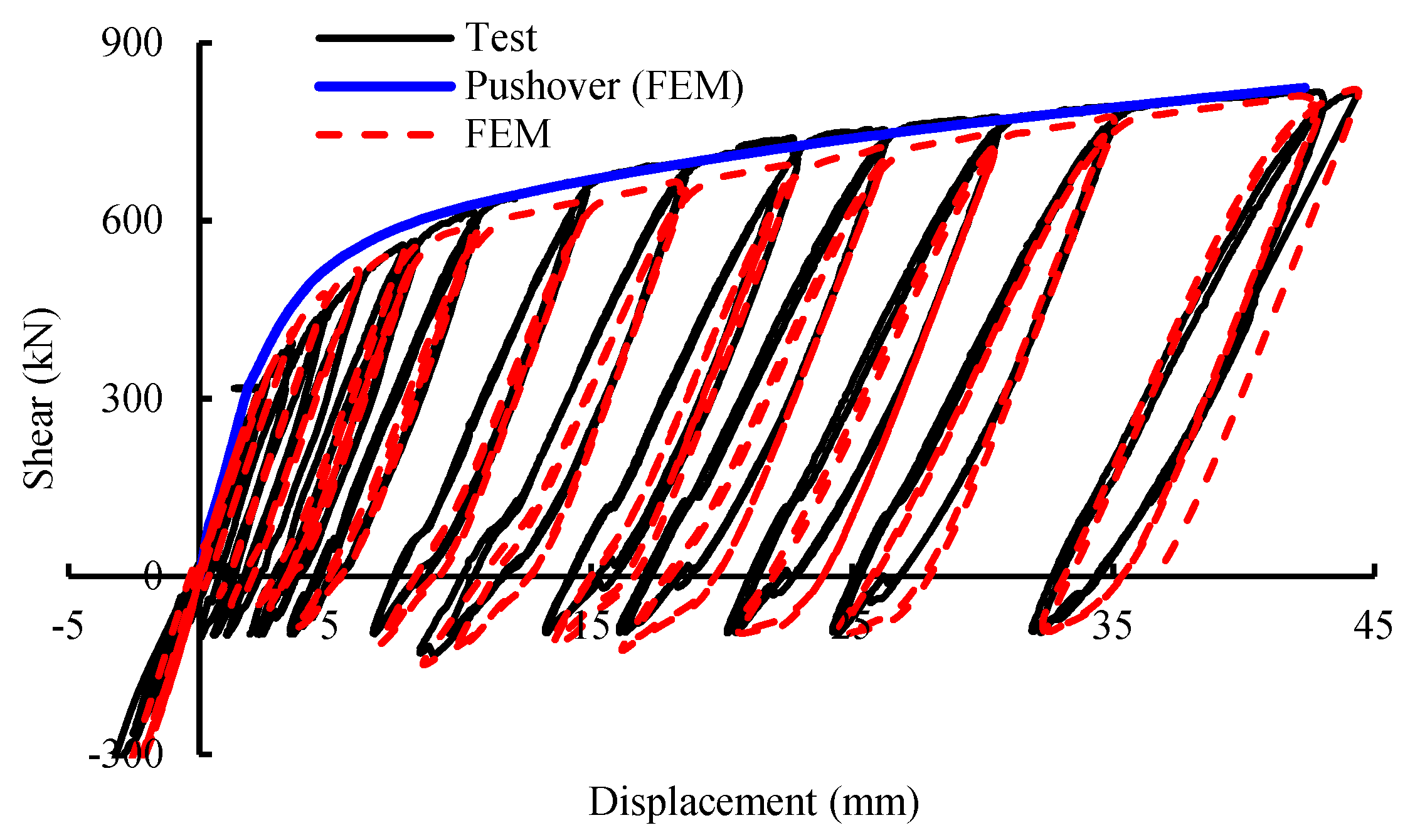
3.1. Finite Element Model and Verification
3.2. Parametric Analysis
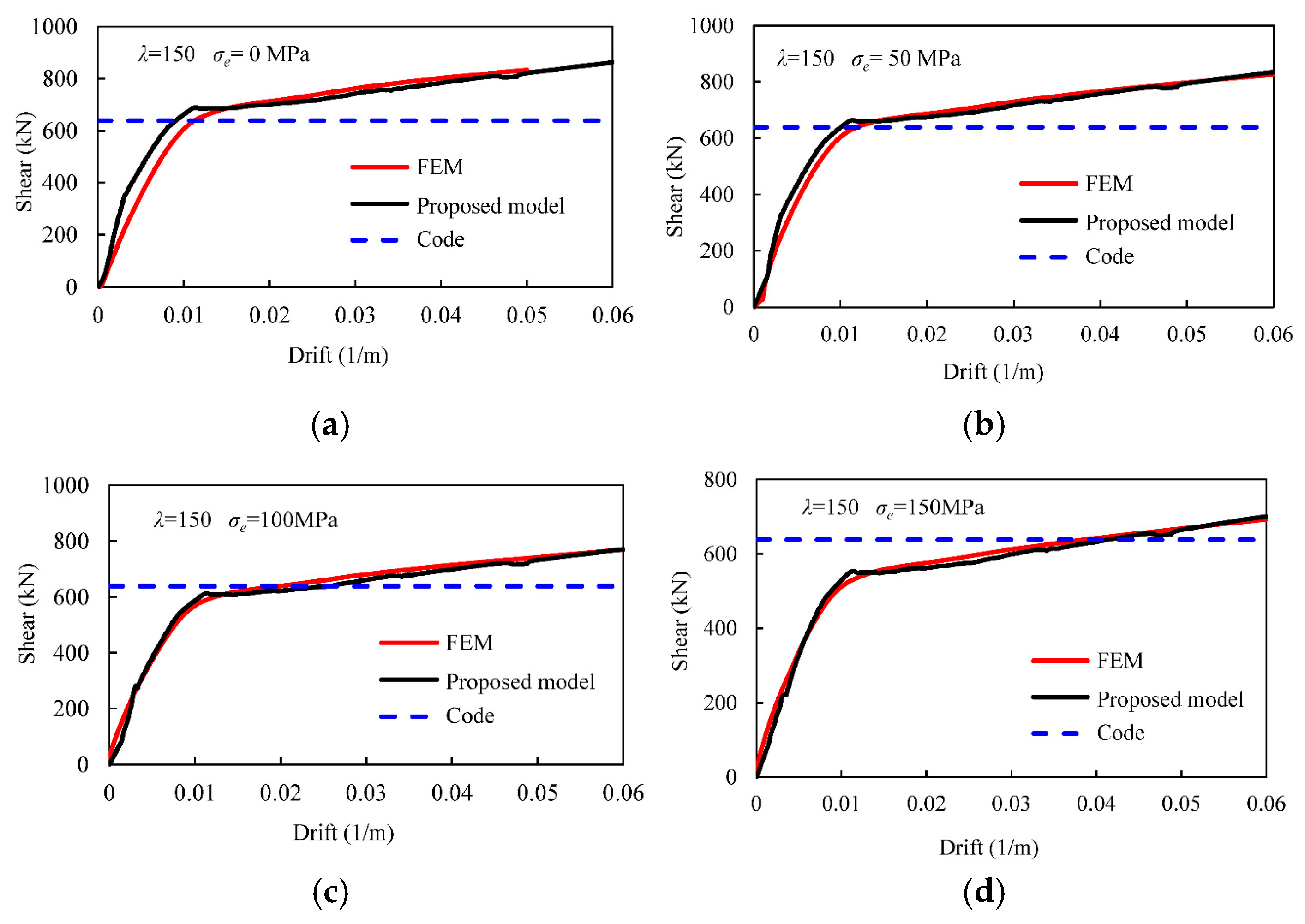
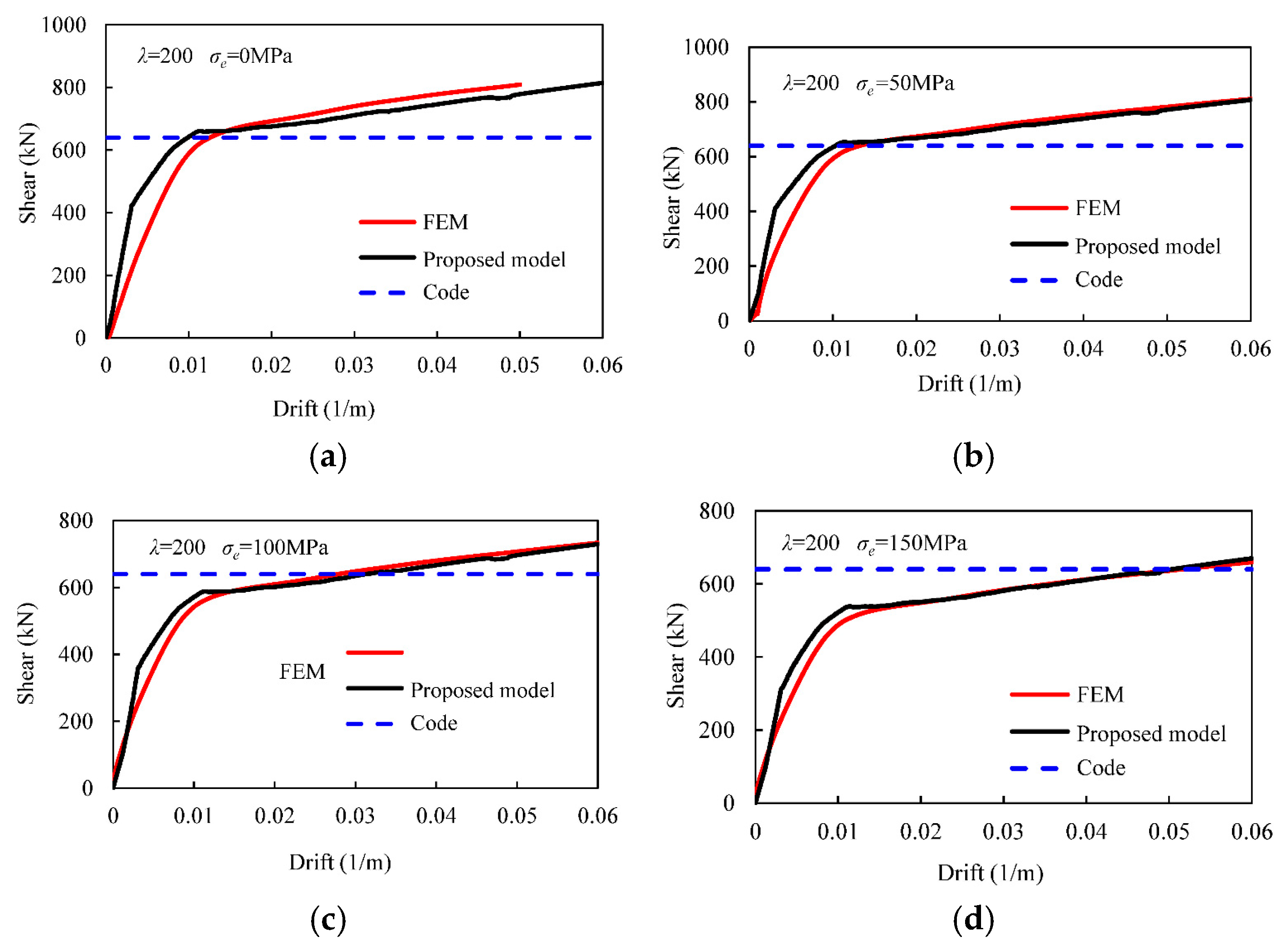
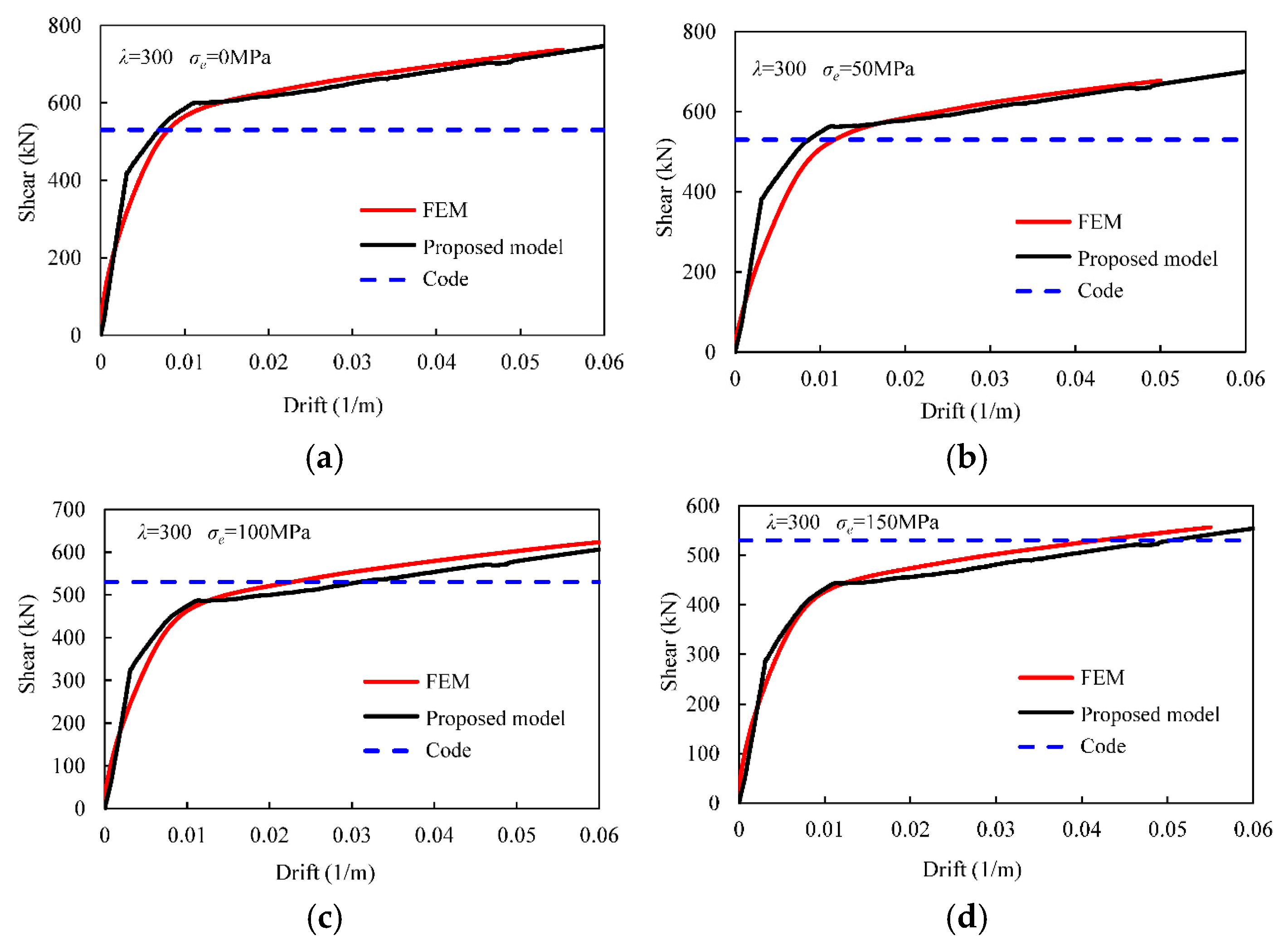
4. Results and Discussions
5. Conclusions
- (1)
- The proposed model offers a significant advancement in accurately predicting the true shear strength of SSWs. Notably, it is capable of generating a complete shear force–displacement curve by utilizing the stress–strain relationships obtained from the tensile testing of steel materials. Furthermore, the model facilitates the precise determination of key parameters, including initial stiffness, yield load, yield displacement, and post-buckling bearing capacity, which are crucial for understanding structural performance during and after yielding.
- (2)
- An important finding is the tendency for some existing code equations to overestimate the seismic performance of SSWs, particularly in cases involving heavily loaded or stocky wall configurations. For example, the CAN/CSA-S16-01 equation may be overestimated by approximately 4%, 9%, and 18% when the vertical compression stress is 50, 100, and 150 MPa for a wall with a slenderness of 150, respectively. This observation highlights the necessity for engineers to exercise caution when employing code equations in situations not fully addressed by current standard provisions.
- (3)
- It is essential to recognize the limitations of the proposed model. Specifically, its application is currently restricted to pushover analysis, thereby necessitating further research to thoroughly assess its validity under cyclic loading conditions typical of seismic events. Future investigations aimed at evaluating the cyclic behavior of SSWs will be vital in establishing the comprehensive practicality and reliability of the proposed model for seismic design applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thorburn, L.J.; Kulak, G.L.; Montgomery, C.J. Analysis of Steel Plate Shear Walls; Report No. 107; Department of Civil Engineering, University of Alberta: Edmonton, AB, Canada, 1983. [Google Scholar]
- Driver, R.G.; Kulak, G.L.; Kennedy, D.J.L.; Elwi, A.E. Cyclic test of a four-storey steel plate shear wall. ASCE J. Struct. Eng. 1998, 124, 112–120. [Google Scholar] [CrossRef]
- Behbahanifard, M.R. Cyclic Behavior of Unstiffened Steel Plate Shear Walls. Ph.D. Dissertation, Department of Civil Engineering, University of Alberta, Edmonton, AB, Canada, 2003. [Google Scholar]
- Moghimi, H.; Driver, R.G. Economical steel plate shear walls for low-seismic regions. ASCE J. Struct. Eng. 2013, 139, 379–388. [Google Scholar] [CrossRef]
- Qu, B.; Bruneau, M.; Lin, C.H.; Tsai, K.C. Testing of full-scale two-storey steel plate shear wall with reduced beam section connections and composite floors. ASCE J. Struct. Eng. 2008, 134, 364–373. [Google Scholar] [CrossRef]
- Han, Q.; Zhang, Y.; Wang, D.; Sakata, H. Seismic behavior of buckling-restrained steel plate shear wall with assembled multi-RC panels. J. Constr. Steel Res. 2019, 157, 397–413. [Google Scholar] [CrossRef]
- Wang, W.; Ren, Y.; Lu, Z.; Song, J.; Han, B.; Zhou, Y. Experimental study of the hysteretic behaviour of corrugated steel plate shear walls and steel plate reinforced concrete composite shear walls. J. Constr. Steel Res. 2019, 160, 136–152. [Google Scholar] [CrossRef]
- Dastfan, M.; Driver, R.G. Test of a Steel Plate Shear Wall with Partially Encased Composite Columns and RBS Frame Connections. J. Struct. Eng. 2018, 144, 04017187. [Google Scholar] [CrossRef]
- Lu, J.; Yu, S.; Xia, J.; Qiao, X.; Tang, Y. Experimental study on the hysteretic behavior of steel plate shear wall with unequal length slits. J. Constr. Steel Res. 2018, 147, 477–487. [Google Scholar] [CrossRef]
- Xu, L.H.; Liu, J.L.; Li, Z.X. Cyclic behaviors of steel plate shear wall with self-centering energy dissipation braces. J. Constr. Steel Res. 2019, 153, 19–30. [Google Scholar] [CrossRef]
- Xu, L.H.; Fan, X.W.; Li, Z.X. Cyclic behavior and failure mechanism of self-centering energy dissipation braces with pre-pressed combination disc springs. Earthq. Eng. Struct. Dyn. 2017, 46, 1065–1080. [Google Scholar] [CrossRef]
- Xu, L.H.; Liu, J.L.; Li, Z.X. Parametric analysis and failure mode of steel plate shear wall with self-centering braces. Eng. Struct. 2021, 237, 112151. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Hao, J.P.; Yu, H.S. Shaking-table test of a novel buckling-restrained multi-stiffened low-yield-point steel plate shear wall. J. Constr. Steel Res. 2018, 145, 128–136. [Google Scholar] [CrossRef]
- Phillips, A.R.; Eatherton, M.R. Computational study of elastic and inelastic ring shaped–steel plate shear wall behavior. Eng. Struct. 2018, 177, 655–667. [Google Scholar] [CrossRef]
- Verma, A.; Sahoo, D.R. Seismic behaviour of steel plate shear wall systems with staggered web configurations. Earthq. Eng. Struct. Dyn. 2018, 47, 660–677. [Google Scholar] [CrossRef]
- Tong, J.Z.; Guo, Y.L.; Zuo, J.Q. Elastic buckling and load-resistant behaviors of double-corrugated-plate shear walls under pure in-plane shear loads. Thin-Walled Struct. 2018, 130, 593–612. [Google Scholar] [CrossRef]
- Bai, J.L.; Chen, H.M.; Zhao, J.X.; Liu, M.; Jin, S. Seismic design and subassemblage tests of buckling-restrained braced RC frames with shear connector gusset connections. Eng. Struct. 2021, 234, 112018. [Google Scholar] [CrossRef]
- Timler, P.A.; Kulak, G.L. Experimental Study of Steel Plate Shear Walls; Structural Engineering Report No. 114; Department of Civil Engineering, University of Alberta: Edmonton, AB, Canada, 1983. [Google Scholar]
- Lv, Y.; Zhao, Z.; Lv, J.Q.; Chouw, N.; Li, Z.X. A stress distribution of thin rectangular steel wall under a uniform compression. Int. J. Struct. Stab. Dyn. 2020, 20, 2050037. [Google Scholar] [CrossRef]
- Lv, Y.; Lv, J.Q.; Zhao, Z. Vertical stress distributions of a thin rectangular steel wall under compression and in-plane bending. Int. J. Struct. Stab. Dyn. 2020, 20, 2050090. [Google Scholar] [CrossRef]
- Lv, Y.; Li, Z.X.; Lu, G.X. Shear capacity prediction of steel plate shear walls with pre-compression from columns. Struct. Des. Tall Spec. Build. 2017, 26, e1375. [Google Scholar] [CrossRef]
- Lv, Y.; Wu, D.; Zhu, Y.H.; Liang, X.; Shi, Y.C.; Yang, Z.; Li, Z.X. Stress state of steel plate shear walls under compression-shear combination load. Struct. Des. Tall Spec. Build. 2018, 27, e1450. [Google Scholar] [CrossRef]
- ANSI-AISC 341-05; Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction, Inc.: Chicago, IL, USA, 2005.
- CAN/CSA-S16-01; Limit States Design of Steel Structures. Canadian Standards Association: Willowdale, ON, Canada, 2001.

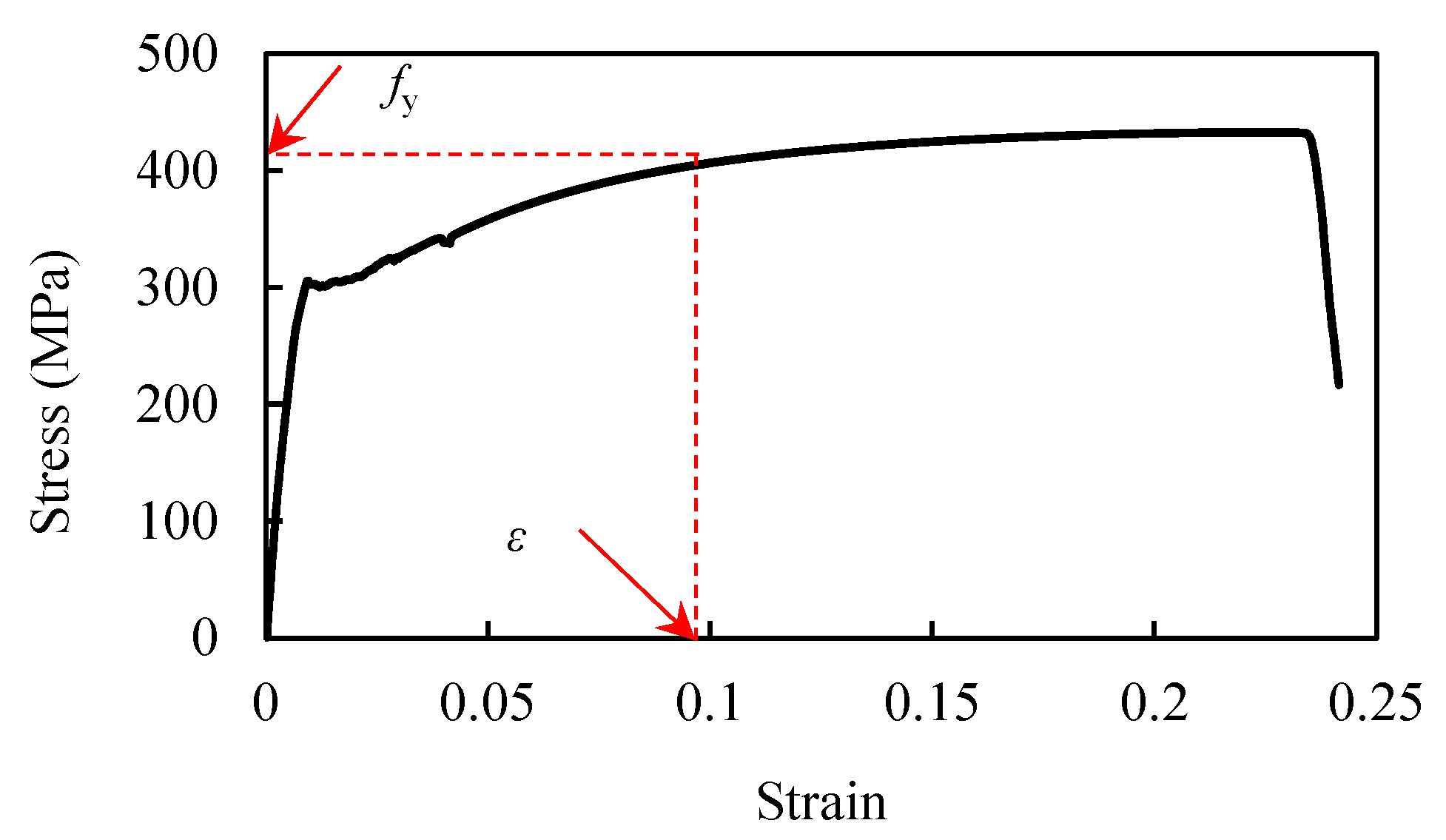
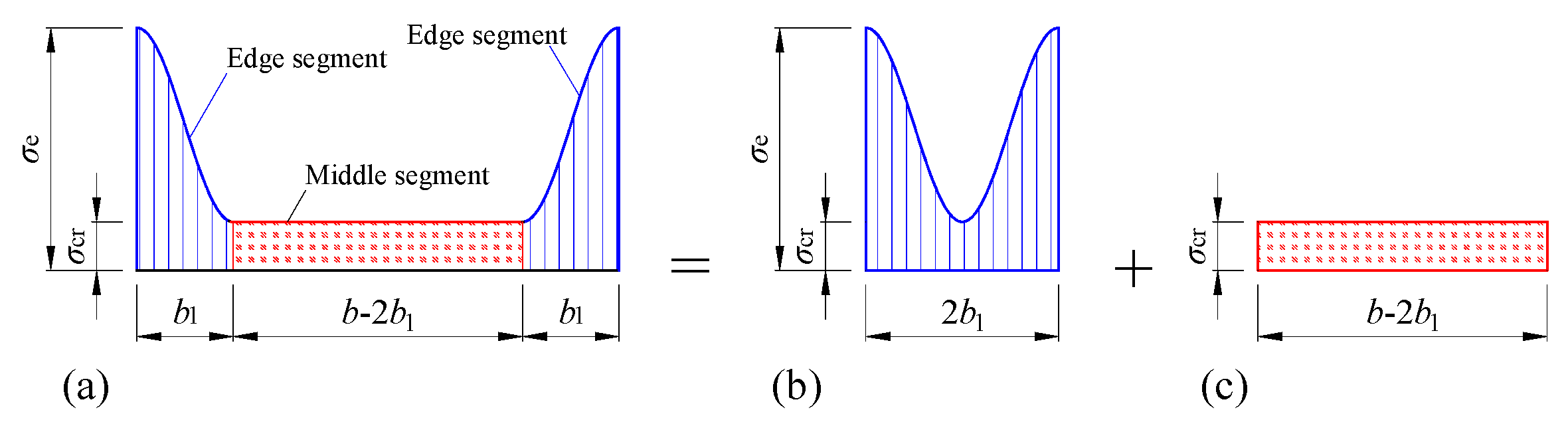
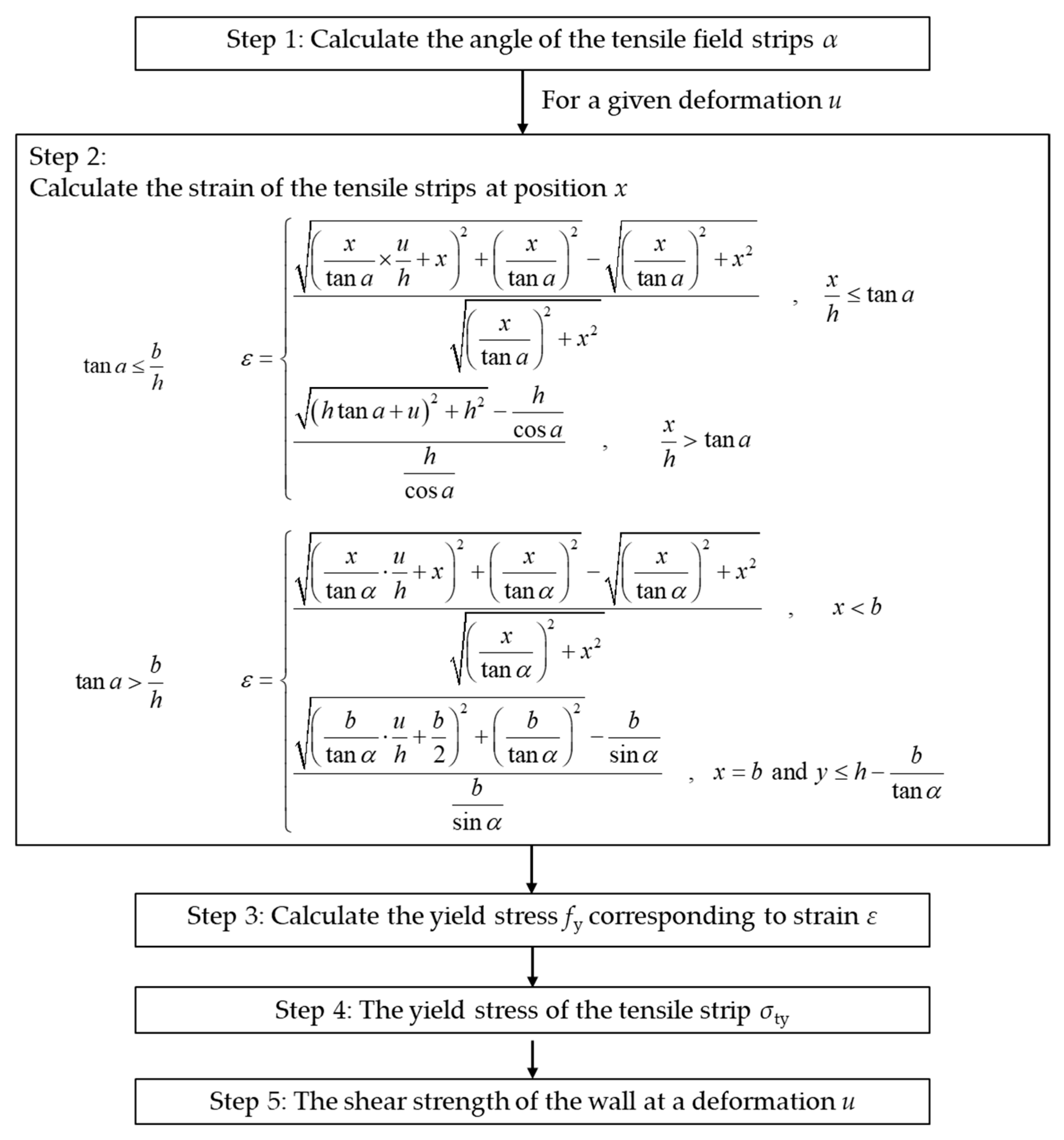
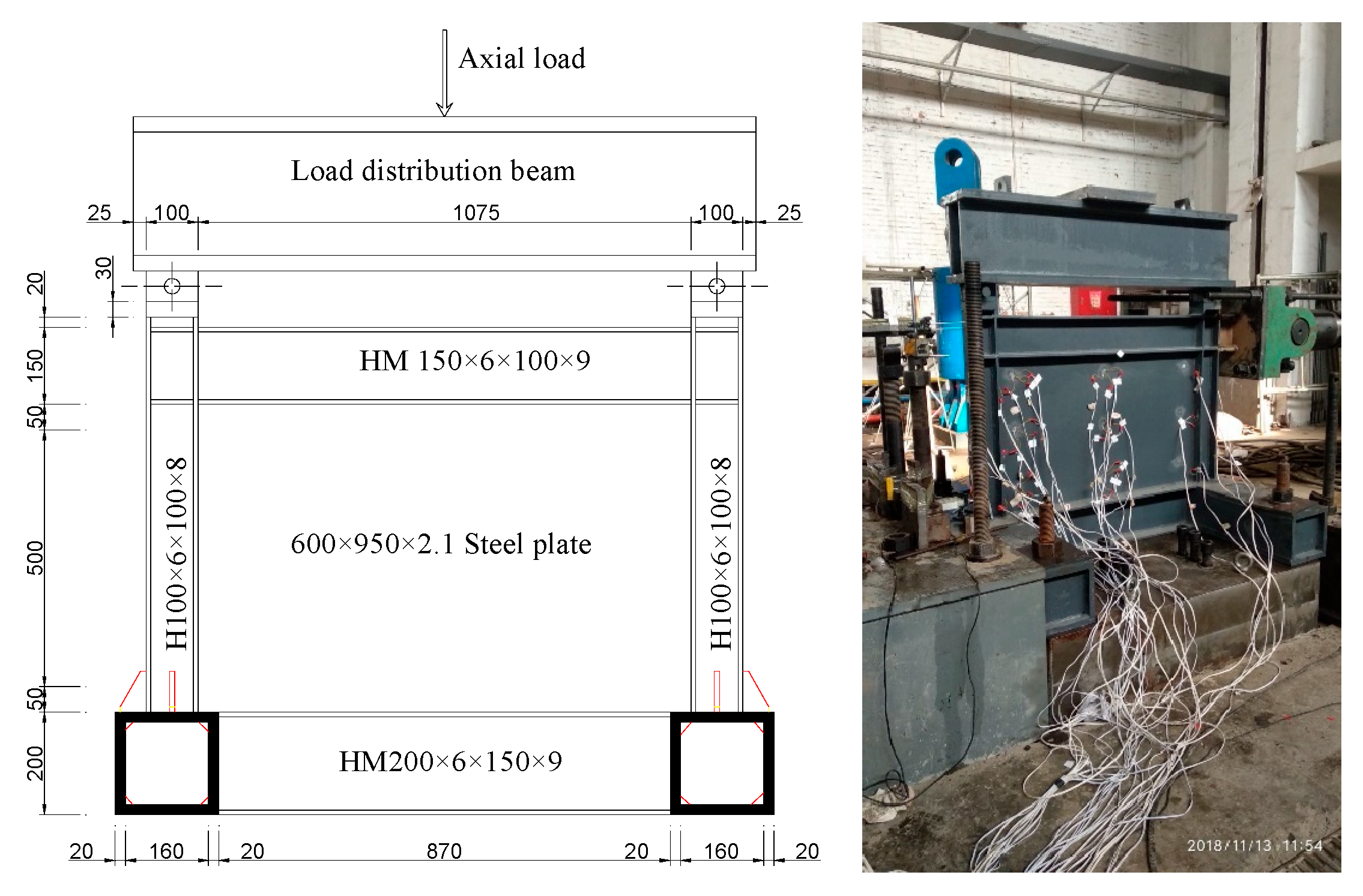


| Steel | t (mm) | fy (MPa) | fu (MPa) | Elongation at Break (%) |
|---|---|---|---|---|
| Q390 | 5.0/10.0 | 456.2 | 562.1 | 21.41 |
| Q235 | 2.10 | 232.1 | 376.2 | 18.30 |
| Cases | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Thickness t (mm) | 4 | 3 | 2 | 4 | 3 | 2 | 4 | 3 | 2 | 4 | 3 | 2 |
| Axial Stress σe (MPa) | 0 | 0 | 0 | 50 | 50 | 50 | 100 | 100 | 100 | 150 | 150 | 150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; He, Y.; Lv, Y. Shear Force–Displacement Curve of a Steel Shear Wall Considering Compression. Buildings 2025, 15, 2112. https://doi.org/10.3390/buildings15122112
Liu Y, He Y, Lv Y. Shear Force–Displacement Curve of a Steel Shear Wall Considering Compression. Buildings. 2025; 15(12):2112. https://doi.org/10.3390/buildings15122112
Chicago/Turabian StyleLiu, Yi, Yan He, and Yang Lv. 2025. "Shear Force–Displacement Curve of a Steel Shear Wall Considering Compression" Buildings 15, no. 12: 2112. https://doi.org/10.3390/buildings15122112
APA StyleLiu, Y., He, Y., & Lv, Y. (2025). Shear Force–Displacement Curve of a Steel Shear Wall Considering Compression. Buildings, 15(12), 2112. https://doi.org/10.3390/buildings15122112







