Advancing Sustainable Road Construction with Multiple Regression Analysis, Regression Tree Models, and Case-Based Reasoning for Environmental Load and Cost Estimation
Abstract
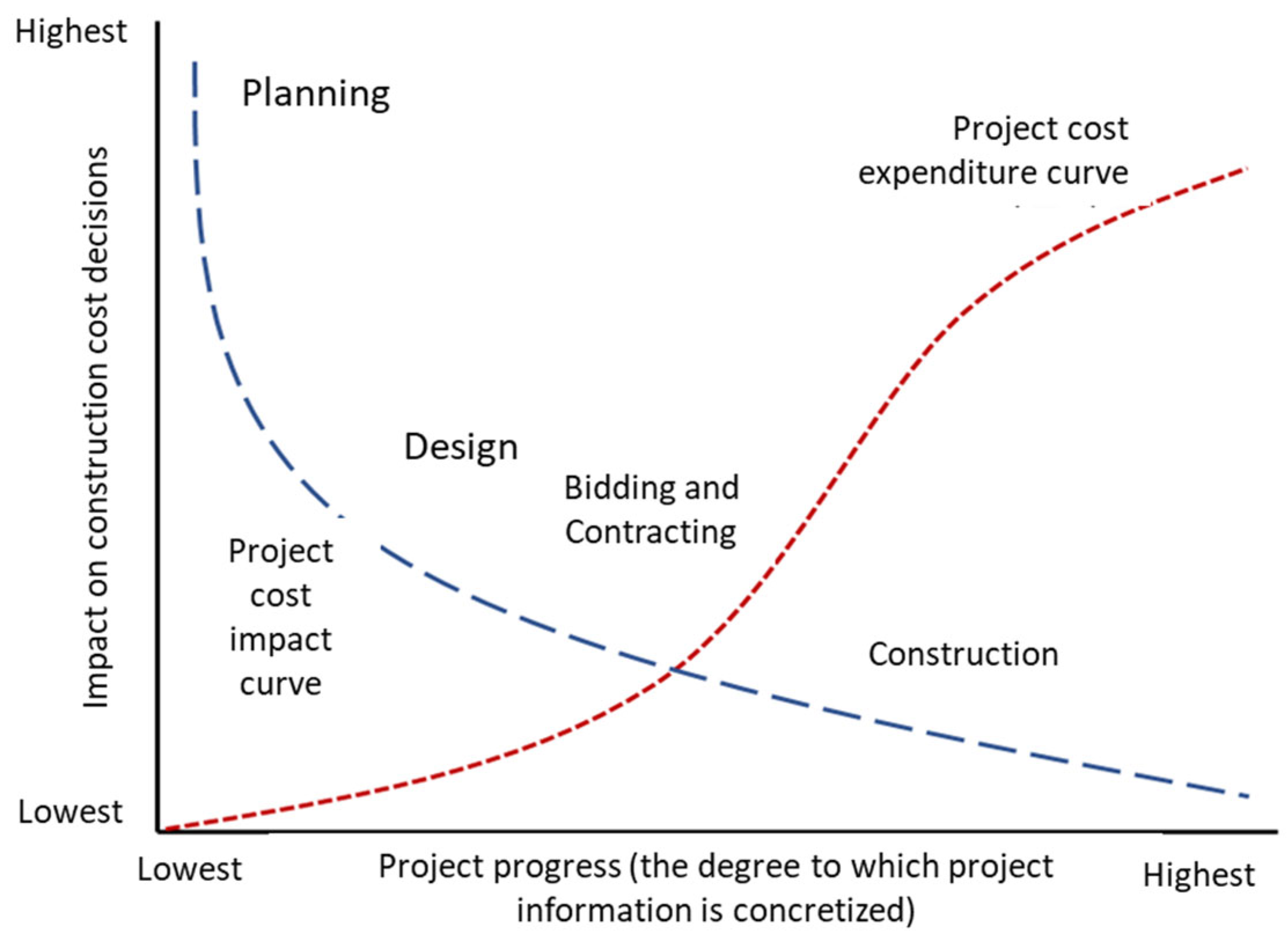
1. Introduction
2. Database Collection and Analysis
2.1. Planning Stage Database Construction Information
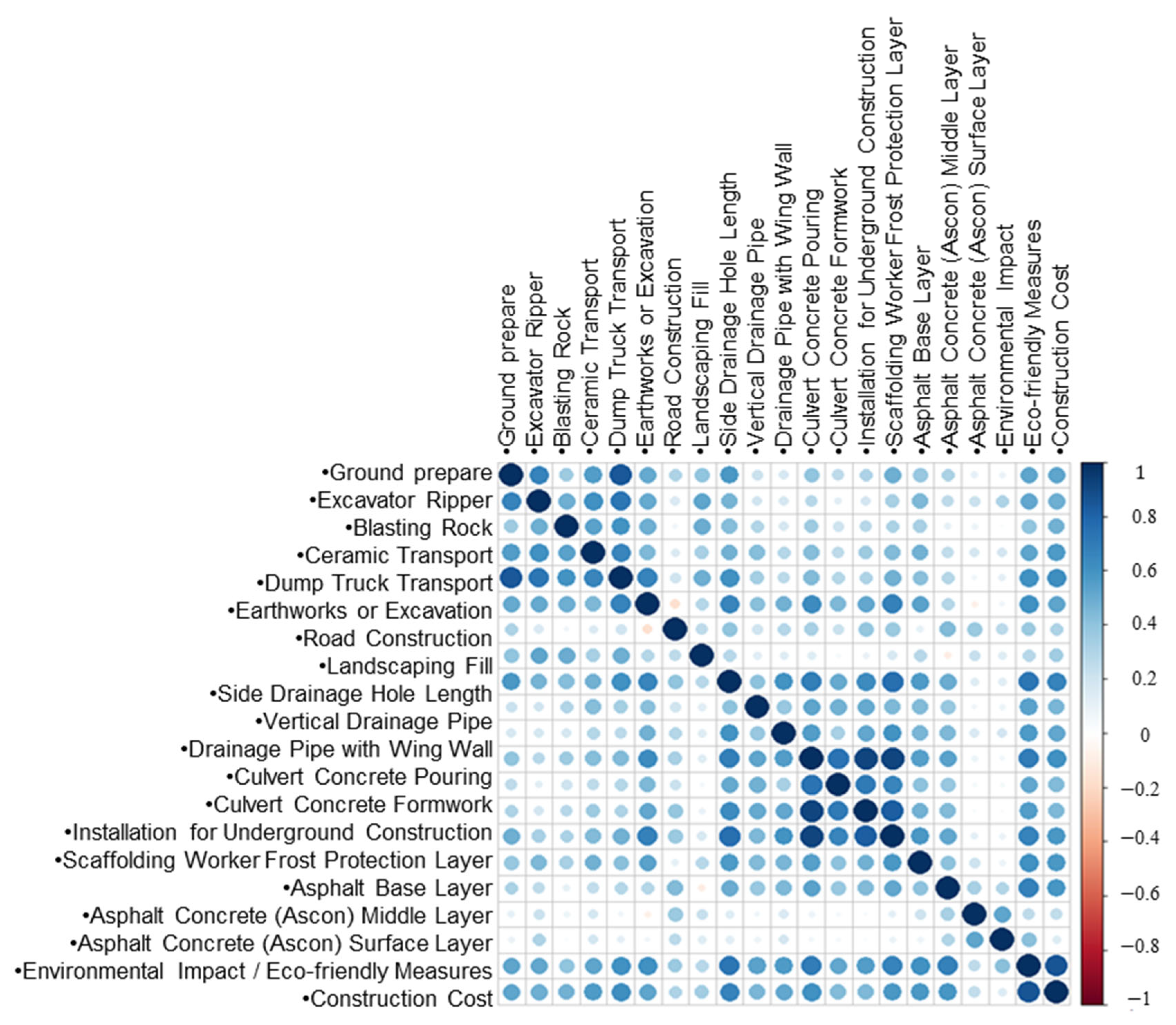
2.2. Design Phase Database Construction Information
3. Machine-Learning Models
3.1. Multiple Regression Analysis
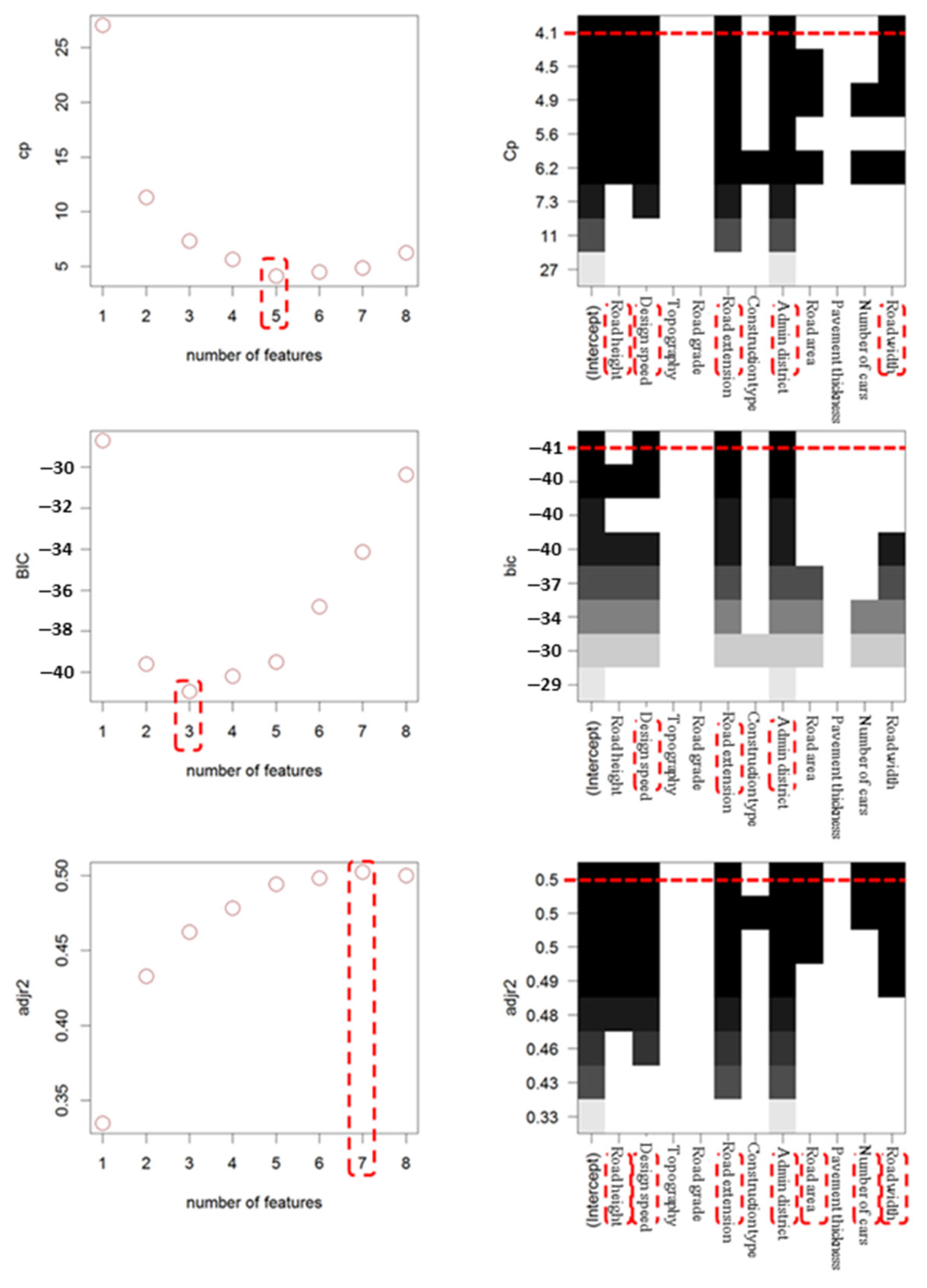
3.1.1. Planning Stage Multiple Regression Analysis Model Construction
- Mallows’ Cp:
- BIC (Bayesian Information Criterion):
- Adjusted R2:
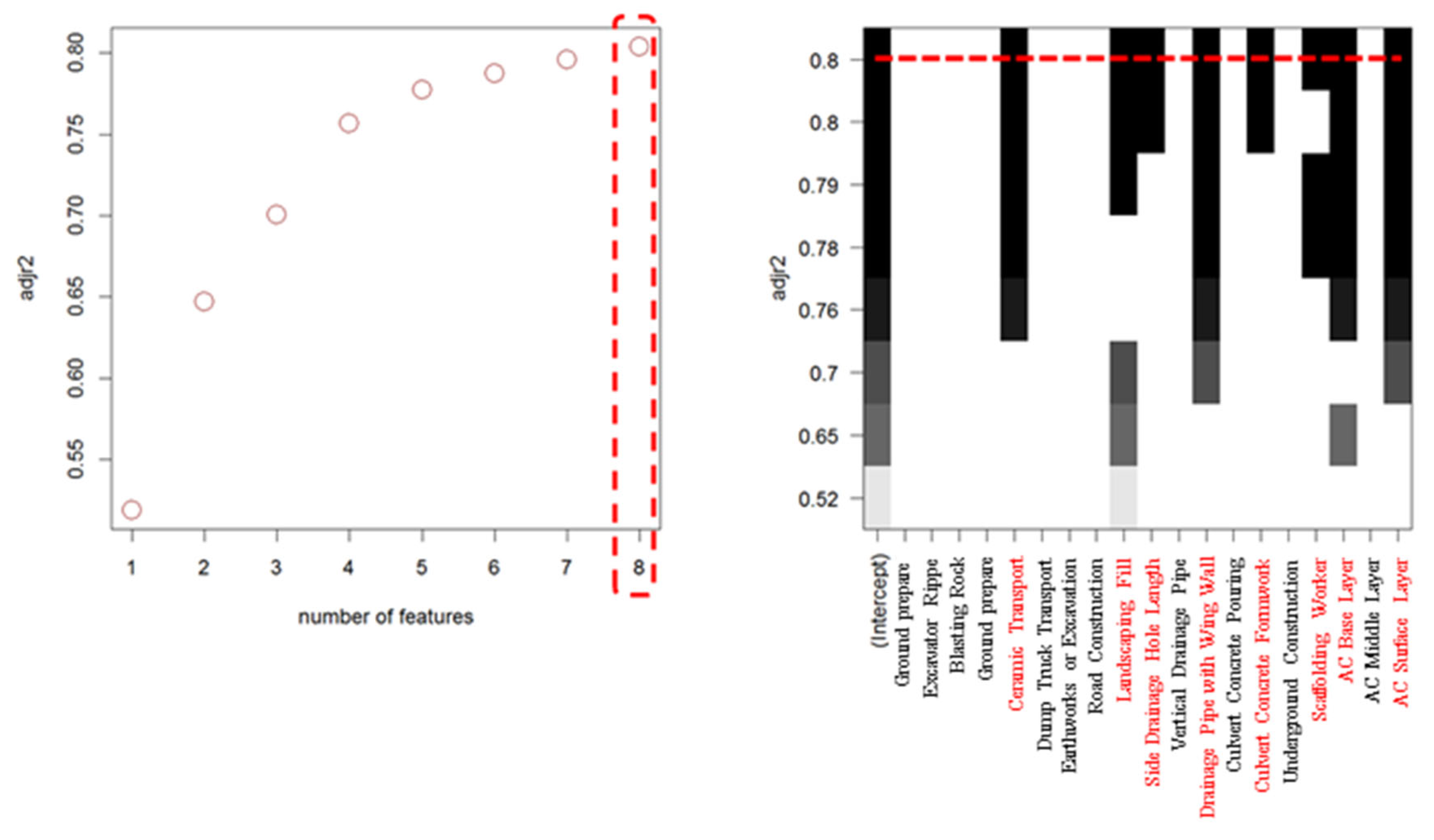
3.1.2. Design-Stage Multiple Regression Analysis Model Construction
3.2. Regression Tree
3.2.1. Planning Stage Regression Tree Model
3.2.2. Design-Stage Regression Tree Model
3.3. Case-Based Reasoning
- = Similarity score of the query case
- = New case
- = Query case
- = Weight of the variable
4. Results and Discussions
4.1. Results
4.2. Discussions
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahn, C. An Integrated Framework for Sustainable Construction Processes: Understanding and Managing the Environmental Performance of Construction Operations. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2012; p. 141. [Google Scholar]
- Ahn, C.R.; Lee, S. Importance of Operational Efficiency to Achieve Energy Efficiency and Exhaust Emission Reduction of Construction Operations. J. Constr. Eng. Manag. 2013, 139, 404–413. [Google Scholar] [CrossRef]
- Bilec, M.M.; Ries, R.J.; Matthews, H.S. Life-Cycle Assessment Modeling of Construction Processes for Buildings. J. Infrastruct. Syst. 2010, 16, 199–205. [Google Scholar] [CrossRef]
- Cass, D.; Mukherjee, A. Calculation of Greenhouse Gas Emissions for Highway Construction Operations by Using a Hybrid Life-Cycle Assessment Approach: Case Study for Pavement Operations. J. Constr. Eng. Manag. 2011, 137, 1015–1025. [Google Scholar] [CrossRef]
- Noh, K.S.; Baek, J.D. Suggestions of the Construction and Management for Sustainable Highways. Ecol. Resilient Infrastruct. 2016, 3, 156–161. [Google Scholar] [CrossRef][Green Version]
- Park, M.C.; Lee, S.H.; Shin, S.W. Case Study of Economic Efficiency Evaluation about Green Residential Complex in Korea. Adv. Mater. Res. 2014, 935, 34–37. [Google Scholar] [CrossRef]
- MOLIT (Ministry of Land, Infrastructure & Transport). Molit Statistics System. 2017. Available online: https://www.molit.go.kr/english/USR/WPGE0201/m_36859/DTL.jsp (accessed on 15 April 2025).
- Xu, Y.; Zhou, Y.; Sekula, P.; Ding, L. Machine Learning in Construction: From Shallow to Deep Learning. Dev. Built Environ. 2021, 6, 100045. [Google Scholar] [CrossRef]
- Dawood, T.; Zhu, Z.; Zayed, T. Machine Vision-Based Model for Spalling Detection and Quantification in Subway Networks. Autom. Constr. 2017, 81, 149–160. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Zheng, C.; Fanijo, E.O.; Wang, L. Improving Asphalt Mix Design Considering International Roughness Index of Asphalt Pavement Predicted Using Autoencoders and Machine Learning. Constr. Build. Mater. 2022, 360, 129439. [Google Scholar] [CrossRef]
- Xu, C.; Chen, X.; Zeng, Q.; Cai, M.; Zhang, W.; Yu, B. A Framework of Integrating Machine Learning Model and Pavement Life Cycle Assessment to Optimize Asphalt Mixture Design. Constr. Build. Mater. 2025, 469, 140481. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Wang, L. Automated, Economical, and Environmentally-Friendly Asphalt Mix Design Based on Machine Learning and Multi-Objective Grey Wolf Optimization. J. Traffic Transp. Eng. (Engl. Ed.) 2024, 11, 381–405. [Google Scholar] [CrossRef]
- Li, Y.; Zou, Z.; Zhang, J.; He, Y.; Huang, G.; Li, J. Refined Evaluation Methods for Preventive Maintenance of Project-Level Asphalt Pavement Based on Confusion-Regression Model. Constr. Build. Mater. 2023, 403, 133105. [Google Scholar] [CrossRef]
- Nguyen, H.L.; Tran, V.Q. Data-Driven Approach for Investigating and Predicting Rutting Depth of Asphalt Concrete Containing Reclaimed Asphalt Pavement. Constr. Build. Mater. 2023, 377, 131116. [Google Scholar] [CrossRef]
- Raza, M.S.; Sharma, S.K. Optimizing Porous Asphalt Mix Design for Permeability and Air Voids Using Response Surface Methodology and Artificial Neural Networks. Constr. Build. Mater. 2024, 442, 137513. [Google Scholar] [CrossRef]
- Ochoa, L.; Hendrickson, C.; Matthews, H.S. Economic Input-Output Life-Cycle Assessment of U.S. Residential Buildings. J. Infrastruct. Syst. 2002, 8, 132–138. [Google Scholar] [CrossRef]
- Sharrard, A.L.; Matthews, H.S.; Ries, R.J. Estimating Construction Project Environmental Effects Using an Input-Output-Based Hybrid Life-Cycle Assessment Model. J. Infrastruct. Syst. 2008, 14, 327–336. [Google Scholar] [CrossRef]
- Guggemos, A.A.; Horvath, A. Decision-Support Tool for Assessing the Environmental Effects of Constructing Commercial Buildings. J. Archit. Eng. 2006, 12, 187–195. [Google Scholar] [CrossRef]
- Kiani, H.; Nasrollahzadeh, K. Fuzzy Logic Approach for Seismic Fragility Analysis of RC Frames with Applications to Earthquake-Induced Damage and Construction Quality. Structures 2023, 55, 1122–1143. [Google Scholar] [CrossRef]
- Taheri, A.; Azimi, N.; Oliveira, D.V.; Tinoco, J.; Lourenço, P.B. Integrating Experimental Analysis and Gradient Boosting for the Durability Assessment of Lime-Based Mortar in Acidic Environment. Buildings 2025, 15, 408. [Google Scholar] [CrossRef]
- Tanguler-Bayramtan, M.; Aktas, C.B.; Yaman, I.O. Environmental Assessment of Calcium Sulfoaluminate Cement: A Monte Carlo Simulation in an Industrial Symbiosis Framework. Buildings 2024, 14, 3673. [Google Scholar] [CrossRef]
- Mohammadi, A.; Karimzadeh, S.; Yaghmaei-Sabegh, S.; Ranjbari, M.; Lourenço, P.B. Utilising Artificial Neural Networks for Assessing Seismic Demands of Buckling Restrained Braces Due to Pulse-like Motions. Buildings 2023, 13, 2542. [Google Scholar] [CrossRef]
- David, A.B.; Olalusi, O.B.; Awoyera, P.O.; Simwanda, L. Suitability of Mechanics-Based and Optimized Machine Learning-Based Models in the Shear Strength Prediction of Slender Beams Without Stirrups. Buildings 2024, 14, 3946. [Google Scholar] [CrossRef]
- Pérez-Acebo, H.; Linares-Unamunzaga, A.; Rojí, E.; Gonzalo-Orden, H. IRI Performance Models for Flexible Pavements in Two-Lane Roads until First Maintenance and/or Rehabilitation Work. Coatings 2020, 10, 97. [Google Scholar] [CrossRef]
- Liu, C.; Chong, X.; Qi, C.; Yao, Z.; Wei, Y.; Zhang, J.; Li, Y. Numerical Investigation of Thermal Parameter Characteristics of the Airfield Runway Adherent Layer in Permafrost Region of Northeast China. Case Stud. Therm. Eng. 2022, 33, 101985. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Y.; Shi, D.; Zhuang, C.; Lin, Z.; Hao, Z. Modelling Residential Outdoor Thermal Sensation in Hot Summer Cities: A Case Study in Chongqing, China. Buildings 2022, 12, 1564. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, B.; Richards, S.H. Calibration and Application of Treatment Performance Models in a Pavement Management System in Tennessee. J. Transp. Eng. 2015, 141, 04014076. [Google Scholar] [CrossRef]
- Polo-Mendoza, R.; Martinez-Arguelles, G.; Peñabaena-Niebles, R. Environmental Optimization of Warm Mix Asphalt (WMA) Design with Recycled Concrete Aggregates (RCA) Inclusion through Artificial Intelligence (AI) Techniques. Results Eng. 2023, 17, 100984. [Google Scholar] [CrossRef]
- Tarefder, R.A.; White, L.; Zaman, M. Neural Network Model for Asphalt Concrete Permeability. J. Mater. Civ. Eng. 2005, 17, 19–27. [Google Scholar] [CrossRef]
- Lanning, S.; Mallek, J. Factors Influencing Information Literacy Competency of College Students. J. Acad. Librariansh. 2017, 43, 443–450. [Google Scholar] [CrossRef]
- Krzywinski, M.; Altman, N. Points of Significance: Multiple Linear Regression. Nat. Methods 2015, 12, 1103–1104. [Google Scholar] [CrossRef]
- Feng, X.; Ning, Z.; Mao, Y.; Yang, Y.; Yang, X. Mechanical Damage Characteristics of CR/PPA Composite Modified Asphalt Pavement under Multi-Factor Coupling Effect in the Seasonally Frozen Region. Case Stud. Constr. Mater. 2023, 19, e02296. [Google Scholar] [CrossRef]
- Lee, S.Y.; Le, T.H.M.; Kim, Y.M. Prediction and Detection of Potholes in Urban Roads: Machine Learning and Deep Learning Based Image Segmentation Approaches. Dev. Built Environ. 2023, 13, 100109. [Google Scholar] [CrossRef]
- Foroutan Mirhosseini, A.; Tahami, S.A.; Hoff, I.; Dessouky, S.; Ho, C.H. Performance Evaluation of Asphalt Mixtures Containing High-RAP Binder Content and Bio-Oil Rejuvenator. Constr. Build. Mater. 2019, 227, 116465. [Google Scholar] [CrossRef]
- Xiao, X.; Skitmore, M.; Yao, W.; Ali, Y. Improving Robustness of Case-Based Reasoning for Early-Stage Construction Cost Estimation. Autom. Constr. 2023, 151, 104777. [Google Scholar] [CrossRef]
- Lu, Y.; Yin, L.; Deng, Y.; Wu, G.; Li, C. Using Cased Based Reasoning for Automated Safety Risk Management in Construction Industry. Saf. Sci. 2023, 163, 106113. [Google Scholar] [CrossRef]
- Okudan, O.; Budayan, C.; Dikmen, I. A Knowledge-Based Risk Management Tool for Construction Projects Using Case-Based Reasoning. Expert Syst. Appl. 2021, 173, 114776. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Skitmore, M.; Zhang, Y. Experience Mining Based on Case-Based Reasoning for Dispute Settlement of International Construction Projects. Autom. Constr. 2019, 97, 181–191. [Google Scholar] [CrossRef]



| Division | Number of Cases | Ratio |
|---|---|---|
| Gangwon | 3 | 3% |
| Gyeonggi-do | 19 | 19% |
| Gyeongnam | 13 | 13% |
| Gyeongbuk | 15 | 15% |
| Jeonnam | 13 | 13% |
| Jeonbuk | 12 | 12% |
| chief mourner | 1 | 1% |
| Chungnam | 15 | 15% |
| Chungbuk | 9 | 9% |
| Division | Number of Cases | Ratio | |
|---|---|---|---|
| Road height | Less than 5 m | 29 | 29% |
| 5~10 m | 41 | 41% | |
| 10~15 m | 22 | 22% | |
| 15 m or more | 8 | 8% | |
| Road grade | National Route 1 | 16 | 16% |
| National Route 2 | 54 | 54% | |
| National Route 3 | 22 | 22% | |
| National Route 4 | 8 | 8% | |
| Design speed | 60 km/h | 11 | 11% |
| 70 km/h | 20 | 20% | |
| 80 km/h | 63 | 63% | |
| 100 km/h | 6 | 6% | |
| Type of construction | New construction | 55 | 55% |
| Expanded packaging | 45 | 45% | |
| Division | Description |
|---|---|
| Earthwork | Digger—Excavation (m3) |
| Excavator Ripper—Excavation for Soil and Rock (m3) | |
| Blasting Rock—Blasting Material (m3) | |
| Earth Moving | Ceramic Transport—Material Transport (m3) |
| Dump Truck Transport—Earthwork Transport (m3) | |
| Excavation—General Earthwork (m3) | |
| Road Construction—Roadwork (m3) | |
| Landscaping Fill—Green Area Fill (m3) | |
| Drainage | Side Drainage Hole—V-shaped and U-shaped Side Gutter (m) |
| Horizontal Drainage Pipe—Horizontal Drain Pipe (m) | |
| Drainage Pipe with Wing Wall—Drainage Pipe Wing Wall (m2) | |
| Underground Tunnel | Concrete Pouring—Concrete Pouring for Tunnel (m3) |
| Formwork—Concrete Formwork for Tunnel (m2) | |
| Rebar Fabrication and Assembly—Rebar Work (ton) | |
| Scaffolding Worker—Scaffolding Worker (ton) | |
| Packer | Frost Protection Layer—Frost Protection Layer Installation (m3) |
| Asphalt Concrete (Ascon) Base Layer—Asphalt Base Layer (ton) | |
| Asphalt Concrete (Ascon) Middle Layer—Asphalt Middle Layer (ton) | |
| Asphalt Concrete (Ascon) Surface Layer—Asphalt Surface Layer (ton) |
| Model | # of Variables Used | Overfitting Controls | Validation Method |
|---|---|---|---|
| Multiple Regression Analysis | 6–8 vars (Stepwise) | Forward stepwise + significance filtering + residual diagnostics | Hold-out (80/20 split) |
| Regression Tree | All variables | Max depth = 4, leaf size = 5, cost-complexity pruning | Pruning + hold-out split |
| Case-Based Reasoning | Normalized inputs | k = 5, weighted similarity by correlation rank | Hold-out test set |
| A | 1 | ||||||||||||
| B | 0 | 1 | |||||||||||
| C | −0.08 | −0.28 | 1 | ||||||||||
| D | 0.05 | 0.14 | −0.26 | 1 | |||||||||
| E | 0.06 | 0.28 | −0.81 | 0.22 | 1 | ||||||||
| F | 0.21 | 0.05 | 0.13 | 0.13 | −0.13 | 1 | |||||||
| G | 0.17 | −0.22 | 0.04 | 0.05 | 0.04 | 0.07 | 1 | ||||||
| H | 0.16 | −0.21 | −0.1 | 0.26 | 0.05 | −0.05 | 0.47 | 1 | |||||
| I | −0.21 | 0.27 | −0.34 | −0.05 | 0.36 | −0.04 | −0.08 | −0.1 | 1 | ||||
| J | −0.06 | −0.07 | −0.47 | 0.2 | 0.43 | −0.04 | −0.04 | 0.29 | 0.39 | 1 | |||
| K | −0.01 | −0.11 | −0.46 | 0.21 | 0.42 | −0.06 | −0.11 | 0.39 | 0.35 | 0.95 | 1 | ||
| L | −0.03 | 0.14 | −0.27 | 0.13 | 0.35 | 0.06 | 0.59 | 0.24 | 0.18 | 0.19 | 0.15 | 1 | |
| M | −0.05 | 0.16 | −0.23 | 0.01 | 0.28 | 0.05 | 0.5 | 0.16 | 0.09 | 0.07 | 0.03 | 0.79 | 1 |
| A | B | C | D | E | F | G | H | I | J | K | L | M | |
| A | B | C | D | E | F | G | H | I | J | K | L | M | |
| Administrative district | Road height | Road grade | Topography | Design speed | Type of construction | Road extension | Road area | Packaging thickness | Number of cars | Road width | Eco | Cost | |
| Variable | Environmental Load (Coefficient) | Construction Costs (Coefficient) |
|---|---|---|
| Section | −5.15 × 103 | 2.91 × 109 |
| Administrative district | −2.03 × 102 | −7.85 × 108 |
| Road height | 1.09 × 102 | 3.75 × 108 |
| Road grade | −2.00 × 102 | −1.72 × 109 |
| Topography | 1.09 × 101 | −2.05 × 109 |
| Design speed | 3.92 × 101 | 9.07 × 107 |
| Type of construction | 3.77 × 102 | 1.61 × 109 |
| Road extension | 7.10 × 101 | 1.99 × 106 |
| Road area | 0.00 × 100 | −1.29 × 104 |
| Packaging thickness | −7.81 × 100 | −1.50 × 108 |
| Number of cars | −9.22 × 102 | −2.74 × 109 |
| Road width | 3.79 × 102 | 9.61 × 108 |
| Metric | ||
| R2 (R-Squared) | 0.55 | 0.43 |
| Modified R2 | 0.48 | 0.35 |
| p-value | 0.00 | 0.00 |
| Planning Stage Environmental Load Multiple Regression Model | Statistical Technique | Variable Names |
|---|---|---|
| Mallow’s Cp | 5 variables | Administrative districts, road height, design speed, road length, road width |
| BIC | 3 variables | Road height, design speed, road length |
| Adjusted R2 | 7 variables | Administrative districts, road height, design speed, road length, road area, number of lanes, road width |
| Planning Stage Construction Cost Multiple Regression Model | Statistical Technique | Variable Names |
| Mallow’s Cp | 4 variables | Administrative districts, road heights, design speeds, road lengths |
| BIC | 3 variables | Road height, design speed, road length |
| Adjusted R2 | 5 variables | Administrative districts, road elevations, road grades, terrain, road length |
| Statistical Technique | Variable | Coefficient | R2 | Adjusted R2 | p-Value |
|---|---|---|---|---|---|
| Mallow’s Cp | Section | −4946.81 | 0.52 | 0.49 | 0.00 |
| Road height | 102.87 | ||||
| Design speed | 57.79 | ||||
| Road extension | 0.59 | ||||
| Administrative district | −169.38 | ||||
| Road width | 100.84 | ||||
| BIC | Section | −5149.37 | 0.48 | 0.46 | 0.00 |
| Road height | 81.39 | ||||
| Design speed | 82.89 | ||||
| Road extension | 0.54 | ||||
| Adjusted R2 | Section | −6210.24 | 0.54 | 0.50 | 0.00 |
| Road height | 111.71 | ||||
| Design speed | 46.99 | ||||
| Road extension | 0.71 | ||||
| Administrative district | −177.13 | ||||
| Road width | 373.22 | ||||
| Number of cars | −881.56 | ||||
| Road area | 0.00 |
| Statistical Technique | Variable | Coefficient | R2 | Modified R2 | p-Value |
|---|---|---|---|---|---|
| Mallow’s Cp | Section | −4946.81 | 0.52 | 0.49 | 0.00 |
| Road height | 102.87 | ||||
| Design speed | 57.79 | ||||
| Road extension | 0.59 | ||||
| Administrative district | −169.38 | ||||
| Road width | 100.84 | ||||
| BIC | Section | −5149.37 | 0.48 | 0.46 | 0.00 |
| Road height | 81.39 | ||||
| Design speed | 82.89 | ||||
| Road extension | 0.54 | ||||
| Modified R2 | Section | −6210.24 | 0.54 | 0.50 | 0.00 |
| Road height | 111.71 | ||||
| Design speed | 46.99 | ||||
| Road extension | 0.71 | ||||
| Administrative district | −177.13 | ||||
| Road width | 373.22 | ||||
| Number of cars | −881.56 | ||||
| Road area | 0.00 |
| Unit: Eco-Point (the Composite Score from Republic of Korea’s Environmental Impact Index) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Division | Actual Value | All Variables | Mallow’s Cp | BIC | |||||
| Predicted Value | Error Rate | Predicted Value | Error Rate | Predicted Value | Error Rate | Predicted Value | Error Rate | ||
| Case 1 | 8174 | 6822 | 16.5% | 7362 | 9.9% | 6645 | 18.7% | 6630 | 18.9% |
| Case 2 | 7852 | 6260 | 20.3% | 5916 | 24.7% | 6125 | 22.0% | 6114 | 22.1% |
| Case 3 | 8490 | 6530 | 23.1% | 6261 | 26.3% | 6360 | 25.1% | 6366 | 25.0% |
| Case 4 | 2917 | 9571 | 228.1% | 6109 | 109.4% | 7602 | 160.6% | 9282 | 218.2% |
| Case 5 | 3892 | 3742 | 3.8% | 4656 | 19.6% | 3869 | 0.6% | 3755 | 3.5% |
| Case 6 | 3716 | 5921 | 59.4% | 4596 | 23.7% | 4453 | 19.8% | 5813 | 56.5% |
| Case 7 | 6690 | 7274 | 8.7% | 6886 | 2.9% | 7325 | 9.5% | 7351 | 9.9% |
| Case 8 | 4273 | 7205 | 68.6% | 5378 | 25.8% | 5565 | 30.2% | 7307 | 71.0% |
| Case 9 | 3337 | 4737 | 42.0% | 2223 | 33.4% | 2641 | 20.8% | 4545 | 36.2% |
| Case 10 | 5474 | 9266 | 69.3% | 8320 | 52.0% | 8883 | 62.3% | 8963 | 63.7% |
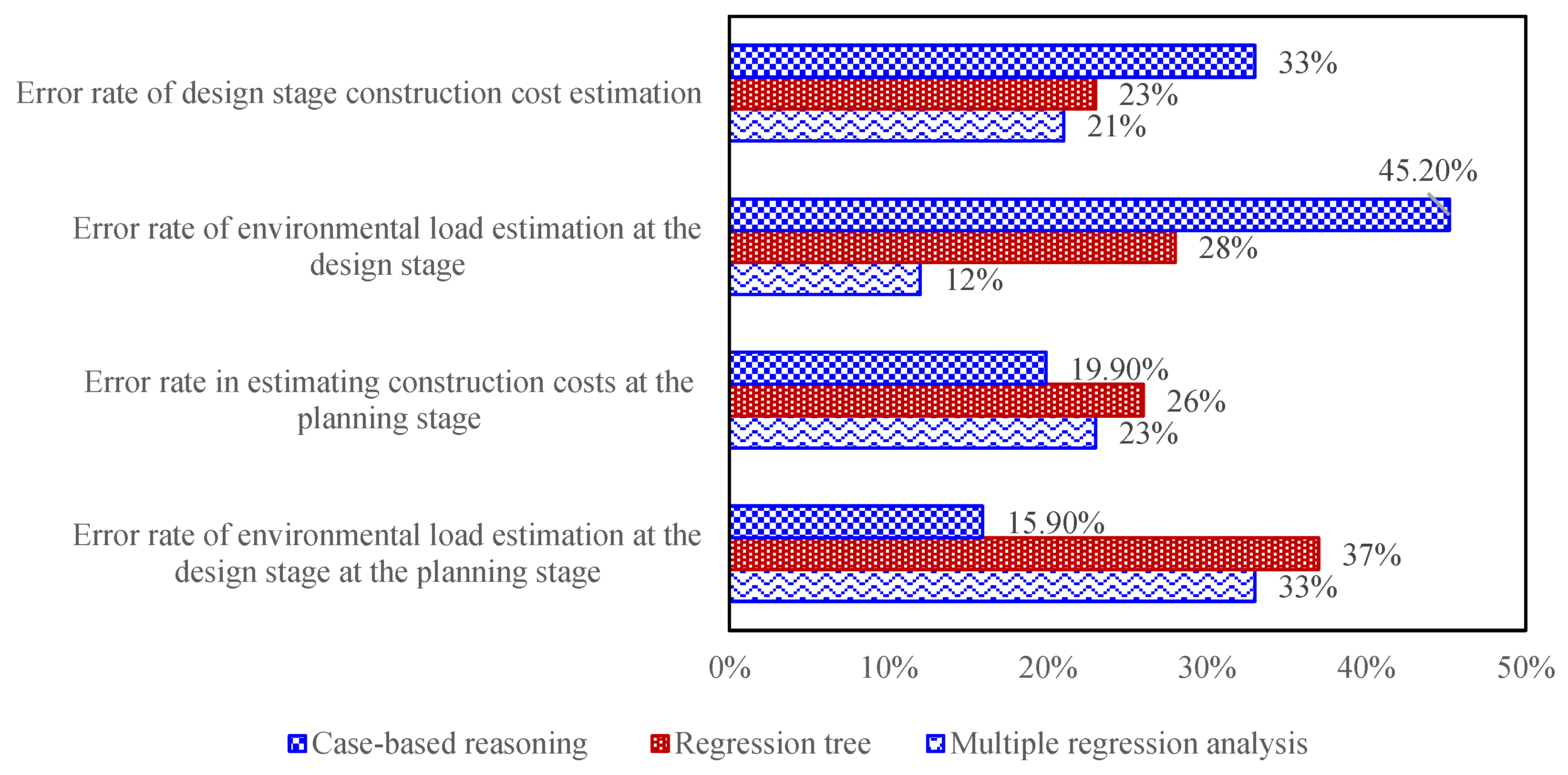
| Error rate average | 54.0% | 32.8% | 37.0% | 52.9% | |||||
| Standard deviation | 62.2% | 28.4% | 43.9% | 59.4% | |||||
| Unit: Ten Million Won (₩10,000,000 KRW) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Division | Actual Value | All Variables | Mallow’s Cp | BIC | |||||
| Predicted Value | Error Rate | Predicted Value | Error Rate | Predicted Value | Error Rate | Predicted Value | Error Rate | ||
| Case 1 | 1838 | 2202 | 19.8% | 1915 | 4.2% | 2115 | 15.1% | 2057 | 11.9% |
| Case 2 | 1891 | 2094 | 10.8% | 1855 | 1.9% | 1734 | 8.3% | 1747 | 7.6% |
| Case 3 | 1942 | 2018 | 3.9% | 1910 | 1.6% | 1843 | 5.1% | 1634 | 15.9% |
| Case 4 | 1061 | 2810 | 164.7% | 1821 | 71.6% | 1751 | 65.0% | 1955 | 84.2% |
| Case 5 | 1128 | 980 | 13.1% | 1189 | 5.4% | 1370 | 21.5% | 878 | 22.1% |
| Case 6 | 1082 | 1658 | 53.2% | 1349 | 24.7% | 1404 | 29.8% | 1218 | 12.6% |
| Case 7 | 1444 | 2318 | 60.5% | 2183 | 51.1% | 1990 | 37.8% | 2334 | 61.6% |
| Case 8 | 1937 | 2003 | 3.4% | 1711 | 11.7% | 1599 | 17.5% | 1671 | 13.7% |
| Case 9 | 1307 | 1628 | 24.6% | 832 | 36.3% | 813 | 37.8% | 1172 | 10.3% |
| Case 10 | 2093 | 2926 | 39.8% | 2596 | 24.0% | 2383 | 13.8% | 2767 | 32.2% |
| Error rate average | 39.4% | 23.3% | 25.2% | 27.2% | |||||
| Standard deviation | 45.8% | 22.4% | 17.1% | 24.3% | |||||
| A | 1 | ||||||||||||||||||||
| B | 0.66 | 1 | |||||||||||||||||||
| C | 0.36 | 0.49 | 1 | ||||||||||||||||||
| D | 0.55 | 0.61 | 0.53 | 1 | |||||||||||||||||
| E | 0.85 | 0.73 | 0.59 | 0.65 | 1 | ||||||||||||||||
| F | 0.51 | 0.5 | 0.48 | 0.45 | 0.67 | 1 | |||||||||||||||
| G | 0.3 | 0.16 | 0.06 | 0.15 | 0.2 | −0.16 | 1 | ||||||||||||||
| H | 0.4 | 0.52 | 0.5 | 0.33 | 0.49 | 0.29 | 0.25 | 1 | |||||||||||||
| I | 0.57 | 0.47 | 0.42 | 0.47 | 0.61 | 0.66 | 0.4 | 0.28 | 1 | ||||||||||||
| J | 0.22 | 0.19 | 0.3 | 0.42 | 0.33 | 0.41 | 0.2 | 0.13 | 0.41 | 1 | |||||||||||
| K | 0.17 | 0.18 | 0.18 | 0.29 | 0.27 | 0.47 | 0.29 | 0.13 | 0.59 | 0.38 | 1 | ||||||||||
| L | 0.39 | 0.27 | 0.35 | 0.43 | 0.44 | 0.62 | 0.33 | 0.14 | 0.68 | 0.53 | 0.56 | 1 | |||||||||
| M | 0.25 | 0.12 | 0.21 | 0.26 | 0.28 | 0.45 | 0.22 | 0.04 | 0.5 | 0.48 | 0.33 | 0.74 | 1 | ||||||||
| N | 0.3 | 0.18 | 0.27 | 0.35 | 0.31 | 0.52 | 0.38 | 0.1 | 0.62 | 0.51 | 0.52 | 0.92 | 0.71 | 1 | |||||||
| O | 0.48 | 0.32 | 0.32 | 0.43 | 0.48 | 0.67 | 0.37 | 0.16 | 0.76 | 0.45 | 0.59 | 0.91 | 0.65 | 0.83 | 1 | ||||||
| P | 0. 37 | 0.44 | 0.33 | 0.47 | 0.42 | 0.54 | 0.11 | 0.28 | 0.56 | 0.43 | 0.45 | 0.54 | 0.4 | 0.47 | 0.57 | 1 | |||||
| Q | 0.32 | 0.25 | 0.11 | 0.25 | 0.28 | 0.28 | 0.43 | −0.1 | 0.5 | 0.38 | 0.44 | 0.53 | 0.38 | 0.43 | 0.52 | 0.4 | 1 | ||||
| R | 0.1 | 0.21 | 0.08 | 0.17 | 0.06 | −0.08 | 0.37 | 0.23 | 0.13 | 0.06 | 0.16 | 0.08 | 0.05 | 0.03 | 0.12 | 0.21 | 0.32 | 1 | |||
| S | 0.09 | 0.31 | 0.03 | 0.18 | 0.11 | 0.06 | 0.26 | 0.14 | 0.13 | 0.08 | 0.19 | 0.06 | 0.05 | 0.03 | 0.09 | 0.08 | 0.3 | 0.52 | 1 | ||
| T | 0.53 | 0.52 | 0.39 | 0.53 | 0.6 | 0.61 | 0.37 | 0.28 | 0.72 | 0.54 | 0.57 | 0.69 | 0.52 | 0.56 | 0.67 | 0.6 | 0.67 | 0.26 | 0.41 | 1 | |
| U | 0.52 | 0.48 | 0.48 | 0.57 | 0.61 | 0.52 | 0.31 | 0.34 | 0.66 | 0.45 | 0.51 | 0.61 | 0.43 | 0.45 | 0.58 | 0.57 | 0.59 | 0.25 | 0.15 | 0.86 | 1 |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | |
| A | B | C | D | E | F | G | H | I | J | ||||||||||||
| Ground preparation | Excavator Ripper | Blasting rock | Ceramic Transport | Dump Truck Transport | Earthworks or Excavation | Road Construction | Landscaping Fill | Side Drainage Hole Length | Vertical Drainage Pipe | ||||||||||||
| K | L | M | N | O | P | Q | R | S | T | ||||||||||||
| Drainage Pipe with Wing Wall | Culvert Concrete Pouring | Culvert Concrete Formwork | Installation for Underground Construction | Scaffolding Worker | Asphalt Base Layer | Frost Protection Asphalt Base Layer | Asphalt Concrete (Ascon) Middle Layer | Asphalt Concrete (Ascon) Surface Layer | Eco-friendly Measures | ||||||||||||
| U | |||||||||||||||||||||
| Construction Cost | |||||||||||||||||||||
| Metric | Variable | Environmental Load Coefficient | Construction Cost Coefficient |
|---|---|---|---|
| Earthwork | Ground preparation | 2.95 × 102 | 1.48 × 109 |
| Excavator Ripper | 8.27 × 10−4 | 1.67 × 103 | |
| Blasting Rock | −2.65 × 10−5 | −3.00 × 103 | |
| Material Transport | Ceramic Transport | −5.66 × 10−4 | 1.56 × 103 |
| Dump Truck Transport | 4.34 × 103 | 4.49 × 104 | |
| Excavation | Excavation | −7.41 × 10−7 | 1.29 × 103 |
| Drainage | Drainage | 7.34 × 10−4 | −4.33 × 102 |
| Roadworks | Green Space Fill | 9.14 × 10−4 | 1.22 × 102 |
| Drainage | Side Drainage Hole | 4.48 × 10−3 | 3.76 × 104 |
| Horizontal Drain Pipe (VR Hall) | 4.32 × 10−2 | 1.44 × 105 | |
| Horizontal Drain Pipe (Wing Wall) | 3.26 × 10−1 | 1.76 × 105 | |
| Underground Tunnel | Concrete Pouring | 3.10 × 10−1 | 2.19 × 106 |
| Concrete Formwork | 4.20 × 10−1 | 1.42 × 106 | |
| Rebar Fabrication and Installation | 7.95 × 10−3 | 3.48 × 104 | |
| Labor | Scaffolding Worker | −1.39 | −6.15 × 106 |
| Protective Layer | Frost Protection Layer | −1.91 × 10−1 | −5.73 × 105 |
| Paving | Asphalt Base Layer (Ascon) | 7.75 × 10−3 | 1.76 × 104 |
| Asphalt Middle Layer (Ascon) | 2.2 × 10−2 | 8.87 × 104 | |
| Asphalt Surface Layer (Ascon) | −6.73 × 10−3 | 1.02 × 104 |
| Model | Statistical Technique | Variable Names | Number of Variables |
|---|---|---|---|
| Design Phase Environmental Load | Mallow’s Cp, BIC, Modified R2 | Dump Truck Transport, Side Trench Construction Length, VR Pipe, Concrete Pouring, Rebar Fabrication and Assembly, Frost Protection Layer, Asphalt Base Layer, Asphalt Surface Layer | 8 |
| Design Phase Construction Cost | Mallow’s Cp | Ceramic Transport, Green Zone Filling, Side Trench Construction Length, Concrete Pouring, Rebar Fabrication and Assembly, Scaffolding, Asphalt Base Layer | 7 |
| BIC | Ceramic Transport, Green Zone Filling, Side Trench Construction Length, Concrete Pouring, Rebar Fabrication and Assembly, Asphalt Base Layer | 6 | |
| Modified R2 | Ceramic Transport, Green Zone Filling, Side Trench Construction Length, Wing Wall, Concrete Pouring, Rebar Fabrication and Assembly, Scaffolding, Asphalt Base Layer | 8 |
| Metric | Dump Transport | Construction Length | VR Hall | Concrete Pouring | Rebar Processing and Assembly | Frost Protection Layer | Ascon Base | Ascon Surface |
|---|---|---|---|---|---|---|---|---|
| Mallow’s Cp | 348.81 | 0 | 0.05 | 0.48 | 0.28 | −1.06 | 0.01 | 0.02 |
| R2 = 0.82; Modified R2 = 0.80; p-value = 0.00 | ||||||||
| Unit: Eco-Point | |||||
|---|---|---|---|---|---|
| Division | Actual Value | All Variables | Mallow’s Cp, BIC, Adjusted R2 | ||
| Predicted Value | Error Rate | Predicted Value | Error Rate | ||
| Case 1 | 8174 | 7720 | 6% | 7767 | 5% |
| Case 2 | 7852 | 6699 | 15% | 6813 | 13% |
| Case 3 | 8490 | 7603 | 10% | 6536 | 23% |
| Case 4 | 2917 | 2258 | 23% | 2313 | 21% |
| Case 5 | 3892 | 3684 | 5% | 3699 | 5% |
| Case 6 | 3716 | 4711 | 27% | 4224 | 14% |
| Case 7 | 6690 | 7196 | 8% | 6504 | 3% |
| Case 8 | 4273 | 5403 | 26% | 5060 | 18% |
| Case 9 | 3337 | 4852 | 45% | 3915 | 17% |
| Case 10 | 5474 | 5616 | 3% | 5269 | 4% |
| Error rate average | 17% | 12% | |||
| Standard deviation | 13% | 7% | |||
| Unit: Ten Million Won (₩10,000,000 KRW) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Division | Actual Value | All Variables | Mallow’s Cp | BIC | Adjusted R2 | ||||
| Predicted Value | Error Rate | Predicted Value | Error Rate | Predicted Value | Error Rate | Predicted Value | Error Rate | ||
| Case 1 | 1838 | 2233 | 21% | 1676 | 9% | 1790 | 3% | 1857 | 1% |
| Case 2 | 1891 | 2210 | 17% | 2173 | 15% | 2307 | 22% | 2229 | 18% |
| Case 3 | 1942 | 2731 | 41% | 1573 | 19% | 1535 | 21% | 2421 | 25% |
| Case 4 | 1061 | 833 | 21% | 1003 | 6% | 969 | 9% | 993 | 6% |
| Case 5 | 1128 | 1114 | 1% | 1009 | 10% | 1051 | 7% | 1034 | 8% |
| Case 6 | 1082 | 1682 | 55% | 1269 | 17% | 1305 | 21% | 1510 | 40% |
| Case 7 | 1444 | 2796 | 94% | 2515 | 74% | 2603 | 80% | 2736 | 89% |
| Case 8 | 1937 | 1791 | 8% | 1547 | 20% | 1585 | 18% | 1577 | 19% |
| Case 9 | 1307 | 1474 | 13% | 1469 | 12% | 1886 | 44% | 1819 | 39% |
| Case 10 | 2093 | 1616 | 23% | 1543 | 26% | 1824 | 13% | 1848 | 12% |
| Error rate average | 29% | 21% | 24% | 26% | |||||
| Standard deviation | 26% | 19% | 22% | 25% | |||||
| Planning stage environmental load estimation regression tree splitting error | |||||
| NO | CP | n-split | relerror | xerror | xstd |
| 1 | 0.40 | 0 | 100% | 102% | 16% |
| 2 | 0.15 | 1 | 60% | 78% | 17% |
| 3 | 0.05 | 2 | 45% | 62% | 15% |
| 4 | 0.02 | 3 | 40% | 61% | 13% |
| 5 | 0.02 | 4 | 38% | 56% | 11% |
| 6 | 0.01 | 5 | 36% | 57% | 11% |
| Planning stage construction cost estimation regression tree splitting error | |||||
| NO | CP | n-split | relerror | xerror | xstd |
| 1 | 0.30 | 0 | 100% | 102% | 16% |
| 2 | 0.08 | 1 | 70% | 88% | 17% |
| 3 | 0.06 | 2 | 63% | 96% | 19% |
| 4 | 0.06 | 3 | 56% | 92% | 18% |
| 5 | 0.02 | 4 | 51% | 84% | 16% |
| 6 | 0.02 | 5 | 48% | 85% | 16% |
| 7 | 0.02 | 6 | 46% | 86% | 16% |
| 8 | 0.02 | 7 | 44% | 87% | 16% |
| 9 | 0.01 | 8 | 42% | 83% | 15% |
| Division | Environmental Load Actual Value Unit: Eco-Point | Planning Stage Estimation of Environmental Load Regression Tree | Construction Cost Actual Value Unit: Ten Million Won (₩10,000,000 KRW) | Planning Stage Estimate Construction Costs Regression Tree | ||
|---|---|---|---|---|---|---|
| Predicted Value | Error Rate | Predicted Value | Error Rate | |||
| Case 1 | 8174 | 8503 | 4.0% | 1838 | 1527 | 56.8% |
| Case 2 | 7852 | 6697 | 14.7% | 1891 | 2754 | 1.9% |
| Case 3 | 8490 | 6697 | 21.1% | 1942 | 2242 | 29.3% |
| Case 4 | 2917 | 8503 | 191.5% | 1061 | 1527 | 21.0% |
| Case 5 | 3892 | 3694 | 5.1% | 1128 | 984 | 9.3% |
| Case 6 | 3716 | 3694 | 0.6% | 1082 | 1559 | 5.0% |
| Case 7 | 6690 | 8503 | 27.1% | 1444 | 1527 | 47.2% |
| Case 8 | 4273 | 5306 | 24.2% | 1937 | 1559 | 17.4% |
| Case 9 | 3337 | 2555 | 23.4% | 1307 | 977 | 48.5% |
| Case 10 | 5474 | 8503 | 55.3% | 2093 | 1527 | 46.1% |
| Average error rate | 36.7% | Average error rate | 28.3% | |||
| Standard deviation | 53.7% | Standard deviation | 19.2% | |||
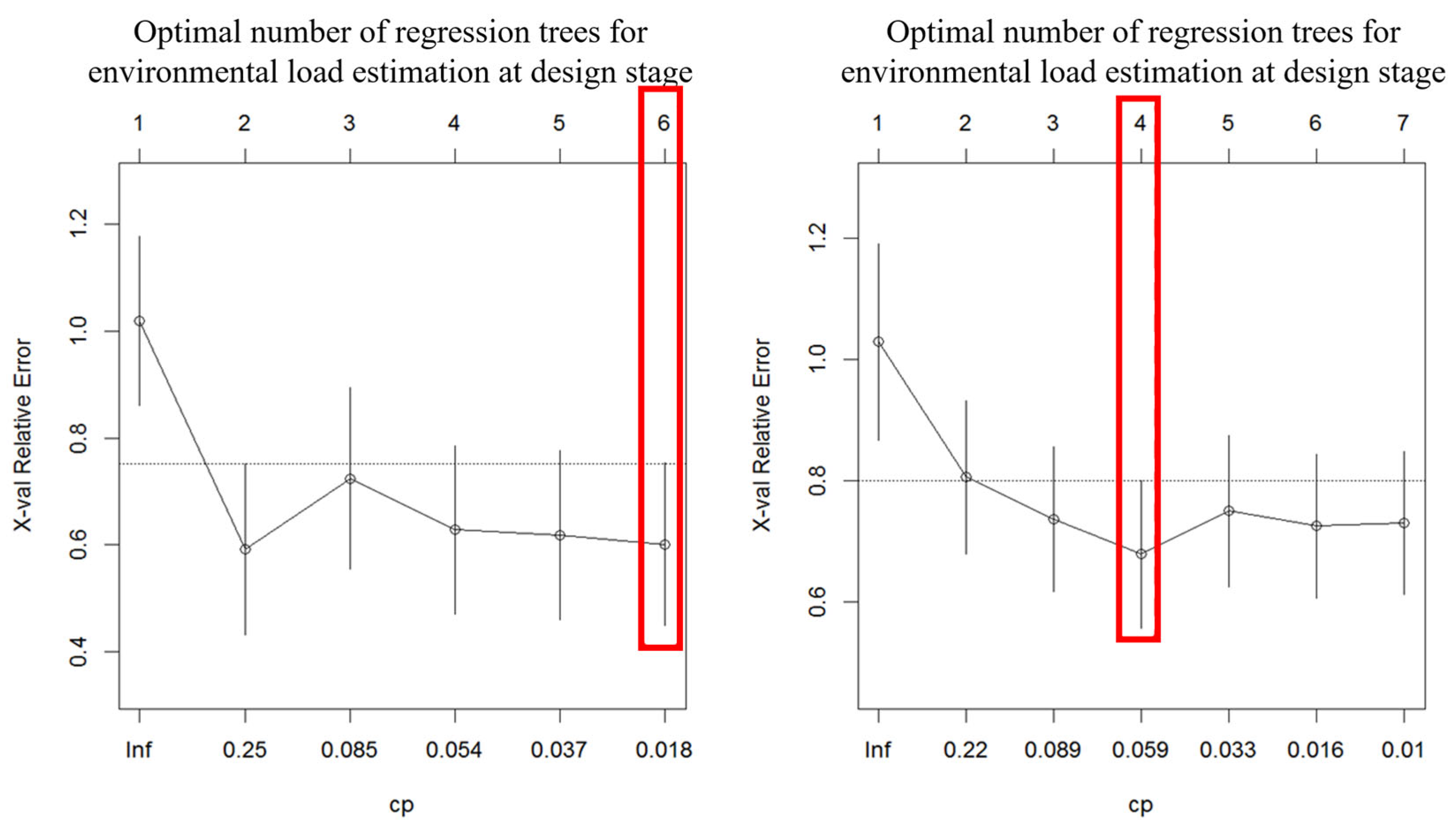
| Design phase environmental load estimation regression tree splitting error | |||||
| NO | CP | n-split | rel error | xerror | xstd |
| 1 | 0.55 | 0 | 100% | 102% | 16% |
| 2 | 0.11 | 1 | 45% | 59% | 16% |
| 3 | 0.06 | 2 | 34% | 72% | 17% |
| 4 | 0.05 | 3 | 27% | 63% | 16% |
| 5 | 0.03 | 4 | 23% | 62% | 16% |
| 6 | 0.01 | 5 | 20% | 60% | 15% |
| Design-stage construction cost estimation regression tree splitting error | |||||
| NO | CP | n-split | rel error | xerror | xstd |
| 1 | 0.44 | 0 | 100% | 103% | 16% |
| 2 | 0.11 | 1 | 56% | 80% | 12% |
| 3 | 0.07 | 2 | 46% | 73% | 12% |
| 4 | 0.05 | 3 | 38% | 68% | 12% |
| 5 | 0.02 | 4 | 33% | 75% | 12% |
| 6 | 0.01 | 5 | 31% | 73% | 12% |
| 7 | 0.01 | 6 | 30% | 73% | 12% |
| Division | Environmental Load Actual Value Unit: Eco-Point | Design Phase Estimation of Environmental Load Regression Tree | Construction Cost Actual Value Unit: Ten Million Won (₩10,000,000 KRW) | Design Phase Estimate Construction Costs Regression Tree | ||
|---|---|---|---|---|---|---|
| Predicted Value | Error Rate | Predicted Value | Error Rate | |||
| Case 1 | 8174 | 3531 | 57% | 1838 | 1252 | 32% |
| Case 2 | 7852 | 8000 | 2% | 1891 | 1715 | 9% |
| Case 3 | 8490 | 5999 | 29% | 1942 | 1715 | 12% |
| Case 4 | 2917 | 3531 | 21% | 1061 | 526 | 50% |
| Case 5 | 3892 | 3531 | 9% | 1128 | 1252 | 11% |
| Case 6 | 3716 | 3531 | 5% | 1082 | 1252 | 16% |
| Case 7 | 6690 | 3531 | 47% | 1444 | 1252 | 13% |
| Case 8 | 4273 | 3531 | 17% | 1937 | 1252 | 35% |
| Case 9 | 3337 | 4956 | 49% | 1307 | 1715 | 31% |
| Case 10 | 5474 | 8000 | 46% | 2093 | 1715 | 18% |
| Average error rate | 28% | Average error rate | 23% | |||
| Standard deviation | 19% | Standard deviation | 13% | |||
| Parameter Name | Setting Value |
|---|---|
| Convergence | 0.0001 |
| Mutation rate | 0.25 |
| Maximum subproblem | 5000 |
| Maximum optimal solution | 5000 |
| Division | Environmental Load Actual Value Unit: Eco-Point | Planning Stage Estimation of Environmental Load Case-Based Reasoning | Construction Cost Actual Value Unit: Ten Million Won (₩10,000,000 KRW) | Planning Stage Estimate Construction Costs Case-Based Reasoning | ||
|---|---|---|---|---|---|---|
| Predicted Value | Error Rate | Predicted Value | Error Rate | |||
| Case 1 | 8174 | 7852 | 3.9% | 1838 | 1627 | 11.5% |
| Case 2 | 7852 | 8174 | 4.1% | 1891 | 2170 | 14.8% |
| Case 3 | 8490 | 3716 | 56.2% | 1942 | 1387 | 28.6% |
| Case 4 | 2917 | 2917 | 0.0% | 1061 | 1333 | 25.6% |
| Case 5 | 3892 | 3892 | 0.0% | 1128 | 1321 | 17.1% |
| Case 6 | 3716 | 6690 | 80.1% | 1082 | 691 | 36.2% |
| Case 7 | 6690 | 8490 | 26.9% | 1444 | 1479 | 2.4% |
| Case 8 | 4273 | 4273 | 0.0% | 1937 | 2265 | 17.0% |
| Case 9 | 3337 | 5474 | 64.1% | 1307 | 1141 | 12.7% |
| Case 10 | 5474 | 3337 | 39.0% | 2093 | 1403 | 33.0% |
| Average error rate | 15.9% | Average error rate | 19.9% | |||
| Standard deviation | 8.6% | Standard deviation | 10.1% | |||
| Division | Environmental Load Actual Value Unit: Eco-Point | Design Phase Estimation of Environmental Load Case-Based Reasoning | Construction Cost Actual Value Unit: (₩10,000,000 KRW) | Design Phase Estimate Construction Costs Case-Based Reasoning | ||
|---|---|---|---|---|---|---|
| Predicted Value | Error Rate | Predicted Value | Error Rate | |||
| Case 1 | 8174 | 4491 | 45.1% | 1838 | 1502 | 18.3% |
| Case 2 | 7852 | 3708 | 52.8% | 1891 | 1172 | 38.0% |
| Case 3 | 8490 | 4011 | 52.8% | 1942 | 1068 | 45.0% |
| Case 4 | 2917 | 5948 | 103.9% | 1061 | 1833 | 72.7% |
| Case 5 | 3892 | 2727 | 29.9% | 1128 | 1139 | 1.0% |
| Case 6 | 3716 | 5948 | 60.1% | 1082 | 1833 | 69.4% |
| Case 7 | 6690 | 7265 | 8.6% | 1444 | 1980 | 37.1% |
| Case 8 | 4273 | 5529 | 29.4% | 1937 | 1068 | 45.0% |
| Case 9 | 3337 | 4483 | 34.4% | 1307 | 1404 | 7.4% |
| Case 10 | 5474 | 7387 | 34.9% | 2093 | 2370 | 13.2% |
| Average error rate | 45.2% | Average error rate | 33.0% | |||
| Standard deviation | 25.5% | Standard deviation | 24.5% | |||
| No. | Model | Stage | Assumed Values/User-Defined Parameters |
|---|---|---|---|
| 1 | Multiple Regression Analysis | Planning | - Variable selection via Best Subsets method - Mallows’ Cp, BIC, and Adjusted R2 as criteria - Normality of residuals assumed |
| Design | - Stepwise forward selection based on Adjusted R2 and p-value threshold (p < 0.05) - Residual homoscedasticity assumed | ||
| 2 | Regression Tree | Planning | - Minimum leaf size: 5 - Max depth: 4 - Pruning based on cost-complexity - Split criterion: Mean Squared Error |
| Design | - Minimum leaf size: 10 - Max depth: 5 - Split criterion: Mean Absolute Error | ||
| 3 | Case-Based Reasoning | Planning | - Similarity measure: Euclidean distance - Number of nearest neighbors (k): 3 - Weighting: Inverse distance weighting |
| Design | - Similarity measure: Weighted Euclidean distance - Number of neighbors: 5 - Attribute weights: Based on correlation analysis |
| Study | Method(s) Used | Application Domain | Dataset Size and Type | Performance (Error/Accuracy) |
|---|---|---|---|---|
| Xiao et al. (2023) [35] | GA-CBR, OLS-CBR, MODLR-CBR | Early-stage construction cost estimation | 11,000 simulated + 1610 real apartment cases | MAPE: 14.60–19.74% (20-fold CV) |
| Kiani and Nasrollahzadeh (2023) [19] | Fuzzy logic model | Seismic fragility modeling for RC frames | 200 probabilistic models (via LHS) | Scenario-dependent error; fuzzy model deviation ≤ 5.2% in base case; accurate fragility prediction across LS1–LS3 |
| This Study—Planning Stage | MRA, RT, CBR | Road construction cost and environmental load | 17 real road projects | MAPE: 23–36% (CBR: 16–20%) |
| This Study—Design Stage | MRA, RT, CBR | Road design cost and environmental load | 22 real road projects | MAPE: 12–28% (MRA best at design stage) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-S. Advancing Sustainable Road Construction with Multiple Regression Analysis, Regression Tree Models, and Case-Based Reasoning for Environmental Load and Cost Estimation. Buildings 2025, 15, 2083. https://doi.org/10.3390/buildings15122083
Kim J-S. Advancing Sustainable Road Construction with Multiple Regression Analysis, Regression Tree Models, and Case-Based Reasoning for Environmental Load and Cost Estimation. Buildings. 2025; 15(12):2083. https://doi.org/10.3390/buildings15122083
Chicago/Turabian StyleKim, Joon-Soo. 2025. "Advancing Sustainable Road Construction with Multiple Regression Analysis, Regression Tree Models, and Case-Based Reasoning for Environmental Load and Cost Estimation" Buildings 15, no. 12: 2083. https://doi.org/10.3390/buildings15122083
APA StyleKim, J.-S. (2025). Advancing Sustainable Road Construction with Multiple Regression Analysis, Regression Tree Models, and Case-Based Reasoning for Environmental Load and Cost Estimation. Buildings, 15(12), 2083. https://doi.org/10.3390/buildings15122083





