Enhancement Analysis of Damaged Masonry Structures Strengthened with Ultra-High-Performance Concrete
Abstract
1. Introduction
2. Numerical Modeling and Structural Analysis
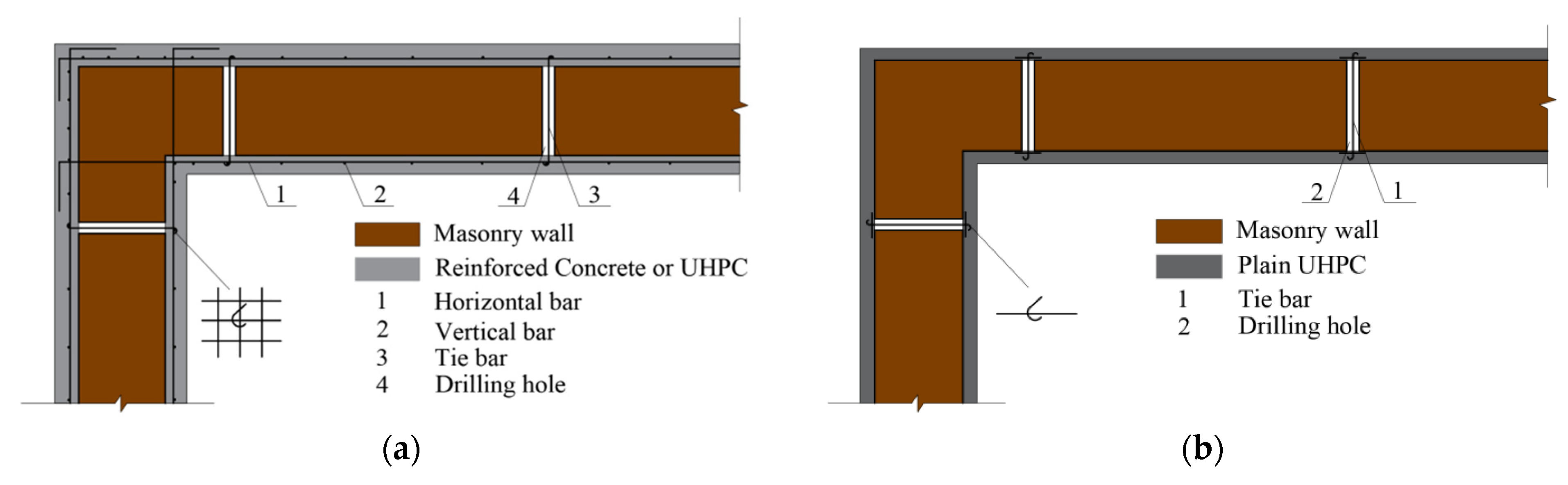
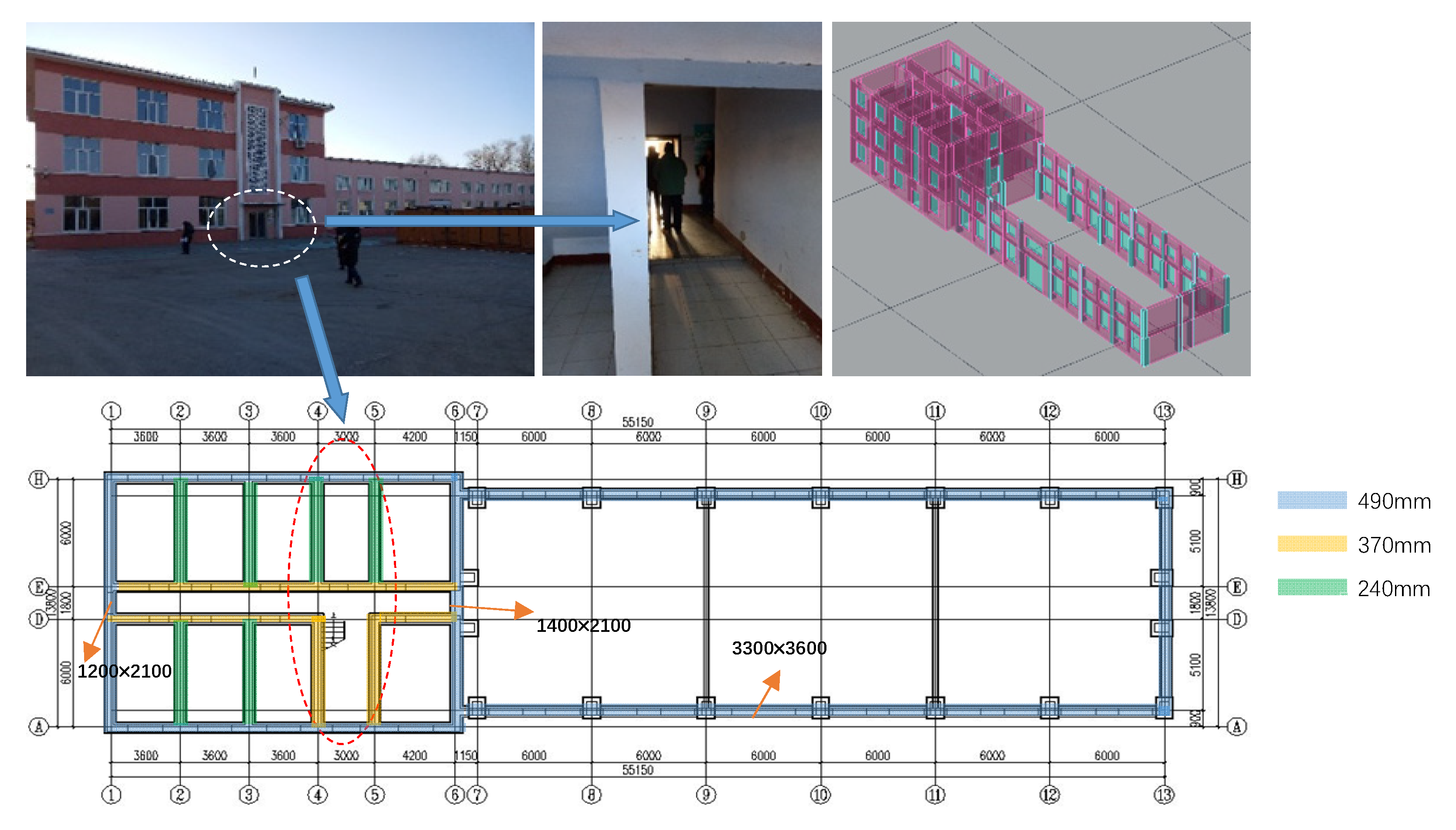
2.1. Description of Existing Masonry Structure Strengthening
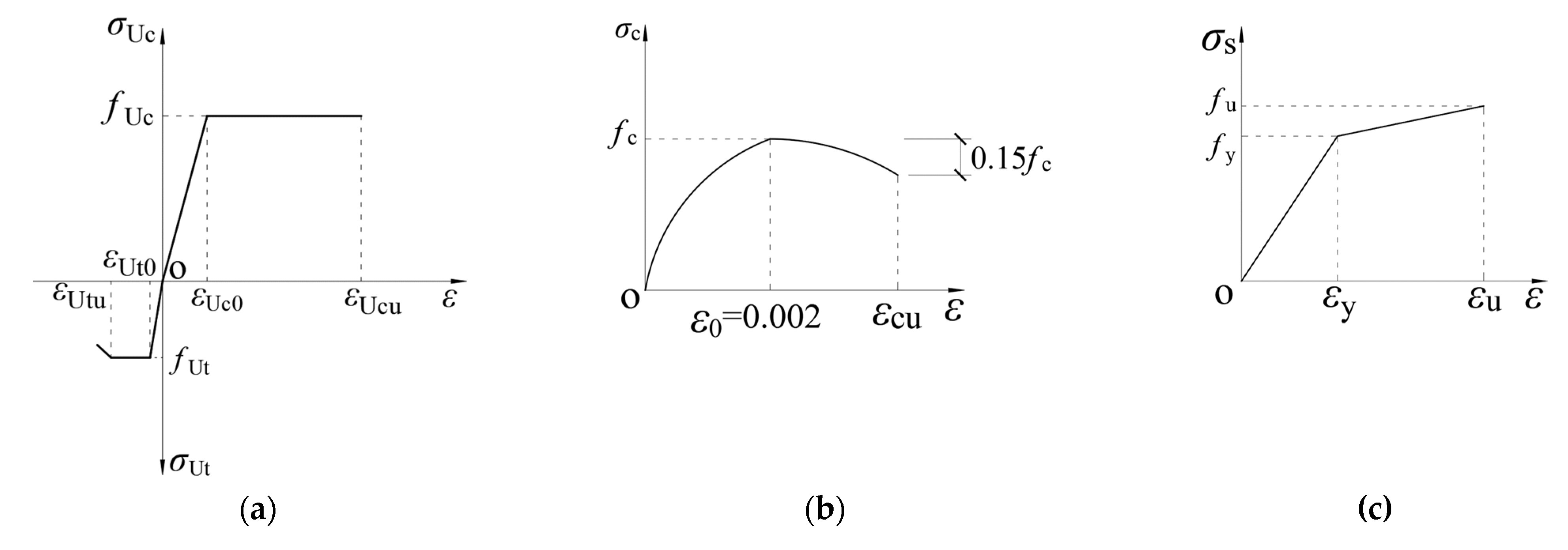
2.2. Material Properties and Stress–Strain Relationships
2.3. Modeling Methodology and Load Cases
3. Results and Discussion
3.1. Structural Performance Before and After Earthquake
3.2. Axial Compression Resistance
3.3. Shear Resistance
3.4. Influence of UHPC Layer Thickness and Rebar Content
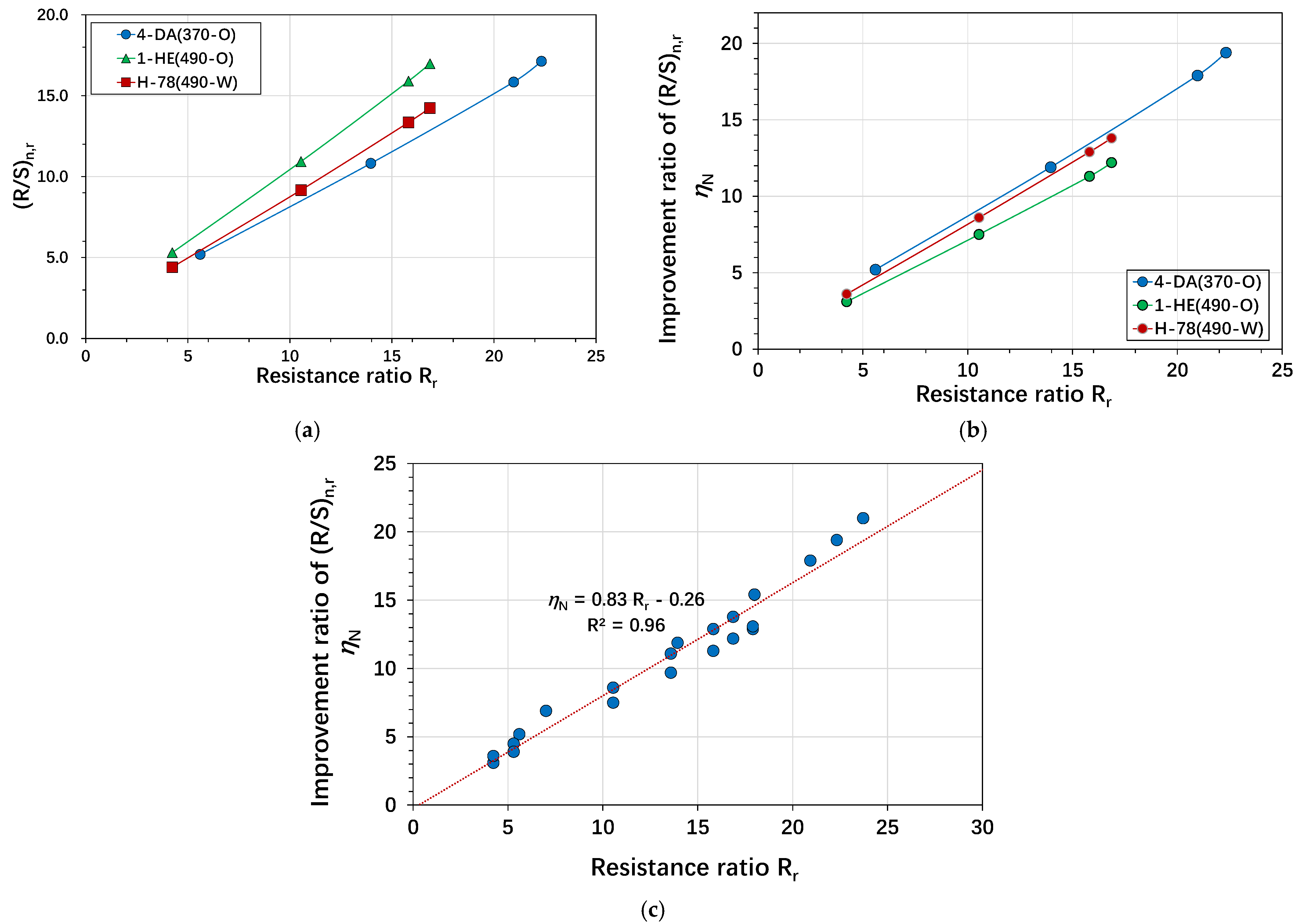
3.5. Regression Analysis of Strengthening Parameters
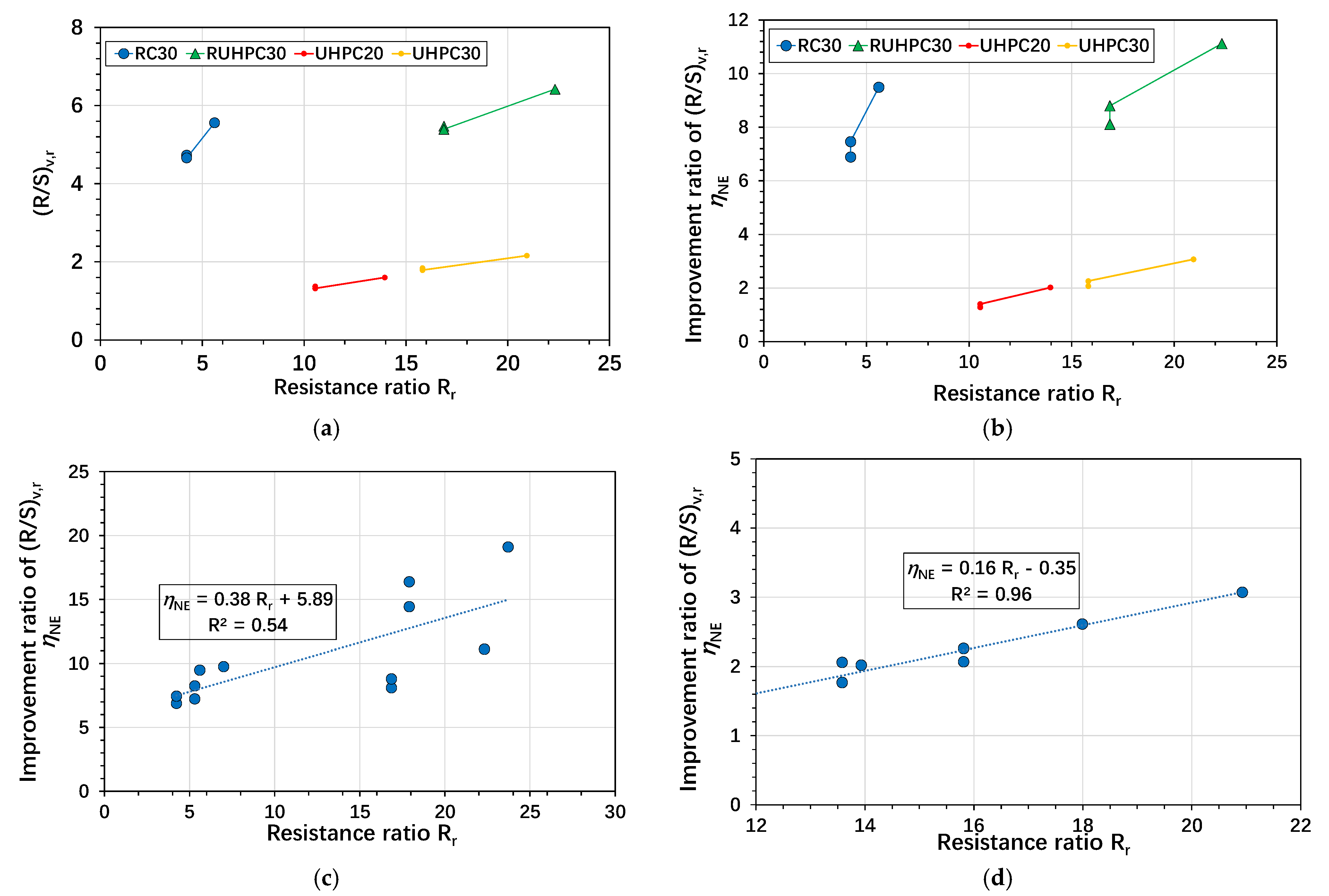
3.5.1. Variations in the Ratio of Compression Resistance
3.5.2. Non-Dimensional Improvement Ratio of Shear Resistance
3.5.3. Effect of the Non-Dimensional Resistance Ratio
4. Comparison of Strengthening Techniques
4.1. RC vs. UHPC Strengthening Performance
4.2. Cost-Effectiveness and Design Coniderations
5. Conclusions
- (1)
- Damaged masonry walls can be retrofitted with plain UHPC layers, and the thickness of the UHPC layers can be appropriately reduced according to design requirements. For typical cases, the compressive resistance of the damaged masonry walls strengthened with 30 mm thick double-sided plain UHPC layers was about 3.0 times that of the corresponding masonry walls strengthened with 30 mm thick double-sided RC layers. When the thickness of the plain UHPC layers was reduced to 20 mm, the compressive resistance of the strengthened masonry walls decreased to about 2.0 times that of the corresponding masonry walls reinforced with 30 mm thick double-sided RC layers. The design thickness of UHPC has a significant impact on the compressive resistance of the existing masonry structures.
- (2)
- The seismic performance of existing brick masonry structures strengthened with UHPC shows a non-linear increase as the thickness of the UHPC layer increases. For typical cases, the axial compression ratio of the masonry walls can be reduced by approximately 60–70% when double-sided plain UHPC layers are used for strengthening. From the perspective of seismic strengthening, the seismic performance of the damaged masonry walls can be improved by about 150%, 250%, and 930% when 20 mm thick double-sided plain UHPC layers, 30 mm thick double-sided plain UHPC layers, and 30 mm thick double-sided RUHPC layers are used for strengthening, respectively.
- (3)
- This article proposes a resistance ratio strengthening parameter and examines its influence on structural behavior. Generally, the regression analysis results showed that the ratio of axial resistance to shear resistance increased linearly with the increase in the resistance ratio. In particular, this relationship was evident in the enhancement effect of axial resistance. To effectively increase the shear resistance, it is recommended to use RC or RUHPC layers with reinforcement.
- (4)
- When the axial compression and shear demands are relatively low, plain UHPC layers can be used without a significant increase in wall thickness. For retrofitting the typical damaged masonry walls described in this paper, the use of 30 mm thick reinforced UHPC layers significantly improved the structural performance. Subsequently, the use of plain UHPC layers provided satisfactory structural performance for the strengthened masonry walls without requiring a minimum thickness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- GB50011-2010[S]; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2016. (In Chinese)
- GB50702-2011[S]; Code for Design of Strengthening Masonry Structures. China Architecture & Building Press: Beijing, China, 2011. (In Chinese)
- Orlowsky, J.; Beßling, M.; Kryzhanovskyi, V. Prospects for the Use of Textile-Reinforced Concrete in Buildings and Structures Maintenance. Buildings 2023, 13, 189. [Google Scholar] [CrossRef]
- Sayin, E.; Calayir, Y. Comparison of linear and non-linear earthquake response of masonry walls. Comput. Concr. 2015, 16, 17–35. [Google Scholar] [CrossRef]
- Karaca, Z.; Turkeli, E.; Pergel, S. Seismic assessment of historical masonry structures: The case of Amasya Tashan. Comput. Concr. 2017, 20, 409–418. [Google Scholar]
- Laib, S.; Meftah, S.A.; Tounsi, A. Vibration and damping characteristics of the masonry wall strengthened with bonded fibre composite patch with viscoelastic adhesive layer. Comput. Concr. 2021, 27, 253–268. [Google Scholar]
- Koksal, H.O.; Jafarov, O.; Karakoc, C. Computational material modeling of masonry walls strengthened with fiber reinforced polymers. Struct. Eng. Mech. 2013, 48, 737–755. [Google Scholar] [CrossRef]
- Mercedes, L.; Bernat-Maso, E.; Gil, L. Numerical simulation of masonry walls strengthened with vegetal fabric reinforced cementitious matrix (FRCM) composites and subjected to cyclic loads. Structures 2022, 35, 1232–1242. [Google Scholar] [CrossRef]
- Deng, M.; Dong, Z.; Ma, P. Cyclic loading tests of flexural-failure dominant URM walls strengthened with engineered cementitious composite. Eng. Struct. 2019, 194, 173–182. [Google Scholar] [CrossRef]
- Choi, H.K.; Bae, B.I.; Choi, C.S. Lateral resistance of unreinforced masonry walls strengthened with engineered cementitious composite. Int. J. Civ. Eng. 2016, 14, 411–424. [Google Scholar] [CrossRef]
- Bui, T.L.; Larbi, A.S.; Reboul, N.; Ferrier, E. Shear behaviour of masonry walls strengthened by external bonded FRP and TRC. Compos. Struct. 2015, 132, 923–932. [Google Scholar] [CrossRef]
- Sharbatdar, M.K.; Tajari, A. Experimental in-plane seismic strengthening of masonry infilled reinforced concrete frames by engineered cementitious composites (ECC). Constr. Build. Mater. 2021, 293, 123529. [Google Scholar] [CrossRef]
- Gul, A.; Alam, B.; Khan, I.U.; Shah, S.A.A.; Khan, S.W.; Shahzada, K. Improving seismic capacity of dry stacked interlocking masonry structurethrough confinement at corners. Soil Dyn. Earthq. Eng. 2023, 165, 107710. [Google Scholar] [CrossRef]
- Tao, Y.; Xu, Z.-D.; Wei, Y.; Miao, C.; Ji, B. Energy-based damage assessment method for masonry walls under seismicand fire loads. Eng. Struct. 2025, 322, 119152. [Google Scholar] [CrossRef]
- Szabó, S.; Funari, M.F.; Lourenço, P.B. Masonry patterns’ influence on the damage assessment of URM walls. Current and future trends. Dev. Built Environ. 2023, 13, 100119. [Google Scholar] [CrossRef]
- Hung, C.-C.; Dai, Y.-X.; Yen, C.-H.; Mosalam, K.M. Comparative studies on in-plane shear behavior of masonrywallettes retrofitted with mortar, UHPC, and ECC ferrocement: Shotcrete and prefabricated panels. Case Stud. Constr. Mater. 2024, 21, e03801. [Google Scholar] [CrossRef]
- T/CBMF 37-2018/T/CCPA 7-2018 [S]; China Building Material Association: Fundamental Characteristics and Test Methods of Ultra-High Performance Concrete. China Architecture Industry Publishing House: Beijing, China, 2018.
- Peng, B.; Wei, S.; Long, L.; Zheng, Q.; Ma, Y.; Chen, L. Experimental Investigation on the Performance of Historical Squat Masonry Walls Strengthened by UHPC and Reinforced Polymer Mortar Layers. Appl. Sci. 2019, 9, 2096. [Google Scholar] [CrossRef]
- Dong, F.; Wang, H.; Jiang, F.; Xing, Q.; Yu, J. In-plane shear behavior of masonry panels strengthened with ultra-high ductile concrete (UHDC). Eng. Struct. 2022, 252, 113609. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Wu, Z.; Bu, F.; Wang, F. Experimental study on seismic strengthening of confined masonry walls using RPC. Adv. Mater. Sci. Eng. 2019, 2019, 5095120. [Google Scholar] [CrossRef]
- Madhavi, K.; Vinay, G.N.; Devi, M.V.R.; Basutkar, S. Shear behavior of brick masonry strengthened with jute fiber reinforced composite. Mater. Today Proc. 2021, 46, 4746–4751. [Google Scholar] [CrossRef]
- Meriggi, P.; De Santis, S.; Fares, S.; de Felice, G. Design of the shear strengthening of masonry walls with fabric reinforced cementitious matrix. Constr. Build. Mater. 2021, 279, 122452. [Google Scholar] [CrossRef]
- Shafighfard, T.; Kazemi, F.; Asgarkhani, N.; Yoo, D.-Y. Machine-learning methods for estimating compressive strength ofhigh-performance alkali-activated concrete. Eng. Appl. Artif. Intell. 2024, 136, 109053. [Google Scholar] [CrossRef]
- ASCE/SEI7-10; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2010.
- European Committee for Standardization. Eurocode 8: Design of Structures for Earthquake Resistance-Part 1:General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- GB50003-2011 [S]; Code for Design of Masonry Structures. China Architecture & Building Press: Beijing, China, 2011. (In Chinese)

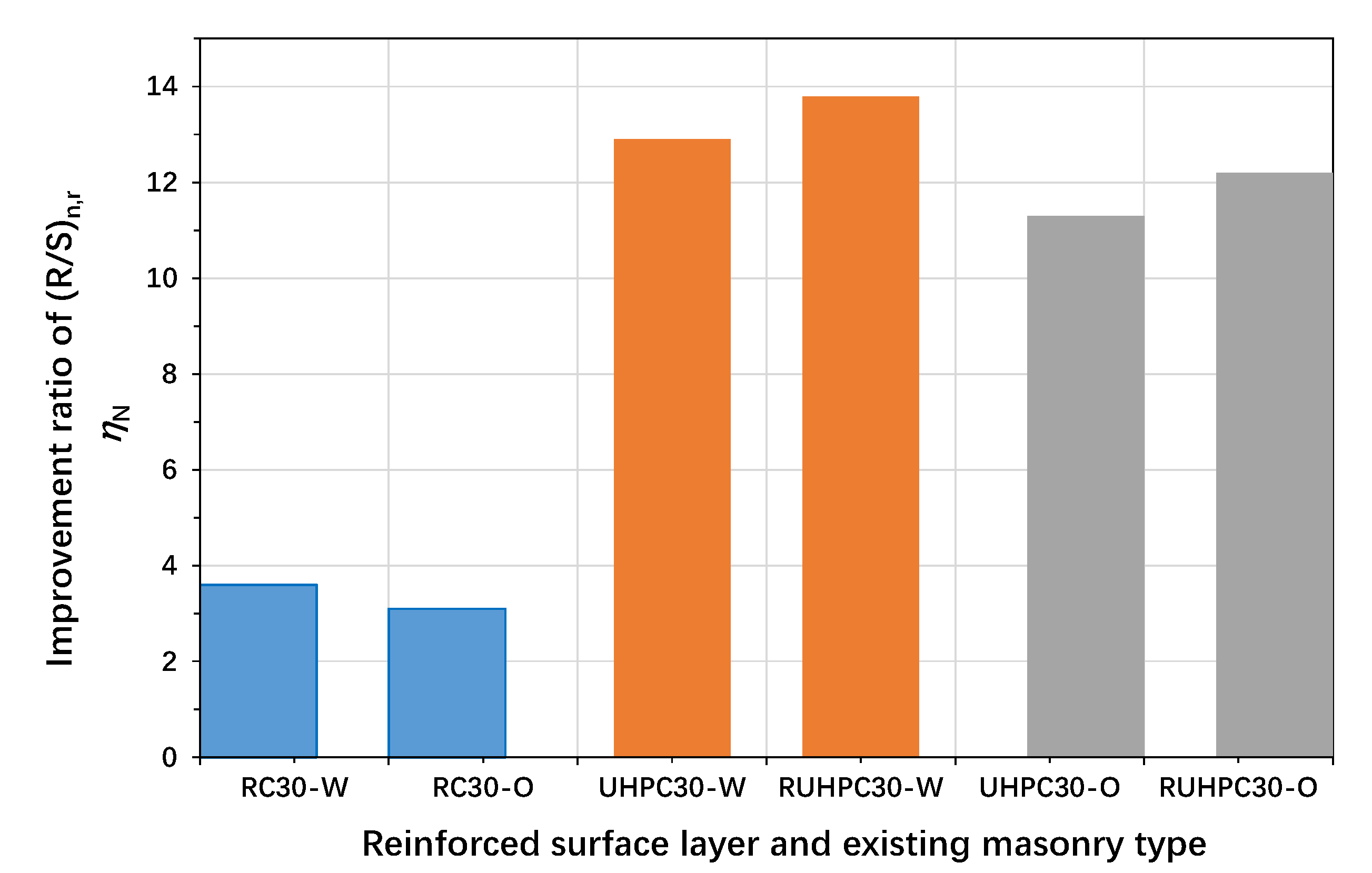

| Materials | Design Compressive Strength/MPa | Design Tensile Strength/MPa | Density/kg/m3 | Elastic Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|---|---|
| UHC150/UHT4.2 | 71 | 2.98 | 2500 | 45 | 0.18 |
| C30 | 14.3 | 1.43 | 2400 | 30 | 0.18 |
| Masonry Walls | 1-HE | 1-DA | E-23 | E-34 | E-45 | E-56 | |
|---|---|---|---|---|---|---|---|
| Wall thickness (mm) | 490 | 490 | 370 | 370 | 370 | 370 | |
| Before earthquake damage | Axial load resistance (R/S) | 3.00 | 3.03 | 1.80 | 2.31 | 1.75 | 13.40 |
| Shear resistance (R/S) | 1.23 | 1.22 | 1.30 | 1.20 | 1.79 | 1.14 | |
| After earthquake damage | Axial load resistance (R/S) | 1.29 | 1.30 | 0.77 | 1.00 | 0.74 | 12.53 |
| Shear resistance (R/S) | 0.55 | 0.54 | 0.61 | 0.55 | 0.84 | 0.51 | |
| Walls | 4-DA (370-O) | 1-HE (490-O) | H-78 (490-W) | |
|---|---|---|---|---|
| Original wall thickness (mm) | 370 | 490 | 490 | |
| Before earthquake damage | Axial load resistance (×103 kN) | 2.57 | 3.79 | 0.713 |
| Axial load demand (×103 kN) | 1.20 | 1.26 | 0.301 | |
| R/S | 2.15 | 3.00 | 2.37 | |
| After earthquake damage | Axial load resistance (×103 kN) | 1.01 | 1.63 | 0.289 |
| Axial load demand (×103 kN) | 1.20 | 1.26 | 0.301 | |
| (R/S)n,d | 0.84 | 1.29 | 0.96 | |
| Double-sided RC layers with 30 mm thickness | Axial load resistance (×103 kN) | 6.24 | 6.67 | 1.33 |
| Axial load demand (×103 kN) | 1.20 | 1.26 | 0.301 | |
| (R/S)n,r | 5.2 | 5.3 | 4.4 | |
| Resistance ratio (Rr) | 5.60 | 4.23 | 4.23 | |
| Improvement ratio (ηN) | 5.2 | 3.1 | 3.6 | |
| Double-sided UHPC layers with 20 mm thickness | Axial load resistance (×104 kN) | 1.30 | 1.38 | 0.276 |
| Axial load demand (×103 kN) | 1.20 | 1.26 | 0.301 | |
| (R/S)n,r | 10.82 | 10.93 | 9.17 | |
| Resistance ratio (Rr) | 13.96 | 10.54 | 10.54 | |
| Improvement ratio (ηN) | 11.9 | 7.5 | 8.6 | |
| Double-sided UHPC layers with 30 mm thickness | Axial load resistance (×104 kN) | 1.90 | 2.01 | 0.402 |
| Axial load demand (×103 kN) | 1.20 | 1.26 | 0.301 | |
| (R/S)n,r | 15.84 | 15.90 | 13.35 | |
| Resistance ratio (Rr) | 20.93 | 15.81 | 15.81 | |
| Improvement ratio (ηN) | 17.9 | 11.3 | 12.9 | |
| Double-sided RUHPC layers with 30 mm thickness | Axial load resistance (×104 kN) | 2.05 | 2.14 | 0.428 |
| Axial load demand (×103 kN) | 1.20 | 1.26 | 0.301 | |
| (R/S)n,r | 17.12 | 16.97 | 14.24 | |
| Resistance ratio (Rr) | 22.32 | 16.86 | 16.86 | |
| Improvement ratio (ηN) | 19.4 | 12.2 | 13.8 | |
| RC Layer or UHPC Layer Strength | C40 (19.1 MPa) | C40 (19.1 MPa) | C40 (19.1 MPa) | UHC130 (61 MPa) | UHC130 (61 MPa) | UHC130 (61 MPa) | UHC150 (71 MPa) | UHC150 (71 MPa) | UHC150 (71 MPa) |
|---|---|---|---|---|---|---|---|---|---|
| rebar ratio | 0.183% | 0.143% | 0.143% | 0 | 0 | 0 | 0.366% | 0.286% | 0.286% |
| wall | H-78 | 1-HE | 4-DA | H-78 | 1-HE | 4-DA | H-78 | 1-HE | 4-DA |
| Rr | 5.30 | 5.30 | 7.00 | 13.58 | 13.58 | 17.99 | 17.90 | 17.90 | 23.71 |
| ηN | 4.50 | 3.90 | 6.90 | 11.10 | 9.70 | 15.40 | 12.90 | 13.10 | 21.00 |
| Walls | 4-DA (370-O) | 1-HE (490-O) | H-78 (490-W) | |
|---|---|---|---|---|
| Before earthquake damage | Shear resistance (×102 kN) | 3.42 | 4.46 | 0.917 |
| Shear demand (×102 kN) | 2.95 | 3.63 | 0.700 | |
| R/S | 1.16 | 1.23 | 1.31 | |
| After earthquake damage | Shear resistance (×102 kN) | 1.56 | 1.99 | 0.420 |
| Shear demand (×102 kN) | 2.95 | 3.63 | 0.700 | |
| (R/S)v,d | 0.53 | 0.55 | 0.60 | |
| Double-sided RC layers with 30 mm thickness | Shear resistance (×103 kN) | 1.768 | 1.757 | 0.354 |
| Shear demand (×103 kN) | 0.318 | 0.377 | 0.0748 | |
| (R/S)v,r | 5.56 | 4.66 | 4.73 | |
| Resistance ratio (Rr) | 5.60 | 4.23 | 4.23 | |
| Improvement ratio (ηNE) | 9.49 | 7.46 | 6.89 | |
| n | 0.192 | 0.189 | 0.225 | |
| Double-sided UHPC layers with 20 mm thickness | Shear resistance (×102 kN) | 4.97 | 4.87 | 1.00 |
| Shear demand (×102 kN) | 3.11 | 3.69 | 0.730 | |
| (R/S)v,r | 1.60 | 1.32 | 1.37 | |
| Resistance ratio (Rr) | 13.96 | 10.54 | 10.54 | |
| Improvement ratio (ηNE) | 2.02 | 1.40 | 1.28 | |
| n | 0.092 | 0.091 | 0.109 | |
| Double-sided UHPC layers with 30 mm thickness | Shear resistance (×102 kN) | 6.87 | 6.76 | 1.38 |
| Shear demand (×102 kN) | 3.18 | 3.77 | 0.748 | |
| (R/S)v,r | 2.16 | 1.79 | 1.84 | |
| Resistance ratio (Rr) | 20.93 | 15.81 | 15.81 | |
| Improvement ratio (ηNE) | 3.07 | 2.26 | 2.07 | |
| n | 0.063 | 0.063 | 0.075 | |
| Double-sided RUHPC layers with 30 mm thickness | Shear resistance (×103 kN) | 2.04 | 2.03 | 0.409 |
| Shear demand (×103 kN) | 0.318 | 0.377 | 0.0748 | |
| (R/S)v,r | 6.42 | 5.39 | 5.47 | |
| Resistance ratio (Rr) | 22.32 | 16.86 | 16.86 | |
| Improvement ratio (ηNE) | 11.12 | 8.80 | 8.11 | |
| n | 0.058 | 0.059 | 0.070 | |
| RC Layer or UHPC Layer Strength | C40 (19.1 MPa) | C40 (19.1 MPa) | C40 (19.1 MPa) | UHC130 (61 MPa) | UHC130 (61 MPa) | UHC130 (61 MPa) | UHC150 (71 MPa) | UHC150 (71 MPa) | UHC150 (71 MPa) |
|---|---|---|---|---|---|---|---|---|---|
| rebar ratio | 0.183% | 0.143% | 0.143% | 0 | 0 | 0 | 0.366% | 0.286% | 0.286% |
| walls | H-78 | 1-HE | 4-DA | H-78 | 1-HE | 4-DA | H-78 | 1-HE | 4-DA |
| Rr | 5.30 | 5.30 | 7.00 | 13.58 | 13.58 | 17.99 | 17.90 | 17.90 | 23.71 |
| ηN | 7.24 | 8.25 | 9.76 | 1.77 | 2.06 | 2.61 | 14.43 | 16.38 | 19.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Wang, W.; Zhang, Y.; Wen, Q.; Wu, X.; Lu, Y.; Wang, D.; Qiu, F. Enhancement Analysis of Damaged Masonry Structures Strengthened with Ultra-High-Performance Concrete. Buildings 2025, 15, 2082. https://doi.org/10.3390/buildings15122082
Wang R, Wang W, Zhang Y, Wen Q, Wu X, Lu Y, Wang D, Qiu F. Enhancement Analysis of Damaged Masonry Structures Strengthened with Ultra-High-Performance Concrete. Buildings. 2025; 15(12):2082. https://doi.org/10.3390/buildings15122082
Chicago/Turabian StyleWang, Rui, Wei Wang, Yuecong Zhang, Quan Wen, Xiangguo Wu, Ya Lu, Daiyu Wang, and Faqiang Qiu. 2025. "Enhancement Analysis of Damaged Masonry Structures Strengthened with Ultra-High-Performance Concrete" Buildings 15, no. 12: 2082. https://doi.org/10.3390/buildings15122082
APA StyleWang, R., Wang, W., Zhang, Y., Wen, Q., Wu, X., Lu, Y., Wang, D., & Qiu, F. (2025). Enhancement Analysis of Damaged Masonry Structures Strengthened with Ultra-High-Performance Concrete. Buildings, 15(12), 2082. https://doi.org/10.3390/buildings15122082






