Study on Vertical Propagation of Power Parameters in RC Frame Under Internal Explosion
Abstract
1. Introduction
2. FE Modeling Approach
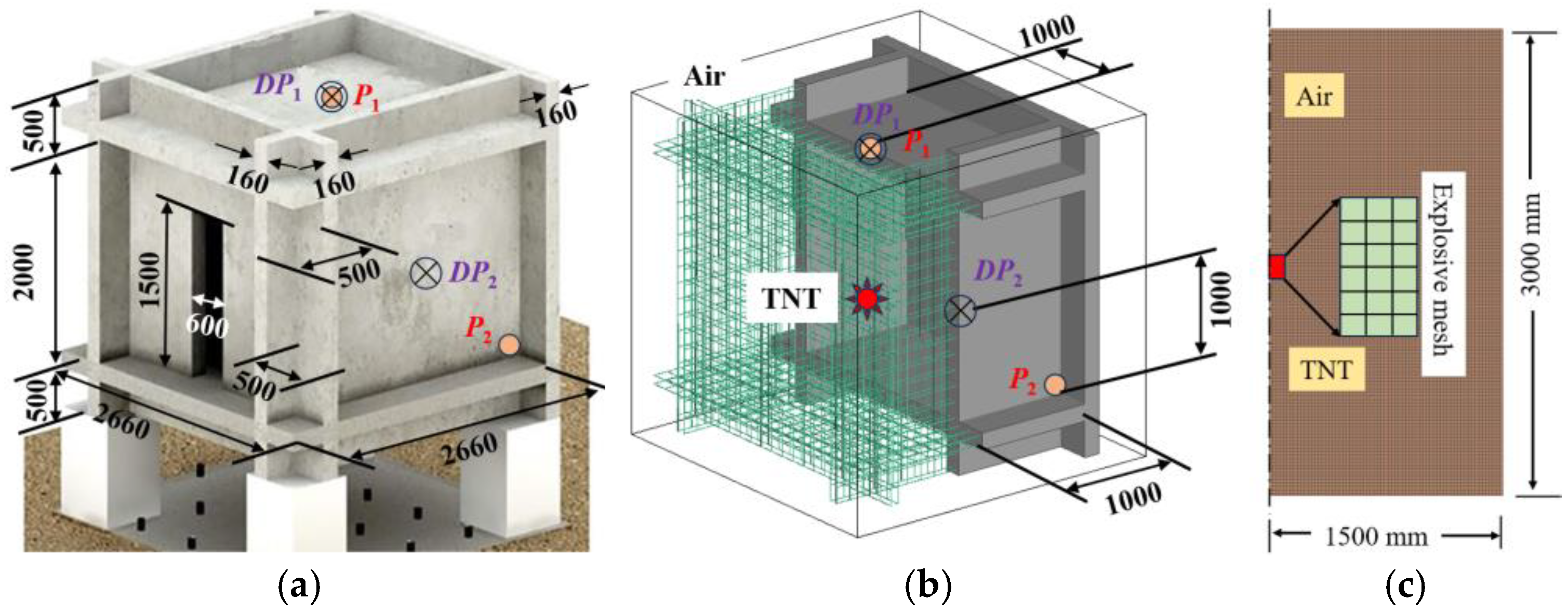
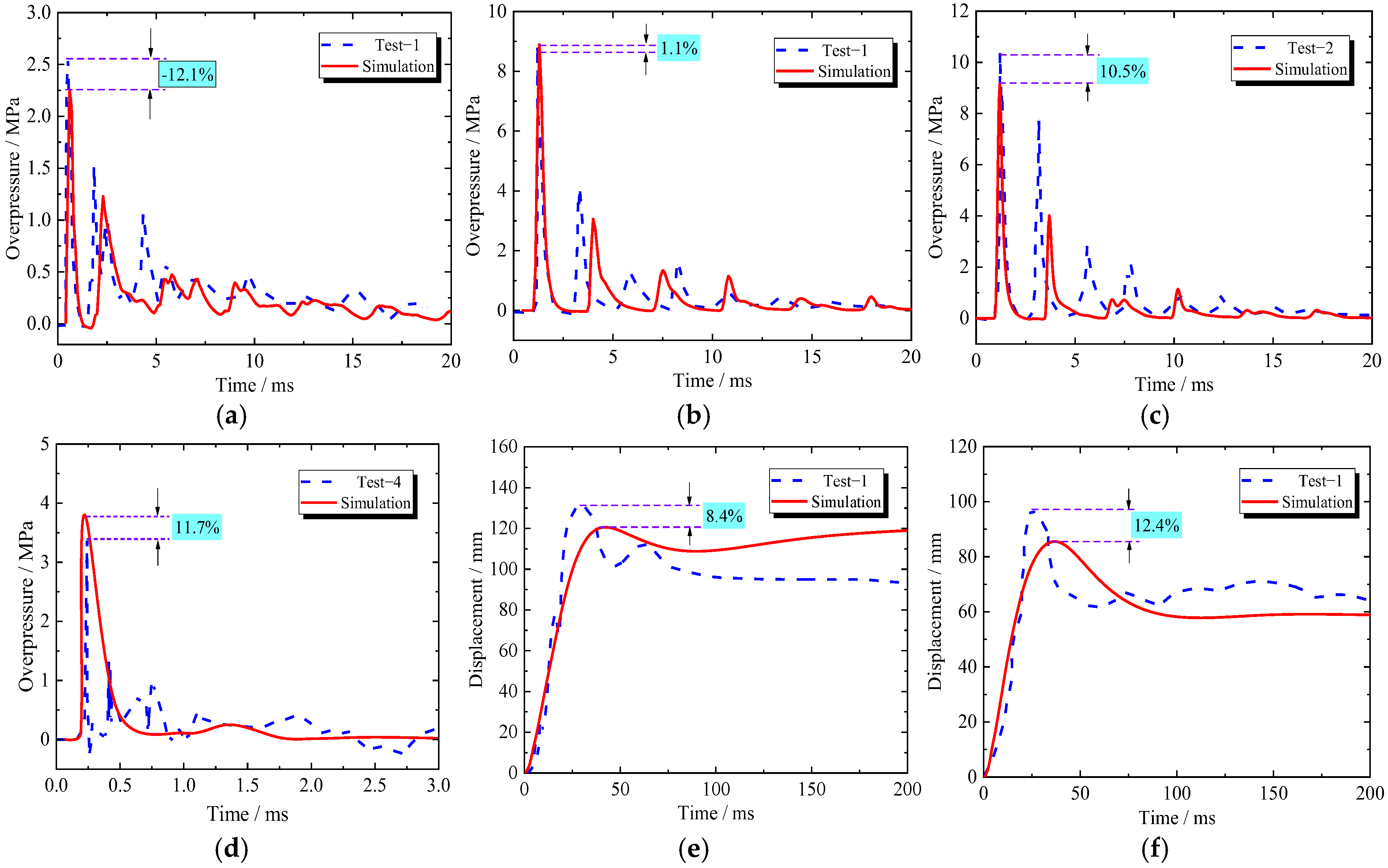
2.1. Internal Explosion Tests on Partially Enclosed RC Structures
- (a)
- test description and FE model
- (b)
- material model and parameters
- (c)
- result comparison
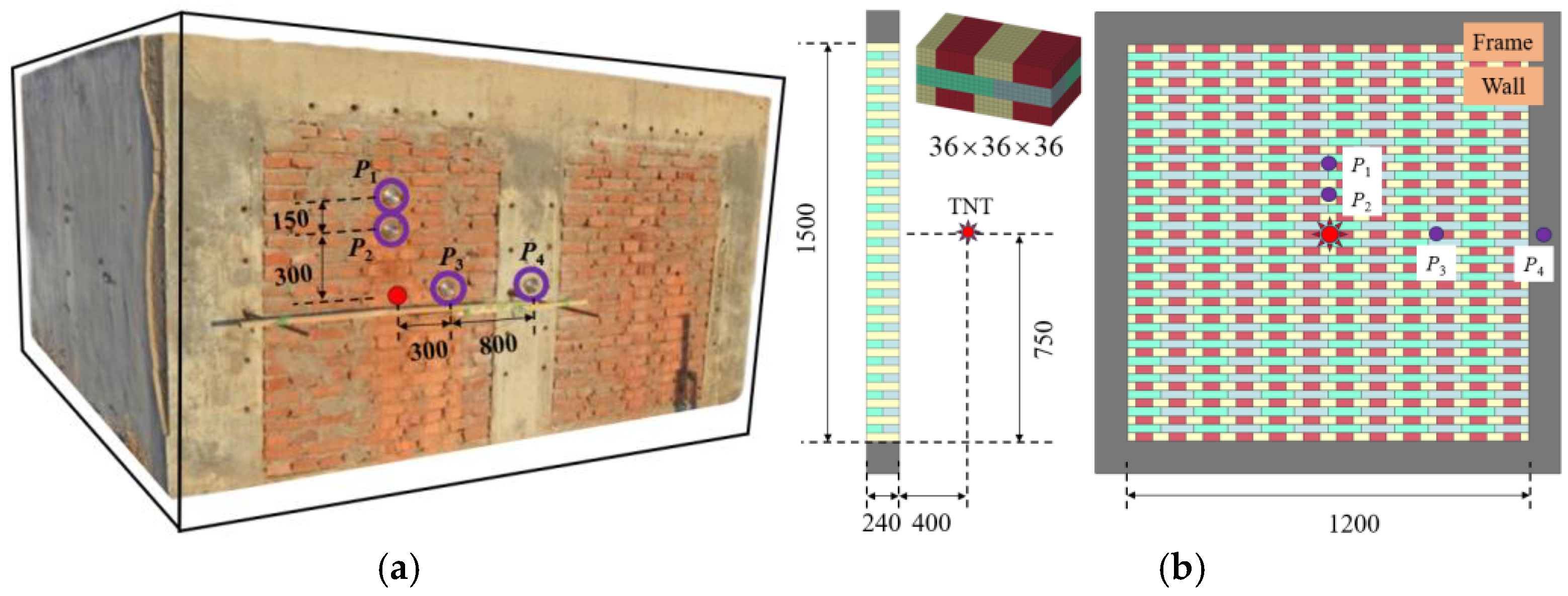
2.2. Close-In Explosions on Masonry Walls
- (a)
- test introduction and modeling approach
- (b)
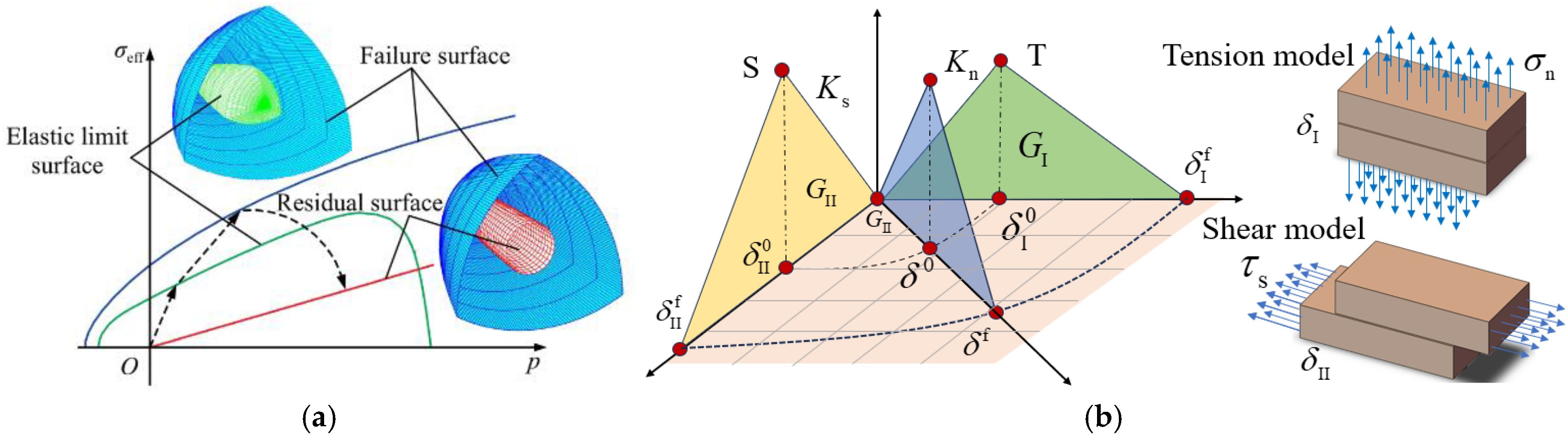
- material model and parameters
- (c)
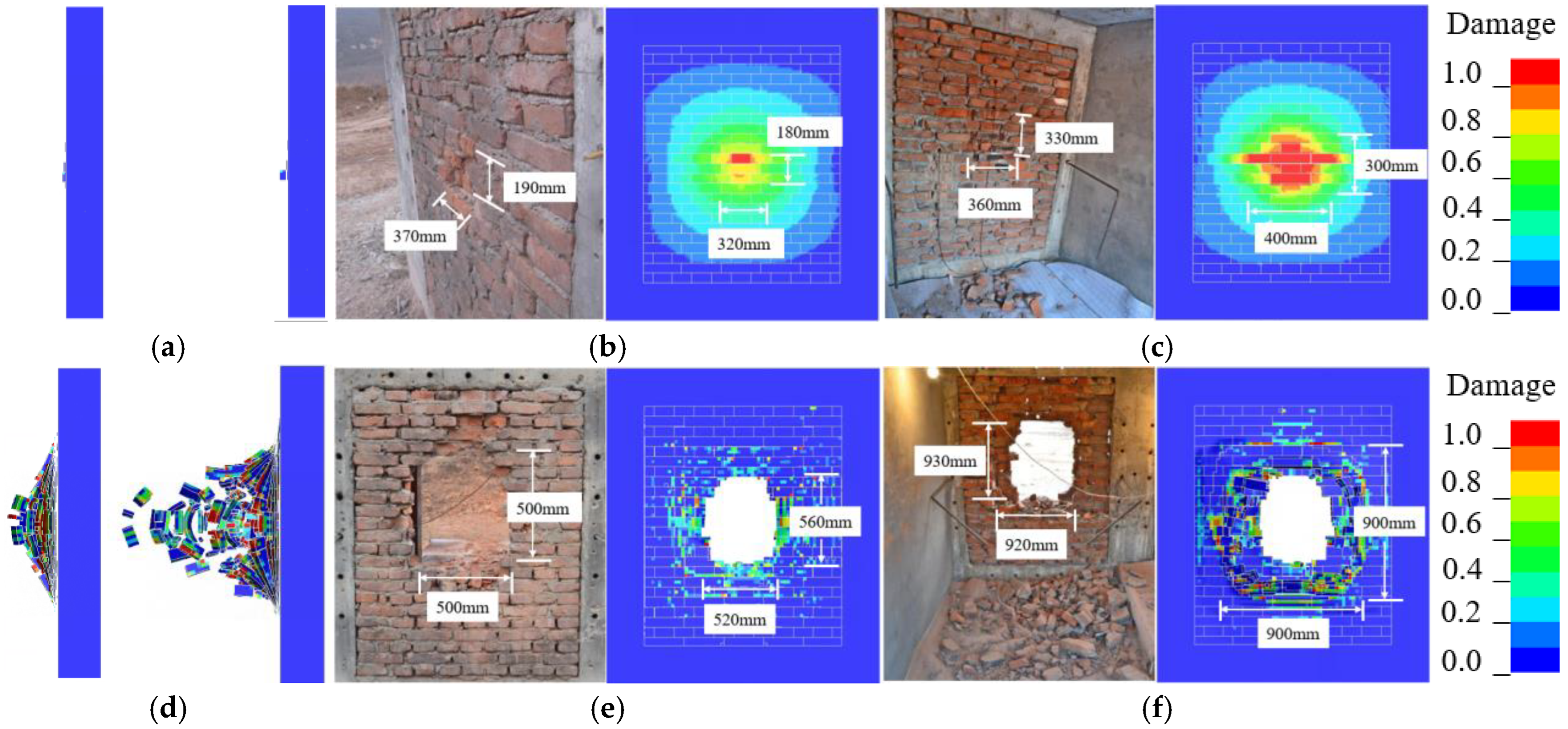
- results comparison
3. Prototypical RC Frame Structure
4. Results Analysis
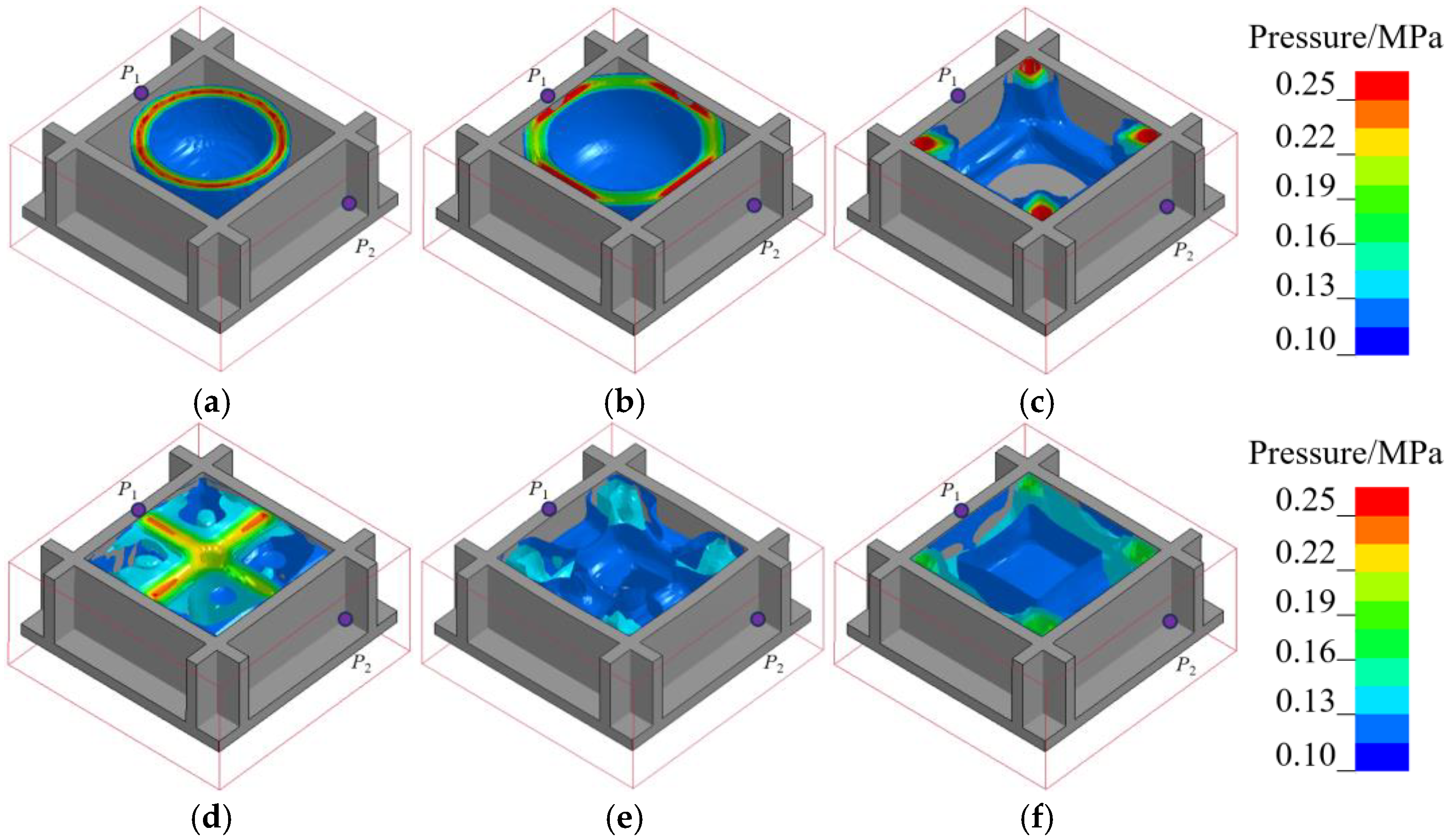
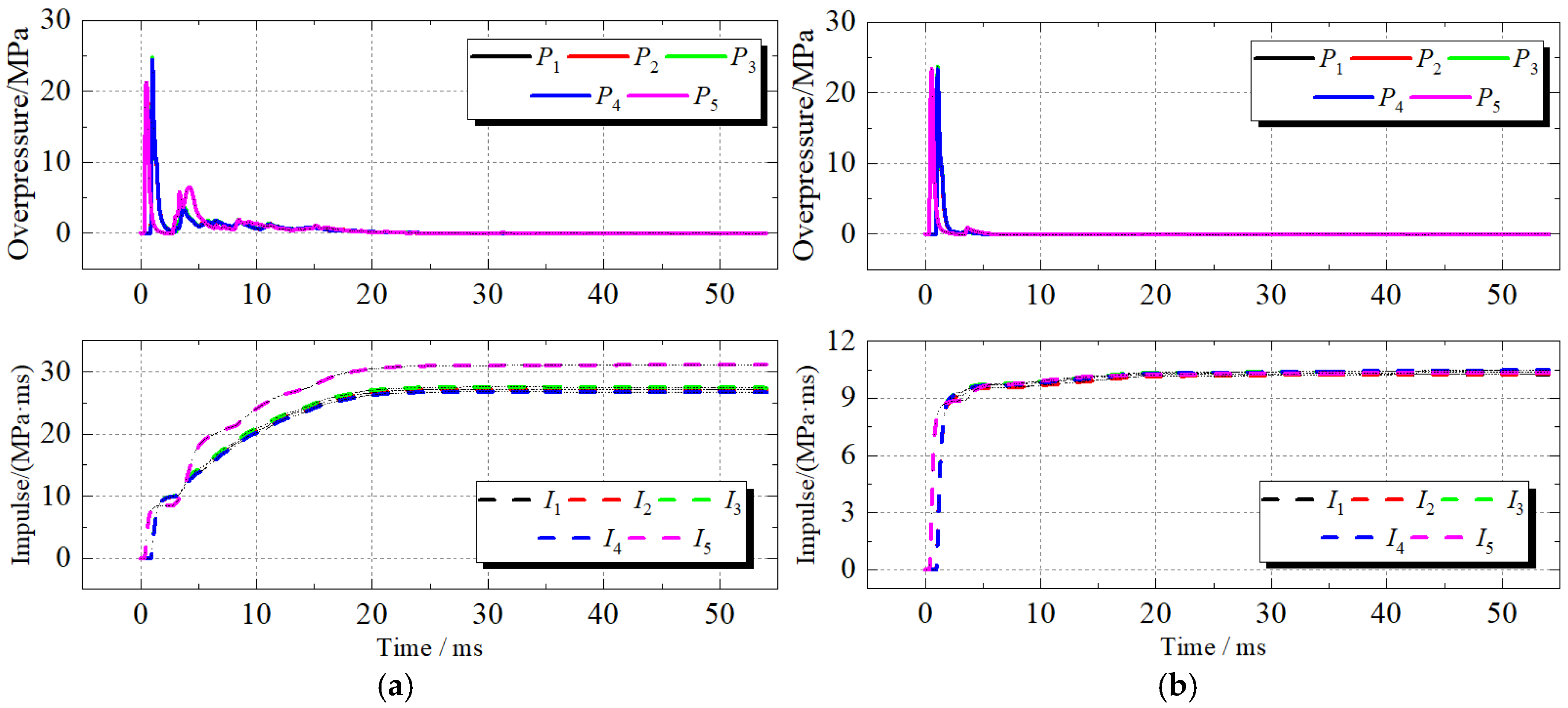
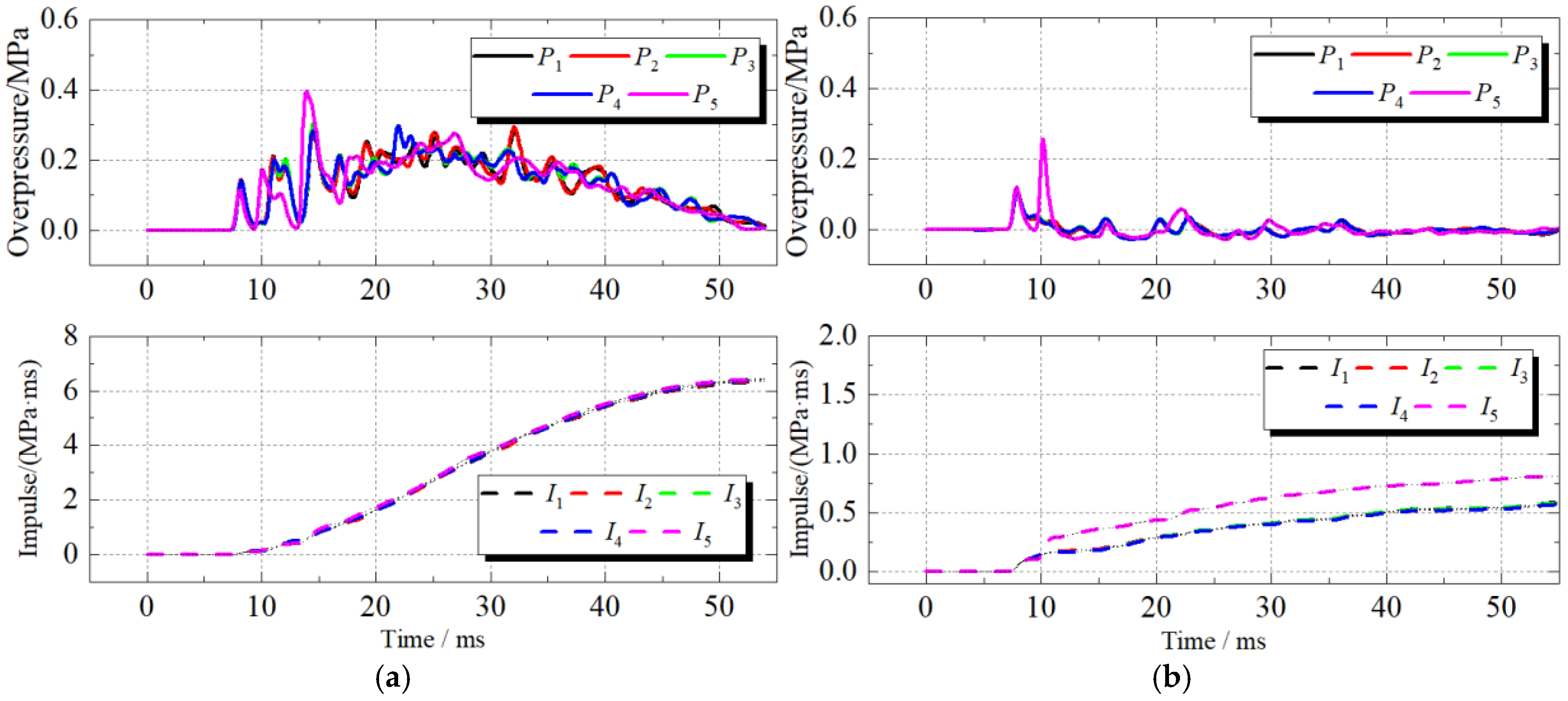
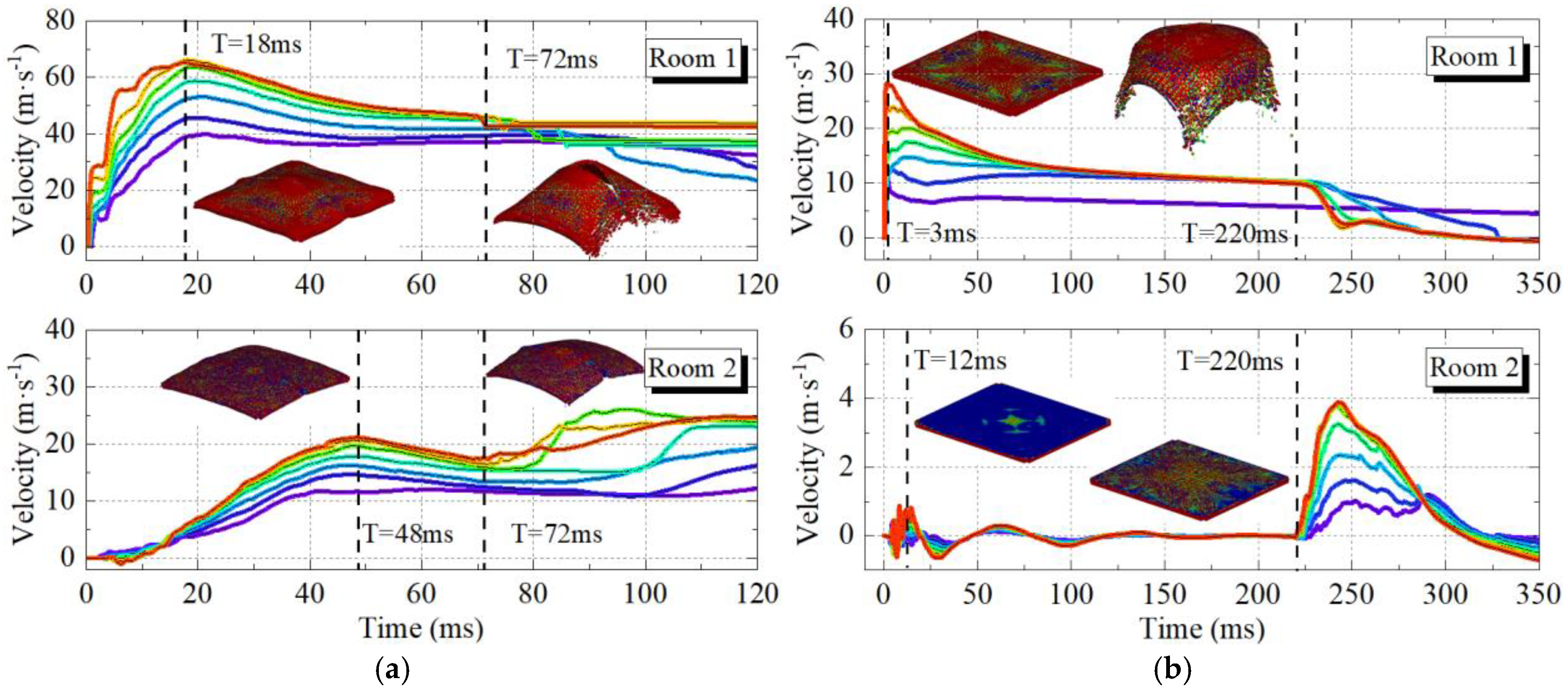
4.1. Blast Wave Propagation
4.2. Load Characteristics in Adjacent Rooms
4.3. Structural Failure Model
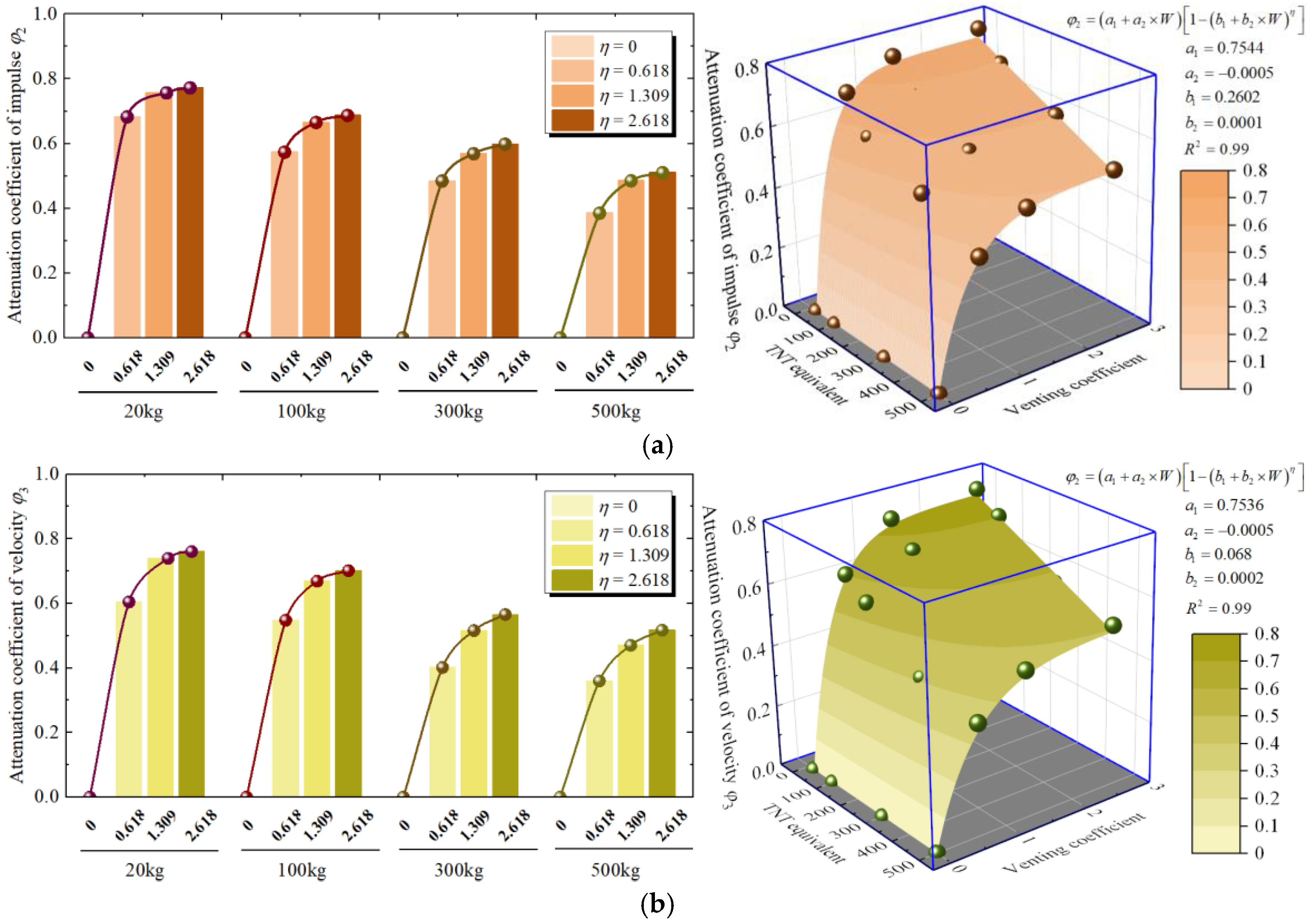
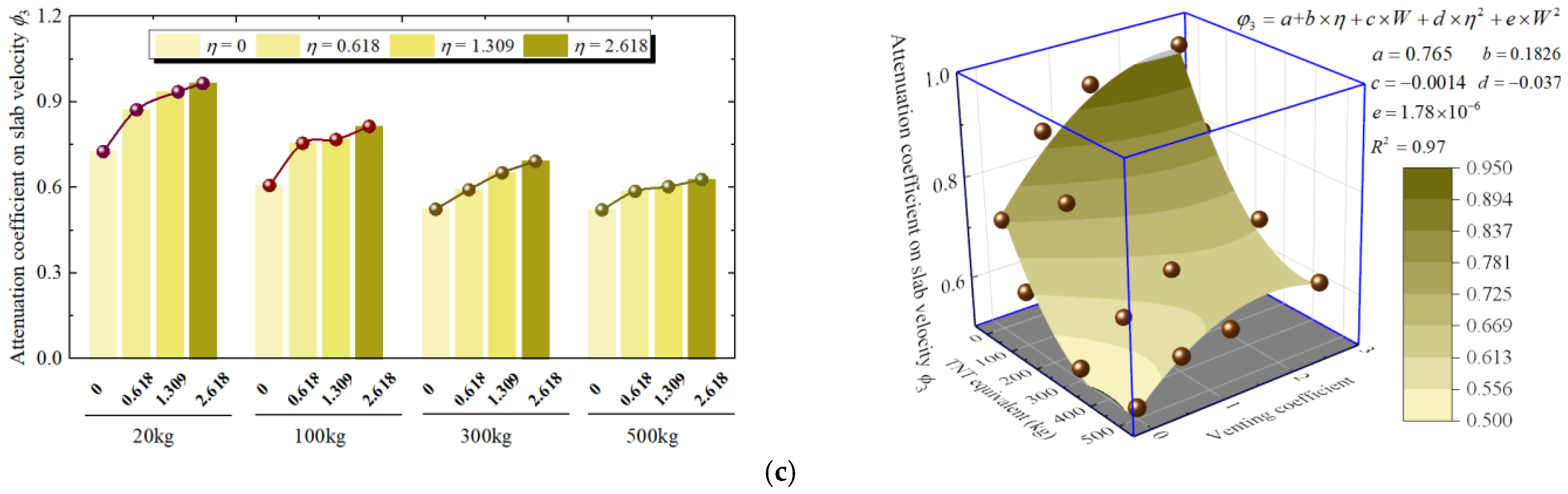
5. Attenuation Coefficient of Power Parameters
5.1. Attenuation Coefficient of Power Parameters in the Explosion Source Room
5.2. Attenuation Coefficient of Power Parameters in the Vertically Adjacent Room
6. Conclusions
- (i)
- The roof slab can effectively block the propagation of shock waves, reducing the shock wave load propagated to the vertically adjacent room by approximately two orders of magnitude for peak overpressure and one order of magnitude for impulse, respectively, compared to the explosion source room. Besides the shock wave load (i.e., peak overpressure, impulse), the explosive ejection of the roof slab significantly impacts the damage to vertically adjacent rooms. Therefore, the vertical damage assessment in RC frame structures must account for both the shock wave load and the explosive ejection of the roof slab.
- (ii)
- The venting coefficient has little influence on peak overpressure in the explosion source room, while rapid energy dissipation leads to significant attenuation of both internal impulse and roof ejection velocity. Compared with a fully enclosed (η = 0) RC building, the maximum attenuation of the impulse and roof ejection velocity in the explosion source room under fully ventilated conditions (η = 2.618) are approximately 76% and 75%, respectively.
- (iii)
- An increase in the venting coefficient can significantly reduce the power parameters propagated to the vertically adjacent rooms. For a 100 kg TNT, increasing the venting coefficient from 0 to 2.618 reduces the power parameters by an 87.5% decrease in peak overpressure, 67.6% in impulse, and 70% in roof ejection velocity, demonstrating that enhancing the venting area can significantly improve structural blast resistance.
- (iv)
- The developed empirical model can accurately predict the attenuation coefficients of power parameters in the explosion source room and the vertically adjacent rooms under varying venting coefficients, enabling rapid damage assessment for RC frame structures under internal explosions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmet, I.T.; Yaşar, A.; Hakan, Y.; Kumbasaroglu, A. An experimental evaluation on structural performance level of corroded reinforced concrete frames. Eng. Struct. 2025, 325, 119479. [Google Scholar] [CrossRef]
- Wang, S.N.; Cheng, X.W.; Li, Y.; Yang, X.; Zhang, H.; Guo, R.; Song, X.; Liang, Z. Assessing progressive collapse regions of reinforced concrete frame structures using Graph Convolutional Networks. Eng. Struct. 2025, 322, 119076. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). The Oklahoma City Bombing: Improving Building Performance Through Multi-Hazard Mitigation, FEMA-277; Building Performance Assessment Team: Washington, DC, USA, 1996. [Google Scholar]
- Sudoyo, H.; Widodo, P.T.; Suryadi, H.; Lie, Y.S.; Safari, D.; Widjajanto, A.; Kadarmo, D.A.; Hidayat, S.; Marzuki, S. DNA analysis in perpetrator identification of terrorism-related disaster: Suicide bombing of the Australian Embassy in Jakarta 2004. Forensic Sci. Int. Genet. 2008, 2, 231–237. [Google Scholar] [CrossRef] [PubMed]
- Souhu. Interception Failed. The Missile Penetrated the Ukrainian Decision-Making Center Building at Twice the Speed of Sound. 2023. Available online: https://www.sohu.com/a/689810854_563497 (accessed on 6 March 2025).
- Wang, Y.S.; Li, W.B.; Zhu, W.; Li, W.; Zhang, Q.; Wang, X. Dynamic response of steel cabin structure under blast loading from adjacent cabin. Eng. Struct. 2024, 311, 118213. [Google Scholar] [CrossRef]
- To, Q.B.; Shin, J.; Kim, J.; Han, S.W.; Lee, K. Finite element analysis-based blast and seismic performance evaluation for RC frame with retrofitted ENTA damper systems. Eng. Struct. 2024, 313, 118300. [Google Scholar] [CrossRef]
- Feldgun, V.R.; Karinski, Y.S.; Edri, I.; Yankelevsky, D.Z. Prediction of the quasi-static pressure in confined and partially confined explosions and its application to blast response simulation of flexible structures. Int. J. Impact Eng. 2016, 90, 46–60. [Google Scholar] [CrossRef]
- Zyskowski, A.; Sochet, I.; Mavrot, G.; Bailly, P.; Renard, J. Study of the explosion process in a small scale experiment-structural loading. J. Loss Prev. Process Ind. 2004, 17, 291–299. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, C.Q.; Lukaszewi, Z.M.; Dragos, J.; Ren, J.; Haskett, M. Characteristics of confined blast loading in unvented structures. Int. J. Prot. Struct. 2011, 2, 21–44. [Google Scholar] [CrossRef]
- Santos, A.P.; Castedo, R.; López, L.M.; Chiquito, M.; Yenes, J.I.; Alañón, A.; Costamagna, E.; Martínez-Almajano, S. Reinforced concrete building with IED detonation: Test and simulation. Appl. Sci. 2022, 12, 7803. [Google Scholar] [CrossRef]
- Liu, S. Study on the distribution range of explosion power field in frame building space. Beijing Acad. Mil. Sci. 2024. (In Chinese) [Google Scholar]
- Guo, X.K.; Li, Y.; Dsniel, P.; Hu, Y.; Bai, Z.; Zhang, H.; Li, Z.; Wang, X. A reinforced concrete shear wall building structure subjected to internal TNT explosions: Test results and numerical validation. Int. J. Impact Eng. 2024, 190, 104950. [Google Scholar] [CrossRef]
- Li, X.D.; Yin, J.P.; Zhao, P.D.; Zhang, L.; Xu, Y.X.; Wang, Q.; Zhang, P. The effect of stand-off distance on damage to clamped square steel plates under enclosed explosion. Structures 2020, 25, 965–978. [Google Scholar] [CrossRef]
- Hu, B.; Fang, X.; Cheng, L.; Wen, J.; Yu, D. Attenuation of impact waves in a nonlinear acoustic metamaterial beam. Nonlinear Dyn. 2023, 111, 15801–15816. [Google Scholar] [CrossRef]
- Khan, M.H.; Li, B.; Tan, K.T. Impact load wave transmission in elastic metamaterials. Int. J. Impact Eng. 2018, 118, 50–59. [Google Scholar] [CrossRef]
- Cai, C.Q.; Zhou, J.X.; Wang, K.; Pan, H.; Tan, D.; Xu, D.; Wen, G. Flexural wave attenuation by metamaterial beam with compliant quasi-zero-stiffness resonators. Mech. Syst. Signal Process. 2022, 174, 109119. [Google Scholar] [CrossRef]
- Kong, X.S.; Zhou, H.; Zheng, C. An experimental study on the mitigation effects of fine water mist on confined-blast loading and dynamic response of steel plates. Int. J. Impact Eng. 2019, 134, 103370. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, L.; Fang, Q. Performance based investigation on the construction of anti-blast water wall. Int. J. Impact Eng. 2015, 81, 17–33. [Google Scholar] [CrossRef]
- Eslami, M.; Keshavarz, M.M.P.; Khalilpour, H.; Parsa, H.; Kodure, V. Experimental and numerical investigation of blast wave attenuation by using barriers in different configurations and shapes. J. Struct. Eng. 2023, 149, 04022224. [Google Scholar] [CrossRef]
- Rose, T.A.; Smith, P.D.; Mays, G.C. The effectiveness of walls designed for the protection of structures against airblast from high explosives. Struct. Build. 1995, 110, 78–85. [Google Scholar] [CrossRef]
- Michaloudis, G.; Gebbeken, N. Modeling masonry walls under far-field and contact detonations. Int. J. Impact Eng. 2019, 123, 84–97. [Google Scholar] [CrossRef]
- Hájek, R.; Foglar, M. The reduction of peak overpressure using concrete blast barriers. WIT Trans. Built Environ. 2014, 141, 265–275. [Google Scholar] [CrossRef]
- MohottiCA1, D.; Wijesooriya, K.; Fernando, P.L.N.; Nishshanka, B.; Lee, C.K.; Remmenikov, A. Experimental investigation of band-beam slabs subjected to close-range blast loading. Eng. Struct. 2024, 309, 118075. [Google Scholar] [CrossRef]
- Mario, J.; Draganić, H.; Gazić, G.; Lukić, S. Post-blast residual static capacity of retrofitted reinforced concrete slabs. Eng. Struct. 2023, 286, 116161. [Google Scholar] [CrossRef]
- Park, D.; Lee, T.H.; Lee, Y.; Choi, Y.; Hong, J.W. Blast simulations of a reinforced concrete slab using the continuous surface cap model (CSCM). J. Build. Eng. 2024, 96, 110603. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Schwarz, S.; Brosh, B. Full scale field blast tests on reinforced concrete residential buildings-from theory to practice. Int. J. Prot. Struct. 2013, 4, 565–590. [Google Scholar] [CrossRef]
- Kim, H.J.; Hwang, K.; Yoon, Y.H.; Lee, H.J. Numerical analysis of the effect of afterburning on damage to the concrete structure under interior explosion. Int. J. Concr. Struct. Mater. 2022, 16, 6. [Google Scholar] [CrossRef]
- Lina, M.; López, A.P.; Anastasio, P.; Santos, A.P.; Diego, Y.G.; Castedo, R.; Chiquito, M. Experimental response and numerical modelling of a full-scale two-span concrete slab frame subjected to blast load. Eng. Struct. 2023, 296, 116969. [Google Scholar] [CrossRef]
- Park, Y.; Kim, K.; Park, S.W.; Yum, S.G.; Baek, J.W. Experimental evaluation on blast resistance of reinforced concrete structures under partially confined explosion. Int. J. Concr. Struct. Mater. 2024, 18, 11–13. [Google Scholar] [CrossRef]
- Gao, C.; Zong, Z.H.; Wu, J. Experimental study on progressive collapse failure of RC frame structures under blast loading. China Civ. Eng. J. 2013, 46, 9–20. (In Chinese) [Google Scholar] [CrossRef]
- Yang, J.; Hao, Y.; Peng, D.; Shi, J.; Zhang, Y. Machine learning-based methods for predicting the structural damage and failure mode of RC slabs under blast loading. Buildings 2025, 15, 1221. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Huang, B.G.; Wang, X.Y.; Xia, Y. Deep learning-based prediction of structural responses of RC slabs subjected to blast loading. Eng. Struct. 2024, 311, 118184. [Google Scholar] [CrossRef]
- Zhao, C.F.; Zhu, Y.F.; Zhou, Z.H. Machine learning-based approaches for predicting the dynamic response of RC slabs under blast loads. Eng. Struct. 2022, 273, 115104. [Google Scholar] [CrossRef]
- Sagaseta, J.; Olmati, P.; Micallef, K.; Cormie, D. Punching shear failure in blast-loaded RC slabs and panels. Eng. Struct. 2017, 147, 177–194. [Google Scholar] [CrossRef]
- Gao, Z.; Chen, Y.Q.; Wang, Z.Q.; Li, S.; Wei, W.; Huang, C. Study on the failure effect of aramid reinforced concrete slab under localized blast loading. Structures 2024, 63, 106292. [Google Scholar] [CrossRef]
- Yao, S.J.; Zhang, D.; Chen, X.G.; Lu, F.; Wang, W. Experimental and numerical study on the dynamic response of RC slabs under blast loading. Eng. Fail. Anal. 2016, 66, 120–129. [Google Scholar] [CrossRef]
- Lukić, S.; Draganić, H.; Grubeša, I.N.; Gazić, G. Influence of blast load on the bond characteristic of retrofitted RC slabs. Constr. Build. Mater. 2022, 319, 126094. [Google Scholar] [CrossRef]
- Maazoun, A.; Matthys, S.; Atoui, O.; Belkassem, B.; Lecompte, D. Finite element modelling of RC slabs retrofitted with CFRP strips under blast loading. Eng. Struct. 2022, 252, 113597. [Google Scholar] [CrossRef]
- Liao, Y.; Shi, S.Q.; Chen, S.; Ming, X.; Ge, L. Numerical evaluation of the retrofit effectiveness for polyurea-woven glass fiber mesh composite retrofitted RC slab subjected to blast loading. Structures 2022, 36, 215–232. [Google Scholar] [CrossRef]
- Wu, J.; Yan, Q.S. Structural design and damage assessment of a chamber for internal blast with explosion vent. Mech. Adv. Mater. Struct. 2020, 27, 2052–2058. [Google Scholar] [CrossRef]
- Anderson, J.R.; Baker, W.E.; Wauters, D.K.; Morris, B.L. Quasi-static pressure, duration, and impulse for explosions (e.g., HE) in structures. Int. J. Mech. Sci. 1982, 25, 455–464. [Google Scholar] [CrossRef]
- Esparza, E.D.; Baker, W.E.; Oldham, G.A. Blast Pressures Inside and Outside Suppressive Structures; Southwest Research Institute: San Antonio, TX, USA, 1975. [Google Scholar]
- Weibull, H.R.W. Pressures recorded in partially closed chambers at explosion of TNT charges. Ann. N Y Acad. Sci. 1968, 152, 357–361. [Google Scholar] [CrossRef]
- Li, J.R.; Lu, Y.G.; Feng, X.W.; Wu, H. Analysis of Internal Explosion Load Characteristics and Dynamic Behavior in RC Box Structures. Explos. Shock Waves 2025, 4, 1–18. (In Chinese) [Google Scholar] [CrossRef]
- Tascon, A. Design of silos for dust explosions: Determination of vent area sizes and explosion pressures. Eng. Struct. 2017, 134, 1–10. [Google Scholar] [CrossRef]
- Qing, C.; Cheng, J.; Wang, Y.; Xie, T. Effect of burst pressure and vented area on vented hydrogen explosions. J. Therm. Anal. Calorim. 2024, 1–13. [Google Scholar] [CrossRef]
- Song, S.C.; Han, Z.W.; Li, Y.N.; Li, J.; Wang, J.; Zhao, Y.; He, G.; He, B.; Wang, B. Influence of Vent Area on Aluminized Explosive Behavior in Fast Cook-off. Propellants Explos. Pyrotech. 2025, 50, 12038. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, K.; Li, B.; Zhang, D.; Mensah, R.A.; Das, O.; Xie, L.; Wang, Y. Effect of hydrogen concentration, vented area, and vented shape on vented hydrogen-air explosions and its consequence analysis. Exp. Therm. Fluid Sci. 2025, 167, 111484. [Google Scholar] [CrossRef]
- Shi, Y.C.; Xiong, W.; Li, Z.X.; Xu, Q. Experimental studies on the local damage and fragments of unreinforced masonry walls under close-in explosions. Int. J. Impact Eng. 2016, 90, 122–131. [Google Scholar] [CrossRef]
- Chen, D.; Wu, H.; Fang, Q. Simplified micro-model for brick masonry walls under out-of-plane quasi-static and blast loadings. Int. J. Impact Eng. 2023, 174, 104529. [Google Scholar] [CrossRef]
- Chen, G.Q.; Lu, J.X.; Wu, H. Dynamic behavior and retrofitting of RC frame building under vehicular bomb explosion. Eng. Fail. Anal. 2023, 143, 106925. [Google Scholar] [CrossRef]
- Chen, D.; Wu, H.; Cheng, Y.H. Dynamic behaviors of unreinforced and spray polyurea retrofitted brick masonry infill walls under blast loads: Shock tube test and analyse. Int. J. Impact Eng. 2024, 190, 104975. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.





| Test No. | TNT Equivalents (kg) | Equivalent Explosive Mesh Density [45] | 2D Finite Element Model | 3D Finite Element Model | ||||
|---|---|---|---|---|---|---|---|---|
| TNT Mesh (mm) | Air Mesh (mm) | TNT Mesh (mm) | Air Mesh (mm) | Structure Mesh (mm) | ||||
| Kim et al. [28] | Test-1 | 2.0 | 255.8 | 107 × 107 | 16 × 16 | / | 24 × 24 × 24 | 24 × 24 × 24 |
| Test-2 | 3.0 | 255.8 | / | / | 122 × 122 × 122 | 24 × 24 × 24 | 24 × 24 × 24 | |
| Shi et al. [50] | Test-3 | 1.0 | 255.8 | 85 × 85 | 13 × 13 | / | 36 × 36 × 36 | 36 × 36 × 36 |
| Test-4 | 6.0 | 255.8 | / | / | 154 × 154 × 154 | 36 × 36 × 36 | 36 × 36 × 36 | |
| Concrete (*MAT_CONCRETE_DAMAGE_REL3) | ||||||||
| Density (kg·m−3) | Compressive strength fc (MPa) | Maximum failure principal strain | ||||||
| 2400 | 40.0/5.0 | 0.3 | ||||||
| Rebar (*MAT_PLASTIC_KINMATIC) | ||||||||
| Density (kg·m−3) | Elasticity modulus GPa | Poisson ratio | Yield strength (MPa) | Strain rate effect C (s−1) | Strain rate parameter P | Failure strain | ||
| 7800 | 206 | 0.3 | 450 (400) | 40 | 5 | 0.14 | ||
| TNT (*MAT_HIGH_ENERGY_BURN&EOS_JWL) | ||||||||
| Density (kg·m−3) | Detonation velocity D (m·s−1) | Burst pressure (GPa) | A/GPa | B/GPa | R1 | R2 | Initial energy E0 (J·m−3) | |
| 1630 | 6930 | 21 | 370 | 3.747 | 4.15 | 0.9 | 0.35 | 7 × 109 |
| Air (*MAT_NULL&*EOS_LINEAR_POLYNOMIAL) | ||||||||
| Density (kg·m−3) | Initial energy E0 (J·m−3) | Dynamic viscosity coefficient | Pressure cutoff Pc (MPa) | C0, C1, C2, C3, C6 | C4, C5 | |||
| 1.29 | 2.5 × 105 | 0 | 0 | 0 | 0.4 | |||
| Masonry wall (*MAT_RHT) | ||||||||
| Density (kg·m−3) | Initial porosity α0 | Crush pressure Pel (MPa) | Compaction pressure Pcomp (MPa) | Porosity exponent | Elasticity modulus E (GPa) | Poisson ratio v | ||
| 1800 | 1.32 | 40 | 2.5 | 3 | 1.44 | 0.2 | ||
| β | Compressive strength fc (MPa) | Relative shear strength fc* | Shear strength ft* | Reference tensile strain rate (s−1) | Conversion strain rate (s−1) | |||
| 0.01244 | 5.43 | 0.27 | 0.54 | 1 × 10−5 | 30 | |||
| *CONTACT_AUTOMATIC_SURFACE_TO_SURFACE_TIEBREAK(OPTION = 9) | ||||||||
| Normal stiffness (MPa·mm−1) | Tangential stiffness (MPa·mm−1) | Normal strength (MPa) | Tangential strength (MPa) | Normal fracture energy (MPa·mm) | Tangential fracture energy (MPa·mm) | λ | ||
| 820 | 352 | 0.32 | 0.56 | 0.01 | 0.027 | −2 | ||
| Parameters | 1 kg TNT | 6 kg TNT | ||
|---|---|---|---|---|
| Blast-Facing Surface | Back-Blast Surface | Blast-Facing Surface | Back-Blast Surface | |
| Simulation | 320 mm × 180 mm | 400 mm × 300 mm | 520 mm × 580 mm | 900 mm × 900 mm |
| Experiment | 370 mm × 190 mm | 360 mm × 330 mm | 500 mm × 500 mm | 920 mm × 930 mm |
| Error | −18.1% | 1.0% | 18.6% | −5.33% |
| Scenario | S (m2) | TNT Equivalent (kg) | Scenario | S (m2) | TNT Equivalent (kg) | ||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.000 | 20 | 9 | 41.68 | 1.309 | 20 |
| 2 | 0 | 0.000 | 100 | 10 | 41.68 | 1.309 | 100 |
| 3 | 0 | 0.000 | 300 | 11 | 41.68 | 1.309 | 300 |
| 4 | 0 | 0.000 | 500 | 12 | 41.68 | 1.309 | 500 |
| 5 | 27.78 | 0.654 | 20 | 13 | 55.57 | 2.618 | 20 |
| 6 | 27.78 | 0.654 | 100 | 14 | 55.57 | 2.618 | 100 |
| 7 | 27.78 | 0.654 | 300 | 15 | 55.57 | 2.618 | 300 |
| 8 | 27.78 | 0.654 | 500 | 16 | 55.57 | 2.618 | 500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Lu, Y.; Miao, H.; Xu, H.; Feng, X.; Yuan, Y. Study on Vertical Propagation of Power Parameters in RC Frame Under Internal Explosion. Buildings 2025, 15, 2080. https://doi.org/10.3390/buildings15122080
Li J, Lu Y, Miao H, Xu H, Feng X, Yuan Y. Study on Vertical Propagation of Power Parameters in RC Frame Under Internal Explosion. Buildings. 2025; 15(12):2080. https://doi.org/10.3390/buildings15122080
Chicago/Turabian StyleLi, Junrun, Yonggang Lu, Haibin Miao, Hengwei Xu, Xiaowei Feng, and Yixin Yuan. 2025. "Study on Vertical Propagation of Power Parameters in RC Frame Under Internal Explosion" Buildings 15, no. 12: 2080. https://doi.org/10.3390/buildings15122080
APA StyleLi, J., Lu, Y., Miao, H., Xu, H., Feng, X., & Yuan, Y. (2025). Study on Vertical Propagation of Power Parameters in RC Frame Under Internal Explosion. Buildings, 15(12), 2080. https://doi.org/10.3390/buildings15122080






