Analysis of Structural Internal Forces and Stratum Deformation in Shaft Construction Using Vertical Shaft Sinking Machine
Abstract
1. Introduction
2. Project Overview
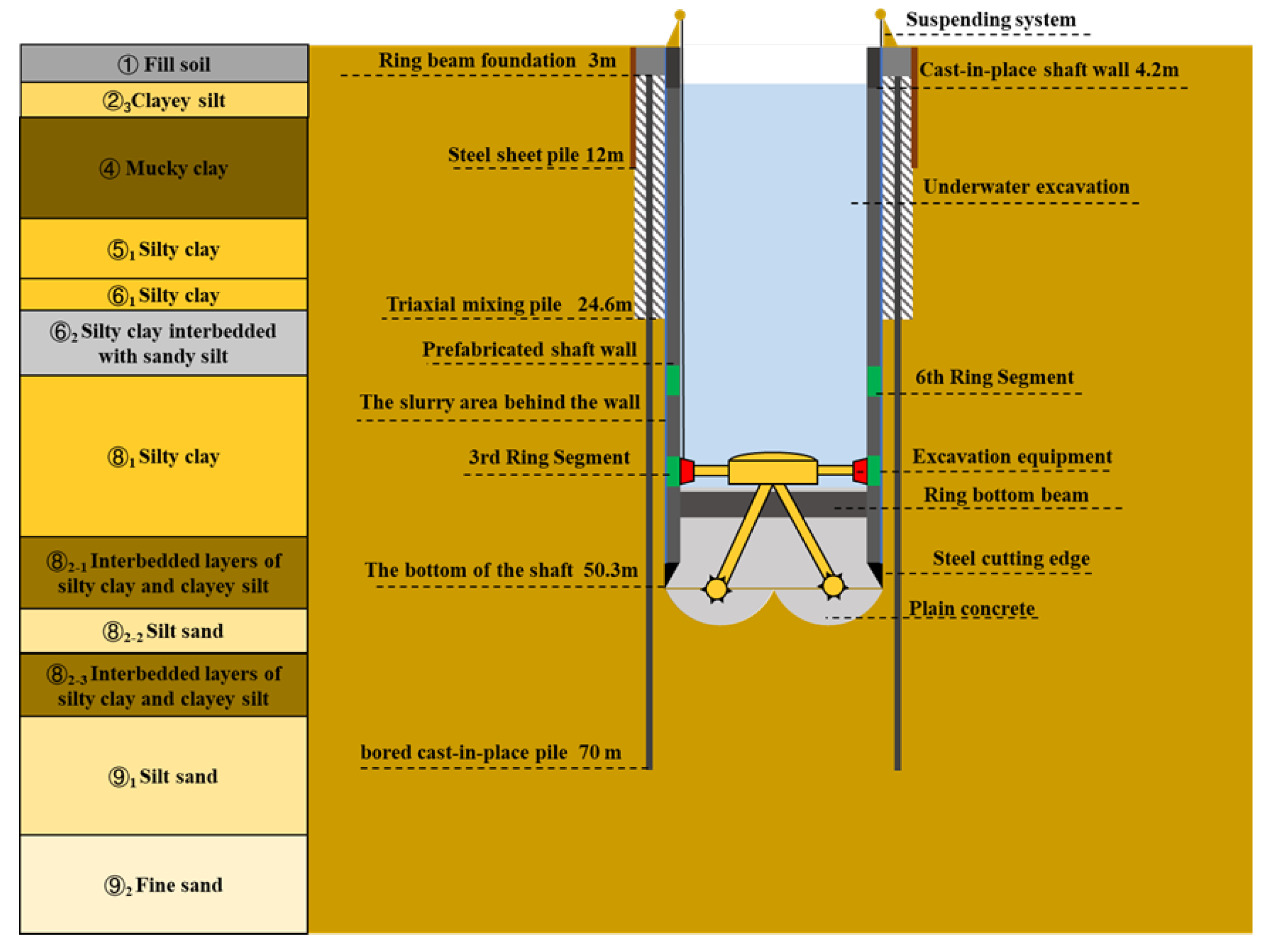
2.1. Geotechnical Conditions
2.2. Vertical Shaft Sinking Method
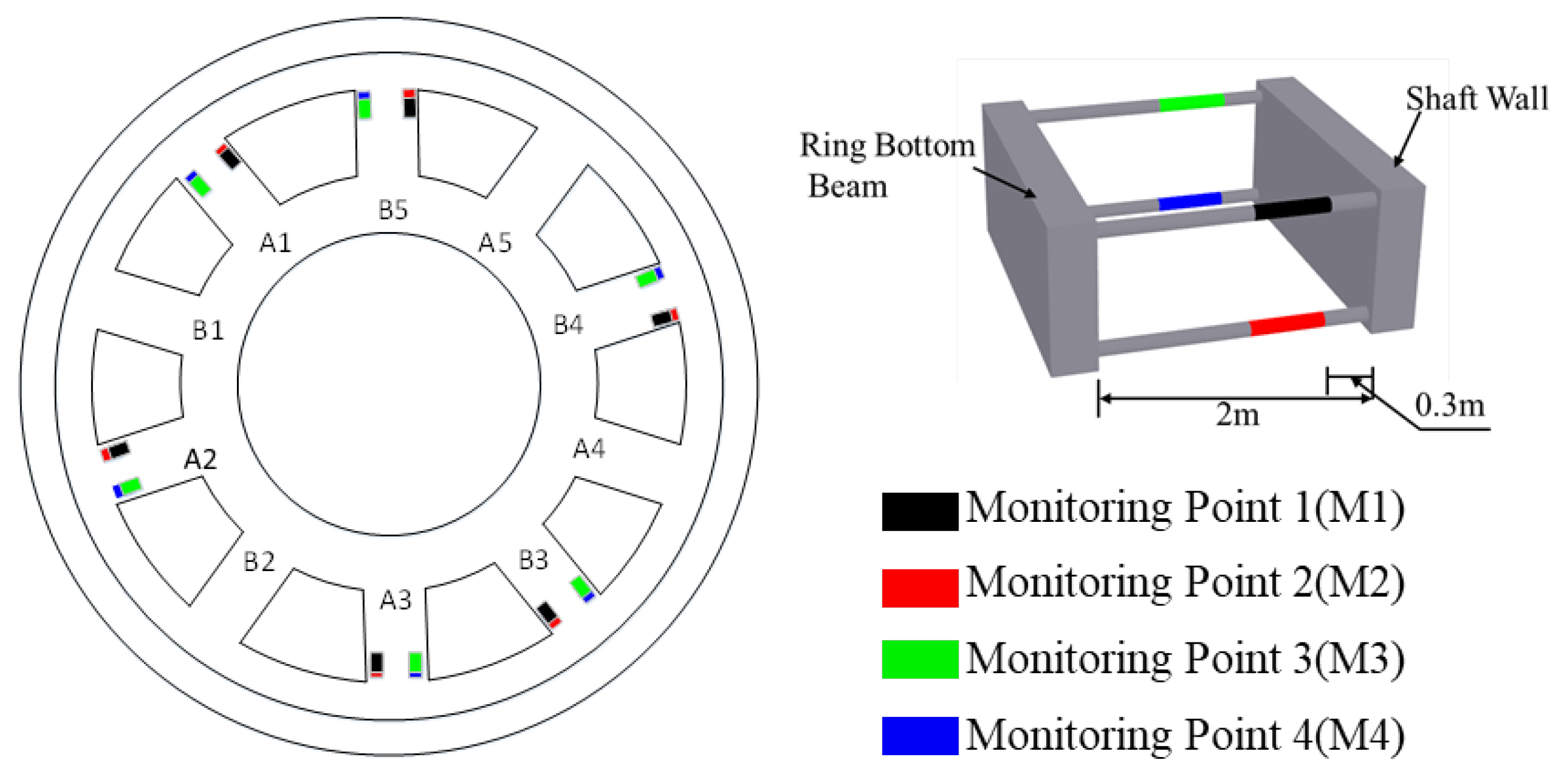
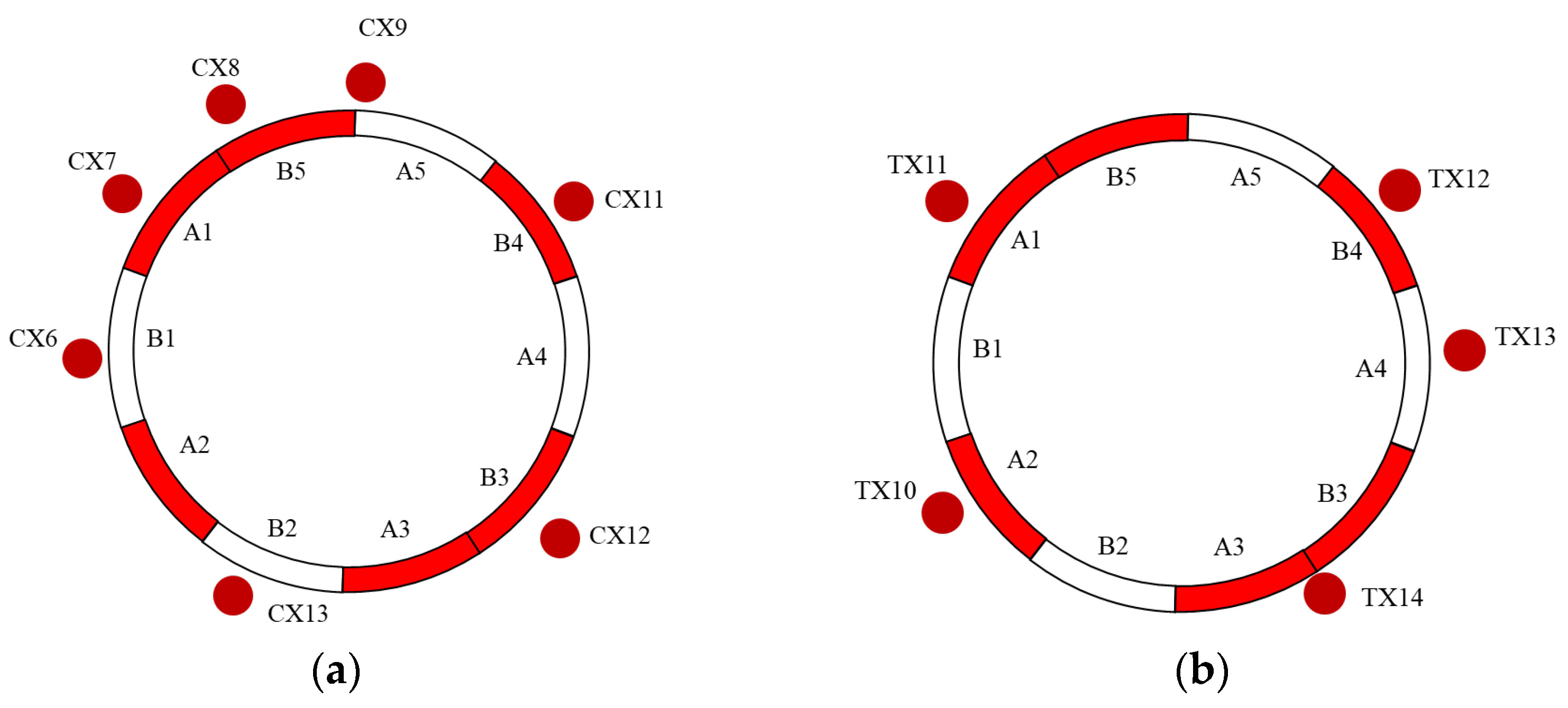
2.3. Monitoring Programs and Date Acquisition
3. Monitoring Analysis of Structural Internal Force
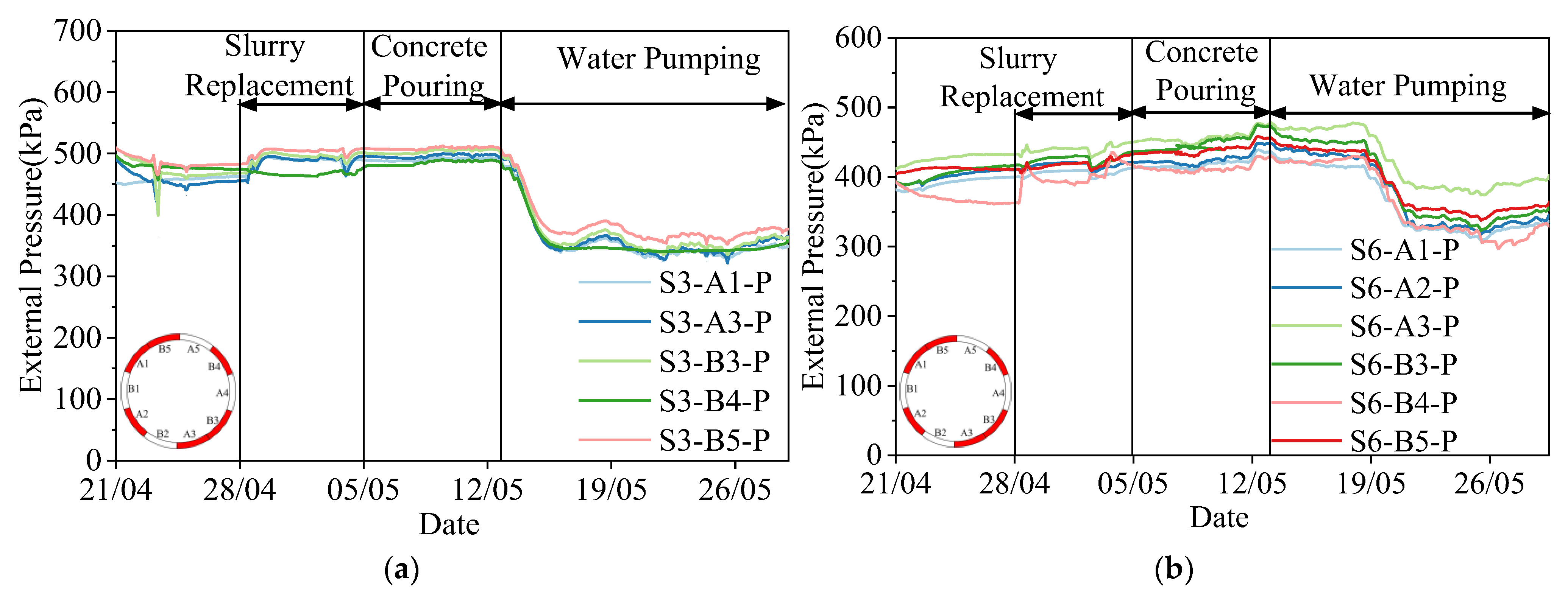
3.1. Analysis of External Pressure on Shaft Segment
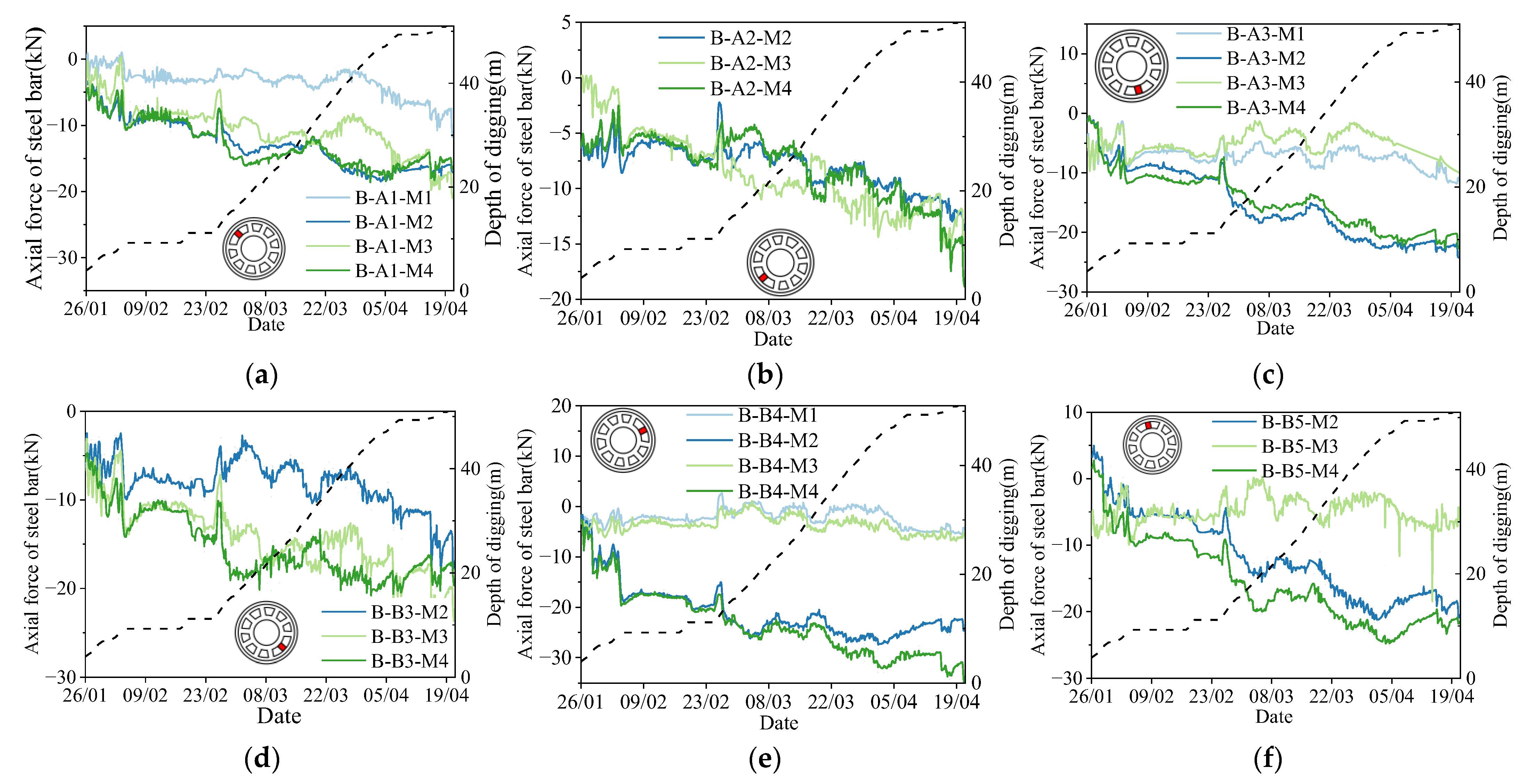
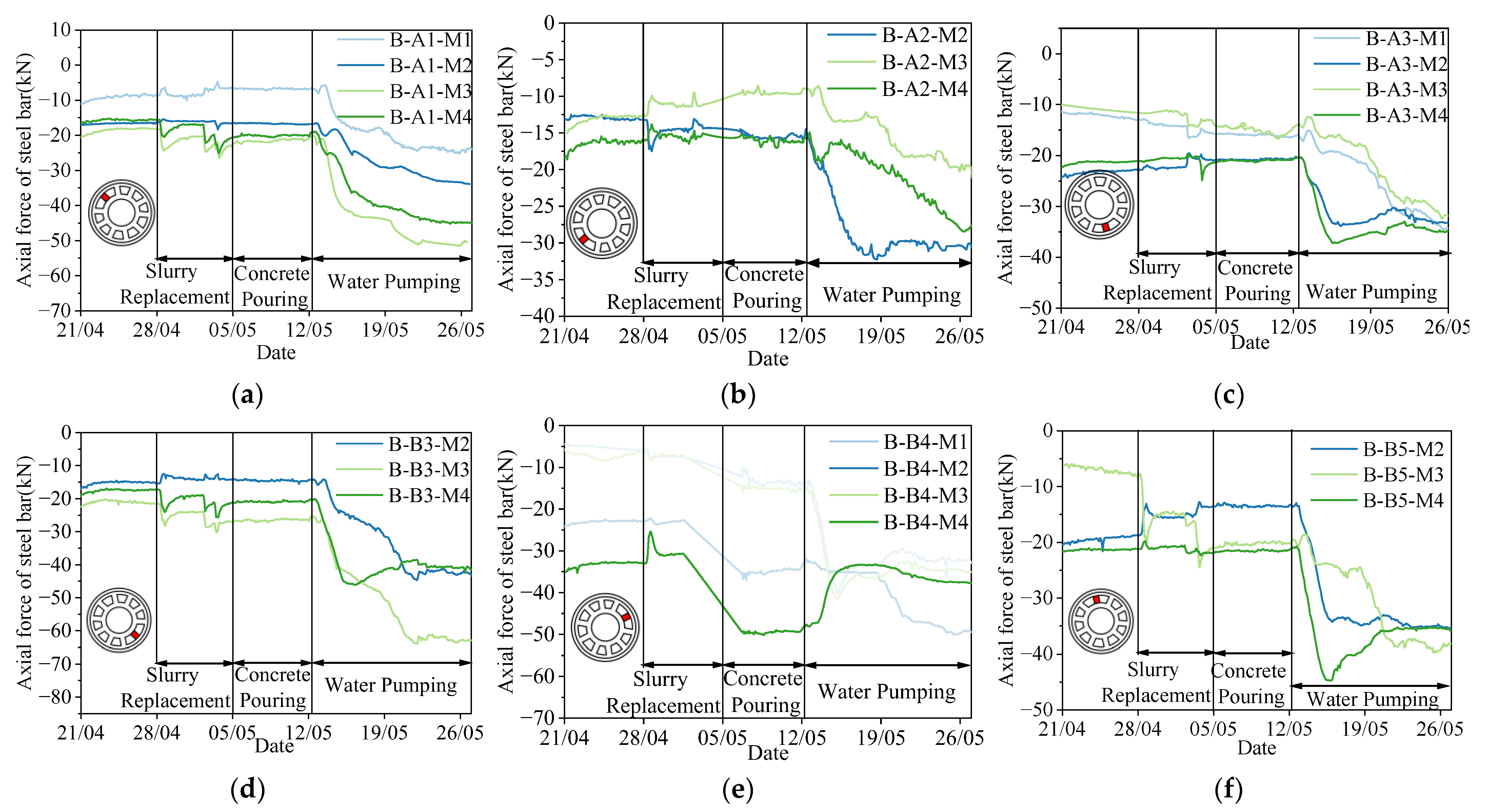
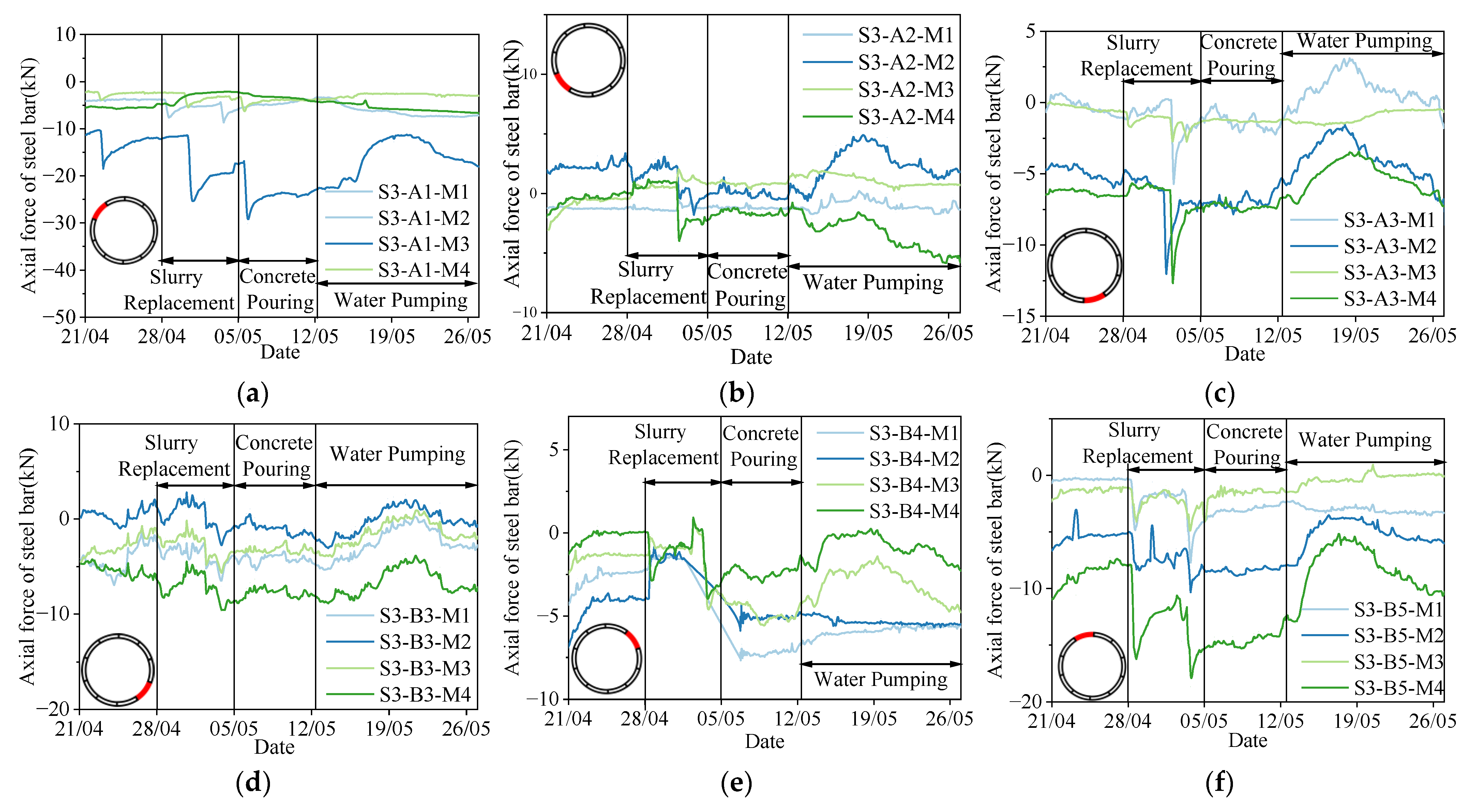
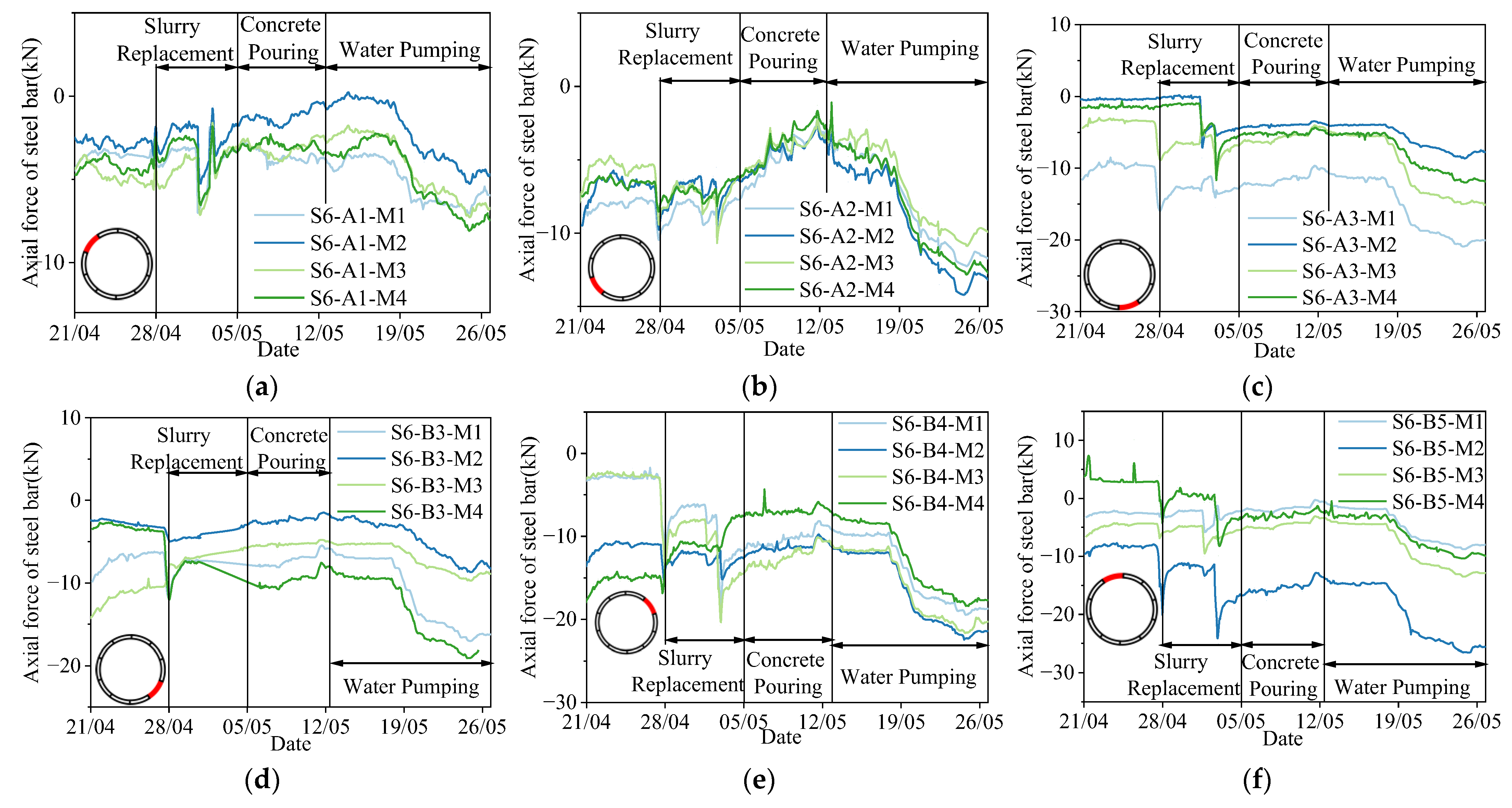
3.2. Axial Force of Steel Bars in the Bottom Connecting Beam
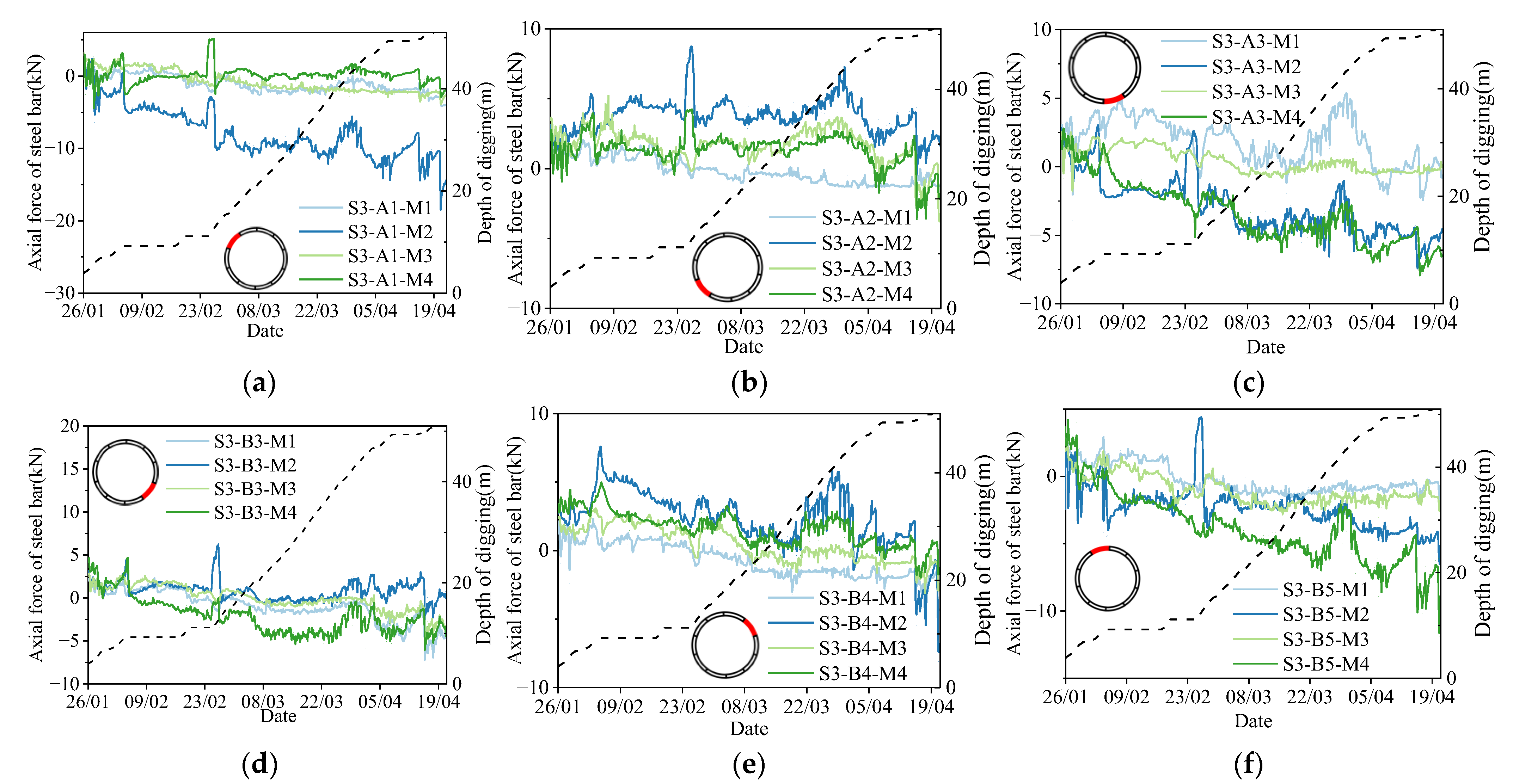
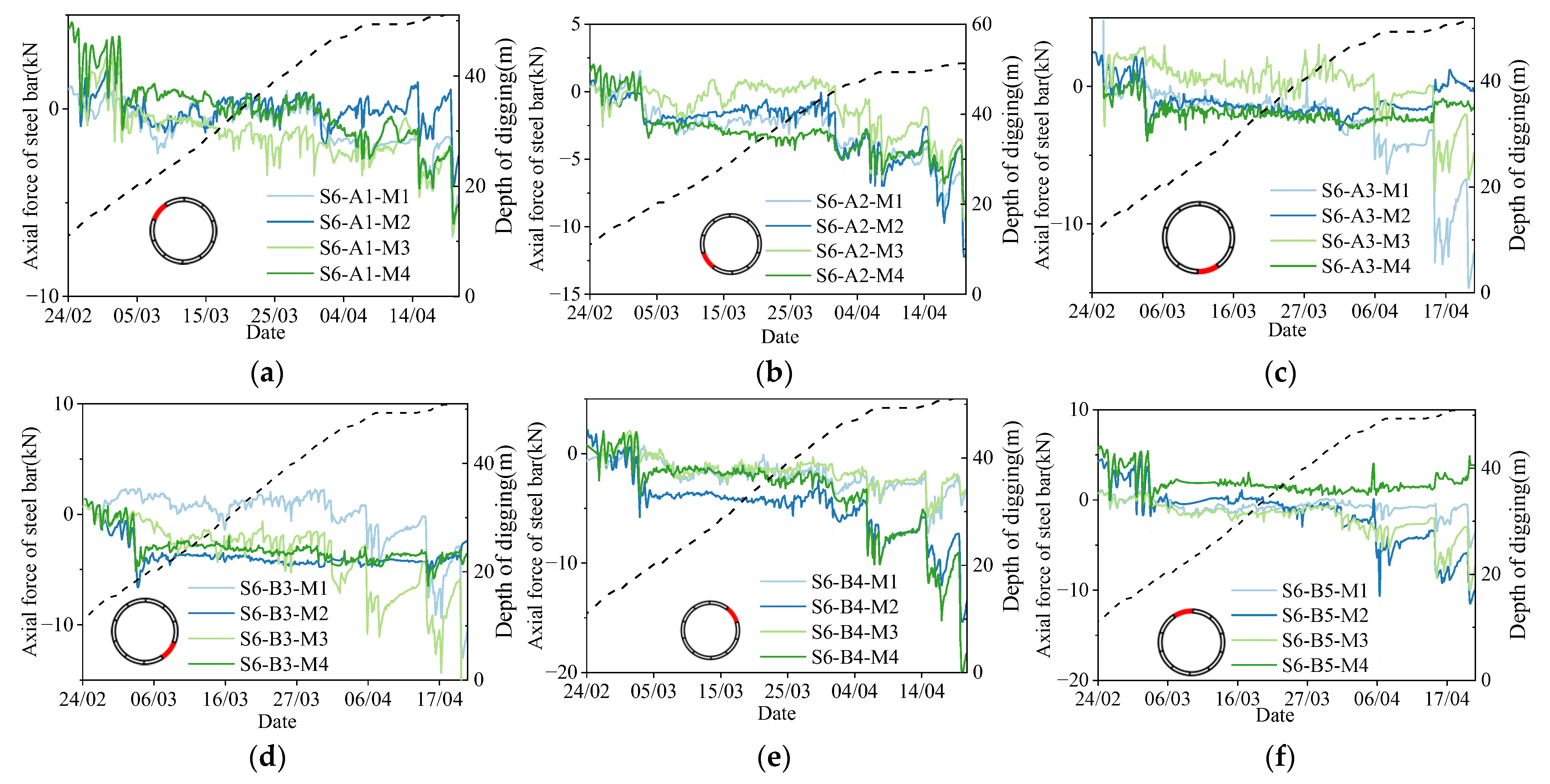
3.3. Axial Forces of Steel Bars in Shaft Segment
4. Monitoring Analysis of Soil Deformation
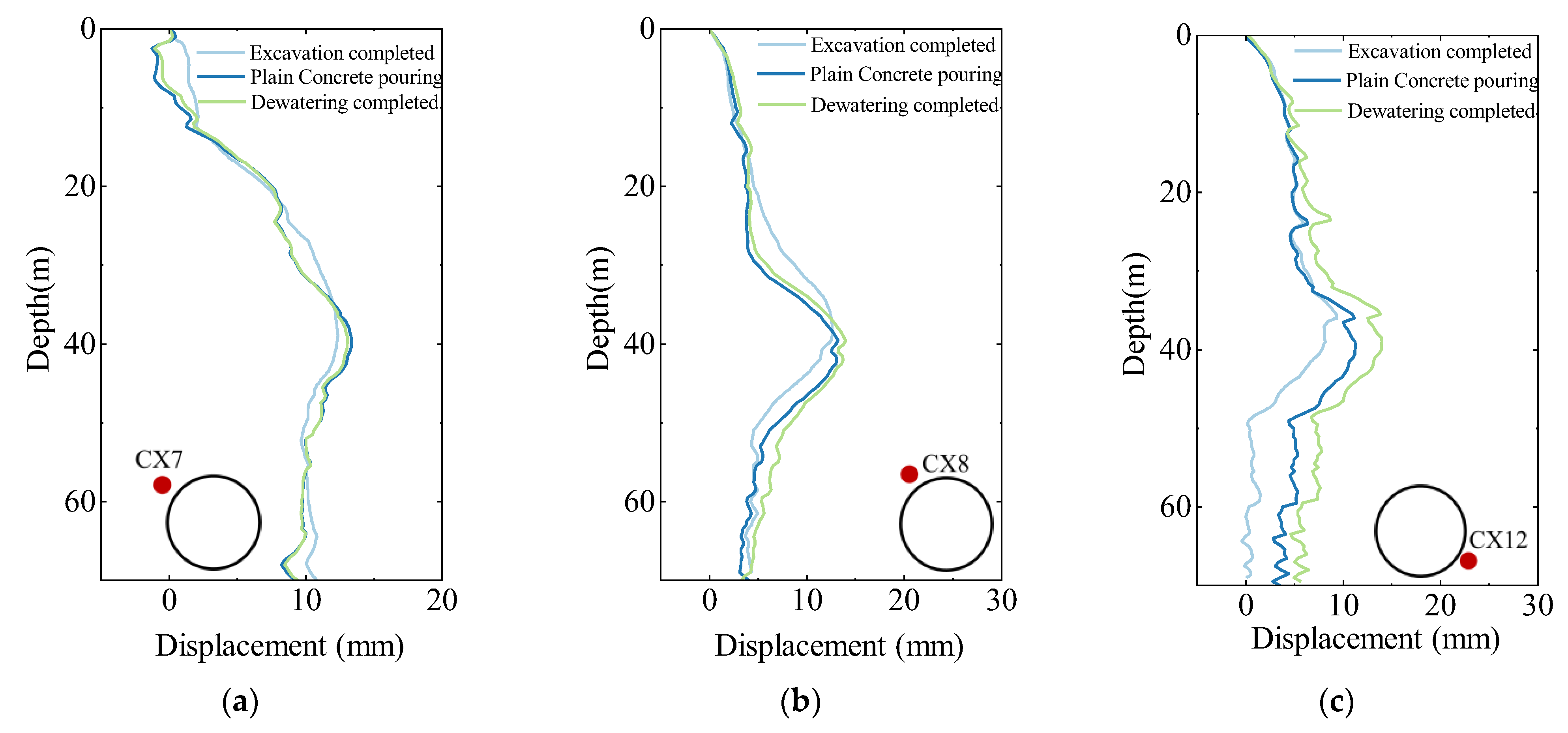
4.1. Horizontal Displacement of Cast-in-Place Piles
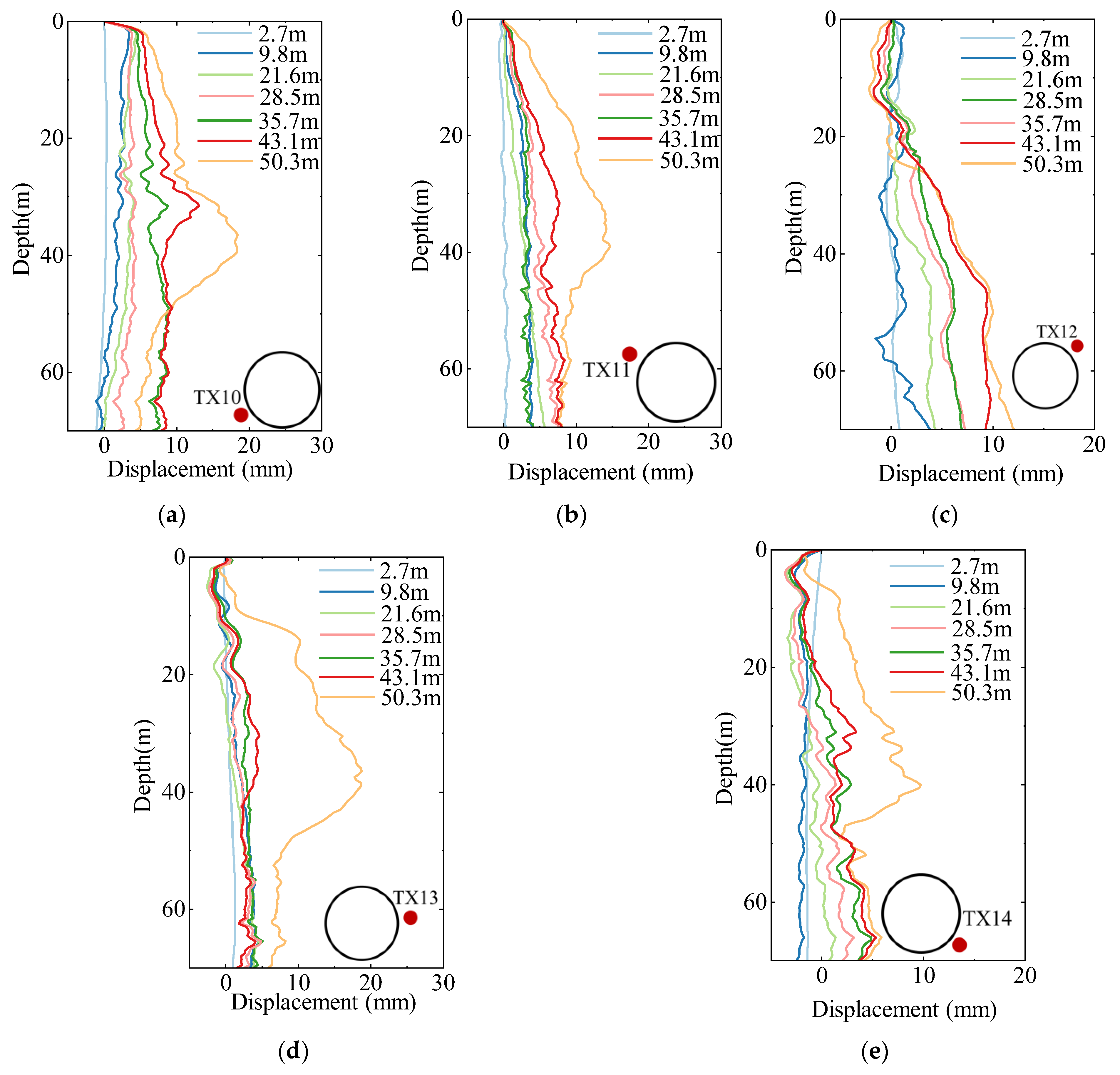
4.2. Horizontal Displacement of Deep Soil
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Abbasi, N.S.; Pan, W.; Alidekyi, S.N.; Li, H.; Ahmed, B.; Asghar, A. A Review of Vertical Shaft Technology and Application in Soft Soil for Urban Underground Space. Appl. Sci. 2025, 15, 3299. [Google Scholar] [CrossRef]
- Ong, D.E.L.; Barla, M.; Cheng, J.W.-C.; Choo, C.S.; Sun, M.; Peerun, M.I. Deep Shaft Excavation: Design, Construction, and Their Challenges. In Sustainable Pipe Jacking Technology in the Urban Environment: Recent Advances and Innovations; Springer: Singapore, 2022; pp. 103–145. ISBN 978-981-16-9372-4. [Google Scholar]
- Leung, C.F.; Shen, R.F. Performance of Gravity Caisson on Sand Compaction Piles. Can. Geotech. J. 2008, 45, 393–407. [Google Scholar] [CrossRef]
- Matsumoto, T.; Gomi, N.; Ikemi, Y. Process for improving open caisson, ‘SS caisson process’ Open keson no kairyo koho ‘SS keson koho’. Denryoku Doboku (Electr. Power Civ. Eng.) 1997, 270, 100–102. [Google Scholar]
- Wang, Y.; Liu, M.; Liao, S.; Yi, Q.; He, J.; Liu, L.; Gong, Z.; Li, K. Investigation on the Stratigraphic Response and Plugging Effect Induced by Press-In Open Caisson in Mucky Soil. KSCE J. Civ. Eng. 2023, 27, 1928–1941. [Google Scholar] [CrossRef]
- Tani, Y.; Nakano, M.; Okoshi, M.; Maeda, S.; Isa, H. Research & Development of Automatic System for Open Caisson Method. In Proceedings of the 13th ISARC, Tokyo, Japan, 11–13 June 1996. [Google Scholar] [CrossRef]
- Tanimura, D.; Ueda, J.; Tani, Y. Large-scale vertical shaft excavation using super-open caisson system. Construction of Tamasato vertical shaft (Ishioka vertical shaft No.5); Jidoka open caisson koho ni yoru daikibo tatekui no kussaku. Tamasato tateko (Ishioka dai5 tateko) shinsetsu koji. Kensetsu No Kikaika 1998, 581, 9–14. [Google Scholar]
- Frenzel, C.; Delabbio, F.; Burger, W.; Potvin, Y. Shaft Boring Systems for Mechanical Excavation of Deep Shafts; Australian Centre for Geomechanics: Perth, Australia, 2010; pp. 289–295. [Google Scholar]
- Peila, D.; Viggiani, G.; Celestino, T. Tunnels and Underground Cities. Engineering and Innovation Meet Archaeology, Architecture and Art: Proceed-ings of the WTC 2019 ITA-AITES World Tunnel Congress (WTC 2019), 3–9 May 2019, Naples, FL, USA; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Neye, E.; Burger, W.; Rennkamp, P. Rapid shaft sinking. Min. Rep. 2013, 149, 250–255. [Google Scholar] [CrossRef]
- Schmäh, P. Vertical Shaft Machines. State of the Art and Vision. Acta Montan. Slovaca 2007, 12, 208–216. [Google Scholar]
- Jiang, H.; Bao, H.; Lin, Y. Research and Application of Design and Construction Technology of Assembled Shaft: A Case Study of a Sinking Shaft Underground Parking Garage in Nanjing, China. Tunn. Constr. 2022, 42, 463–470. [Google Scholar]
- Khine, H.Y.; Marcus Tong, S.Y.; Chen, Y.K. The First Circular Shaft in Asia with the Use of Vertical Shaft Sinking Machine. In Proceedings of the ITA-AITES World Tunnel Congress, Copenhagen, Denmark, 2–8 September 2022. [Google Scholar]
- Schmäh, P.; Berblinger, S. VSM Shaft Sinking Technology: Mechanized Shaft Sinking with the VSM in Different Projects for Subway Ventilation Shafts. In Proceedings of the World Tunnel Congress 2014—Tunnels for a Better Life, Iguassu Falls, Brazil, 9–15 May 2014; Volume 3, p. 123. [Google Scholar]
- Mingliang, H.; Zhenguang, Z.; Jie, X.; Hong, J.; Heli, B.; Xian, L. Measuring of Shaft Wall Stress in Caisson Construction Process Based on Vertical Shaft Sinking Machine: A Case Study of Caisson-Type Underground Intelligent Parking Garage Project in Nanjing, China. Suidao Jianshe (Zhong Ying Wen) 2022, 42, 1033–1043. [Google Scholar]
- Ma, C.; Hong, H.; Yu, L.; Liu, K.; Huang, J. A Numerical Study of Reinforcement Structure in Shaft Construction Using Vertical Shaft Sinking Machine (VSM). Buildings 2024, 14, 2402. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Z.; Ma, C.; Xu, Z.; Yu, L.; Zhang, X.; Liu, K. A Numerical Analysis of the Role of Pile Foundations in Shaft Sinking Using the Vertical Shaft Sinking Machine (VSM). Buildings 2024, 14, 3383. [Google Scholar] [CrossRef]
- Lu, P.; Chen, F.; Nie, D.; Han, J. Analysis of Strata Deformation Patterns Induced by Vertical Shaft Sinking Machine Based on Soil Deformation Zoning: A Case Study of the Zhuyuan Bailonggang Sewage Connecting Pipe Project in Shanghai, China. Appl. Sci. 2025, 15, 1705. [Google Scholar] [CrossRef]
- Abualghethe, D.A.H.; Mu, B.; Dai, G.; Liu, S.; Li, Z.; Liu, S.; Han, L. Optimization of Reinforced Ring Base Depth for Vertical Shaft Sinking in Soft Soil Using VSM Method. Undergr. Space 2025, 22, 280–302. [Google Scholar] [CrossRef]
- Chu, J.; Ma, J.; Jiang, B.; Li, M.; Zhang, K. Experimental Study on Side Friction Distribution of Caissons during Sinking in Water. Chin. J. Geotech. Eng 2019, 41, 707–716. [Google Scholar]
- Templeman, J.O.; Phillips, B.M.; Sheil, B.B. Cutting Shoe Design for Open Caissons in Sand: Influence on Vertical Bearing Capacity. Proc. Inst. Civ. Eng. Geotech. Eng. 2023, 176, 58–73. [Google Scholar] [CrossRef]
- Guo, M.; Dong, X.; Li, J. Study on the Earth Pressure during Sinking Stage of Super Large Caisson Foundation. Appl. Sci. 2021, 11, 10488. [Google Scholar] [CrossRef]
- Yan, F.Y.; Shi, G. Analysis of Limiting Soil Resistance beneath Cutting Curb during Sinking of Open Caisson. Rock Soil Mech. 2013, 34, 80–87. [Google Scholar]
- Mu, B.G.; Bie, Q.; Zhao, X.L.; Gong, W.M. Meso-Experiment on Caisson Load Distribution Characteristics during Sinking. China J. Highw. Transp. 2014, 27, 49–56. [Google Scholar]
- Royston, R.; Sheil, B.B.; Byrne, B.W. Undrained Bearing Capacity of the Cutting Face for an Open Caisson. Géotechnique 2022, 72, 632–641. [Google Scholar] [CrossRef]
- Kim, K.-Y.; Lee, D.-S.; Cho, J.; Jeong, S.-S.; Lee, S. The Effect of Arching Pressure on a Vertical Circular Shaft. Tunn. Undergr. Space Technol. 2013, 37, 10–21. [Google Scholar] [CrossRef]
- Qiao, Y.; Xie, F.; Bai, Z.; Lu, J.; Ding, W. Deformation Characteristics of Ultra-Deep Circular Shaft in Soft Soil: A Case Study. Undergr. Space 2024, 16, 239–260. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, B.C. Instrumentation and Numerical Analysis of Cylindrical Diaphragm Wall Movement during Deep Excavation at Coastal Area. Mar. Georesources Geotechnol. 2005, 23, 117–136. [Google Scholar] [CrossRef]
- Wang, R.; Liu, S.; Xu, L.; Zhao, C.; Ni, P.; Zheng, W. Performance of a 56 m Deep Circular Excavation Supported by Diaphragm and Cut-off Double-Wall System in Shanghai Soft Ground. Can. Geotech. J. 2023, 60, 521–540. [Google Scholar] [CrossRef]
- Jia, J.; Zhai, J.-Q.; Li, M.-G.; Zhang, L.-L.; Xie, X.-L. Performance of Large-Diameter Circular Diaphragm Walls in a Deep Excavation: Case Study of Shanghai Tower. J. Aerosp. Eng. 2019, 32, 04019078. [Google Scholar] [CrossRef]
- Kumagai, T.; Ariizumi, K.; Kashiwagi, A. Behaviour and Analysis of a Large-Scale Cylindrical Earth Retaining Structure. Soils Found. 1999, 39, 13–26. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, D. Characteristics of a Large-Scale Deep Foundation Pit Excavated by the Central-Island Technique in Shanghai Soft Clay. I: Bottom-Up Construction of the Central Cylindrical Shaft. J. Geotech. Geoenvironmental Eng. 2013, 139, 1875–1893. [Google Scholar] [CrossRef]
- Terzaghi, K. General Wedge Theory of Earth Pressure. Trans. Am. Soc. Civ. Eng. 1941, 106, 68–80. [Google Scholar] [CrossRef]
- Sherif, M.A.; Ishibashi, I.; Lee, C.D. Earth Pressures against Rigid Retaining Walls. J. Geotech. Eng. Div. 1982, 108, 679–695. [Google Scholar] [CrossRef]
- Zhao, T.; Ding, W.; Qiao, Y.; Duan, C. A Large-Scale Synchronous Grouting Test for a Quasi-Rectangular Shield Tunnel: Observation, Analysis and Interpretation. Tunn. Undergr. Space Technol. 2019, 91, 103018. [Google Scholar] [CrossRef]







| Location | Diameter/(m) | Depth/(m) | Shaft Type | Geological Conditions |
|---|---|---|---|---|
| Girona, Spain | 5.25 | 20 | Ventilation | Soft ground; loamy coarse boulders |
| Barcelona, Spain | 9.2 | 47 | Sand, gravel, quartz, slate | |
| Paris, France | 11.9 | 45 | Soft and heterogeneous ground | |
| Honolulu, HI, USA | 10 | 36 | Microtunneling shafts | Hard basalt as well as coral |
| St. Petersburg, Russia | 7.7 | 85 | Sewage collector shafts | clay, sand, boulders |
| Dortmund, Germany | 9.0 | 23 | Launch shaft | Soft ground; sand, silt, marl |
| Nanjing, China | 12.8 | 68 | Parking garage shafts | Sand, gravel, limestone |
| Guangzhou, China | 14 | 27 | Launch shaft | Clay, gravel, granite |
| Shanghai, China | 22.6 | 50.5 | Parking garage shafts | Mucky clay, silty clay, silty sand |
| Stage | Construction Processes | Date (dd-mm-yyyy) |
|---|---|---|
| 1 | Shaft excavation and sinking stage | 24/01/2024–21/04/2024 |
| Construction of the cast-in-place shaft wall | 14/04/2024–25/04/2024 | |
| 2 | Slurry replacement behind the shaft wall | 28/04/2024–03/05/2024 |
| Underwater pouring of bottom plain concrete of the shaft | 07/05/2024–11/05/2024 | |
| pumping water inside the shaft | 11/05/2024–23/05/2024 |
| Monitoring Points * | Monitoring Items | Monitoring Target | Monitoring Area | Monitoring Point |
|---|---|---|---|---|
| S3/S6-A1/A2/A3/B3/B4/B5-P | External Pressure | 3rd/6th ring segment | A1/A2/A3/ B3/B4/B5 | |
| S3/S6-A1/A2/A3/B3/B4/B5-M1/M2/M3/M4 | Axial force of the steel bar | 3rd/6th ring segment | A1/A2/A3/ B3/B4/B5 | M1/M2/M3/M4 |
| B-A1/A2/A3/B3/B4/B5-M1/M2/M3/M4 | Bottom connecting beam | A1/A2/A3/ B3/B4/B5 | M1/M2/M3/M4 | |
| CX6/CX7/CX8/CX9/CX11/CX12/CX13 | Horizontal Deformation | cast-in-place piles | ||
| TX10/TX11/TX12/TX13/TX14 | Horizontal Deformation | Stratum |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baoyin, H.; Xu, Z.; Yu, L.; Zhang, X.; Wang, X.; Liu, Y. Analysis of Structural Internal Forces and Stratum Deformation in Shaft Construction Using Vertical Shaft Sinking Machine. Buildings 2025, 15, 2043. https://doi.org/10.3390/buildings15122043
Baoyin H, Xu Z, Yu L, Zhang X, Wang X, Liu Y. Analysis of Structural Internal Forces and Stratum Deformation in Shaft Construction Using Vertical Shaft Sinking Machine. Buildings. 2025; 15(12):2043. https://doi.org/10.3390/buildings15122043
Chicago/Turabian StyleBaoyin, Hexige, Zhibing Xu, Long Yu, Xu Zhang, Xiaoxiao Wang, and Yang Liu. 2025. "Analysis of Structural Internal Forces and Stratum Deformation in Shaft Construction Using Vertical Shaft Sinking Machine" Buildings 15, no. 12: 2043. https://doi.org/10.3390/buildings15122043
APA StyleBaoyin, H., Xu, Z., Yu, L., Zhang, X., Wang, X., & Liu, Y. (2025). Analysis of Structural Internal Forces and Stratum Deformation in Shaft Construction Using Vertical Shaft Sinking Machine. Buildings, 15(12), 2043. https://doi.org/10.3390/buildings15122043





