Research on the Mechanical Behavior of External Composite Steel Bar Under Cyclic Tension-Compression Loading
Abstract
1. Introduction
2. Experimental Investigation on External Composite Steel Bars
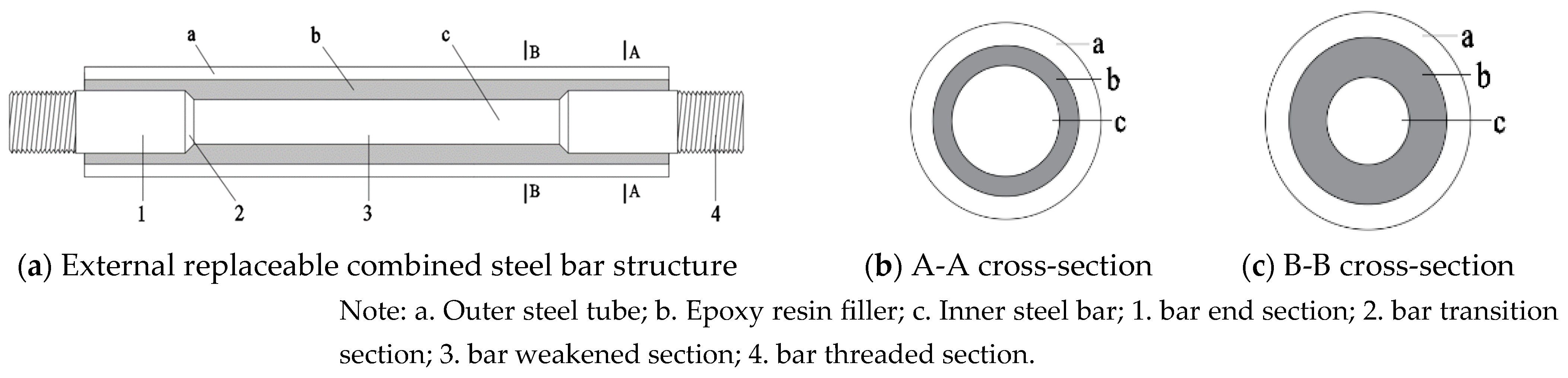
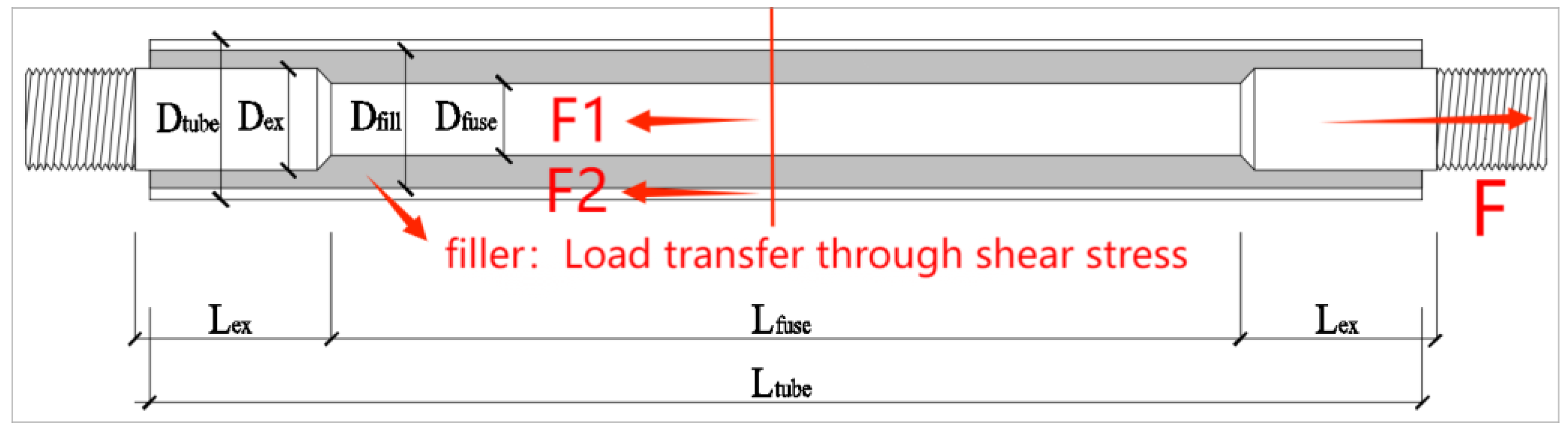
2.1. Specimen Design
- Afuse is the cross-sectional area of the weakened section of the inner steel bar;
- Atube is the cross-sectional area of the outer steel tube;
- Ifuse is to the moment of inertia of the weakened section of the inner steel bar;
- Itube is the moment of inertia of the outer steel tube;
- Aeff,fill is the effective cross-sectional area of the internal filler material;
- Ieff,fill is the moment of inertia of the internal filler material.
| Specimen Group Number | Specimen Identification Number | Dw (mm) | Dex/Dfuse | Lfuse (mm) | Ltube (mm) | λfuse | λtot |
|---|---|---|---|---|---|---|---|
| Group 1 | D14L210-Q345B | 10 | 1.7 | 210 | 310 | 60.0 | 20.8 |
| D16L200-Q345B | 8 | 1.5 | 200 | 300 | 50.0 | 20.0 | |
| D16L240-Q345B | 8 | 1.5 | 240 | 340 | 60.0 | 24.0 | |
| D16L280-Q345B | 8 | 1.5 | 280 | 380 | 70.0 | 28.0 | |
| D18L270-Q345B | 6 | 1.3 | 270 | 370 | 60.0 | 27.2 | |
| Group 2 | D20L300-Q345B | 10 | 1.5 | 300 | 400 | 60.0 | 30.5 |
| D22L275-Q345B | 8 | 1.36 | 275 | 375 | 50.0 | 28.2 | |
| D22L330-Q345B | 8 | 1.36 | 330 | 430 | 60.0 | 33.8 | |
| D22L385-Q345B | 8 | 1.36 | 385 | 485 | 70.0 | 39.5 | |
| D24L360-Q345B | 6 | 1.25 | 360 | 460 | 60.0 | 37.2 | |
| Group 3 | D26L390-Q345B | 10 | 1.4 | 390 | 490 | 60.0 | 40.5 |
| D28L350-Q345B | 8 | 1.3 | 350 | 450 | 50.0 | 36.4 | |
| D28L420-Q345B | 8 | 1.3 | 420 | 520 | 60.0 | 43.7 | |
| D28L490-Q345B | 8 | 1.3 | 490 | 590 | 70.0 | 51.0 | |
| D30L450-Q345B | 6 | 1.2 | 450 | 550 | 60.0 | 46.9 | |
| Group 4 | D14L210-30 | 10 | 1.7 | 210 | 310 | 60.0 | 20.8 |
| D16L200-30 | 8 | 1.5 | 200 | 300 | 50.0 | 20.0 | |
| D16L240-30 | 8 | 1.5 | 240 | 340 | 60.0 | 24.0 | |
| D16L280-30 | 8 | 1.5 | 280 | 380 | 70.0 | 28.0 | |
| D18L270-30 | 6 | 1.3 | 270 | 370 | 60.0 | 27.2 | |
| Group 5 | D20L300-30 | 10 | 1.5 | 300 | 400 | 60.0 | 30.5 |
| D22L275-30 | 8 | 1.36 | 275 | 375 | 50.0 | 28.2 | |
| D22L330-30 | 8 | 1.36 | 330 | 430 | 60.0 | 33.8 | |
| D22L385-30 | 8 | 1.36 | 385 | 485 | 70.0 | 39.5 | |
| D24L360-30 | 6 | 1.25 | 360 | 460 | 60.0 | 37.2 | |
| Group 6 | D26L390-30 | 10 | 1.4 | 390 | 490 | 60.0 | 40.5 |
| D28L350-30 | 8 | 1.3 | 350 | 450 | 50.0 | 36.4 | |
| D28L420-30 | 8 | 1.3 | 420 | 520 | 60.0 | 43.7 | |
| D28L490-30 | 8 | 1.3 | 490 | 590 | 70.0 | 51.0 | |
| D30L450-30 | 6 | 1.2 | 450 | 550 | 60.0 | 46.9 |
2.2. Material Properties
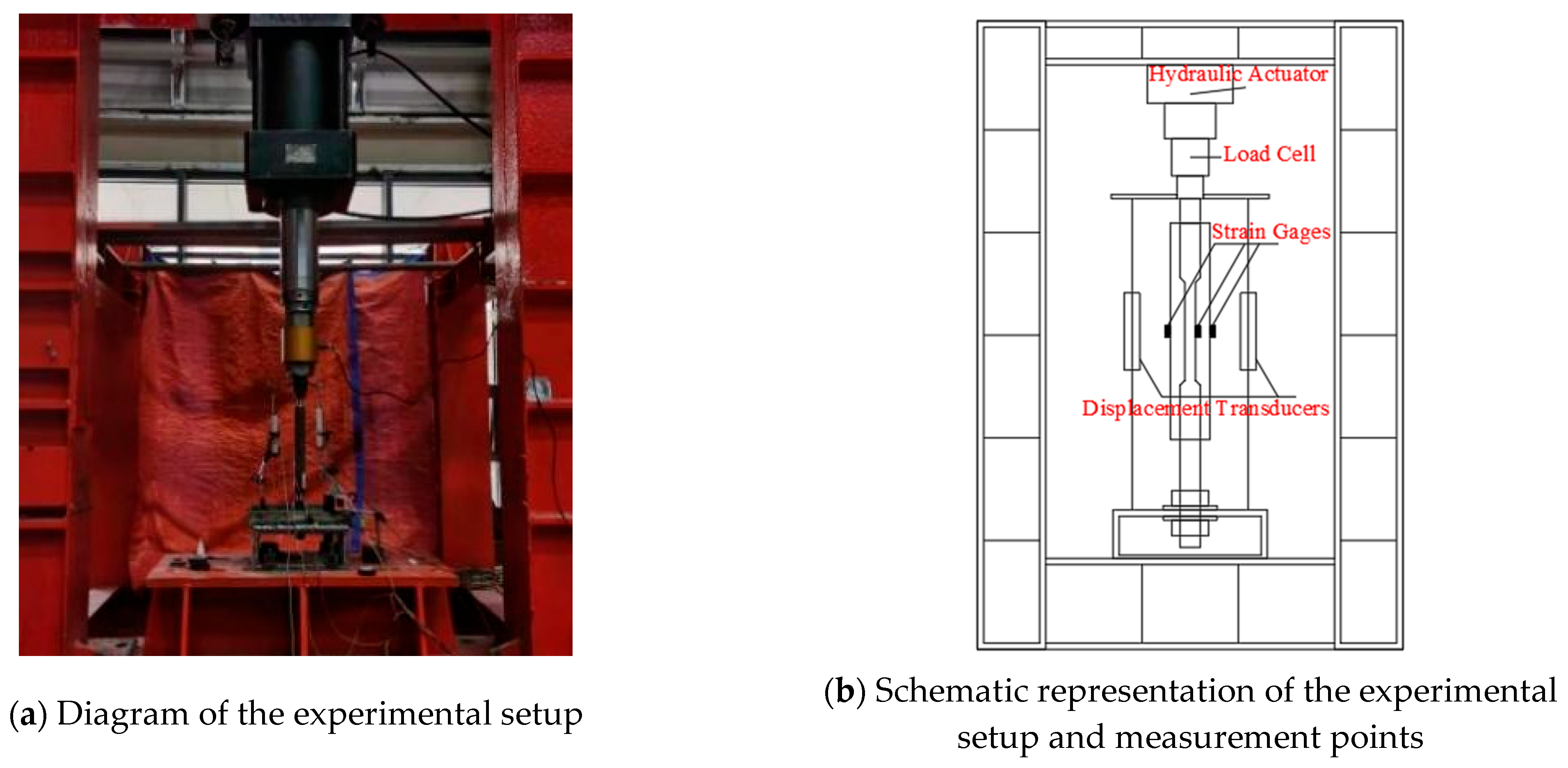
2.3. Test Loading and Measurement
2.4. Experimental Phenomena
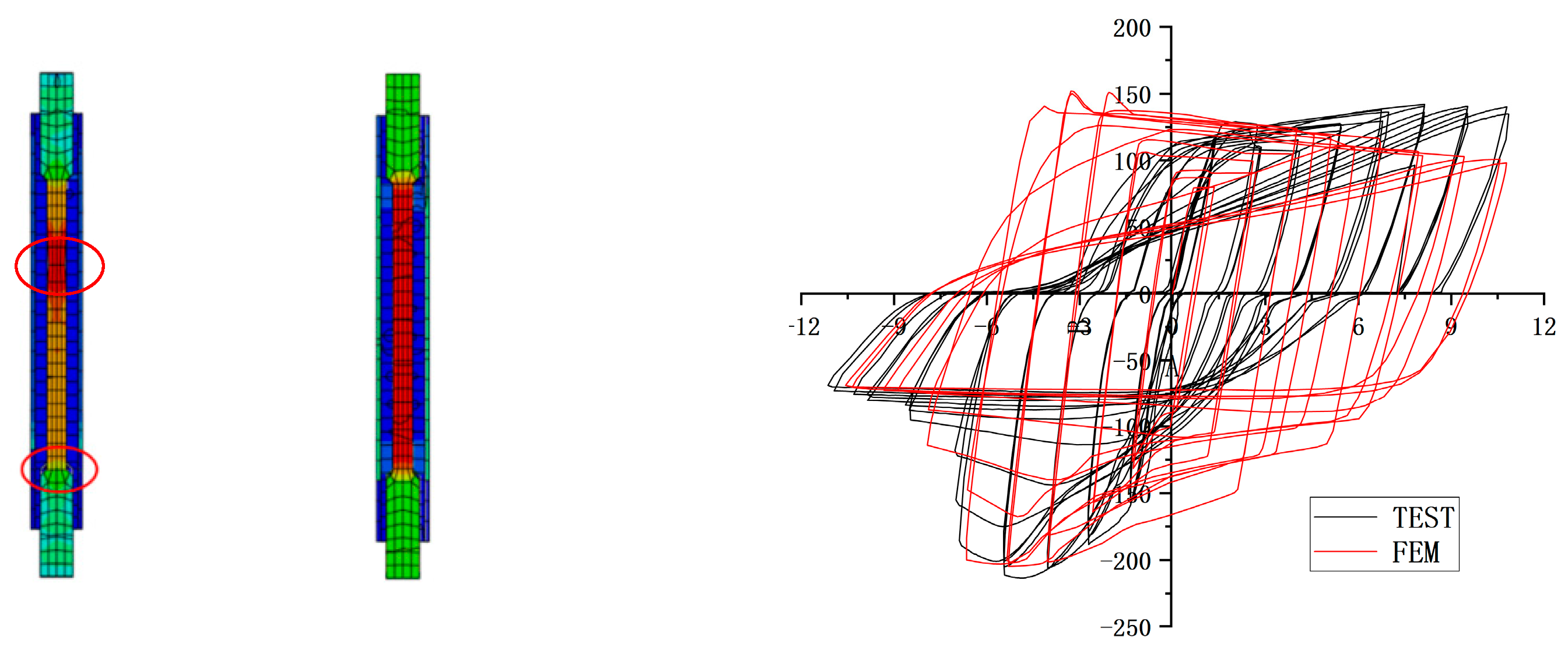
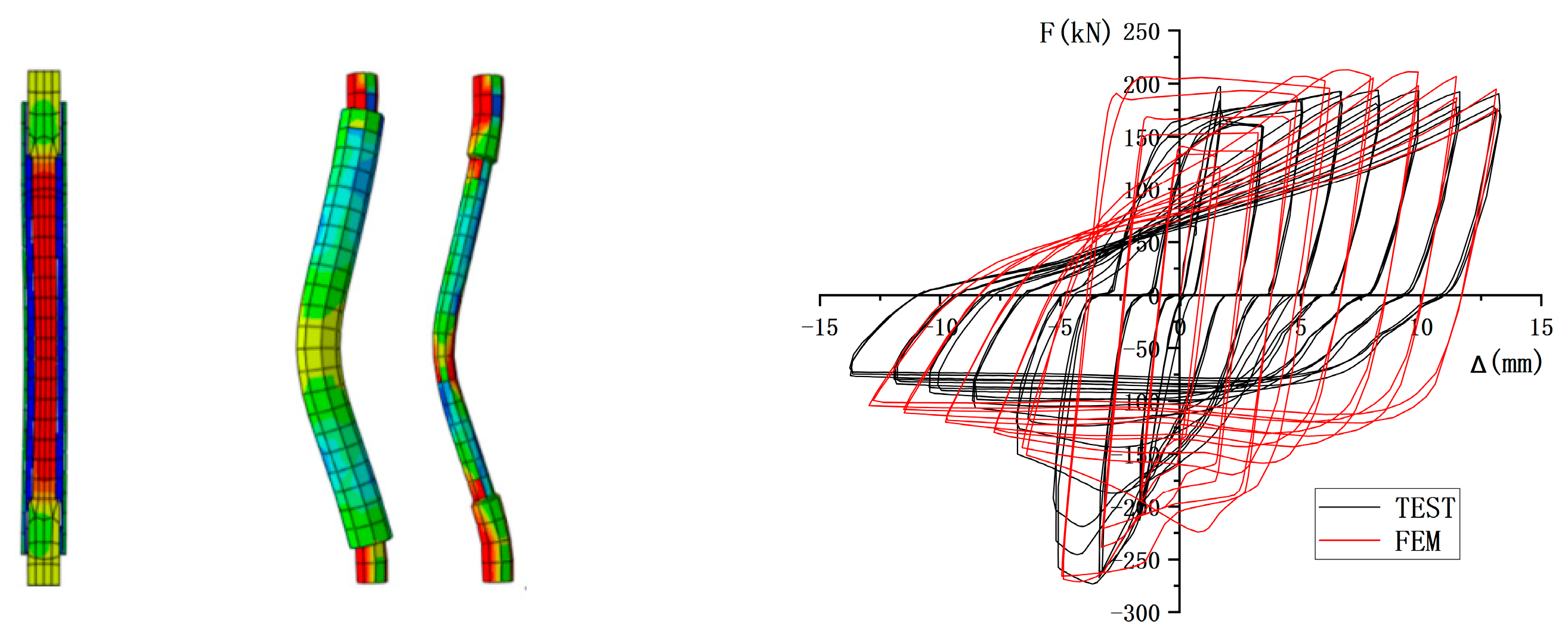
2.4.1. Failure Mode
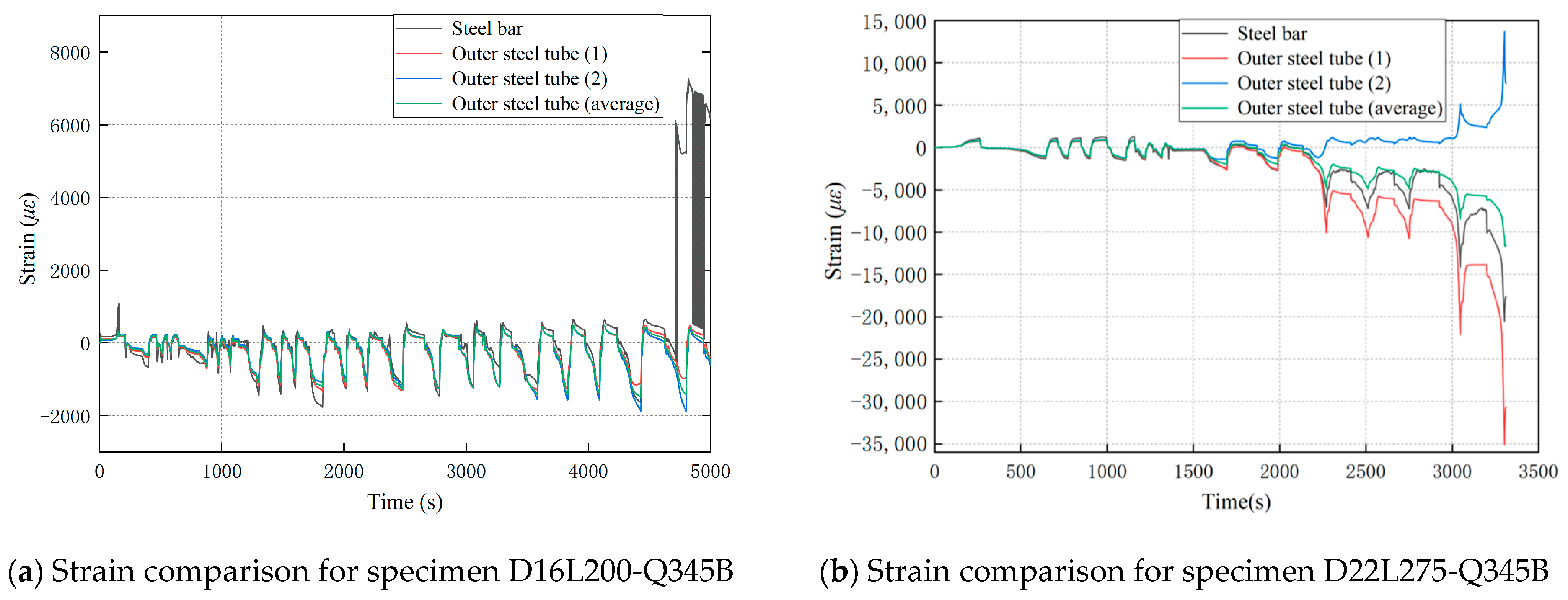
2.4.2. Strain Analysis
2.5. Analysis of Experimental Results
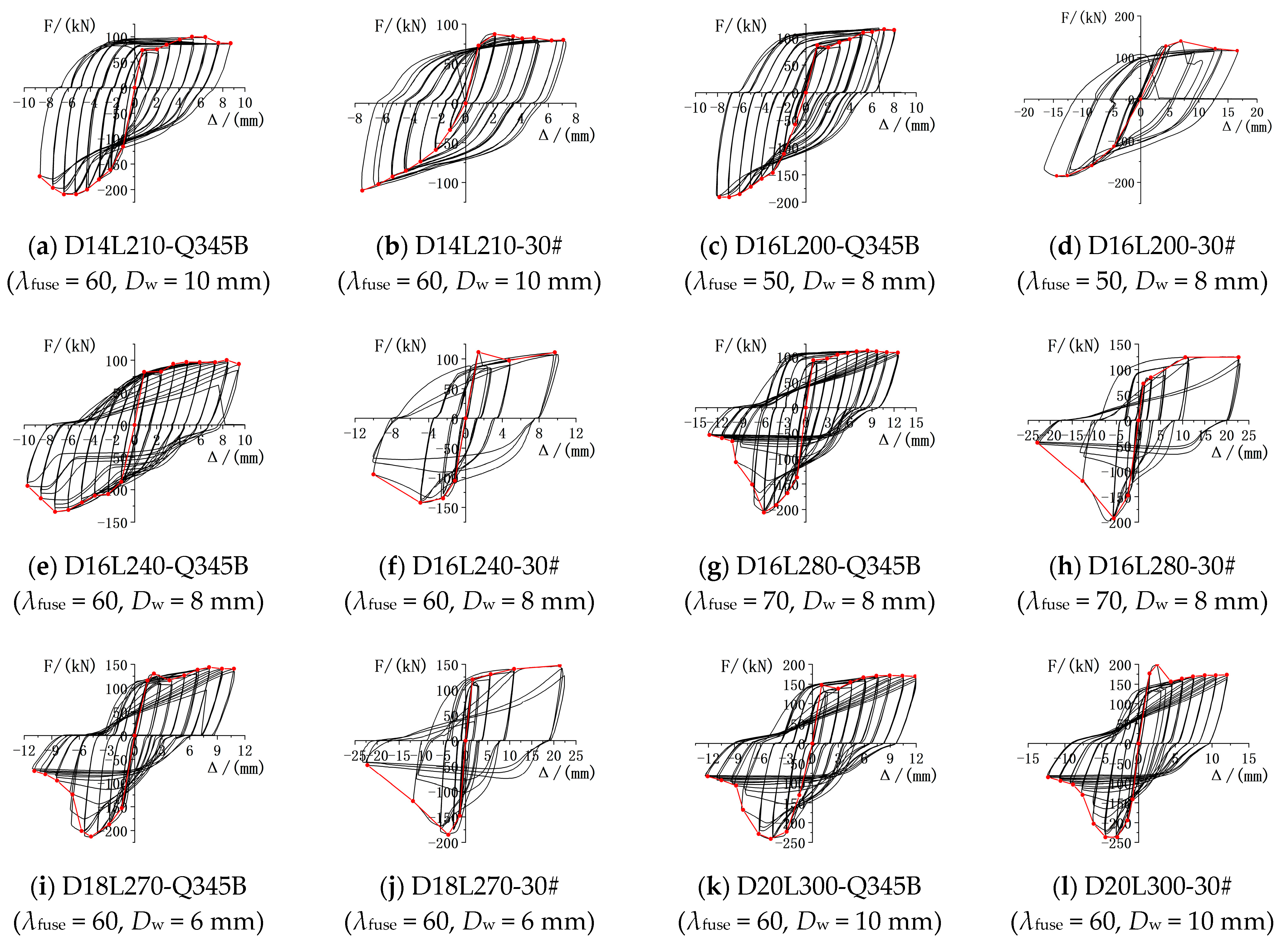
2.5.1. Hysteresis Curve
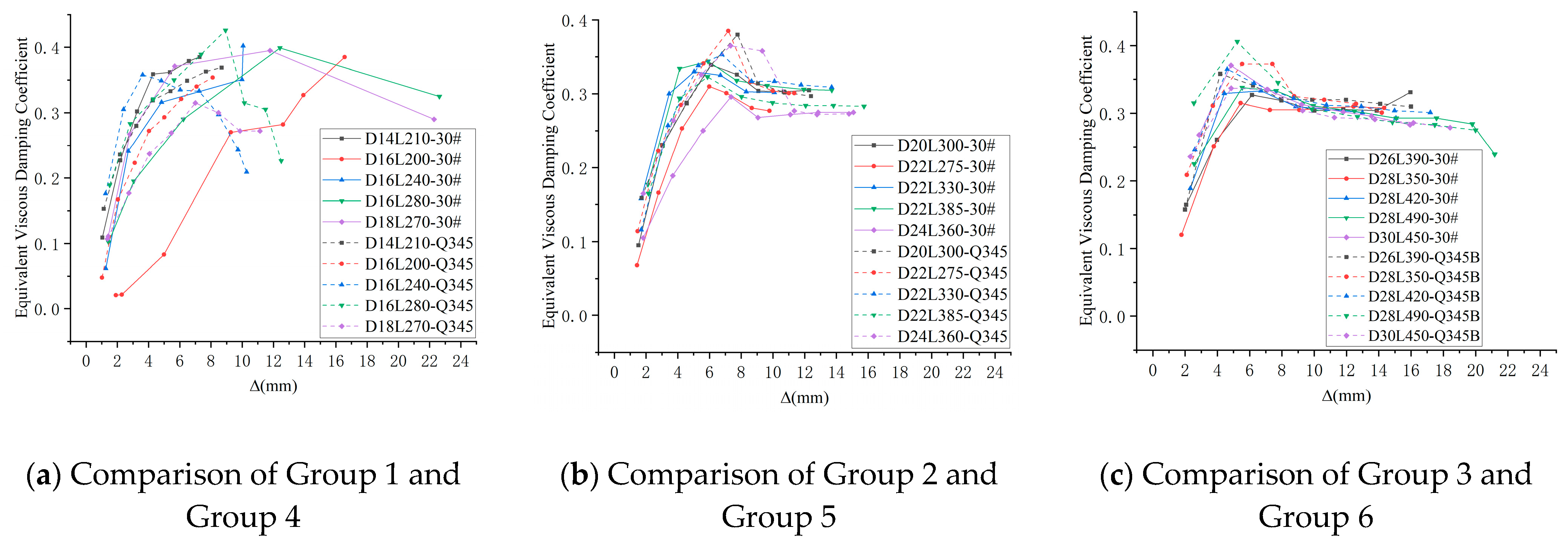
2.5.2. Displacement Ductility
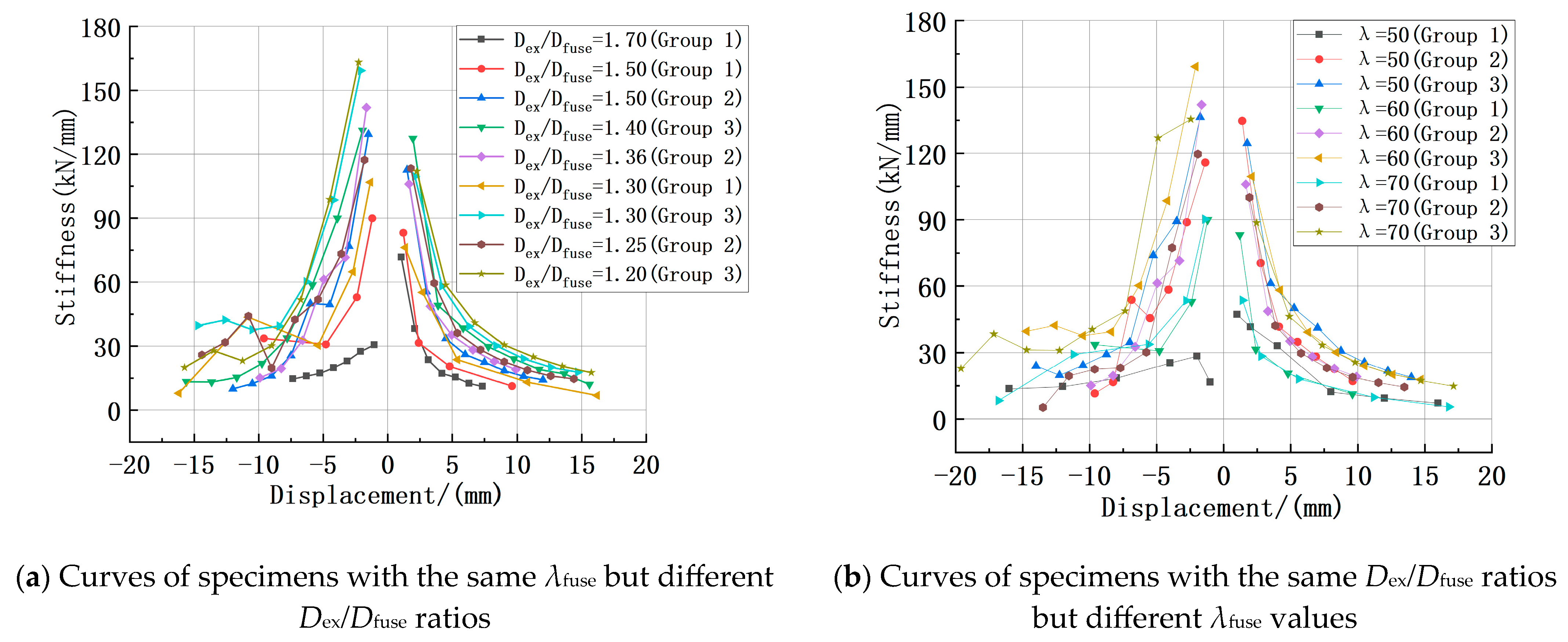
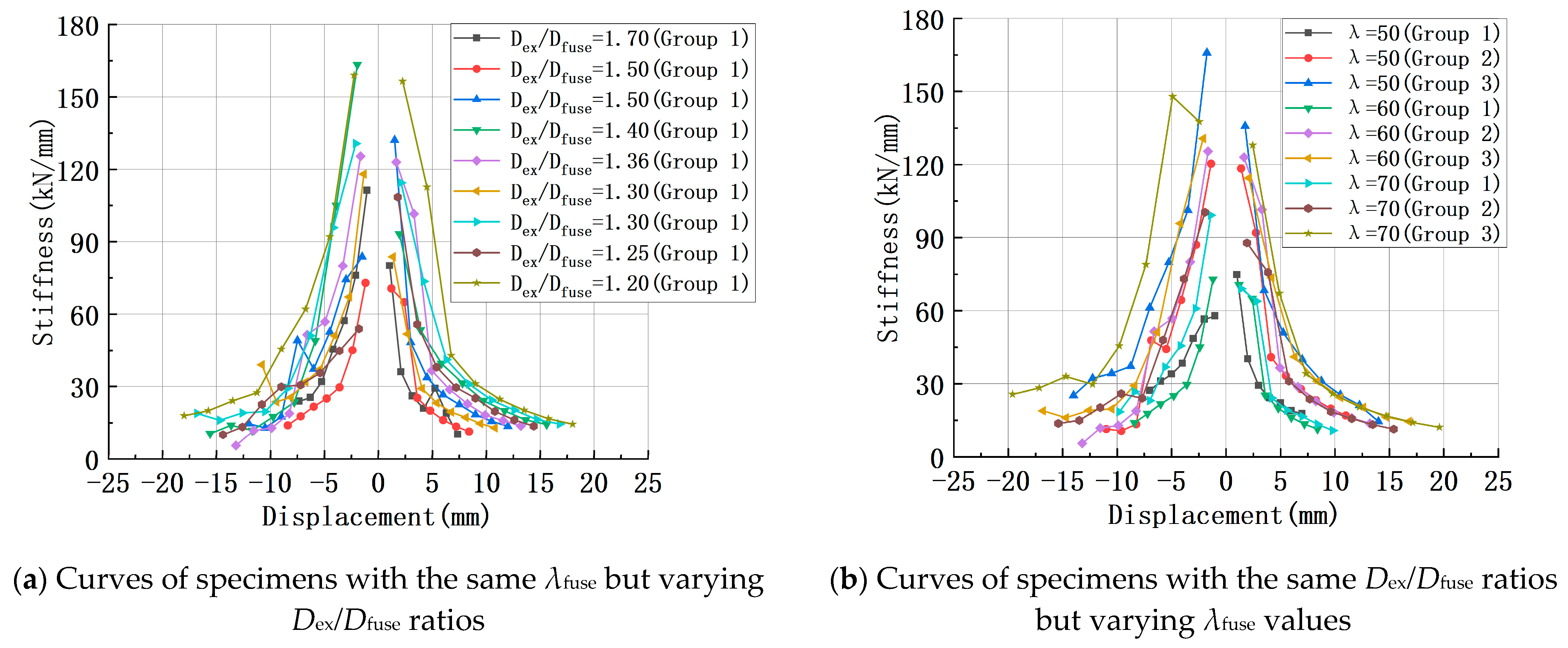
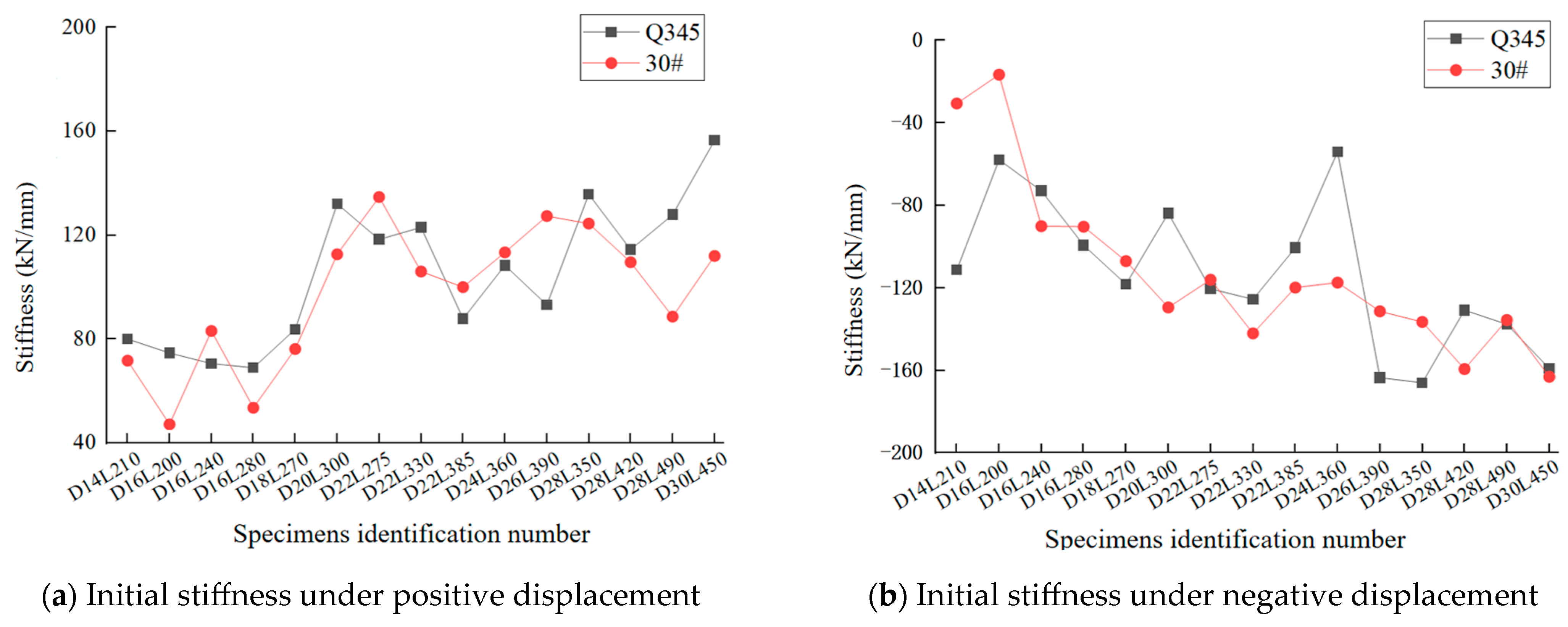
2.5.3. Stiffness Degradation
3. Numerical Simulation of External Composite Steel Bars
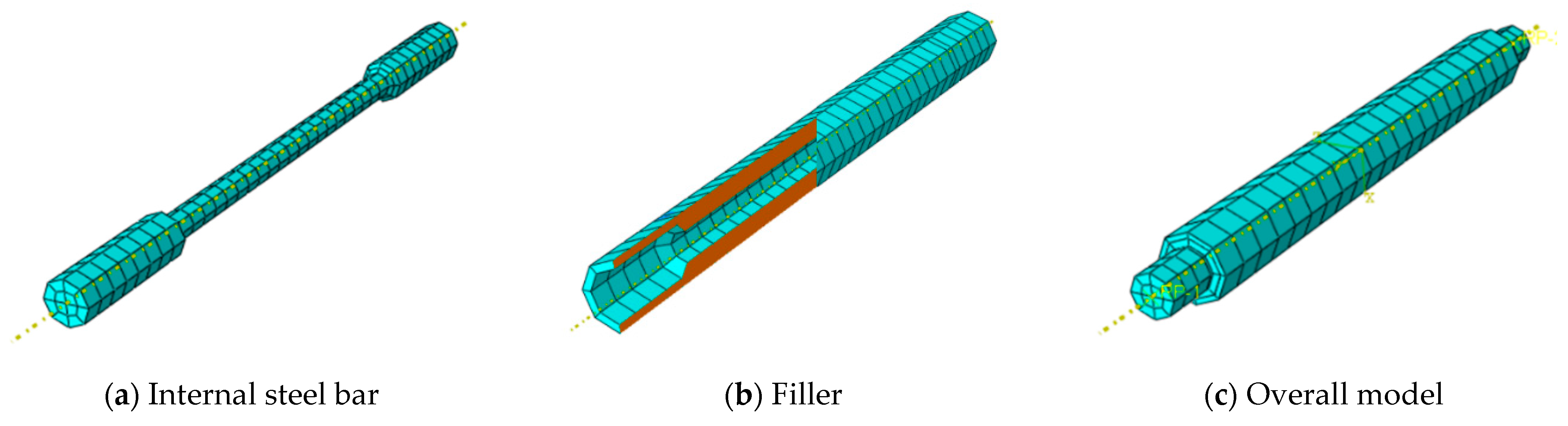
3.1. Model Establishment
3.2. Finite Element Analysis Results
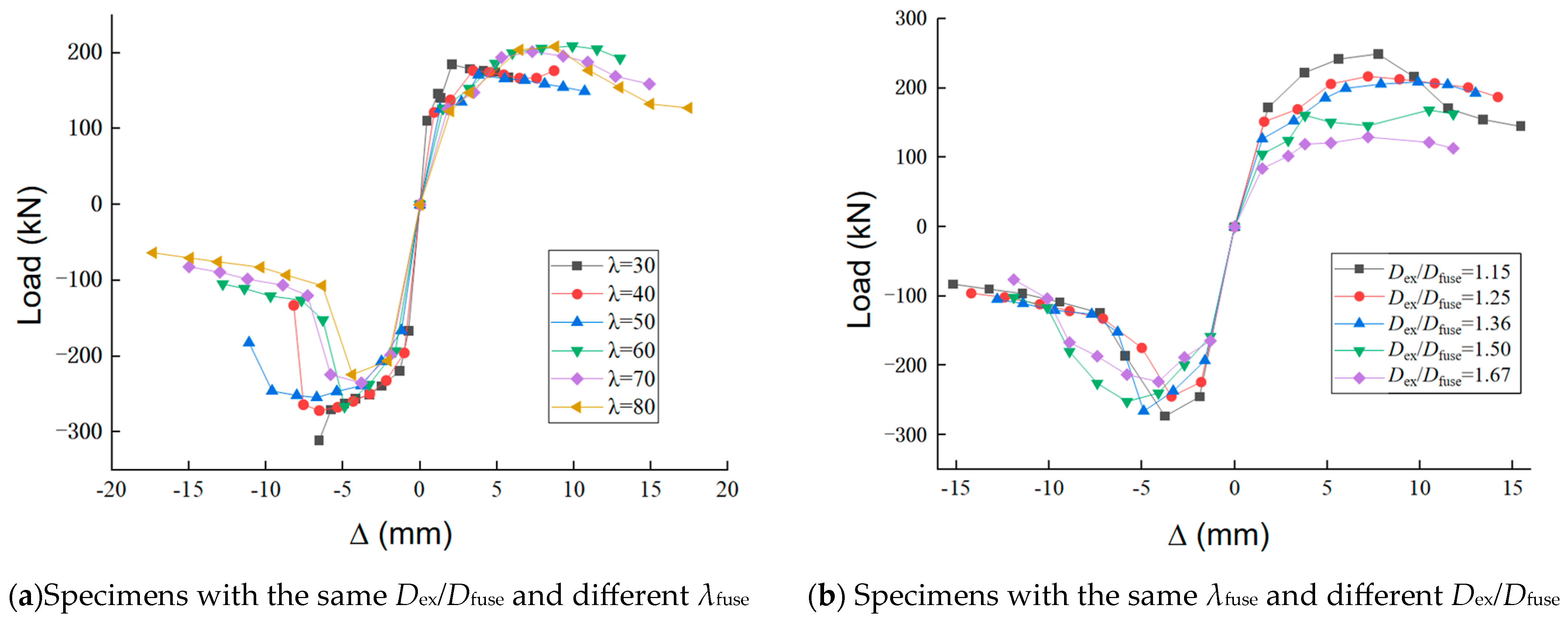
3.3. Parametric Numerical Analysis
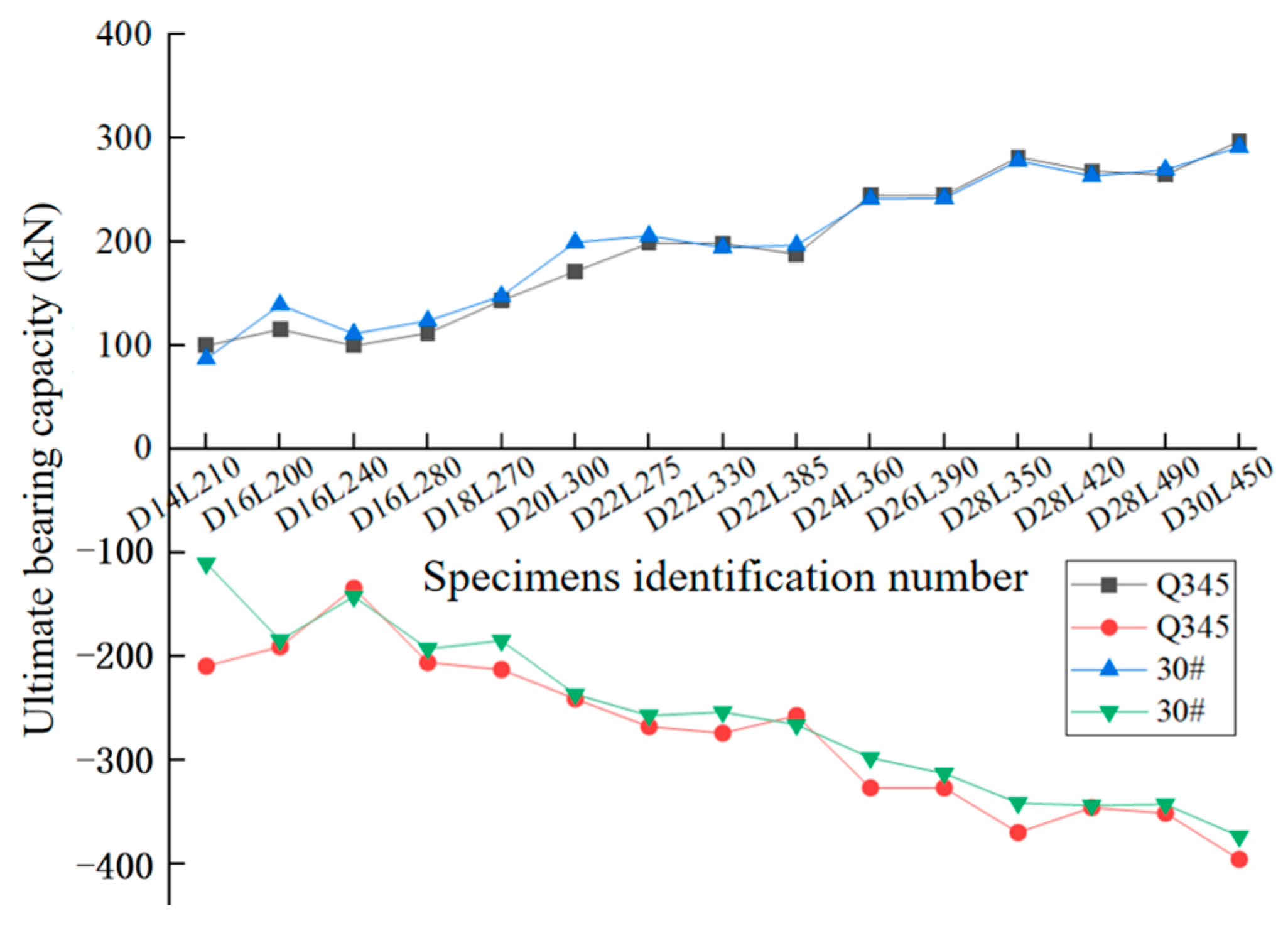
3.3.1. Comparison of Materials of Steel Bars
3.3.2. Slenderness Ratio of Test Specimens and Diameter Ratio of Core Steel Bar Segments
4. Theoretical Calculation of the Initial Stiffness
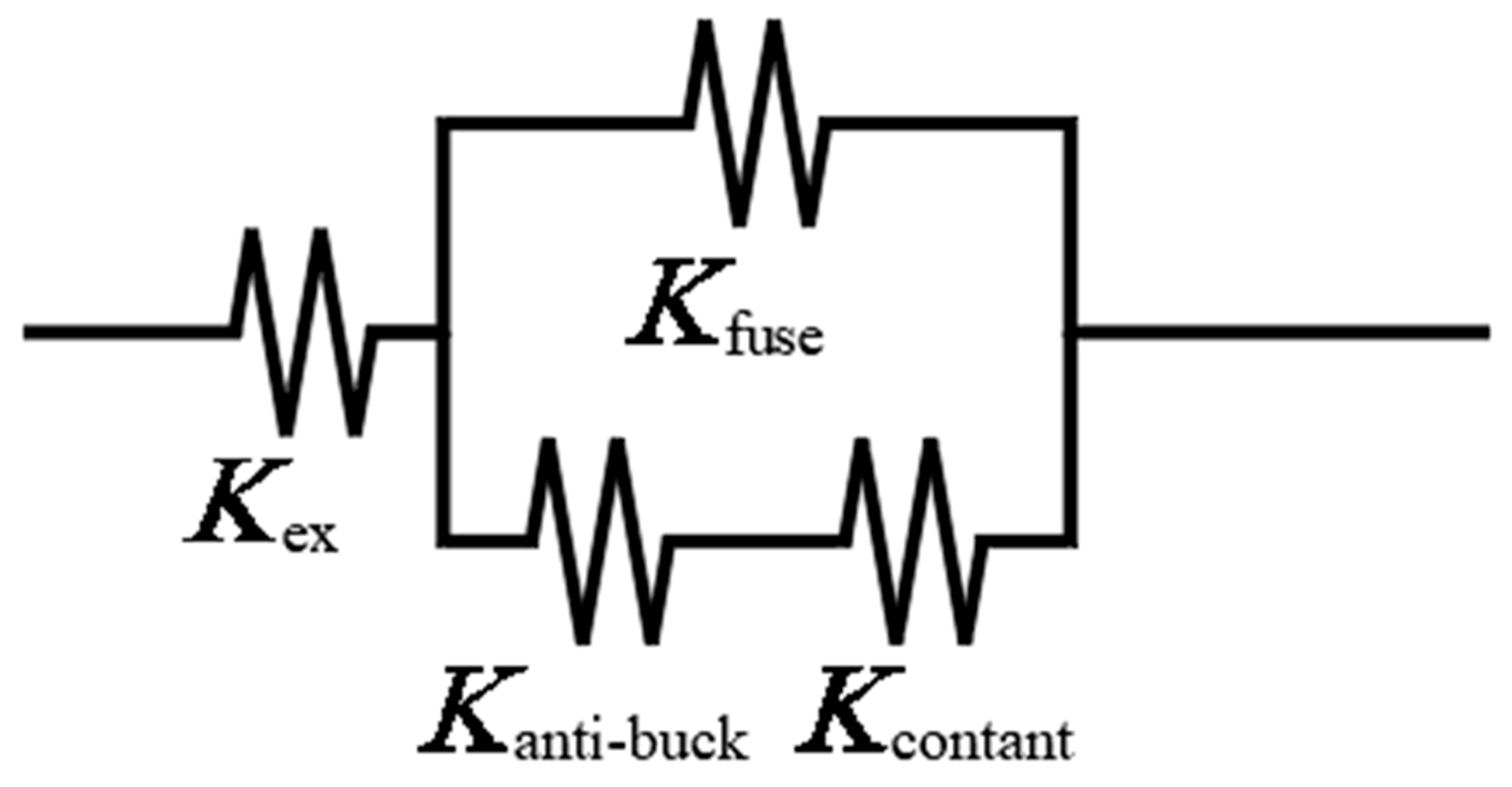
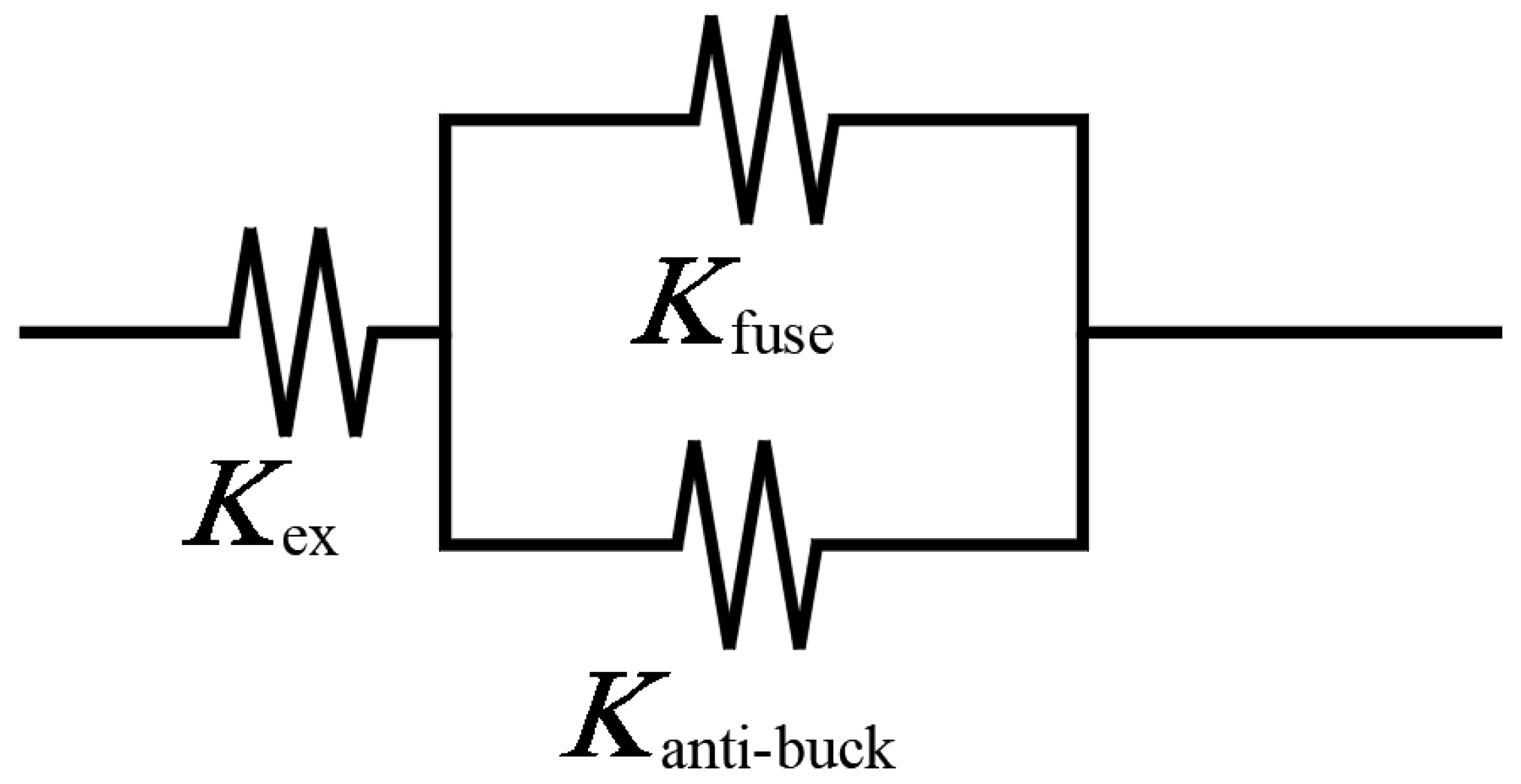
4.1. Theoretical Calculation of Initial Tensile Stiffness
- Kfuse: stiffness of the steel bar;
- Kanti-buck: stiffness of the outer steel tube;
- Kcontact: stiffness of the filling material.
4.2. Theoretical Calculation of Initial Compressive Stiffness
4.3. Analysis of Initial Stiffness
5. Conclusions
- The composite steel bar specimens exhibited two failure modes: buckling and necking. For specimens exhibiting buckling failure, the compressive bearing capacity of the composite steel bar rapidly decreased to below 85% during the mid-to-later loading stages. Necking failure was observed in specimens with both low slenderness ratios and small diameters, typically occurring in the core steel bar or at its ends.
- Analysis of the seismic performance indicators obtained from the experiments reveals that the composite steel bars demonstrated substantial deformation capacity and stable deformability. For most specimens, the tensile ductility factor exceeded the compressive ductility factor, indicating strong deformation capacity and high compressive stiffness, which reduces the likelihood of compression-induced failure. The slenderness ratio and the diameter ratio between the steel bar ends and the weakened segment had a pronounced influence on performance, whereas their influence on stiffness was less significant.
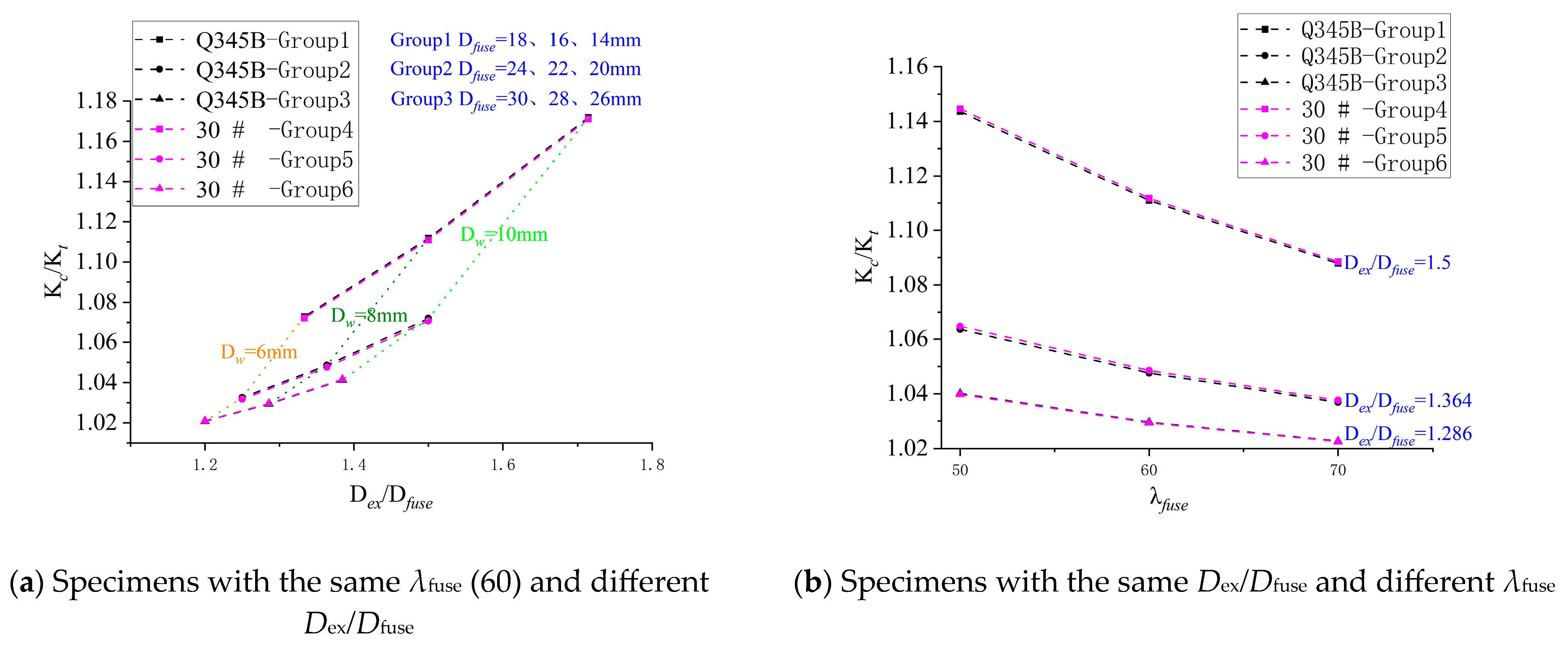
- For the design and application of external composite steel bars, it is recommended to comprehensively consider the basic slenderness ratio λfuse and the diameter ratio between the loading end and the weakened section Dex/Dfuse. Based on experimental and numerical analysis, a stable energy dissipation performance can generally be achieved when λfuse is between 60 and 80 (λtot = 33.8–45.1) and Dex/Dfuse ranges from 1.25 to 1.50.
- Analysis of the initial tensile-compressive stiffness of the externally replaceable composite steel bars suggests that when the diameter of the energy-dissipating segment is less than or equal to 18 mm, the diameter ratio of Dex/Dfuse should be below 1.25; when the diameter is greater than or equal to 20 mm, the diameter ratio of Dex/Dfuse should be below 1.5. These parameters help ensure optimal stiffness ratios and more stable energy dissipation.
- It is recommended to use materials with a low yield point (lower than the connecting main reinforcement), high elongation capacity (elongation > 20%) and anti-fatigue for the composite steel bars to ensure lower yield loads and larger deformation displacements, thereby improving the failure mode and enhancing energy dissipation capacity. Meanwhile, the limitations of this study are the lack of consideration of the effect of the roughness of the metal surface bonded to the epoxy resin on the performance, and the lack of dynamic load tests to guide future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite element mode |
References
- Zhou, Y. Design and Application of Anti-Buckling Energy Consumption Braced Structures; Architecture & Building Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Priestley, M.N. Overview of PRESSS Research Program. PCI J. 1991, 36, 50–57. [Google Scholar] [CrossRef]
- Priestley, M.N.; Sritharan, S.; Conley, J.R.; Pampanin, S. Preliminary Results and Conclusions from the PRESSS Five-Story Precast Concrete Test Building. PCI J. 1999, 44, 42–67. [Google Scholar] [CrossRef]
- Huang, L.; Clayton, P.M.; Zhou, Z. Seismic Design and Performance of Self-Centering Precast Concrete Frames with Variable Friction Dampers. Eng. Struct. 2021, 245, 112863. [Google Scholar] [CrossRef]
- Wang, H.; Marino, E.M.; Pan, P.; Liu, H.; Nie, X. Experimental Study of a Novel Precast Prestressed Reinforced Concrete Beam-to-Column Joint. Eng. Struct. 2018, 156, 68–81. [Google Scholar] [CrossRef]
- Wang, C.-L.; Liu, Y.; Zheng, X.; Wu, J. Experimental Investigation of a Precast Concrete Connection with All-Steel Bamboo-Shaped Energy Dissipaters. Eng. Struct. 2019, 178, 298–308. [Google Scholar] [CrossRef]
- Chen, S.; Zheng, L.; Yan, W.; Kim, K.-S. Seismic Performance of Post-Tensioned Precast Concrete Joints Improved with Curved Steel Braces. J. Earthq. Eng. 2022, 26, 1461–1479. [Google Scholar] [CrossRef]
- Kim, S.; Kang, T.H.K.; Jung, D.; LaFave, J.M. Seismic behavior of precast and post-tensioned exterior connections with ductile headed rods. ACI Struct. J. 2021, 118, 87–100. [Google Scholar] [CrossRef]
- Yang, C.; Xie, L.; Li, A.; Wang, X. A Dry-Connected Rotational Friction Dissipative Beam-to-Column Joint for Precast Concrete Frame: Full-Scale Experimental and Numerical Investigations. J. Build. Eng. 2022, 54, 104685. [Google Scholar] [CrossRef]
- Yam, M.C.H.; Ke, K.; Huang, Y.; Zhou, X.; Liu, Y. A Study of Hybrid Self-Centring Beam-to-Beam Connections Equipped with Shape-Memory-Alloy-Plates and Washers. J. Constr. Steel Res. 2022, 198, 107526. [Google Scholar] [CrossRef]
- Zhu, L.; Ning, Q.; Han, W.; Zhao, C. Seismic Performance of Self-Centering Concrete-Filled Square Steel Tubular Column-to-Steel Beam Connection Equipped with SMA Bolts. Thin-Walled Struct. 2023, 183, 110351. [Google Scholar] [CrossRef]
- Li, Z.; Qi, Y.; Teng, J. Experimental Investigation of Prefabricated Beam-to-Column Steel Joints for Precast Concrete Structures under Cyclic Loading. Eng. Struct. 2020, 209, 110217. [Google Scholar] [CrossRef]
- Huang, W.; Hu, G.; Zhang, J. Experimental Study on the Seismic Performance of New Precast Concrete Beam-Column Joints with Replaceable Connection. Structures 2022, 35, 856–872. [Google Scholar] [CrossRef]
- Bai, J.; He, J.; Li, C.; Jin, S.; Yang, H. An RBS-Based Replaceable Precast Concrete Beam-Column Joint: Design Approach and Experimental Investigation. J. Build. Eng. 2022, 51, 104212. [Google Scholar] [CrossRef]
- Dai, K.; Sun, T.; Liu, Y.; Li, T.; Camara, A. Concept and Numerical Analysis of a Double-Stage Coupling Damper for Multilevel Seismic Protection. Thin-Walled Struct. 2023, 185, 110581. [Google Scholar] [CrossRef]
- Lu, Y.; Lv, Q.; Sun, T.; Liu, Y.; Tang, H. Experimental and Numerical Studies on Hysteretic Behavior of a Novel Bending-Friction Coupled Damper. Thin-Walled Struct. 2023, 183, 110385. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, W.; Zhang, M.; Li, Y. A Novel Energy Dissipation Damper for Multi-Level Earthquakes. J. Constr. Steel Res. 2022, 192, 107214. [Google Scholar] [CrossRef]
- Wang, J.; Men, J.; Zhang, Q.; Fan, D.; Zhang, Z.; Huang, C.-H. Seismic Performance Evaluation of a Novel Shape-Optimized Composite Metallic Yielding Damper. Eng. Struct. 2022, 268, 114714. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Li, W.; Xue, Y. Development of a Buckling Restrained Shear Panel Damper. J. Constr. Steel Res. 2015, 106, 311–321. [Google Scholar] [CrossRef]
- Lin, X.; Wu, K.; Skalomenos, K.A.; Lu, L.; Zhao, S. Development of a Buckling-Restrained Shear Panel Damper with Demountable Steel-Concrete Composite Restrainers. Soil Dyn. Earthq. Eng. 2019, 118, 221–230. [Google Scholar] [CrossRef]
- Li, F.; Du, Y.; Hong, N.; Li, H.; Chi, P. Seismic Performance of Prefabricated Replaceable Graded-Yielding Energy-Dissipating Connectors. Eng. Struct. 2023, 297, 116962. [Google Scholar] [CrossRef]
- Marriott, D.; Pampanin, S.; Palermo, A. Quasi-static and Pseudo-dynamic Testing of Unbonded Post-tensioned Rocking Bridge Piers with External Replaceable Dissipaters. Earthq. Eng. Struct. Dyn. 2009, 38, 331–354. [Google Scholar] [CrossRef]
- Pampanin, S. Reality-Check and Renewed Challenges in Earthquake Engineering: Implementing Low-Damage Systems–from Theory to Practice. Bull. New Zealand Soc. Earthq. Eng. 2012, 45, 137–160. [Google Scholar] [CrossRef]
- Sarti, F.; Palermo, A.; Pampanin, S. Quasi-Static Cyclic Testing of Two-Thirds Scale Unbonded Posttensioned Rocking Dissipative Timber Walls. J. Struct. Eng. 2016, 142, E4015005. [Google Scholar] [CrossRef]
- Wang, H.; Marino, E.M.; Pan, P. Design, Testing and Finite Element Analysis of an Improved Precast Prestressed Beam-to-Column Joint. Eng. Struct. 2019, 199, 109661. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Zhang, J.; Tong, C. Experimental Study on Seismic Performance of Precast Concrete Frame with Replaceable Energy-Dissipating Connectors. Eng. Struct. 2021, 231, 111719. [Google Scholar] [CrossRef]
- Qu, X.S.; Fu, X.; Sun, Y.B.; Liu, B. Study of hysteretic behavior of mild steel dissipaters under cyclic tension loading. Earthq. Resist. Eng. Retrofit. 2021, 43, 109–117. (In Chinese) [Google Scholar] [CrossRef]
- ACI Innovation Task Group 5. Acceptance Criteria for Special Unbonded Post-Tensioned Precast Structural Walls Based on Validation Testing and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- Yan, X.; Reiner, J.; Bacca, M.; Altintas, Y.; Vaziri, R. A Study of Energy Dissipating Mechanisms in Orthogonal Cutting of UD-CFRP Composites. Compos. Struct. 2019, 220, 460–472. [Google Scholar] [CrossRef]
- Kaddour, A.S.; Hinton, M.J.; Smith, P.A.; Li, S. Mechanical Properties and Details of Composite Laminates for the Test Cases Used in the Third World-Wide Failure Exercise. J. Compos. Mater. 2013, 47, 2427–2442. [Google Scholar] [CrossRef]
- Naik, N.K.; Shankar, P.J.; Kavala, V.R.; Ravikumar, G.; Pothnis, J.R.; Arya, H. High Strain Rate Mechanical Behavior of Epoxy under Compressive Loading: Experimental and Modeling Studies. Mater. Sci. Eng. A 2011, 528, 846–854. [Google Scholar] [CrossRef]
- Fiedler, B.; Hobbiebrunken, T.; Hojo, M.; Schulte, K. Influence of Stress State and Temperature on the Strength of Epoxy Resins. In Proceedings of the 11th International Conference on Fracture 2005, ICF11, Turin, Italy, 20–25 March 2005; Volume 3, pp. 2271–2275. [Google Scholar]
- Chen, J.; Ma, Y.W.; Yoon, K.B. Finite Element Study for Determination of Material’s Creep Parameters from Small Punch Test. J. Mech. Sci. Technol. 2010, 24, 1195–1201. [Google Scholar] [CrossRef]



| Filler Material | Elastic Modulus (GPa) | Shear Strength (MPa) | Tensile Strength (MPa) |
|---|---|---|---|
| E-44 epoxy resin | 3.3 | 12 | 80 |
| Type of Internal Steel Bar | Specimen Number | Elastic Modulus E (GPa) | Yield Strength fy (MPa) | Ultimate Tensile Strength fu (MPa) | Elongation δ (%) |
|---|---|---|---|---|---|
| Q345B | 1 | 177 | 399.68 | 577.82 | 20.44 |
| 2 | 183 | 402.48 | 573.54 | ||
| 3 | 194 | 390.67 | 549.69 | ||
| 30# | 4 | 170 | 379.80 | 589.70 | 20.00 |
| 5 | 174 | 403.57 | 601.04 | ||
| 6 | 197 | 391.58 | 588.72 |
| Specimen Number | Loading Direction | Yield-Displacement Point | Peak-Load Point | Failure-Displacement Point | Ductility Coefficient μ | |||
|---|---|---|---|---|---|---|---|---|
| Δy/mm | Py/kN | Δm/mm | Fm/kN | Δu/mm | Fu/kN | |||
| D14L210-Q345B | + (tension) | 2.20 | 77.75 | 5.20 | 100.30 | 8.70 | 87.60 | 3.95 |
| − (compression) | −2.91 | −174.44 | −6.40 | −209.50 | −8.38 | −178.08 | 2.88 | |
| D16L200-Q345B | + | 3.05 | 92.03 | 7.10 | 115.70 | 8.00 | 114.30 | 2.62 |
| − | −4.25 | −160.60 | −6.95 | −190.60 | −6.95 | −190.60 | 1.64 | |
| D16L240-Q345B | + | 1.70 | 82.67 | 8.35 | 100.30 | 9.45 | 94.40 | 5.56 |
| − | −3.30 | −108.32 | −7.20 | −134.00 | −8.44 | −113.90 | 2.56 | |
| D16L280-Q345B | + | 2.30 | 95.27 | 8.37 | 112.20 | 12.50 | 108.30 | 5.43 |
| − | −2.80 | −172.79 | −5.70 | −206.00 | −6.60 | −175.10 | 2.36 | |
| D18L270-Q345B | + | 3.11 | 122.27 | 8.10 | 143.80 | 10.80 | 140.70 | 3.47 |
| − | −2.58 | −182.34 | −4.74 | −212.70 | −6.02 | −180.80 | 2.33 | |
| D20L300-Q345B | + | 2.49 | 141.20 | 8.94 | 171.90 | 11.88 | 169.50 | 4.77 |
| − | −3.10 | −224.09 | −4.80 | −240.90 | −6.90 | −204.77 | 2.23 | |
| D22L275-Q345B | + | 3.00 | 158.47 | 6.68 | 199.00 | 10.90 | 194.00 | 3.63 |
| − | −2.69 | −238.19 | −4.12 | −267.80 | −6.45 | −227.63 | 2.40 | |
| D22L330-Q345B | + | 2.20 | 184.86 | 1.60 | 199.00 | 2.94 | 169.15 | 1.34 |
| − | −2.49 | −235.18 | −3.66 | −274.00 | −5.45 | −232.90 | 2.19 | |
| D22L385-Q345B | + | 2.52 | 175.39 | 9.70 | 188.30 | 15.40 | 186.50 | 6.11 |
| − | −2.71 | −220.66 | −3.90 | −257.00 | −4.60 | −218.45 | 1.70 | |
| D24L360-Q345B | + | 2.98 | 207.75 | 10.90 | 227.10 | 14.30 | 210.60 | 4.80 |
| − | −4.60 | −215.60 | −7.26 | −218.90 | −8.41 | −186.07 | 1.83 | |
| D26L390-Q345B | + | 2.69 | 225.83 | 11.63 | 245.20 | 15.60 | 236.70 | 5.80 |
| − | −3.00 | −315.20 | −1.75 | −327.00 | −4.43 | −277.95 | 1.48 | |
| D28L350-Q345B | + | 2.20 | 262.50 | 7.05 | 281.90 | 14.20 | 266.70 | 6.45 |
| − | −2.70 | −323.26 | −4.30 | −370.20 | −5.93 | −314.67 | 2.20 | |
| D28L420-Q345B | + | 2.25 | 246.96 | 10.60 | 268.70 | 16.80 | 262.20 | 7.47 |
| − | −2.89 | −303.19 | −4.00 | −346.00 | −4.66 | −294.10 | 1.61 | |
| D28L490-Q345B | + | 1.80 | 257.97 | 9.70 | 265.10 | 19.70 | 256.00 | 10.94 |
| − | −2.25 | −328.74 | −3.20 | −351.30 | −5.16 | −298.61 | 2.29 | |
| D30L450-Q345B | + | 2.72 | 276.77 | 11.20 | 297.60 | 17.96 | 279.90 | 6.60 |
| − | −2.59 | −363.34 | −4.30 | −396.00 | −5.18 | −336.60 | 2.00 | |
| D14L210-30 | + | 1.29 | 77.43 | 2.11 | 87.30 | 7.08 | 80.10 | 5.49 |
| − | −5.26 | −92.49 | −7.48 | −110.23 | −7.48 | −110.23 | 1.42 | |
| D16L200-30 | + | 4.89 | 129.85 | 6.90 | 139.50 | 14.99 | 118.58 | 3.07 |
| − | −8.90 | −162.32 | −14.43 | −184.30 | −14.43 | −184.30 | 1.62 | |
| D16L240-30 | + | 2.43 | 107.08 | 1.40 | 111.50 | 9.70 | 111.10 | 3.99 |
| − | −1.95 | −124.02 | −4.90 | −142.10 | −7.18 | −120.79 | 3.68 | |
| D16L280-30 | + | 5.31 | 96.97 | 10.60 | 124.20 | 22.66 | 124.20 | 4.27 |
| − | −3.70 | −165.67 | −5.60 | −192.60 | −8.38 | −163.71 | 2.26 | |
| D18L270-30 | + | 4.48 | 127.45 | 21.30 | 147.80 | 21.30 | 147.80 | 4.75 |
| − | −2.07 | −158.39 | −3.90 | −184.80 | −7.26 | −157.08 | 3.51 | |
| D20L300-30 | + | 1.79 | 183.52 | 2.54 | 200.00 | 3.83 | 170.00 | 2.14 |
| − | −1.80 | −203.07 | −4.50 | −236.70 | −6.13 | −201.20 | 3.41 | |
| D22L275-30 | + | 1.70 | 196.00 | 7.20 | 206.00 | 9.67 | 206.00 | 5.69 |
| − | −2.45 | −226.45 | −4.33 | −257.00 | −6.06 | −218.45 | 2.47 | |
| D22L330-30 | + | 2.40 | 174.53 | 9.90 | 194.80 | 9.90 | 194.80 | 4.13 |
| − | −1.78 | −236.33 | −2.33 | −253.70 | −4.36 | −215.65 | 2.45 | |
| D22L385-30 | + | 1.68 | 191.52 | 2.70 | 197.00 | 13.50 | 197.00 | 8.04 |
| − | −1.78 | −236.71 | −2.80 | −266.00 | −3.57 | −226.10 | 2.01 | |
| D24L360-30 | + | 2.37 | 211.97 | 4.70 | 241.80 | 14.40 | 211.20 | 6.08 |
| − | −3.39 | −254.17 | −5.30 | −298.00 | −6.06 | −253.30 | 1.79 | |
| D26L390-30 | + | 3.00 | 213.49 | 13.60 | 242.40 | 15.56 | 241.30 | 5.19 |
| − | −2.50 | −276.19 | −3.50 | −313.00 | −6.01 | −266.05 | 1.73 | |
| D28L350-30 | + | 3.05 | 234.66 | 8.80 | 278.50 | 13.90 | 272.60 | 4.56 |
| − | −2.85 | −297.00 | −3.60 | −341.60 | −4.86 | −290.36 | 1.74 | |
| D28L420-30 | + | 2.72 | 247.77 | 10.60 | 264.00 | 14.80 | 262.00 | 5.44 |
| − | −2.30 | −344.00 | −2.30 | −344.00 | −3.29 | −292.40 | 1.43 | |
| D28L490-30 | + | 3.28 | 241.55 | 17.00 | 270.00 | 19.60 | 251.80 | 5.98 |
| − | −2.38 | −342.80 | −2.38 | −342.80 | −4.15 | −291.38 | 1.71 | |
| D30L450-30 | + | 2.33 | 285.80 | 13.40 | 292.10 | 15.80 | 293.40 | 6.78 |
| − | −2.35 | −350.39 | −3.00 | −373.70 | −4.07 | −317.65 | 2.40 | |
| Dex (mm) | Dex/Dfuse | λfuse |
|---|---|---|
| ≤18 | ≤1.25 | 60~80 |
| ≥20 | ≤1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, X.; Yang, J.; Liu, H.; Sun, K. Research on the Mechanical Behavior of External Composite Steel Bar Under Cyclic Tension-Compression Loading. Buildings 2025, 15, 2019. https://doi.org/10.3390/buildings15122019
Qu X, Yang J, Liu H, Sun K. Research on the Mechanical Behavior of External Composite Steel Bar Under Cyclic Tension-Compression Loading. Buildings. 2025; 15(12):2019. https://doi.org/10.3390/buildings15122019
Chicago/Turabian StyleQu, Xiushu, Jialong Yang, Hongmeng Liu, and Kexin Sun. 2025. "Research on the Mechanical Behavior of External Composite Steel Bar Under Cyclic Tension-Compression Loading" Buildings 15, no. 12: 2019. https://doi.org/10.3390/buildings15122019
APA StyleQu, X., Yang, J., Liu, H., & Sun, K. (2025). Research on the Mechanical Behavior of External Composite Steel Bar Under Cyclic Tension-Compression Loading. Buildings, 15(12), 2019. https://doi.org/10.3390/buildings15122019






