Seismic Performance Research of Self-Centering Single-Column Bridges Using Equivalent Stiffness Theory
Abstract
1. Introduction
2. Theory of Equivalent Elastic Stiffness for SHR-SCSAB
2.1. Finite Strip Method
2.2. A Comprehensive Theoretical Framework for Sectional Collapse Analysis
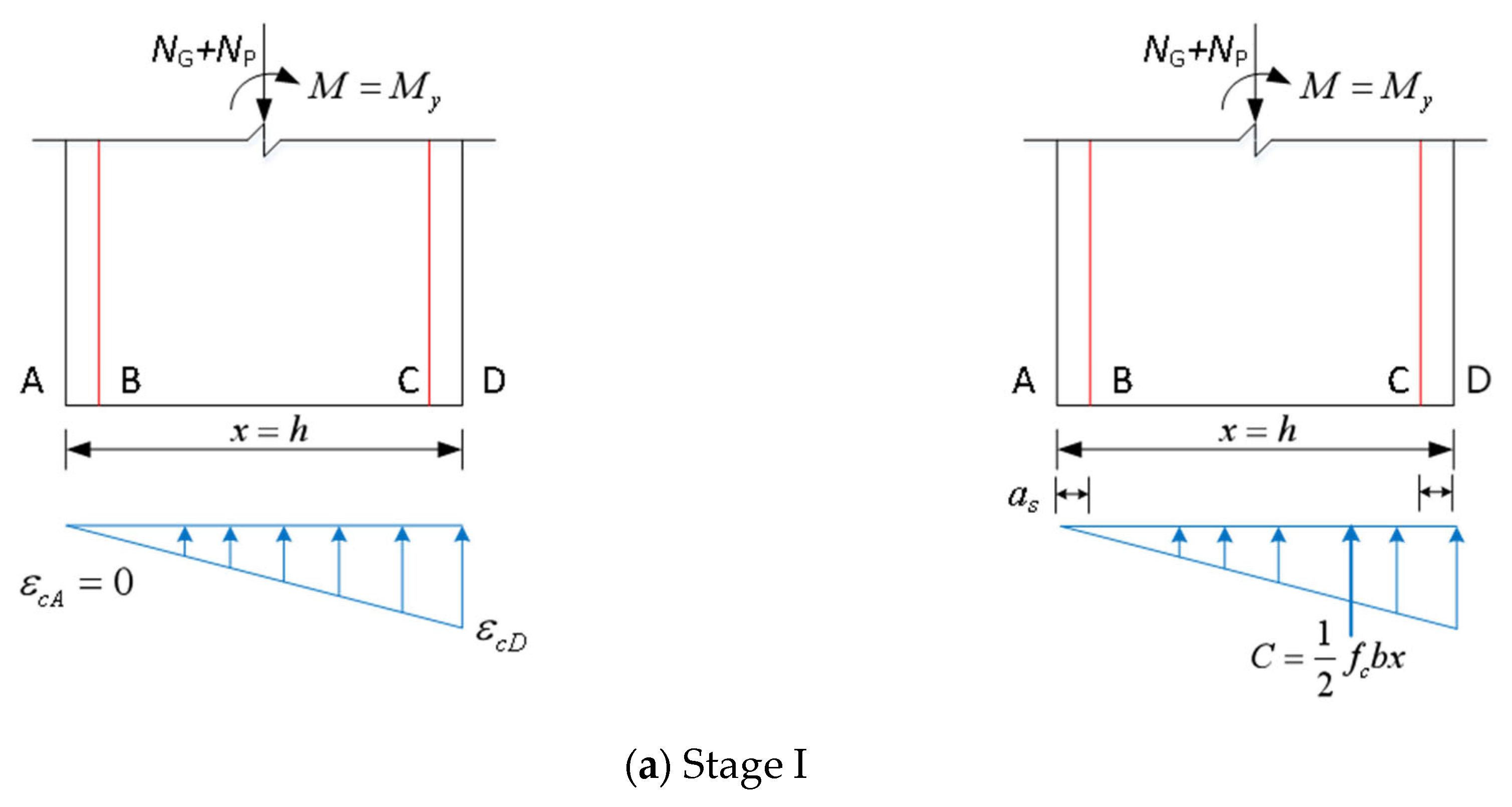
2.2.1. Stage I: Full Cross-Section Compression Stage, Increase in Bending Moment from Zero to Dissipating Bending Moment
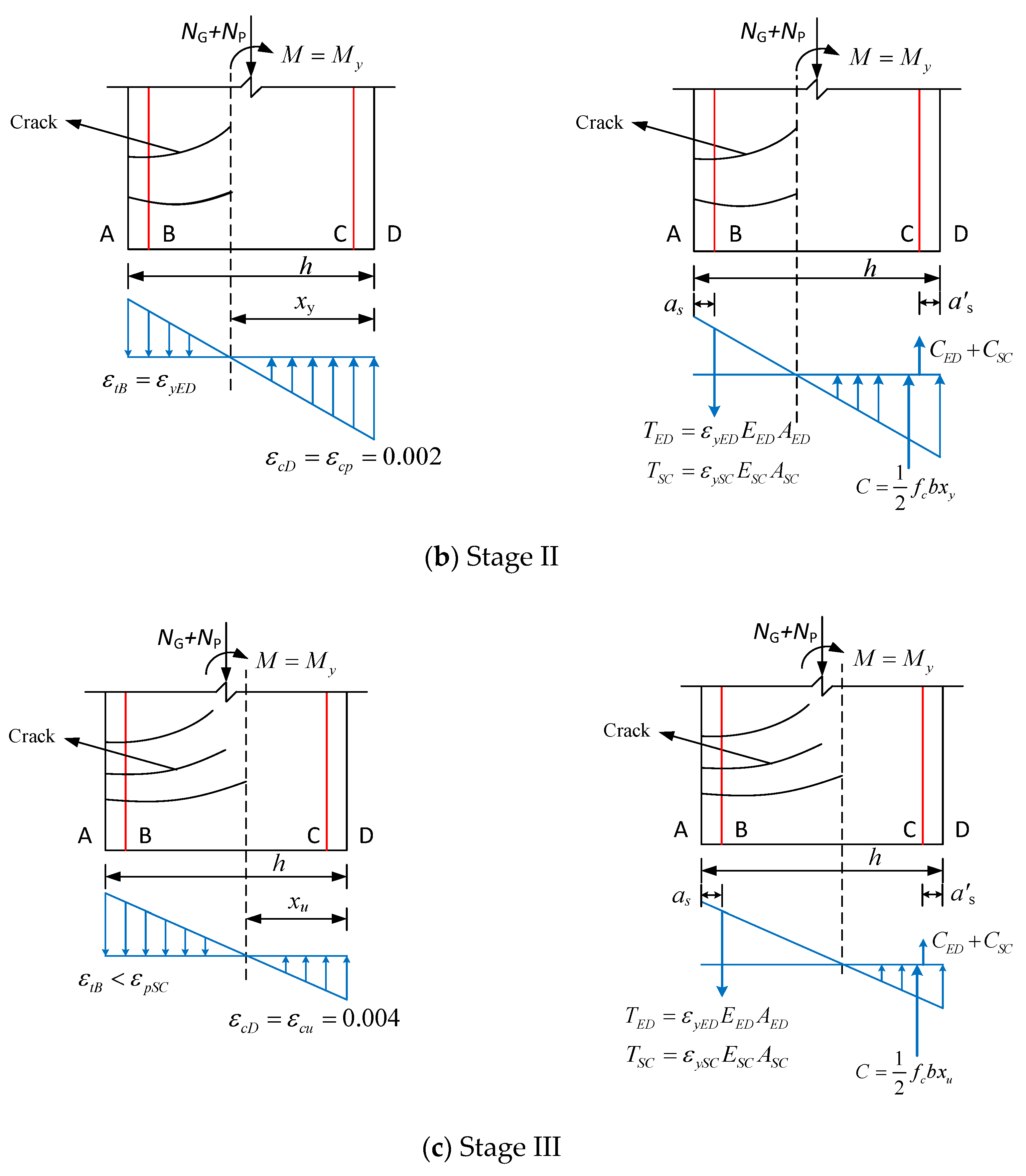
2.2.2. Stage II: The Bending Moment Continues to Increase Until the Energy-Consuming Reinforcement Enters the Yield State
2.2.3. Stage III: The Bending Moment Continues to Increase Until the Section Breaks
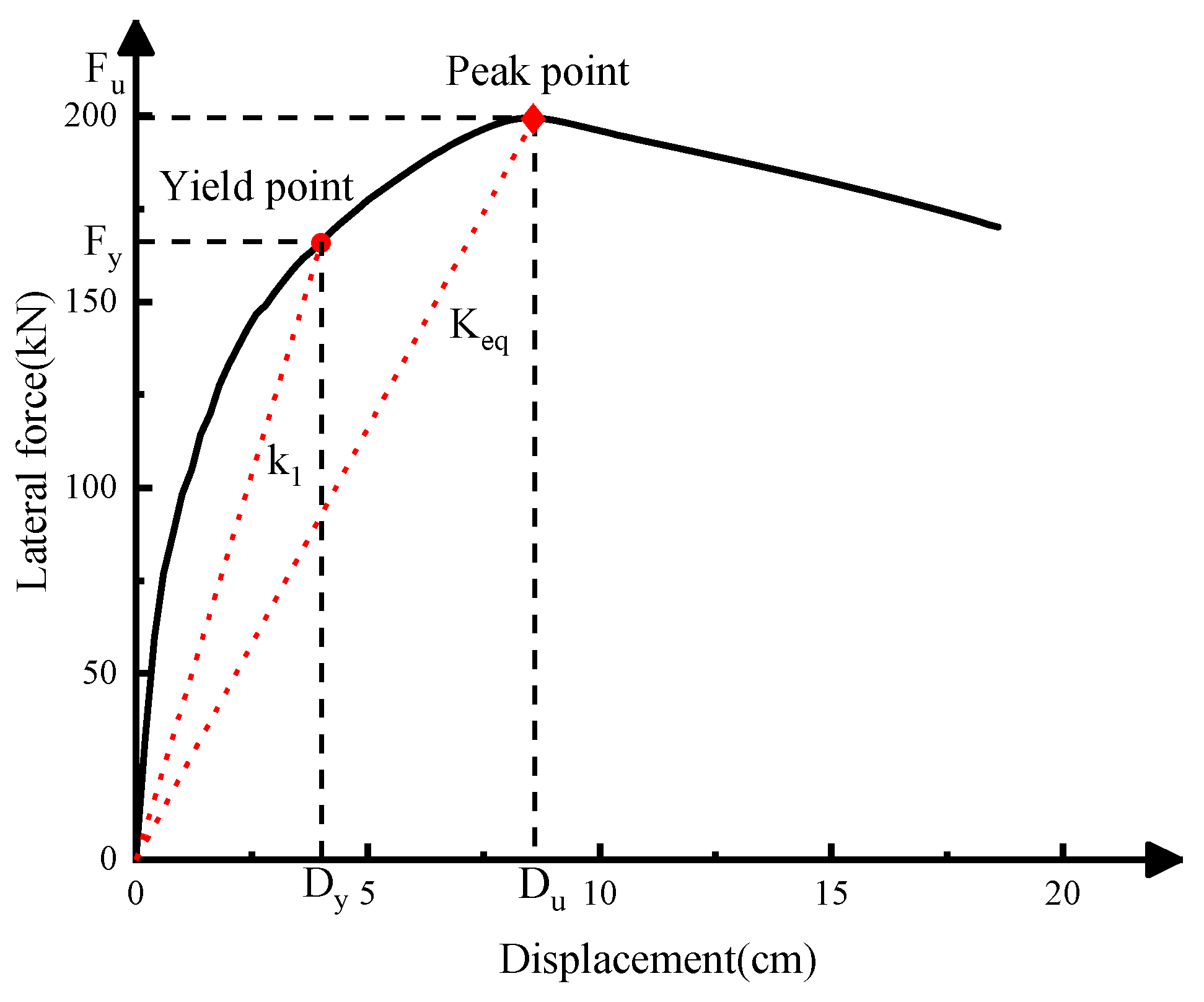
2.3. Equivalent Elastic Stiffness Derivation
3. Analytical Models for Hybrid Systems
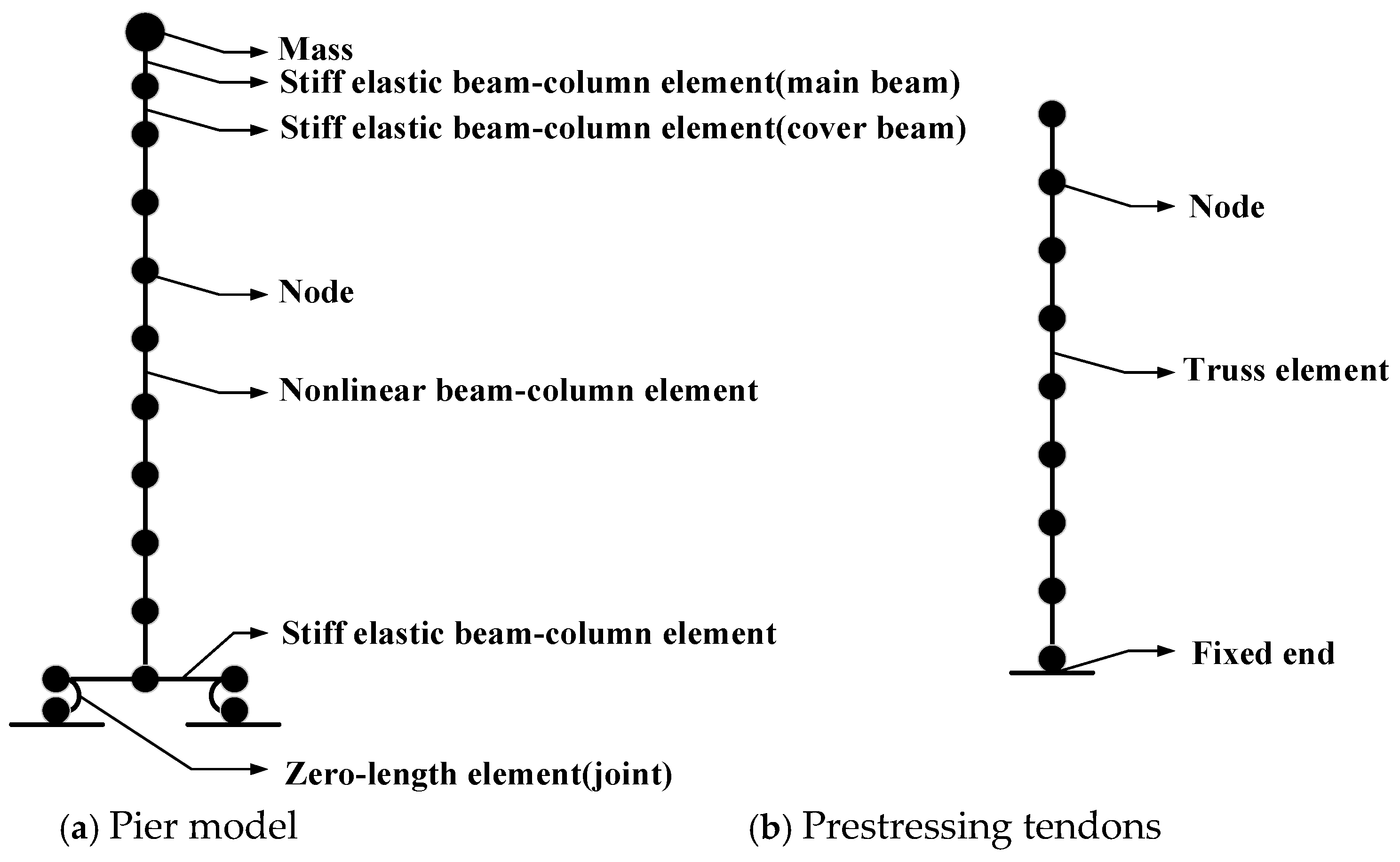
3.1. Finite Element Modelling
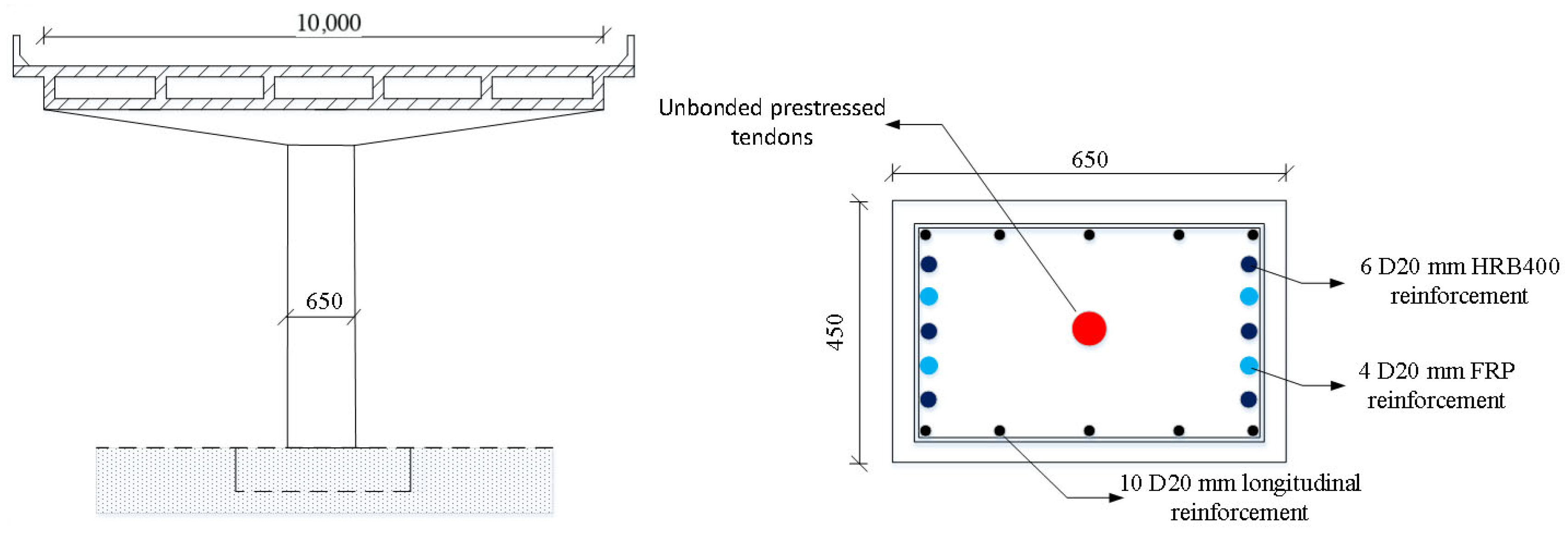
3.2. Description of Bridge
4. Numerical Modelling
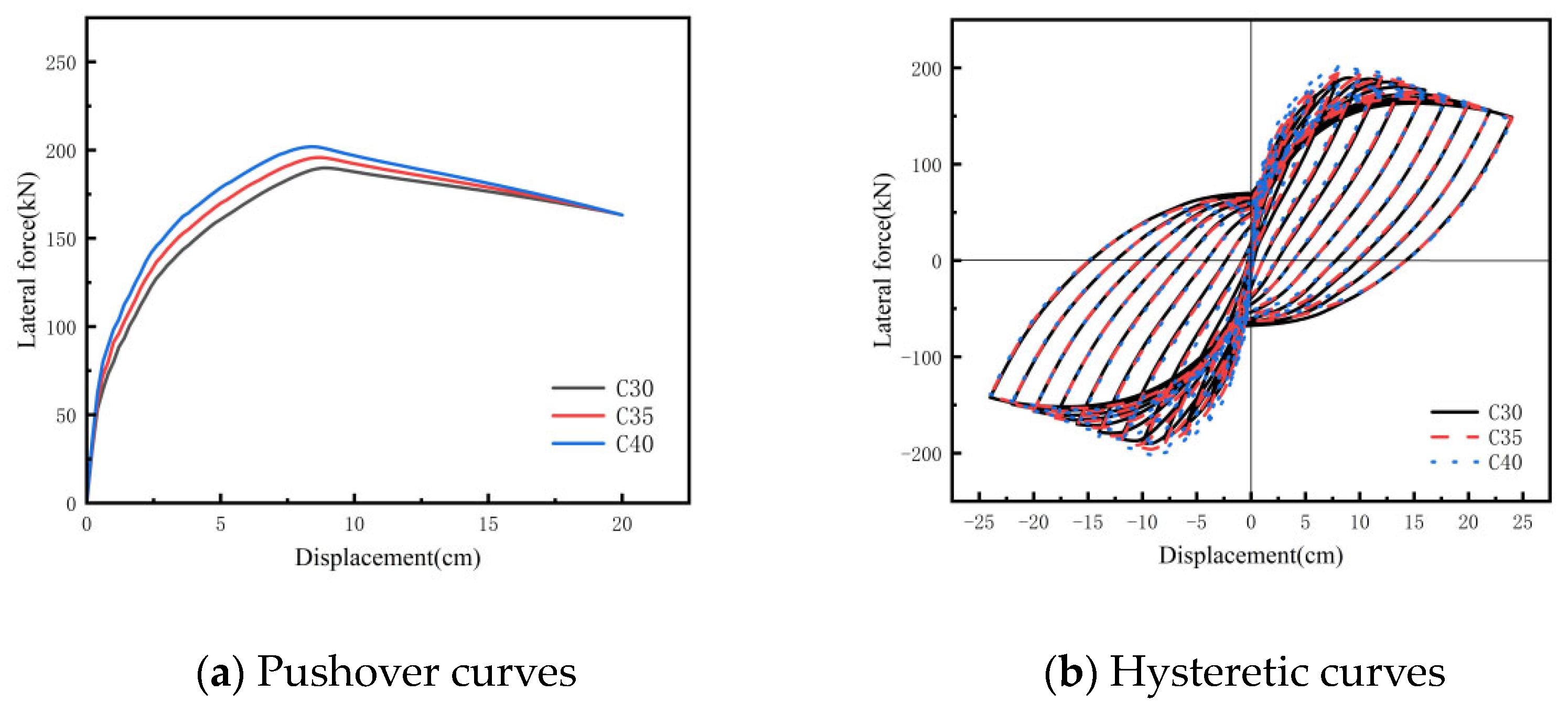
4.1. Pushover Analysis
4.2. Hysteretic Response Analysis
4.3. Concrete Material Deterioration Effects
5. Summary
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.; Wu, J.; Zhang, J.; Xie, L.; Wei, Y.; Tong, C. Experimental and theoretical investigations of post-tensioned precast reinforced concrete bridge pier with external replaceable energy dissipaters. Eng. Struct. 2023, 294, 116719. [Google Scholar] [CrossRef]
- Yang, M.; Deng, S.; Dong, Z. Study on Anchoring Characteristics and Freeze–Thaw Degradation Law of the Cement-Based Early-Strength Anchor in Freeze–Thaw Regions. Sustainability 2023, 15, 7773. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, G.; Qi, Z.; Li, P.; Ren, H. Stress analysis of segmental assembly structures for large-tonnage steel truss flexible arch bridges. J. Water Conserv. Archit. Eng. 2024, 22, 134–139. [Google Scholar]
- Bu, Z.-Y.; Ou, Y.-C.; Song, J.-W. Cyclic loading test of unbonded and bonded posttensioned precast segmental bridge columns with circular section. J. Bridge Eng. 2016, 21, 04015043. [Google Scholar] [CrossRef]
- Priestley, M.J.N. Myths and Fallacies in Earthquake Engineering—Conflicts Between Design and Reality. Bull. N. Z. Soc. Earthq. Eng. 1993, 26, 329–341. [Google Scholar]
- Priestley, M.J.N.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridges; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Priestley, M.J.N.; Seible, F.; Calvi, G.M. Seismic Design Principles for Bridge Retrofitting. Struct. Eng. Int. 1996, 3, 12–20. [Google Scholar]
- Kowalsky, M.J.; Priestley, M.J.N.; MacRae, G.A. Displacement-Based Design of RC Bridge Columns in Seismic Regions. Earthq. Eng. Struct. Dyn. 2000, 29, 583–607. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M.J. Displacement-Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007. [Google Scholar]
- Hewes, J.T. Seismic Design and Performance of Precast Concrete Segmental Bridge Columns. Ph.D. Thesis, University of California, San Diego, CA, USA, 2002. [Google Scholar]
- Xiong, E.; Zhang, J.; Shang, D.; Feng, A.; Mei, Z. Seismic performance of precast segmental double-column bridge piers. J. Cent. South Univ. (Nat. Sci. Ed.) 2023, 54, 3609–3620. [Google Scholar]
- Xiong, E.; Gong, Z.; Yu, S.; Shi, Q. Seismic Performance and Deformation Analysis of Plastic Hinge Zones of a New Type of Precast Segmental Assembled Bridge Piers. China Civ. Eng. J. 2024, 57, 68–83. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, H.; Wen, J.; Li, C.; Gao, X.; Zhao, X.; Teng, Q. Analysis of the prefabricated scheme and seismic performance of thin-walled wall pier structures. J. Southeast Univ. (Nat. Sci. Ed.) 2024, 54, 911–920. [Google Scholar]
- Liu, Z.; Tang, J.; Zhang, W.; Chen, X.; Ma, H. The Hysteresis Characteristics of Steel Tube-Embedded Replaceable Rubber Through-Rotors and Their Application in Self-Resetting Bridges. J. Jilin Univ. (Eng. Ed.) 2024, 1–10. [Google Scholar] [CrossRef]
- Sezgin, S.K.; Ahmadi, E.; Kashani, M.M. Seismic performance of resilient self-centring bridge piers equipped with SMA bars. Proc. Inst. Civ. Eng. Bridge Eng. 2025, 178, 248–261. [Google Scholar] [CrossRef]
- Chen, M.; Jia, J.; Cheng, S.; Zhou, S.; Pang, W. Seismic Performance of Precast Segmental Pier Columns with Stainless Steel and FRP Reinforcements. J. Build. Struct. 2023, 44, 368–379. [Google Scholar]
- Gao, H.; Lu, H. Seismic Performance Study of Hybrid Reinforced Precast Segmental Bridge Piers. Sichuan Cem. 2023, 3, 38–41. [Google Scholar]
- Cai, Z.K.; Yuan, W.; Wang, Z.; Smith, S.T. Seismic behavior of precast segmental bridge columns reinforced with hybrid FRP-steel bars. Eng. Struct. 2021, 228, 111484. [Google Scholar] [CrossRef]
- Tan, X.; Yin, C.; Wang, C.; Wang, X.; Chen, B.; Wu, X.; Liu, R. Experimental study on influence of external steel plate strength on seismic performance of segmental assembled CFST bridge piers. J. Earthq. Eng. 2025, 2, 300–308. [Google Scholar] [CrossRef]
- Motaref, S.; Saiidi, M.S. Multi-spring modeling for segmental columns. Earthq. Eng. Struct. Dyn. 2023, 52, 189–211. [Google Scholar] [CrossRef]
- Gao, H.; Song, Y.; Yuan, W.; Lu, H.; Cao, S. Seismic Design Method of Self-Centring-Segment Bridge Piers with Tensile-Type Viscoelastic Dampers; Hindawi Limited: London, UK, 2021. [Google Scholar] [CrossRef]
- Gao, H.; Xia, W.; Liu, G. Analysis of Seismic Performance for Segmentally Assembled Double-Column Bridge Structures Based on Equivalent Stiffness. Buildings 2025, 15, 1919. [Google Scholar] [CrossRef]
- JTG/T B02-1-2010; Industry Standard of the People’s Republic of China. Seismic Design Details for Highway Bridges. People’s Communications Press: Beijing, China, 2008.
- Xue, G.; Guo, X. Nonlinear full-process analysis of bending stiffness of reinforced concrete beams. J. Inn. Mong. Univ. Sci. Technol. 2007, 3, 250–252. [Google Scholar]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-Strain Behaviour of Concrete Confined by Overlapping Hoops at Low and High Strain Rates. Aci Struct. J. 1982, 79, 13–27. [Google Scholar]
- Tavassoli, A.; Liu, J.; Sheikh, S. Glass fiber-reinforced polymer-reinforced circular columns under simulated seismic loads. ACI Struct. J. 2015, 112, 103. [Google Scholar] [CrossRef]
- Deitz, D.H.; Harik, I.E.; Gesund, H. Physical properties of glass fiber reinforced polymer rebars in compression. J. Compos. Constr. 2003, 7, 363–366. [Google Scholar] [CrossRef]
- Gong, Y. Study on the Compressive and Seismic Performance of High-Performance CFRP-Strengthened Concrete Columns. Ph.D. Thesis, Southeast University: Nanjing, China, 2007. [Google Scholar]
- Cai, Z. Seismic Performance and Design Methods of Hybrid Reinforced Prefabricated Segmental Bridge Piers. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Spacone, E.; Filippou, F.C.; Taucer, F.F. Fibre beam–column model for non-linear analysis of R/C frames: Part I. Formulation. Earthq. Eng. Struct. Dyn. 1996, 25, 711–725. [Google Scholar] [CrossRef]
- Saenz, L.P. discussion of “Equation for the Stress-Strain Curve of Concrete” by Desayi and Krishnan. J. Am. Concr. Inst. 1964, 61, 1229–1235. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- Kawashima, K.; Nagaya, K.; Hoshikuma, J.-I.; MacRae, G.A. Residual Displacement Response Spectrum. J. Struct. Eng. 1998, 124, 523–530. [Google Scholar] [CrossRef]







| Concrete | Posttensioned Tendon | Energy-Consuming Reinforcement | FRP Reinforcement | Stirrup | |||||
|---|---|---|---|---|---|---|---|---|---|
| Compressing strength | Elastic modulus | Yield strength | Ultimate strength | Elastic modulus | Yield strength | Elastic modulus | Ultimate strength | Elastic modulus | Yield strength |
| 40.0 | 32.5 | 1670 | 1860 | 195 | 400 | 200 | 2100 | 140 | 286 |
| Bridge Pier Stiffness | Simulated Value (kN/m) | Analytical Solution (kN/m) | Discrepancy (%) |
|---|---|---|---|
| 4054 | 4155 | 2.43 | |
| 2420 | 2321 | 4.09 |
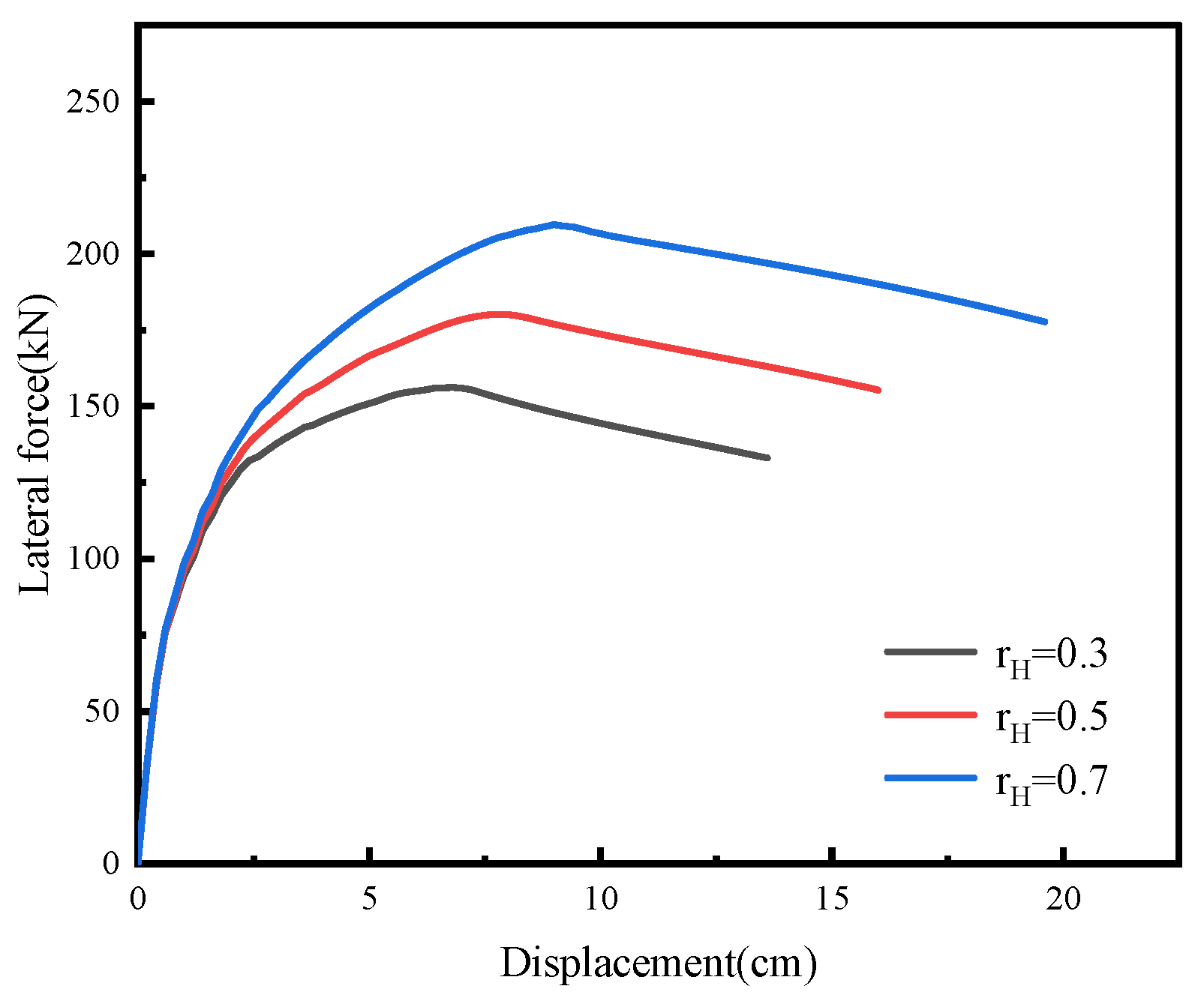
| Hybrid Ratio | Yield Displacement (cm) | Yield Force (kN) | Peak Displacement (cm) | Peak Force (kN) | Ultimate Displacement (cm) | Yield Stiffness (kN/m) | Equivalent Elastic Stiffness (kN/m) | Ductility Factor |
|---|---|---|---|---|---|---|---|---|
| 0.3 | 2.4 | 132 | 6.8 | 156 | 13.6 | 5500 | 2294 | 5.67 |
| 0.5 | 3.2 | 149 | 7.8 | 180 | 16.0 | 4656 | 2307 | 5.00 |
| 0.7 | 4.0 | 170 | 9.0 | 210 | 19.6 | 4250 | 2333 | 4.90 |
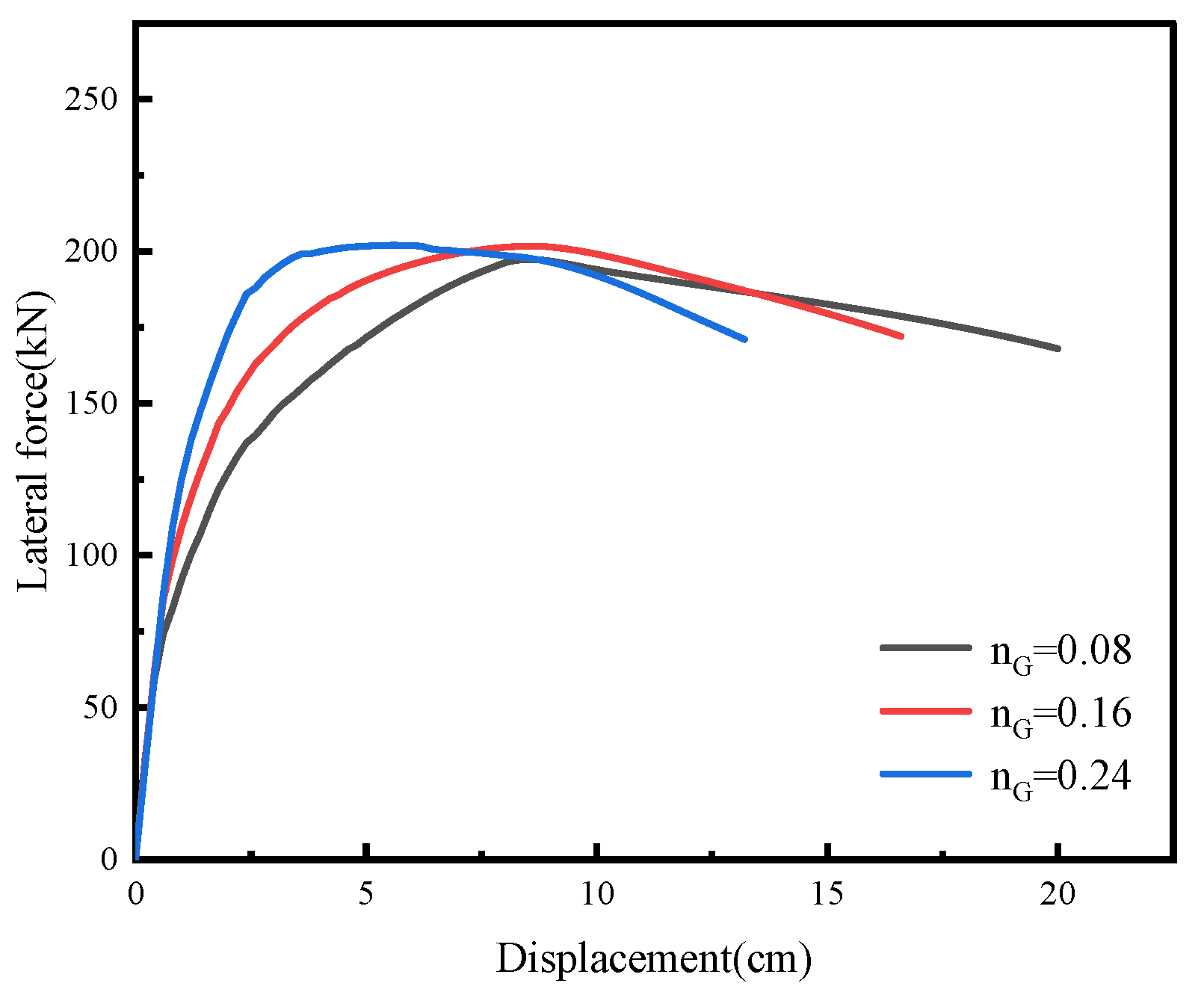
| Axial Pressure Ratio | Yield Displacement (cm) | Yield Force (kN) | Peak Displacement (cm) | Peak Force (kN) | Ultimate Displacement (cm) | Yield Stiffness (kN/m) | Equivalent Elastic Stiffness (kN/m) | Ductility Factor |
|---|---|---|---|---|---|---|---|---|
| 0.08 | 3.5 | 160 | 8.6 | 197 | 20.0 | 4571 | 2295 | 5.70 |
| 0.16 | 3.0 | 169 | 8.4 | 201 | 16.6 | 5633 | 2401 | 5.53 |
| 0.24 | 2.5 | 173 | 5.6 | 202 | 13.2 | 6920 | 3606 | 5.28 |
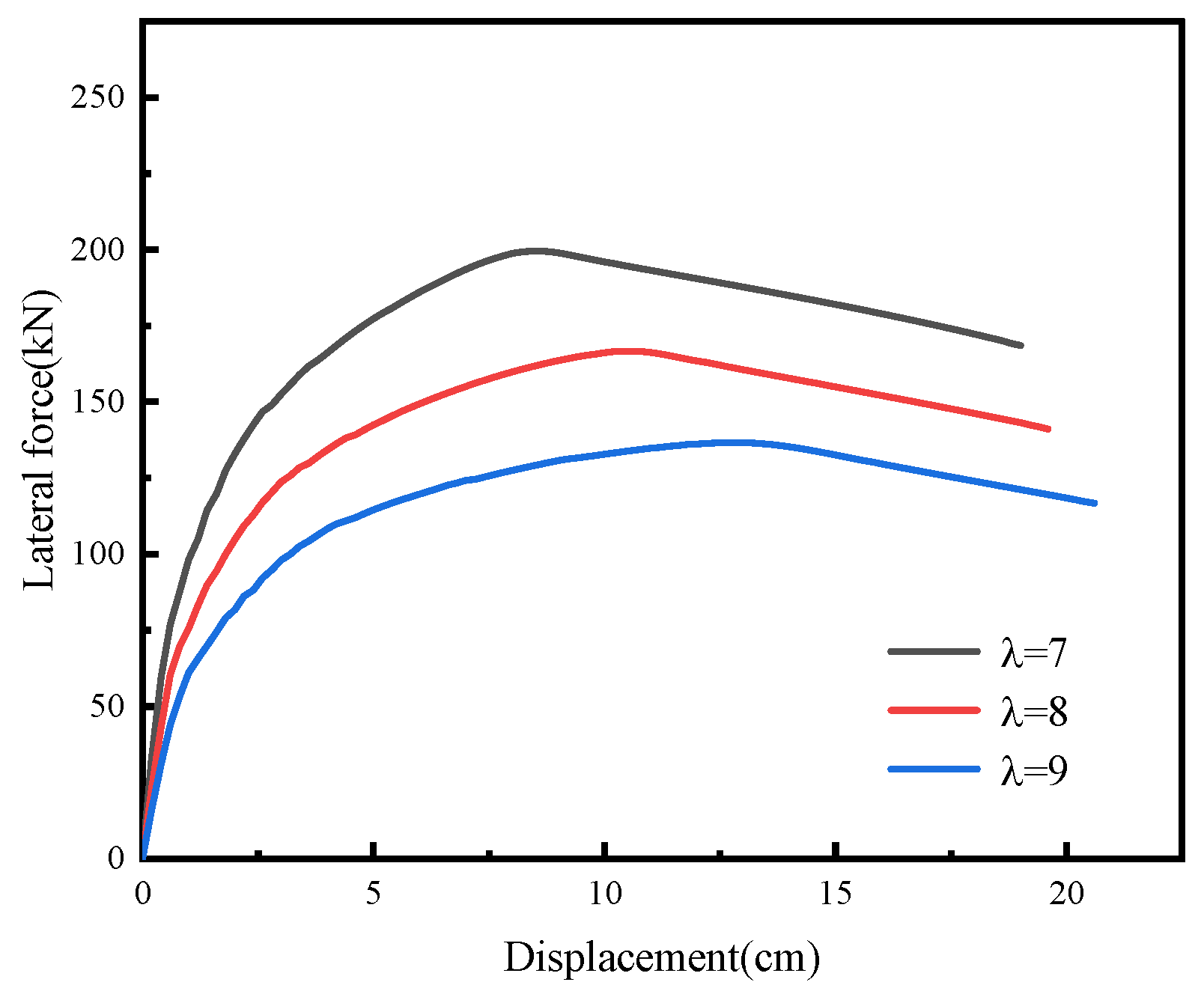
| Shear-to-Span Ratio | Yield Displacement (cm) | Yield Force (kN) | Peak Displacement (cm) | Peak Force (kN) | Ultimate Displacement (cm) | Yield Stiffness (kN/m) | Equivalent Elastic Stiffness (kN/m) | Ductility Factor |
|---|---|---|---|---|---|---|---|---|
| 7 | 3.8 | 164 | 8.6 | 200 | 19.0 | 4316 | 2320 | 5.00 |
| 8 | 4.4 | 138 | 10.6 | 167 | 19.6 | 3136 | 1572 | 4.45 |
| 9 | 4.9 | 114 | 12.8 | 137 | 20.6 | 2327 | 1067 | 4.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Xia, W.; Lu, H. Seismic Performance Research of Self-Centering Single-Column Bridges Using Equivalent Stiffness Theory. Buildings 2025, 15, 2000. https://doi.org/10.3390/buildings15122000
Gao H, Xia W, Lu H. Seismic Performance Research of Self-Centering Single-Column Bridges Using Equivalent Stiffness Theory. Buildings. 2025; 15(12):2000. https://doi.org/10.3390/buildings15122000
Chicago/Turabian StyleGao, Huixing, Wenjing Xia, and Hongxu Lu. 2025. "Seismic Performance Research of Self-Centering Single-Column Bridges Using Equivalent Stiffness Theory" Buildings 15, no. 12: 2000. https://doi.org/10.3390/buildings15122000
APA StyleGao, H., Xia, W., & Lu, H. (2025). Seismic Performance Research of Self-Centering Single-Column Bridges Using Equivalent Stiffness Theory. Buildings, 15(12), 2000. https://doi.org/10.3390/buildings15122000




