Abstract
The rapid development of urban subway network is prompting higher requirements for daylighting in subway stations. The skylight daylighting space of shallow buried subway stations not only improves the quality of light environment but also brings challenges for the optimization of light and thermal performance, especially in areas with hot summers and cold winters. In this paper, key parameters such as illumination, air temperature, and the black sphere temperature of skylight and artificial lighting areas at stations A and B in Shanghai were tested with a field test system. The results show that the light environment in the skylight areas was significantly improved, but the need for regulation and control of the thermal environment increased. Combined with response surface analysis, 10 sample models for two types of daylighting space (partitioned and open atrium styles) were studied and constructed, including 254 simulated working conditions. The results reveal that design parameters such as the number, aspect ratio, depth of light openings, and skylight angle have significant effects on combined energy consumption. The decentralized double slope roof daylighting space has the best performance in partitioned and open atrium-style public areas, and combined energy consumption can be reduced to 385.14 kWh/m2. The optimization strategies proposed in this study can provide a quantitative basis for the skylight design of shallow buried subway stations and an important reference for the design of low-carbon and energy-saving underground spaces.
1. Introduction
The urban subway network is becoming increasingly more dense in order to relieve the pressure of surface traffic and increase people’s time in subway stations; therefore, the demand for light and thermal environments in subway stations is becoming more and more prominent, especially in areas with hot summers and cold winters [1]. Shallow buried subway stations face unique challenges in space design due to their small buried depth (the thickness of covered soil is only 3–8 m). They have a complex internal structure and high passenger density, and the demand for illumination and thermal comfort has significantly increased. In areas with hot summers and cold winters, external solar radiation enters the stations through skylights, which can not only improve natural daylighting but also introduce additional heat, thereby leading to a significant increase in cooling load [2,3]. In view of this conflict between light and heat, optimizing the daylighting design of skylights is key if we are to ensure energy conservation and passengers’ comfort in subway stations.
At present, subway stations are mostly lit by artificial light sources, resulting in large power consumption. In order to reduce energy consumption, some subway stations introduce natural light through skylights [4]. Although natural daylighting improves illumination and reduces energy consumption, it also introduces solar radiation into the interior, affecting the indoor thermal environment of subway stations. Research on skylight daylighting mainly focuses on the influence of the building atrium on space. For instance, Dussault et al. [5] tested the impact of the window-to-wall ratio of skylights on building energy consumption and found that an appropriate window-to-wall ratio could reduce building energy consumption. Tsikaloudaki et al. [6] and Kim et al. [7] used EnergyPlus software (V9.4) to simulate the solar heat gain coefficient of skylights and revealed its impact on building energy consumption. It was verified that the visible light transmittance of skylights had a significant impact, and it was proposed that building energy consumption can be reduced by adjusting transmittance [8,9]. In recent years, studies on skylights in subway stations have shown that skylights can effectively improve the utilization efficiency of natural light [10], but they can also easily cause problems such as over-brightness and a decrease in thermal comfort in summer [11]. From a field test and multi-objective optimization [12], it was found that adjusting design parameters such as skylight ratio, light transmittance, and U value can not only reduce the annual energy consumption of air conditioning (by 28.1%) but also significantly improve light performance (by 31.5%) and thermal comfort (by 43.8%). This study provides a concrete quantitative method and theoretical support for the optimized design of skylights in shallow buried subway stations. Nevertheless, research on the form, distribution, and dynamic control strategy of skylights is still insufficient, especially in the practical application of shallow buried subway stations with high-density passenger flow.
Research on the thermal environment of subway stations mainly focuses on thermal comfort and temperature control optimization. For example, Wang et al. [13] studied the thermal comfort of passengers in subway stations in Changchun in a cold area, and the results provided references for the thermal environmental design of underground stations. Katavoutas et al. [14] conducted a field test on the internal thermal environment of a subway station in Athens and found that the thermal comfort of passengers was related to platform design. Pan et al. [15] studied two underground stations in Beijing and pointed out that the thermal sensation of passengers in the subway stations alternated between cold and hot during the waiting process. Passi et al. [16] investigated the thermal environment on the platforms and in the carriages of Jinnai subway station in India, and the results showed that passengers’ dissatisfaction on the platforms was significantly higher than that in the carriages. Li et al. [17] conducted a field test on the platform thermal environment of metro line 1 in Beijing and found that passengers’ dissatisfaction on the platforms was significantly higher than that in the carriages. Through a field test and questionnaire survey on thermal comfort, the thermal environment of different underground buildings was evaluated, and it was found that passengers’ thermal comfort was significantly different from the theoretical calculated value of the Predicted Mean Vote (PMV). In addition, Zhao et al. [10] tested the microclimate of a sunken square in Shenzhen and revealed its impact on the environment inside a subway station. Liu et al. [9] analyzed the operating temperature of air conditioning in a subway station of Tianjin and its variation trend with outdoor temperature and studied the changes in passengers’ thermal comfort (represented by RWI values) during the process of entering and leaving the station. Moreover, some scholars have studied the thermal comfort of subway stations in different seasons, control units, and time periods, and they have put forward some control strategies.
At present, there have been some studies on the light and thermal environment of subway stations, but there are still some shortcomings. Specifically, most studies focus on the evaluation of a single performance (metric such as daylighting or shading) and fail to comprehensively evaluate light and thermal performance. Moreover, there are relatively few studies on the light and thermal environment of shallow buried subway stations with high personnel density and compact spatial layout. There is no effective regulation and control scheme for skylights according to light and thermal characteristics in different seasons and time periods.
These studies have collectively provided a solid foundation for understanding daylighting and thermal comfort in underground spaces. However, a comprehensive review of skylight-related research in both building and metro station contexts has also been integrated into the Introduction to clarify the academic background and highlight the research gap addressed in this paper.
In this paper, the daylighting spatial form and its proportional relationship in public areas of shallow buried subway stations were systematically investigated and tested, and the key form elements affecting the light and thermal environment were extracted. This study focuses on subway stations in Shanghai in an area with hot summers and cold winters. Based on test data from summer and winter, the light environment quality and thermal comfort conditions were analyzed. The daylighting spatial models of two typical public areas (in partitioned and open atrium styles) were established based on response surface analysis, covering 254 working conditions. The relationship between skylight daylighting form and energy consumption was quantitatively analyzed by using DesignBuilder software (V7) through numerical simulation, and the range of design parameters were optimized based on multiple regression models. This study can provide systematic theoretical support and practical guidance for optimizing the light and thermal performance of skylights in shallow buried subway stations.
The remainder of this paper is organized as follows. Section 2 presents the research methodology, including field measurements, simulation modeling, and the application of response surface methodology. Section 3 discusses the results of both field tests and simulations, highlighting key findings related to illumination, temperature, energy performance, and optimal skylight configurations. Section 4 concludes the study and offers practical recommendations and future research directions.
2. Methodology
In this study, field measurements, simulation analysis, and optimization modeling were comprehensively applied to analyze the spatial characteristics of the skylight lighting area and its impact on the light and thermal environment in public areas of shallow-buried subway stations (Shanghai, China). This study followed a three-stage research process. First, field measurements were conducted in summer and winter at two subway stations in Shanghai to assess the actual illumination and thermal conditions under skylight and artificial lighting. Second, simulation models were developed using DesignBuilder (V7) and Energy Plus (V9.4) to reproduce the measured conditions and evaluate the effects of different skylight configurations across 254 working conditions. Finally, a response surface methodology (RSM) was applied to identify the quantitative influence of key design parameters—such as skylight angle, depth, number, and aspect ratio—on combined energy consumption, and to determine the optimal skylight spatial form.
2.1. Field Investigation
2.1.1. Investigation of Spatial Features and Form Parameterization
To clarify the form elements of daylighting space in public areas of subway stations, typical shallow buried subway stations were investigated. The detailed contents of the investigation are shown in Supplementary S1. The statistical analysis of spatial form and daylighting space was conducted using the aspect ratio of light openings [18,19], window-to-floor ratio [20], depth of light openings [21], number of atriums [22,23], number of light openings [24], and type of daylighting skylights [25]. Based on the interface form as well as the number of light openings, they can be partitioned into centralized and decentralized types, and their roofs can be divided into flat, double slope and arched roofs according to skylight angle. In order to comprehensively study the influence of daylighting spatial form of skylights on the light and thermal performance of public areas, 10 sample models of common skylight daylighting space in public areas in subway stations were identified based on basic models of partitioned and open atrium-style public areas (Table 1).

Table 1.
Value ranges of skylight daylighting spatial form parameters.
2.1.2. Site for Field Measurement
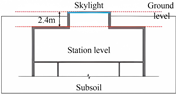
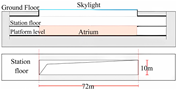
Shanghai is located in an area with hot summers and cold winters and has the typical characteristics of light and thermal environments in summer and winter. In this study, we conducted a field test on the light and thermal environment of public spaces in subway stations A and B of Shanghai. Their geographical locations are shown in Figure 1. The two subway stations, which are standard shallow buried island subway stations, are adjacent on the same subway line and have a uniform outdoor climate environment. Station A is an underground standard station with a two-floor island platform and has a partitioned public area. The skylight of the station hall is a rectangle 28 m long and 5.2 m wide, and the public area is located in the middle of the subway station. Station B is also a standard underground station with a two-floor island platform and features an open atrium-style public area. The skylight of the station hall is a rectangle 82 m long and 10 m wide, and the public area is situated in the middle of the subway station. In the center of the public area, there are four atriums (18 m × 10 m). The two stations have different types of space and skylights, and it is easy to compare and analyze the influence on their light and thermal environment. Therefore, the light and thermal environment in the areas under the skylights of stations A and B were tested.
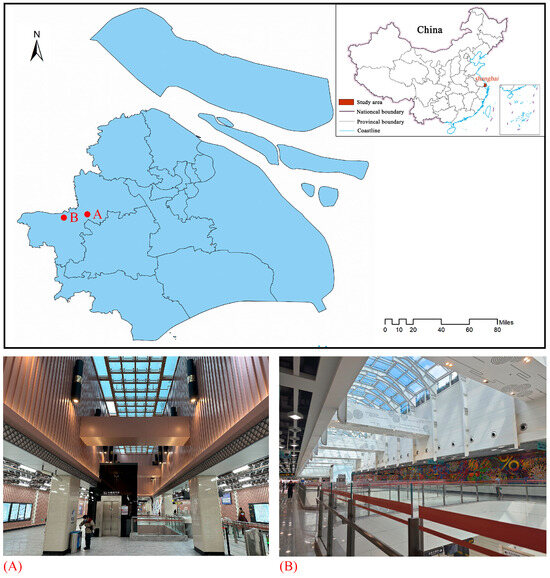
Figure 1.
Sites for field test. (A) Station A; (B) Station B.
2.1.3. Time and Content of the Field Test
The field test was conducted from July 25 to 29 in 2023 (summer) and from January 7 to 9 in 2024 (winter). During a day, the test time was 07:00–18:00, once every hour on the hour. The test lasted for 1–2 d at each station. The skylights were closed during the test. The illumination, air temperature, black sphere temperature, ground temperature, wind speed, surface temperature under the skylights of the subway stations, and outdoor solar radiation were tested. In addition, the PMV index was calculated to evaluate thermal comfort based on the measured air temperature, black globe temperature, and air velocity at each test point. The calculation considered standard values of relative humidity (60%), metabolic rate (1.2 met), and clothing insulation (0.5 clo in summer, 1.0 clo in winter).
2.1.4. Test Instruments and Position of Test Points
Tests were conducted at stations A and B, with measurement points distinguishing natural and artificial lighting zones shown in Figure 2. Test parameters, including spatial dimensions, point spacing, and skylight types, are detailed in Table 2. Instruments for lighting and thermal measurements were used, with specifications in Table 3. The layout, instrument selection, and performance evaluation follow relevant national standards for daylighting, lighting, and energy efficiency (GB/T 5699-2017, GB/T 5700-2008, GB 50033-2013, GB 50034-2013, and GB 50189-2015). Sensors were placed 0.15 m above the floor in accordance with the applicable daylighting standard (GB/T 5699-2017).
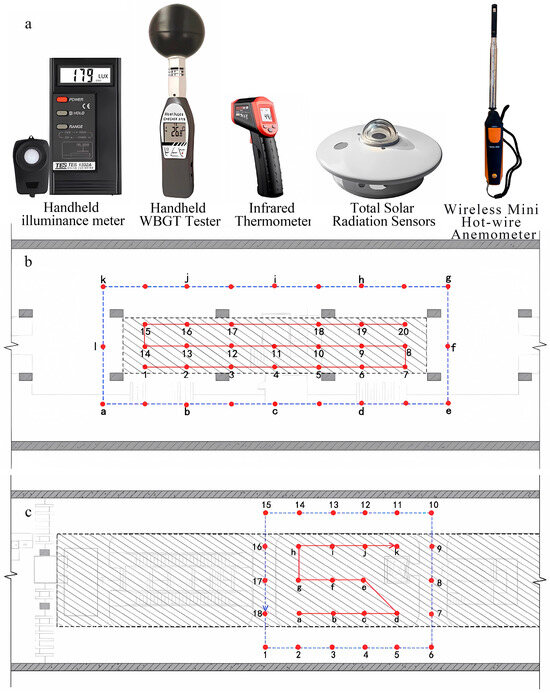
Figure 2.
Test instruments and points. (a) Test instruments; (b) test points of station A; (c) test points of station B.

Table 2.
Overview of test station configurations, skylight types and sizes, testing schedules, and measurement layout.

Table 3.
Basic information of test instruments.
2.2. Simulation of Light and Thermal Environment
The analysis of light and thermal environment in the public areas of the subway stations should be combined with annual meteorological conditions and indoor parameters, but it was difficult to carry out an annual test due to the limitations of field conditions. Hence, it was necessary to simulate the light and thermal environment of the underground bus hub and then conduct response surface analysis, thereby determining the optimal parameters of skylights in the public areas of the subway stations.
2.2.1. Simulation of Light Environment
Based on the DesignBuilder(V7) platform, the influence of skylights of two shallow buried subway stations (stations A and B in Shanghai) on the light and thermal environment of the underground public spaces was simulated. The basic model information and software modeling of stations A and B are shown in Figure 3.
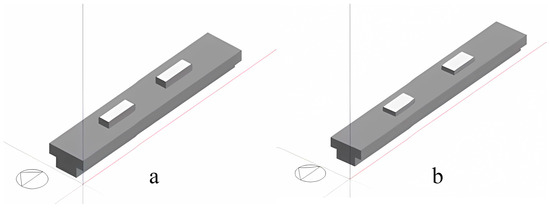
Figure 3.
Software modeling. (a) Station A; (b) Station B.
Meteorological parameters of Shanghai City were derived from meteorological data of representative years and obtained in CSWD format from the official website of EnergyPlus (V9.4). The meteorological dataset was jointly developed by the China Meteorological Administration and Tsinghua University based on five decades of real-time monitoring data from 194 meteorological stations in China. It covers summer and winter design days and annual hourly meteorological parameters, including temperature, humidity, solar radiation, wind speed, sunshine duration, and atmospheric pressure. The setting of the building envelope according to the actual field investigation is listed in Table 4. In addition, the Perez sky model was used to simulate the dynamic natural daylighting effect throughout the year [26]. This threshold was determined as 300 lx according to the Standard for Daylighting Design of Buildings (GB 50033-2013). UDI is the percentage of time between 200 lx and 2000 lx of daylight received by the analysis point during the actual use of a building. This 300 lx threshold was used to calculate the Daylight Autonomy (DA) for different skylight configurations, which is defined as the percentage of occupied hours during which the illuminance at the analysis point exceeds 300 lx.

Table 4.
Design type of the building envelope.
2.2.2. Simulation of Energy Consumption and Thermal Environment
The energy consumption of stations A and B in Shanghai was simulated based on the DesignBuilder (V7) platform. Heat transfer is the basis of energy consumption calculation. The heat transfer of the wall was calculated based on conduction transfer function (CTF) [27]. The heat transferred through the inner and outer surfaces of the wall at the jth time step is as follows:
where Xj is the CTF coefficient for the outside surface of the wall, j = 0, 1, …, n; Yj is the CTF coefficient for the intermediate layer of the wall, j = 0, 1, …, n; Zj is the CTF coefficient for the inner surface of the wall, j = 0, 1, …, n; Φj is the heat flow CTF coefficient, j = 0, 1, …, n; Ti is the inner surface temperature; To is the outside surface temperature; qko is the outside surface heat transfer; and qki is the inner surface heat transfer.
The control equation of heat transfer in double glazing glass is as follows:
where Eₒ and Eᵢ are the intensity of longwave radiation on the outside and inner surfaces of the glass, respectively; k1 and k2 are heat transfer coefficients for layers 1 and 2, respectively; hₒ and hᵢ are the convective heat transfer coefficients of the outside and inside surfaces, respectively; Sᵢ is the intensity of shortwave radiation absorbed by surface i and longwave radiation from indoor heat sources; θi and θo are the indoor and outdoor temperatures, respectively; εi is the longwave emissivity of surface i; hj is the heat transfer coefficient of the gas between the glass layers; and σ is the Stefan–Boltzmann constant.
The heat balance model equation of heat gain in the air conditioning area is as follows:
where is the total convective heat transfer from the internal heat source; is the convective heat transfer from the surface of the zone; is the heat transfer from the outdoor infiltration air; is the mixed heat transfer from the air in the inner zone; is the output energy of the air conditioning system; and is the energy stored in the air. These equations are derived from the Conduction Transfer Function (CTF) method used in EnergyPlus (V9.4). EnergyPlus simulations (refer to EnergyPlus (V9.4). Engineering Reference, U.S. Department of Energy (DOE), 2023 Edition).
The parameters required for the calculation of energy consumption were determined based on the field test data. The heat transfer coefficient of the skylights was 3.0 W/(m2·K), and the heat transfer coefficient of the roofs was 0.38 W/(m2·K). In addition, according to the operation time of the underground public transportation hubs, the operation time of station A in Shanghai was from 5:30 to 22:30, and the presence rate of passengers was determined based on the passenger flow observed in the field test. According to the HVAC design parameters of station A in Shanghai, the primary return air conditioning system was adopted. The interior design temperature was 26 °C, and the humidity was 65%. The passenger flow density was 1 person/m2. The equipment power density was 4.5 W/m2, and the lighting power density was 12 W/m2. The fresh air volume was 20 m3/(person·h). Mechanical ventilation was used in other seasons.
2.3. Response Surface Methodology
Response surface methodology (RSM) is a statistical technique used for modeling and optimizing processes where multiple variables influence one or more outcomes [28,29]. RSM can be used to analyze the influence of form parameters of skylights on the light and thermal environmental performance in the public areas of the subway stations to seek the optimal skylight design scheme and then balance the light and thermal environmental performance. A central composite design (CCD) was adopted, and key form parameters of skylights (such as aspect ratio, window-to-floor ratio, and angle, etc.) were selected as input variables, while light and thermal performance indicators (such as illumination uniformity and thermal gain, etc.) were used as response variables. The quadratic polynomial regression model was used to establish the model relationship between the input variables and response variables. The model equation is as follows:
where represents the input variable or factor of the system. In the response surface analysis of light and thermal environment, the input variable can be the key form parameter of the skylight. represents the baseline response value of the system, and when input variable is zero, the response variable of the system is equal to , which is the intercept of the regression model. is the linear regression coefficient of input variable , and is the degree of linear influence of input variable on response variable . is the quadratic regression coefficient of the input variable, and represents the quadratic nonlinear influence of input variable on response variable . This term can reflect the degree of curvature of response surface in the parameter space. is the interaction regression coefficient between input variables and , and means the impact of the interaction of two input variables on response variable . ϵ is a random error term. Energy use was simulated on an annual basis using typical meteorological year (TMY) weather data, and all results are reported in kWh/m2, representing annual energy intensity. This quadratic polynomial model is commonly used in response surface methodology (RSM) as described in Montgomery, D. C., Design and Analysis of Experiments, 9th ed., Wiley, 2020. In this study, a central composite design (CCD) was adopted to generate the experimental matrix with four independent variables: skylight number (A), aspect ratio (B), opening depth (C), and skylight angle (D), each set at three levels. The energy consumption under each configuration was simulated using DesignBuilder(V7) and taken as the response variable. All variables were coded using standard RSM transformation formulas. The regression model was evaluated using the coefficient of determination (R2), adjusted R2, and p-values to verify its statistical significance and predictive performance. A total of 254 combinations were simulated, and representative data are available in the Supplementary Material.
2.4. Comparison Between Simulated and Field Test Data
In order to verify the accuracy of the simulation, the data of illumination at the test points under the skylight of station A in summer were compared with the simulated data. As shown in Figure 4, the simulated data were consistent with the test data, but there were also errors. The main reason is that the simulation environment was relatively ideal, and the changes in the actual meteorological environment were transient and non-characteristic, resulting in large fluctuations of the data at some test points. In addition, there were no buildings or obstacles directly blocking the light in the actual test environment, but there were surrounding objects such as the ground and reflective surfaces at the actual test scene, which increased the test illumination in the model. During the simulation, the surrounding environment was not set, so the simulated illumination was lower than the test value.
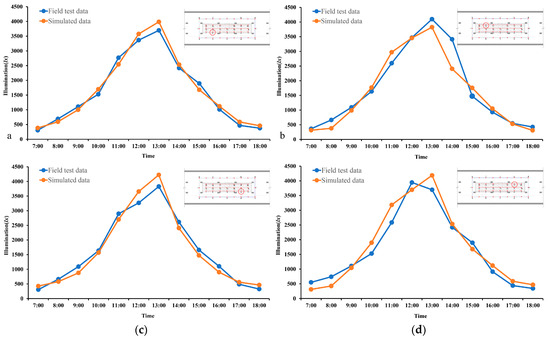
Figure 4.
Comparison between the field test and simulated data of illumination. (a) Position 2 (b) Position 16 (c) Position 6 (d) Position 19.
3. Results and Discussion
3.1. Field Test Results
Some indicators were tested in the skylight and artificial lighting areas at stations A and B in Shanghai in summer and winter, including illumination, air temperature, black sphere temperature, ground temperature, surface temperature under skylights, and outdoor solar radiation intensity. The specific analysis results are as follows.
3.1.1. Summer Experimental Results
- 1.
- Analysis of illumination
As shown in Figure 5a, the average illumination of the skylight areas showed an obvious changing trend during the day and peaked at 13:00–14:00 at stations A and B, reaching up to 3672 lx and 7214 lx, respectively. The illumination in the artificial lighting areas was relatively stable, with a range of 260–851 lx, and there was little fluctuation throughout the day. At station B, the average illumination of the skylight area on the first underground floor (d1) was 3091.75 lx, which was 33.23% higher than that of the second underground floor (d2, 2356.17 lx). This difference is statistically supported, with standard deviations of ±2336.68 lx (d1) and ±1661.16 lx (d2), and 95% confidence intervals ranging from 1607.09–4576.41 lx and 1300.72–3411.62 lx, respectively. These results indicate that the daylighting design of the upper floor contributed significantly to improving the light environment. According to the Standard for Daylighting Design of Buildings (GB 50033-2013) and Standard for Lighting Design of Buildings (GB 50034-2013), the illumination of the skylight areas could meet the natural daylighting standard (≥300 lx) from 08:00 to 17:00. This indicates that the Daylight Autonomy (DA) of the skylight areas in summer reached nearly 100%, satisfying the visual comfort requirements for the entire occupied period. In the artificial lighting areas, illumination was insufficient in the morning and evening hours, so additional light sources were needed to ensure the visual needs of passengers.
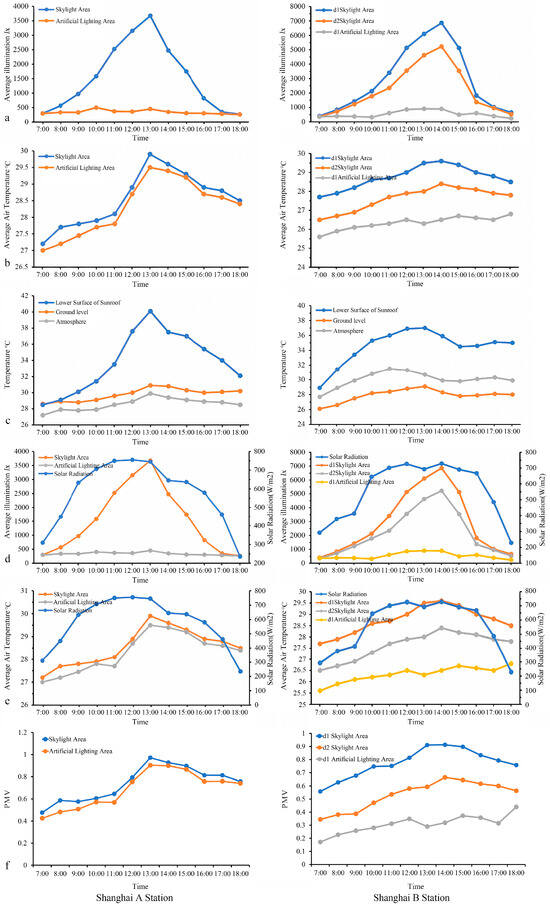
Figure 5.
Field test data of stations A and B in Shanghai. (a). Indoor illumination. (b). Indoor air temperature. (c). Surface temperature under the skylights, air temperature, and ground temperature. (d). Outdoor solar radiation and indoor illumination. (e). Outdoor solar radiation and indoor air temperature. (f). Predicted Mean Vote (PMV) for indoor environments.
In addition, based on the average measured illumination values on the first and second underground floors (3091.75 lx and 2356.17 lx, respectively), the attenuation coefficient of daylight with depth was calculated to be 0.762. This indicates that illumination at the lower level retained approximately 76.2% of the upper level’s value. Fitting an exponential decay model gave an attenuation factor of k = 0.272, which may serve as a reference for natural light predictions in multi-level underground design.
- 2.
- Analysis of air temperature
The daily variation of air temperature can be seen in Figure 5b. The temperature in the skylight areas was higher than that in the artificial lighting areas most of the time, with an increase of 0.3 °C on average. The temperature difference in the skylight areas was 2.7 °C, which was significantly higher than 2.4 °C in the artificial lighting areas, reflecting the direct influence of solar radiation on the temperature fluctuation in the skylight areas. The daily variation range of air temperature on the first underground floor was larger than that on the second underground floor, at 1.1 °C higher on average. Although the air conditioning system effectively regulated the temperature, the design of the skylights still had a direct effect on the thermal environment.
- 3.
- Analysis of surface and air temperature
As shown in Figure 5c, the surface temperature under the skylights was most significantly affected by solar radiation, with an average temperature of 33.6 °C and a fluctuation range of 10.6 °C. The ground temperature was the second most affected, with an average temperature of 29.7 °C and a fluctuation range of 2.3 °C. Air temperature was the least affected, with an average temperature of 28.6 °C and a fluctuation range of 2.7 °C. The data show that the heat load of the skylights was significant, but the air conditioning system effectively controlled the temperature of passengers’ activity areas, keeping it within the comfortable range. This temperature difference can be attributed to the relatively low thermal inertia of surface materials, which respond more quickly to solar radiation than the air.
- 4.
- Relation between outdoor solar radiation and indoor illumination
Figure 5d shows that the variation of outdoor solar radiation intensity was highly positively correlated with the illumination of the skylight areas. At station A, the illumination of the skylight area reached a peak of 3672 lx at 13:00, and the average of the whole day was 1534 lx, which was 4.43 times that of the artificial lighting areas. At station B, the average illumination of the skylight area on the first and second underground floors was 6855 lx and 5220 lx, respectively, indicating that natural light could meet indoor lighting needs at most times.
- 5.
- Relationship between outdoor solar radiation and indoor air temperature
As shown in Figure 5e, the variation trend of air temperature in the skylight and artificial lighting areas was highly correlated with outdoor solar radiation intensity. The average temperature of the whole day in the skylight areas was 28.6 °C, 0.3 °C higher than that of the artificial lighting areas (28.3 °C). The difference was small, but it further validates the impact of skylight design on the thermal environment. The air conditioning system effectively reduced the additional heat load introduced by the skylights to ensure temperature comfort.
- 6.
- Indoor PMV Analysis
Figure 5f illustrates the hourly PMV variations in the skylight and artificial lighting areas for both stations. At station A, PMV values peaked at 0.97 in the skylight area, indicating a slightly warm to warm sensation, while values in the artificial lighting area remained below 0.9. Station B presented a notable vertical gradient, with PMV values of 0.91 and 0.59 in d1 and d2 skylight areas, respectively. These results reflect the influence of both spatial configuration and daylighting strategy on thermal comfort.
3.1.2. Winter Experimental Results
- 1.
- Analysis of indoor illumination
As shown in Figure 6a, the illumination of the skylight areas was significantly affected by weather conditions, and the illumination at noon was higher than that in the morning and evening. At station A, illumination peaked at 13:00, reaching 1465 lx. At station B, the peak was up to 4823 lx on the first underground floor and 3452 lx on the second underground floor. That is, the latter was only 71.6% of the former, reflecting a significant vertical illumination gradient. In contrast, the illumination in the artificial lighting areas was more stable, with a small changing range, and the peak appeared during 12:00–14:00. The measured peak illuminance at station B in winter reached 4823 lx on the first underground floor and 3452 lx on the second, resulting in an attenuation coefficient of 0.716, or a 28.4% reduction in daylight between levels. The corresponding exponential decay coefficient was k = 0.334, confirming a consistent vertical attenuation pattern during colder seasons. Despite lower seasonal radiation, daylight levels in the skylight areas exceeded 300 lx during most of the occupied hours, corresponding to a DA above 85%, and thus still provided effective daylighting.
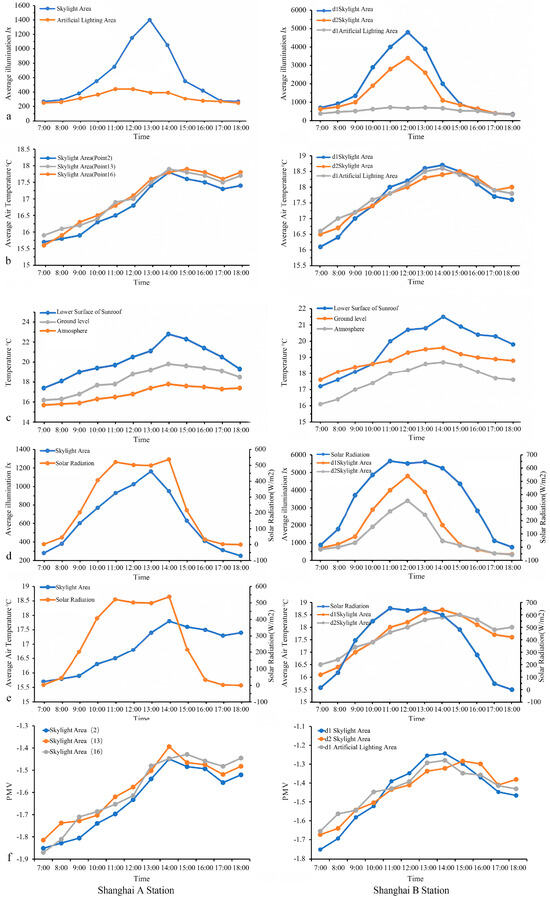
Figure 6.
Field test data of stations A and B in Shanghai. (a). Indoor illumination. (b). Indoor air temperature. (c). Surface temperature under the skylights, air temperature, and ground temperature. (d). Outdoor solar radiation and indoor illumination. (e). Outdoor solar radiation and indoor air temperature. (f). Predicted Mean Vote (PMV) for indoor environments.
- 2.
- Analysis of indoor air temperature
As shown in Figure 6b, the air temperature at stations A and B showed a fluctuating upward trend before 14:00, with an average increase of 2–2.6 °C, and gradually declined with the decrease in outdoor radiation intensity after 14:00. At 18:00 in the evening peak period, the temperature at each test point increased slightly due to the increase in passengers, but the range was limited. The diurnal variation in the natural daylighting areas was consistent with that of solar radiation intensity, which further reveals the internal relationship between light and thermal environment.
- 3.
- Analysis of surface and air temperature
Figure 6c shows that the surface temperature under the skylights varied most greatly, and the maximum daily temperature difference at stations A and B was 5.3 °C and 4.3 °C, respectively. The ground temperature difference was 3.6 °C, and the air temperature difference was 2.1 °C. The surface temperature under the skylights rose slowly in the morning and rapidly at noon because of direct solar radiation, being 3–5 °C higher than the air temperature, and it had a significant impact on ground and air temperature. This observation reveals that the thermal effect of skylights plays an important role in indoor thermal environments. This greater variability in surface temperature is likely due to the low thermal inertia of the exposed surfaces, which leads to faster heating and cooling cycles compared to the surrounding air.
- 4.
- Relation between outdoor solar radiation and indoor illumination
As shown in Figure 6d, the peak of outdoor solar radiation intensity was 638 W/m², which was consistent with the peak trend of illumination in the skylight areas. However, due to the occlusion of the surrounding buildings, the peak of illumination in the skylight areas appeared later than that of outdoor radiation, and its duration was shorter. At station B, the illumination on the first underground floor was higher than that of the second underground floor, and the former was 1.41 times the latter at 12:00, indicating that the daylighting level of the skylights was significantly affected by outdoor radiation and occlusion.
- 5.
- Relationship between outdoor solar radiation and indoor air temperature
As shown in Figure 6e, the outdoor solar radiation intensity at station A was above 400 W/m² from 10:00 to 14:00, which was consistent with the changing trend of indoor air temperature, and the peak appeared at 14:00. During the evening peak period (18:00), because of the increase in passengers, air temperature rose slightly. At station B, the fluctuation range of air temperature on the first underground floor was 2.6 °C, while that of the second underground floor was only 2.0 °C, indicating that the first underground floor was more sensitive to solar radiation, and the temperature on the second underground floor was more stable. The analysis shows that indoor air temperature was significantly affected by solar radiation, and there was a certain lag effect.
- 6.
- Indoor PMV Analysis
As shown in Figure 6f, all PMV values during winter remained negative, indicating cold thermal sensations. In station A, PMV reached as low as −1.85 in the skylight zone, while station B showed slightly milder values around −1.6. The observed differences across layers (e.g., d1 vs. d2 skylight areas) highlight the impact of vertical distance from the skylight and occupant density on perceived comfort.
3.1.3. Comparison of Test Results Between the Two Stations
Based on the field test data, the light and thermal environments of the skylight and artificial lighting areas at stations A and B in Shanghai were compared to reveal the significant differences in the lighting and thermal environmental performance of the two stations. The results reveal that the illumination of the skylight areas at station B was significantly higher than that at station A. In summer, the peak of illumination on the first underground floor reached 7214 lx, almost twice that of station A (3672 lx). In winter, the peak of illumination at station B was also significantly higher than that of station A, which is mainly due to the larger daylighting area of station B and more optimized skylight design. However, the illumination gradient of station B (for example, the difference between the first and second underground floor was 33.23%) and the fluctuation amplitude of the skylight surface temperature (up to 10.6 °C in summer and 5.3 °C in winter) were more significant than those of station A, reflecting the deficiencies in the control of thermal environment uniformity and local heat load while the lighting efficiency was improved. In terms of thermal environment, the fluctuation of daily temperature in the skylight areas at the two stations was significantly higher than that in the artificial lighting areas, but it was larger at station B, reaching up to 2.7 °C in summer, which was 12.5% higher than that of station A (2.4 °C). At station B, the first underground floor was more sensitive to solar radiation, and the range of change in air temperature was larger than that of the second underground floor, revealing the important influence of the location of light openings and surrounding occlusion on the light and thermal environmental performance.
In addition, the predicted percentage of dissatisfied (PPD) values derived from the measured PMV data revealed further insights into thermal comfort conditions. During summer, the PPD in skylight areas remained below 15%, indicating acceptable thermal comfort. However, in winter, PPD values in most skylight areas exceeded 60%, particularly on the second underground floor of station B, where values approached 70%, reflecting significant thermal discomfort. These results highlight the need for improved insulation or auxiliary heating in deeper underground zones to ensure year-round comfort.
3.2. Simulation Results
In order to further verify and analyze the comprehensive characteristics of the energy consumption of 10 sample models, a regression model of variance analysis was carried out to clarify the significance and interaction of factors such as the number, aspect ratio and depth of light openings, and skylight angle on combined energy consumption (Supplementary S2). Moreover, experimental models for the working conditions of 10 samples are listed in this study, including the form design of partitioned and open atrium-style daylighting spaces (Supplementary S3), which provide a quantitative basis and practical reference for optimal design.
3.2.1. Influence of Daylighting Spatial Form on Light and Thermal Performance in the Partitioned Public Area
- 1.
- Decentralized flat roof skylight
The influence of the lighting spatial form (the number A, aspect ratio B and depth C of light openings) of a decentralized flat roof skylight on the light and thermal performance was analyzed. The results show that the main effect of A, B and C on combined energy consumption is significant, and the interaction terms (such as AB and AC) also play an important role. The single factor analysis revealed that the number of light openings and aspect ratio were negatively correlated with combined energy consumption, while the depth had a relatively weak influence. The simulation range of combined energy consumption was 394.45–400.03 kWh/m2, among which refrigeration energy consumption dominated combined energy consumption (Figure 7). Based on the response surface analysis, the optimized daylighting form was obtained as follows. The number of light openings was 6, and aspect ratio was 3, and depth was 4 m. Under this working condition, combined energy consumption was the lowest, at only 394.17 kWh/m2.
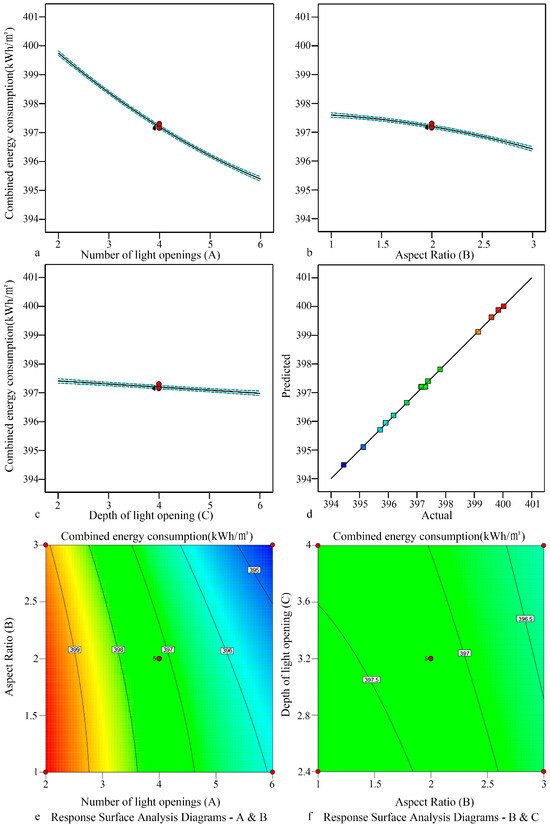
Figure 7.
Fitting relationship of combined energy consumption in the partitioned public area of sample 1.
- 2.
- Decentralized double slope roof skylight
The influence of the form elements (the number A, aspect ratio B, and depth C of light openings and skylight angle D) of a decentralized double slope roof skylight on the light and thermal performance was studied. The results indicate that the main effects of the number (A) and aspect ratio (B) of light openings and skylight angle (D) were significant (p < 0.01). The single factor analysis revealed that the number of light openings was negatively correlated with combined energy consumption, while skylight angle was positively correlated with combined energy consumption. The influence of aspect ratio was weak, and the influence of depth was the smallest. Upon interaction analysis, the interaction between the number of light openings and skylight angle (AD) was significant, and combined energy consumption varied from 387.49 to 403.44 kWh/m2 (Figure 8). According to the response surface analysis, the optimized daylighting form was obtained as follows. The number of light openings was 6, aspect ratio was 2.6, depth was 4 m, and the skylight angle was 15°. The minimum of combined energy consumption was 385.14 kWh/m2. The results show that the double slope roof can reduce combined energy consumption more effectively than the flat roof.
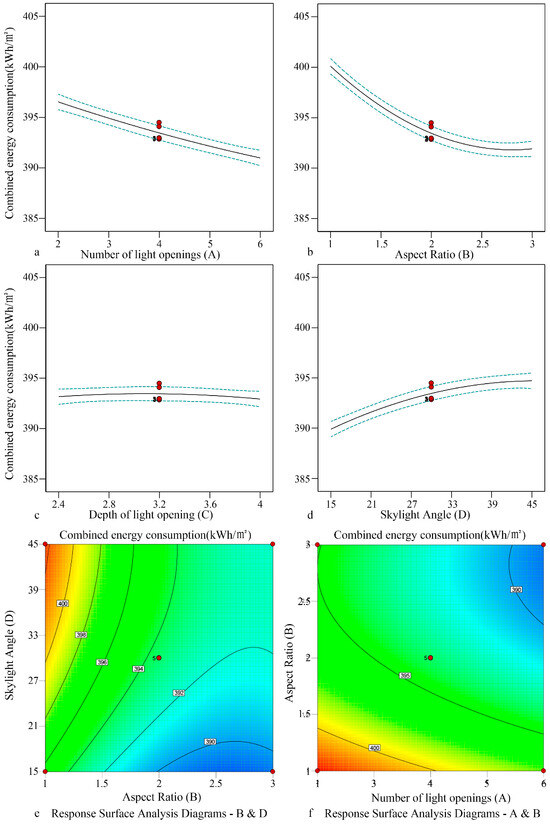
Figure 8.
Fitting relationship of combined energy consumption in the partitioned public area of sample 2.
- 3.
- Centralized flat roof skylight
The influence of form elements (window-to-floor ratio A, aspect ratio B, and depth C of light openings) of a centralized flat roof skylight on the light and thermal performance was discussed. The results revealed that window-to-floor ratio had the greatest influence on combined energy consumption, and they were positively correlated, while the aspect ratio and depth of light openings were negatively correlated with combined energy consumption. The interaction effect between window-to-floor ratio and the aspect ratio of light openings was significant (p < 0.05). Combined energy consumption ranged from 398.63 to 405.69 kWh/m2 (Figure 9). According to the response surface analysis, the optimized daylighting form was obtained as follows. The window-to-floor ratio was 0.08, the aspect ratio of light openings was 8, and depth was 4 m. Under this working condition, the combined energy consumption was the lowest (only 398.48 kWh/m2).
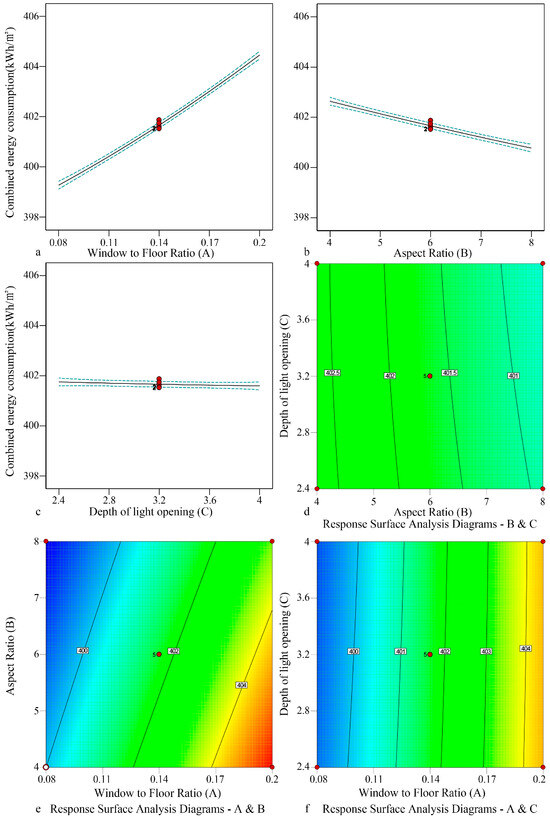
Figure 9.
Fitting relationship of combined energy consumption in the partitioned public area of sample 3.
- 4.
- Centralized double slope roof skylight
The influence of the window-to-floor ratio (A), aspect ratio (B), and depth (C) of light openings and skylight angle (D) of a centralized double slope roof skylight on the light and thermal performance was analyzed. Skylight angle was positively correlated with combined energy consumption, while the aspect ratio of light openings was negatively correlated with combined energy consumption, and window-to-floor ratio and depth had little influence. The interaction analysis showed that there was a significant interaction between the aspect ratio of light openings and skylight angle (BD) (p < 0.05). Combined energy consumption ranged from 392.23 to 398.22 kWh/m2 (Figure 10). The optimized design parameters were as follows. The window-to-ground ratio was 0.18, and the aspect ratio of light openings was 8; depth was 2.962 m, and the skylight angle was 15°. The corresponding combined energy consumption was 392.28 kWh/m2.
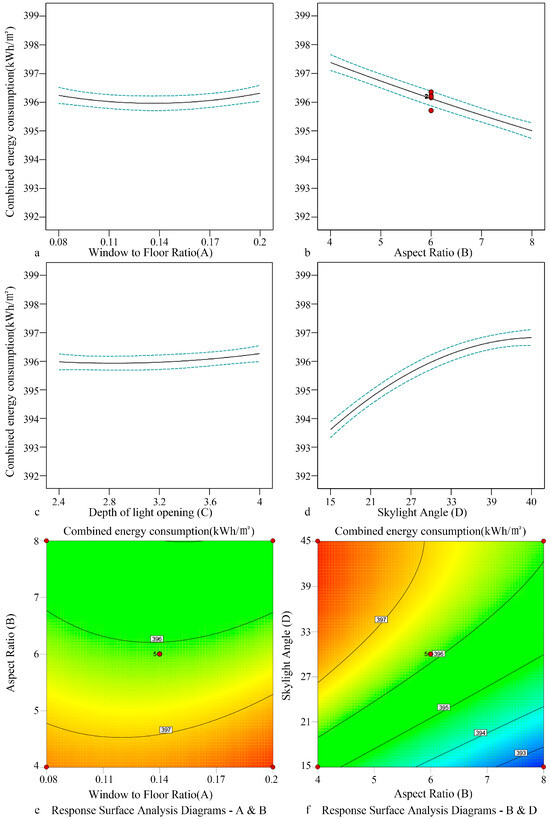
Figure 10.
Fitting relationship of combined energy consumption in the partitioned public area of sample 4.
- 5.
- Centralized arched roof skylight
The influence of the form elements (window-to-floor ratio A, aspect ratio B, the depth C of light openings, and the skylight angle D) of a centralized arched roof skylight on the light and thermal performance was studied. It was found that the window-to-floor ratio was positively correlated with combined energy consumption, while the skylight angle was negatively correlated with combined energy consumption, and the influence of the depth and aspect ratio of light openings was weak. Interaction analysis revealed that the interaction effect between window-to-floor ratio and skylight angle (AD) was significant. Combined energy consumption ranged from 397.88 to 412.99 kWh/m2 (Figure 11). For the optimized parameters, the window-to-ground ratio was 0.08, and the aspect ratio of light openings was 7.198; depth was 4 m, and the skylight angle was 22.282°. The corresponding combined energy consumption was 397.582 kWh/m2.
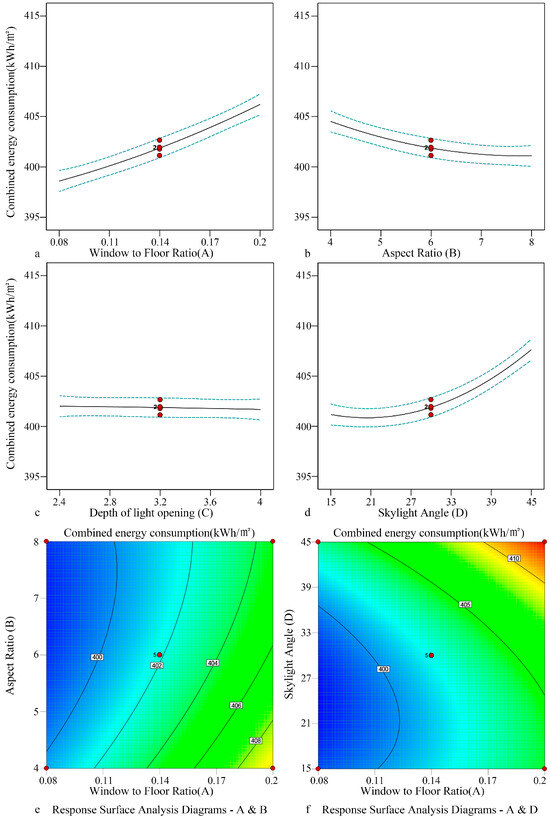
Figure 11.
Fitting relationship of combined energy consumption in the partitioned public area of sample 5.
3.2.2. Influence of Daylighting Spatial Form on Light and Thermal Performance in the Open Atrium-Type Public Area
- 1.
- Decentralized flat roof skylight
The influence of the lighting spatial form (the number A, aspect ratio B, the depth C of light openings, and the number of atriums D) of a decentralized flat roof skylight on the light and thermal performance was analyzed. The results revealed that the effect of the number of light openings and atriums on combined energy consumption was the most significant (p < 0.01), and these factors are negatively correlated, while the aspect ratio and depth of light openings have a relatively weak effect. The combined energy consumption varied from 417.97 to 423.54 kWh/m2 (Figure 12). The optimized parameters were as follows. The number of light openings was 6, and the aspect ratio was 3; depth was 4 m, and the number of atriums was 5. The corresponding combined energy consumption was 411.819 kWh/m2.
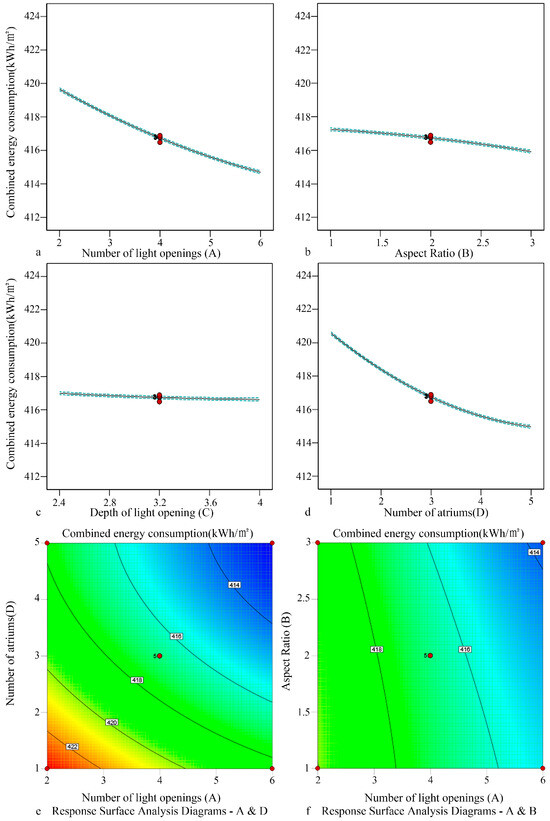
Figure 12.
Fitting relationship of combined energy consumption in the open atrium-style public area of sample 1.
- 2.
- Decentralized double slope roof skylight
The influence of form elements (the number A and aspect ratio B of light openings, the number of atriums C, and the skylight angle D) of a decentralized double slope roof skylight on the light and thermal performance was studied. It was found that both the number of light openings and atriums are negatively correlated with combined energy consumption, while the skylight angle is positively correlated with combined energy consumption. The influence of aspect ratio was small. Combined energy consumption ranged from 406.11 to 422.8 kWh/m2 (Figure 13). In terms of the optimized parameters, the number of light openings was 6, and the aspect ratio was 3; the number of atriums was 5, and the skylight angle was 15°. The corresponding combined energy consumption was 403.476 kWh/m2.
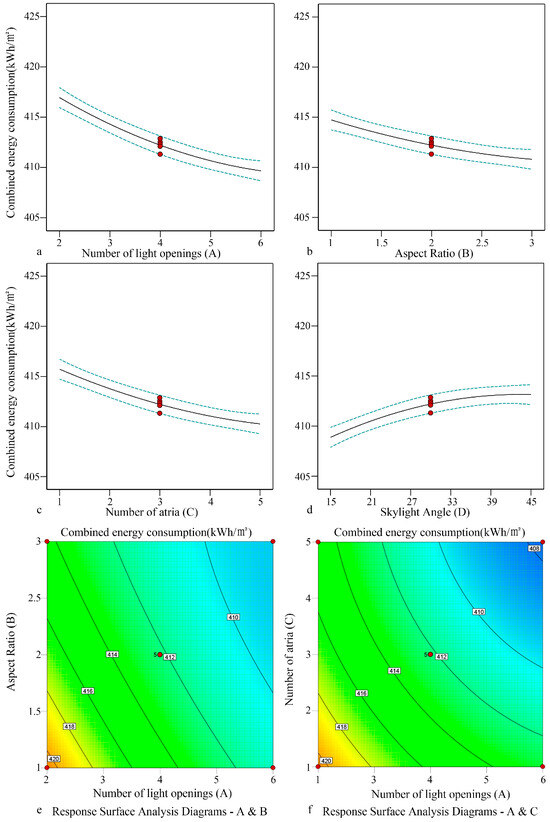
Figure 13.
Fitting relationship of combined energy consumption in the open atrium-style public area of sample 2.
- 3.
- Centralized flat roof skylight
The effect of form elements (the window-to-floor ratio A and depth B of light openings, and the number of atriums C) of a centralized flat roof skylight on the light and thermal performance was analyzed. The window-to-floor ratio had the greatest influence on combined energy consumption, and they were positively correlated, while the influence of the number of atriums was small, and the depth made almost no difference. The combined energy consumption varied from 417.47 to 442.4 kWh/m2 (Figure 14). The optimized parameters were as follows. The window-to-floor ratio was 0.1, and depth was 4 m; the number of atriums was 5. The corresponding combined energy consumption was 417.151 kWh/m2.
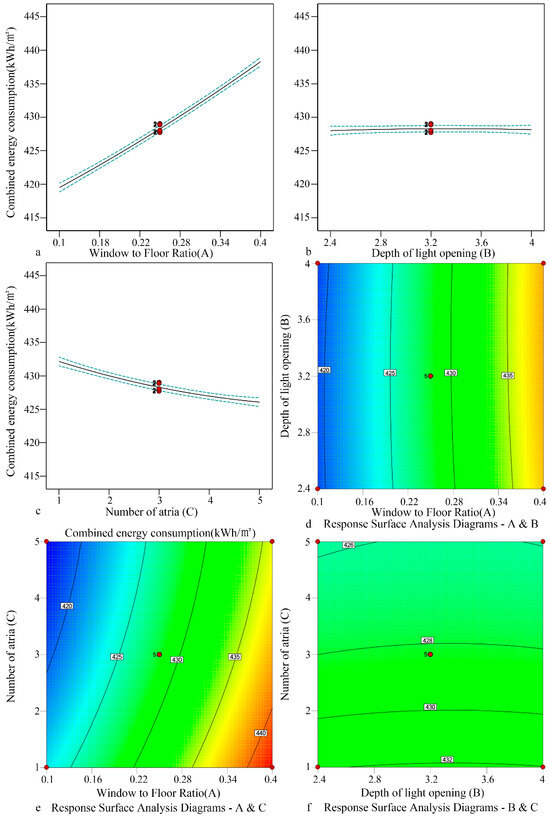
Figure 14.
Fitting relationship of combined energy consumption in the open atrium-style public area of sample 3.
- 4.
- Centralized double slope roof skylight
The influence of form elements (the window-to-floor ratio A and depth B of light openings, the number of atriums C, and the skylight angle D) of a decentralized double slope roof skylight on the light and thermal performance was studied. The results revealed that the window-to-floor ratio was positively correlated with combined energy consumption, while the skylight angle and the depth of light openings were negatively correlated with combined energy consumption. The effect of the number of atriums was weak. The combined energy consumption was between 408.76 and 421 kWh/m2 (Figure 15). In terms of the optimized parameters, the window-to-floor ratio was 0.1, and depth was 2.401; the number of atriums was 5, and the skylight angle was 26.548°. The corresponding combined energy consumption was 414.811 kWh/m2.
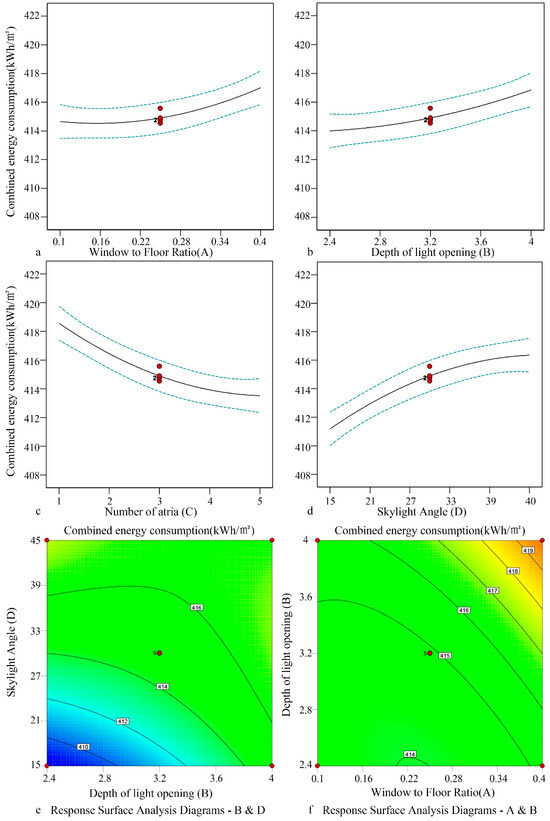
Figure 15.
Fitting relationship of combined energy consumption in the open atrium-style public area of sample 4.
- 5.
- Centralized arched roof skylight
The effect of form elements (the window-to-floor ratio A and depth B of light openings, the number of atriums C, and skylight angle D) of a centralized arched roof skylight on the light and thermal performance was analyzed. It was found that the window-to-floor ratio was positively correlated with combined energy consumption, while the skylight angle was negatively correlated with combined energy consumption. The influence of the depth was weak. The combined energy consumption changed from 417.36 to 467.01 kWh/m2 (Figure 16). The optimized parameters were as follows. The window-to-floor ratio was 0.1, and depth was 2.401; the number of atriums was 5, and skylight angle was 26.548°. The corresponding combined energy consumption was 414.811 kWh/m2.
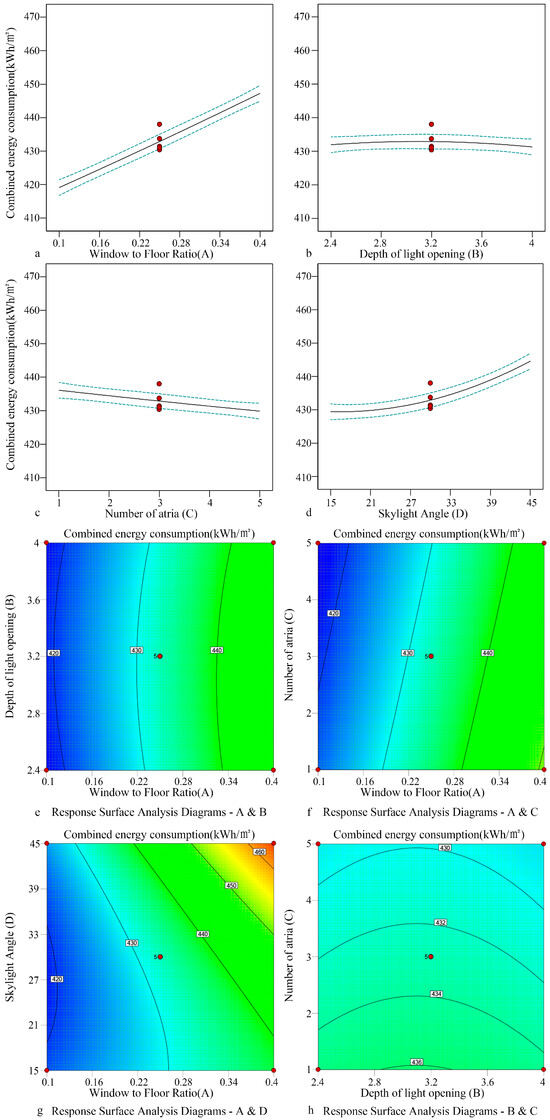
Figure 16.
Fitting relationship of combined energy consumption in the open atrium-style public area of sample 5.
3.2.3. Comparison of Simulation Results Between the Two Stations
From the comparative analysis of 10 sample models of daylighting space at the two stations, it can be seen that the light and thermal performance of the partitioned daylighting space was superior to that of the open atrium-style daylighting space (Figure 17, Table 5). Decentralized double slope roof skylights performed best in the two layouts, with a combined energy consumption of 385.14 kWh/m2 for the partitioned style and of 403.48 kWh/m2 for the open atrium style. Centralized flat and arched roofs have higher energy consumption and should be used under specific constraints. It is recommended to preferentially use decentralized double slope roof skylights and appropriately adjust the number and aspect ratio of light openings as well as skylight angle to optimize light and thermal environmental performance.
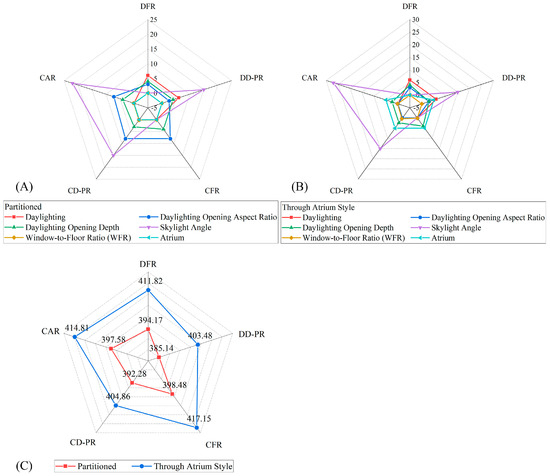
Figure 17.
Comparative analysis of sample models of daylighting space. (A). Partitioned style. (B). Open atrium style, (C). Comparison of combined energy consumption between the two.

Table 5.
Summary of skylight design parameters and energy performance.
3.3. Optimization Strategies
3.3.1. Partitioned Daylighting Space
For the decentralized skylight daylighting space, the number, aspect ratio, and depth of light openings are key factors affecting combined energy consumption [30,31,32]. Optimization strategies should be refined according to specific working conditions. ① When a decentralized flat roof is adopted, six light openings should be recommended to ensure sufficient natural light entry and reduce the need for artificial lighting; the aspect ratio of light openings should be 2.5–3 to optimize daylighting efficiency, and depth should ideally be 4 m to balance the cooling load and lighting energy consumption. ② When a decentralized double slope roof is used, a 15° skylight angle should be recommended, and the number and aspect ratio of light openings should be consistent with those of the flat roof. In this study, it was further pointed out that the double slope roof design had a significant advantage in terms of reducing the heat load. Through the above strategies, combined energy consumption could be optimized to 385.14 kWh/m2.
For the centralized skylight daylighting space, the window-to-floor ratio is the key factor influencing combined energy consumption. The increase in window-to-floor ratio will significantly improve cooling load and combined energy consumption but at the same time will reduce heating load and lighting energy consumption [33,34]. Optimization strategies should be formulated according to the type of skylights (flat roof, double slope roof, and arched roof). For the design of flat and arched roofs, the window-to-floor ratio should ideally be 0.08 to limit excessive heat entering the room and maintain a suitable level of natural light; the aspect ratio of light openings should be 7–8, and the depth is recommended to be 3–4 m. For the design of a double slope roof, the window-to-floor ratio can be appropriately increased to 0.18 to enhance the natural lighting effect; the skylight angle should be 15–25°, and the depth of light openings should be 3–4 m. The optimized design can significantly decrease artificial lighting energy consumption and cooling load and meet thermal comfort requirements.
3.3.2. Open Atrium-Style Daylighting Space
The optimization analysis of the open atrium-style skylight daylighting space shows that the number of light openings is significantly negatively correlated with cooling load and combined energy consumption, and increasing the number of light openings can effectively reduce energy consumption [35,36,37]. The aspect ratio of light openings has a significant influence on cooling load, lighting energy consumption, and combined energy consumption and is negatively correlated with them, with a best value of 3. The influence of the depth of light openings is weak, and it only has a small positive correlation with heating load. The number of atriums is negatively correlated with combined energy consumption, so the number of atriums should be 5 in order to achieve the best energy consumption performance. Moreover, the skylight angle is positively correlated with cooling load and combined energy consumption and should be within 15°. It is recommended that the number of light openings is 6, and the aspect ratio of light openings should be 3; the depth of light openings should be 3–4 m, and the skylight angle should be 15°. The number of atriums should be 5. After optimization, the lowest combined energy consumption of the decentralized distributed double slope roof was 403.48 kWh/m2, that is, the energy conservation performance proved to be good.
For the centralized skylight daylighting space, the window-to-floor ratio has the most significant influence on combined energy consumption. That is, with the increase in the window-to-floor ratio, cooling load and combined energy consumption rose, but heating load and lighting energy consumption decreased [24]. The depth of light openings had little influence on combined energy consumption, while the number of atriums was significantly negatively correlated with combined energy consumption. The number of atriums should be ideally 5. Furthermore, skylight angle was positively correlated with cooling load and combined energy consumption, and the skylight angle should ideally be 15–30°. The window-to-floor ratio of flat and arched roofs should be 0.1, and that of double slope roofs should be 0.4. The depth of light openings should ideally be 2.4–4 m, and the skylight angle should be 15–30°. In the optimized configuration, the combined energy consumption of the centralized double slope roof was the lowest, at only 404.86 kWh/m2, which is better than other centralized types.
According to our comprehensive analysis of optimization strategies of partitioned and open atrium-style skylight daylighting spaces, the partitioned double slope roof design had the best performance in terms of energy conservation and the regulation of light and the thermal environment, followed by the open atrium-style double slope roof design. The window-to-floor ratio and number and aspect ratio of light openings had the most significant influence on combined energy consumption, while the depth of light openings and skylight angle should be adjusted according to the specific type of design. In the actual design, a skylight in the form of a double slope roof is preferentially recommended, and the optimal configuration can be selected according to the specific spatial form and functional requirements of the public area of a subway station, so as to achieve a comprehensive improvement of light and thermal performance and the realization of energy conservation.
3.3.3. Practical Feasibility and Cost Considerations
In addition to energy performance optimization, the construction feasibility and cost implications of skylight configurations are critical for practical implementation. Decentralized skylights with flat or double slope roofs require simpler structural modifications and align with modular construction workflows, making them cost-effective for standard subway station designs (e.g., $20–30% lower costs than centralized types [38]). Their integration is particularly feasible given the shallow burial depth (3–8 m) and standardized layouts of subway stations. Conversely, centralized skylights with large spans or arched roofs demand complex structural support, customized glazing, and enhanced waterproofing to address soil pressure and groundwater risks, thereby significantly increasing construction and maintenance costs. Thus, while centralized configurations offer acceptable performance, their higher costs and complexity render them less suitable for widespread adoption unless specific architectural or functional priorities are emphasized.
4. Conclusions
Through a combination of field testing and numerical simulation, the light and thermal environment of underground public transportation hubs with skylights were systematically evaluated. The characteristics of the light and thermal environment in summer and winter at stations A and B in Shanghai were analyzed, and relationship models between daylighting spatial form and energy consumption were established. The main conclusions are as follows.
- 1.
- In terms of skylight daylighting and thermal environmental characteristics, the illumination of skylight areas was significantly affected by external solar radiation and climate conditions, fluctuating with time, while the illumination of artificially lit areas was more stable. The daily fluctuation range of the surface temperature under the skylights was significantly larger than that of ground and air temperature. However, due to the effective adjustment of air conditioning system, the difference in air temperature between the skylight and artificial lighting areas was small, and the overall temperature was kept within a comfortable range. The daylighting effect of station B in Shanghai was better than that of station A. At station B, with a large skylight daylighting area, the quality of light environment improved, but the demand for the adjustment of thermal environment also increased.
- 2.
- Ten sample models of common skylight daylighting in the public areas of subway stations were summarized. They can be divided into centralized and decentralized types according to the number of light openings, and the roofs can be partitioned into flat, double slope, and arched roofs according to skylight angle. Among them, decentralized daylighting space usually does not use arched roofs. According to the spatial classification of partitioned and open atrium-style public areas, 10 sample models of common skylight daylighting space were formed. This study revealed that under the premise of ensuring indoor light and thermal environmental comfort, the decentralized double slope roof structure is preferable, followed by the centralized double slope roof structure.
- 3.
- Aiming to optimize combined energy consumption through design, the optimized parameters of skylight daylighting space were determined as follows. In the decentralized daylighting space, the number of light openings was 6, and the aspect ratio of light openings was 2.5–3; depth was 4 m, and the skylight angle of a double slope roof skylight was 15°. In the centralized daylighting space in the partitioned public area, the window-to-floor ratio of flat and arched roofs was 0.08, and that of a double slope roof was 0.18; the aspect ratio of light openings was 7–8, and depth was 3–4 m; skylight angle was 15–25°. In the open atrium-style public area, the window-to-floor ratio of flat and arched roofs was 0.1, and that of a double slope roof was 0.4; the depth of light openings was 2.4–4 m, and the number of atriums was 5. The skylight angle was 15–30°.
Although this study provides theoretical and practical support for the optimization of skylight daylighting of shallow buried subway stations, there are still some limitations. For instance, the influence of ground materials (i.e., reflective tiles, concrete, carpets) and interior layout elements (i.e., the partition wall and seat layout) on light reflection and heat absorption has not been fully explored. These factors should be included in future research, and advanced skylight materials (EC mirror and low-radiation coating) and dynamic control strategies (automatic sunshade shutters or sensor drive systems) should be explored. The layout parameters should be optimized using a multi-objective algorithm, and it should extend to diversified underground transportation hubs to improve energy efficiency and comfort.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/buildings15111926/s1, Supplementary S1: Investigation of skylight daylighting space in the public areas of subway stations; Supplementary S2: Variance analysis of regression models; Supplementary S3: Experimental models for the working conditions of 10 samples.
Author Contributions
Conceptualization, X.L., B.S., H.Z. and X.J.; data curation, X.L. and B.S.; formal analysis, X.L. and H.Z.; funding acquisition, X.L.; methodology, X.L., B.S., C.H. and Y.C.; resources, B.S. and X.J.; software, X.L., B.S. and C.H.; supervision, X.L. and B.S.; validation, B.S.; visualization, X.L. and C.H.; writing–original draft, X.L., B.S. and C.H.; writing—review and editing, X.L. and B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Foundation for Young Doctors of Jiangsu Collaborative Innovation Center for Building Energy Saving and Construction Technology (No. SJXTBS2108).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Chen Hua was employed by the company Changzhou Metro Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ma, C.; Peng, F.; Qiao, Y.; Li, H. Evaluation of spatial performance of metro-led urban underground public space: A case study in Shanghai. Tunn. Undergr. Space Technol. 2022, 124, 104484. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, Y.; Jia, L. Discrete modeling approach for emergency guidance signage system design in underground spaces: A case study in transportation hubs. Tunn. Undergr. Space Technol. 2022, 120, 104275. [Google Scholar] [CrossRef]
- Passi, A.; Nagendra, S.M.S.; Maiya, M.P. Characteristics of indoor air quality in underground metro stations: A critical review. Build. Environ. 2021, 198, 107907. [Google Scholar] [CrossRef]
- Wu, Z.; Ji, X.; Zhou, X.; Tong, S. Research on Environmental Suitability Evaluation of the Transfer Spaces in Urban Subway Stations. Buildings 2022, 12, 2209. [Google Scholar] [CrossRef]
- Dussault, J.; Gosselin, L.; Galstian, T. Integration of smart windows into building design for reduction of yearly overall energy consumption and peak loads. Sol. Energy 2012, 86, 3405–3416. [Google Scholar] [CrossRef]
- Tsikaloudaki, K.; Laskos, K.; Theodosiou, T.; Bikas, D. The energy performance of windows in Mediterranean regions. Energy Build. 2015, 92, 180–187. [Google Scholar] [CrossRef]
- Kim, J.T.; Todorovic, M.S. Tuning control of building glazing’s transmittance dependence on the solar radiation wavelength to optimize daylighting and building’s energy efficiency. Energy Build. 2013, 63, 108–118. [Google Scholar] [CrossRef]
- Pu, J.; Shen, C.; Wang, J.; Zhang, Y.; Zhang, C.; Kalogirou, S.A. Near-infrared absorbing glazing for energy-efficient windows: A critical review and performance assessments from the building requirements. Nano Energy 2023, 110, 108334. [Google Scholar] [CrossRef]
- Liu, X.; Shen, C.; Yang, H.; Wang, J. Comprehensive investigation on lighting and energy-saving performance of lighting/heating coupled tubular daylighting devices integrated with nanofluids. Appl. Therm. Eng. 2024, 239, 122094. [Google Scholar] [CrossRef]
- Zhao, J.; Dong, J.; Zhang, X.; Na, Y.; Jiang, C.; He, F.; Cui, Q.; Liu, J. Field measurement of microclimate of sunken square and its effect on indoor environment of underground metro station in subtropical region. Build. Environ. 2023, 228, 109873. [Google Scholar] [CrossRef]
- Huang, S.; Hao, S.; Li, J.; Dong, J.; Liu, J. Effects of large skylights on lighting and thermal environments in underground public transport hubs: A case study in Shenzhen. Build. Environ. 2024, 250, 111182. [Google Scholar] [CrossRef]
- Yuan, J.; Yu, Q.; Yao, S.; Ma, X.; Sun, Z. Multi-objective optimization for the daylighting and thermal comfort performance of elevated subway station buildings in cold climate zone of China. J. Build. Eng. 2023, 78, 107771. [Google Scholar] [CrossRef]
- Wang, C.; Li, C.; Xie, L.; Wang, X.; Chang, L.; Wang, X.; Li, H.; Liu, Y. Thermal environment and thermal comfort in metro systems: A case study in severe cold region of China. Build. Environ. 2023, 227, 109758. [Google Scholar] [CrossRef]
- Katavoutas, G.; Assimakopoulos, M.N.; Asimakopoulos, D.N. On the determination of the thermal comfort conditions of a metropolitan city underground railway. Sci. Total Environ. 2016, 566–567, 877–887. [Google Scholar] [CrossRef]
- Pan, S.; Liu, Y.; Xie, L.; Wang, X.; Yuan, Y.; Jia, X. A thermal comfort field study on subway passengers during air-conditioning season in Beijing. Sustain. Cities Soc. 2020, 61, 102218. [Google Scholar] [CrossRef]
- Passi, A.; Nagendra, S.M.; Maiya, M.P. Evaluation of comfort perception of passengers in urban underground metro stations. Energy Sustain. Dev. 2022, 68, 273–288. [Google Scholar] [CrossRef]
- Li, Y.; Geng, S.; Zhang, X.; Zhang, H. Study of thermal comfort in underground construction based on field measurements and questionnaires in China. Build. Environ. 2017, 116, 45–54. [Google Scholar] [CrossRef]
- Li, X.; Shi, W.; Liu, Y.; Zhang, N. Optimization Strategy for Thermal Comfort in Railway Stations above Ground Level in Beijing. Buildings 2024, 14, 2843. [Google Scholar] [CrossRef]
- Futrell, B.J.; Ozelkan, E.C.; Brentrup, D. Bi-Objective optimization of building enclosure design for thermal and lighting performance. Build. Environ. 2015, 92, 591–602. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.; Wojtasiak, A.; Owyong, S.; Sun, B.; Fang, Y.; Vassigh, S.; Lin, A. Biomimetic self-shading walls via 3D-printing for reduced heat gain: Multiscale learning using graph neural networks to predict solar radiation absorption. Build. Environ. 2025, 279, 113048. [Google Scholar] [CrossRef]
- Motamedi, S.; Liedl, P. Integrative algorithm to optimize skylights considering fully impacts of daylight on energy. Energy Build. 2017, 138, 655–665. [Google Scholar] [CrossRef]
- Fang, Y.; Cho, S. Design Optimization of building geometry and fenestration for daylighting and energy performance. Sol. Energy 2019, 191, 7–18. [Google Scholar] [CrossRef]
- Shi, L.; Li, Y.; Tao, L.; Zhang, Y.; Jiang, X.; Yang, Z.; Qi, X.; Qiu, J. Sporters’ visual comfort assessment in gymnasium based on subjective evaluation & objective physiological response. Build. Environ. 2022, 225, 109678. [Google Scholar]
- Bian, Y.; Luo, Y.; Hu, L.; Liu, L.; Pang, Y. Visual discomfort assessment in an open-plan space with skylights: A case study with POE survey and retrofit design. Energy Build. 2021, 248, 111215. [Google Scholar] [CrossRef]
- Loy-Benitez, J.; Li, Q.; AIfaei, P.; Nam, K.; Heo, S.; Yoo, C. A dynamic gain-scheduled ventilation control system for a subway station based on outdoor air quality conditions. Build. Environ. 2018, 144, 159–170. [Google Scholar] [CrossRef]
- Albatayneh, A.; Juaidi, A.; Abdallah, R.; Manzano-Agugliaro, F. Influence of the advancement in the LED lighting technologies on the optimum windows-to-wall ratio of Jordanians residential buildings. Energies 2021, 14, 5446. [Google Scholar] [CrossRef]
- Al-Janabi, A.; Kavgic, M.; Mohammadzadeh, A.; Azzouz, A. Comparison of EnergyPlus and IES to model a complex university building using three scenarios: Free-floating, ideal air load system, and detailed. J. Build. Eng. 2019, 22, 262–280. [Google Scholar] [CrossRef]
- Pan, Y.; Zhu, M.; Lv, Y.; Yang, Y.; Liang, Y.; Yin, R.; Yang, Y.; Jia, X.; Wang, X.; Zeng, F.; et al. Building energy simulation and its application for building performance optimization: A review of methods, tools, and case studies. Adv. Appl. Energy 2023, 10, 100135. [Google Scholar] [CrossRef]
- Sun, W.; Feng, L.; Abed, A.M.; Sharma, A.; Arsalanloo, A. Thermoeconomic assessment of a renewable hybrid RO/PEM electrolyzer integrated with Kalina cycle and solar dryer unit using response surface methodology (RSM). Energy 2022, 260, 124947. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, W.; Wang, Q. Multi-objective parametric optimization of the composite external shading for the classroom based on lighting, energy consumption, and visual comfort. Energy Build. 2022, 275, 112441. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, D.; Zhen, M.; Jing, W.; Luo, W.; Feng, W. Combined effects of the thermal-acoustic environment on subjective evaluations in outdoor public spaces. Sustain. Cities Soc. 2022, 77, 103522. [Google Scholar] [CrossRef]
- Wang, H.; Owyong, S.; Shi, A.; Shin, S.; Nguyen, T.H.; Lin, A. Investigating on thermal insulation in concrete partition wall with insulation-material-infilled Voronoi sections. J. Build. Eng. 2024, 96, 110437. [Google Scholar] [CrossRef]
- Bi, Y.; Lin, Y.; Qin, L.; Wang, H.; Sun, R. Performance optimization of a solar air conditioning with a three-phase accumulator based on the energy-economic analysis. J. Build. Eng. 2022, 59, 105065. [Google Scholar] [CrossRef]
- Yu, Z.; Zhu, X.; Liu, X. Characterizing metro stations via urban function: Thematic evidence from transit-oriented development (TOD) in Hong Kong. J. Transp. Geogr. 2022, 99, 103299. [Google Scholar] [CrossRef]
- Su, S.; Zhang, H.; Wang, M.; Weng, M.; Kang, M. Transit-oriented development (TOD) typologies around metro station areas in urban China: A comparative analysis of five typical megacities for planning implications. J. Transp. Geogr. 2021, 90, 102939. [Google Scholar] [CrossRef]
- Kumar, P.; Sekhar, P.C.H.; Ravi, C.H.; Parida, M. Identification of neighborhood typology for potential transit-oriented development. Transp. Res. D 2020, 78, 102218. [Google Scholar]
- Hu, M.; Liu, M.; You, D.; Zhang, Y. Influence of train arrival characteristics on unorganized ventilation in underground subway station with platform screen doors. J. Wind Eng. Ind. Aerod. 2020, 198, 104089. [Google Scholar] [CrossRef]
- Antoniou, F.; Aretoulis, G.; Giannoulakis, D.; Konstantinidis, D. Cost and material quantities prediction models for the construction of underground metro stations. Buildings 2023, 13, 382. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).