Analysis of Seismic Performance for Segmentally Assembled Double-Column Bridge Structures Based on Equivalent Stiffness
Abstract
1. Introduction
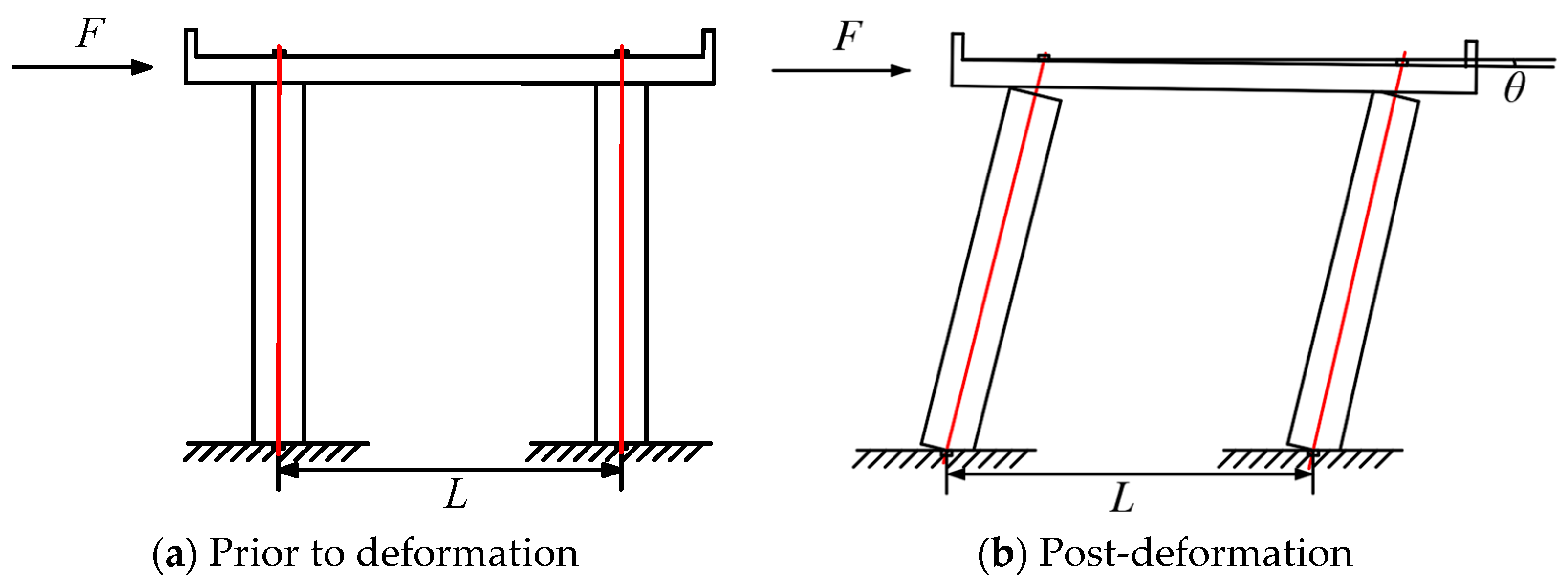
2. Equivalent Stiffness Theoretical Model and Derivation Formula
2.1. Finite Strip Method
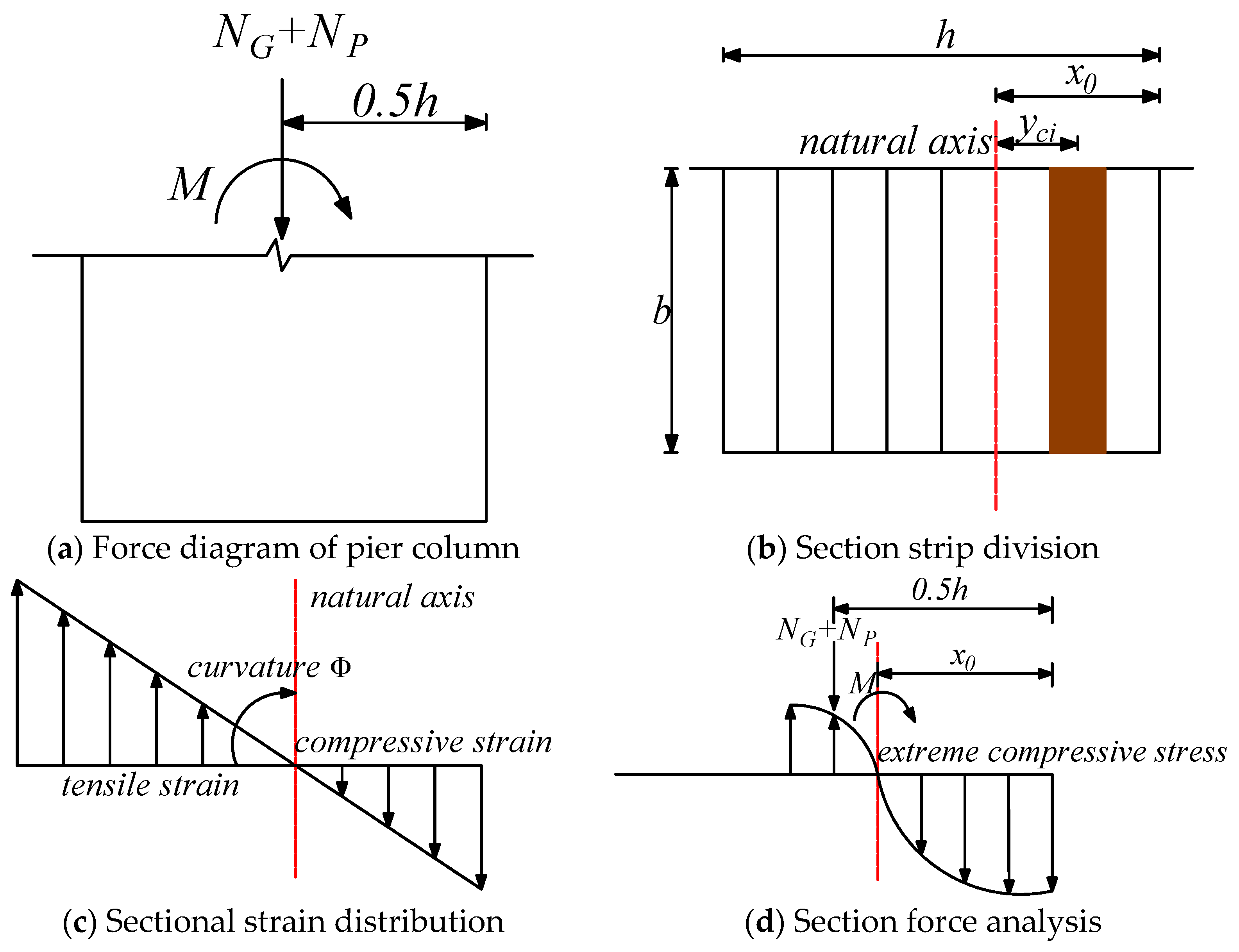
2.2. Cross-Section Damage-State Analysis
2.2.1. Decompression State
2.2.2. Yield State
2.2.3. Design-Limit States
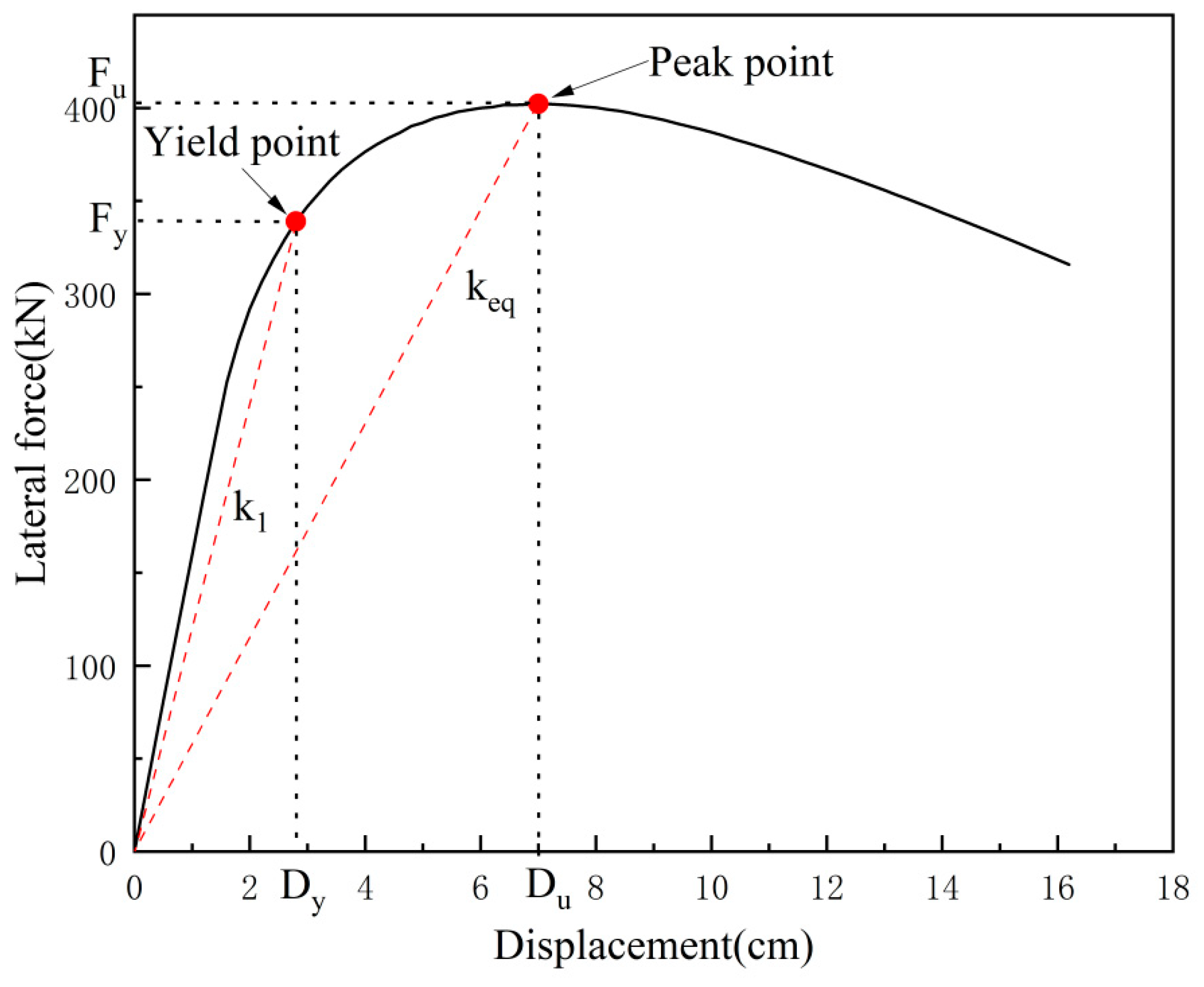
2.3. Equivalent Stiffness Theory Derivation
3. Software Modeling
3.1. Establish Finite Element Model
3.2. Key Issues
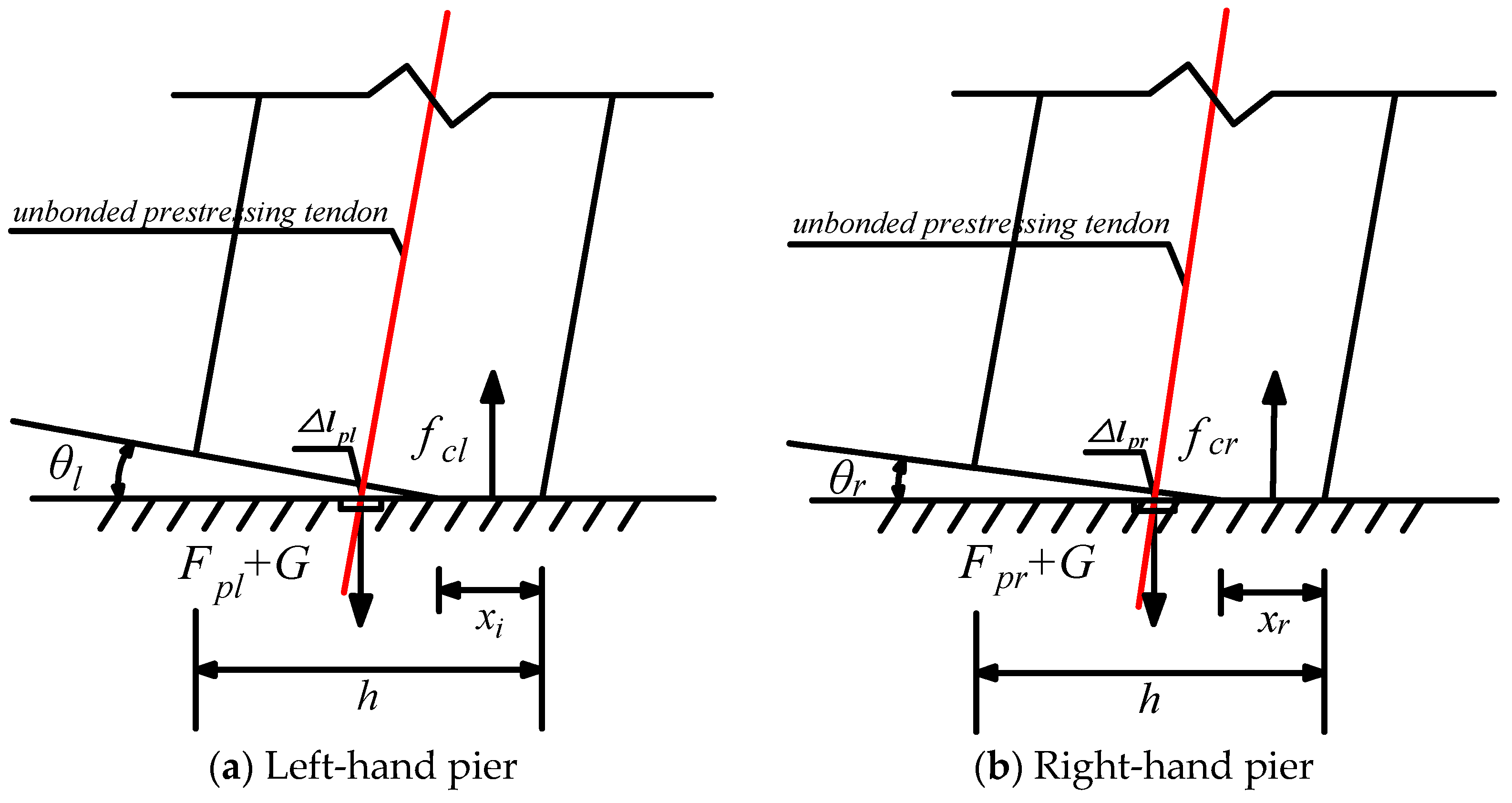
3.2.1. Prestressed Tendons
3.2.2. Joints
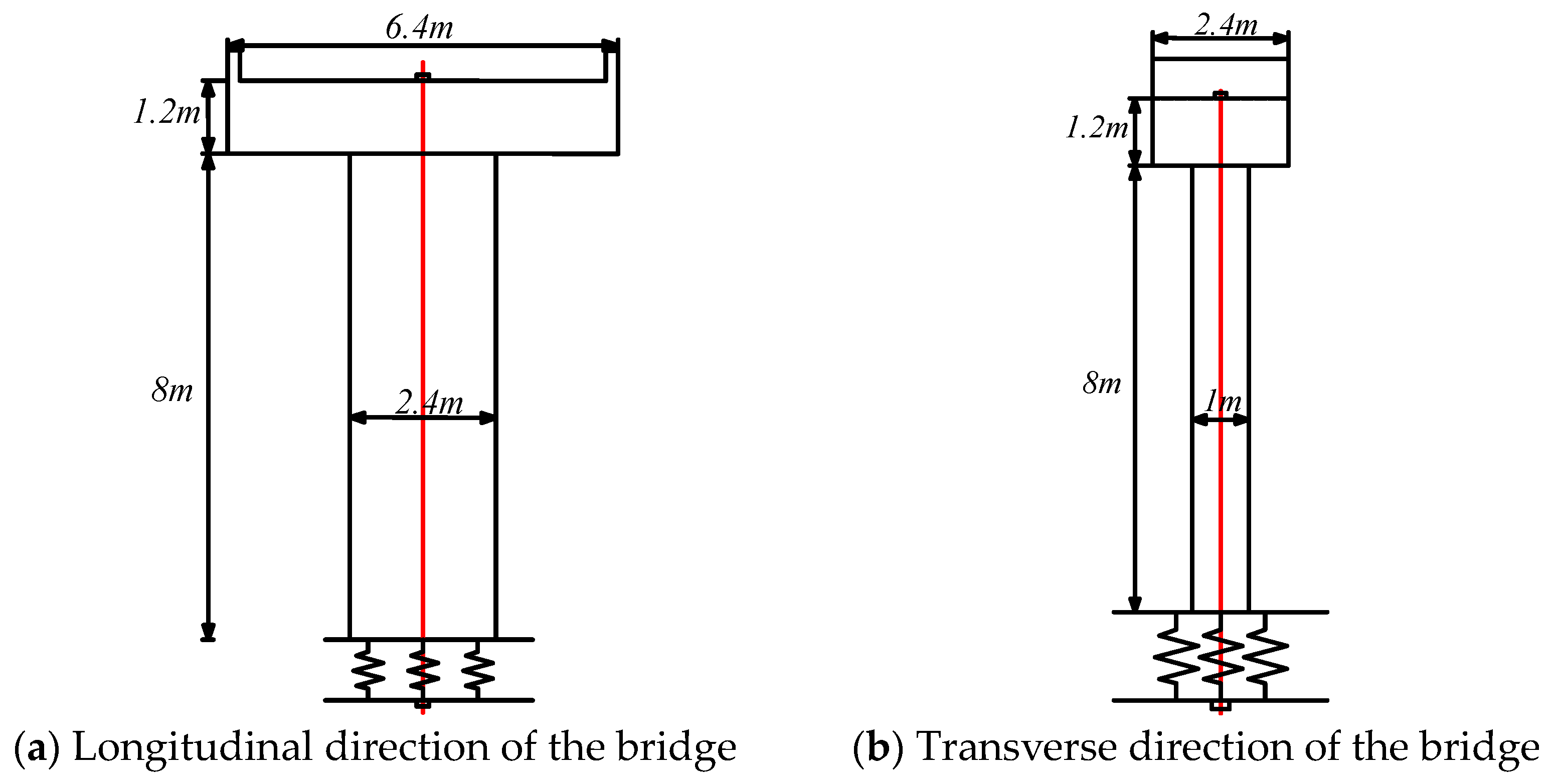
3.3. Double-Column SC-SAB Structure
3.4. Single-Column SC-SAB Structure
4. Numerical Study
4.1. Pushover Analysis
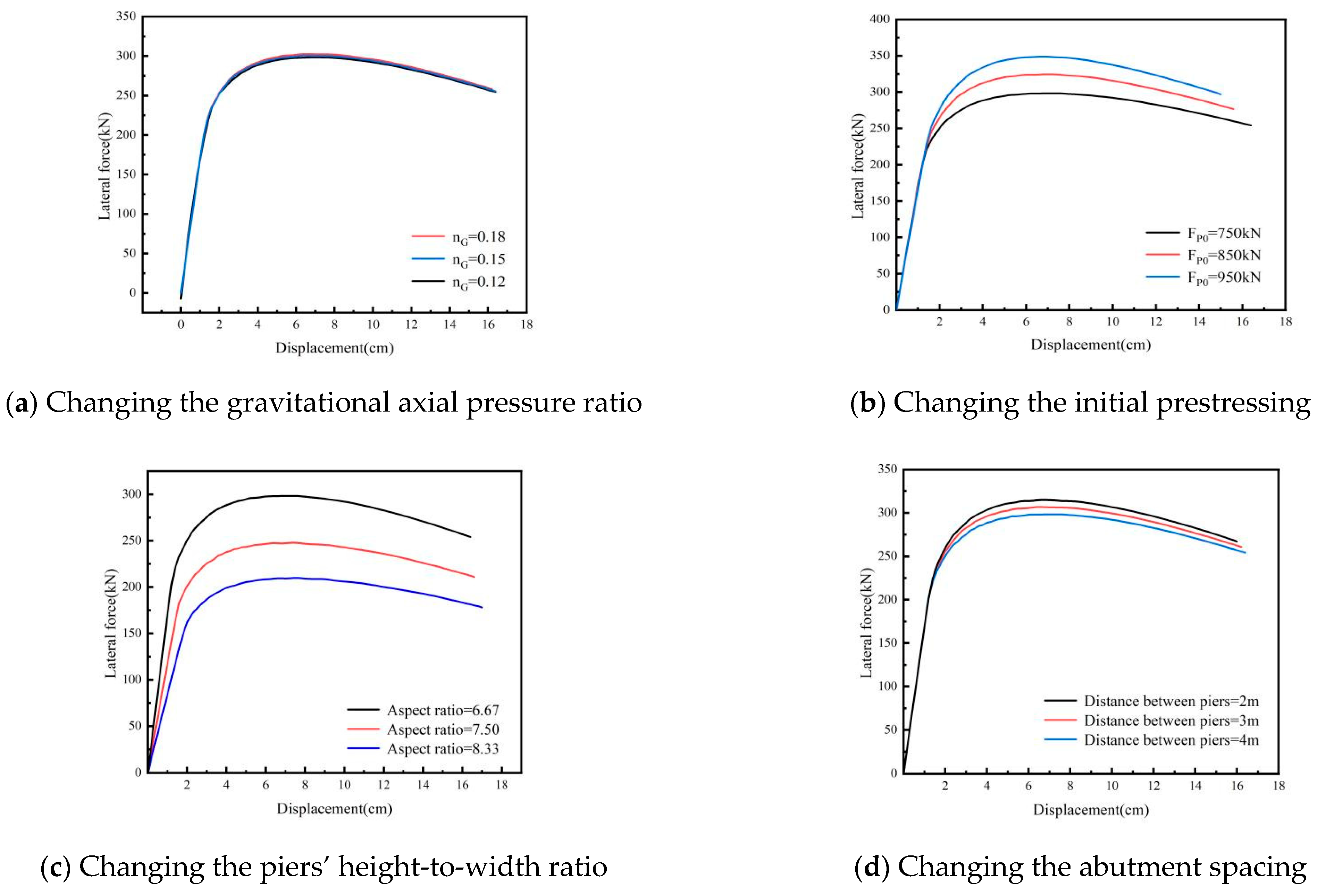
4.1.1. Gravitational Axial Pressure Ratio Under Pushover Analysis
4.1.2. Initial Prestressing Under Pushover Analysis
4.1.3. Piers’ Height-to-Width Ratios Under Pushover Analysis
4.1.4. Abutment Spacing Under Pushover Analysis
4.2. Hysteretic Response Analysis
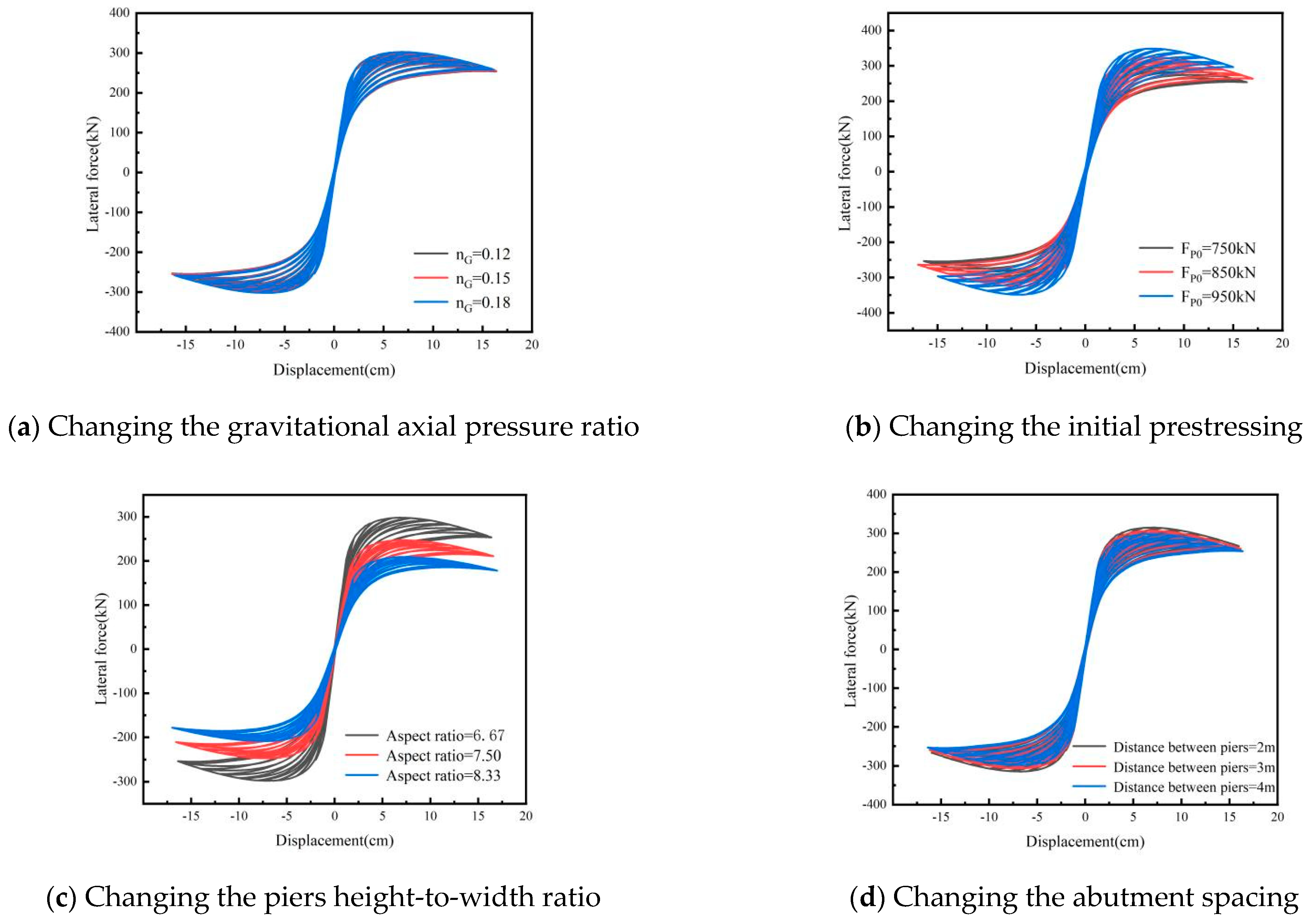
4.2.1. Gravitational Axial Pressure Ratio Under Hysteretic Analysis
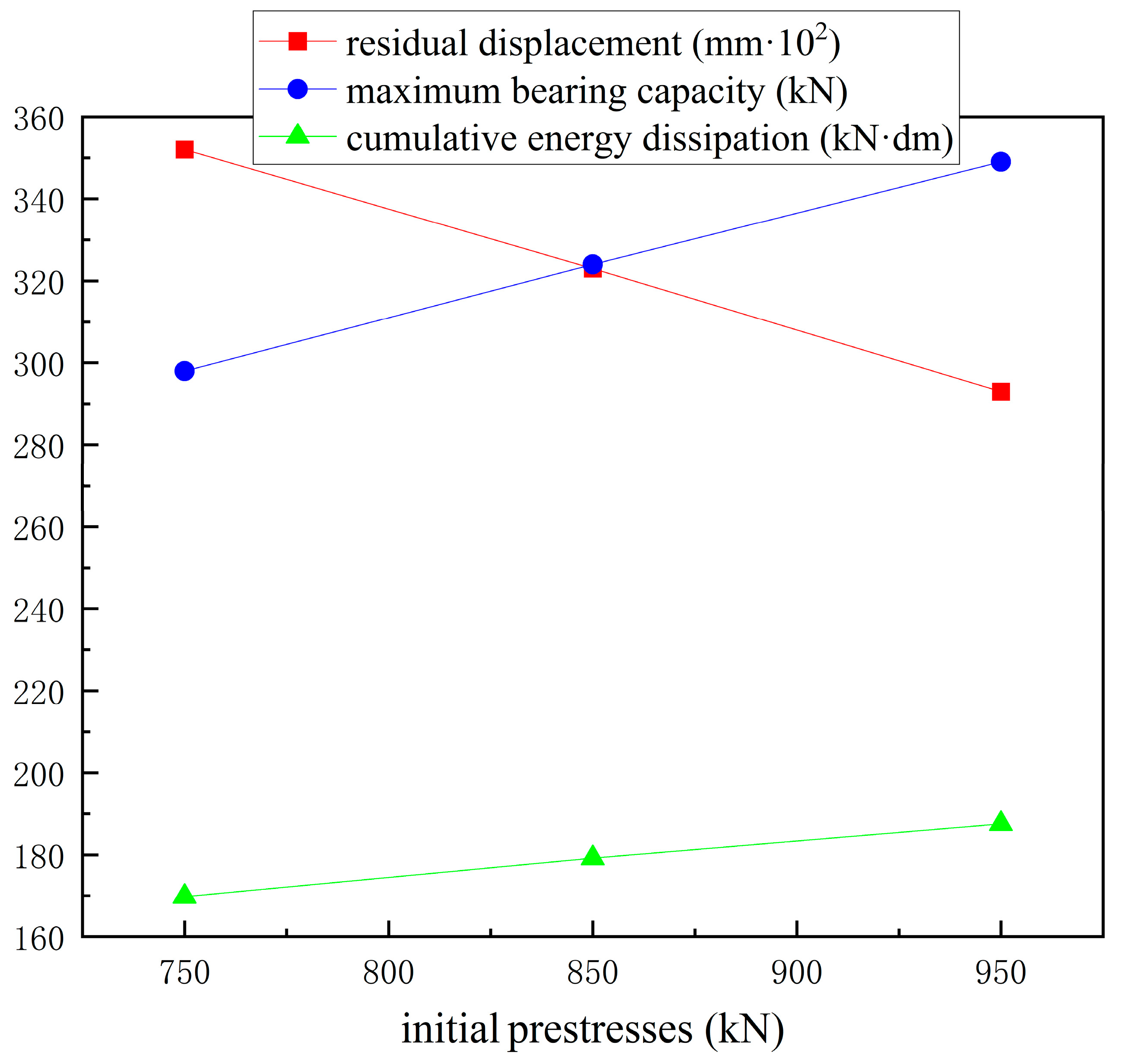
4.2.2. Initial Prestressing Under Hysteretic Analysis
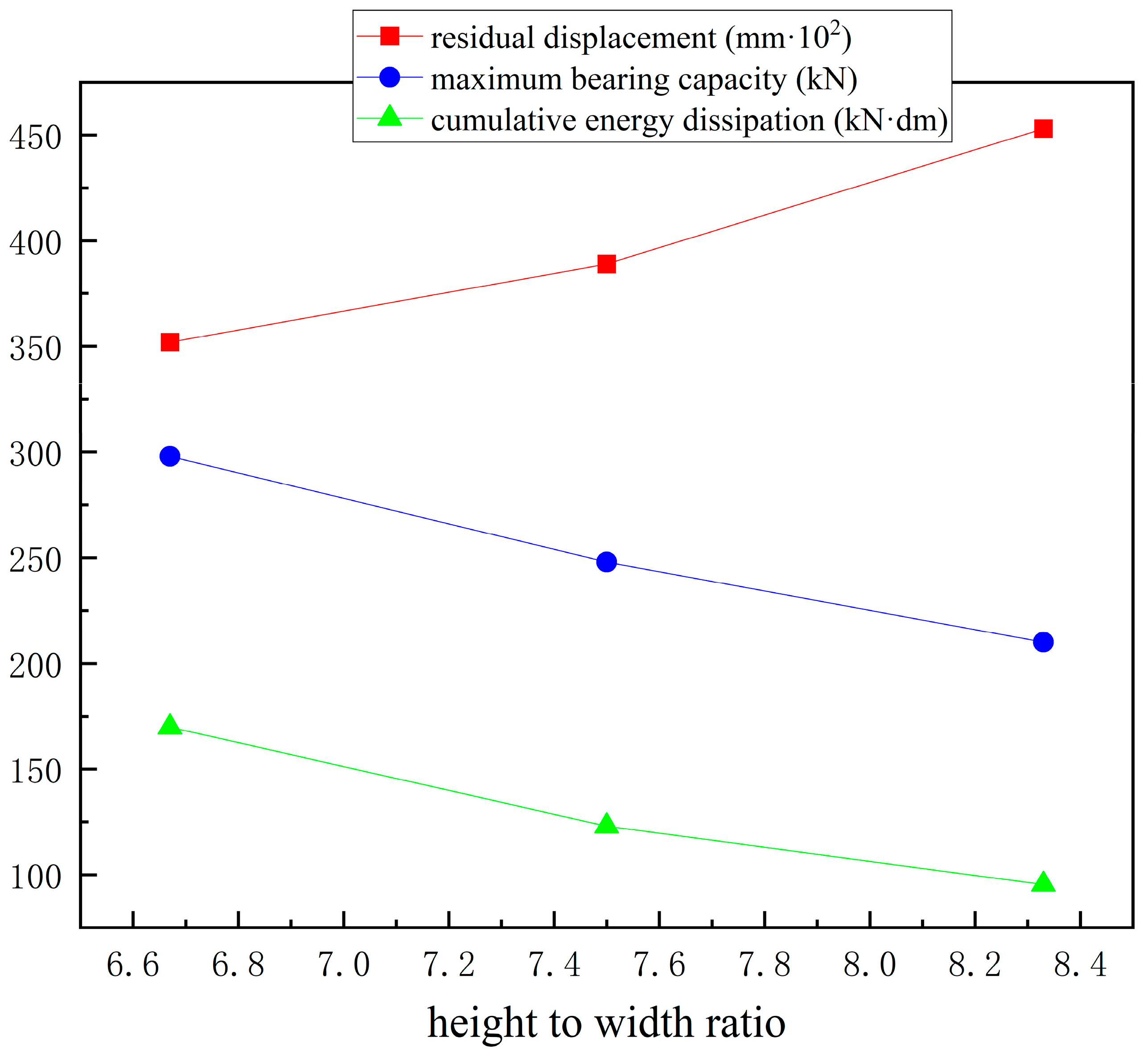
4.2.3. Piers’ Height-to-Width Ratio Under Hysteretic Analysis
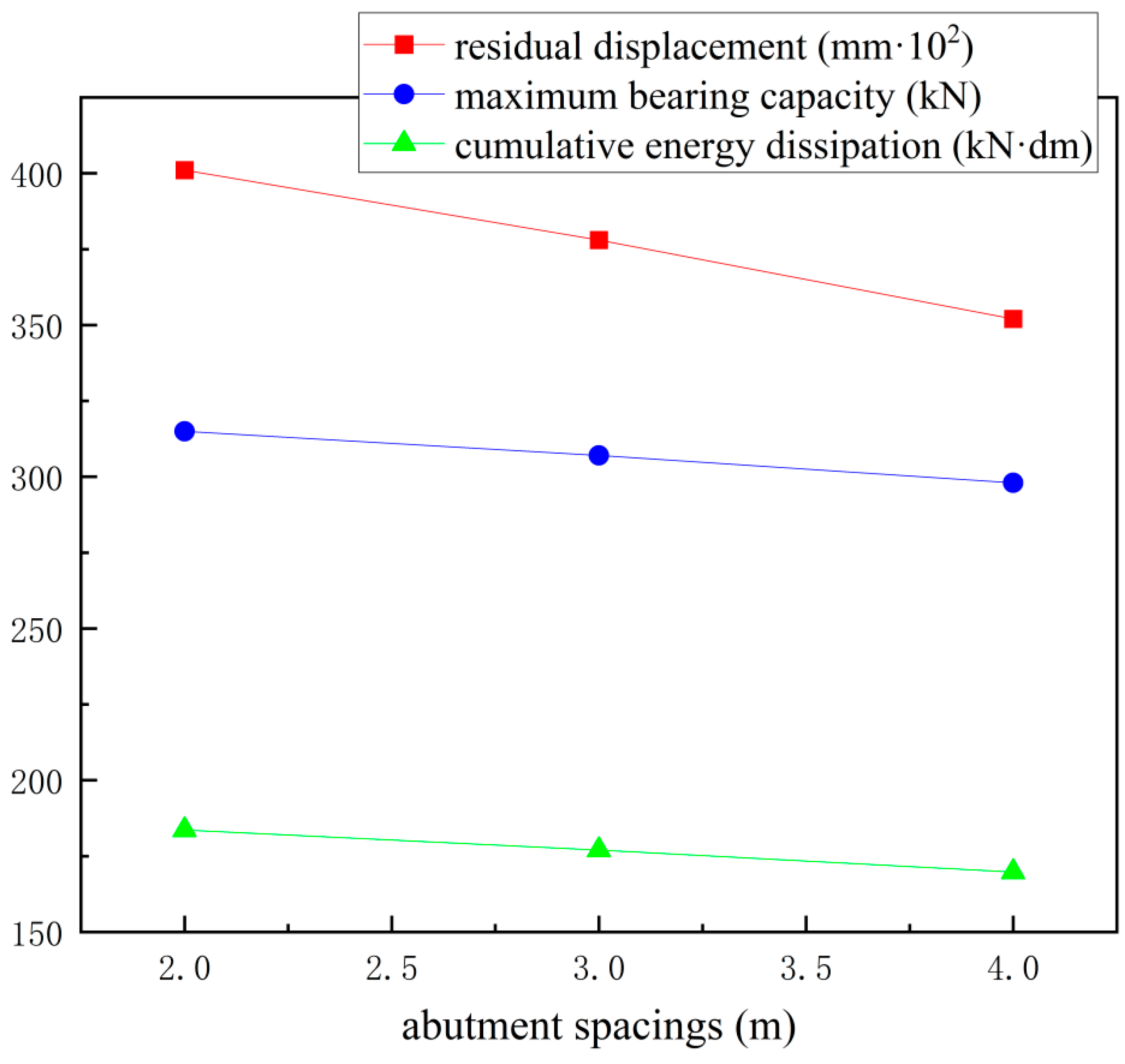
4.2.4. Abutment Spacing Under Hysteretic Analysis
5. Conclusions
Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, H.; Han, Q.; Du, X. Seismic resilience evaluation of self-centering bridge systems: A state-of-the-art review. Eng. Struct. 2021, 242, 112532. [Google Scholar] [CrossRef]
- Wang, J.; Guo, A.; Li, C. Residual drift control in self-centering bridge piers: A meta-analysis of 62 experimental studies. Eng. Struct. 2020, 213, 110602. [Google Scholar] [CrossRef]
- Palermo, A.; Mashal, M.; Tani, M. Flag-shaped hysteresis in post-tensioned concrete structures: Theoretical modeling and experimental validation. J. Struct. Eng. 2021, 147, 04020354. [Google Scholar] [CrossRef]
- Marriott, D.; Pampanin, S.; Bull, D. Minimum prestress requirements for self-centering capability in segmental bridge columns. Earthq. Spectra 2022, 38, 456–478. [Google Scholar]
- Kavianipour, F.; Saiidi, M.S. Accelerated construction of self-centering bridges: Case studies. J. Bridge Eng. 2021, 26, 04021012. [Google Scholar] [CrossRef]
- Bu, Z.; Ou, Y.; Song, J. Energy dissipation in unbonded post-tensioned bridge piers: Experimental quantification and modeling. Eng. Struct. 2020, 223, 111156. [Google Scholar] [CrossRef]
- JTG/T 3360-2-2018; Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts. China Communications Press: Beijing, China, 2018.
- Nikoukalam, M.; Sideris, P. Damping characteristics of hybrid self-centering bridge columns with replaceable dissipaters. J. Earthq. Eng. 2021, 25, 1531–1552. [Google Scholar] [CrossRef]
- Dong, H.; Du, X.; Han, Q.; Bi, K.; Hao, H. Hysteretic performance of RC double-column bridge piers with self-centering buckling-restrained braces. Bull. Earthq. Eng. 2019, 17, 3255–3281. [Google Scholar] [CrossRef]
- Dong, H.; Han, Q.; Du, X. Replaceable energy-dissipating devices for self-centering bridge piers: Experimental and numerical study. J. Struct. Eng. 2020, 146, 04020177. [Google Scholar] [CrossRef]
- Qian, H.; Yan, C.; Jin, G. Superelastic SMA bars as supplemental dampers in self-centering bridge piers: Full-scale validation. Constr. Build. Mater. 2022, 319, 126065. [Google Scholar] [CrossRef]
- Zhao, Z.; He, H.S.; Yuan, L.; Li, J. Review of experimental investigations on seismic performance of precast segmental bridge columns in seismic regions. Adv. Struct. Eng. 2023, 26, 1161–1186. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, Y.; He, S.; Chen, X. Study on the seismic performance of unbonded prestressed combination. Bridge Constr. 2022, 52, 58–65. [Google Scholar]
- Qian, H.; Yang, Y.; Yang, C. Experimental study on the seismic performance of self-centering bridge piers incorporating ECC and superelastic SMA bars. Structures 2022, 46, 1955–1967. [Google Scholar] [CrossRef]
- Qian, H.; Qiu, P.; Jin, G. Study on seismic performance of SMA/ECC pier column. Eng. Mech. 2023, 40, 172–183. [Google Scholar]
- Zhao, Z.; Yuan, L.; Chao, M. Quasi-static cyclic tests on seismic performance of partial precast bridge columns. KSCE J. Civ. Eng. 2023, 27, 4288–4299. [Google Scholar] [CrossRef]
- Jia, J.; Tan, Y.; Bai, B. Seismic performance analysis of self-resetting prefabricated RC piers. J. Appl. Basic Eng. Sci. 2022, 30. [Google Scholar]
- Jia, J.; Bian, J.; Li, Y. Numerical simulation of self-centering double-column piers. J. Vib. Shock 2023, 42, 89–96. [Google Scholar]
- He, S.; Zhu, L.; Zhu, Z. Analysis of seismic design parameters for prefabricated bridge piers. J. Chongqing Jiaotong Univ. 2023, 42, 89–98. [Google Scholar]
- Liu, Z.; He, S.; Zhu, Z. Seismic performance analysis of partial precast piers. Highway. Transp. Tech. 2023, 40, 82–90. [Google Scholar]
- Sideris, P. Seismic Analysis and Design of Precast Concrete Segmental Bridges. Ph.D. Thesis, State University of New York, Buffalo, NY, USA, 2012. [Google Scholar]
- Wu, J.; Zhang, J.; Xie, L.; Wei, Y.; Tong, C. Experimental and theoretical investigations of post-tensioned precast reinforced concrete bridge pier with external replaceable energy dissipaters. Eng. Struct. 2023, 294, 116719. [Google Scholar] [CrossRef]
- Motaref, S.; Saiidi, M.S. Influence of column coupling on seismic response of self-centering bridge bents. Eng. Struct. 2023, 278, 115466. [Google Scholar] [CrossRef]
- Motaref, S.; Saiidi, M.S. Multi-spring modeling for segmental columns. Earthq. Eng. Struct. Dyn. 2023, 52, 189–211. [Google Scholar] [CrossRef]
- Gao, H.; Song, Y.; Yuan, W.; Lu, H.; Cao, S. Seismic Design Method of Self-Centring-Segment Bridge Piers with Tensile-Type Viscoelastic Dampers. Adv. Civ. Eng. 2021, 2021, 6688006. [Google Scholar] [CrossRef]
- JTG/T B02-1-2010; Seismic Design Specifications for Highway Bridges. China Communications Press: Beijing, China, 2008.
- Xue, G.; Guo, X. Nonlinear full process analysis of flexural stiffness of reinforced concrete beams. J. Inn. Mong. Univ. Sci. Technol. 2007, 3, 250–252. [Google Scholar]
- Cai, Z. Seismic Performance and Design Method of Hybrid Reinforced Precast Segmental Bridge Columns. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Kurama, Y.C. Hybrid post-tensioned precast concrete walls for use in seismic regions. PCI J. 2002, 47, 36–59. [Google Scholar] [CrossRef]





| Concrete | Prestressed Reinforcement | ||||
|---|---|---|---|---|---|
| Compressive Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) |
| 30 | 30 | 0.2 | 1670 | 1860 | 195 |
| Pier Stiffness | Simulated Value (kN/m) | Theoretical Value (kN/m) | Error (%) |
|---|---|---|---|
| yield stiffness | 12,108 | 11,977 | 1.08 |
| equivalent stiffness | 5745 | 5509 | 4.11 |
| Double-Column | Single-Column | Error (%) | |
|---|---|---|---|
| peak displacement (cm) | 7.0 | 7.2 | 2.86 |
| peak bearing capacity (kN) | 402 | 403 | 0.25 |
| Axial Compression Ratio | Yield Displacement (cm) | Yield Stiffness (kN/m) | Peak Displacement (cm) | Peak Bearing Capacity (kN) | Ultimate Displacement (cm) | Ultimate Bearing Capacity (kN) |
|---|---|---|---|---|---|---|
| 0.12 | 2.8 | 9679 | 7.0 | 298 | 16.4 | 254 |
| 0.15 | 2.8 | 9832 | 6.4 | 301 | 16.4 | 255 |
| 0.18 | 3.0 | 9875 | 6.2 | 303 | 16.2 | 258 |
| Initial Prestress (kN) | Yield Displacement (cm) | Yield Stiffness (kN/m) | Peak Displacement (cm) | Peak Bearing Capacity (kN) | Ultimate Displacement (cm) | Ultimate Bearing Capacity (kN) |
|---|---|---|---|---|---|---|
| 750 | 2.8 | 9679 | 7.0 | 298 | 16.4 | 254 |
| 850 | 2.6 | 11,038 | 7.0 | 324 | 15.6 | 276 |
| 950 | 2.4 | 12,333 | 6.8 | 349 | 15.0 | 297 |
| Height-to-Width Ratio | Yield Displacement (cm) | Yield Stiffness (kN/m) | Peak Displacement (cm) | Peak Bearing Capacity (kN) | Ultimate Displacement (cm) | Ultimate Bearing Capacity (kN) |
|---|---|---|---|---|---|---|
| 6.67 | 2.8 | 9679 | 7.0 | 298 | 16.4 | 254 |
| 7.50 | 3.0 | 7500 | 7.4 | 248 | 16.6 | 211 |
| 8.33 | 3.2 | 5938 | 7.6 | 210 | 17.0 | 178 |
| Abutment Spacing (m) | Yield Displacement (cm) | Yield Stiffness (kN/m) | Peak Displacement (cm) | Peak Bearing Capacity (kN) | Ultimate Displacement (cm) | Ultimate Bearing Capacity (kN) |
|---|---|---|---|---|---|---|
| 2.0 | 3.2 | 9156 | 6.6 | 315 | 16.0 | 267 |
| 3.0 | 3.0 | 9433 | 6.6 | 307 | 16.2 | 261 |
| 4.0 | 2.8 | 9679 | 7.0 | 298 | 16.4 | 254 |
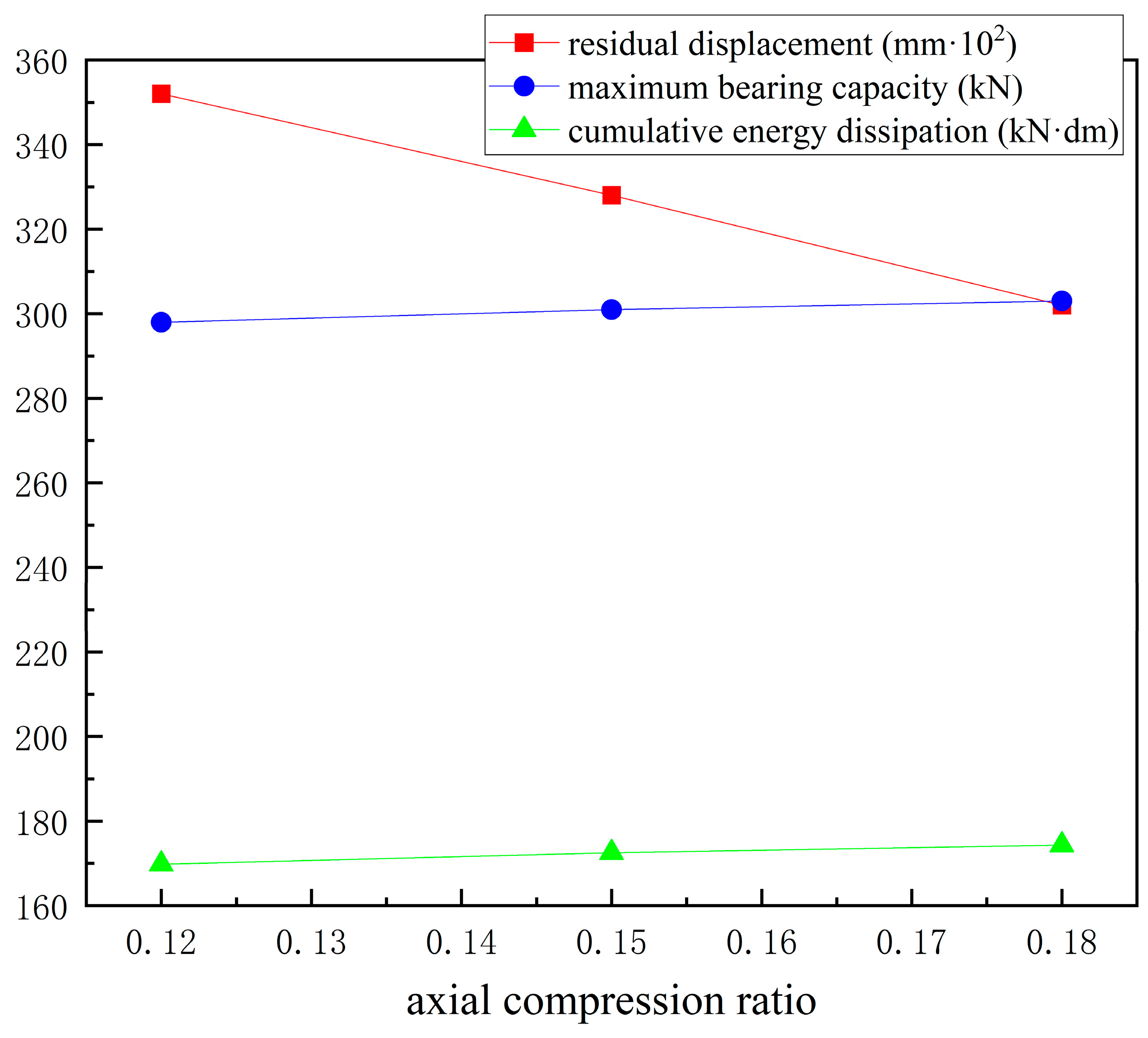
| Axial Compression Ratio | Residual Displacement (mm) | Cumulative Energy Dissipation (kN·m) | Maximum Bearing Capacity (kN) |
|---|---|---|---|
| 0.12 | 3.52 | 16.98 | 298 |
| 0.15 | 3.28 | 17.25 | 301 |
| 0.18 | 3.02 | 17.43 | 303 |
| Initial Prestresses (kN) | Residual Displacement (mm) | Cumulative Energy Dissipation (kN·m) | Maximum Bearing Capacity (kN) |
|---|---|---|---|
| 750 | 3.52 | 16.98 | 298 |
| 850 | 3.23 | 17.92 | 324 |
| 950 | 2.93 | 18.75 | 349 |
| Height-to-Width Ratios | Residual Displacement (mm) | Cumulative Energy Dissipation (kN·m) | Maximum Bearing Capacity (kN) |
|---|---|---|---|
| 6.67 | 3.52 | 16.98 | 298 |
| 7.50 | 3.89 | 12.30 | 248 |
| 8.33 | 4.53 | 9.54 | 210 |
| Abutment Spacings (m) | Residual Displacement (mm) | Cumulative Energy Dissipation (kN·m) | Maximum Bearing Capacity (kN) |
|---|---|---|---|
| 2.0 | 4.01 | 18.36 | 315 |
| 3.0 | 3.78 | 17.70 | 307 |
| 4.0 | 3.52 | 16.98 | 298 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Xia, W.; Liu, G. Analysis of Seismic Performance for Segmentally Assembled Double-Column Bridge Structures Based on Equivalent Stiffness. Buildings 2025, 15, 1919. https://doi.org/10.3390/buildings15111919
Gao H, Xia W, Liu G. Analysis of Seismic Performance for Segmentally Assembled Double-Column Bridge Structures Based on Equivalent Stiffness. Buildings. 2025; 15(11):1919. https://doi.org/10.3390/buildings15111919
Chicago/Turabian StyleGao, Huixing, Wenjing Xia, and Guoqing Liu. 2025. "Analysis of Seismic Performance for Segmentally Assembled Double-Column Bridge Structures Based on Equivalent Stiffness" Buildings 15, no. 11: 1919. https://doi.org/10.3390/buildings15111919
APA StyleGao, H., Xia, W., & Liu, G. (2025). Analysis of Seismic Performance for Segmentally Assembled Double-Column Bridge Structures Based on Equivalent Stiffness. Buildings, 15(11), 1919. https://doi.org/10.3390/buildings15111919




