Abstract
Addressing the shortcomings of currently available concrete reinforcement techniques, a new method using sprayed Glass Fibre Epoxy Mortar (GFEM) reinforcement is proposed. To investigate the effect of this method on the frost durability of concrete, a total of 156 specimens in four groups were designed, and related freezing and thawing cycle tests were conducted. The apparent morphology, mass loss rate, ultrasonic velocity, freeze–thaw damage, and strength loss rate of each group of specimens after different freeze–thaw cycles were analysed comparatively. The test results show that the concrete specimens reinforced with GFEM have a better mass loss rate after freeze–thaw cycles and ultrasonic wave velocity than the unreinforced concrete specimens. The compressive strength of specimens in group A is 24.04 MPa, and the compressive strengths of specimens in groups B, C, and D are 35.28 MPa, 35.73 MPa, and 36.37 MPa, respectively, which is higher than that of group A by 46.76%, 48.63%, and 51.29%, respectively, and 46.76%, 48.63%, and 51.29% higher than group A, respectively. It can be seen that the concrete specimens reinforced with sprayed Glass Fibre Epoxy Mortar can effectively improve the frost durability of concrete; the reinforcing effect is obvious, and in a certain range of fibre mixing, the larger the better the frost resistance. The integration of GFEM is cost-effective and improves viscosity, and the best glass fibre mix percentage is about 0.8%. A freeze–thaw damage model for GFEM-reinforced concrete was developed using the Weibull distribution theory, and an improved strength attenuation model under freeze–thaw cycles was established. By correlating the strength attenuation model with the freeze–thaw damage model, a damage evolution equation for the reinforced specimens was formulated, allowing for the prediction of freeze–thaw damage based on the number of cycles and the relative compressive strength.
1. Introduction
In buildings exposed to the natural environment over extended periods, external materials gradually erode the structure, weakening material properties. Consequently, a building’s structural safety, functionality, and durability may no longer meet the unified standards of structural reliability design. To address varying degrees of ageing [1] or weakened structural performance, targeted reinforcement is required to restore structural capacity, stiffness, and durability.
Currently, the common reinforcement methods mainly include the increase section reinforcement method [2,3], the external steel reinforcing method [4,5], the adhesive steel reinforcement method [6], the prestressed reinforcement method [7,8,9], and the paste fibre-reinforced composite reinforcement method [10,11,12]. However, the current reinforcement methods used in China have various shortcomings, including complex construction processes, significant on-site wet work, high costs, and uncontrollable bond strength. Therefore, this paper proposes a new reinforcement method: spray GFEM technology on the external surfaces of buildings or component nodes. Glass fibre [13] has high tensile strength, high modulus, and good plasticity and toughness, which can give full play to the role of crack-blocking and toughening so that the number of micro-cracks in the early stage of hydration of the GFEM-reinforced layer is significantly reduced, effectively inhibiting the cracks and expansion, and reducing the possibility of internal micro-porosity expansion and penetration, whereas epoxy mortar [14,15,16] is a widely used repair material in civil engineering. Epoxy mortar is composed of epoxy resin, diluent, curing agent, coupling agent, and other organic components, along with cement, sand, and other inorganic components in specific proportions. This combination yields new building structural materials with high compressive strength and durability. Applying this mixture using an air compressor for spraying offers easy construction, excellent durability, and broad applicability, making it an effective structural reinforcement method.
Regarding the current status of research on the freeze durability of concrete, Cao, D.F [17] and others found that the degree of decrease in concrete quality and dynamic elastic modulus gradually increased with the increase in the number of freezing and thawing cycles, while the higher the strength grade, the slower the decrease. Li, W.S [18] found that after 50 cycles of freezing and thawing, the rate of loss of quality and strength of ordinary concrete decreased below the specification requirements and the concrete failed.
Yu, X.M. [19] pointed out through experimental research that the essence of freeze–thaw damage is the process of concrete under the freeze–thaw environment. The internal damage gradually accumulates and expands, leading to the volume expansion of concrete, the structure becomes crispy and then causes cracking and damage to the concrete.
Shang, H.S’s [20] study is based on the fatigue cumulative damage theory and the freeze–thaw damage characteristics of concrete reliability analysis.
Powers, T.C. [21] pointed out that the main reason for the freeze–thaw damage of concrete structures is the pore water infiltration pressure.
Li, J.Y. [22] proposed that freeze–thaw damage is a phenomenon in which already hardened concrete is saturated with immersion water or is in a wet state and is subjected to a freeze–thaw environment, which results in the gradual denudation and destruction of the concrete from the outside and the inside.
Li, J.Z. [23] investigated the deterioration characteristics of concrete properties during the freeze–thaw cycle and discussed the changes in concrete flexural strength and split tensile strength under a freeze–thaw environment.
Tang, G.P. [24] established the material damage evolution equation by applying the damage mechanics method according to the mechanism of concrete freeze–thaw cycle damage, and established the evolution model of concrete freeze–thaw damage surface in the principal stress space by applying the concept of “effective stress”.
The current status of research on the frost durability of reinforced concrete is as follows:
Moceikis, R. et al. [25] found that glass fibre concrete showed good frost resistance after 112 freeze–thaw cycles in de-icing salt solution.
Meng, S.Y. et al. [26] investigated the effect of different types of fibre concrete on resistance to freeze–thaw cycles, and the test results showed that glass fibres can effectively improve the frost resistance of concrete.
Xu, L.N. et al. [27] found that glass fibre concrete has less strength loss, higher peak strength, and less destructive strain than basalt fibre concrete during freeze–thaw cycle tests.
Shen, R.X. [28], of the China Academy of Building Materials Science, added synthetic fibres to ordinary concrete as a way to study its mechanism of action on concrete, while the enhancement mechanism of synthetic fibres on concrete was concluded based on the experimental data and results, i.e., improved crack-resisting and toughening properties of concrete.
Cheng, Y.H. et al. [29] compared the frost resistance of three types of fibre concrete (steel fibre, alkali-resistant glass fibre, and polypropylene fibre) and determined that polypropylene fibre concrete had the best frost resistance through tests such as dynamic modulus of elasticity and mass loss.
Ning, B.K. et al. [30] investigated the changes in mechanical properties of concrete beams reinforced with carbon fibre cloth under the coupling of prestressing and freeze–thaw cycles.
Liu, L.N. et al. [31] compared and analysed the effects of freeze–thaw cycles and pre-existing bond defects on the bond performance of carbon fibre-reinforced members, and used a non-destructive Pulse Imaging Tester (PPT) to assess the performance of bonded surfaces.
Wei, C.Y. et al. [32] considered the effect of freeze–thaw cycling on double-layer glass fibre tube concrete members and carried out a study on the axial compression and seismic performance of combined columns under freeze–thaw cycling.
These national and international studies indicate extensive research on freeze–thaw concrete with many important findings. However, current studies on fibre concrete’s frost resistance typically involve mixing fibres into the concrete to form specimens. There has been no research on applying GFEM to the concrete surface for reinforcement followed by freeze–thaw cycle testing. A GFEM reinforcement layer can effectively prevent the crack expansion inside the concrete specimen, and then ensure the overall frost resistance of the specimen. At present, the research direction of concrete structure reinforcement technology is increasingly diversified, and domestic and foreign research based on the traditional reinforcement methods is constantly developing and innovating, so the study of GFEM reinforcement of concrete structure frost resistance and durability is of practical significance.
In this paper, four groups of 156 concrete specimens were reinforced and subjected to freeze–thaw cycle tests using the sprayed GFEM reinforcement technique. The objective was to determine the impact of different fibre contents on the frost durability of the reinforced specimens. Additionally, a freeze–thaw damage model of GFEM-reinforced concrete was developed based on Weibull’s distribution theory [33], leading to the establishment of a strength attenuation model for the sprayed GFEM-reinforced concrete members.
2. Materials and Methods
2.1. Raw Materials and Mixing Ratios
This paper follows the Chinese code “Ordinary Concrete Proportion Design Regulations [34]” to select materials and prepare standard concrete. The C20 proportion of the matrix concrete is as follows: water, 175 kg/m3; cement, 343 kg/m3; sand, 621 kg/m3; gravel, 1261 kg/m3; slag powder, 20 kg/m3; and water reducing agent, 5.2 kg/m3. The test cement is P.O 42.5 grade ordinary Portland cement. The fine aggregate is river sand with a fineness modulus of 2.7, and the coarse aggregate is crushed stone with a good grading of 5–20 mm in diameter. The water-reducing agent is a hydroxyl agent with a water reduction rate of 20%. Following the Chinese code “Technical Specification for the Application of Mineral Admixtures [35]”, grade II fly ash and ordinary tap water were used. The epoxy mortar used in this test is a waterborne epoxy resin mortar produced by Dongguan Ruinard Building Materials Co. (Dongguan Ruina Building Materials Co., Ltd., Dongguan City, China), with its physical parameters and properties shown in Table 1. The glass fibre used in this test is made by Yangzhou Chaoheng Chemical Fiber Co. (Yangzhou Chaoheng Chemical Fibre Co., Ltd., Yangzhou, China), and its physical parameters and properties are shown in Table 2. The grouping of the test specimens and their parameters are detailed in Table 3.

Table 1.
Physical properties of epoxy mortar.

Table 2.
Physical properties of glass fibres.

Table 3.
Grouping of test specimens and parameters.
2.2. Preparation of Specimens
Different specifications and sizes of specimens are used to test compressive, tensile, and flexural strengths. Usually, small-sized specimens show higher strength than large-sized specimens, so the size of the specimen needs to be specified in the test design to obtain consistent test results.
Plain concrete specimens were produced by standards for the mechanical properties of concrete. Specimens with dimensions of 100 mm × 100 mm × 100 mm and 100 mm × 100 mm × 400 mm were fabricated to test mass, ultrasonic wave velocity, compressive strength, and relative dynamic elastic modulus. The total amount of materials used in the concrete was measured with an accuracy of ±0.4%, and cement and aggregate within ±1.2%. The concrete was moulded and vibrated to shape, with the formwork removed after approximately 24 h. The specimens were then placed in a curing room at a temperature of (20 ± 2) °C and a relative humidity of over 95% for curing. After 28 days of curing, the specimens were removed for the application of sprayed GFEM reinforcement.
After curing was completed, the surface of the specimen was polished to increase its roughness and improve adhesion between the GFEM and the specimen. The surface was then cleaned thoroughly. Epoxy mortar was prepared using a cement sand mixer, with different amounts of glass fibre added according to the required proportions. Following the Chinese code “Technical Specification for Epoxy Resin Mortar [36]”, a cementitious sand mixer was used to blend the epoxy mortar. First, the three components, epoxy resin emulsion (a), hardener (b), and powder (c) were mixed in a 3:1:21 ratio at low speed for 30 s. During this process, the specified amount of glass fibre was added. The mixer was then switched to high speed for another 30 s. After mixing, the process was paused for 90 s to scrape the epoxy mortar from the blades, pot walls, and bottom back into the pot. Mixing resumed at high speed for 60 s to ensure the fibre was evenly distributed within the epoxy mortar. Once mixing was complete, the GFEM was sprayed onto the surface of the specimens using an air compressor. The specimens were sprayed uniformly, one side at a time, with an infrared laser used to control the required thickness. After the initial setting, the process was repeated until all six surfaces were reinforced. The freeze–thaw cycle test was conducted after 28 days of curing under standard conditions.
2.3. Test Methods
The freeze–thaw cycle test was conducted using a fast freeze–thaw cycle testing machine for concrete, The instrument used is the HC-HDK9/F type concrete rapid freeze-thaw testing machine, using the following fast freeze method specified in the Chinese code “Test Procedure for Hydraulic Concrete” [37]: Firstly, put the test piece in the blast dryer at 100 °C (±5 °C) and dry for 24 h, weighing its initial mass, m0. After the test specimen has cooled, place it in water at 10–20 °C and soak for 24 h. then remove it after it has become fully saturated and weigh its saturated mass m1. After weighing, place the specimen in a rapid freeze-thaw machine pre-cooled to −15 °C, where it is frozen for 2 h at low temperature. Subsequently, control the rapid freeze–thaw machine to raise the temperature to an ambient temperature of 10 °C to 20 °C and thaw for 2 h, thereby completing one freeze–thaw cycle. The test process is shown in Figure 1. Every 25 cycles, the dynamic elastic modulus, ultrasonic wave velocity, mass, and compressive strength of the specimens were measured. The degree of visible damage was recorded. The test was stopped when any of the following conditions were met: the specified number of cycles was reached; the compressive strength loss rate reached 25%; the mass loss rate reached 5%; or the relative dynamic elastic modulus of the specimen decreased to less than 60%. Spraying GFEM equipment: This test uses a Shengtian oil-free air compressor to spray GFEM for the reinforcement test of concrete specimens, and the test apparatus is shown in Figure 2. The power of the instrument is 1.6 KW, the pressure is 0.8 Mpa, the exhaust volume is 150 L/min, and the capacity of the gas tank is 70 L, which meets the test requirements.

Figure 1.
Concrete specimen freeze–thaw cycle test.

Figure 2.
Shengtian oil-free air compressor.
3. Results
3.1. Analysis of Apparent Damage Patterns
Concrete freeze–thaw damage manifests as freeze cracking and surface spalling. As the number of freeze–thaw cycles increases, the damage worsens from the surface to the interior. Initially, small holes appear on the specimen, accompanied by slight slurry shedding. In the middle stage, significant slurry peeling occurs, the number of holes increases markedly, defects appear at the corners, and fine aggregate is gradually exposed. In the later stage, a substantial amount of fine aggregate is dislodged, exposing coarse aggregate, the surface becomes pitted, and macroscopic cracks develop. Figure 2 illustrates the apparent morphology of each group of concrete specimens throughout the freeze–thaw cycles.
As shown in Figure 3, the surface integrity of specimens A0, B0, C0, and D0 is well preserved after 0 freeze–thaw cycles. After 50 freeze–thaw cycles, surface spalling begins in specimen A2, while specimens B2, C2, and D2 exhibit increased holes but no concrete spalling. After 100 freeze–thaw cycles, specimen A4 is significantly damaged, with extensive surface spalling, loss of fine aggregate, numerous exposed coarse aggregates, and severe edge defects. In contrast, specimens B4, C4, and D4 show increased holes and larger hole diameters but no concrete spalling. After 150 freeze–thaw cycles, small areas of surface spalling appear in specimens B6, C6, and D6. The number and diameter of holes continue to increase, but D6 has the fewest and most minor holes and the smallest spalling area. Generally, with the same number of freeze–thaw cycles, specimens with higher fibre doping within a specific range have fewer and smaller holes and less spalling. The presence of glass fibres allows for a more uniform distribution of the pressure generated within the GFEM material during icing, reducing damage in localized areas. At the same time, the GFEM reinforcement layer effectively protects the matrix concrete from internal damage, thus reducing mass loss.

Figure 3.
Apparent damage pattern of the concrete specimen after freeze–thaw cycles. (a) Concrete group A. (b) Concrete group B. (c) Concrete group C. (d) Concrete group D.
3.2. Mass Loss Analysis
The mass loss rate can reflect the degree of concrete damage to a certain extent, defined as W. The mass loss rate calculation formula is shown in Equation (1):
where M0 (kg) and Mn (kg) are the mass of the concrete specimens without the freeze–thaw cycle and after the nth freeze–thaw cycle, respectively.
The specimen is placed in a blast dryer for 24 h prior to the freeze–thaw cycle and weighed at its mass M0 after drying, and after the freeze–thaw cycle, the specimen is placed in a blast dryer for 24 h and weighed at its post-freeze mass Mn (n is the number of freezes and thaws). Based on the freeze–thaw cycle test data, the mass of each group of concrete specimens was measured, and the testing process is illustrated in Figure 4. The rate of mass loss was then calculated. Table 4 presents the mass loss rate of each group of concrete specimens under different numbers of freeze–thaw cycles. The trend of the mass loss rate for each group after the freeze–thaw cycles is shown in Figure 5. All test curves were plotted using Origin 2024.

Figure 4.
Testing the mass of concrete specimens.

Table 4.
Concrete specimen mass loss rate.
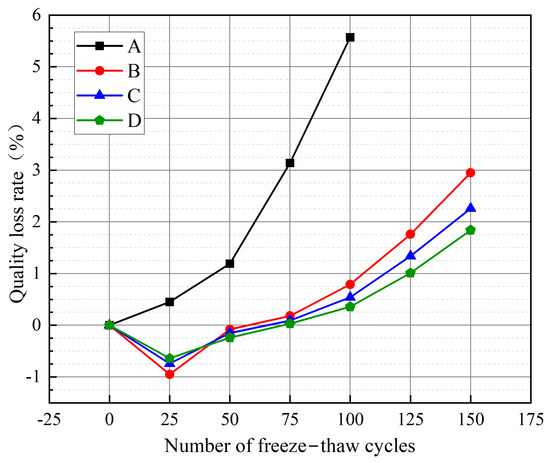
Figure 5.
Trend of the mass loss rate of concrete specimens.
As seen in Figure 5, the mass loss rate of the group A concrete specimen increases consistently with the number of freeze–thaw cycles. Initially, internal pore damage accumulates, creating new tiny connecting pores. These pores expand under freezing and expansion forces, reducing densification. Moisture penetrates these cracks, increasing the concrete specimen’s weight, while the surface concrete paste gradually peels off. The mass of moisture in the internal voids is less than the mass loss of the concrete itself. As the number of freeze–thaw cycles increases, the surface holes multiply, fine aggregate is lost, and the damage progresses from the surface to the interior, gradually increasing in mass loss. The mass initially decreases and then increases for groups B, C, and D. This is because moisture penetrating the cracks initially increases the specimen’s weight. However, the GFEM reinforcement layer prevents internal concrete mass loss, leading to an initial increase in mass. As the number of freeze–thaw cycles increases, holes in the reinforcement layer surface multiply, eventually leading to mass loss.
The rate of concrete mass loss in group A is significantly higher than in groups B, C, and D. The rate of concrete mass loss in group D is the smallest, with D, C, B, and A in descending order. At 25 freeze–thaw cycles, the negative growth rate of D1 was the smallest, followed by C1, and B1 was the largest. This is because at the beginning of the freeze–thaw cycle, the higher the fibre admixture within a specific range, the better the frost resistance; moreover, the fewer cracks inside the concrete, the less water enters into the cracks, and the less the mass increases. At 50 freeze–thaw cycles, the mass loss rate of B2 becomes the highest, but still negative, followed by C2 and D2. This is because with the increase in freeze–thaw cycles, holes begin to appear on the surface of the concrete, and the higher the fibre content within a certain range, the fewer the holes. The mass loss rate of the concrete in groups B, C, and D becomes positive after 75 freeze–thaw cycles and the mass loss rate increases rapidly after 100 freeze–thaw cycles. After 100 cycles, the mass loss rate increases quickly. In group A, the mass loss rate becomes positive after 50 freeze–thaw cycles, and the mass loss rate increases rapidly after 100 freeze–thaw cycles. The GFEM reinforcement layer can effectively reduce the mass loss of concrete. In addition, the integration of glass fibres helps to improve the compactness and reduce the porosity of the GFEM material, thus reducing water infiltration and effectively preventing internal stresses caused by icing expansion during freeze–thaw cycles.
3.3. Ultrasonic Velocity Analysis
The propagation of ultrasonic velocity is closely related to the density of the material. The ultrasonic velocity remains constant in concrete with good density and few original defects, which can be considered a homogeneous medium. However, in materials with poor density and internal defects, the ultrasonic waves are refracted during propagation, reducing their speed and thus resulting in a lower propagation velocity. The freeze–thaw cycle of concrete causes fatigue damage, altering the internal structure and subsequently affecting the ultrasonic velocity. Therefore, changes in ultrasonic velocity can reflect the internal compactness of concrete. To carry out the test, the coupling agent is applied at the measurement point, the transducer is pressed firmly on the measurement point, and the gain is adjusted so that the amplitude of the first half-wave of the received signal of all tested pieces is reduced to the same amplitude of a certain amplitude, and the time readings are taken. Each specimen is evaluated based on five points using the arithmetic average of the measured value to test the ultrasonic wave velocity measurements in concrete.
Based on the freeze–thaw cycle test data, ultrasonic velocity tests were conducted on each group of concrete specimens, as shown in Figure 6. Table 5 presents the ultrasonic velocity of each group of concrete specimens under different numbers of freeze–thaw cycles. The trend in ultrasonic velocity after the freeze–thaw cycles is illustrated in Figure 7.

Figure 6.
Ultrasonic velocity of tested concrete specimens.

Table 5.
Ultrasonic velocity of concrete specimens.
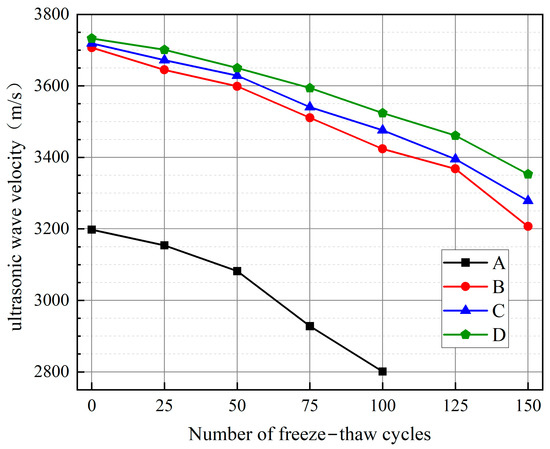
Figure 7.
Trend of the ultrasonic velocity of concrete specimens.
As can be seen in Figure 7, at 0 freeze–thaw cycles, the ultrasonic velocity values of B0, C0, and D0 were higher than that of A0, which were elevated by 15.92%, 16.29%, and 16.72%, respectively, relative to A0. From the beginning to the end of the freeze–thaw cycle, the decreasing rates of the ultrasonic velocity of concrete in group A were 1.37%, 3.63%, 8.44%, and 12.41%. The decreasing rates of ultrasonic velocity of concrete in group B were 1.67%, 2.91%, 5.29%, 7.63%, 9.14%, and 13.49%; the decreasing rates of ultrasonic velocity of concrete in group C were 1.26%, 2.42%, 4.79%, 6.53%, 8.71%, and 11.83%; and the decreasing rate of ultrasonic velocity of concrete in group D was 0.86%, 2.22%, 3.72%, 5.60%, 7.29%, and 10.18% in that order. The decrease rate of A4 at 100 freeze–thaw cycles was about twice as much as that of B4, C4 and D4. The decline rate of group A concrete at the same number of freeze–thaw cycles was higher than that of B, C, and D concrete, and all of them showed a trend of decreasing all the time with the increase in the number of freeze–thaw cycles. When the number of freeze–thaw cycles is the same, the higher the glass fibre dosage in a particular range, the higher the ultrasonic velocity, the more minor the internal damage, and the better the reinforcement effect. The GFEM reinforcement layer can influence the movement of moisture within the matrix concrete so that the moisture is not concentrated in a particular location during the freeze–thaw process, reducing localized damage.
3.4. Freeze–Thaw Cycle Damage Analysis
Based on the freeze–thaw cycle test data, the dynamic elastic modulus of prismatic specimens was evaluated, The dynamic modulus of elasticity was tested using a NELD-DTV dynamic modulus of elasticity tester manufactured in Beijing, China, as detailed in Figure 8. The dynamic elastic modulus test of each group of prismatic specimens using the forced resonance method applies to specimens with the ratio of length to the maximum side length of the cross-section between 3 and 5. The dynamic elastic modulus measuring apparatus should be preheated for more than 15 min before the test. The specimen should be removed after reaching the test age. Before the test, the specimen should be saturated in water in a surface-dry state, wiping the surface of the specimen clean with a wringing wet cloth, weighing the mass accurately to 0.01 kg, and measuring the specimen size accurately to 1 mm. The changes in the relative dynamic elastic modulus were calculated accordingly. Table 6 presents the relative dynamic elastic modulus of each concrete specimen group subjected to varying freeze–thaw cycles.

Figure 8.
Testing the dynamic elastic modulus of concrete specimens.

Table 6.
Relative dynamic elastic modulus of concrete specimens.
Various standards exist for evaluating concrete damage, which is typically carried out using compressive strength and mass loss rate indicators. However, these indicators are not suitable for assessing actual engineering structures. To study concrete freeze–thaw cycle damage [38], we assume that crack extension in the concrete during the freeze–thaw process is isotropic and uniform. By combining this with the macroscopic damage mechanics definition, we use the dynamic elastic modulus of concrete as an evaluation index for damage. The degree of freeze–thaw damage, Dn, is defined by the calculation formula shown in Equation (2):
where E0 (MPa) and En (MPa) are the dynamic modulus of elasticity of the concrete specimens without the freeze–thaw cycle and after the nth freeze–thaw cycle, respectively.
The degree of freeze–thaw damage for each group of concrete specimens was calculated using Equation (2). Figure 9 illustrates the relationship between the number of freeze–thaw cycles and the degree of freeze–thaw damage.
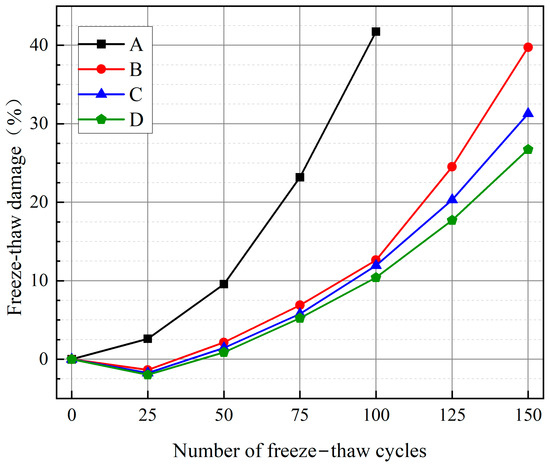
Figure 9.
Trend of the degree of freeze–thaw damage of the concrete specimens.
As shown in Figure 9, the degree of freeze–thaw damage for specimens B1, C1, and D1 increased negatively during the pre-freeze–thaw cycle. This can be attributed to the expansion of water within the concrete due to freezing, which created more empty spaces within the cement paste. Consequently, the fit between cement particles improved, enhancing volume stability and the dynamic elastic modulus. During the freeze–thaw cycle, the degree of damage for group A concrete was higher compared to groups B, C, and D. After 100 freeze–thaw cycles, the damage degree of A4 exceeded 40%. In contrast, the damage degrees for B4, C4, and D4 were 12.63%, 11.95%, and 10.41%, respectively, indicating better durability. Upon reaching 150 freeze–thaw cycles, the damage degree for B6 was 39.75%, approaching critical levels of destruction. C6 demonstrated a damage degree of 31.29%, while D6 showed the most minor damage at 26.74%, exhibiting the best resistance against freeze–thaw cycles. Furthermore, when the number of freeze–thaw cycles was constant, an increase in glass fibre doping within a specific range resulted in better reinforcement and improved resistance against freeze–thaw cycles. Consequently, the sprayed GFEM reinforcement technology effectively suppressed the development of freeze–thaw damage in concrete, with the glass fibre admixture inhibiting crack expansion during repeated freeze–thaw cycles and enhancing the concrete’s frost resistance. The addition of glass fibres also improves the thermal expansion properties of GFEM materials during temperature changes, which helps to reduce thermal cracking caused by temperature differences and better cope with freeze–thaw cycles.
3.5. Rate of Loss of Compressive Strength Analysis
The mechanical properties of concrete materials play a crucial role in evaluating freezing resistance and analysing durability, as they visually reflect the material’s structural characteristics. This study examined the fundamental mechanical properties of regular concrete and GFEM concrete with varying dosages under the influence of freeze–thaw cycles. This analysis aimed to understand the stress progression in the specimens and investigate the mechanism behind the impact of the number of freeze–thaw cycles and fibre dosage on concrete compressive strength. A universal testing machine was used to test the compressive strength of the specimens. Universal testing machine adopts WAW-1000 electro-hydraulic servo universal testing machine from Jinan, China. For each group of three specimens, the average of the measured values of the three specimens is the specimen groups’ compressive strength test results. When there is a measured value and the difference between the intermediate value is more than 15% of the intermediate value, take the intermediate value as the test result. When the difference between two measured values and the median value is more than 15% of the median value, the test results of this group are invalid. When reaching the specified test age, take out the specimen from the curing room, cover the specimen with a wet cloth, and keep the specimen in a moist state. During the test, wipe the upper and lower platens of the testing machine clean, and place the specimen in the middle of the lower platen of the testing machine, with the side of the mould used as the pressure-bearing surface. If necessary, add steel pads between the upper and lower platens of the testing machine and the specimen, and clamp a steel ball seat between the upper platen and the specimen at the centre position.
The definition μ of the rate of strength loss [39] is calculated as shown in Equation (3):
where F0 (MPa) and Fn (MPa) are the compressive strength of the concrete specimens without the freeze–thaw cycle and after the nth freeze–thaw cycle, respectively.
The test procedure shown in Figure 10 was conducted based on the measured compressive strength of each group of concrete specimens. The rate of compressive strength loss was calculated using Equation (3), and Table 7 presents the rate of compressive strength loss for each group under varying numbers of freeze–thaw cycles. The relationship between the number of freeze–thaw cycles and the compressive strength loss rate is illustrated in Figure 11.

Figure 10.
Testing the compressive strength of concrete specimens.

Table 7.
Loss of compressive strength of concrete specimens.
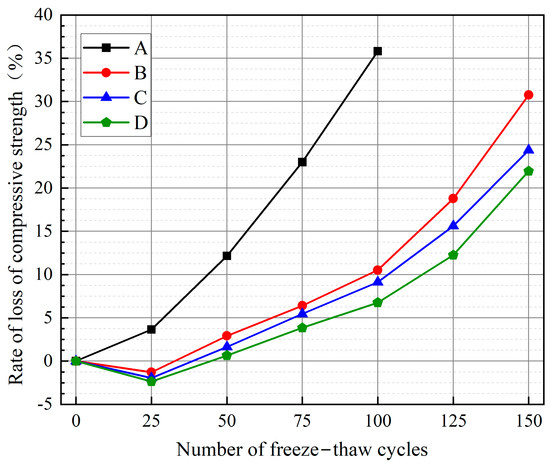
Figure 11.
Trend of the compressive strength loss rate of concrete specimens.
As depicted in Figure 11, the compressive strengths of B1, C1, and D1 initially exhibited negative growth up to 25 freeze–thaw cycles, reaching their lowest point. This can be attributed to the same reason that caused the negative growth in the degree of freeze–thaw damage during the early stages of the cycles. Furthermore, group A concrete’s compressive strength loss rate was higher than that of the concrete of groups B, C, and D during the freeze–thaw cycles. At 75 freeze–thaw cycles, A3 experienced a compressive strength loss rate of 23.00%, nearing the damage threshold. At the same time, B3, C3, and D3 had lower rates of 6.41%, 5.46%, and 3.85%, respectively, indicating a significant reinforcement effect and lower loss rates. At 150 freeze–thaw cycles, B6 exhibited a compressive strength loss rate of 30.75%, reaching a damaged state. C6 and D6 had compressive strength loss rates of 24.39% and 21.96%, respectively, approaching the damage threshold without surpassing it. Remarkably, for a constant number of freeze–thaw cycles, increasing the fibre doping within a specific range resulted in lower rates of compressive strength loss, demonstrating a more substantial reinforcement effect and improved frost resistance.
After 100 freeze–thaw cycles, the loss rate of compressive strength for group B, C, and D concrete notably increased. The loss of compressive strength from 0 to 100 freeze–thaw cycles was 10.52%, 9.13%, and 6.76%, respectively, while the loss from 100 to 150 freeze–thaw cycles was 20.23%, 15.62%, and 15.20%, which is approximately two times higher than the previous loss rate. Comparing each group’s compressive strength loss rates after freeze–thaw cycles, it was evident that the GFEM reinforcement layer effectively mitigated the compressive strength loss caused by repeated freezing and thawing. The uniform dense structure formed by the hydration products of glass fibre, slurry, and aggregate cemented and the weak zone of the interface reduced, while the incorporation of glass fibre was accompanied by air, which optimizes the hydration environment of the GFEM-reinforced layer, increases the air content, and mitigates the freeze–thaw damage.
3.6. The Effect of Sprayed GFEM Reinforcement Technology Analysis
Glass fibres, consisting of monofilaments, can be oriented in a single direction or multiple directions, effectively determining the structural properties of the composite. As a bonding medium, epoxy mortar facilitates stress transfer between distributed fibres, ensuring their integration into a cohesive whole. Including fibre-reinforced composites in reinforced concrete technology can enhance the ultimate load-bearing capacity, durability, and seismic resistance of concrete structures.
Significant improvements were observed in the compressive strength of specimens reinforced with sprayed GFEM. Figure 12 illustrates the compressive strengths of the concrete in groups A, B, C, and D at 0, 25, 50, 75, and 100 freeze–thaw cycles, as well as the corresponding rate of compressive strength increase. As highlighted in Figure 12, the compressive strength of A0 was initially 24.04 MPa with no freeze–thaw cycles. Conversely, B0, C0, and D0 exhibited compressive strengths of 35.28 MPa, 35.73 MPa, and 36.37 MPa, respectively, representing increases of 46.76%, 48.63%, and 51.29% compared to A0. The reinforcing effect was significant. While a specific range of fibre doping resulted in a slight increase in compressive strength, the improvement was not substantial. Despite the freeze–thaw cycles, the concrete groups B, C, and D maintained higher compressive strengths than group A, with the enhancement rate gradually increasing. After 100 freeze–thaw cycles, A4 was damaged, whereas B4, C4, and D4 demonstrated good frost resistance, indicating that the reinforced concrete specimens exhibited excellent frost resistance and substantial reinforcing effects.
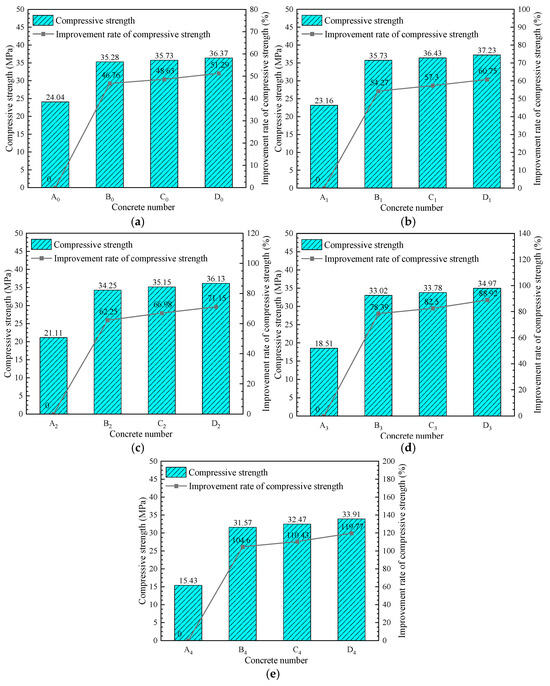
Figure 12.
The compressive strength of concrete specimens and rate of compressive strength increase. (a) Freeze–thaw cycle 0 times; (b) freeze–thaw cycle 25 times; (c) freeze–thaw cycle 50 times; (d) freeze–thaw cycle 75 times; and (e) freeze–thaw cycle 100 times.
4. Freeze–Thaw Damage Modelling of GFEM-Reinforced Concrete
4.1. Damage Model for Fibre Concrete Based on Weibull Distribution
Currently, the freeze–thaw damage model for concrete is primarily described by exponential and quadratic functions. However, these functions do not satisfy the boundary condition that the freeze–thaw damage rate is zero. The quadratic function is an empirical formula based on testing and is not precise enough to describe the random damage occurring within the concrete. Therefore, it is necessary to employ a probabilistic method to accurately predict the service life of the concrete [40]. The Weibull distribution is a model representing the probability distribution of material failure and serves as the theoretical foundation for reliability analysis and life inspection. This study employs a wide range of Weibull distribution models to describe the freeze–thaw damage of each group of concrete specimens. By using these models, a more accurate representation of the damage process can be achieved, enhancing the reliability of predictions related to the service life of the concrete.
According to the two-parameter Weibull distribution model, define fn as the probability density function of the number of freeze–thaw cycles nth, which is calculated as shown in Equation (4):
where β denotes the Weibull shape factor and η denotes the scale factor.
Integrating Equation (4) yields the probability distribution function, which is calculated as shown in Equation (5):
where Fn denotes the failure probability of the concrete specimen after n freeze–thaw cycles.
During the freeze–thaw cycles, both the failure probability and the extent of damage in a concrete specimen accumulate simultaneously. The failure probability of the specimen after the nth cycle is represented as Fn, while the degree of damage is denoted as Dn. When the freeze–thaw cycle eventually leads to failure, the failure probability reaches Fn = 1 and the damage degree becomes Dn = 1. Consequently, the failure probability and the extent of damage in the concrete specimen can be considered as equivalent, expressed as Fn = Dn. This equivalence allows for a unified approach to analysing and quantifying the specimen’s deterioration over freeze–thaw cycles.
To summarize, the degree of freeze–thaw damage is equated with the distribution function of the probability of failure, which is calculated as shown in Equation (6):
To facilitate the analysis and calculations, both sides of Equation (6) are taken twice in natural logarithms to obtain Equation (7):
Equation (7) is a linear formula in the form of y = ax + b, so that y = ln[ln(1/(1 − Dn))], x = lnn, a = β, b = βln(1/η), using linear fitting in mathematical statistics to obtain the value of the characteristic parameters a, b. Table 8 shows the results of the calculation of the characteristic parameters of the Weibull distribution function of each group of concrete. The fitting accuracy R2 of the fitting equations for each group of tests is more significant than 0.97, which is a good fit, indicating that the model can better predict the freeze–thaw damage of each group of concrete specimens.

Table 8.
Characteristic parameters of the Weibull distribution function.
By substituting the determined values of β and η from Table 5 into the equations a = β and b = βln(1/η), we can obtain the values of β and η. These values are then applied to Equation (6) to derive the freeze–thaw damage evolution based on the characteristic parameters of the Weibull distribution, as shown in Figure 13. Table 9 shows the freeze–thaw damage evolution function for each group of specimens. The figure shows that the early-stage freeze–thaw damage of concrete progresses at a slower rate with a gentler curve. Comparatively, the freeze–thaw damage curve of group A concrete consistently remains at the highest level, indicating the most severe damage among groups A, B, C, and D. After 100 freeze–thaw cycles, the freeze–thaw damage curve for groups B, C, and D shows a significant increase in slope, indicative of an accelerated damage rate. Regarding frost resistance, before experiencing damage, the group D concrete exhibited the best performance among all tested specimens during the first 200 freeze–thaw cycles.
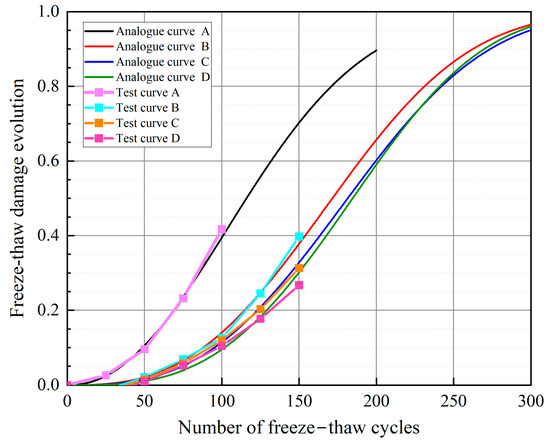
Figure 13.
Freeze–thaw damage evolution.

Table 9.
Freeze–thaw damage evolution function.
4.2. Concrete Strength Decay Model
Extensive investigations by scholars, both national and international, have explored the attenuation model for concrete specimen strength through numerous mechanical property tests following freeze–thaw cycles. Building upon the understanding of the decline in concrete strength due to freezing and thawing [41], Equation (8) presents a formula that relates the strength f after a freeze–thaw cycle to the number of cycles n:
where f 0, f n represent the compressive strength of the concrete specimens without the freeze–thaw cycle and after the nth freeze–thaw cycle, respectively; A and B are constants related to materials.
Equation (8) must satisfy the boundary condition of the number of freeze–thaw cycles n = 0 and A = 1. To better fit the relationship law between the number of freeze–thaw cycles and the strength of concrete specimens, Equation (8) is improved to obtain Equation (9):
Taking the natural logarithm twice for both sides of Equation (9) yields Equation (10):
Let Y = ln[ln(f0/fn)], X = lnn, θ = A, γ = Aln(1/B), then Equation (10) becomes a unitary linear function:
The compressive strength of concrete specimens from each group, subjected to varying numbers of freeze–thaw cycles, was analysed using linear analysis to determine the parameters θ and γ for the compressive strength attenuation model, as presented in Table 9. Using the relations θ = A and γ = Aln(1/B) and the data from Table 7, values for A and B were obtained. Subsequently, with Equation (9), concrete’s compressive strength decay model was determined for groups A, B, C, and D.
Table 10 displays that the accuracy, as measured by R2, of the relevant parameters in the compressive strength attenuation model for each group of concrete specimens exceeds 0.97. This excellent accuracy signifies a robust fit of the concrete’s strength attenuation model under freezing and thawing cycles. Consequently, the model offers improved predictive capabilities for determining the strength decay pattern of concrete following freeze–thaw cycles.

Table 10.
Parameters of the concrete strength decay model and related parameters.
Find A and B from θ = A, γ = A ln(1/B) and the data in Table 9, then substitute A and B into Equation (9). Table 11 shows the compressive strength decay function for each group of specimens.

Table 11.
Decay function of compressive strength.
4.3. Modelling of Freeze–Thaw Damage and Compressive Strength Evolution
The strength decay model in Equation (9) satisfies the boundary conditions of the number of freezing and thawing cycles n = 0, f n/f 0 = 1, and the constant deformation of Equation (9) yields Equation (12):
From Table 5 and Table 6, it can be seen that the number of freeze–thaw cycles fits the strength decay model and the freeze–thaw damage model with high accuracy and good correlation, and the coupling of Equations (6) and (12) eliminates the number of freeze–thaw cycles nth required to obtain the equation of the evolution of the degree of freeze–thaw damage of concrete expressed by the relative strength (13):
Table 12 shows the values of freeze–thaw damage parameters for each group of concrete specimens, and the relative compressive strength attenuation rate and freeze–thaw damage degree of groups A, B, C, and D concrete under the action of freeze–thaw cycles were converted by substituting each parameter in Table 10 into Equation (13). Table 13 shows the relative compressive strength decay rate and freeze–thaw damage conversion relationship equation.

Table 12.
Concrete freeze–thaw damage parameters.

Table 13.
Equation for conversion.
5. Microstructure Analysis
This paper uses the Phenom XL desktop scanning electron microscope produced by Funan Scientific Instruments (Shanghai) Co., Ltd. of Xi’an University of Technology to test the microstructure of concrete. The deterioration of the GFEM reinforcement in group B specimens after freeze–thaw cycles was analysed by SEM [42], as shown in Figure 14.

Figure 14.
Microstructure of group B specimens. (a) B0 (300×); (b) B2 (300×); (c) B4 (300×); (d) B6 (300×); (e) B0 (2000×); and (f) B6 (2000×).
In Figure 14a–d, it is evident that crack width increases progressively with the number of freeze–thaw cycles, causing internal structural damage within the reinforcement layer and weakening interfacial bonds. This degradation results in reduced strength of the reinforcement layer. The analysis attributes this phenomenon to freezing temperatures, where water within the reinforcement layer’s pores freezes, expands, and exerts pressure on the structure. With repeated freeze–thaw cycles, accumulated damage progressively compromises the reinforcement layer’s integrity, eventually leading to structural failure. The freeze–thaw environment induces osmotic pressure due to water freezing in pore spaces, further contributing to concrete reinforcement layer deterioration.
Figure 14e illustrates the condition prior to the onset of freeze–thaw cycles, revealing distinct layering and staggered hydration products within the reinforcement layer, with no apparent cracks or voids. Figure 14f shows the result after 150 freeze–thaw cycles, where fibre surfaces are enveloped in dense mortar, integrating seamlessly with other components. This consolidation enhances the stability and integrity of the reinforcement layer.
In summary, the glass fibre has a certain crack-blocking and toughening capacity. In the reinforced layer structure, the glass fibre plays a “reinforcing” role, effectively enhancing the tensile strength of the reinforced layer and frost resistance.
6. Conclusions
This paper proposes a new structural reinforcement method—Glass Fibre Epoxy Mortar (GFEM) reinforcement technology—through a systematic comparative test to study the performance evolution of ordinary concrete specimens and GFEM-reinforced concrete specimens in the freeze–thaw environment. The macroscopic performance indexes and microscopic structural characteristics of the specimens of the four different schemes were comprehensively analysed, and a freeze–thaw damage prediction model was established based on the Weibull distribution theory. The main research results are as follows:
- (1)
- Significantly improved frost resistance: GFEM reinforcement technology improves the frost resistance of concrete by more than 50%. Ordinary concrete has serious spalling and aggregate exposure after 100 cycles of freezing and thawing, while GFEM-reinforced specimens still maintain good integrity after 150 cycles of freezing and thawing, which indicates that the reinforced layer effectively slows down the development of freezing and thawing damage.
- (2)
- Optimization of material ratio: Through ultrasonic testing, it was found that the specimen density was optimal when the glass fibre dosage was 1.0%, but considering the comprehensive economy and construction performance, 0.8% is recommended as the optimal fibre dosage. In this study, the wave speed was only reduced by 2.1% and the cost–benefit ratio was improved significantly.
- (3)
- Mechanical property maintenance: After 75 times of freezing and thawing, the loss rate of the compressive strength of ordinary concrete reached 23% (close to the damage threshold), while the loss rate of the strength of GFEM-reinforced specimens (groups B, C, and D) was less than 6.5%. The group C specimens with 0.8% fibre dosage showed the optimal strength retention rate (the loss rate is only 5.46%).
- (4)
- Micro-mechanism: SEM analysis shows that the glass fibres form a three-dimensional network structure in the mortar matrix, which inhibits crack expansion through the "fibre bridging" effect and enhances the performance of the interfacial transition zone, which is the key mechanism to improve the tensile strength and freeze–thaw durability of the reinforced layer.
- (5)
- Model establishment and validation: A freeze–thaw damage model based on Weibull distribution (R2 > 0.97) was innovatively constructed, and the evolution equation of the damage degree characterised by the relative strength was derived by the associative strength attenuation model. The model realised the quantitative conversion between the number of freeze–thaw cycles, the strength attenuation rate, and the degree of damage, and provided a new method for the prediction of the freeze–thaw life of concrete structures in engineering practice.
Author Contributions
Conceptualization, J.S. and Y.L.; methodology, Y.L.; software, W.S.; validation, W.S.; formal analysis, J.S.; investigation, W.S.; resources, X.N.; data curation, W.S.; writing—original draft preparation, Y.L.; writing—review and editing, J.S.; visualization, J.J. and J.X.; supervision, L.H. and X.N.; project administration, J.X. and J.J.; funding acquisition, L.H. and X.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Xiaoyu Niu, Junpeng Ju, Lizhe He and Junlin Xiang were employed by Shaanxi Ancient Construction Garden Construction Group Co. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GFEM | Glass Fibre Epoxy Mortar |
| GF | Glass fibre |
References
- Marie, S.L.; Ioannis, B.; Krešimir, N.; Jan, V.; Roman, W.W. Relationship of LDPM meso-scale parameters and aging for normal and high strength concretes. Mater. Struct. 2022, 55, 219. [Google Scholar] [CrossRef]
- Zhou, J.H.; Kang, T.B.; Wang, F.C.; Wang, X.D. Finite Element Analysis of Increasing Column Section and CFRP Reinforcement Method under Different Axial Compression Ratio. IOP Conf. Ser. Mater. Sci. Eng. 2017, 269, 012029. [Google Scholar]
- Ma, H.X.; Li, Z.G.; Yue, Z.; Xu, H.R. Research on the Bearing Capacity of the Cross Section of Reinforced Concrete Beams Strengthened with Increasing Section Method Considering the Effect of the Second Loading. Adv. Res. 2015, 5, 1–9. [Google Scholar] [CrossRef]
- Bobalo, T.; Blikharskyy, Y.; Selejdak, J.; Kopiika, N.; Blikharskyy, Z. Concrete Beams Reinforced with High Strength Rebar in Combination with External Steel Tape. Appl. Sci. 2023, 13, 4528. [Google Scholar] [CrossRef]
- Medvedev, V.; Semeniuk, S. Durability and deformability of braced bending elements with external sheet reinforcement. Mag. Civ. Eng. 2016, 63, 3–15. [Google Scholar] [CrossRef]
- Chen, J.H.; Bai, L.H.; Zhao, S.B.; Yu, X.H.; Chen, C. Construction Technology of Transverse Bonded Structural Steel for Strengthening PPC Hollow Slab Bridge. Appl. Mech. Mater. 2012, 238, 697–700. [Google Scholar] [CrossRef]
- Gong, S.; Su, M.; Yoshitake, I.; Zhu, C.X.; Peng, H. Factors affecting flexural properties of RC beams strengthened with gradually prestressed NSM CFRP strips. Eng. Struct. 2024, 306, 117865. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, H.D. Shear strengthening effect by external post-tensioning steel rods in damaged reinforced concrete beams. Struct. 2024, 62, 106327. [Google Scholar] [CrossRef]
- Xie, J.H.; Li, J.L.; Lu, Z.Y.; Liu, D.; Huang, P.Y. Effects of pre-existing damage and cyclic overloading on the flexural behaviour of RC beams strengthened with prestressed CFRP plates. Eng. Struct. 2021, 247, 113078. [Google Scholar] [CrossRef]
- Kim, Y.J.; Hassani, A. Stepped Reinforced Concrete Beams Retrofitted with Carbon Fiber-Reinforced Polymer Sheets and Ultra-High-Performance Concrete. ACI Struct. J. 2023, 120, 91–104. [Google Scholar] [CrossRef]
- Sven, B.; Josef, H.; Martin, C. Dowel action of textile CFRP shear reinforcement in carbon reinforced concrete. Constr. Build. Mater. 2024, 411, 134106. [Google Scholar] [CrossRef]
- Hieu, N.T.; Tuan, N.V.; Dat, P.X.; Hung, N.M.; Lanh, L.P. Experimental Study on the Strengthening Effect of CFRP Sheets on Corrosion-Damaged, Eccentrically Loaded Reinforced Concrete Columns. Int. J. Civ. Eng. 2023, 22, 535–547. [Google Scholar]
- Liu, Y.F.; Wu, C.F. Experimental study on the modulus of elasticity of glass fiber concrete. Concrete 2017, 6, 64–66+79. [Google Scholar]
- Xu, Z.G.; Sun, T. The effect of wetness at the bonding interface on the bond strength of epoxy mortars for repairing hydraulic concrete. J. Phys. Conf. Ser. 2023, 2553, 012035. [Google Scholar] [CrossRef]
- Cai, L.H.; Qian, L.; Rui, G. Study on the shear behavior of RC beams strengthened by CFRP grid with epoxy mortar. Compos. Struct. 2021, 275, 114419. [Google Scholar] [CrossRef]
- Sun, Y.F.; He, J.J.; Ma, L.Y.; Di, S.J.; Zhang, Y.; Liu, J.; Xing, R.J. Experimental Study on Thermal Expansion Property of Epoxy Mortar in Hydraulic Structure Repairing. IOP Conf. Ser. Earth Environ. Sci. 2021, 636, 012009. [Google Scholar] [CrossRef]
- Cao, D.F.; Fu, L.Z. Experimental study on mechanical properties of ordinary concrete under freeze-thaw environment. Concrete 2010, 10, 34–36+40. [Google Scholar]
- Li, W.S.; Wang, M.L.; Yang, N. Study on freeze-thaw properties of recycled aggregate concrete and ordinary concrete. Eng. Constr. 2010, 42, 1–4. [Google Scholar]
- Yu, X.M.; Ren, Q.W. Experimental study on fracture energy of ordinary concrete under freeze-thaw cycles. J. Hohai Univ. (Nat. Sci.) 2010, 38, 80–82. [Google Scholar]
- Shang, H.S.; Ou, J.P.; Song, Y.P. Theory of freeze-thaw damage and reliability analysis of concrete structures. Eng. Mech. 2011, 28, 70–74. [Google Scholar]
- Powers, T.C. A working hypothesis for further studies of frost resistance. J. Am. Concr. Inst. 1945, 16, 245–272. [Google Scholar]
- Li, J.Y.; Cao, J.G. Research and Application of Durability of Hydraulic Concrete; China Electric Power Press: Beijing, China, 2004. [Google Scholar]
- Li, J.Z.; Zhou, S.H.; Shi, Y. Study on performance deterioration of concrete during freeze-thaw cycles. J. Yangtze River Sci. Res. Inst. 2011, 28, 171–174. [Google Scholar]
- Tang, G.P.; Liu, X.L.; Shi, S.S. Study on evolution model of concrete failure surface under freeze-thaw conditions. Chin. J. Rock Mech. Eng. 2006, 25, 2573–2578. [Google Scholar]
- Moceikis, R.; Kičaitė, A.; Sahmenko, G.; Selsekienė, A. Durability characterisation of glass fibre reinforced concrete by resistance to freezing and thawing. J. Sustain. Archit. Civ. Eng. 2020, 26, 98–109. [Google Scholar] [CrossRef]
- Meng, S.Y.; Zuo, J.Q.; Wang, C. Study on durability of concrete with different fibers. Compr. Util. Fly Ash 2013, 1, 19–21+24. [Google Scholar]
- Xu, L.N.; Lei, N. Influence of fibre type on unconfined compressive strength of fibre-reinforced cemented soil under freeze-thaw cycling. Int. J. Mater. Prod. Technol. 2022, 65, 248–257. [Google Scholar] [CrossRef]
- Shen, R.X. Mechanism of synthetic fibers with low dosage in concrete. In Proceedings of the Academic Symposium on 60 Years of Professor Wu Zhongwei’s Scientific and Educational Work, Beijing, China, 2004; Chinese Ceramic Society: Beijing, China, 2004; pp. 22–25. [Google Scholar]
- Cheng, Y.H.; Wang, H.W.; Wang, Y. Experimental study on frost resistance of fiber reinforced concrete. Highway 2012, 3, 179. [Google Scholar]
- Ning, B.K.; Li, S.; Liu, W.; Zhang, J.X. Experiment on freeze-thaw characteristics of concrete beams strengthened with prestressed fiber sheets. J. Shenyang Univ. Technol. 2017, 39, 567–571. [Google Scholar]
- Liu, L.N.; Zheng, B.S. Application of infrared thermography in impact detection of CFRP strengthened components. New Technol. New Process 2015, 11, 122–124. [Google Scholar]
- Wei, C.Y. Study on Mechanical Properties of Double GFRP Tube Concrete Composite Columns with Different Strengths Under Freeze-Thaw Cycles. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2023. [Google Scholar]
- Xia, D.T.; Feng, C.L.; Zheng, Z.; Wu, H. Modeling of salt-freezing damage of mixed-fiber concrete under coupled salt-freeze-thaw cycles. J. Wuhan Univ. (Eng. Ed.) 2024, 57, 55–63. [Google Scholar]
- JGJ 55-2011; Ordinary Concrete Proportion Design Regulations. China Construction Industry Press: Beijing, China, 2011.
- GB/T 51003-2014; Technical Specification for the Application of Mineral Admixtures. China Construction Industry Press: Beijing, China, 2015.
- DL/T 5193-2021; Technical Specification for Epoxy Resin Mortar. China Electric Power Press: Beijing, China, 2021.
- SL/T 352-2020; Test Procedure for Hydraulic Concrete. China Water Conservancy and Hydropower Press: Beijing, China, 2020.
- Guan, H.; Qiu, J.S.; Pan, D.; Zheng, J.J.; Wang, M.H. Research on the assessment method of damage degree of gangue concrete under freeze-thaw environment. Mater. Rev. 2018, 32, 3546–3552. [Google Scholar]
- Zhang, G.T.; Liu, S.T.; Geng, T.J.; Peng, R.; Chen, Y. Fiber concrete damage model under freeze-thaw cycle based on Weibull distribution. Sci. Technol. Eng. 2020, 20, 12078–12084. [Google Scholar]
- Qiao, H.X.; Guo, X.K.; Zhu, B.R. Accelerated life test of concrete under multifactorial action with three-parameter Weibull distribution. Mater. Rev. 2019, 33, 639–643. [Google Scholar]
- Luo, X.; Wei, J. Study on the correlation between damage evolution and strength of concrete under freeze-thaw conditions. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2006, 1, 98–100. [Google Scholar]
- Sun, C.W.; Wang, X.Z.; Xin, M.; He, J.J. Study on frost resistance of basalt-cellulose hybrid fiber concrete. Concr. Cem. Prod. 2024, 65–69. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).