Multiple Regression-Based Dynamic Amplification Factor Investigation of Monorail Tourism Transit Systems

Abstract

The monorail tourism transit system (MTTS) is a large-scale amusement facility. Currently, there is limited theoretical research on the vehicle–bridge coupling vibration and dynamic amplification factor (DAFs) of this system. The values specified in relevant standards are not entirely reasonable; for instance, the calculated value of the DAFs in the “Large-scale amusement device safety code (GB 8408-2018)” only takes speed into account and is set at 0.44 when the speed is between 20 and 40 km/h. This is overly simplistic and obviously too large. This paper aims to establish a reasonable expression of the DAFs for the MTTS and improve the design code of the industry. Firstly, using on-site trials of the project and the dynamics numerical simulation method, the dynamic response characteristics of the MTTS and the influencing factors of the DAFs were systematically analyzed. The rationality and accuracy of the model were verified. Secondly, combined with the joint simulation model, the dynamic influence mechanism of multifactor coupling on the DAFs was revealed. On this basis, the key regression parameters were selected by using the Pearson correlation coefficient method and the random forest algorithm, and the DAFs prediction model was constructed based on the least absolute shrinkage and selection operator (LASSO) regression theory. Finally, through cross-comparison of simulation data and specification verification, a recommended calculation expression of the DAFs for the MTTS was proposed. The research results show that the established prediction model can predict 94.50% of the variation information of the DAFs of the MTTS and pass the 95% confidence level and 0.05 significance test. The accuracy is high and relatively reasonable and can provide a reference for the design of the MTTS.

1. Introduction

With the rapid development of the tourism industry around the world and the increasing awareness of natural landscape protection, the monorail tourism transit system (MTTS), as an innovative solution for the low-carbon upgrading of scenic spots, has been widely applied all over the world with the advantages of lightweight construction and eco-friendly design concepts. Companies such as Intamin in Switzerland, Mack Rides in Germany, S&S in the United States, and CRRC in China have carried out a lot of work in this regard. As a key parameter in the design of MTTS, the DAFs is crucial to the safety design and comfort evaluation of MTTS. However, there is a significant gap between the theoretical research and engineering practice of the vehicle–bridge coupling and dynamic amplification factors (DAFs) of MTTS. The industry design standards need to be improved, and there is a lack of research on key technical standards. The calculation and value selection of the DAFs are relatively rough. All these issues have restricted its development [1]. The design of this system is based on the “Large-scale amusement device safety code (GB 8408-2018) [2]”. However, there are issues such as the DAFs being set less safely at low speeds and too conservatively at high speeds, with relatively single considerations. Adhering to the values stipulated in the code may lead to overly conservative designs and economic losses. MTTS has developed rapidly by taking advantage of the strengths of the traditional urban monorail transportation system, but there are also certain differences between the two. Specifically, the traditional urban monorail transportation system mainly uses prestressed concrete track beams and column structures, with a relatively large overall stiffness and a minimum curve radius of 100 m. In contrast, MTTS typically employs steel box girders and steel columns, and the modular construction can significantly reduce the construction period. Moreover, the minimum curve radius can be as small as 20 m, allowing it to flexibly adapt to the complex terrain of scenic areas. The diversity of structural parameters leads to significant differences in dynamic characteristics and impact effects between the two [3,4,5]. Therefore, the research on DAFs of MTTS is of positive significance for improving its design and evaluation system.

At present, the vibration characteristics of the transportation system are usually achieved through numerical simulation, such as solving the vehicle–bridge coupling vibration equation by programming with MATLAB [6,7,8]. However, during the derivation of the vibration equation, mechanical simplifications are made to the train and bridge, etc., which can easily cause a significant deviation between the numerical results and the actual running state of the train. The use of the finite element method (FEM) combined with multi-body dynamics (MBD) can effectively improve such problems [9]: Liu et al. established a simulation model of straddle-type monorail transportation using the multi-body dynamics software SIMPACK and analyzed the dynamic performance of monorail vehicles [10]. The results indicated that straddle-type monorail vehicles have good curve passing performance, and all static and dynamic performance evaluation indicators of the vehicles meet the requirements. Gao et al. developed a co-simulation model using the finite element method and MBD software to study the influence of vehicle speed and pier height on railway systems [11]. In addition, many studies have also considered the diversity and coupling effects of influencing factors in monorail transportation systems. For instance, Zhou et al. [12] improved the tire wear of monorail vehicles through dynamic parameter research and conducted a coupled dynamic analysis of monorail vehicles equipped with single-axle bogies [13]. Li et al. analyzed the dynamic response of long-span railway cable-stayed bridges and discussed the influence of factors such as train formation, track irregularity, driving direction, and train type on the impact coefficients of various components of cable-stayed bridges [14]. For the MTTS, Wang et al. [15] proposed a method for detecting the unevenness of the track beam in the MTTS, conducted multiple projects of unevenness measurement and spectral fitting, and compared the applicability of monorail spectral analysis with various spectral estimation and fitting methods. Finally, a joint model was established using ANSYS and UM software to analyze the dynamic response characteristics of the MTTS. Zhang et al. [16] established a general monorail vertical and horizontal unevenness spectrum for the MTTS based on measured data. GUO et al. established a comfort evaluation index for the monorail spectrum based on the vehicle–bridge coupling analysis model [17]. Zhang et al. established a wind–vehicle–bridge coupling model for the MTTS and analyzed the stiffness limit of the track beam under the influence of track unevenness and wind load [18]. The above studies mainly focus on the traditional transportation system and relatively few studies on MTTS; of course, these studies can also provide a methodology for MTTS.

Research on DAFs has been very extensive and in-depth in traditional transportation systems. Shervan et al. investigated the effect of train formation, train speed, span length, rise/span ratio, the first natural frequencies in vertical and lateral directions, and the combined elastic modulus of masonry and mortar on DAFs [19]. Babatope et al. investigated the deflection curve and the response characteristics of the DAFs of axially prestressed continuous beams under non-uniform speed loading [20]. Zhu et al. [21] established an 11-degrees-of-freedom three-dimensional vehicle model and a finite element model using MATLAB and ANSYS, respectively, and studied the DAFs of a three-span continuous arch-rigid frame bridge by using the vehicle–bridge coupling iteration method. They also proposed an improved damage identification method based on the DAFs [22], which enabled rapid detection and assessment of long-span suspension bridges. Zhou et al. took simply supported T-beam bridges, box girder bridges, and hollow slab bridges with standard spans as the research objects, derived the expression of the DAFs of simply supported beams under the action of three-axle vehicles based on the modal superposition method, and verified the variation law of the DAFs under different influencing factors through numerical simulation and field measurement [23]. Li et al. studied the DAFs and influencing factors of stay cables of cable-stayed bridges based on the vehicle–bridge coupling theory. The research shows that the pavement grade is the main influencing factor, and a reasonable value of the DAFs is proposed [24]. Deng et al. [25] compared the DAFs of strain and deflection of simply supported beam bridges and continuous beam bridges based on theoretical derivation and numerical simulation. The results showed that the DAFs of strain were basically less than those of deflection. In addition, they used the vehicle–bridge coupling vibration model to study and analyze the influence of parameters such as stiffness, mass, and damping of the vehicle model on the DAFs of the bridge [26] and verified the validity of the model through measured data. In summary, the existing research mainly focuses on traditional transportation systems and lacks studies on the DAFs of MTTS. Therefore, from the perspective of engineering application requirements and theoretical research value, it is of significant importance to conduct research on the DAFs of MTTS and establish a relatively reasonable calculation expression.

Based on a comprehensive analysis of existing research, the research approach of this paper is shown in Figure 1. Firstly, on-site tests of vehicle–bridge coupling were conducted based on actual projects, the dynamic response of the MTTS was analyzed, and a joint simulation model was established. Secondly, the joint model was used to analyze the influencing factors of the DAFs. Finally, due to the numerous influence factors of the DAFs and the interaction among them, the LASSO regression theory can effectively address such issues. Therefore, this paper employed the LASSO regression method to conduct a multiple regression analysis on the DAFs, establishing the calculation expression of the DAFs for the MTTS. Its rationality and accuracy were verified through comparison with simulation data and standards. Compared with the model established by the traditional research methods of monorail systems, the joint model established in this paper is more in line with the actual operation state, and the DAFs prediction model is more accurate and reasonable. This has a positive significance for improving the safety design and comfort evaluation of MTTS.

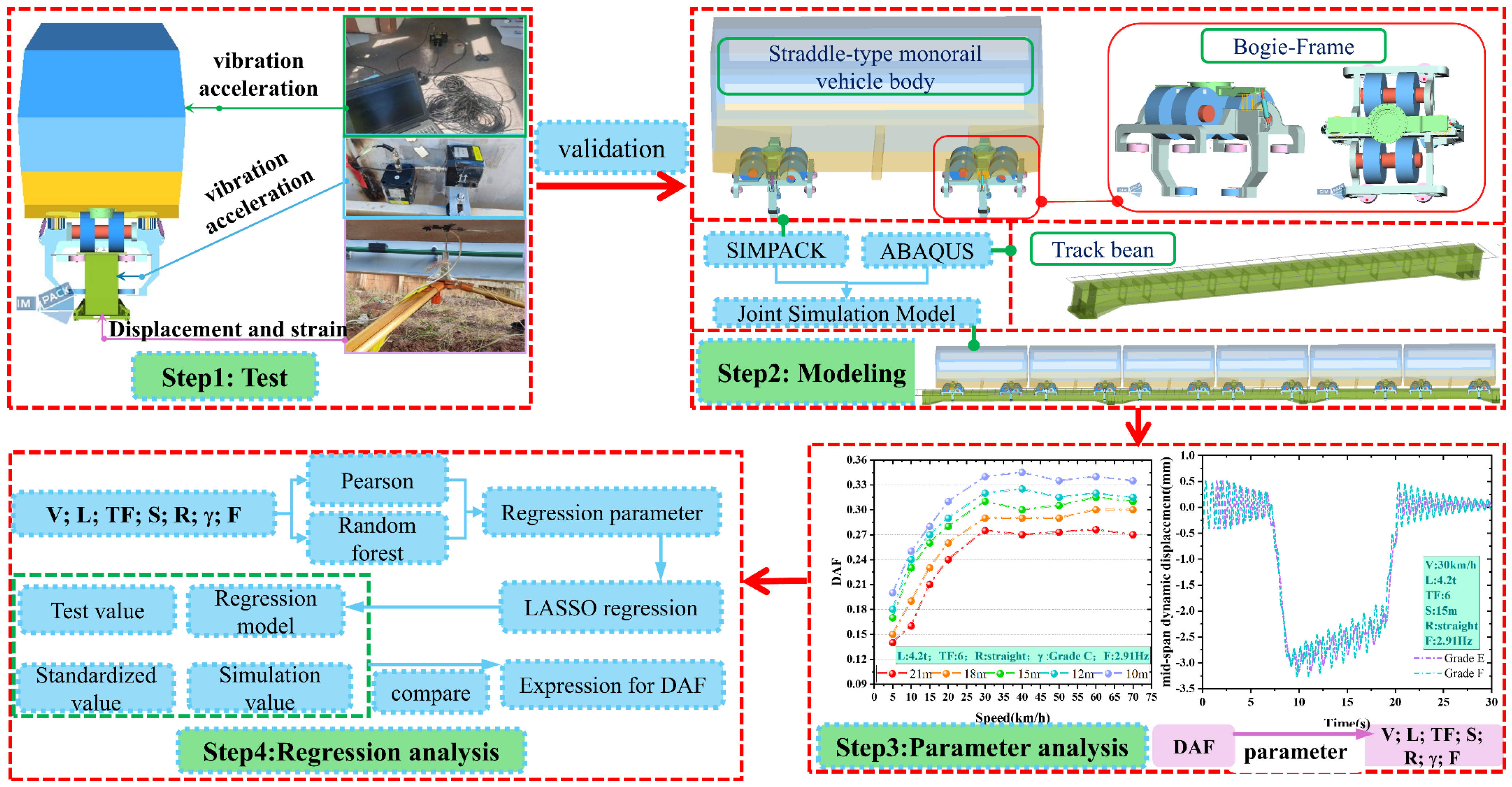
2. Methodologies

This section first established a joint simulation model of the MTTS based on the actual project structure parameters. Then, on-site tests were carried out at the project site to analyze the influencing factors and variation patterns of the DAFs. Finally, through the comparative analysis of the test data and the simulation results, the rationality and accuracy of the joint simulation model were verified, which will provide a methodological basis for the subsequent expansion analysis of the DAFs influencing parameters.

2.1. Joint Simulation Model of MTTS

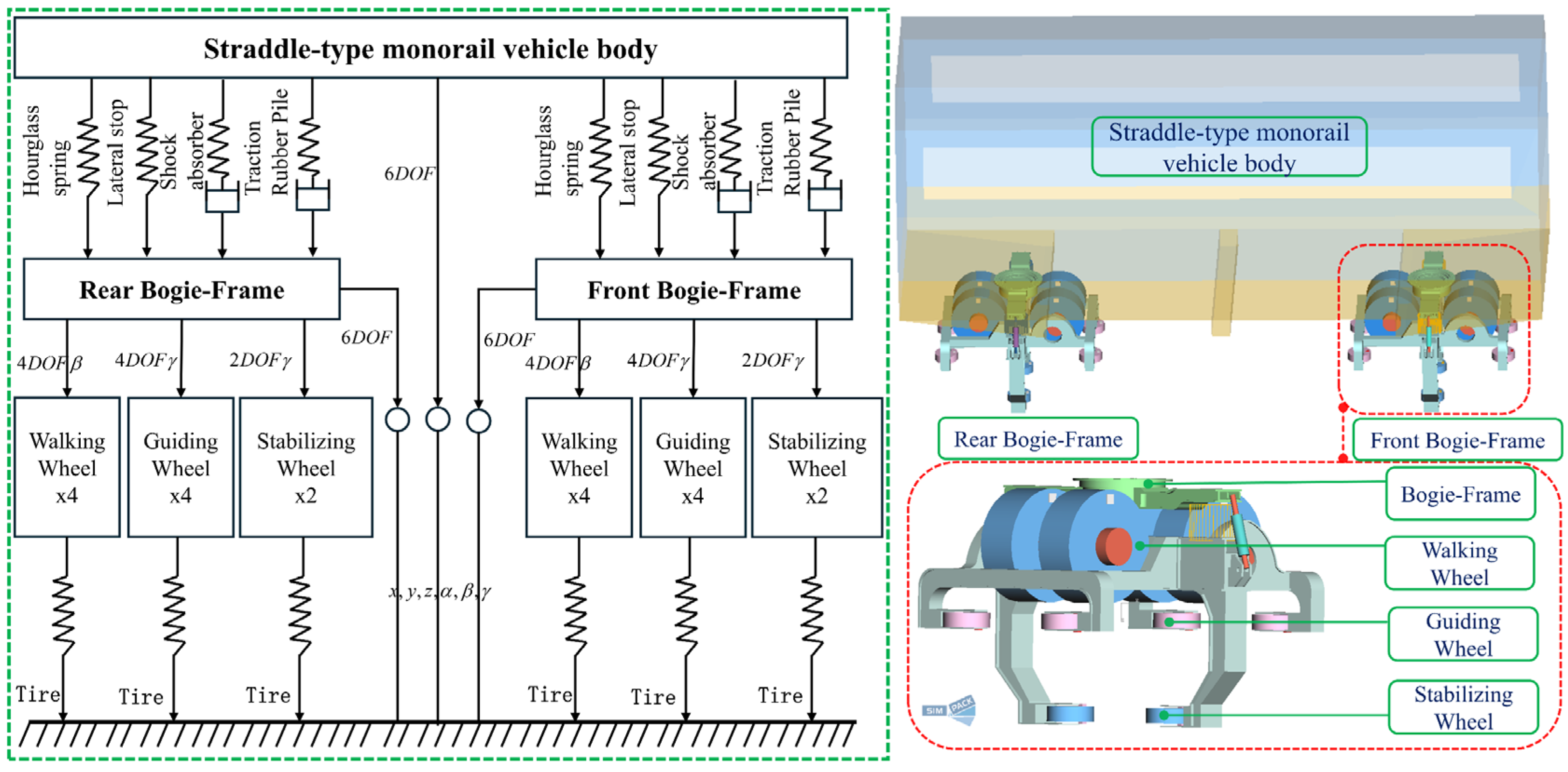
2.1.1. Modeling Monorail Trains

Based on the actual structural parameters of the CRRC Zhuzhou test line project, a 38-degree-of-freedom MTTS monorail vehicle dynamic model topology was established using the multi-body dynamics software SIMPACK (version 2021X) [27], as illustrated in Figure 2. In the SIMPACK modeling process, component appearances serve solely for visualization purposes, influencing only the graphical representation without materially affecting structural dynamics calculations or analyses. This study ensures strict consistency between core modeling parameters and the actual structure while appropriately simplifying the geometric characteristics of complex components, such as the monorail bogie. Specifically, the bogie and carriage are defined as independent subsystems, with the MTTS monorail vehicle structural dynamics analysis model constructed through primary and secondary suspension joints connecting the carriage and bogie subsystems.

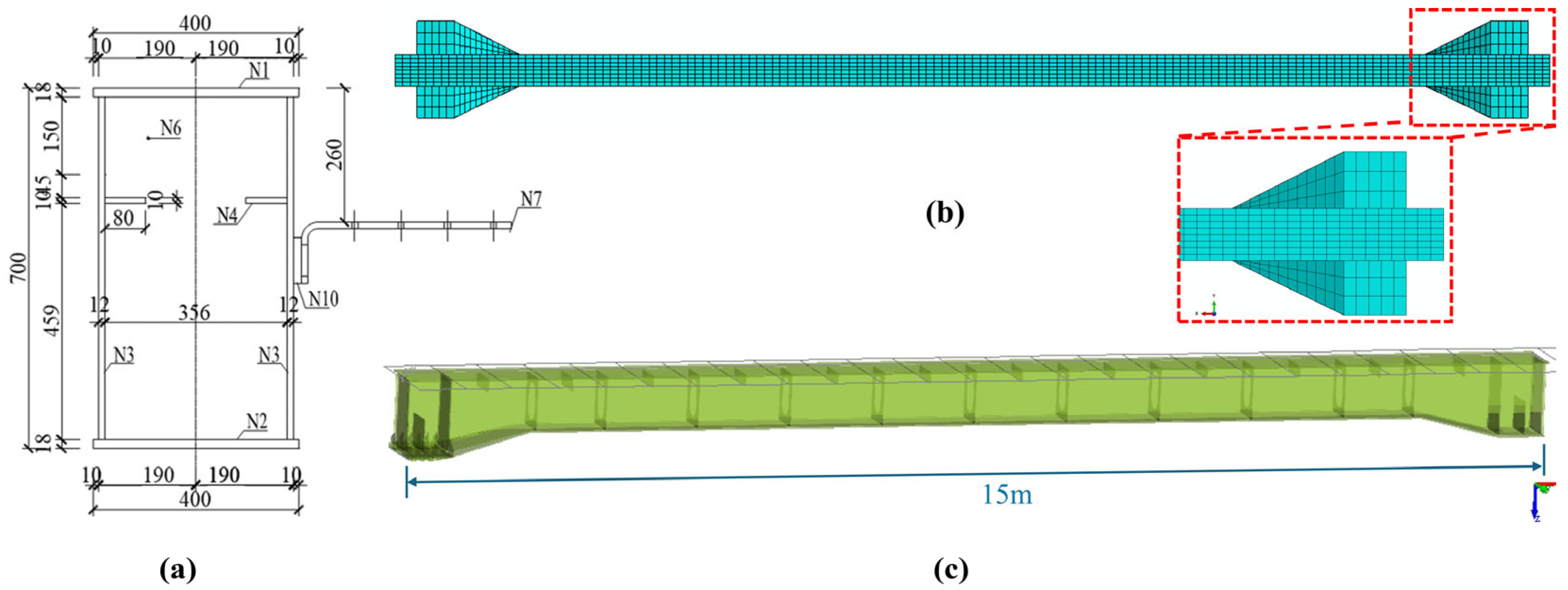
2.1.2. Modeling Track Beams

Based on the structural parameters of the CRRC Zhuzhou test line, a track beam model was established as shown in Figure 3 (using the 15 m span as an example). Figure 3a illustrates the cross-sectional parameters of the track beam, while Figure 3b presents the finite element model developed in ABAQUS [28]. The model employed solid elements, with simplifications applied to the stiffening ribs to balance computational efficiency and accuracy. Core parameters such as structural stiffness were calibrated to align with the actual structure. Subsequently, modal analysis and substructure generation were performed. Finally, through the ABAQUS-SIMPACK interface, the flexible track beam model was imported into SIMPACK, as depicted in Figure 3c.

2.1.3. Joint Simulation Modeling

The main steps of the joint model establishment are shown in Figure 4 and can be described as follows: (1) ABAQUS was used to establish the rail beam model and generate inp and sim model data files that could be linked with SIMPACK; (2) SIMPACK was utilized to develop the car body, bogie, and tire models, respectively, and realized the coupling connection between the car body, bogie, and tires through the force element to establish the monorail car model; and (3) through the interface between SIMPACK and ABAQUS, the track beam data files were imported and Fbi model files were generated. Subsequently, the Ftr file was utilized to read the Fbi file information and write the track beam model data, establishing the track beam flexible body model. Finally, the wheel-rail contact relationship equations were employed to achieve the coupling of the monorail train with the track beam, completing the establishment of the ABAQUS-SIMPACK joint model. This approach enabled the simulation and analysis of the MTTS vehicle–bridge coupling system.

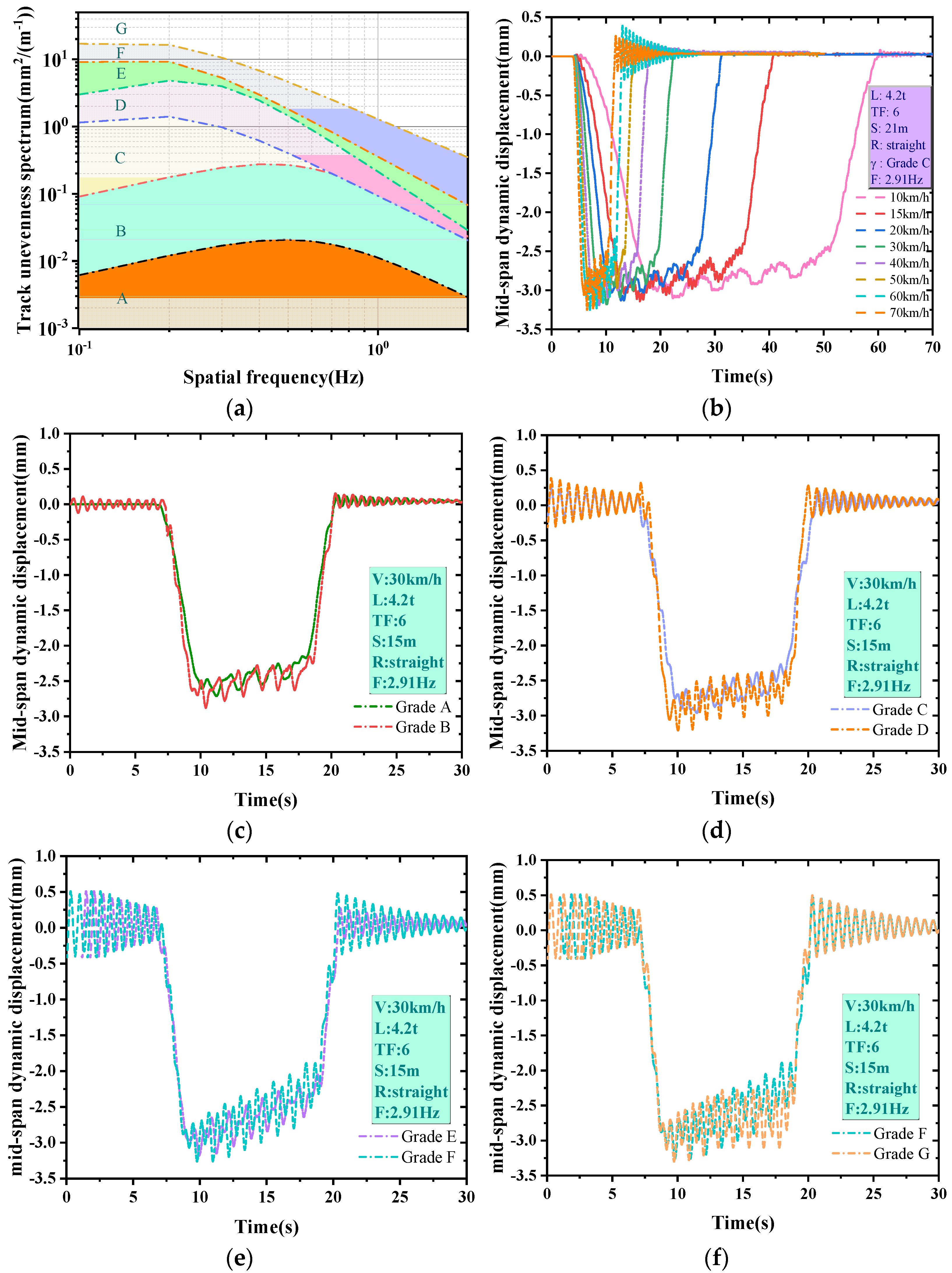
2.2. Vehicle–Bridge Coupling Field Trials of MTTS

To verify the rationality and accuracy of the joint simulation model, a typical beam span from the Zhuzhou MTTS test line project was employed for vehicle–bridge coupling dynamic response measurements. The monorail train speed was set across 2–15 km/h, with a total of five gears. The test group consisted of a 6-car formation fully loaded to 4.2 t; the train weighed approximately 24 t. The test spans were distributed as 12 m, 15 m, and 18 m. The MTTS vehicle–bridge coupling field test arrangement is shown in Figure 5 (taking the 15 m track beam as an example, the figure shows the specific distribution position of the 15 m span test section track in the line and the spans of the adjacent track beams on the left and right are 15 m and 18 m, respectively). Test monitoring equipment included a top bar displacement gauge, strain gauges, and vibration sensors (pickup). The data acquisition and analysis system utilized the YSV dynamic collector and DHDAS static collector. By varying parameters of the monorail train (speed, load) and track beam parameters (span), the dynamic and static responses of the track beam and vibration responses during the monorail train’s travel were tested under different working conditions.

The test results of the dynamic response and DAFs of the vehicle–bridge coupling of the MTTS are shown in Figure 6. The analysis reveals the following: (1) Within the speed range of 2 km/h to 10 km/h, both the displacement and strain DAFs show a positive correlation with the increase in speed and the growth rate is significant. After 10 km/h to 15 km/h, the increase in the strain DAFs gradually slows down and reaches its peak at 15 km/h, while the displacement DAFs still have room for increase, indicating that it has not yet reached the peak value. At the same time, it can be seen from the figures that the load has a certain influence on the DAFs, especially on the strain DAFs, which is more obvious. Compared with the light load, the maximum difference in the displacement and strain DAFs under heavy load is about 0.02. Within the current speed and load calculation range, the displacement DAFs are always greater than the strain DAFs, indicating that the displacement DAFs are more sensitive to the change in speed. (2) As the span increases, the DAFs show a significant negative correlation and change markedly. Under heavy load conditions, within the three calculated spans, the extreme differences between the maximum and minimum values of the DAFs are 0.08 (displacement DAFs) and 0.07 (strain DAFs), respectively. The increase in the displacement and strain DAFs under heavy load is more significant, indicating that the DAFs of the monorail train are more susceptible to span changes under heavy load, which is the result of their coupling effect. Moreover, under the same working conditions, the displacement DAFs is greater than the strain DAFs, and relevant research [25] also supports this conclusion.

2.3. Joint Simulation Model Validation

When a train with a speed of 15 km/h passed through a 15 m span track beam, the dynamic response at the mid-span was tested and compared with the simulation data, fully verifying the validity of the combined model. The results are shown in Figure 7. The analysis indicates that the extreme value differences of the vibration acceleration are 0.02 (in the lateral direction) and 0.21 (in the vertical direction), respectively; the extreme value difference of the mid-span dynamic displacement between the test and simulation is 0.05 mm. Overall, the simulation data are in good agreement with the test data, with the overall error extreme value being only 1.96%. This indicates that the combined simulation model has high rationality, reliability, and accuracy.

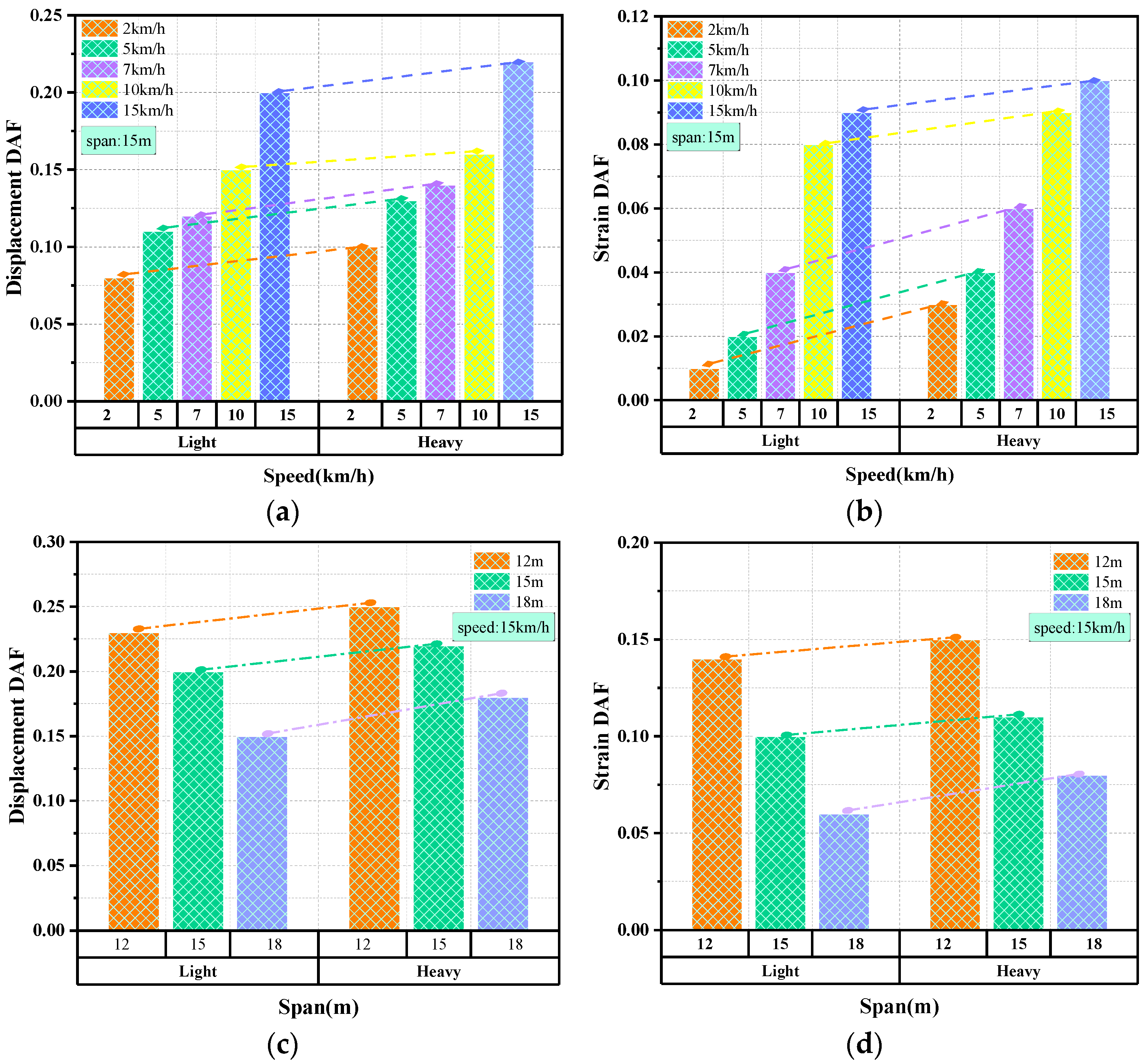
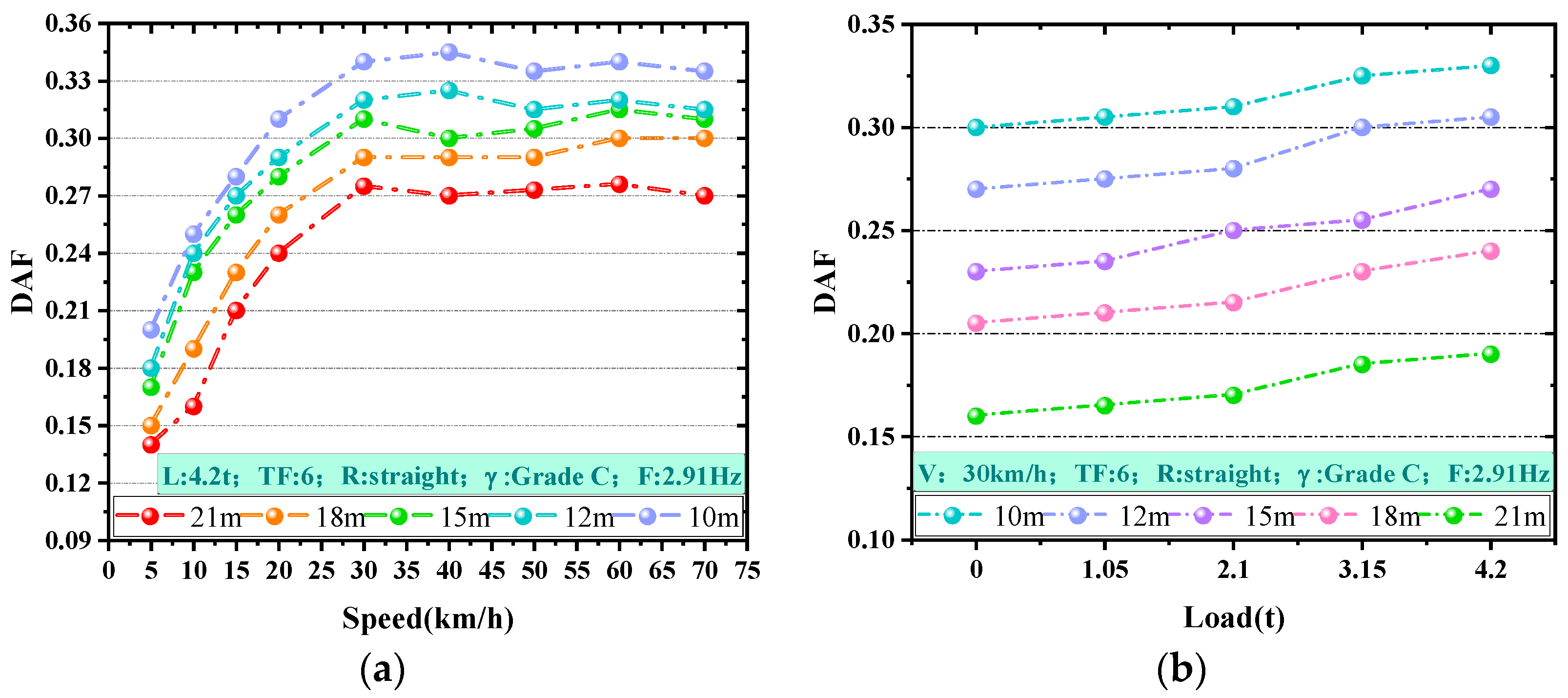
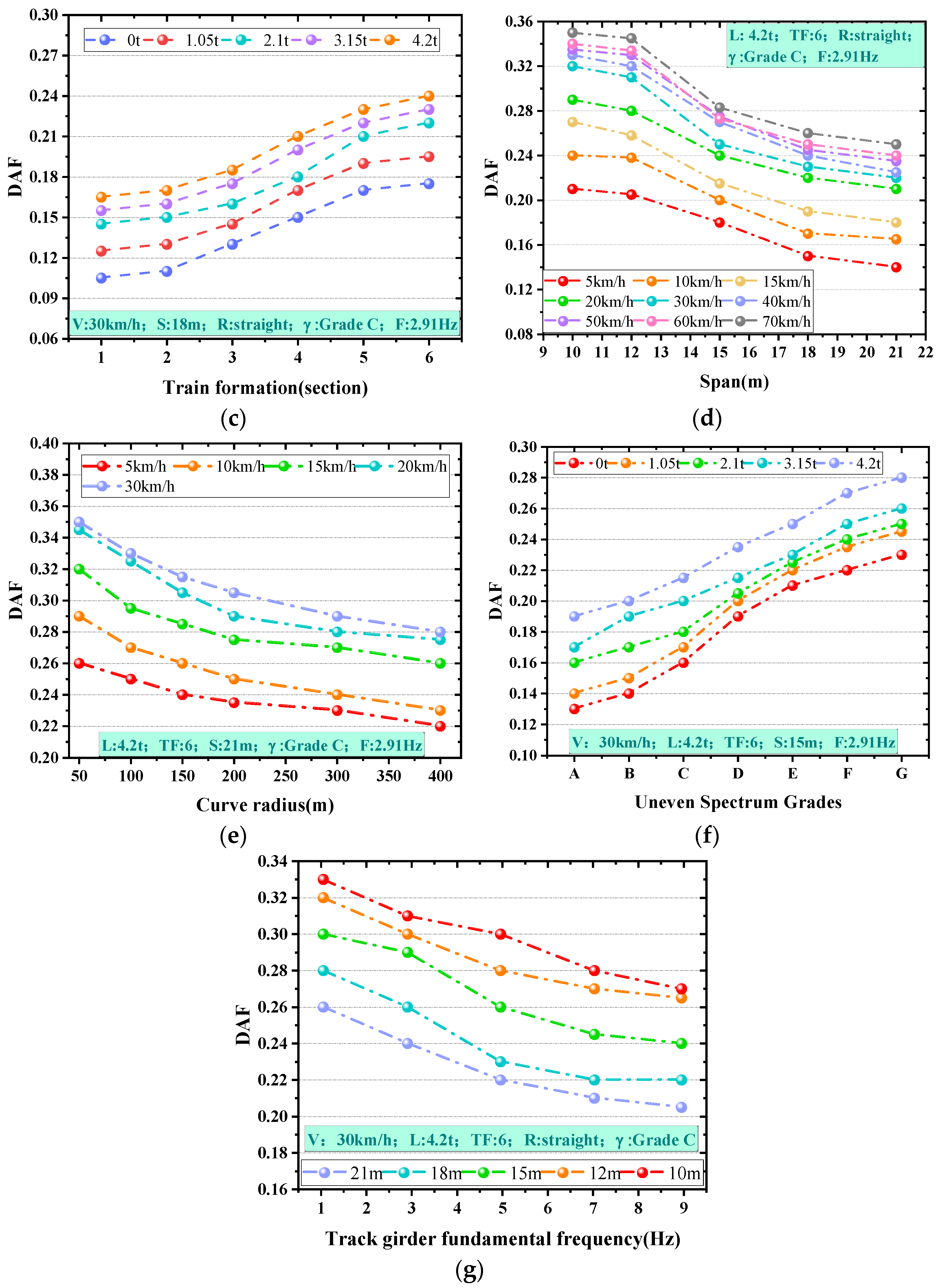
3. Analysis of Factors Influencing the DAFs

This section conducted an analysis of the influencing factors of the DAFs of the MTTS based on the joint simulation model established in the previous section, exploring the influence mechanisms of train characteristic parameters (speed, load, and formation) and track beam characteristic parameters (span, curve radius, track unevenness spectrum classification, and fundamental frequency) on the DAFs. Based on the actual project operational conditions of MTTS and relevant specification requirements. The working conditions were set as follows: (1) speed (V): 10 km/h, 15 km/h, 20 km/h, 30 km/h, 40 km/h, 50 km/h, 60 km/h, and 70 km/h; (2) load (L): empty, 1/4 full load (1.05 t), half load (2.1 t), 3/4 full load (3.15 t), and full load (4.2 t); (3) train formation (TF): 1 to 6 train formations; (4) Span (S): 10 m, 12 m, 15 m, 18 m, and 21 m; (5) curve radius (R): 21 m span beams with radii of 50 m, 100 m, 150 m, 200 m, 300 m, 400 m; (6) track unevenness spectrum (γ): an irregularity spectrum based on measured data fitting was adopted, which was classified into seven grades from A to G in order of superiority [29], see Figure 8a; and (7) track beam fundamental frequency (F): 1.05 Hz (0.5 times stiffness), 2.91 Hz (1 times stiffness), 4.96 Hz (2 times stiffness), 7.03 Hz (3 times stiffness), 8.95 Hz (4 times stiffness), a total of five calculation conditions.

The mid-span dynamic displacement response result when the train speed was set at 0.1 km/h was taken as the static response. Based on the control variable method, the variation law of the DAFs under the influence of each control factor was explored. Due to the high consistency of the dynamic response curves of the track beam under the influence of various factors, this section only took the variation law of the mid-span dynamic response of the track beam under the influence of speed and irregularity as an example for a brief analysis. The results are as follows:

Based on the analysis of the dynamic displacement time curve shown in Figure 8b–f, with speed and track unevenness as control factors, it was observed that the dynamic displacement in the span exhibited a positive correlation with speed. As the speed increased, the extreme value of dynamic displacement demonstrated rapid growth below 30 km/h. When the speed exceeded 30 km/h, the growth rate of the dynamic displacement extreme value began to decelerate, reaching its peak at 70 km/h. Additionally, the dynamic displacement in the span demonstrated strong sensitivity to variations in track beam unevenness. With the deterioration of the track unevenness grading spectrum (from Grade A to Grade G), the dynamic displacement in the span is correspondingly accompanied by a marked increase in the overall volatility of the time curve. The density and amplitude of curve fluctuation sections exhibited a positive correlation and an approximately linear relationship with spectral grading changes.

The parameter analysis results for DAFs are shown in Figure 9. The conclusions are as follows: (1) Figure 9a shows that the train speed has a significant impact on the DAFs of the monorail track beam. Within the speed range of 0–30 km/h, the impact coefficient shows a logarithmic nonlinear growth trend overall with respect to the train speed and reaches its extreme value at 30 km/h. When the speed exceeds 30 km/h, the DAFs vary periodically around their extreme value with the train speed. (2) Figure 9b indicates that train loads constitute a minor proportion of the total loading effect and have a relatively insignificant impact on the structural impact effect. (3) Figure 9c demonstrates that the train formation significantly influences the dynamic load on the track beam DAFs. When the total train length is smaller than the track beam span, the DAFs exhibit strong sensitivity to train formation variations. However, when the total train length exceeds the track beam span, further increases in formation length no longer cause significant DAF growth. (4) Figure 9d reveals that the DAFs are significantly affected by the track beam span. Within the calculated span range, the DAF values exhibit an exponential decrease as the span increases. For small-span track beams, higher train loads intensify the dynamic response of key cross-sections, resulting in abrupt DAF changes. (5) Figure 9e illustrates that the DAFs of the track beam show an exponential nonlinear negative correlation with variations in curve radius. Compared with straight beams, smaller curve radii enhance the bending-twisting coupling effect, leading to significant fluctuations in the DAFs. (6) Figure 9f highlights that track unevenness substantially affects the vibration response of the monorail track beam. As the track irregularity grading spectrum deteriorates (from A to G), the sensitivity of the DAFs response exhibits gradual growth characterized by an S-shaped curve. (7) Figure 9g additionally indicates that fundamental frequency influenced the dynamic response of monorail track beams, with lower fundamental frequencies causing resonance phenomena and, consequently, larger DAF values.

4. LASSO-Based Regression Analysis of DAFs for Multifactor Coupling Effects

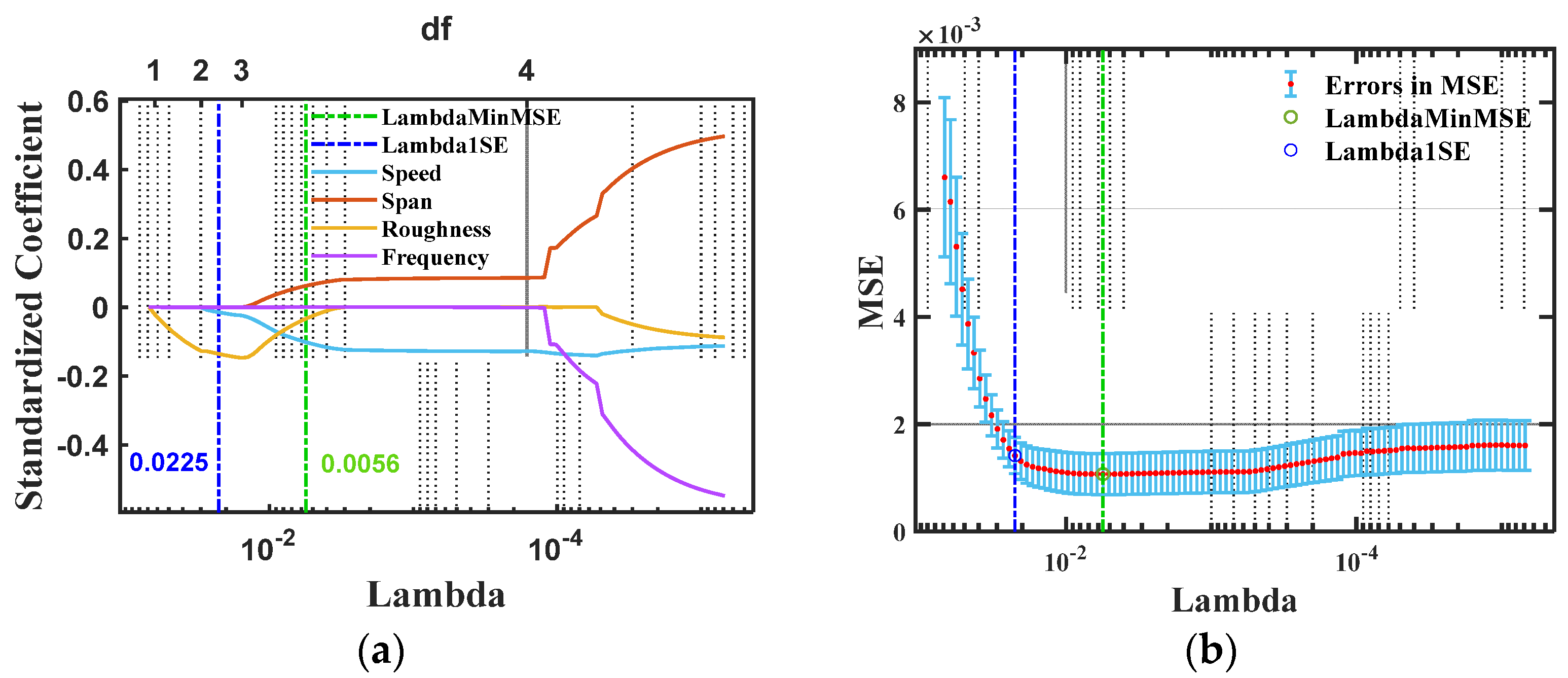
4.1. Regression Parameter Screening

The DAFs have many influencing factors, and there are mutual influences. This section using the Pearson correlation coefficient method and random forest algorithm to study the correlation between the influencing factors and the impact coefficients and multifactor coupling in the impact coefficients process of the degree of contribution to the screening of the regression parameters; however, there is a significant multiple covariance between the regression parameters, if the direct traditional regression analysis will increase the regression model overfitting and not. However, there is significant multicollinearity among the regression parameters, and direct traditional regression analysis will increase the risk of overfitting and instability of the regression model, while LASSO regression can better deal with the problem of multicollinearity, and at the same time, it can also further screen the regression variables of the model, which can increase the spatial dimension of the characteristics of the regression expression and simplicity at the same time of ensuring the model stability.

Based on the previous research results, this section used the Pearson correlation coefficient method [30] to explore the degree of correlation between each influencing factor and the DAFs and used the random forest algorithm [31] to explore the importance of each influencing factor in the coupling effect on the DAFs. The results were comprehensively analyzed to screen the regression parameters, reduce the dimension of the DAFs feature space, and improve the accuracy of the regression model.

The results of Pearson correlation analysis are shown in Figure 10a. The results indicate that the correlation coefficients between span, speed, track irregularity, fundamental frequency, and the DAFs are all greater than 0.8, suggesting a significant correlation. Moreover, the correlation coefficients among these four parameters are relatively large, indicating the existence of multicollinearity. The correlation coefficients of load, formation, and curve radius are relatively small, suggesting a slightly weaker correlation. The results of the feature importance analysis of the impact coefficient based on the random forest algorithm are shown in Figure 10b. It can be seen from the analysis that the importance proportion of the four influencing factors of span, speed, track irregularity, and fundamental frequency is 94.93%, indicating that these four factors cover most of the information in the process of multiple factors coupling to affect the DAFs. Therefore, these four influencing factors are selected as the regression parameters.

4.2. Multiple Regression Analysis of DAFs Based on LASSO Regression Theory

Based on the research results from the previous section, span, speed, unevenness, and base frequency were selected as regression parameters. However, there is multicollinearity among these characteristic factors. In this section, based on the LASSO regression theory [32], Python software (3.10.2) programming was used to conduct a multiple regression analysis of the DAFs. LASSO regression can effectively handle the problem of parameter multicollinearity and further screen the regression parameters by sacrificing some unbiasedness to reduce the dimension of the DAFs feature space, ensuring the stability of the regression model and increasing the simplicity and intuitiveness of the DAFs calculation expression. Since the relationship between a single control factor and the DAFs is approximately nonlinear, to facilitate subsequent calculations, the function relationship between a single factor and the DAFs was linearized first (

Table 1. Regression parameters linearization correlation parameters.

Regression Parameters	Linearization Equation	Parameters
		m	n
Speed (V)	$x^{*}={\displaystyle \frac{1}{1+{(\frac{x}{m})}^n}}$	14.535	2.786
Span (S)		12.436	7.350
Frequency (F)		3.774	2.338
Unevenness (γ)		3.842	3.658

).

After linearizing the regression parameters, the Z-score method was used to standardize the original data to eliminate the influence of differences in the dimensions of various variables and ensure the accuracy of the regression model. As shown in Figure 11a,b, based on the LASSO regression theory, the regularization path diagram and MSE cross-validation diagram during the establishment of the multiple regression model of the DAFs are presented. Where Lambda denotes the regularization parameter, MSE represents the mean square error, and the standardization coefficient serves as an eigenvalue to quantify the influencing factors during the regularization calculation process. When the standardization coefficients of each regression parameter start to stabilize with the change of the regularization parameter Lambda, that is, the curve in the figure shows a relatively gentle trend, and the mean square error (MSE) of the established regression model reaches the minimum, the regularization parameter Lambda achieves the optimal value. At this point, the established regression model is the most stable and can effectively avoid the problem of multicollinearity. The analysis reveals that when Lambda is taken as 0.0056, the MSE reaches its minimum value. However, at this point, the regularization path diagram shows a relatively large degree of dispersion. Therefore, the Lambda1SE value obtained when Lambda is 0.0225 is selected as the optimal MSE.

Based on the optimal value, a LASSO regression model of the DAFs was established, and the regression expression is shown in Equation (1). The analysis reveals that the track beam fundamental frequency (F) and track unevenness (γ) are screened out of the LASSO model, while speed (V) and span (S) are retained as regression parameters. The calculation results from the program demonstrated that the coefficient of determination (R²) of the LASSO regression model is 0.948, the adjusted R² is 0.945, and the root mean square error (RMSE) is 0.0154. These results indicate that the regression model can predict 94.50% of the variation information of DAFs. Moreover, both the model and the variables have passed the 95% confidence interval test with a significance level of 0.05, indicating that the regression effect of the model is accurate and reliable.

$$\mu =0.187+{\displaystyle \frac{0.185}{1+{(\frac{S}{14.535})}^{7.35}}}-{\displaystyle \frac{0.133}{1+{(\frac{V}{12.436})}^{2.786}}}$$

(1)

Here, $\mu$ is the DAFs, S is the span (m), and V is the traveling speed (km/h).

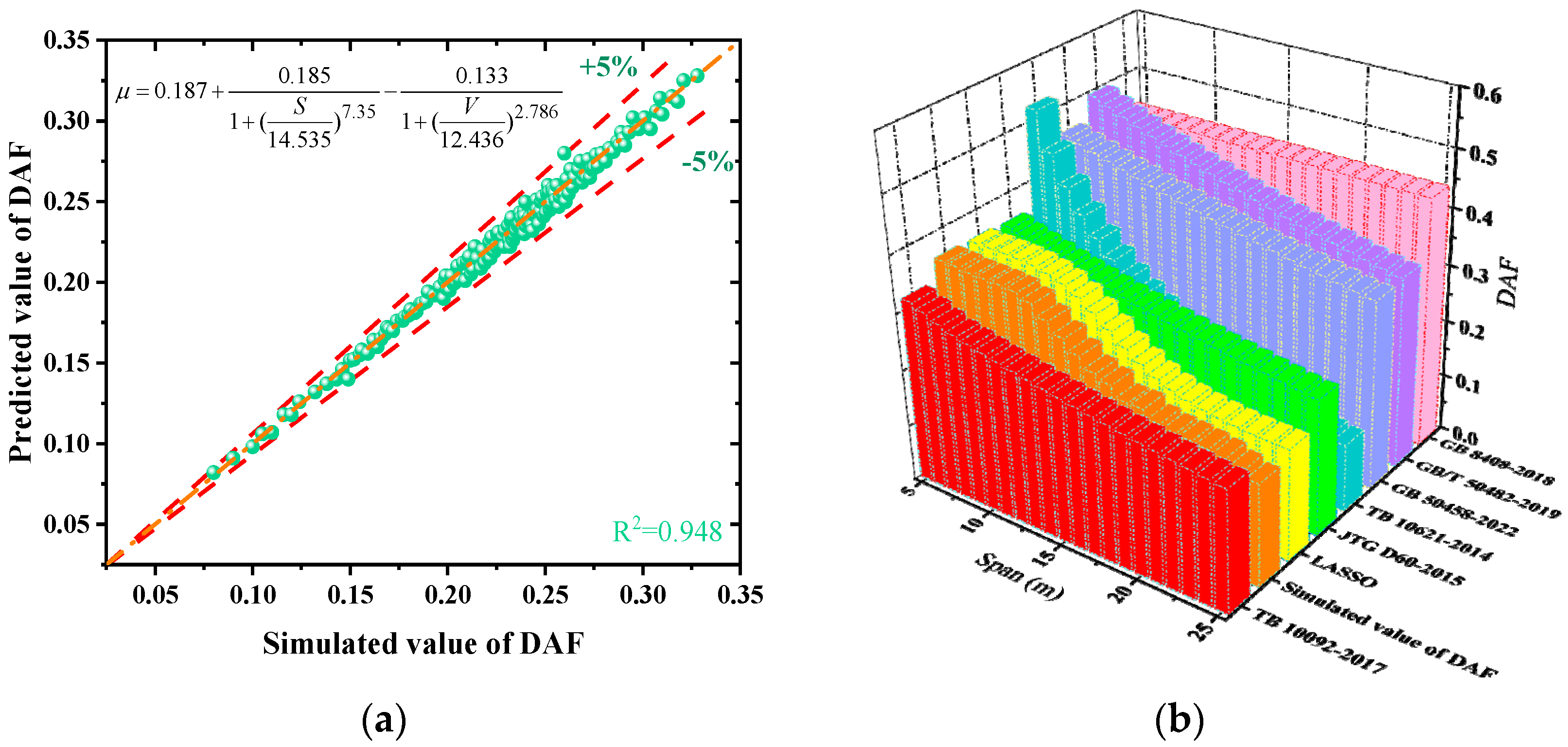
4.3. Regression Model Validation

To verify the validity and accuracy of the LASSO regression model, this section calculated the intersection diagram of the DAFs for 200 groups of samples under the same operating conditions using both the regression model and the joint simulation model in Figure 12a. Considering the characteristics of the DAFs as a span function in most specifications, the predicted DAF values are calculated with span as the independent variable when the speed is set to 40 km/h. The comparison results are presented in Figure 12b.

Analysis of Figure 12a shows that the predicted values from the regression model are in good agreement with the simulated values, and the DAFs values are basically in line with the characteristics of the normal distribution. Analysis of Figure 12b demonstrates that: (1) For the “Large-scale amusement device safety code (GB 8408-2018) [2]”, “General Specifications for Design of Highway Bridges and Culverts (JTG D60-2015) [33]”, “Standard for Design of Straddle Monorail Transit (GB 50458-2022) [34]”, and “Code for Design of Urban Rail Transit Bridge (GB/T 51234-2017) [35]”, the calculated DAFs values are consistently higher than the simulated DAFs values of the MTTS across different spans, with errors exceeding 10% in all cases. (2) For the “Code for Design on Railway Bridge and Culvert (TB 10092-2017) [36]”, when the span is relatively small, the code-specified DAFs are lower than the simulated value. As the span increases, the difference between the two gradually decreases. When the span reaches 15 m, the difference becomes the smallest. However, as the span continues to increase, the code-specified value gradually exceeds the simulated value, and the difference shows a positive correlation with the span. Additionally, the DAFs values specified in GB 8408-2018 were overly simplified, and their direct adoption could potentially lead to significant errors. (3) The DAFs expression established based on the LASSO regression is generally consistent with the simulated values overall, with the error remaining within 4%, indicating that the DAFs expression can effectively represent the vast majority of the actual impact effect information.

The above research shows that the DAFs multiple regression model established based on LASSO has high reliability and accuracy and can be used as the recommended expression of DAFs for MTTS. This is of positive significance for improving the design and evaluation system of MTTSs.

4.4. Limitations and Future Work

MTTS and traditional monorail systems exhibit significant differences; therefore, the DAFs prediction model proposed in this paper is more suitable for large-scale amusement facilities that conform to the structural characteristics of MTTS. Furthermore, in the research of civil engineering, when the influencing factors of the research object are numerous, screening out the factors with significant correlation and high contribution and then conducting subsequent research (such as regression analysis, establishing prediction models, etc.) is important research content. When encountering such problems, the systematic research method proposed in this paper can be considered. This can not only avoid cumbersome analysis and derivation but also obtain conclusions that meet the requirements of analysis accuracy. In future research, the following work still needs to be carried out to make the research on the MTTS more complete.

i.

A field of theoretical research requires extensive on-site trials of the project to provide support. Currently, the on-site trials for MTTS project research are relatively insufficient, especially in areas such as bearing force states, cross-sectional changes in steel box beams, train bogie structures, and tire forces and wear. Future studies could focus on conducting more detailed field tests on these aspects to enhance and refine the research system.

ii.

There is still room for improvement in the research on the DAFs of MTTSs. Future studies could develop a probabilistic algorithmic prediction model for the DAFs and enhance prediction accuracy by comprehensively considering the uncertainty and complexity of influencing factors.

5. Conclusions

To address the limited knowledge of the DAFs for MTTS and general monorail systems, this study performed a comprehensive parametric analysis and predictive modeling based on a validated joint model. The main conclusions are summarized as follows:

i.

Relying on the CRRC Zhuzhou test line project, a vehicle–bridge coupling field test of MTTS was conducted. The results show that the influence degrees of each test parameter on the DAFs are different, and the displacement DAFs are greater than the strain DAFs.

ii.

The joint simulation model established based on the vehicle–bridge coupling test parameters of the MTTS and the actual project parameters was demonstrated to be reasonable and reliable, and the simulation results of the structural dynamic response model were in good agreement with the test results.

iii.

Based on the joint simulation model for analyzing DAF impact parameters, the results showed that each impact parameter exhibited varying degrees of influence on the variability of the DAFs. Notably, the span and speed were identified as having the most significant impact.

iv.

Based on the Pearson correlation coefficient method and the random forest algorithm, the regression parameters of the DAFs were screened. The results show that there is a significant correlation between speed, span, unevenness, fundamental frequency and the DAFs, and the total contribution degree of these factors in the process of the DAFs under the coupling effect of multiple factors is 94.93%. Therefore, speed, span, unevenness, and fundamental frequency were selected as the regression parameters of the DAFs.

v.

Utilizing LASSO regression theory to establish the DAFs multivariate regression model, the calculation results of the regression model and the simulation model were compared with the specifications. The results indicated that the regression model was reasonable and effective, passing the 95% confidence level and 0.05 significance test while demonstrating high precision. Therefore, it is recommended as a calculation expression for the DAFs of MTTSs.