Soil Parameter Inversion in Dredger Fill Strata Using GWO-MLSSVR for Deep Foundation Pit Engineering
Abstract
1. Introduction
2. Materials and Methods
2.1. Machine Learning Model
2.1.1. The Gray Wolf Optimization Algorithm
2.1.2. Least Squares Support Vector Regression
2.1.3. Gray Wolf Optimization for Multi-Output LSSVR
2.2. Engineering Background and Numerical Simulation
2.2.1. Engineering Background
2.2.2. FLAC3D Numerical Simulation
2.3. Orthogonal Experiment
2.3.1. Determination of Parameter Inversion Intervals
2.3.2. Training Samples
3. Results
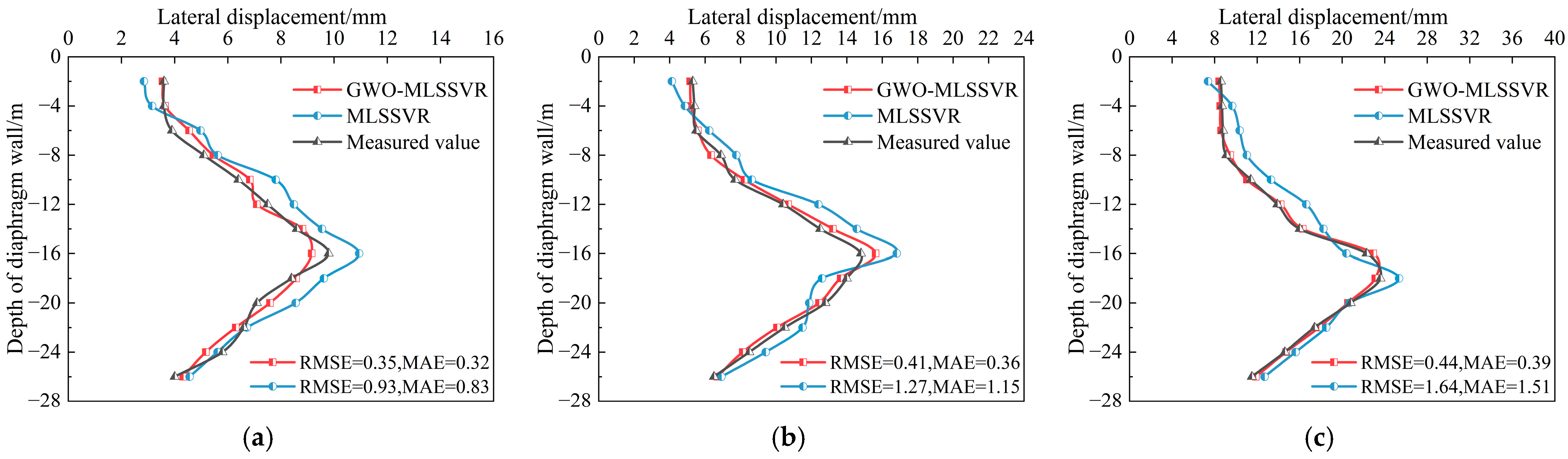
3.1. Inversion Results of Soil Parameters
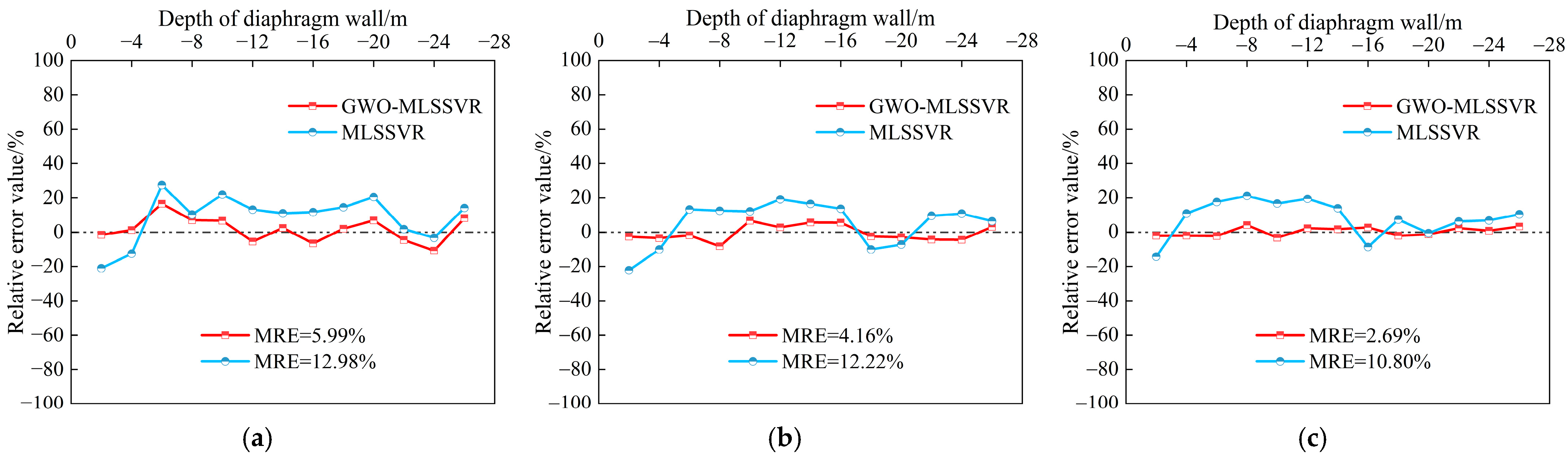
3.2. Assessment of Inversion Performance
4. Discussion
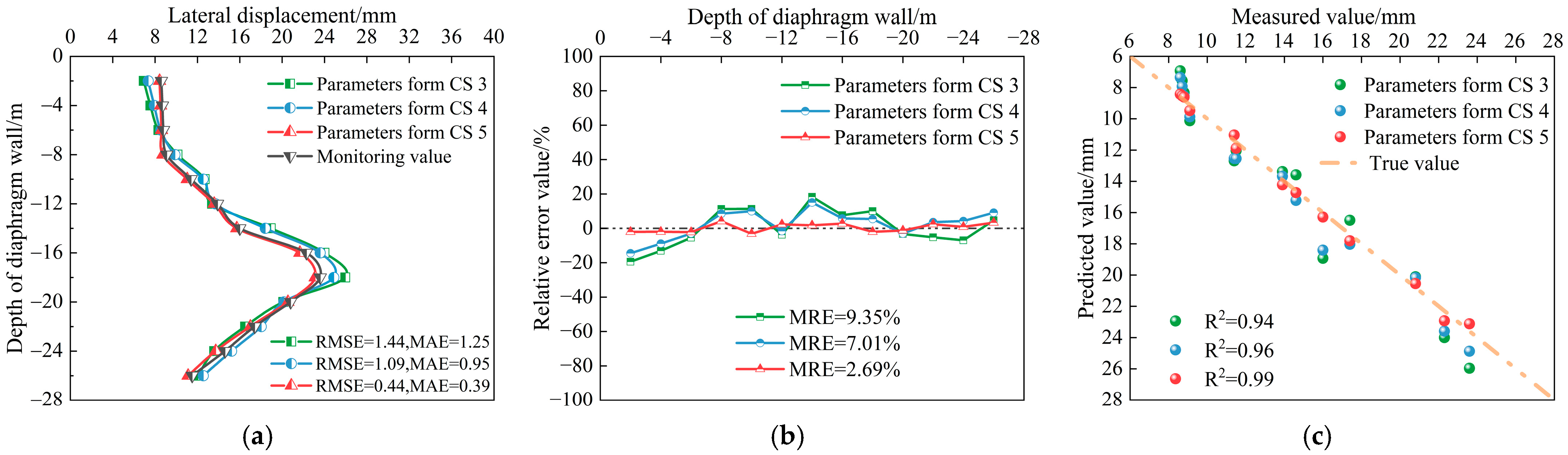
4.1. Effect of Construction Stage
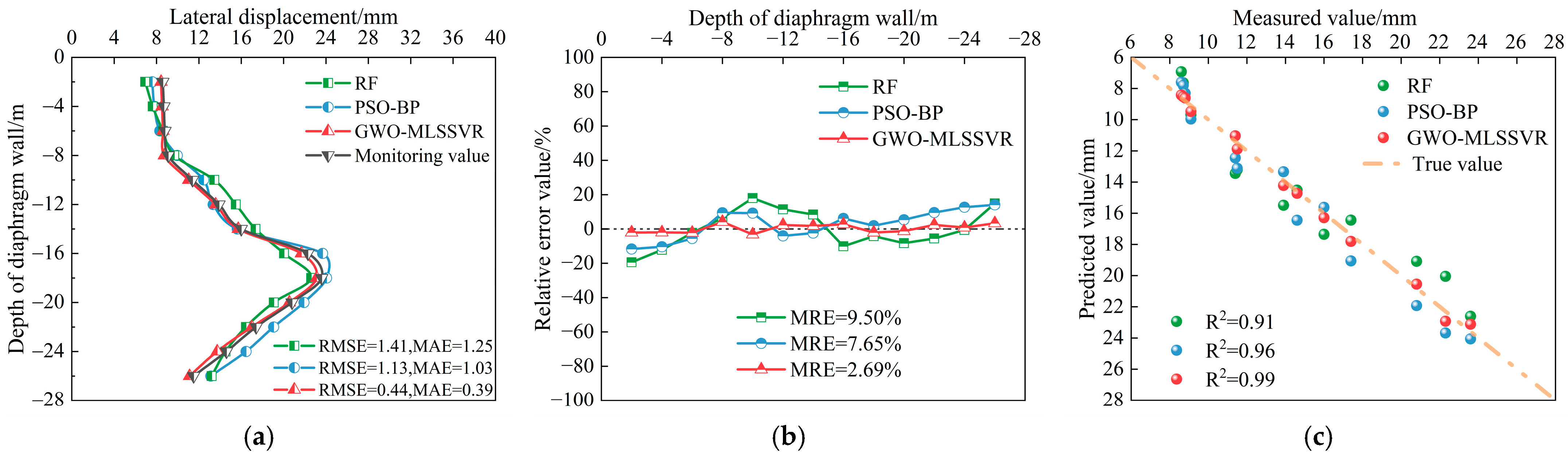
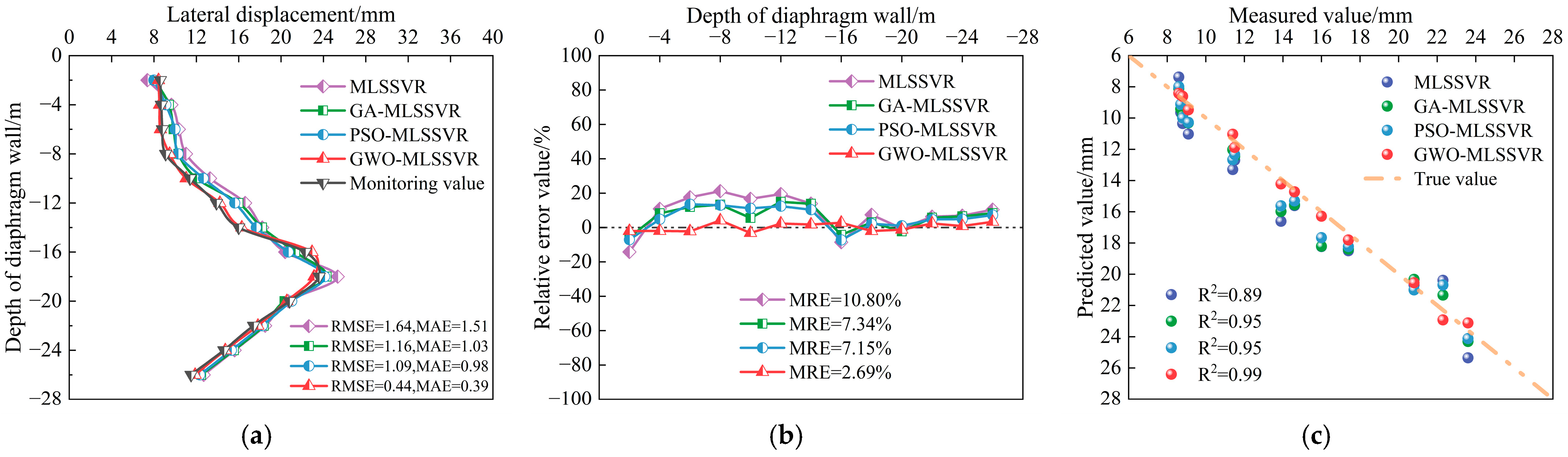
4.2. Compared with Other Inversion Methods
4.3. Compared with Other Optimization Algorithms
4.4. Effect of Node Number in the Input Layer
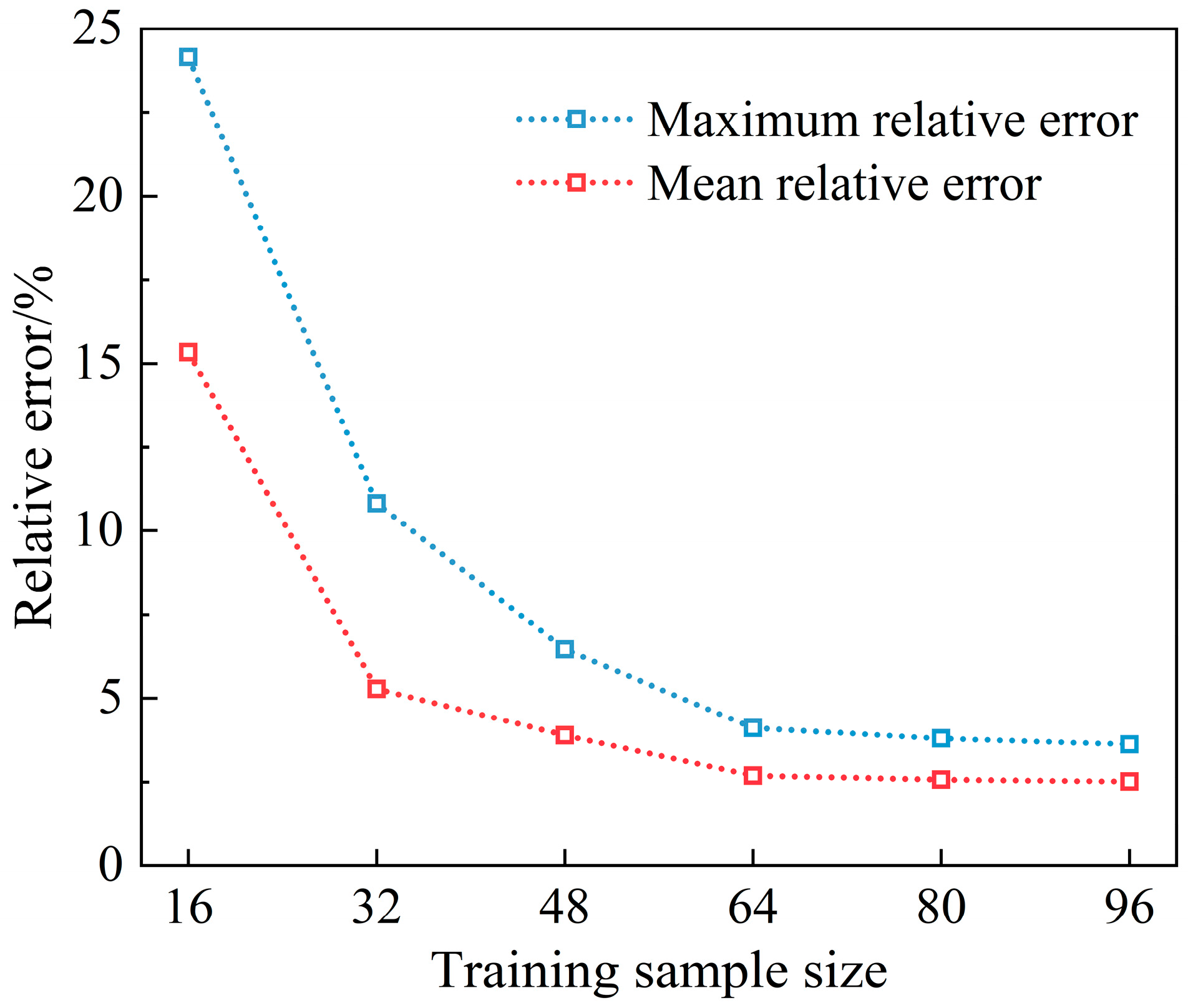
4.5. Effect of the Number of Training Samples
4.6. Research Limitation
5. Conclusions
- The displacement curves of the retaining structure, obtained from the inversion of MLSSVR and GWO-MLSSVR, align with the variations in the actual displacement curves, indicating that the lateral displacement of the retaining structure can be accurately inverted to yield precise HS parameters. The lateral displacement values derived via GWO-MLSSVR closely align with the measured monitoring data, exhibiting reduced relative errors.
- With the progression of foundation pit excavation, the relative error in the inverted lateral displacements of the retaining structure tends to decrease. Hence, it is advisable to perform parameter inversion based on excavation stages with larger horizontal displacements, as this can lead to improved inversion accuracy.
- In the inversion method proposed in this study, increasing the number of input layer nodes can help reduce errors to a certain extent. However, when the error falls within the acceptable range for engineering applications, it is advisable to select an appropriate number of input nodes to avoid unnecessary computational costs and potential overfitting.
- The size of the training dataset has a certain impact on the inversion outcomes. In this study, 64 training samples were employed, which proved adequate to satisfy the accuracy requirements of parameter inversion.
- Compared with other commonly adopted inversion methods, the GWO-MLSSVR method proposed in this study shows superior inversion performance. The lateral displacements of the retaining structure at various depths, calculated using the inverted parameters, differ from the measured values by less than 5%. This indicates that GWO-MLSSVR is an innovative and practical approach for inverting constitutive parameters of foundation soils, characterized by high accuracy and robustness.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Sample ID | / (kPa) | (°) | / (MPa) | / (kPa) | (°) | / (MPa) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 10 | 4 | 3 | 6 | 10 | 5 | 3 |
| 2 | 4 | 12 | 6 | 4.5 | 10 | 20 | 11 | 6.5 |
| 3 | 4 | 14 | 8 | 6 | 11 | 24 | 6 | 4.5 |
| 4 | 4 | 16 | 10 | 5.5 | 7 | 14 | 12 | 5 |
| 5 | 4 | 18 | 9 | 3.5 | 13 | 16 | 7 | 6 |
| 6 | 4 | 20 | 11 | 4 | 9 | 22 | 9 | 3.5 |
| 7 | 4 | 22 | 5 | 6.5 | 8 | 18 | 8 | 5.5 |
| 8 | 4 | 24 | 7 | 5 | 12 | 12 | 10 | 4 |
| 9 | 5 | 10 | 7 | 4 | 11 | 18 | 12 | 6 |
| 10 | 5 | 12 | 5 | 3.5 | 7 | 12 | 6 | 3.5 |
| 11 | 5 | 14 | 11 | 5 | 6 | 16 | 11 | 5.5 |
| 12 | 5 | 16 | 9 | 6.5 | 10 | 22 | 5 | 4 |
| 13 | 5 | 18 | 10 | 4.5 | 8 | 24 | 10 | 3 |
| 14 | 5 | 20 | 8 | 3 | 12 | 14 | 8 | 6.5 |
| 15 | 5 | 22 | 6 | 5.5 | 13 | 10 | 9 | 4.5 |
| 16 | 5 | 24 | 4 | 6 | 9 | 20 | 7 | 5 |
| 17 | 6 | 10 | 10 | 5 | 13 | 20 | 8 | 3.5 |
| 18 | 6 | 12 | 8 | 6.5 | 9 | 10 | 10 | 6 |
| 19 | 6 | 14 | 6 | 4 | 8 | 14 | 7 | 4 |
| 20 | 6 | 16 | 4 | 3.5 | 12 | 24 | 9 | 5.5 |
| 21 | 6 | 18 | 7 | 5.5 | 6 | 22 | 6 | 6.5 |
| 22 | 6 | 20 | 5 | 6 | 10 | 16 | 12 | 3 |
| 23 | 6 | 22 | 11 | 4.5 | 11 | 12 | 5 | 5 |
| 24 | 6 | 24 | 9 | 3 | 7 | 18 | 11 | 4.5 |
| 25 | 7 | 10 | 9 | 6 | 8 | 12 | 9 | 6.5 |
| 26 | 7 | 12 | 11 | 5.5 | 12 | 18 | 7 | 3 |
| 27 | 7 | 14 | 5 | 3 | 13 | 22 | 10 | 5 |
| 28 | 7 | 16 | 7 | 4.5 | 9 | 16 | 8 | 4.5 |
| 29 | 7 | 18 | 4 | 6.5 | 11 | 14 | 11 | 3.5 |
| 30 | 7 | 20 | 6 | 5 | 7 | 24 | 5 | 6 |
| 31 | 7 | 22 | 8 | 3.5 | 6 | 20 | 12 | 4 |
| 32 | 7 | 24 | 10 | 4 | 10 | 10 | 6 | 5.5 |
| 33 | 8 | 10 | 5 | 5.5 | 9 | 24 | 11 | 4 |
| 34 | 8 | 12 | 7 | 6 | 13 | 14 | 5 | 5.5 |
| 35 | 8 | 14 | 9 | 4.5 | 12 | 10 | 12 | 3.5 |
| 36 | 8 | 16 | 11 | 3 | 8 | 20 | 6 | 6 |
| 37 | 8 | 18 | 8 | 5 | 10 | 18 | 9 | 5 |
| 38 | 8 | 20 | 10 | 6.5 | 6 | 12 | 7 | 4.5 |
| 39 | 8 | 22 | 4 | 4 | 7 | 16 | 10 | 6.5 |
| 40 | 8 | 24 | 6 | 3.5 | 11 | 22 | 8 | 3 |
| 41 | 9 | 10 | 6 | 6.5 | 12 | 16 | 6 | 5 |
| 42 | 9 | 12 | 4 | 5 | 8 | 22 | 12 | 4.5 |
| 43 | 9 | 14 | 10 | 3.5 | 9 | 18 | 5 | 6.5 |
| 44 | 9 | 16 | 8 | 4 | 13 | 12 | 11 | 3 |
| 45 | 9 | 18 | 11 | 6 | 7 | 10 | 8 | 4 |
| 46 | 9 | 20 | 9 | 5.5 | 11 | 20 | 10 | 5.5 |
| 47 | 9 | 22 | 7 | 3 | 10 | 24 | 7 | 3.5 |
| 48 | 9 | 24 | 5 | 4.5 | 6 | 14 | 9 | 6 |
| 49 | 10 | 10 | 11 | 3.5 | 10 | 14 | 10 | 4.5 |
| 50 | 10 | 12 | 9 | 4 | 6 | 24 | 8 | 5 |
| 51 | 10 | 14 | 7 | 6.5 | 7 | 20 | 9 | 3 |
| 52 | 10 | 16 | 5 | 5 | 11 | 10 | 7 | 6.5 |
| 53 | 10 | 18 | 6 | 3 | 9 | 12 | 12 | 5.5 |
| 54 | 10 | 20 | 4 | 4.5 | 13 | 18 | 6 | 4 |
| 55 | 10 | 22 | 10 | 6 | 12 | 22 | 11 | 6 |
| 56 | 10 | 24 | 8 | 5.5 | 8 | 16 | 5 | 3.5 |
| 57 | 11 | 10 | 8 | 4.5 | 7 | 22 | 7 | 5.5 |
| 58 | 11 | 12 | 10 | 3 | 11 | 16 | 9 | 4 |
| 59 | 11 | 14 | 4 | 5.5 | 10 | 12 | 8 | 6 |
| 60 | 11 | 16 | 6 | 6 | 6 | 18 | 10 | 3.5 |
| 61 | 11 | 18 | 5 | 4 | 12 | 20 | 5 | 4.5 |
| 62 | 11 | 20 | 7 | 3.5 | 8 | 10 | 11 | 5 |
| 63 | 11 | 22 | 9 | 5 | 9 | 14 | 6 | 3 |
| 64 | 11 | 24 | 11 | 6.5 | 13 | 24 | 12 | 6.5 |
References
- Fu, Y.B.; He, S.Y.; Zhang, S.Z.; Yang, Y. Parameter Analysis on Hardening Soil Model of Soft Soil for Foundation Pits Based on Shear Rates in Shenzhen Bay, China. Adv. Mater. Sci. Eng. 2020, 2020, 7810918. [Google Scholar] [CrossRef]
- Zhu, M.; Chen, X.S.; Zhang, G.T.; Pang, X.C.; Su, D.; Liu, J.Q. Parameter back-analysis of hardening soil model for granite residual soil and its engineering applications. Rock Soil Mech. 2022, 43, 1061–1072. [Google Scholar] [CrossRef]
- Shi, X.M.; Sun, J.L.; Qi, Y.; Zhu, X.Y.; Zhang, X.M.; Liang, R.S.; Chen, H.J. Study on Stiffness Parameters of the Hardening Soil Model in Sandy Gravel Stratum. Appl. Sci. 2023, 13, 2710. [Google Scholar] [CrossRef]
- Yan, X.; Tong, L.Y.; Li, H.J.; Liu, W.Y.; Xiao, Y.; Wang, W. Effects of the excavation of deep foundation pits on an adjacent double-curved arch bridge. Undergr. Space 2025, 21, 164–177. [Google Scholar] [CrossRef]
- Cao, Y.M.; Li, Z.Y.; Chen, J.L.; Xia, C.Y. Stochastic inversion of soil dynamic parameters based on non-intrusive data. Soil Dyn. Earthq. Eng. 2024, 181, 108640. [Google Scholar] [CrossRef]
- Pu, X.S.; Huang, J.; Peng, T.; Wang, W.Z.; Li, B.; Zhao, H.T. Application of Parameter Inversion of HSS Model Based on BP Neural Network Optimized by Genetic Algorithm in Foundation Pit Engineering. Buildings 2025, 15, 531. [Google Scholar] [CrossRef]
- Cheng, Q.; Yang, Z.; Qin, S.; Zhang, L.; Miao, Q.; Zhang, Y. Application of soil parameters inversion based on psomlssvr in deep foundation pit engineering. J. Eng. Geol. 2022, 30, 520–532. [Google Scholar]
- Zhang, J.J.; Li, H.B.; Zhang, G.Z.; Gu, Y.P.; Liu, Z.F. Rock physics inversion based on an optimized MCMC method. Appl. Geophys. 2021, 18, 288–298. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Raja, M.N.A.; Abdoun, T.; El-Sekelly, W. Exploring the Potential of Machine Learning in Stochastic Reliability Modelling for Reinforced Soil Foundations. Buildings 2024, 14, 954. [Google Scholar] [CrossRef]
- Tang, R.; Luo, W. Parameter inversion of soft soil subgrade based on support vector machine optimized by gravitational search algorithm. J. Rail Way Sci. Eng. 2022, 19, 1568–1576. [Google Scholar]
- Yu, H.; Chen, X.B.; Yi, L.Q.; Qiu, J.; Gu, Z.H.; Zhao, H. Parameter inversion and application of soft soil modified Cambridge model. Rock Soil Mech. 2023, 44, 3318–3326. [Google Scholar] [CrossRef]
- Sun, P.M.; Bao, T.F.; Gu, C.S.; Jiang, M.; Wang, T.; Shi, Z.W. Parameter sensitivity and inversion analysis of a concrete faced rock-fill dam based on HS-BPNN algorithm. Sci. China-Technol. Sci. 2016, 59, 1442–1451. [Google Scholar] [CrossRef]
- Ruan, Y.; Yu, D.; Yang, J.; Wu, L.; Tan, G. Inversion of Mechanical Parameters of Reinforced Soft Soil around Tunnel Based on PSO-SVM. J. Highw. Transp. Res. Dev. 2020, 37, 87–96. [Google Scholar]
- Cui, J.Q.; Wu, S.C.; Cheng, H.Y.; Kui, G.; Zhang, H.R.; Hu, M.L.; He, P.B. Composite interpretability optimization ensemble learning inversion surrounding rock mechanical parameters and support optimization in soft rock tunnels. Comput. Geotech. 2024, 165, 105877. [Google Scholar] [CrossRef]
- Xiao, J.F.; Wang, Q.W.; Zhang, Q.H.; Hei, Y.P.; Zhang, Y.L. Multiple Parameters Determination Method of Hardening Soil Model Based on Particle Swarm Optimization. Adv. Civ. Eng. 2024, 2024, 5561981. [Google Scholar] [CrossRef]
- Balogun, A.L.; Rezaie, F.; Pham, Q.B.; Gigovic, L.; Drobnjak, S.; Aina, Y.A.; Panahi, M.; Yekeen, S.T.; Lee, S. Spatial prediction of landslide susceptibility in western Serbia using hybrid support vector regression (SVR) with GWO, BAT and COA algorithms. Geosci. Front. 2021, 12, 101104. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Ahmed, A.N.; Kisi, O.; El-Shafie, A. Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (GWO) algorithm. J. Hydrol. 2020, 582, 124435. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, R.; Gong, C.; Zhao, L. Study on improvement of gray wolf algorithm. Appl. Res. Comput. 2017, 34, 3603. [Google Scholar]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.G.; Zhu, S.L.; Armaghani, D.J.; Li, C.Q.; Nguyen, H.; Yagiz, S. Optimization of support vector machine through the use of metaheuristic algorithms in forecasting TBM advance rate. Eng. Appl. Artif. Intell. 2021, 97, 104015. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Wang, Y.K.; Tang, H.M.; Huang, J.S.; Wen, T.; Ma, J.W.; Zhang, J.R. A comparative study of different machine learning methods for reservoir landslide displacement prediction. Eng. Geol. 2022, 298, 106544. [Google Scholar] [CrossRef]
- Zhang, L.M.; Wu, X.G.; Zhu, H.P.; AbouRizk, S.M. Performing Global Uncertainty and Sensitivity Analysis from Given Data in Tunnel Construction. J. Comput. Civ. Eng. 2017, 31, 04017065. [Google Scholar] [CrossRef]
- Bao, T.F.; Li, J.M.; Lu, Y.F.; Gu, C.S. IDE-MLSSVR-Based Back Analysis Method for Multiple Mechanical Parameters of Concrete Dams. J. Struct. Eng. 2020, 146, 04020155. [Google Scholar] [CrossRef]
- Ye, J.; He, X. Performance of batter pile walls in deep excavation: Laboratory test and numerical analysis. Mech. Adv. Mater. Struct. 2022, 29, 5301–5310. [Google Scholar] [CrossRef]
- Li, Y.D.; Wang, C.X.; Sun, Y.; Wang, R.C.; Shao, G.J.; Yu, J. Analysis of Corner Effect of Diaphragm Wall of Special-Shaped Foundation Pit in Complex Stratum. Front. Earth Sci. 2022, 10, 794756. [Google Scholar] [CrossRef]
- Shi, Y.; Ruan, J.; Wu, C. Xiamen area typical stratum of HS-small model for small strain parameters sensitivity analysis. Sci. Technol. Eng. 2017, 17, 105–110. [Google Scholar]
- Ye, J.; He, X. Response of dual-row retaining pile walls under surcharge load. Mech. Adv. Mater. Struct. 2022, 29, 1614–1625. [Google Scholar] [CrossRef]
- Wang, S.H.; Han, B.W.; Jiang, J.H.; Telyatnikova, N. Machine learning and FEM-driven analysis and optimization of deep foundation pits in coastal area: A case study in Fuzhou soft ground. Undergr. Space 2025, 22, 55–76. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.L.; Yao, A.J.; Gong, Y.F.; Liang, X.M. Simplified Calculation Method of Wall-Brace Coordinated Deformation in the Excavation Process of a Foundation Pit under Multifactor Coupling. Int. J. Geomech. 2025, 25, 04024354. [Google Scholar] [CrossRef]
- Hu, D.; Hu, Y.J.; Yi, S.; Liang, X.Q.; Li, Y.S.; Yang, X. Prediction method of surface settlement of rectangular pipe jacking tunnel based on improved PSO-BP neural network. Sci. Rep. 2023, 13, 5512. [Google Scholar] [CrossRef] [PubMed]
- Pichler, B.; Lackner, R.; Mang, H.A. Back analysis of model parameters in geotechnical engineering by means of soft computing. Int. J. Numer. Methods Eng. 2003, 57, 1943–1978. [Google Scholar] [CrossRef]
- Zhu, C.; Zhao, H.; Zhao, M. Back Analysis of Geomechanical Parameters in Underground Engineering Using Artificial Bee Colony. Sci. World J. 2014, 2014, 693812. [Google Scholar] [CrossRef]

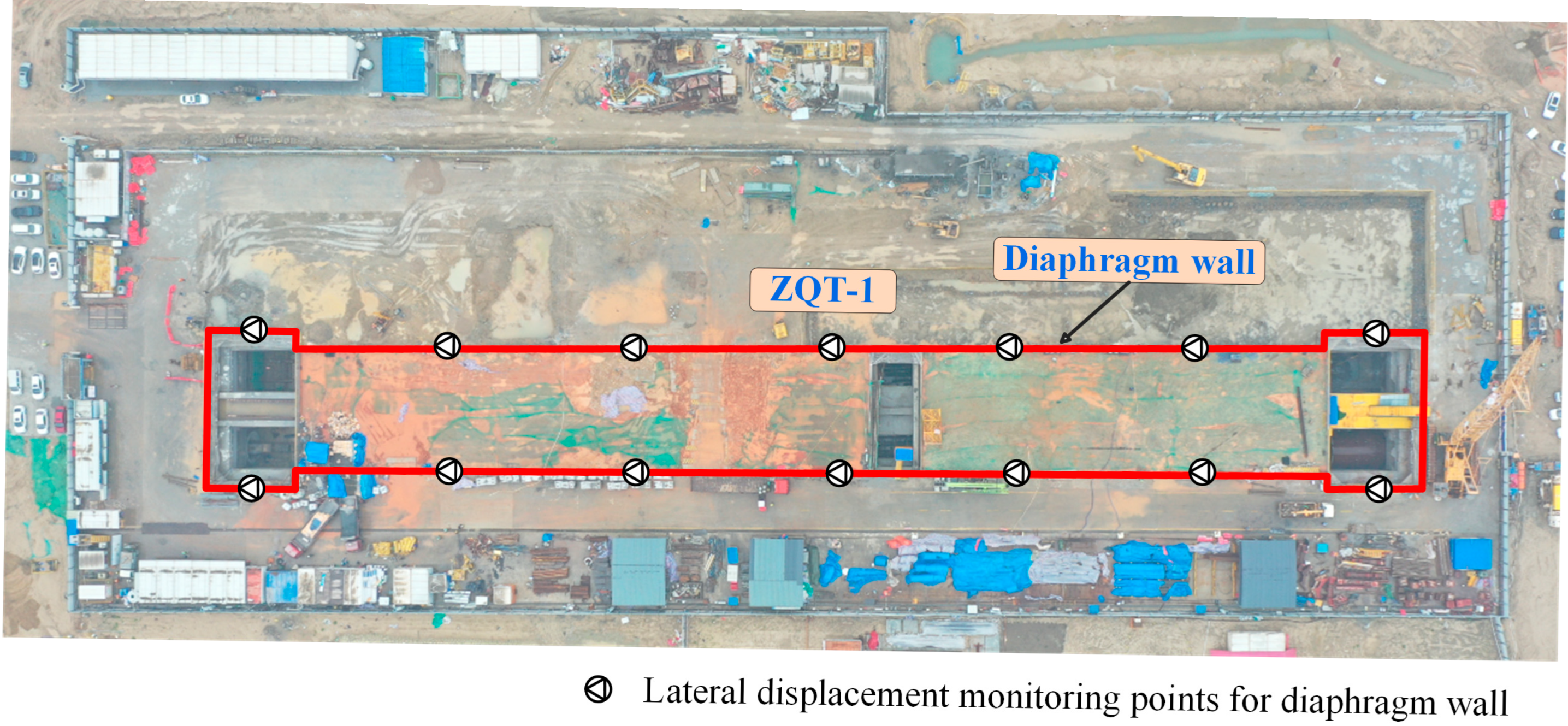
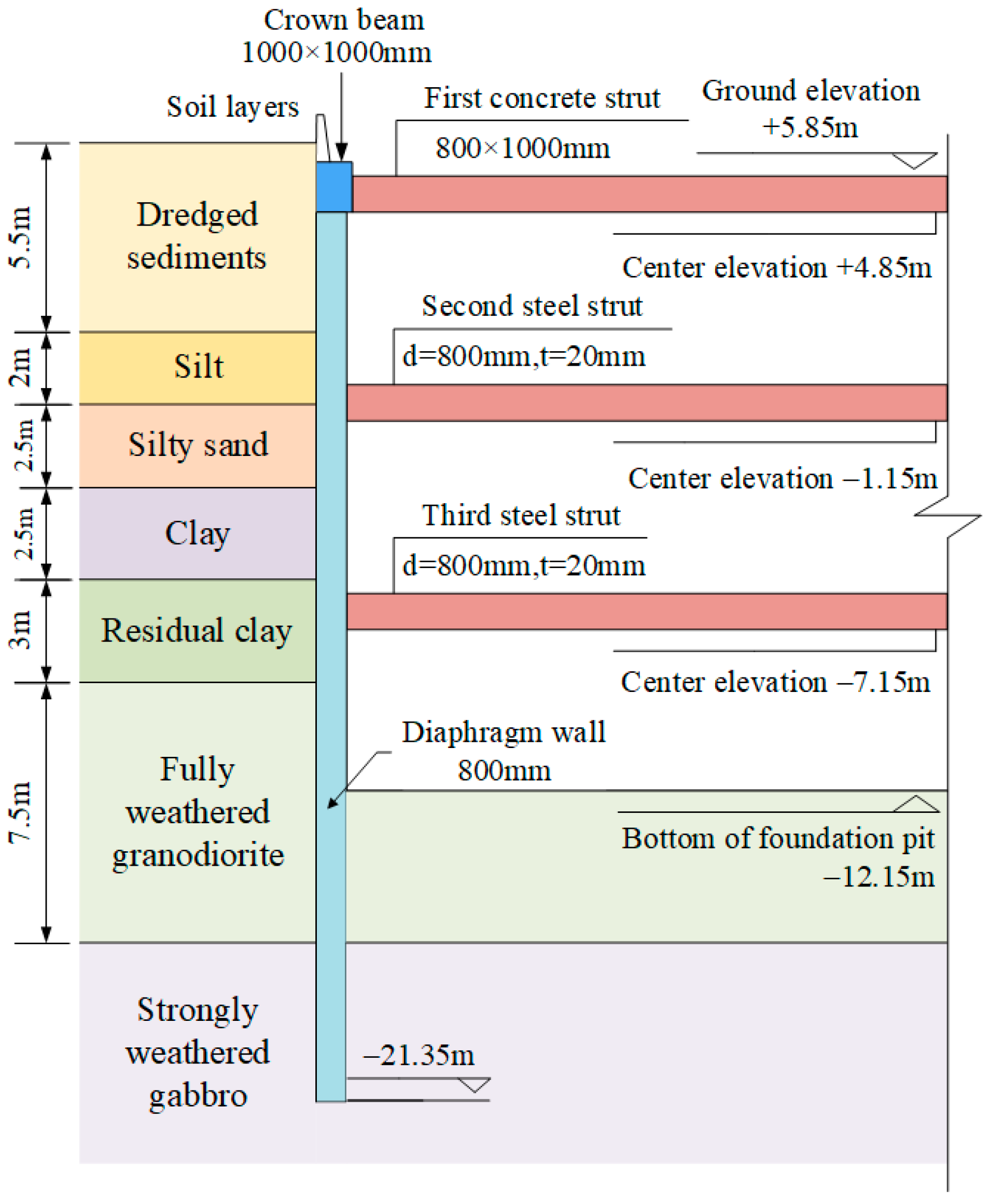
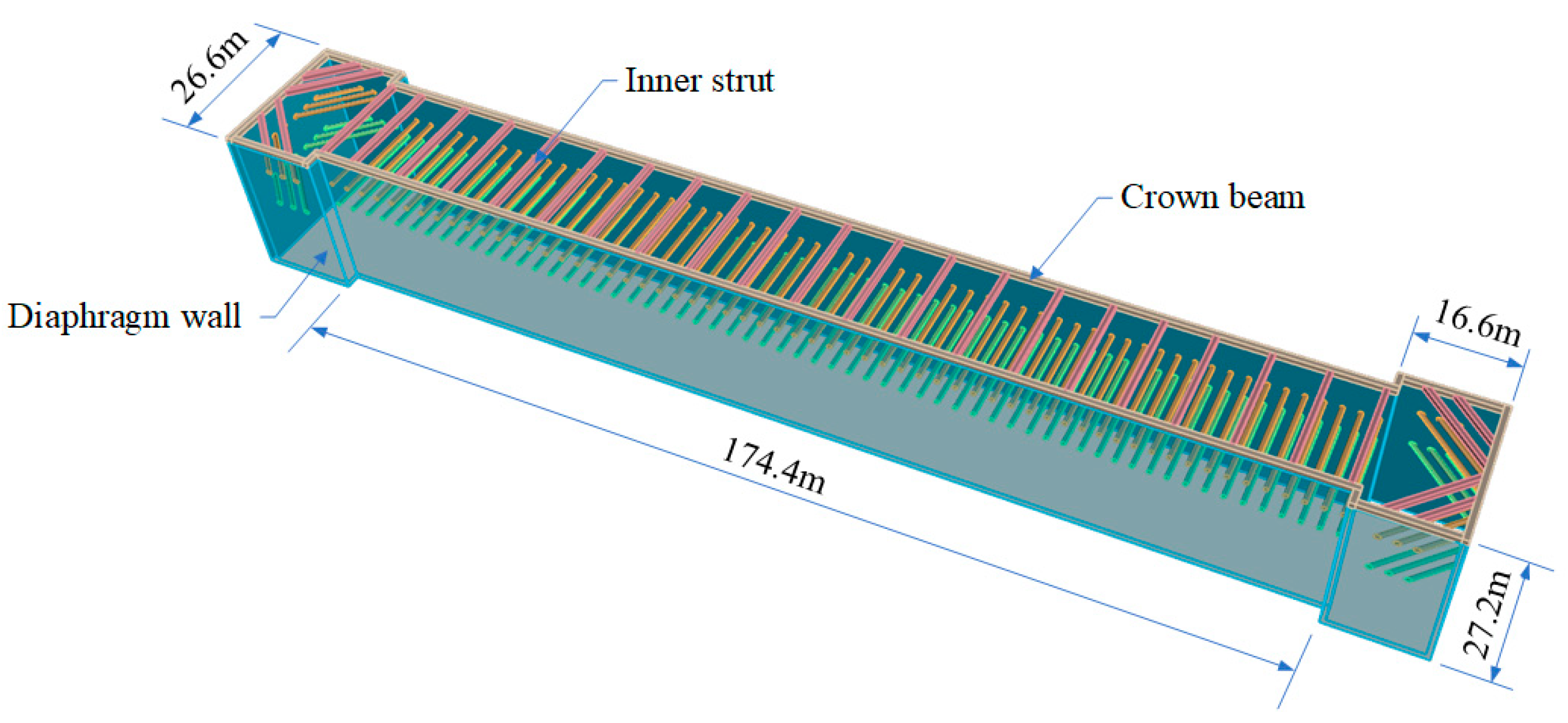
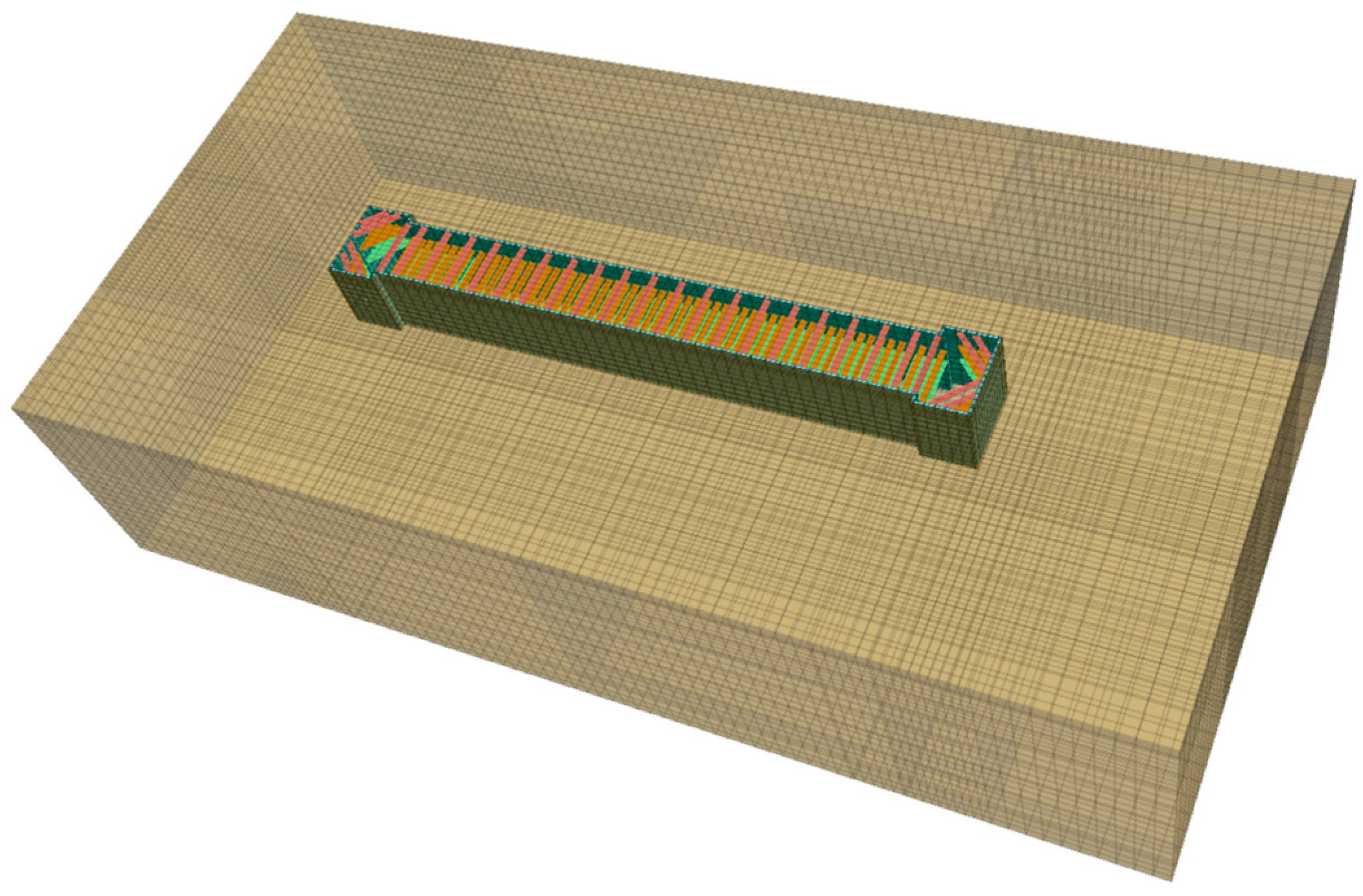

| Stage | Construction | Excavation Depth/m |
|---|---|---|
| CS 1 | Excavate at 4.05~5.85 m, install the first level inner strut | 1.5 |
| CS 2 | Excavate at −1.65~4.05 m, install the second level inner strut | 7.5 |
| CS 3 | Excavate at −7.65~−1.65 m, install the third level inner strut | 13.5 |
| CS 4 | Excavate at −9.65~−7.65 m | 15 |
| CS 5 | Excavate at −12.15~−9.65 m | 18 |
| Materials | Density/(kg/m3) | Elasticity Modulus/(GPa) | Poisson’s Ratio | Size/(mm) |
|---|---|---|---|---|
| diaphragm wall | 25 | 30 | 0.2 | |
| concrete inner struts | 25 | 30 | 0.2 | |
| steel inner struts | 78 | 174 | 0.3 | d = 800, t = 20 |
| Soil Layer | (kg/m3) | /(kPa) | (°) | /(MPa) | /(MPa) | /(MPa) | ||
|---|---|---|---|---|---|---|---|---|
| Dredged sediments | 18.1 | - | - | - | 0.6 | 5.5 | ||
| Silt | 17.4 | 5 | 0 | 5 | 5 | 20 | 0.7 | 2 |
| Silty sand | 17.4 | - | - | - | 0.7 | 2.5 | ||
| Clay | 19.8 | 17 | 15 | 15 | 15 | 60 | 0.77 | 2.5 |
| Residual clay | 18.5 | 23 | 14.9 | 20 | 20 | 80 | 0.75 | 3 |
| Fully weathered granodiorite | 21.0 | 35 | 26 | 40 | 40 | 150 | 0.7 | 7.5 |
| Strongly weathered gabbro | 24.0 | 45 | 30 | 60 | 60 | 200 | 0.58 | - |
| Value | Dredged Sediments | Silty Sand | ||||||
|---|---|---|---|---|---|---|---|---|
| / (kPa) | (°) | / (MPa) | / (kPa) | (°) | / (MPa) | |||
| Level 1 | 4 | 10 | 4 | 3 | 6 | 10 | 5 | 3 |
| Level 2 | 5 | 12 | 5 | 3.5 | 7 | 12 | 6 | 3.5 |
| Level 3 | 6 | 14 | 6 | 4 | 8 | 14 | 7 | 4 |
| Level 4 | 7 | 16 | 7 | 4.5 | 9 | 16 | 8 | 4.5 |
| Level 5 | 8 | 18 | 8 | 5 | 10 | 18 | 9 | 5 |
| Level 6 | 9 | 20 | 9 | 5.5 | 11 | 20 | 10 | 5.5 |
| Level 7 | 10 | 22 | 10 | 6 | 12 | 22 | 11 | 6 |
| Level 8 | 11 | 24 | 11 | 6.5 | 13 | 24 | 12 | 6.5 |
| Construction Stage | Sample ID | Lateral Displacement of Diaphragm Wall at Different Depth/(mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| −4 m | −8 m | −12 m | −14 m | −16 m | −18 m | −22 m | −26 m | ||
| CS 3 | 1 | 3.79 | 5.33 | 7.04 | 8.69 | 9.01 | 8.37 | 6.25 | 4.31 |
| 5 | 3.57 | 4.97 | 6.98 | 8.78 | 9.20 | 8.66 | 6.32 | 4.32 | |
| 9 | 3.44 | 4.64 | 6.87 | 8.81 | 9.27 | 8.75 | 6.49 | 4.46 | |
| 13 | 3.57 | 5.24 | 6.98 | 8.41 | 8.51 | 7.87 | 5.96 | 4.17 | |
| 17 | 3.55 | 4.98 | 6.62 | 8.08 | 8.25 | 7.65 | 5.88 | 4.05 | |
| 21 | 3.57 | 4.96 | 6.95 | 8.60 | 8.87 | 8.24 | 6.18 | 4.26 | |
| 25 | 3.40 | 4.70 | 7.20 | 9.06 | 9.45 | 8.87 | 6.53 | 4.43 | |
| 29 | 3.55 | 5.21 | 7.21 | 8.98 | 9.36 | 8.77 | 6.40 | 4.38 | |
| 33 | 3.49 | 5.07 | 6.98 | 8.73 | 9.12 | 8.58 | 6.30 | 4.33 | |
| 37 | 3.58 | 5.08 | 7.05 | 8.77 | 9.08 | 8.46 | 6.26 | 4.28 | |
| 41 | 3.60 | 5.07 | 6.93 | 8.53 | 8.76 | 8.13 | 6.09 | 4.16 | |
| 45 | 3.49 | 4.97 | 6.97 | 8.59 | 8.85 | 8.28 | 6.31 | 4.30 | |
| 49 | 3.54 | 4.93 | 6.87 | 8.55 | 8.85 | 8.33 | 6.31 | 4.36 | |
| 53 | 3.44 | 4.64 | 6.92 | 8.94 | 9.45 | 8.85 | 6.49 | 4.47 | |
| 56 | 3.66 | 5.31 | 7.03 | 8.40 | 8.45 | 7.74 | 5.84 | 4.04 | |
| 61 | 3.57 | 5.18 | 7.15 | 8.88 | 9.22 | 8.59 | 6.27 | 4.29 | |
| CS 4 | 2 | 4.76 | 5.97 | 9.87 | 11.69 | 13.83 | 13.46 | 10.07 | 6.78 |
| 6 | 4.91 | 6.39 | 9.73 | 11.38 | 13.30 | 12.81 | 9.61 | 6.54 | |
| 10 | 4.99 | 6.61 | 9.81 | 11.96 | 14.08 | 13.70 | 10.25 | 6.94 | |
| 14 | 4.88 | 6.15 | 9.44 | 11.90 | 14.16 | 13.86 | 10.34 | 6.94 | |
| 18 | 4.94 | 6.24 | 9.48 | 11.97 | 14.18 | 13.81 | 10.11 | 6.77 | |
| 22 | 4.89 | 6.56 | 9.83 | 11.88 | 14.05 | 13.75 | 10.11 | 6.76 | |
| 26 | 4.91 | 6.39 | 9.61 | 11.96 | 14.19 | 13.89 | 10.19 | 6.72 | |
| 30 | 4.93 | 6.36 | 9.65 | 11.80 | 13.97 | 13.65 | 10.12 | 6.78 | |
| 34 | 4.99 | 6.18 | 9.57 | 11.39 | 13.39 | 13.00 | 9.74 | 6.58 | |
| 38 | 4.87 | 6.25 | 9.53 | 11.69 | 13.79 | 13.36 | 9.96 | 6.68 | |
| 42 | 4.85 | 6.20 | 9.54 | 11.79 | 14.04 | 13.72 | 10.01 | 6.81 | |
| 46 | 5.04 | 6.40 | 9.71 | 11.88 | 13.97 | 13.60 | 10.00 | 6.68 | |
| 50 | 4.90 | 6.30 | 9.62 | 11.71 | 13.87 | 13.49 | 10.00 | 6.70 | |
| 54 | 4.97 | 6.45 | 9.77 | 11.76 | 13.93 | 13.58 | 10.12 | 6.79 | |
| 57 | 4.98 | 6.31 | 9.64 | 11.65 | 13.73 | 13.33 | 9.95 | 6.64 | |
| 62 | 4.85 | 6.14 | 9.41 | 11.98 | 14.25 | 13.94 | 10.42 | 6.99 | |
| CS 5 | 3 | 8.12 | 8.79 | 13.33 | 15.56 | 21.71 | 23.07 | 16.57 | 10.99 |
| 5 | 8.41 | 8.83 | 13.65 | 15.69 | 21.65 | 23.06 | 16.87 | 11.05 | |
| 8 | 8.60 | 8.84 | 13.81 | 15.85 | 21.82 | 23.27 | 17.03 | 11.22 | |
| 11 | 8.51 | 8.85 | 14.01 | 16.36 | 22.26 | 23.90 | 17.06 | 11.39 | |
| 16 | 8.66 | 8.88 | 13.83 | 15.84 | 21.78 | 23.18 | 16.98 | 11.12 | |
| 20 | 8.31 | 8.81 | 13.53 | 15.61 | 21.62 | 23.09 | 17.00 | 11.23 | |
| 26 | 8.42 | 8.80 | 13.79 | 16.18 | 22.35 | 23.60 | 16.89 | 10.91 | |
| 33 | 8.57 | 8.77 | 13.69 | 15.62 | 21.55 | 23.01 | 16.81 | 11.03 | |
| 36 | 8.48 | 8.84 | 13.72 | 15.70 | 21.61 | 22.97 | 16.80 | 10.95 | |
| 38 | 8.25 | 8.74 | 13.65 | 16.09 | 22.33 | 23.58 | 16.69 | 10.89 | |
| 42 | 8.43 | 8.76 | 13.64 | 15.69 | 21.66 | 23.05 | 16.94 | 11.11 | |
| 46 | 8.56 | 8.95 | 13.90 | 16.08 | 22.19 | 23.56 | 16.90 | 11.21 | |
| 50 | 8.47 | 8.80 | 13.68 | 15.72 | 21.73 | 23.15 | 16.83 | 11.04 | |
| 53 | 8.13 | 8.70 | 13.56 | 15.89 | 22.10 | 23.59 | 17.21 | 11.28 | |
| 59 | 8.37 | 8.74 | 13.69 | 15.89 | 21.96 | 23.38 | 17.01 | 11.12 | |
| 64 | 8.25 | 8.59 | 13.95 | 16.49 | 22.82 | 24.15 | 16.92 | 11.00 | |
| Construction Stage | Inversion Method | Dredged Sediments | Silty Sand | ||||||
|---|---|---|---|---|---|---|---|---|---|
| / (kPa) | (°) | / (MPa) | / (kPa) | (°) | / (MPa) | ||||
| CS 3 | GWO-MLSSVR | 8.15 | 20.22 | 7.26 | 4.83 | 10.21 | 18.69 | 8.33 | 4.66 |
| MLSSVR | 6.92 | 17.25 | 6.52 | 5.03 | 9.18 | 15.09 | 7.85 | 5.15 | |
| CS 4 | GWO-MLSSVR | 8.36 | 23.47 | 7.03 | 5.01 | 13.19 | 17.34 | 8.85 | 4.78 |
| MLSSVR | 6.01 | 19.04 | 5.23 | 4.82 | 11.23 | 14.68 | 8.24 | 5.31 | |
| CS 5 | GWO-MLSSVR | 8.55 | 22.64 | 6.52 | 4.52 | 12.01 | 17.14 | 8.74 | 4.86 |
| MLSSVR | 6.13 | 20.30 | 5.14 | 4.44 | 10.12 | 15.55 | 8.28 | 5.10 | |
| Inversion Method | MRE (%) | 95% CI (%) | 99% CI (%) |
|---|---|---|---|
| RF | 9.50 | [−5.80, 7.10] | [−8.40, 9.70] |
| PSO-BP | 7.65 | [−1.78, 8.60] | [−3.86, 10.68] |
| GWO-MLSSVR | 2.69 | [−0.88, 3.18] | [−1.49, 3.79] |
| Number of Nodes in the Input Layer | Maximum Relative Error/% | Mean Relative Error/% | R2 | Total CPU Time/s |
|---|---|---|---|---|
| 5 | 24.03 | 13.32 | 0.73 | 193 |
| 6 | 19.67 | 8.20 | 0.88 | 330 |
| 7 | 9.34 | 5.61 | 0.94 | 524 |
| 8 | 4.12 | 2.69 | 0.99 | 667 |
| 9 | 4.01 | 2.62 | 0.99 | 1004 |
| 10 | 3.89 | 2.57 | 0.99 | 1760 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Li, S.; Ye, J.; Chen, F.; Wu, Y.; Yu, J.; Cai, Y.; Lin, J.; Zhou, X. Soil Parameter Inversion in Dredger Fill Strata Using GWO-MLSSVR for Deep Foundation Pit Engineering. Buildings 2025, 15, 1864. https://doi.org/10.3390/buildings15111864
Chen C, Li S, Ye J, Chen F, Wu Y, Yu J, Cai Y, Lin J, Zhou X. Soil Parameter Inversion in Dredger Fill Strata Using GWO-MLSSVR for Deep Foundation Pit Engineering. Buildings. 2025; 15(11):1864. https://doi.org/10.3390/buildings15111864
Chicago/Turabian StyleChen, Changrui, Sifan Li, Jinbi Ye, Fangjian Chen, Yibin Wu, Jin Yu, Yanyan Cai, Jinna Lin, and Xianqi Zhou. 2025. "Soil Parameter Inversion in Dredger Fill Strata Using GWO-MLSSVR for Deep Foundation Pit Engineering" Buildings 15, no. 11: 1864. https://doi.org/10.3390/buildings15111864
APA StyleChen, C., Li, S., Ye, J., Chen, F., Wu, Y., Yu, J., Cai, Y., Lin, J., & Zhou, X. (2025). Soil Parameter Inversion in Dredger Fill Strata Using GWO-MLSSVR for Deep Foundation Pit Engineering. Buildings, 15(11), 1864. https://doi.org/10.3390/buildings15111864






