Performance Evaluation of Education Infrastructure Public–Private Partnership Projects in the Operation Stage Based on Limited Cloud Model and Combination Weighting Method
Abstract
1. Introduction
2. Literature Review
2.1. Application of the PPP Model in Educational Infrastructure Projects
2.2. Performance Evaluation Indicator System for PPP Projects
2.3. Performance Evaluation Models for PPP Projects
3. Methods and Materials
3.1. Performance Evaluation Indicator System for the Operation Stage of Education PPP Projects
3.1.1. Identifying the Subject of Performance Evaluation
3.1.2. Designing the Performance Evaluation Indicator System
3.1.3. Questionnaire Survey
3.1.4. Determination of the Performance Evaluation Indicator System
3.2. COWA-Critic-Game Theory Combination Weighting Method
3.2.1. COWA Method
3.2.2. CRITIC Method
- Step 1: Calculate the standard deviation of each indicator.
- Step 2: Calculate the correlation coefficient between each pair of indicators.
- Step 3: Calculate the objective weights of each level of indicators.
3.2.3. Game Theory-Based Combined Weighting
3.3. Limited Cloud Model
3.3.1. Cloud Uncertainty Reasoning
3.3.2. Forward and Backward Generators
3.3.3. Calculation of the Comprehensive Cloud
4. Case Study
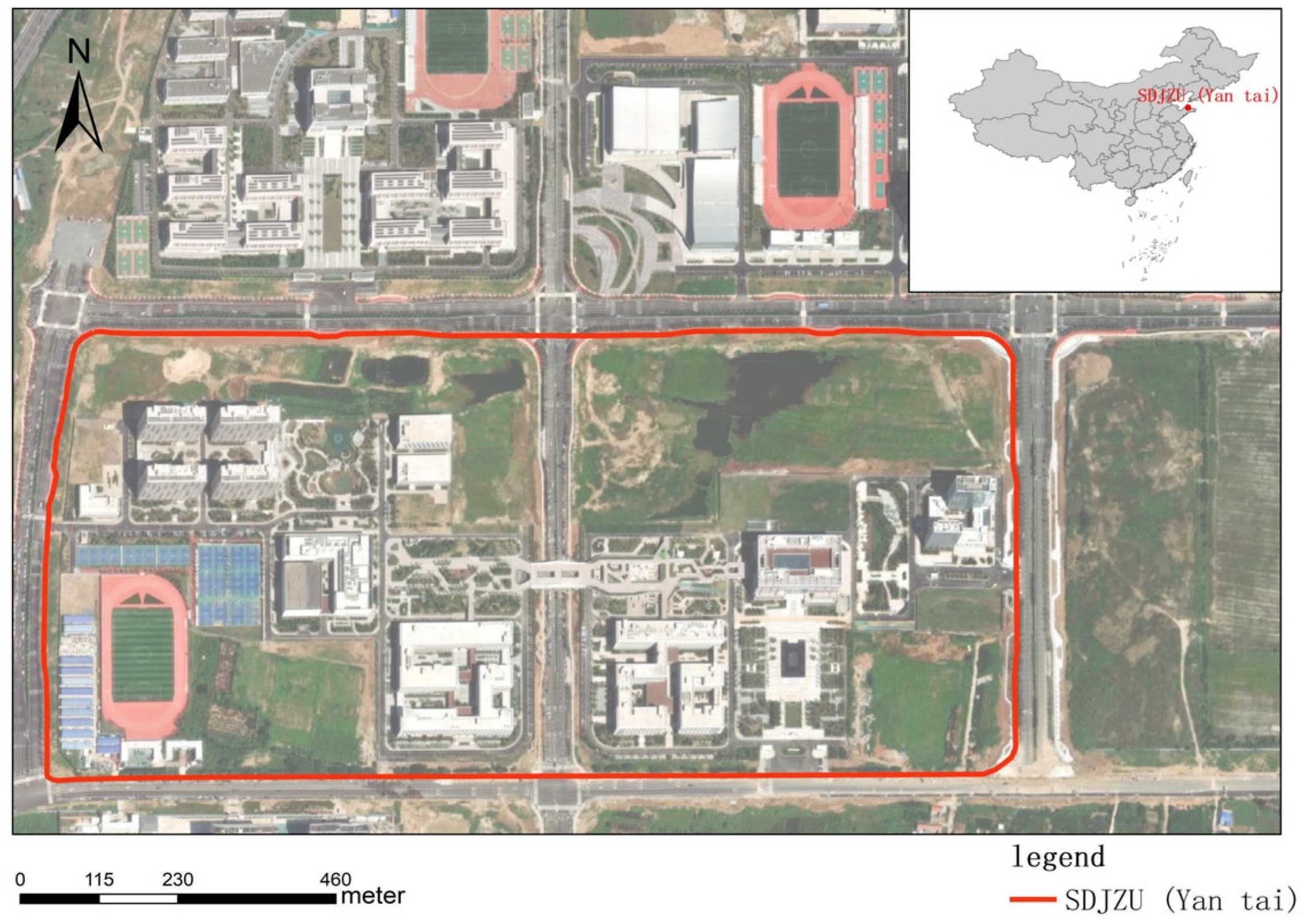
4.1. Case Description
4.2. Data Sources and Processing
4.2.1. Data Sources
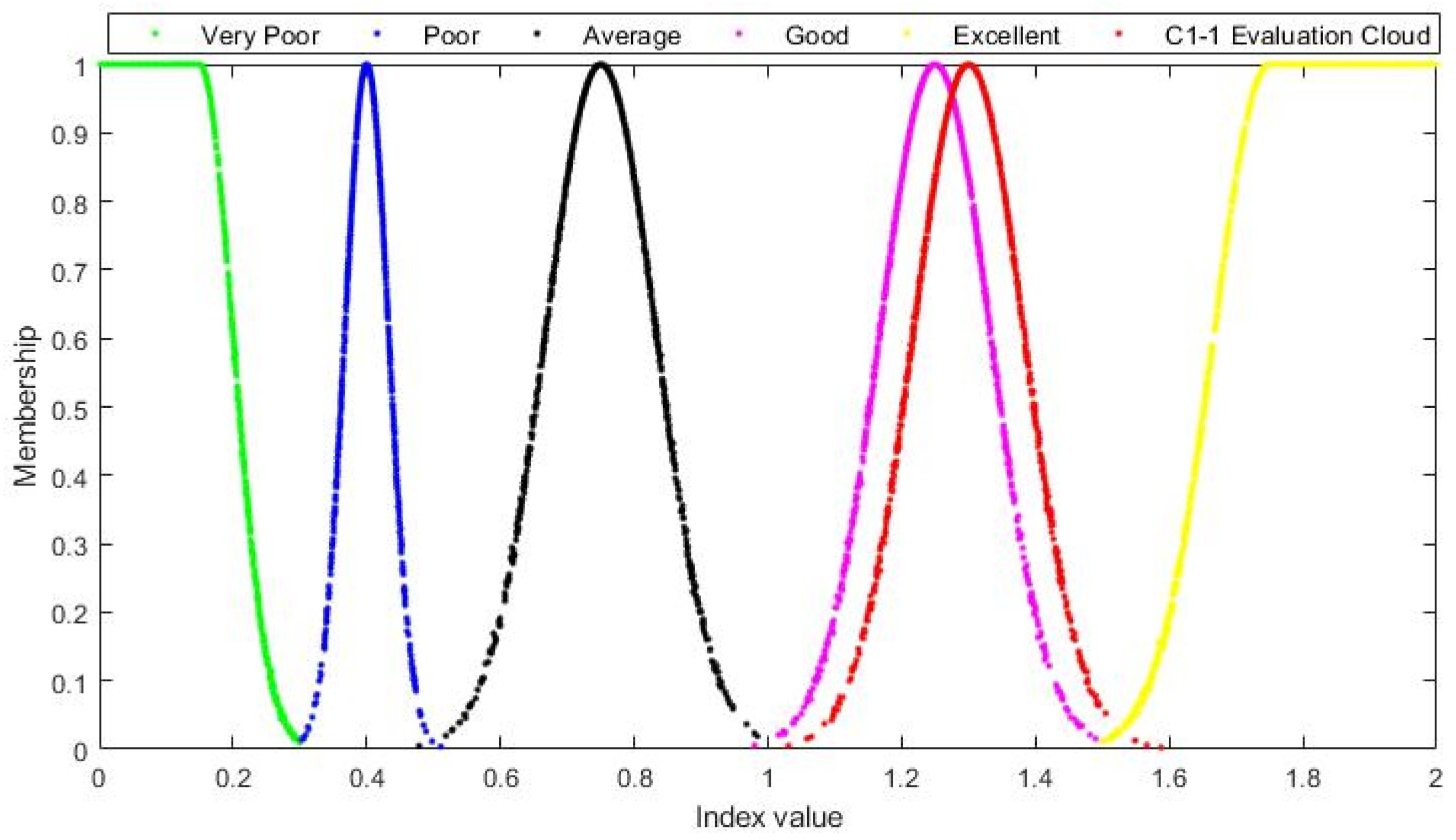
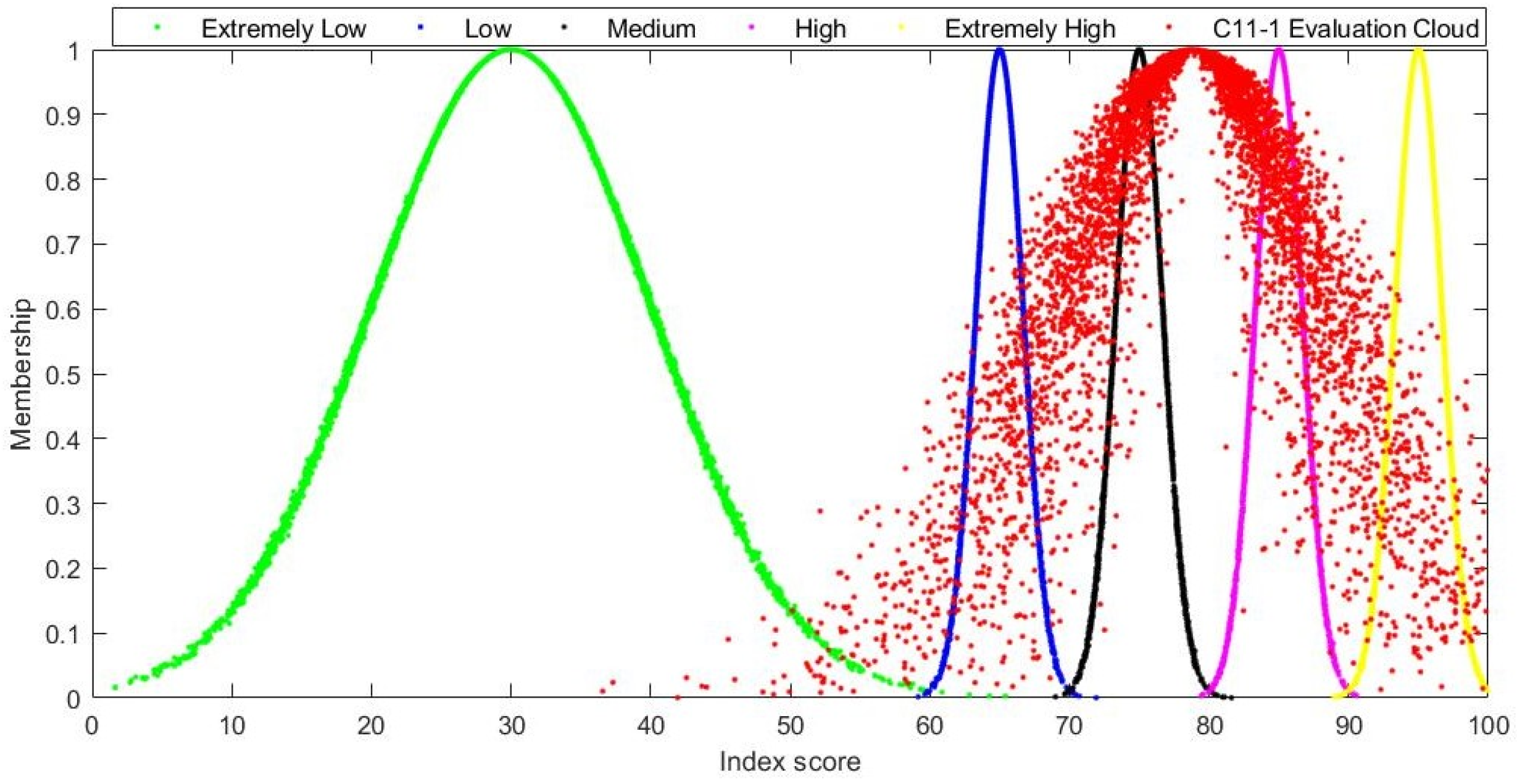
4.2.2. Performance Evaluation Data Processing Based on the Limited Cloud Model
4.3. Performance Evaluation Results
5. Discussion
5.1. Discussion of the Evaluation Model
5.1.1. Discussion on the Reliability of Data Processing
5.1.2. Comparative Analysis
5.1.3. Innovations and Contributions to the Evaluation Model
5.2. Comprehensive Discussion
5.2.1. The Relationship Between Operational Revenue and User Scale
5.2.2. Operational Experience in Education Projects
5.2.3. Contract and Relationship Governance
5.2.4. Differences in Stakeholder Needs During Project Operation
5.3. Limitations and Future Research
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PPP | Public–private partnership |
| SPV | Special purpose vehicle |
| RII | Relative Importance Indicator |
| COWA | Combined ordered weighted averaging |
| CRITIC | Intercriteria correlation |
References
- Khallaf, R.; Kang, K.; Hastak, M.; Othman, K. Public–Private Partnerships for Higher Education Institutions in the United States. Buildings 2022, 12, 1888. [Google Scholar] [CrossRef]
- Caves, K.; Oswald-Egg, M.E. The Networked Role of Intermediaries in Education Governance and Public-Private Partnership. J. Educ. Policy 2024, 39, 40–63. [Google Scholar] [CrossRef]
- Fabre, A.; Straub, S. The Impact of Public–Private Partnerships (PPPs) in Infrastructure, Health, and Education. J. Econ. Lit. 2023, 61, 655–715. [Google Scholar] [CrossRef]
- Jiang, W.; Jiang, J.; Martek, I.; Jiang, W. Critical Risk Management Strategies for the Operation of Public–Private Partnerships: A Vulnerability Perspective of Infrastructure Projects. ECAM 2024. [Google Scholar] [CrossRef]
- The World Bank. Available online: https://Ppp.Worldbank.Org/ (accessed on 5 January 2025).
- Available online: https://saiindia.gov.in/en (accessed on 15 May 2025).
- Public Private Partnerships in Educational Governance: A Case Study of Bogota’s Concession Schools. Available online: https://www.Academia.Edu/24476781/Public_Private_Partnerships_in_Educational_GOVERNANCE_a_Case_Study_of_Bogotas_Concession_Schools (accessed on 15 May 2025).
- Wang, Y.; Liang, Y.; Li, C.; Zhang, X. Operation Performance Evaluation of Urban Rail Transit PPP Projects: Based on Best Worst Method and Large-Scale Group Evaluation Technology. Adv. Civ. Eng. 2021, 2021, 4318869. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H. Exploring Risk Factors Affecting Sustainable Outcomes of Global Public–Private Partnership (PPP) Projects: A Stakeholder Perspective. Buildings 2023, 13, 2140. [Google Scholar] [CrossRef]
- Stafford, A.; Stapleton, P. The Impact of Hybridity on PPP Governance and Related Accountability Mechanisms: The Case of UK Education PPPs. AAAJ 2022, 35, 950–980. [Google Scholar] [CrossRef]
- Sajida; Kusumasari, B. Critical Success Factors of Public-Private Partnerships in the Education Sector. PAP 2023, 26, 309–320. [Google Scholar] [CrossRef]
- Ansari, A.H. Bridging the Gap? Evaluating the Effectiveness of Punjab’s Public–Private Partnership Programmes in Education. Int. J. Educ. Res. 2024, 125, 102325. [Google Scholar] [CrossRef]
- Hong, S.; Kim, T.K. Public–Private Partnership Meets Corporate Social Responsibility—The Case of H-JUMP School. Public Money Manag. 2018, 38, 297–304. [Google Scholar] [CrossRef]
- Vecchi, V.; Cusumano, N.; Casalini, F. Investigating the Performance of PPP in Major Healthcare Infrastructure Projects: The Role of Policy, Institutions, and Contracts. Oxf. Rev. Econ. Policy 2022, 38, 385–401. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, C.; Luo, X.; Martek, I. Determining Concessionary Items for “Availability Payment Only” PPP Projects: A Holistic Framework Integrating Value-For-Money and Social Values. J. Civ. Eng. Manag. 2024, 30, 149–167. [Google Scholar] [CrossRef]
- Liu, B.; Ji, J.; Chen, J.; Qi, M.; Li, S.; Tang, L.; Zhang, K. Quantitative VfM Evaluation of Urban Rail Transit PPP Projects Considering Social Benefit. Res. Transp. Bus. Manag. 2023, 49, 101015. [Google Scholar] [CrossRef]
- Lagzi, M.D.; Sajadi, S.M.; Taghizadeh-Yazdi, M. A Hybrid Stochastic Data Envelopment Analysis and Decision Tree for Performance Prediction in Retail Industry. J. Retail. Consum. Serv. 2024, 80, 103908. [Google Scholar] [CrossRef]
- Sadeghi, M.; Mahmoudi, A.; Deng, X.; Luo, M. A Novel Performance Measurement of Innovation and R&D Projects for Driving Digital Transformation in Construction Using Ordinal Priority Approach. KSCE J. Civ. Eng. 2024, 28, 5427–5440. [Google Scholar]
- Carnero, M.C.; Martínez-Corral, A.; Cárcel-Carrasco, J. Fuzzy Multicriteria Evaluation and Trends of Asset Management Performance: A Case Study of Spanish Buildings. Case Stud. Constr. Mater. 2023, 19, e02660. [Google Scholar] [CrossRef]
- Du, J.; Wang, W.; Gao, X.; Hu, M.; Jiang, H. Sustainable operations: A systematic operational performance evaluation framework for public–private partnership transportation infrastructure projects. Sustainability 2023, 15, 7951. [Google Scholar] [CrossRef]
- Anjomshoa, E. Key Performance Indicators of Construction Companies in Branding Products and Construction Projects for Success in a Competitive Environment in Iran. ECAM 2024, 31, 2151–2175. [Google Scholar] [CrossRef]
- Assaf, G.; Assaad, R.H. Developing a Scoring Framework to Assess the Feasibility of the Design–Build Project Delivery Method for Bundled Projects. J. Manag. Eng. 2024, 40, 04024058. [Google Scholar] [CrossRef]
- Tabejamaat, S.; Ahmadi, H.; Barmayehvar, B. Boosting Large-scale Construction Project Risk Management: Application of the Impact of Building Information Modeling, Knowledge Management, and Sustainable Practices for Optimal Productivity. Energy Sci. Eng. 2024, 12, 2284–2296. [Google Scholar] [CrossRef]
- Jiang, F.; Lyu, Y.; Zhang, Y.; Guo, Y. Research on the Differences between Risk-Factor Attention and Risk Losses in PPP Projects. J. Constr. Eng. Manag. 2023, 149, 04023090. [Google Scholar] [CrossRef]
- Lu, Y.; Nie, C.; Zhou, D.; Shi, L. Research on Programmatic Multi-Attribute Decision-Making Problem: An Example of Bridge Pile Foundation Project in Karst Area. PLoS ONE 2023, 18, e0295296. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, X. Risk Assessment Method and Application of Urban River Ecological Governance Project Based on Cloud Model Improvement. Adv. Civ. Eng. 2023, 2023, 8797522. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, X.; Xiao, Y.; Yuan, J. Modeling and Performance Evaluation of PPP Projects Utilizing IFC Extension and Enhanced Matter-Element Method. ECAM 2020, 27, 1763–1794. [Google Scholar] [CrossRef]
- Jiao, H.; Cao, Y.; Li, H. Performance Evaluation of Urban Water Environment Treatment PPP Projects Based on Cloud Model and OWA Operator. Buildings 2023, 13, 417. [Google Scholar] [CrossRef]
- Zhang, Y.; He, N.; Li, Y.; Chen, Y.; Wang, L.; Ran, Y. Risk Assessment of Water Environment Treatment PPP Projects Based on a Cloud Model. Discret. Dyn. Nat. Soc. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Wu, M.; Liu, Y.; Ye, Y.; Luo, B. Assessment of Clean Production Level in Phosphate Mining Enterprises: Based on the Fusion Group Decision Weight and Limited Interval Cloud Model. J. Clean. Prod. 2024, 456, 142398. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, J.; Zhang, K.; Han, X. Research on the Value Improvement Model of Private Parties as “Investor–Builder” Dual-Role Entity in Major River Green Public–Private Partnership Projects. Buildings 2023, 13, 2881. [Google Scholar] [CrossRef]
- Geng, L.; Herath, N.; Hui, F.K.P.; Liu, X.; Duffield, C.; Zhang, L. Evaluating Uncertainties to Deliver Enhanced Service Performance in Education PPPs: A Hierarchical Reliability Framework. ECAM 2023, 30, 4464–4485. [Google Scholar] [CrossRef]
- Zhang, Q.; Iqbal, S.; Shahzad, F. Role of Environmental, Social, and Governance (ESG) Investment and Natural Capital Stocks in Achieving Net-Zero Carbon Emission. J. Clean. Prod. 2024, 478, 143919. [Google Scholar] [CrossRef]
- Akomea-Frimpong, I.; Jin, X.; Osei-Kyei, R. A Holistic Review of Research Studies on Financial Risk Management in Public–Private Partnership Projects. ECAM 2021, 28, 2549–2569. [Google Scholar] [CrossRef]
- Ghorbany, S.; Noorzai, E.; Yousefi, S. BIM-Based Solution to Enhance the Performance of Public-Private Partnership Construction Projects Using Copula Bayesian Network. Expert Syst. Appl. 2023, 216, 119501. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, S.; Zhao, F.; Ye, X.; Qi, H. A Study on the Impact of Team Interdependence on Cooperative Performance in Public–Private Partnership Projects: The Moderating Effect of Government Equity Participation. Sustainability 2023, 15, 12684. [Google Scholar] [CrossRef]
- Gunduz, M.; Naji, K.K.; Maki, O. Evaluating the Performance of Campus Facility Management through Structural Equation Modeling Based on Key Performance Indicators. J. Manag. Eng. 2024, 40, 04023056. [Google Scholar] [CrossRef]
- Menichelli, F.; Bullock, K.; Garland, J.; Allen, J. The Organisation and Operation of Policing on University Campuses: A Case Study. Criminol. Crim. Justice 2024, 17488958241254444. [Google Scholar] [CrossRef]
- Yuan, J.; Ji, W.; Guo, J.; Skibniewski, M.J. Simulation-Based Dynamic Adjustments of Prices and Subsidies for Transportation PPP Projects Based on Stakeholders’ Satisfaction. Transportation 2019, 46, 2309–2345. [Google Scholar] [CrossRef]
- Liu, W.; Wang, X.; Jiang, S. Decision Analysis of PPP Project’s Parties Based on Deep Consumer Participation. PLoS ONE 2024, 19, e0299842. [Google Scholar] [CrossRef]
- Hou, W.; Wang, L. Research on the Refinancing Capital Structure of Highway PPP Projects Based on Dynamic Capital Demand. ECAM 2022, 29, 2047–2072. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Li, M.; Jim, C.Y. A Performance Evaluation System for PPP Sewage Treatment Plants at the Operation-Maintenance Stage. KSCE J. Civ. Eng. 2023, 27, 1423–1440. [Google Scholar] [CrossRef]
- Flores-Salgado, B.; Gonzalez-Ambriz, S.-J.; Martínez-García-Moreno, C.-A.; Beltrán, J. IoT-Based System for Campus Community Security. Internet Things 2024, 26, 101179. [Google Scholar] [CrossRef]
- Pan, H.; Pan, Y.; Liu, X. Identifying the Critical Factors Affecting the Operational Performance of Characteristic Healthcare Town PPP Projects: Evidence from China. J. Infrastruct. Syst. 2023, 29, 05023007. [Google Scholar] [CrossRef]
- He, M.; Hu, Y.; Wen, Y.; Wang, X.; Wei, Y.; Sheng, G.; Wang, G. The Impacts of Forest Therapy on the Physical and Mental Health of College Students: A Review. Forests 2024, 15, 682. [Google Scholar] [CrossRef]
- Seva, R.R.; Tangsoc, J.C.; Madria, W.F. Determinants of University Students’ Safety Behavior during a Pandemic. Int. J. Disaster Risk Reduct. 2024, 106, 104441. [Google Scholar] [CrossRef]
- Guo, Y.; Su, Y.; Chen, C.; Martek, I. Inclusion of “Managing Flexibility” Valuations in the Pricing of PPP Projects: A Multi-Objective Decision-Making Method. ECAM 2024, 31, 4562–4584. [Google Scholar] [CrossRef]
- Nose, M. Evaluating Fiscal Supports on the Public–Private Partnerships: A Hidden Risk for Contract Survival. Oxf. Econ. Pap. 2025, gpaf001. [Google Scholar] [CrossRef]
- Li, J.; Liu, B.; Wang, D.; Casady, C.B. The Effects of Contractual and 15Relational Governance on Public-private Partnership Sustainability. Public Adm. 2024, 102, 1418–1449. [Google Scholar] [CrossRef]
- Wang, J.; Luo, L.; Sa, R.; Zhou, W.; Yu, Z. A Quantitative Analysis of Decision-Making Risk Factors for Mega Infrastructure Projects in China. Sustainability 2023, 15, 15301. [Google Scholar] [CrossRef]
- Abdul Nabi, M.; Assaad, R.H.; El-adaway, I.H. Modeling and Understanding Dispute Causation in the US Public–Private Partnership Projects. J. Infrastruct. Syst. 2024, 30, 04023035. [Google Scholar] [CrossRef]
- Nemati, M.A.; Rastaghi, Z. Quality Assessment of On-Campus Student Housing Facilities through a Holistic Post-Occupancy Evaluation (A Case Study of Iran). Archit. Eng. Des. Manag. 2024, 20, 719–740. [Google Scholar] [CrossRef]
- Yoon, B.; Jun, K. Effects of Campus Dining Sustainable Practices on Consumers’ Perception and Behavioral Intention in the United States. Nutr. Res. Pract. 2023, 17, 1019. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Cai, X.; Peng, Y.; Liu, S.; Lai, W.; Chang, Y.; Liu, Y.; Yu, L. The Relation between Barrier-Free Environment Perception and Campus Commuting Satisfaction. Front. Public Health 2023, 11, 1294360. [Google Scholar] [CrossRef] [PubMed]
- Sampson, C.S.; Maberry, M.D.; Stilley, J.A. Football Saturday: Are Collegiate Football Stadiums Adequately Prepared to Handle Spectator Emergencies? J. Sports Med. Phys. Fit. 2023, 64, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Michalski, L.; Low, R.K.Y. Determinants of Corporate Credit Ratings: Does ESG Matter? Int. Rev. Financ. Anal. 2024, 94, 103228. [Google Scholar] [CrossRef]
- Spohr, J.; Wikström, K.; Ronikonmäki, N.-M.; Lepech, M.; In, S.Y. Are Private Investors Overcompensated in Infrastructure Projects? Transp. Policy 2024, 152, 1–8. [Google Scholar] [CrossRef]
- Xiahou, X.; Tang, L.; Yuan, J.; Zuo, J.; Li, Q. Exploring Social Impacts of Urban Rail Transit PPP Projects: Towards Dynamic Social Change from the Stakeholder Perspective. Environ. Impact Assess. Rev. 2022, 93, 106700. [Google Scholar] [CrossRef]
- Bu, Z.; Liu, J.; Zhang, X. Collaborative Government-Public Efforts in Driving Green Technology Innovation for Environmental Governance in PPP Projects: A Study Based on Prospect Theory. Kybernetes 2025, 54, 1684–1715. [Google Scholar] [CrossRef]
- Park, S.; Cho, K.; Choi, M. A Sustainability Evaluation of Buildings: A Review on Sustainability Factors to Move towards a Greener City Environment. Buildings 2024, 14, 446. [Google Scholar] [CrossRef]
- Li, W.-W.; Gu, X.-B.; Yang, C.; Zhao, C. Level Evaluation of Concrete Dam Fractures Based on Game Theory Combination Weighting-Normal Cloud Model. Front. Mater. 2024, 11, 1344760. [Google Scholar] [CrossRef]
- Huang, L.; Lv, W.; Huang, Q.; Zhang, H.; Jin, S.; Chen, T.; Shen, B. Transforming Medical Equipment Management in Digital Public Health: A Decision-Making Model for Medical Equipment Replacement. Front. Med. 2024, 10, 1239795. [Google Scholar] [CrossRef]
- Das, U.; Behera, B. Geospatial Assessment of Ecological Vulnerability of Fragile Eastern Duars Forest Integrating GIS-Based AHP, CRITIC and AHP-TOPSIS Models. Geomat. Nat. Hazards Risk 2024, 15, 2330529. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, B.; Qin, J.; Zhu, Q.; Lyu, S. Integrated Performance Assessment of Prefabricated Component Suppliers Based on a Hybrid Method Using Analytic Hierarchy Process–Entropy Weight and Cloud Model. Buildings 2024, 14, 3872. [Google Scholar] [CrossRef]
- Viner, R.M.; Russell, S.J.; Croker, H.; Packer, J.; Ward, J.; Stansfield, C.; Mytton, O.; Bonell, C.; Booy, R. School Closure and Management Practices during Coronavirus Outbreaks Including COVID-19: A Rapid Systematic Review. Lancet Child Adolesc. Health 2020, 4, 397–404. [Google Scholar] [CrossRef] [PubMed]
- Bugalia, N.; Maemura, Y.; Dasari, R.; Patidar, M. A system dynamics model for effective management strategies of High-Speed Railway (HSR) projects involving private sector participation. Transp. Res. Part A Policy Pract. 2023, 175, 103779. [Google Scholar] [CrossRef]
- Helmy, R.; Khourshed, N.; Wahba, M.; Bary, A.A.E. Exploring Critical Success Factors for Public Private Partnership Case Study: The Educational Sector in Egypt. J. Open Innov. Technol. Mark. Complex. 2020, 6, 142. [Google Scholar] [CrossRef]
- Ramu, P.; Osman, M.; Abdul Mutalib, N.A.; Aljaberi, M.A.; Lee, K.-H.; Lin, C.-Y.; Hamat, R.A. Validity and Reliability of a Questionnaire on the Knowledge, Attitudes, Perceptions and Practices toward Food Poisoning among Malaysian Secondary School Students: A Pilot Study. Healthcare 2023, 11, 853. [Google Scholar] [CrossRef]
- Reyes, G.A.; Zagorsky, J.; Lin, Y.; Prescott, M.P.; Stasiewicz, M.J. Quantitative Modeling of School Cafeteria Share Tables Predicts Reduced Food Waste and Manageable Norovirus-Related Food Safety Risk. Microb. Risk Anal. 2022, 22, 100229. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Panjaburee, P.; Chang, S.-C. Effects of Integrating Maternity VR-Based Situated Learning into Professional Training on Students’ Learning Performances. Interact. Learn. Environ. 2022, 32, 2121–2135. [Google Scholar] [CrossRef]


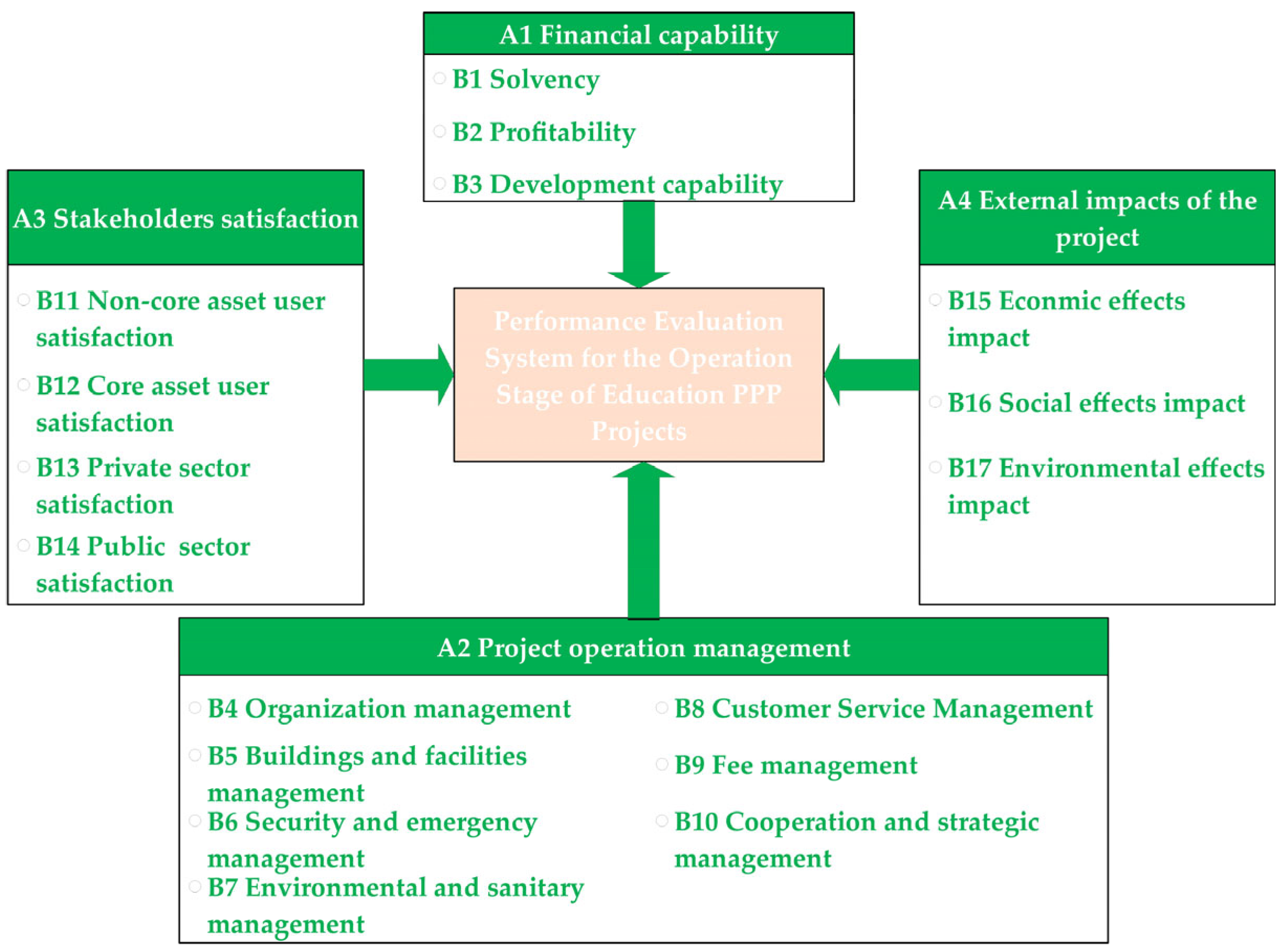



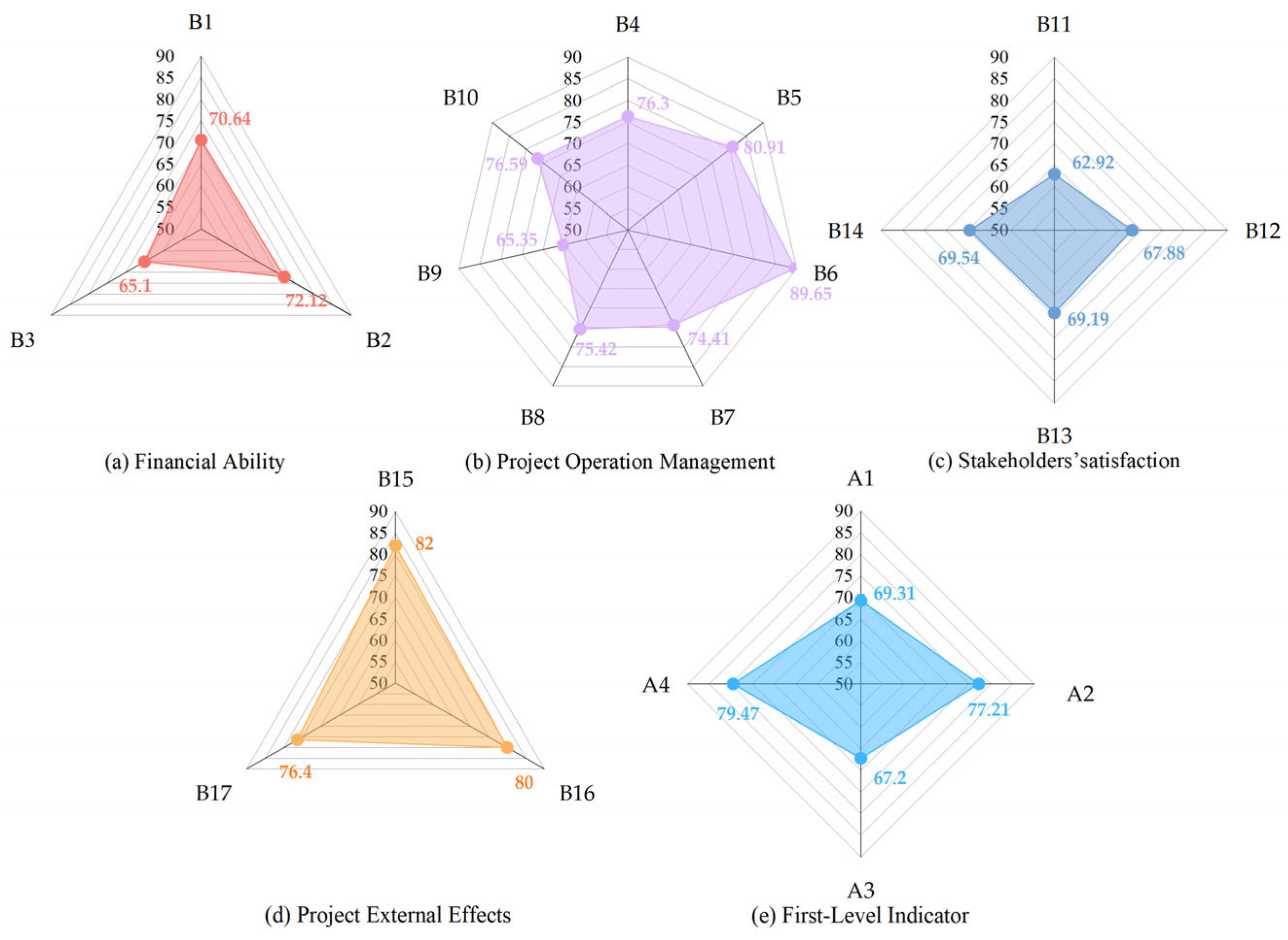

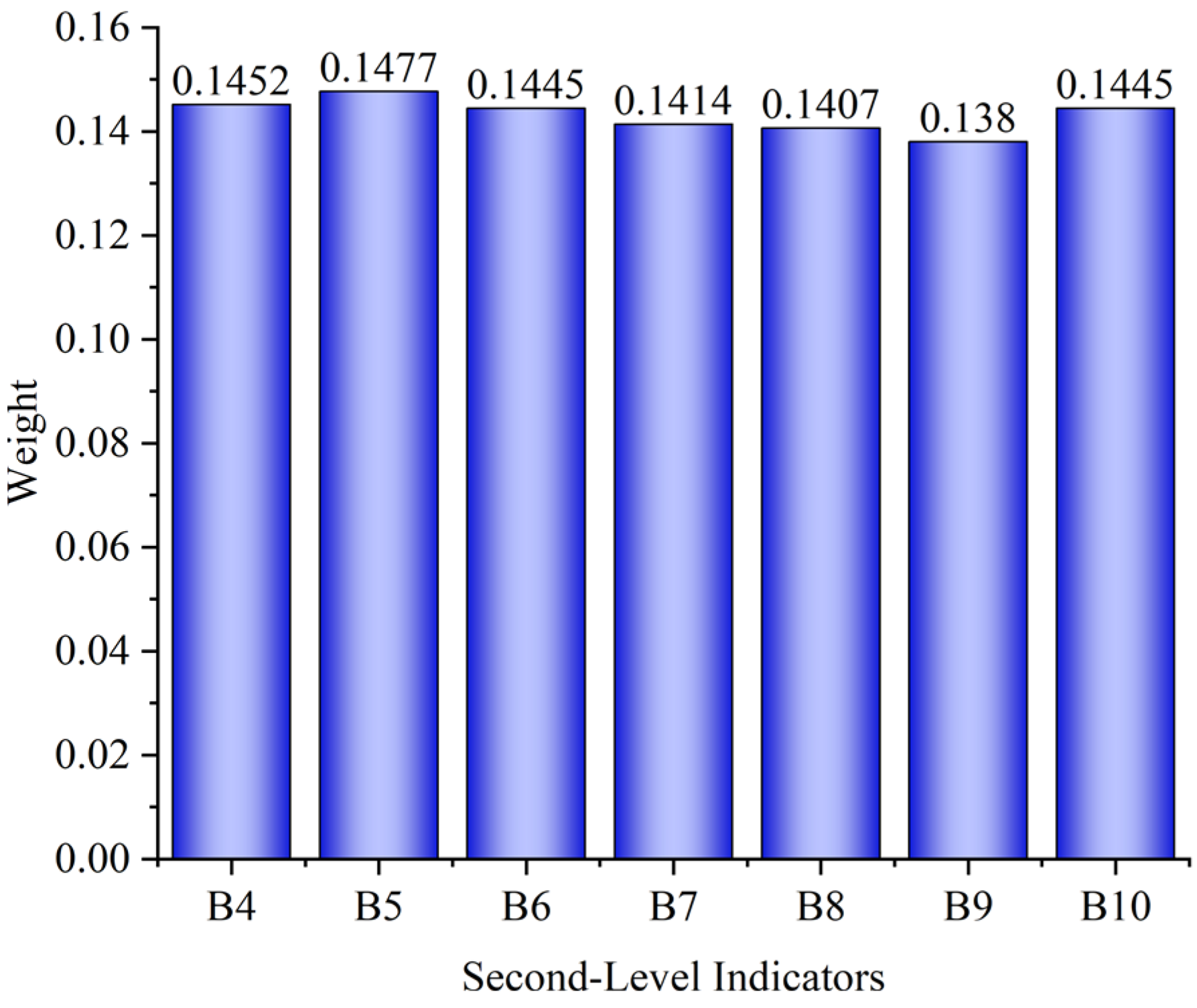
| First-Level A | Second-Level B | Third-Level C | Source |
|---|---|---|---|
| Financial capability A1 | Solvency B1 | Current ratio C1-1 | [20,34,35] |
| Assets–liability ratio C1-2 | |||
| Profitability B2 | Total assets turnover C2-1 | ||
| Input–output ratio C2-2 | |||
| Development capability B3 | Capital accumulation ratio C3-1 | ||
| Revenue growth ratio C3-2 | |||
| Project operation management A2 | Organization management B4 | Institutional framework C4-1 | [3,8,36,37,38] |
| Management system C4-2 | |||
| Information management C4-3 | |||
| Human resource management C4-4 | |||
| Corporate culture C4-5 | |||
| Buildings and facilities management B5 | Civil structure management C5-1 | [19,20,39,40] | |
| Public facility management C5-2 | |||
| Equipment room management C5-3 | |||
| Power supply system management C5-4 | |||
| Weak current system management C5-5 | |||
| Elevator system management C5-6 | |||
| Water supply and drainage system management C5-7 | |||
| HVAC system management C5-8 | |||
| Fire protection system management C5-9 | |||
| Security and emergency management B6 | Access and monitoring management C6-1 | [37,41,42,43] | |
| Inspection management C6-2 | |||
| Parking management C6-3 | |||
| Emergency plan C6-4 | |||
| Emergency drill C6-5 | |||
| Environmental and sanitary management B7 | Cleaning management C7-1 | [39,44,45,46] | |
| Garbage disposal C7-2 | |||
| Landscape maintenance C7-3 | |||
| Disinfection management C7-4 | |||
| Health management C7-5 | |||
| Customer service management B8 | Service system digitization rate C8-1 | [9,32,37] | |
| User complaint management C8-2 | |||
| Employee service quality C8-3 | |||
| Timeliness of service C8-4 | |||
| Campus activities management C8-5 | |||
| Fee management B9 | Integrity of the pricing mechanism C9-1 | [39,47] | |
| Flexibility of the price adjustment mechanism C9-2 | |||
| Cooperation and strategic management B10 | Relational governance C10-1 | [41,44,48,49,50,51] | |
| Contractual governance C10-2 | |||
| Integrity of conflict resolution | |||
| mechanism C10-3 | |||
| Integrity of refinancing strategy C10-4 | |||
| Stakeholders’ satisfaction A3 | Non-core asset user satisfaction B11 | Cafeteria service satisfaction C11-1 | [32,52,53,54,55] |
| Dormitory service satisfaction C11-2 | |||
| Commercial areas service satisfaction C11-3 | |||
| Commuting satisfaction C11-4 | |||
| Core asset user satisfaction B12 | Property service charges satisfaction C12-1 | [37,55] | |
| Special times service satisfaction C12-2 | |||
| Property service quality satisfaction C12-3 | |||
| Private sector satisfaction B13 | Comprehensive benefits for the SPV C13-1 | [56,57] | |
| Realization of strategic plan C13-2 | |||
| Public sector satisfaction B14 | Achievement of social benefits C14-1 | [58,59] | |
| Contract fulfillment C14-2 | |||
| External impacts of the project A4 | Economic effects impact B15 | Promote economic development C15-1 | [53,56,60] |
| Social effects impact B16 | Offer employment opportunities C16-1 | ||
| Environmental effects | Energy conservation and emission | ||
| impact B17 | reduction C17-1 |
| Quantitative Evaluation Set | Qualitative Comments |
|---|---|
| Excellent (1.75, 0.083, 0.0008) | Extremely High (90, 3.3, 0.03) |
| Good (1.25, 0.083, 0.0008) | High (70, 3.3, 0.03) |
| Average (0.75, 0.083, 0.0008) | Medium (50, 3.3, 0.03) |
| Poor (0.4, 0.033, 0.0003) | Low (30, 3.3, 0.03) |
| Very Poor (0.15, 0.05, 0.0005) | Extremely Low (10, 3.3, 0.03) |
| Indicator | Indicator Score | Weight | Indicator | Indicator Score | Weight |
|---|---|---|---|---|---|
| C1-1 | 72 | 0.4955 | C8-1 | 85 | 0.3355 |
| C1-2 | 69.30 | 0.5045 | C8-2 | 62.7 | 0.3506 |
| C2-1 | 76.20 | 0.5142 | C8-3 | 79.4 | 0.3139 |
| C2-2 | 67.80 | 0.4858 | C9-1 | 65.4 | 0.4879 |
| C3-1 | 65.10 | 0.5098 | C9-2 | 65.3 | 0.5121 |
| C3-2 | ~ | 0.4902 | C10-1 | 77.65 | 0.2085 |
| C4-1 | 71.5 | 0.2477 | C10-2 | 75.85 | 0.2798 |
| C4-2 | 72.1 | 0.1919 | C10-3 | 77 | 0.25 |
| C4-3 | 71.7 | 0.2204 | C10-4 | 76.1 | 0.2618 |
| C4-4 | 72.75 | 0.2371 | C11-1 | 57.6 | 0.2281 |
| C4-5 | 60.00 | 0.1956 | C11-2 | 66.92 | 0.2499 |
| C5-1 | 81 | 0.1094 | C11-3 | 63.6 | 0.2324 |
| C5-2 | 80 | 0.1225 | C11-4 | 63.2 | 0.2894 |
| C5-3 | 80.8 | 0.1067 | C12-1 | 67.98 | 0.4688 |
| C5-4 | 81.7 | 0.0991 | C12-2 | 67.80 | 0.5312 |
| C5-5 | 80.65 | 0.0951 | C13-1 | 69.3 | 0.5069 |
| C5-6 | 81.45 | 0.1312 | C13-2 | 69.08 | 0.4931 |
| C5-7 | 81.25 | 0.0902 | C14-1 | 68.8 | 0.4909 |
| C5-8 | 80.6 | 0.116 | C14-2 | 70.27 | 0.5091 |
| C5-9 | 81 | 0.1296 | C15-1 | 82 | 0.3368 |
| C6-1 | 80.85 | 0.3111 | C16-1 | 80 | 0.3278 |
| C6-2 | 72 | 0.2315 | C17-1 | 76.4 | 0.3354 |
| C6-3 | 71.9 | 0.3223 | |||
| C6-4 | 100 | 0.2466 | |||
| C7-1 | 68.65 | 0.1604 | |||
| C7-2 | 79.25 | 0.1826 | |||
| C7-3 | 71.95 | 0.1797 | |||
| C7-4 | 72 | 0.2545 | |||
| C7-5 | 79.25 | 0.223 |
| Performance Evaluation Methods | Evaluation Set |
|---|---|
| Matter-Element Method | {Extremely High, High, Medium, Low, Extremely Low} |
| Fuzzy Comprehensive Evaluation | {Extremely High (80–100), High (60–80), Medium (40–60), Low (20–40), Extremely Low (0–20)} |
| Performance Evaluation Methods | Score/Membership | Performance Level |
|---|---|---|
| Matter-Element Method | {−0.124, 0.038, −0.353, −0.566, −0.679} | High |
| Fuzzy Comprehensive Evaluation | 78.84 | High |
| The Proposed Method | 73.14 | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Li, X. Performance Evaluation of Education Infrastructure Public–Private Partnership Projects in the Operation Stage Based on Limited Cloud Model and Combination Weighting Method. Buildings 2025, 15, 1833. https://doi.org/10.3390/buildings15111833
Ma J, Li X. Performance Evaluation of Education Infrastructure Public–Private Partnership Projects in the Operation Stage Based on Limited Cloud Model and Combination Weighting Method. Buildings. 2025; 15(11):1833. https://doi.org/10.3390/buildings15111833
Chicago/Turabian StyleMa, Junhao, and Xiangjun Li. 2025. "Performance Evaluation of Education Infrastructure Public–Private Partnership Projects in the Operation Stage Based on Limited Cloud Model and Combination Weighting Method" Buildings 15, no. 11: 1833. https://doi.org/10.3390/buildings15111833
APA StyleMa, J., & Li, X. (2025). Performance Evaluation of Education Infrastructure Public–Private Partnership Projects in the Operation Stage Based on Limited Cloud Model and Combination Weighting Method. Buildings, 15(11), 1833. https://doi.org/10.3390/buildings15111833




