Numerical Simulation-Based Study on Influence of Different Connection Configurations of Viscous Dampers on Seismic Performance

Abstract

To investigate the influence of different connection configurations of viscous dampers on seismic mitigation performance, this study conducts a numerical simulation analysis of a 10-story inpatient building in Bazhou People’s Hospital, comparing the energy dissipation efficacy of viscous dampers under three connection types: diagonal bracing, chevron bracing, and wall-mounted connections. The results demonstrate that both chevron and wall-mounted configurations exhibit superior seismic mitigation performance compared to diagonal bracing. Specifically, chevron bracing is more suitable for mid- to high-rise structures, while wall-mounted connections achieve marginally better performance in low-rise buildings. However, the latter’s efficacy diminishes in mid- to high-rise structures due to the influence of wall self-weight. This study provides practical insights for optimizing the arrangement and application of viscous dampers in engineering projects.

1. Introduction

With accelerating urbanization and increasingly complex building structures, concerns regarding structural dynamic responses and safety under seismic loads have intensified. As stipulated in China’s Classification Standard for Seismic Fortification of Buildings, critical medical facilities in tertiary hospitals—including outpatient, diagnostic, and inpatient units—are classified as special fortification structures, while similar facilities in secondary and tertiary hospitals are designated as priority fortification structures [1,2,3]. Traditional seismic design relies on structural strength and ductility for energy dissipation, yet such approaches risk severe damage or collapse under intense seismic events, failing to meet safety requirements for hospital buildings. Consequently, supplemental damping devices that dissipate seismic energy have emerged as a key strategy for enhancing structural resilience. Among these, viscous dampers are widely adopted in engineering practice due to their high energy dissipation capacity, minimal impact on structural stiffness, and stable force transmission. However, the connection configuration of viscous dampers critically influences their energy dissipation efficiency and overall seismic mitigation performance, necessitating further research into optimal placement strategies. This study evaluates the seismic mitigation efficacy of different connection configurations, particularly brace-type and wall-mounted systems, through a case study of a 10-story frame structure at Bazhou People’s Hospital in Korla City.

Recent research has extensively explored the seismic mitigation mechanisms, connection configurations, and engineering applications of viscous dampers. Michael C. Constantinou [4] compared diagonal, chevron, and toggle-brace connections, highlighting the superior energy dissipation of toggle-brace systems via geometric amplification effects, validated through engineering case studies. Abdalla Mahamad Affan Alhamdany [5] introduced energy dissipation techniques using viscous dampers in school buildings. Mohammed Samier Sebaq [6] investigated damage indices for viscous dampers under low-intensity earthquakes through experiments and simulations, though their findings were limited to steel structures and excluded complex systems like frame shear wall structures. Li Yi et al. [7] studied the influence of different damper connection modes on the seismic reduction performance of a teaching building through numerical simulation, with a particular focus on the working state of the lasso structure. Wang and Huang et al. [8] systematically and comprehensively investigated the seismic performance of a 14-story-frame shear wall structure under two different connection modes by organically combining multiple platforms, such as ETABS, adopting the response spectrum method, the elastic time–history analysis method, and the elastoplastic time–history analysis method. Hua Chenglong et al. [9] studied the relationship between different connection modes and damping coefficients by studying the mechanical properties of different connection modes of viscous dampers in a steel frame model. Xu Xiao et al. [10] conducted numerical simulations to study the influence of different connection modes on the seismic performance of reinforced concrete frame structures and carried out time–history analysis under rare earthquakes. Zhu Lin et al. [11] proposed an objective function to compare the advantages and disadvantages of structural seismic performance under different connection modes and derived the optimal layout mode. Yang Xiaofeng et al. [12] studied the frame structure of bottom-story buildings, adopted different types of damper layout modes, compared the displacement, inter-story displacement, and acceleration of the structure in two principal axis directions, and verified the seismic performance of energy-dissipating and shock-absorbing structures equipped with viscous dampers. Song Lixun et al. [13] studied the influence of different connection modes on the mechanical properties of long-span cable-stayed bridges through numerical analysis. Wang Runze et al. [14] investigated the influence of different connection modes on the seismic performance of steel structure frame factories using ETABS 22.0.0. Lu Mingkuan et al. [15] identified the optimal installation positions of dampers by comparing the layout modes of damper systems in super high-rise buildings. This paper systematically investigates the influence of different connection modes on the shock absorption performance based on the ETABS platform and a practical engineering model. Taking the maximum inter-story displacement and hysteretic curves of viscous dampers under different connection modes as the judgment basis, we can obtain the general rules between connection modes and seismic performance, providing more universal design bases for engineering practice.

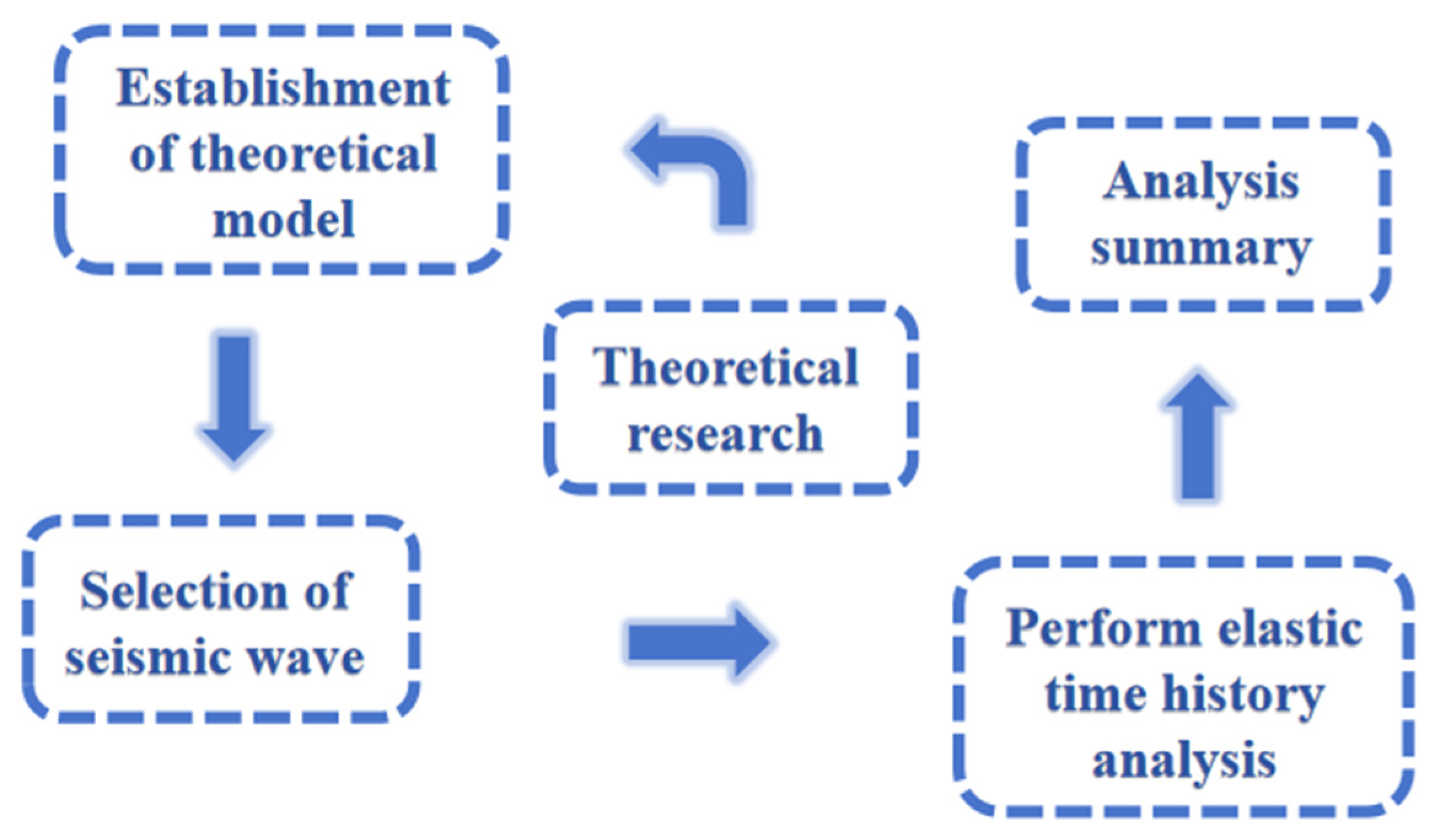
2. Research Methodology

Due to the complexity of seismic research and significant limitations imposed by physical experimental constraints, this study employs numerical simulation analysis using ETABS 22.0.0. Theoretical models are established within the platform to simulate the operational states of different viscous dampers during seismic events. The fast time–history analysis method is utilized to obtain response data for the building models, which are subsequently analyzed and synthesized to derive deeper insights or patterns. The specific research methodology is illustrated in Figure 1.

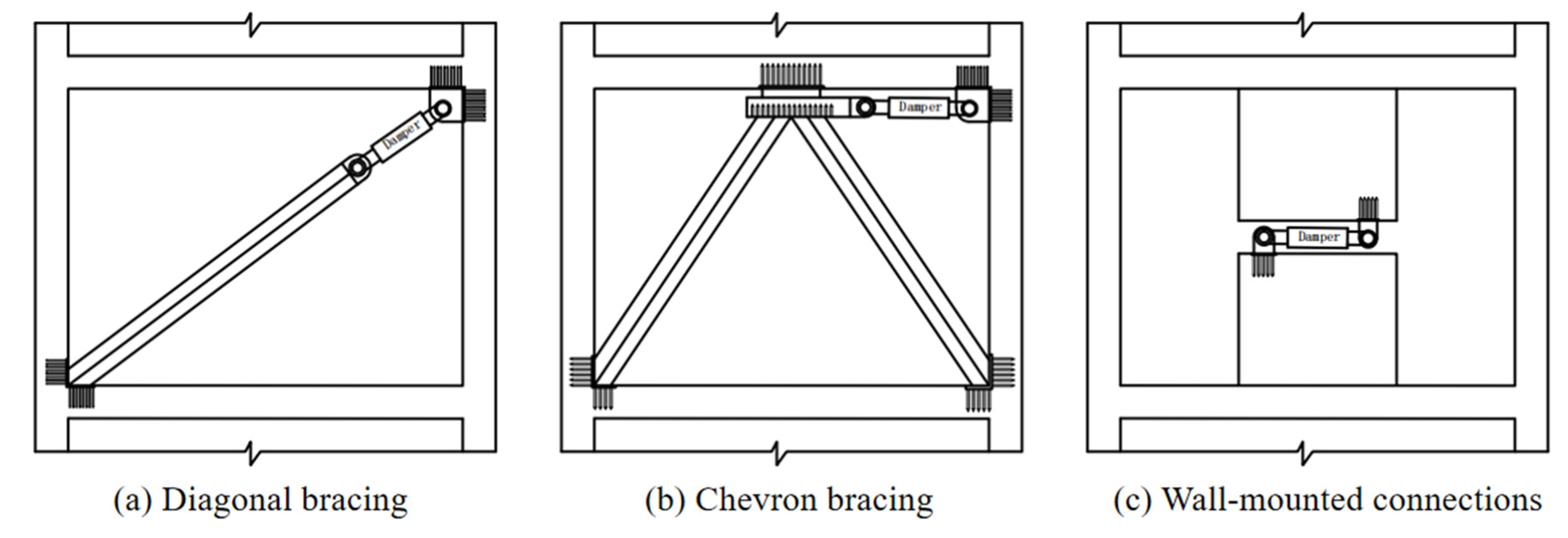
3. Working Mechanism of Viscous Damper Connection Configurations

Walls were used to form damper systems. Common configurations include inclined rod, herringbone, and wall-mounted connections. Under seismic loading, the lateral displacement of the structure induces inter-story shear deformation, driving relative motion at the ends of steel braces or between walls. This forces the damper to undergo compression or extension along its piston axis, generating diagonal or horizontal damping forces opposing structural displacement, thereby dissipating seismic energy.

The working mechanism is expressed as follows [4]:

$$\mathrm{u}=f\cdot {\mathrm{u}}_{\mathrm{F}}$$

(1)

Here, $\mathrm{u}$ = relative displacement at both ends of the damper; $f$ = displacement amplification coefficient; and ${\mathrm{u}}_F$ = inter-story displacement of the floor where the damper is installed.

For inclined rod connections (Figure 2a), the relative displacement between the two ends of the damper is less than the inter-story displacement of the floor where it is located;

For Chevron bracings (Figure 2b) and wall-mounted connections (Figure 2c), the relative displacement given by the two ends of the damper is equal to the inter-story displacement of the floor where it is located.

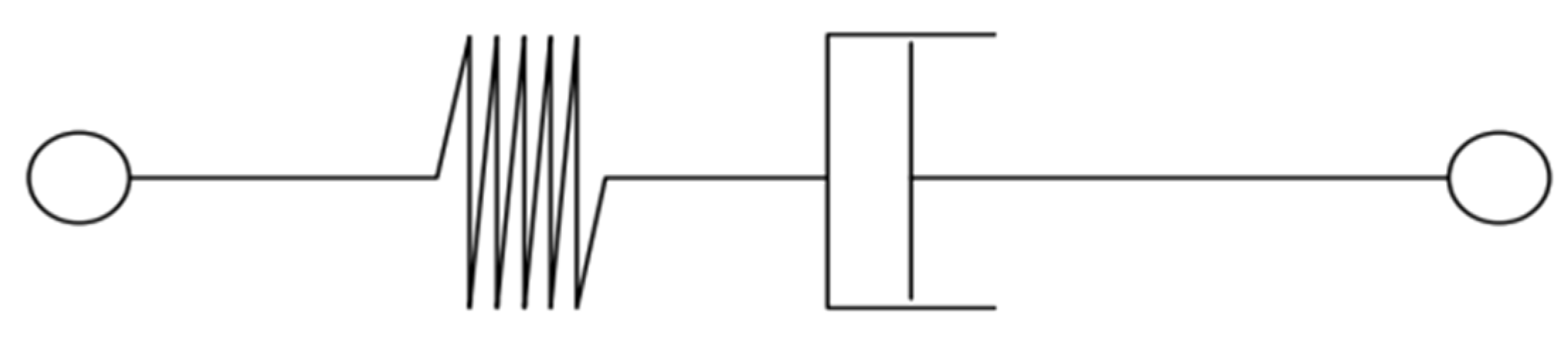
4. Seismic Mitigation Mechanism of Viscous Dampers

A viscous damper is a velocity-dependent energy dissipation device based on fluid dynamics principles. It exhibits negligible inherent stiffness, with damping forces solely proportional to velocity. The device demonstrates a well-defined elliptical hysteresis loop, and its mechanical behavior can be mathematically represented by a first-order Maxwell model [16]:

$$F_{\mathrm{d}}+\lambda {\stackrel{•}{F}}_{\mathrm{d}}=C_0\stackrel{•}{\mathrm{u}}$$

(2)

Here, $F_{\mathrm{d}}$ = damping force; $\lambda$ = relaxation time coefficient; $C_0$ = generalized damping coefficient; and $\stackrel{•}{\mathrm{u}}$ = relative velocity at both ends of the damper.

A comparison between experimental and theoretical values derived from the Maxwell model reveals that the $\lambda \stackrel{•}{F_{\mathrm{d}}}$ term can be neglected when the frequency is below 4 Hz [17]. Since most engineering structures subjected to wind or seismic loads exhibit vibrations below 4 Hz (i.e., low-frequency vibrations), Equation (1) can be simplified as follows:

$$F_{\mathrm{d}}=C_0\stackrel{•}{\mathrm{u}}$$

(3)

Building on this, Taylor Devices Inc. optimized the mechanical model expression for viscous dampers. For horizontally installed viscous dampers, the following is used [18]:

$$F_{\mathrm{d}}=C_0|\stackrel{•}{u}{|}^{\alpha }\hspace{1em}sign(\stackrel{•}{u})$$

(4)

For inclined installations, the following is used:

$$F_{\mathrm{d}}=C_0|\stackrel{•}{u}{|}^{\alpha }\hspace{1em}sign(\stackrel{•}{u})$$

(5)

Here, $\theta$ = angle between the damper and the horizontal plane; $C_0$ = generalized damping coefficient; $\stackrel{•}{\mathrm{u}}$ = relative velocity at both ends of the damper; and $\alpha$ = velocity exponent, typically ranging from 0.3 to 1.0 in practical engineering.

When $\alpha$ = 1.0, the damper exhibits linear behavior. For $\alpha$ < 1.0, the damper becomes nonlinear, with damping force increasing rapidly at low velocities and decelerating as velocity rises.

5. Engineering Case Study

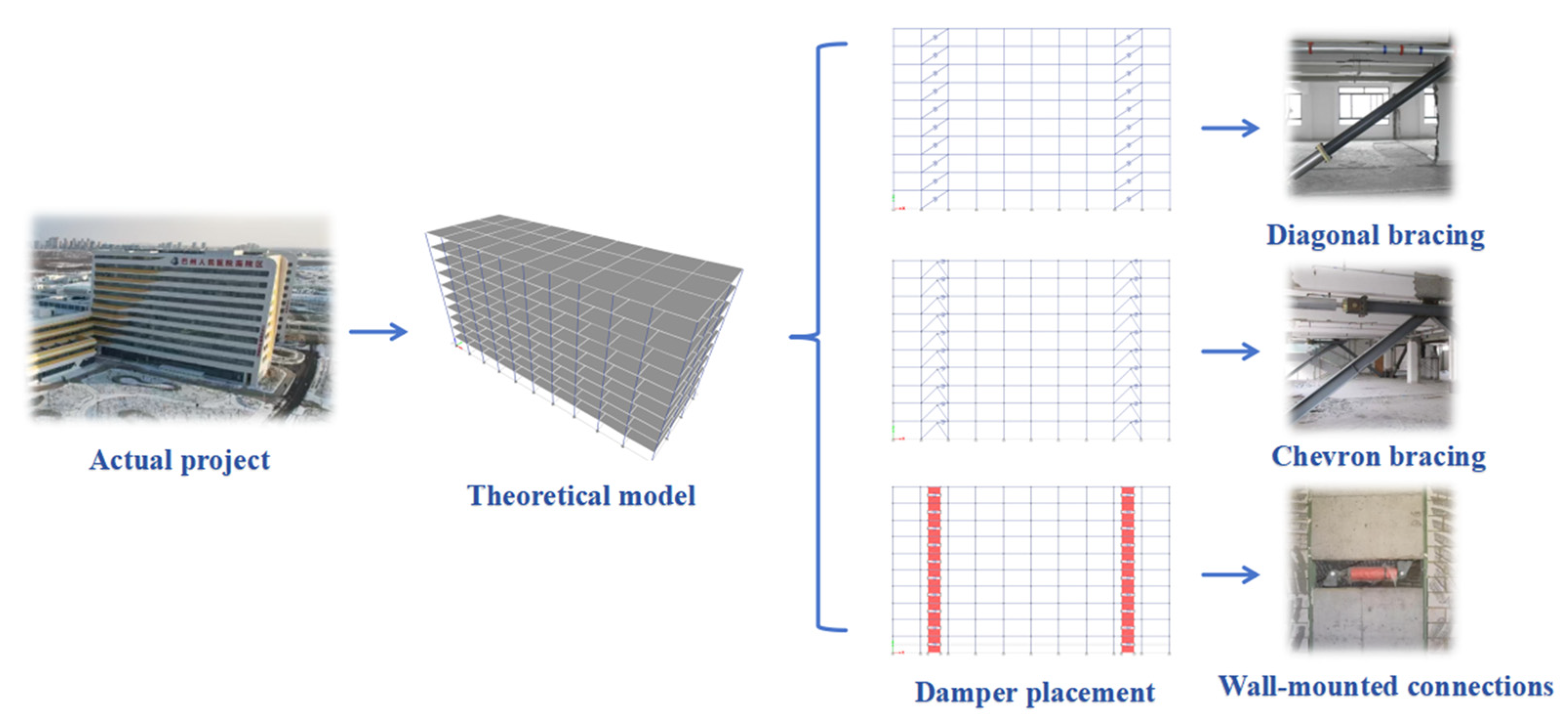
5.1. Project Overview

This case study focuses on an inpatient building at Bazhou People’s Hospital in Korla City, the capital of Bazhou Prefecture. The structure comprises a 10-story reinforced concrete frame system with a total height of 43.8 m. The site is classified as having a seismic fortification intensity of 8 degrees (peak ground acceleration 0.2 g), belonging to design earthquake group II and site class II, with a characteristic period (T_g) of 0.40 s. The structure is categorized as a priority fortification facility (Class B). Seismic actions were calculated for an 8-degree intensity (0.2 g PGA), while seismic detailing adhered to 9-degree requirements. To systematically evaluate the influence of connection configurations on the seismic mitigation performance of viscous dampers, this case study employs elastic time–history analysis, focusing exclusively on the structural response along the X-direction under frequent earthquake levels. The maximum inter-story drift ratio is selected as the primary evaluation metric. The specific research process are shown in Figure 3.

5.2. Model Development

Numerical simulations were conducted using structural elements native to the analysis software used. The key material parameters are summarized in

Table 1. Material parameters.

Unit Type	Material	Dimension (mm)
Beam	C30	500 × 300
Column	C40	500 × 500

. Permanent floor loads were set at 3.5 kN/m², and live loads at 2.0 kN/m², with fully fixed base supports applied. The viscous dampers are modeled using spring–damper elements based on the Maxwell model (the specific theoretical derivation of this model can be found in Section 4), a classical viscoelastic constitutive model designed to describe the mechanical behavior of materials exhibiting both elastic and viscous properties. This model is composed of a spring element and a damper element connected in series (See Figure 4 for the specific model), and it is widely used to simulate the dynamic responses of fluids, polymeric materials, and dampers in engineering structures. Notably, the stiffness of the dampers is neglected in the calculations. The arrangement positions and parameters of the dampers in the three connection configurations are identical, with the specific damper parameters as reported in Reference [19], as presented in

Table 2. Damper parameters.

Connection Unit Type	Damping Index	Damping Coefficient (KN×(s/m))	Number of Dampers
Damper Exponential	0.3	1000	60

.

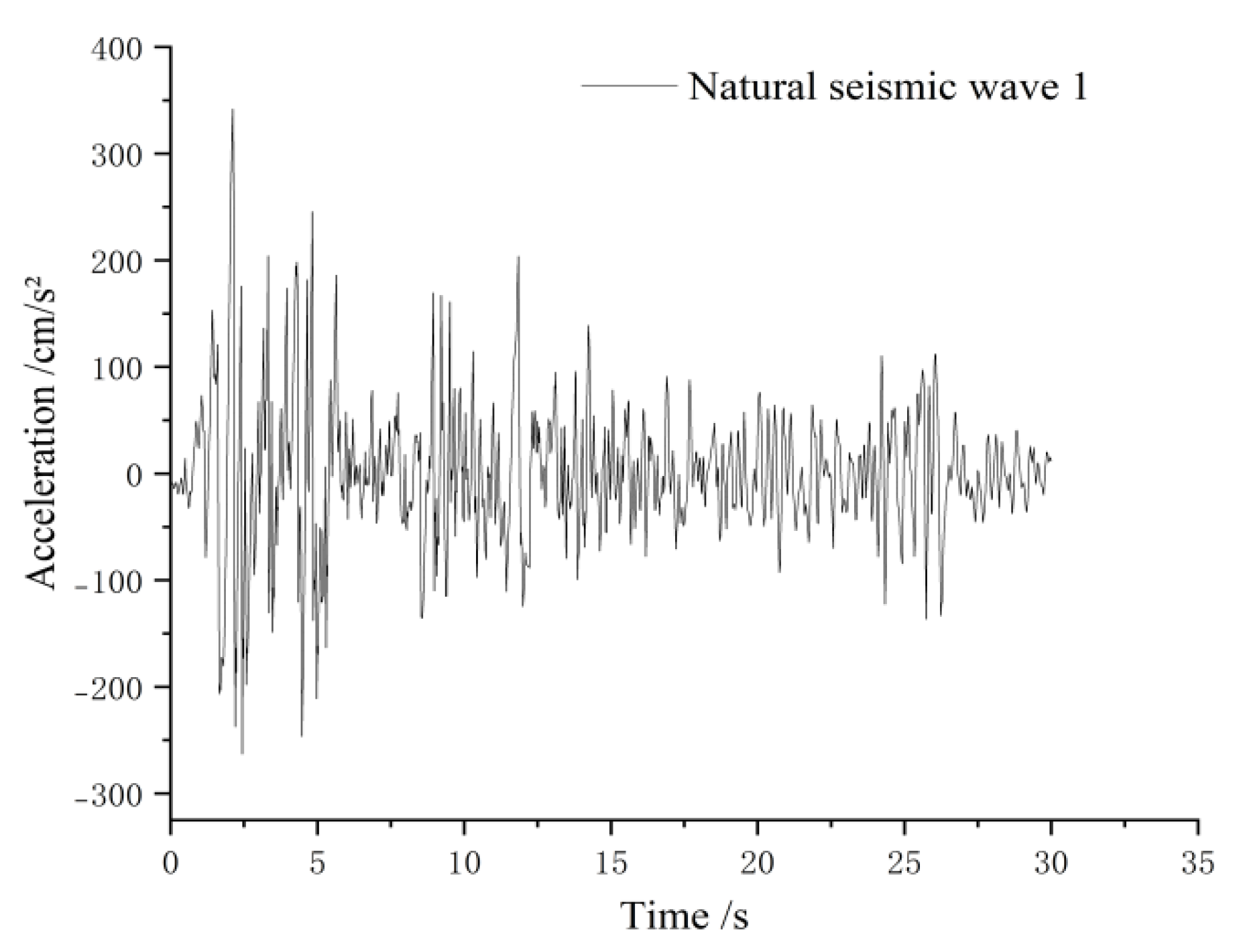
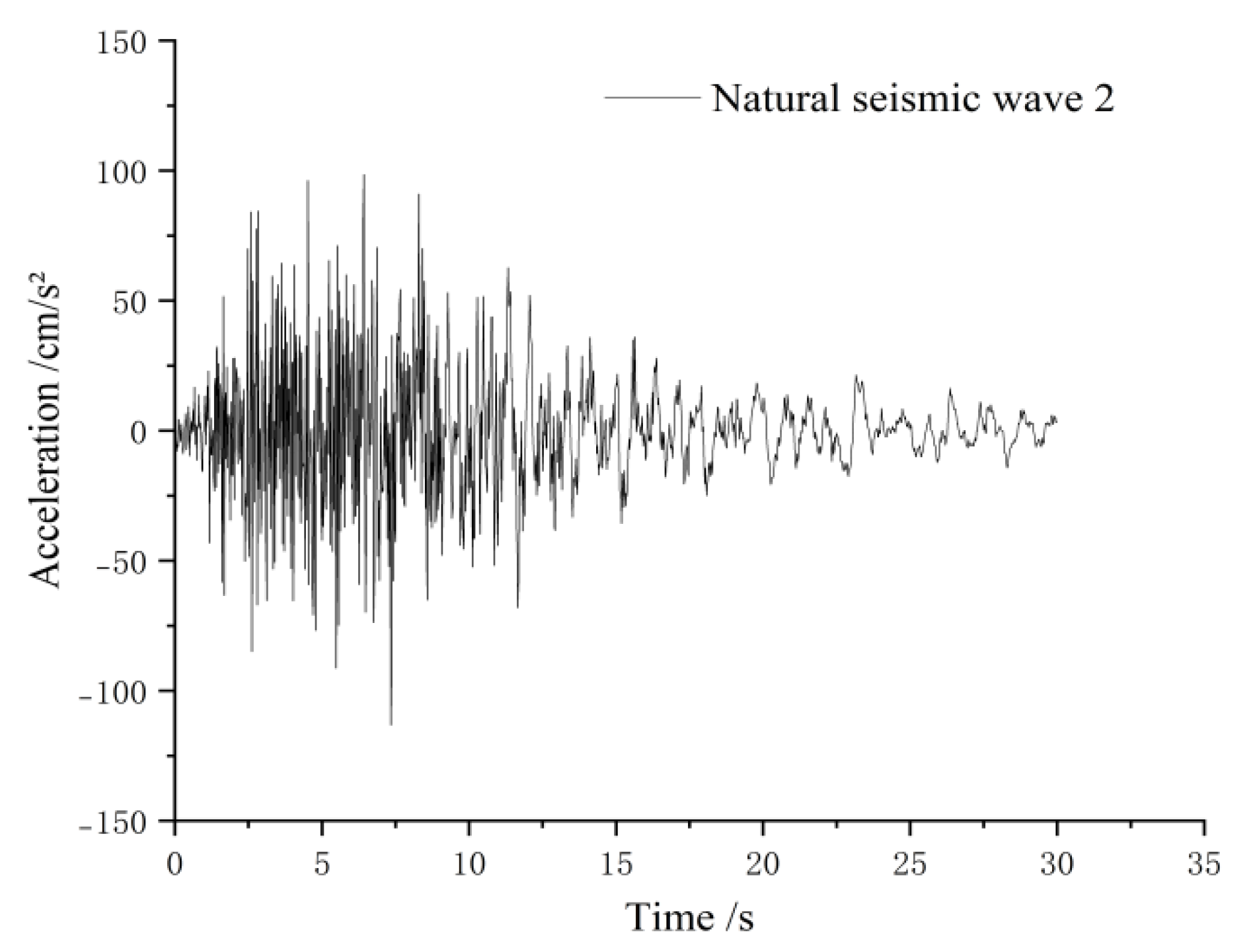
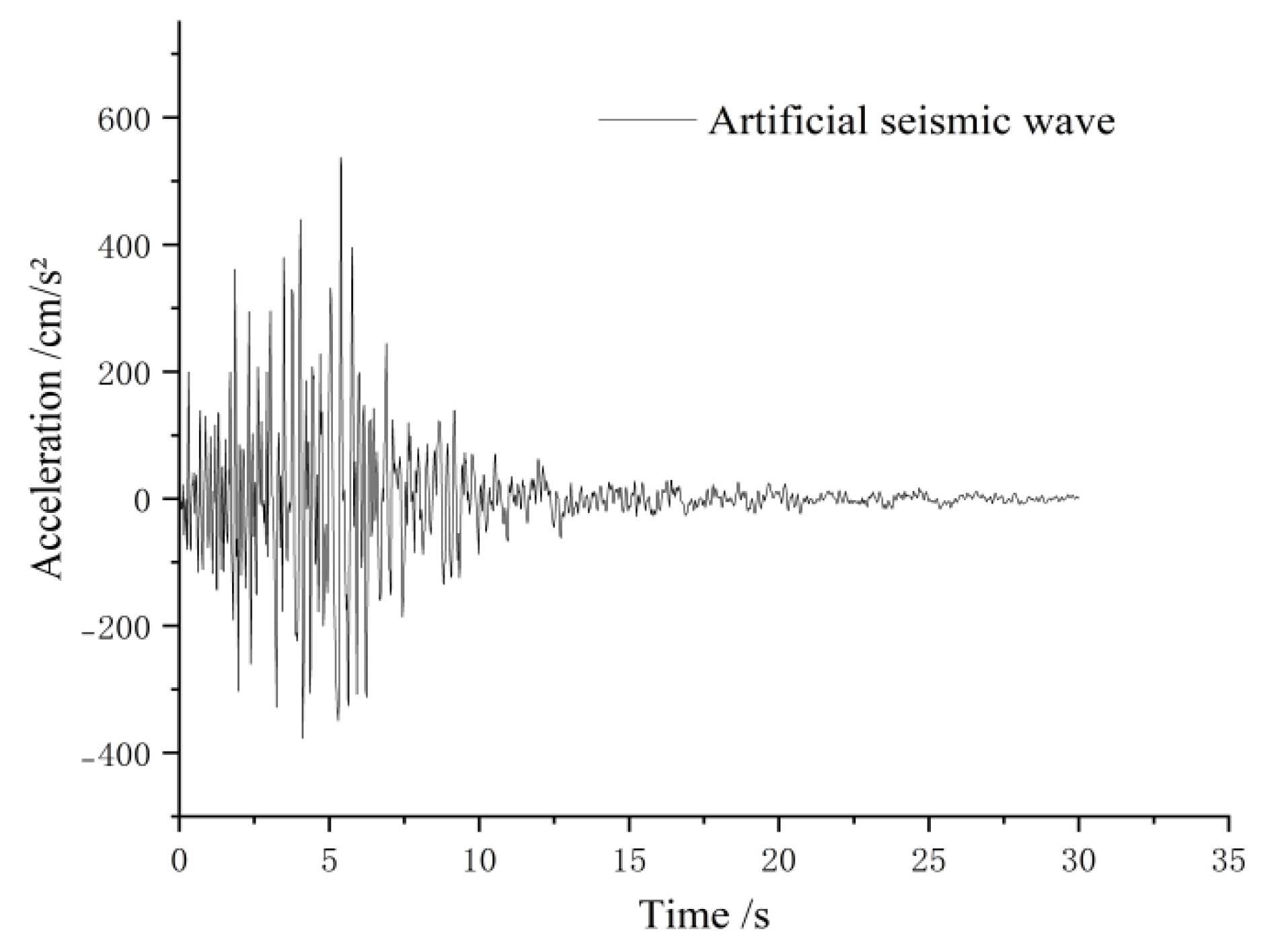
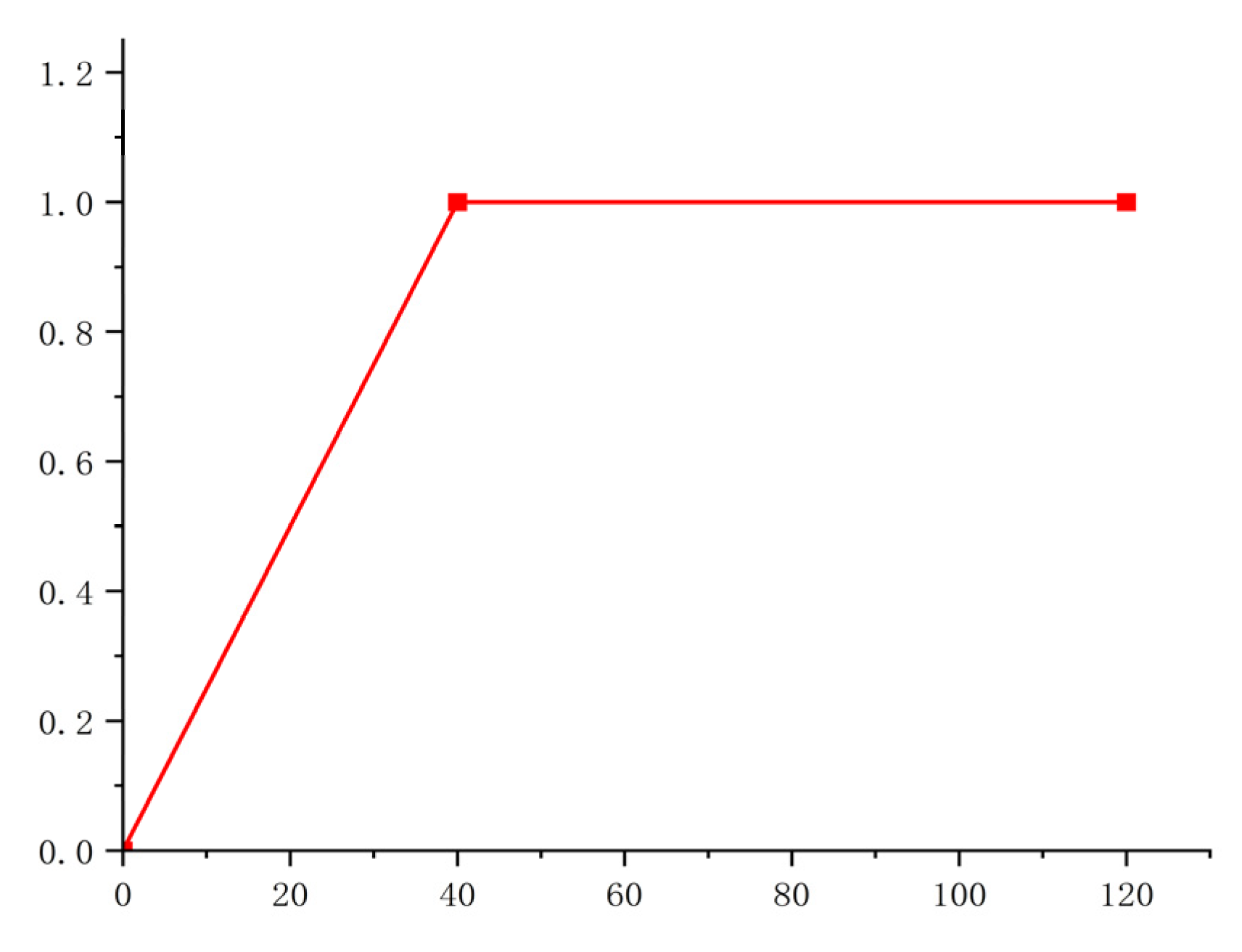
5.3. Selection of Seismic Waves

To ensure a rational investigation of the structural model, appropriate seismic waves must be selected as inputs for elastic time–history analysis. This study focuses on verifying and validating the seismic performance of designed or existing structures in practical engineering. To reduce computational effort while aligning with code-based design objectives, a seismic wave selection method grounded in the design response spectrum was adopted [20,21,22]. The selected seismic waves, comprising two natural waves and one artificial wave, were sourced from the National Seismic Network and the ETABS platform database. These waves were chosen in compliance with code requirements [23], considering engineering practicality and representativeness, to perform elastic time–history analysis under frequent earthquake conditions. The specific waveform is shown in Figure 5, Figure 6 and Figure 7.

5.4. Elastic Time–History Analysis

After inputting the seismic time–history functions into the software, the load cases for elastic time–history analysis were defined. To balance research objectives and computational efficiency, the Ritz vector method [24] was employed for modal analysis due to its rapid iteration and computational convenience. The applied load types included acceleration and link loads, with the maximum number of modes determined as 60 through trial calculations to ensure that the cumulative modal participation mass reached at least 90% of the total structural mass.

To simplify the analysis and enhance computational speed, the Fast Nonlinear Analysis (FNA) method was utilized in defining the time–history module [25,26]. Four load cases—FNA-RTH, FNA-TR1, FNA-TR2, and FNA-RG—were established. The FNA-RTH case employed the slope function shown in Figure 8 as its time–history curve, serving as a precursor to simulate the force–displacement relationships and restore force characteristics of nonlinear connection elements. The remaining three seismic load cases were derived based on this precursor. During the definition of these seismic load cases, scaling coefficients were applied to adjust the amplitude of the seismic time–history functions [27], ensuring that the peak accelerations of the waves did not exceed the maximum limits specified for frequent earthquakes in the codes. Detailed parameter definitions are illustrated in Figure 9 and Figure 10.

6. Results Analysis

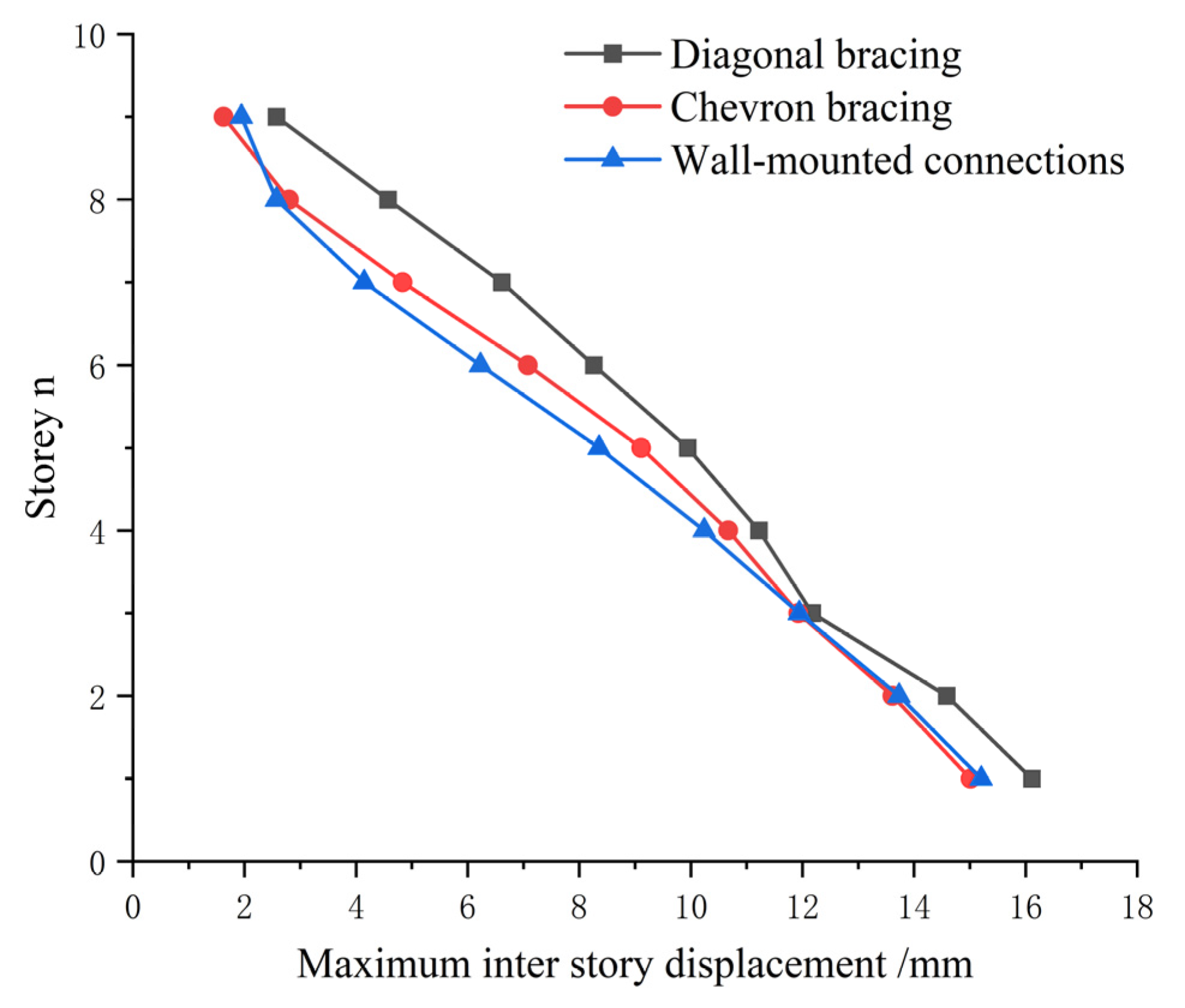
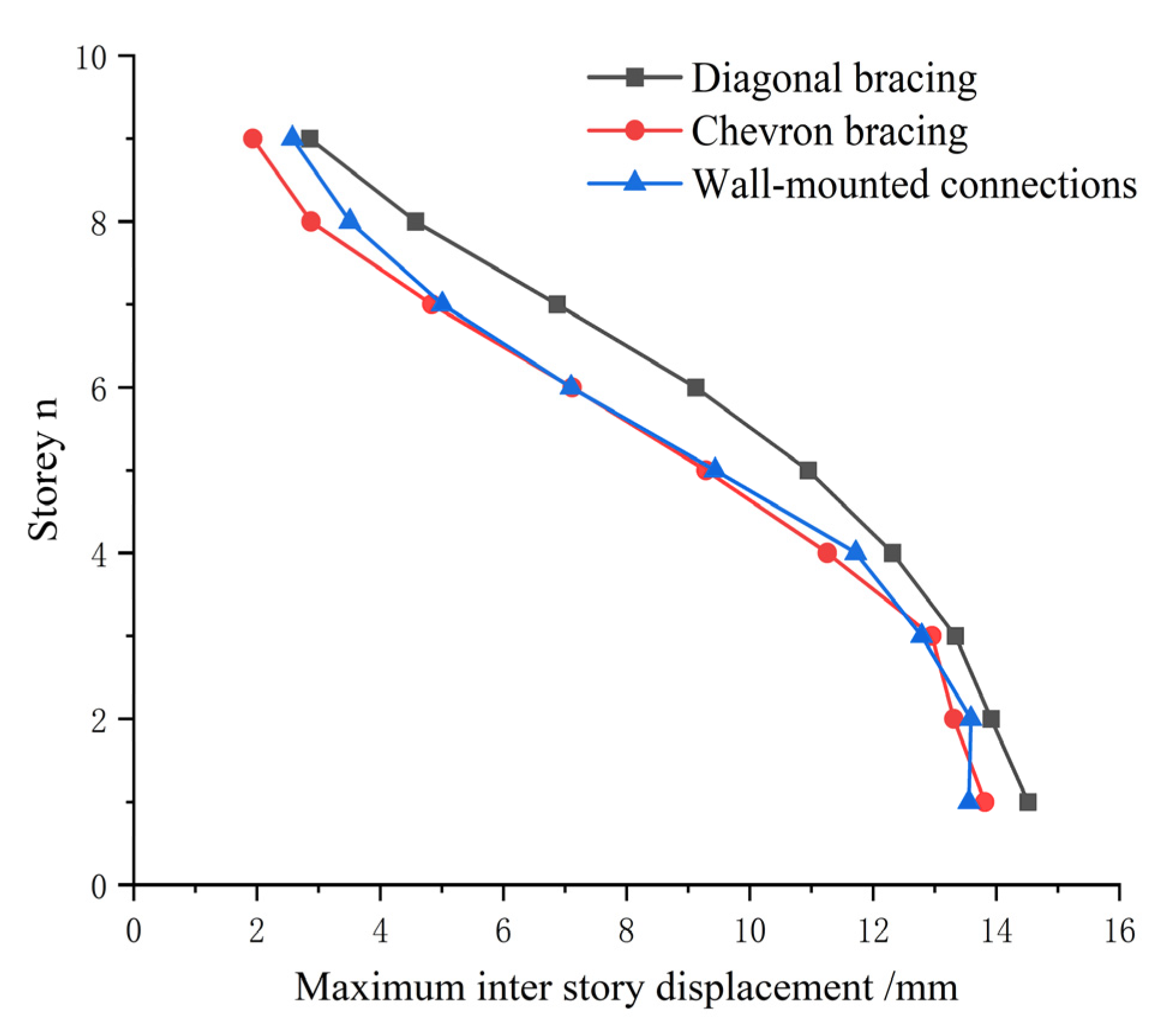
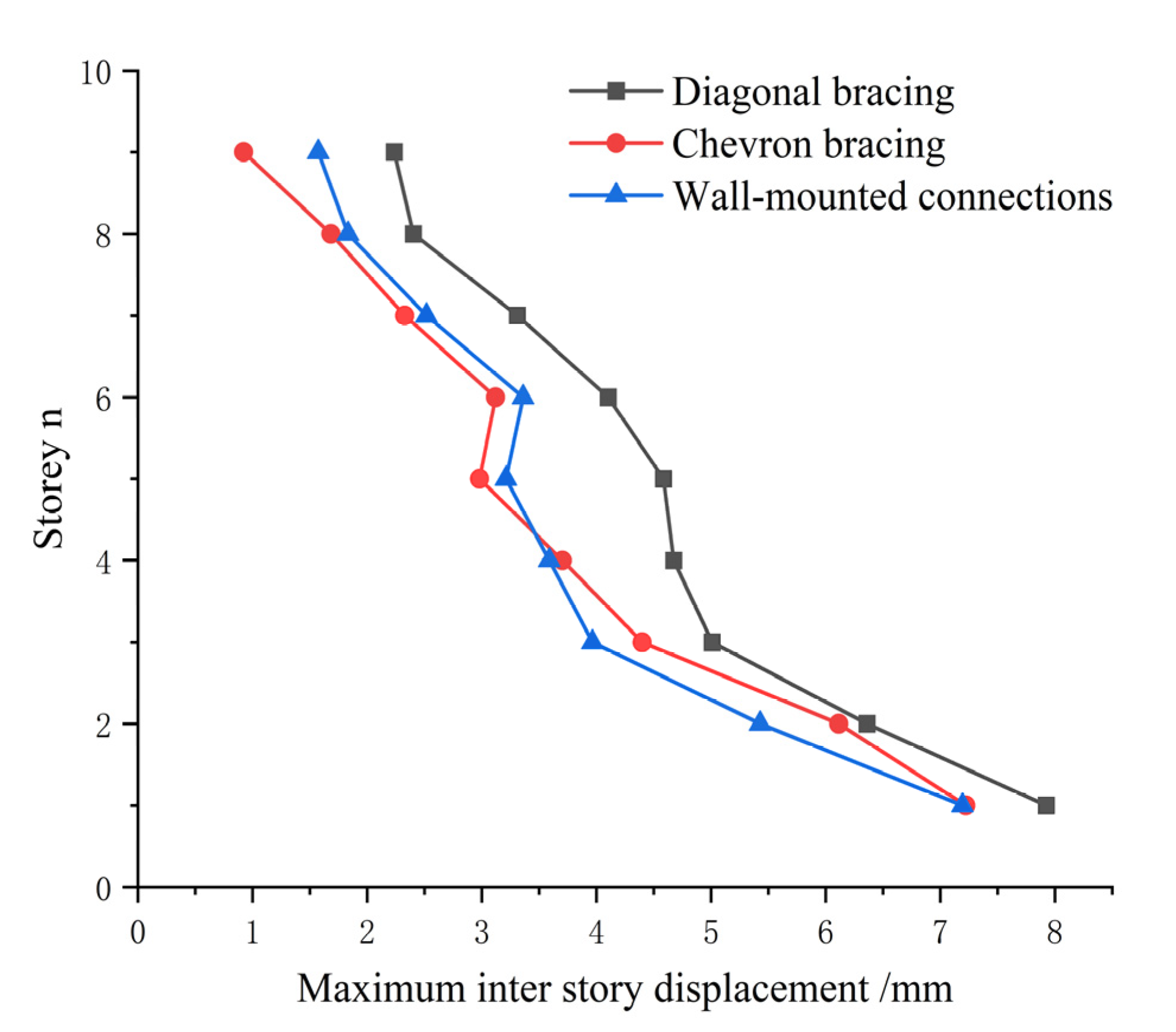
6.1. Maximum Inter-Story Drift

By comparing the analysis results and extracting the stress cloud diagram of the most typical building model (see Figure 11 for details), it can be concluded that the building model undergoes significant deformation under the action of seismic waves, and the viscous dampers undergo relative displacement, fully entering the working state. The stress state of the model shows a significant change with the change in floors, and the closer it is to the bottom, the greater the degree of deformation.

The damping analysis results for the maximum inter-story drifts of the building model are summarized in

Table 3. Comparison of maximum interlayer displacement under TR1 action.

Story	Diagonal Bracing (mm)	Chevron Bracing (mm)	Wall-Mounted Connections (mm)
1–2	16.114	15.013	15.204
2–3	14.587	13.612	13.732
3–4	12.178	11.927	11.941
4–5	11.222	10.671	10.239
5–6	9.944	9.110	8.354
6–7	8.261	7.079	6.228
7–8	6.612	4.833	4.143
8–9	4.572	2.798	2.574
9–10	2.575	1.625	1.946

,

Table 4. Comparison of maximum interlayer displacement under TR2 action.

Story	Diagonal Bracing (mm)	Chevron Bracing (mm)	Wall-Mounted Connections (mm)
1–2	14.517	13.815	13.555
2–3	13.917	13.312	13.588
3–4	13.337	12.956	12.788
4–5	12.316	11.257	11.720
5–6	10.947	9.289	9.439
6–7	9.123	7.117	7.099
7–8	6.873	4.838	5.008
8–9	4.576	2.876	3.508
9–10	2.858	1.933	2.574

and

Table 5. Comparison of maximum interlayer displacement under RG action.

Story	Diagonal Bracing (mm)	Chevron Bracing (mm)	Wall-Mounted Connections (mm)
1–2	7.924	7.223	7.194
2–3	6.360	6.115	5.428
3–4	5.009	4.400	3.966
4–5	4.674	3.704	3.590
5–6	4.586	2.980	3.211
6–7	4.102	3.121	3.360
7–8	3.310	2.327	2.518
8–9	2.403	1.685	1.834
9–10	2.237	0.923	1.574

and Figure 12, Figure 13 and Figure 14. Under the TR1 wave (X direction), the controlled structure with diagonal brace connections exhibited the largest maximum inter-story drift, peaking at 16.114 mm. The wall-type connections ranked second with a peak drift of 15.204 mm, while the chevron connections showed the smallest peak drift of 15.013 mm. Under the TR2 wave (X-direction), the diagonal brace connections again yielded the largest maximum drift (14.517 mm), followed by chevron connections (13.815 mm), and wall-type connections (13.555 mm). For the RG wave (X-direction), diagonal brace connections remained the least effective, with a peak drift of 7.924 mm, followed by chevron connections (7.223 mm) and wall-type connections (7.194 mm).

Thus, under identical damping conditions, the maximum inter-story drifts of floors equipped with chevron and wall-type connections were consistently smaller than those with diagonal brace connections. This indicates that chevron and wall-type connections generally outperform diagonal brace connections in terms of seismic energy dissipation effectiveness. Analysis of the curve trends in the figures reveals that the maximum inter-story drift values and damping performance of chevron and wall-type connections vary across different floors and seismic load cases, demonstrating context-dependent advantages under the three earthquake scenarios.

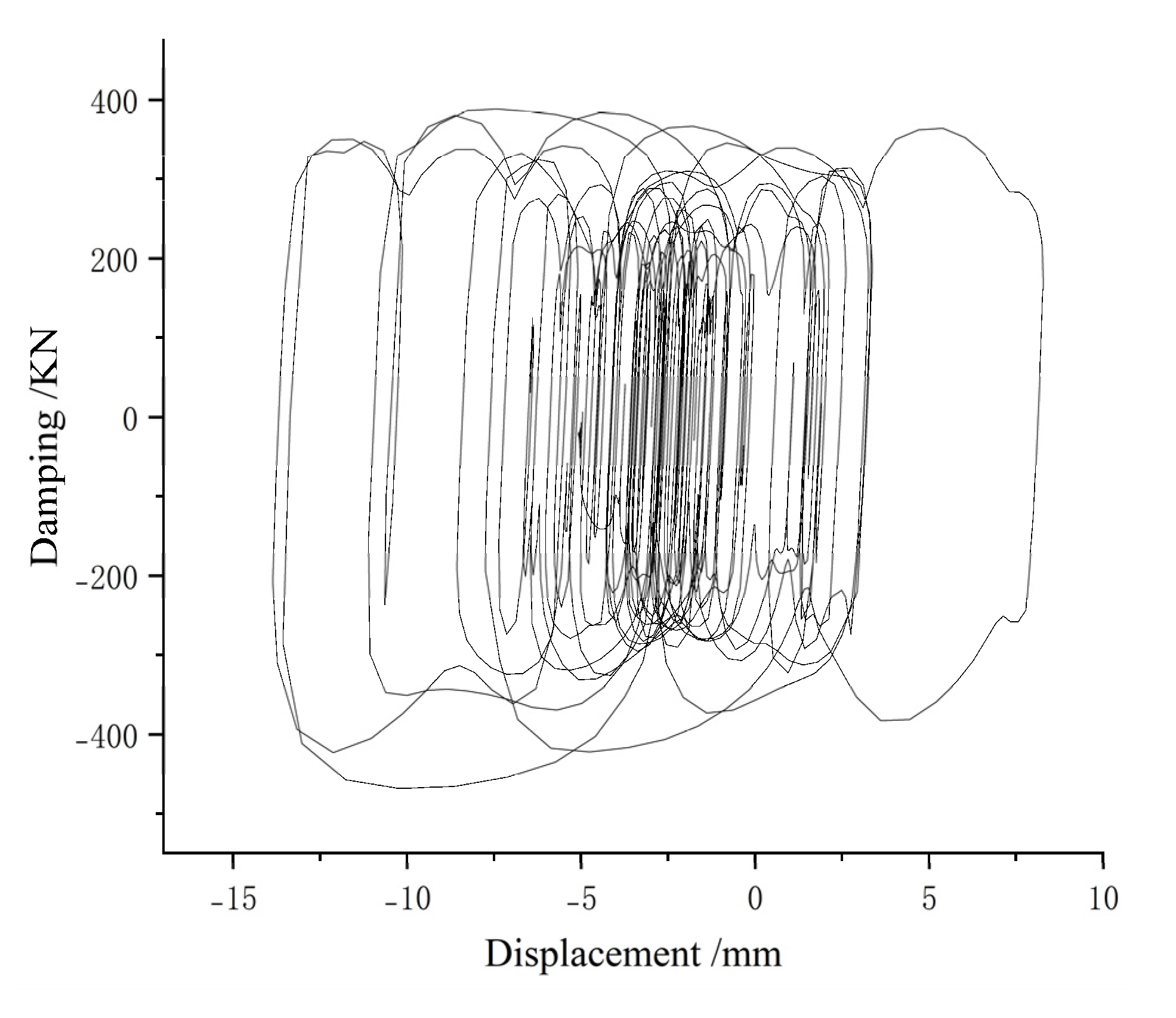
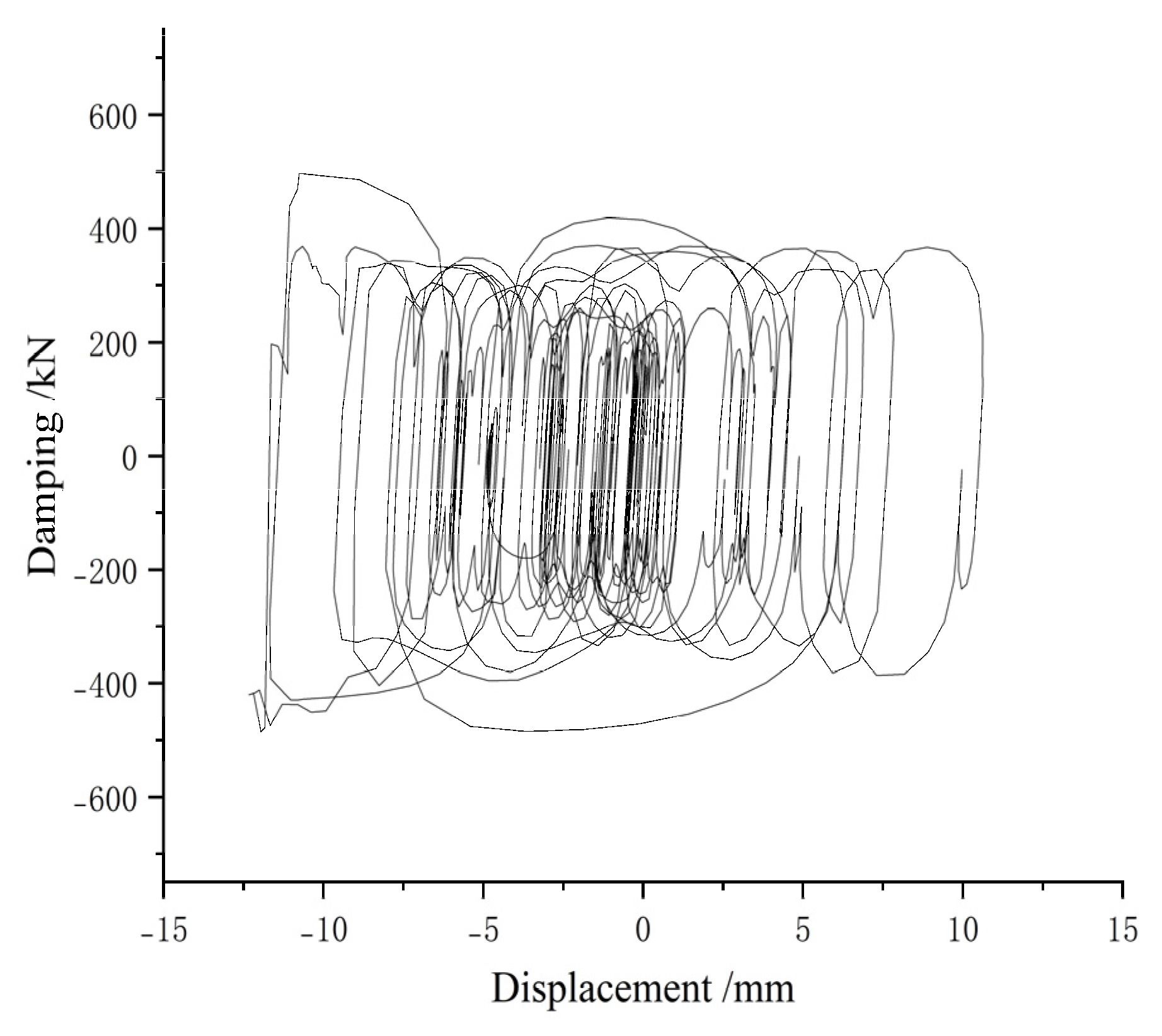
6.2. Energy Dissipation Characteristics of Viscous Dampers

During earthquakes, seismic energy is transferred through structural connections to viscous dampers, where it is absorbed and dissipated. This mechanism achieves the seismic design objectives of “economical performance under minor earthquakes, operational integrity under moderate earthquakes, and repairability under major earthquakes.” The energy dissipation mechanism of viscous dampers can be summarized through their energy distribution characteristics.

$$E_T=E_S+E_C+E_P+E_D$$

(6)

Here, $E_T$ = total seismic input energy; $E_S$ = mechanical energy of structural vibration; $E_C$ = energy dissipated by structural damping; $E_P$ = energy dissipated by structural inelastic deformation; and $E_D$ = energy dissipated by viscous dampers.

To illustrate the energy dissipation efficacy of viscous dampers, hysteretic curves under different connection configurations were randomly selected. Figure 15, Figure 16 and Figure 17 show the hysteretic curves of viscous dampers in the X direction under seismic loading. These curves exhibit a typical velocity-dependent energy dissipation process, characterized by irregular elliptical shapes with full hysteresis loops. This indicates that the dampers effectively dissipate energy, significantly attenuating the total seismic input energy and achieving robust vibration mitigation.

7. Discussion

Numerical simulations reveal that, in practical engineering applications, both herringbone and wall-mounted connections demonstrate superior seismic mitigation performance compared to diagonal bracings. However, these two connection types exhibit distinct characteristics. The chevron bracing, installed between upper- and lower-frame beams and connected to columns via steel braces, offers lightweight construction and excellent energy dissipation. In contrast, the wall-mounted connections employ two concrete walls with embedded steel plates and anchor bolts between frame beams, with viscous dampers installed in the pre-reserved mid-wall space. While this method provides convenient installation and effective energy dissipation, the self-weight of concrete walls in mid- to high-rise buildings introduces additional structural loads, adversely affecting seismic resistance.

A comparative analysis of the maximum inter-story drift values across different floors (

Table 6. Statistics of minimum value of maximum interlayer displacement.

Storey	Chevron Bracing	Wall-Mounted Connections
1–7	44.44%	55.56%
8–10	77.78%	22.22%

, Figure 18 and Figure 19) shows that for low-rise structures, wall-mounted connections yield slightly smaller drift values than chevron bracings, indicating marginally better performance. However, in mid- to high-rise buildings, chevron bracings exhibit significantly smaller drift values than floor height increases. This trend highlights the diminishing effectiveness of wall-mounted connections due to self-weight impacts, whereas chevron bracings demonstrate enhanced adaptability and superior energy dissipation in taller structures.

8. Conclusions

A numerical simulation study on the seismic mitigation performance of viscous dampers in a hospital building in Bazhou was conducted, analyzing three connection types: inclined rod, herringbone, and wall-mounted connections. The key conclusions are as follows:

(1)

Under identical seismic mitigation conditions, for frame structures similar to the hospital structure, both the herringbone and wall-mounted connections exhibit superior seismic reduction performance compared to the diagonal bracings. This is evidenced by the fact that under different seismic loads, the maximum inter-story drifts of structures employing herringbone and wall-mounted connections are consistently smaller than those using diagonal bracing connections.

(2)

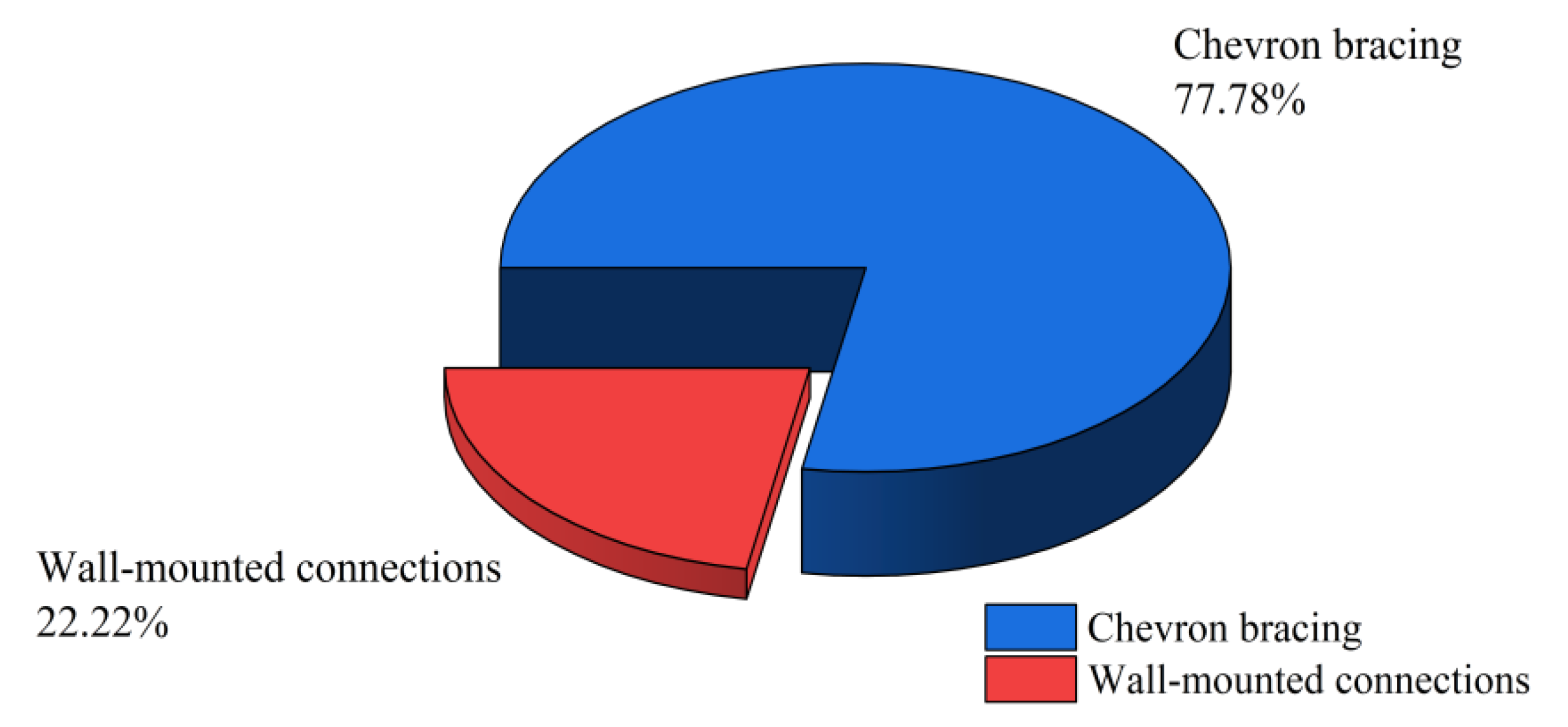
In terms of the applicability of connection types, the chevron bracings are suitable for medium-to-high-rise frame structures similar to the hospital structure, where its seismic reduction effect is more pronounced. While the wall-mounted connections demonstrate slightly better seismic performance than the chevron connection in low-rise frame structures of a similar type, their effectiveness is diminished in medium- to high-rise frame structures due to the influence of wall self-weight, resulting in less optimal seismic reduction compared to chevron bracings.

(3)

Energy Dissipation Mechanism: Viscous dampers effectively dissipate seismic energy, as evidenced by their velocity-dependent hysteretic curves. The hysteretic curves confirm robust energy absorption, validating their role in seismic mitigation.

In engineering practice, the selection of viscous damper connection types should consider building height and structural characteristics to optimize seismic performance. Numerical simulations reveal that, in practical engineering applications, both herringbone and wall-mounted connections demonstrate superior seismic mitigation performance.