Vibration Characteristics of Double-Shield TBM Cutterhead Under Rock–Machine Interaction Excitation
Abstract
1. Introduction
2. Project Overview and TBM Vibration Monitoring System Deployment
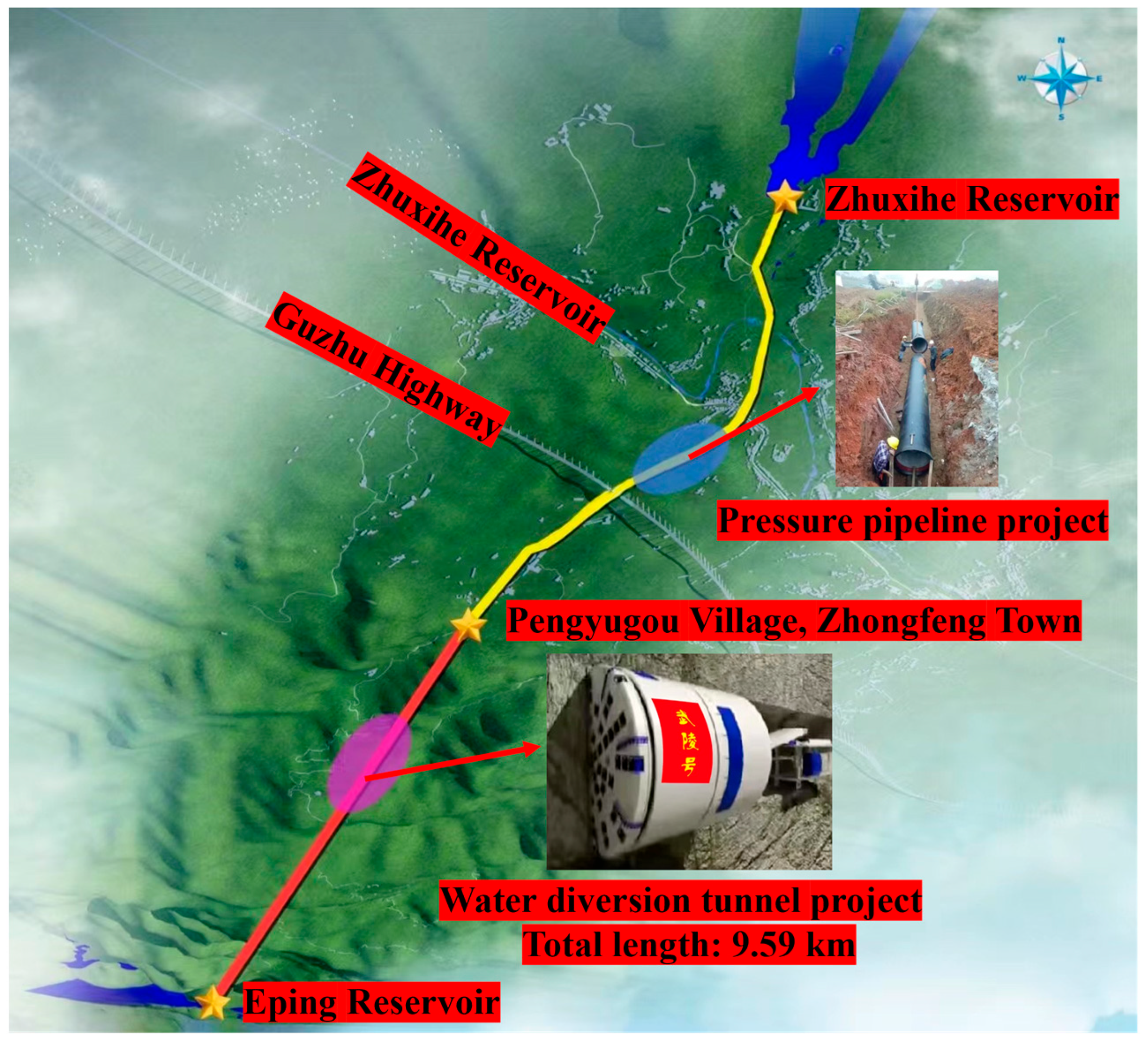
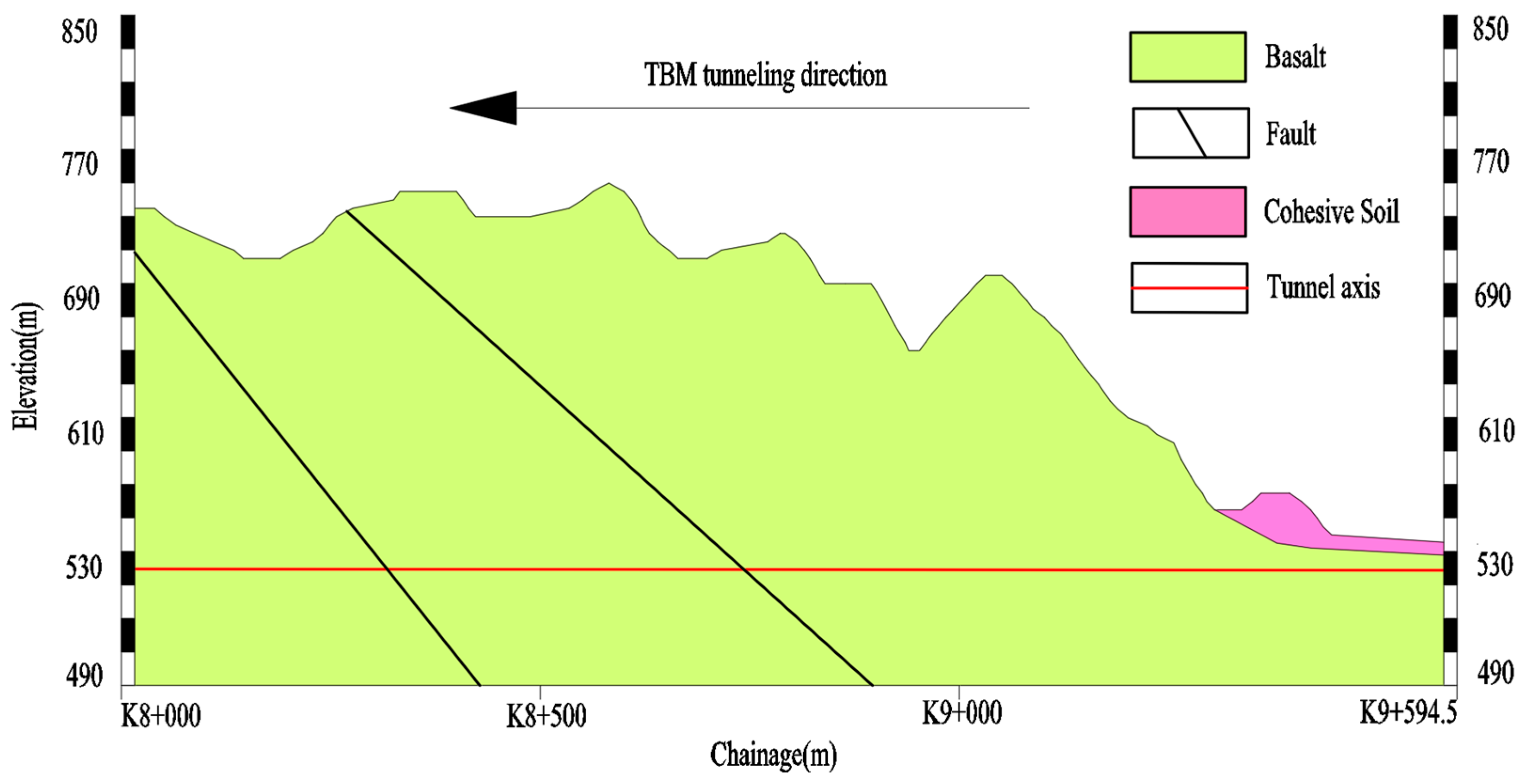
2.1. Project Overview
2.2. Double-Shield TBM
2.3. Deployment of the Double-Shield TBM Vibration Monitoring System
3. Vibration Signal Reconstruction and Feature Selection for Double-Shield TBM
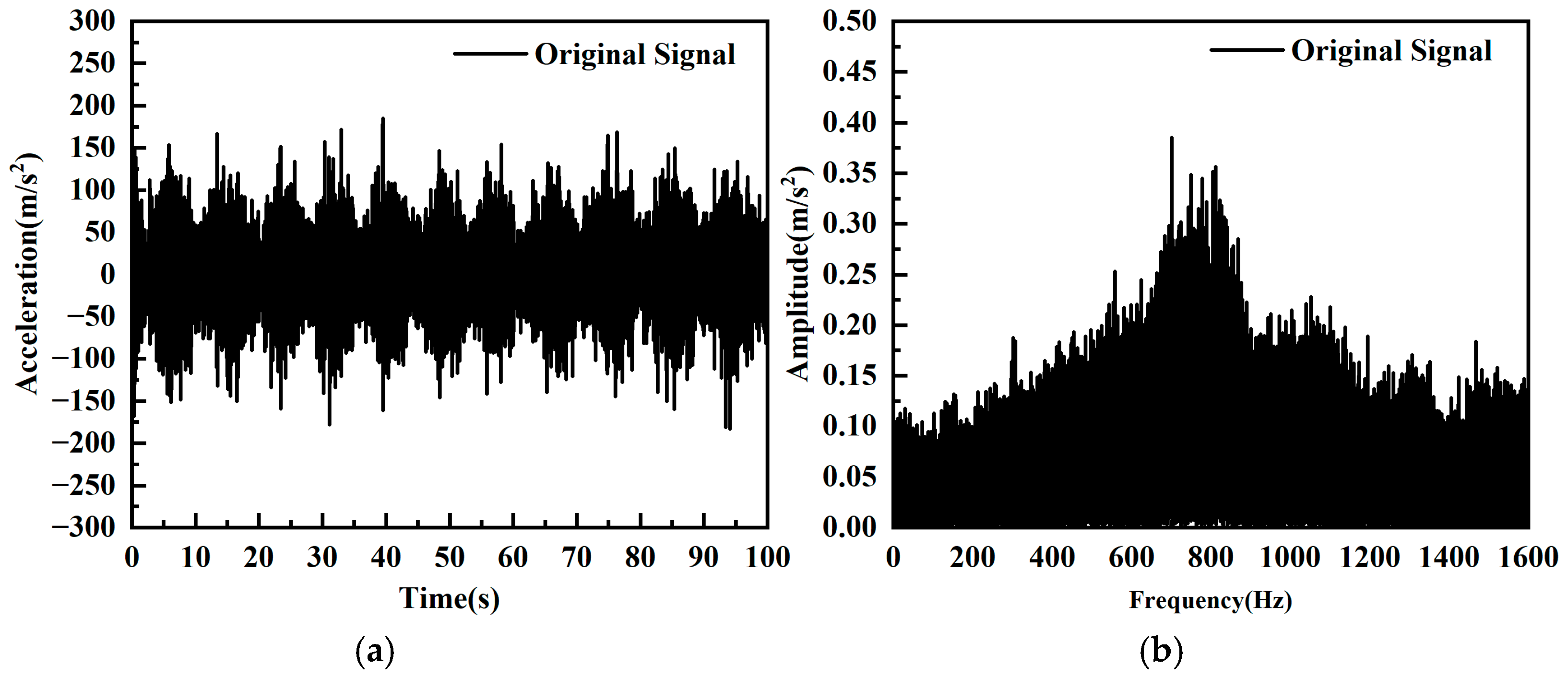
3.1. Acquisition of Vibration Signals
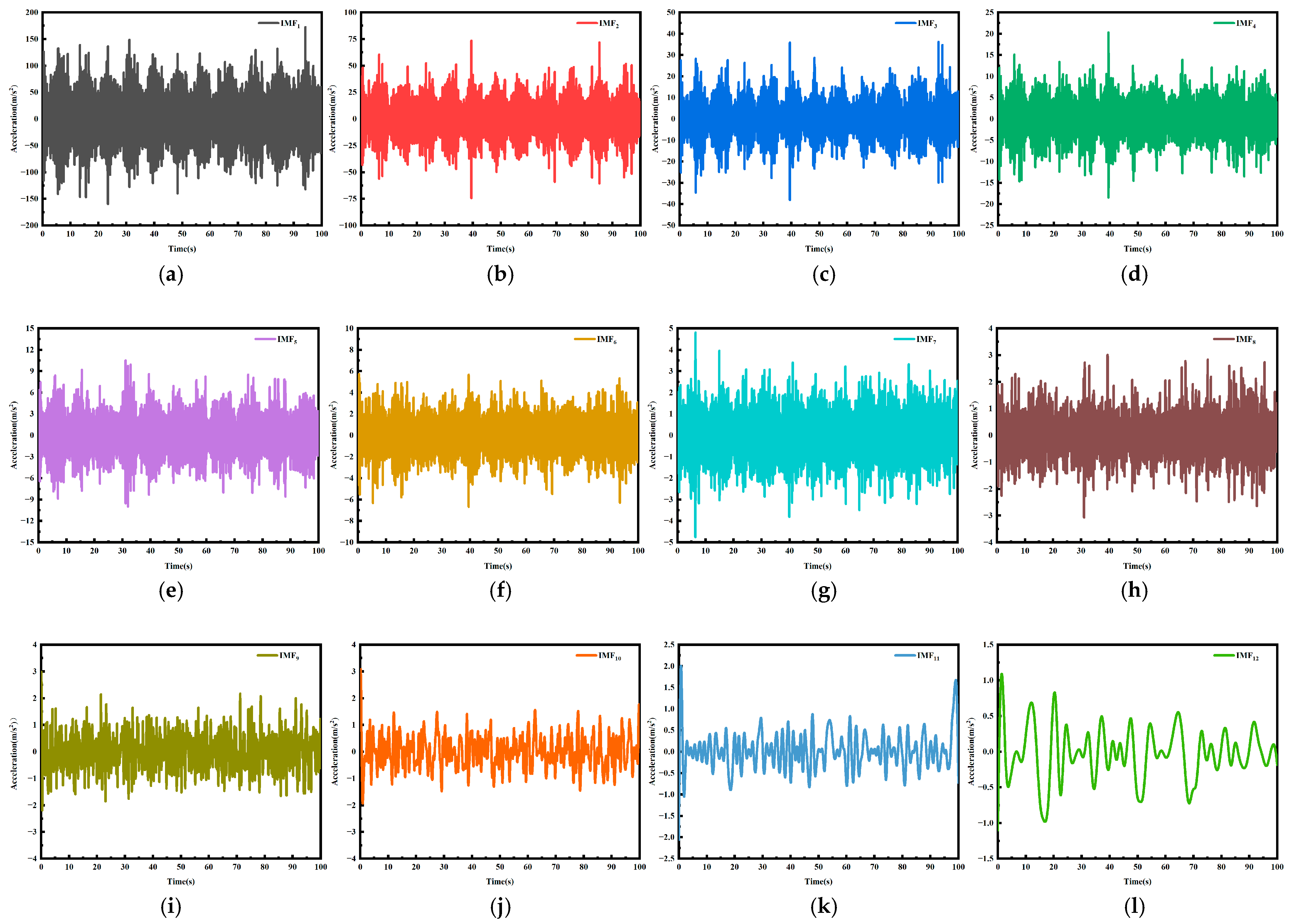
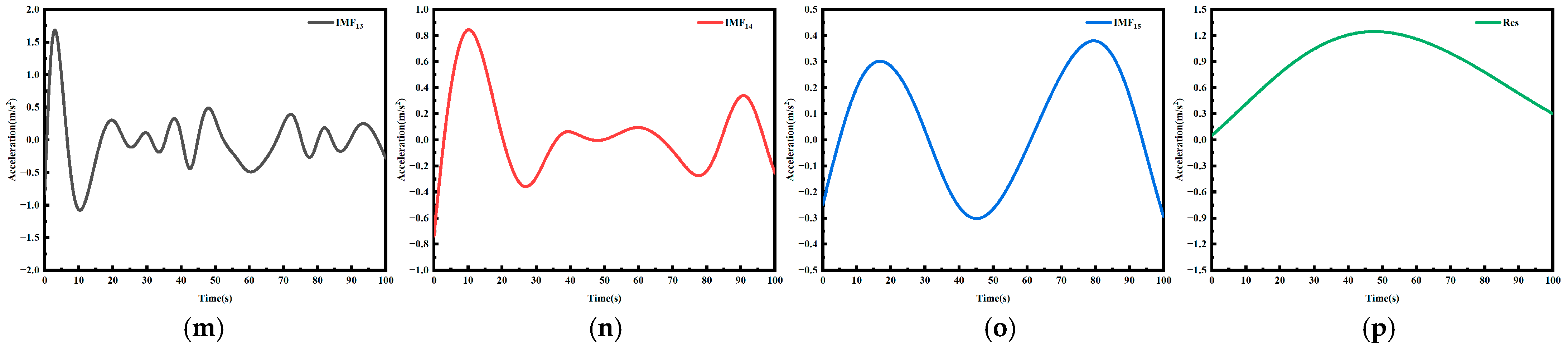
3.2. Empirical Mode Decomposition of Vibration Signals
3.3. Intrinsic Mode Function Screening and Processing
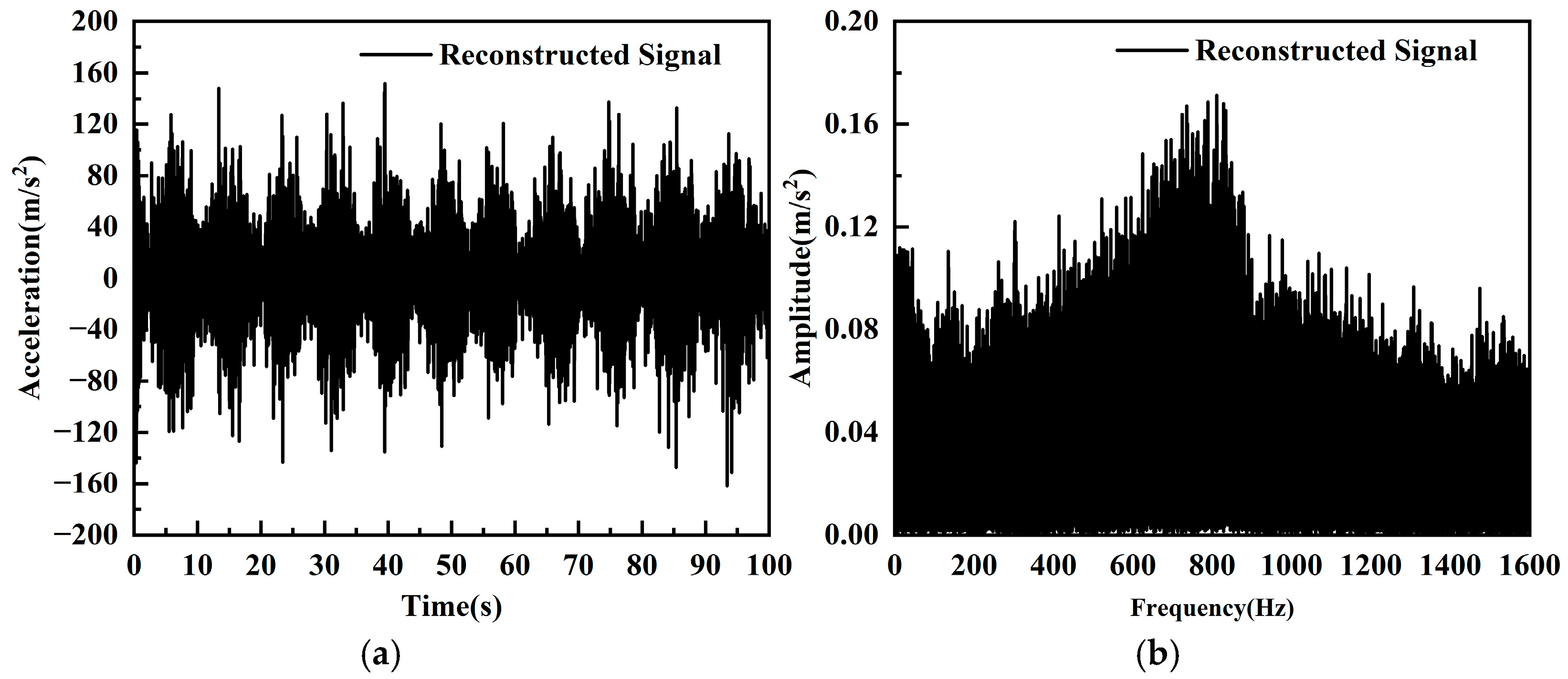
3.4. Vibration Signal Reconstruction and Feature Selection
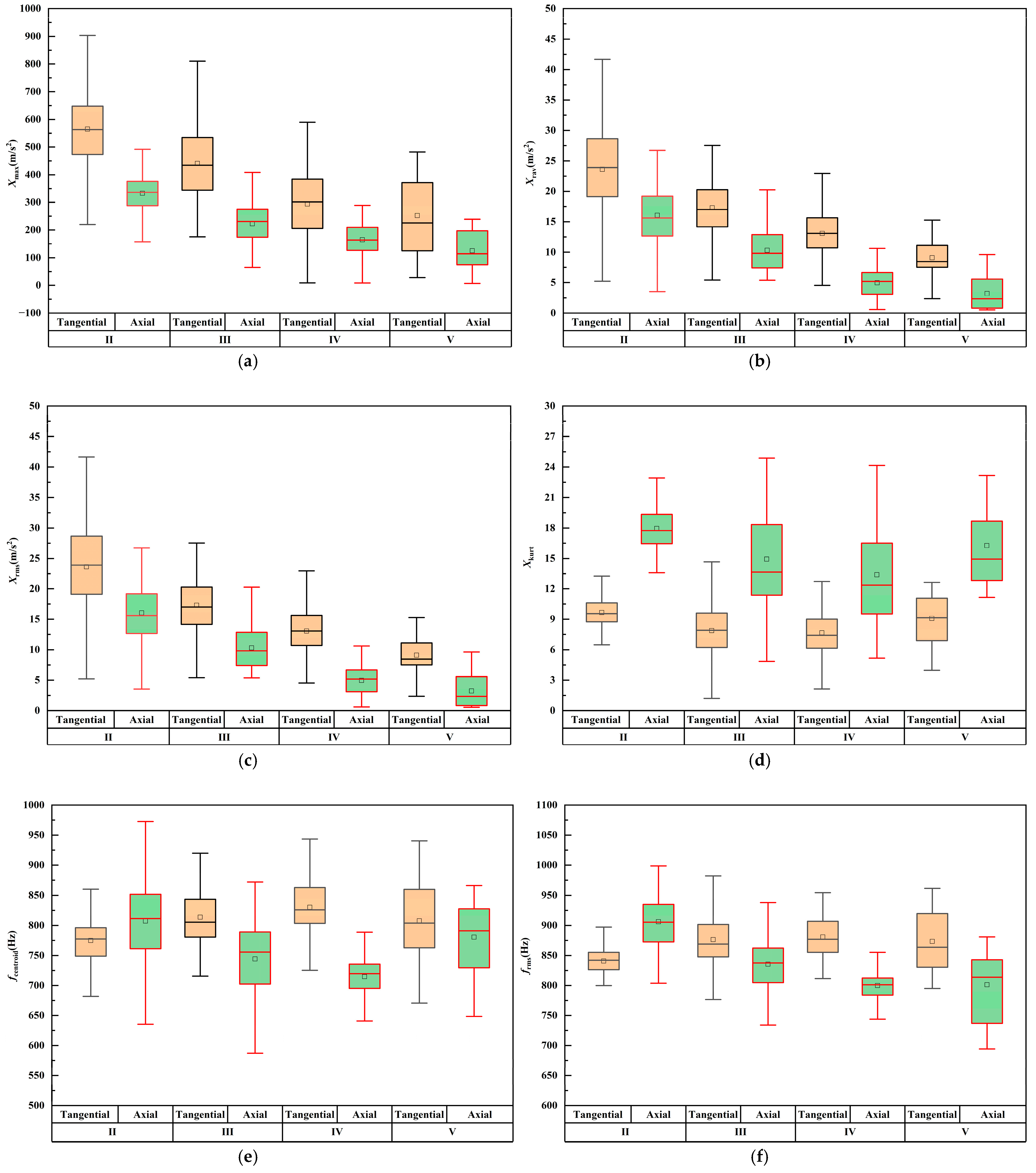
4. Vibration Characteristics of Double-Shield TBM Cutterhead
5. Analysis of Factors Influencing Vibration of Double-Shield TBM Cutterhead
5.1. Influence of Surrounding Rock Classes on Vibration of Double-Shield TBM Cutterhead
5.2. Influence of Tunneling Parameters on Vibration of Double-Shield TBM Cutterhead
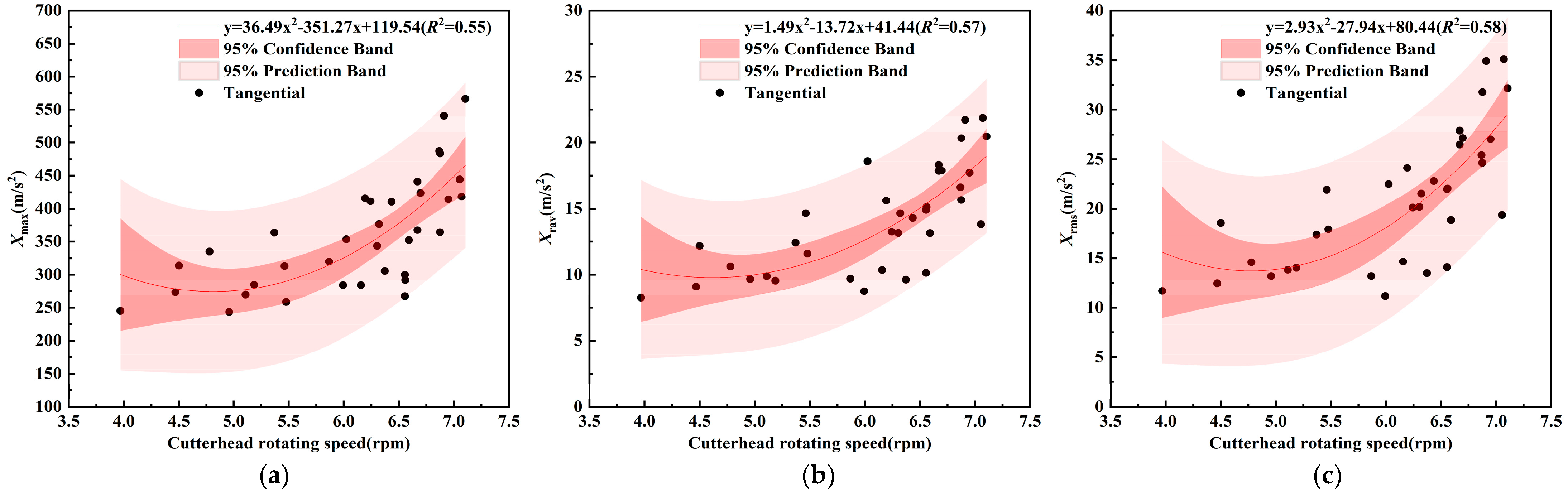
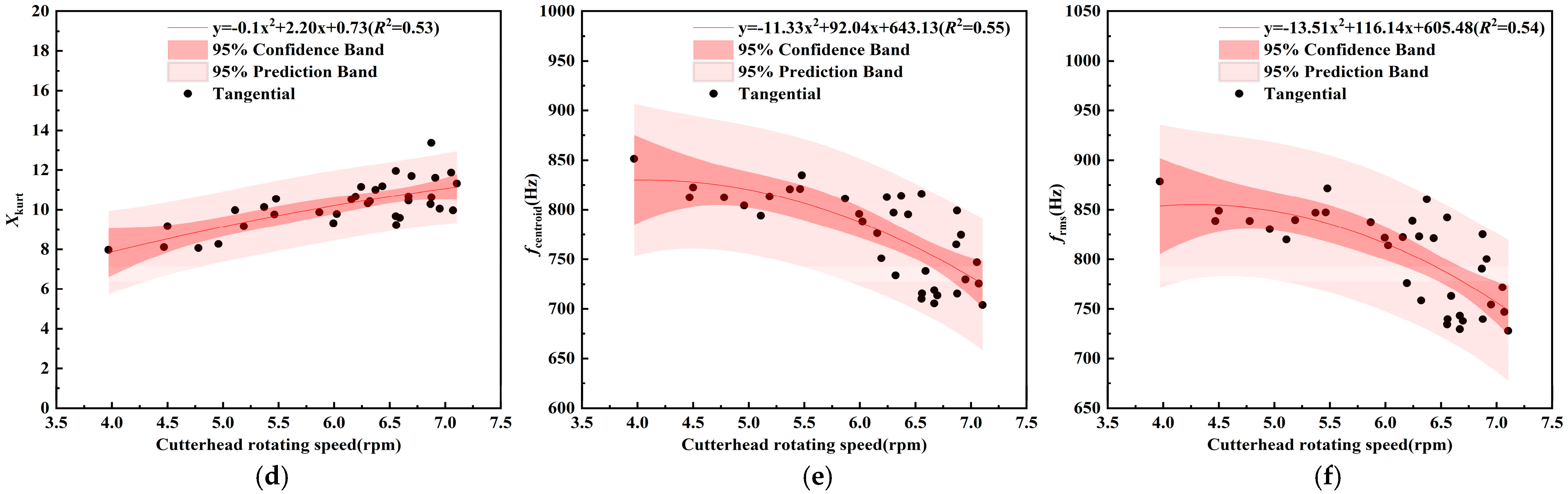
5.2.1. Influence of Cutterhead Rotational Speed on Vibration of Double-Shield TBM Cutterhead
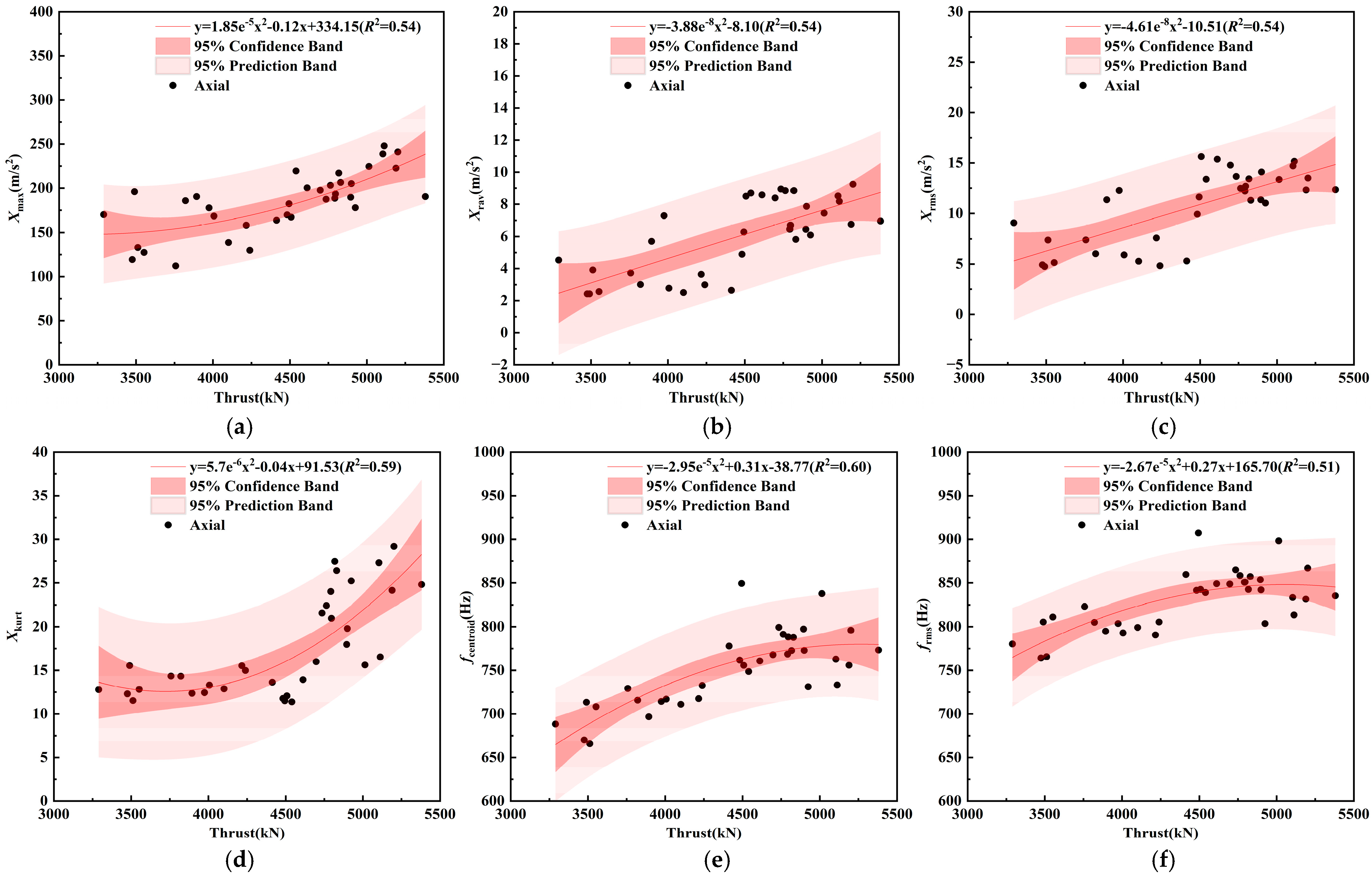
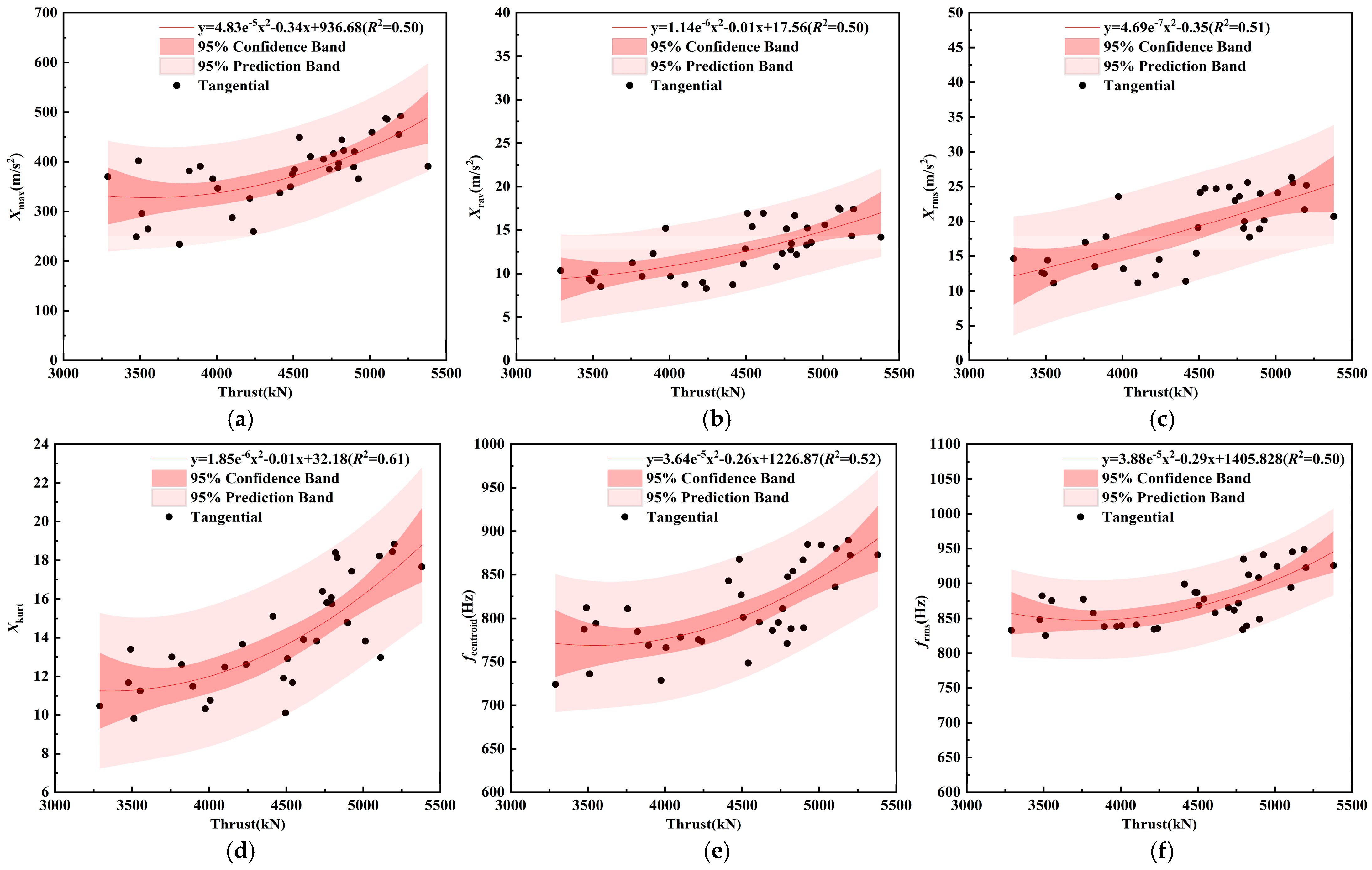
5.2.2. Influence of Thrust on Vibration of Double-Shield TBM Cutterhead
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, K.R.; Du, Y.L.; Chen, K.; Feng, H.H.; Jia, L.H.; Xu, F. Development history, achievements, and prospects of full-face tunnel boring machines in China. J. Tunn. Constr. 2022, 42, 739–756. [Google Scholar]
- Zhang, Z.H.; Song, C.N.; Li, Z. Analysis of vibration characteristics of TBM cutterhead under multi-point excitation. J. Mining Mach. 2020, 48, 1. [Google Scholar]
- Ling, J.X.; Sun, W.; Yang, X.J.; Tong, X. Analysis of vibration response of TBM cutterhead system under multi-point distributed loads. J. Eng. Des. 2017, 24, 317–322. [Google Scholar]
- Huo, J.Z.; Ouyang, X.Y.; Zhang, X.; Chen, J. The influence of front support on vibration behaviors of TBM cutterhead under impact heavy loads. J. Appl. Mech. Mater. 2014, 541, 641–644. [Google Scholar] [CrossRef]
- Sun, H.K.; Gao, Y. Dynamic cutting force model and vibration analysis of the cutterhead in TBM. J. Rock Mech. Rock Eng. 2023, 56, 7883–7903. [Google Scholar] [CrossRef]
- Zou, X.Y.; Heng, H.; Mi, Y.Z.; Xie, X. A study on vibration of tunnel boring machine and the induced shield tangential force. J. Vib. Eng. Technol. 2016, 4, 373–381. [Google Scholar]
- Xia, Y.M.; Ma, J.S.; Li, Z.G.; Mei, Y.B.; Ji, Z.Y. Influence of key structural parameters on the dynamic characteristics of main beam TBM. J. Vib. Shock 2020, 9, 193–201. [Google Scholar]
- Xia, Y.M.; Qian, C.; Li, Z.G.; Mei, Y.B. Vibration characteristics of the thrust and support system of tunnel boring machines. J. Zhejiang Univ. (Eng. Sci.) 2018, 52, 233–239. [Google Scholar]
- Zou, X.Y.; Mi, Y.Z.; Zheng, H. Vibration characteristics of hard rock tunnel boring machine based on field tests. J. Vib. Meas. Diagn. 2017, 37, 990–995. [Google Scholar]
- Liu, D.X.; Xiao, Y.H.; Zhou, X.X.; Gong, Q.M.; Liu, J.H. Research on vibration characterization parameters of TBM rock-breaking cutterhead. J. Mod. Tunn. Technol. 2023, 60, 153–162. [Google Scholar]
- Duan, Z.Y.; Gong, Q.M.; Wang, J.; Ma, H.S.; Huang, L.; Liu, D.X.; Peng, Z.Y. Analysis of influencing parameters on rock-breaking vibration of Beishan No. 1 TBM cutterhead. J. World Nucl. Geosci. 2024, 41, 805–816. [Google Scholar]
- Yang, Y.L.; Du, L.J.; Li, Q.W.; Wei, F.; Zhang, X.W.; Zhao, X.B.; Wang, Z.; Liu, Y. Vibration characteristics of TBM main beam under different surrounding rock and tunneling parameters. J. Vib. Shock 2023, 42, 88–97. [Google Scholar]
- Wu, F.; Gong, Q.M.; Li, Z.G.; Qiu, H.F.; Jin, C.; Huang, L.; Yin, L.J. Development and application of cutterhead vibration monitoring system for TBM tunnelling. Int. J. Rock Mech. Min. Sci. 2021, 146, 104887. [Google Scholar] [CrossRef]
- Ugur, A.; Hanifi, C. Investigation of parameters affecting vibration patterns generated during excavation by EPB TBMs. J. Tunn. Undergr. Space Technol. 2023, 138, 105185. [Google Scholar]
- Liu, M.B.; Liao, S.M.; Men, Y.Q.; Xing, H.T.; Liu, H.; Sun, L.Y. Field monitoring of TBM vibration during excavating changing stratum: Patterns and ground identification. Rock Mech. J. Rock Eng. 2022, 55, 1481–1498. [Google Scholar] [CrossRef]
- Tang, Q.S.; Gong, Q.M.; Liu, Y.; Guli, M.; Bieke, A.; Liu, S. Tunnel face rock mass class identification based on multi-domain feature extraction and selection of TBM cutterhead vibration signals. Int. J. Rock Mech. Min. Sci. 2025, 188, 106066. [Google Scholar] [CrossRef]
- Ma, H.W.; Zhang, D.W.; Cao, X.G.; Dong, M.; Li, C.H. Research on vibration signal denoising method based on EMD. J. Vib. Shock 2016, 35, 38–40. [Google Scholar]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. J. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. J. Adv. Adapt. Data Anal. 2010, 4, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics; Speech and Signal Processing, Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. J. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Li, R.; Fan, Y.G. Fault diagnosis of high-pressure diaphragm pump check valve based on CEEMDAN Multi-scale Permutation Entropy and SO-RELM. J. Vib. Shock 2023, 42, 127–135. [Google Scholar]
- Li, Z.L.; Tan, Z.S.; Zhou, Z.L.; Li, L.F.; Yang, Y.; Zheng, X.H. Research on surrounding rock parameter perception technology based on TBM vibration monitoring. J. Railw. Sci. Eng. 2025, 22, 1853–1869. [Google Scholar]
- GB 50487-2008; Code for Engineering Geological Investigation of Water Resources and Hydropower. China Planning Press: Beijing, China, 2009.
- Zheng, J.D.; Cheng, J.S.; Yang, Y. Improved EEMD algorithm and its application research. J. Vib. Shock 2013, 32, 21–26. [Google Scholar]







| Mounting Position | Range (G) | Resolution (bit) | Accuracy (mg·LSB⁻1) | Sampling Frequency (Hz) | Sampling Time (s) | Transmission Method | Shock Resistance (G) | Operating Temperature (°C) |
|---|---|---|---|---|---|---|---|---|
| Cutterhead | ±200 | 16 | ≤4 | 3200 | 120 | Wireless | 10,000 | −40~85 |
| IMF | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 |
|---|---|---|---|---|---|---|---|---|
| MPE | 0.9814 | 0.8914 | 0.7407 | 0.6405 | 0.5712 | 0.4880 | 0.4404 | 0.4137 |
| IMF | IMF9 | IMF10 | IMF11 | IMF12 | IMF13 | IMF14 | IMF15 | IMF16 |
| MPE | 0.4003 | 0.3932 | 0.3899 | 0.3880 | 0.3874 | 0.3868 | 0.3866 | 0.3863 |
| Characteristics | Xmax (m/s2) | Xrav (m/s2) | Xrms (m/s2) | Xkurt | fcentroid (Hz) | frms (Hz) |
|---|---|---|---|---|---|---|
| Original Signal | 184.71 | 13.96 | 19.90 | 3.68 | 802.58 | 871.95 |
| Reconstructed Signal | 161.45 | 6.16 | 10.97 | 15.10 | 724.40 | 818.59 |
| Reduction | 12.59% | 55.86% | 44.88% | −310.24% | 9.74% | 6.12% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Song, Q.; Gong, Q.; Liu, D.; Li, D.; Sun, M. Vibration Characteristics of Double-Shield TBM Cutterhead Under Rock–Machine Interaction Excitation. Buildings 2025, 15, 1824. https://doi.org/10.3390/buildings15111824
Zhang G, Song Q, Gong Q, Liu D, Li D, Sun M. Vibration Characteristics of Double-Shield TBM Cutterhead Under Rock–Machine Interaction Excitation. Buildings. 2025; 15(11):1824. https://doi.org/10.3390/buildings15111824
Chicago/Turabian StyleZhang, Guang, Qing Song, Qiuming Gong, Dongxing Liu, Dongwei Li, and Minghao Sun. 2025. "Vibration Characteristics of Double-Shield TBM Cutterhead Under Rock–Machine Interaction Excitation" Buildings 15, no. 11: 1824. https://doi.org/10.3390/buildings15111824
APA StyleZhang, G., Song, Q., Gong, Q., Liu, D., Li, D., & Sun, M. (2025). Vibration Characteristics of Double-Shield TBM Cutterhead Under Rock–Machine Interaction Excitation. Buildings, 15(11), 1824. https://doi.org/10.3390/buildings15111824





