Quantitative Evaluation of Water Vapor Permeability Coefficients of Earth Materials Under the Influence of Density and Particle Size Distribution
Abstract
1. Introduction
1.1. Background
1.2. Problem
1.3. Focus and Research Questions
2. Materials and Methods
2.1. Experimental Principle
2.2. Test Block Preparation
2.2.1. Earth Materials
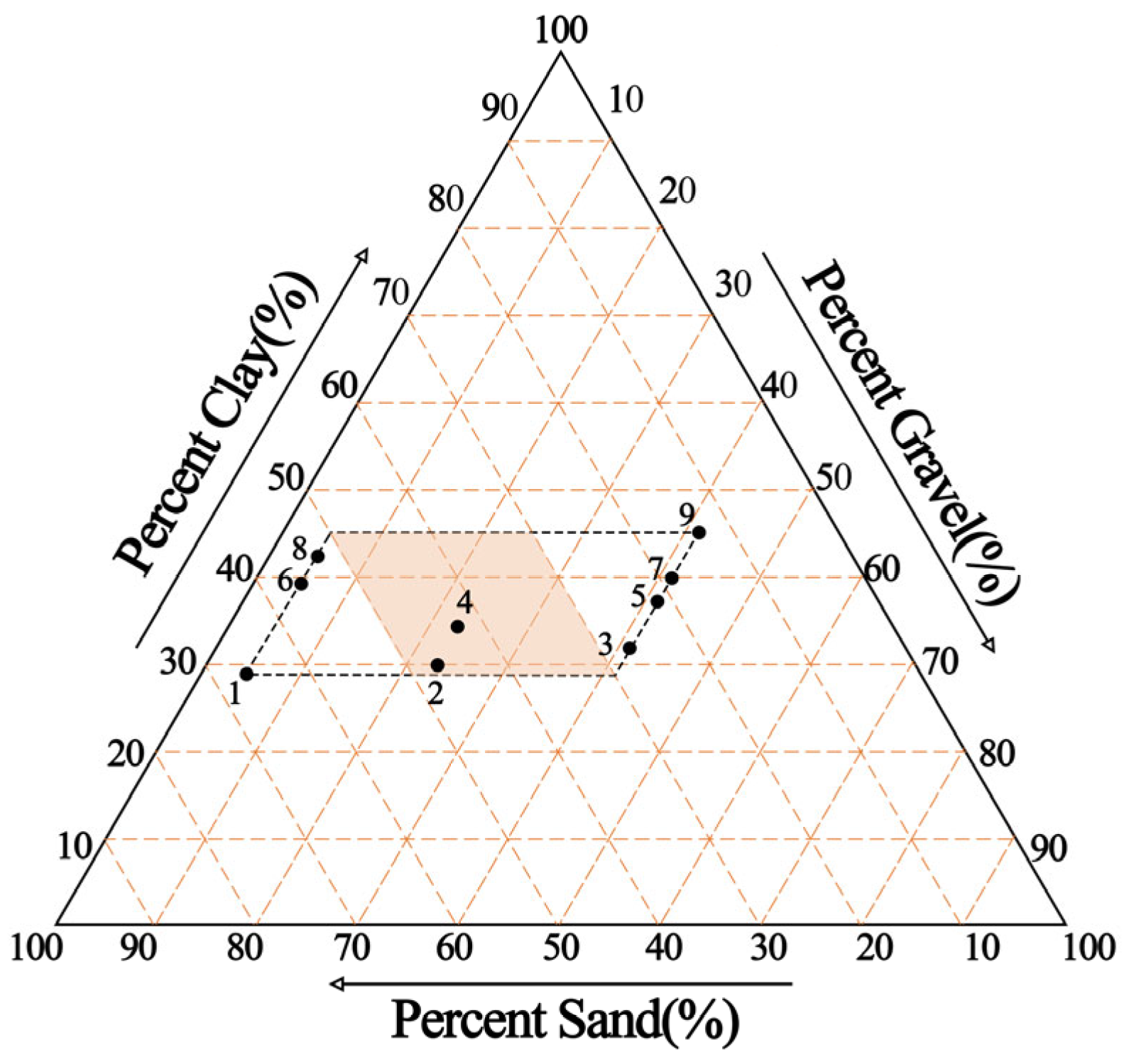
2.2.2. Test Block Gradation
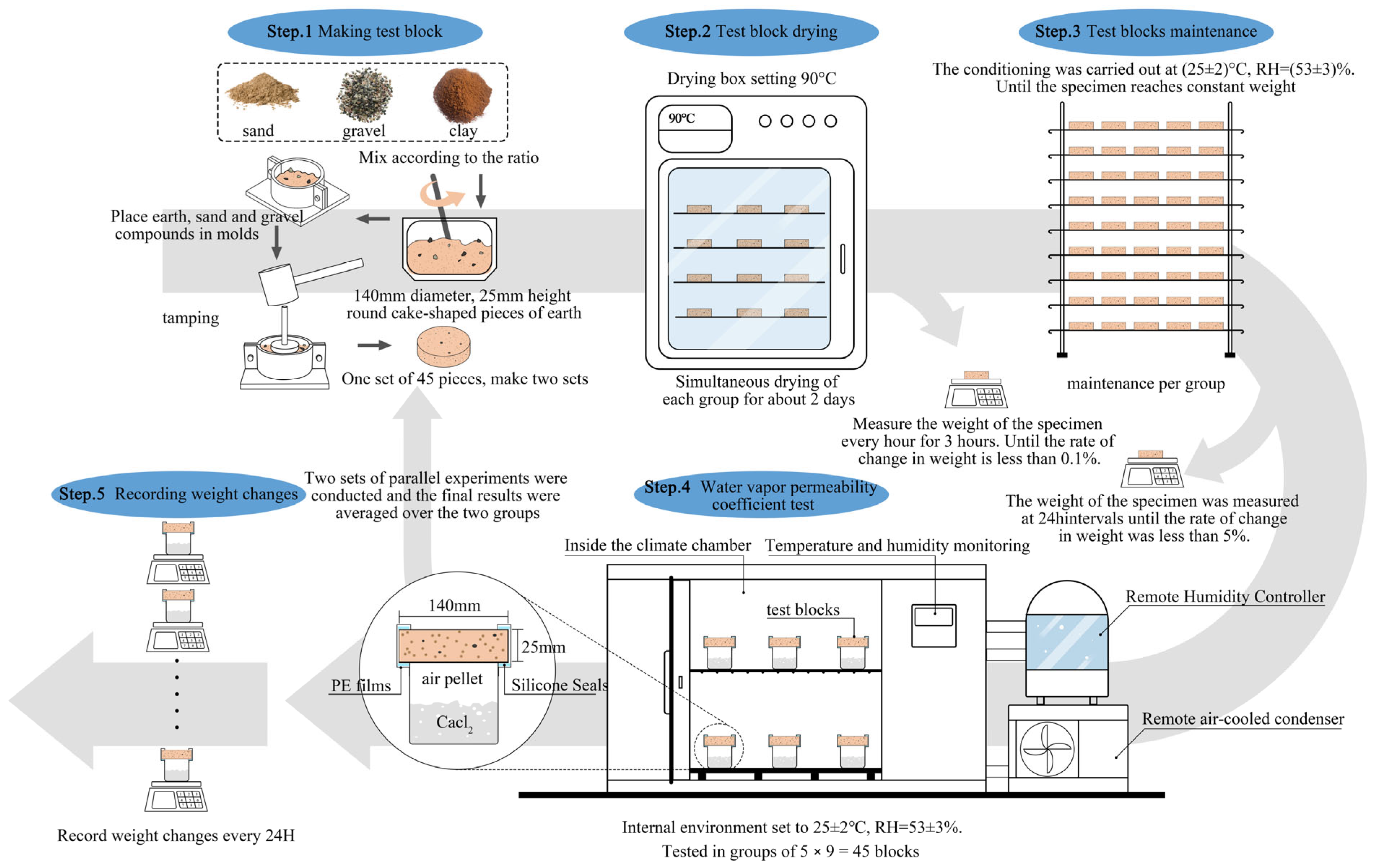
2.3. Making the Test Blocks
2.4. Experimental Methods
3. Mathematical Model of the Water Vapor Permeability Coefficient
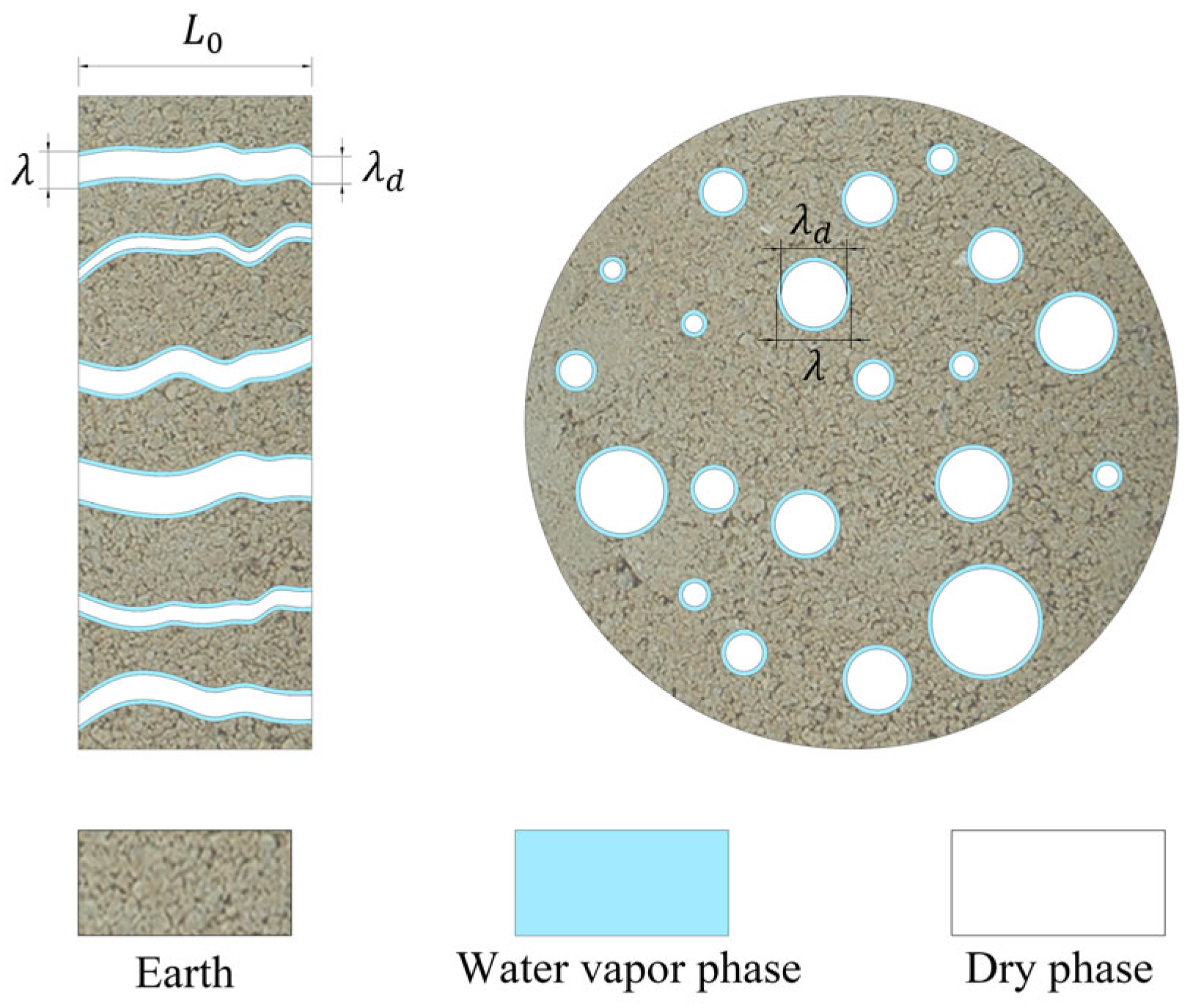
3.1. Fractal Theory
3.2. Mathematical Model Building
3.3. Calculation
4. Results and Discussion
4.1. Porosity Analysis of Earth Materials
4.2. Analysis of Water Vapor Permeability Coefficient of Earth Materials
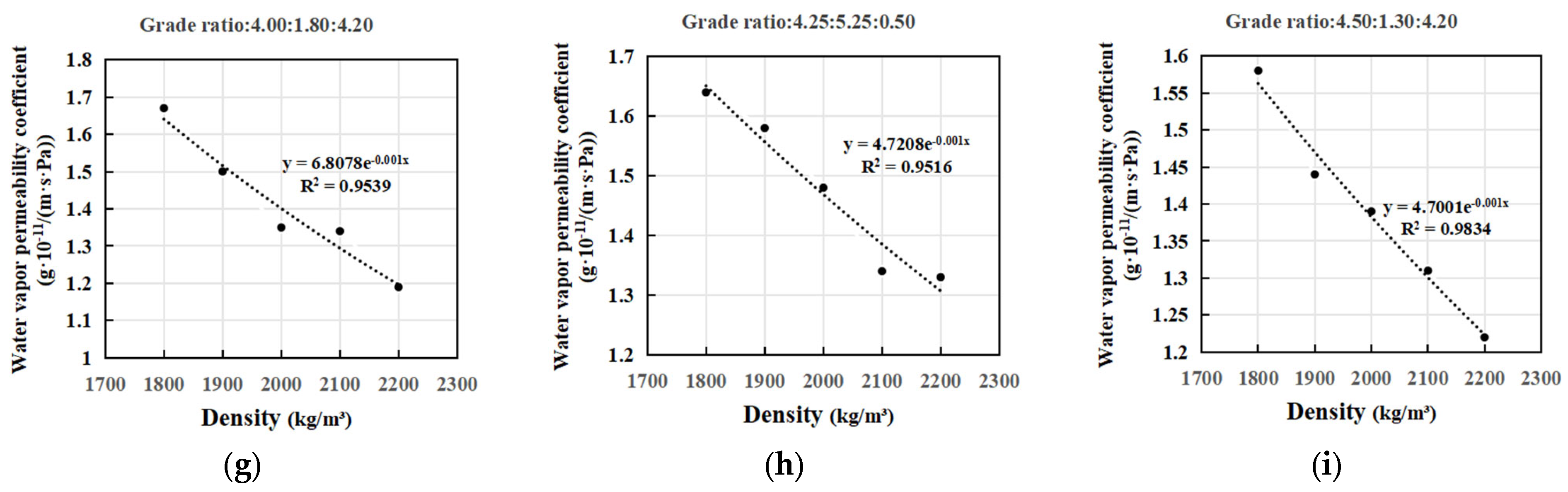
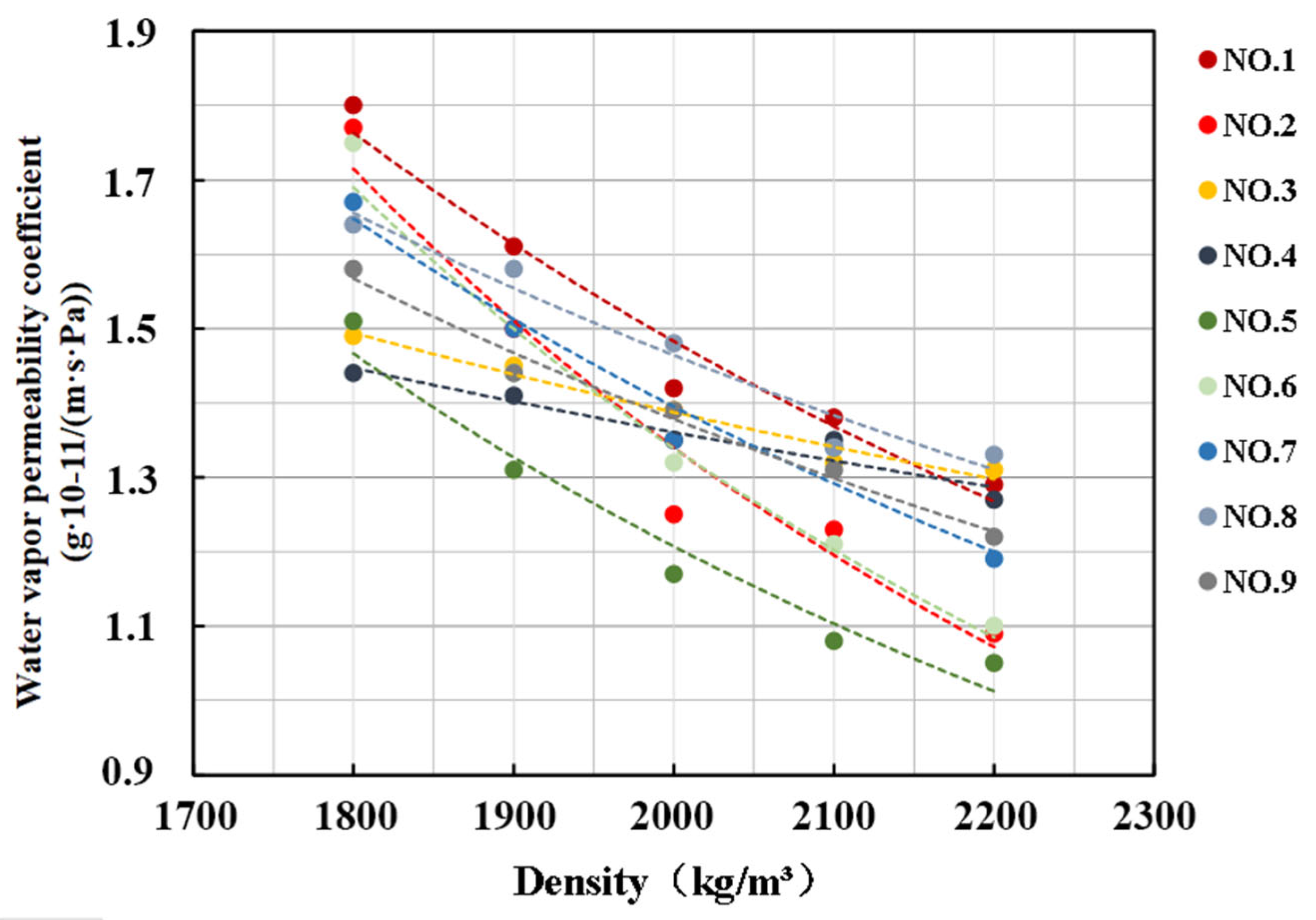
4.2.1. Water Vapor Permeability Coefficient Experimental Results
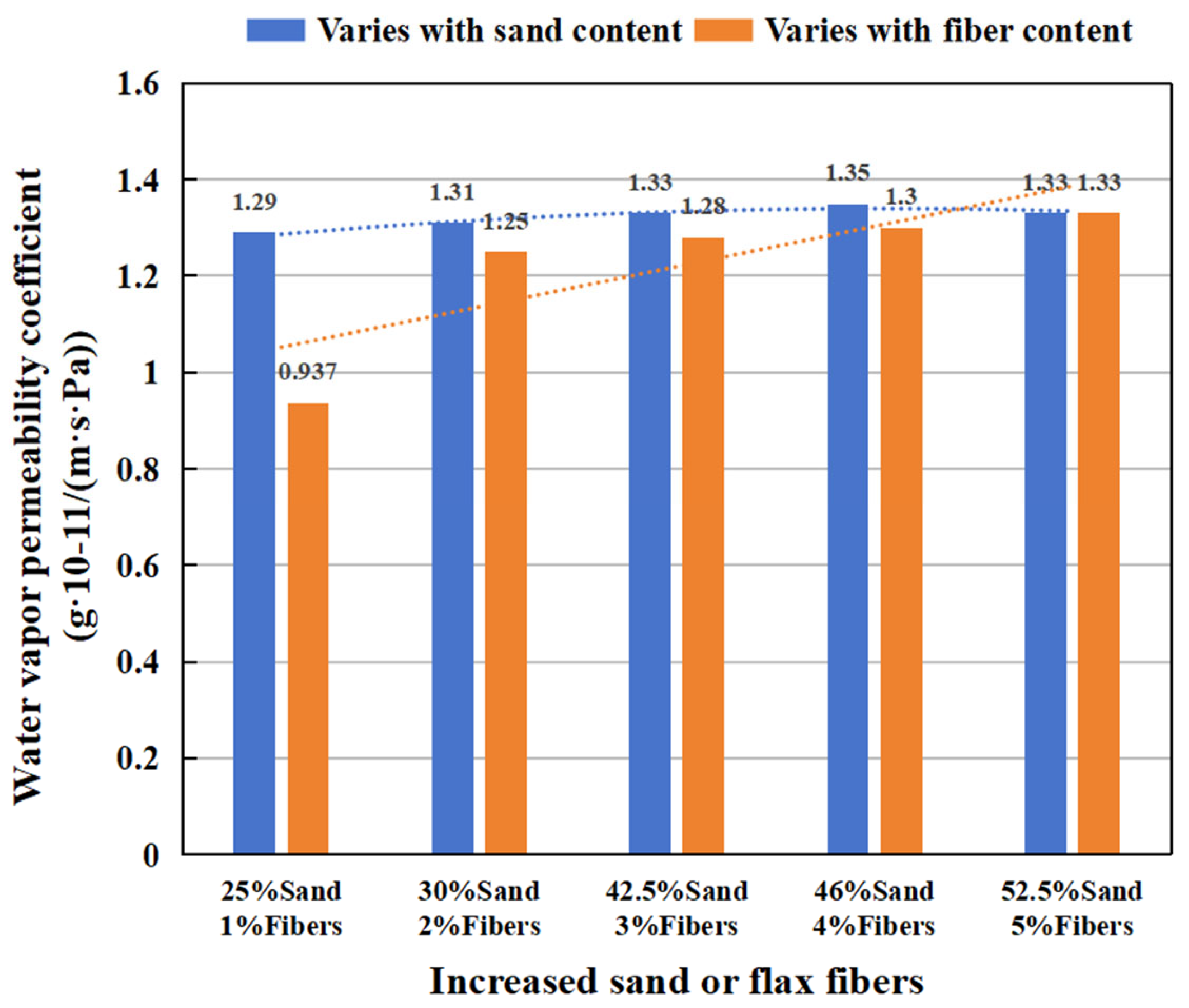
4.2.2. Comparison of Earth Materials with Flax Fibers
4.3. Validation of the Mathematical Model
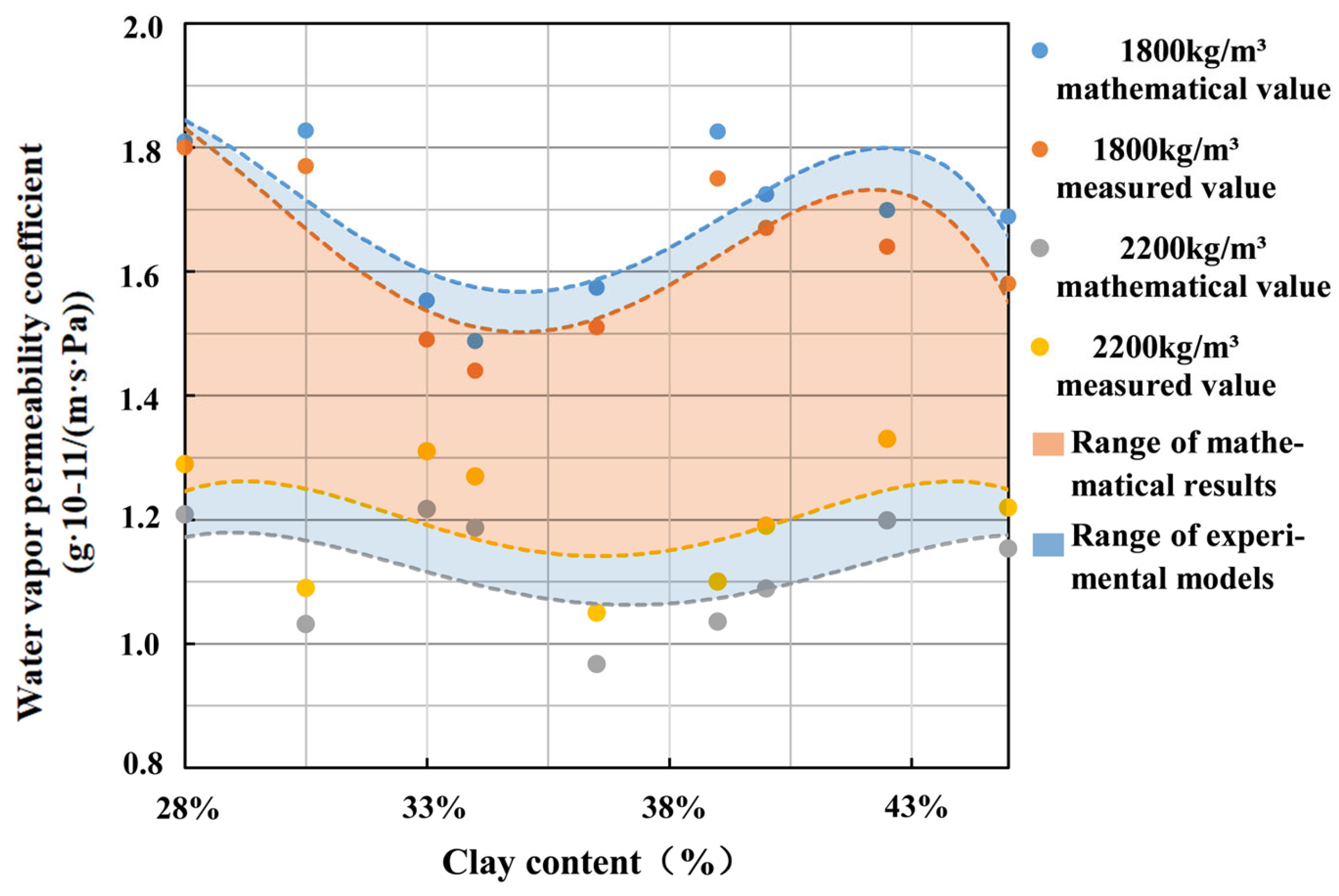
4.3.1. Error Analysis of the Mathematical Results and Experimental Results
4.3.2. Correction of the Mathematical Model
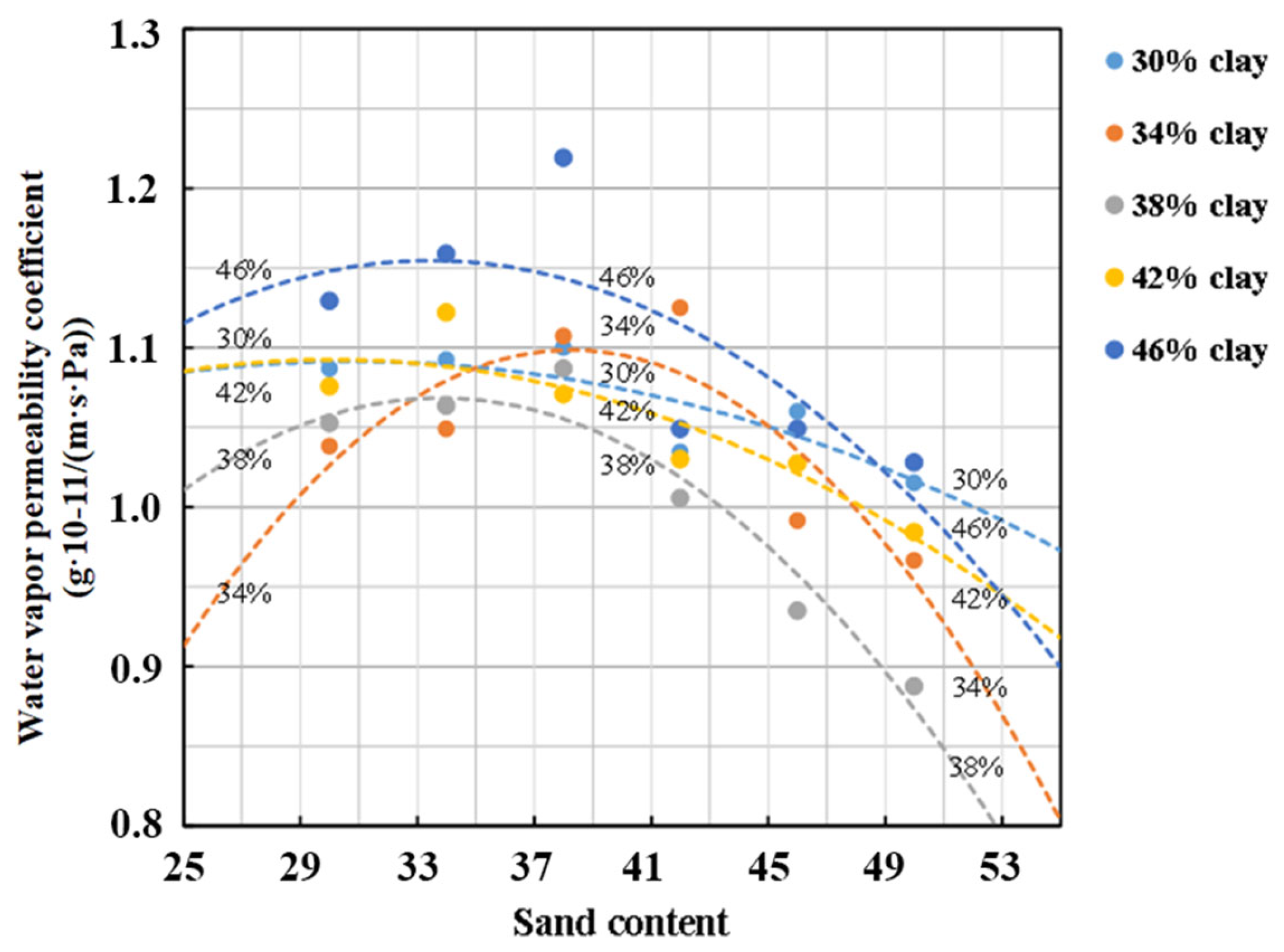
4.4. Effects of Density and Gradation on the Water Vapor Permeability Coefficient
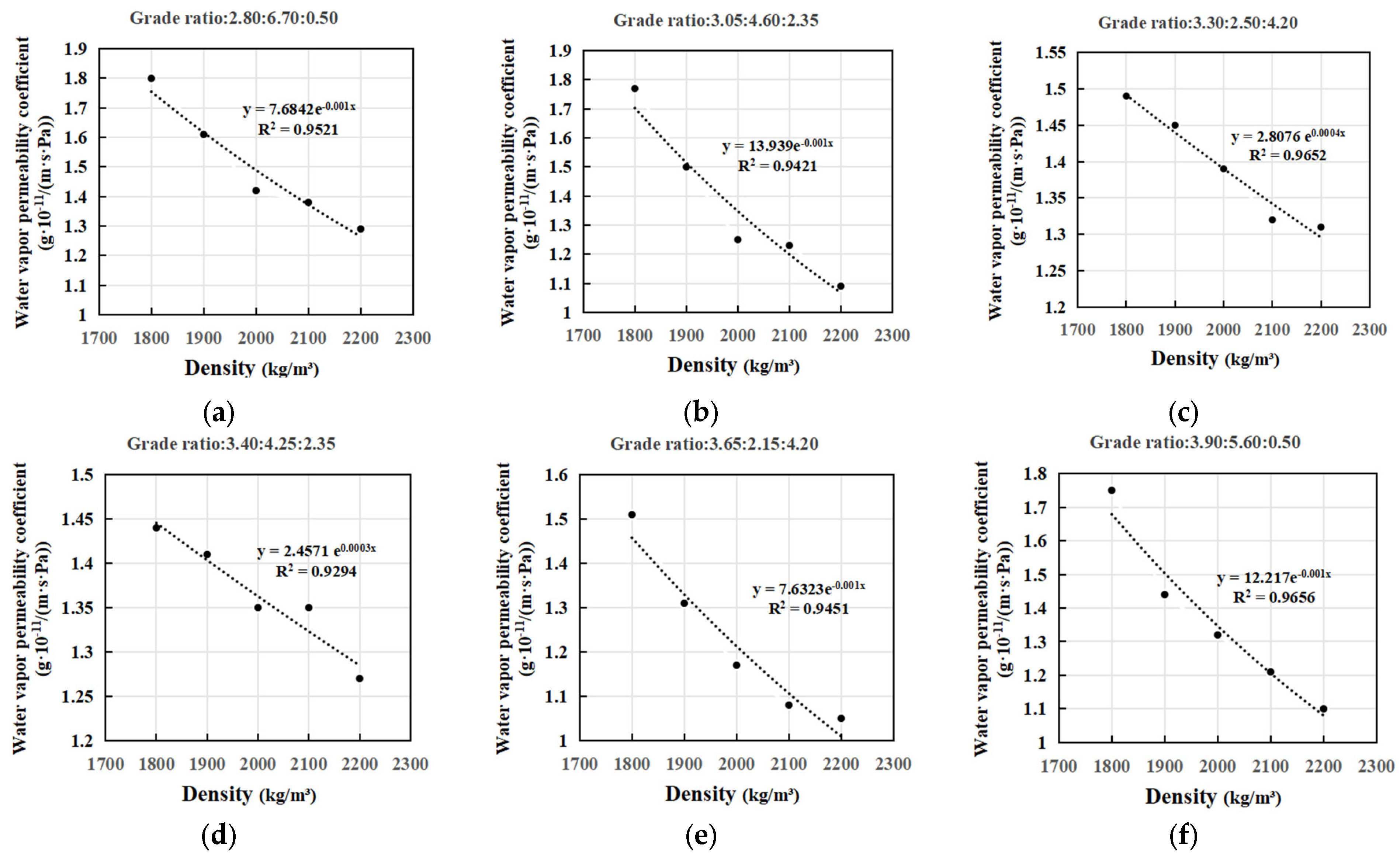
4.4.1. Effect of Density
4.4.2. Effect of Gradation
5. Conclusions
- The water vapor permeability coefficient of earth materials is influenced by both density and clay–sand gradation.
- Utilizing fractal theory, a model was developed to predict the water vapor permeability coefficient of earth materials. By comparing and analyzing the experimental data with the calculated data, the model was further refined, and the final average prediction error was approximately 1.3%.
- The impacts of clay, sand, and gravel contents on the water vapor permeability coefficient of earth materials were analyzed. The results indicate that as the clay content increases from 30% to 38%, the water vapor permeability continuously decreases. However, when the clay content increases from 38% to 46%, the water vapor permeability begins to increase. For sand content ranging from 30% to 38%, the water vapor permeability increases as the sand content increases. Nevertheless, when the sand content exceeds 42%, the water vapor permeability decreases with the increase in sand content.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Loli, A.; Bertolin, C. Towards Zero-Emission Refurbishment of Historic Buildings: A Literature Review. Buildings 2018, 8, 22. [Google Scholar] [CrossRef]
- Schroeder, H. Structures Built of Earth Building Materials—Impacts, Structural Damage and Preservation; Springer: Berlin/Heidelberg, Germany, 2016; pp. 393–503. [Google Scholar] [CrossRef]
- Champire, F.; Fabbri, A.; Morel, J.C.; Wong, H.; McGregor, F. Impact of Relative Humidity on The Mechanical Behavior of Compacted Earth as a Building Material. Constr. Build. Mater. 2016, 110, 70–78. [Google Scholar] [CrossRef]
- Cagnon, H.; Aubert, J.E.; Coutand, M.; Magniont, C. Hygrothermal Properties of Earth Bricks. Energy Build. 2014, 80, 208–217. [Google Scholar] [CrossRef]
- Allinson, D.; Hall, M. Hygrothermal Analysis of a Stabilised Rammed Earth Test Building in the UK. Energy Build. 2010, 42, 845–852. [Google Scholar] [CrossRef]
- Ávila, F.; Puertas, E.; Gallego, R. Characterization of the Mechanical and Physical Properties of Unstabilized Rammed Earth: A Review. Constr. Build. Mater. 2020, 270, 121435. [Google Scholar] [CrossRef]
- Hall, M.; Allinson, D. Assessing the Effects of Soil Grading on the Moisture Content-Dependent Thermal Conductivity of Stabilised Rammed Earth Materials. Appl. Therm. Eng. 2009, 29, 740–747. [Google Scholar] [CrossRef]
- Hall, M.; Allinson, D. Analysis of the Hygrothermal Functional Properties of Stabilised Rammed Earth Materials. Build. Environ. 2009, 44, 1935–1942. [Google Scholar] [CrossRef]
- McGregor, F.; Heath, A.; Shea, A.; Lawrence, M. The Moisture Buffering Capacity of Unfired Clay Masonry. Build. Environ. 2014, 82, 599–607. [Google Scholar] [CrossRef]
- Minke, G. Building with Earth: Design and Technology of a Sustainable Architecture; Birkhäuser: Basel, Switzerland, 2013. [Google Scholar]
- Allinson, D.; Hall, M. Humidity Buffering Using Stabilised Rammed Earth Materials. Proc. Inst. Civ. Eng.-Constr. Mater. 2012, 165, 335–344. [Google Scholar] [CrossRef]
- Galán-Marín, C.; Rivera-Gómez, C.; Petric, J. Clay-Based Composite Stabilized with Natural Polymer and Fibre. Constr. Build. Mater. 2010, 24, 1462–1468. [Google Scholar] [CrossRef]
- Hibouche, A. Sol Traités Aux Liants: Performances Hydro-Mécaniques et Hygro-Thermiques: Application en BTP. Ph.D. Thesis, 2013. Available online: http://www.theses.fr/2013LEHA0023 (accessed on 5 November 2023).
- Adam, E.A.; Jones, P.J. Thermophysical Properties of Stabilised Soil Building Blocks. Build. Environ. 1995, 30, 245–253. [Google Scholar] [CrossRef]
- Sindanne, S.A.; Ntamack, G.E.; Sanga, R.P.L.; Moubeke, C.A.; Sallaboui, E.S.K.; Bouabid, H.; Mansouri, K.; D’ouazzane, S.C. Thermophysical Characterization of Earth Blocks Stabilized by Cement, Sawdust and Lime. J. Build. Mater. Struct. 2014, 1, 58–64. [Google Scholar] [CrossRef]
- Dondi, M.; Principi, P.; Raimondo, M.; Zanarini, G. Water Vapour Permeability of Clay Bricks. Constr. Build. Mater. 2003, 17, 253–258. [Google Scholar] [CrossRef]
- Fabbri, A.; Soudani, L.; McGregor, F.; Morel, J.-C. Analysis of the Water Absorption Test to Assess the Intrinsic Permeability of Earthen Materials. Constr. Build. Mater. 2019, 199, 154–162. [Google Scholar] [CrossRef]
- Chinese National Standard GB/T 21650.1-2008; Determination of Pore Size Distribution and Porosity of Solid Materials by Mercury Intrusion and Gas Adsorption—Part 1: Mercury Intrusion Method. Standards Press of China: Beijing, China, 2008.
- CEN/ISO. NF EN ISO 5167-4; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-section Conduits Running Full—Part 4: Criteria for Practice. European Committee for Standardization: Brussels, Belgium, 2022.
- Musa, H.H.; Hussein, A.M.; Hanoon, A.N.; Hason, M.M.; Abdulhameed, A.A. Phases of Urban Development Impact on the Assessment of Thermal Comfort: A Comparative Environmental Study. Civ. Eng. J. 2022, 8, 951–966. [Google Scholar] [CrossRef]
- Houben, H.; Guillard, H. Earth Construction; Intermediate Technology Publications: Rugby, UK, 1989. [Google Scholar] [CrossRef]
- Bourlieu, C.; Guillard, V.; Vallès-Pamiès, B.; Guilbert, S.; Gontard, N. Edible Moisture Barriers: How to Assess of Their Potential and Limits in Food Products Shelf-Life Extension? Crit. Rev. Food Sci. Nutr. 2009, 49, 474–499. [Google Scholar] [CrossRef]
- Yu, B.; Lee, L.J.; Cao, H. Factal Characters of Pore Microstructures of Textile Fabrics. Fractals 2001, 09, 155–163. [Google Scholar] [CrossRef]
- Xu, P.; Qiu, S.; Yu, B.; Jiang, Z. Prediction of Relative Permeability in Unsaturated Porous Media with a Fractal Approach. Int. J. Heat Mass Transf. 2013, 64, 829–837. [Google Scholar] [CrossRef]
- Yu, B.; Li, J.; Li, Z.; Zou, M. Permeabilities of Unsaturated Fractal Porous Media. Int. J. Multiph. Flow 2003, 29, 1625–1642. [Google Scholar] [CrossRef]
- Wheatcraft, S.W.; Tyler, S.W. An Explanation of Scale-Dependent Dispersivity in Heterogeneous Aquifers Using Concepts of Fractal Geometry. Water Resour. Res. 1988, 24, 566–578. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. A Geometry Model for Tortuosity of Flow Path in Porous Media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. Some Fractal Characters of Porous. Media 2001, 09, 365–372. [Google Scholar] [CrossRef]
- Denn, M.M. Polymer Melt Processing; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Tian, S.-Q.; Wang, K.; Fan, L.-W.; Yu, Z.-T.; Ge, J. Effects of Sample Length on the Transient Measurement Results of Water Vapor Diffusion Coefficient of Porous Building Materials: A Case Study of Autoclave Aerated Concrete (AAC) with Various Porosities. Int. J. Heat Mass Transf. 2019, 135, 209–219. [Google Scholar] [CrossRef]
- Zhang, L.; Sang, G.C.; Cui, X.L.; Han, W.X.; Guo, X.N. Hygrothermal Properties of Cement Stabilized Earth Material and Both Temperature and Relative Humidity Distribution of Wall under Periodic Boundary Conditions. J. Xi’an Univ. Technol. 2022, 38, 1. [Google Scholar] [CrossRef]
- Hamrouni, I.; Ouahbi, T.; El Hajjar, A.; Taibi, S.; Jamei, M.; Zenzri, H. Water Vapor Permeability of Flax Fibers Reinforced Raw Earth: Experimental and Micro-Macro Modeling. Eur. J. Environ. Civ. Eng. 2022, 27, 3020–3039. [Google Scholar] [CrossRef]






| Particle Size Range (mm) | Clay ≤0.005 | Silt 0.005~0.08 | Sand 0.08~2 | Gravel 2~10 |
|---|---|---|---|---|
| Percentage (%) | 66.85 | 24.91 | 7.59 | 0.65 |
| Sample Address | Liquidity Index | Liquid Limit (%) | Plastic Limit (%) | Plastic Index | Classification |
|---|---|---|---|---|---|
| Ruhei Village | <0.25 | 70.1 | 45.1 | 24.6 | High liquid Mit (MHR) |
| NO. | Grade Ratio (a:b:c) | Mass Ratios (a:b:c) | ||||
|---|---|---|---|---|---|---|
| 1800 (kg/m3) | 1900 (kg/m3) | 2000 (kg/m3) | 2100 (kg/m3) | 2200 (kg/m3) | ||
| 1 | 2.80:6.70:0.50 | 1.13:2.71:0.20 | 1.20:2.86:0.21 | 1.20:2.86:0.21 | 1.20:2.86:0.21 | 1.20:2.86:0.21 |
| 2 | 3.05:4.60:2.35 | 1.24:1.86:0.95 | 1.30:1.97:1.00 | 1.30:1.97:1.00 | 1.30:1.97:1.00 | 1.30:1.97:1.00 |
| 3 | 3.30:2.50:4.20 | 1.34:1.01:1.70 | 1.41:1.07:1.80 | 1.41:1.07:1.80 | 1.41:1.07:1.80 | 1.41:1.07:1.80 |
| 4 | 3.40:4.25:2.35 | 1.38:1.72:0.95 | 1.45:1.82:1.00 | 1.45:1.82:1.00 | 1.45:1.82:1.00 | 1.45:1.82:1.00 |
| 5 | 3.65:2.15:4.20 | 1.48:0.87:1.70 | 1.56:0.92:1.80 | 1.56:0.92:1.80 | 1.56:0.92:1.80 | 1.56:0.92:1.80 |
| 6 | 3.90:5.60:0.50 | 1.58:2.27:0.20 | 1.67:2.39:0.21 | 1.67:2.39:0.21 | 1.67:2.39:0.21 | 1.67:2.39:0.21 |
| 7 | 4.00:1.80:4.20 | 1.62:0.73:1.70 | 1.71:0.77:1.80 | 1.71:0.77:1.80 | 1.71:0.77:1.80 | 1.71:0.77:1.80 |
| 8 | 4.25:5.25:0.50 | 1.72:2.13:0.20 | 1.82:2.24:0.21 | 1.82:2.24:0.21 | 1.82:2.24:0.21 | 1.82:2.24:0.21 |
| 9 | 4.50:1.30:4.20 | 1.82:0.53:1.70 | 1.92:0.56:1.80 | 1.92:0.56:1.80 | 1.92:0.56:1.80 | 1.92:0.56:1.80 |
| Bulk Density (kg/m3) | Porosity (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1800 (kg/m3) | 28.13 | 26.43 | 26.25 | 25.94 | 26.67 | 30.33 | 27.28 | 28.81 | 27.05 |
| 1900 (kg/m3) | 27.09 | 25.71 | 24.72 | 25.58 | 25.94 | 26.40 | 25.38 | 28.40 | 26.79 |
| 2000 (kg/m3) | 23.88 | 23.57 | 21.85 | 24.54 | 25.38 | 22.47 | 23.86 | 26.26 | 24.95 |
| 2100 (kg/m3) | 23.30 | 22.38 | 21.47 | 23.64 | 24.69 | 22.45 | 23.07 | 24.68 | 23.79 |
| 2200 (kg/m3) | 21.54 | 22.28 | 20.98 | 21.99 | 23.64 | 22.10 | 22.21 | 22.45 | 22.37 |
| NO. | Density (kg/m3) | Porosity | d | (mm) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2000 | 23.88% | 2 | ~0.666 | 0.01 | 1.7962 | 1.1201 | 0.0545 |
| 2 | 2000 | 23.57% | 2 | ~0.664 | 0.01 | 1.7907 | 1.1214 | 0.0555 |
| 3 | 2000 | 21.85% | 2 | ~0.659 | 0.01 | 1.7798 | 1.1295 | 0.0562 |
| 4 | 2000 | 24.54% | 2 | ~0.0671 | 0.01 | 1.7966 | 1.1172 | 0.0542 |
| 5 | 2000 | 25.38% | 2 | ~0.677 | 0.01 | 1.8014 | 1.1137 | 0.0505 |
| 6 | 2000 | 22.47% | 2 | ~0.655 | 0.01 | 1.7838 | 1.1265 | 0.055 |
| 7 | 2000 | 23.86% | 2 | ~0.666 | 0.01 | 1.7925 | 1.1201 | 0.0538 |
| 8 | 2000 | 26.26% | 2 | ~0.683 | 0.01 | 1.8064 | 1.1102 | 0.0529 |
| 9 | 2000 | 24.95% | 2 | ~0.674 | 0.01 | 1.7990 | 1.1155 | 0.052 |
| NO. | Grade Ratio (a:b:c) | Water Vapor Transmission Rate ) | ||||
|---|---|---|---|---|---|---|
| 1800 (kg/m3) | 1900 (kg/m3) | 2000 (kg/m3) | 2100 (kg/m3) | 2200 (kg/m3) | ||
| 1 | 2.80:6.70:0.50 | 1.810 × 10−11 | 1.555 × 10−11 | 1.340 × 10−11 | 1.304 × 10−11 | 1.208 × 10−11 |
| 2 | 3.05:4.60:2.35 | 1.827 × 10−11 | 1.437 × 10−11 | 1.204 × 10−11 | 1.173 × 10−11 | 1.031 × 10−11 |
| 3 | 3.30:2.50:4.20 | 1.554 × 10−11 | 1.401 × 10−11 | 1.330 × 10−11 | 1.249 × 10−11 | 1.217 × 10−11 |
| 4 | 3.40:4.25:2.35 | 1.488 × 10−11 | 1.360 × 10−11 | 1.307 × 10−11 | 1.262 × 10−11 | 1.187 × 10−11 |
| 5 | 3.65:2.15:4.20 | 1.574 × 10−11 | 1.274 × 10−11 | 1.115 × 10−11 | 1.014 × 10−11 | 9.673 × 10−12 |
| 6 | 3.90:5.60:0.50 | 1.825 × 10−11 | 1.469 × 10−11 | 1.279 × 10−11 | 1.146 × 10−11 | 1.036 × 10−11 |
| 7 | 4.00:1.80:4.20 | 1.725 × 10−11 | 1.437 × 10−11 | 1.291 × 10−11 | 1.258 × 10−11 | 1.089 × 10−11 |
| 8 | 4.25:5.25:0.50 | 1.699 × 10−11 | 1.534 × 10−11 | 1.432 × 10−11 | 1.260 × 10−11 | 1.199 × 10−11 |
| 9 | 4.50:1.30:4.20 | 1.689 × 10−11 | 1.394 × 10−11 | 1.364 × 10−11 | 1.213 × 10−11 | 1.153 × 10−11 |
| NO. | Grade Ratio (a:b:c) | Water Vapor Transmission Rate ) | ||||
|---|---|---|---|---|---|---|
| 1800 (Kg/m3) | 1900 (Kg/m3) | 2000 (Kg/m3) | 2100 (Kg/m3) | 2200 (Kg/m3) | ||
| 1 | 2.80:6.70:0.50 | 1.80 × 10−11 | 1.61 × 10−11 | 1.42 × 10−11 | 1.38 × 10−11 | 1.29 × 10−11 |
| 2 | 3.05:4.60:2.35 | 1.77 × 10−11 | 1.50 × 10−11 | 1.25 × 10−11 | 1.23 × 10−11 | 1.09 × 10−11 |
| 3 | 3.30:2.50:4.20 | 1.49 × 10−11 | 1.45 × 10−11 | 1.39 × 10−11 | 1.32 × 10−11 | 1.31 × 10−11 |
| 4 | 3.40:4.25:2.35 | 1.44 × 10−11 | 1.41 × 10−11 | 1.35 × 10−11 | 1.35 × 10−11 | 1.27 × 10−11 |
| 5 | 3.65:2.15:4.20 | 1.51 × 10−11 | 1.31 × 10−11 | 1.17 × 10−11 | 1.08 × 10−11 | 1.05 × 10−11 |
| 6 | 3.90:5.60:0.50 | 1.75 × 10−11 | 1.44 × 10−11 | 1.32 × 10−11 | 1.21 × 10−11 | 1.10 × 10−11 |
| 7 | 4.00:1.80:4.20 | 1.67 × 10−11 | 1.50 × 10−11 | 1.35 × 10−11 | 1.34 × 10−11 | 1.19 × 10−11 |
| 8 | 4.25:5.25:0.50 | 1.64 × 10−11 | 1.58 × 10−11 | 1.48 × 10−11 | 1.34 × 10−11 | 1.33 × 10−11 |
| 9 | 4.50:1.30:4.20 | 1.58 × 10−11 | 1.44 × 10−11 | 1.39 × 10−11 | 1.31 × 10−11 | 1.22 × 10−11 |
| Bulk Density (kg/m3) | Deviation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1800 (kg/m3) | 6.55% | 3.22% | 4.27% | 3.34% | 4.24% | 4.30% | 5.28% | 3.60% | 8.99% |
| 1900 (kg/m3) | 3.40% | 4.17% | 3.42% | 3.38% | 2.78% | 1.99% | 4.19% | 2.89% | 3.22% |
| 2000 (kg/m3) | 5.58% | 3.63% | 7.26% | 3.18% | 4.70% | 3.07% | 4.37% | 3.22% | 5.58% |
| 2100 (kg/m3) | 5.49% | 4.61% | 5.34% | 6.55% | 6.12% | 5.30% | 6.13% | 5.99% | 7.44% |
| 2200 (kg/m3) | 6.33% | 5.37% | 7.10% | 6.52% | 7.87% | 5.86% | 8.48% | 9.88% | 5.46% |
| Bulk Density (kg/m3) | Deviation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1800 (kg/m3) | 2.76% | 0.18% | −0.84% | 0.06% | −0.81% | −0.87% | 0.12% | −0.20% | −3.35% |
| 1900 (kg/m3) | 1.96% | 2.75% | 1.99% | 1.94% | 1.34% | −3.51% | 2.76% | 1.44% | 1.78% |
| 2000 (kg/m3) | 0.87% | −1.17% | −0.51% | −1.65% | −0.05% | −1.76% | −0.40% | −1.61% | −3.07% |
| 2100 (kg/m3) | −1.03% | −1.97% | −1.19% | 0.10% | −0.36% | −1.24% | −0.35% | −0.50% | 1.04% |
| 2200 (kg/m3) | −0.27% | −1.30% | 0.55% | −0.07% | 1.37% | −0.78% | 2.02% | 3.52% | −1.21% |
| NO. | Sand (%) | ||||||
|---|---|---|---|---|---|---|---|
| 30 | 34 | 38 | 42 | 46 | 50 | ||
| Clay (%) | 30 | 1.09 × 10−11 | 1.09 × 10−11 | 1.10 × 10−11 | 1.03 × 10−11 | 1.06 × 10−11 | 1.02 × 10−11 |
| 34 | 1.04 × 10−11 | 1.05 × 10−11 | 1.11 × 10−11 | 1.12 × 10−11 | 9.92 × 10−12 | 9.67 × 10−12 | |
| 38 | 1.05 × 10−11 | 1.06 × 10−11 | 1.09 × 10−11 | 1.01 × 10−11 | 9.35 × 10−12 | 8.88 × 10−12 | |
| 42 | 1.08 × 10−11 | 1.12 × 10−11 | 1.07 × 10−11 | 1.03 × 10−11 | 1.03 × 10−11 | 9.84 × 10−12 | |
| 46 | 1.13 × 10−11 | 1.16 × 10−11 | 1.22 × 10−11 | 1.05 × 10−11 | 1.05 × 10−11 | 1.03 × 10−11 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, J.; Yu, S. Quantitative Evaluation of Water Vapor Permeability Coefficients of Earth Materials Under the Influence of Density and Particle Size Distribution. Buildings 2025, 15, 1821. https://doi.org/10.3390/buildings15111821
Mu J, Yu S. Quantitative Evaluation of Water Vapor Permeability Coefficients of Earth Materials Under the Influence of Density and Particle Size Distribution. Buildings. 2025; 15(11):1821. https://doi.org/10.3390/buildings15111821
Chicago/Turabian StyleMu, Jun, and Shenwei Yu. 2025. "Quantitative Evaluation of Water Vapor Permeability Coefficients of Earth Materials Under the Influence of Density and Particle Size Distribution" Buildings 15, no. 11: 1821. https://doi.org/10.3390/buildings15111821
APA StyleMu, J., & Yu, S. (2025). Quantitative Evaluation of Water Vapor Permeability Coefficients of Earth Materials Under the Influence of Density and Particle Size Distribution. Buildings, 15(11), 1821. https://doi.org/10.3390/buildings15111821





