Stress–Strain Prediction for Steam-Cured Steel Slag Fine Aggregate Concrete Based on Machine Learning Algorithms
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
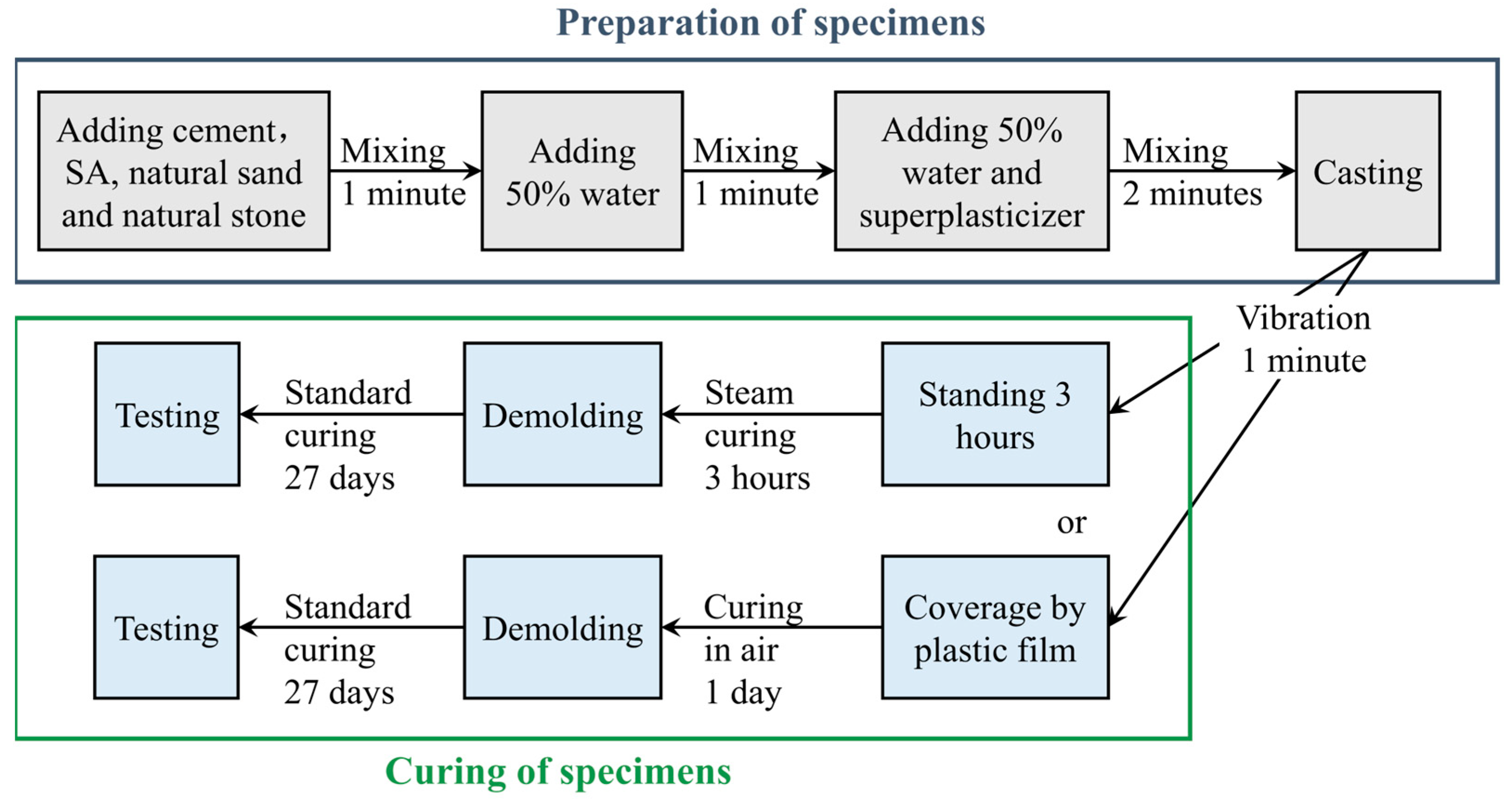
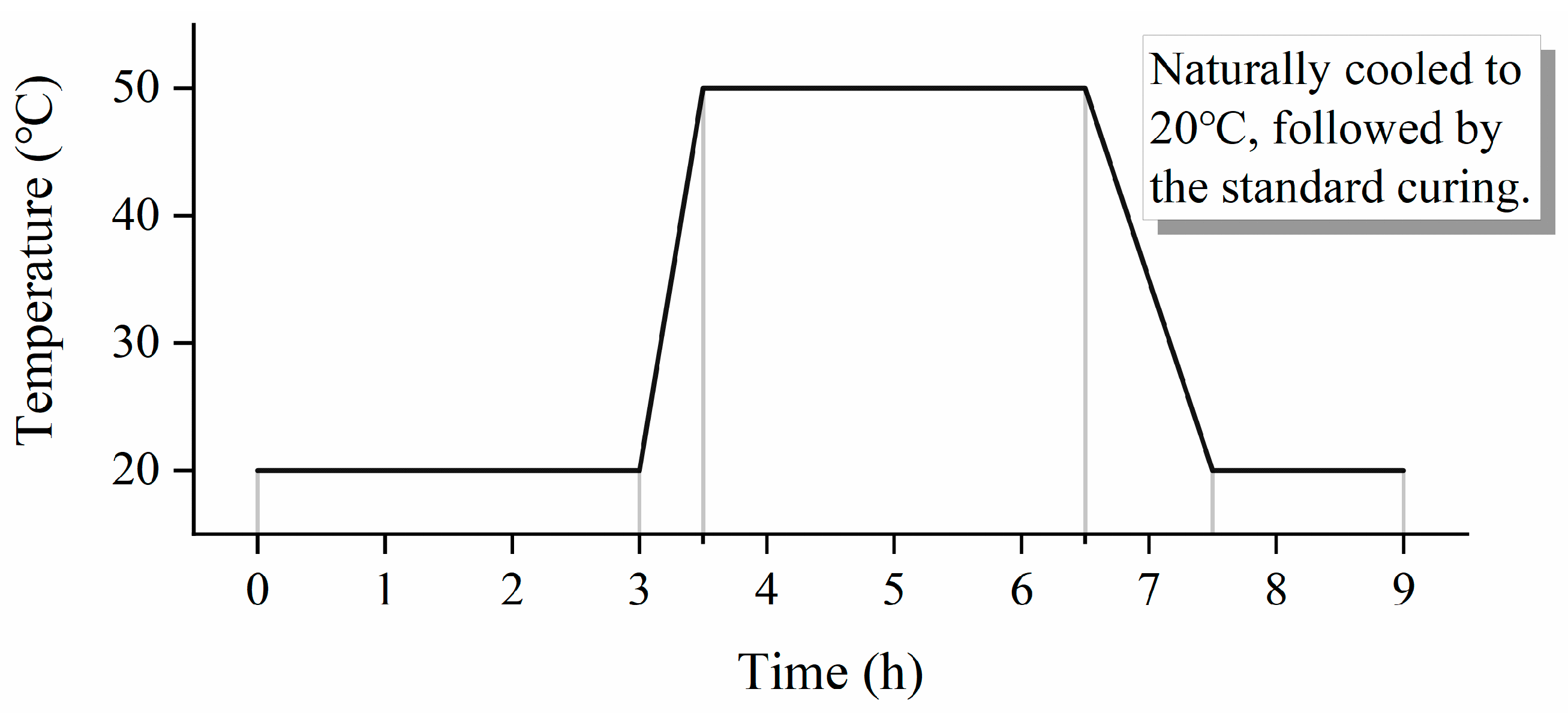
2.2. Specimen Fabrication and Mix Proportion
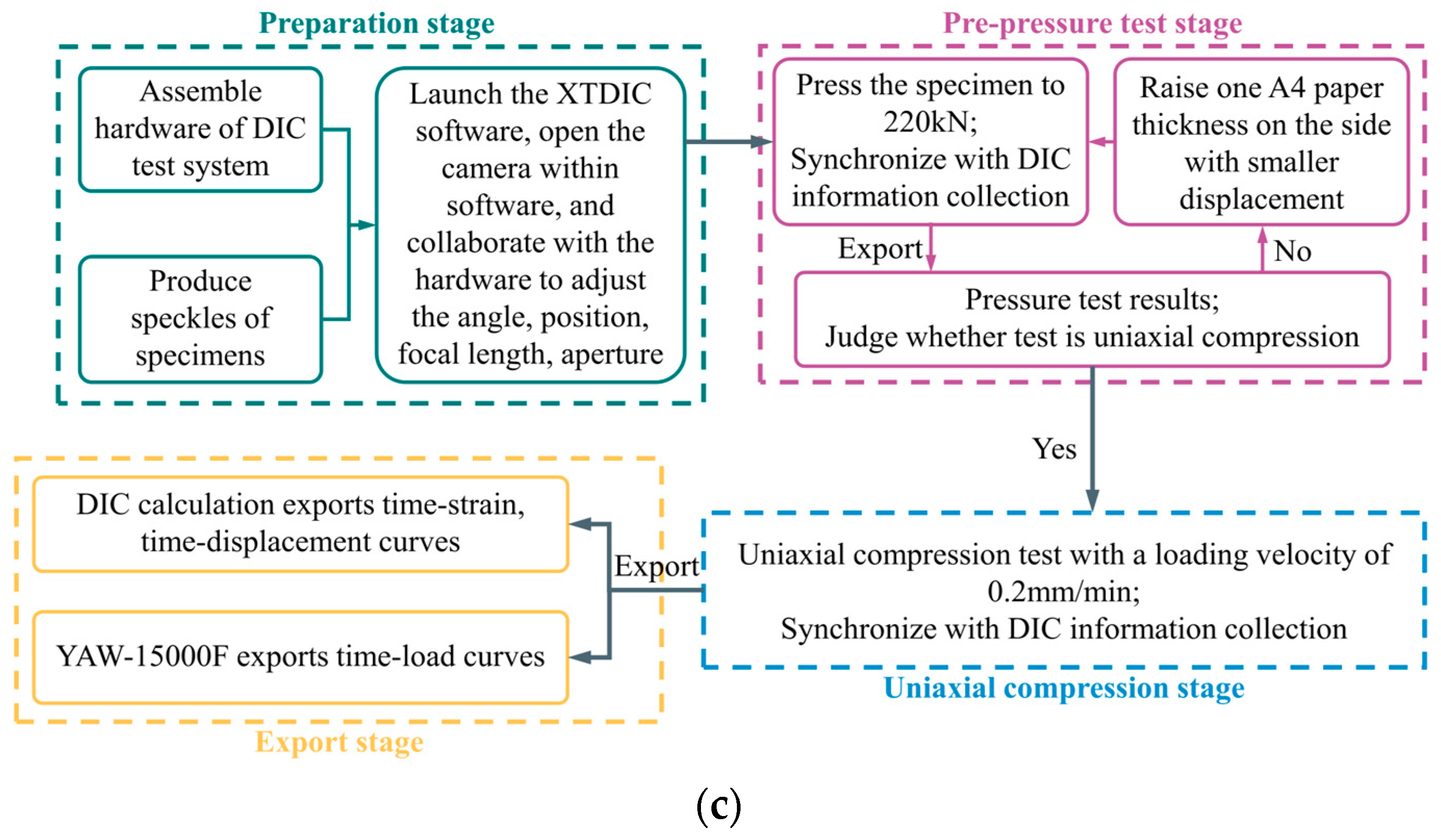
2.3. Uniaxial Compression Test Method
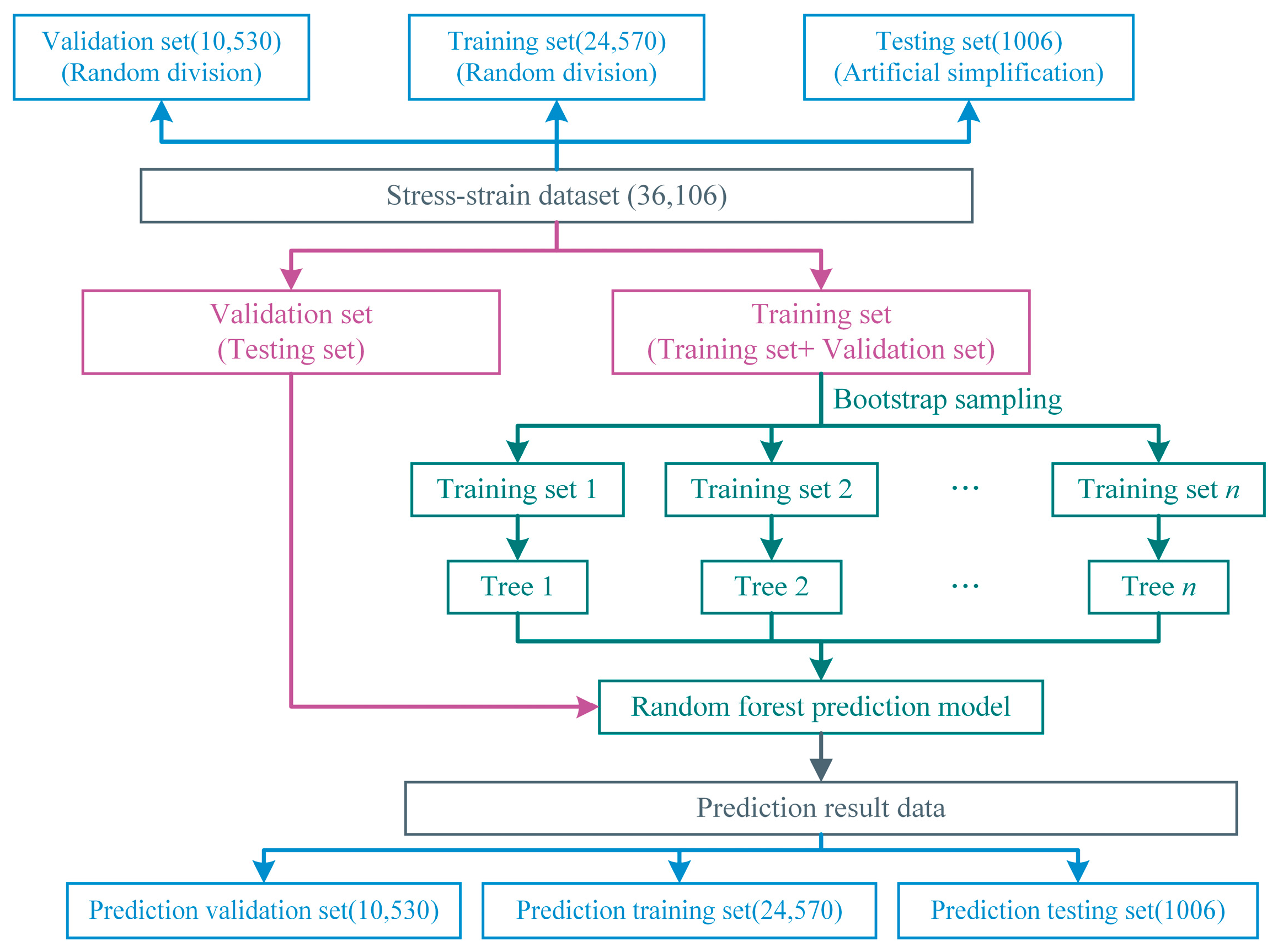
2.4. Random Forest (RF) Prediction Model
2.5. Backpropagation Neural Network (BPNN) Prediction Model
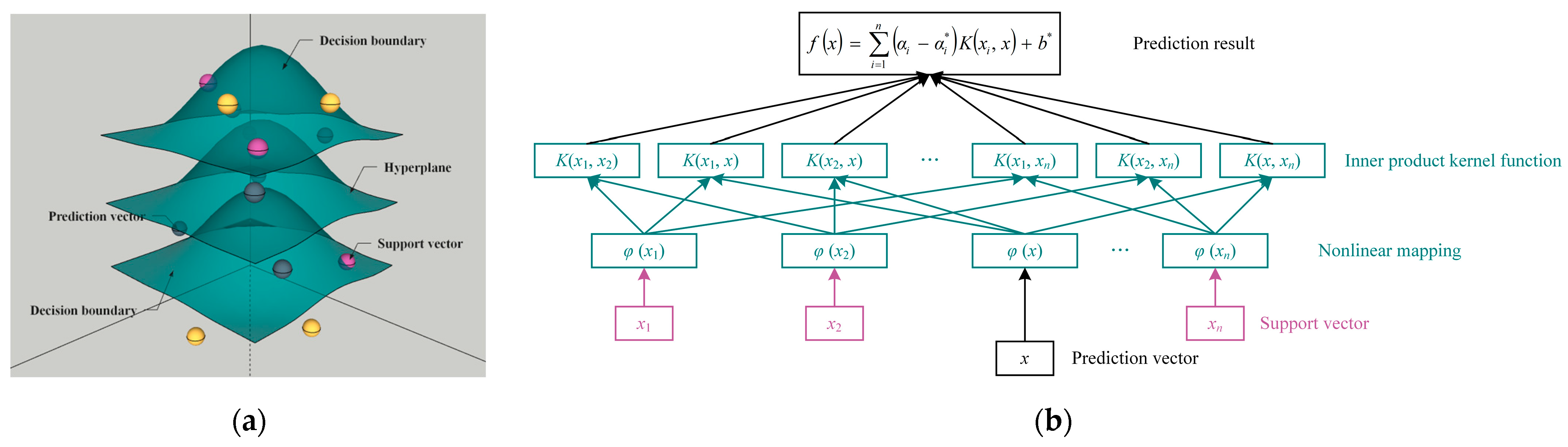
2.6. Support Vector Regression (SVR) Prediction Model
3. Results and Discussion
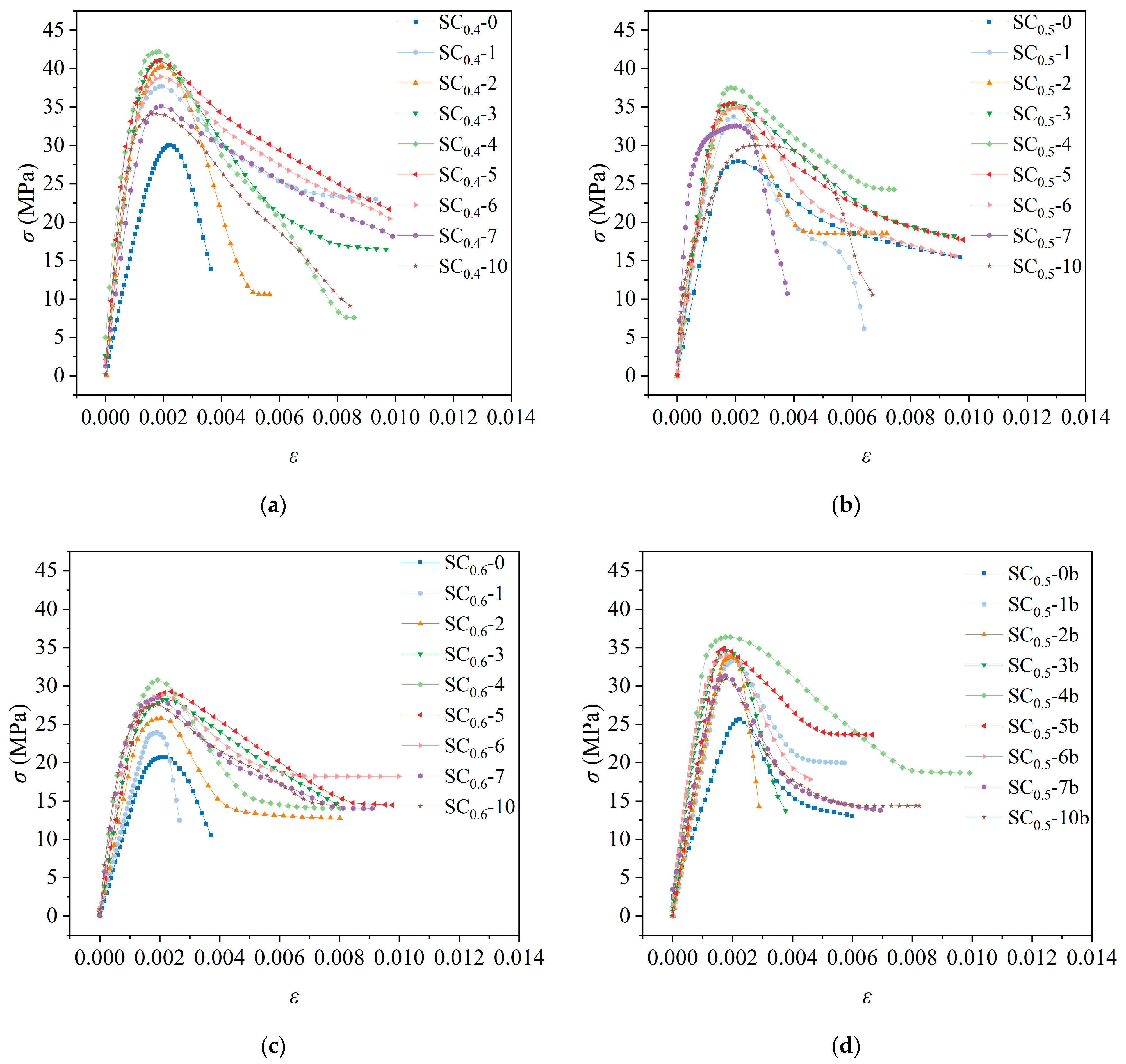
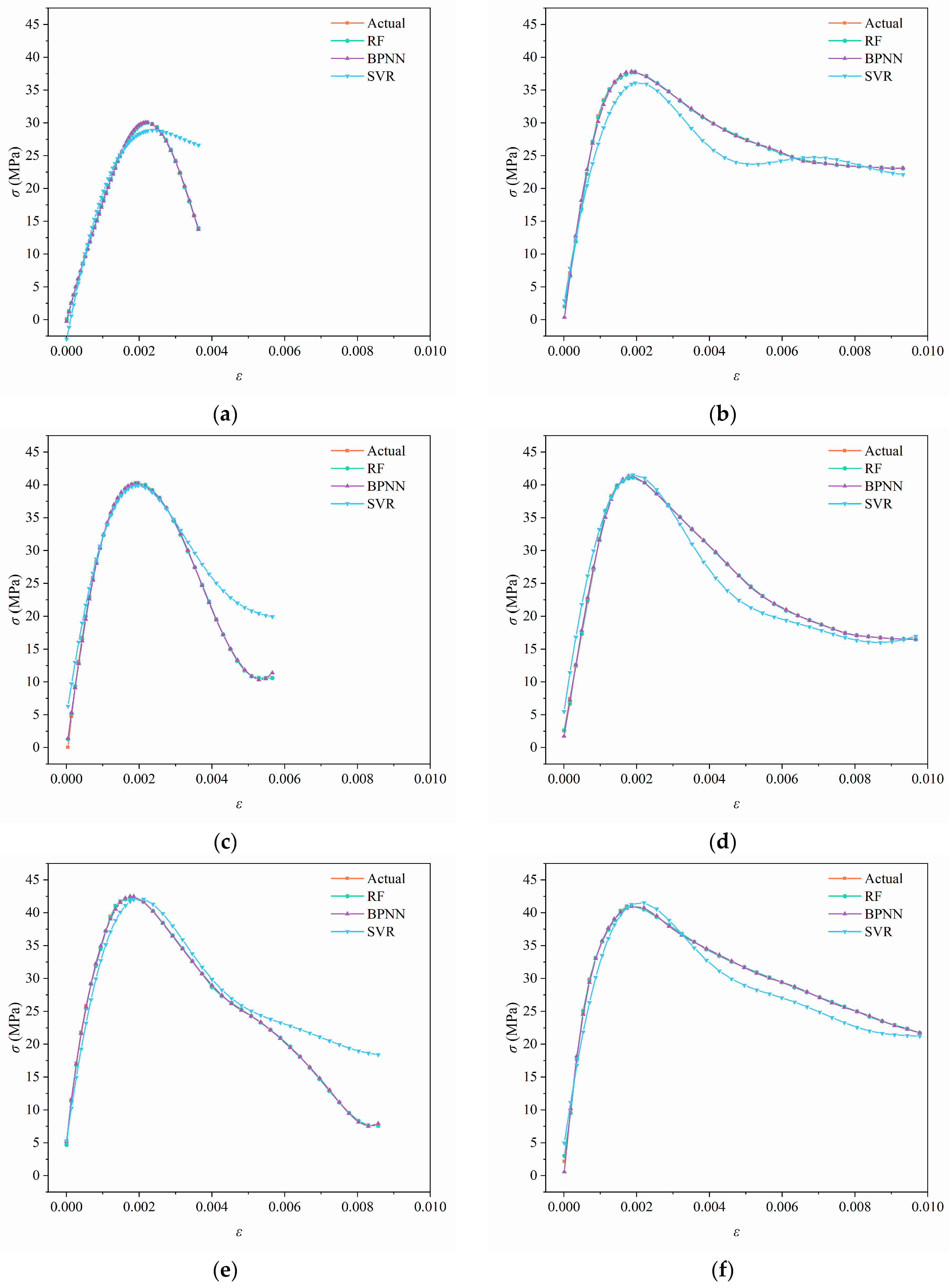
3.1. Uniaxial Compression Failure and Stress–Strain Curves
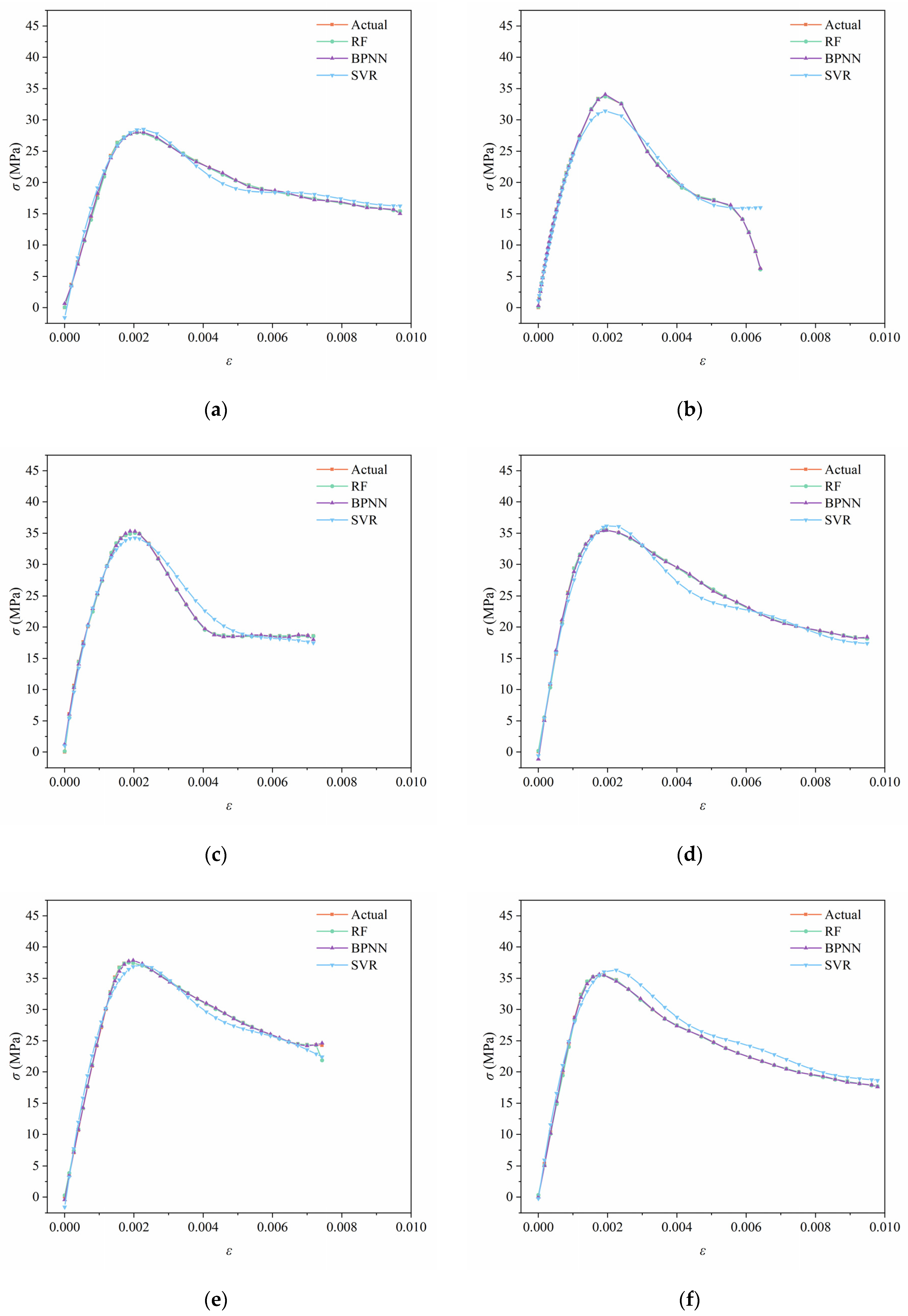
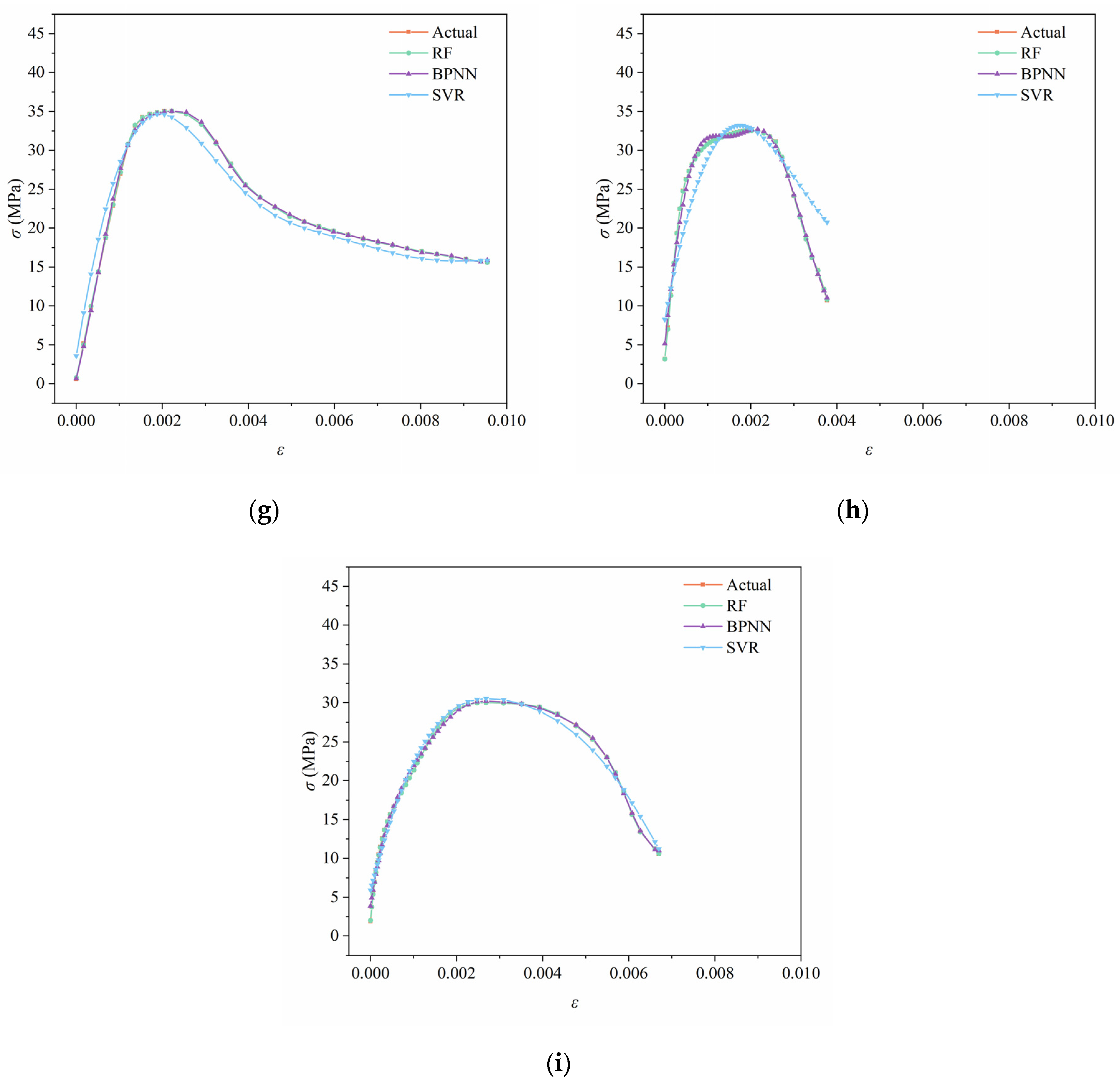
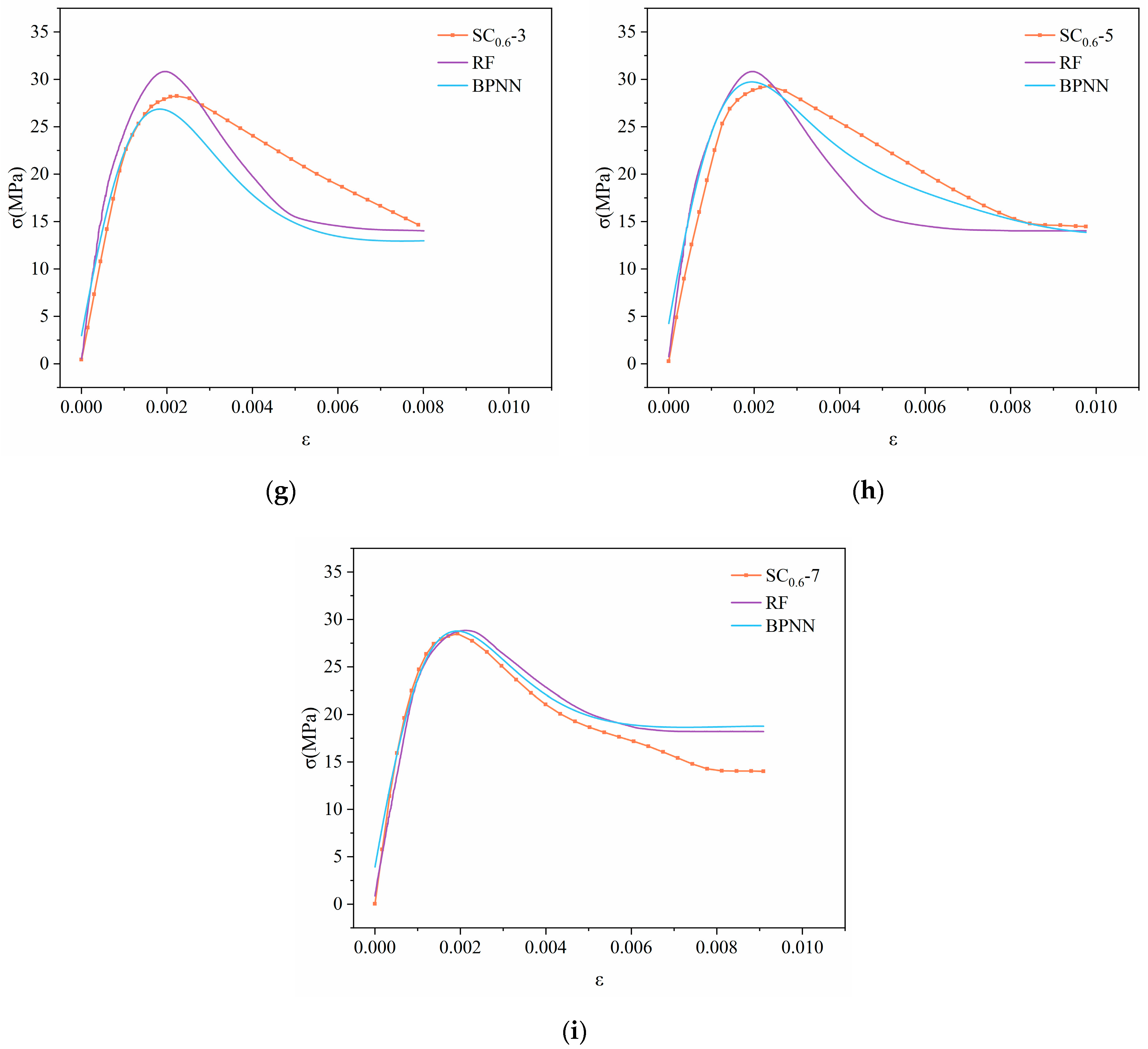
3.2. Stress–Strain Prediction Models Based on RF, BPNN, and SVR
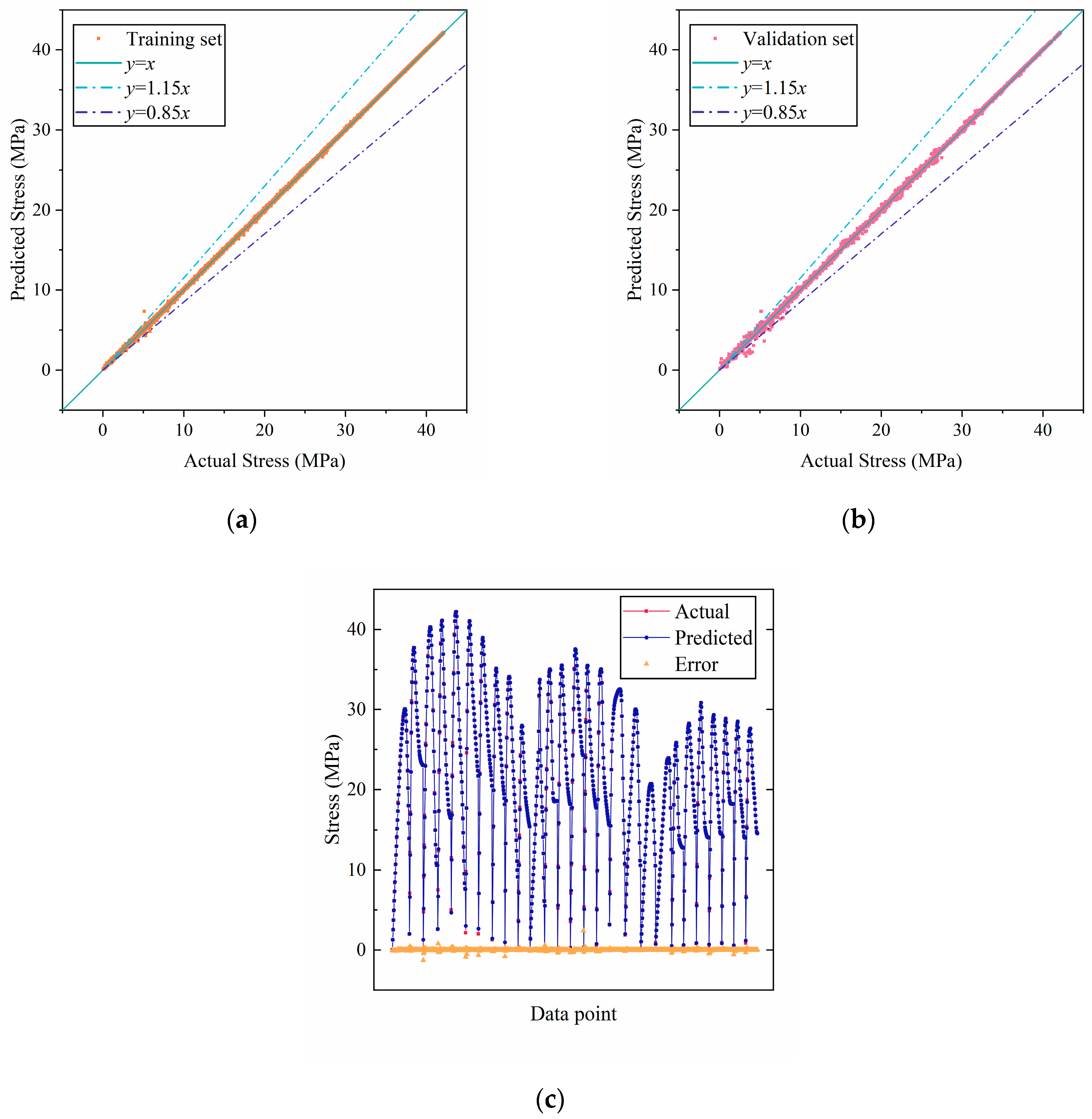
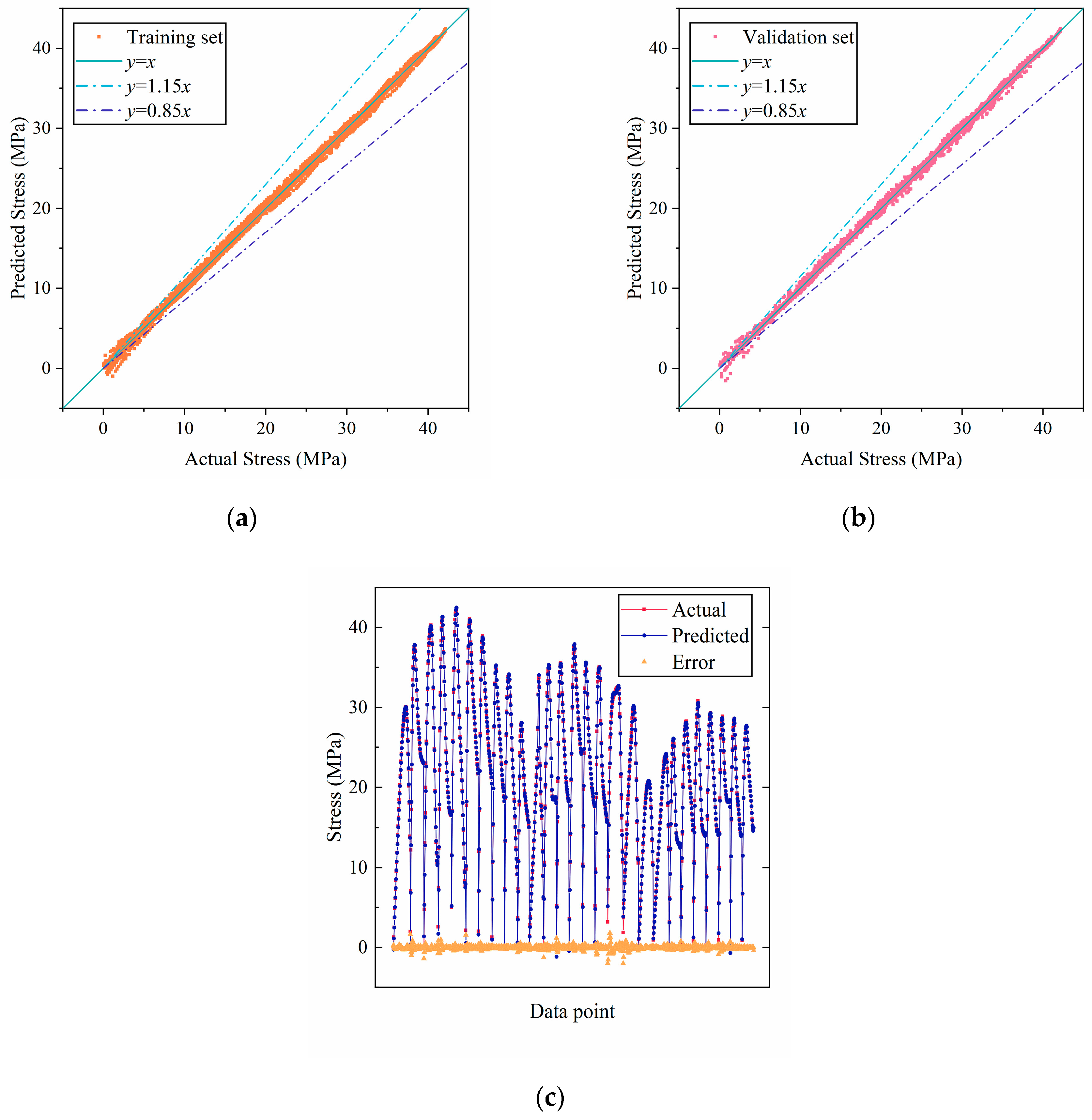
3.3. Evaluation of the Accuracy of RF, BPNN, and SVR Prediction Models
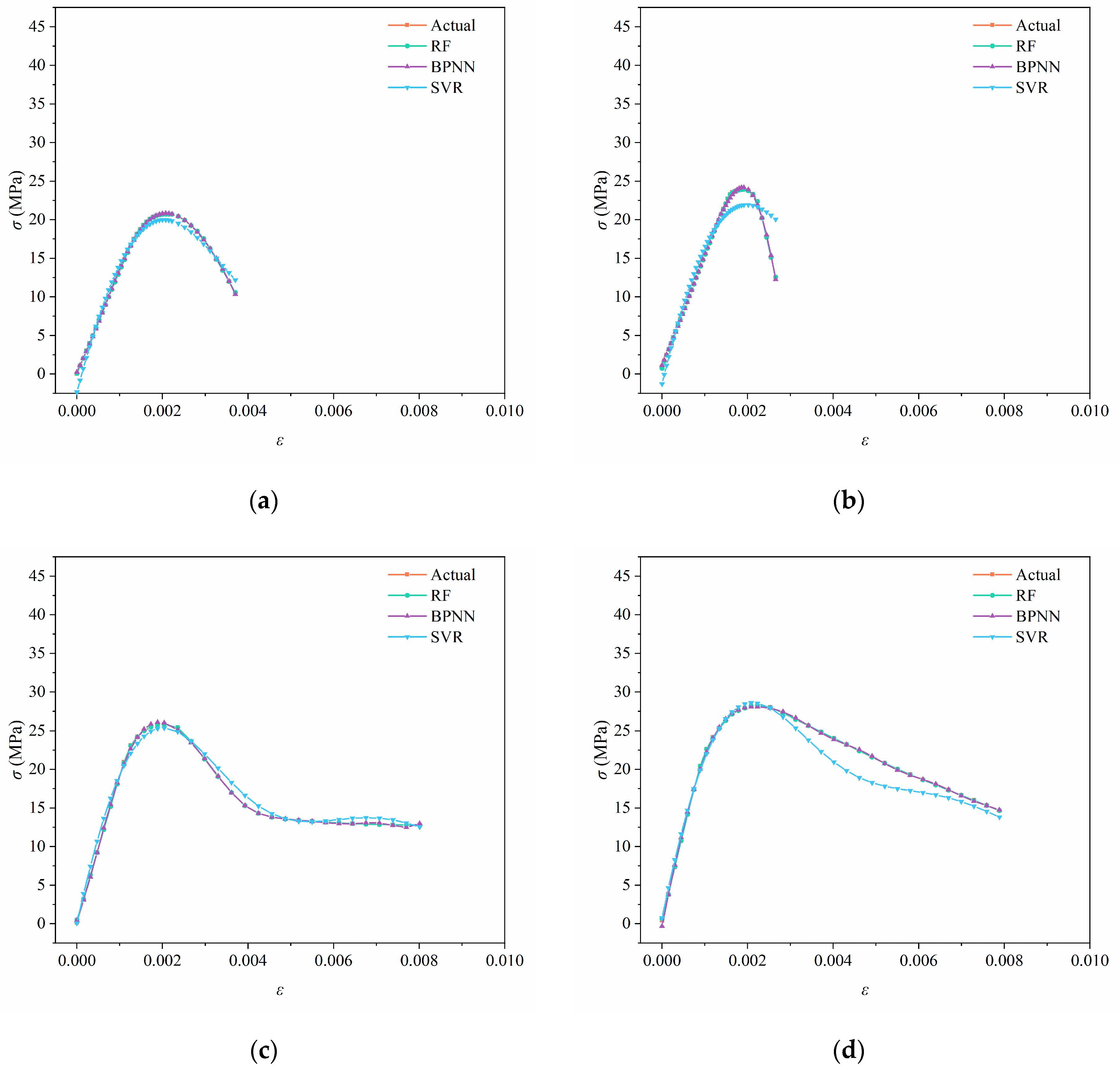
3.3.1. Prediction Results of the Testing Set
3.3.2. Model Prediction Accuracy
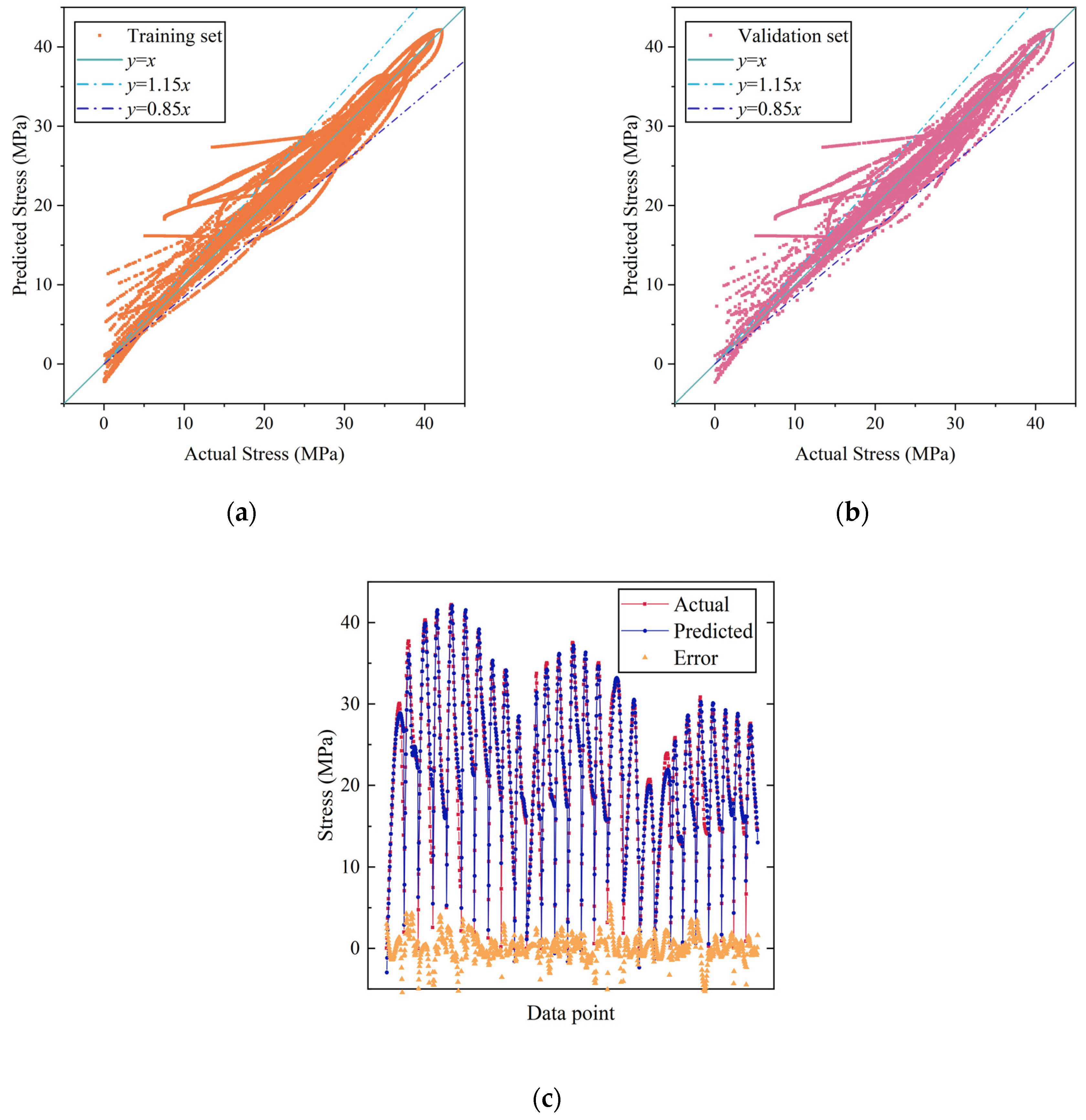
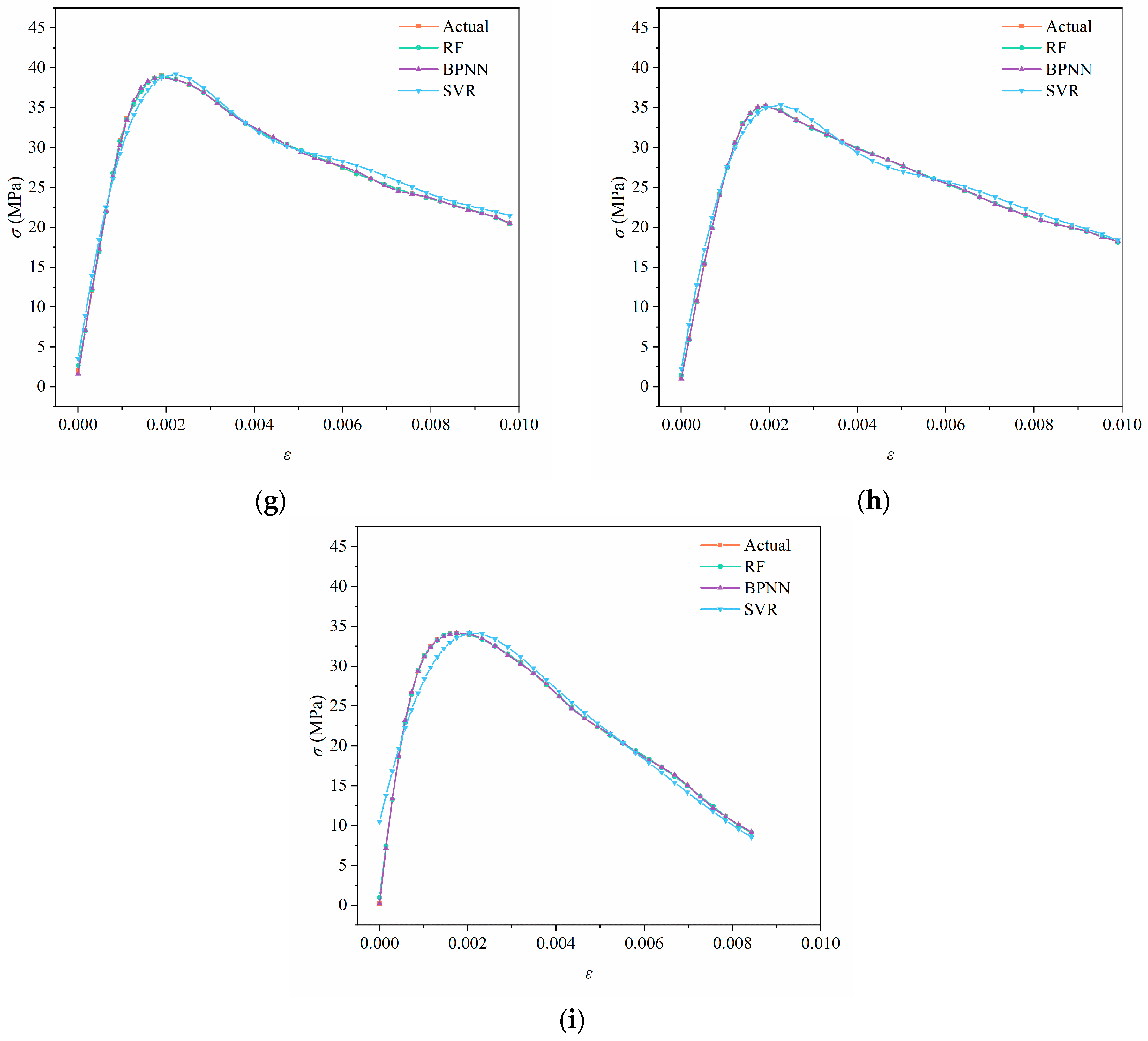
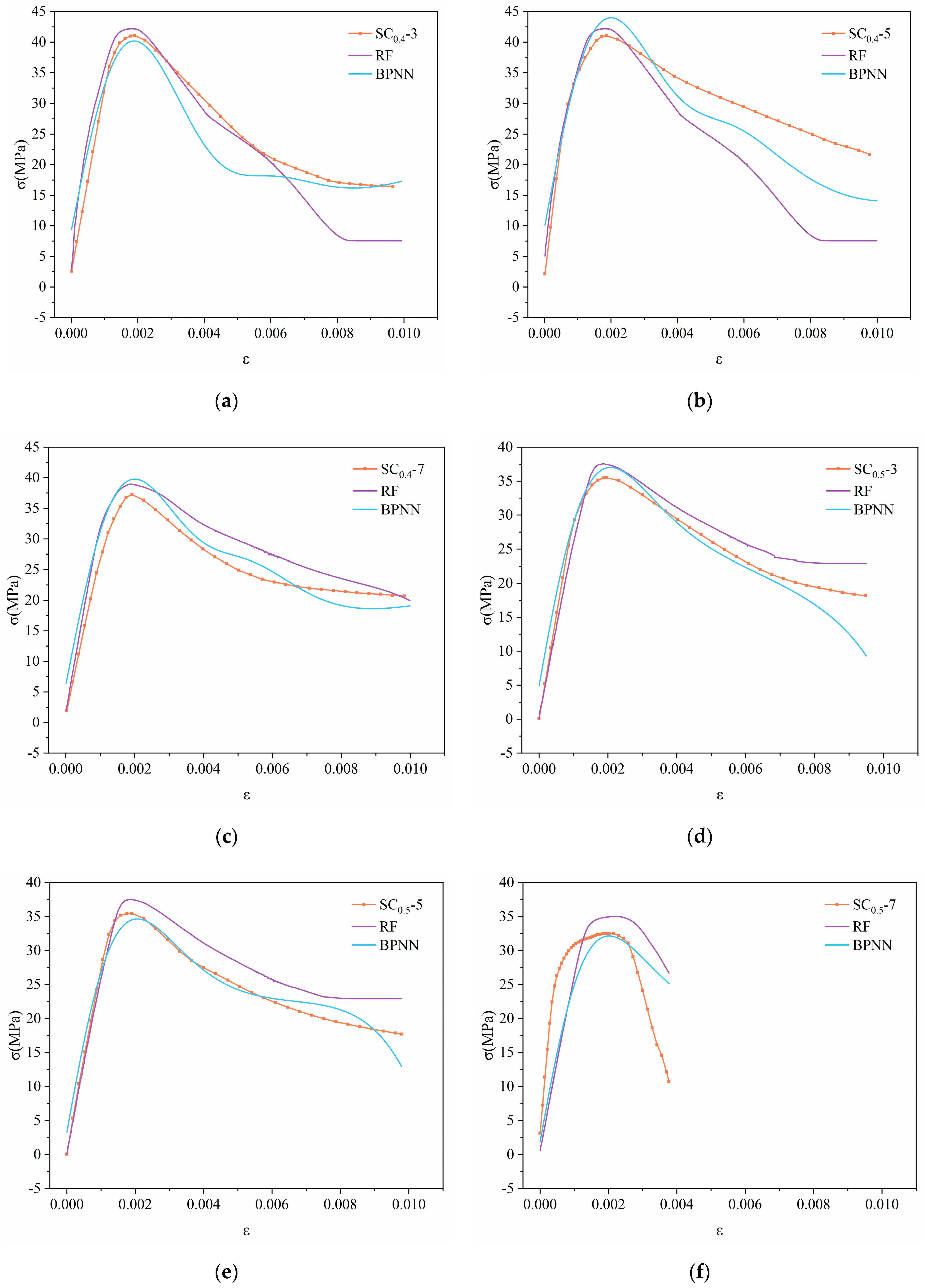
4. Applicability of the Models
4.1. Reconstruction of RF and BPNN Models
4.2. Prediction Results
5. Conclusions
- (1)
- Steam curing significantly enhances the mechanical properties of SC. The peak stress of the specimens is increased, the ultimate strain is raised, and the descending segment of the uniaxial compressive stress–strain curve of SC becomes more gentle. The peak stress of SC initially increases and then decreases with the rise in the SA volume replacement ratio, reaching its maximum when the SA replacement ratio is 40%. The main cracking surface of SC specimens under uniaxial compression failure is the side surface. Standard-cured specimens exhibit more pronounced brittle failure characteristics, while steam-cured specimens show more ductile failure modes.
- (2)
- By artificial thinning and randomly dividing the uniaxial compressive stress–strain data of steam-cured SC, the prediction performance of the RF, BPNN, and SVR models was compared. It was found that the RF model performed the best (R2 = 1.00), with over 95% of the data points falling within the ±15% error band. The BPNN model was the next best. However, the SVR model, due to its large prediction point dispersion and significant errors, is not suitable for this type of stress prediction (testing set R2 = 0.943). The prediction results of the RF and BPNN models are in very good agreement with the test results.
- (3)
- The RF and BPNN models were reconstructed and rerun to test their generalization ability in predicting the stress–strain relationship of SC specimens across mix proportions. It was found that after optimization (reducing the number of hidden layer neurons from sixty-four to eight), the BPNN model showed enhanced stability in cross-content prediction, with an R2 of 0.8 or higher for six groups of specimens and a peak value of 0.956. However, the RF model overestimated the peak stress when predicting the stress of SC specimens with untrained SA contents, indicating that its robustness needs improvement. Transfer learning validation showed that the BPNN model has the most engineering value, with prediction errors for SC with untrained contents of 30%, 50%, and 70% stably within 6 MPa. This validation method not only confirmed the BPNN model’s generalization capability across various mix proportions but also highlighted its practical utility in engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, N.; Lou, L.; Amirkhanian, A.; Amirkhanian, S.N.; Xiao, F. Assessment of Effective Patching Material for concrete Bridge Deck—A Review. Constr. Build. Mater. 2021, 293, 123520. [Google Scholar] [CrossRef]
- Tang, S.W.; Yao, Y.; Andrade, C.; Li, Z.J. Recent Durability Studies on Concrete Structure. Cem. Concr. Res. 2015, 78, 143–154. [Google Scholar] [CrossRef]
- Khan, M.; Rehman, A.; Ali, M. Efficiency of Silica-Fume Content in Plain and Natural Fiber Reinforced Concrete for Concrete Road. Constr. Build. Mater. 2020, 244, 118382. [Google Scholar] [CrossRef]
- Shamass, R.; Limbachiya, V.; Ajibade, O.; Rabi, M.; Lopez, H.U.L.; Zhou, X. Carbonated Aggregates and Basalt Fiber-Reinforced Polymers: Advancing Sustainable Concrete for Structural Use. Buildings 2025, 15, 775. [Google Scholar] [CrossRef]
- Al-Kheetan, M.J.; Jweihan, Y.S.; Rabi, M.; Ghaffar, S.H. Durability Enhancement of Concrete with Recycled Concrete Aggregate: The Role of Nano-ZnO. Buildings 2024, 14, 353. [Google Scholar] [CrossRef]
- Guo, J.; Bao, Y.; Wang, M. Steel Slag in China: Treatment, Recycling, and Management. Waste Manag. 2018, 78, 318–330. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, G.; Chen, X.; Tan, J.; Gu, X. Recycling of Steel Slag Aggregate in Portland Cement Concrete: An Overview. J. Clean. Prod. 2021, 282, 124447. [Google Scholar] [CrossRef]
- Rashad, A.M. Behavior of Steel Slag Aggregate in Mortar and Concrete—A Comprehensive Overview. J. Build. Eng. 2022, 53, 104536. [Google Scholar] [CrossRef]
- Guo, Y.; Xie, J.; Zheng, W.; Li, J. Effects of Steel Slag as Fine Aggregate on Static and Impact Behaviours of Concrete. Constr. Build. Mater. 2018, 192, 194–201. [Google Scholar] [CrossRef]
- Qasrawi, H.; Shalabi, F.; Asi, I. Use of Low CaO Unprocessed Steel Slag in Concrete as Fine Aggregate. Constr. Build. Mater. 2009, 23, 1118–1125. [Google Scholar] [CrossRef]
- Xue, G.; Fu, Q.; Xu, S.; Li, J. Macroscopic Mechanical Properties and Microstructure Characteristics of Steel Slag Fine Aggregate Concrete. J. Build. Eng. 2022, 56, 104742. [Google Scholar] [CrossRef]
- Fu, Q.; Xue, G.; Xu, S.; Li, J.; Dong, W. Mechanical Performance, Microstructure, and Damage Model of Concrete Containing Steel Slag Aggregate. Struct. Concr. 2022, 24, 2189–2207. [Google Scholar] [CrossRef]
- Guo, Y.; Xie, J.; Zhao, J.; Zuo, K. Utilization of Unprocessed Steel Slag as Fine Aggregate in Normal- and High-Strength Concrete. Constr. Build. Mater. 2019, 204, 41–49. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, L.; Yan, L.; Li, S.; Cai, H.; Li, Y.; Luo, X. Characterising Mechanical Properties and Failure Criteria of Steel Slag Aggregate Concrete under Multiaxial Stress States. Constr. Build. Mater. 2024, 424, 135903. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, P. Hydration Properties of Basic Oxygen Furnace Steel Slag. Constr. Build. Mater. 2010, 24, 1134–1140. [Google Scholar] [CrossRef]
- Belhadj, E.; Diliberto, C.; Lecomte, A. Properties of Hydraulic Paste of Basic Oxygen Furnace Slag. Cem. Concr. Compos. 2014, 45, 15–21. [Google Scholar] [CrossRef]
- Shi, C.; Hu, S. Cementitious Properties of Ladle Slag Fines under Autoclave Curing Conditions. Cem. Concr. Res. 2003, 33, 1851–1856. [Google Scholar] [CrossRef]
- Zhou, Z.; Jin, Q.; Hu, D.; Zhu, L.; Li, Z.; Su, W. Long-term Volume Stability of Steel Slag Sand Mortar and Concrete. Case Stud. Constr. Mater. 2025, 22, e04179. [Google Scholar] [CrossRef]
- Feng, P.; Li, Z.; Zhang, S.; Yang, J.Q. Steel Slag Aggregate Concrete Filled-In FRP Tubes: Volume Expansion Effect and Axial Compressive Behaviour. Constr. Build. Mater. 2022, 318, 125961. [Google Scholar] [CrossRef]
- Cai, Y.; Gao, S.; Wang, F.; Zhang, Z.; Zhao, Z.; Ma, B. Early Hydration Heat Temperature Field of Precast Concrete T-Beam under Steam Curing: Experiment and Simulation. Case Stud. Constr. Mater. 2023, 18, e02067. [Google Scholar] [CrossRef]
- Shao, Y.; Zhang, Z.; Liu, X.; Zhu, L.; Han, C.; Li, S.; Du, W. Comprehensive Utilization of Industry By-Products in Precast Concrete: A Critical Review from the Perspective of Physicochemical Characteristics of Solid Waste and Steam Curing Conditions. Materials 2024, 17, 4702. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Wang, Q.; Long, Z.; Wang, X. Investigating the Impact of Fly Ash on the Strength and Micro-Structure of Concrete during Steam Curing and Subsequent Stages. Materials 2023, 16, 1326. [Google Scholar] [CrossRef]
- GB/T 37439-2019; Precast Post-Tensioned Prestressed Concrete Simply-Supported Beam of High-Speed Railway. Chinese Standard Press: Beijing, China, 2019. (In Chinese)
- Li, H.; Lin, J.; Zhao, D.; Shi, G.; Wu, H.; Wei, T.; Li, D.; Zhang, J. A BFRC Compressive Strength Prediction Method Via Kernel Extreme Learning Machine-Genetic Algorithm. Constr. Build. Mater. 2022, 344, 128076. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Mascolo, I.; Modano, M.; Guarracino, F. Application of Artificial Intelligence to Support Design and Analysis of Steel Structures. Metals 2025, 15, 408. [Google Scholar] [CrossRef]
- Jweihan, Y.S.; Al-Kheetan, M.J.; Rabi, M. Empirical Model for the Retained Stability Index of Asphalt Mixtures Using Hybrid Machine Learning Approach. Appl. Syst. Innov. 2023, 6, 93. [Google Scholar] [CrossRef]
- Rabi, M. Bond Prediction of Stainless-Steel Reinforcement Using Artificial Neural Networks. Proc. Inst. Civ. Eng.-Constr. Mater. 2023, 2, 177. [Google Scholar] [CrossRef]
- Shang, H.; Wu, P.; Lou, Y.; Wang, J.; Chen, Q. Machine Learning-Based Modeling of the Coupling Effect of Strain Rate and Temperature on Strain Hardening for 5182-O Aluminum Alloy. J. Mater. Process. Technol. 2022, 302, 117501. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Mohr, D. Machine-Learning Based Temperature- and Rate-Dependent Plasticity Model: Application to Analysis of Fracture Experiments on DP Steel. Int. J. Plast. 2019, 118, 320–344. [Google Scholar] [CrossRef]
- Zhou, M.; Ye, G.; Yuen, K.V.; Yu, W.; Jin, Q. A Graph Attention Reasoning Model for Prefabricated Component Detection. Comput.-Aided Civ. Infrastruct. Eng. 2025, 40, 13373. [Google Scholar] [CrossRef]
- Ye, G.; Yuen, K.V.; Jin, Q.; Zhou, M.; Yin, C.; Jiang, Q.; Zhao, S.; Su, W. Evaluation Method for Uniformity of Steel Slag Concrete Aggregate Based on Improved YOLOv8. J. Build. Eng. 2024, 73, 111046. [Google Scholar] [CrossRef]
- Sun, Y.; Cheng, H.; Zhang, S.; Mohan, M.K.; Ye, G.; De Schutter, G. Prediction & Optimization of Alkali-Activated Concrete Based on the Random Forest Machine Learning Algorithm. Constr. Build. Mater. 2023, 385, 131519. [Google Scholar] [CrossRef]
- Kim, T.K.; Hwang, S.-H.; Kim, J.; Jung, W.-T.; Yoon, J. Analysis of Bond Strength of CFRP Cables with Concrete Using Random Forest Model. J. Build. Eng. 2024, 96, 110658. [Google Scholar] [CrossRef]
- Dada, T.E.; Gong, G.; Xia, J.; Sarno, L.D. Stress-Strain Behaviour of Axially Loaded FRP-Confined Natural and Recycled Aggregate Concrete Using Design-Oriented and Machine Learning Approaches. J. Build. Eng. 2024, 95, 110256. [Google Scholar] [CrossRef]
- Zheng, C.; Liu, Y.; Li, L.; Yang, L. Effect of Sulfate Freeze-Thaw on the Stress-Strain Relationship of Recycled Coarse Aggregate Self-Compacting Concrete: Experimental and Machine Learning Algorithms. Constr. Build. Mater. 2024, 449, 138383. [Google Scholar] [CrossRef]
- GB 175-2007; Common Portland Cement. National Standards of the People’s Republic of China: Beijing, China, 2007. (In Chinese)
- JGJ 55-2011; Specification for Mix Proportion Design of Ordinary Concrete. National Standards of the People’s Republic of China: Beijing, China, 2011. (In Chinese)
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. National Standards of the People’s Republic of China: Beijing, China, 2019. (In Chinese)
- Allen, D.H.; Searcy, C.R. A Micromechanical Model for a Viscoelastic Cohesive Zone. Int. J. Fract. 2001, 107, 159–176. [Google Scholar] [CrossRef]
- Masad, E.; Castelo Branco, V.T.F.; Little, D.N.; Lytton, R. A Unified Method for the Analysis of Controlled-Strain and Controlled-Stress Fatigue Testing. Int. J. Pavement Eng. 2008, 9, 233–246. [Google Scholar] [CrossRef]
- Zhou, K.; Lei, D.; He, J.; Zhang, P.; Bai, P.; Zhu, F. Real-Time Localization of Micro-Damage in Concrete Beams Using DIC Technology and Wavelet Packet Analysis. Cem. Concr. Compos. 2021, 123, 104198. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Jin, Z.; Chen, F.; Zhong, P.; Zhang, L. Real-Time Strain Monitoring of Reinforced Concrete under the Attacks of Sulphate and Chloride Ions Based on XCT and DIC Methods. Cem. Concr. Compos. 2022, 125, 104314. [Google Scholar] [CrossRef]
- Guo, J.; Gao, S.; Liu, A.; Wang, H.; Guo, X.; Xing, F.; Zhang, H.; Qin, Z.; Ji, Y. Experimental Study on Failure Mechanism of Recycled Coarse Aggregate Concrete under Uniaxial Compression. J. Build. Eng. 2023, 63, 105548. [Google Scholar] [CrossRef]
- Xue, G.; Fu, Q.; Zhou, H.; Sun, L. Experimental Study on Stress-Strain Relationship of Steel Slag Fine Aggregate Concrete under Uniaxial Compression. J. Southwest Jiaotong Univ. 2022, 57, 1165–1174. (In Chinese) [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wu, Y.; Peng, S.; Xie, Q.; Xu, P. Nonlinear Least Squares with Local Polynomial Interpolation for Quantitative Analysis of IR Spectra. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 206, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Coelho, A.A. Optimum Levenberg–Marquardt Constant Determination for Nonlinear Least-Squares. J. Appl. Crystallogr. 2018, 51, 428–435. [Google Scholar] [CrossRef]
- Petrović, M.; Rakočević, V.; Kontrec, N.; Panić, S.; Ilić, D. Hybridization of Accelerated Gradient Descent Method. Numer. Algorithms 2018, 79, 769–786. [Google Scholar] [CrossRef]
- Yuvaraj, P.; Murthy, A.R.; Iyer, N.R.; Sekar, S.; Samui, P. Support Vector Regression Based Models to Predict Fracture Characteristics of High Strength and Ultra High Strength Concrete Beams. Eng. Fract. Mech. 2013, 98, 29–43. [Google Scholar] [CrossRef]
- Myers, R.H. Classical and Modern Regression with Applications, 2nd ed.; Duxbury Press: Belmont, CA, USA, 2000. [Google Scholar]
- Lai, S.; Serra, M. Concrete Strength Prediction by Means of Neural Network. Constr. Build. Mater. 1997, 11, 93–98. [Google Scholar] [CrossRef]
- Feng, D.C.; Liu, Z.T.; Wang, X.D.; Chen, Y.; Chang, J.Q.; Wei, D.F.; Jiang, Z.M. Machine Learning-Based Compressive Strength Prediction for Concrete: An Adaptive Boosting Approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.-N.; Moayedi, H. A Novel Artificial Intelligence Technique to Predict Compressive Strength of Recycled Aggregate Concrete Using ICA-XGBoost Model. Eng. Comput. 2021, 37, 3329–3346. [Google Scholar] [CrossRef]
- Chou, J.S.; Pham, A.D. Enhanced Artificial Intelligence for Ensemble Approach to Predicting High Performance Concrete Compressive Strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Chou, J.S.; Roy, A.F.V.; Wu, Y.W. High-Performance Concrete Compressive Strength Prediction Using Time-Weighted Evolutionary Fuzzy Support Vector Machines Inference Model. Autom. Constr. 2012, 28, 106–115. [Google Scholar] [CrossRef]
- Wang, C.; Ye, G.; Jin, Q.; Zhou, Z.; Hu, D.; Wei, Y. The Uniaxial Compressive Stress-Strain Relations of Steel Slag Fine Aggregate Concrete under Steam Curing. Constr. Build. Mater. 2025, 459, 139820. [Google Scholar] [CrossRef]
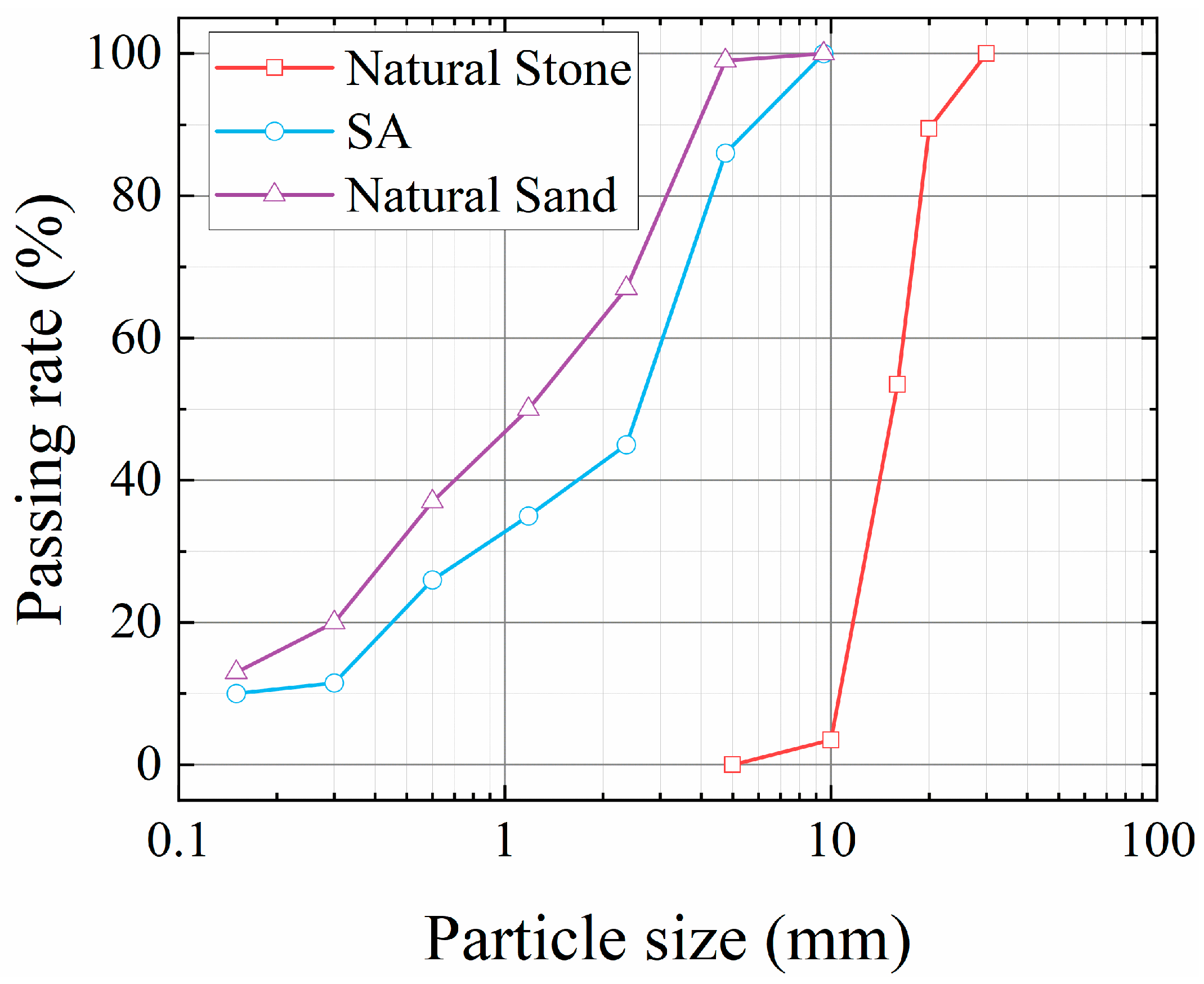




| Fine Aggregate | Apparent Density (kg/m3) | Loose Bulk Density (kg/m3) | Compact Bulk Density (kg/m3) | Crushing Value (%) | Silt Content (%) | Water Absorption (%) | Void Ratio (%) |
|---|---|---|---|---|---|---|---|
| Natural Sand | 2677 | 1583 | 1653 | 15.96 | 2.81 | 0.84 | 41.0 |
| SA | 3261 | 1890 | 1950 | 9.59 | 3.66 | 2.87 | 40.6 |
| W/C | Series | Cement (kg/m3) | Fine Aggregate (m3/m3) | SA Replacement Rate by Volume | Natural Coarse Aggregate (kg/m3) | Water (kg/m3) | Water Reducer (kg/m3) |
|---|---|---|---|---|---|---|---|
| 0.4 | SC0.4-0~SC0.4-7, SC0.4-10 | 375.00 | 0.37 | 0%~70%, 100% | 949.13 | 150.00 | 3.75~4.50 |
| 0.5 | SC0.5-0~SC0.5-7, SC0.5-10 | 300.00 | 0.38 | 981.96 | 3.00~3.60 | ||
| 0.6 | SC0.6-0~SC0.6-7, SC0.6-10 | 250.00 | 0.39 | 1003.52 | 2.50~3.00 | ||
| 0.5 | SC0.5-0b~SC0.5-7b, SC0.5-10b | 300.00 | 0.38 | 981.96 | 3.00~3.60 |
| Prediction Models and Data Subsets | R2 | MAE | RMSE | |
|---|---|---|---|---|
| RF | Training set | 1.0000 | 0.0185 | 0.0450 |
| Validation set | 1.0000 | 0.0464 | 0.1497 | |
| Testing set | 1.0000 | 0.0473 | 0.1282 | |
| BPNN | Training set | 0.9993 | 0.1403 | 0.2176 |
| Validation set | 0.9994 | 0.1416 | 0.2203 | |
| Testing set | 0.9990 | 0.1831 | 0.2896 | |
| SVR | Training set | 0.9214 | 1.4820 | 2.3493 |
| Validation set | 0.9221 | 1.4658 | 2.3271 | |
| Testing set | 0.9432 | 1.3955 | 2.2109 | |
| Specimens | Models | R2 | MAE | RMSE |
|---|---|---|---|---|
| SC0.4-3 | RF | 0.6964 | 3.7321 | 5.0259 |
| BPNN | 0.8262 | 2.8909 | 3.8029 | |
| SC0.4-5 | RF | −0.8609 | 7.8362 | 9.7264 |
| BPNN | 0.5315 | 4.2346 | 4.8801 | |
| SC0.4-7 | RF | 0.8122 | 2.7112 | 2.8596 |
| BPNN | 0.8233 | 2.1961 | 2.7740 | |
| SC0.5-3 | RF | 0.8603 | 2.4646 | 2.6623 |
| BPNN | 0.8671 | 1.8523 | 2.5975 | |
| SC0.5-5 | RF | 0.7764 | 3.0443 | 3.2559 |
| BPNN | 0.9558 | 1.1254 | 1.4476 | |
| SC0.5-7 | RF | 0.6713 | 6.6785 | 8.0771 |
| BPNN | 0.7766 | 5.0750 | 6.6589 | |
| SC0.6-3 | RF | 0.6342 | 3.1214 | 3.5023 |
| BPNN | 0.4438 | 3.7704 | 4.3184 | |
| SC0.6-5 | RF | 0.5816 | 3.2714 | 3.9553 |
| BPNN | 0.8886 | 1.6571 | 2.0408 | |
| SC0.6-7 | RF | 0.8322 | 1.9463 | 2.2727 |
| BPNN | 0.8127 | 1.8592 | 2.4015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Hu, D.; Jin, Q. Stress–Strain Prediction for Steam-Cured Steel Slag Fine Aggregate Concrete Based on Machine Learning Algorithms. Buildings 2025, 15, 1817. https://doi.org/10.3390/buildings15111817
Wang C, Hu D, Jin Q. Stress–Strain Prediction for Steam-Cured Steel Slag Fine Aggregate Concrete Based on Machine Learning Algorithms. Buildings. 2025; 15(11):1817. https://doi.org/10.3390/buildings15111817
Chicago/Turabian StyleWang, Chuanshang, Di Hu, and Qiang Jin. 2025. "Stress–Strain Prediction for Steam-Cured Steel Slag Fine Aggregate Concrete Based on Machine Learning Algorithms" Buildings 15, no. 11: 1817. https://doi.org/10.3390/buildings15111817
APA StyleWang, C., Hu, D., & Jin, Q. (2025). Stress–Strain Prediction for Steam-Cured Steel Slag Fine Aggregate Concrete Based on Machine Learning Algorithms. Buildings, 15(11), 1817. https://doi.org/10.3390/buildings15111817





