Parametric Analysis and Control of Bedding-Inclined Asymmetric Stress in Double-Arch Tunnels: A 3DEC-Based Study on Jointed Rock Masses
Abstract
1. Introduction
2. Numerical Simulations Using 3DEC
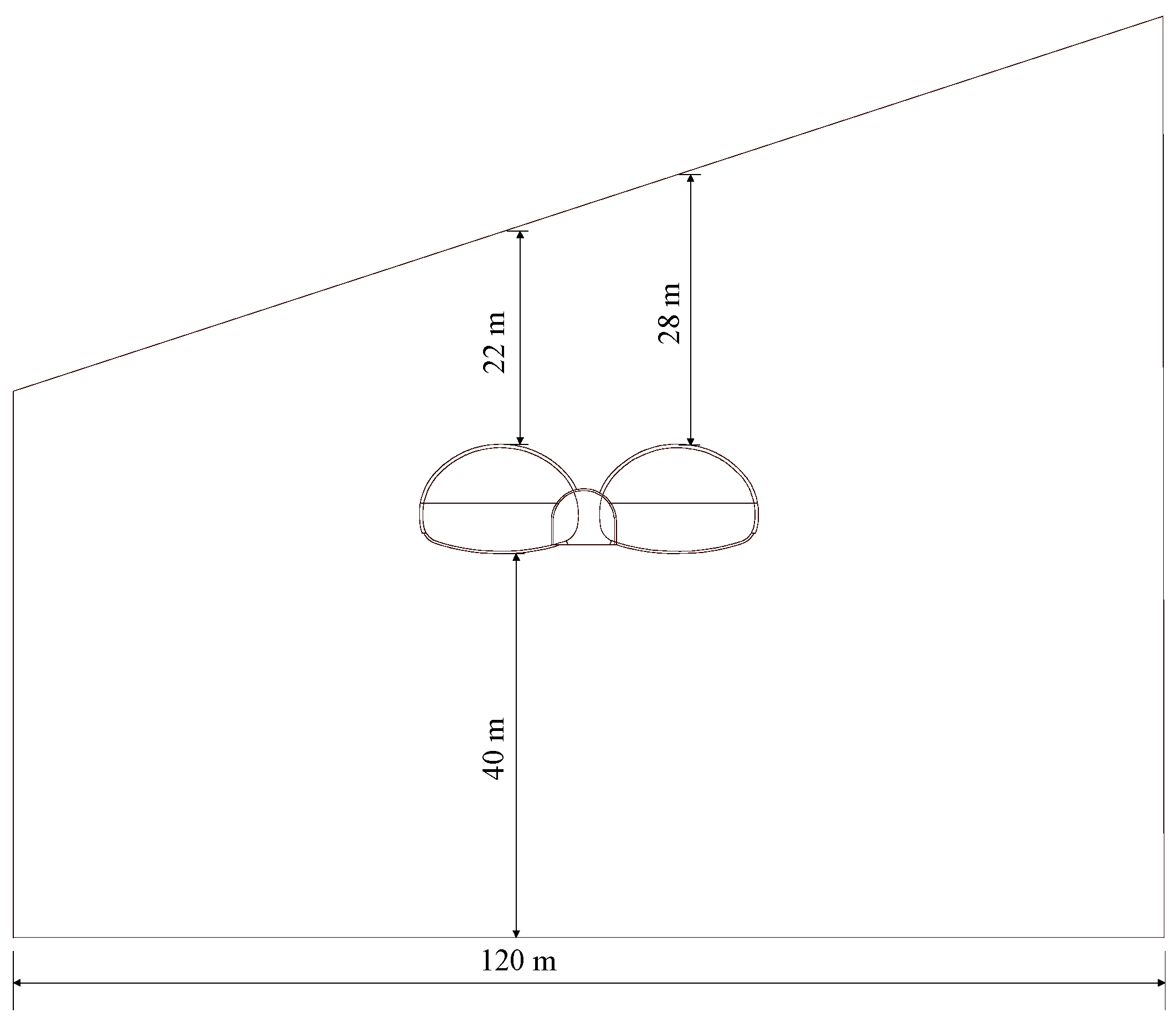
2.1. Implementation of the Numerical Model
2.2. Excavation and Support Simulation Sequence
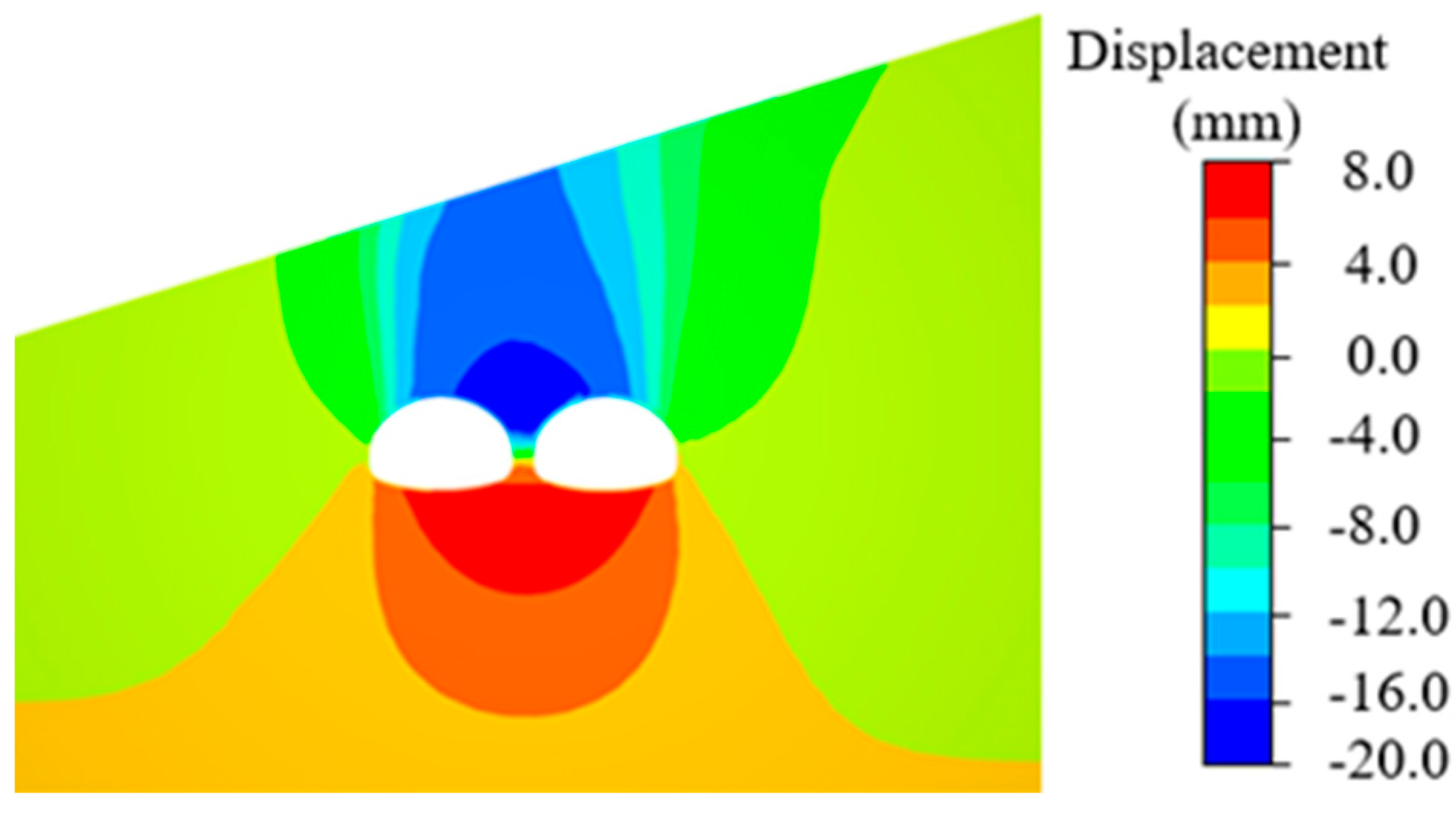
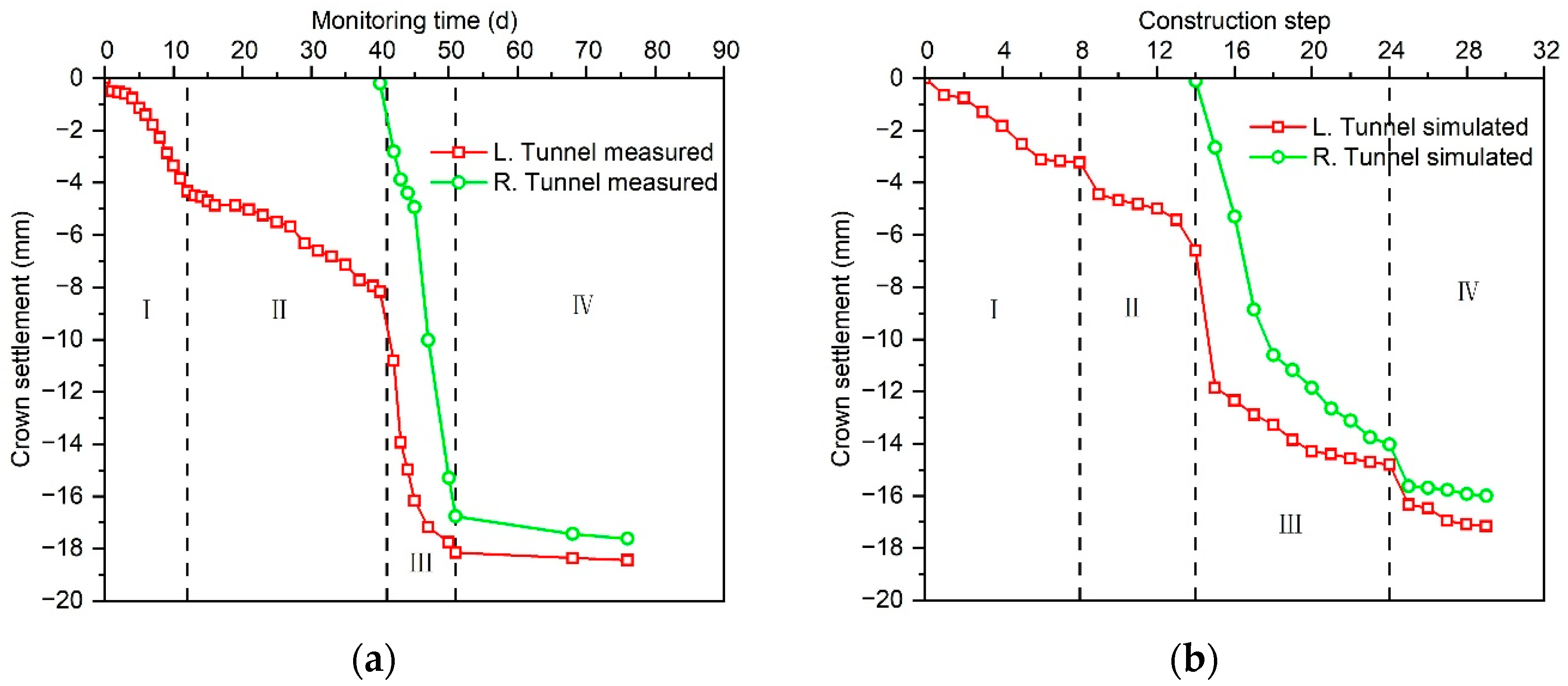
2.3. Verification of Numerical Modeling
2.4. Numerical Model Parameters of the Double-Arch Tunnel
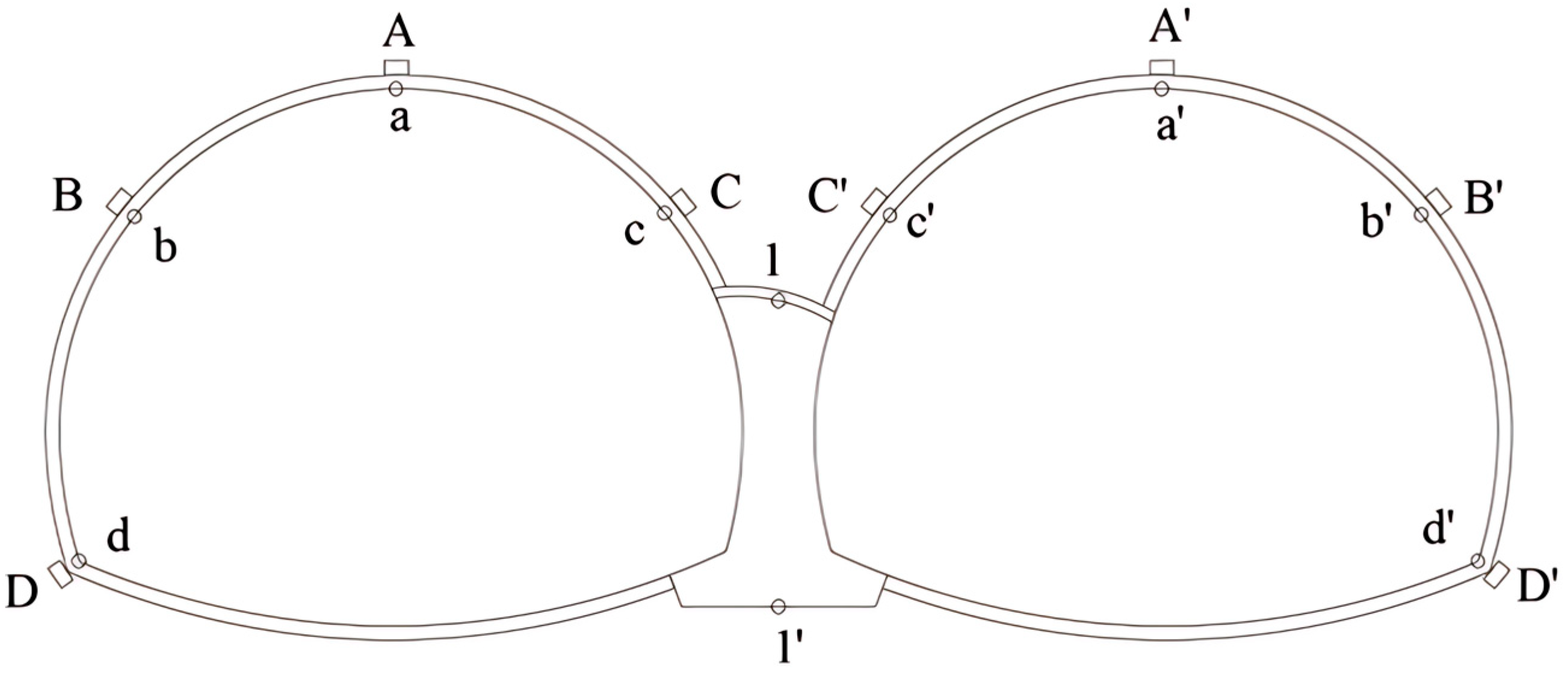
2.5. Placement of Data Sampling Points for Model Analysis
3. Parametric Analysis of Joint Characteristics
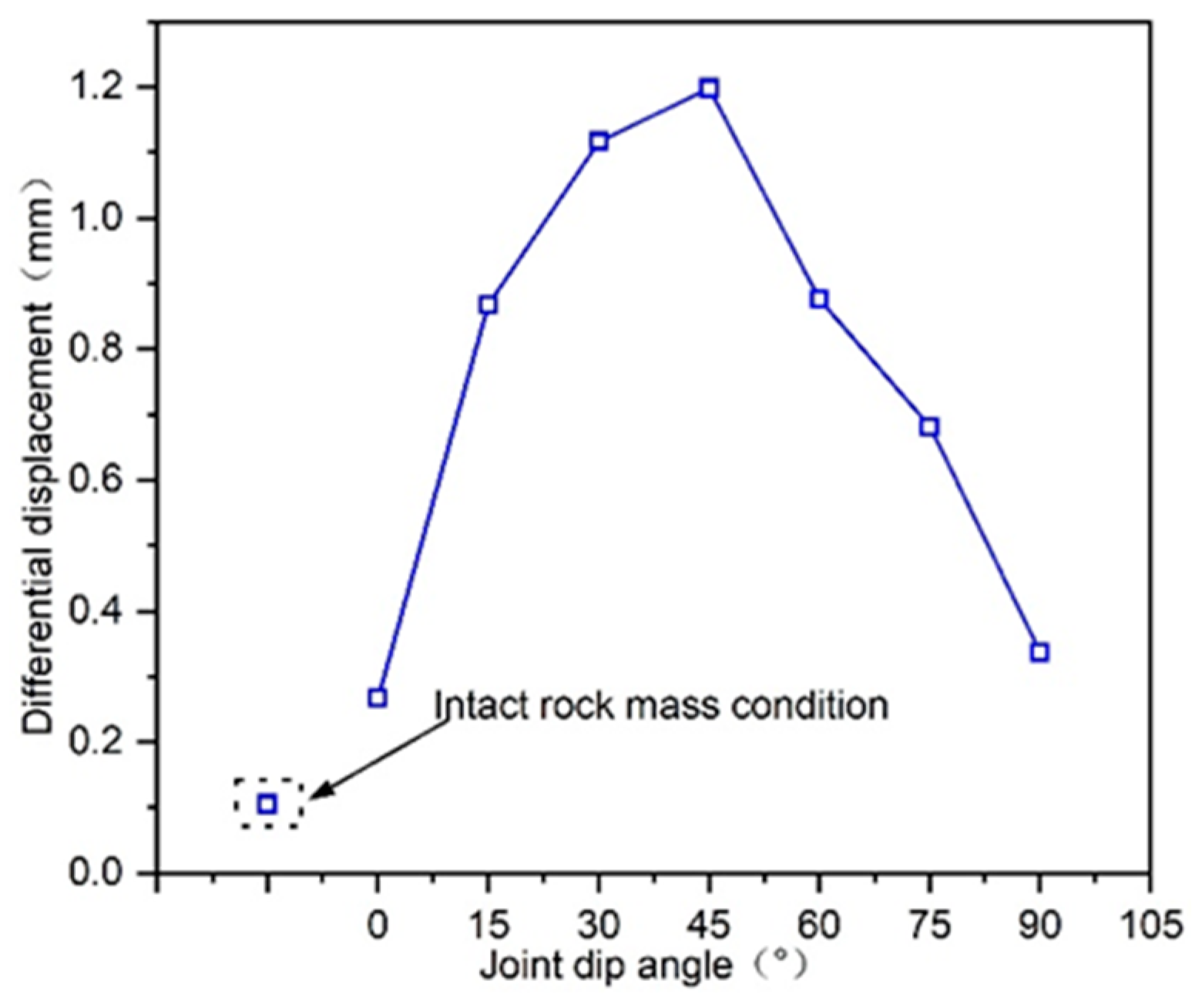
3.1. Effect of Joint Dip Angle on BIAS and Deformation
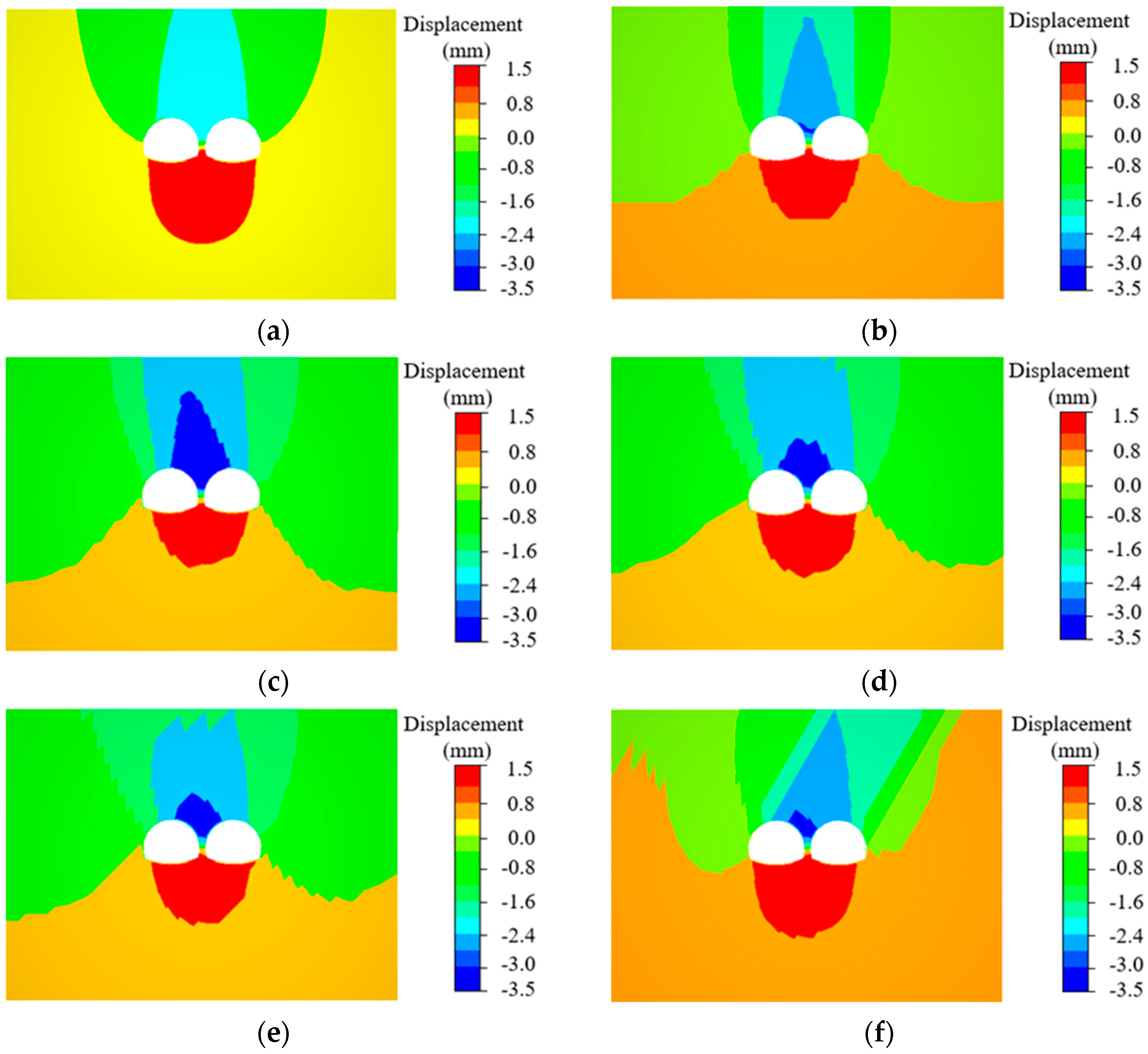
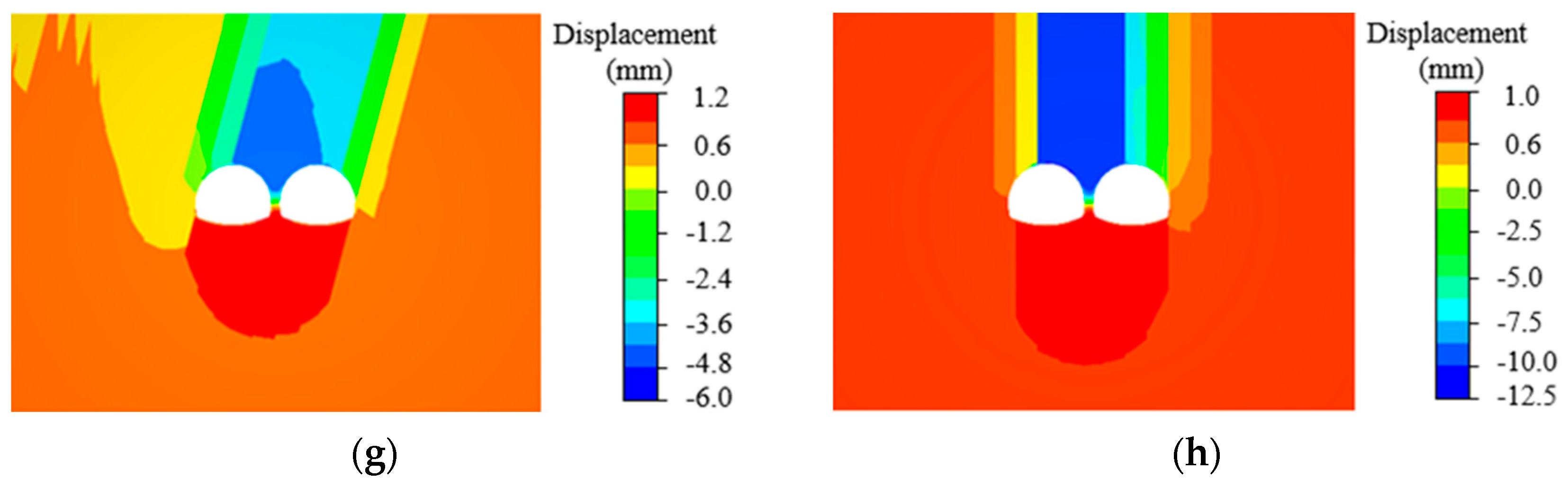
3.1.1. Surrounding Rock Deformation Patterns
3.1.2. Differential Displacement of Middle Partition Wall
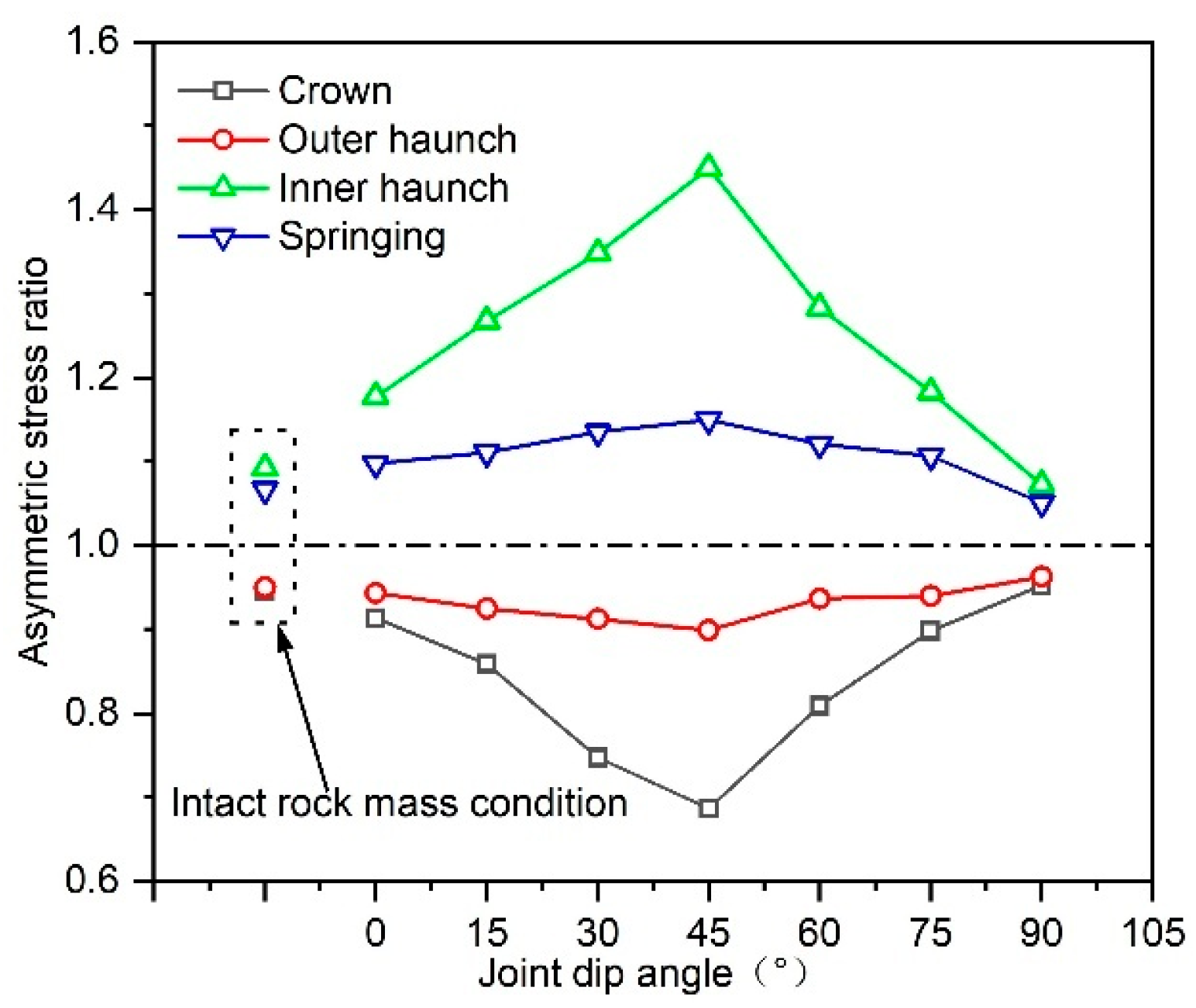
3.1.3. Quantification of BIAS Magnitude
3.2. Effect of Joint Spacing on Rock Mass Integrity
3.2.1. Effect of Joint Spacing on Surrounding Rock Deformation
3.2.2. Differential Displacement of Middle Partition Wall Under Different Joint Spacings
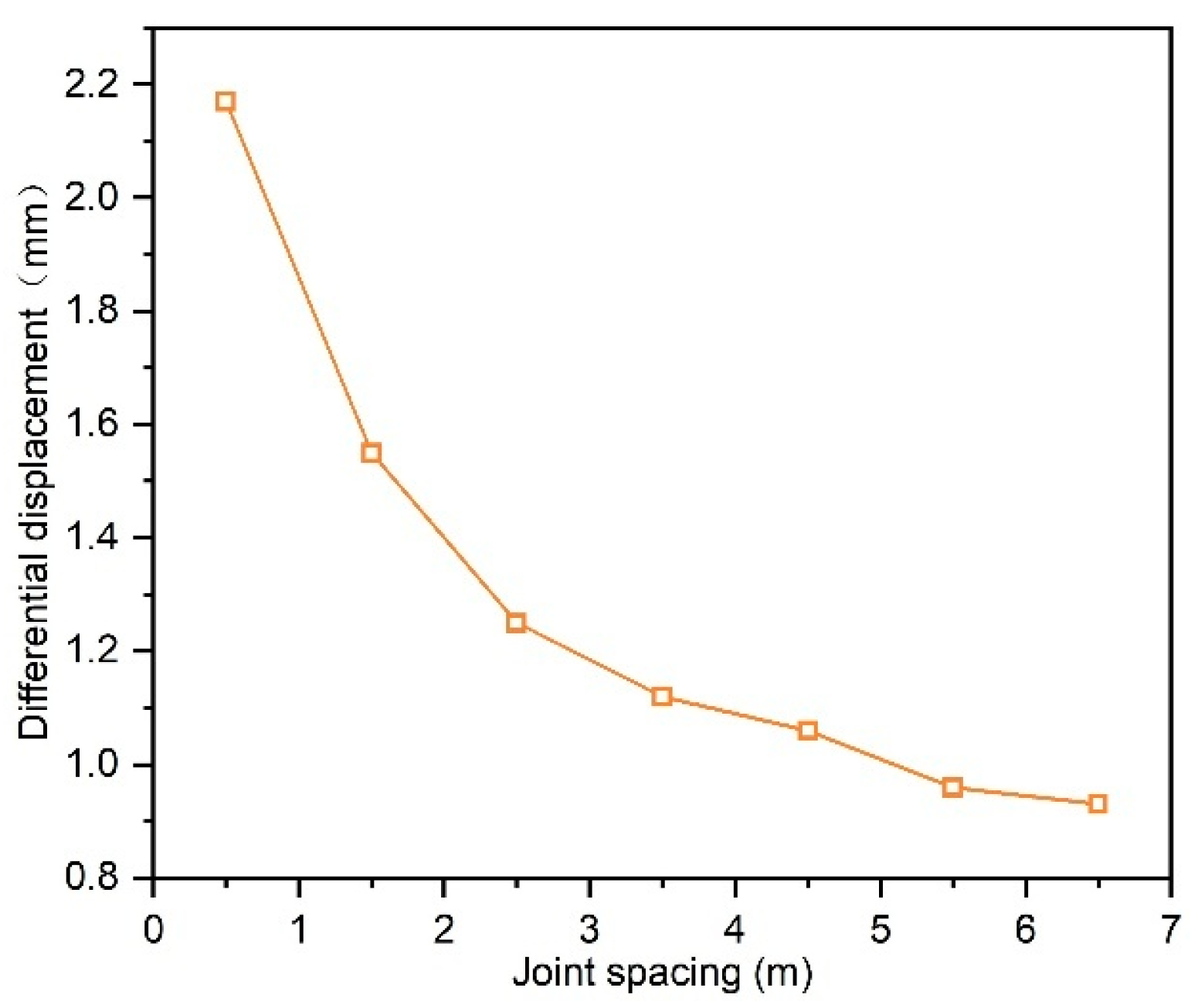
3.2.3. Quantification of BIAS Magnitude Under Different Joint Spacings
4. Analysis of Control Measures for BIAS
4.1. Optimization of Construction Methods
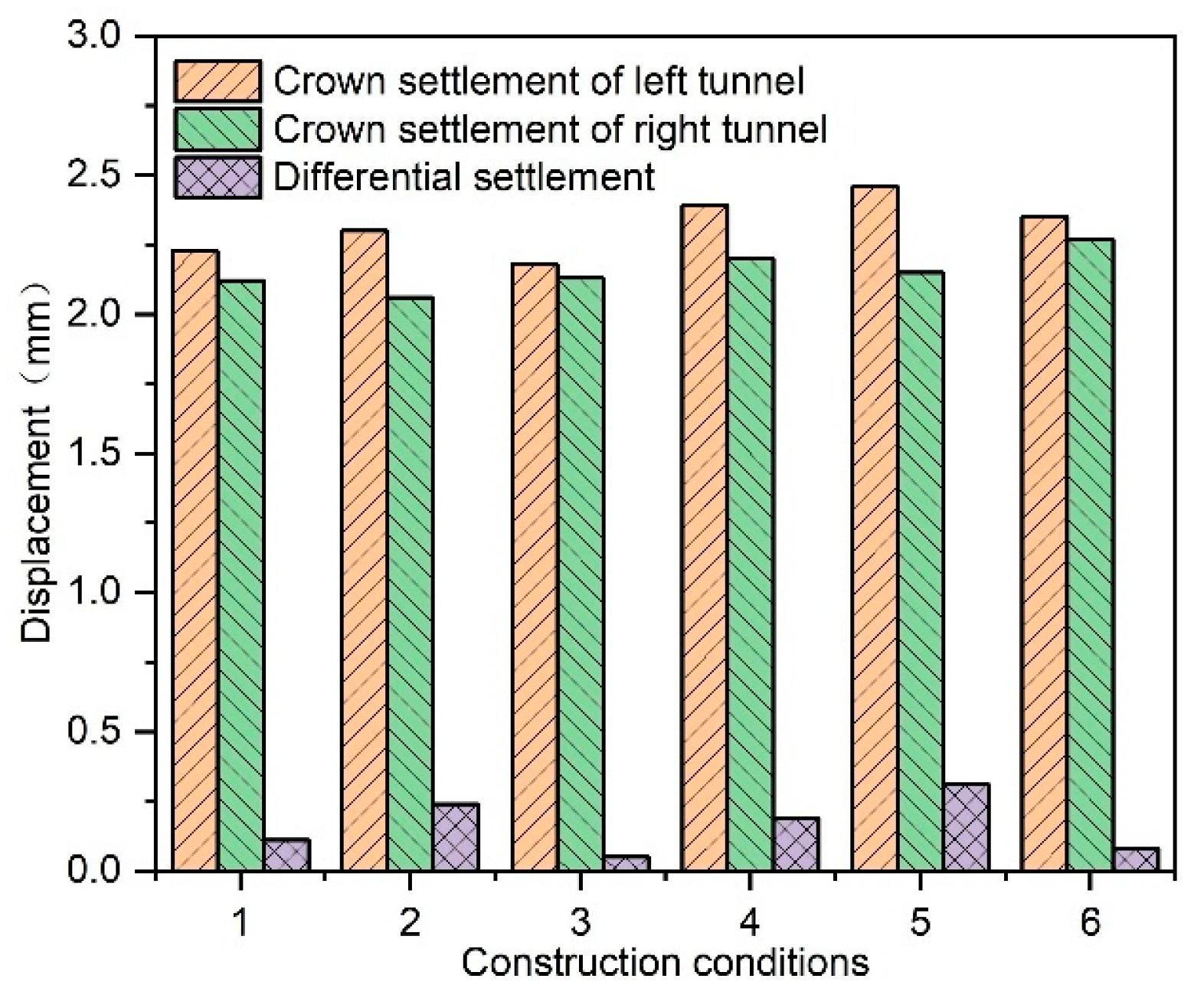
4.1.1. Influence of Excavation Sequence on Surrounding Rock Deformation
4.1.2. Stability Enhancement of the Middle Partition Wall
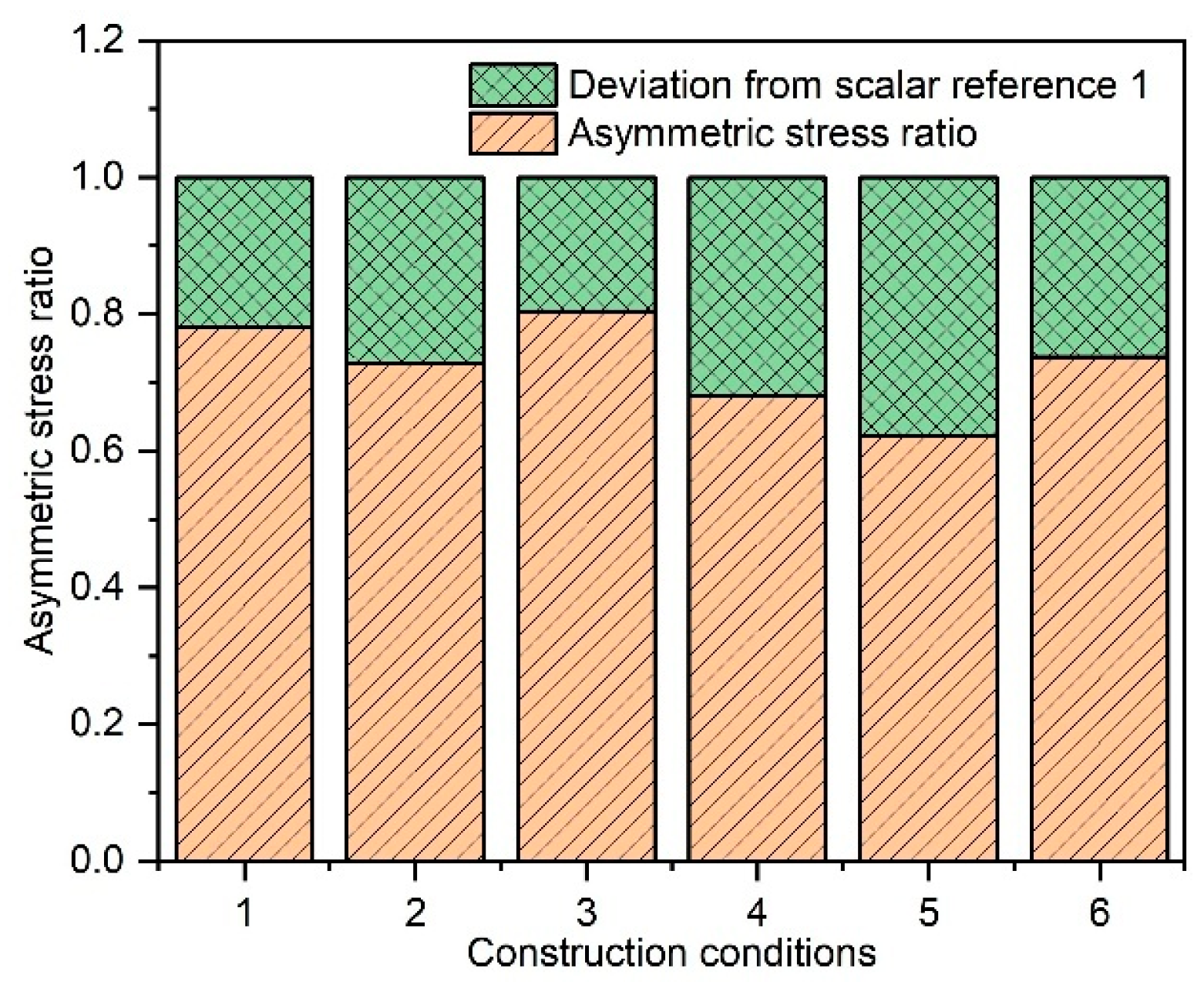
4.1.3. Reduction of Asymmetric Stress Ratios
4.2. Optimization of Rock Bolt Configuration
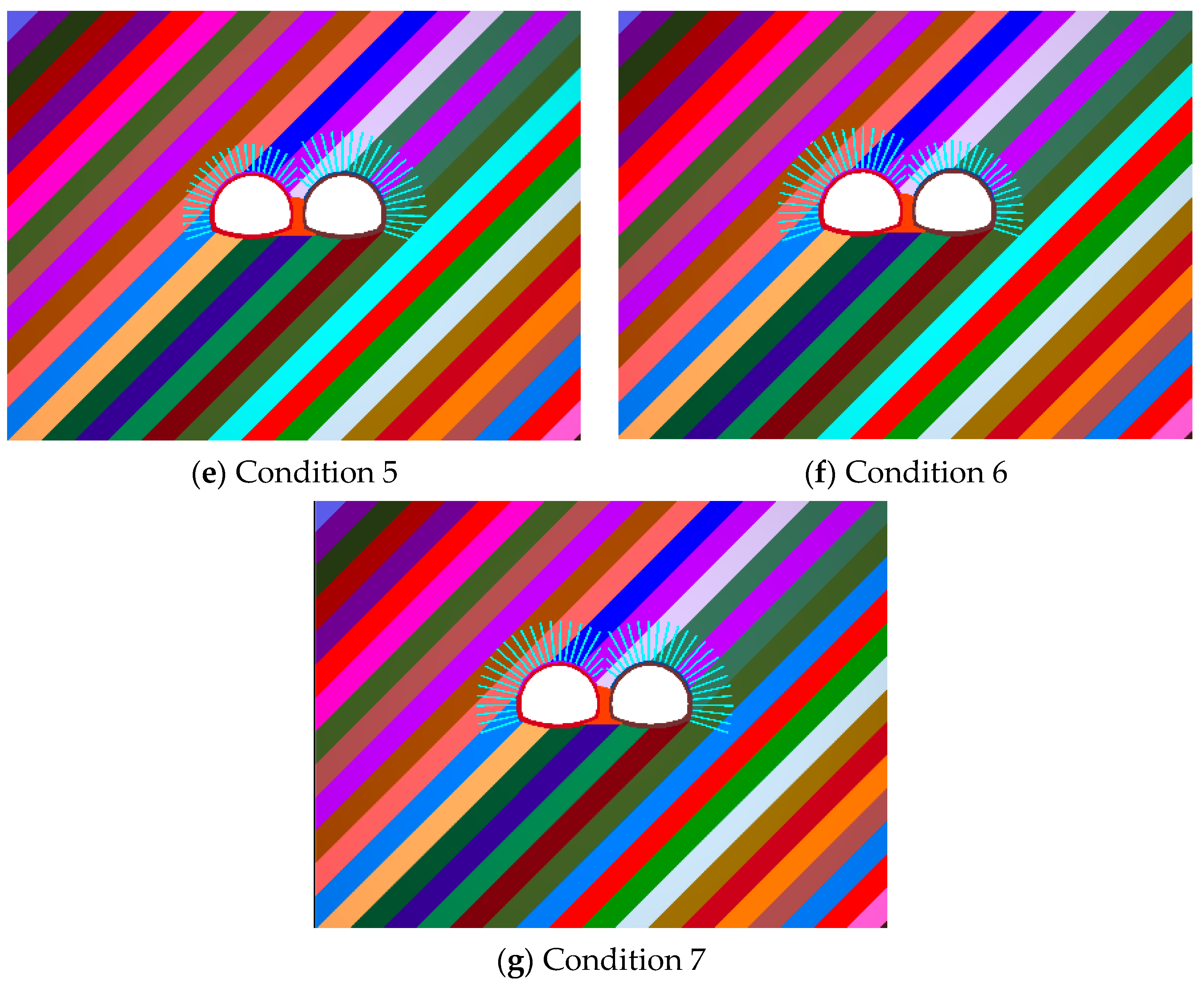
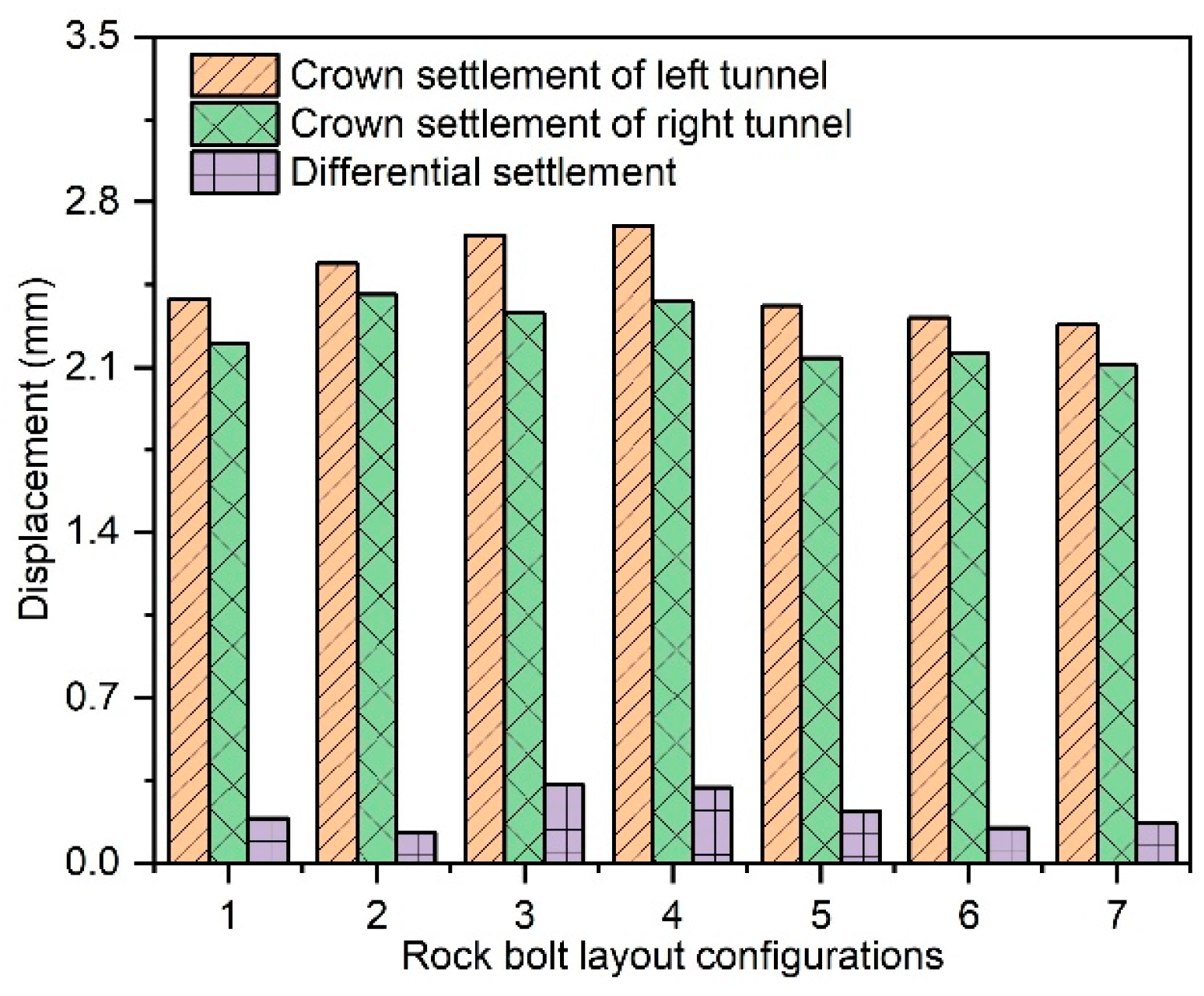
4.2.1. Surrounding Rock Deformation Patterns Under Different Bolt Arrangements
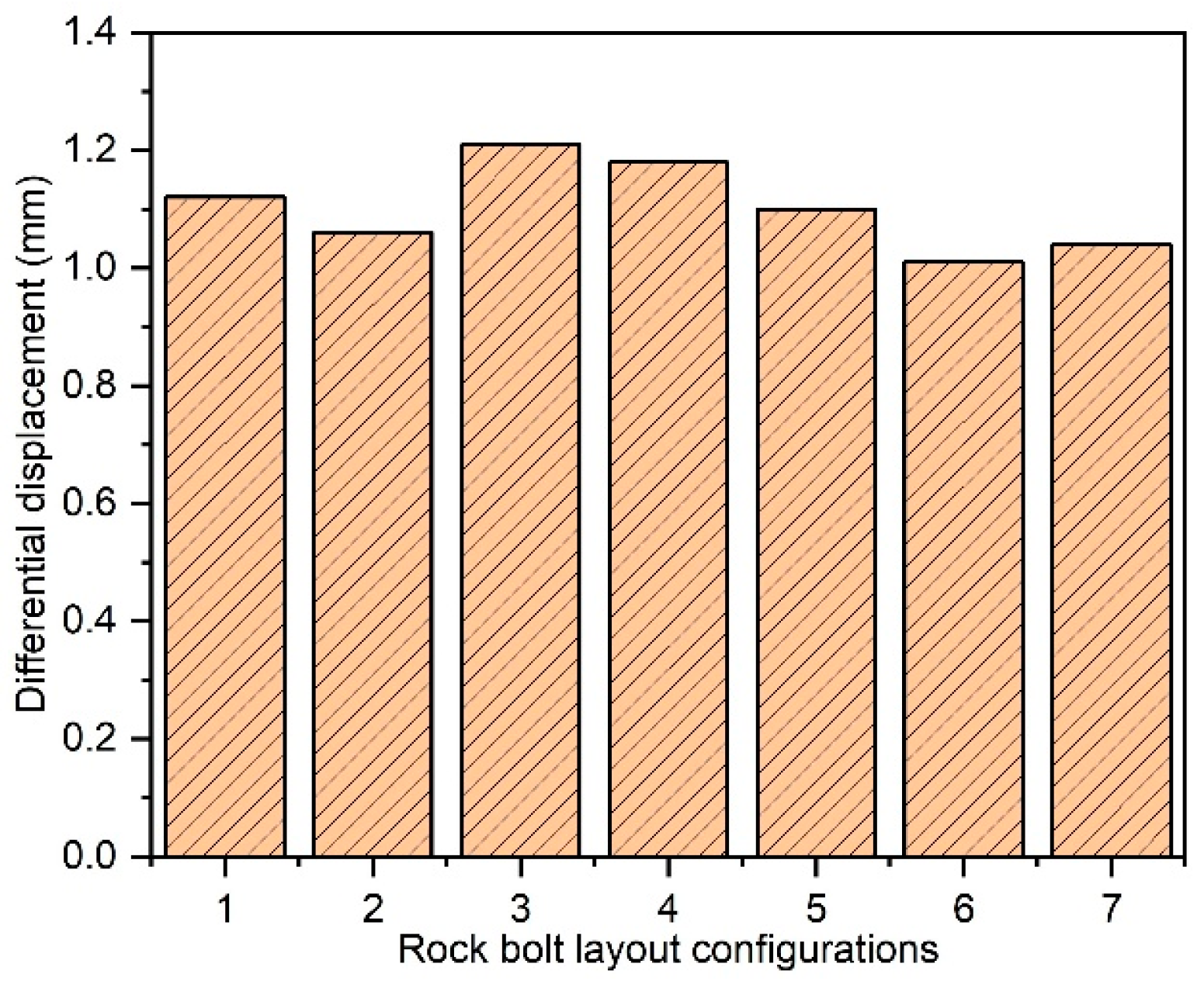
4.2.2. Stability Enhancement of the Middle Partition Wall Under Different Bolt Arrangements
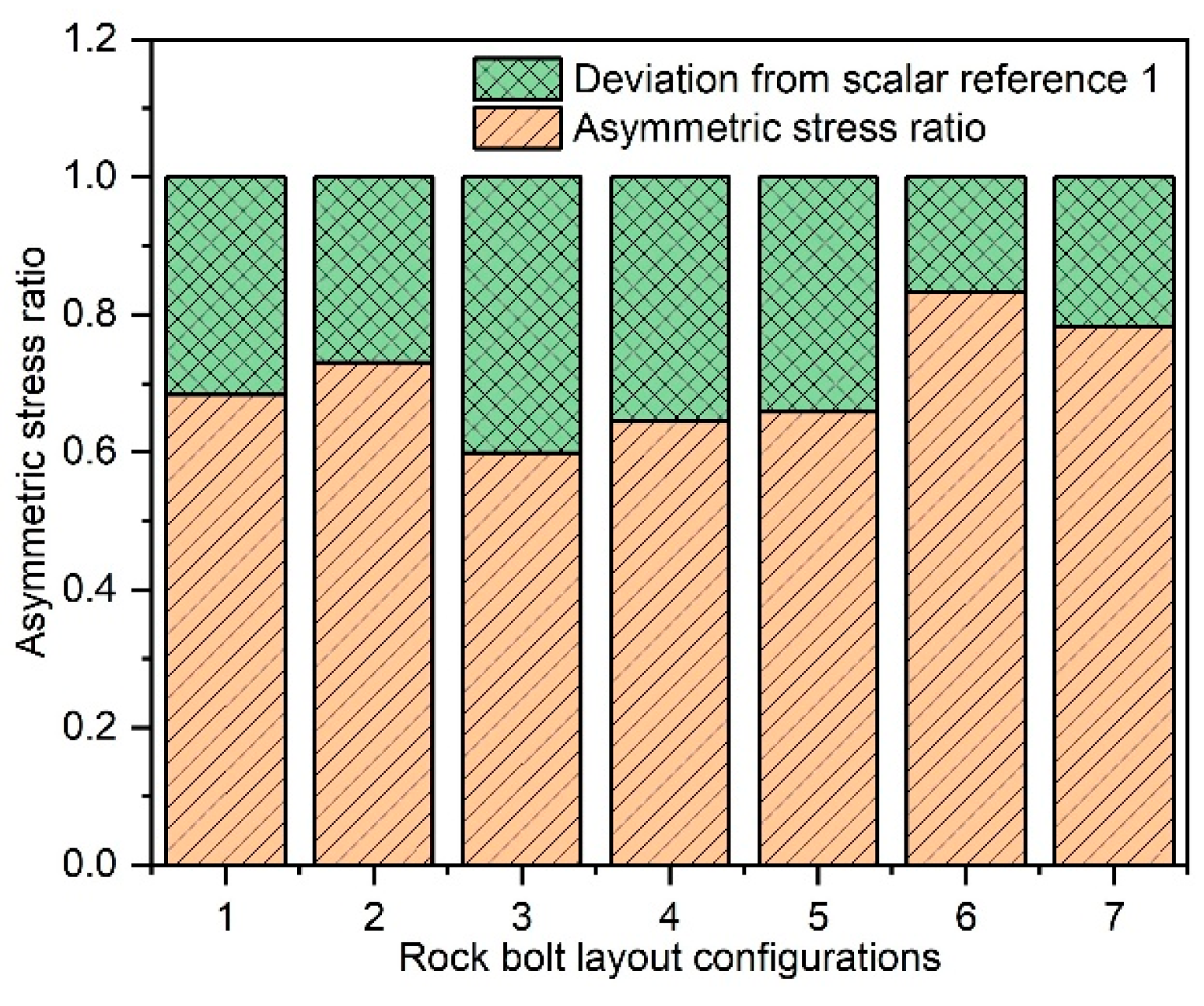
4.2.3. Quantification of BIAS Magnitude Under Different Bolt Arrangements
- (1)
- Angular configuration optimization: dip side bolts perpendicular to rock strata significantly alleviate BIAS.
- (2)
- Length adjustment strategy: counter-dip side bolt lengthening delivers the most pronounced control effect.
5. Conclusions and Outlook
- (1)
- Deformation and stress patterns: In inclined layered jointed rock masses, the maximum downward deformation of surrounding rock occurs at the top of the middle partition wall, while the maximum upward deformation is observed at its base. Counter-dip side deformation exceeds that of the dip side, with crown settlement significantly surpassing convergence deformation. Stress concentrations are higher at the crown and outer haunch on the counter-dip side, whereas the invert and inner haunch on the dip side exhibit greater stress. The BIAS intensity at the crown and inner haunch surpasses that at other locations.
- (2)
- Joint parameter influences: The BIAS intensity initially increases and subsequently decreases with rising joint dip angles, reaching its peak magnitude at approximately 45°. Meanwhile, BIAS progressively diminishes as joint spacing increases, with its influence becoming negligible when spacing exceeds 3.5 m.
- (3)
- Optimization strategies: Construction sequencing with dip-side pilot excavation demonstrates superior BIAS control compared to other sequences. Full-face excavation outperforms the bench method in stress redistribution management. Vertical bolting (90° to bedding planes) on the dip side effectively mitigates BIAS. Lengthening counter-dip side bolts provide enhanced control compared to dip-side adjustments. These findings provide theoretical guidance and technical references for the design and construction of double-arch tunnels in layered jointed rock masses under BIAS configurations.
- (1)
- Conducting multi-physics coupling analyses (e.g., hydro–mechanical–thermal interactions) to elucidate regulatory mechanisms of groundwater seepage and thermal gradients on BIAS evolution in stratified rock masses.
- (2)
- Validating current conclusions through comparative studies across diverse geological settings, particularly high-stress mountainous terrains and soft surrounding rock environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Li, P. A Statistical Analysis of China’s Traffic Tunnel Development Data. Engineering 2018, 4, 3–5. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Xu, Y.; Kulatilake, P.H.S.W.; Huang, X. Physical model test and numerical analysis on the behavior of stratified rock masses during underground excavation. Int. J. Rock Mech. Min. Sci. 2011, 49, 134–147. [Google Scholar] [CrossRef]
- Xing, Y.; Kulatilake, P.; Sandbak, L.A. Rock Mass Stability Investigation Around Tunnels in an Underground Mine in USA. Geotech. Geol. Eng. 2017, 35, 45–67. [Google Scholar] [CrossRef]
- Chen, R.; Luo, Z.Y.; Zhang, L.L.; Li, Z.F.; Tan, R.Q. A new flexible-wall triaxial permeameter for localized characterizations of soil suffusion. Q. J. Eng. Geol. Hydrogeol. 2025, 58, qjegh2023-124. [Google Scholar] [CrossRef]
- Saroglou, C.; Qi, S.W.; Guo, S.; Wu, F. ARMR, a new classification system for the rating of anisotropic rock masses. Bull. Eng. Geol. Environ. 2019, 78, 3611–3626. [Google Scholar] [CrossRef]
- Hatzor, Y.H.; Feng, X.T.; Li, S.J.; Yagoda-Biran, G.; Jiang, Q.; Hu, L.X. Tunnel reinforcement in columnar jointed basalts: The role of rock mass anisotropy. Tunn. Undergr. Space Technol. 2015, 46, 1–11. [Google Scholar] [CrossRef]
- Exadaktylos, G.E.; Stavropoulou, M.C. A closed-form elastic solution for stresses and displacements around tunnels. Int. J. Rock Mech. Min. Sci. 2002, 39, 905–916. [Google Scholar] [CrossRef]
- Cui, Z.D.; Liu, D.A.; Wu, F.Q. Influence of dip directions on the main deformation region of layered rock around tunnels. Bull. Eng. Geol. Environ. 2014, 73, 441–450. [Google Scholar] [CrossRef]
- Mostafaei, H.; Behnamfar, F.; Alembagheri, M. Nonlinear analysis of stability of rock wedges in the abutments of an arch dam due to seismic loading. Struct. Monit. Maint. Int. J. 2020, 7, 295–317. [Google Scholar]
- Yao, Z.; Liu, X.; Pu, J.; Yu, T.; Fang, Y.; Yue, J.; Zhang, W. Influence of Thickness of the Partition Wall on the Bearing Capacity of Double-Arch Tunnel Under Different Buried Depth. Geotech. Geol. Eng. 2024, 42, 5891–5906. [Google Scholar] [CrossRef]
- Yao, S.G.; He, J.N.; Xu, P. The Change in Dynamic Response Distribution of Double-Track Tunnel Structure Caused by Adding Middle Partition Wall. Buildings 2022, 12, 1711. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Huang, D.; Zhong, Z.; Liu, Y.; Peng, J.B. Restraint effect of partition wall on the tunnel floor heave in layered rock mass. J. Mt. Sci. 2024, 21, 2462–2479. [Google Scholar] [CrossRef]
- Min, B.; Zhang, X.; Zhang, C.; Gong, Y.; Yuan, T. Mechanical Behavior of Double-Arch Tunnels under the Effect of Voids on the Top of the Middle Wall. Symmetry 2018, 10, 703. [Google Scholar] [CrossRef]
- Wang, S.Q.; Qiao, C.S.; Xu, G.C.; Zhu, Z.G. Deformation and stress distribution of middle-wall for asymmetrically-loaded double-arch tunnel under complicated geological conditions. Rock Soil Mech. 2007, 28, 449–454. [Google Scholar]
- Yang, S.Q.; Li, X.L.; Zhang, W.; Fan, S.Y.; Liu, L.B. Optimization Analysis of Partition Wall Support Scheme of Multi-Arch Tunnel. Buildings 2024, 14, 490. [Google Scholar] [CrossRef]
- Wang, H.; Chen, R.; Leung, A.K.; Garg, A.; Jiang, Z.L. Pore-Based Modeling of Hydraulic Conductivity Function of Unsaturated Rooted Soils. Int. J. Numer. Anal. Methods Geomech. 2025, 49, 1790–1803. [Google Scholar] [CrossRef]
- Han, C.R.; Bai, S.W.; Wang, Y.P.; Zhang, D.H. Optimum design of rock bolts supporting long-deep tunnel in layered surrounding rock mass. Rock Soil Mech. 2016, 37, 409–414. [Google Scholar]
- Boon, C.W. Study of reinforcement support mechanisms for wide-span horse-shoe-shaped openings in horizontally layered jointed rock using the distinct element method. Rock Mech. Rock Eng. 2019, 52, 1179–1191. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Liu, J.; Chen, R.; Xu, J. Physical and numerical modeling of an inclined three-layer (silt/gravelly sand/clay) capillary barrier cover system under extreme rainfall. Waste Manag. 2015, 38, 210–221. [Google Scholar] [CrossRef]
- Li, Z.F.; Wang, Y.H.; Li, X.; Yuan, Q. Validation of discrete element method by simulating a 2D assembly of randomly packed elliptical rods. Acta Geotech. 2017, 12, 541–557. [Google Scholar] [CrossRef]
- Shi, X.S.; Nie, J.; Zhao, J.; Gao, Y. A homogenization equation for the small strain stiffness of gap-graded granular materials. Comput. Geotech. 2020, 121, 103440. [Google Scholar] [CrossRef]
- Min, B.; Zhang, C.; Zhang, X.; Wang, H.; Li, P.; Zhang, D. Cracking performance of asymmetric double-arch tunnels due to the voids behind linings. Thin-Walled Struct. 2020, 154, 106856. [Google Scholar] [CrossRef]
- Li, C.L.; Wang, S.R.; Wang, Y.G.; Cui, F.; Yang, F. Skewed Pressure Characteristics of Equivalent Load in Double-Arch Tunnel. J. Eng. Technol. Sci. 2016, 48, 345–358. [Google Scholar] [CrossRef][Green Version]
- Dancygier, A.N.; Karinski, Y.S.; Chacha, A. A model to assess the response of an arched roof of a lined tunnel. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2016, 56, 211–225. [Google Scholar] [CrossRef]
- Wang, F.; Ren, Q.; Yang, X.; Chen, B.; Cui, S.; Zhang, Z. Study on Dynamic Response Characteristics of Shallow-Buried and Unsymmetrical-Loaded Double-Arch Tunnel. Geotech. Geol. Eng. 2022, 41, 257–269. [Google Scholar] [CrossRef]
- Dang, B.; Weng, X.; Qin, C.; Chen, Y.; Hu, J. Modeling test study on influence mechanism of large-span double-arch tunnels in proximity to existing tracks. Eng. Fail. Anal. 2024, 165, 108821. [Google Scholar] [CrossRef]
- Wang, J.; Cao, A.; Wu, Z.; Sun, Z.; Lin, X.; Sun, L.; Liu, X.; Li, H.; Sun, Y. Numerical Simulation on the Response of Adjacent Underground Pipelines to Super Shallow Buried Large Span Double-Arch Tunnel Excavation. Appl. Sci. 2022, 12, 621. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Liu, J.; Chen, R. Numerical Investigation on Gas Emission from Three Landfill Soil Covers under Dry Weather Conditions. Vadose Zone J. 2015, 14, vzj2014-12. [Google Scholar] [CrossRef]
- Ma, T.; Li, S.; Li, S.; Xu, X.; Zhang, L.; Ping, Y. Model experimental study of deformation and failure law in excavation of deep rock mass with multi-cleftiness of different angles. Rock Soil Mech. 2016, 37, 2899–2908. [Google Scholar]
- Wang, S.R.; Li, C.L.; Wang, Y.G.; Zou, Z.S. Evolution characteristics analysis of pressure-arch in a double-arch tunnel. Teh. Vjesn.-Tech. Gaz. 2016, 23, 181–189. [Google Scholar]
- Li, W.T.; He, P.; Wang, G.; Zheng, W.; Fan, K.R.; Wang, L.T.; Zheng, C.C. Elastoplastic Solution for Tunnel Composite Support Structures Based on Mohr-Coulomb Criterion. Buildings 2024, 14, 3657. [Google Scholar] [CrossRef]
- Sui, Y.; Cheng, X.; Wei, J. Distributed fibre optic monitoring of damaged lining in double-arch tunnel and analysis of its deformation mode. Tunn. Undergr. Space Technol. 2021, 110, 103812. [Google Scholar] [CrossRef]
- Li, Z.F.; Zhang, Y.F.; Chen, R.; Tai, P.; Zhang, Z.T. Numerical investigation of morphological effects on crushing characteristics of single calcareous sand particle by finite-discrete element method. Powder Technol. 2025, 453, 120592. [Google Scholar] [CrossRef]
- Chen, R.; Chen, Q.; Li, Z.F.; Li, Y.F.; Zhou, Y.F.; Tai, P. An integrated recycling strategy of utilising excavation waste soil in marine clay improvement. Eur. J. Environ. Civ. Eng. 2025, 1–17. [Google Scholar] [CrossRef]
- Niu, Q.F.; Revil, A.; Li, Z.F.; Wang, Y.H. Relationship between electrical conductivity anisotropy and fabric anisotropy in granular materials during drained triaxial compressive tests: A numerical approach. Geophys. J. Int. 2017, 210, 1–17. [Google Scholar] [CrossRef]
- Shi, X.S.; Zhao, J. Practical Estimation of Compression Behavior of Clayey/Silty Sands Using Equivalent Void-Ratio Concept. J. Geotech. Geoenviron. Eng. 2020, 146, 4020046. [Google Scholar] [CrossRef]
- Li, L.; Tian, Z.S.; Guo, X.L.; Yu, Y.; Luo, L.L. Research on large deformation of tunnels with small intervals in squeezing steeply dipping phyllite strata. Chin. J. Rock Mech. Eng. 2019, 38, 276–286. [Google Scholar]
- Bian, X.; Gao, Z.; Zhao, P.; Li, X. Quantitative analysis of low carbon effect of urban underground space in Xinjiekou district of Nanjing city, China. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2024, 143, 105502. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, C.; Lin, G.; Wang, B. Field Monitoring of Deformations and Internal Forces of Surrounding Rocks and Lining Structures in the Construction of the Gangkou Double-Arched Tunnel—A Case Study. Appl. Sci. 2017, 7, 169. [Google Scholar] [CrossRef]
- Sui, Y.; Cheng, X.; Zhao, Z.; Ma, W. Investigation of cracking mechanism of the first tunnel lining during double-arch tunnel construction. Undergr. Space 2024, 14, 1–17. [Google Scholar] [CrossRef]
- Chen, R.; Ng, C.W.W. Impact of wetting-drying cycles on hydro-mechanical behavior of an unsaturated compacted clay. Appl. Clay Sci. 2013, 86, 38–46. [Google Scholar] [CrossRef]
- Zhang, X.; Ye, Z.; Min, B.; Xu, Y. Effect of Voids Behind Lining on the Failure Behavior of Symmetrical Double-Arch Tunnels. Symmetry 2019, 11, 1321. [Google Scholar] [CrossRef]
- Wu, S.; Wu, J.; Liu, D. Research on Construction Sequences and Construction Methods of the Small Clear-Distance, Double-Arch Tunnel under an Asymmetrical Load. Appl. Sci. 2023, 13, 8242. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, J.Y.; Zhu, J.; Zhang, H.X.; Ren, Y.; Wu, J.L.; Lai, J.B.; Zhang, H.; Zhao, H.Y.; Zeng, X. Data-knowledge hybrid driven intelligent prediction method of tunnel excavation profiles geometric deformation. Int. J. Digit. Earth 2025, 18, 2459317. [Google Scholar] [CrossRef]
- Hu, Z.H.; Wu, B.B.; Xu, N.W.; Wang, K. Effects of discontinuities on stress redistribution and rock failure: A case of underground caverns. Tunn. Undergr. Space Technol. 2022, 127, 104583. [Google Scholar] [CrossRef]
- Li, Z.F.; Wang, Y.H.; Chow, J.K. Density Effect and Associated Unjamming Events on the Aging-Induced Stiffness Increase in Sand. Int. J. Geomech. 2018, 18, 4018173. [Google Scholar] [CrossRef]
- Bian, X.; Fan, Z.; Liu, J.; Li, X.; Zhao, P. Regional 3D geological modeling along metro lines based on stacking ensemble model. Undergr. Space 2024, 18, 65–82. [Google Scholar] [CrossRef]
- Tsesarsky, M. Deformation mechanisms and stability analysis of undermined sedimentary rocks in the shallow subsurface. Eng. Geol. 2012, 133, 16–29. [Google Scholar] [CrossRef]
- Oğuzhan, Ç. Nonlinear Constitutive Soil Models for the Soil–Structure Interaction Modeling Issues with Emphasis on Shallow Tunnels: A Review. Arab. J. Sci. Eng. 2023, 48, 12657–12691. [Google Scholar]
- Liu, B.; He, K.; Han, M.; Hu, X.; Wu, T.; Wu, M.; Ma, G. Dynamic process simulation of the Xiaogangjian rockslide occurred in shattered mountain based on 3DEC and DFN. Comput. Geotech. 2021, 134, 104122. [Google Scholar] [CrossRef]
- He, X.; Li, Y. Analysis of stress disturbed zone of tunnel and its influence factors. J. Railw. Sci. Eng. 2019, 16, 2782–2790. [Google Scholar]
- Li, Z.F.; Chow, J.K.; Li, J.H.; Tai, P.; Zhou, Z.S. Modeling of flexible membrane boundary using discrete element method for drained/undrained triaxial test. Comput. Geotech. 2022, 145, 104687. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.H.; Ma, C.H.; Mok, C.M.B. Experimental characterization and 3D DEM simulation of bond breakages in artificially cemented sands with different bond strengths when subjected to triaxial shearing. Acta Geotech. 2017, 12, 987–1002. [Google Scholar] [CrossRef]
- Zhao, J.P.; Wang, X.Y.; Tan, Z.S.; Zhang, C.; Wang, Z.X. Study on the reasonable construction layout of main tunnel in unsymmetrical loading multi-arch tunnel with weak rock. China Civ. Eng. J. 2017, 50, 66–74. [Google Scholar]
- JTG3370.1-2018; Code for Design of Road Tunnel Section 1 Civil Engineering. China Communications Press: Beijing, China, 2019.
- Manquehual, C.J.; Li, C.C.; Shabanimashcool, M.; Grindheim, B.; Lia, L. 3D Numerical Modeling of Rock Mass Failure in an Uplift Test of a Rock Anchor with Focus on the Role of Rock Joints. Rock Mech. Rock Eng. 2025, 58, 2847–2875. [Google Scholar] [CrossRef]
- Peng Dingchao, Y.Y.; Zhang, Y. Spatial Analysis of the Influence of Excavation Construction Methods on the Central Wall of Multi-Arch Tunnels. Mod. Tunn. Technol. 2002, 1, 47–53. [Google Scholar]
- Yu, Q.; Liu, W.; Nie, L.; Dai, S. Characteristic Analysis on Stress Ratio of Unsymmetrical Load Tunnel. J. Jilin Univ. (Earth Sci. Ed.) 2018, 48, 1797–1803. [Google Scholar]
- He, C.; Feng, J.; Jiang, N.; Zhang, Y.; Huang, L. Analysis on the Influence of Rock Joint Characteristics on Failure Mode and Stability of Bedding Tunnel. Chin. J. Undergr. Space Eng. 2020, 16, 599–607. [Google Scholar]
- Wang, W.; Zhu, W. Stability Analysis of Tunnels in Jointed Rock Masses. Mod. Tunn. Nnelling Technol. 2014, 51, 66–72. [Google Scholar]





| Material Type | (kN/m3) | (GPa) | (°) | (GPa) | |
|---|---|---|---|---|---|
| Rock Mass | 20.0 | 1.2 | 0.35 | 25 | 0.2 |
| Primary Support | 23.0 | 27.2 | 0.25 | — | — |
| Middle Partition Wall | 25.0 | 32.5 | 0.20 | — | — |
| Settlement Parameter | Measured Value (mm) | Simulated Value (mm) | Difference (mm) | Error |
|---|---|---|---|---|
| Left Tunnel Crown Settlement | 18.7 | 17.2 | 1.5 | 8.0% |
| Right Tunnel Crown Settlement | 17.6 | 16.0 | 1.6 | 9.1% |
| Material Type | (kN/m3) | (GPa) | (°) | (MPa) | |
|---|---|---|---|---|---|
| Rock Mass | 24.0 | 13.0 | 0.35 | 45 | 1.1 |
| Primary Support | 24.9 | 30.5 | 0.20 | — | — |
| Middle Partition Wall | 25.0 | 31.5 | 0.20 | — | — |
| Secondary Lining | 25.0 | 31.5 | 0.20 | — | — |
| Rock Bolt | 7.8 | 200.0 | 0.31 | — | — |
| Normal Stiffness (GPa) | Tangential Stiffness (GPa) | Tensile Stiffness (kPa) | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|
| 7.5 | 5.0 | 6.0 | 60.0 | 25.0 |
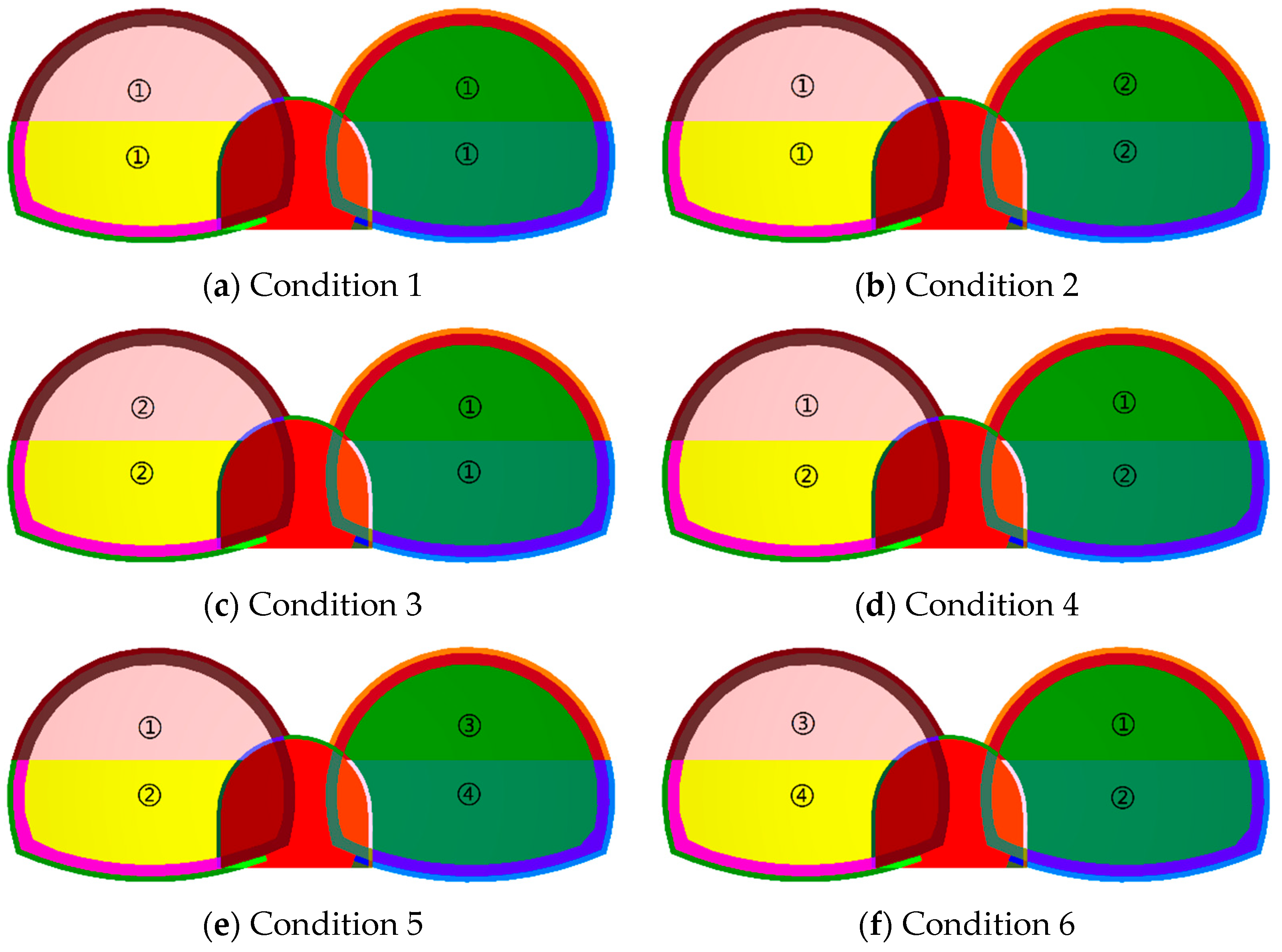
| Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | Condition 6 |
|---|---|---|---|---|---|
| Simultaneous Excavation | Left Tunnel Precedence | Right Tunnel Precedence | Simultaneous Advancement | Left Tunnel Precedence | Right Tunnel Precedence |
| Full-face Excavation Method | Full-face Excavation Method | Full-face Excavation Method | Bench Method | Bench Method | Bench Method |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Li, W.; Xu, L.; Wu, F.; Li, Z.; Tai, P.; Liu, L. Parametric Analysis and Control of Bedding-Inclined Asymmetric Stress in Double-Arch Tunnels: A 3DEC-Based Study on Jointed Rock Masses. Buildings 2025, 15, 1816. https://doi.org/10.3390/buildings15111816
Zhang P, Li W, Xu L, Wu F, Li Z, Tai P, Liu L. Parametric Analysis and Control of Bedding-Inclined Asymmetric Stress in Double-Arch Tunnels: A 3DEC-Based Study on Jointed Rock Masses. Buildings. 2025; 15(11):1816. https://doi.org/10.3390/buildings15111816
Chicago/Turabian StyleZhang, Pai, Wangrong Li, Liqiang Xu, Fengwei Wu, Zaihong Li, Pei Tai, and Leilei Liu. 2025. "Parametric Analysis and Control of Bedding-Inclined Asymmetric Stress in Double-Arch Tunnels: A 3DEC-Based Study on Jointed Rock Masses" Buildings 15, no. 11: 1816. https://doi.org/10.3390/buildings15111816
APA StyleZhang, P., Li, W., Xu, L., Wu, F., Li, Z., Tai, P., & Liu, L. (2025). Parametric Analysis and Control of Bedding-Inclined Asymmetric Stress in Double-Arch Tunnels: A 3DEC-Based Study on Jointed Rock Masses. Buildings, 15(11), 1816. https://doi.org/10.3390/buildings15111816





