Abstract
The overturning resistance of curved single-column pier bridges has garnered increasing attention with the rise in infrastructure demands. However, aspects such as the secondary effects of overturning and the dynamic interactions between vehicles and bridges have not been fully explored. Hence, a refined finite element model incorporating Vehicle–Bridge Interaction (VBI) dynamics has been applied to a highway ramp bridge in this study, aiming to elucidate how VBI-induced vibrations contribute to bridge overturning and to develop effective reinforcement strategies for enhanced stability under eccentric loads. The analysis suggests that the rotation of the main girder, influenced by eccentric overload, is a significant factor in the overturning process. The initial overturning stability coefficient was found to be 0.948, pointing to potential areas for improvement. By implementing targeted reinforcement measures, specifically the addition of cover beams, the stability coefficient was improved to 2.626. The study provides insights into VBI-induced overturning in curved single-column pier bridges, offering a reinforcement strategy aimed at enhancing stability under eccentric loads.
1. Introduction
Single-column pier curved girder bridges have emerged as a preferred choice for urban viaducts due to their small footprint, flexible layout, linear esthetics, and economic advantages [1,2]. However, the safety of these bridges is challenged by off-center and overloaded vehicles [3,4], causing significant social and economic impacts [5,6,7,8]. As illustrated in Figure 1, numerous collapses of single-column pier bridges have occurred in China over the past decade, highlighting the need for a thorough investigation into their overturning stability [9,10,11,12]. Statistical analyses of these accidents indicate that the rollover resistance of single-column pier bridges is often inadequate, particularly under the influence of biased loads from heavy vehicles [13,14,15,16,17]. Nevertheless, the structural integrity of these bridges is generally maintained during overturning, with no significant strength deterioration observed. Consequently, the necessity for reinforcing single-column pier bridges to enhance their overturning resistance is underscored. Currently, four main reinforcement strategies are commonly employed: (i) pier and beam consolidation, (ii) the addition of cover beams, (iii) the widening of pier columns, and (iv) the installation of supplementary anti-draft restraints [18].
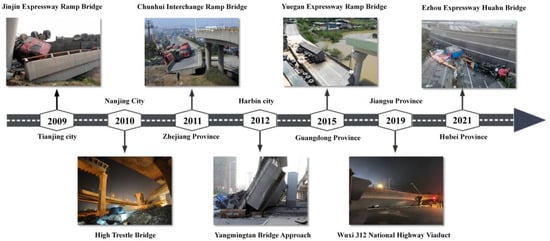
Figure 1.
Summary of overturning accidents of single-pillar pier bridges after 2009.
In recent years, extensive research has been conducted on the overall overturning stability of bridges [19,20,21,22]. Studies on the overturning of curved girder bridges with single-column piers have primarily focused on analyzing the overturning process and developing assessment methods for accidental bridge failures. For instance, Satoko et al. [23] calculated the ratio of flexural and shear capacity of each pier by analyzing the 1995 Hanshin Expressway collapse. The results indicate that flexural failure occurs when is greater than 1.0, while shear failure occurs when is less than 1.0. Fan et al. [24] summarize bridge collapses into three typical overturning failure modes and propose corresponding failure assessment criteria. Peng et al. [25] suggested a new method to predict the overturning loads of single-column pier bridges. The method is called AOLA and has been tested on data and simulations of two collapsed bridges. Dan et al. [26] proposed two technical routes for assessing the potential overturning risk of bridges: traffic load monitoring based on overturning stability coefficients and structural response monitoring based on support angle control. Ge et al. [27] proposed a method to evaluate the overturning risk by monitoring the disengagement state of the support by deriving the support reaction force for multi-point elastic support and the torque for a linkage with a multi-point torsion spring. Cao et al. [28] investigate the stability of bridges against overturning by obtaining the support reactions. He treats the bridge deck as an orthotropic isotropic thin plate, sets up point supports in the domain, and uses the Grey Wolf Optimizer to derive a semi-analytical formulation for the support reaction force. The analysis results show that the proposed method is accurate, efficient, and effective. In the above studies, analytical methods are used to assess and monitor the risk of bridge overturning in the limit state. However, finite element analysis can be used to model actual overturning, which is geometrically, materially, and contact nonlinear. Shi et al. [3] established an ANSYS finite element model based on a field collapse accident of a box truss bridge and investigated the mechanism of toppling failure in the case of eccentric heavy vehicles on box truss bridges. Based on the explicit dynamic finite element method, Ji et al. [29] carried out a nonlinear analysis of the lateral tilting process of steel-concrete composite box girders and established a formula for calculating the risk of overturning. Zhuang et al. [30] used a nonlinear finite element model to evaluate the overturning instability process of the girder under the action of an eccentric heavy vehicle and established the lateral slip equilibrium equations. The results show that typical bridge damage begins with bulging and ends with sliding rather than rigid body overturning. Existing studies are mostly for straight bridges, large radius of curvature, and other typical cases, while for curved girders under the action of flexure-torsion coupling, the force mechanism is more complex. No systematic analysis of the overturning resistance of various forms of single-column arched beams exists [31].
While discrete element and finite element methods have been extensively used for the theoretical analysis and numerical simulation of bridge overturning and collapse, relatively few studies have focused on the variations in the center of gravity of girders during overturning or on the impact of supports on secondary overturning mechanisms [13,32]. Furthermore, in many studies, the beams are often simplified as rigid bodies, with the influence of vehicle–bridge coupled vibrations frequently overlooked. Although there are well-established evaluation and reinforcement methods for straight girder bridges, these approaches are less applicable to single-column pier curved girder bridges due to their unique bending, shear, and torsion characteristics [33,34]. As a result, a comprehensive understanding of the overturning mechanisms in these structures remains incomplete, and there is a need to develop more cost-effective and practical reinforcement strategies tailored to their specific demands.
In this study, a highway ramp bridge in Guangdong was selected as the case study. Two key superstructure modes were identified during the overturning process in a bridge collapse scenario. To thoroughly investigate the overturning mechanism, numerical analysis and finite element simulations were conducted, incorporating the effects of geometric and contact nonlinearity, vehicle–bridge interaction (VBI), and secondary overturning effects. The analysis provided insights into the behavior of single-column pier curved bridges under these conditions and proposed reinforcement strategies that do not significantly alter the original stress distribution of the bridge. The results indicate that the proposed methods align with current design codes [35] and effectively enhance the bridge’s resistance to overturning.
2. Overturning Mechanism of Single-Column Pier Curved
2.1. Overturning Principle
The axis of rotation serves as the foundation for calculating the overturning of single-column piers. Specifically, if the overturning moment generated by the prestressed vehicle on one side exceeds the lateral overturning moment due to the deadweight on the opposite side, the superstructure will rotate around the overturning axis. This calculation method is widely adopted in related research fields for its simplicity. As illustrated in Figure 2, the overturning process of a single-column pier curved girder bridge typically begins with the failure of the support on one side, leading to torsional deformation of the superstructure. This deformation causes lateral instability, resulting in the slipping of the girder, squeezing of the support, and eventual overturning of the bridge.

Figure 2.
Typical failure process of a single-column pier curved bridge.
The issue of support not-loading in single-column pier curved girder bridges during actual overturning is difficult to address. When a multi-span continuous girder partially loses its end support, it effectively transitions into a single-span simply supported girder with a larger span, complicating the achievement of the required flexural load capacity due to the positive cross-section. Furthermore, it has been observed in investigations of bridge overturning accidents that actual overturning in these structures typically initiates well before complete overturning occurs, with damages such as main girder slippage or support extrusion. The continuously changing boundary contact conditions during overturning add to the complexity. To address these challenges, the finite element method has been employed in this study to explicitly analyze and simulate the overturning process, accounting for both geometric and contact nonlinearities.
2.2. Calculation of Anti-Overturning Stability Coefficient Considering the Secondary
For the calculation of bridge overturning stability, SHI et al. [36] propose a method for calculating the anti-overturning moment , overturning moment and overturning stability coefficient based on the rigid body principle, as follows:
where is the support reaction force under the condition of the superstructure; is the vertical distance between the support and the overturning shaft; is the weight of each vehicle; is the vertical distance between the vehicle’s center of mass and the overturned axle.
The aforementioned method assumes that the overturning axis passes through the center of the beam and that the vehicle’s center of gravity remains constant during loading. However, in practice, as the rotation of the main beam increases, the distance between the center of gravity of the main beam and the overturning axis, as well as the distance between the center of gravity of the vehicle and the overturning axis, continuously changes. Additionally, the position of the reaction force generated by the pivot also shifts due to variations in the pivot’s width, as shown in Figure 3.
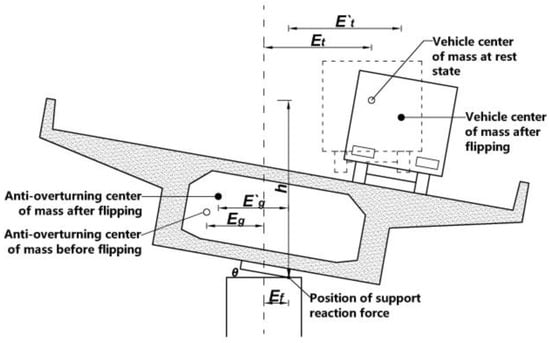
Figure 3.
Torque arm changes in the rotation of the main beam.
In Figure 3, represents the initial distance between the vehicle’s center of mass and the overturned shaft, represents the distance between the center of mass of the vehicle and the position where the reaction force is generated by the support after the main beam is rotated, represents the initial distance between the center of gravity of the main beam and the overturning shaft, represents the distance between the center of gravity of the main beam after rotation and the position where the reaction force is generated.
As can be seen from Figure 3, due to the rotation of the main beam, becomes , and becomes . Since it is difficult to determine the position of the center of gravity of the main beam, the anti-overturning moment is calculated according to the support reaction force. When considering secondary effects, the overturning stability factor is calculated as follows [36]:
where is the anti-overturning moment considering the secondary overturning effect; is the overturning moment considering the secondary overturning effect; represents the height from the vehicle’s center of gravity to the position of the reaction force of the support; represents the distance from the initial position of the reaction force to the position of the final reaction force.
3. Simulation of Bridge Overturning Process
3.1. Project Overview
The ramp bridge is a continuous curved girder bridge consisting of three spans, each with a diameter of 25 m and a total length of 75 m. It features a pier diameter of 1.3 m and a bridge deck width of 8.5 m. The bridge is supported by double support piers at both ends and single-column piers in the middle. There were four heavily loaded vehicles, i.e., C1–4, at the scene of the bridge collapse accident, as shown in Figure 4a, of which C4 drove onto the main girder after the bridge had collapsed and had no effect on the bridge overturning. Due to the presence of a toll station ahead, three overloaded vehicles C1–3 were driving at the same time on the same side of the bridge, slowing down on the side. The main cause of the accident was the overturning and deceleration of C1–3 on the same side of the bridge in the middle of the span. In Figure 4b, the bridge is reversed to the right under the influence of vehicle loads. The anti-overturning center of mass position of the overturned main beam has changed. At the same time, the center of mass of the truck also tilts to the right.

Figure 4.
Accident case. (a) Accident scene. (b) Bridge flipping process.
3.2. Establish Vehicle–Bridge Interaction Model
The motion equation for controlling the vertical vibration of a vehicle can be expressed as follows [37]:
where is the overall mass matrix of the vehicle. is the overall damping matrix of the vehicle. is the overall stiffness matrix of the vehicle. is the vehicle motion matrix. is the matrix of vehicle contact force.
The cross-sectional dimensions of the bridge are shown in Figure 5 and Figure 6, along with the plan view. Based on the structural plan of the collapsed bridge, the dimensions of the main girder were determined, as shown in Figure 7. The main girder was 1.4 m high with a width of 8.5 m at the top flange and 4.0 m at the bottom flange. The two end supports were provided with standard circular rubber supports of 600 mm diameter and 150 mm total thickness, with a distance of 2.55 m between the supports. The single-column pier support at the center of the span is fitted with a standard circular rubber support with a diameter of 850 mm and a total thickness of 150 mm. According to the parameters of the real bridge at the accident site, the modeled main girder is made of C50 concrete with a density of 2500 kg/m3, Young’s modulus of 35.5 GPa, and Poisson’s ratio of 0.2. All piers and abutments were constructed from C30 concrete with a density of 2500 kg/m3, Young’s modulus of 30 GPa, and Poisson’s ratio of 0.2. The supports were modeled using an elastic material with a density of 2200 kg/m3 and Young’s modulus of 400 MPa. Both bridge and vehicle models are modeled using solids [38]. In this study, it is assumed that concrete and rubber support exhibit linear elastic behavior. The model unit is a 3D simplified integral unit C3D8R, with adequate stiffness for contact analysis.
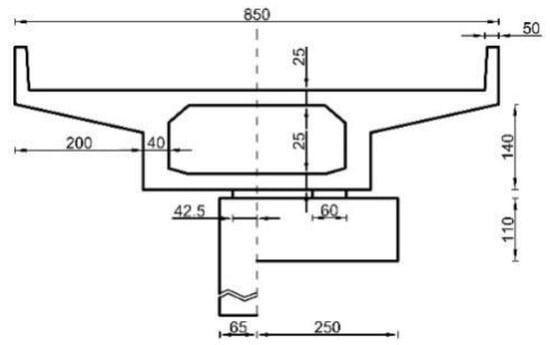
Figure 5.
Section size of the main beam (cm).

Figure 6.
Bridge plan.
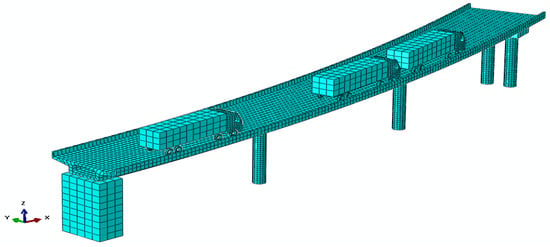
Figure 7.
Finite element model.
The specific parameters of the vehicle are shown in Table 1.

Table 1.
Vehicle parameters.
According to the vehicle survey of the accident at the scene, three vehicles were involved in the overturning of the bridge. According to a simplified calculation considering the loss of cargo, the weight of the vehicles is estimated to be 120 tons. The vehicle parameters are simplified, and the Solid Unit is used to create the complete vehicle model in this paper. The vehicle model is shown in Figure 8, which consists of four parts: body, front end, wheels, and suspension. The suspension part uses multi-point constraints to establish the elastic damping unit to simulate the vehicle suspension system. In the model, the vehicle is not fixed on the bridge deck, as it refers to the actual situation due to gravity driving on the bridge deck. To simulate the overturning of the whole bridge due to overloaded vehicles traveling on the exterior of the bridge deck, a power display analysis is required [39,40]. In the vehicle driving simulation, the vehicle model is based on the following assumptions [41]: (1) all wheels are activated; (2) the vehicle is operated under realistic driving conditions; and (3) the suspension is linear and the damping is viscous. The motion of the vehicle is driven by the rotational angular velocity of the wheels, which determines its direction and velocity.
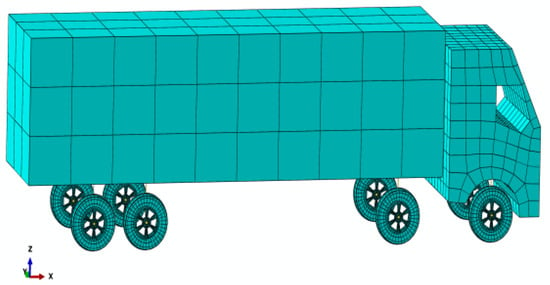
Figure 8.
Vehicle model.
To achieve contact of the vehicle with the bridge, the VBI model is simulated using a surface contact algorithm, which outputs the contact force between the tire and the bridge deck, as shown in Figure 9. The contact property tangential behavior is based on a generic friction formula with a friction coefficient of 0.6, while the normal behavior is based on ‘hard’ contact and allows for separation after contact. To ensure the accuracy of the calculation results of the mutual contact between the wheels and the bridge deck, as well as to ensure the convergence of the VBI model, the wheels and the bridge deck are meshed with hexahedral meshes.
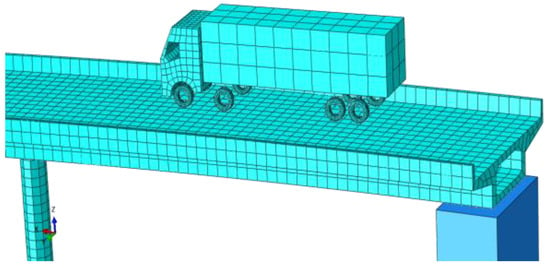
Figure 9.
Axle surface contact interaction.
The vehicle motion uses the set rotational angular velocity of the wheels per unit time to provide power to the vehicle and give it direction and speed of travel. There are three analysis steps established for setting the boundary conditions of vehicle travel, among which the first analysis step (Initial) fixes the bridge boundary and vehicle model to ensure stable deformation of the bridge. In step two of the analysis (Contact step), only the vertical displacement of the vehicle body, front end, and wheels is released. At this time, the wheels and bridge deck enter a contact state and stabilize, and the suspension system enters a working state. In step three of the analysis (Move step), all constraints on the vehicle body and front end are released, and the vehicle mass is borne by the suspension system. At the same time, the vertical and horizontal constraints on each wheel are released, and the rotational angular velocity in the direction of wheel travel is given. At this point, the vehicle begins to move.
3.3. Bridge Overturning Process Analysis
At present, there is no official announcement of the specific driving speed of the vehicle involved in this reference accident. However, based on engineering principles and similar cases, the vehicle’s driving speed is set at 28.8 km/h, which is 8 m/s. Based on the analysis of this accident, the main cause of bridge overturning is severe overloading, which resulted in the overturning of the bridge. The speed of vehicles is considered constant during the time period of the accident.
This model simulates an actual accident scenario, where two vehicles, C2 and C3, are parked in the middle section of the bridge, while the moving vehicle C1 travels from one end of the bridge towards the middle section of the bridge where C2 and C3 are located. The travel time of the vehicle is the time that the moving vehicle C1 travels, and the time required for the vehicle to travel between its actual position and the initial point when the bridge overturns is 1.9 s.
Based on the model analysis, the bridge collapse process is classified into three distinct stages: minor rotation, extensive rotation, and complete overturning. There are two characteristic states, the rotational limit state and the overturning stability limit state, as shown in Figure 10 and Figure 11.

Figure 10.
Rotational limit state.
Figure 11.
Rotation phase.
Under the action of overloaded vehicles, when a vehicle travels to a substantial eccentric position, the rotation angle of the primary beam progressively magnifies, leading to eventual overturning and structural collapse. When the vehicle travel time is 1.90 s, the end support is empty, and the bridge is in the rotation limit state. When the driving vehicle enters the middle span, the rotation angle of the main beam is 3.97°. Subsequently, the main beam experiences a substantial increase in rotation angle, entering the stage of large rotation, as shown in Figure 12. At 2.50 s, the middle pier support was emptied, reaching the limit state of overturning stability, and the bridge completely overturned. The simulation model precisely depicts the structural mechanics from initial support de-emptying until the point of complete overturning. The calculation outcomes align well with the ramp bridge’s inclination during overturning.
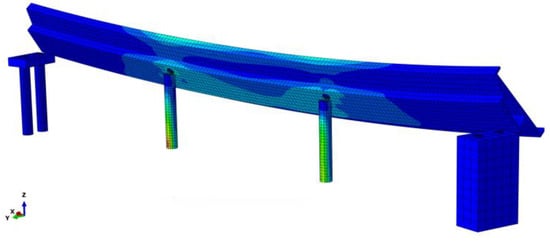
Figure 12.
Overturning stable limit state.
3.4. The Relative Vertical Displacement of the Main Beam During the Overturning Process
The two characteristic points, a and b, located at the bottom of the main beam and the ends of the coplanar surface, are designated as reference points. They were used to calculate the change in vertical relative displacement of the main beam as shown in Figure 13. The results in the figure show that as the overloaded vehicle traveled forward, vertical relative displacements occurred at points a and b during the initial moment. This indicates that the supports P1-2 and P4-2 started to unload, and the main beam started to rotate slightly, and was in the stage of minor rotation. After 1.20 s, the vertical relative displacements at points a and b continued to increase sharply. This indicates that the secondary effect of overturning caused by the rotation of the main girder had a significant impact, leading to the beginning of a large rotation. The slope of the vertical displacement curve at the point starts to increase steeply after 1.90 s, indicating that the bridge is in the limit state of overturning at 1.90 s, and then enters the state of complete overturning.
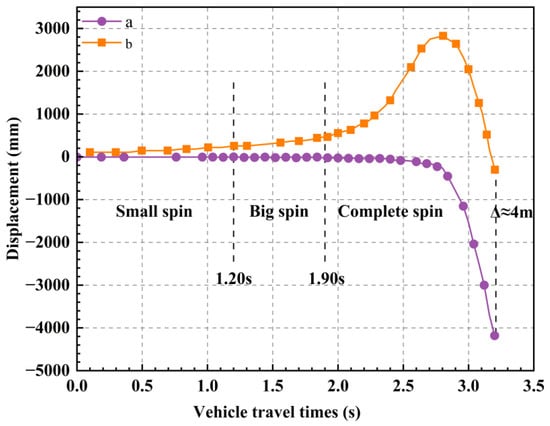
Figure 13.
Vertical relative displacement between a and b.
3.5. Comparison of Calculation Methods for Anti-Overturning Stability
Figure 14 shows the variation in the anti-overturning moment and overturning moment considering the overturning secondary effect. Among them, when the rotation angle of the central pillar support is zero, the overturning secondary effect is not considered because the main beam is not rotated, and the calculation results at this time are equal to the results of Equations (1)–(3). As can be seen from Figure 14, when the overturning secondary effect is not considered, the anti-overturning moment is greater than the overturning moment even under 100% of the total vehicle load. When the overturning secondary effect is considered, the anti-overturning moment reaches the maximum, as the angle of rotation increases and then begins to decrease while the overturning moment continues to increase and finally reaches the critical overturning angle, which causes the bridge to overturn. Table 2 shows a comparison of the results of the overturning stability coefficient calculated by the two calculation methods under different vehicle load ratios.
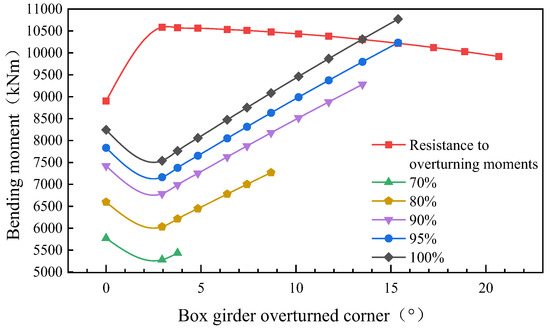
Figure 14.
Overturning and resistance moment under vehicle load for different girder rotations.

Table 2.
Comparison of overturning stability with and without rotation effects.
In Table 2, is the overturning stability coefficient without considering the overturning secondary effect, and is the overturning stability coefficient considering the overturning secondary effect. When the applied load reaches 95% of the total vehicle load, if the overturning secondary effect is not considered, is 1.14; if the overturning secondary effect is considered, is 0.998 less than 1, indicating that the bridge reaches the critical overturning state at this time, and the critical overturning angle of the main beam is θ = 15.9°.
Theoretical analysis and finite element simulation results show that the rotating large deformation of the main beam has a significant effect on the support force position and the overturning force arm. This effect causes the redistribution of support reaction force and overturning moment, which causes overturning and collapse. Therefore, when determining the stability of the bridge against overturning, not only the rotation of the rigid body should be calculated, but also the secondary effect caused by the rotation of the main beam should be considered.
4. Reinforcement Scheme Design
4.1. Reinforcement and Retrofit Principles
According to the structural characteristics, overturning process, force mechanism, bridge operation status, and traffic status of single-column pier curved bridges, the following reinforcement and transformation principles are proposed [42,43,44,45]:
- (1)
- Reinforcement can significantly improve the overturning resistance of single-column pier bridges, and the overturning resistance after reinforcement and transformation meets the requirements of current specifications.
- (2)
- The reinforcement and transformation do not significantly change the stress system of the bridge structure, and minimize the impact on the existing components.
- (3)
- The reinforced bridge fulfills original functional requirements, such as clearance under the bridge and transportation, and minimizes traffic disruption.
- (4)
- Considering the spatial layout of the bridge and its surrounding environment, the transformed appearance accommodates the local surroundings.
4.2. Selection of Reinforcement Program
To meet the requirements of an in-service single-column pier curved girder bridge for overturning resistance, it is common to use the following reinforcement methods in the actual project: pier and beam consolidation, additional cover girders, widening of piers, and additional setting of the restraints against pull-outs [46,47,48].
4.2.1. Pier and Beam Consolidation
Change the support mode of bridge piers, through the radial limit device, which will be the main box girder and abutment connection, leading the original pier single support to solidification. The advantage of this reinforcement scheme is that it can enhance the overturning resistance of the bridge by changing the support mode of the piers, without having to make large-scale changes to the entire bridge structure. This type of reinforcement will increase the construction difficulty, but it remains relatively economical and effective.
4.2.2. Additional Cover Beams
The addition of cover beams, usually made of steel or concrete, can increase the number of pier supports in a curved girder bridge. The addition of steel cover beams and bracing can make the forces on the beams more uniform, reducing the overturning moment due to unbalanced loads. At the same time, due to the high strength and stability of steel, the addition of steel cover beams can effectively enhance the bridge’s load-carrying capacity and overall stability. This method does not require large-scale modification of the bridge structure, reducing the complexity and cost of construction, as shown in Figure 15 and Figure 16.

Figure 15.
Add concrete cover beams.

Figure 16.
Add steel cover beams.
4.2.3. Widening of Piers
When the original width of the bridge piers cannot provide enough support area, wider piers can make up for this deficiency, as shown in Figure 17. A common method of increasing the stability and load-bearing capacity of bridge piers by increasing their cross-sectional area and reinforcement is the concrete outsourcing reinforcement method. This not only increases the cross-sectional stiffness of the piers but also changes the self-oscillation frequency, improving the performance of the bridge during normal use.

Figure 17.
Wider piers and columns.
4.2.4. Additional Setting of the Restraints Against Pull-Outs
The setting of the restraints against pull-outs on both sides of the abutment connects the main girder and the abutment, realizing the close combination between the main girder and the abutment. Under the action of external forces, the force on the piers is more uniform, reducing the deformation of the bridge. It can effectively prevent the accident of bridge overturning caused by the support emptying, and ensure the safety of traveling and the overall stability of the bridge. As shown in Figure 18 [47].

Figure 18.
Additional setting of the restraints against pull-outs.
Considering the particular circumstances of the accident site and taking into account the spatial orientation of the bridge, the clearance under the bridge, and the construction cost constraints, this paper proposes a strengthening solution involving the installation of cover beams and double supports. This approach will effectively strengthen the piers without significantly changing the stress system of the structure.
4.2.5. Comparison and Selection of Reinforcement Schemes
The advantages and disadvantages of the single column pier reinforcement method are summarized in Table 3.

Table 3.
Comparison and selection of reinforcement schemes for single column piers.
4.3. Numerical Simulation Results and Analysis
For the actual situation of the ramp bridge site, the general idea of reinforcement is to change the single support system to a multiple support system to improve the stability of anti-overturning. Specific practice is to increase the cover beam, in the middle pier of the single column to increase the double support. The main function of the support is to absorb the lateral overturning moment and then transfer the moment of the superstructure to the substructure. This effectively reduces the eccentric load effect of the car.
The pier’s cover beam is 1.2 m high and gradually decreases in height on either side to facilitate the support of the cantilevered structure. The cover beam length extends to 5000 mm, with newly added supports positioned at a center distance of 2250 mm. The lower part of the cover beam features a cylindrical reinforcement structure, expanding outward by 0.3 m as illustrated in Figure 19.
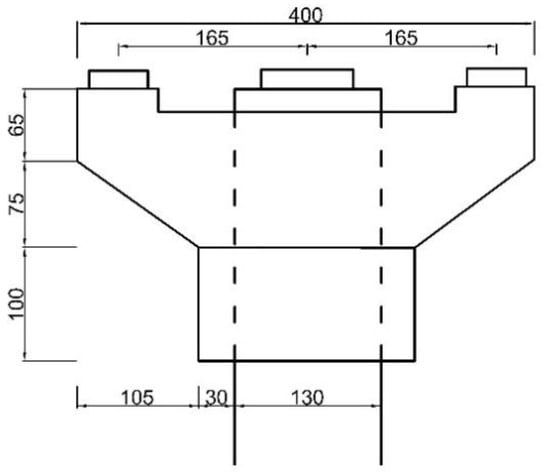
Figure 19.
Schematic diagram of pier reinforcement (cm).
4.4. Reinforcement Pier Column Modeling
The single-column pier reinforcement model is composed of a total of 16,895 elements and 25,878 nodes. The piers, cover beams, and supports are simulated through solid elements. The established model is presented in Figure 20 and Figure 21. Generally, automatic meshing is employed for regular-shaped parts while mapping meshing is used for irregularly shaped parts. After several test comparisons, tetrahedral meshing was used for the model to ensure convergence of the vehicle-axle coupling model. This was due to limitations in the shape of the cover beam structure. The support has been meshed using hexahedral meshing, and the circular middle pier support has been meshed through a neutral axis algorithm, allowing for the effective calculation of contact force for the component.
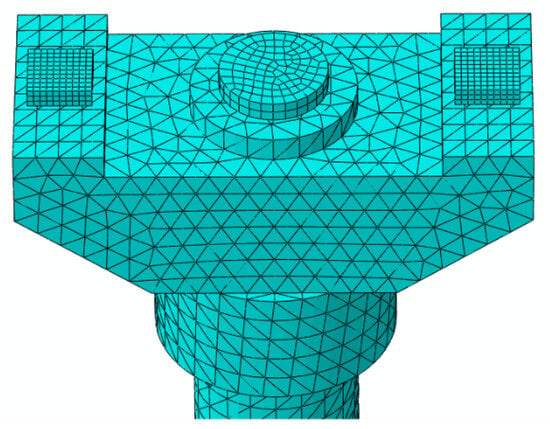
Figure 20.
Reinforced middle pier columns and supports.
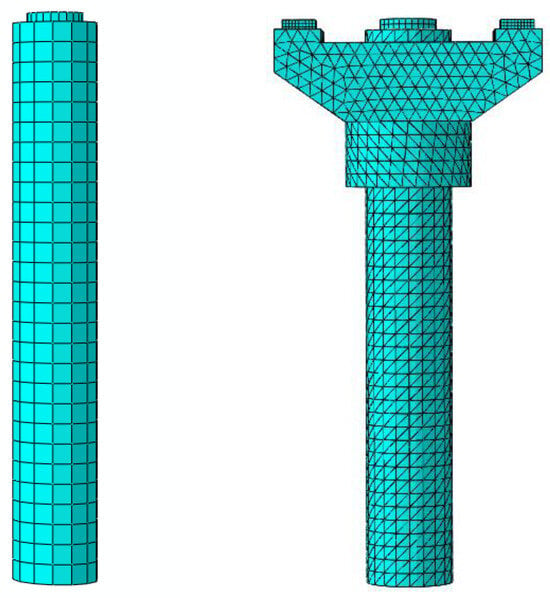
Figure 21.
Comparison of the model of the middle pier column before and after reinforcement.
5. Reinforcement and Retrofit Evaluation
The reinforcement model is an improvement based on the overturning model in Section 3. There are three trucks driving on the bridge, each weighing 120 tons. The bridge is still a continuous curved beam bridge, consisting of three spans, each with a diameter of 25 m and a total length of 75 m. The bridge piers will be improved using the reinforcement measures described in Section 4.
Table 4 displays the reaction force of the bridge support before and after reinforcement. The reinforcement and transformation have led to the redistribution of the reaction forces, with P2-2 and P3-2 of the middle pier support now distributed to the double supports on the reinforced cover beam. As a result, the reaction force of the middle pier support has significantly reduced. Regarding the end supports, the disparity in reaction forces between the strengthened front end supports P1-1 and P1-2 amounts to 493.13 kN, while the variation in reaction forces between P4-1 and P4-2 supports is 499.93 kN. As a result of the bridge structure’s redistribution following reinforcement, the reaction force disparity between the rear end support’s P1-1 and P1-2 supports was measured at 52.68 kN, with the reaction force for P4-1 and P4-2 support registering at 94.09 .

Table 4.
Contrast of reaction forces of reinforced front and rear supports.
The stress distribution diagram of the middle pier support before and after reinforcement is presented in Figure 22. It can be seen that the maximum stress in the center pier support before reinforcement is located at the edge of the support and is distributed in a fan shape. This indicates that, during the overturning process, the middle pier support experienced eccentric load extrusion, leading to rotation and extrusion. This phenomenon corresponds to the collapse of the central pier beam at the accident site. After the reinforcement, the stress on the center pier support was significantly reduced, and the maximum stress value was found at the ipsilateral edge of the double support of the reinforced cover beam. This indicates that the double support of the reinforced cover beam optimizes the stress distribution and confirms the effectiveness of the reinforced structure.
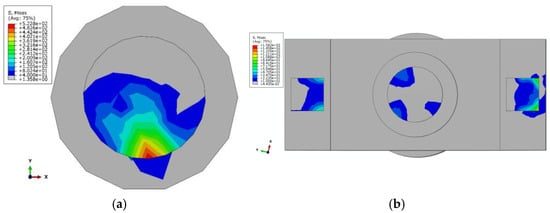
Figure 22.
Stress cloud of reinforcement front and rear supports (MPa). (a) Middle pier support stress before reinforcement. (b) Stress of middle pier support after reinforcement.
The theoretical calculation involves comparing the anti-overturning stability coefficient of the bridge both before and after reinforcement when subjected to secondary forces. As the results are shown in Table 5, the coefficient of stability against overturning of the strengthened bridge increased significantly with an increased ratio of 1.68, which is by the specification criteria. In this study, the reinforcing method of adding cover girders was used to improve the overturning stability coefficient of the single-pier curved girder bridge from the original 0.948 to 2.626. The effectiveness and feasibility of this reinforcement scheme are demonstrated.

Table 5.
Comparison of anti-overturning stability coefficient before and after reinforcement (kN·m).
Two coplanar reference points, a and b, located at both ends of the main beam bottom, were selected to monitor vertical relative displacement and assess overturning stability. The vertical relative displacement of the main beam before and after reinforcement was calculated and plotted in Figure 23. Figure 23 shows the negative vertical displacement of the beam under load. No significant change in displacement was observed during the monitoring period, indicating that the support was empty. In addition, the displacement of the left and right side beams did not show a marked contrast and showed a consistent changing pattern. This indicated that the bridge had no clear tendency to overturn under the operating load of the vehicle. This finding implies the effectiveness of reinforcing the superstructure by adding cover beams.
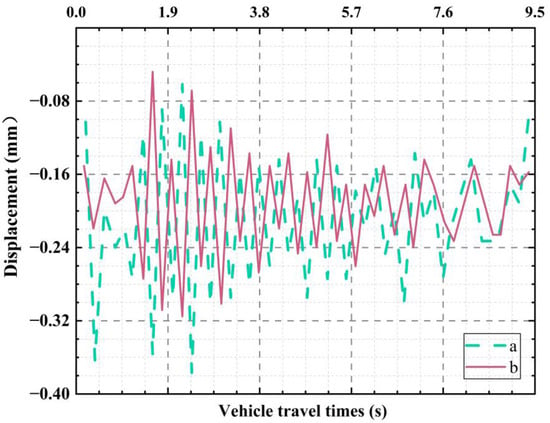
Figure 23.
Maximum displacement monitoring of measurement points.
In this study, a reinforcement method involving the addition of cover beams was implemented to enhance the overturning stability coefficient of single-column pier curved girder bridges. The original coefficient of 0.948 was significantly improved, reaching 2.626, and the overall support force of the bridge was optimized accordingly. The results demonstrate that the proposed technique of incorporating cover girders to augment support significantly improves the overturning stability coefficient of single-column pier curved girder bridges, thereby affirming the efficacy and viability of the reinforcement scheme.
6. Conclusions
This study investigated the overturning mechanism of curved single-column pier girder bridges through the simulation of a vehicle–bridge interaction (VBI) model, leading to the development of a feasible reinforcement scheme. The following conclusions were drawn:
- (1)
- The finite element analysis indicates that the eccentric driving of overloaded vehicles is a primary cause of overturning in single-column pier bridges. The simulation accurately captured the structural-mechanical behavior from the onset of support deflation to complete overturning, establishing both the rotational limit state and the overturning stability limit state. The calculated results closely matched the observed overturning inclination of the ramp bridge.
- (2)
- The analysis revealed that the secondary effect of overturning, caused by the rotation of the main beam, is a critical factor in the stability of the bridge. This effect, influenced by changes in support size and moment arm during rotation, significantly impacts the overturning stability coefficient. Therefore, it is crucial to limit the maximum rotation angle of the main beam and consider the dimensions of the support during the design and reinforcement of bridges to mitigate this secondary effect and enhance stability.
- (3)
- To improve lateral stability in single-column pier curved bridges with insufficient overturning resistance, reinforcement should target the overturning force mechanism. Effective strategies include strengthening piers and girders, adding cover beams, widening piers, and installing additional restraints against pull-out. The design of these reinforcements must consider the specific location and traffic requirements of the bridge.
- (4)
- The addition of cover beams increased the overturning stability coefficient of the original bridge from 0.948 to 2.626, reducing the load on the central pier support and optimizing the overall bridge support system. This study demonstrates that the proposed reinforcement method is effective in improving the overturning stability of curved girder bridges with single-column piers. The analysis and proposed reinforcement scheme offer significant practical value for addressing lateral stability and safety issues in such bridges.
Author Contributions
X.H.: original draft, visualization, software; L.C.: review and editing, formal analysis; Y.Q.: review and editing, formal analysis; X.Y.: review and editing, funding acquisition, methodology, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 52078057); and the Natural Science Foundation of Hunan Province (Grant No. 2023JJ30044).
Data Availability Statement
Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Xu, H.; Li, Q.Y.; Li, D.C.; Jiang, H.N.; Wang, T.; Gao, Q.F. Experimental and Numerical Investigation of the Anti-Overturning Theory of Single-Column Pier Bridges. Sustainability 2023, 15, 1545. [Google Scholar] [CrossRef]
- Xiong, W.; Cai, C.S.; Kong, B.; Ye, J.S. Overturning-Collapse Modeling and Safety Assessment for Bridges Supported by Single-Column Piers. J. Bridge Eng. 2017, 22, 04017084. [Google Scholar] [CrossRef]
- Shi, X.F.; Zhou, Z.J.; Ruan, X. Failure Analysis of a Girder Bridge Collapse under Eccentric Heavy Vehicles. J. Bridge Eng. 2016, 21, 05016009. [Google Scholar] [CrossRef]
- Deng, L.; Wang, W.; Yu, Y. State-of-the-Art Review on the Causes and Mechanisms of Bridge Collapse. J. Perform. Constr. Facil. 2016, 30, 04015005. [Google Scholar] [CrossRef]
- Wardhana, K.; Hadipriono, F.C. Analysis of Recent Bridge Failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef]
- Huber, T.; Kollegger, J.; Suza, D.; Huber, P. The Wieselburg Bridge collapse—Analysis of the shear capacity based on forensic data. Struct. Concr. 2024, 25, 2784–2799. [Google Scholar] [CrossRef]
- Scattarreggia, N.; Salomone, R.; Moratti, M.; Malomo, D.; Pinho, R.; Calvi, G.M. Collapse analysis of the multi-span reinforced concrete arch bridge of Caprigliola, Italy. Eng. Struct. 2022, 251, 113375. [Google Scholar] [CrossRef]
- Schaap, H.S.; Caner, A. Bridge collapses in Turkey: Causes and remedies. Struct. Infrastruct. Eng. 2022, 18, 694–709. [Google Scholar] [CrossRef]
- Xu, F.Y.; Zhang, M.J.; Wang, L.; Zhang, J.R. Recent Highway Bridge Collapses in China: Review and Discussion. J. Perform. Constr. Facil. 2016, 30, 04016030. [Google Scholar] [CrossRef]
- Liu, B.; Han, W.S.; Wang, T.; Feng, Y.; Wang, J.F.; Xu, K. Analytical method for overturning risk assessment of curved girder bridges with single-column piers under heavy-duty vehicles. Structures 2023, 57, 105084. [Google Scholar] [CrossRef]
- Fan, Y.X.; Zhu, J.; Pei, J.J.; Li, Z.; Wu, Y.G. Analysis for Yangmingtan Bridge collapse. Eng. Fail. Anal. 2015, 56, 20–27. [Google Scholar] [CrossRef]
- Saritaş, F. Performance-based seismic assessment of a base-isolated bridge-pier. Eur. J. Environ. Civ. Eng. 2022, 26, 21–38. [Google Scholar] [CrossRef]
- Song, T.Y.; Deng, Q.E.; Li, G.P. Collapse Mechanism and Full-Range Analysis of Overturning Failure of Continuous Girder Bridges. Adv. Mater. Sci. Eng. 2021, 2021, 5547300. [Google Scholar] [CrossRef]
- Song, G.H.; Che, D.L.; Li, M.H. Overturning Axis Selection in Curved Box-Girder Bridges with Single-Column Piers. Math. Probl. Eng. 2018, 2018, 9206138. [Google Scholar] [CrossRef]
- Dong, F.H.; Zhang, H.H. Probabilistic Safety Factor Calculation of the Lateral Overturning Stability of a Single-Column Pier Curved Bridge under Asymmetric Eccentric Load. Symmetry 2022, 14, 1534. [Google Scholar] [CrossRef]
- Wang, Y.L.; Zhou, Y.J.; Xue, Y.X.; Yao, C.W.; Wang, K.L.; Luo, X.C. Failure Analysis for Overall Overturning of Concrete Single-Column Pier Bridges Induced by Temperature and Overloaded Vehicles. Materials 2024, 17, 2650. [Google Scholar] [CrossRef]
- Liu, X.; Jian, S.G.; Song, H.J.; Bo, S.J.; Xu, H.Z. Stability analysis of gravity anchorage: A case study of Taizhou Yangtze River Bridge. Eur. J. Environ. Civ. Eng. 2021, 25, 1002–1024. [Google Scholar] [CrossRef]
- Peng, W.B.; Dai, F.; Taciroglu, E. Research on Mechanism of Overturning Failure for Single-Column Pier Bridge. In Proceedings of the Computing in Civil and Building Engineering (2014), Orlando, FL, USA, 23–25 June 2014; pp. 1747–1754. [Google Scholar]
- Lee, K.; Andrawes, B.; Lim, J.; Kim, H.; Kang, Y. A study on overturning failure of horizontally curved single steel box girders. Eng. Fail. Anal. 2019, 97, 20–31. [Google Scholar] [CrossRef]
- Wang, Y.L.; Tian, J.; Zheng, D.; Jing, D.Y.; Cai, B.Z.; Liu, X.F. A Failure Analysis of the Long-Term Overturning Stability of Concrete Continuous Single-Column Pier Bridges Considering Creep and Overloaded Vehicles. Buildings 2024, 14, 1987. [Google Scholar] [CrossRef]
- Zhang, K.F.; Chen, L.; Cheng, T.; Hu, Z.L. Analysis of stability against lateral overturning during construction period using small-radius curved girder bridge step-by-step method. In Proceedings of the International Conference on Computer Application and Information Security (ICCAIS 2024), Wuhan, China, 25 April 2025; Volume 13562. [Google Scholar]
- Yang, X.Q.; Wang, T.; Liu, B. Overturning Stability Evaluation of Single-Column Pier Bridge Under Eccentric Load of Customized Transport Vehicle. In Proceedings of the 11th International Conference on Traffic and Transportation Studies, Singapore, 10–11 November 2025; pp. 259–267. [Google Scholar]
- Hashimoto, S.; Abe, M.; Fujino, Y. Damage analysis of Hanshin Expressway viaducts during 1995 Kobe earthquake. III: Three-span continuous girder bridges. J. Bridge Eng. 2005, 10, 61–68. [Google Scholar] [CrossRef]
- Fan, D.B.; Zhu, Z.X.; Gu, H.Y.; Wei, J.X.; Peng, W.B. Analytical Method for Bridge Overturning Analysis Coupled with Rigid and Deformable Body Rotation. Int. J. Struct. Stab. Dyn. 2024, 24, 2450166. [Google Scholar] [CrossRef]
- Peng, W.B.; Zhao, H.; Dai, F.; Taciroglu, E. Analytical Method for Overturning Limit Analysis of Single-Column Pier Bridges. J. Perform. Constr. Facil. 2017, 31, 04017007. [Google Scholar] [CrossRef]
- Dan, D.H.; Yu, X.W.; Yan, X.F.; Zhang, K.L. Monitoring and Evaluation of Overturning Resistance of Box Girder Bridges Based on Time-Varying Reliability Analysis. J. Perform. Constr. Facil. 2020, 34, 04019101. [Google Scholar] [CrossRef]
- Ge, L.F.; Dan, D.H.; Yan, X.F.; Zhang, K.L. Real time monitoring and evaluation of overturning risk of single-column-pier box-girder bridges based on identification of spatial distribution of moving loads. Eng. Struct. 2020, 210, 110383. [Google Scholar] [CrossRef]
- Cao, L.; Zhou, H.L.; Peng, W.B.; Liu, J.P.; Chen, Y.F. Analytical analysis on the static support reactions of single-column pier bridges using the grey wolf optimizer. Structures 2023, 55, 2003–2012. [Google Scholar] [CrossRef]
- Ji, X.L.; Zhu, L.; Kai-Leung Su, R.; Wang, G.M. Lateral overturning process and failure mechanism of curved steel-concrete composite box-girder bridges under specific overloading vehicles. Structures 2022, 35, 638–649. [Google Scholar] [CrossRef]
- Zhuang, D.L.; Xiao, R.C.; Jia, L.J.; Sun, B. Failure analysis for overall stability against sliding and overturning of a girder bridge. Eng. Fail. Anal. 2020, 109, 104271. [Google Scholar] [CrossRef]
- Liu, B.; Wang, T.; Mao, M.F.; Han, W.S.; Wang, J.F.; Xu, K. Response characteristics of curved girder bridges with single-column piers during the whole overturning process: Experimental and numerical study. Structures 2024, 66, 106848. [Google Scholar] [CrossRef]
- Scattarreggia, N.; Galik, W.; Calvi, P.M.; Moratti, M.; Orgnoni, A.; Pinho, R. Analytical and numerical analysis of the torsional response of the multi-cell deck of a collapsed cable-stayed bridge. Eng. Struct. 2022, 265, 114412. [Google Scholar] [CrossRef]
- Tang, L.Y.; Yong, Q.P.; She, Y.G.; Mi, X.J.; Wu, D. An approach to simplify the vehicle load in excavation-supporting structures design. Eur. J. Environ. Civ. Eng. 2020, 24, 1589–1605. [Google Scholar] [CrossRef]
- Chen, L.K.; Jiang, L.Z.; Li, R.; Li, Q.; Zhang, M.; Zhang, N.; Luo, J.Z.; Ling, L.; Zhu, S.Y. A feasible vibration measurement and active control method of reinforced concrete lightweight pier railway bridges for heavy-haul monorail trains. Eur. J. Environ. Civ. Eng. 2022, 26, 360–378. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Design Specifications for Strengthening Highway Bridges; China Communications Press: Beijing, China, 2008. [Google Scholar]
- Shi, X.F.; Cao, Z.; Ma, H.Y.; Ruan, X. Failure Analysis on a Curved Girder Bridge Collapse under Eccentric Heavy Vehicles Using Explicit Finite Element Method: Case Study. J. Bridge Eng. 2018, 23, 05018001. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yau, J.D. Vehicle-Bridge Interaction Element for Dynamic Analysis. J. Struct. Eng. 1997, 123, 1512–1518. [Google Scholar] [CrossRef]
- Lu, X.Z.; Kim, C.W.; Chang, K.C. Finite Element Analysis Framework for Dynamic Vehicle-Bridge Interaction System Based on ABAQUS. Int. J. Struct. Stab. Dyn. 2020, 20, 2050034. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, N.; Xia, H.; De Roeck, G. A Compaison Of Diffent Solution Algorithms For The Numerical Analysis of Vehlcle–Bridge Interaction. Int. J. Struct. Stab. Dyn. 2014, 14, 1350065. [Google Scholar] [CrossRef]
- Yang, J.P.; Wu, C.H. Vehicle-Bridge Interaction System with Non-Uniform Beams. Int. J. Struct. Stab. Dyn. 2021, 21, 2150170. [Google Scholar] [CrossRef]
- Greco, F.; Paolo, L.; Pascuzzo, A. A moving mesh FE methodology for vehicle–bridge interaction modeling. Mech. Adv. Mater. Struct. 2020, 27, 1256–1268. [Google Scholar] [CrossRef]
- Zhuang, L.D.; Zhao, J.Z.; Wang, C.; Liang, H.Q.; Tang, M.X. Experimental study on the composite reinforcement method for single-column piers in existing bridges. Structures 2024, 65, 106734. [Google Scholar] [CrossRef]
- Li, T.; Liu, Z.; Zhang, W.M. Analysis of suspension bridges in construction and completed status considering the pylon saddles. Eur. J. Environ. Civ. Eng. 2022, 26, 4280–4295. [Google Scholar] [CrossRef]
- Peng, W.B.; Zhu, Z.X.; Li, C.H.; Shen, Z.N.; Taciroglu, E. Modified Method for Accurate Evaluation of Overturning Limit on Restrainer-Reinforced Single-Column Pier Bridges. J. Bridge Eng. 2024, 29, 04024067. [Google Scholar] [CrossRef]
- Li, J.; Ma, L. Research on quality inspection and reinforcement technology of road bridge. AJST 2024, 10, 51–54. [Google Scholar] [CrossRef]
- Andrawes, B.; DesRoches, R. Comparison between Shape Memory Alloy Seismic Restrainers and Other Bridge Retrofit Devices. J. Bridge Eng. 2007, 12, 700–709. [Google Scholar] [CrossRef]
- Shrestha, B.; Hao, H.; Bi, K.M. Effectiveness of using rubber bumper and restrainer on mitigating pounding and unseating damage of bridge structures subjected to spatially varying ground motions. Eng. Struct. 2014, 79, 195–210. [Google Scholar] [CrossRef]
- Liu, A.R.; Liu, C.H.; Fu, J.Y.; Pi, Y.L.; Huang, Y.H.; Zhang, J.P. A Method of Reinforcement and Vibration Reduction of Girder Bridges Using Shape Memory Alloy Cables. Int. J. Struct. Stab. Dyn. 2017, 17, 1750076. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).