A Stacking Ensemble-Based Multi-Channel CNN Strategy for High-Accuracy Damage Assessment in Mega-Sub Controlled Structures
Abstract
1. Introduction
2. Damage Mechanism and Damage Setting of MSCSS
2.1. MSCSS Modeling
2.2. Damage Mechanism Study of MSCSS
2.3. Damage Modes Setting for MSCSS
2.4. Damage Signal Acquisition and Dataset Preparation for MSCSS
3. Relevant Theories and the Proposed Damage Recognition Method
3.1. Related Theories
- (i)
- Data preparation: Prepare the training dataset, including input features and their corresponding labels.
- (ii)
- Feature selection: Conduct feature selection on the input features, choosing a subset of important features as support vectors.
- (iii)
- Data standardization: Standardize the selected features, ensuring they exhibit zero mean and unit variance characteristics.
- (iv)
- Solving sparse SVM: Solve the optimization problem to obtain the parameters of the sparse SVM model. The objective function for sparse SVM can be expressed as:
- (v)
- Model prediction: Utilize the obtained sparse SVM model to predict new samples. The prediction formula is:
3.2. Methodology
3.3. Experimental Dataset Setting and Training of Damage Recognition Model
- (i)
- Dividing the training samples into k-fold cross-validation samples and performing 5-fold cross-validation experiments for all four base learners, creating training samples for the base learners.
- (ii)
- Training the four base learners on the cross-validation samples, obtaining the prediction results for each base learner, and saving them.
- (iii)
- Concatenating the prediction results of the 12 base learners from the three 1DCNN models and inputting them into the meta-learner.
- (iv)
- The meta-learner takes the concatenated results of the base learners’ outputs as training samples, with the training set labels marked as structural damage types.
- (v)
- Comparing the predictions of the meta-learner with those of the base learners to assess whether the model’s performance after employing the stacking ensemble strategy is superior to that of individual models.
- (i)
- Inputting the test samples into the trained base learners to obtain the prediction results for each base learner.
- (ii)
- Concatenating the prediction results of the base learners from the multi-channel 1DCNN model and inputting them into the meta-learner. The input samples for the meta-learner testing are the concatenated results, and the labels of the test samples are marked as structural damage types.
- (iii)
- Comparing the predictions of the meta-learner with those of the base learners to test whether the performance of the model after using the stacking ensemble strategy is better than that of a single model.
4. Results and Discussion
4.1. Evaluation Indexes
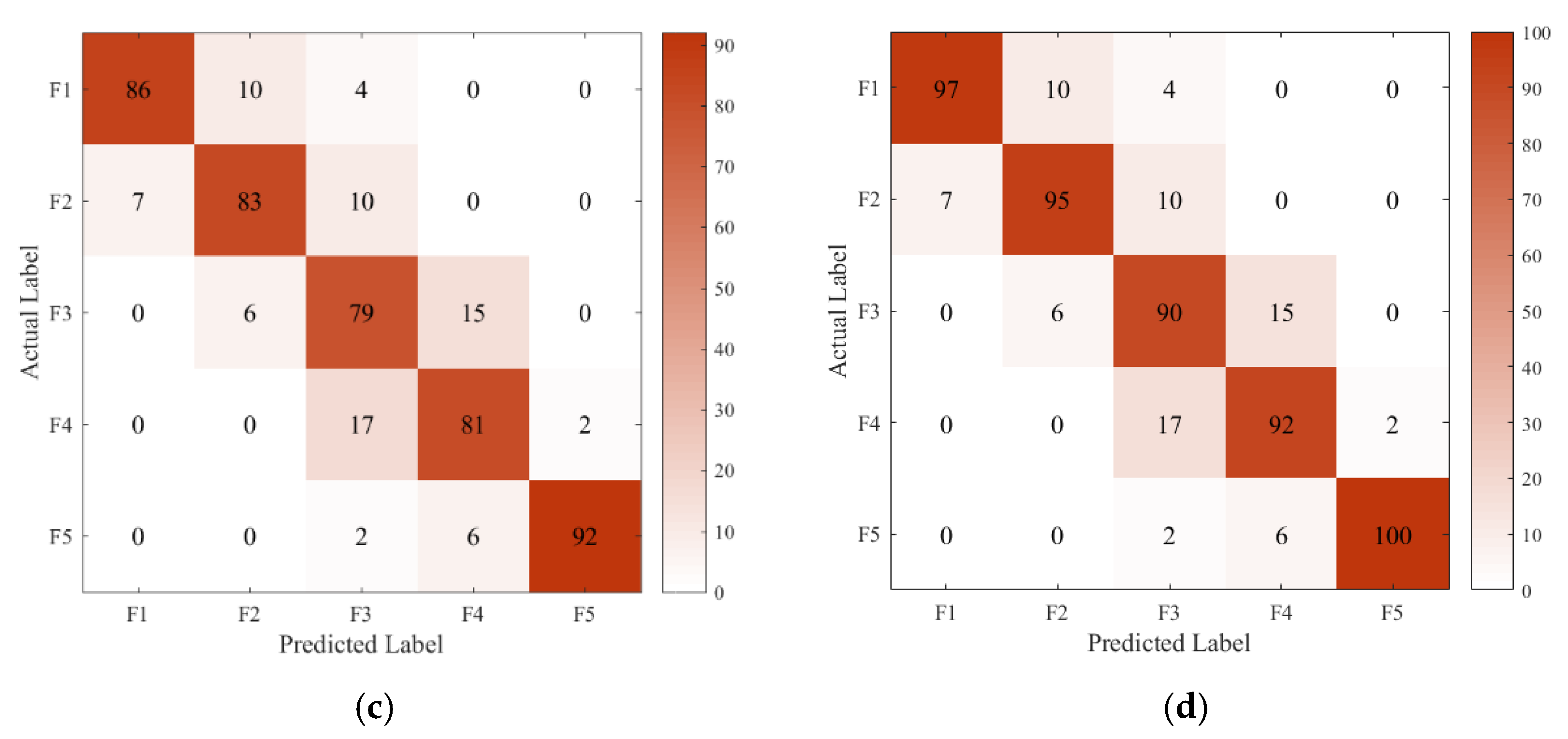
4.2. The Results of Structural Damage Detection
4.3. The Setting of Comparison Methods
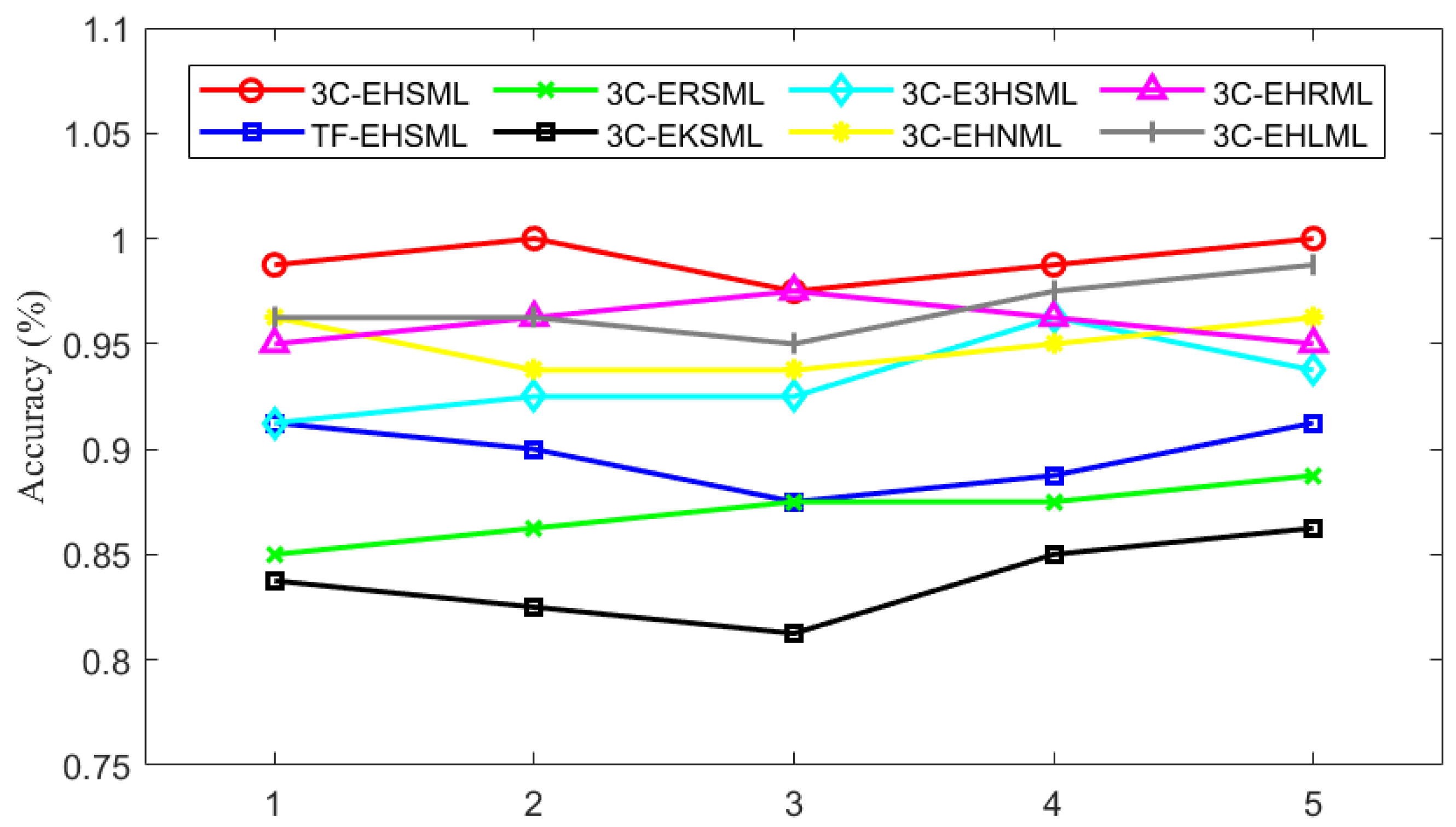
4.4. Performance Comparison of Different Recognition Methods
4.4.1. Comparison of Model Training Performance
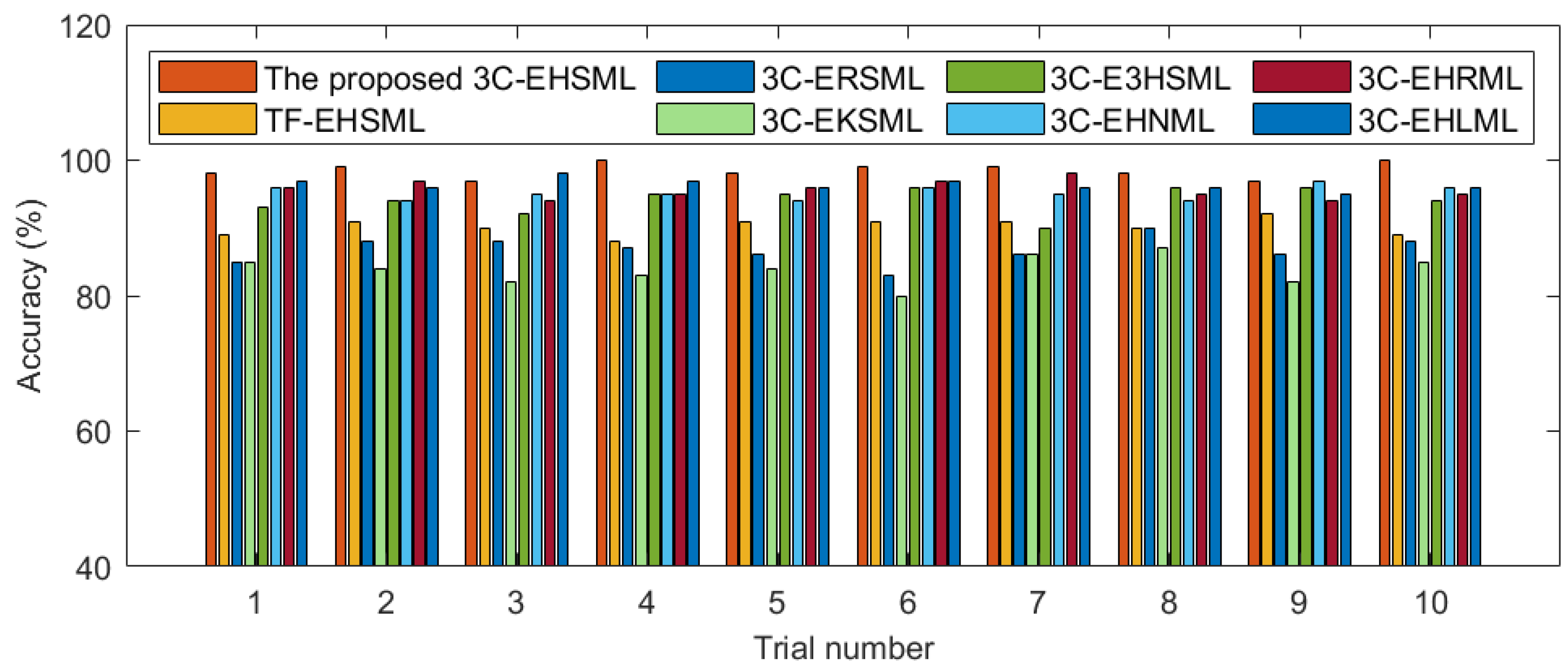
4.4.2. Different Models’ Test Performance Comparison
4.4.3. The Comparison Experiment for Imbalanced Data
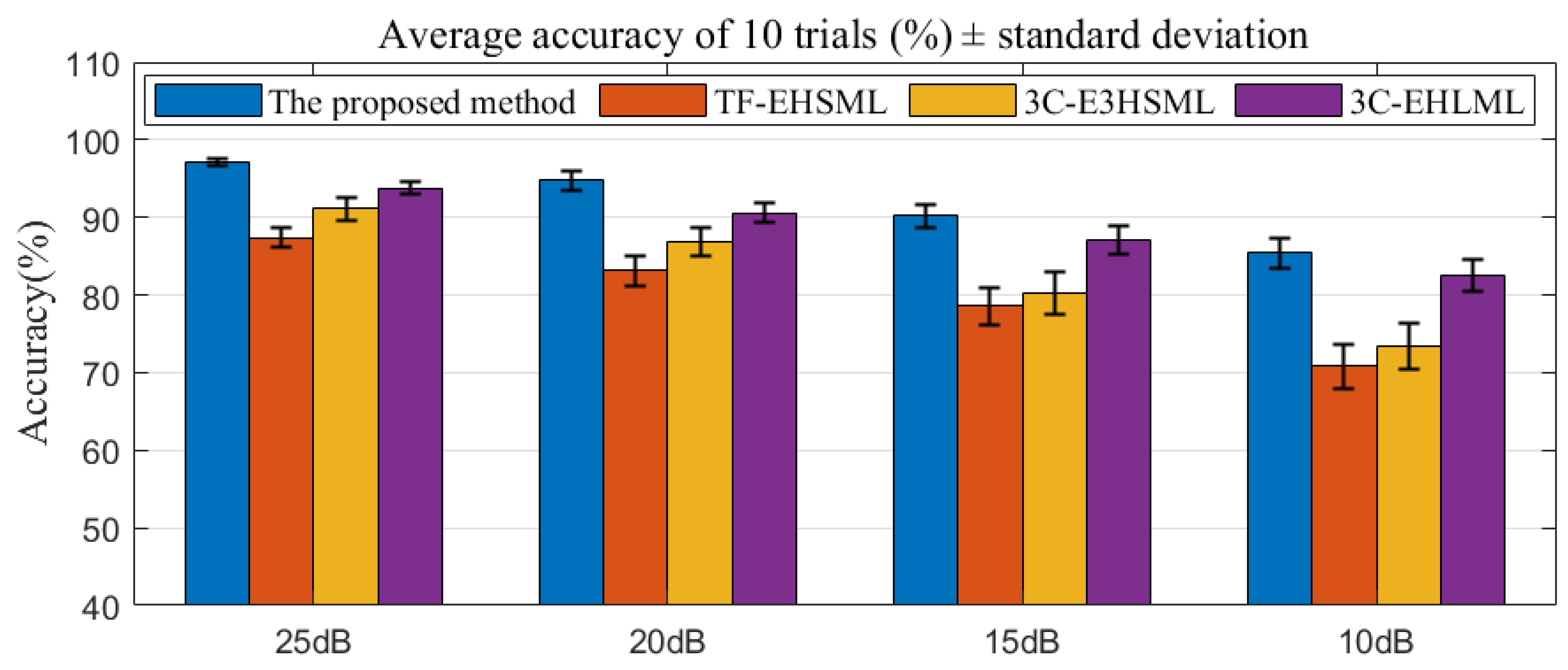
4.4.4. Noise Robustness Analysis
5. Conclusions
- (i)
- The proposed three-channel 1DCNN model eliminates the need for signal selection from three signals and efficiently extracts features from the acceleration response signals of the top structures of the three main components of the MSCSS automatically.
- (ii)
- Damage features extracted based on multi-channel automatic extraction are more representative than time-frequency domain features extracted from damage signals. The average accuracy of damage recognition in the proposed method is 98.5%, which is 8.3% higher than the method based on time-frequency domain features.
- (iii)
- Stacking heterogeneous ensemble learning classifiers avoids the impact of improper classifier selection on the classification effectiveness of damage modes. The superiority of stacking heterogeneous ensemble learning classifiers over homogeneous ensemble learning classifiers has been demonstrated, with the accuracy of heterogeneous ensemble learning classifiers being at least 7% higher.
- (iv)
- The proposed method performs better than the comparison methods in handling imbalanced datasets. Additionally, the noise robustness of the proposed damage recognition method is demonstrated when noise is added to the structural acceleration response signals.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bao, Y.; Chen, Z.; Wei, S.; Xu, Y.; Tang, Z.; Li, H. The State of the Art of Data Science and Engineering in Structural Health Monitoring. Engineering 2019, 5, 234–242. [Google Scholar] [CrossRef]
- Wang, R.; Li, J.; An, S.; Hao, H.; Liu, W.; Li, L. Densely Connected Convolutional Networks for Vibration Based Structural Damage Identification. Eng. Struct. 2021, 245, 112871. [Google Scholar] [CrossRef]
- Ardani, S.; Akintunde, E.; Linzell, D.; Azam, S.E.; Alomari, Q. Evaluating POD-Based Unsupervised Damage Identification Using Controlled Damage Propagation of Out-of-Service Bridges. Eng. Struct. 2023, 286, 116096. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H. Structural Health Monitoring by a New Hybrid Feature Extraction and Dynamic Time Warping Methods under Ambient Vibration and Non-Stationary Signals. Measurement 2019, 134, 548–568. [Google Scholar] [CrossRef]
- Fan, G.; Li, J.; Hao, H. Vibration Signal Denoising for Structural Health Monitoring by Residual Convolutional Neural Networks. Measurement 2020, 157, 107651. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal Processing Techniques for Vibration-Based Health Monitoring of Smart Structures. Arch. Comput. Methods Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, Y.; Mi, J.; Liu, W.; Liu, L. Detecting Structural Damage under Unknown Seismic Excitation by Deep Convolutional Neural Network with Wavelet-Based Transmissibility Data. Struct. Health Monit. 2021, 20, 1583–1596. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A Review of Vibration-Based Damage Detection in Civil Structures: From Traditional Methods to Machine Learning and Deep Learning Applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Ding, Z.; Hou, R.; Xia, Y. Jaya-Based Long Short-Term Memory Neural Network for Structural Damage Recognition with Consideration of Measurement Uncertainties. Int. J. Struct. Stab. Dyn. 2022, 22, 2250161. [Google Scholar] [CrossRef]
- Han, F.; Dan, D.; Xu, Z.; Wu, Y.; Wang, C.; Zhang, Y. A Vibration-Based Approach for Damage Recognition and Monitoring of Prefabricated Beam Bridges. Struct. Health Monit. 2022, 21, 169–184. [Google Scholar] [CrossRef]
- Gao, K.; Chen, Z.D.; Weng, S.; Zhu, H.P.; Wu, L.Y. Detection of Multi-Type Data Anomaly for Structural Health Monitoring Using Pattern Recognition Neural Network. Smart Struct. Syst. 2022, 29, 129–140. [Google Scholar]
- Arul, M.; Kareem, A. Data Anomaly Detection for Structural Health Monitoring of Bridges Using Shapelet Transform. Smart Struct. Syst. 2022, 29, 93–103. [Google Scholar]
- Cawley, P. Structural Health Monitoring: Closing the Gap between Research and Industrial Deployment. Struct. Health Monit. 2018, 17, 1225–1244. [Google Scholar] [CrossRef]
- Fujino, Y.; Siringoringo, D.M.; Ikeda, Y.; Nagayama, T.; Mizutani, T. Research and Implementations of Structural Monitoring for Bridges and Buildings in Japan. Engineering 2019, 5, 1093–1119. [Google Scholar] [CrossRef]
- Shan, J.; Zhang, H.; Shi, W.; Lu, X. Health Monitoring and Field-Testing of High-Rise Buildings: A Review. Struct. Concr. 2020, 21, 1272–1285. [Google Scholar] [CrossRef]
- Çelebi, M.; Sanli, A.; Sinclair, M.; Gallant, S.; Radulescu, D. Real-Time Seismic Monitoring Needs of a Building Owner—And the Solution: A Cooperative Effort. Earthq. Spectra 2004, 20, 333–346. [Google Scholar] [CrossRef]
- Wu, J.; Hu, N.; Dong, Y.; Zhang, Q.; Yang, B. Wind Characteristics Atop Shanghai Tower during Typhoon Jongdari Using Field Monitoring Data. J. Build. Eng. 2021, 33, 101815. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Xia, Y.; Liao, W.Y.; Ko, J.M. Technology Innovation in Developing the Structural Health Monitoring System for Guangzhou New TV Tower. Struct. Control Health Monit. 2009, 16, 73–98. [Google Scholar] [CrossRef]
- Feng, M.Q.; Chai, W. Design of a Mega-Sub Controlled Building System under Stochastic Wind Loads. Probab. Eng. Mech. 1997, 12, 149–162. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, X.; Cherry, S.; Zhou, Y. A New Proposed Passive Mega-Sub Controlled Structure and Response Control. J. Earthq. Eng. 2009, 13, 252–274. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Jiang, J. The Controlling Mechanism and the Controlling Effectiveness of Passive Mega-Sub-Controlled Frame Subjected to Random Wind Loads. J. Sound Vib. 2005, 283, 543–560. [Google Scholar]
- Wang, X.; Zhang, X.; Shahzad, M.M.; Shi, X. Fragility Analysis and Collapse Margin Capacity Assessment of Mega-Sub Controlled Structure System under the Excitation of Mainshock-Aftershock Sequence. J. Build. Eng. 2022, 49, 104080. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Shahzad, M.M.; Shi, X. Research on Dynamic Response Characteristics and Control Effect of Mega-Sub Controlled Structural System under Long-Period Ground Motions. Structures 2021, 29, 225–234. [Google Scholar] [CrossRef]
- Li, X.; Tan, P.; Wang, Y.; Zhang, X. Shaking Table Test and Numerical Simulation on a Mega-Sub Isolation System under Near-Fault Ground Motions with Velocity Pulses. Int. J. Struct. Stab. Dyn. 2022, 22, 2250026. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Olsen, K.B.; Singh, S.K. Wave-Guide Effects in Subduction Zones: Evidence from Three-Dimensional Modeling. Geophys. Res. Lett. 2000, 27, 433–436. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, Y.; Li, M.; Xin, J.; Peng, L. Long Period Ground Motion Simulation and Its Application to the Seismic Design of High-Rise Buildings. Soil Dyn. Earthq. Eng. 2021, 143, 106619. [Google Scholar] [CrossRef]
- Gunes, N. Effects of Near-Fault Pulse-Like Ground Motions on Seismically Isolated Buildings. J. Build. Eng. 2022, 52, 104508. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, H.; Qian, H.; Liu, J. Comparative Vulnerability Analysis of Decomposed Signal for the LRB Base-Isolated Structure under Pulse-Like Ground Motions. J. Build. Eng. 2022, 59, 105106. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, S.; Zhao, K.; Li, Z.; Yang, Q.; Liu, Z. An Efficient Diagnostic Strategy for Intermittent Faults in Electronic Circuit Systems by Enhancing and Locating Local Features of Faults. Meas. Sci. Technol. 2024, 35, 036107. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Z.; Jia, Z.; Li, Z. Incipient Fault Diagnosis of Analog Circuit with Ensemble HKELM Based on Fused Multi-Channel and Multi-Scale Features. Eng. Appl. Artif. Intell. 2023, 117, 105633. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.; Zhang, F.; Li, J.; Liu, X. An Ensemble Method with DenseNet and Evidential Reasoning Rule for Machinery Fault Diagnosis under Imbalanced Condition. Meas. Sci. Technol. 2023, 214, 112806. [Google Scholar] [CrossRef]
- Li, G.; Zheng, Y.; Liu, J.; Zhou, Z.; Xu, C.; Fang, X.; Yao, Q. An Improved Stacking Ensemble Learning-Based Sensor Fault Detection Method for Building Energy Systems Using Fault-Discrimination Information. J. Build. Eng. 2021, 43, 102812. [Google Scholar] [CrossRef]
- Lin, G.; Zhang, Y.; Cai, E.; Li, J.; Wang, X. An Ensemble Learning Based Bayesian Model Updating Approach for Structural Damage Recognition. Smart Struct. Syst. 2023, 32, 61–81. [Google Scholar]
- Sarmadi, H.; Entezami, A.; Saeedi Razavi, B.; Yuen, K.-V. Ensemble Learning-Based Structural Health Monitoring by Mahalanobis Distance Metrics. Struct. Control Health Monit. 2021, 28, e2663. [Google Scholar] [CrossRef]
- Zou, H.; Wei, Z.; Su, J.; Zhang, Y.; Wang, X. Relation-CNN: Enhancing Website Fingerprinting Attack with Relation Features and NFS-CNN. Expert Syst. Appl. 2024, 247, 123236. [Google Scholar] [CrossRef]
- Fang, Y.L.; Li, C.P.; Wu, S.X.; Yan, M.H. A New Approach to Structural Damage Identification Based on Power Spectral Density and Convolutional Neural Network. Int. J. Struct. Stab. Dyn. 2024, 22, 2250056. [Google Scholar] [CrossRef]
- Roshid, M.H.; Maeda, K.; Phan, L.T.; Manavalan, B.; Kurata, H. Stack-DHUpred: Advancing the Accuracy of Dihydrouridine Modification Sites Detection via Stacking Approach. Comput. Biol. Med. 2024, 169, 107848. [Google Scholar]
- Aval, S.B.B.; Mohebian, P. Joint Damage Identification in Frame Structures by Integrating a New Damage Index with Equilibrium Optimizer Algorithm. Int. J. Struct. Stab. Dyn. 2022, 22, 2250056. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, Z.; Gan, Y.; Li, Z. A Deep Forest-Based Fault Diagnosis Scheme for Electronics-Rich Analog Circuit Systems. IEEE Trans. Ind. Electron. 2021, 68, 10087–10096. [Google Scholar] [CrossRef]
- Hamidian, P.; Soofi, Y.J.; Bitaraf, M. A Comparative Machine Learning Approach for Entropy-Based Damage Detection Using Output-Only Correlation Signal. J. Civ. Struct. Health Monit. 2022, 12, 975–990. [Google Scholar] [CrossRef]
- Zhang, J.; Sato, T.; Iai, S.; Hutchinson, T. A Pattern Recognition Technique for Structural Identification Using Observed Vibration Signals: Linear Case Studies. Eng. Struct. 2008, 30, 1439–1446. [Google Scholar] [CrossRef]
- Ebrahimi-Mamaghani, A.; Koochakianfard, O.; Rafiei, M.; Alibeigloo, A.; Saeidi Dizaji, A.; Borjialilou, V. Machine Learning, Analytical, and Numerical Techniques for Vibration Analysis of Submerged Porous Functional Gradient Piezoelectric Microbeams with Movable Supports. Int. J. Struct. Stab. Dyn. 2024, 22, 22500549. [Google Scholar] [CrossRef]
- Vettoruzzo, A.; Bouguelia, M.-R.; Rögnvaldsson, T. Meta-Learning for Efficient Unsupervised Domain Adaptation. Neurocomputing 2024, 574, 127264. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, X.; Xing, S.; Sun, C.; Chen, X. Sparse Representation Theory for Support Vector Machine Kernel Function Selection and Its Application in High-Speed Bearing Fault Diagnosis. ISA Trans. 2021, 118, 207–218. [Google Scholar] [CrossRef]

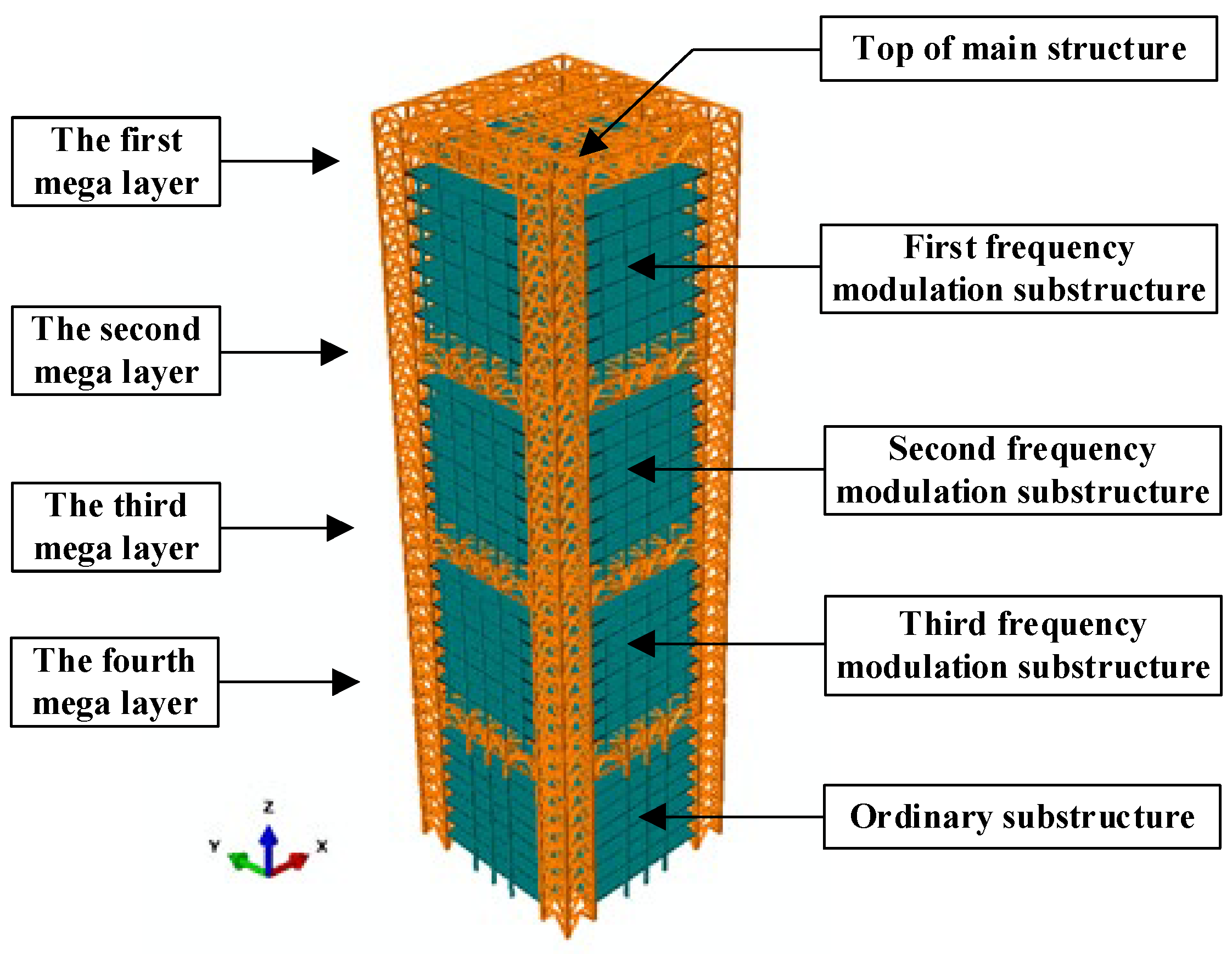
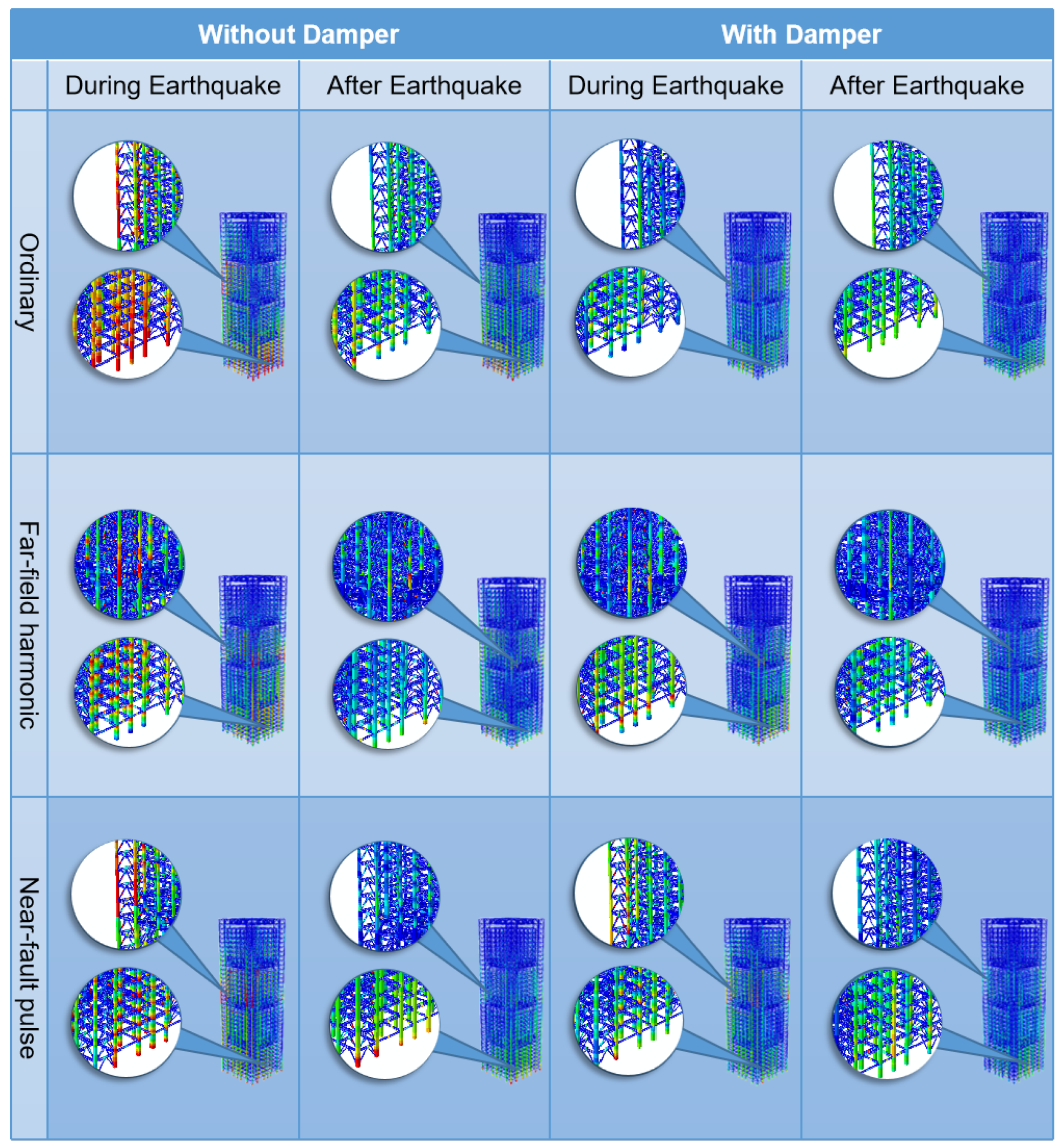


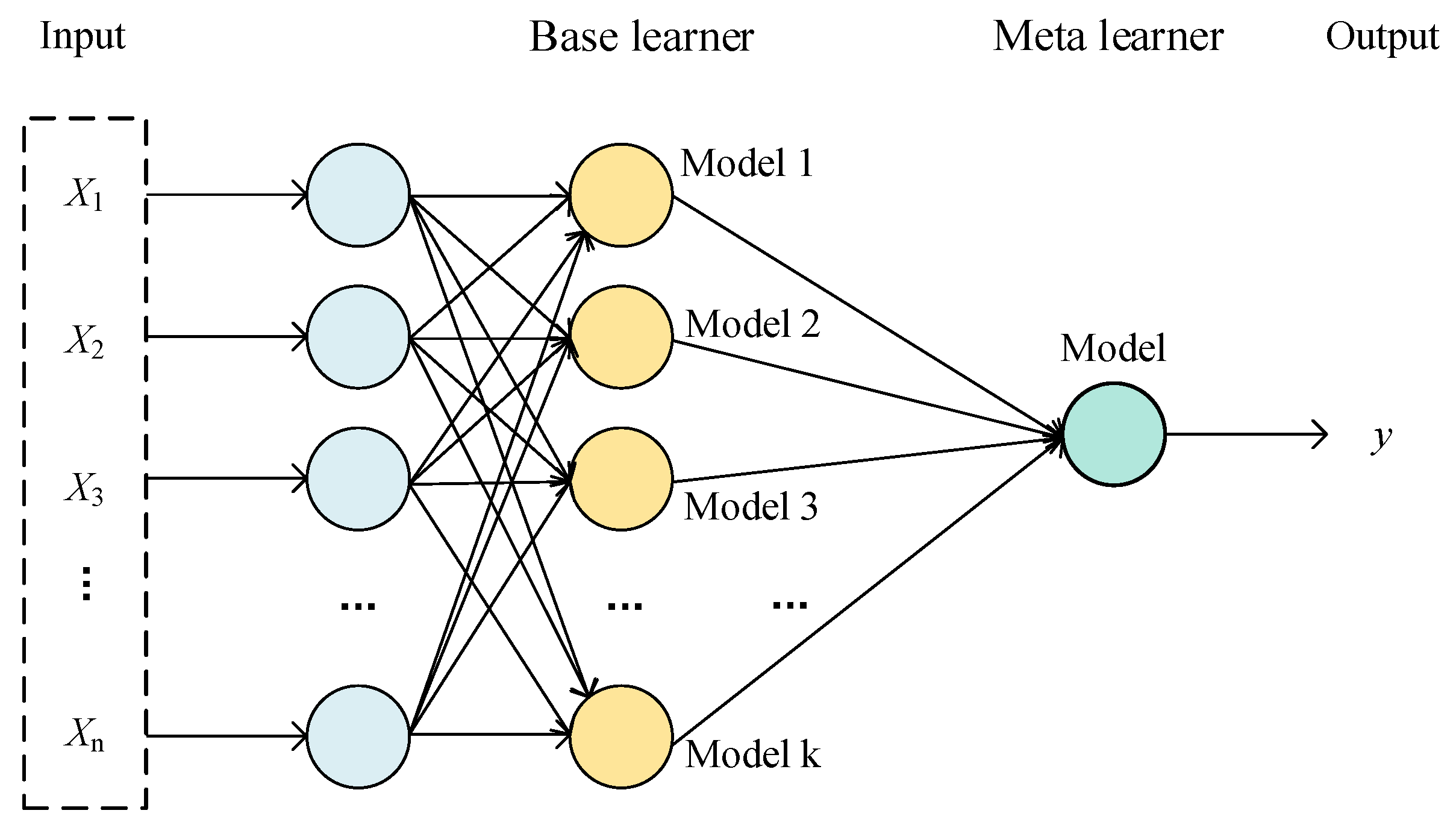
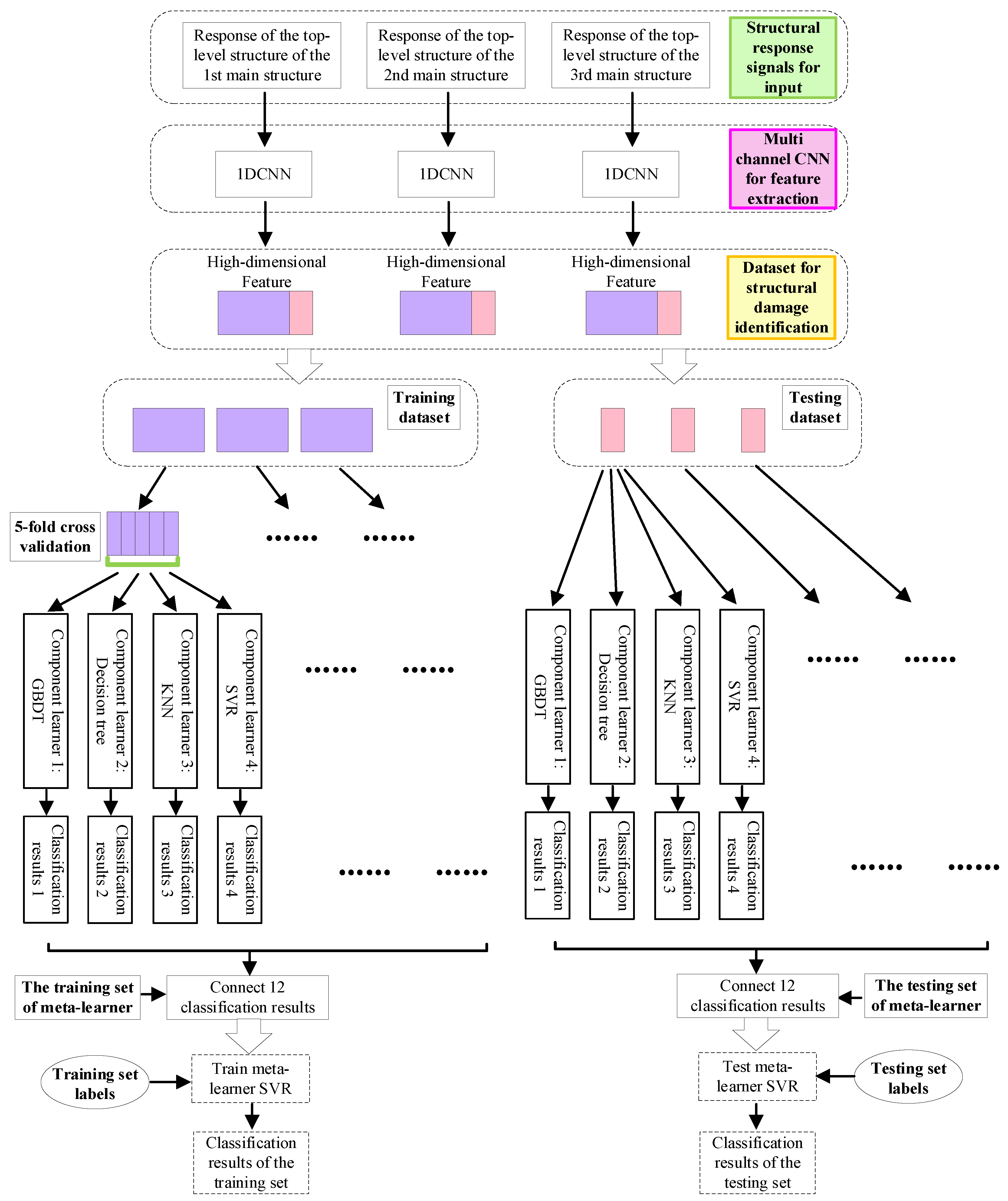


| Component | Section Codes | Section Dimensions (mm) | Area (m2) | Ix (m4) | Iy (m4) |
|---|---|---|---|---|---|
| Giant columns | MC1-2 MC3-4 | ☐ 800 × 800 × 34 × 34 ☐ 600 × 600 × 20 × 20 | 0.1042 0.0464 | 0.0102 2.61 × 10−3 | 0.0102 2.61 × 10−3 |
| Giant beams | MB1 MB2-4 | H 588 × 300 × 12 × 20 H 582 × 300 × 12 × 17 | 0.0186 0.0168 | 1.133 × 10−3 9.79 × 10−4 | 9.008 × 10−5 7.66 × 10−5 |
| Giant layer beam braces | MBBr1-3 MBBr4 | ☐ 350 × 350 × 20 × 20 ☐ 300 × 300 × 16 × 16 | 0.0264 0.0182 | 4.809 × 10−4 2.451 × 10−4 | 4.809 × 10−4 2.451 × 10−4 |
| Giant layer column support | MCBr | ☐ 250 × 250 × 14 × 14 | 0.0132 | 1.231 × 10−4 | 1.231 × 10−4 |
| Beams in giant columns | MCB1-2 MCB3-4 | H 582 × 300 × 12 × 17 H 500 × 250 × 10 × 18 | 0.0168 0.0137 | 9.79 × 10−4 6.101 × 10−4 | 7.66 × 10−5 4.730 × 10−5 |
| Substructure beam | SC1-2 SC3-4 | ☐ 800 × 800 × 28 × 28 ☐ 600 × 600 × 20 × 20 | 0.0865 0.0464 | 8.600 × 10−3 2.61 × 10−3 | 8.600 × 10−3 2.61 × 10−3 |
| Substructure column | SB | H 500 × 250 × 10 × 18 | 0.0136 | 6.06 × 10−4 | 4.69 × 10−5 |
| Damage Mode Code | Damage State Descriptions |
|---|---|
| MSCSS-F1 | Undamaged State |
| MSCSS-F2 | Setting 30% damage to all components in the second giant layer |
| MSCSS-F3 | Setting 50% damage to all components in the second giant layer |
| MSCSS-F4 | Setting 30% damage to all components in the fourth giant layer |
| MSCSS-F5 | Setting 50% damage to all components in the fourth giant layer |
| GBDT | RF | SVR | KNN | ||||
|---|---|---|---|---|---|---|---|
| n_estimators | 200 | n_estimators | 230 | C | 10 | n_neighbors | 12 |
| learning_rate | 0.15 | max_depth | 20 | epsilon | 0.6 | weights | uniform |
| max_depth | 6 | min_samples_split | 30 | kernel | sigmoid | algorithm | auto |
| min_samples_split | 30 | min_samples_leaf | 25 | gamma | auto | leaf_size | 25 |
| min_samples_leaf | 20 | max_features | 0.3 | ||||
| Trial Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy (%) | 98.6 | 98.0 | 98.2 | 99.2 | 98.0 | 99.6 | 1.00 | 98.6 | 99.4 | 99.8 |
| Acc_ave + Var | 98.9% ± 0.21 | |||||||||
| F1 | F2 | F3 | F4 | F5 | Precision | Recall | F1-Score | |
|---|---|---|---|---|---|---|---|---|
| F1 | 100 | 0.9901 | 1 | 0.9950 | ||||
| F2 | 1 | 98 | 1 | 0.9899 | 0.98 | 0.9849 | ||
| F3 | 1 | 96 | 3 | 0.96 | 0.96 | 0.96 | ||
| F4 | 3 | 97 | 0.97 | 0.97 | 0.97 | |||
| F5 | 100 | 1 | 1 | 1 |
| Channel Settings | 1 | 2 | 3 | 1 + 2 | 1 + 3 | 2 + 3 |
|---|---|---|---|---|---|---|
| Accuracy (%) | 94.5 | 94.3 | 93.9 | 96.8 | 96.5 | 96.3 |
| Imbalanced Case | Imbalanced Ratio | The Number of Samples for Normal State | The Number of Samples for Each Damage State | ||||
|---|---|---|---|---|---|---|---|
| Training Dataset | Validation Dataset | Testing Dataset | Testing Dataset | Validation Dataset | Testing Dataset | ||
| Case 1 | 1:1 | 320 | 80 | 100 | 320 | 80 | 100 |
| Case 2 | 1:0.9 | 320 | 80 | 100 | 288 | 72 | 100 |
| Case 3 | 1:0.8 | 320 | 80 | 100 | 256 | 64 | 100 |
| Case 4 | 1:0.7 | 320 | 80 | 100 | 224 | 56 | 100 |
| Case 5 | 1:0.6 | 320 | 80 | 100 | 192 | 48 | 100 |
| Imbalanced Case | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | The Degree of Decline |
|---|---|---|---|---|---|---|
| Proposed method | 98.5 ± 1.05 | 95.2 ± 1.35 | 91.7 ± 1.46 | 87.2 ± 1.68 | 82.8 ± 1.89 | 15.7 |
| TF-EHSML | 90.2 ± 1.36 | 87.1 ± 1.58 | 82.8 ± 1.87 | 77.2 ± 2.04 | 71.8 ± 2.79 | 18.4 |
| 3C-ERSML | 86.7 ± 3.41 | 82.0 ± 3.64 | 76.9 ± 3.93 | 70.3 ± 4.11 | 62.1 ± 4.51 | 24.6 |
| 3C-EKSML | 83.8 ± 3.96 | 79.6 ± 4.27 | 76.1 ± 4.67 | 72.6 ± 5.12 | 66.5 ± 5.40 | 25.3 |
| 3C-E3HSML | 94.1 ± 3.49 | 90.7 ± 3.73 | 85.3 ± 3.99 | 79.4 ± 4.54 | 70.9 ± 5.02 | 23.2 |
| 3C-EHNML | 95.2 ± 0.96 | 91.8 ± 1.24 | 86.2 ± 1.67 | 80.1 ± 1.93 | 73.6 ± 2.26 | 21.6 |
| 3C-EHRML | 95.7 ± 1.61 | 92.3 ± 1.93 | 87.0 ± 2.25 | 80.8 ± 2.67 | 74.4 ± 3.14 | 21.3 |
| 3C-EHLML | 96.4 ± 0.64 | 94.7 ± 1.14 | 89.6 ± 1.54 | 84.3 ± 1.88 | 78.4 ± 2.13 | 18.3 |
| Index | Balanced State | Imbalanced Case 3 | ||||
|---|---|---|---|---|---|---|
| Precision | Recall | F1-Score | Precision | Recall | F1-Score | |
| F1 | 0.9901 | 1 | 0.9950 | 0.9588 | 0.93 | 0.9442 |
| F2 | 0.9899 | 0.98 | 0.9849 | 0.92 | 0.92 | 0.92 |
| F3 | 0.96 | 0.96 | 0.96 | 0.8365 | 0.87 | 0.8529 |
| F4 | 0.97 | 0.97 | 0.97 | 0.8713 | 0.88 | 0.8756 |
| F5 | 1 | 1 | 1 | 0.9898 | 0.97 | 0.9797 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Wang, X.; Fan, B.; Shahzad, M.M. A Stacking Ensemble-Based Multi-Channel CNN Strategy for High-Accuracy Damage Assessment in Mega-Sub Controlled Structures. Buildings 2025, 15, 1775. https://doi.org/10.3390/buildings15111775
Wei Z, Wang X, Fan B, Shahzad MM. A Stacking Ensemble-Based Multi-Channel CNN Strategy for High-Accuracy Damage Assessment in Mega-Sub Controlled Structures. Buildings. 2025; 15(11):1775. https://doi.org/10.3390/buildings15111775
Chicago/Turabian StyleWei, Zheng, Xinwei Wang, Buqiao Fan, and Muhammad Moman Shahzad. 2025. "A Stacking Ensemble-Based Multi-Channel CNN Strategy for High-Accuracy Damage Assessment in Mega-Sub Controlled Structures" Buildings 15, no. 11: 1775. https://doi.org/10.3390/buildings15111775
APA StyleWei, Z., Wang, X., Fan, B., & Shahzad, M. M. (2025). A Stacking Ensemble-Based Multi-Channel CNN Strategy for High-Accuracy Damage Assessment in Mega-Sub Controlled Structures. Buildings, 15(11), 1775. https://doi.org/10.3390/buildings15111775






