Mechanical Response of Pipeline Leakage to Existing Tunnel Structures: Insights from Numerical Modeling

Abstract

Pipeline leakage can induce ground surface settlements and structural responses in existing tunnels. A thorough understanding of pipeline–tunnel interactions is crucial for optimizing urban underground design and establishing construction guidelines. As urban underground spaces undergo rapid, large-scale development, their layouts have grown increasingly complex. Previous studies have mainly focused on the leakage propagation range and the resulting strata instability during tunnel excavation, while paying limited attention to the effects of pipeline leakage on existing tunnels. This study systematically investigated the mechanical response of existing tunnel structures to pipeline leakage under different layout configuration conditions using numerical modeling. A two-dimensional numerical model was developed to simulate the pipeline leakage process and its impact on adjacent tunnels. The research established a correlation between surrounding rock strength parameters and the saturation degree while examining the evolution patterns of leakage effects in various tunnel–pipeline arrangements. The analysis specifically focused on the mechanical influence of horizontal pipeline–tunnel distance, quantitatively determining the relationships among pipeline–tunnel spacing, leakage duration, and structural internal force. The horizontal pipeline–tunnel distance did not influence the development of the leakage zone above the tunnel vault but significantly altered the seepage path length and interface contact area. The complete encapsulation of the tunnel periphery by the leakage zone required progressively longer durations with increasing horizontal offsets: 16 days (0 m), 20 days (3 m), and 33 days (6 m). Corresponding circumferential contact ratios at 10 days were measured at 68.9%, 56.4%, and 30.6%, respectively. Furthermore, prolonged seepage duration led to increased ground subsidence with expanded affected areas, while the maximum settlement decreased proportionally with greater horizontal separation from the tunnel. These findings provide valuable insights for planning, designing, and maintaining “old tunnel-new pipeline” systems in urban underground development.

1. Introduction

Urban underground pipelines play a key role in ensuring the safe operation of cities [1,2,3]. However, with the aging of pipeline infrastructure [4] and increasing disturbances from underground space development, pipeline leakage has become a critical issue [5]. Such leakage induces soil erosion in surrounding strata, consequently triggering ground subsidence that seriously threatens public property and safety (Figure 1). This growing phenomenon of urban sinkholes has consequently drawn significant attention from both academic communities and societal stakeholders. The macroscopic manifestations of underground pipeline failures can be categorized into two typical modes: sudden failure and progressive failure. Sudden failure predominantly occurs in high-pressure pipeline systems [1,6,7], where its mechanical characteristics manifest as brittle fractures in the pipe wall within a short duration, generating instantaneous dynamic loading on surrounding soils and structures. In contrast, progressive failure represents a time-dependent material degradation process involving long-term damage accumulation mechanisms such as corrosion fatigue and stress corrosion cracking [8,9,10,11], demonstrating distinct spatiotemporal evolution characteristics. Despite their divergent temporal characteristics, both failure modes induce irreversible damage to surface infrastructure [12].

Extensive research has been conducted on pipeline leakage-induced ground subsidence or collapse through numerical simulations, laboratory model tests, and theoretical methods. Chao et al. [1] conducted extensive experimental tests, along with a finite difference method, to investigate the ground movements, soil erosion, and failure mechanism caused by pipe bursts and concluded that pipe bursts undergo three evolution stages, i.e., seepage diffusion, erosion cavity expansion, and soil fluidization. Yuan et al. [13] used the discrete element software PFC 5.0 and the coupled CFD-DEM method to study the ground collapse induced by buried sewage pipeline breakage and soil leakage. Long et al. [14] used numerical simulation coupled with the finite difference method and discrete element method (FDM-DEM) to elucidate the damage mechanism of tunnel destabilization due to leakage in the water-rich sand stratum. Tang et al. [15] analyzed the mechanical properties of the type B sleeve structure by considering the effects of pipeline–soil interaction and penetration. Sato et al. [16] analyzed the spatial distribution of soil strength reduction caused by underground pipeline leakage and conducted laboratory model tests to investigate the correlation between pipeline location and subsurface cavity development. Tarek et al. [17] conducted a series of small-scale model tests simulating sewer pipe cracks and different groundwater flow modes to investigate ground subsidence mechanisms induced by sewer pipe leakage. Zhang et al. [18] investigated the internal erosion process around defective pipes through a series of indoor tests and proposed a new method to quantify this process. Young et al. [19] used large-scale model chambers of different soils to conclude that uniform soil with no fine content was more vulnerable to ground cavities than well-graded soil with fine content. Liu et al. [20] combined experimental tests with 3D CFD-DEM coupling numerical simulations to investigate the behaviors and micro-mechanism of cavity failure under erosion conditions and ground collapse induced by the exfiltration of a shallowly buried defective pipe. Chen et al. [21] developed a computational model based on Manning’s equation by investigating the effects of soil particle size, hydraulic gradient, rough span ratio, and full pipe flow velocity on ground settlement around a defective underwater pipe. Gao et al. [22] experimentally investigated the occurrence, mechanism, and evolution process of strata collapse disasters induced by soil–water leakage in partially failed tunnels. It can be seen that the impact of water on underground engineering cannot be ignored, and it can introduce great safety hazards to tunnel engineering.

Meanwhile, numerous studies have investigated the mechanisms by which underground pipeline leakage affects existing tunnels. Shi et al. [23] used 3D numerical simulation to study ground settlement caused by shield tunneling under pipeline leakage conditions. Yuan et al. [24] developed a unified 3D upper-bound finite element method incorporating suction stress-based effective stress, the analysis of tunnel support pressures near leaking pipelines, and the evolution of collapse mechanisms. Dohyun Park [25] performed a coupled hydro-mechanical (HM) analysis via a Python-based TOUGH-FLAC simulator to examine water leakage effects on tunnel stability. Zhang et al. [26] studied the failure behavior of composite strata caused by tunnel excavation under seepage conditions via finite difference methods. Therefore, the accurate characterization of soil strength degradation becomes imperative when employing numerical simulations [27,28] to investigate tunnel mechanical responses induced by pipeline leakage. Zhang et al. [29] conducted a study on the internal erosion process around defective pipes and proposed a new method for quantifying this erosion process. Shao et al. [30] conducted a series of laboratory tests to obtain the yield characteristics of unsaturated loess under different matric suction conditions and calculated the internal force of an EERW using the obtained strength criterion of unsaturated loess. Liu et al. [31] developed a seepage diffusion model of pipeline leakage fluid in an unsaturated stratum using the Green–Ampt model, the VG–Mualen permeability coefficient function, and the stepwise algorithm. At present, some scholars have conducted research on the stability of strata under seepage conditions, emphasizing the importance of seepage on the mechanical response of tunnel structures.

However, previous studies have insufficiently examined the influence of varying horizontal pipeline–tunnel distances on existing tunnels. This research systematically investigates leakage-induced evolution patterns in different geometric configurations through numerical simulations, offering a comprehensive analysis of how pipeline–tunnel horizontal spacing mechanically affects tunnel structures. This paper is organized as follows: Section 2 establishes a two-dimensional numerical model of an existing tunnel subjected to pipeline leakage, integrating key processes, including tunnel face excavation and soil strength–saturation relationships. The model’s validity is confirmed through comparison with laboratory-scale physical model test results from the existing literature. Section 3 quantitatively evaluates ground surface settlements and lining responses to pipeline leakage at different horizontal distances from the tunnel. Section 4 summarizes the key findings from the analysis.

2. Two-Dimensional Number Modeling

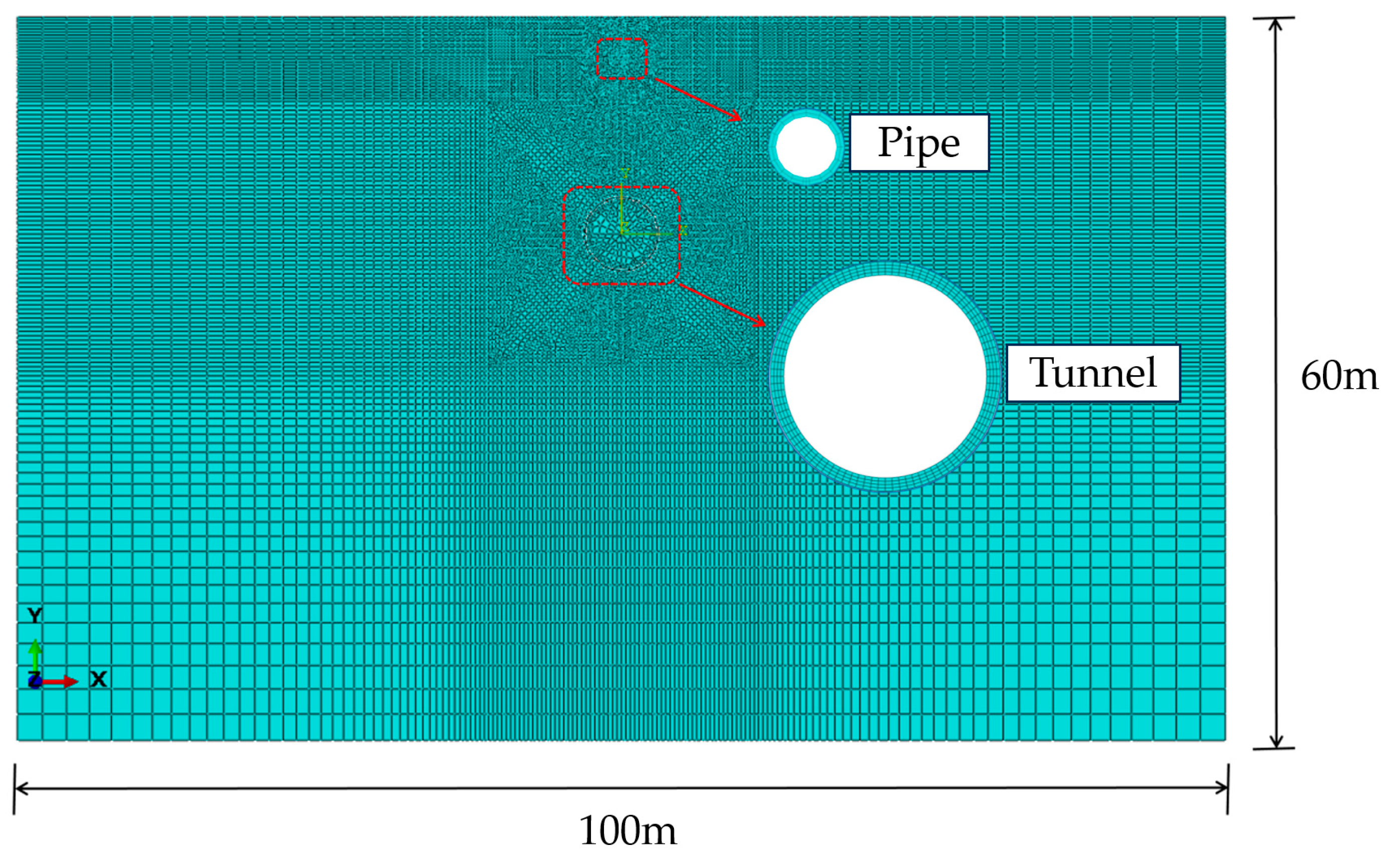
2.1. Overview of Two-Dimensional Numerical Model

This study establishes a two-dimensional “pipe-tunnel-stratum” numerical model using the finite element software ABAQUS 2016. As illustrated in Figure 2, the modeling domain has dimensions of 100 × 60 m. To facilitate computational efficiency, the stratum is simplified as homogeneous moderately permeable soil with a saturated permeability coefficient k of 5 × 10⁻⁶ m/s. The tunnel is embedded at a depth of 15 m, featuring a lining structure with an external diameter (D) of 6.2 m and a lining thickness of 0.35 m. A pipeline with a nominal diameter of 1 m is positioned 12 m above the tunnel vault. Given that the numerical simulation focuses on leakage tests in underground pipelines where internal water pressure typically remains below 0.1 MPa, an initial hydraulic pressure of 0.06 MPa is specified [32]. The leakage condition is simulated through pore pressure constraints applied at the pipeline invert, with the leakage zone encompassing a 10° circumferential extent. Except for the top boundary, horizontal X-direction displacements are constrained on both lateral boundaries, while Y-direction displacements are restricted at the base. Since the primary focus of this study is the geometric layout of the pipeline leakage, specifically examining the impact of lateral offset distance between the pipeline centerline and tunnel centerline (D_h), other variables, such as tunnel burial depth (D_T) and pipeline radius (D_P), are held constant.

2.2. Modeling of Tunnel Excavation

The finite element analysis software ABAQUS, which is renowned for its capabilities in multi-physics coupling, large deformation analysis, nonlinear material behavior, and complex geometric modeling, is extensively applied in geotechnical and tunneling engineering. To eliminate boundary effects on tunnel mechanical responses, the lateral boundaries are positioned 50 m horizontally from the tunnel centerline, while the lower boundary extends 40 m below the tunnel bottom, resulting in a total model height of 60 m. The mesh discretization employs four-node plane strain quadrilateral pore pressure elements (CPE4P elements), with localized refinement implemented around the pipeline and tunnel structures. The soil is idealized as a homogeneous unsaturated medium, with the analysis conducted under plane strain conditions [32,33,34,35,36]. The stratum is classified as Grade V surrounding rock. Given the unsaturated soil conditions and negligible groundwater influence, hydrogeological effects are excluded from the analysis. Post-leakage water pressure remains stable, with fluid migration approximated as homogeneous isotropic seepage through the surrounding rock. The tunnel lining comprises C50 concrete segments interconnected by longitudinal and circumferential bolts. To simulate the joint effects between precast segments, the lining is idealized as a continuous ring with stiffness reduction using the modified conventional method. The equivalent bending stiffness is defined as ηEI, where EI represents the transverse flexural rigidity of intact segments and η denotes the transverse rigidity efficiency factor (η = 0.8) [37]. Material parameters for the stratum and support structures are listed in

Table 1. Mechanical parameters of the surrounding rock and support system.

Parameters	Density (g/m3)	Permeability Coefficient (m/s)	Elastic Modulus (Gpa)	Poisson’s Ratio	Friction Angle (°)	Cohesion (kPa)
Surrounding rock	2300	1.7 × 10−5	0.282	0.32	33	280
Grouting layer	2300	1 × 10−7	25.5	-	-	-
Secondary lining	2500	20.1	27.6	-	-	-

. The thickness of the grouting layer between the segments and the formation is 0.12 m.

2.3. Modeling Fluid–Structure Coupling

This study primarily simulates the water leakage process in unsaturated soils following pipeline rupture. During the fluid–solid coupling analysis, the inherent Mohr–Coulomb criterion in ABAQUS cannot account for the variation of soil strength parameters with saturation levels, particularly the water-induced softening behavior. To address this limitation, a soil strength degradation model is integrated with an ideal elastoplastic framework to simulate the strength attenuation of unsaturated soils. Several studies [38,39] have employed the USDFLD subroutine to simulate soil softening, enabling the customization of material properties (e.g., elastic modulus, shear modulus, stress–strain relationships) while incorporating nonlinearity, time-dependency, and failure effects. Building on this approach, a Fortran-based USDFLD (Figure 3) subroutine is developed to establish functional relationships between soil strength parameters (cohesion c and internal friction angle φ) and saturation levels. This implementation dynamically updates strength parameters during saturation to replicate water-induced softening. The methodology involves three key steps (Figure 4): Step Ⅰ: the initial and final states of soil strength parameters are defined in the ABAQUS preprocessing module. A seepage analysis is subsequently conducted to obtain saturation variations at each incremental step. Step Ⅱ: based on the established formula describing the relationship between unsaturated soil strength parameters and water content, a correlation between saturation degree and strength indicators is developed. Step Ⅲ: the saturation degree (S_r), cohesion (c), and internal friction angle (φ) are assigned as field variables and state variables. Through a customized programming implementation, specific interdependencies among these variables are established to enable their progressive updating during seepage computation. This methodology facilitates the controlled degradation of soil strength parameters within predefined initial–final state boundaries according to specified attenuation patterns, thereby effectively simulating the water-induced softening behavior of soil materials. This study primarily referenced the shear strength degradation behavior and empirical formulas of unsaturated soils established by Cai [40] through laboratory experimental investigations. The cohesion (c) of soil exhibits an exponential decrease with increasing saturation, while the internal friction angle (φ) decreases linearly with saturation. The specific expressions are as follows:

$$c=8.69469+117.6773{\mathrm{e}}^{-0.05425S_r}$$

(1)

$$\phi =42.3587-0.327235S_r$$

(2)

To establish the relationship between soil shear strength indices and saturation using the USDFLD subroutine, Fortran is used to programmatically assign soil element saturation at each step to predefined field variables. The soil strength parameters (c and φ) are then defined as functions of these variables based on Equations (1) and (2). This method enables continuous parameter updates during the fluid–solid coupling analysis, effectively simulating strength reduction with rising saturation.

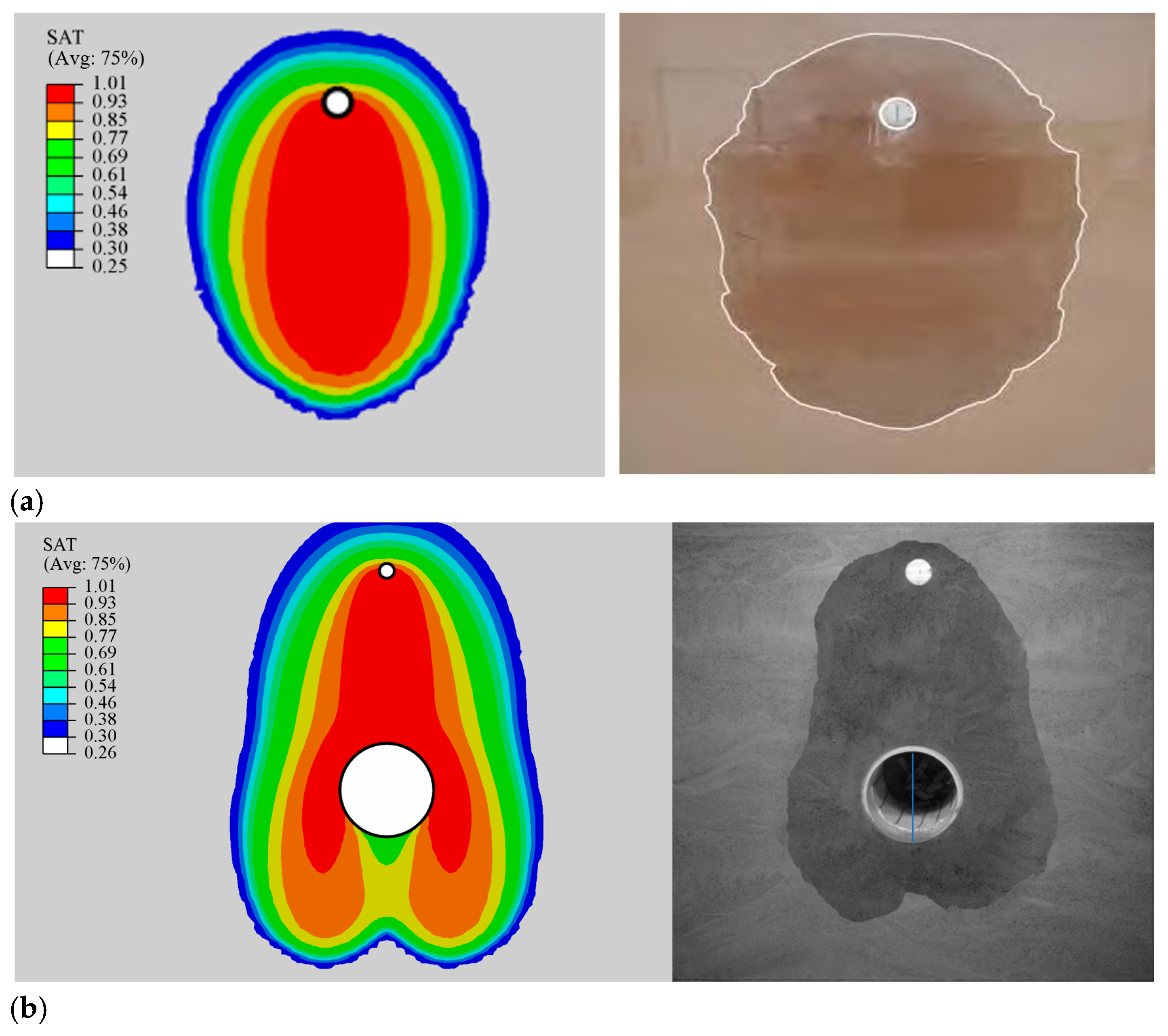
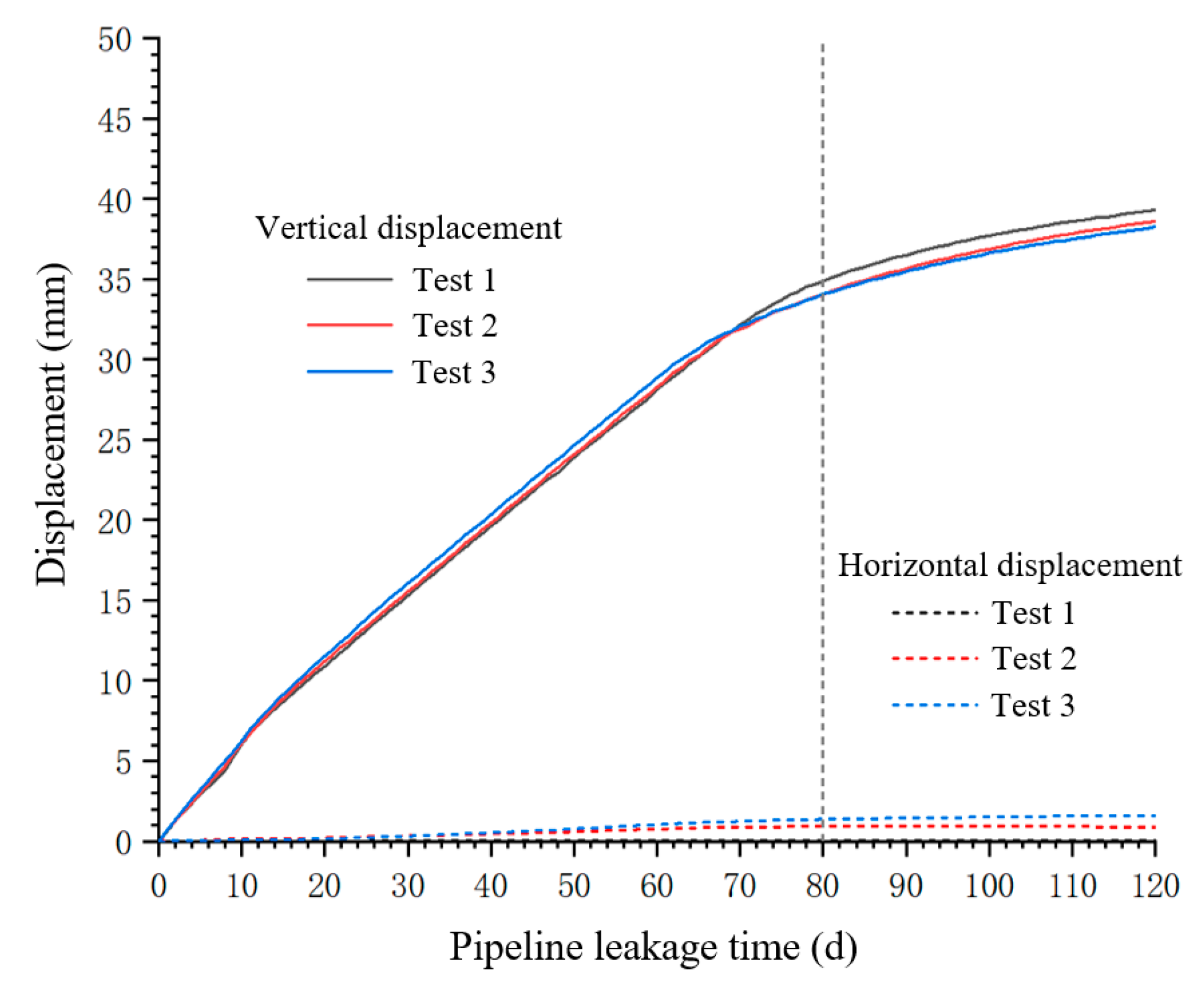
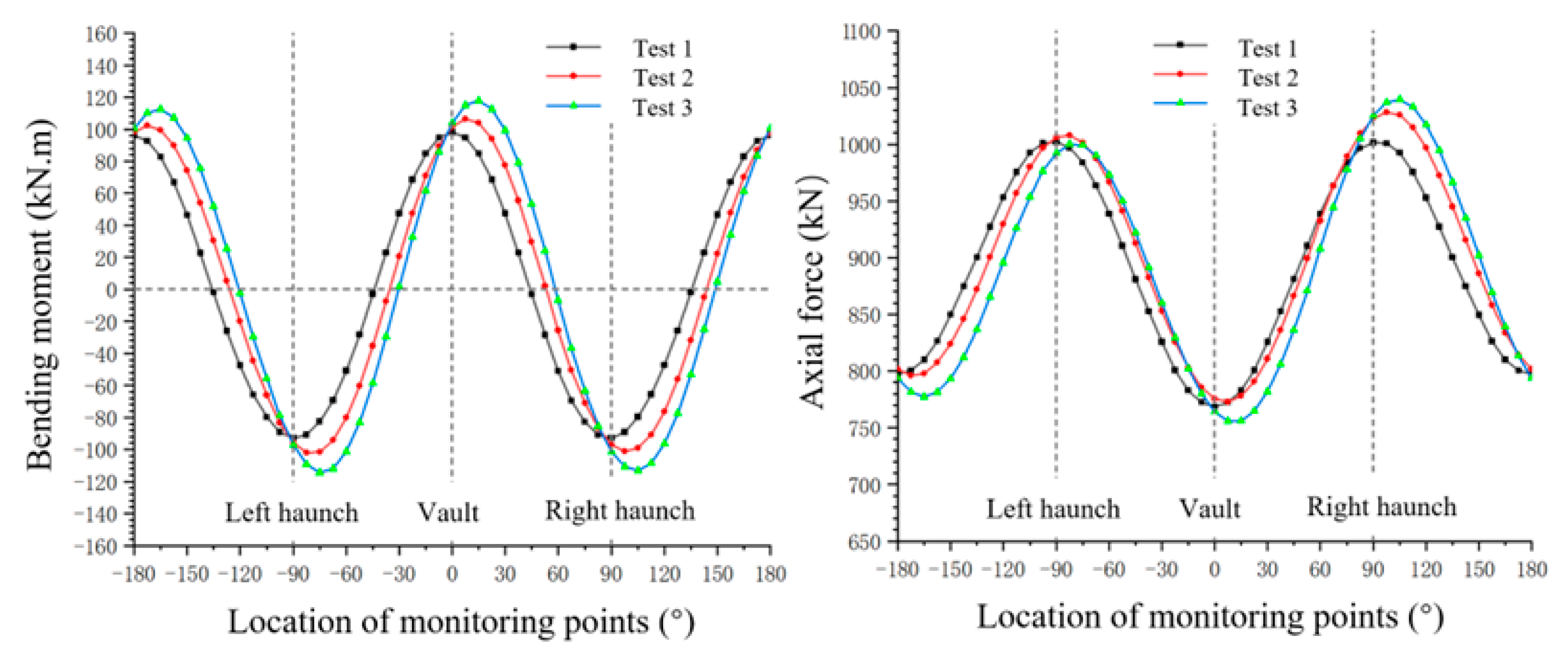
2.4. Validation Based on Case History

To validate the numerical modeling method used in this study, the numerical results were compared with measured data from case studies in the literature [41,42]. Figure 5 presents the numerical simulation results with laboratory-scale physical model test results for seepage patterns under two testing conditions: pipeline leakage without pre-existing tunnels and pipeline leakage beneath existing tunnels. The results demonstrate that in the absence of existing tunnels, the leakage zone exhibits radial expansion with significantly greater vertical development beneath the pipeline compared to its upper region, forming a flattened elliptical profile that maintains bilateral symmetry around the pipeline axis. Under the influence of pre-existing tunnels, seepage pathways are redirected; wastewater migrates along both sides of the tunnel lining, converges at the tunnel invert, and subsequently propagates downward, enveloping the lining structure in a characteristic pear-shaped morphology. The comparative results demonstrate good agreement between the numerical simulation and physical modeling. For free pipeline leakage conditions, the simulated and experimental leakage zone heights were 4.19D and 3.95D (6% error), respectively, while the widths were 3.18D and 2.82D (12% error). When a tunnel was present beneath the pipeline, the corresponding heights measured 3.86D and 3.98D (3% error), with widths of 2.91D and 3.59D (18% error), as shown in

Table 2. Leakage zone dimensions of the numerical simulation and model test.

	Height			Width
	Numerical Simulation	Model Test	Error	Numerical Simulation	Model Test	Error
Pipeline leakage area	4.19D	3.95D	6%	3.18D	2.82D	12%
Pipeline leakage area under the existing tunnel conditions	3.86D	3.98D	3%	2.91D	3.59D	18%

. The height measurements showed excellent consistency (<6% error), while the width discrepancies remained within 20%, potentially due to boundary friction effects in the physical model. Overall, the close correlation between both methods validates the reliability of the numerical simulation approach.

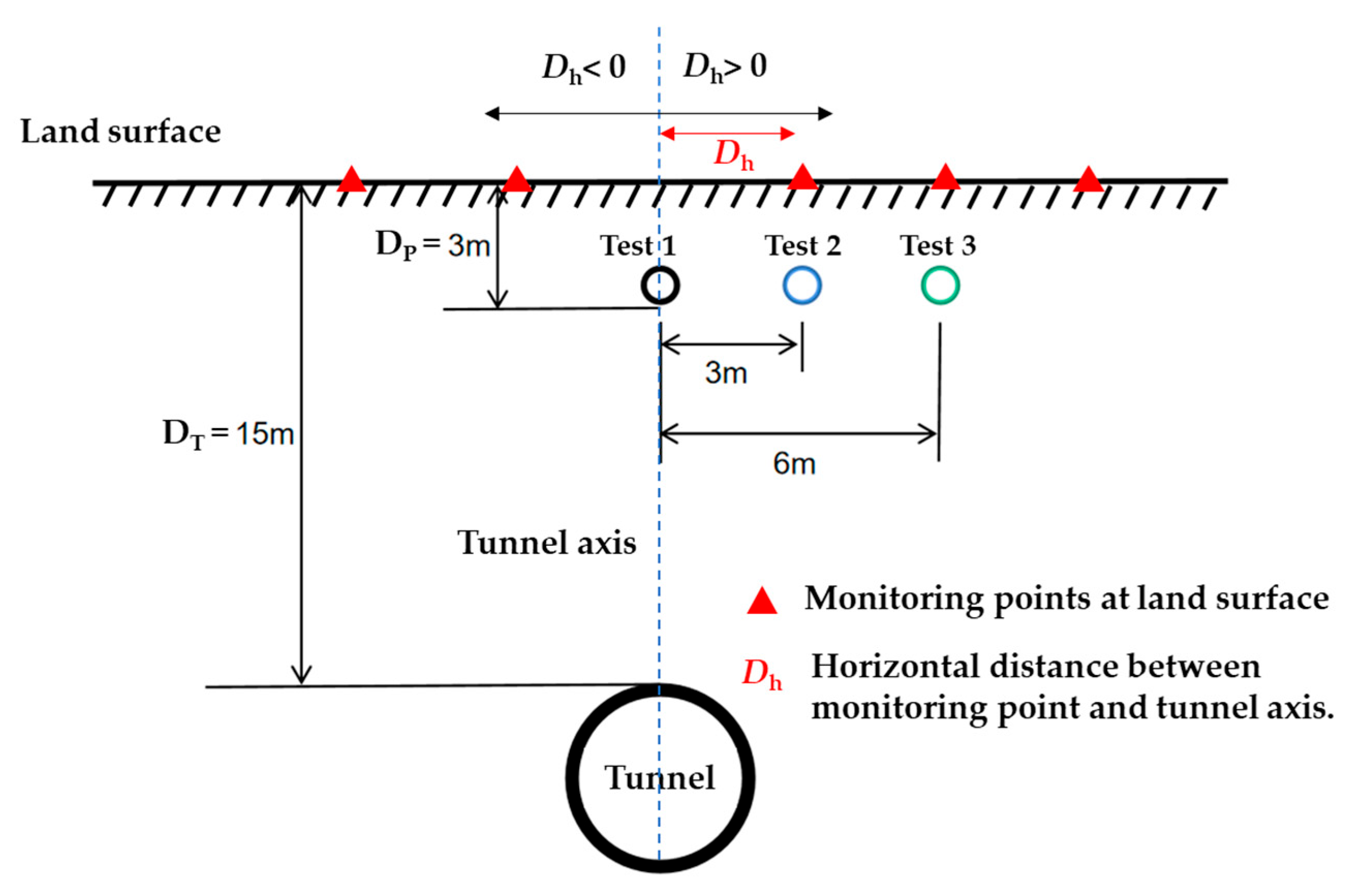
2.5. Analysis Cases

In urban metro construction, where new tunnels frequently intersect existing sewer pipelines, either passing straight through or sideways through them, aging pipelines often develop leakage incidents that have non-negligible impacts on adjacent tunnel structures. To study the effects of pipeline leakage at different positions above a shield tunnel on ground deformation and tunnel structural forces, a simplified 2D homogeneous numerical model was developed, ignoring rock heterogeneity and stratification. Three test cases were modeled: the pipeline directly above the tunnel (0D), a 3 m right offset (0.5D) from the center line, and a 6 m right offset (1D) from the center line (Figure 6). The simulation included the following steps: (1) geometric modeling of the strata, pipelines, linings, and grouting layers, followed by meshing; (2) the application of gravity loads and pore pressures, with geostatic equilibrium established through automatic balancing; (3) the simulation of pipeline installation and tunnel excavation using element removal/reactivation techniques; and (4) the application of hydraulic pressure at the leakage point to simulate water leakage.

3. Results and Discussion

This section focuses on the ground settlements and lining responses resulting from the pipeline under various layout conditions.

3.1. Influence of the Pipeline Leakage Process on the Strata

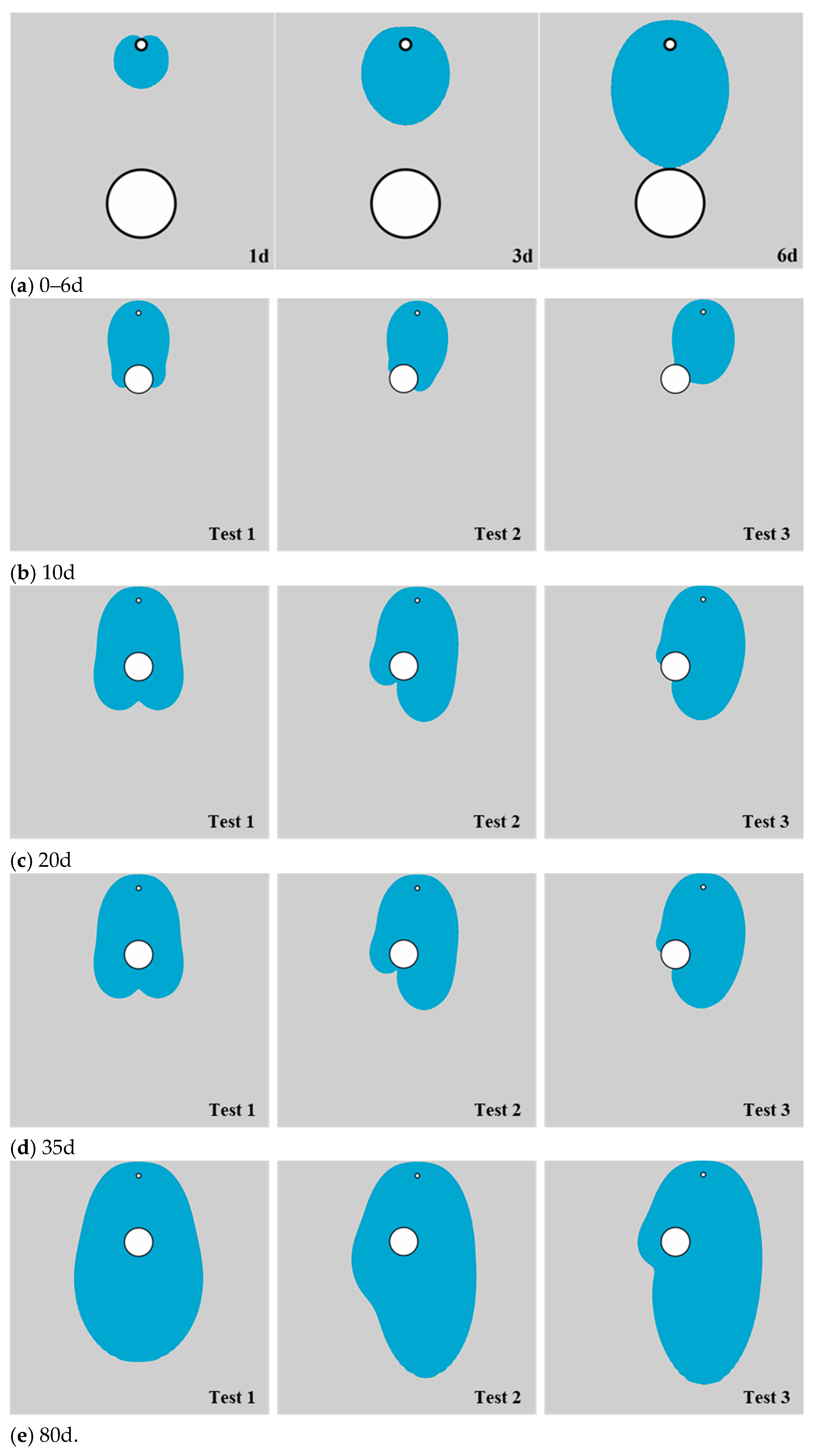
3.1.1. Analysis of Strata Infiltration Range

When a leak occurred at the bottom of the pipeline, the soil around the pipe’s bottom became saturated first. Water began to spread from the leakage point in all directions, forming a leakage zone, with the soil saturation decreasing in layers from the inside to the outside (Figure 7a). Before the leakage zone reached the arch, the extent of the leakage at any given moment was essentially the same. Therefore, the tunnel structure below the pipeline did not affect the development of the leakage zone before the leakage water reached the arch. Consequently, the comparative analysis of the impact range of the leakage under three test conditions began at the 6-day mark. For ease of analysis, the tunnel structure was considered to be a circle, with each position represented by angles from 0° to 360°, with the arch position being 0° (360°) and the angle increasing clockwise.

As shown in Figure 7b, the leakage zone started to extend downward along the tunnel contour from both sides, and by 10 days, both sides had reached the center height of the tunnel. When the time passed reached 20 days, in Figure 7c, the water in Test 2 had seeped to the bottom of the tunnel arch, and the leakage zone had surrounded the entire tunnel structure. As the water continued to seep downward, the shape of the leakage zone in Test 1 gradually evolved into an approximate pear shape. Tests 2 and 3 showed differences after 6 days. In Figure 7b, at 10 days, due to the longest horizontal distance between the pipeline and the tunnel in Test 3, the time required for water to reach the position of the tunnel was relatively longer; thus, the leakage zone had the smallest contact area with the outer contour of the tunnel. At that point, the range of the tunnel surrounded by water ranged from 236° to 360° to 124° in Test 1, 294° to 360° to 137° in Test 2, and 353° to 360° to 103° in Test 3, accounting for 68.9%, 56.4%, and 30.6% of the entire circle, respectively. By 15 days, the leakage zones of all three tests had surrounded more than half of the tunnel. The leakage zones in Tests 1 and 2 surrounded the entire tunnel structure for 20 days, while Test 3 required approximately 35 days. Furthermore, in Tests 2 and 3, the pipeline offset diminished the flow-blocking effect of the underlying tunnel structure, resulting in greater vertical infiltration depths compared to Test 1 at equivalent time intervals. This differential behavior became increasingly evident during the advanced phases of the simulation.

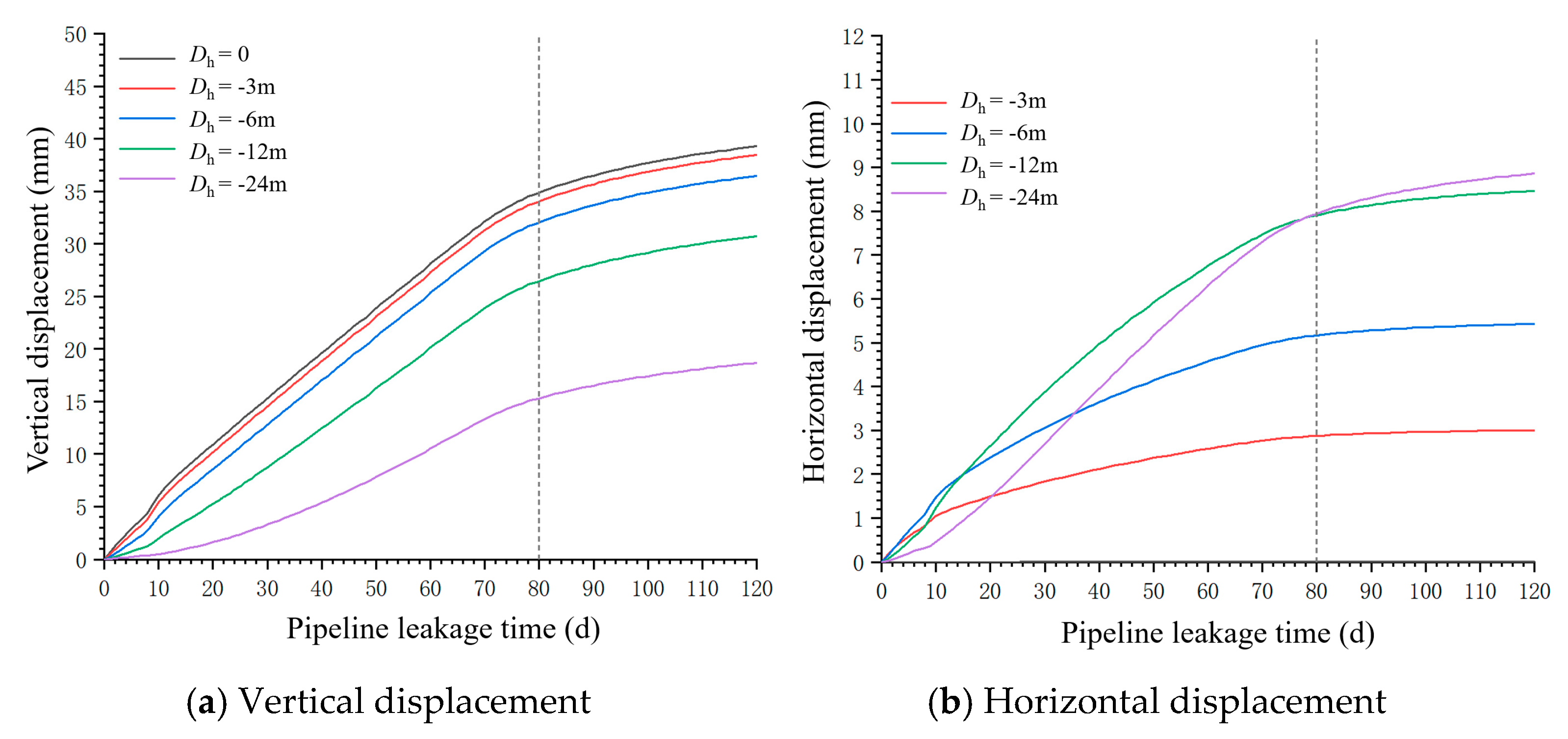
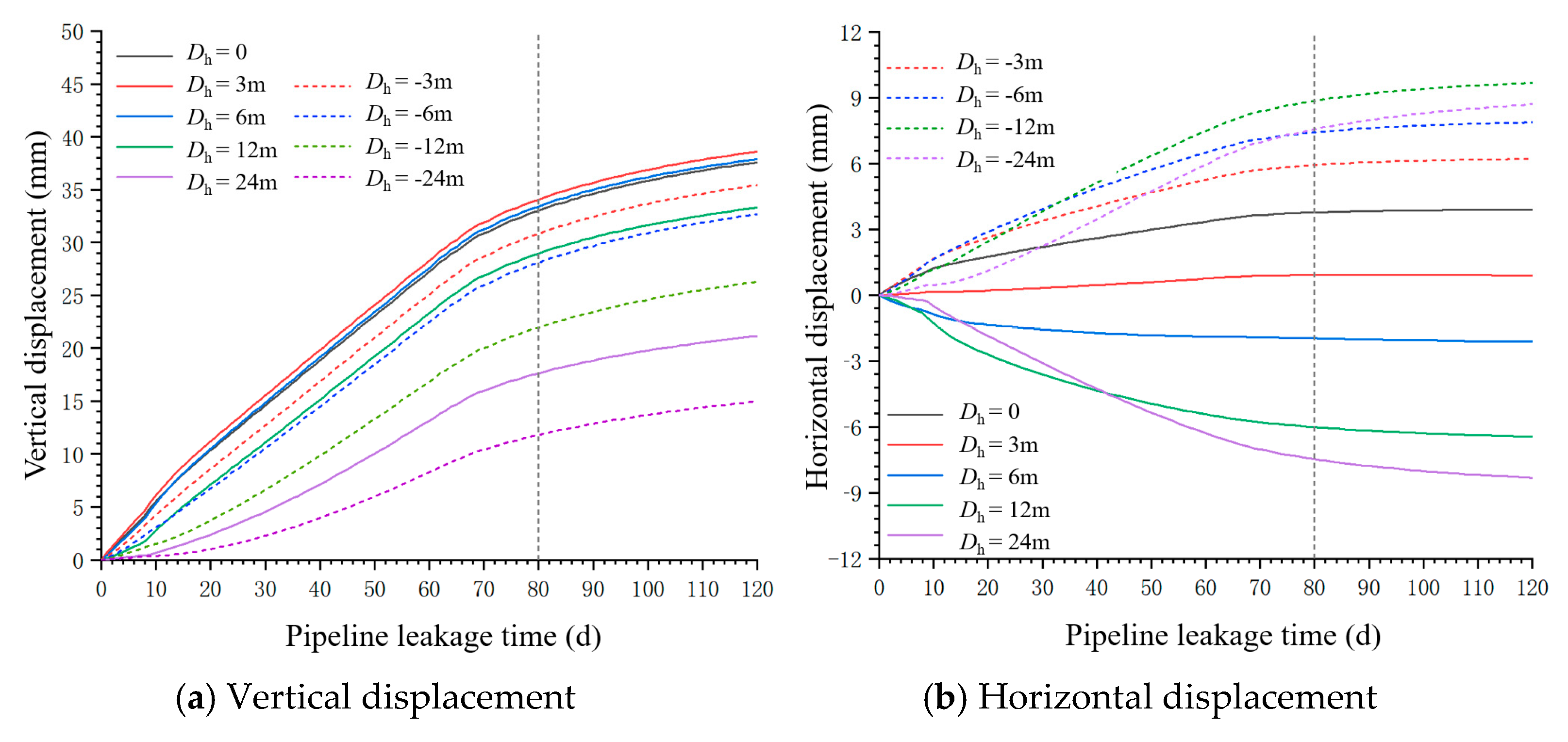
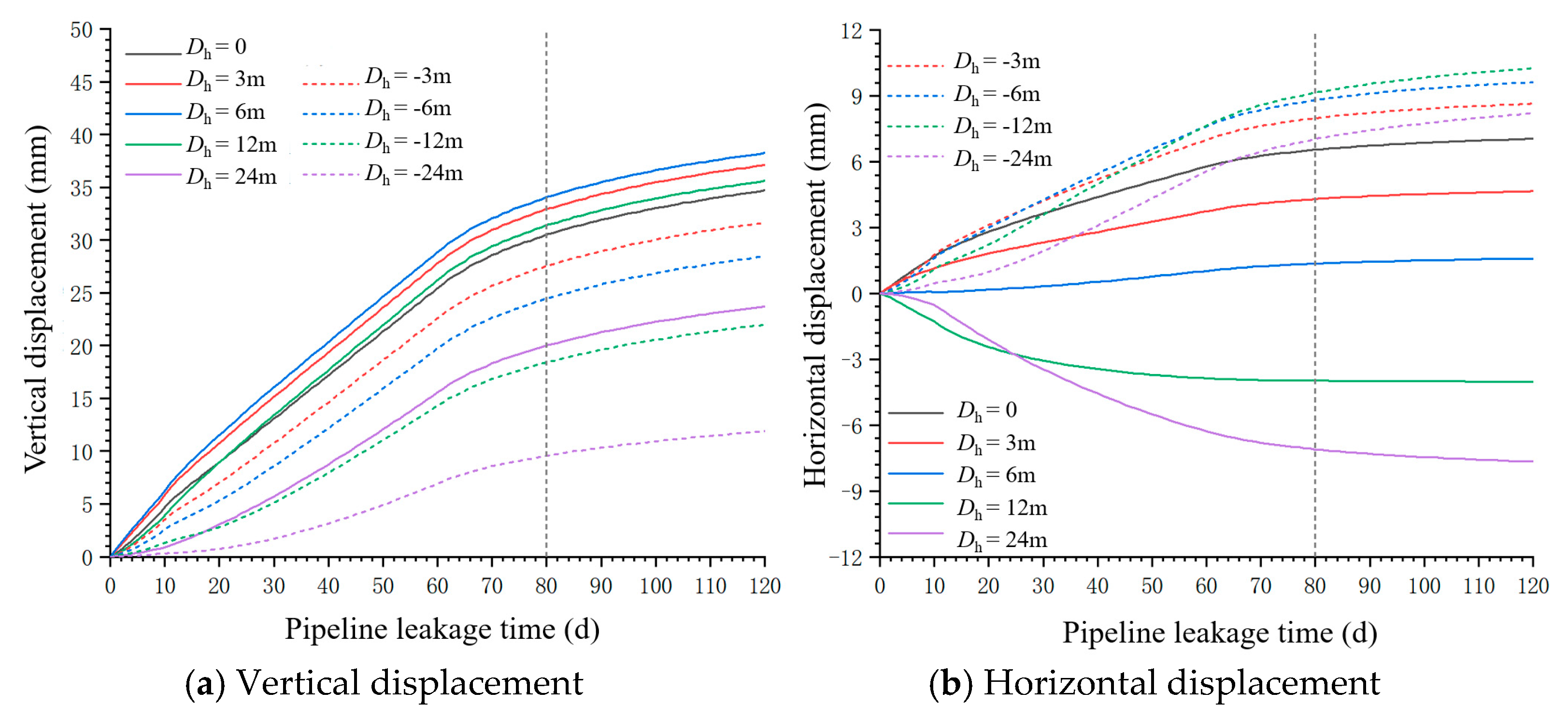
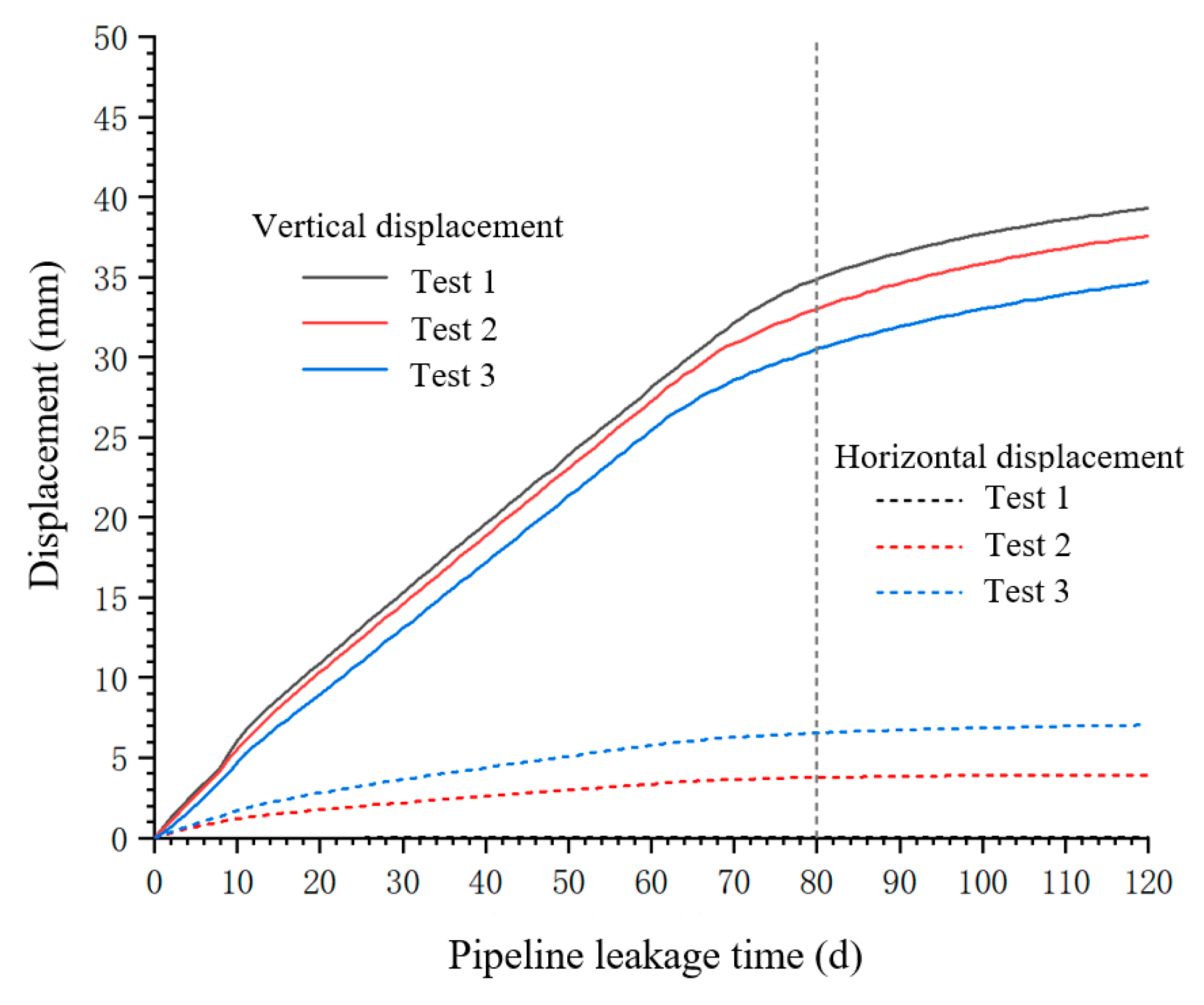
3.1.2. Analysis of Surface Displacement

In Test 1, the surface displacements on both sides of the shield tunnel centerline exhibited comparable magnitudes. Consequently, the left-side monitoring points were selected for plotting time–history curves in Figure 8. As shown in Figure 8a, the vertical displacement at the surface directly above the tunnel vault consistently exceeded those at other positions throughout the leakage process, with the maximum settlement reaching 39.29 mm at 120 days. Settlement magnitudes decreased progressively with increasing distance from the tunnel centerline. Notably, the settlement increment at the 24 m offset location remained relatively minor during the initial 10 days due to reduced influence from the limited initial extent of the seepage zone on distal regions. Figure 8b illustrates horizontal displacement variations across monitoring points. Horizontal displacement at the tunnel centerline demonstrated negligible variation, while displacement curves at 12 m and 24 m left offsets intersected at 78 days, indicating equivalent displacements at these positions. The 24 m left offset location attained the peak horizontal displacement of 8.86 mm by 120 days.

In Test 2, the pipeline was positioned 3 m rightward from the tunnel centerline above the vault. Figure 9 compares the vertical and horizontal displacements at symmetrically aligned left- and right-side monitoring points relative to the tunnel axis. As illustrated in Figure 9a, the maximum surface settlement throughout the leakage process consistently occurred at the 3 m rightward offset location, peaking at 38.59 mm by 120 days. Settlements directly above the tunnel vault remained consistently lower than those at the 6 m rightward offset. Furthermore, at equivalent distances from the tunnel centerline, right-side settlements invariably exceeded those at corresponding left-side positions. By 120 days, settlements at right-side offsets of 3 m, 6 m, 12 m, and 24 m surpassed left-side counterparts by measurable margins. Figure 9b reveals negligible horizontal displacement (approaching zero) at the 3 m rightward offset. The maximum horizontal displacement (9.68 mm) was recorded at the 12 m leftward offset, whereas the peak right-side horizontal displacement (8.24 mm) occurred at the 24 m rightward offset.

Test 3 involved a 3 m horizontal rightward offset of the pipeline relative to Test 2; the displacement evolution profiles are presented in Figure 10. As shown in Figure 10a, the surface settlement at the 6 m rightward offset consistently exceeded those at other positions throughout the leakage duration, peaking at 38.26 mm by 120 days, while the minimum settlement (11.91 mm) occurred at the 24 m leftward offset. Similar to Test 1, the settlements exhibited asymmetric distribution across the tunnel centerline, with those on the right side of the tunnel axis exceeding those on the left side. Figure 10b demonstrates negligible horizontal displacement (1.59 mm at 120 days) at the surface directly above the pipeline. However, the maximum horizontal displacement (10.26 mm) was recorded at the 12 m leftward offset by the end of the simulation period.

Figure 11 compares displacement at the ground surface directly above the pipeline across all three tests. The final vertical settlement in Test 1 marginally exceeded those in Tests 2 and 3 by approximately 1 mm. The horizontal displacement order is as follows: Test 3 > Test 2 > Test 1, with consistent trends and minor numerical differences throughout the leakage process. Notably, the incremental rate of surface displacement decelerated after approximately 80 days, gradually stabilizing. Figure 12 illustrates displacement variations at the ground surface directly above the tunnel vault. Test 1 exhibited the largest vertical settlement (39.29 mm at 120 days), followed by Test 2 (37.57 mm) and Test 3 (34.7 mm). Horizontal displacements displayed an inverse trend, with magnitudes ranked as follows: Test 3 > Test 2 > Test 1.

In summary, prolonged leakage caused the progressive saturation of surrounding unsaturated soils, leading to soil strength reduction and time-dependent ground subsidence. Maximum vertical settlement consistently appeared directly beneath the pipeline, decreasing with lateral distance, while horizontal displacements remained minimal at this location. This resulted from gravity-driven downward seepage along the pipeline axis, which maximized both seepage zone height and symmetry about the centerline. Consequently, vertical settlements dominated the near-pipeline region, with minimal horizontal displacements due to symmetrical fluid migration patterns.

The preceding analysis focused on displacement evolution at discrete monitoring points along both sides of the tunnel. The subsequent investigation evaluates ground settlement patterns within a 24 m-wide zone symmetrically distributed around the tunnel centerline. Ground settlement profiles at specified time intervals (1 d, 5 d, 15 d, 30 d, 50 d, 80 d, and 120 d) are plotted based on the computational results, as illustrated in Figure 13. In Test 1 (Figure 13a), with the pipeline centered above the tunnel, all settlement profiles maintain symmetrical distribution around the tunnel centerline throughout the leakage process. The initial stages exhibit limited spatial influence, with maximum settlement reaching merely 0.66 mm at 1 d. Tests 2–3 (Figure 13b,c) demonstrate shifted settlement patterns due to pipeline–tunnel eccentricity. Maximum settlements consistently occur above the pipeline axis, with profiles exhibiting near-symmetrical distribution around the pipeline centerline.

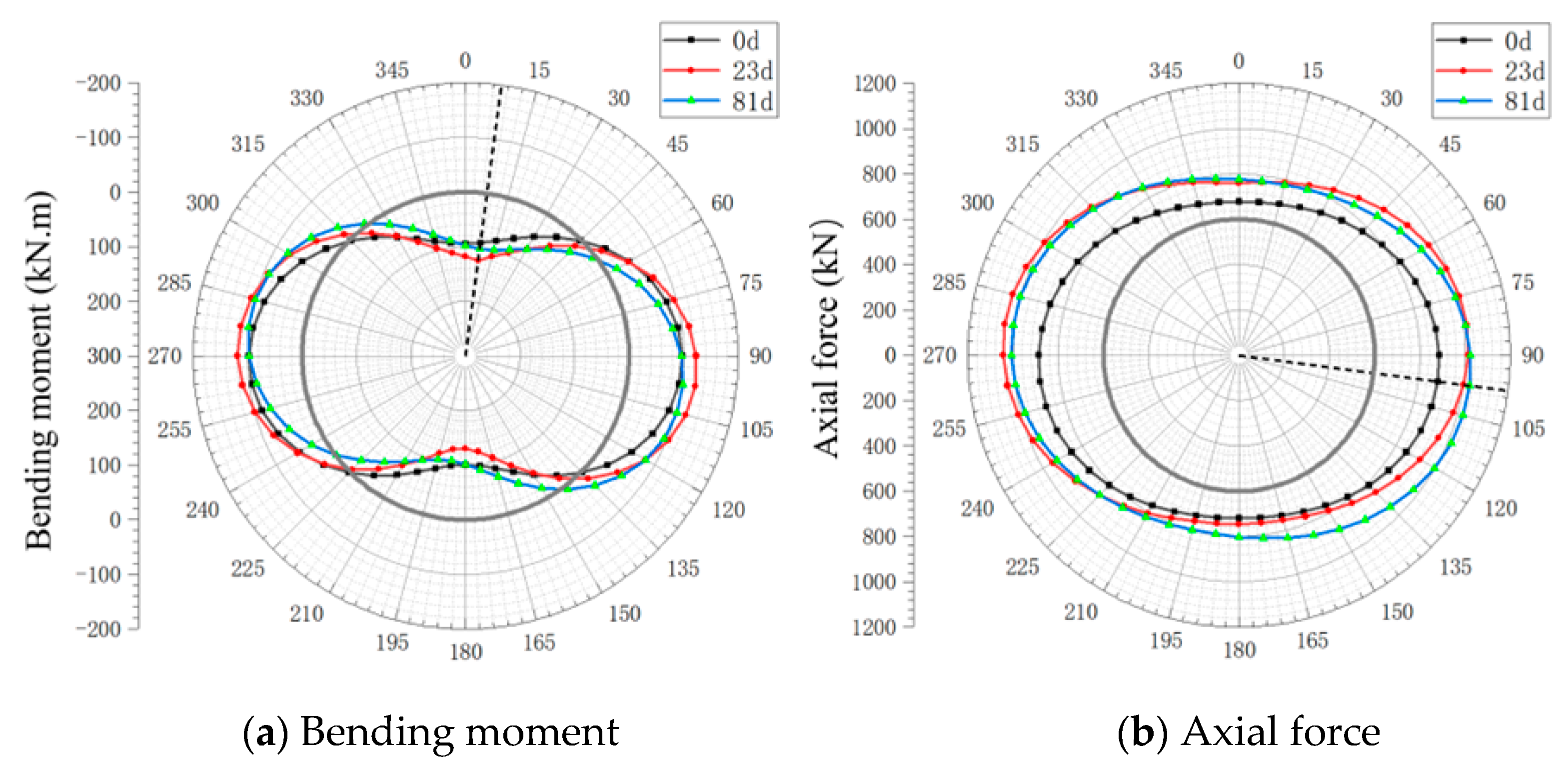
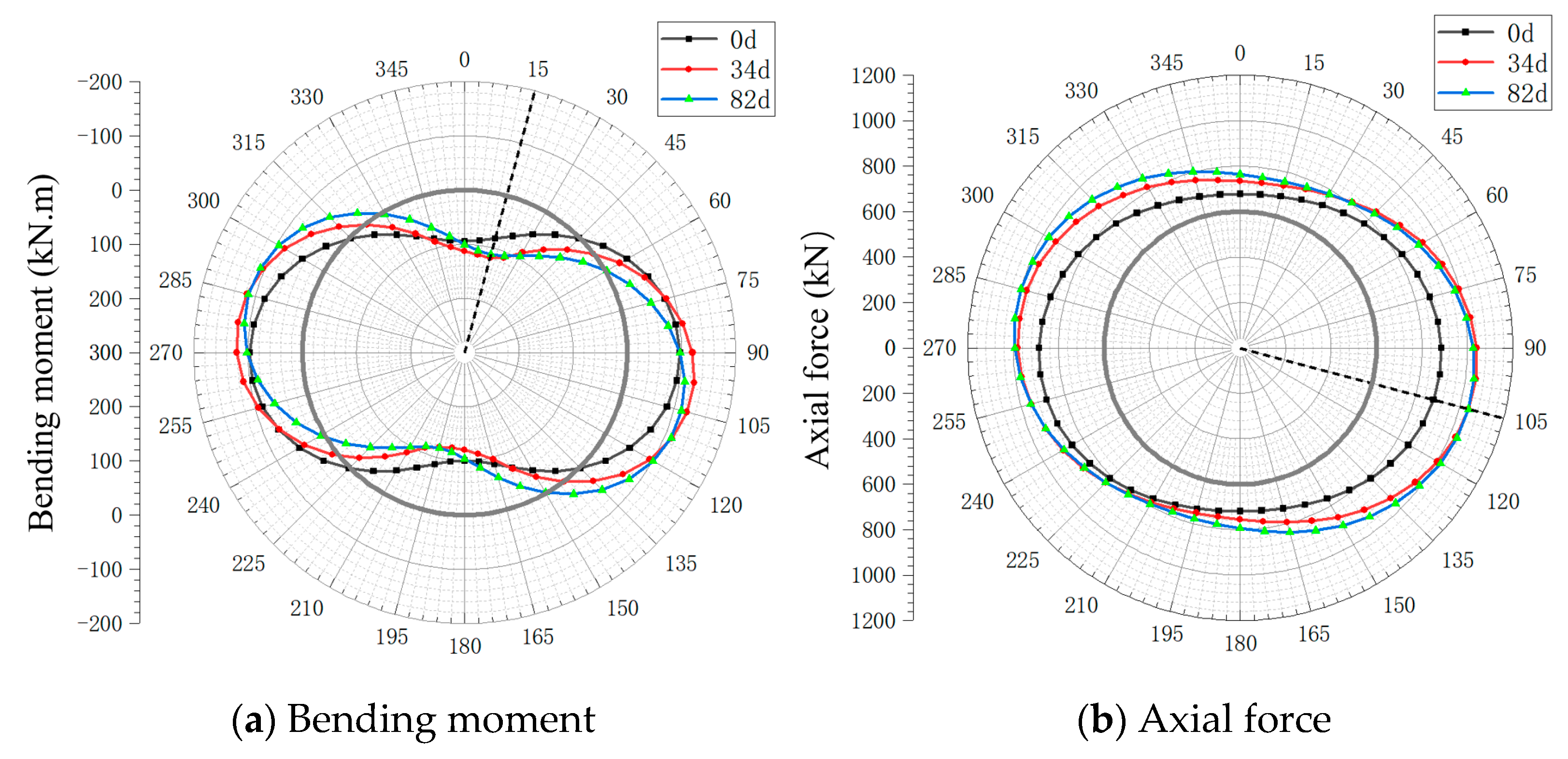
3.2. Mechanical Response of the Lining Structure Under Segment Leakage Conditions

During pipeline leakage, the surrounding soil undergoes a transition from an unsaturated state to a saturated state, modifying soil properties and mechanically interacting with the tunnel lining as the seepage zone develops. This section analyzes leakage-induced changes in lining axial forces (positive for compression, negative for tension) and bending moments (positive when the outer lining surface is compressed and inner surface tensioned).

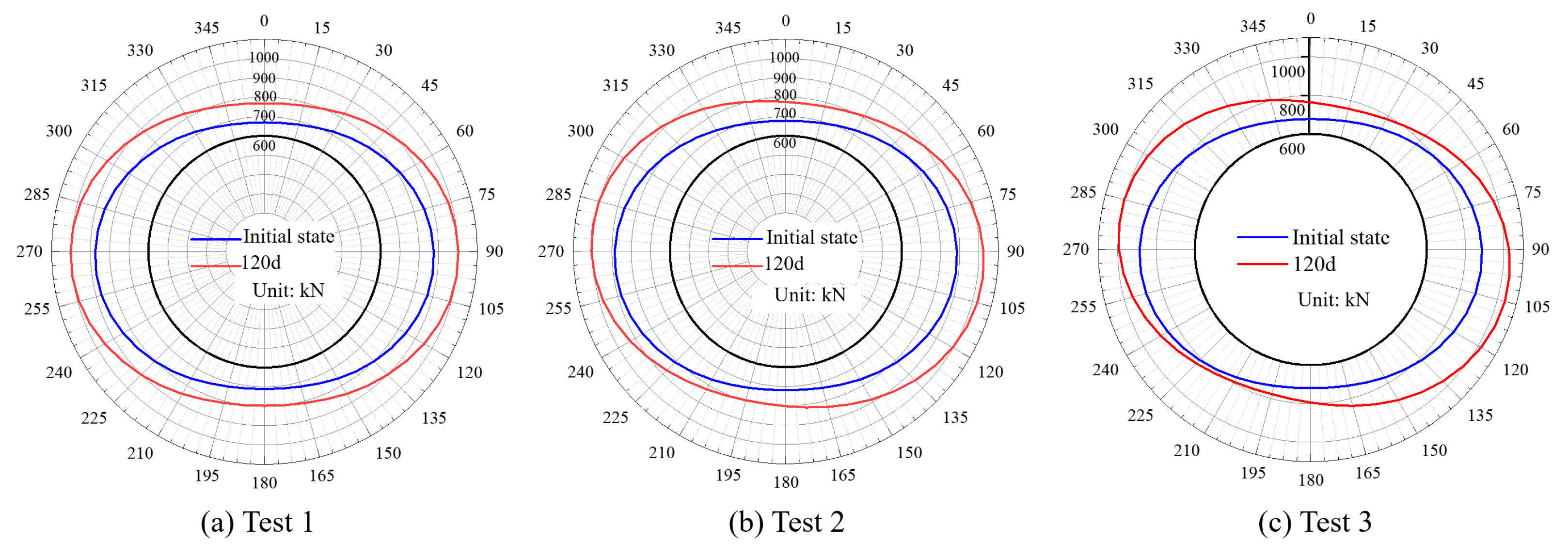
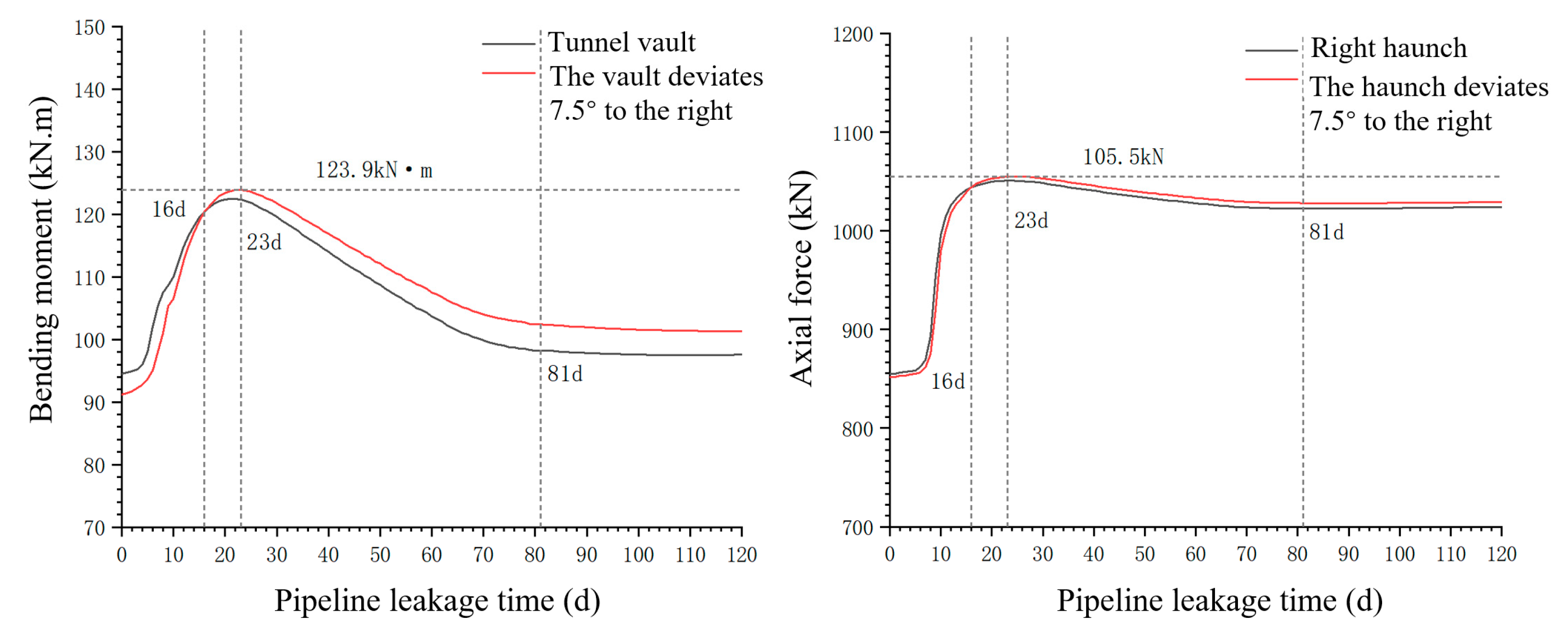
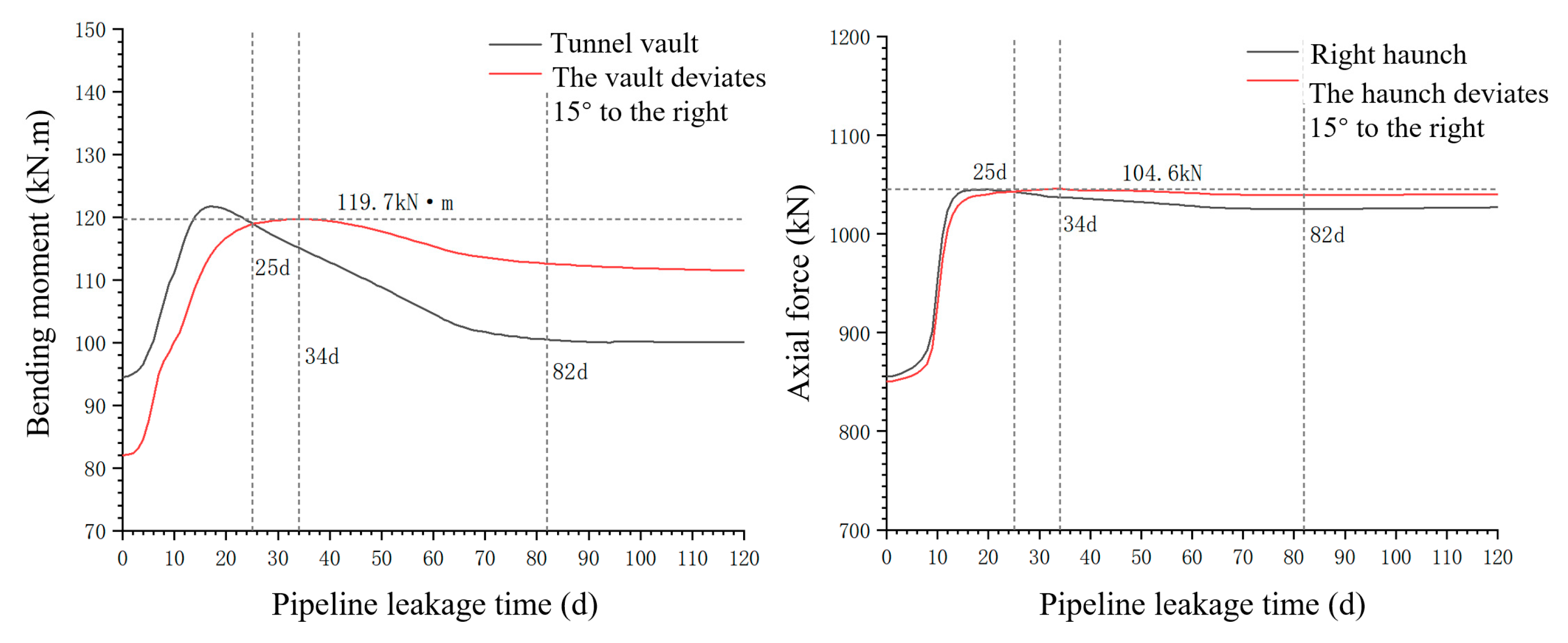
3.2.1. Analysis of the Positional Variation of the Maximum Internal Force Value

Figure 14 presents the distributions of lining axial forces and bending moments under three test conditions, including under the initial conditions and after 120 days of leakage. Before leakage initiation, the internal force distributions of the linings were nearly identical across all tests, whereas distinct patterns emerged in their final states. During leakage progression, Test 1 exhibited persistent localization of bending moment extremes at the tunnel vault and haunch, with marginal variation in bending moments but significant axial force amplification (Figure 15). In Test 2, the peak bending moment migrated 7.5° rightward from the vault, while the axial force shifted 7.5° downward along the right haunch. Test 3 demonstrated more pronounced mechanical responses, with bending moment and axial force extremes displacing 15° rightward from the vault and downward along the right haunch, respectively.

Time–history curves of maximum bending moments and axial forces were extracted across the tests. Figure 16 delineates the evolutionary behavior of lining vault internal forces in Test 1, revealing four sequential phases: an initial steady phase (0–5 d) with negligible bending moment variation, followed by a rapid growth phase (5–19 d) where bending moments and axial forces abruptly increased to peak values of 126.3 kN·m and 1045.7 kN at 19 d, subsequently transitioning into an attenuation phase (19–80 d) characterized by gradual force reduction to 98.2 kN·m and 999.5 kN at 80 d, and ultimately entering a stabilization phase (80–120 d) with minimal force fluctuations. Notably, the leakage process induced merely a 4% bending moment increase versus 18.6% cumulative axial force amplification, highlighting the greater susceptibility of axial forces to surrounding rock saturation softening effects.

Figure 17 presents the mechanical response observed in Test 2. Simultaneous bending moment increases occurred at both the vault and the 7.5° right position after 5 days of leakage. The moment curves intersected at 16 days, indicating a shift in peak bending moment (reaching 123.9 kN·m at the right position by day 23). Axial forces followed a similar trend, with the 7.5° downward haunch position becoming dominant after 16 days and peaking at 105.5 kN at 23 days. Both axial forces and moments stabilized after 81 days.

Figure 18 illustrates the mechanical behavior in Test 3. The vault bending moment reached its peak at 14 days before decreasing, while the 15° right position attained its maximum value (119.7 kN·m) at 34 days after the moment curves crossed at 25 days. Axial forces demonstrated identical temporal–spatial evolution patterns. These observations demonstrate the asymmetric load redistribution caused by seepage path deviation, with a 10-day response delay compared to Test 2.

3.2.2. Analysis of the Overall Internal Force Variation of the Lining

The analysis identified characteristic temporal patterns of lining internal forces across the three tests: Tests 1, 2, and 3 reached peak internal force states at 19, 23, and 34 days, achieving stabilization at 80, 81, and 82 days, respectively. These key states were classified as “peak state” and “stabilized state”, with the non-leakage condition serving as the “initial state” for comparative mechanical analysis. Figure 19 shows Test 1′s symmetric bending moment and axial force distributions around the tunnel centerline. The bending moment curves at the initial (0 days) and stabilized (80 days) states (Figure 19a) nearly overlapped, demonstrating negligible leakage impact. The 19-day bending moment profile exhibited concave upward and convex lateral deformations, with maximum amplification at the vault, invert, and haunches, as well as inflection points at the 45°, 135°, 225°, and 315° positions. Axial force evolution (Figure 19b) showed higher stabilized state values in the vault (315°–45°) and invert (150°–210°) regions compared to the peak state (19 days), while other sectors displayed reduced magnitudes.

Figure 20 presents the asymmetric mechanical evolution in Test 2. The bending moment distribution (Figure 20a) displayed stronger amplification in the right semicircle during peak state (23 days), evolving into a quasi-symmetric distribution around the 7.5° axis at stabilization (81 days). Axial forces (Figure 20b) initially followed inverted dominant patterns before redistributing along seepage paths, eventually forming an elliptical distribution with a 97.5°-oriented major axis upon stabilization. Figure 21 shows similar mechanisms in Test 3, with symmetric stabilized bending moments around the 15° axis and axial forces forming an elliptical pattern with a 105° major axis orientation.

Figure 22 presents a comparative analysis of stabilized mechanical states across the three tests to assess pipeline–tunnel positional effects. The lining circumference was divided into four quadrants: BL (−180° to −90°), TL (−90° to 0°), TR (0° to 90°), and BR (90° to 180°). Bending moments displayed a Test 3 > Test 2 > Test 1 hierarchy in the BL and TR quadrants, while showing an inverse pattern (Test 1 > Test 2 > Test 3) in the TL and BR quadrants. Notably, bending moment curves converged near the 0°, ±90°, and 180° positions, revealing minimal sensitivity to pipeline offset in these regions. Axial force distributions followed similar quadrant-based patterns.

4. Conclusions

This study establishes a soil strength–saturation constitutive relationship for pipeline leakage to simulate pipeline–tunnel interaction. A validated 2D fluid–solid coupled numerical model is developed and verified against laboratory data. Systematic analyses reveal how pipeline–tunnel geometries affect lining mechanics, particularly highlighting horizontal spacing’s critical impact on surface settlements and lining responses. The key findings are as follows:

(1)

This study reveals a “blockage threshold” effect in seepage–structure interactions, showing that horizontal pipe–tunnel offsets nonlinearly influence seepage evolution. Before reaching the tunnel crown, fluid diffusion follows radial patterns with negligible offset impact on leakage zone development. After contact, offsets control flow path lengths and contact areas, creating heterogeneous hydraulic gradients that produce divergent seepage velocities. Larger offsets significantly delay seepage progression: full encapsulation takes 16 days (0 m), 20 days (3 m), and 33 days (6 m), with corresponding 10-day contact ratios of 68.9%, 56.4%, and 30.6%.

(2)

This study reveals multiscale coupling mechanisms between seepage and deformation fields. Surface settlement patterns demonstrate how seepage-induced stratum softening governs deformation characteristics. Ground subsidence progressively intensifies over time in terms of both magnitude and affected area. Maximum settlements consistently occur directly above the pipeline centerline (reaching ~39 mm at 120 days) and decreased radially, confirming a “source-controlled” damage propagation mechanism.

(3)

This study reveals time-dependent correlations between structural responses and seepage damage. The analysis of the lining internal force redistribution shows how seepage erosion affects structural integrity. Pipeline–tunnel horizontal offsets significantly alter internal force distributions; at 3 m and 6 m offsets, maximum bending moments shift 7.5° and 15° clockwise from the crown, while peak axial forces move downward at corresponding angles from the haunch region. These findings demonstrate the spatial redistribution of structural stresses under seepage conditions.

For tunnel–proximal pipeline deployment, optimizing horizontal offsets can delay seepage front progression toward tunnels. Complementary gradient anti-seepage layers or peripheral drainage systems should be implemented to counteract circumferential seepage erosion. Leakage source identification and damage control can be achieved by analyzing surface settlement trough patterns to guide timely interventions. While field conditions involving geological heterogeneity and transient leakage pressures introduce additional complexities, this study focused on isolating horizontal offset effects through controlled parameterization. Future research will expand to examine coupled leakage–geotechnical interactions under multifactorial conditions.