Abstract
Superabsorbent polymers (SAPs) are widely employed as an internal curing agent to enhance the durability and shrinkage–cracking resistance of concrete. However, while its macroscopic effects on concrete properties (e.g., strength reduction) have been documented, the nanoscale mechanisms governing the mechanical behavior of calcium silicate hydrate (C-S-H) gel in SAP-modified concrete remain poorly understood. This knowledge gap limits the optimization of SAP content for balancing durability and strength, a critical challenge in high-performance concrete design. In this paper, we address this scientific problem by combining experimental characterization and molecular dynamics (MD) simulations to systematically investigate how SAP-induced pore structure modifications dictate the mechanical performance of C-S-H gel. First, we analyzed the effects of SAP on concrete pore structure and compressive strength, revealing its role in refining capillary pores into gel pores. Next, MD simulations were employed to construct C-S-H gel models with controlled pore size distributions at three SAP contents (0.2%, 0.3%, and 0.5%), to establish a quantitative relationship between pore characteristics and material performance. The results reveal that pores of ~0.74 nm diameter, predominantly located in weak interfacial regions, critically govern the mechanical behavior of C-S-H gel. At 0.2% SAP content, the C-S-H gel exhibits the highest bulk modulus (10.61 GPa) and optimal mechanical properties, whereas 0.3% SAP leads to a dominant pore cluster at 1.12 nm, resulting in significant reductions in bulk modulus (30.8%), shear modulus (29%), and Young’s modulus (22.3%). These findings establish a quantitative pore-property relationship, providing a mechanistic basis for tailoring SAP content to enhance both durability and mechanical performance in concrete, ultimately advancing the design of longer-lasting infrastructure.
1. Introduction
Cement concrete is extensively utilized in infrastructure projects, including construction engineering (e.g., floors, beams, columns), transportation systems (e.g., roads, bridges, tunnels), hydraulic structures (e.g., dams, channels), and specialized applications (e.g., airport runways, ports, docks), owing to its material availability, cost-effectiveness, constructability, and high compressive strength. However, concrete durability remains a critical challenge [1,2,3]. The actual service life of concrete structures often falls significantly short of their engineering-designed targets, such as concrete dams (50–150 years vs. observed <30–80 years), bridges (50–100 years vs. observed <20–50 years), and pavements (20~30 years vs. observed <10–15 years).
It is widely recognized that material composition and structural configuration significantly influence the service life of concrete. To enhance durability, extensive research has focused on optimizing the material mix design. Beyond cement, supplementary cementitious materials (e.g., slag, fly ash) are incorporated to enhance long-term strength [4,5], while chemical admixtures (e.g., water reducers, air-entraining agents) improve impermeability and frost resistance. Fibers are further added to augment tensile capacity [6,7,8]. In 1950, the National Institute of Standards and Technology (NIST) and the American Concrete Institute (ACI) introduced the concept of high-performance concrete (HPC), defined by its superior early-age strength, enhanced toughness, and volumetric stability after hardening. From a material–structure perspective, concrete exhibits a multi-phase internal architecture [9,10,11], comprising solid phases (aggregates, hardened cement paste), liquid phase (pore water), and voids spanning macroscopic to nanoscopic scales. Theoretical models predict that concrete strength could exceed 600 MPa [12], with service life significantly prolonged, provided internal defects are minimized through advanced material engineering. The development of 80 MPa high-strength concrete (HSC) and 120 MPa ultra-high-performance concrete (UHPC) relies on critical strategies: (1) minimizing water-to-binder ratios, (2) optimizing particle size distributions, and (3) maximizing pore-filling efficiency to achieve superior compactness [13,14].
However, a critical challenge arises in low water-binder ratio systems: unhydrated cementitious materials cease further hydration, leading to increased shrinkage crack formation within the concrete matrix [15,16,17]. To address this, the American Concrete Institute (ACI) proposed internal curing concrete in 2001. This method incorporates pre-absorbent materials (e.g., porous ceramsite, superabsorbent polymers/SAPs) to sustain hydration under water-deficient conditions, thereby enhancing gel formation, compactness, and defect resistance [18,19]. In contrast, SAP is more widely used in internal curing concrete [20,21,22]. As illustrated in Figure 1, SAPs feature a 3D polymer network with hydrophilic side chains (-COOH, -OH, -CONH2) that dissociate into anions, expanding the structure via electrostatic repulsion while binding water through hydrogen bonds [23,24,25]. When ambient humidity drops, concentration difference and osmotic gradients trigger SAP dehydration: the network contracts, releasing stored water into the cement paste [26,27]. Post-dehydration, SAP particles shrink volumetrically by 50–80%, adopting flattened or concave morphologies dependent on material properties and dehydration kinetics [28]. While SAP effectively enhances hydration and durability, its impact on the formation and nanomechanical behavior of calcium silicate hydrate (C-S-H) gel remains poorly understood [29]. This knowledge gap creates a dual deficit: (1) Scientific: Current models fail to resolve how SAP-induced pore alter C-S-H gel nanostructure. (2) Engineering: Without mechanistic insights, optimizing SAP content to balance strength loss and durability gains relies on trial-and-error approaches, limiting the design of next-generation internal curing systems.
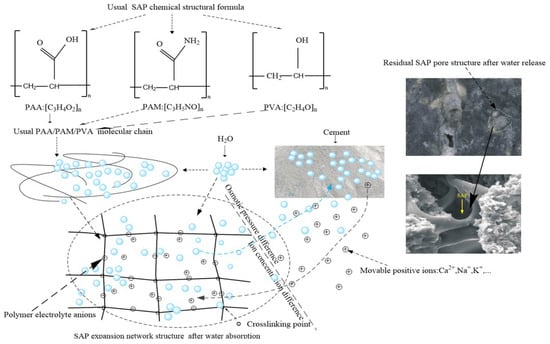
Figure 1.
Schematic diagram of SAP water absorption and release during cement hydration and hardening.
Existing studies demonstrate two primary roles of superabsorbent polymers (SAPs) in concrete: (1) enhancing cement hydration to increase C-S-H gel production [30,31] and (2) forming pore defects upon water release [32,33]. C-S-H gel, the primary hydration product of cement-based materials, constitutes 60–70% of the hardened paste by volume and largely dictates the nanomechanical behavior of these materials [34]. In the composition of concrete structures, the focus of research is on the composition and structure of C-S-H gel, as these cannot be accurately analyzed through existing experimental techniques (e.g., nanoindentation, TEM, or X-ray tomography) face fundamental limitations in probing the nanoscale porosity effects on C-S-H gel mechanics [35,36,37]. While molecular dynamics simulations (MDs) have been widely adopted to study the C-S-H gel mechanics and have yielded numerous reliable results [35,38], the current limitations include: (1) Oversimplified pore models (e.g., unquantified pore distribution) that neglect realistic SAP-modified pore space arrangement and interfacial water structures [39,40]; (2) Limited understanding of how pore size, spatial arrangement, and hydration state modulate nanoscale stress changes [41,42,43]; (3) A realistic molecular model of cement hydrates is necessary to accurately predict their mechanical behaviors [44,45]. To bridge this gap, our study addresses two unresolved questions: (1) How do SAP-generated gel pores (<1.5 nm) govern the nanoscale stress distribution in C-S-H gel? (2) What is the quantitative relationship among SAP content, dominant pore size, and nanomechanical degradation? First, we systematically analyzed pore structure evolution in SAP-modified concrete. Subsequently, molecular dynamics simulations were employed to construct a C-S-H gel model incorporating different sizes of SAP-modified gel pores. The nanomechanical behavior of the pore-containing C-S-H gel was then quantified through MD analysis. These findings provide critical insights for: (1) explaining the strength mechanisms of internal-cured concrete, (2) optimizing SAP synthesis methods, and (3) advancing performance-enhanced SAP-based internal curing concrete systems.
As illustrated in Figure 2, our multiscale approach combines the analysis of existing research results of SAP-modified concrete with molecular dynamics simulations of C-S-H gel mechanics.
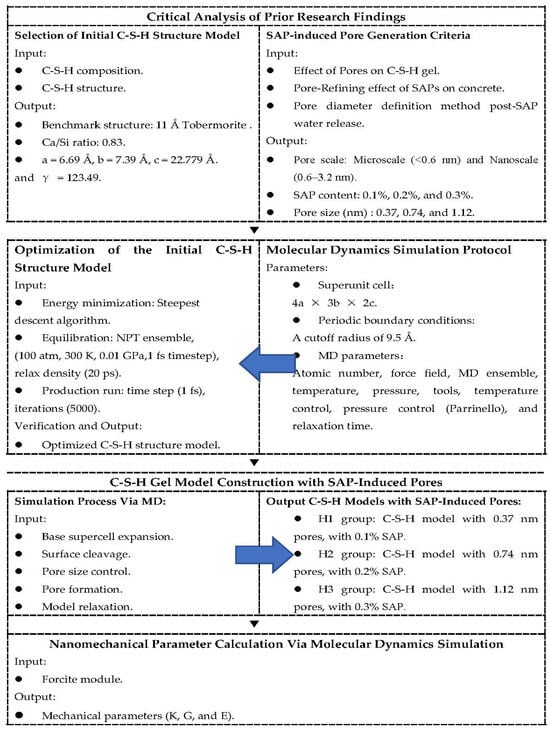
Figure 2.
A comprehensive block diagram of the multiscale research framework.
2. Materials and Methods
2.1. Model Construction of C-S-H Gel
2.1.1. Selection of Initial C-S-H Structure Model
Regarding C-S-H composition: Henri Le Chatelier [46] proposed the basic hydration phase CaO·SiO2·2.5H2O; Taylor [47,48,49] introduced a structural formula: Ca4 [Si6−Δ□ΔO18−2Δ)H2pCa2−p]q·(OH)8(1−q)·mH2O, where C-S-H (I) corresponds to Ca4(Si6O18H2)Ca·4H2O (Ca/Si ratio = 0.83) and C-S-H (II) corresponds to Ca9Si6O18(OH)6·8H2O (Ca/Si ratio = 1.5). The Ca/Si ratio can exceed 0.83, when bridging tetrahedra are partially replaced by interlayer Ca2+ ions. Newberry [50] suggested that its composition ranges from 1.5 to 2 CaO·SiO2(aq). Bogue [51] proposed a composition of 1.5CaO·SiO2(aq). Bernal [52] reported a lower Ca/Si ratio for C-S-H gel, ranging from 0.67 to 1. Richardson [53,54,55,56] proposed a structural formula for C-S-H: Ca2n/wSi(3n−1)O(9n−2)·(OH)w+n(y−2)·Cany/2·mH2O, where the Ca/Si ratio is defined as n(4 + y)/(2n − 1) (Equation (3)), with n representing the average silicate chain length, w the number of silanol groups, and y a parameter constrained to 0 ≤ y ≤ 2. Groves [57] proposed a C-S-H formula of Ca6.33H6.33Si8.5O26.5·mH2O, with a Ca/Si ratio of 0.7–0.8. Therefore, the C-S-H composition can be generalized as yCaO·SiO2·xH2O, where the Ca/Si ratio (y) varies approximately from 1 to 2.5. Currently, the C-S-H structure is primarily analogous to the layered structures of Tobermorite or Jennite, though differing in interlayer spacing.
Taylor [48,49] proposed that C-S-H (I) has a layered structure analogous to the silicon-containing tetrahedral single chain of Tobermorite, with an interlayer spacing of 1.0–1.25 nm. C-S-H (II) closely resembles the layered structure of Jennite. Richardson [55,56] suggested that the characteristic size of C-S-H gel ranges from 4 to 8 nm. Groves [57] estimated via TEM imaging that the pores in Ip-type C-S-H are smaller than 10 nm. Bernal [50] reported that the Tobermorite-like structure in the C-S-H gel exhibits a layer spacing of 0.9–1.4 nm, which can be reduced to 0.9 nm upon heating at 80–300 °C. The composition of the C-S-H gel is primarily governed by the Ca/Si ratio and hydrogen-to-silicon ratio (H/Si). Variability in these ratios leads to structural heterogeneity in C-S-H gel. Specifically, the Ca/Si ratio dictates the structural framework of C-S-H gel, whereas the H/Si ratio predominantly influences its interlayer spacing.
Current research on the properties of C-S-H primarily focuses on the structure of Tobermorite. For different Ca/Si ratios, C-S-H gels exhibit higher structural variability, and their atomic configurations remain challenging to characterize with current experimental techniques. In contrast, the C-S-H gel model with a Ca/Si ratio of 0.83, proposed by Hamid [58] was derived from X-ray diffraction data and has been a widely accepted proxy for C-S-H gel in molecular simulations [59,60,61]. Comparative studies between this model and experimental data, including stiffness and strength measurements, have demonstrated its strong agreement with empirical observations [62]. This simplification allows us to isolate the mechanical effects of SAP-induced pores while maintaining computational tractability. However, we acknowledge that real C-S-H gels exhibit Ca/Si ratios ranging from 0.6 to 1.7 depending on hydration conditions and additives [63]. Variations in Ca/Si ratio alter the silicate chain polymerization degree and interlayer calcium density, which may modulate pore-gel interfacial bonding strength [64]. Future work will incorporate dynamic Ca/Si ratio adjustments to explore this coupled effect.
In this study, an initial 11 Å C-S-H gel model with a Ca/Si ratio of 0.83 was developed and validated. The molecular formula of Hamid’s model is Ca2.25[Si3O7.5(OH)1.5]·3.5H2O. The space group and atomic coordinates were retrieved from the Crystallography Open Database (COD). In Materials Studio, the monoclinic cell parameters were defined as a = 6.69 Å, b = 7.39 Å, c = 22.779 Å, and γ = 123.49°, with the space group P21 selected for the simulation. The initial C-S-H structural model generated using these parameters is shown in Figure 3a.
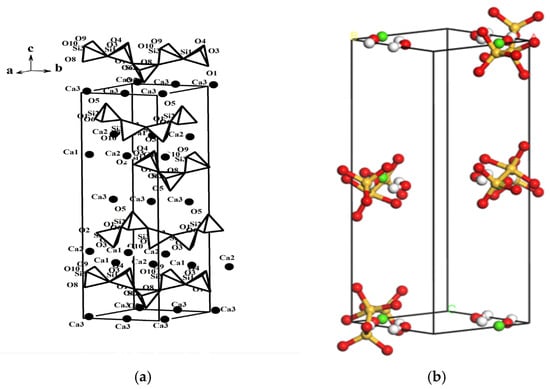
Figure 3.
Initial and optimized C-S-H structure models. (a) Hamid C-S-H structure model. (b) Optimized C-S-H structure model; Si: yellow, Ca: hoary, O: red, OH: green.
Prior to molecular dynamics simulations, the initial structure was energy-minimized to achieve a stable configuration. The geometric optimization parameters (Table 1) resulted in rapid energy convergence, reaching stability within 500 iterations. The optimized C-S-H structure model is presented in Figure 3b.

Table 1.
Geometrical optimization parameters setting of the c-s-h gel structure model via md.
2.1.2. Molecular Dynamics Simulation Protocol
Following the construction and basic geometric optimization of the preliminary C-S-H gel model, further computational refinement was performed. All simulations were performed using Materials Studio with the COMPASS force field, which has been widely validated in simulating the nanomechanical behavior and atomic configurations of C-S-H gels [65,66]. The simulation workflow included: (1) Energy minimization: Steepest descent algorithm to eliminate initial atomic overlaps. (2) Equilibration: NPT ensemble (100 atm, 300 K, 0.01 GPa, 1 fs timestep) for 20 ps to relax density. (3) Production run: The optimization protocol included NPT ensemble relaxation with a time step of 1 fs for 5000 iterations. As demonstrated in prior studies [67,68], NPT ensemble relaxation effectively minimizes the system’s potential energy, achieving a stable equilibrium state.
To facilitate the future pore size analysis, the unit cell dimensions were scaled to 4a × 3b × 2c (a = 6.69 Å, b = 7.39 Å, c = 22.779 Å). Periodic boundary conditions were applied to minimize edge artifacts, enhance simulation realism, and ensure computational reproducibility. A cutoff radius of 9.5 Å was assigned to van der Waals interactions, beyond which their contributions were truncated. The molecular dynamics parameters for structural optimization are summarized in Table 2. The nanomechanical behavior of the optimized C-S-H model are summarized in Table 3, with structural details shown in Figure 4. The results exhibit strong agreement with the C-S-H models reported [35,36], validating the accuracy of our computational framework. Finally, molecular dynamics simulations were executed on the optimized system, yielding target properties (e.g., elastic modulus) through the post-processing of selected output parameters.

Table 2.
Selection of parameters for C-S-H structure optimization via MD.

Table 3.
Nanomechanical behavior of the optimized C-S-H gel.
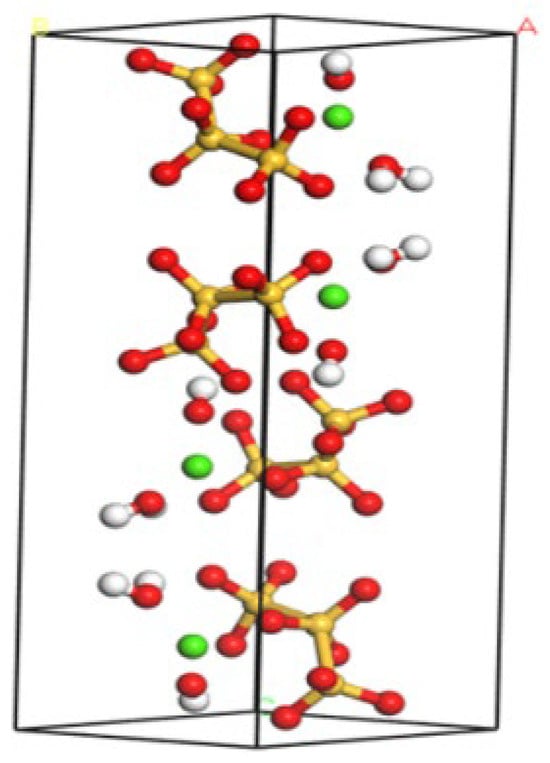
Figure 4.
Optimized C-S-H structure model. Si: yellow, Ca: hoary, O: red, OH: green.
2.2. SAP-Induced Pore Generation Criteria
2.2.1. Effect of Pores on Concrete Strength
Concrete is inherently heterogeneous, containing numerous pores and cracks within its microstructure. This study specifically investigates the impact of pore defects on strength. From a physical standpoint, pores can be categorized into microscopic, nanoscopic, and mesoscopic scales, depending on characterization techniques: (1) Imaging methods: Optical Microscopy (OM), Scanning Electron Microscopy (SEM), Transmission Electron Microscopy (TEM), Focused Ion Beam (FIB), X-ray Computed Tomography (X-CT); (2) Analytical techniques: Mercury Intrusion Porosimetry (MIP), Small-Angle X-ray Scattering (SAXS); (3) Probing tools: Atomic Force Microscopy (AFM) [37,69,70,71]. Pores at these scales exhibit distinct effects on concrete strength.
According to the pore classification proposed by the International Union of Pure and Applied Chemistry (IUPAC) in 1985, pores are classified as micropores (<2 nm), mesopores (2–50 nm), and macropores (>50 nm). In 2015, IUPAC further subdivided and supplemented these categories into nanopores (including micropores, mesopores, and macropores, but with an upper limit of 100 nm), ultramicropores (<0.7 nm), and supermicropores (0.7–100 nm). Separately, F.H. Wittmann first introduced the concept of concrete porosology at the 7th International Congress on the Chemistry of Cement in 1980 [72].
Subsequently, research on pore classification gradually expanded to include parameters such as size, grading, morphology, and other pore characteristics. Pores can now be categorized based on size, distribution, and characterization methods, as illustrated in Figure 5. According to T.C. Powers’ theory [73], pores in concrete structures include: crystal pores (formed within cement hydration products), capillary pores (spaces left after water evaporates during hydration), and transition pores (voids created by the growth of hydration products). Feldman [74,75] further classified pores into interlayer gap pores, adsorption pores, and coarse pores. Other notable classifications include: Brunauer [76]: Super-micropores (<0.6 nm), micropores (0.6–1.6 nm), medium pores (1.6–100 nm), and coarse pores (>100 nm). Kondo Lianyi [77]: Internal crystalline pores (<1.2 nm), gel pores (1.2–3.2 nm), intergel pores (3.2–200 nm), and capillary pores (>200 nm). Mikhail [78]: Internal small pores (<0.6 nm), internal large pores (0.6–1.6 nm), external large pores (1.6–100 nm), and coarse pores (>100 nm). Wu [79]: Harmless pores (<20 nm), less harmful pores (20~50 nm), harmful pores (50~200 nm), and multiple harmful pores (>200 nm). Hansen [80]: Gel pores (<10 nm), transition pores (10~100 nm), capillary pores (100–1000 nm), and macropores (>1000 nm). Jawed [81]: C-S-H gel pores (<2.6 nm), slurry interstitial pores (2.6–50 nm), capillary macropores (50–5000 nm), and macropores (>5000 nm).
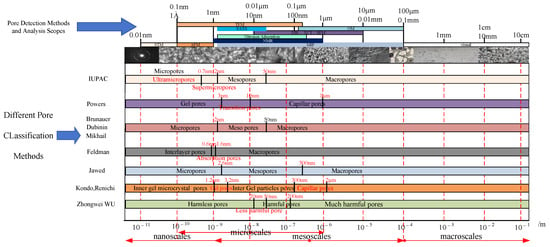
Figure 5.
Classification of pore types and sizes in concrete according to the literature.
Next, the relationship between these pores and concrete strength was further analyzed. Tracing back to 1896, French scholar Feret [82] proposed that concrete strength inversely correlates with void volume (i.e., an inverse proportional function). Later, T.C. Powers [83] established an exponential relationship between strength and the gel–space ratio, which became a cornerstone for subsequent theories linking pores to strength. Mathematical models describing the relationship between porosity and concrete strength, including exponential, power, logarithmic, and linear functions, were subsequently proposed by Balshin [84], Ryshkewitch [85], Jambor [41], Schiller [42], Hasselman [43], and Diamond [86]. However, these formulas fail to explain why concrete with similar porosity can exhibit different strengths. To address this, scholars began systematically studying the effect of pore size on concrete strength (Table 4): Older [39] classified pores into three size ranges affecting strength: <10 nm, 10~100 nm (most detrimental, a 3.7-fold reduction in response to porosity changes), and >100 nm; Atzeni [40] categorized pores into four groups: >106 nm (greatest strength reduction), 53–106 nm, 10.6–53 nm, and <10.6 nm; Ma [87] defined critical pore sizes as: <50 nm, 50–100 nm, and >100 nm.

Table 4.
Mathematical models linking pore parameters to concrete strength (based on the literature).
In summary, the influence of pores on concrete strength should be evaluated synthetically based on three factors: pore size, pore location, and their impact on strength (in addition to porosity). Accordingly, the pore classification for concrete materials is provided in Table 5, which includes microcrystalline pores (<0.6 nm), gel pores (0.6–3.2 nm), capillary pores (3.2–50 nm), and coarse pores (>1000 nm).

Table 5.
Pore classification in concrete structures (proposed in this study).
2.2.2. Pore-Refining Effect of SAPs on Concrete
The influence of superabsorbent polymers (SAPs) on the strength of concrete. including ultra-high-performance concrete [88], high-strength concrete [89], ordinary concrete [90], and mortar [91]. Depending on factors such as SAP particle size, dosage, water/cement ratio, and hydration age, SAP-modified concrete exhibits two distinct strength trends [92]: (1) Strength enhancement (SAP increases concrete strength), (2) Strength reduction (SAP decreases concrete strength). Zhang et al. [93] demonstrated that SAP addition promotes the hydration of unhydrated cement particles and refines the pore structure of calcium silicate hydrate (C-S-H). Specifically, SAP facilitates the transformation of macropores into capillary pores or gel pores, while capillary pores are further reduced to gel pores. Kong et al. [94] found that the bulk reduction in SAPs after water release left large pores (similar in size to the original SAP particles) within the concrete. While this generally increases the total porosity, the threshold pore size (critical pore diameter) remained largely unchanged. Table 6 compares results from several key studies. According to Shen et al. [95], the proportion of gel pores (<10 nm) in SAP-modified concrete increases significantly, accounting for 39.81% of the total porosity. This refining effect is most evident in the reduction in transition pores and capillary pores, which are converted into gel pores. The most pronounced improvement in pore structure occurred with 0.18% content of 40–80 mesh SAP. Qin et al. [96] observed that SAP addition shifted the peak of the differential pore size distribution curve for gel pores toward smaller diameters, indicating a reduction in the maximum pore size. At 0.2% SAP content, a distinct peak emerged at 0.74 nm, suggesting substantial pore refinement to sizes below 1.5 nm. Kong [94] further demonstrated that SAP reduces the proportion of 100–1000 nm pores while increasing the porosity of <10 nm pores and >1000 nm pores. Jensen et al. [97] highlighted that the influence of the pore distribution (0.1–1 μm) introduced by SAPs on the hydration kinetics was verified through experiments, and SAP pores can reduce early strength.

Table 6.
Typical pore parameters of SAP-modified concrete (Based on the literature).
A comprehensive analysis reveals that the influence of superabsorbent polymers (SAP) on the mechanical properties of concrete stems primarily from two mechanisms: (1) enhancing hydration reactions and (2) altering pore structure. The hydration-enhancing effect can be quantified by measuring the volume of hydration products [96,97,98]. However, there remains no robust method to evaluate the mechanical implications of SAP-induced pore structure modifications. Previous studies on pore structure characterization have relied on techniques such as scanning electron microscopy (SEM) and mercury intrusion porosimetry (MIP) [89,90,91], yet these methods lack resolution at the molecular scale and often overlook the role of gel pores (<10 nm) in traditional cement concrete performance analyses. Notably, recent research demonstrates that SAP addition significantly increases the proportion of gel pores in concrete, with profound implications for its mechanical behavior [99,100]. The interlayer distance between cleaved C-S-H surfaces (i.e., pore size) was calibrated using experimental data from atomic force microscopy (AFM) measurements on hydrated C-S-H gel [101], which revealed a strong correlation between interlayer spacing (1–8 nm) and mechanical properties.
2.2.3. Pore Diameter Definition Method Post-SAP Water Release
Based on the above analysis, SAP addition primarily increases the porosity of large pores and gel pores in cement concrete, leading to altered nanomechanical behavior. Recent studies have extensively discussed macropores (>1000 nm) and established theoretical frameworks for their behavior [102,103]. Combined with the pore classification in Table 5, pores below 10 nm are categorized as: microcrystalline pores (<0.6 nm) and gel pores (0.6–3.2 nm). As shown in Qin [96], adding SAP with 0.1%, 0.2%, and 0.3% mass content to concrete results in distinct typical pore sizes within 1.5 nm: approximately 0.3 nm, 0.7 nm, and 1.1 nm, respectively [96]. Recent research on the relationship between the SAP content and representative pore sizes (<10 nm) is summarized in Table 7 [36,104,105,106,107,108,109]. Notably, SAP refines pore structures below 10 nm, with a greater refinement observed at a lower SAP content. A quantitative relationship between three SAP contents (0.1%, 0.2%, and 0.3%) and typical pore sizes (0.3–1.5 nm) was established, as detailed in Table 8. Building on this, simulations of C-S-H nanomechanical behavior with these gel pores can partially reflect the mechanical behavior of concrete with the corresponding pore structures.

Table 7.
Summary of the influence of SAP content on the gel pore size in domestic and international studies.

Table 8.
Remaining pore sizes in the experimental group after SAP water-release setting.
2.3. C-S-H Gel Model Construction with SAP-Induced Pores
The pore size distribution in SAP-modified C-S-H gels was modeled based on experimentally observed pore characteristics reported in SAP–concrete systems. Specifically, SAP particles (typically 20–500 μm in diameter) create nanoscale gel pores (<10 nm) during hydration, as characterized by mercury intrusion porosimetry (MIP) and nitrogen adsorption. To replicate this, three representative pore sizes (0.37 nm, 0.74 nm, and 1.12 nm) were selected, corresponding to the dominant pore ranges identified in SAP-modified cement pastes. The C-S-H gel model was constructed as follows: (1) Base supercell: A 4 × 6 × 2 supercell of Tobermorite 11 Å (single C-S-H crystal) was expanded along the [001] direction, preserving the Ca-O-Si layered structure. (2) Surface cleavage: The supercell was cleaved along the (001) plane to generate two parallel surfaces terminated by hydroxyl (-OH) and non-bridging oxygen (≡Si-O−) groups, mimicking the natural interfaces of C-S-H gel sheets. (3) Pore size control: The interlayer spacing between the cleaved surfaces was adjusted to match target pore sizes (0.37, 0.74, and 1.12 nm). (4) Pore formation: The structure of the models was formed through a controlled computational method of incorporating the pore regions with a density of 1.0 g/cm3 [61,62,63], and the validated three initial C-S-H gel models with distinct pore structures were built using the Materials Studio software 2023 (Figure 6a–c). (5) Model relaxation: Molecular dynamics geometry optimization was performed on the initial models. Energy minimization was achieved via the Newton–Raphson algorithm, followed by dynamic relaxation under the COMPASS force field to reach stable configurations (Figure 6d–f). The nanomechanical behavior during relaxation is summarized in Appendix A (Table A1). The optimized models revealed progressively finer pore structures from H3 to H1 groups, consistent with increasing the SAP content. This refinement in pore size provides a foundation for subsequent mechanical analysis.
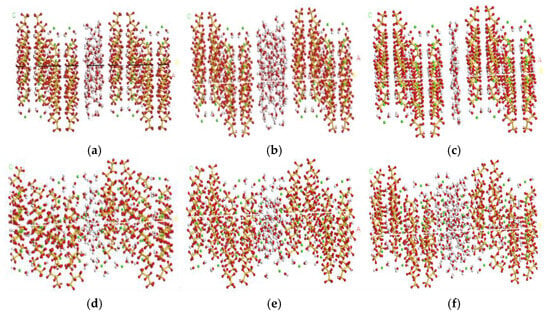
Figure 6.
Preliminary and optimized models of H1, H2, and H3 groups. (a) Preliminary model of H1. (b) Preliminary model of H2. (c) Preliminary model of H3. (d) Optimized model of H1. (e) Optimized model of H2. (f) Optimized model of H3; Si: yellow, Ca: hoary, O: red, OH: green.
3. Results
As a mature commercial software for molecular dynamics simulations, Materials Studio provides the Forcite module, which enables the direct calculation of mechanical parameters for equilibrated systems. In this study, Forcite was employed to compute the nanomechanical behavior of the established models. The workflow included the following steps: (1) Calculation of the elastic stiffness matrix using the Forcite module; (2) Derivation of the compliance matrix from the stiffness matrix. The bulk modulus (K) and shear modulus (G) were derived via matrix analysis; (3) The bulk modulus (K) and shear modulus (G) were calculated according to the Hill [110] formulas shown in Equations (1) and (2), which is the arithmetic mean of Voigt [111] and Reuss [112]. The calculation of Young’s modulus (E) using Equation (3). The stiffness and compliance matrices for H1, H2, and H3 groups are presented in Appendix B (Table A2(a)–(f)). The analysis of the diagonal elements reveals that both stiffness and compliance values along the diagonals are substantially larger than off-diagonal terms, consistent with the moderately isotropic nature of the models. Based on these matrices, the key mechanical parameters (K, G, and E) were quantified.
E = 9G/(3 + G/K)
3.1. C-S-H Weak Region Bulk Modulus Evolution
The bulk modulus (K), a critical mechanical property, quantifies the resistance of C-S-H gel to compressive deformation. As shown in Figure 7:
- The bulk modulus of the three C-S-H gel groups exhibits an initial increase followed by a decrease as the pore size reduces within the 0.3–1.5 nm range. The maximum bulk modulus occurs at 0.2% SAP content, indicating optimal mechanical performance. Controlling the SAP content to 0.2% ensures that pore sizes within 0.3–1.5 nm exert the most favorable influence on concrete mechanics;
- For group H1, the bulk modulus of the C-S-H system with 0.37 nm pores is 9.214 GPa. Increasing the pore size to 0.74 nm elevates the modulus to 10.606 GPa. This trend may arise from the minimal impact of pore size variation on K within the H1-H2 range (ultra-small pores), coupled with heightened system energy and water molecule mobility due to increased hydration, which collectively enhance K;
- In contrast, at 0.3% SAP content (H3 group, 1.12 nm pores), K drops sharply to 7.343 GPa. This decline suggests that pore expansion-induced weakening of compressibility resistance outweighs any modulus enhancement from additional water molecules, resulting in a net reduction in the mechanical stability.
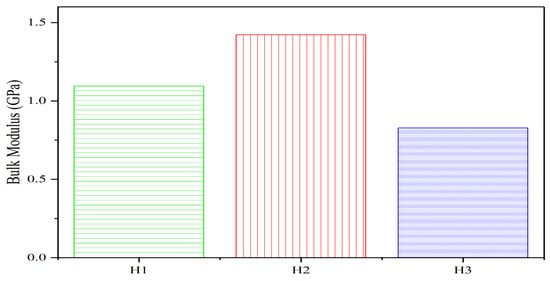
Figure 7.
Effect of SAP content variations on the C-S-H gel bulk modulus.
3.2. C-S-H Weak Region Shear Modulus Evolution
The shear modulus (G) quantifies a material’s resistance to shear deformation. As shown in Figure 8:
- The shear modulus of the three C-S-H gel groups exhibits a non-monotonic relationship with pore size within the 0.3–1.5 nm range: it initially increases and then decreases as pore size reduces.
- Specifically, for the H2 group (pore size reduced from 1.12 nm to 0.74 nm), G rises to 5.315 GPa. For the H1 group (pore size further reduced to 0.37 nm), G declines to 4.877 GPa.
- This trend may arise from two competing mechanisms:
- (1)
- Enhanced interlayer contact: Smaller pores increase the contact area between C-S-H gel layers, restricting relative sliding and thereby improving shear resistance.
- (2)
- Reduced viscous resistance: At a fixed water density (1 g/cm3), fewer water molecules occupy smaller pores, lowering viscous damping between layers. These opposing effects lead to an initial increase in G followed by a decrease.
- The highest shear modulus (5.315 GPa) occurs at 0.2% SAP content, corresponding to an optimal pore size of 0.74 nm within the 0.3–1.5 nm range.
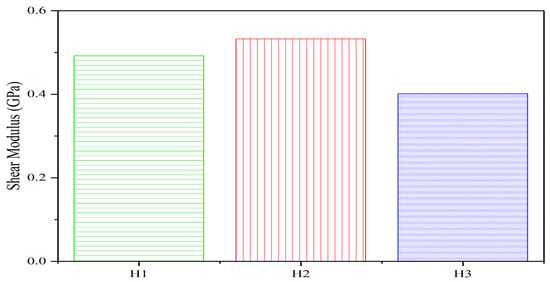
Figure 8.
Effect of SAP content variations on the C-S-H gel shear modulus.
3.3. C-S-H Weak Region Young Modulus Evolution
Young’s modulus (E) characterizes the linear elastic stress–strain behavior of solids under uniaxial loading. As illustrated in Figure 9:
- E initially increases from 12.437 GPa to 13.663 GPa but subsequently decreases to 9.657 GPa as pore size expands within the 0.3–1.5 nm range.
- This non-monotonic trend stems from two competing mechanisms:
- (1)
- Enhanced energy from hydration: Increased water molecule density at smaller pores elevates system energy, improving deformation resistance.
- (2)
- Structural weakening: Larger pores reduce structural integrity, facilitating compressive strain.
- When the pore size grows from 0.37 nm to 0.74 nm (H1 to H2 groups), the hydration effect dominates, increasing E. The further expansion to 1.12 nm (H3 group) shifts the balance toward pore-induced structural weakening, causing E to decline.
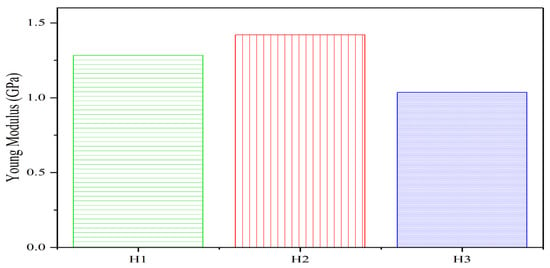
Figure 9.
Effect of SAP content variations on the C-S-H gel Young modulus.
4. Nanomechanical Behavior of SAP-Modified C-S-H: Verification and Discussion
4.1. Verification
Based on the tobermorite-type C-S-H gel structure with a Ca/Si ratio of 0.83 proposed by Hamid, C-S-H gels incorporating different SAP sizes pore were constructed, and their nanomechanical behavior was analyzed using molecular dynamics (MD). The analysis of the three SAP-modified groups revealed optimal mechanical performance at 0.2% SAP content (with a predominant pore size of ~0.74 nm). Conversely, 0.3% SAP content (pore size ~1.1 nm) yielded the lowest nanomechanical behavior within the studied range. The nanomechanical parameters K, G, and E results were compared with those of previous studies using Reuss–Voigt–Hill (R-V-H) for calculations, results summarized in Table 9. According to Shahsavari [113] and Li Zongli [63], for 11 Å Jennite models with 1.0–2.0 nm pores, the bulk modulus (K) of the C-S-H gel increased by 50.8–58.65%, while the shear modulus (G) and Young’s modulus (E) increased by 0.18–13.8% and 16.7–12.04%, respectively. In contrast, Shahsavari reported differences of 28.17 GPa (K), 10.6 GPa (G), and 28.74 GPa (E) between the 11 Å Jennite and Tobermorite models. Hajilar [108] calculated the mechanical parameters (K, G, and E) for 1a × 1b × 1c and 2a × 2b × 2c supercells based on the Jennite model and found discrepancies of 12.3–17 GPa (K), 9.1–12.6 GPa (G), and 24.6–28.2 GPa (E) compared to Li Zongli’s single-cell pore-containing model. So, the values of bulk modulus K, shear modulus G, and Young’s modulus E in this study all fall within a reasonable range, indicating the reliability of the adopted model.

Table 9.
Elastic mechanical parameters of C-S-H with pores in comparison with the previous 11 Å Tobermorite or Jennite structure C-S-H MD simulations or experiments.
4.2. Discussion
4.2.1. Fundamental Insights into SAP-Modified C-S-H Mechanics
When the structural size of the C-S-H gel is maintained at 11 Å, its bulk modulus (K), shear modulus (G), and Young’s modulus (E) are influenced by: (1) The base model of C-S-H (Jennite or Tobermorite), (2) the supercell size, and (3) the gel pore diameter variation. Our results align with those of Shahsavari et al. [113], who reported K = 58 GPa, G = 32.56 GPa, and E = 82.89 GPa and for pristine Tobermorite-based C-S-H. However, the introduction of SAP-induced pores (0.37–1.12 nm) reduced these values by 81–88%, highlighting the critical role of nanoscale porosity in interfacial weakening. This degradation mechanism contrasts with the pore-filling hypothesis proposed by Mechtcherine et al. [114], where SAPs were assumed to enhance mechanics via hydration refinement. Instead, our MD simulations reveal that pores below 0.74 nm dominate energy dissipation, whereas larger pores (>0.74 nm) act as stress concentrators, reconciling the conflicting experimental observations of SAP’s dual role in strength loss and fracture energy gain [115].
4.2.2. Engineering Implications for Concrete Design
The critical pore size threshold of 0.74 nm provides actionable guidelines for SAP selection in construction practice:
- (1)
- SAP particle size control: Smaller SAP particles (<50 μm) generate sub ~0.74 nm pores during swelling, minimizing mechanical degradation while sustaining internal curing efficiency [116]. The smaller SAP-induced pores (0.37–1.12 nm) promote distributed microcracking at the nanoscale [117]. This aligns with experimental observations of increased fracture energy (25–40%) in SAP-modified concrete proposed by Mechtcherine et al. [114], where 40 μm SAPs improved pavement durability by 35% without compromising the 28-day strength.
- (2)
- Dosage optimization: Nonlinear mechanical degradation (e.g., 41% G, 44% K, 41% E reduction at 0.3% SAP vs. 0.2% SAP) suggests an optimal SAP dosage of 0.1–0.2 wt% cement, balancing pore refinement (desirable for curing) and strength retention (critical for load-bearing structures).
- (3)
- Material–structure synergy: The observed nanoscale mechanical degradation and pore refinement induced by SAPs have profound implications for macroscale concrete performance. In cast-in-place concrete structures (e.g., high-performance concrete bridge deck presented in Appendix C (Figure A1a,b)), the targeted SAPs used in low-stress zones could enhance crack resistance, whereas SAP exclusion from high-stress regions (e.g., beam tension faces) preserves structural integrity.
4.2.3. Limitations and Future Directions
While this study bridges nanoscale mechanisms and macroscale performance, several limitations warrant attention:
- (1)
- Simplified pore morphology: Spherical pores in simulations neglect real SAP-induced pore anisotropy observed via TEM. Future work should incorporate irregular pore geometries.
- (2)
- Multi-ion effects: Simulations assumed pure pore water, whereas real cement pore solutions contain Ca2+, K+, Na+, and SO42−, which may alter the interfacial water structure.
- (3)
- Scale integration: The current MD-to-macro correlation relies on phenomenological models. Multiscale frameworks (e.g., FE-MD coupling) are needed to predict component-level performance.
5. Conclusions and Prospects
5.1. Key Findings
- (1)
- Pore classification and SAP refinement mechanism: SAP addition refines transition/capillary pores into gel pores (0.6–3.2 nm), with a distinct 0.74 nm peak in pore size distribution. Pores < 0.74 nm dominate interfacial energy dissipation, whereas larger pores (>0.74 nm) trigger localized stress concentrations.
- (2)
- Molecular dynamics framework: We established a validated MD workflow for C-S-H gel with SAP-induced pores (0.37–1.12 nm), enabling the atomic-scale analysis of pore–property relationships.
- (3)
- Optimal SAP content: A 0.2% SAP dosage generates ~0.74 nm pores, maximizing interfacial bulk (10.61 GPa), shear (5.31 GPa), and Young’s modulus (13.66 GPa) values.
5.2. Scientific Prospects
This study opens new avenues for fundamental research:
- (1)
- Pore morphology realism: Replace idealized spherical pores with TEM-informed irregular geometries to capture anisotropic stress distributions.
- (2)
- Multiscale bridging: Integrate MD-predicted nanomechanics into phase-field or FEM frameworks to predict macroscale crack propagation in SAP-modified concrete.
5.3. Applied Engineering Prospects
The findings directly inform construction practice:
- (1)
- SAP material design: Prioritize SAPs with crosslinked networks (e.g., acrylic acid-co-acrylamide) to limit swelling and stabilize pore sizes <0.74 nm.
- (2)
- Optimize particle size distribution (e.g., 20–50 μm) to enhance pore refinement efficiency.
- (3)
- Concrete mix optimization: Apply 0.1–0.2% SAPs in high-stress zones (e.g., bridge decks) for crack suppression, while minimizing SAPs in compression-critical regions (e.g., columns). Combine SAPs with nano-silica to offset strength loss via pozzolanic reactivity.
Author Contributions
Software, S.L.; validation, K.L. and J.W.; investigation, S.Z., K.L., G.L., S.L. and X.S.; resources, J.C.; writing—original draft, S.Z.; project administration, S.Z.; funding acquisition, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Suqian Sci&Tech Program, grant number: H202313; the Natural Science Research Project of Jiangsu Province Higher Education Institutions, grant number: 23KJA560007; the Open Project of the Technical Innovation Center of Mine Geological Environmental Restoration Engineering in Southern Karst Area, Ministry of Natural Resources, grant number: NFSS2023029; the Jiangsu Civil Architecture Society Project, grant number: 2023 No. 4 Item 9; and the Suqian University Talent Introduction Research Start-up Fund, grant number: Suqian University 2022XRC087.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Xiaohu Sun was employed by the company Shandong Tangzheng Testing Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A

Table A1.
Nanomechanical behavior of H1, H2, and H3 groups during relaxation stages.
Table A1.
Nanomechanical behavior of H1, H2, and H3 groups during relaxation stages.
| Items | H1 Group | H2 Group | H3 Group | |||
|---|---|---|---|---|---|---|
| Initial | Final | Initial | Final | Initial | Final | |
| Tot. energy (kcal/mol) | −21,346.382 | −20,712.823 | −21,346.382 | −20,712.823 | −21,814.6649 | −21,216.576 |
| Pot. energy (kcal/mol) | −22,763.189 | −22,091.413 | −22,763.189 | −22,091.413 | −23,364.698 | −22,830.948 |
| Kin. energy (kcal/mol) | 1416.807 | 1378.590 | 1416.807 | 1378.590 | 1550.049 | 1614.372 |
| Tot. enthalpy (kcal/mol) | −24,500.171 | −23,483.741 | −24,500.171 | −23,483.741 | −24,595.401 | −23,306.257 |
| Temperature (K) | 298.000 | 289.962 | 298.000 | 289.962 | 298.000 | 310.366 |
| Pressure (GPa) | −0.980 | −0.861 | −0.980 | −0.861 | −0.810 | −0.609 |
| Volume (Å3) | 22,361.199 | 22,361.199 | 22,361.199 | 22,361.199 | 23,838.302 | 23,838.302 |
| Density (g/cm3) | 1.756 | 1.756 | 1.756 | 1.756 | 1.710 | 1.710 |
Appendix B

Table A2.
(a)–(f) Stiffness and flexibility matrices of H1, H2, and H3 groups from MD simulations.
Table A2.
(a)–(f) Stiffness and flexibility matrices of H1, H2, and H3 groups from MD simulations.
| (a) Stiffness Matrix of H1 | (b) Flexibility Matrix of H1 |
| (c) Stiffness Matrix of H2 | (d) Flexibility Matrix of H2 |
| (e) Stiffness Matrix of H3 | (f) Flexibility Matrix of H3 |
Appendix C

Figure A1.
(a,b) SAP particles with sizes of 20–50 μm and the 0.2% SAP-modified concrete bridge deck pavement engineering applications. (a) Polyacrylic acid–acrylamide SAP. (b) The cured concrete bridge deck pavement project along the Chongzuo–Jingxi Expressway (middle picture) and on the Matan Hongshui River Special Bridge (right picture) in China.
References
- Mostafaei, H.; Keshavarz, Z.; Rostampour, M.A.; Mostofinejad, D.; Wu, C. Sustainability Evaluation of a Concrete Gravity Dam: Life Cycle Assessment, Carbon Footprint Analysis, and Life Cycle Costing. Structures 2023, 53, 279–295. [Google Scholar] [CrossRef]
- Hadizadeh-Bazaz, M.; Navarro, I.J.; Yepes, V. Life Cycle Assessment of a Coastal Concrete Bridge Aided by Non-Destructive Damage Detection Methods. J. Mar. Sci. Eng. 2023, 11, 1656. [Google Scholar] [CrossRef]
- Kaya, O.; Citir, N.; Ceylan, H.; Kim, S.; Waid, D.R. Development of Pavement Performance and Remaining Service Life Prediction Tools for Iowa Jointed Plain Concrete Pavement Systems. J. Transp. Eng. Part B-Pavements 2022, 149, 04022070. [Google Scholar] [CrossRef]
- Wu, R.; Shen, Y.; Li, J.; Cheng, L.; Zhang, G.; Zhang, Y. Effect of Iron Tailings and Slag Powders on Workability and Mechanical Properties of Concrete. Front. Mater. 2021, 8, 723119. [Google Scholar]
- Alaj, A.; Krelani, V.; Numao, T. Effect of Class F Fly Ash on Strength Properties of Concrete. Civ. Eng. J.-Tehran 2023, 9, 2249–2258. [Google Scholar] [CrossRef]
- Masanaga, M.; Hirata, T.; Kawakami, H.; Morinaga, Y.; Nawa, T.; Elakneswaran, Y. Effects of a New Type of Shrinkage-Reducing Agent on Concrete Properties. Materials 2020, 13, 3018. [Google Scholar] [CrossRef]
- Dąbrowski, M.; Glinicki, M.A. Air void system parameters and frost resistance of air-entrained concrete containing calcareous fly ash. Roads Bridges-Drog. I Mosty 2013, 12, 41–55. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, W.; Han, J.; Liu, Z.; Liu, J.; Huang, Y. Experimental Research on Crack Resistance of Steel–Polyvinyl Alcohol Hybrid Fiber-Reinforced Concrete. Materials 2024, 17, 3097. [Google Scholar] [CrossRef]
- Velichko, E.G.; Vatin, N.I. Reactive Powder Concrete Microstructure and Particle Packing. Materials 2022, 15, 2220. [Google Scholar] [CrossRef]
- Oneschkow, N.; Scheiden, T.; Hüpgen, M.; Rozanski, C.; Haist, M. Fatigue-Induced Damage in High-Strength Concrete Microstructure. Materials 2021, 14, 5650. [Google Scholar] [CrossRef]
- Sagar, B.; Sivakumar, M.V.N. Mechanical and Microstructure Characterization of Alccofine Based High Strength Concrete. Silicon 2022, 14, 795–813. [Google Scholar] [CrossRef]
- Wu, Z. Research and application of high strength and super high strength cement-based materials. Concr. Cem. Prod. 1992, 5, 4–9. [Google Scholar]
- Prado, L.P.; Carrazedo, R.; El Debs, M.K. Interface strength of High-Strength concrete to Ultra-High-Performance concrete. Eng. Struct. 2022, 252, 113591. [Google Scholar] [CrossRef]
- Du, J.; Meng, W.; Khayat, K.H.; Bao, Y.; Guo, P.; Lyu, Z.; Abu-obeidah, A.; Nassif, H.; Wang, H. New development of ultra-high-performance concrete (UHPC). Compos. Part B-Eng. 2021, 224, 109220. [Google Scholar] [CrossRef]
- Škvára, F.; Kolář, K.; Novotný, J.; Zadák, Z. Cement pastes and mortars with low water-to-cement ratio I. Cem. Concr. Res. 2003, 10, 253–262. [Google Scholar] [CrossRef]
- Huang, F.; Hu, Z.; Li, S.; Liu, J.; Han, F.; Liu, J. Long-term deformation and mechanical properties evolution of cement paste with ultra-low water-to-cement ratio driven by water migration. J. Build. Eng. 2023, 76, 107250. [Google Scholar] [CrossRef]
- An, M.; Liu, Y.; Zhang, G.; Wang, Y. Properties of Cement-Based Materials with Low Water–Binder Ratios and Evaluation Mechanism under Further Hydration Effect. Appl. Sci. 2023, 13, 9946. [Google Scholar] [CrossRef]
- Suzuki, M.; Meddah, M.S.; Sato, R. Use of porous ceramic waste aggregates for internal curing of high-performance concrete. Cem. Concr. Res. 2009, 39, 373–381. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, Z.; Li, Y.; Ang, Y.; Zhang, K. A Method for Internal Curing Water Calculation of Concrete with Super Absorbent Polymer. Adv. Civ. Eng. 2021, 2021, 6645976. [Google Scholar] [CrossRef]
- Justs, J.; Wyrzykowski, M.; Winnefeld, F.; Bajare, D.; Lura, P. Influence of superabsorbent polymers on hydration of cement pastes with low water-to-binder ratio. J. Therm. Anal. Calorim. 2013, 115, 425–432. [Google Scholar] [CrossRef]
- AzariJafari, H.; Kazemian, A.; Rahimi, M.; Yahia, A. Effects of pre-soaked super absorbent polymers on fresh and hardened properties of self-consolidating lightweight concrete. Constr. Build. Mater. 2016, 113, 215–220. [Google Scholar] [CrossRef]
- Liu, J.; Wang, M.; Liu, N.; Teng, L.; Wang, Y.; Chen, Z.; Shi, C. Development of ultra-fine SAP powder for lower-shrinkage and higher-strength cement pastes made with ultra-low water-to-binder ratio. Compos. Part B-Eng. 2023, 262, 110810. [Google Scholar] [CrossRef]
- Shah, T.-U.-H.; Tahir, M.H.; Rahman, A.U.; Liu, H.-W. Superabsorbent capability and high retention ability of China clay (Kaolinite)/polyacrylic acid composites for aqueous solution. Chin. J. Chem. Phys. 2019, 32, 508–512. [Google Scholar] [CrossRef]
- Bai, H.; Li, Z.; Zhang, S.; Wang, W.; Dong, W. Interpenetrating polymer networks in polyvinyl alcohol/cellulose nanocrystals hydrogels to develop absorbent materials. Carbohydr. Polym. 2018, 200, 468–476. [Google Scholar] [CrossRef]
- Yu, K.; Liu, J.; Li, H.; Li, B.; Guo, J. Preparation and properties of super water-retaining agent with sulfonic acid and carboxylic acid groups assisted by ultrasounds. Polym. Bull. 2024, 81, 13607–13627. [Google Scholar] [CrossRef]
- Lee, P.I. Absorbent polymer technology. J. Control. Release 2002, 17, 297–298. [Google Scholar] [CrossRef]
- Qi, Z.; Hu, X. Water absorbency of super absorbent polymer based on flexible polymeric network. Eur. Polym. J. 2022, 166, 111045. [Google Scholar] [CrossRef]
- Watanabe, N.; Hosoya, Y.; Tamura, A.; Kosuge, H. Characteristics of water-absorbent polymer emulsions. Polym. Int. 2007, 30, 525–531. [Google Scholar] [CrossRef]
- Rahman, M.M.; Jyoti, L.T.Z.; Paul, S.; Ishmam, A.; Hossain, M.A. Mechanical and Thermal Performance of Cement Mortar Incorporating Super Absorbent Polymer (SAP). Civ. Eng. J.-Tehran 2020, 6, 2231–2244. [Google Scholar] [CrossRef]
- Liu, J.; Farzadnia, N.; Shi, C. Microstructural and micromechanical characteristics of ultra-high performance concrete with superabsorbent polymer (SAP). Cem. Concr. Res. 2021, 149, 106560. [Google Scholar] [CrossRef]
- Xie, F.; Zhang, C.; Cai, D.; Ruan, J. Comparative Study on the Mechanical Strength of SAP Internally Cured Concrete. Front. Mater. 2020, 7, 588130. [Google Scholar] [CrossRef]
- Kim, M.; Moon, J.; Hong, S.-G. Theoretical study on the freeze resistance of concrete mixed with superabsorbent polymer (SAP) considering the reabsorption behavior of SAP. J. Sustain. Cem.-Based Mater. 2022, 12, 292–304. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Wyrzykowski, M.; Schröfl, C.; Snoeck, D.; Lura, P.; De Belie, N.; Mignon, A.; Van Vlierberghe, S.; Klemm, A.J.; Almeida, F.C.R.; et al. Application of super absorbent polymers (SAP) in concrete construction—Update of RILEM state-of-the-art report. Mater. Struct. 2021, 54, 80. [Google Scholar] [CrossRef]
- De Souza, F.B.; Sagoe-Crentsil, K.; Duan, W. A century of research on calcium silicate hydrate (C-S-H): Leaping from structural characterization to nanoengineering. J. Am. Ceram. Soc. 2022, 105, 3081–3099. [Google Scholar] [CrossRef]
- Bedi, R.; Sharma, S.; Sonwani, Y.K. Prediction of Mechanical Properties of Epoxy Concrete Using Molecular Dynamics Simulation. Compos.-Mech. Comput. Appl. 2021, 12, 25–39. [Google Scholar] [CrossRef]
- Ma, X.; Liu, J.; Wu, Z.; Shi, C. Effects of SAP on the properties and pore structure of high performance cement-based materials. Constr. Build. Mater. 2017, 131, 476–484. [Google Scholar] [CrossRef]
- Sutter, L.L.; Peterson, K.R.; Van Dam, T.J.; Smith, K. Using Epifluorescence Optical Microscopy to Identify Causes of Concrete Distress: Case Study. Transp. Res. Rec. 2007, 1798, 22–30. [Google Scholar] [CrossRef]
- Barbhuiya, S.; Das, B.B. Molecular dynamics simulation in concrete research: A systematic review of techniques, models and future directions. J. Build. Eng. 2023, 76, 107267. [Google Scholar] [CrossRef]
- Older, I.; Rossler, M. Investigations on the relationship between porosity structure and strength of hydrated Portland cement pastes II. Effects of pore structure and degree of hydration. Cem. Concr. Res. 1985, 4, 401–410. [Google Scholar]
- Atize, C.; Massidda, L. Effect of pore size distribution on strength of hardened cement paste. Cem. Concr. Res. 1986, 1, 56–62. [Google Scholar]
- Jambor, J. Pore structure and strength of hardened cement pastes. In Proceedings of the 8th ICCC, Vienna, Austria, 7–11 September 1964. [Google Scholar]
- Schiller, K.K. Strength of porous materials. Cem. Concr. Res. 1971, 1, 419–422. [Google Scholar] [CrossRef]
- Hasselman, D.P.H. Relation between effects of porosity on strength and on Young’s modulus of elasticity of polycrystalline materials. J. Am. Ceram. Soc. 1963, 46, 564–565. [Google Scholar] [CrossRef]
- Pellenq, R.J.M.; Kushima, A.; Shahsavari, R.; Van Vliet, K.J.; Buehler, M.J.; Yip, S.; Ulm, F.J. A realistic molecular model of cement hydrates. Proc. Natl. Acad. Sci. USA 2009, 106, 16102–16107. [Google Scholar] [CrossRef]
- Bauchy, M.; Qomi, M.J.A.; Bichara, C.; Ulm, F.-J.; Pellenq, R.J.-M. Transition in Materials: Hardness is Driven by Weak Atomic Constraints. Phys. Rev. Lett. 2015, 114, 125502. [Google Scholar] [CrossRef]
- Le Chatelier, H. Experimental researches on the constitution of cements and the theory of their setting. Comptes Rendus Acad. Sci. 1882, 94, 867–869. [Google Scholar]
- Taylor, H.F.W.; Howison, J.W. Relationships between calcium silicates and clay minerals, Clay Mineral. Bulletin 1956, 3, 98–111. [Google Scholar]
- Taylor, H.F.W. Proposed structure for calcium silicate hydrate gel. J. Am. Ceram. Soc. 1986, 69, 464–467. [Google Scholar] [CrossRef]
- Taylor, H.F.W. A discussion of the papers “Models for the composition and structure of calcium silicate hydrate (C-S-H) gel in hardened tricalcium silicate pastes” and “The incorporation of minor and trace elements into calcium silicate hydrate (C-S-H) gel in hardened cement pastes”. Cem. Concr. Res. 1993, 23, 995–998. [Google Scholar]
- Newberry, S.B.; Smith, M.M. Constitution of hydraulic cements. J. Soc. Chem. Ind. 1903, 22, 94–95. [Google Scholar]
- Bogue, R.H. The Chemistry of Portland Cement, 2nd ed.; Reinhold Publishing Corporation: New York, NY, USA, 1955. [Google Scholar]
- Bernal, J.D.; Jeffery, J.W.; Taylor, H.F.W. Crystallographic research on the hydration of Portland cement. A first report on investigations in progress. Mag. Concr. Res. 1952, 4, 49–54. [Google Scholar] [CrossRef]
- Richardson, I.G.; Groves, G.W. The structure of the calcium silicate hydrate phases present in hardened pastes of white Portland cement/blast-furnace slag blends. J. Mater. Sci. 1997, 32, 4793–4802. [Google Scholar] [CrossRef]
- Richardson, I.G.; Brough, A.R.; Groves, G.W.; Dobson, C.M. The characterization of hardened alkali- activated blast-furnace slag pastes and the nature of the calcium silicate hydrate (C-S-H) phase. Cem. Concr. Res. 1994, 24, 813–829. [Google Scholar] [CrossRef]
- Richardson, I.G.; Brough, A.R.; Brydson, R.; Groves, G.W.; Dobson, C.M. The location of aluminum in substituted calcium silicate hydrate (C-S-H) gels as determined by 29Si and 27Al nmR and EELS. J. Am. Chem. Soc. 1993, 76, 2285–2288. [Google Scholar] [CrossRef]
- Richardson, I.G. Tobermorite/jennite and tobermorite/calcium hydroxide-based models for the structure of C-S-H: Applicability to hardened pastes of tricalcium silicate, h-dicalcium silicate, Portland cement, and blends of Portland cement with blast-furnace slag, metakaolin, or silica fume. Cem. Concr. Res. 2004, 34, 1733–1777. [Google Scholar]
- Richardson, I.G.; Groves, G.W. Microstructure and microanalysis of hardened ordinary Portland cement pastes. J. Mater. Sci. 1993, 28, 265–277. [Google Scholar] [CrossRef]
- Hamid, S.A. The crystal structure of the 11 Å natural tobermorite Ca2.25 [Si3O7.5(OH)1.5].3.5H2O. Z. Krist. 1981, 154, 189–198. [Google Scholar]
- Bauchy, M.; Qomi, M.J.A.; Ulm, F.-J.; Pellenq, R.J.-M. Order and disorder in calcium–silicate–hydrate. Phys. Rev. Lett. 2015, 114, 195502. [Google Scholar] [CrossRef]
- Richardson, I.G. The calcium silicate hydrates. Cem. Concr. Res. 2008, 38, 137–158. [Google Scholar] [CrossRef]
- Qomi, M.J.A.; Krakowiak, K.J.; Bauchy, M.; Stewart, K.L.; Shahsavari, R.; Jagannathan, D.; Brommer, D.B.; Baronnet, A.; Buehler, M.J.; Yip, S.; et al. Combinatorial molecular optimization of cement hydrates. Nat. Commun. 2014, 5, 4960. [Google Scholar]
- Hou, D.; Yu, J.; Wang, P. Molecular dynamics modeling of the structure, dynamics, energetics and mechanical properties of cement-polymer nanocomposite. Composites 2019, 162, 433–444. [Google Scholar] [CrossRef]
- Li, Z.; Liu, S.; Tong, T.; Xiao, S.; Li, Y. Effect of Gel Pore on the Mechanical Properties of Calcium Silicate Hydrate by Molecular Dynamics Simulation. J. Mater. Sci. Eng. 2023, 41, 703–709+774. [Google Scholar]
- Roopa, A.K.; Hunashyal, A.M.; Patil, A.Y.; Kamadollishettar, A.; Patil, B.; Soudagar, M.E.M.; Shahapurkar, K.; Khan, T.M.Y. Study on Interfacial Interaction of Cement-Based Nanocomposite by Molecular Dynamic Analysis and an RVE Approach. Adv. Civ. Eng. 2023, 6, 1–18. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mohamed, A.K.; Geissbühler, D.; Manzano, H.; Jamil, T.; Shahsavari, R.; Kalinichev, A.G.; Galmarini, S.; Tao, L. Cemff: A force field database for cementitious materials including validations, applications and opportunities. Cem. Concr. Res. 2017, 102, 68–89. [Google Scholar] [CrossRef]
- Hue, K.Y.; Lew, J.H.; Thant, M.M.M.; Matar, O.K.; Luckham, P.F.; Müller, E.A. Molecular Dynamics Simulation of Polyacrylamide Adsorption on Calcite. Molecules 2023, 28, 6367. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, M.; Hou, D. EVA enhances the interfacial strength of EPS concrete: A molecular dynamics study. J. Exp. Nanosci. 2021, 16, 382–396. [Google Scholar]
- Fan, D.; Yang, S. Mechanical properties of C-S-H globules and interfaces by molecular dynamics simulation. Constr. Build. Mater. 2018, 176, 573–582. [Google Scholar] [CrossRef]
- Mohan, M.K.; Rahul, A.V.; Van Stappen, J.F.; Cnudde, V.; De Schutter, G.; Van Tittelboom, K. Assessment of pore structure characteristics and tortuosity of 3D printed concrete using mercury intrusion porosimetry and X-ray tomography. Cem. Concr. Compos. 2023, 140, 105104. [Google Scholar] [CrossRef]
- Ghods, P.; Isgor, O.B.; Carpenter, G.J.C.; Li, J.; McRae, G.A.; Gu, G.P. Nano-scale study of passive films and chloride-induced depassivation of carbon steel rebar in simulated concrete pore solutions using FIB/TEM. Cem. Concr. Res. 2013, 47, 55–68. [Google Scholar] [CrossRef]
- Brisard, S.; Davy, C.A.; Michot, L.; Troadec, D.; Levitz, P. Mesoscale pore structure of a high-performance concrete by coupling focused ion beam/scanning electron microscopy and small angle X-ray scattering. J. Am. Ceram. Soc. 2018, 102, 2905–2923. [Google Scholar] [CrossRef]
- Bikbaou, M. 7th international congress on the chemistry of cement (Paris). Cem. Concr. Res. 1980, 9, i–ii. [Google Scholar]
- Powers, T.C. Physical Properties of Cement Paste. In Proceedings of the Fourth International Symposium on the Chemistry of Cement, Washington, DC, USA, 2–7 October 1960; Volume 2, p. 577. [Google Scholar]
- Feldman, R.F.; Ramachandran, V.S. New Accelerated Methods for Redictin Durability of Cementitious Materials. ASTM 1978, 691, 313–325. [Google Scholar]
- Feldman, R.F. Pore Structure Formation During Hydration of Fly-Ash and Slag Cement Blends. In Proceedings of the Materials Research Society Annual Meeting, Boston, MA, USA, 16 November 1981; Volume 11, pp. 16–19. [Google Scholar]
- Brunauer, S. Pore Structure of Solids. Pure Appl. Chem. 1976, 48, 401–405. [Google Scholar] [CrossRef]
- Lianyi, K.; Zhengji, D. Phase compositon of hardened cement slurry. In Proceedings of the 6th International Cement Chemistry Conference, II; China Building Industry Press: Beijing, China, 1982. [Google Scholar]
- Brunauer, S.; Mikhail, R.S.H.; Bodor, E.E. Pore Structure Analysis without a Pore Shape Model. J. Colloid Interface Sci. 1967, 24, 451–463. [Google Scholar] [CrossRef]
- Wu, Z.; Lian, H. High-Performance Concrete; China Railway Publishing House: Beijing, China, 1992; pp. 218–244. [Google Scholar]
- Hansen, T.C. Physical structure of hardened cement paste: A classical approach. Mater. Struct. 1986, 14, 210–219. [Google Scholar] [CrossRef]
- Shen, A. Cement and Concrete; Beijing Communications Press: Beijing, China, 2000; pp. 93–103. [Google Scholar]
- Rao, G.A. Generalization of Abram’s law for cement mortars. Cem. Concr. Res. 2001, 31, 495–502. [Google Scholar] [CrossRef]
- Powers, T.C. Structure and physical properties of hardened Portland cement paste. J. Am. Ceram. Soc. 1958, 41, 1–6. [Google Scholar] [CrossRef]
- Balshin, M.Y. The Mechanics of Powder Material Compaction. Dokl. Akad. Nauk. SSSR 1949, 67, 831–834. [Google Scholar]
- Ryshkewitch, E. Compression Strength of Porous Sintered Alumina and Zirconia. J. Am. Ceram. Soc. 1953, 36, 65–68. [Google Scholar] [CrossRef]
- Jin, N.; Jin, X.; Guo, J. Relationship modeling of pore structure and strength of concrete. J. Zhejiang Univ. (Eng. Sci.) 2005, 39, 1680–1684. [Google Scholar]
- Ma, C.; Feng, N.; Wu, Z. The relationship between the pore structure and the flexural and compressive strength of zeolite rock. Concrete 1994, 6, 6–12. [Google Scholar]
- Tan, Y.; Li, B.; Chen, Y.-T.; Ling, Y.; Shi, W. Effects of Superabsorbent Polymer and Natural Zeolite on Shrinkage, Mechanical Properties, and Porosity in Ultra-High Performance Concretes. Dev. Built Environ. 2024, 20, 100568. [Google Scholar] [CrossRef]
- Olawuyi, B.J.; Babafemi, A.J.; Boshoff, W.P. Early-age and long-term strength development of high-performance concrete with SAP. Constr. Build. Mater. 2020, 267, 121798. [Google Scholar] [CrossRef]
- Borito, S.M.; Zhu, H.; Yu, Y.; Al-shawafi, A. Effect of superabsorbent polymers on mechanical strength and cracking of mortar and concrete with water to cement ratios of 0.4 and 0.5. Struct. Concr. 2022, 23, 3974–3994. [Google Scholar] [CrossRef]
- Beushausen, H.; Gillmer, M.; Alexander, M. The influence of superabsorbent polymers on strength and durability properties of blended cement mortars. Cem. Concr. Compos. 2014, 52, 73–80. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, L.; Zhang, P. Factors Influencing Strength of Super Absorbent Polymer (SAP) Concrete. Trans. Tianjin Univ. 2017, 23, 245–257. [Google Scholar] [CrossRef]
- Zhang, Z. Influence and Mechanism of SAP on the Properties of Cement Concrete. Master’s Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Kong, X.; Zhang, Z. Investigation on the shrinkage-reducing effect of super-absorbent polymer in high-strength concrete and its mechanism. J. Build. Mater. 2014, 17, 559–565+571. [Google Scholar]
- Shen, A.; Li, D.; Guo, Y.; Qian, Y.; Wang, W.; Qin, X.; Lv, Z.; Zhao, M.; Wang, Z. Correlation Investigation between Impermeability and Mesostructure of Internal Curing Concrete with SAP. Bull. Chin. Ceram. Soc. 2019, 38, 3993–4001. [Google Scholar]
- Qin, H.; Gao, M.; Pang, C.; Wei, S. Research on performance improvement of expansive concrete with internal curing agent SAP and its action mechanism. J. Build. Mater. 2011, 14, 394–399. [Google Scholar]
- Jensen, O.M.; Hansen, P.F. Water-entrained cement-based materials: I. Principles and theoretical background. Cem. Concr. Res. 2001, 31, 647–654. [Google Scholar] [CrossRef]
- Kang, S.-H.; Hong, S.-G.; Moon, J. Absorption kinetics of superabsorbent polymers (SAP) in various cement-based solutions. Cem. Concr. Res. 2017, 97, 73–83. [Google Scholar] [CrossRef]
- Liu, M.; Hu, Y.; Li, J.; Liu, X.; Sun, H.; Di, Y.; Wu, X.; Zhang, J. Insights into Hydration Kinetics of Cement Pastes Evaluated by Low-Field Nuclear Magnetic Resonance: Effects of Super-Absorbent Polymer as Internal Curing Agent and Calcium Oxide as Expansive Agent. Materials 2025, 18, 836. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Brochard, L.; Vandamme, M.; Ren, Q.; Li, C.; Jiang, Z. A hierarchical C-S-H/organic superstructure with high stiffness, super-low porosity, and low mass density. Cem. Concr. Res. 2024, 176, 107407. [Google Scholar] [CrossRef]
- Ulm, F.J.; Vandamme, M.; Jennings, H.M. Nanogranular origin of concrete creep. J. Am. Ceram. Soc. 2010, 93, 1239–1252. [Google Scholar]
- Xun, W.; Wu, C.; Leng, X.; Li, J.; Xin, D.; Li, Y. Effect of Functional Superplasticizers on Concrete Strength and Pore Structure. Appl. Sci. 2020, 10, 3496. [Google Scholar] [CrossRef]
- Kim, I.-S.; Choi, S.-Y.; Choi, Y.-S.; Yang, E.-I. Effect of Internal Pores Formed by a Superabsorbent Polymer on Durability and Drying Shrinkage of Concrete Specimens. Materials 2021, 14, 5199. [Google Scholar] [CrossRef]
- Kang, S.-H.; Hong, S.-G.; Moon, J. The effect of superabsorbent polymer on various scale of pore structure in ultra-high performance concrete. Constr. Build. Mater. 2018, 172, 29–40. [Google Scholar] [CrossRef]
- Wang, F.; Fei, Y.; Peng, B. Autogenous Shrinkage of Concrete with Super-Absorbent Polymer. ACI Mater. J. 2009, 106, 123–127. [Google Scholar]
- Klemm, A.J.; Sikora, K.S. The effect of Superabsorbent Polymers (SAP) on microstructure and mechanical properties of fly ash cementitious mortars. Constr. Build. Mater. 2013, 49, 134–143. [Google Scholar] [CrossRef]
- Tong, Y.; Lai, J.; Bi, Y.; Sun, J.; Zhan, S.; Zhan, Y. Effect of adding methods of super absorbent polyer on performance of cement mortar. Concrete 2019, 3, 111–114. [Google Scholar]
- Snoeck, D.; Pel, L.; De Belie, N. Comparison of different techniques to study the nanostructure and the microstructure of cementitious materials with and without superabsorbent polymers. Constr. Build. Mater. 2019, 223, 244–253. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, K.; Zhu, D.; Meng, Q.; Cui, L. Hydration and pore structure characteristics of concrete incorporating internal curing materials in a dry and large-temperature-difference environment. Mater. Res. Express 2022, 9, 035502. [Google Scholar] [CrossRef]
- Hill, T.R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der kristallphysic; Teubner: Leibzig, Germany, 1928. [Google Scholar]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM-Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Shahsavari, R.; Buehler, M.J.; Pellenq, R.J.-M.; Ulm, F.-J. First-Principles Study of Elastic Constants and Interlayer Interactions of Complex Hydrated Oxides: Case Study of Tobermorite and Jennite. J. Am. Ceram. Soc. 2009, 92, 2323–2330. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Dehn, F.; Plank, J. Superabsorbent polymers in concrete: Pore-filling mechanism and its effect on mechanical properties. Cem. Concr. Res. 2016, 89, 228–237. [Google Scholar]
- Lee, S.; Kim, J.; Park, H. Optimizing Strength and Ductility in SAP-Modified Concrete Mixtures. ACI Mater. J. 2021, 118, 123–134. [Google Scholar]
- Schröfl, C.; Snoeck, D.; Mechtcherine, V. Effect of particle size and solution concentration on the swelling capacity of superabsorbent polymers in cementitious materials. Cem. Concr. Compos. 2015, 65, 15–24. [Google Scholar]
- Yang, J.; Sun, Z.; De Belie, N.; Snoeck, D. Self-healing ability of cracks in alkali-activated slag systems incorporating superabsorbent polymers. Cem. Concr. Res. 2023, 89, 228–237. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).