From Signal to Safety: A Data-Driven Dual Denoising Model for Reliable Assessment of Blasting Vibration Impacts
Abstract
1. Introduction
2. Method
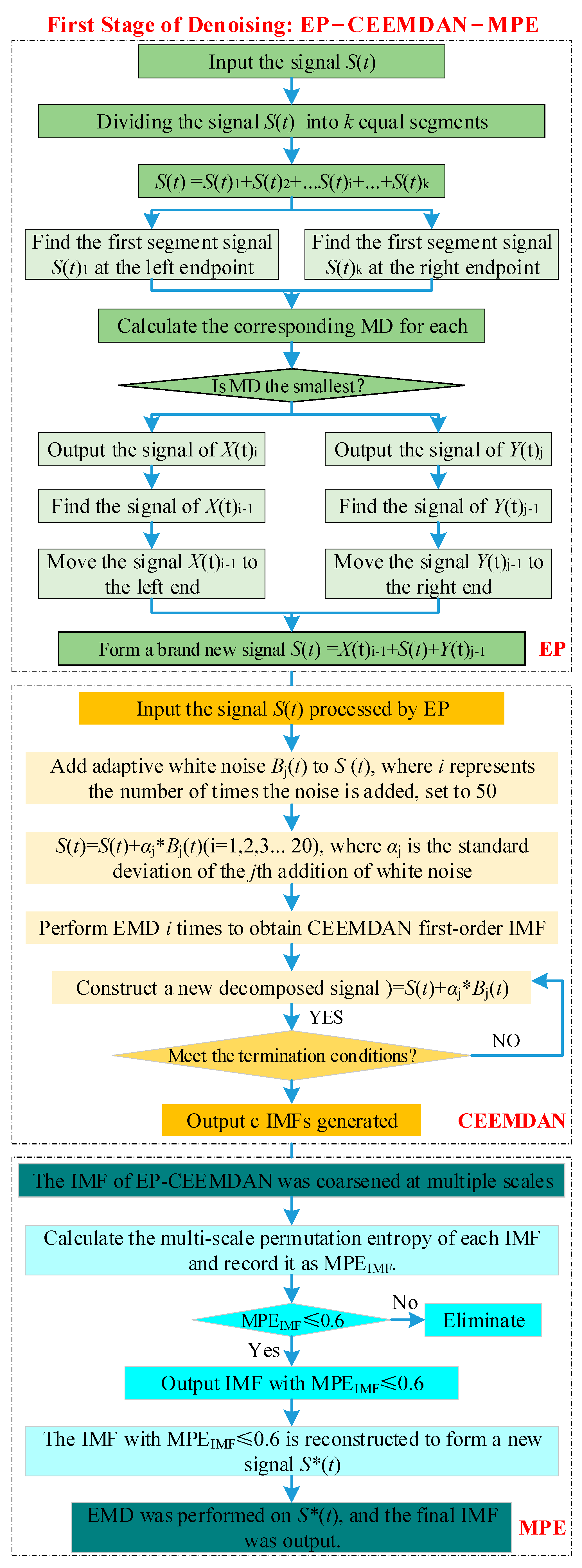
2.1. First Stage of Denoising: EP-CEEMDAN-MPE
2.1.1. Endpoint Processing (EP)
2.1.2. CEEMDAN-MPE
2.1.3. EP-CEEMDAN-MPE
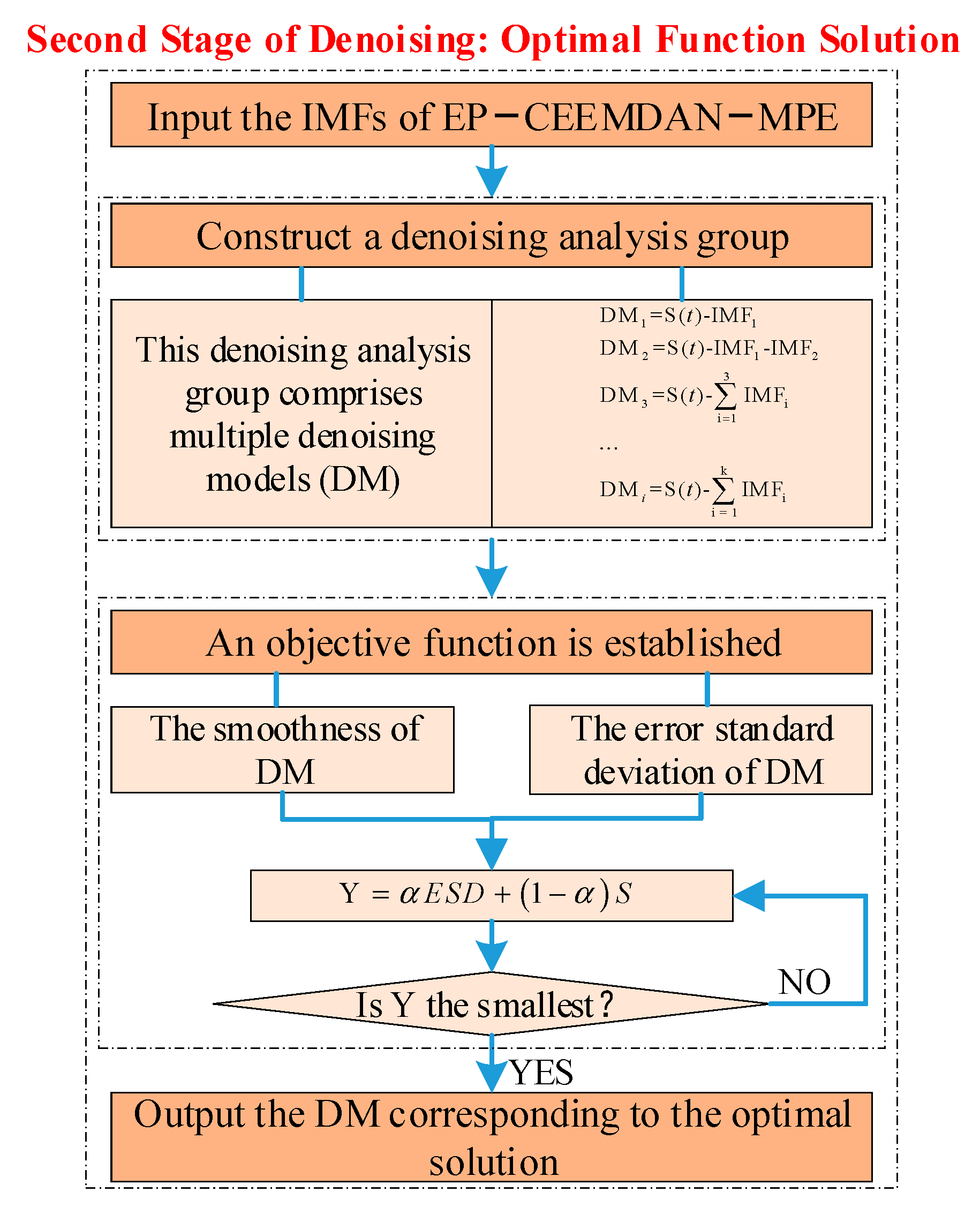
2.2. Second Stage of Denoising: Optimal Function Solution
2.2.1. Construction of the Denoising Analysis Group
2.2.2. Optimal Function Solution
- Protection of the true components of the original signal: This is quantified by the error standard deviation (ESD) between the DM and the original signal.
- Degree of denoising: This is reflected by the smoothness (S) of the DM.
3. Evaluation of the Denoising Performance of the Denoising Model
3.1. Generation of Simulated Blasting Vibration Signals with a Given Signal-to-Noise Ratio
3.2. Construction of the Denoising Model for Simulated Signals
- (1)
- As β increases, Y increases. When β = 0.6, the optimal function reaches its minimum value of 0.1578, and the denoising model is identified as DM2.
- (2)
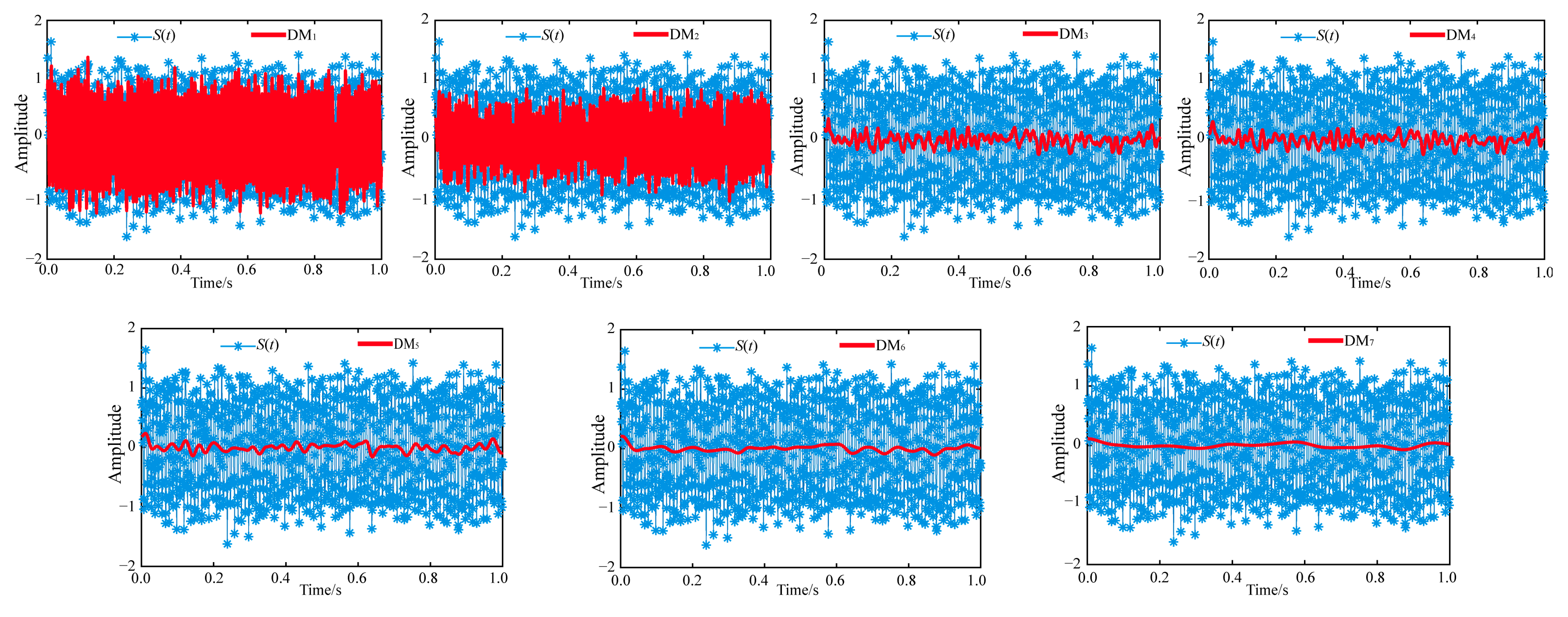
- From DM1 to DM7, the reconstruction ESD between the DM and S(t) gradually increases, indicating a higher degree of denoising. However, DM7 shows poor correlation with the original signal, resulting in over-denoising.
- (3)
- Critical state: When β = 0.8845, the DM no longer has a unique solution.
3.3. Evaluation of Denoising Performance for Simulated Signals
- (1)
- It assesses the denoising capability of the DM.
- (2)
- It validates the correctness of the optimal equation solution (using β = 0.7 as an example).
3.4. Analysis of Noise Reduction Results of Simulated Blasting Vibration Signals
- 1.
- Simulated signal generation and denoising model construction occurred as follows:
- (1)
- A simulated blasting vibration signal S(t) with a specified signal-to-noise ratio (SNR = 10) was generated by combining a noise-free sinusoidal signal x(t) and scaled random noise n(t). The DM, incorporating endpoint processing (EP), CEEMDAN, and MPE, was applied to S(t).
- (2)
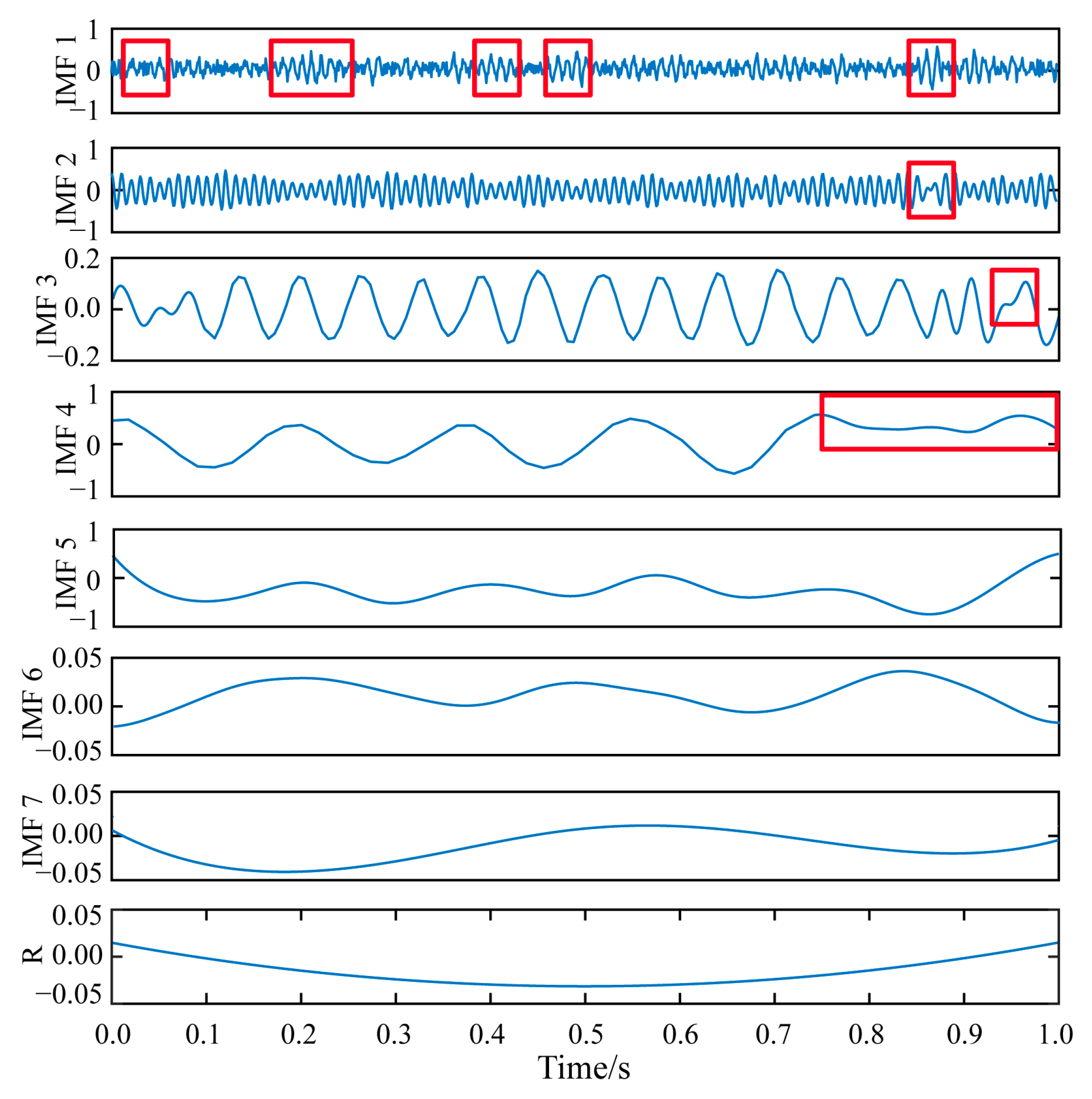
- The results demonstrated that EP-CEEMDAN-MPE effectively suppressed endpoint divergence and mode confusion, particularly in mid- to high-frequency modes, while preserving the original signal’s authenticity. In contrast, CEEMDAN-MPE without endpoint processing exhibited severe mode confusion, especially in IMF1 and IMF4, highlighting the necessity of endpoint processing.
- 2.
- Optimization and performance of denoising models occurred as follows:
- (1)
- Seven denoising models (DM1 to DM7) were constructed based on the IMFs obtained from EP-CEEMDAN-MPE. The error standard deviation (ESD) and smoothness (S) of each model were calculated, and an objective function was optimized to balance denoising intensity and signal fidelity.
- (2)
- The analysis revealed that DM2 achieved the optimal balance, minimizing the objective function (Y = 0.1578, β = 0.6). Models DM5 to DM7 exhibited over-denoising, leading to signal distortion, while DM1 showed insufficient denoising. This confirmed the importance of the dual-stage approach in achieving effective denoising without compromising signal integrity.
- 3.
- Denoising performance evaluation occurred as follows:
- (1)
- The denoising performance was evaluated using the improved signal-to-noise ratio (ISNR), which measures the reduction in noise power. DM2 demonstrated the highest ISNR improvement (ISNR−SNR = 7.2480), indicating its superior denoising capability.
- (2)
- Models DM4 to DM7 failed to preserve the original signal’s authenticity, as their noise reduction power (PDM-Pn) resulted in negative values, rendering ISNR calculations meaningless. This further validated the effectiveness of DM2 in achieving optimal denoising while maintaining signal fidelity.
4. Application of the Model in Practical Engineering
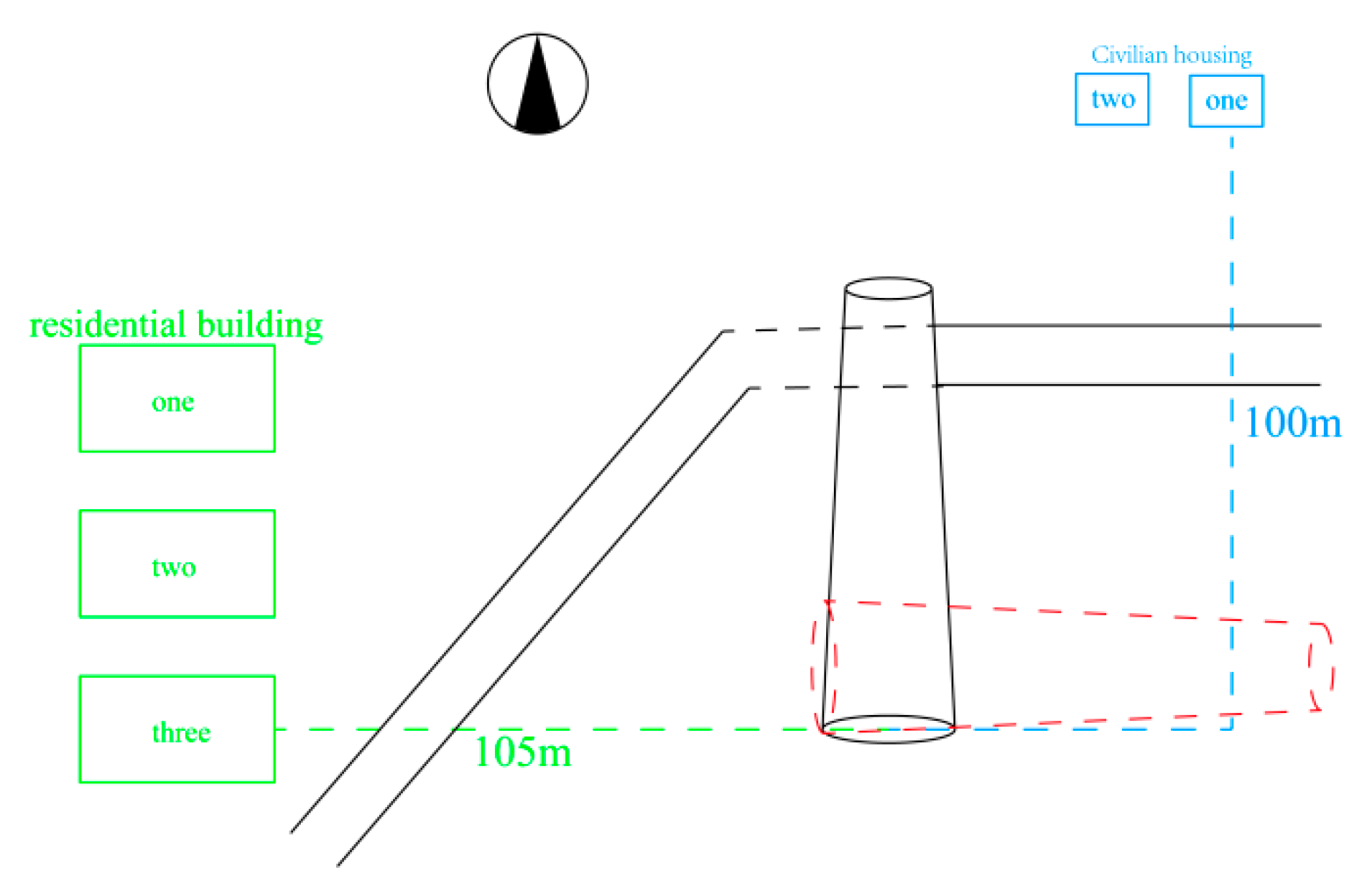
4.1. Engineering Background
4.2. Construction of the Model for Blasting Seismic Wave Signals
4.3. Evaluation of Denoising Performance for Blasting Seismic Wave Signals
4.4. Analysis of Results
- 1.
- Signal processing and denoising model construction occurred as follows:
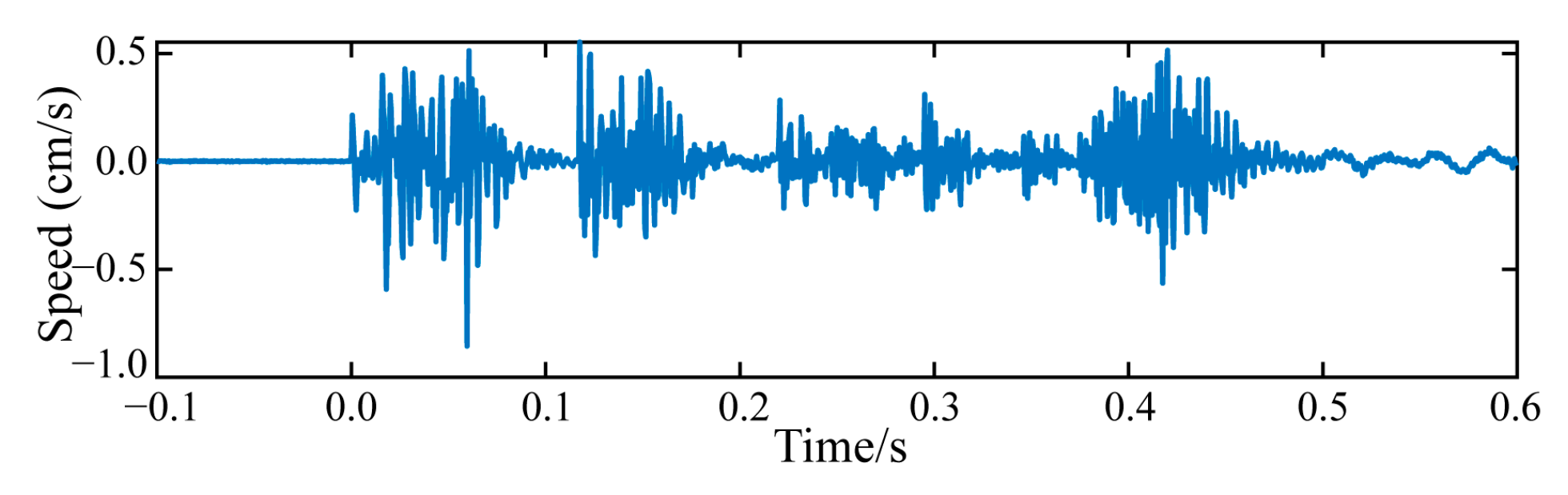
- (1)
- A typical seismic wave signal S(t) (Figure 8) was decomposed using EP-CEEMDAN-MPE, yielding eight IMFs and a residual term (Figure 9). The decomposition demonstrated high stability in mid- and low-frequency signals, with no significant mode confusion or endpoint divergence, validating the effectiveness of endpoint processing.
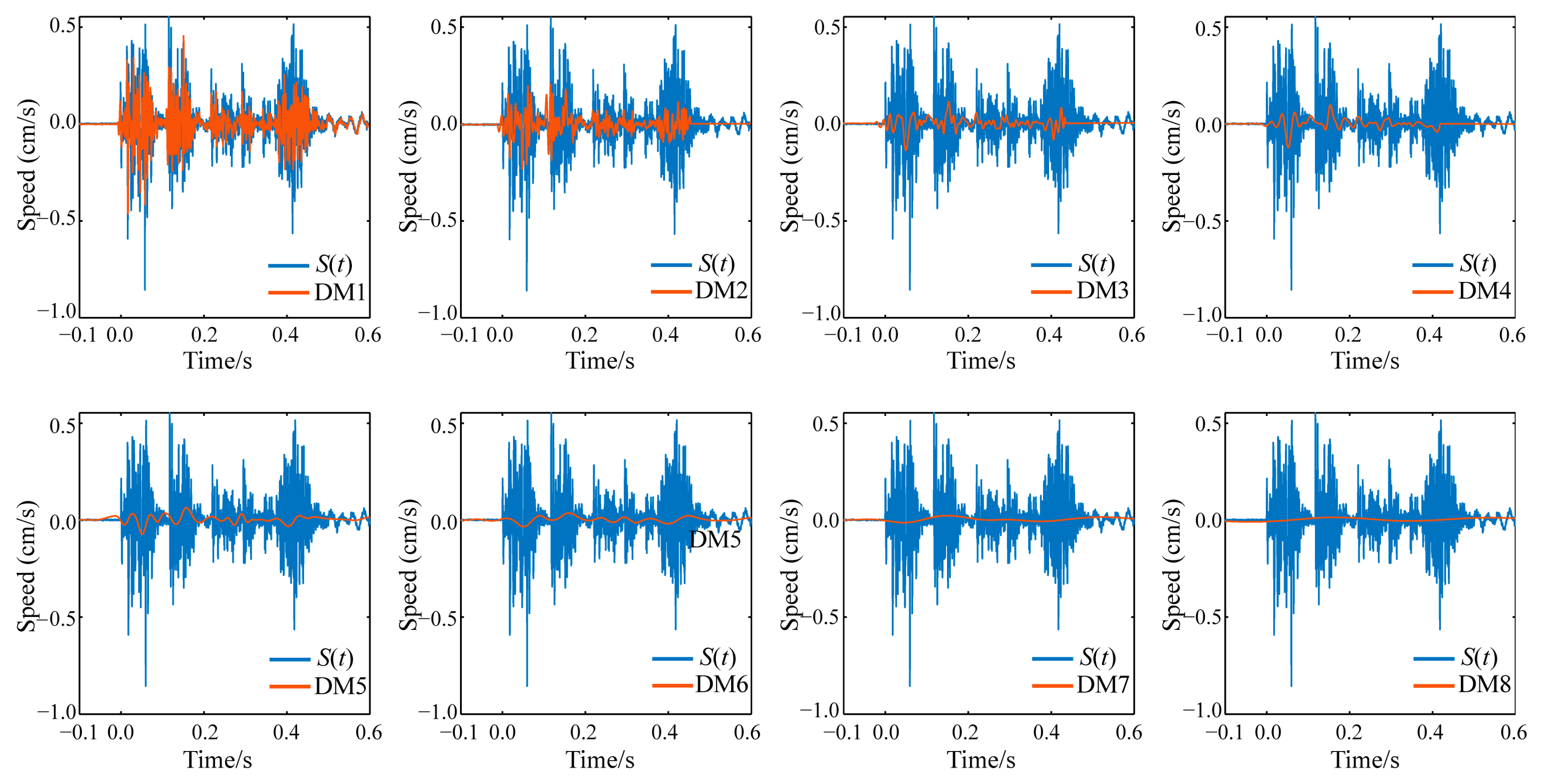
- (2)
- Eight denoising models (DM1 to DM8) were constructed, and their performance was evaluated using error standard deviation (ESD) and smoothness (S). The objective function Y was optimized for different weighting coefficients (β = 0.6,0.7,0.8). DM2 emerged as the optimal model, balancing denoising intensity and signal fidelity, while DM6 to DM8 exhibited over-denoising, leading to signal distortion (Table 3).
- 2.
- Denoising performance evaluation occurred as follows:
- (1)
- The improved signal-to-noise ratio (ISNR) was utilized to evaluate the denoising performance. DM2 achieved the highest ISNR improvement, indicating a superior denoising capability while maintaining the authenticity of the original signal. In contrast, DM6 to DM8 resulted in negative noise reduction power, rendering ISNR calculations meaningless and emphasizing the risks of over-denoising (Table 4).
- (2)
- A comparison plot (Figure 10) further validated DM2’s effectiveness, demonstrating its ability to retain critical signal features while reducing noise. This aligns with the results from the simulated signal analysis, confirming the model’s consistency and reliability.
5. Discussion
- (1)
- Endpoint processing (EP).
- (2)
- CEEMDAN-MPE algorithm.
- (3)
- Dual-stage denoising framework.
- (4)
- Validation with simulated signals.
- (5)
- Application to real engineering data.
- (6)
- Scientific and practical contributions.
6. Conclusions
- (1)
- The denoising model significantly enhances urban controlled blasting safety by precisely extracting authentic vibration characteristics, enabling accurate hazard assessment and effective vibration control measures for the protection of critical infrastructure.
- (2)
- By applying endpoint processing to the blasting seismic wave monitoring signals, the interference of endpoint effects inherent in the denoising model on the evaluation of denoising performance is effectively eliminated.
- (3)
- The CEEMDAN-MPE algorithm, which combines the adaptability of CEEMDAN and its strong suppression capability for low-frequency noise with the robustness of MPE and its control over high-frequency noise, effectively mitigates the impact of noise on modal decomposition, yielding IMFs with clearer physical significance.
- (4)
- Based on the optimization principles of advanced mathematics, a denoising model is identified that enhances denoising performance while preserving the authentic components of the original monitoring signals. The denoising capability of the dual-stage denoising model is quantitatively analyzed using simulated blasting vibration signals with a specified signal-to-noise ratio (SNR).
- (5)
- The denoising results for both the simulated signals with a specified signal-to-noise ratio (SNR) and the actual engineering blasting seismic wave signals are consistent, demonstrating the reliability and effectiveness of the denoising model in noise reduction applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| S(t) | Signal |
| S(t)i | The i-th part of the signal |
| MD | Matching degree |
| d | Distances |
| r | Correlation coefficient |
| ysj | Multi-scale time series |
| Bj(t) | The adaptive white noise |
| αj | The standard deviation of the j-th white noise |
| IMFi | Intrinsic mode function |
| R(t) | The remainder |
| DM | Denoising model |
| β | The weighting coefficient |
| ESD | The error standard deviation |
| f(x); u(x); v(x) | The smooth curve |
| u’-(w0) | The left limit of u(x) at w0 |
| v’+ (w0) | The right limit of v(x) at w0 |
| Ku|w=w0 | The curvatures of u(x) |
| Kv|w=w0 | The curvatures of v(x) |
| u’’(w0) | The second derivatives of u(x) at w0 |
| v’’(w0) | The second derivatives of v(x) at w0 |
| S | The smoothness |
| Y | The objective function |
| N | The total number of sampling points |
| x0 | Any arbitrary point within N |
| h | The sampling interval |
| SNR | Signal-to-noise ratio |
| Pn | The effective power of the noise |
| Ps | The effective power of the signal |
| x(t) | A noise-free signal |
| n(t) | A noise signal |
| ISNR | Improved signal-to-noise ratio |
| PDM | The power of the denoising model |
References
- Zhao, Z.Y.; Zhang, Y.; Bao, H.R. Tunnel blasting simulations by the discontinuous deformation analysis. Int. J. Comput. Methods 2011, 8, 277–292. [Google Scholar] [CrossRef]
- Meng, X.Z.; Wang, Z.S.; Zhang, Z.Z.; Wang, F.Q. A Method for Monitoring the Underground Mining Position Based on the Blasting Source Location. Meas. Sci. Rev. 2013, 13, 45–49. [Google Scholar] [CrossRef]
- Abbaszadeh Shahri, A.; Pashamohammadi, F.; Asheghi, R.; Abbaszadeh Shahri, H. Automated intelligent hybrid computing schemes to predict blasting induced ground vibration. Eng. Comput. 2021, 38, 3335–3349. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, Z.; Li, M.; Luo, X. Prediction of Ground Vibration Induced by Rock Blasting Based on Optimized Support Vector Regression Models. Comput. Model. Eng. Sci. 2024, 139, 3147–3165. [Google Scholar] [CrossRef]
- Huang, W.X.; Liu, D.W. Mine microseismic signal denosing based on variational mode decomposition and independent component analysis. J. Vib. Shock 2019, 38, 56–63. (In Chinese) [Google Scholar]
- Liu, J.C.; Gao, W.X. Vibration Signal Analysis of Water Seal Blasting Based on Wavelet Threshold Denoising and HHT Transformation. Adv. Civ. Eng. 2020, 2020, 4381480. [Google Scholar] [CrossRef]
- Zhao, M.S.; Zhang, J.H.; Yi, C.P. Time-frequency characteristics of blasting vibration signals measured in milliseconds. Min. Sci. Technol. 2011, 21, 349–352. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Wang, E.; Feng, J.; Chen, L.; Li, N.; Kong, X. Extraction of microseismic waveforms characteristics prior to rock burst using Hilbert—Huang transform. Measurement 2016, 2016, 101–113. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, X.; Liu, Y.; Bian, H.; Chen, W.; Wang, Y. Analysis of Acoustic Wave Frequency Spectrum Characters of Rock Mass under Blasting Damage Based on the HHT Method. Adv. Civ. Eng. 2018, 2018, 9207476. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Zheng, J.D.; Chen, J.S.; Yang, Y. Modified EEMD algorithm and its applications. J. Vib. Shock 2013, 32, 21–26. (In Chinese) [Google Scholar] [CrossRef]
- Gaci, S. A New Ensemble Empirical Mode Decomposition (EEMD) Denoising Method for Seismic Signals. Energy Procedia 2016, 97, 84–91. [Google Scholar] [CrossRef]
- Cheng, J.S.; Wang, J.; Gui, L. An improved EEMD method and its application in rolling bearing fault diagnosis. J. Vib. Shock 2018, 37, 51–56. (In Chinese) [Google Scholar] [CrossRef]
- Sun, M.; Wu, L.; Yang, J.K. Application research on time-frequency analysis of underground tunnel blasting vibration based on CEEMDAN-INHT. Blasting 2024, 41, 14–20. Available online: https://www.sciopen.com/article/10.3963/j.issn.1001-487X.2024.01.003 (accessed on 25 April 2025). (In Chinese).
- Ditommaso, R.; Mucciarelli, M.; Parolai, S.; Picozzi, M. Monitoring the structural dynamic response of a masonry tower: Comparing classical and time-frequency analyses. Bull. Earthq. Eng. 2012, 10, 1221–1235. [Google Scholar] [CrossRef]
- Zhong, G.S.; Xu, G.Y.; Jiang, W.W. Application of de-noising in blasting seismic signals based on wavelet transform. J. Cent. South Univ. 2006, 37, 155–159. [Google Scholar]
- Beenamol, M.; Prabavathy, S.; Mohanalin, J. Wavelet based seismic signal de-noising using Shannon and Tsallis entropy. Comput. Math. Appl. 2012, 64, 3580–3593. [Google Scholar] [CrossRef]
- Srivardhan, V. Stratigraphic correlation of wells using discrete wavelet transform with fourier transform and multi-scale analysis. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 137–150. [Google Scholar] [CrossRef]
- Huang, N.E. New method for nonlinear and nonstationary time series analysis: Empirical mode decomposition and Hilbert spectral analysis. Proc. SPIE—Int. Soc. Opt. Eng. 2000, 4056, 197–209. [Google Scholar] [CrossRef]
- Ditommaso, R.; Mucciarelli, M.; Ponzo, F. Analysis of non-stationary structural systems by using a band-variable filte. Bull. Earthq. Eng. 2012, 2012, 10. [Google Scholar] [CrossRef]
- Li, X.; Wang, E.; Li, Z.; Bie, X.; Chen, L.; Feng, J.; Li, N. Blasting wave pattern recognition based on Hilbert-Huang transform. Geomech. Eng. 2016, 11, 607–624. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Vashishtha, G.; Kumar, R. Autocorrelation energy and aquila optimizer for MED filtering of sound signal to detect bearing defect in Francis turbine. Meas. Sci. Technol. 2022, 33, 015006. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H. Adaptive noise reduction method for DSPI fringes based on bi-dimensional ensemble empirical mode decomposition. Opt. Express 2011, 19, 18207–18215. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, Y.; Sun, B.; Han, Y.; Hong, Y. Study on the Improvement of the Application of Complete Ensemble Empirical Mode Decomposition with Adaptive Noise in Hydrology Based on RBFNN Data Extension Technology. Comput. Model. Eng. Sci. 2021, 126, 755–770. [Google Scholar] [CrossRef]
- Peng, Y.X.; Liu, Y.S.; Zhang, C.; Wu, L. A Novel Denoising Model of Underwater Drilling and Blasting Vibration Signal Based on CEEMDAN. Arab. J. Sci. Eng. 2021, 46, 4857–4865. [Google Scholar] [CrossRef]
- Wang, Y.S.; Ma, Q.H.; Zhu, Q.; Liu, X.T.; Zhao, L.H. An intelligent approach for engine fault diagnosis based on Hilbert-Huang transform and support vector machine. Appl. Acoust. 2014, 1, 1–9. [Google Scholar] [CrossRef]
- Jiao, Y.X.; Li, K.Z.; Yue, Z.; Ban, H.F.; Liang, L.F.; Tian, C.D.; Shen, Y.Y. CEEMDAN combined wavelet denoising improved the MW cycle slip detection algorithm. Sci. Rep. 2025, 14, 23487. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Lu, W.B.; Qiao, X.M.; Chen, M.; Yan, P. Signal processing and response analysis of blasting vibration induced by high rock slope excavation. J. China Coal Soc. 2011, 39, 401–405. (In Chinese) [Google Scholar]
- Zhao, Y.; Shan, R.L.; Wang, H.L.; Tong, X.; Li, Y.H. Regression analysis of the blasting vibration effect in cross tunnels. Arab. J. Geosci. 2021, 14, 1925. [Google Scholar] [CrossRef]
- Lou, J.W.; Long, Y. Research on Feature Extraction and Recognition Technology of Blasting Vibration Signal. Vib. Shock 2003, 22, 4. [Google Scholar]
- Yuan, H.P.; Zou, Y.Y.; Li, H.Z.; Ji, S.J.; Gu, Z.A.; He, L.; Hu, R.C. Assessment of peak particle velocity of blast vibration using hybrid soft computing approaches. J. Comput. Des. Eng. 2025, 12, 154–176. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP, Prague, Czech Republic, 22–27 May 2011; pp. 4143–4147. [Google Scholar] [CrossRef]
- Yao, W.P.; Liu, T.B.; Dai, J.F.; Wang, J. Multiscale permutation entropy analysis of electroencephalogram. Acta Phys. Sin. 2014, 63, 427–433. [Google Scholar] [CrossRef]
- Chen, S.J.; Shang, P.J.; Wu, Y. Multivariate multiscale fractional order weighted permutation entropy of nonlinear time series. Phys. A: Stat. Mech. Its Appl. 2019, 515, 217–231. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Yang, Z.X.; Du, X.L.; Luo, X.Y. A New Method for Denoising Underwater Acoustic Signals Based on EEMD, Correlation Coefficient, Permutation Entropy, and Wavelet Threshold Denoising. J. Mar. Sci. Appl. 2024, 23, 222–237. [Google Scholar] [CrossRef]
- Li, J.; Li, Q. Medium term electricity load forecasting based on CEEMDAN-permutation entropy and ESN with leaky integrator neurons. Electr. Mach. Control. 2015, 19, 70–80. (In Chinese) [Google Scholar] [CrossRef]



| DM | ESD | S | Y | |||
|---|---|---|---|---|---|---|
| β = 0.6 | β = 0.7 | β = 0.8 | β = 0.8845 | |||
| DM1 | 0.0628 | 1.0000 | 0.4377 | 0.3440 | 0.2502 | 0.1710 |
| DM2 | 0.1762 | 0.1303 | 0.1578 | 0.1624 | 0.1670 | 0.1709 |
| DM3 | 0.4187 | 0.0088 | 0.2547 | 0.2957 | 0.3367 | 0.3714 |
| DM4 | 0.5397 | 0.0011 | 0.3243 | 0.3781 | 0.4320 | 0.4775 |
| DM5 | 0.9154 | 0.0002 | 0.5493 | 0.6408 | 0.7324 | 0.8097 |
| DM6 | 0.9637 | 0.00002 | 0.5782 | 0.6746 | 0.7710 | 0.8524 |
| DM7 | 1.0000 | 1.1361 × 10−7 | 0.6000 | 0.7000 | 0.8000 | 0.8845 |
| DM | SNR | ISNR | ISNR-SNR |
|---|---|---|---|
| DM1 | 10 | 12.8758 | 2.8758 |
| DM2 | 17.2480 | 7.2480 | |
| DM3 | 10.0914 | 0.0914 | |
| DM4 | (PDM-Pn) < 0, Logarithmically meaningless | (PDM-Pn) < 0, Logarithmically meaningless | |
| DM5 | (PDM-Pn) < 0, Logarithmically meaningless | (PDM-Pn) < 0, Logarithmically meaningless | |
| DM6 | (PDM-Pn) < 0, Logarithmically meaningless | (PDM-Pn) < 0, Logarithmically meaningless | |
| DM7 | (PDM-Pn) < 0, Logarithmically meaningless | (PDM-Pn) < 0, Logarithmically meaningless |
| DM | ESD | S | Y(β = 0.6) | Y(β = 0.7) | Y(β = 0.8) |
|---|---|---|---|---|---|
| DM1 | 0.0628 | 1.0000 | 0.4377 | 0.3440 | 0.2502 |
| DM2 | 0.1762 | 0.1303 | 0.1578 | 0.1624 | 0.1670 |
| DM3 | 0.4187 | 0.0088 | 0.2547 | 0.2957 | 0.3367 |
| DM4 | 0.5397 | 0.0011 | 0.3243 | 0.3781 | 0.4320 |
| DM5 | 0.9154 | 0.0002 | 0.5493 | 0.6408 | 0.7324 |
| DM6 | 0.9637 | 0.00002 | 0.5782 | 0.6746 | 0.7710 |
| DM7 | 0.9991 | 8.7264 × 10−7 | 0.5995 | 0.6994 | 0.7993 |
| DM8 | 1.0000 | 1.1361 × 10−7 | 0.6000 | 0.7000 | 0.8000 |
| DM | Ps | PDM | ISNR |
|---|---|---|---|
| DM1 | 1.3874 × 10−2 | 1.2476 × 10−2 | 2.3321 |
| DM2 | 1.3782 × 10−2 | 0.0289 | |
| DM3 | 1.3365 × 10−2 | 0.2938 | |
| DM4 | 1.3277 × 10−2 | 0.1910 | |
| DM5 | 1.3146 × 10−2 | 0.2341 | |
| DM6 | 1.3032 × 10−2 | 0.2719 | |
| DM7 | 1.2904 × 10−2 | 0.3148 | |
| DM8 | 1.2774 × 10−2 | 0.3587 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Wu, J.; Yang, J.; Wu, L.; Lu, Y.; Zhou, H. From Signal to Safety: A Data-Driven Dual Denoising Model for Reliable Assessment of Blasting Vibration Impacts. Buildings 2025, 15, 1751. https://doi.org/10.3390/buildings15101751
Sun M, Wu J, Yang J, Wu L, Lu Y, Zhou H. From Signal to Safety: A Data-Driven Dual Denoising Model for Reliable Assessment of Blasting Vibration Impacts. Buildings. 2025; 15(10):1751. https://doi.org/10.3390/buildings15101751
Chicago/Turabian StyleSun, Miao, Jing Wu, Junkai Yang, Li Wu, Yani Lu, and Hang Zhou. 2025. "From Signal to Safety: A Data-Driven Dual Denoising Model for Reliable Assessment of Blasting Vibration Impacts" Buildings 15, no. 10: 1751. https://doi.org/10.3390/buildings15101751
APA StyleSun, M., Wu, J., Yang, J., Wu, L., Lu, Y., & Zhou, H. (2025). From Signal to Safety: A Data-Driven Dual Denoising Model for Reliable Assessment of Blasting Vibration Impacts. Buildings, 15(10), 1751. https://doi.org/10.3390/buildings15101751





