Crack Propagation Behavior Modeling of Bonding Interface in Composite Materials Based on Cohesive Zone Method
Abstract
1. Introduction
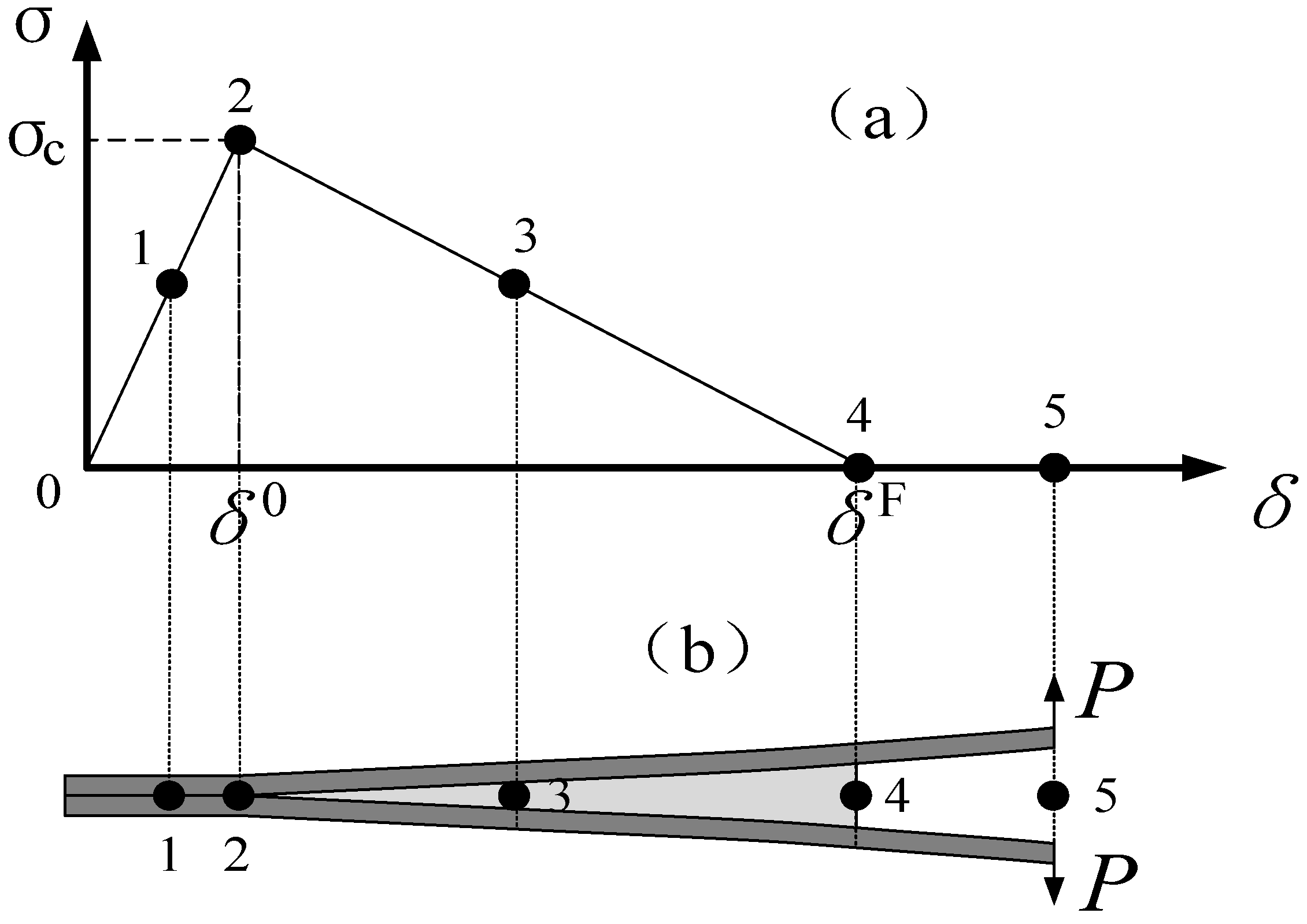
2. Theory of the Cohesive Zone Method (CZM)
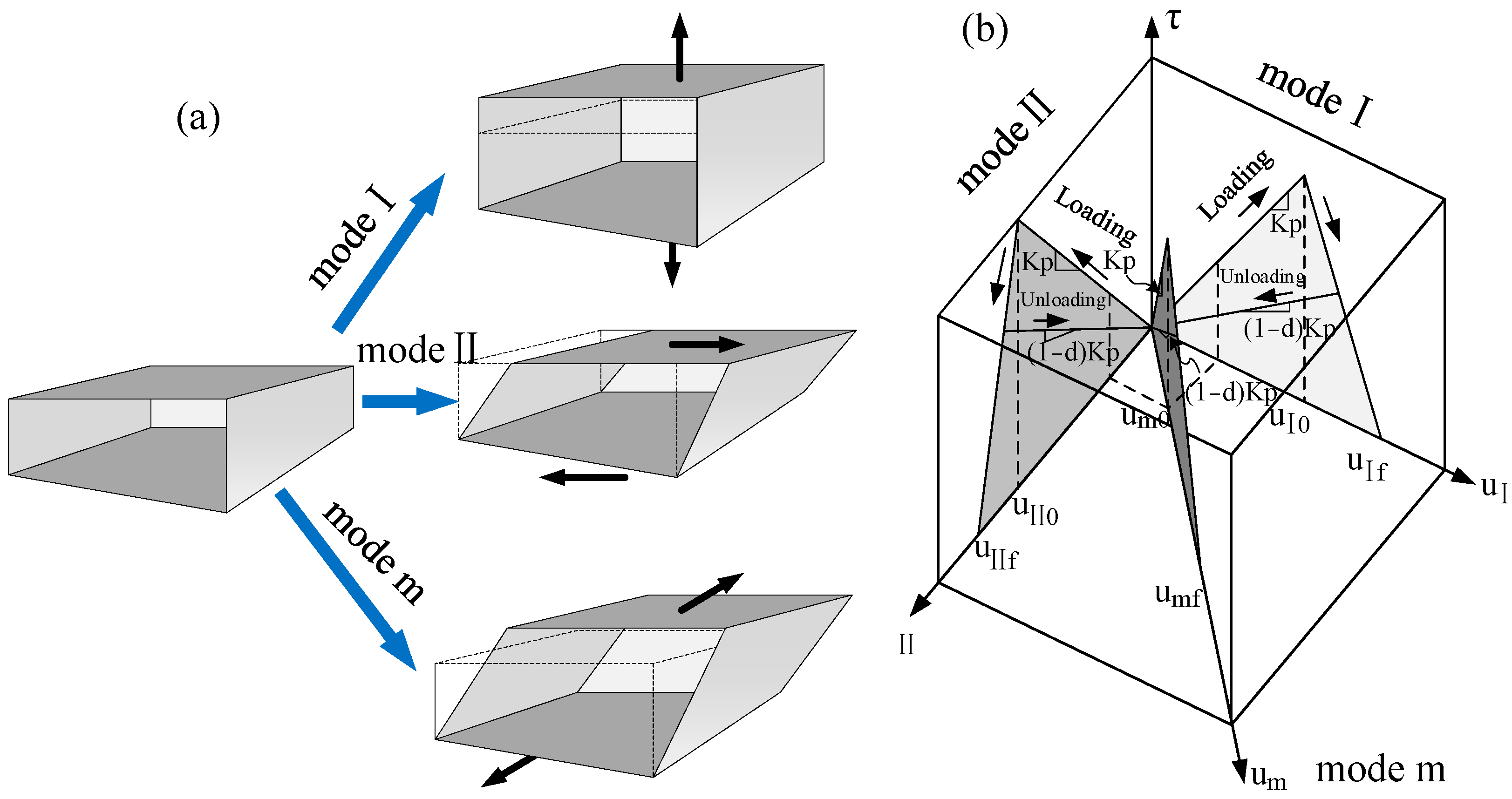
2.1. Numerical Implementation of Debonding Zones for Delamination Modeling in Composite Materials
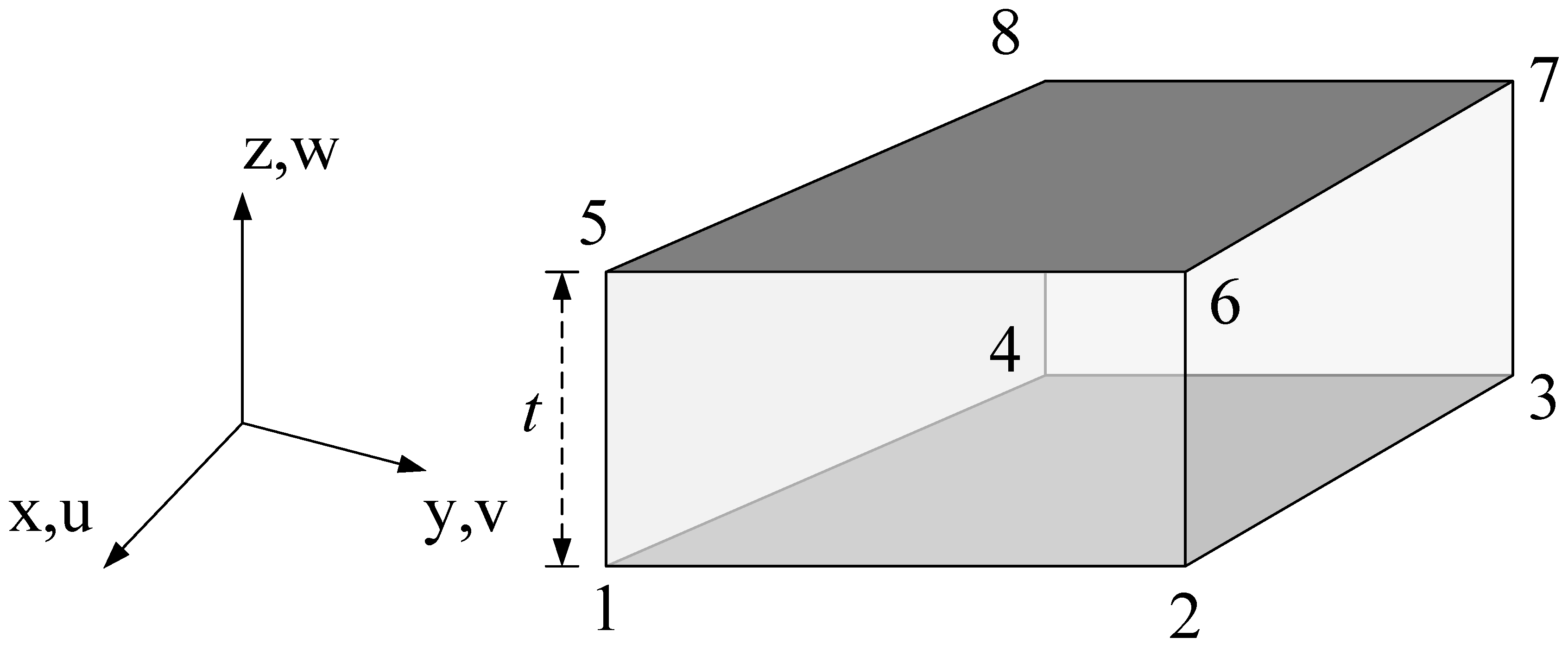
2.2. Geometric Configuration and Constitutive Framework of the Bonding Element in CZM
3. Mechanical Behavior and Failure Mechanisms of Bonding Interface in GLT Structures
3.1. Mesh Convergence Analysis
3.2. Numerical Model and Material Properties of GLT
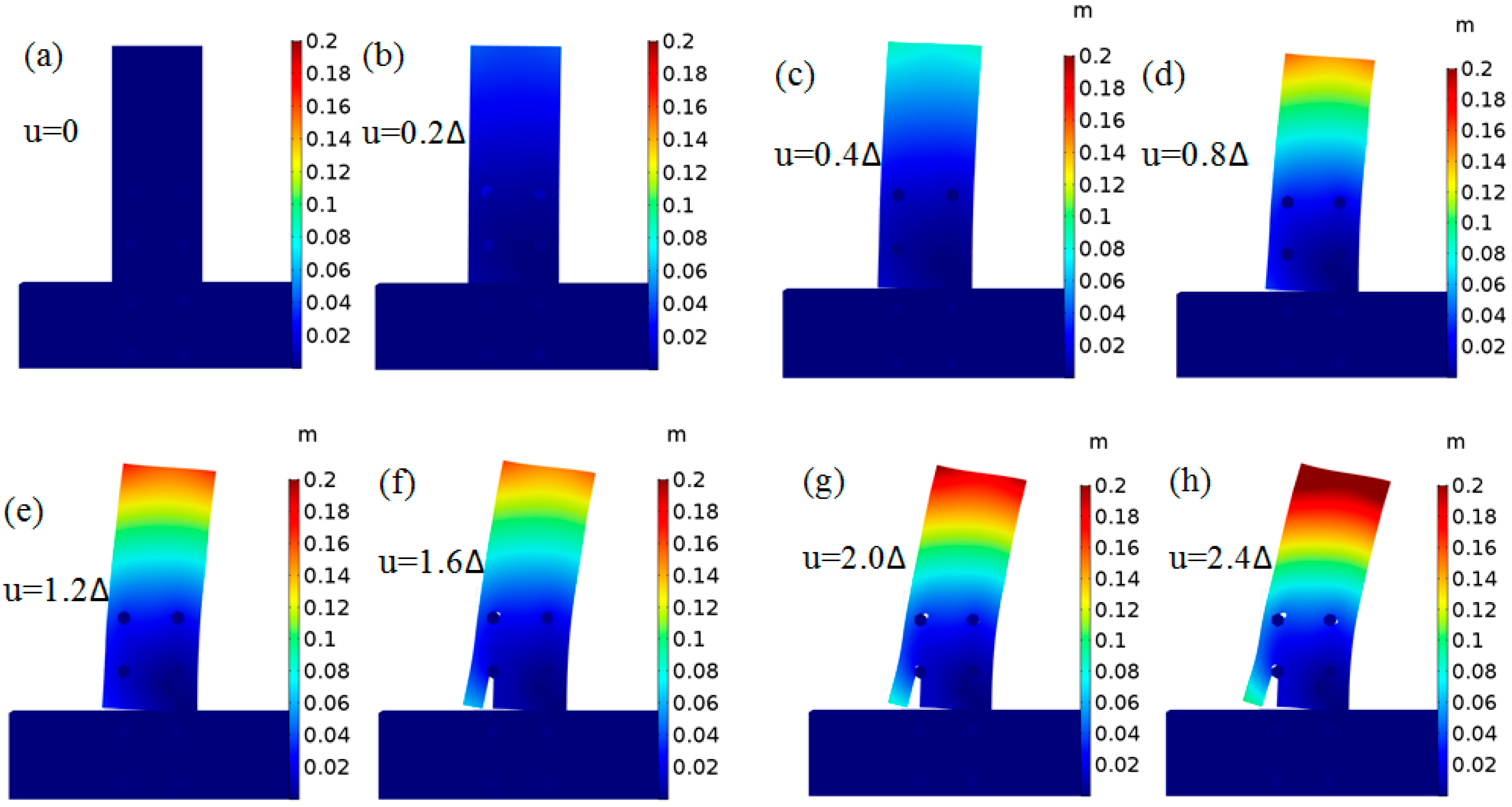
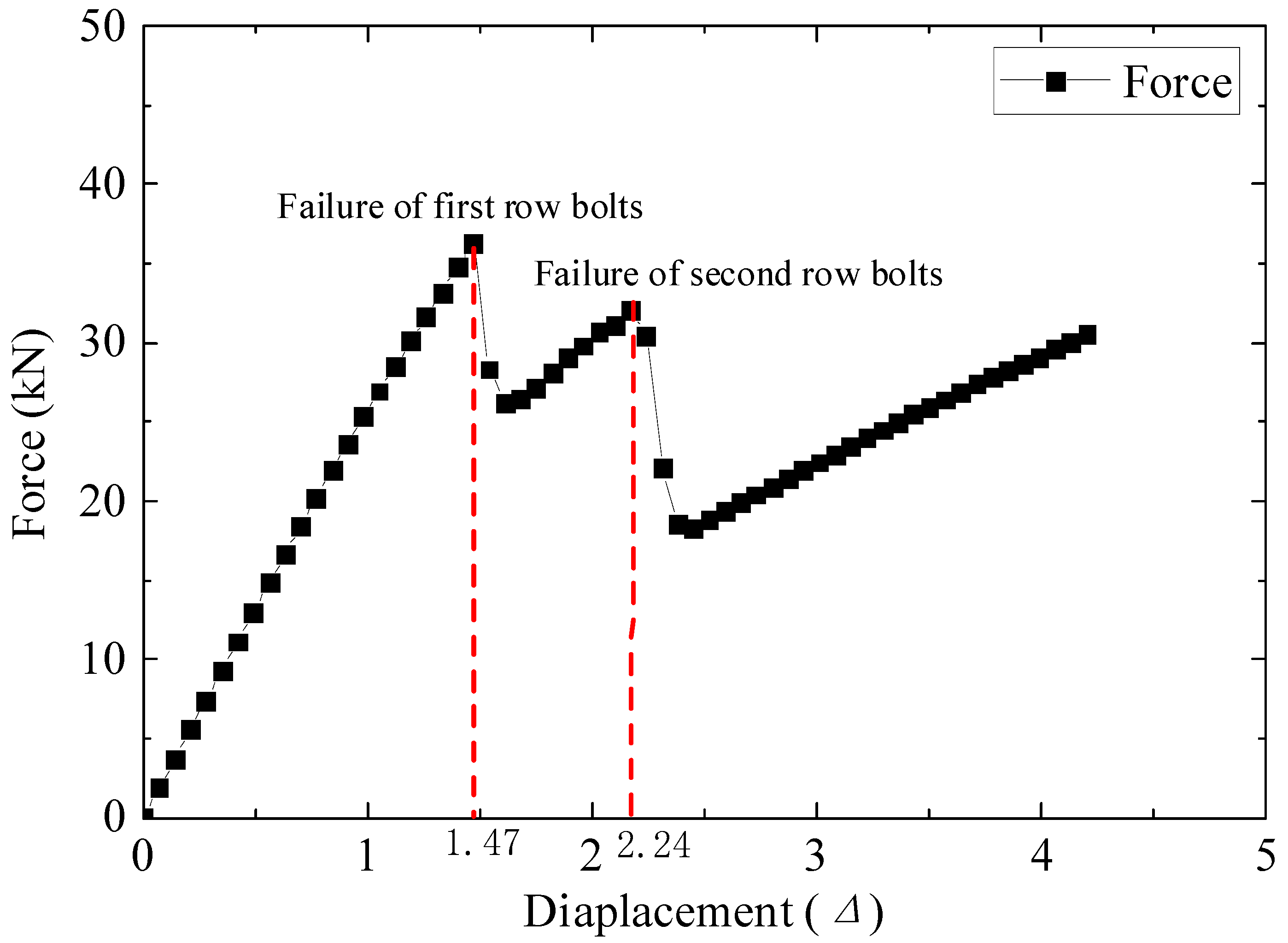
3.3. Numerical Results of GLT Cracking Behavior
4. Mechanical Behavior and Failure Mechanisms of Bonding Interface in RC Beam
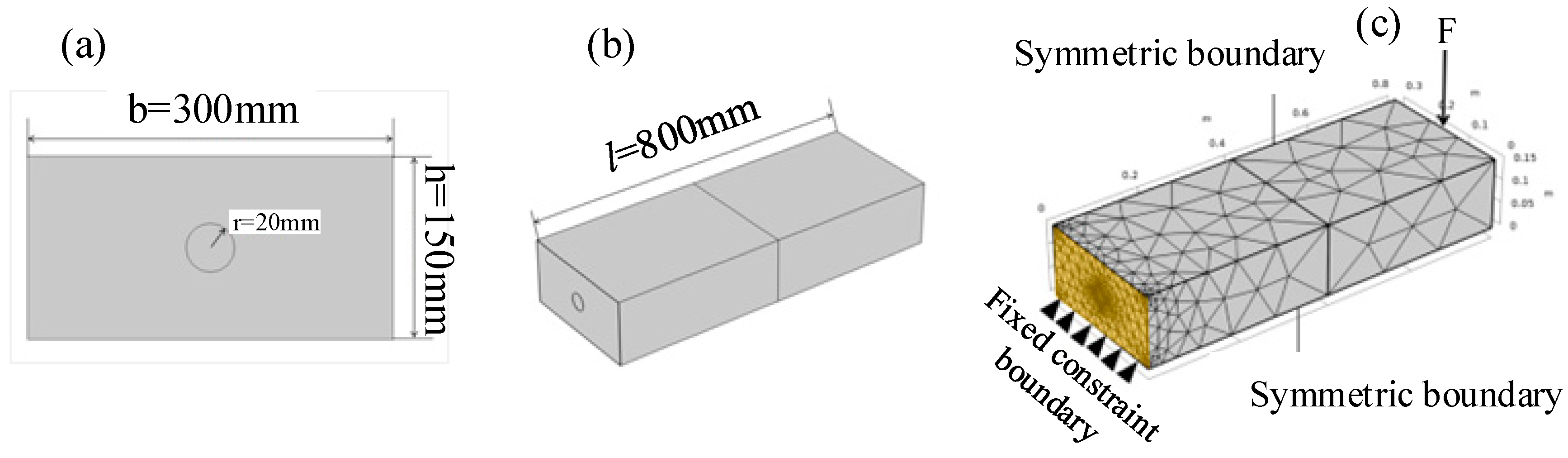
4.1. Numerical Model and Material Properties of RC Beam
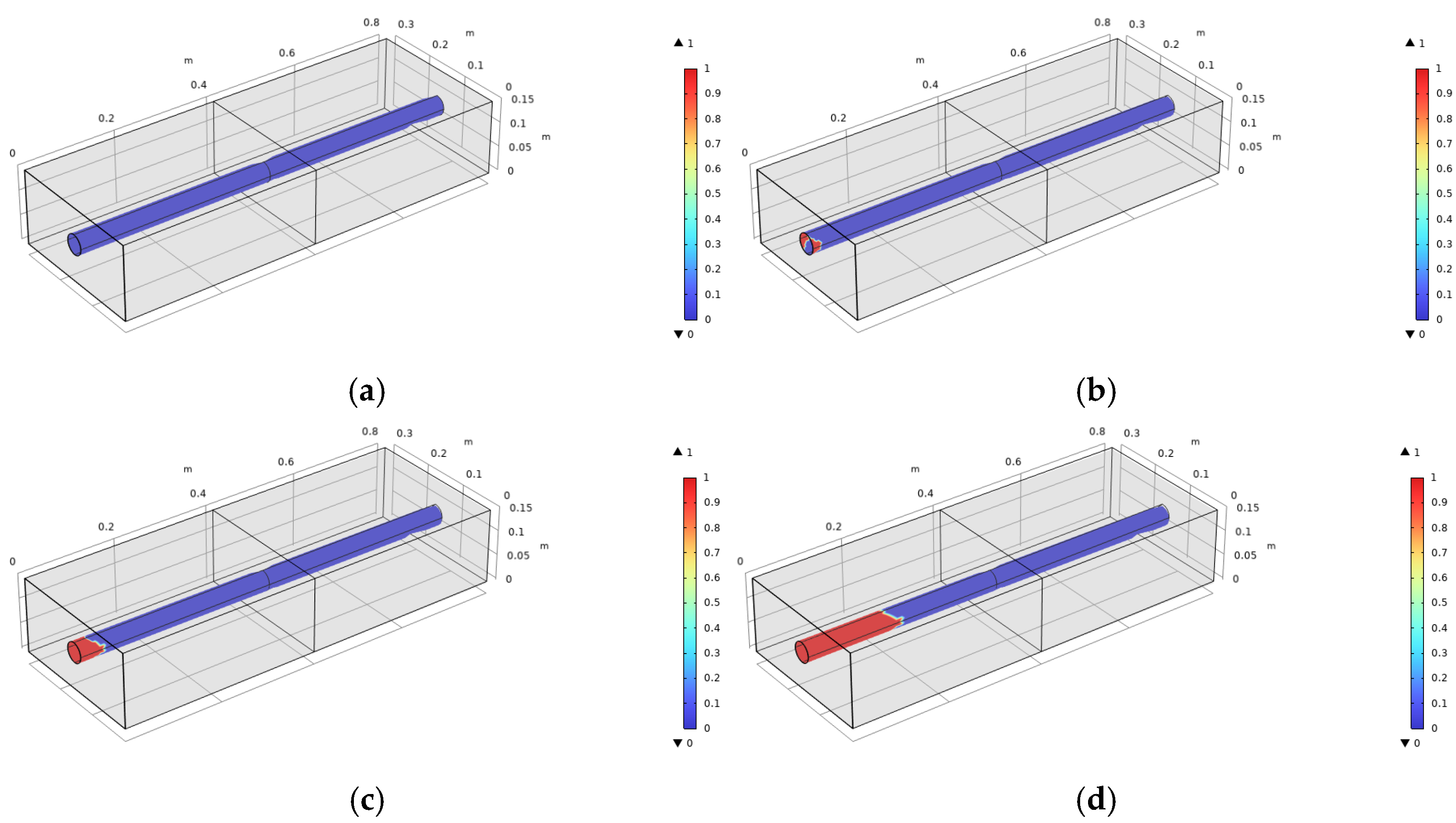
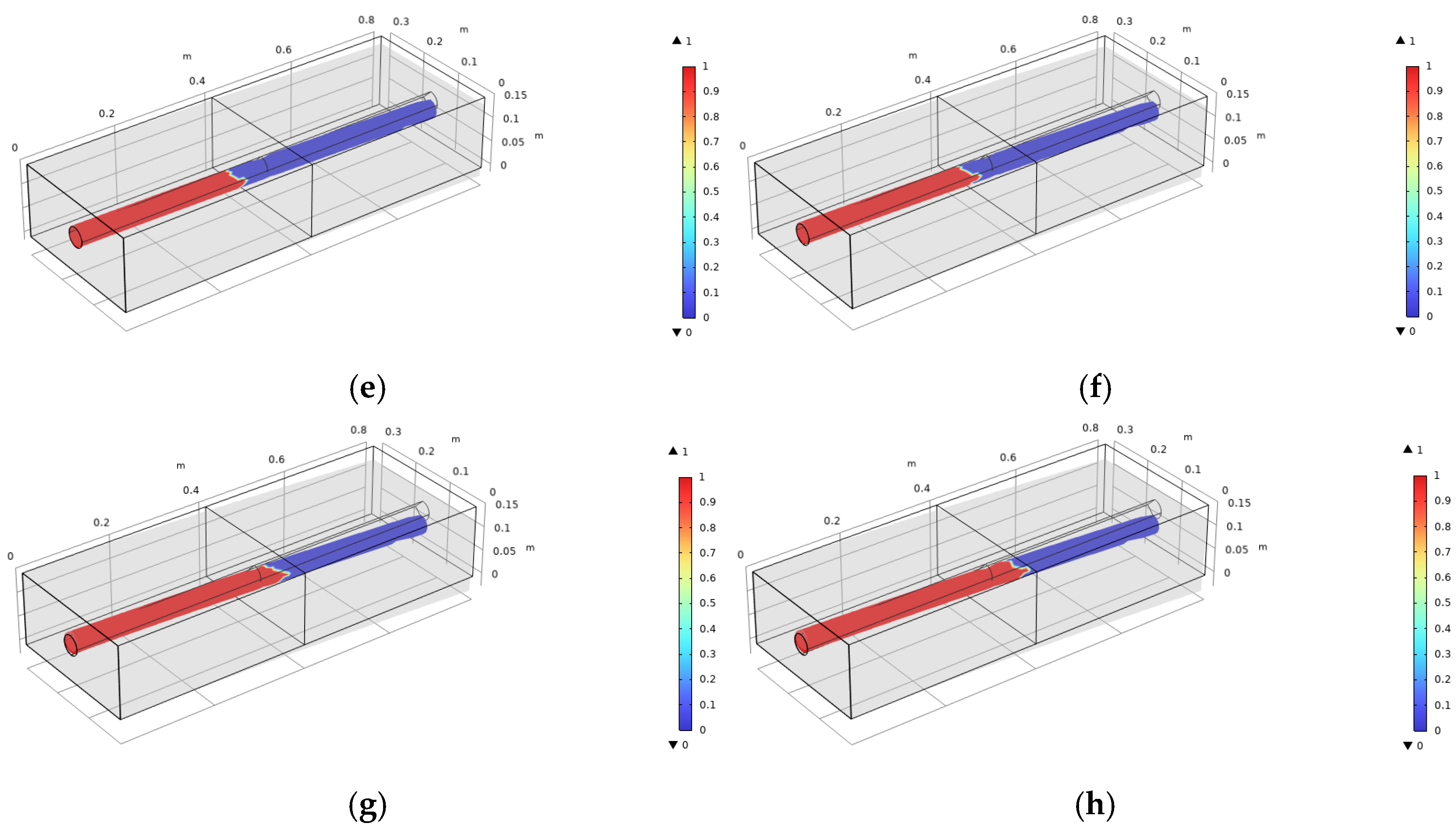
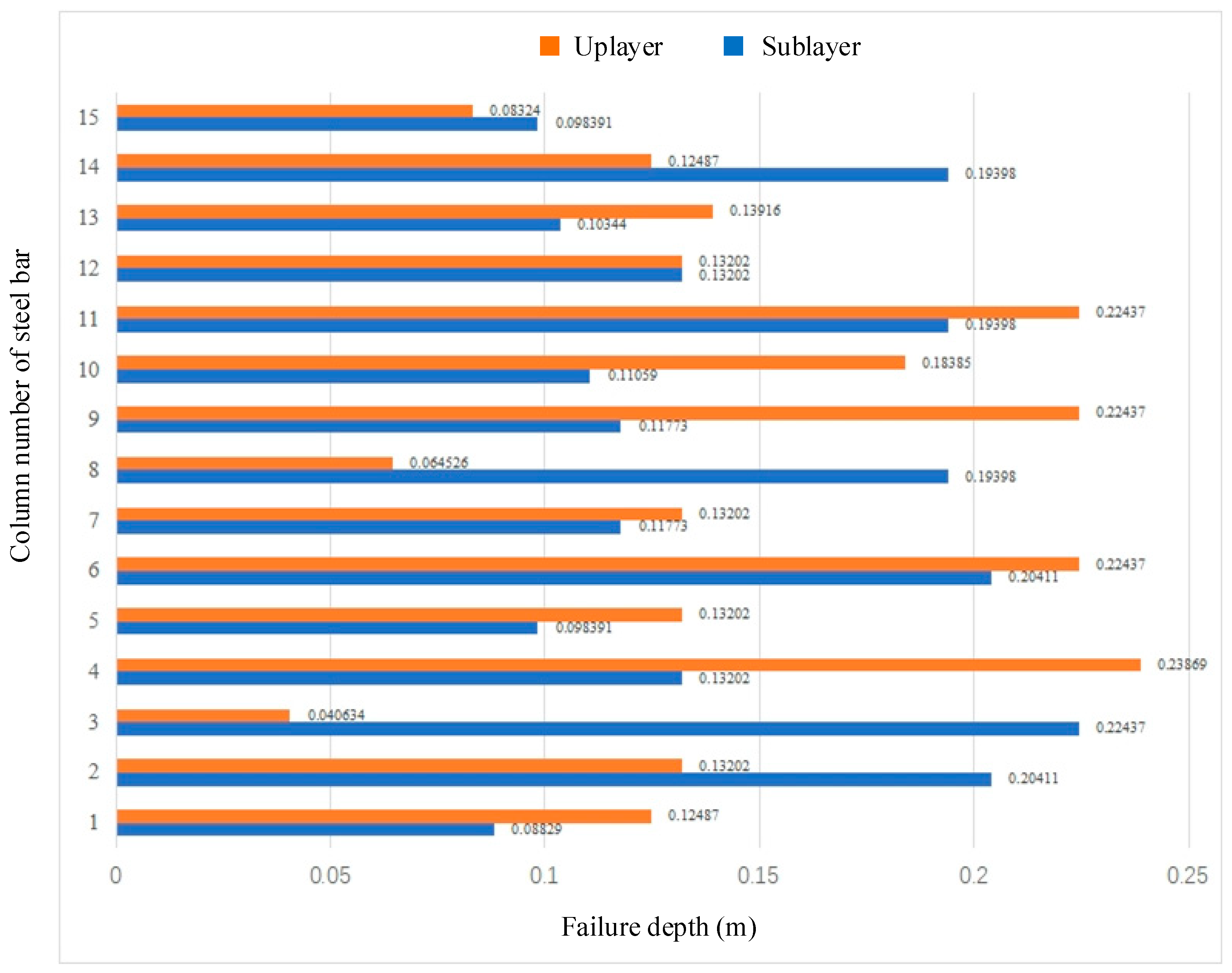
4.2. Numerical Results of RC Beam Cracking Behavior
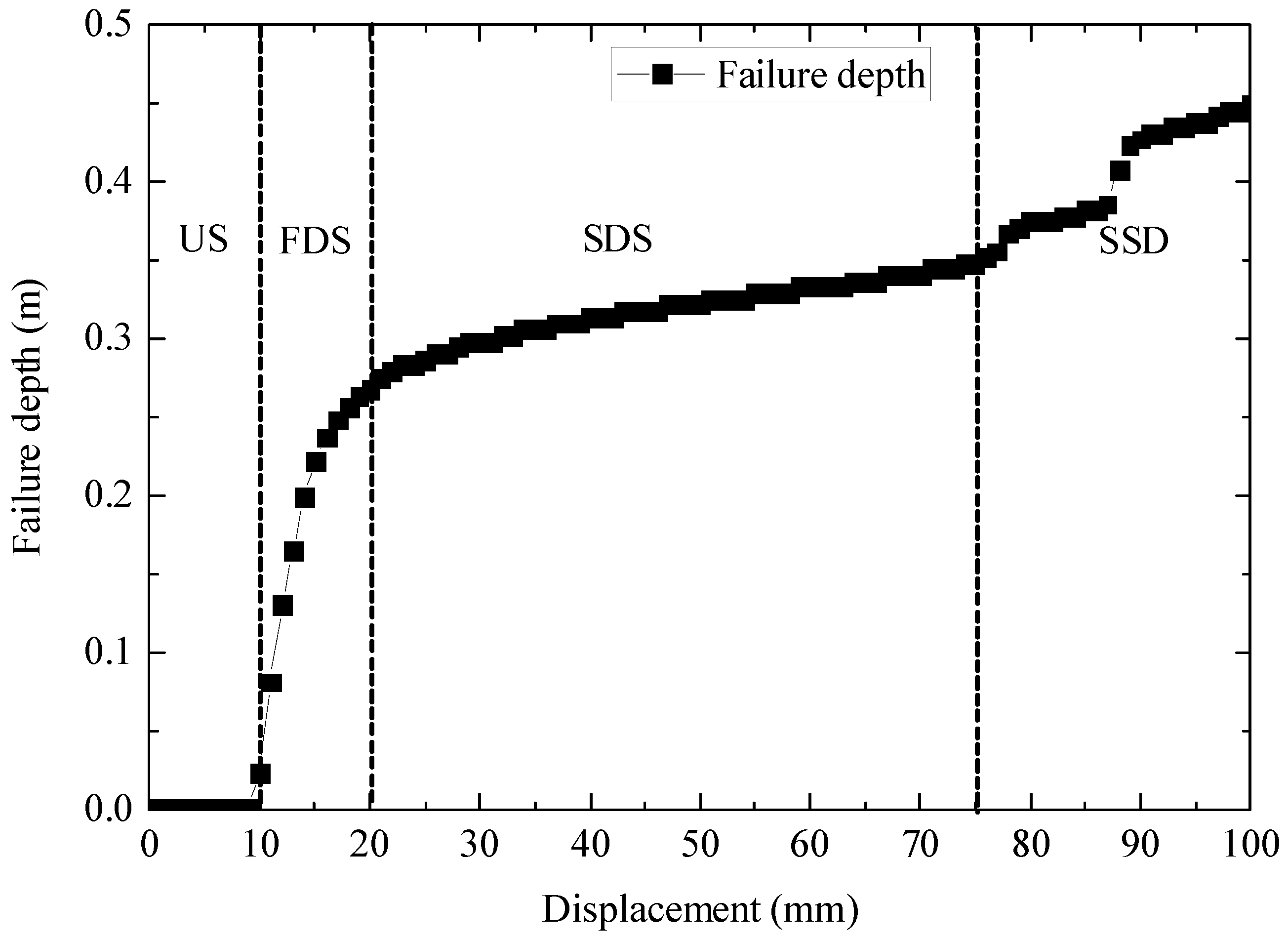
5. Mechanical Behavior and Failure Mechanisms of Bonding Interface in RC Slab
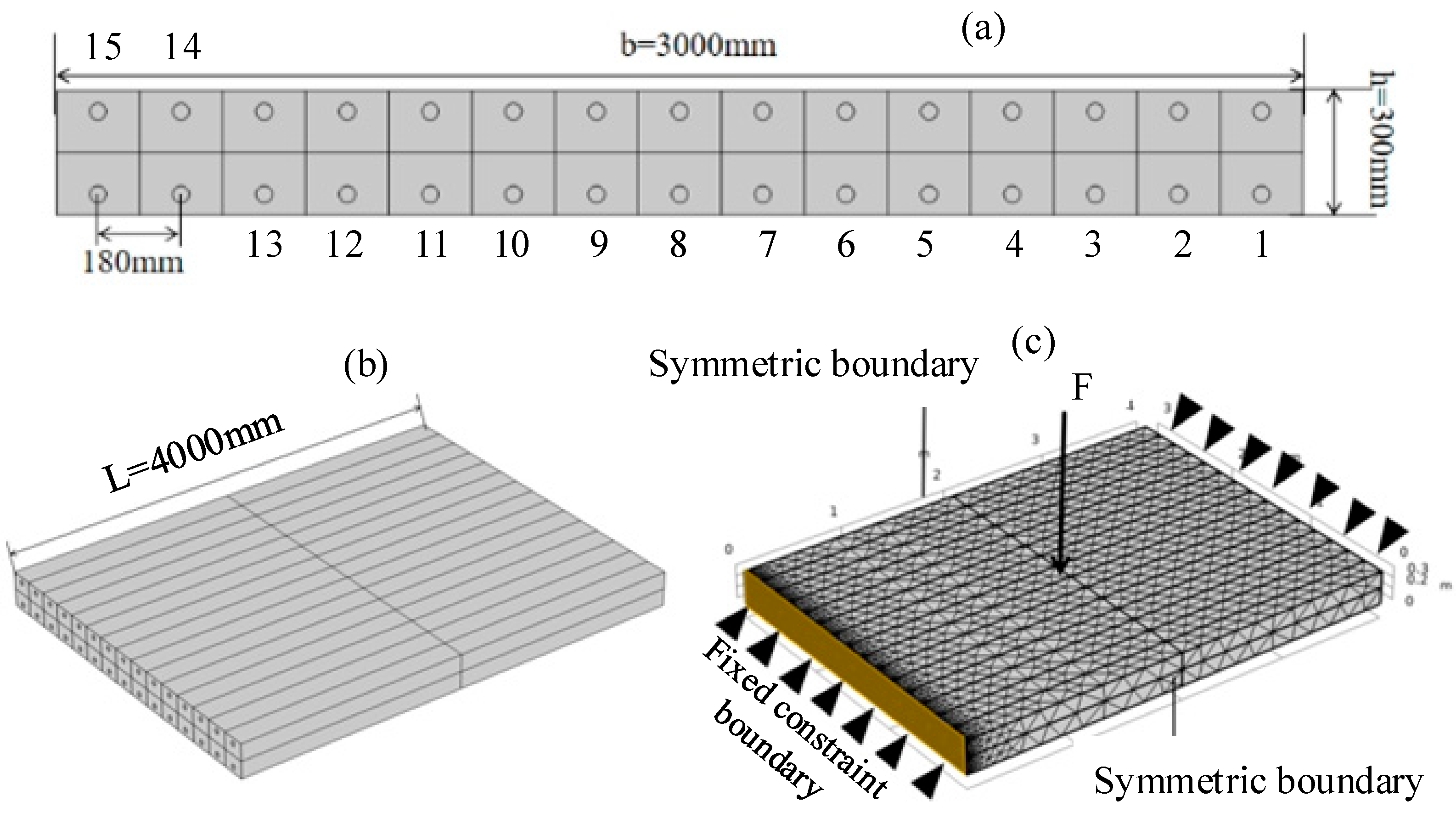
5.1. Numerical Model and Material Properties of RC Slab
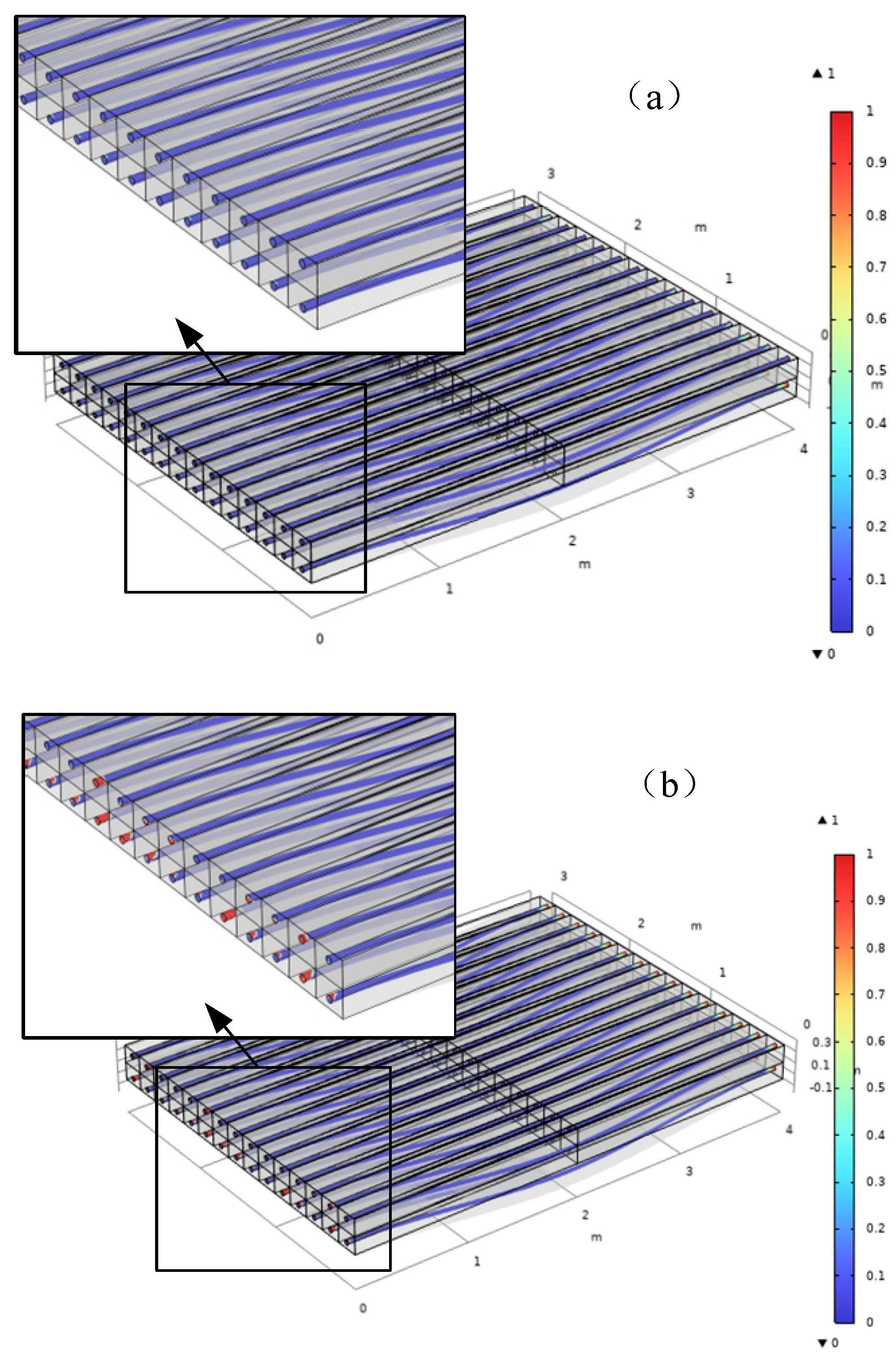
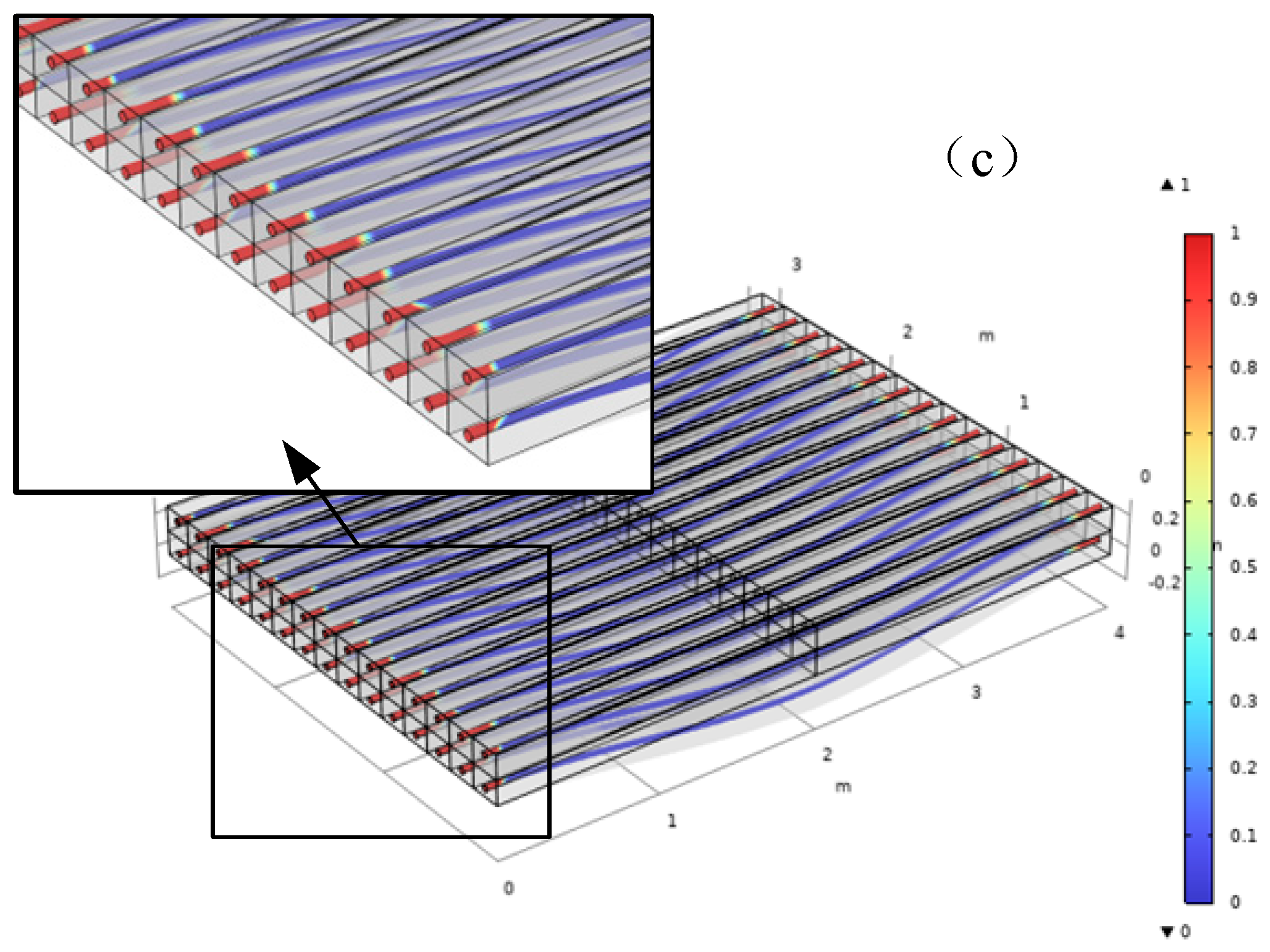
5.2. Numerical Results of RC Slab Cracking Behavior
6. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schlopschnat, C.; Pérez, M.G.; Zechmeister, C.; Estrada, R.D.; Kannenberg, F.; Rinderspacher, K.; Knippers, J.; Menges, A. Co-design of fibrous walls for multi-story buildings. J. Clean. Prod. 2023, 235, 235–248. [Google Scholar]
- Wang, Y.; Li, G.Q.; Zhu, S. Collapse modes and mechanisms of planar multi-story large-span steel frames under fire. J. Build. Eng. 2024, 94, 109924. [Google Scholar] [CrossRef]
- Malladi, B.P.; Venkateshwaran, A.; Nayaka, R.R. Design and economic implications of using steel fibers in elevated slabs of multi-story buildings. Struct. Concrete 2025, 26, 162–178. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Kumar, R.; Pruncu, C.I. Recent progress of reinforcement materials: A comprehensive overview of composite materials. J. Mater. Res. Technol. 2019, 8, 6354–6374. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Xie, T.; Yang, J. Flexural behaviour and cost effectiveness of layered UHPC-NC composite beams. Eng. Struct. 2022, 273, 115060. [Google Scholar] [CrossRef]
- Jonnala, S.N.; Gogoi, D.; Devi, S.; Kumar, M.; Kumar, C. A comprehensive study of building materials and bricks for residential construction. Constr. Build. Mater. 2024, 425, 135931. [Google Scholar] [CrossRef]
- Cao, J.; Du, J.; Fan, Q.; Yang, J.; Bao, C.; Liu, Y. Reinforcement for earthquake-damaged glued-laminated timber knee-braced frames with self-tapping screws and CFRP fabric. Eng. Struct. 2024, 306, 117787. [Google Scholar] [CrossRef]
- Palieraki, V.; Vintzileou, E.; Silva, J.F. Behavior of RC interfaces subjected to shear: State-of-the art review. Constr. Build. Mater. 2021, 306, 124855. [Google Scholar] [CrossRef]
- Bader, T.K.; Ormarsson, S. Modeling the mechanical behavior of wood materials and timber structures. In Springer Handbook of Wood Science and Technology; Springer: Cham, Switzerland, 2023; pp. 507–568. [Google Scholar]
- Kallioras, S.; Bournas, D.; Smiroldo, F.; Giongo, I.; Piazza, M.; Molina, F.J. Cross-laminated timber for seismic retrofitting of RC buildings: Substructured pseudodynamic tests on a full-scale prototype. Earthq. Eng. Struct. Dyn. 2024, 53, 4354–4378. [Google Scholar] [CrossRef]
- Gao, Z.; Gong, M.; Mohammadi, M.; Li, L. In-situ characteristic elastic properties of bond-lines in laminated engineered wood products using microscopic digital image correlation. Int. J. Adhes. Adhes. 2024, 132, 103715. [Google Scholar] [CrossRef]
- Kytka, T.; Gašparík, M.; Sahula, L.; Karami, E.; Teterin, D.; Das, S.; Kvietková, M.S. Bending characteristics of glued laminated timber depending on the alternating effects of freezing and heating. Constr. Build. Mater. 2022, 350, 128916. [Google Scholar] [CrossRef]
- Wang, M.; Song, X.; Gu, X.; Zhang, Y.; Luo, L. Rotational behavior of bolted beam-to-column connections with locally cross-laminated glulam. J. Struct. Eng. 2015, 141, 04014121. [Google Scholar] [CrossRef]
- Ling, Z.; Zhang, H.; Mu, Q.; Xiang, Z.; Zhang, L.; Zheng, W. Shear performance of assembled shear connectors for timber–concrete composite beams. Constr. Build. Mater. 2022, 329, 127158. [Google Scholar] [CrossRef]
- Hänsel, A.; Sandak, J.; Sandak, A.; Mai, J.; Niemz, P. Selected previous findings on the factors influencing the gluing quality of solid wood products in timber construction and possible developments: A review. Wood Mater. Sci. Eng. 2022, 17, 230–241. [Google Scholar] [CrossRef]
- Subhani, M.; Lui, H.Y. Effect of Primer and Fibre Orientation on Softwood–Hardwood Bonding. J. Compos. Sci. 2024, 8, 192. [Google Scholar] [CrossRef]
- De Moura, M.; Gonçalves, J.P.M.; Marques, A.T. Modeling compression failure after low velocity impact on laminated composites using interface elements. J. Compos. Mater. 1997, 31, 1462–1479. [Google Scholar] [CrossRef]
- Gonçalves, J.P.M.; De Moura, M.; De Castro, P.M.S.T. Interface element including point-to-surface constraints for three-dimensional problems with damage propagation. Eng. Comput. 2000, 17, 28–47. [Google Scholar] [CrossRef]
- Reedy, E.D., Jr.; Mello, F.J.; Guess, T.R. Modeling the initiation and growth of delaminations in composite structures. J. Compos. Mater. 1997, 31, 812–831. [Google Scholar] [CrossRef]
- Petrossian, Z.; Wisnom, M.R. Prediction of delamination initiation and growth from discontinuous plies using interface elements. Compos. Part A Appl. Sci. Manuf. 1998, 29, 503–515. [Google Scholar] [CrossRef]
- Mi, Y.; Crisfield, M.A.; Davies, G.A.O. Progressive delamination using interface elements. J. Compos. Mater. 1998, 32, 1246–1272. [Google Scholar] [CrossRef]
- Chen, M.; Crisfield, M.; Kinloch, A.J.; Busso, E.P.; Matthews, F.L.; Qiu, Y. Predicting progressive delamination of composite material specimens via interface elements. Mech. Compos. Mater. Struct. 1999, 6, 301–317. [Google Scholar] [CrossRef]
- Schellekens, J.C.J.; De Borst, R. On the numerical integration of interface elements. Int. J. Numer. Methods Eng. 1993, 36, 43–66. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; De Moura, M.F. Numerical simulation of mixed-mode progressive delamination in composite materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Needleman, A. A continuum model for void nucleation by inclusion debonding. J. Appl. Mech. 1987, 54, 525–531. [Google Scholar] [CrossRef]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Davila, C.; Camanho, P.; de Moura, M. Mixed-mode decohesion elements for analyses of progressive delamination. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, AIAA, Anaheim, CA, USA, 11–14 June 2001; p. 1486. [Google Scholar]
- Daudeville, L.; Allix, O.; Ladeveze, P. Delamination analysis by damage mechanics: Some applications. Compos. Eng. 1995, 5, 17–24. [Google Scholar] [CrossRef]
- Cui, W.; Wisnom, M.R.; Jones, M. A comparison of failure criteria to predict delamination of unidirectional glass/epoxy specimens waisted through the thickness. Composites 1992, 23, 158–166. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Liu, Y. Perpendicular to Grain Fracture of Curved Glulam Beams-Experiment and Numerical Modelling. Master’s Thesis, Harbin University of Technology, Harbin, China, 2015. [Google Scholar]
- He, X.; Yam, M.C.; Zhou, Z.; Zayed, T.; Ke, K. Inhomogeneity in mechanical properties of ductile iron pipes: A comprehensive analysis. Eng. Fail. Anal. 2024, 163, 108459. [Google Scholar] [CrossRef]
- Masoumi, M.; Loureiro, R.C.; Mohtadi-Bonab, M.A.; Béreš, M.; de Abreu, H.F. Analysis of crystallographic orientation and crack behavior in armor wire with spheroidized pearlite: Simulation and modeling with linear elastic fracture mechanics. Eng. Fail. Anal. 2024, 159, 108126. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Wang, Y.; Poh, L.H. A simple implementation of localizing gradient damage model in Abaqus. Int. J. Damage Mech. 2022, 31, 1562–1591. [Google Scholar] [CrossRef]
- Mercuri, M.; Pathirage, M.; Gregori, A.; Cusatis, G. Influence of self-weight on size effect of quasi-brittle materials: Generalized analytical formulation and application to the failure of irregular masonry arches. Int. J. Fract. 2024, 246, 117–144. [Google Scholar] [CrossRef]




| Materials | Density/(kg/m3) | Young’s Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|
| Steel plate | 7870 | 206 | 0.29 |
| Bolt | 7850 | 206 | 0.33 |
| Moment (kN∙m) | Yielding Moment | Maximum Moment | Failure Moment |
|---|---|---|---|
| Experiment data from Wang et al. [13] | 33.9 | 38.4 | 27.9 |
| Simulation data | 30.1 | 30.1 | 26.6 |
| Materials | Density/(kg/m3) | Young’s Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|
| Concrete | 2350 | 28 | 0.2 |
| Steel bar | 7870 | 206 | 0.29 |
| Properties | Value |
|---|---|
| Normal tensile strength, T | 2.31 MPa |
| Shear strength, R = S | 11.4 MPa |
| Penalty stiffness, Kp | 106 N/mm3 |
| Tension critical energy release rate, GIc | 93.8 J/m2 |
| Shear critical energy release rate, GIIc | 3363.6 J/m2 |
| B-K standard index, η | 2.284 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhang, Y.; Xiang, L. Crack Propagation Behavior Modeling of Bonding Interface in Composite Materials Based on Cohesive Zone Method. Buildings 2025, 15, 1717. https://doi.org/10.3390/buildings15101717
Zhu Y, Zhang Y, Xiang L. Crack Propagation Behavior Modeling of Bonding Interface in Composite Materials Based on Cohesive Zone Method. Buildings. 2025; 15(10):1717. https://doi.org/10.3390/buildings15101717
Chicago/Turabian StyleZhu, Yulong, Yafen Zhang, and Lu Xiang. 2025. "Crack Propagation Behavior Modeling of Bonding Interface in Composite Materials Based on Cohesive Zone Method" Buildings 15, no. 10: 1717. https://doi.org/10.3390/buildings15101717
APA StyleZhu, Y., Zhang, Y., & Xiang, L. (2025). Crack Propagation Behavior Modeling of Bonding Interface in Composite Materials Based on Cohesive Zone Method. Buildings, 15(10), 1717. https://doi.org/10.3390/buildings15101717






